Open Access Article
Open Access ArticleEvaluation of quantum chemistry calculation methods for conformational analysis of organic molecules using A-value estimation as a benchmark test†
Ken-ichi Yamada *ab and
Tsubasa Inokuma
*ab and
Tsubasa Inokuma ab
ab
aGraduate School of Pharmaceutical Sciences, Tokushima University, Shomachi, Tokushima 770-8505, Japan. E-mail: yamak@tokushima-u.ac.jp
bResearch Cluster on “Key Material Development”, Tokushima University, Shomachi, Tokushima 770-8505, Japan
First published on 12th December 2023
Abstract
A-values of 20 substituents were estimated by quantum chemistry calculations of different theoretical levels. Comparison with the reported experimental values provided a good benchmark to evaluate the theoretical levels for the conformational analysis of organic molecules.
Introduction
These days, quantum chemistry calculation such as density-functional theory (DFT) is an indispensable tool for experimental chemists to understand obtained results and predict an unknown property of molecules.1 Among the utilities of DFT calculations, estimating nuclear magnetic resonance (NMR) and electronic circular dichroism (ECD) is a powerful approach to determine organic molecules' absolute and relative configuration.2,3 When the molecule of concern has conformers, it is important to accurately determine the relative population of conformers for a good estimation of the spectra because each conformer demonstrates a different spectrum, and the observable spectrum is a weighted average of each spectrum based on the population of conformers. Although it is desirable to use a large basis set with a method at a high theoretical level for accurate energy calculations, geometry optimization, and frequency calculations, such calculations of large molecules require considerable time and high computational power. They thus are often not realistic for most organic chemists. Therefore, geometry optimization and frequency calculations are often performed with a smaller basis set such as 6-31G* to save time and computational cost, and the provided geometry and thermal correction are used for energy calculations with a larger basis set at the same theoretical level or often at a higher theoretical level. DFTs, such as B3LYP,4 ωB97X-D,5 and M06-2X,6 and second order Møller–Plesset perturbation theory (MP2)7 are popular and have often been used for structural analysis and energy calculation of organic molecules among experimental chemists. However, no criteria are known for selecting the best method for calculating conformer distribution because there has been no quantitative benchmark to evaluate these methods.Ring flipping of cyclohexane is one of the most fundamental conformational changes in organic chemistry. The free energy difference of the cyclohexane conformers of a monosubstituted cyclohexane, the so-called A-value,8 is well-studied and has been used to estimate the steric bulkiness of a certain substituent. However, the energy difference of the conformers depends not only on steric repulsion, so-called 1,3-diaxial interaction, but also on Baeyer strain, torsional strain, electrostatic interaction, and dispersion forces.9 Thus, these interactions must be properly allowed for to estimate an A-value accurately. Because of this fact and the availability of experimental A-values of many substituents, we expected that a comparison of calculated A-values with those experimentally observed would be a good benchmark test for the calculation methods of conformer distribution. The aim of this work is to provide experimental chemists with a guide for selecting a suitable calculation method.
Results and discussion
We first calculated the A-values of methyl (Me), tert-butyl (t-Bu), trifluoromethyl (CF3), trimethylsilyl (TMS), ethynyl (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH), cyano (CN), fluoro (F), chloro (Cl), bromo (Br), and iodo (I) substituents for simplicity because monosubstituted cyclohexanes bearing these substituents have only two conformers, eq and ax (Scheme 1). The reported A-values of these substituents and solvents used for the measurement are shown in Table 1. Geometry optimization and frequency calculations were performed using seven popular methods for organic molecules, i.e., Hartree–Fock approximation (HF), B3LYP, B3LYP-D3, M06-2X, ωB97X-D, ωB97X-V, and MP2 with LANL2DZ (bromine and iodine atoms) or 6-31G* basis set (other atoms). The energy of the optimized geometry of each conformer was calculated with solvent correction of the Polarizable Continuum Model (PCM) at the B3LYP-D3, M06-2X, ωB97X-D, ωB97X-V, MP2 theoretical levels, in which dispersion force is taken into account, using def2-TZVPD (bromine and iodine atoms) or 6-311+G(2df,2p) basis set (other atoms). The energy calculations were performed also at the B3LYP and HF theoretical levels to evaluate the importance of dispersion correction and electron correlation, respectively. These calculations were performed using the Gaussian 09W program except for the calculations with ωB97X-V functional, where the Spartan 18W program was used with LANL2DZ as basis set (an iodine atom) or 6-31G* (other atoms) for geometry optimization and frequency calculations, and 6-311+G(2df,2p) for energy calculations.
CH), cyano (CN), fluoro (F), chloro (Cl), bromo (Br), and iodo (I) substituents for simplicity because monosubstituted cyclohexanes bearing these substituents have only two conformers, eq and ax (Scheme 1). The reported A-values of these substituents and solvents used for the measurement are shown in Table 1. Geometry optimization and frequency calculations were performed using seven popular methods for organic molecules, i.e., Hartree–Fock approximation (HF), B3LYP, B3LYP-D3, M06-2X, ωB97X-D, ωB97X-V, and MP2 with LANL2DZ (bromine and iodine atoms) or 6-31G* basis set (other atoms). The energy of the optimized geometry of each conformer was calculated with solvent correction of the Polarizable Continuum Model (PCM) at the B3LYP-D3, M06-2X, ωB97X-D, ωB97X-V, MP2 theoretical levels, in which dispersion force is taken into account, using def2-TZVPD (bromine and iodine atoms) or 6-311+G(2df,2p) basis set (other atoms). The energy calculations were performed also at the B3LYP and HF theoretical levels to evaluate the importance of dispersion correction and electron correlation, respectively. These calculations were performed using the Gaussian 09W program except for the calculations with ωB97X-V functional, where the Spartan 18W program was used with LANL2DZ as basis set (an iodine atom) or 6-31G* (other atoms) for geometry optimization and frequency calculations, and 6-311+G(2df,2p) for energy calculations.
 | ||
Scheme 1 Two conformers of monosubstituted cyclohexanes (X = Me, t-Bu, CF3, TMS, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, CN, F, Cl, Br, or I). CH, CN, F, Cl, Br, or I). | ||
| X | A-valuea | Solvent | Method | Ref. |
|---|---|---|---|---|
| a The numbers of digits are as reported in the literature. | ||||
| Me | 1.74 | CFCl3/CDCl3 (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
1H NMR | 10 |
| t-Bu | 4.9 | CD2Cl2 | 13C NMR | 11 |
| CF3 | 2.5 | CFCl3 | 19F NMR | 12 |
| TMS | 2.50 | CDCl3/CD2Cl2 (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) 4) |
13C NMR | 13 |
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH CH |
0.515 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| CN | 0.21 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| F | 0.36 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| Cl | 0.507 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| Br | 0.485 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| I | 0.490 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| Et | 1.79 | CFCl3/CDCl3 (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
1H NMR | 10 |
| i-Pr | 2.21 | CFCl3/CDCl3 (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
1H NMR | 10 |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
1.68 | CD2Cl2 | 13C NMR | 15 |
| Ph | 2.7 | Propane-d8 | 13C NMR | 16 |
| Ac | 1.21 | Toluene-d8 | 13C NMR | 17 |
| OMe | 0.75 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| OAc | 0.785 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| NMe2 | 1.35 | Toluene-d8 | 13C NMR | 18 |
| NO2 | 1.13 | CFCl3/TMS (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
13C NMR | 14 |
| SMe | 1.00 | CDCl3 | 13C NMR | 19 |
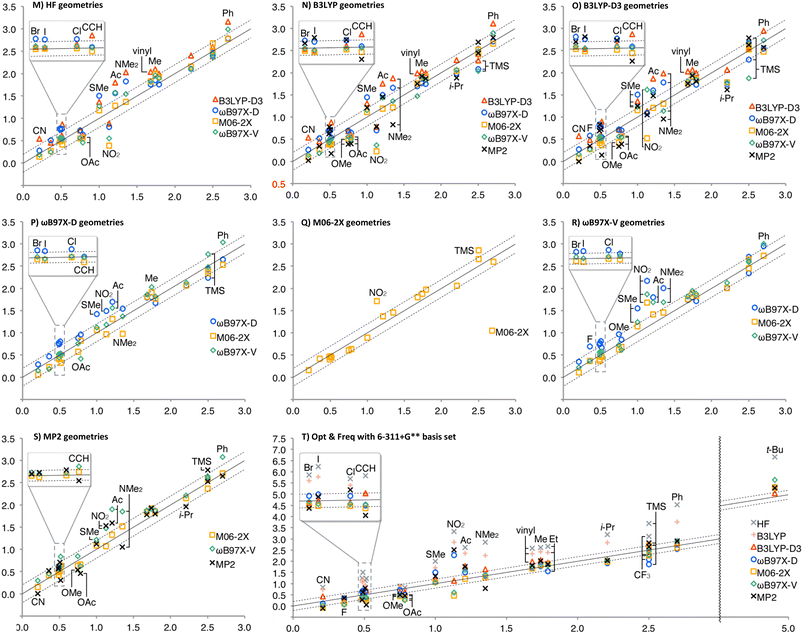
The A-values calculated at different theoretical levels were summarized in Fig. 1, where the horizontal axes are the experimental values and the vertical axes are those calculated (see ESI† for details, such as individual geometries, energies, thermal corrections, and A-values in numerical form). The two broken lines show ±0.2 kcal mol−1 errors, and the solid lines are the centres. In Fig. 1, Charts A–G are summaries by the method for geometry optimization and frequency calculations. In general, HF and B3LYP energy calculations (gray × and coral +, respectively) overestimate A-values more than the other theoretical levels. This clearly shows the significance of the dispersion force as well as the electron correlation to be considered in evaluating the 1,3-diaxial interaction. As expected, the effect of solvation correction was negligible for non-polar substituents, such as Me, t-Bu, and TMS; the average differences between A-values with and without solvation correction were +0.02 kcal mol−1 (solvation enlarged A-values). In contrast, significant solvation effect was observed for polar substituents, CF3, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, CN, F, Cl, Br, and I (A-values decreased by 0.15 kcal mol−1 on average).
CH, CN, F, Cl, Br, and I (A-values decreased by 0.15 kcal mol−1 on average).
 | ||
| Fig. 1 The calculated A-values for Scheme 1 the values were plotted on the vertical axis versus the experimental values on the horizontal axis. Charts A–G are summaries by the geometry calculation method, and H–L are those by the energy calculation method. | ||
As shown in Charts A–C, HF, B3LYP, and B3LYP-D3 geometries generally provided good performance with the energy calculation methods other than HF and B3LYP, except for TMS, for which ωB97X-D and ωB97X-V energies for B3LYP geometry, and ωB97X-V energy for B3LYP-D3 geometry significantly underestimated the A-value (the blue ○ and green ◊ in Chart B, and the green ◊ in Chart C, respectively). ωB97X-D geometry also provided good fit to the experimental values, except for t-Bu, whose A-value was generally overestimated (Chart D). In M06-2X geometry, A-values of F, CF3 and TMS also tended to be overestimated in addition to t-Bu (Chart E). The overestimation in F and t-Bu was also observed in ωB97X-V and MP2 geometries (Charts F and G).
Charts H–L are summaries by the method for energy calculation. In general, the use of ωB97X-D and MP2 geometries (the blue ○ and the black ×), and M06-2X geometry (the orange □) provided overestimated the A-value of t-Bu and TMS, respectively. Chart H shows the tendency of B3LYP-D3 energy calculation to overestimate the A-values of C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, CN, and t-Bu. ωB97X-D energy calculation provided better performance; however, it overestimates the A-value of F (Chart I). M06-2X energy calculation generally provided good fit, except for overestimation of the A-value of t-Bu (Chart J). ωB97X-V and MP2 energy calculations also overestimate the A-value of t-Bu (Charts K and L). The calculated A-values of TMS were highly geometry-dependent in ωB97X-V energy calculation, overestimated for M06-2X geometry and underestimated for B3LYP and B3LYP-D3 geometries (Chart K). In contrast to B3LYP-D3, MP2 energy calculation tends to underestimate the A-values of triple bonds, C
CH, CN, and t-Bu. ωB97X-D energy calculation provided better performance; however, it overestimates the A-value of F (Chart I). M06-2X energy calculation generally provided good fit, except for overestimation of the A-value of t-Bu (Chart J). ωB97X-V and MP2 energy calculations also overestimate the A-value of t-Bu (Charts K and L). The calculated A-values of TMS were highly geometry-dependent in ωB97X-V energy calculation, overestimated for M06-2X geometry and underestimated for B3LYP and B3LYP-D3 geometries (Chart K). In contrast to B3LYP-D3, MP2 energy calculation tends to underestimate the A-values of triple bonds, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH and CN (Chart L).
CH and CN (Chart L).
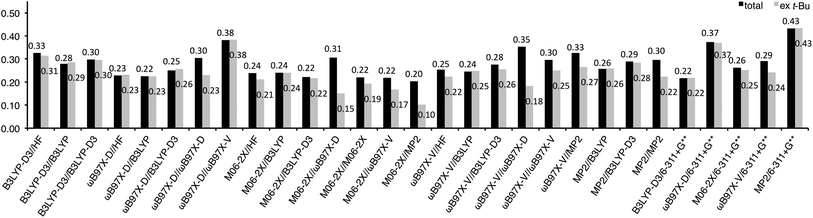
Root means squared errors (RMSEs) from the experimental values were calculated for each method and shown in Fig. 2 as solid bars to evaluate the goodness of fit. The RMSEs of the B3LYP-D3 energies for HF, B3LYP, and B3LYP-D3 geometries were 0.20–0.26 kcal mol−1, while those for ωB97X-D, M06-2X, ωB97X-V, and MP2 geometries were lager (0.37–0.48 kcal mol−1). Interestingly, the same tendency was also observed for the other methods, ωB97X-D (0.17–0.20 vs. 0.24–0.34 kcal mol−1), M06-2X (0.12–0.20 vs. 0.22–0.40 kcal mol−1), ωB97X-V (0.18–0.28 vs. 0.25–0.45 kcal mol−1), and MP2 energies (0.21–0.30 vs. 0.33–0.47 kcal mol−1). This is mainly attributable to large RMSEs for the nonpolar substituents (Me, t-Bu, and TMS) with these methods (horizontal stripe bars in Fig. 2), except for ωB97X-D energy with M06-2X, ωB97X-V, and MP2 geometries, in which the RMSEs for the polar substituents are also large (oblique stripe bars in Fig. 2). This might indicate a problem in estimating steric repulsion and/or dispersion force with ωB97X-D, M06-2X, ωB97X-V, and MP2 using a smaller basis set such as 6-31G*.
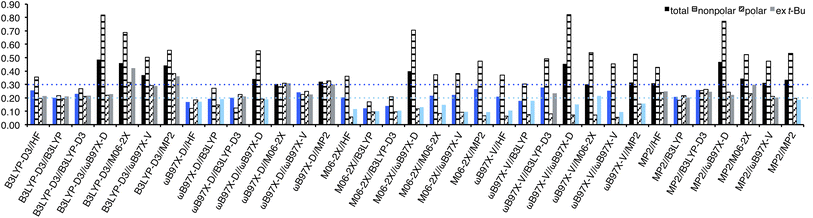 | ||
Fig. 2 The RMSE of the A-values calculated for Scheme 1 at each theoretical level: solid, horizontal stripe, oblique stripe, and pale bars stand for RMSE calculated with all the substituents; nonpolar substituents (Me, t-Bu, and TMS); polar substituents (CF3, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, CN, F, Cl, Br, and I); and t-Bu excluded, respectively. The broken lines show 0.20 and 0.30 kcal mol−1 criteria. CH, CN, F, Cl, Br, and I); and t-Bu excluded, respectively. The broken lines show 0.20 and 0.30 kcal mol−1 criteria. | ||
For a measure of the difficulty of estimating an A-value, RMSEs were also calculated for each substituent (see ESI† for details). The results indicate that estimating the A-value of t-Bu is rather difficult, providing a large RMSE (0.70 kcal mol−1). As discussed above, the A-value of t-Bu (4.9 kcal mol−1) was generally overestimated in HF, ωB97X-D, M06-2X, ωB97X-V, and MP2 geometries; especially for ωB97X-D geometries, 5.82–6.27 kcal mol−1 were provided. It is noteworthy that slightly better performance was obtained for Br when basis sets with an effective core potential, LANL2DZ and def2-TZVPD, were applied to a bromine atom than those with full electron included, 6-31G* and 6-311+G(2df,2p) (0.18 vs. 0.25 kcal mol−1 RMSE).
The large RMSE for t-Bu might be attributable to limitation of the present methods in application to highly congesting systems. However, the possibility cannot be totally excluded that it would be due to experimental error in the reported A-value, which was indirectly determined based on the additivity of A-values in tri-substituted cyclohexane system, and that the true value might be larger. Therefore, we also calculated RMSE with the results for t-Bu excluded, and chose the 19 methods having t-Bu-included RMSE of less than 0.30 kcal mol−1 (the blue bars in Fig. 2) and, in addition, the 5 methods having t-Bu-excluded RMSE of less than 0.20 kcal mol−1 (the sky blue bars), and undertook further evaluation.
As other alkyl substituents, ethyl (Et) and isopropyl (i-Pr) groups were investigated. For ethyl- and isopropylcyclohexane, six conformers, three conformers each for the axial and equatorial conformers, were found (see ESI† for details). As sp2 carbon substituents, vinyl (CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2) and phenyl (Ph) groups were investigated. For vinylcyclohexane, six conformers, three conformers each for the axial and equatorial conformers, were found. For phenylcyclohexane, four conformers, one equatorial and three axial conformers were found. To evaluate the applicability of hetero atoms, acetyl (Ac), methoxy (OMe), acetoxy (OAc), dimethylamino (NMe2), nitro (NO2), and methylthio (SMe) groups were investigated. For acetylcyclohexane, six conformers, two sets of two equivalent equatorial conformers, and two equivalent axial conformers were found. For methoxy-, N,N-dimethylamino-, and methylthiocyclohexane, there are six conformers, three conformers each, two of which are equivalent, were found for equatorial and axial conformers. For acetoxycyclohexane, three equatorial and two axial conformers were found within 5.5 kcal mol−1. For nitrocyclohexane, there are five conformers, three equatorial conformers, two of which are equivalent, and two axial conformers were found. Population of each conformer was determined on the basis of Boltzmann distribution, and those of axial and equatorial conformers were separately summed up to determine axial/equatorial ratios (ax/eq), with which the following formula provided A-values: −1.36
CH2) and phenyl (Ph) groups were investigated. For vinylcyclohexane, six conformers, three conformers each for the axial and equatorial conformers, were found. For phenylcyclohexane, four conformers, one equatorial and three axial conformers were found. To evaluate the applicability of hetero atoms, acetyl (Ac), methoxy (OMe), acetoxy (OAc), dimethylamino (NMe2), nitro (NO2), and methylthio (SMe) groups were investigated. For acetylcyclohexane, six conformers, two sets of two equivalent equatorial conformers, and two equivalent axial conformers were found. For methoxy-, N,N-dimethylamino-, and methylthiocyclohexane, there are six conformers, three conformers each, two of which are equivalent, were found for equatorial and axial conformers. For acetoxycyclohexane, three equatorial and two axial conformers were found within 5.5 kcal mol−1. For nitrocyclohexane, there are five conformers, three equatorial conformers, two of which are equivalent, and two axial conformers were found. Population of each conformer was determined on the basis of Boltzmann distribution, and those of axial and equatorial conformers were separately summed up to determine axial/equatorial ratios (ax/eq), with which the following formula provided A-values: −1.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(ax/eq).
log(ax/eq).
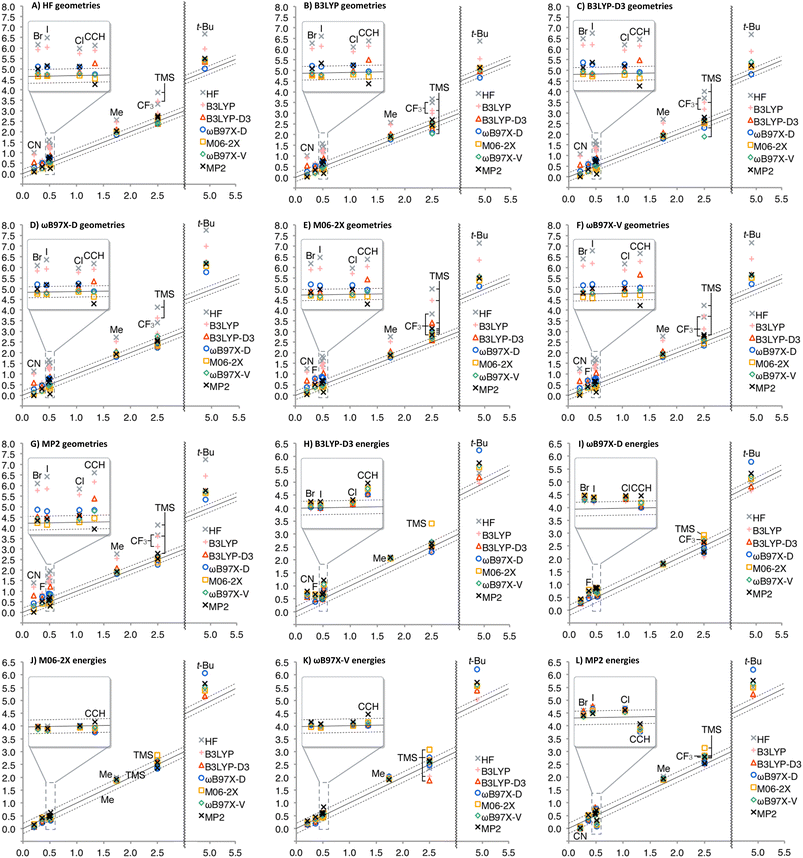
The calculated A-values were summarized in Fig. 3 (see ESI† for details, such as individual geometries, energies, thermal corrections, and A-values in numerical form). As expected, solvation effect is negligible for nonpolar Et and i-Pr; A-values were only increased by 0.01 kcal mol−1 on average. Interestingly, solvation effect is moderate for CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, Ph, and OAc, for which A-values were decreased by 0.05 kcal mol−1 on average, while significant effect (decrease by 0.23 kcal mol−1 on average) was observed for other polar substituents.
CH2, Ph, and OAc, for which A-values were decreased by 0.05 kcal mol−1 on average, while significant effect (decrease by 0.23 kcal mol−1 on average) was observed for other polar substituents.
Similarity of Charts M and N shows that the use of B3LYP geometry in place of HF geometry only slightly improves the A-value calculation. With these geometries, the A-value of NO2 was significantly underestimated. The dispersion correction amended the underestimation (B3LYP-D3), but the A-value of i-Pr was underestimated, instead (Chart O). Although ωB97X-D, M06-2X, and MP2 geometries produced better performance (Charts P, Q, and S), the use of ωB97X-V functional for geometry optimization and frequency calculation didn't improve goodness of fit, and the A-values of SMe, NO2, Ac, and NMe2 were significantly overestimated (Chart R) even though this functional is quite time-consuming. The overestimation of the NO2 A-value in M06-2X and ωB97X-V geometries is probably explainable by the extra equatorial conformers that were local minimum only at the M06-2X and ωB97X-V/6-31G* theoretical levels (Scheme 2). In these conformers, the N–O bond almost eclipses the C–C bond and likely interacts electrostatically with one of the axial β-hydrogen atoms. These conformers were only ca. 0.1 kcal mol−1 less stable than the most stable equatorial conformer, and contribute to increase the population of the equatorial conformers. This may suggest the tendency of these functionals to overestimate electrostatic interaction at least with 6-31G* basis set. Nevertheless, the RMSE for NO2 is quite large (0.63 kcal mol−1), which clearly suggests that estimation of the A-value for NO2 was challenging.
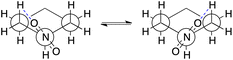 | ||
| Scheme 2 The Newman projection of the extra equatorial conformers found at the M06-2X and ωB97X-V/6-31G* theoretical levels: the blue dash lines represent the possible hydrogen-bonding (O⋯H 2.53 Å). | ||
Finally, geometry optimization and frequency calculations with a relatively large 6-311+G** basis set were performed for comparison, although these methods are impractical for application to most of the molecules that may concern synthetic chemists. The results were summarized in Chart T (Fig. 3). As expected, the improvement from HF to B3LYP, and from B3LYP to B3LYP-D3 show the significance of the electron correlation and the dispersion force to be considered, respectively. The overestimation of the t-Bu A-value and the high method-dependence in calculating a NO2 A-value were also observed. This indicates that the discrepancy is not due to the difference of functionals used for the geometry optimization and the energy calculations.
RMSEs from the experimental values were calculated for each method and shown in Fig. 4. In general, the use of B3LYP geometry in place of HF slightly improved RMSEs; for B3LYP-D3, ωB97X-D, and ωB97X-V/6-311+G(2df,2p) energies, HF/6-31G* geometry provided RMSE of 0.30, 0.23, and 0.25 kcal mol−1, respectively, while B3LYP geometry provided RMSE of 0.28, 0.22, and 0.24 kcal mol−1, respectively, although it failed to improve RMSE of M06-2X energy (both 0.24 kcal mol−1). In general, no benefit to use B3LYP-D3 in place of B3LYP for geometry optimization and frequency calculation was observed, except for M06-2X energy, for which B3LYP-D3 geometry provided better RMSE (0.22 kcal) than B3LYP (0.24 kcal mol−1). Energy calculation at the M06-2X/6-311+G(2df,2p) theoretical level generally provided good performance (RMSE 0.20–0.31 kcal mol−1). It is noteworthy that the use of time-consuming methods such as ωB97X-V and MP2/6-311+G** failed to improve the result (0.29 and 0.43 kcal mol−1), and relatively low-cost B3LYP-D3/6-311+G**, ωB97X-D/6-311+G(2df,2p)//B3LYP/6-31G*, and M06-2X/6-311+G(2df,2p)//B3LYP-D3/6-31G* provided better results (0.22 kcal mol−1). The five lowest RMSEs were provided by M06-2X//MP2 (0.20 kcal mol−1), ωB97X-D//B3LYP, M06-2X//B3LYP-D3, M06-2X//M06-2X, M06-2X//ωB97X-V (0.22 kcal mol−1 each), and those excluding t-Bu A-values were provided by M06-2X//MP2, M06-2X//ωB97X-D, M06-2X//ωB97X-V, ωB97X-V//ωB97X-D, and M06-2X//M06-2X (0.10, 0.15, 0.17, 0.18, and 0.19 kcal mol−1, respectively).
Experimental
The calculations were performed using the Gaussian 09W program,20 except for those with the ωB97X-V functional, for which the Spartan'18W program21 was used. Conformational search were systematically performed by changing dihedral angles by 60° in initial geometries of axial and equatorial conformers. Geometry optimization was performed with the tight convergent criteria option followed by calculations of thermal corrections. A larger grid (99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590) was applied to integral computation using the B3LYP, B3LYP-D3, ωB97X-D, M06-2X, and ωB97X-V functionals. The optimized geometries were provided as xyz files and the calculated energies were summarized as tables in ESI.†
590) was applied to integral computation using the B3LYP, B3LYP-D3, ωB97X-D, M06-2X, and ωB97X-V functionals. The optimized geometries were provided as xyz files and the calculated energies were summarized as tables in ESI.†
Conclusions
Equatorial/axial equilibrium of twenty monosubstituted cyclohexanes was estimated using forty two theoretical levels and compared with those experimentally observed. With these results as a benchmark, we identified ωB97X-D or M06-2X/6-311+G(2df,2p) are good candidates for energy calculation when molecular size allows the use of only HF or B3LYP/6-31G* for geometry optimization and frequency calculation. When more time-consuming B3LYP-D3 geometry and frequency are available, the use of M06-2X/6-311+G(2df,2p) for energy calculation is expected to give better fit. Although M06-2X and ωB97X-V/6-311+G(2df,2p) energy calculations for ωB97X-D/6-31G* geometry would also be candidates, they should be carefully applied to a highly congested system as they provided large error for the t-Bu A-value. The use of M06-2X energy for M06-2X, ωB97X-V, or MP2 geometry is also expected to give good fit, but is impractical for large molecules because of the highly time-consuming frequency calculations as well as geometry optimization. These results provide experimental chemists with a guide for choosing an appropriate computational method.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported in part by JSPS (KAKENHI JP22H05569), the Mochida Memorial Foundation for Medical and Pharmaceutical Research, and Tokushima University (Research Clusters program No. 2201004).Notes and references
- (a) A. H. Mazurek and Ł. Szeleszczuk, Molecules, 2022, 27, 3874 CrossRef CAS; (b) K. N. Houk, F. Liu, Z. Yang and J. I. Seeman, Angew. Chem., Int. Ed., 2021, 60, 12660 CrossRef CAS PubMed; (c) F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814 CrossRef CAS PubMed; (d) M. Bursch, E. Caldeweyher, A. Hansen, H. Neugebauer, S. Ehlert and S. Grimme, Acc. Chem. Res., 2019, 52, 258 CrossRef CAS PubMed; (e) C. Puzzarini and V. Barone, Acc. Chem. Res., 2018, 51, 548 CrossRef CAS; (f) D. L. Davies, S. A. Macgregor and C. L. McMullin, Chem. Rev., 2017, 117, 8649 CrossRef CAS PubMed; (g) X. Zhang, L. W. Chung and Y.-D. Wu, Acc. Chem. Res., 2016, 49, 1302 CrossRef CAS; (h) S. Santoro, M. Kalek, G. Huang and F. Himo, Acc. Chem. Res., 2016, 49, 1006 CrossRef CAS; (i) J. M. Herbert, X. Zhang, A. F. Morrison and J. Liu, Acc. Chem. Res., 2016, 49, 931 CrossRef CAS; (j) G.-J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y.-D. Wu, J. Am. Chem. Soc., 2015, 137, 1706 CrossRef CAS; (k) J. G. Brandenburg and S. Grimme, Top. Curr. Chem., 2014, 345, 1 CAS; (l) P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Celebi-Olcum and K. N. Houk, Chem. Rev., 2011, 111, 5042 CrossRef CAS.
- W. Hehre, P. Klunzinger, B. Deppmeier, A. Driessen, N. Uchida, M. Hashimoto, E. Fukushi and Y. Takata, J. Nat. Prod., 2019, 82, 2299 CrossRef CAS.
- (a) A. E. Nugroho and H. Morita, J. Nat. Med., 2014, 68, 1 CrossRef CAS PubMed; (b) K. Yamasaki, A. Yamauchi, T. Inokuma, Y. Miyakawa, Y. Wang, R. Oriez, Y. Yamaoka, K. Takasu, N. Tanaka, Y. Kashiwada and K. Yamada, Asian J. Org. Chem., 2021, 10, 1828 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- (a) S. Winstein and N. J. Holness, J. Am. Chem. Soc., 1955, 77, 5562 CrossRef CAS; (b) J. A. Hirsch, Top. Stereochem., 1967, 1, 199 CAS; (c) F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, 5th edn, Plenum, New York, 1990, pp. 156–159 Search PubMed; (d) P. Muller, Pure Appl. Chem., 1994, 66, 1077 CrossRef; (e) K. B. Wiberg, J. D. Hammer, H. Castejon, W. F. Bailey, E. L. DeLeon and R. M. Jarret, J. Org. Chem., 1999, 64, 2085 CrossRef CAS.
- (a) J. E. Anderson, Dynamic Chemistry; Topics in Current Chemistry Fortschritte der Chemischen Forschung, Springer, Berlin, Heidelberg, 1974, vol. 45, pp 139–167 Search PubMed; (b) R. Bjornsson and I. Arnason, Phys. Chem. Chem. Phys., 2009, 11, 8689 RSC; (c) E. Solel, M. Ruth and P. R. Schreiner, J. Am. Chem. Soc., 2021, 143, 20837 CrossRef CAS.
- H. Booth and J. R. Everett, J. Chem. Soc., Perkin Trans. 2, 1980, 255 RSC.
- M. Manoharan and E. L. Eliel, Tetrahedron Lett., 1984, 25, 3267 CrossRef CAS.
- E. W. Della, J. Am. Chem. Soc., 1967, 89, 5221 CrossRef CAS.
- W. Kitching, H. A. Olszowy, G. M. Drew and W. Adcock, J. Org. Chem., 1982, 47, 5153–5156 CrossRef CAS.
- H. J. Schneider and V. Hoppen, J. Org. Chem., 1978, 43, 3866 CrossRef CAS.
- E. L. Eliel and M. Manoharan, J. Org. Chem., 1981, 46, 1959 CrossRef.
- M. E. Squillacote and J. M. Neth, J. Am. Chem. Soc., 1987, 109, 198 CrossRef CAS.
- G. W. Buchanan, S. H. Preusser and V. L. Webb, Can. J. Chem., 1984, 62, 1308 CrossRef CAS.
- The value was recalculated using 1.74 as an A-value of Me in place of 1.7: H. Booth and M. L. Jozefowicz, J. Chem. Soc., Perkin Trans. 2, 1976, 895 RSC.
- E. L. Eliel and D. Kandasamy, J. Org. Chem., 1976, 41, 3899 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
- Spartan'18 Wavefunction, Inc., Irvine, CA.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra06783a |
| This journal is © The Royal Society of Chemistry 2023 |