Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Discovery of unexpectedly complex reaction pathways for the Knorr pyrazole synthesis via transient flow†
Linden
Schrecker
 a,
Joachim
Dickhaut
b,
Christian
Holtze
b,
Philipp
Staehle
b,
Marcel
Vranceanu
b,
Klaus
Hellgardt
c and
King Kuok (Mimi)
Hii
a,
Joachim
Dickhaut
b,
Christian
Holtze
b,
Philipp
Staehle
b,
Marcel
Vranceanu
b,
Klaus
Hellgardt
c and
King Kuok (Mimi)
Hii
 *a
*a
aDepartment of Chemistry, Imperial College London, Molecular Sciences Research Hub, 82 Wood Lane, London W12 0BZ, UK. E-mail: mimi.hii@imperial.ac.uk
bBASF SE, 38 Carl-Bosch-Straße, 67056, Ludwigshafen/Rhein, Germany
cDepartment of Chemical Engineering, Imperial College London, South Kensington, London SW7 2AZ, UK
First published on 12th September 2022
Abstract
Kinetic data for reactions between phenyl hydrazine and 1,3-diketones (Knorr pyrazole synthesis) were acquired by using transient flow methods. Supported by further spectroscopic and mass spectrometry data, a microkinetic model was subsequently constructed, which provided new insights into the mechanism, including autocatalysis and the involvement of an unexpected reaction intermediate. During this work, a novel reactant stoichiometry transient flow methodology was demonstrated, allowing the robustness of these models to be asserted.
Introduction
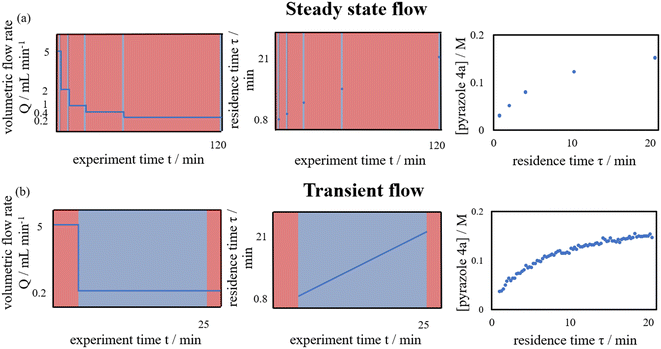
Flow chemistry can offer certain advantages over batch chemistry for the investigation of reaction kinetics in situ. In a batch reactor, reaction progress is monitored temporally (% conversion vs. time, t). For homogeneous reactions where mixing or mass transfer is not an issue, this is the preferred method for determining reaction kinetics.1 However, as reactions are initiated by the addition of a reactant to a stirred and pre-heated solution, the initial rate of the reaction during mixing can be ill-defined, particularly for fast reactions.In contrast, in a flow reactor, the reaction progresses spatially, along the length of the reactor with increasing residence time. Provided good mixing at the point of contact, the measurement of reaction rates can be much more precise, as residence times can be accurately defined. Kinetic data can be collected by changing the flow rate (% conversion vs. residence time, τ). This can be achieved in a stepwise manner, where each data point is collected at a specific flow rate under ‘steady state’ conditions (Fig. 1a). This method of data collection is slow and requires a large amount of material. Alternatively, time-series data collection can also be performed continuously in ‘transient flow’, whereby a step change to the flow rate is introduced to the system, with simultaneous collection of the data during the produced residence time gradient (Fig. 1b). First introduced by Littlejohn et al. in 2011,2 the method greatly facilitates the data acquisition while using less material emulating batch experiments. In the ensuing decade, the concept was further explored by others to determine technical best practice,3 and to acquire kinetic data for different chemistries.4,5 More recently, it has been extended to changes in other reaction parameters, such as temperature6 and the effect of additives (Table 1).7 Collection of data over this change in conditions affords means to access data series that are otherwise time-consuming to collect using batch reactors.
The data collection can be enhanced even further beyond the capability of a batch reactor, by the application of multi-variable ramps simultaneously. Recently, both mono- and bi-variable transient flow ramps were combined with model-based design of experiments (MBDoE) to elucidate kinetic parameters.8 The approach has also been extended successfully to automatically distinguish between predefined kinetic models in simple chemical systems.9
Results and discussion
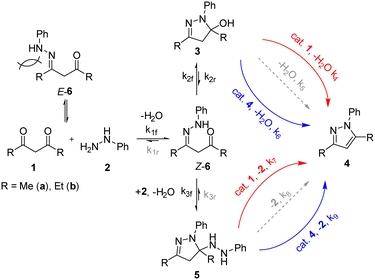
The pyrazole structure can be found in many agrochemicals and active pharmaceutical ingredients. The Knorr pyrazole synthesis is one of the most popular ways of preparing the 5-membered heterocycle, given the availability of 1,3-diketone and hydrazine precursors.10 One of the limitations is the mixture of regioisomers that can result from an unsymmetrical 1,3-diketone substrate (Scheme 1).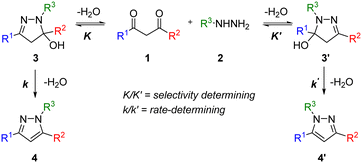 | ||
| Scheme 1 The Knorr pyrazole synthesis of an unsymmetric 1,3-diketone 1 and mono substituted hydrazine 2via the widely accepted mechanism to form pyrazoles 4 and 4′. | ||
Previous mechanistic studies have established a correlation between the regioselectivity with several reaction parameters; including: pH, solvent, as well as the electronic and steric characteristics of the substituents (R1 and R2).11–13 These studies were largely based on empirical observations of product distributions under different reaction conditions. Often, a hydroxylpyrazolidine intermediate 3 was observed,12,14 and can be isolated in certain cases.13,15 Thus, the dehydration of 3 to form the pyrazole is generally accepted to be the rate-determining step under pH neutral conditions. To date, there had been only one reported kinetic study of the Knorr pyrazole synthesis, where the reactions between arylhydrazine (R3 = Ar) with trifluoromethyl-substituted diketones (where R1 = CF3)16 were found to be first order in both reactants at pH > 1.6 (eqn (1)).
| Rate = k[diketone][phenylhydrazine] | (1) |
Kinetic studies performed in transient flow
With ethanol as the solvent (boiling point 78 °C), the kinetic study was performed in flow to enable a wider operating window for the kinetic experiments. A continuous flow system was constructed, where programmable piston pumps were used to deliver pre-heated reactant solutions into to a T-piece mixer; with a back-pressure regulator to maintain volatile components in solution at elevated temperatures. The reaction mixture was allowed to dwell for a given residence time (τ) at temperature (T) in a tubular reactor, before it was thermally quenched, passed through an in-line FTIR, and eventually collected for HPLC-MS analysis (Fig. S1†).Multiple flow rate step changes can be implemented semi-automatically to deliver reactants 1a and 2 with a cumulative flow rate between 5 to 0.2 mL min−1, while the product formation was monitored in-line by infrared spectroscopy. Adopting the transient flow methodology, a number of kinetic experiments were initially performed at different concentrations and reaction stoichiometries, to delineate the reaction order of each reactant, as well as product and by-products (Table 2).
The ‘different excess’ experiments (Fig. 2, experiments A–C) confirmed that the kinetic model was more complex than initially thought: experiments B and C were not superimposable, implying that the effect of changing the concentration of diketone 1a and phenyl hydrazine 2 is not the same, as will be the case if the rate equation (eqn (1)) is true. Interestingly, while the presence of extraneous water had no effect on the reaction rate (Fig. 2, experiments F and G), product autocatalysis was occurring (Fig. 2, experiments E and F).
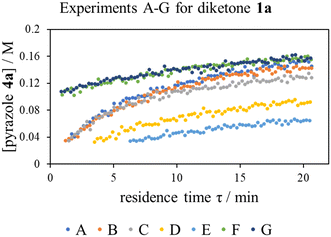 | ||
| Fig. 2 Time series data collected for the reaction of diketone 1a and phenyl hydrazine 2 using residence time ramps over a range of experiments, described in Table 2. | ||
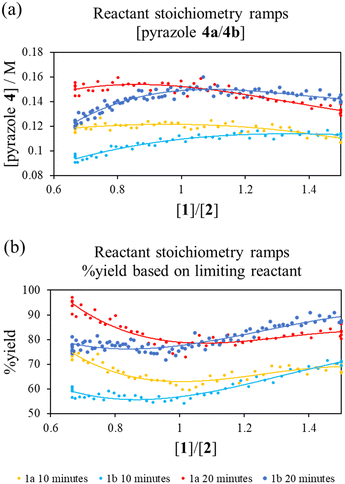
To interrogate this further, a new transient flow method was also developed: by varying flow rate of each pump, but maintaining the same cumulative flow rate, to provide independent data to verify the results of different excess experiments obtained by varying cumulative flow rates. By varying reactant stoichiometry at a fixed residence time (τ), a data series of different initial reactant stoichiometries can easily be produced (Fig. 3a). With a simple linear kinetic model, we would expect the data to overlap when plotted against [1a]/[2] and [2]/[1a], as within such a kinetic model [1a] and [2] are interchangeable (eqn (1)). However, we observed considerable discrepancy between the two plots (Fig. 3b), further verifying our previous observations that the simple rate law does not apply to this reaction.
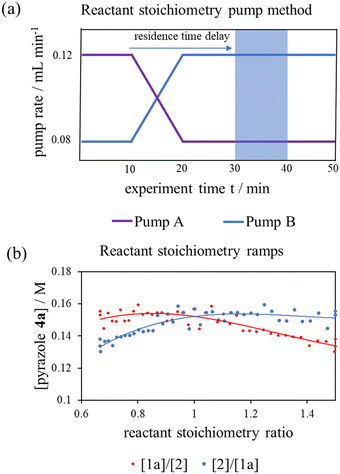 | ||
Fig. 3 (a) Pump method for 20 minute residence time reactant stoichiometry ramp; (b) reactant stoichiometry ramp at a 20 minute residence time, 70 °C and using 0.4 M stock solutions of 1a and 2 between ratios of [1a]/[2] of 0.16 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.24 M to 0.24 M 0.24 M to 0.24 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.16 M plotted against [1a]/[2] and [2]/[1a] demonstrating clear conflict with the simple rate law (eqn (1)). The fitted 3° lines are as a visual aid. 0.16 M plotted against [1a]/[2] and [2]/[1a] demonstrating clear conflict with the simple rate law (eqn (1)). The fitted 3° lines are as a visual aid. | ||
Interestingly, the HPLC-MS data of the reaction mixtures revealed the presence of two reaction intermediates: the hydroxylpyrazolidine 3a, and another that results from the di-addition of phenylhydrazine, 5a (Scheme 2). Both of these intermediates can also be generated by the addition of 1a to 2 in ethanol, which slowly converts into the pyrazole product when left at ambient conditions.
 | ||
| Scheme 2 The possible forms of the mono-addition intermediate (3a/6a) and di-addition intermediate (5a/7a). | ||
Both intermediates can exist either in a closed (3a and 5a) or open form (6a and 7a), although the former is presumably more stable thermodynamically. While the observation of 3a is somewhat expected,12,14 the involvement of 5a is not, although there is some precedent for similar molecules, which are unable to eliminate and aromatise.17 Attempts to verify the structures of these intermediates by NMR spectroscopy led only to the observation of intractable complex mixtures (Fig. S13 and S14†).
Microkinetic model fitting
Based on the experimental observations, microkinetic models were constructed and tested against the kinetic data obtained for the reaction of 2 with 1a, using an ODE solver (Fig. S19–S22†).18 Unsurprisingly, initial models based on the previously proposed mechanism (Scheme 1) produced poor fits; a reasonable fit can only be obtained by including both intermediates 3 and 5, as well as the involvement of either the diketone 1 or product 4 in the aromatisation step (Scheme 3). The proposed model was fitted to the seven experiments outlined in Fig. 4 A–G, and then simplified by iteratively fitting the model and dropping kinetically non-competitive steps (k < 1 × 10−5), and then retrained based on this new reaction pathway framework. This produced a well-fitting model in a simple interpretable form (Scheme 3).The complexity of the model means there are multiple equivalent optimal solutions that can be fitted to the available data. Nevertheless, after a few iterations, we were able to arrive at a set of kinetic rate constants (Table 3) that appear to fit most consistently across the reactions of both 1a and 1b (Table 2, experiments A–G for 1a and A–E for 1b). The key features of the model are highlighted below:
| R | Me | Et |
|---|---|---|
| k 1f | 2.23589 | 6.22879 |
| k 1r | 0 | 0 |
| k 2f | 1753.989 | 81.44262 |
| k 2r | 0.25614 | 0.01174 |
| k 3f | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860.73 860.73 |
551.6668 |
| k 3r | 0 | 0 |
| k 4 | 0.63061 | 0.74228 |
| k 5 | 0 | 0 |
| k 6 | 0.0399 | 0.44781 |
| k 7 | 11.87965 | 3.26931 |
| k 8 | 0 | 0 |
| k 9 | 3.69715 | 4.97573 |
| RMSE | 0.01755 | 0.01801 |
1. The initial nucleophilic attack (k1f) of the phenyl hydrazine appear to be faster with the diethyl-substituted diketone (R = Et, 1b) than acetylacetone (R = Me, 1a). This can be rationalised by taking into account the two geometrical forms of the hydrazone intermediate 6: where only the Z-form can proceed to form the ring-closed intermediates 3 or 5, and the unproductive E-form dissociating back to 1 and 2. Presumably, the formation of E-6b is more facile than that for E-6a, due to unfavourable 1,3-(aza)allylic strain present in its Z-isomer.19
2. As may be expected, the formation of the hydroxypyrazolidine intermediate 3 is kinetically favoured, with similar K2 values (k2f/k2r ∼ 7000). In contrast, the formation of hydrazidopyrazolidine 5a (R = Me, k3f) proceeds 25 times faster than 5b (R = Et), which is attributed to steric strain at the highly substituted carbon.
3. Neither aromatisation of 3 nor 5 proceed in any appreciable amount (k5/8 ≈ 0) unless catalysed by the product 4 (k6/9) or diketone 1 (k4/7). The role of the diketone (pKa 9) is presumably to provide an acid-catalysed pathway. We speculate that 1 could be acting as a base/proton-acceptor to promote the elimination. NMR studies confirmed there is no significant ion pair effects between the product and the diketone, and hence it is plausible that both pathways can occur concurrently.
4. Overall, the aromatisation of 5 is considerably faster than that of 3, by orders of magnitude (k7/9 ≫ k4/6), consistent with our earlier postulation of the higher steric strain of 5.
Subsequently, the addition of phenyl hydrazine to a number of symmetric diketone substrates (1b–e, where R = Et, i-Pr, i-Bu and t-Bu, respectively) was performed, to confirm the presence of different intermediates by HPLC-MS. Apart from 1e (which did not react under these conditions), mono-addition intermediates 3 (or E-6) were detected. However, the presence of 5 was only observed with 5b (R = Et) and 5d (R = i-Bu), suggesting its formation is strongly dictated by steric effects.
Unsymmetric methyl-ethyl pyrazole
Reactant stoichiometry ramps for diketones 1a and 1b showed a strong dependence of reaction rates on the initial reactant stoichiometry (Fig. 4). This suggested that the regioisomeric ratio for the corresponding reaction of the unsymmetrical hexan-2,4-dione 1f could be affected by varying the ratio of diketone 1f and phenyl hydrazine. To the best of our knowledge, the ratio of reactants has not previously been used to effect the regioselectivity of a reaction, although more invasive condition changes have been used for similar purposes.20Subsequently, the reaction of the unsymmetrical hexan-2,4-dione (R1 = Me, R2 = Et, 1f) and phenyl hydrazine were performed under different excess conditions (Scheme 4). Although neither excess experiment produced regioselectivity, we found that the ratio of regioisomeric pyrazole products (4f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4f′) does indeed vary, depending on which reactant was in excess. Pyrazole 4f was identified as the major product in both cases, however the ratio of products was more equal with an excess of phenyl hydrazine (1.7
4f′) does indeed vary, depending on which reactant was in excess. Pyrazole 4f was identified as the major product in both cases, however the ratio of products was more equal with an excess of phenyl hydrazine (1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), compared to when diketone 1f was present in excess (2.5
1), compared to when diketone 1f was present in excess (2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). This is contrary to that expected from the reactant stoichiometry ramps for the symmetric substrates, which showed a greater difference in the relative rates with an excess of phenyl hydrazine. This suggests a more complex interplay between the two R groups may be occurring.
1). This is contrary to that expected from the reactant stoichiometry ramps for the symmetric substrates, which showed a greater difference in the relative rates with an excess of phenyl hydrazine. This suggests a more complex interplay between the two R groups may be occurring.
 | ||
| Scheme 4 The reaction of unsymmetrical diketone 1f and phenyl hydrazine to form regioisomeric pyrazole products 4f and 4f′. | ||
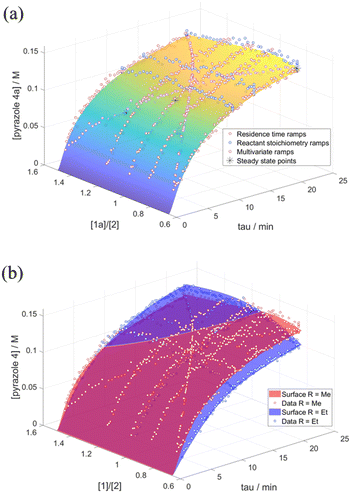
Last but not least, the microkinetic model was further validated by the construction of a response surface generated in MATLAB. This was compared with the experimental data obtained from reactant stoichiometry ramps, different excess experiments and bi-variable transient ramps (Fig. 5). The good overlay between the experimental data to the model response surface confirms the accuracy and robustness of the model: the extra transient experiments, as well as steady state flow data points, acted as independent verification for the model and the different transient flow methods through repeated points. These surface comparisons allowed us to visually discard models which, despite good RMSE scores, did not compare well for the rest of the independent data due to overfitting.
Conclusions
The previously proposed rate equation for the Knorr pyrazole synthesis was investigated with the aim of predicting regioselectivity for unsymmetric diketone substrates. However, it transpired the kinetics were more complex than previously reported, including autocatalytic reaction pathways and previously unreported intermediates. Transient flow methodology allowed efficient accurate data collection on this reaction, revealing the non-first order nature of the reaction under neutral conditions.Microkinetic modelling revealed autocatalysis and the prominence of unusual kinetic pathways via an unexpected di-addition intermediate 5. Surprisingly, different kinetic pathways dominate between acetyl acetone 1a and heptane-2,4-dione 1b, despite only a small change of the R substituent from a methyl to an ethyl group. DFT studies are currently underway to study the prominence of different reaction pathways between the reaction with 1a and 1b, and will be reported elsewhere.
Development of novel reactant stoichiometry ramps allowed us to better investigate this mechanistic change and suggested that the regioisomeric outcome of the reaction of the corresponding unsymmetric diketone 1f could be perturbed by reactant stoichiometry, subsequently confirmed by further experimentation.
Orthogonal transient flow methods, including novel reactant stoichiometry ramps and multivariate ramps, allowed quick access to data which would take much more time, material and effort to emulate with batch methods. The robustness of the microkinetic model, and of our novel transient flow methods, was further validated by comparison of the microkinetic model response surface with independent transient experimentation. It is envisaged that this approach could be applied to other challenging kinetic elucidation problems in the future.
Author contributions
All of the authors contributed to the conceptualization of the project. LS performed the experiments, collected and analysed the data, with inputs from the others. The original draft of the paper was created by LS, which was reviewed and edited by KKH, and subsequently forwarded to the others for comment.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to BASF for financial support. This project was supported by access to instruments and expertise at the Centre for Rapid Online Analysis of Reactions (ROAR) at Imperial College London [EPSRC, EP/R008825/1 and EP/V029037/1]. We are grateful to Imperial College Advanced Hackspace for their help in constructing the Peltier cooling device.Notes and references
- F. E. Valera, M. Quaranta, A. Moran, J. Blacker, A. Armstrong, J. T. Cabral and D. G. Blackmond, Angew. Chem., Int. Ed., 2010, 49, 2478–2485 CrossRef CAS PubMed.
- S. Mozharov, A. Nordon, D. Littlejohn, C. Wiles, P. Watts, P. Dallin and J. M. Girkin, J. Am. Chem. Soc., 2011, 133, 3601–3608 CrossRef CAS PubMed.
- T. Durand, C. Henry, D. Bolien, D. C. Harrowven, S. Bloodworth, X. Franck and R. J. Whitby, React. Chem. Eng., 2016, 1, 82–89 RSC.
- C. A. Hone, N. Holmes, G. R. Akien, R. A. Bourne and F. L. Muller, React. Chem. Eng., 2017, 2, 103–108 RSC.
- C. P. Haas, S. Biesenroth, S. Buckenmaier, T. Van De Goor and U. Tallarek, React. Chem. Eng., 2020, 5, 912–920 RSC.
- K. C. Aroh and K. F. Jensen, React. Chem. Eng., 2018, 3, 94–101 RSC.
- B. M. Wyvratt, J. P. McMullen and S. T. Grosser, React. Chem. Eng., 2019, 4, 1637–1645 RSC.
- C. Waldron, A. Pankajakshan, M. Quaglio, E. Cao, F. Galvanin and A. Gavriilidis, React. Chem. Eng., 2020, 5, 112–123 RSC.
- C. J. Taylor, M. Booth, J. A. Manson, M. J. Willis, G. Clemens, B. A. Taylor, T. W. Chamberlain and R. A. Bourne, Chem. Eng. J., 2021, 413, 127017 CrossRef CAS.
- S. Fustero, M. S. Anchez-Rosell, P. Barrio and A. Sim On-Fuentes, Chem. Rev., 2011, 111, 6984–7034 CrossRef CAS.
- S. K. Singh, M. Srinivasa Reddy, S. Shivaramakrishna, D. Kavitha, R. Vasudev, J. M. Babu, A. Sivalakshmidevi and Y. K. Rao, Tetrahedron Lett., 2004, 45, 7679–7682 CrossRef CAS.
- T. Norris, R. Colon-Cruz and D. H. B. Ripin, Org. Biomol. Chem., 2005, 3, 1844–1849 RSC.
- S. P. Singh, D. Kumar, H. Batra, R. Naithani, I. Rozas and J. Elguero, Can. J. Chem., 2000, 78, 1109–1120 CrossRef CAS.
- S. I. Selivanov, K. G. Golodova and B. A. Ershov, Zh. Org. Khim., 1986, 22, 2073–2081 CAS.
- S. P. Singh, V. Kumar, R. Aggarwal and J. Elguero, J. Heterocycl. Chem., 2006, 43, 1003–1014 CrossRef CAS.
- J. C. Sloop, B. Lechner, G. Washington, C. L. Bumgardner, W. D. Loehle and W. Creasy, Int. J. Chem. Kinet., 2008, 40, 370–383 CrossRef CAS.
- K. N. Zelenin, M. Y. Malov, I. P. Bezhan, V. A. Khrustalev and S. I. Yakimovich, Chem. Heterocycl. Compd., 1985, 21, 713–714 CrossRef.
- Berkeley Madonna, https://berkeley-madonna.myshopify.com/, (accessed 17 February 2022).
- R. W. Hoffmann, Chem. Rev., 1989, 89, 1841–1860 CrossRef CAS.
- S. Fustero, R. Román, J. F. Sanz-Cervera, A. Simón-Fuentes, A. C. Cuñat, S. Villanova and M. Murguía, J. Org. Chem., 2008, 73, 3523–3529 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2re00271j |
| This journal is © The Royal Society of Chemistry 2023 |