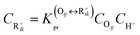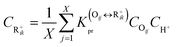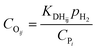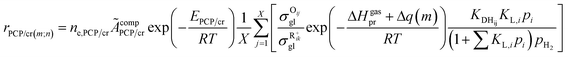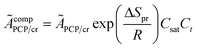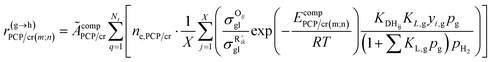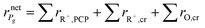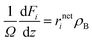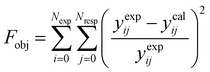Single event kinetic modeling for paraffin hydrocracking over an industrial Ni–W silica–aluminum catalyst†
Received
17th July 2022
, Accepted 6th October 2022
First published on 7th October 2022
Abstract
The hydrocracking of n-octane on a Ni–W silica–aluminum catalyst was performed over a fixed-bed reactor. A detailed reaction network was generated based on the hydrocracking behavior and the carbenium ion chemistry. By introducing Golender's potential energy concept, a computer-aided method was developed to calculate the global symmetry numbers of the species and their transition states accurately and conveniently. The single event kinetic models for n-octane hydrocracking were derived and the related physicochemical properties were calculated. A re-lump method to extend the real application of the model was mentioned. Totally, 19 independent kinetic parameters were drawn from the rate equations and were estimated by the genetic algorithm and the Marquardt algorithm. The predicted component evolutions (e.g., the changes of C3, n-C4, mono-C4, n-C5, mono-C5, n-C8, mono-C8, di-C8 and tri-C8) along the reactor corresponded to existing experience in hydrocracking and were logically reasonable. The calculated results at the reactor outlet were in good agreement with the experimental data. This kinetic modeling method is of great significance in kinetic studies and hydrocracking reactor simulation.
1 Introduction
Hydrocracking is one of the key processes in the refining industry in which heavy feedstocks are catalyzed to form olefinic species and subsequently protonated into carbenium ions, thereafter isomerized and cracked to convert into light fractions under higher reaction pressure and temperature. The presence of hydrogen can effectively inhibit the coke formation and catalyst deactivation in this reaction process as compared to the fluid catalytic cracking process. Different kinds of heavy feeds, e.g., vacuum gas oil (VGO), bitumen and Fischer–Tropsch wax, are used to be treated by hydrocracking and to produce lighter transportation fuels such as gasoline, kerosene, and diesel, lubricants or feedstocks for catalytic cracking for olefinic products in industrial applications.
During the past decades, hydrocracking of heavy feedstocks has been studied comprehensively, e.g., the development and utilization of catalysts,1–6 the investigation and design of reactors, the analysis of the reaction mechanisms and the influence of operating conditions7–9 and the reaction kinetic studies based on different degrees of mathematical models.10–18 The kinetic study is helpful in reactor simulation, optimization and design of industrial units and prediction of the optimum reaction conditions. Some models could also provide suggestions for equilibrium between metal sites and active sites in catalyst development which is a better guide for industrial application.16 At present, the most widely used industrial kinetic models are lumped models in which the parameters are significantly affected by the feedstock, reaction conditions and reactor used. Though with slow application progress, more and more molecular-level kinetic models (such as Monte Carlo model,19,20 structural-oriented model,21–23 structural model24 and single event kinetic model10,25–32) are gradually favored by many researchers. The single event kinetic method developed by Froment et al.33 is in a true elementary-step level. Compared with the traditional empirical models and lumped models, single event kinetic models have significant advantages. They involve fewer independent kinetic parameters, and the parameters are almost not affected by the feed,34 even kinetic parameters obtained in one catalyst can be used to predict the product distribution in another catalyst by adjusting the protonation enthalpy.35
This fundamental kinetic method was applied to the hydroisomerization of n-octane into methylheptane on a Pt/USY zeolite by Baltanas.36 Vynckier and Froment33 introduced the single event method into complex processes such as hydrocracking of paraffins and cycloalkanes. Wu et al.37 generated a reaction network for n-decane catalytic cracking (including the elementary steps both on Lewis and Brønsted acid sites), and developed related kinetic models. Schweitzer et al.38 developed a single event kinetic model for n-hexadecane cracking and confirmed that the kinetic parameters obtained were independent of the length of the carbon chain and could even be used to predict the product fractions of Fischer–Tropsch product hydrocracking. Chavarría et al.39 introduced the single event concept into a non-ideal hydroisomerization and hydrocracking reactions of n-octane, considering more general situations and establishing kinetic models for the reactions on the metal sites and acid sites. Guillaume et al.40 extended the concept and applied it to the kinetic modeling of butane isomerization. Surla et al.41 confirmed that n-butane isomerization obeyed a bimolecular reaction mechanism and established a kinetic model of n-butane isomerization based on a detailed reaction network.
In this work, the kinetic data of n-octane hydrocracking over an industrial Ni–W amorphous silica–aluminum catalyst are collected. A detailed reaction network of n-octane hydrocracking is specified on the basis of Boolean adjacency matrixes. Golender's potential energy concept is introduced to calculate the global symmetry numbers of species and activate the complex by computer-aided programs accurately and conveniently. The detailed rate equations for the elementary steps and a re-lump method for practical application of the model are mentioned. A chain-length related factor is introduced to reflect the differences in the activities of the hydrocarbon species with different carbon numbers. The kinetic parameters are estimated based on the experimental data. The model has potential to be extended to long-chain paraffin (e.g., Fischer–Tropsch wax) hydrocracking because of its intrinsic merits. The results can be used for operating condition optimization and industrial reactor simulation in hydrocracking reactions. The methods in this paper are of great significance in computer-aided fundamental kinetic modeling.
2 Experimental section
2.1 Experimental setup and catalysts
The hydrocracking of n-octane was carried out in a tubular fixed-bed reactor. The schematic diagram is shown in Fig. 1. The n-octane used in the experiment was of analytical grade (>99%). A commercial Ni–W over amorphous silica–aluminum (FC-14) developed by Fushun Research Institute of Petroleum and Petrochemical in China was used in this study. The average particle size and loading capacity of the catalyst in the reactor were 0.25 mm and 2.33 g, respectively. The chemical composition and physical properties of the catalyst are shown in Table 1. A pre-sulfuration step is necessary before experimental data collection to obtain a high activity of the catalyst.
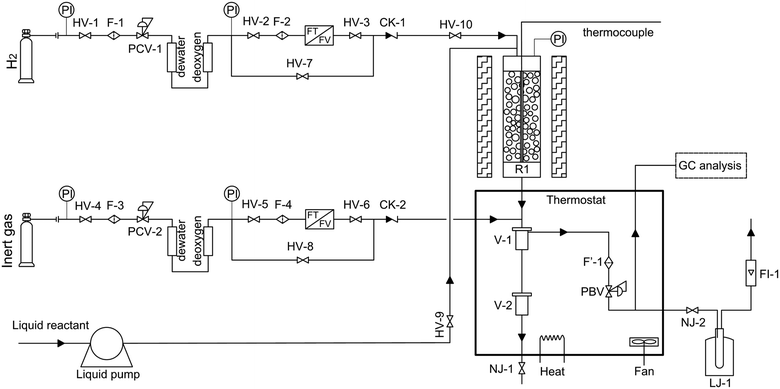 |
| | Fig. 1 Schematic diagram of the experimental setup (HV, globe valves; F, filter; CK, non-return valves; PCV, pressure reducing valves; F′, thermal resistant filter; NJ, thermal resistant globe valves; R1, fixed-bed reactor; PBV, back-pressure regulator; LJ, cold trap; FI, flow meter; V, gas–liquid separator). | |
Table 1 Chemical composition and physical properties of the catalyst
| Items |
Values |
| Main chemical composition |
| WO3, wt% |
22.1 |
| NiO, wt% |
5.3 |
| SiO2, wt% |
22.5 |
| Physical properties |
| Pore volume, cm3 g−1 |
0.35 |
| BET, m2 g−1 |
186 |
| Density, g cm−3 |
0.89 |
2.2 Reaction conditions and product analysis
The reaction conditions of the experiments are at temperature of 573–654 K, pressure of 2.0–8.0 MPa, liquid hourly space velocity (LHSV) of 1–4 h−1, and hydrogen/oil volume ratio of 400–1200 mL/mL. The orthogonal design method is adopted in the experiments of the hydrocracking of n-octane in the range of the above reaction conditions. The internal and external diffusions were checked before cracking data collection (see details in the ESI†). The products were directly analyzed by online and offline gas chromatography. The detailed experimental point, conversion and mass balance information are listed in Table S1 of the ESI.† The experimental data obtained were used for kinetic parameter estimation and model validation.
2.3 Reaction mechanism and the types of elementary steps
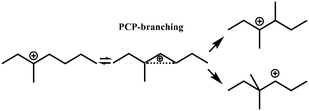
In general, hydrocracking of alkanes over a bifunctional catalyst involves dehydrogenation and hydrogenation reactions on the active metal sites and carbenium ion elementary steps on the acid sites. The reaction mechanism and instances are shown in Table 2. An alkane molecule entered the pore of the catalyst and was adsorbed on the metal sites, then dehydrogenation occurred and the corresponding olefin species were formed. The olefin species migrated to the acid sites, then underwent protonation to form carbenium ions. Subsequently, the carbenium ions underwent rearrangements, such as hydride shift (HS), methyl shift (MS), and protonated cyclopropyl branching (PCP-branching) to produce isomerized products with different degrees of branching. These isomerized species underwent cracking reactions (e.g., β-scission) to obtain lighter carbenium ions and olefins. Cyclization, aromatization and oligomerization are not considered in this study because the contents of cycloalkanes, aromatics and other higher carbon number components are negligible in the hydrocracking reactions at the current situation. In addition, C6/C2 and C7/C1, with total selectivity normally less than 1% under current situations, were believed to be produced through hydrogenolysis.42,43 Considering such minor amounts of the hydrogenolysis products in industrial catalytic performance,44–48 the formation of C6/C2 and C7/C1 was neglected in the kinetic modeling process.
Table 2 Elementary steps involved in the hydrocracking of n-octane on the catalyst
| Types |
Elementary steps |
Example |
|
R+pq stands for all the possible branched carbenium ions (e.g., type A, B and C in Fig. S2 of the ESI†). The direct cracking of a linear secondary carbenium ion is not considered (e.g., type D in Fig. S2 of the ESI†) because of the high energy barrier of this reaction route.49,50
|
| Metal sites |
| (De)hydrogenation |
Pgasi + m ↔ Pim |
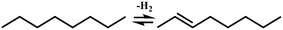
|
| Pim ↔ Oijm + H2 |
| Oijm ↔ Oij + m |
| Acid sites |
| (De)protonation |
Oijm + H+ ↔ R+ik |
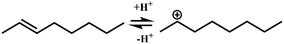
|
| Isomerization |
R+ik → R+pq |

|

|
|
| Crackinga |
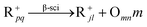
|

|
2.4 Theoretical basis
The rate coefficient k of an elementary step based on the single event concept51 is expressed in eqn (1) in terms of the transition state theory.52| | 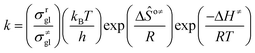 | (1) |
where 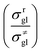 is called the number of single events, viz. ne, and is relevant to the structures of the reactants and the activated complex. ΔŜo≠ represents the intrinsic entropy change upon transformation of the reactant into the activated complex.
is called the number of single events, viz. ne, and is relevant to the structures of the reactants and the activated complex. ΔŜo≠ represents the intrinsic entropy change upon transformation of the reactant into the activated complex. ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) in eqn (2) is defined as the single event rate coefficient, and according to the Arrhenius equation, Ã in eqn (3) is called the single event frequency factor. The rate coefficient is regarded as the product of the single event rate coefficient
in eqn (2) is defined as the single event rate coefficient, and according to the Arrhenius equation, Ã in eqn (3) is called the single event frequency factor. The rate coefficient is regarded as the product of the single event rate coefficient ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and the structure related parameter ne.
and the structure related parameter ne.| | 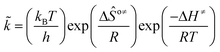 | (2) |
| | 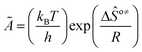 | (3) |
In addition, the linear relationship between the activation energy (ΔH≠ ≈ Ea) and the reaction enthalpy of the elementary step is expressed by the Evans–Polanyi relationship,53 in which eqn (4) and (5) are for the exothermic and endothermic reactions, respectively.| | | Ea = E0 + αΔHsurfr (ΔHsurfr < 0) | (4) |
| | | Ea = E0 + (1 − α)ΔHsurfr (ΔHsurfr > 0) | (5) |
E0 and α are the intrinsic activation energy and transfer factor (0 < α < 1) of a specific type of elementary step, respectively. ΔHsurfr is the reaction enthalpy of an elementary step occurring on the surface of the catalyst.
2.5 Detailed reaction network generation
In our previous work, detailed reaction networks about hydrocracking of long-chain paraffins had been generated by computer algorithms based on digital representations of species and elementary steps. Automatic transformation between a characteristic vector with nine elements and a matrix representing the species made the generation of reaction networks of large molecules accurate and efficient.54 A summary of the number of intermediates and elementary steps in n-octane hydrocracking is shown in Table 3. Here the number of the β-scission steps is relatively small because the maximum chain length of the feedstock is only n-octane and no more secondary cracking occurred. The number of isomerization steps is large, meaning a variety of rearrangement possibilities.
Table 3 Results of the reaction networks of n-octane hydrocracking
| Types |
Number |
| Number of the elementary steps involved |
| (De)protonation |
107 |
| Hydride-shift |
63 |
| Methyl-shift |
44 |
| PCP-branching |
52 |
| β-Scission |
15 |
| Total intermediate species involved |
| Olefins |
65 |
| Carbenium ions |
49 |
The whole reaction paths in terms of carbenium chemistry and some proposed reaction rules are recorded and saved during the generation of the reaction networks. These paths could be read and identified during the rate equation generation and parameter estimation. Table 4 lists the information involved in each reaction path during our reaction network generation, including the type of elementary step, chain length of the species, number of the side-chains, nature of the carbenium ions, global symmetry number σgl of the species, number of single events ne, reaction enthalpy of the elementary steps and dehydrogenation equilibrium constants.
Table 4 Information involved during the generation of the reaction paths
| Items |
Explanation |
| Ty |
The type of elementary step, e.g., PCP-branching and β-scission |
|
σ
rgl, σ≠gl |
The global symmetry number of the species and activated complex |
|
n
e
|
Number of single events of the elementary steps |
|
N
r, Np |
Chain length of the reactants and products |
|
B
r, Bp |
Number of the side-chain of the reactants and products |
| ΔHgpr, ΔHgPCP, ΔHgcr |
Reaction enthalpies of the elementary steps |
|
K
DH
|
Dehydrogenation equilibrium constants |
| (m;n) |
Transformation from an m type carbenium ion to an n type carbenium ion, where m and n stand for secondary or tertiary carbenium ions |
2.6 Symmetry number calculation based on computer algorithms
Traditionally, the global symmetry number of a species could be estimated by artificial analysis of the symmetry properties and then calculated by eqn (6),55 where σext is the external symmetry number,56n′ and n′′ are the numbers of the two-fold and three-fold symmetry axes, respectively. n′′′ is the number of the chiral center.| | 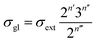 | (6) |
In reality, it is easy to get wrong in estimating the values of σext, n′, n′′ and n′′′ of the species and activated complex, especially when the molecules involved are structure complicated.
In this study, we introduced a computer-aided symmetry number calculation method based on a theory proposed by Ercolani,57 who described that like atoms in a molecule could be distinguished by labels and the global symmetry number of this molecule is the ratio of the label information as defined in eqn (7). The numerator item Πini! represents the total number of equilibrium configurations of the labeled molecule and the denominator item N is the number of distinguishable label-isomers which are created by the labeling procedure that makes like atoms distinguishable.
| | 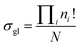 | (7) |
By introducing a concept of Golender's potential energy,
58 it is very convenient to know the conditions of the atoms in the species so that we could estimate the number of distinguishable label-isomers accurately and easily.
59 The equations for calculating the global symmetry number of paraffins, olefins and carbenium ions are derived in
eqn (8)–(10).
| | 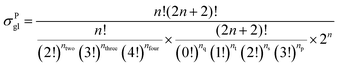 | (8) |
| | 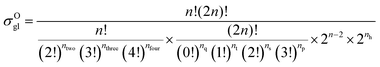 | (9) |
| | 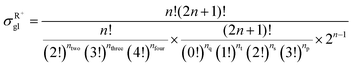 | (10) |
in which
np,
ns,
nt, and
nq represent the numbers of the primary carbon atoms, the secondary carbon atoms, the tertiary carbon atoms and the quaternary carbon atoms in the species, respectively. In the computer procedure, we can execute an initial estimation of the
np,
ns,
nt and
nq values based on the carbon skeleton information. Subsequently, the carbon atoms with sp
2 hybridization must be checked. Every time we find one sp
2 hybridized primary carbon atom, the initial
np value will be reduced by one, while the initial
ns value will be added by one. Similar rules should be executed to recalculate the
ns,
nt and
nq values sequentially.
nh represents the total number of permutations of carbon atoms with the same Golender's potential energy and connected to sp
2 hybridized carbon atoms.
nh only appears in calculating the global symmetry number of an unsaturated species (
e.g., olefins). If the sp
2 hybridized carbon atom in the olefin species is a primary carbon atom or it is connected to two carbon atoms with the same Golender's potential energy,
nh = 1, or else
nh = 0.
ntwo counts for the occurrence of the situation where two carbon atoms with the same Golender's potential energy are connected directly or are connected to the same carbon atom.
nthree and
nfour count for the occurrence of the situation where three and four carbon atoms with the same Golender's potential energy are connected to the same carbon atom, respectively.
Take the 2,4-dimethyl-3-hexane carbenium ion (see the structure in Fig. 2) as an example, the specific details in calculating the global symmetry number are as follows. The Boolean adjacency matrix representing the carbon skeleton structure of the 2,4-dimethyl-3-hexane carbenium ion is shown as matrix M and the constructed matrix G is a transformation of matrix M (see in Fig. 3). The carbon atom with a positive charge or connected with an unsaturated bond is categorized into the sp2 hybridization state. The other carbon atoms are categorized into the sp3 hybridization state. The elements of matrix M and matrix G are marked by mij and gij, respectively. The value of each element gij in matrix G is determined using eqn (11).
| | 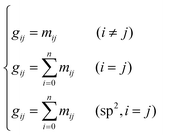 | (11) |
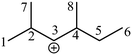 |
| | Fig. 2 The numbering of the carbon skeleton of the 2,4-dimethyl-3-hexane carbenium ion. | |
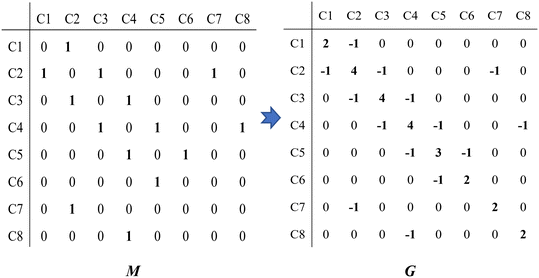 |
| | Fig. 3 The Boolean adjacency matrix M of the 2,4-dimethyl-3-hexane carbenium ion and its transformation to matrix G. | |
The series of each carbon atom in a species is recorded in vector C. The values of the elements in vector C are determined by the sum of the elements in each row of matrix M, as shown in eqn (12).
| | 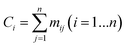 | (12) |
If Ci = 1, the ith carbon is classified as primary.
If Ci = 2, the ith carbon is classified as secondary.
If Ci = 3, the ith carbon is classified as tertiary.
If Ci = 4, the ith carbon is classified as quaternary.
Combining the value Ci (see in Fig. 4) and the reality that the 3rd carbon atom in the 2,4-dimethyl-3-hexane carbenium ion is in sp2 hybridization, we can obtain np = 4, ns = 1, nt = 3 and nq = 0.
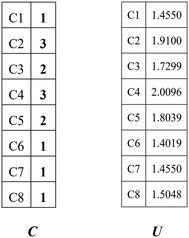 |
| | Fig. 4 Vector C and vector U of the 2,4-dimethyl-3-hexane carbenium ion. | |
The vector U defined by eqn (13) stores the potential energies of the carbon atoms of the species, where G−1 is the inverse of G.
The 1st carbon atom and 7th carbon atom in the 2,4-dimethyl-3-hexane carbenium ion have the same potential energy (see vector
U in
Fig. 4) and they are connected to the same 2nd carbon atom. Accordingly, we can obtain
ntwo = 1,
nthree = 0 and
nfour = 0. The above values of the paraffins and olefins could be calculated similarly.
The global symmetry number of the activated complex could also be calculated by this method. Take the PCP-branching reaction of the 2-hexane carbenium ion as an example, PCP-branching is usually considered as a two-step reaction, including cyclization and cleavage, as shown in Fig. 5. The transition states of the elementary step were discussed in detail elsewhere.55 The matrix M1 in Fig. 6 represents the relationships of the carbon atoms of the 2-hexane carbenium ion. M2 and M3 stand for two possible cleavage positions for two branched isomers. The 2nd carbon atom, 3rd carbon atom and 4th carbon atom in the 2-hexane carbenium ion form a ternary ring in its transition state, so m24 = m42 = 1 in the matrices M2 and M3. If the cleavage occurs between the 2nd carbon atom and the 3rd carbon atom, then these two carbons form a half bond in the transition state, so that m23 = m32 = 0.5 in matrix M2. If the cleavage occurs between the 3rd carbon atom and the 4th carbon atom, then these two carbons form a half bond in the transition state, accordingly m43 = m34 = 0.5 in matrix M3. The global symmetry number of the activated complex in PCP-branching is defined in eqn (14).
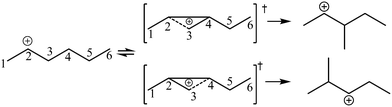 |
| | Fig. 5 The PCP-branching reaction of the 2-hexane carbenium ion. | |
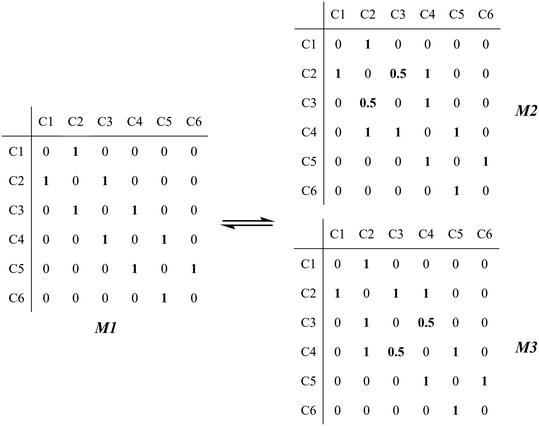 |
| | Fig. 6 The matrix transformation from reactants to transition states in the PCP-branching step. | |
| |
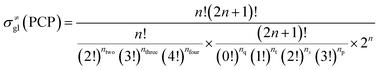
| (14) |
The β-scission of the 3,4-dimethyl-2-pentane carbenium ion is shown in Fig. 7. Its carbon relationships are described by matrix M4 and these transition states are described by matrix M5 (see in Fig. 8). A double bond will be formed between the 2nd carbon atom and the 3rd carbon atom during the β-scission step, and simultaneously a cleavage will occur between the 3rd carbon atom and the 4th carbon atom. Accordingly, we define one and a half bond between the 2nd carbon atom and the 3rd carbon atom, meaning m23 = m32 = 1.5, and a half bond between the 3rd carbon atom and the 4th carbon atom, meaning m43 = m34 = 0.5 in matrix M5. The global symmetry number of the activated complex in β-scission is expressed by eqn (15).
 |
| | Fig. 7 The β-scission of the 3,4-dimethyl- 2-pentane carbenium ion. | |
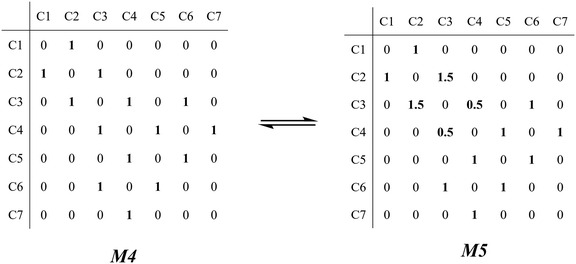 |
| | Fig. 8 The matrix transformation from reactants to transition states in β-scission. | |
| |
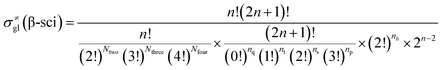
| (15) |
It should be noted that the global symmetry numbers calculated in eqn (8)–(10), (14) and (15) assume that the species are in free state. In reality, the species are adsorbed and bonded on the surface of the catalysts during the catalytic reactions, meaning some decrease of the degrees of freedom compared with the values in the above equations. However, the number of the single events ne is always the ratio of the global symmetry numbers of the reactants and their transition state. We assume that the numerator and the denominator have the same degrees of freedom loss when bonding with the active sites of the catalysts, so that the ne values have no more changes in these two situations.
3 Model equations
Based on the experimental data analysis, the elementary steps involved in n-octane hydrocracking are mentioned in Table 2. The (de)hydrogenation, (de)protonation, hydride shift and methyl shift steps reach quasi-equilibrium.16 The PCP-branching and β-scission steps are assumed the rate determining steps. According to the carbenium chemistry, the chain length of the carbenium ions involved in the PCP branching and β-scission steps is not less than 4 and 6, respectively. The mono-branched products could easily be produced from the n-alkane feedstock. The multi-branched hydrocarbons are much less in the products and are preferred to be cracked.
3.1 Rate equations based on the single event concept
The concentration of an alkane species adsorbed on the surface of the catalyst is described by eqn (16) according to Langmuir isotherm adsorption,15,16,39,60 where KL,i is the Langmuir coefficient of alkane i, and Csat,i is the saturated concentration of alkane i. The KL,i value is assumed to be independent of the chain length and only relevant to the number of the side chains.| | 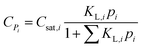 | (16) |
The reaction equilibrium constants could also be expressed by the single event concept. Take the protonation step as an example, its equilibrium constant is defined in eqn (17), in which ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) pr is called the single event protonation equilibrium constant and defined in eqn (18).
pr is called the single event protonation equilibrium constant and defined in eqn (18). ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) pr is independent of the rotational entropy change and only related to the non-structure-affected intrinsic entropy change ΔŜpr and the reaction enthalpy of the step ΔHsurfpr.
pr is independent of the rotational entropy change and only related to the non-structure-affected intrinsic entropy change ΔŜpr and the reaction enthalpy of the step ΔHsurfpr.
| | 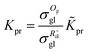 | (17) |
| | 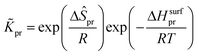 | (18) |
The reaction enthalpy of the protonation ΔHsurfpr is defined as the algebraic sum of the heat formations of the products and the reactants, as shown in eqn (19). The heat of formation of each species on the surface can be obtained by subtracting the stabilization energy q and the heat of sorption of the species into the zeolite pores ΔHsorp from its gas phase heat of formation, as shown in eqn (20)–(22).16,55
| | | ΔHsurfpr = ΔHsurff(R+) − ΔHsurff(O) − ΔHsurff(H+) | (19) |
| | | ΔHsurff(R+) = ΔHgasf(R+) − ΔHsorp(R+) − q(R+) | (20) |
| | | ΔHsurff(O) = ΔHgasf(O) − ΔHsorp(O) | (21) |
| | | ΔHsurff(H+) = ΔHgasf(H+) − q(H+) | (22) |
Substituting
eqn (20)–(22) into
eqn (19), Δ
Hsurfpron the surface of the catalysts is obtained
| | | ΔHsurfpr = ΔHgaspr − [ΔHsorp(R+) − ΔHsorp(O)] + [q(H+) − q(R+)] | (23) |
The second term on the right side of
eqn (23) can be ignored by assuming that a similar carbon skeleton structure of species has similar heat of sorption values.
q(R
+) is defined as the difference between the energy value of an adsorbed carbenium ion and that of its corresponding surface-bonded state on a solid acid site. Δ
q(
m) is defined as the difference between the stabilization energy of a proton and that of a carbenium ion
| | | Δq(m) = q(H+) − q(R+) | (24) |
where
m represents the nature of the carbenium ion R
+,
e.g., secondary or tertiary. Substituting
eqn (24) into
eqn (23), we finally obtain the expression of Δ
Hsurfpr in
eqn (25).
| | | ΔHsurfpr = ΔHgaspr + Δq(m) | (25) |
| | | ΔHsurfPCP(m;n) = ΔHgasPCP + [Δq(n) − Δq(m)] | (26) |
| | | ΔHsurfcr(m;n) = ΔHgascr + [Δq(n) − Δq(m)] | (27) |
Similarly, the reaction enthalpies of PCP-branching and β-scission can be defined by
eqn (26) and
(27), where
m and
n represent the nature of the reactant carbenium ion and the product carbenium ion. That is to say, (
m;
n) stand for one of the situations (s;s), (s;t), (t;s) and (t;t).
Theoretically, Δq(m) might be related to the nature of carbenium ions and the chain length. Therefore, we detailed Δq(m) through eqn (28), where λ is a chain-length-related factor, Δq0(m) is only relevant to the type of the carbenium ion, and NC is the carbon number of the m type carbenium ion.
The rate equation of PCP-branching and β-scission expressed in terms of the single event concept is shown in eqn (29). The concentration of the reactant carbenium ion can be calculated from the protonation equilibrium step, as shown in eqn (30).
| | rPCP/cr = ne,PCP/cr![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) PCP/crCR+ik PCP/crCR+ik | (29) |
| | 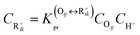 | (30) |
If there are
X olefins in equilibrium with a carbenium ion R
+ik, the average concentration of R
+ik can be obtained by
eqn (31).
| | 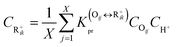 | (31) |
where
X will equal to 2 or 3, depending on the nature of the carbenium ion R
+ik, secondary or tertiary.
The total concentration of the acid active sites Ct is the sum of the concentration of all the carbenium ions and the concentration of the proton CH+. Normally, it is assumed that the concentration of the intermediate carbenium ions is negligible compared with the proton CH+, viz. CH+ ≈ Ct. The concentration of the adsorbed olefin COij can be calculated from the dehydrogenation equilibrium step, as shown in eqn (32). Substituting eqn (16)–(18), (31) and (32) into eqn (29), the final rate equation of PCP-branching or β-scission could be given in eqn (33).
| | 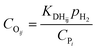 | (32) |
| | 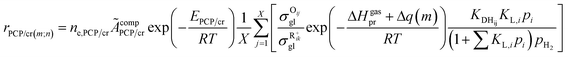 | (33) |
in which
ÃcompPCP/cr is a composite frequency factor defined in
eqn (34), and
EPCP/cr is the activation energy of the reaction and can be expressed as
eqn (35) according to the Evans–Polanyi relation. By substituting
eqn (26) and
(27) into
eqn (35), the specific activation energies for PCP-branching and β-scission are obtained by
eqn (36) and
(37).
| | 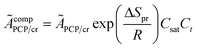 | (34) |
| | | EPCP/cr = E0,PCP/cr + aPCP/crΔHsurfPCP/cr | (35) |
| | | EPCP(m;n) = E0,PCP/cr + aPCP[ΔHgasPCP + Δq0(n) − Δq0(m)] | (36) |
| | | Ecr(m;n) = E0,cr(m;n) + acr[ΔHgascr + Δq0(n) − Δq0(m) + λ(Np − Nr)] | (37) |
Eqn (33) is a truly fundamental rate equation that could generally describe the rate determining steps of the elementary steps in the hydrocracking reaction. It means that this single event kinetic model can describe all the components that appear in the reaction networks. However, the detailed composition analysis of the complex feedstocks and products (e.g., vacuum gas oil and Fischer–Tropsch wax) is still very challenging although great progress has been achieved in the past years. To extend the fundamental model to practical fields, we can re-lump the components in the modeling to match the reality. For example, paraffin with a given carbon number can be grouped into four components based on the number of the methyl branches: normal, mono-, di- and tri-branched paraffins. What we need to emphasize is the lump mentioned here is quite different from the traditional lump concept because this lump method is backed by strict thermodynamic principles and the fundamental single event concept.17 The detailed reaction paths are kept intact in the model equations. For instance, a paraffinic lump g converts to lump h, in which the reaction paths are shown in Fig. 9. Numerous equilibrium reactions of the isomeric intermediates are incorporated into the lumps. The PCP branching and β-scission will occur between lump g and lump h so that the reaction rate is the sum of the net reaction rates of each carbenium ion in the lump. This can be expressed by eqn (38), in which pg is the partial pressure of lump g, yi,g is the equilibrium molar fraction of ith paraffin in lump g and Nt is the total number of elemental steps that occur from lump g.
| | 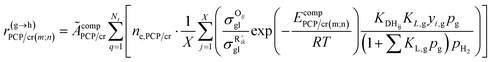 | (38) |
The net rate of formation of the alkane g component is equal to the sum of the net rates of formation of carbenium ions and olefins which have the same skeleton structure as alkane g, as expressed
| | 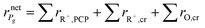 | (39) |
where ∑
rR+,PCP and ∑
rR+,cr are the net rates of formation of the carbenium ions due to PCP-branching and β-scission, respectively. ∑
rO,cr is the net rate of formation of the olefins produced by β-scission.
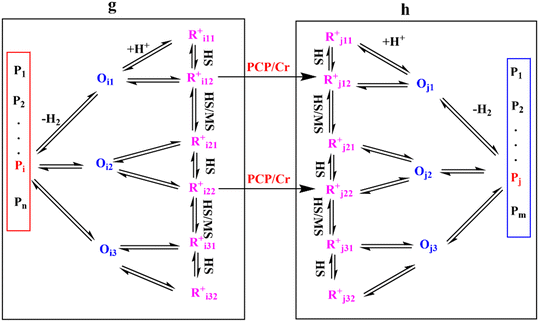 |
| | Fig. 9 Reaction paths from lump g to lump h. | |
3.2 Reactor model and the numerical methods
In our octane hydrocracking experiments, we used a lab-scale tubular reactor with a catalyst bed length (L) of 30 mm, a reactor diameter (D) of 10 mm and a particle size of the catalysts (dp) around 0.25 mm. The ratio of the reactor diameter to catalyst particle diameter was 40 here, thus reasonably assuming the elimination of the wall effects (a widely accepted value D/dp > 10).61 The intensity of the axial dispersion was estimated by Peclet number analysis, in which a new empirical correlation (considering both the molecular diffusion factor and the bed voidage factor in the axial dispersion coefficient calculation) developed by Rastegar and Gu was used to calculate the Peclet number under experimental operating conditions.62 The values of the Peclet number under current conditions ranged from 113 to 162 (see the detailed information of the calculation in the ESI†). We assumed that the flow regime could be approximately simplified as ideal plug flow.
The diameters of the catalyst particles are within sufficiently small values so that the transport limitations are negligible. The continuity equations of the species are expressed as follows
| | 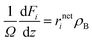 | (40) |
where
i stands for the product species (
i = C
3,
n-C
4, mono-C
4,
n-C
5, mono-C
5,
n-C
8, mono-C
8, di-C
8 and tri-C
8),
rneti is the net reaction rate of species
i,
ρB is the catalyst bulk density,
Ω is the cross section of the reactor, and
Fi is the molar flow rate of the species
i. The molar flow rates of the reaction outlet were obtained by solving the set of nonlinear equations. The ordinary differential equations corresponding to the species were solved by the fourth order Runge–Kutta method.
The parameter values of the kinetic equations were estimated by minimizing a multi-response objective function which is the sum of the squares of the relative errors between the experimental and calculated data.
| | 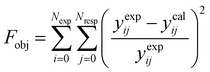 | (41) |
in which
Nexp is the number of experiments,
Nresp is the number of responses (
e.g., the product species), and
yexpij and
ycalij are the experimental and calculated molar fractions of the response
j in the
ith experiment.
The genetic algorithm (GA) was used as a global optimization method to screen the parameter values initially, to avoid falling into local traps. Subsequently, the Marquardt method was followed to guarantee that a global minimum could be obtained. The parameter estimation was performed first with the isothermal data at 654 K and 636 K, respectively. The values were then used for the mixed condition estimation.
4 Results and discussion
Totally, 19 independent parameters were drawn from the kinetic equations and the estimated results are listed in Table 5. The activation energy values of the rate determining steps were calculated and listed in Table 6 based on the fundamental parameters in Table 5. In the PCP-branching reaction, type (s;t) has the lowest activation energy of 39 kJ mol−1, while the value of type (t;s) is as high as 101 kJ mol−1. This may be attributed to the fact that the t type carbenium ion is more stable than the s type carbenium ion. The activation energies of the other two types (s;s) and (t;t) in PCP-branching were 70 kJ mol−1 and 80 kJ mol−1, respectively. As a whole, the activation energies of the PCP-branching reactions were remarkably lower than those of the β-scission reactions in which type (s;t) is 98 kJ mol−1 and the other three are from 110 kJ mol−1 to 121 kJ mol−1.
Table 5 Parameter estimation
| Parameter |
Value |
Unit |
Parameter |
Value |
Unit |
|
E
0,PCP(s;s)
|
73 |
kJ mol−1 |
E
0,cr(s;s)
|
101 |
kJ mol−1 |
|
E
0,PCP(s;t)
|
76 |
kJ mol−1 |
E
0,cr(s;t)
|
114 |
kJ mol−1 |
|
E
0,PCP(t;s)
|
72 |
kJ mol−1 |
E
0,cr(t;s)
|
78 |
kJ mol−1 |
|
E
0,PCP(t;t)
|
83 |
kJ mol−1 |
E
0,cr(t;t)
|
92 |
kJ mol−1 |
|
Ã
compPCP
|
9.6 × 106 |
h−1 |
Ã
compcr
|
3.3 × 1012 |
h−1 |
|
α
PCP
|
0.25 |
— |
α
cr
|
0.19 |
— |
| Δq0(s) |
749 |
kJ mol−1 |
Δq0(t) |
805 |
kJ mol−1 |
|
λ
|
0.49 |
kJ mol−1 |
|
|
|
|
K
L,nor
|
10.9 |
MPa−1 |
K
L,mono
|
1.9 |
MPa−1 |
|
K
L,di
|
3.4 |
MPa−1 |
K
L,tri
|
13.7 |
MPa−1 |
Table 6 Activation energies of the elementary steps
| Parameter |
Value |
Unit |
Parameter |
Value |
Unit |
|
E
PCP(s;s)
|
70 |
kJ mol−1 |
E
cr(s;s)
|
121 |
kJ mol−1 |
|
E
PCP(s;t)
|
39 |
kJ mol−1 |
E
cr(s;t)
|
98 |
kJ mol−1 |
|
E
PCP(t;s)
|
101 |
kJ mol−1 |
E
cr(t;s)
|
120 |
kJ mol−1 |
|
E
PCP(t;t)
|
80 |
kJ mol−1 |
E
cr(t;t)
|
110 |
kJ mol−1 |
Δq0(t) is higher than Δq0(s) (see in Table 5), which is in agreement with the traditional understanding that the tertiary carbenium ions are more stable than the secondary carbenium ions. According to eqn (37), by introducing parameter λ, components with a higher carbon number will have larger stabilization energy on the surface of the catalysts and could be cracked (by β-scission) more easily, which could predict long-chain paraffin hydrocracking reasonably. This is in agreement with the experimental phenomenon in publication.63 The λ value of 0.49 is obtained from the current experimental data. It is hard to find similar λ information in the publications on hydrocracking kinetic models, but this can be found in some polymerization reactions, e.g., the value λ with carbon number is 0.653 in Fischer–Tropsch synthesis64 and 2.51 in the alkylation reaction,55 respectively. Jin et al.65 did not consider the effect of chain length on the energy changes, but still got good prediction results in the ethene oligomerization reaction. From our point of view, the λ item might be negligible in low-carbon-number component reactions, but it will become increasingly important as the reactant chain-length grows. Moreover, the adsorption equilibrium constants of paraffins with different numbers of side chains were estimated simultaneously. The values of n-paraffins and tri-branched paraffins were larger than those of mono- and di-branched paraffins. Fig. 10 exhibits the fitting results of the experimental and the calculated molar fraction of the components in hydrocracking of n-octane under various reaction conditions. Most of the calculated results are in good agreement with the experimental data. It should be noted that the 19 parameters developed for C8 paraffin hydrocracking have no chain-length-dependent information involved; theoretically the model has potential to be extended to high-carbon-number hydrocarbon hydrocracking, e.g., Fischer–Tropsch wax hydrocracking. However, the universality of the model is still just a reasonable hypothesis; more experimental and calculated results are needed to verify the efficiency.
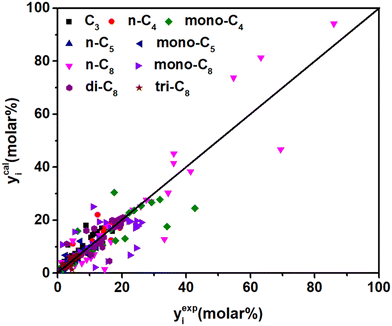 |
| | Fig. 10 Parity plot between the experimental and the calculated molar fraction of the components under different reaction conditions. | |
Fig. 11 and 12 are reactor simulation results based on the developed kinetic model and the estimated parameter values, at reaction temperature of 636 K and 654 K, respectively. The curves in the figures clearly reflect the evolution of the components along the axial direction of the tubular reactor at lower conversion and higher conversion, which correspond to existing experience in hydrocracking and are logically reasonable. The predicted reactor effluent components are in good agreement with the experimental data, especially at higher conversion (see in Table 7). Generally speaking, the feed n-C8 is converted gradually along with the catalyst bed and the products are mainly isomerized C8 at low conversion, but the cracked products increase quickly at high conversion. The flow rate of mono-C8 increases remarkably at the initial stage of the reaction and reaches a maximum in some position of the catalyst bed, and the specific position of the peak would move forward or backward, depending on the conversion of n-C8. The flow rates of di-C8 and tri-C8 components also increase with the catalyst bed. The selectivity to di-C8 is close to that for the mono-C8 at the reactor outlet, but almost 4 times higher than that for tri-C8. di-C8 and tri-C8 contents have maxima at high conversion of the feed, but are less obvious at low conversion. The peaks of the mono-C8, di-C8 and tri-C8 components appear in order, suggesting the PCP-branching from mono-C8 to di-C8 and then to tri-C8 in reality. Light components, including the normal and the branched ones, increase remarkably at the latter stage of the catalyst bed, especially at high conversion of the feed. These phenomena are consistent with the hydrocracking reaction mechanism that the isomerization reaction has a relatively lower activation energy than the β-scission reaction and thus occurs easily. The initial isomers undergo β-scission and crack for light hydrocarbons. The multi-branched hydrocarbons can be cracked easily compared with the mono-branched ones.
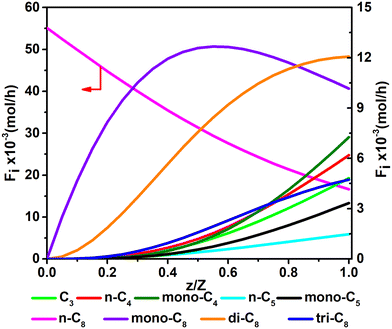 |
| | Fig. 11 The simulated contents of the components against the dimensionless height of the reactor in hydrocracking of n-octane (T = 636 K, P = 5 MPa, H2/octane (v./v.) = 200, LHSV = 3 h−1, n-octane conversion of 71.2%). | |
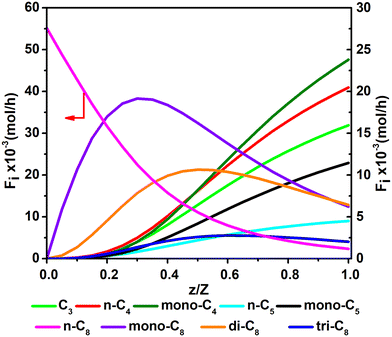 |
| | Fig. 12 The simulated contents of the components against the dimensionless height of the reactor in hydrocracking of n-octane (T = 654 K, P = 5 MPa, H2/octane (v./v.) = 200, LHSV = 3 h−1, n-octane conversion of 95.7%). | |
Table 7 The experimental and simulated results of the reactor effluent components
| Reaction conditionsa |
636 K |
654 K |
| Items |
Experimental |
Simulated |
Experimental |
Simulated |
|
P = 5.0 MPa, H2/oil = 200 (v./v.), LHSV = 3.0 h−1.
|
| Conversion (%) |
83.5 |
71.2 |
96.1 |
95.7 |
| Specific components, mmol h−1 |
| C3 |
6.95 |
4.82 |
14.37 |
15.94 |
|
n-C4 |
7.3 |
6.29 |
17.28 |
20.47 |
| Mono-C4 |
10.54 |
7.46 |
23.4 |
23.8 |
|
n-C5 |
1.8 |
1.48 |
4.05 |
4.5 |
| Mono-C5 |
4.46 |
3.44 |
9.62 |
11.44 |
|
n-C8 |
9.1 |
15.9 |
2.15 |
2.37 |
| Mono-C8 |
11.24 |
10.16 |
5.71 |
6.24 |
| Di-C8 |
11.61 |
12.17 |
5.89 |
6.44 |
| Tri-C8 |
3.63 |
4.73 |
1.84 |
2.03 |
In reality, the quantities of C3 are close to the sum of the C5 components, which obeys the carbenium ion mechanism63,66 in the absence of hydrogenolysis. The flow rate of mono-C5 is always higher than that of n-C5, which can be attributed to the fact that mono-C5 are formed by PCP-branching of n-C5 and β-scission of di-C8 or tri-C8. n-C4 can be produced by β-scission of all C8 isomers, but mono-C4 can only be produced by β-scission of di-C8 and tri-C8 in the reaction network, so the flow rate of mono-C4 is always higher than that of n-C4, reflecting the truth that the multi-branched hydrocarbons can be cracked easily.
5 Conclusions
A set of kinetic data for the hydrocracking of n-octane has been collected over an industrial Ni–W silica–aluminum catalyst. Combining the types of the hydrocracking products and the carbenium ion chemistry, a detailed reaction network of the hydrocracking has been generated by computer algorithms, providing all the key elementary steps needed in the fundamental kinetic modeling. The physicochemical properties of the species are calculated and involved in the reaction network procedure. A computer-aided method has been developed for the analysis of the symmetry properties of the species and their transition states, the calculation of the global symmetry numbers and the calculation of the number of the single events of the elementary steps.
On the basis of the assumption that PCP-branching and β-scission are the rate determining steps and the others are in quasi-equilibrium, the fundamental kinetic equations are derived based on the single event kinetic concept. Considering the challenges in the detailed analysis of a complex mixture, e.g., the position of the side chains in the linear high-carbon-number paraffin mixture, a re-lump method and rate equations have been provided to extend the practical application of the models. Totally, 19 independent parameters are confirmed and estimated based on the experimental data. The genetic algorithm and the Marquardt algorithm are combined to make sure that a global minimum of the objective function is obtained. Most of the calculated data are in good agreement with the experimental data. The kinetic model and the estimated parameters were used to simulate the hydrocracking at different feed conversions. The predicted evolutions of the species along the catalyst bed are consistent with the commonly observed phenomena in hydrocracking, e.g., isomerization occurs before cracking, multi-branched components can be cracked easier than the linear and mono-branched components, and isomerization is dominant at low conversion but cracking is dominant at high conversion. The computer-aided modeling methods could be extended to long-chain paraffin hydrocracking, such as Fischer–Tropsch wax hydrocracking, and are useful in reaction condition optimization and reactor simulation.
Nomenclature
|
Ã
compPCP/cr
| Composite single event frequency factor for PCP-branching or β-scission, h−1 |
|
C
Pi
| Concentration of paraffin i, mol gcat.−1 |
|
C
Oij
| Concentration of Oij, mol gcat.−1 |
|
C
H+
| Concentration of proton, mol gcat.−1 |
|
C
R+
| Concentration of R+, mol gcat.−1 |
|
C
t
| Total concentration of acid active sites, mol gcat.−1 |
|
C
sat
| Saturation concentration in the zeolite pore, mol gcat.−1 |
|
E
0,PCP/cr
| Intrinsic activation energy for PCP-branching or β-scission, kJ mol−1 |
|
F
i
| Molar flow of component i, mol h−1 |
|
g
ij
| The element in ith row and jth column in matrix G |
| ΔHgasf(i) | Heat of formation of species i in the gas phase, kJ mol−1 |
| ΔHsurff(i) | Heat of formation of species i on the catalyst surface, kJ mol−1 |
| ΔHsorp(i) | Heat of sorption of species i from gas phase to the adsorbed phase, kJ mol−1 |
|
K
DH
| Dehydrogenation equilibrium constant, MPa |
|
K
pr
| Protonation equilibrium constant, gcat. mol−1 |
|
K
L,n
| Sorption equilibrium constant of n-alkanes, MPa−1 |
|
K
L,mono
| Sorption equilibrium constant of the mono-branched alkane lump, MPa−1 |
|
K
L,di
| Sorption equilibrium constant of the di-branched alkane lump, MPa−1 |
|
K
L,tri
| Sorption equilibrium constant of the tri-branched alkane lump, MPa−1 |
|
m
ij
| The element in ith row and jth column in matrix M |
|
N
p
| The carbon chain length of the product carbenium ion |
|
N
r
| The carbon chain length of the reactant carbenium ion |
|
N
t
| Total number of elemental steps that occur from lump g |
|
p
g
| Partial pressure of lumped g, MPa |
|
p
H2
| Partial pressure of hydrogen, MPa |
|
q(m) | Heat of stabilization of an m type of carbenium ion, from the adsorbed phase to the surface, kJ mol−1 |
| Δq(m) | Relative heat of stabilization of a proton with respect to an m type of carbenium ion, kJ mol−1 |
|
R
| Ideal gas constant, 8.314 J mol−1 K−1 |
|
r
PCP/cr
| Reaction rate for PCP-branching or β-scission, mol gcat.−1 h−1 |
| ΔŜpr | Intrinsic entropy of protonation, J mol−1 K−1 |
|
T
| Temperature, K |
|
X
| The number of isomerized olefins by deprotonation of a carbenium ion |
|
y
i,g
| Equilibrium mole fraction of ith alkane in lump g, dimensionless |
|
z
| Axial length along the bed of the catalyst (m) |
Symbol
| C3 | Propane |
|
n-C4 |
n-Butane |
|
n-C5 |
n-Pentane |
|
n-C8 |
n-Octane |
| mono-C4 | iso-Butane |
| mono-C5 | iso-Pentane |
| mono-C8 | Monomethyl-heptane |
| di-C8 | Dimethyl-hexane |
| tri-C8 | Trimethyl-pentane |
Greek
|
α
PCP/cr
| Transfer factor of PCP-branching or β-scission, dimensionless |
|
λ
| Chain length factor, kJ mol−1 |
|
Ω
| Reactor cross-sectional area, m2 |
|
σ
i
gl
| Global symmetry number of species i, dimensionless |
|
ρ
B
| Density of catalyst bulk, gcat m−3 |
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 21908234) and the National Natural Science Foundation of China (No. 22025804). The authors are also grateful to the experimental data support from Lei Jia.
References
- T. Li, L. Zhang, Z. Tao, C. Hu, C. Zhao, F. Yi, X. Gao, X. Wen, Y. Yang and Y. Li, Fuel, 2020, 279 Search PubMed.
- U. Ghosh, K. Kulkarni, A. D. Kulkarni and P. L. Chaudhari, Chem. Process Eng. Res., 2015, 34, 51–55 Search PubMed.
- M.-g. Seo, D.-W. Lee, K.-Y. Lee and D. J. Moon, Fuel, 2015, 143, 63–71 CrossRef CAS.
- Y. Liu, K. Murata and K. Sakanishi, Fuel, 2011, 90, 3056–3065 CrossRef CAS.
- S. Cui, G. Wang, Y. Yang and B. Liu, Fuel, 2018, 225, 10–17 CrossRef CAS.
- B. E. Browning, I. Pitault, F. Couenne and M. Tayakout-Fayolle, Ind. Eng. Chem. Res., 2018, 57, 16579–16592 CrossRef CAS.
- D. Leckel and M. Liwanga-Ehumbu, Energy Fuels, 2006, 20, 2330–2336 CrossRef CAS.
- D. Leckel, Energy Fuels, 2005, 19, 1795–1803 CrossRef CAS.
- V. Calemma, S. Peratello, F. Stroppa, R. Giardino and C. Perego, Ind. Eng. Chem. Res., 2004, 43, 934–940 CrossRef CAS.
- T. Zhang, C. Leyva and G. F. Froment, Ind. Eng. Chem. Res., 2015, 54, 858–868 CrossRef CAS.
- S. Sánchez, M. A. Rodríguez and J. Ancheyta, Ind. Eng. Chem. Res., 2005, 44, 9409–9413 CrossRef.
- L. Pellegrini, S. Locatelli, S. Rasella, S. Bonomi and V. Calemma, Chem. Eng. Sci., 2004, 59, 4781–4787 CrossRef CAS.
- M. Mitsios, D. Guillaume, P. Galtier and D. Schweich, Ind. Eng. Chem. Res., 2009, 48, 3284–3292 CrossRef CAS.
- G. G. Martens, J. W. Thybaut and G. B. Marin, Ind. Eng. Chem. Res., 2001, 40, 1832–1844 CrossRef CAS.
- G. G. Martens, G. B. Marin, J. A. Martens, P. A. Jacobs and G. V. Baron, J. Catal., 2000, 195, 253–267 CrossRef CAS.
- H. Kumar and G. F. Froment, Ind. Eng. Chem. Res., 2007, 46, 4075–4090 CrossRef CAS.
- H. Kumar and G. F. Froment, Ind. Eng. Chem. Res., 2007, 46, 5881–5897 CrossRef CAS.
- J. Ancheyta, S. Sánchez and M. A. Rodríguez, Catal. Today, 2005, 109, 76–92 CrossRef CAS.
- D. O. L. Pereira, J. J. Verstraete and M. Kolb, Sci. China: Chem., 2013, 56, 1608–1622 CrossRef.
- M. Neurock, C. Libanati, A. Nigam and M. T. Klein, Chem. Eng. Sci., 1990, 45, 2083–2088 CrossRef CAS.
- L. Ye, J. Liu, B. Xing, X. Qin, W. Yu, J. Xie, L. Hou, H. Wang, Y. Ji and D. Lu, Chem. Eng. Sci., 2021, 246 Search PubMed.
- R. J. Quann and S. B. Jaffa, Ind. Eng. Chem. Res., 1992, 31, 2483–2497 CrossRef CAS.
- S. B. Jaffe, H. Freund and W. N. Olmstead, Ind. Eng. Chem. Res., 2005, 44, 9840–9852 CrossRef CAS.
- D. K. Liguras and D. T. Allen, Ind. Eng. Chem. Res., 1989, 28, 674–683 CrossRef CAS.
- J. W. Thybaut, I. R. Choudhury, J. F. Denayer, G. V. Baron, P. A. Jacobs, J. A. Martens and G. B. Marin, Top. Catal., 2009, 52, 1251–1260 CrossRef CAS.
- K. Surla, D. Guillaume, J. J. Verstraete and P. Galtier, Oil Gas Sci. Technol., 2011, 66, 343–365 CrossRef CAS.
- J. C. Chavarría-Hernández, J. Ramírez and M. A. Baltanás, Catal. Today, 2008, 130, 455–461 CrossRef.
- J. C. Chavarria-Hernandez and J. Ramirez, Ind. Eng. Chem. Res., 2009, 48, 1203–1207 CrossRef CAS.
- M. Mitsios, D. Guillaume, P. Galtier and D. Schweich, Ind. Eng. Chem. Res., 2009, 48, 3284–3292 CrossRef CAS.
- I. R. Choudhury, K. Hayasaka, J. W. Thybaut, C. S. Laxmi Narasimhan, J. F. Denayer, J. A. Martens and G. B. Marin, J. Catal., 2012, 290, 165–176 CrossRef CAS.
- B. Browning, P. Afanasiev, I. Pitault, F. Couenne and M. Tayakout-Fayolle, Chem. Eng. J., 2016, 284, 270–284 CrossRef CAS.
- M. A. Baltanas, K. K. V. Raemdonck, G. F. Froment and S. R. Moheda, Ind. Eng. Chem. Res., 1989, 28, 899–910 CrossRef CAS.
-
E. Vynckier and G. F. Froment, Kinetic & Thermodynamic Lumping of Multicomponent Mixtures, 1991, vol. 12, pp. 131–161 Search PubMed.
- S. Standl, M. Tonigold and O. Hinrichsen, Ind. Eng. Chem. Res., 2017, 56, 13096–13108 CrossRef CAS.
- J. W. Thybauta, G. B. Marin, G. V. Baron, P. A. Jacobs and J. A. Martens, J. Catal., 2001, 202, 324–339 CrossRef.
- M. A. Baltanas, K. K. V. Raemdonck, G. F. Froment and S. R. Mohedad, Ind. Eng. Chem. Res., 1989, 28, 899–910 CrossRef CAS.
- F. Wu, E. Vynckier and G. F. Froment, Ind. Eng. Chem. Res., 1993, 32, 2997–3005 CrossRef CAS.
- J.-M. Schweitzer, P. Galtier and D. Schweich, Chem. Eng. Sci., 1999, 54, 2441–2452 CrossRef CAS.
- J. C. Chavarría, J. Ramírez, H. González and M. A. Baltanas, Catal. Today, 2004, 98, 235–242 CrossRef.
- D. Guillaume, K. Surla and P. Galtier, Chem. Eng. Sci., 2003, 58, 4861–4869 CrossRef CAS.
- K. Surla, H. Vleeming, D. Guillaume and P. Galtier, Chem. Eng. Sci., 2004, 59, 4773–4779 CrossRef CAS.
- G. C. Bond, J. Calhoun and A. D. Hooper, J. Chem. Soc., Faraday Trans., 1996, 92, 5117–5128 RSC.
- G. C. Bond, J. Catal., 1989, 115, 286–288 CrossRef CAS.
- R. de Haan, G. Joorst, E. Mokoena and C. P. Nicolaides, Appl. Catal., A, 2007, 327, 247–254 CrossRef CAS.
- C. Gambaro, V. Calemma, D. Molinari and J. Denayer, AIChE J., 2011, 57, 711–723 CrossRef CAS.
- V. Calemma, C. Gambaro, W. O. Parker, R. Carbone, R. Giardino and P. Scorletti, Catal. Today, 2010, 149, 40–46 CrossRef CAS.
- V. Calemma and C. Gambaro, ACS Symp. Ser., 2011, 1084, 239–253 CrossRef CAS.
- C. Gambaro, V. Calemma, D. Molinari and J. Denayer, AIChE J., 2011, 57, 711–723 CrossRef CAS.
- D. Guillaume, Ind. Eng. Chem. Res., 2006, 45, 4554–4557 CrossRef CAS.
- J. Planelles, J. Sánchez-Marin, F. Tomás and A. Corma, J. Chem. Soc., 1985, 333–340 CAS.
- G. F. Froment, Rev. Chem. Eng., 2013, 29, 385–412 CAS.
-
S. W. Benson, Thermochemical Kinetics, Wiley-Interscience, New York, 3rd edn, 1976, pp. 56–60 Search PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- J. Wang, W. Zhao, K. Song, H. Xiang, L. Zhou, Y. Yang and Y. Li, Chin. J. Chem. Eng., 2022, 41, 342–349 CrossRef.
- J. M. Martinis and G. F. Froment, Ind. Eng. Chem. Res., 2006, 45, 954–967 CrossRef CAS.
- C. Muller, G. Scacchi and G. M. Come, Comput. Chem., 1991, 15, 17–27 CrossRef CAS.
- G. Ercolani, C. Piguet, M. Borkovec and J. Hamacek, J. Phys. Chem. B, 2007, 111, 12195–12203 CrossRef CAS.
- V. E. Golender, V. V. Drboglav and A. B. Rosenblit, J. Chem. Inf. Model., 1981, 21, 196–204 CrossRef CAS.
- M. Shi, H. Wen and H. Jiang, J. East China Univ. Sci. Technol., 2011, 04, 396–403 Search PubMed.
- G. G. Martens and G. F. Froment, Stud. Surf. Sci. Catal., 1999, 122, 333–340 CrossRef CAS.
- R. K. Reddy and J. B. Joshi, Particuology, 2010, 8, 37–43 CrossRef CAS.
- S. O. Rastegar and T. Gu, J. Chromatogr. A, 2017, 1490, 133–137 CrossRef CAS PubMed.
- I. Rossetti, C. Gambaro and V. Calemma, Chem. Eng. J., 2009, 154, 295–301 CrossRef CAS.
- L. Zhou, G. F. Froment, Y. Yang and Y. Li, AIChE J., 2016, 62, 1668–1682 CrossRef CAS.
- F. Jin, Y. Fan, M. Yuan, F. Min, G. Wu, Y. Ding and G. F. Froment, Catal. Today, 2018, 316, 129–141 CrossRef CAS.
- F. Regali, M. Boutonnet and S. Järås, Catal. Today, 2013, 214, 12–18 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *b,
Yong
Yang
*b,
Yong
Yang
 abc and
Yongwang
Li
abc
abc and
Yongwang
Li
abc
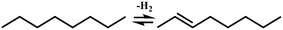
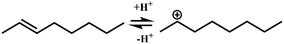



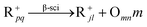

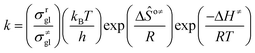
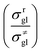 is called the number of single events, viz. ne, and is relevant to the structures of the reactants and the activated complex. ΔŜo≠ represents the intrinsic entropy change upon transformation of the reactant into the activated complex.
is called the number of single events, viz. ne, and is relevant to the structures of the reactants and the activated complex. ΔŜo≠ represents the intrinsic entropy change upon transformation of the reactant into the activated complex. ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) in eqn (2) is defined as the single event rate coefficient, and according to the Arrhenius equation, Ã in eqn (3) is called the single event frequency factor. The rate coefficient is regarded as the product of the single event rate coefficient
in eqn (2) is defined as the single event rate coefficient, and according to the Arrhenius equation, Ã in eqn (3) is called the single event frequency factor. The rate coefficient is regarded as the product of the single event rate coefficient ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and the structure related parameter ne.
and the structure related parameter ne.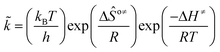
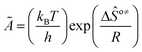
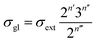
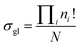
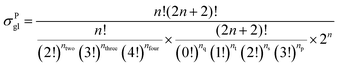
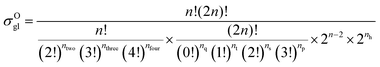
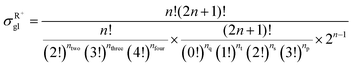
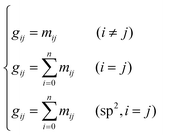

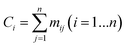
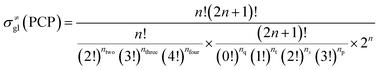
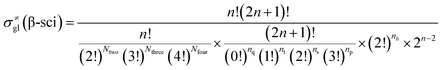
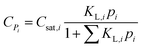
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) pr is called the single event protonation equilibrium constant and defined in eqn (18).
pr is called the single event protonation equilibrium constant and defined in eqn (18). ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) pr is independent of the rotational entropy change and only related to the non-structure-affected intrinsic entropy change ΔŜpr and the reaction enthalpy of the step ΔHsurfpr.
pr is independent of the rotational entropy change and only related to the non-structure-affected intrinsic entropy change ΔŜpr and the reaction enthalpy of the step ΔHsurfpr.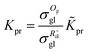
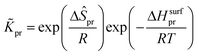
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) PCP/crCR+ik
PCP/crCR+ik