Open Access Article
Open Access ArticleDesigning negative feedback loops in enzymatic coacervate droplets†
Nisha
Modi
 a,
Siwei
Chen
a,
Siwei
Chen
 a,
Imelda N. A.
Adjei
b,
Briana L.
Franco
a,
Kyle J. M.
Bishop
a,
Imelda N. A.
Adjei
b,
Briana L.
Franco
a,
Kyle J. M.
Bishop
 *a and
Allie C.
Obermeyer
*a and
Allie C.
Obermeyer
 *a
*a
aDepartment of Chemical Engineering, Columbia University, New York, USA. E-mail: kyle.bishop@columbia.edu; aco2134@columbia.edu
bDepartment of Biomedical Engineering, Columbia University, New York, USA
First published on 19th April 2023
Abstract
Membraneless organelles within the living cell use phase separation of biomolecules coupled with enzymatic reactions to regulate cellular processes. The diverse functions of these biomolecular condensates motivate the pursuit of simpler in vitro models that exhibit primitive forms of self-regulation based on internal feedback mechanisms. Here, we investigate one such model based on complex coacervation of the enzyme catalase with an oppositely charge polyelectrolyte DEAE-dextran to form pH-responsive catalytic droplets. Upon addition of hydrogen peroxide “fuel”, enzyme activity localized within the droplets causes a rapid increase in the pH. Under appropriate conditions, this reaction-induced pH change triggers coacervate dissolution owing to its pH-responsive phase behavior. Notably, this destabilizing effect of the enzymatic reaction on phase separation depends on droplet size owing to the diffusive delivery and removal of reaction components. Reaction-diffusion models informed by the experimental data show that larger drops support larger changes in the local pH thereby enhancing their dissolution relative to smaller droplets. Together, these results provide a basis for achieving droplet size control based on negative feedback between pH-dependent phase separation and pH-changing enzymatic reactions.
Introduction
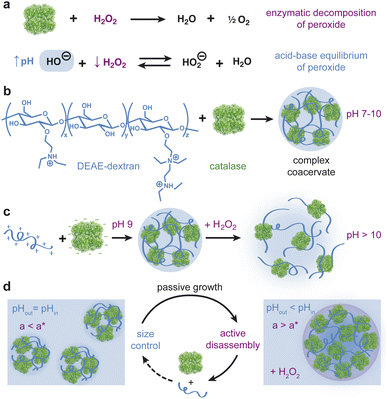
Living cells use phase separation of biopolymer mixtures to form membraneless organelles (MLOs) that regulate biochemical reactions and cellular processes.1–3 The formation and function of MLOs and other condensates can be understood—to a large extent—using concepts of equilibrium thermodynamics. The existence, stability, and composition of these condensed phases depend on molecular interactions (e.g., electrostatic, hydrophobic) and thermodynamic variables (e.g., temperature, pH, ionic strength) as described by equilibrium phase diagrams.4,5 The molecular environments of each phase enable the selective enrichment or exclusion of chemical species, offering enhanced control over reaction rates—for example, by concentrating enzymes and their substrates.6,7Coupling between phase separation and chemical reaction(s) provides a basis for feedback control whereby reaction products promote or inhibit the formation of biomolecular condensates which, in turn, accelerate or decelerate the reaction rate.8,9 For example, RNA condensation serves to accelerate RNA transcription by enriching critical factors within transcriptional condensates.10–14 At low concentrations, transcription of RNA promotes condensation creating positive feedback between the two mutually enhancing processes. By contrast, reentrant phase behavior at high RNA concentration leads to negative feedback whereby transcription inhibits condensation.15 These feedback mechanisms enable homeostatic regulation of transcription and other intracellular processes.1,2 Moreover, through coupling with biochemical reactions, cells can gain dynamic control over condensate properties such as size,16–18 number,16 and position,19 which are difficult to control at equilibrium.
Understanding the function of MLOs in vivo benefits from simpler in vitro models that combine biomolecular condensation and enzymatic reaction(s) to create elements of feedback control. Complex coacervates based on phase separation of oppositely-charged polyelectrolytes provide a useful model for MLOs as they readily incorporate enzymes and other reaction components within a responsive dynamic environment.20–22 Coacervate droplets respond to changes in temperature,23 ionic strength, and pH24–26 among other factors that alter the molecular interactions mediating phase separation. In addition to these thermodynamic variables, active coacervates respond also to chemically-fueled reactions that modify the charge27 or concentration of the participating biomolecules.28–30 Active coacervate droplets have been shown to grow due to positive feedback whereby reactions promoted within the drop produce material components that feed drop growth.30 Such positive feedback between chemical production and coacervate formation can lead to transient non-spherical shapes among populations of growing droplets.28
Active droplets exhibiting negative feedback between coacervate formation and reaction-induced dissolution provide a basis for controlling droplet size (Fig. 1).17,31 Theoretical models of active size control have shown how enzymes enriched in the condensed phase can drive reactions therein that destabilize the coacervate—for example, by modifying phase separating components. Importantly, this type of reaction-induced destabilization depends on droplet size owing to the diffusive delivery and removal of participating components. Droplets evolve in time to a stable size at which the rates of droplet growth and dissolution are balanced. Recent experimental models based on pH-responsive coacervates of glucose oxidase and an oppositely charged polyelectrolyte have achieved some of the key requirements necessary for controlling droplet size.32 The enzyme catalyzes the production of gluconic acid which lowers the pH causing dissolution of the coacervate droplets. However, the slow rate of reaction compared to diffusion within micron-scale droplets prohibits the type of size-dependent inhibition needed to close the feedback loop and regulate droplet size.
Here, we present an active, pH-responsive coacervate based on catalase and the weak polycation DEAE-dextran that enables two-way coupling between phase separation and enzymatic activity (Fig. 1). The diffusion-limited enzyme catalyzes the rapid decomposition of hydrogen peroxide “fuel” causing a concomitant increase in the pH under mild basic conditions. We quantify and explain the magnitude and rate of the reaction-induced pH increase as a function of the initial pH, peroxide concentration, and enzyme loading. We further demonstrate that catalase and DEAE dextran form pH-dependent coacervate droplets that dissolve in response to reaction-induced pH increases initiated by the addition of hydrogen peroxide fuel. In addition to the inhibitory influence of reaction on coacervation, we show that coacervate size can alter the rate of fuel consumption due to diffusion limitations in droplets larger than a characteristic size. Using reaction-diffusion models informed by experimental data, we discuss how this and related systems could enable the formation of monodisperse coacervate droplets of tunable size. Such coacervate systems could potentially emulate active size control in biological condensates as seen in centrosomes16 and membrane receptors.33
Results and discussion
Our design of active coacervates capable of negative feedback control relies on the coupling between reaction-induced pH change and pH-responsive phase separation. In this context, a suitable reaction should induce a pH change that is (i) sufficiently large (i.e., >1 pH unit) to alter coacervate phase behavior, (ii) locally enhanced within coacervate droplets to inhibit their growth, and (iii) suitably fast to compete with diffusive exchange with the surrounding solution. The enzymatic decomposition of hydrogen peroxide by catalase satisfies all of these criteria. While the effect of pH on catalase activity is well established,34 the ability of catalase to modify the solution pH is less widely appreciated. We therefore begin by characterizing the magnitude and rate of pH increase induced by this reaction. We then consider the incorporation of the enzyme within coacervate droplets and characterize the two-way coupling between phase separation and enzymatic reaction.Enzymatic decomposition of H2O2 causes rapid pH increase
The pH increase induced by the decomposition of H2O2 is predicted by a kinetic model that accounts for the acid-base equilibrium of H2O2 and its enzymatic decomposition by catalase (Fig. 2a). Hydrogen peroxide is a weak acid that dissociates to form HO2− anion under basic conditions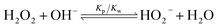 | (1) |
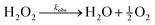 | (2) |
 | ||
| Fig. 2 Reaction-induced pH increase ΔpH due to the enzymatic decomposition of H2O2. (a) Measured pH increase (markers) as a function of the initial pH for an initial H2O2 concentration of 100 mM. The shaded region denotes ±1 standard deviation above/below the mean of three replicates. The curves show the predictions of the equilibrium model with (solid) and without (dashed) 8 μM Tris buffer present in the experiments (see ESI Section 1†). (b) Measured pH increase (markers) as a function of the initial H2O2 concentration for an initial pH of 9. The solid curve shows the prediction of the equilibrium model. (c) Measured pH as a function of time upon addition of 100 mM H2O2 to an aqueous solution of 0.235 mg mL−1 catalase at pH 9 (green markers). The time scale t* is defined graphically as the time required to increase from the initial pH0 (dotted line) to final pH∞ (dashed line) at the initial rate. A control experiment shows no pH increase in the absence of catalase (gray markers) (see ESI Section 1.5†). | ||
To validate these model predictions, we measure the enzyme-catalyzed pH change for a series of 100 mM peroxide solutions at different initial pH values (Fig. 2a). The initial value pH0 is measured before the addition of a small volume of buffered catalase solution. The pH is then monitored over time until it reaches an asymptotic value pH∞. The pH change for the assay, ΔpHassay = pH∞ − pH0, is compared to that of a control reaction ΔpHcontrol wherein a buffered solution without catalase is added to the H2O2 solution. Near neutral pH, the control experiments without catalase show non-zero pH change due to the presence of 8 μM Tris buffer. The reported pH change in Fig. 2a represents the difference between that of the assay and the control: ΔpH = ΔpHassay − ΔpHcontrol. Comparing experimental measurements to model predictions, we find that the equilibrium model based on reaction (1) agrees well with the measured pH increase at basic conditions (pH0 > 8) but fails at lower pH values (cf. dashed curve and solid markers in Fig. 2a). These discrepancies are largely reconciled by augmenting the model to include the effects of buffer present in the catalase solution (Fig. 2a, bold curve and ESI Section 1.4†).
Under basic conditions (pH0 = 9), the measured pH change increases monotonically with the initial peroxide concentration in close agreement with model predictions (Fig. 2b). For consistency, the reported pH change is given by ΔpH = ΔpHassay − ΔpHcontrol as above; however, the control experiment without catalase shows only a negligible pH change due to the small amount of added buffer. These results indicate that large pH changes (>1 unit) require relatively high peroxide concentrations (>50 mM). At such concentrations, the rapid catalytic decomposition of H2O2 produces many bubbles due to the low solubility of oxygen in water. As discussed below, the formation of bubbles complicates the imaging of active coacervates enriched with catalase. Further experiments make use of 100 mM peroxide solutions at pH 9 to create significant pH changes despite undesired bubble formation.
The characteristic time required for the reaction-induced pH change is controlled by the enzyme kinetics (Fig. 2c). To facilitate comparison between kinetic assays, we define a characteristic time for pH change t* using the geometric construction shown in Fig. 2c. Assuming that acid-base equilibration is fast, the time required for the pH change is controlled by the enzymatic consumption of peroxide (ESI Section 1.5†). For the 0.22 mg mL−1 catalase concentration used here, the t* value of 5.5 s agrees with expectations based on kinetic parameters obtained directly by measuring the rate of H2O2 consumption (ESI Section 4.2 and Table SI†).
Phase separation of catalase & DEAE-dextran is pH dependent
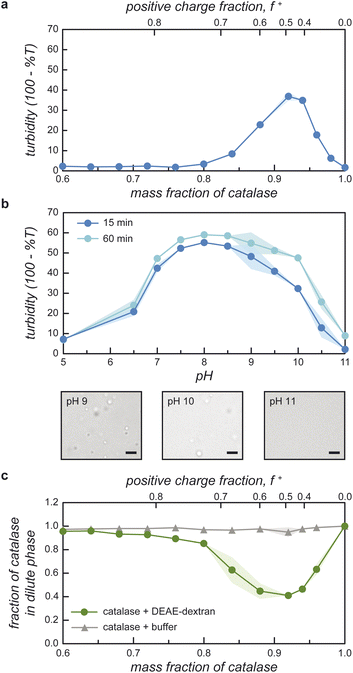
Guided by the constraints of the enzymatic reaction, we now seek to design a pH-responsive coacervate that forms liquid droplets at pH 9 but dissolves at higher pH. The isoelectric point of catalase is pI = 5.3, as estimated using the Henderson–Hasselbalch equation applied to charged amino acid residues and in agreement with previously reported values.34 At the conditions of interest (pH = 9 to 11 > pI), catalase is negatively charged and forms the anionic component of a complex coacervate. To make the coacervate pH-responsive, we require a weak polycation with a pKa ≈ 9 such that reaction-induced pH changes cause a significant reduction in polycation charge and thereby the electrostatic interactions driving phase separation. Based on preliminary experiments with different weak polycations—including poly(2-(dimethylamino)ethyl methacrylate), poly(allylamine hydrochloride), and poly-L-lysine—we identify diethylaminoethyl (DEAE)-dextran as the most promising candidate. The presence of strong tertiary amines with an apparent pKa of 8.8 suggests that DEAE-dextran will exhibit significant charge reduction upon increasing the pH from 9 to 10.32 Moreover, DEAE-dextran is soluble over the desired pH range (9 to 11) and shows a higher tendency to form liquid droplets with catalase as compared to other polycations tested, which formed solid-like precipitates.Turbidity measurements indicate that catalase phase separates with DEAE-dextran to form complex coacervates at mixing ratios close to charge neutrality (Fig. 3a). Turbidity is used as an indicator of phase separation, which is subsequently confirmed by optical microscopy. To detect phase separation at pH 9, we measure the turbidity of catalase and DEAE-dextran mixtures as a function of mixing ratio with the total macromolecule concentration kept constant. The mixing ratio is expressed both as the mass fraction of catalase x and as the positive charge fraction f+ defined as
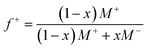 | (3) |
Phase separation of catalase with DEAE-dextran is pH-dependent (Fig. 3b). To verify this, we measure the turbidity as a function of pH for a constant mixing ratio corresponding to 0.94 mass fraction of catalase. The turbidity shows a broad peak centered at pH 8–9 and decreases rapidly as the pH increases to 11 (Fig. 3b). In these experiments, the mixing ratio is selected to maximize the difference in turbidity between pH 9 and 10.5 and thereby facilitate reaction-induced inhibition of phase separation. The observed pH dependence is consistent with expectations based on macromolecular charge imbalance. The positive charge fraction at 0.94 mass fraction catalase is predicted to decrease from 0.4 at pH 9 to 0.1 at pH 10 with further reduction at higher pH. The pH-responsive phase behavior is further confirmed by optical microscopy, which shows that micron-scale coacervate droplets form at pH 9 but not at pH 11 (Fig. 3b).
Catalase is significantly enriched within the coacervate phase at mixing ratios approaching charge neutrality (Fig. 3c). We quantify enzyme partitioning between the two phases using absorption spectroscopy to measure the concentration of fluorescently labeled catalase in the dilute phase. For a total macromolecule concentration of 0.5 mg mL−1 at pH 9, the fraction of catalase remaining in the dilute phase reaches a minimum value of 0.41 at mixing ratios close to charge neutrality. The fraction of catalase in the condensed phase is therefore maximal at this mixing ratio, which corresponds closely to that of the turbidity maximum (cf.Fig. 3a and c). Together, the agreement between the turbidity measurements and these concentration measurements supports the hypothesis that catalase is incorporated within the coacervate phase as reported previously for other protein-polymer coacervates.37–39
Importantly, the local enzyme concentration within the coacervate droplets at 0.94 mass fraction of catalase is estimated to be ∼103 times higher than in the surrounding solution. This order-of-magnitude estimate assumes a macromolecule concentration of ∼120 mg mL−1 in the condensed phase for a two-phase system with a total macromolecule concentration of 0.25 mg mL−1.40,41 This concentration estimate is based on the measured fraction of catalase that remains in the supernatant (0.47, Fig. 3c) and the assumption that the volume fraction of the condensed phase is ∼0.001.39–41 The rate of enzyme-catalyzed peroxide decomposition should be similarly enhanced assuming that the rate is proportional to the local enzyme concentration and that the enzyme activity is not significantly altered by the coacervate environment.30,42
H2O2 fuel destabilizes catalase/DEAE-dextran coacervates
Coacervate droplets formed at pH 9 dissolve rapidly upon addition of H2O2 fuel due to the reaction-induced pH increase catalyzed by the enzyme (Fig. 4a). To demonstrate this inhibitory influence of reaction on coacervation, we mix catalase and DEAE-dextran at pH 9 with a catalase mass fraction of 0.94 to form stable coacervate droplets as evidenced by turbidity analysis (Fig. 4b, − buffer). Upon addition of 100 mM H2O2, we observe a rapid increase in pH and a simultaneous decrease in turbidity, which is evident by eye as a transition from cloudy to transparent, bubbly solutions (Fig. 4c). When the same experiment is conducted in the presence of 100 mM Tris buffer, the pH of the coacervate solution remains unchanged as does the measured turbidity (Fig. 4b and d, + buffer). These results suggest that coacervate dissolution is caused by the pH increase induced by the enzymatic reaction. A similar effect was reported previously for a pH-responsive, protein-polymer coacervate based on glucose oxidase.32 However, this type of reaction-induced destabilization alone does not establish a closed feedback loop between the enzymatic reaction and coacervate formation. To close this loop, it remains to be demonstrated that the enrichment of the enzyme within coacervate droplets can create and potentially sustain local conditions that inhibit coacervate stability. In the present context, the reaction should create significant pH differences between the droplet interior and the surrounding solution despite the diffusion of species between the two phases. We attempted to monitor pH differences between the supernatant and coacervate phase with pH indicator dyes, but the presence of the enzyme and/or polycation interfered with the absorption spectrum of the dyes and prevented this quantitative comparison (ESI Section 8†).Coacervation slows pH increase due to diffusion limitations
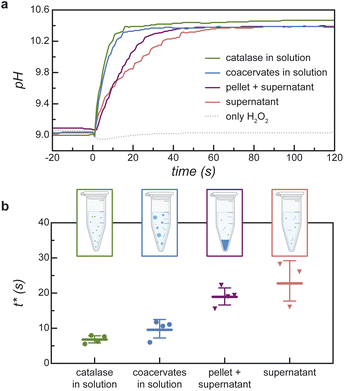
The time scale t* for the chemically fueled pH increase depends on the size of the condensed phase (Fig. 5). To show this, we compare the transient pH increase in catalase/DEAE-dextran mixtures for two limiting cases—that of many micron-scale coacervate droplets and a single macro-scale coacervate pellet prepared by centrifugation (ESI Section 6†). Importantly, the composition of each mixture is identical; they differ only in the spatial distribution of the condensed phase. Upon addition of 100 mM H2O2, the pH of the coacervate dispersion increases quickly with a characteristic time scale t* = 9.9 ± 2.3 s (Fig. 5a and b; coacervate in solution). By contrast, the pH of the coacervate after centrifugation increases more slowly with t* = 19.1 ± 2.4 s (Fig. 5a and b; pellet + supernatant). For comparison, the transient pH increase for catalase in solution without DEAE-dextran is statistically indistinguishable from that of the coacervate dispersion (Fig. 5a and b; catalase in solution, t* = 6.9 + 1.0 s, effect sizes ESI Fig. S13†). Catalase shows similar activity for H2O2 decomposition when it's incorporated in micron-scale coacervate droplets as when it's dispersed in solution (ESI Table SII and Section 6.4†).These experimental observations are reproduced and explained by a reaction-diffusion model that considers the diffusion of H2O2 into spherical coacervate droplets of radius a and its enzymatic decomposition with a rate constant proportional to the local enzyme concentration (ESI Section 2.1†). The corresponding rates of diffusion and reaction are balanced for a characteristic droplet radius of a* = 3(DH2O2/kinobs)1/2, where DH2O2 is the diffusivity of H2O2 inside the coacervate, and kinobs is the rate constant for H2O2 decomposition therein. Assuming a total macromolecule concentration of 120 mg mL−1 in the condensed phase, the rate constant inside the coacervate is estimated to be kinobs ∼ 300 s−1 based on the observed value kobs = 0.51 s−1 for catalase in solution and the measured fraction of catalase in the dilute phase. Approximating the H2O2 diffusivity by the solution-phase value DH2O2 = 1.4 × 10−9 m2 s−1, the reaction-diffusion length is estimated to be a* ∼ 7 μm. This estimate is highly uncertain as the reaction rate constant and the H2O2 diffusivity inside the coacervate are not measured directly. Regardless of its precise value, droplets larger than this length scale (a ≫ a* ∼ 10 μm) experience diffusion limitations whereby H2O2 fuel does not reach the drop interior but is rather consumed within a boundary layer of thickness a*. Catalase present within the interior of large drops is kinetically inaccessible thereby reducing the apparent rate of peroxide decomposition and the accompanying pH increase (ESI Fig. S3†).
Analysis of the model reveals that the apparent rate constant for peroxide decomposition catalyzed by a dispersion of coacervate droplets is well approximated as
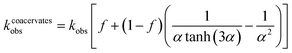 | (4) |
By contrast, for a single large droplet (a ≫ a*), eqn (4) for the apparent rate constant is well approximated as kcoacervateobs ≈ fkobs when α ≫ (1 − f)/f. In this limit, only catalase present in the dilute phase contributes appreciably to peroxide decomposition; the vast majority of catalase present in the condensed phase is kinetically inaccessible to the H2O2 fuel. Consistent with this prediction, the measured time scales t* for ‘pellet + supernatant’ and for ‘supernatant’ alone are equal within the experimental uncertainty (Fig. 5b and ESI Section 6.4†). Moreover, the ratio between t* for ‘coacervates in solution’ and for ‘pellet + supernatant’ is 0.31 ± 0.082, which is similar to the fraction of catalase in the dilute phase f = 0.47 measured independently (cf.Fig. 3c and 5b). In addition to experimental uncertainty, the discrepancy between these quantities may be caused by errors in the measured catalase concentration due to incomplete separation of the labelled enzyme from the unreacted fluorophore (ESI Section 6.4†).
Together, the results of Fig. 5 suggest that the reaction-diffusion length a* is bounded between the sizes of the micron-scale coacervate droplets and the macro-scale coacervate pellet: 1 μm ≪ a* ≪ 1 mm. To narrow these bounds, we measure additional t* values for coacervate solutions aged for different times to promote the coarsening of larger drops (ESI Section 7†). Coacervate solutions stirred for 4 h to promote coarsening lead to a slower pH increase upon addition of H2O2 as compared to otherwise identical solutions aged without stirring for the same time: t* = 8.1 ± 2.0 s vs. 4.7 ± 1.6 s for stirred and unstirred solutions, respectively. This difference is attributed to the presence of larger droplet sizes in the stirred solutions as evidenced by optical microscopy; however, significant polydispersity in the size distribution prevented quantitative analysis. Subsequent centrifugation of the stirred coacervate leads to a further increase in t* to 14.2 ± 2.0 s. These results remain consistent with the above order of magnitude estimate for the reaction-diffusion length, a* ∼ 10 μm; however, the precise value remains uncertain.
According to the reaction-diffusion model, large coacervate droplets (a ≫ a*) support reaction-induced pH differences between the droplet interior and the surrounding solution (Fig. 6, ESI Fig. S3†). Peroxide decomposition in the boundary layer near the droplet surface results in the localized production of OH− therein and a transient pH increase throughout the drop interior. Such local pH changes are expected to destabilize coacervate droplets larger than a critical size. By contrast, pH variations within smaller droplets (a ≪ a*) remain spatially uniform due to the peroxide decomposition becoming increasingly reaction limited with decreasing droplet size. For a closed system (as in our experiments), the distinction between large and small droplets does not alter the final outcome: the reaction-induced pH increase causes coacervate dissolution. However, for an open system maintained at constant H2O2 concentration and solution pH, the model suggests that coacervate droplets will grow to a characteristic size of order a*, above which the local pH increase triggers droplet dissolution (ESI Section 2.2 and Fig. S4†).
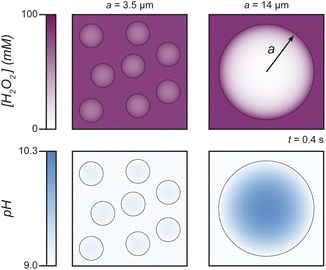 | ||
| Fig. 6 Computed profiles for H2O2 concentration (top) and pH (bottom) in and around small (left) and large (right) coacervate droplets at time t = 0.4 s after addition of H2O2. The parameters and conditions of the reaction-diffusion model are chosen to match those of the experiments in Fig. 5 (see ESI Section 2.1 and Fig. S3† for details). For droplets smaller than the reaction-diffusion length a* = 7 μm, H2O2 diffuses throughout the drop interior before being consumed by the reaction (top, left); the local pH increase within the droplet is limited by diffusive exchange with the surrounding solution (bottom, left). For large drops, peroxide decomposition is localized near the drop interface (top, right), and the local pH rises significantly within the drop interior (bottom, right). | ||
Unfortunately, experiments designed to demonstrate reaction-induced size control were inconclusive due to vigorous bubble formation. Using external feedback control, we fix the solution pH to a constant value by addition of acid to counteract the effects of the enzymatic reaction. However, owing to the steady addition of peroxide fuel, the production of oxygen bubbles creates a rapidly growing foam that sequesters much of the coacervate material, which adsorbs at the gas–liquid interface. As a result, we are unable to maintain the reaction conditions predicted to drive coacervate dissolution and/or growth toward a stable size. Nevertheless, the present experiments on the catalase system provide useful insights in the design of future coacervate materials with activity-induced size control.
General requirements for activity-induced size control
To summarize, the present approach for controlling the size of active coacervate drops relies on the catalytic production of a destabilizing species within the drop interior. The stability of the dense phase must be responsive to this species (here, OH−) such that phase separation occurs only below a threshold concentration. The catalytic production of the destabilizing species should exceed this threshold within large drops, for which the diffusive removal of the species from the drop is slower than its reactive production inside the drop. Based on the reaction-diffusion model (ESI, Section 2†), the maximum stable drop size is proportional to the characteristic length a* over which reaction and diffusion compete: a* = 3(Din/kin)1/2 where Din and kin are the diffusivity of the chemical fuel and the (first order) rate constant for its consumption inside the coacervate drop.Different chemistries with faster or slower reaction kinetics are capable of stabilizing smaller or larger drops. For an enzyme-polymer coacervate based on glucose oxidase,32 the catalytic oxidation of glucose produces gluconolactone, which hydrolyzes to form gluconic acid, thereby lowering the pH and destabilizing the coacervate. Under the reported conditions (pH 7.5), the rate limiting step for the reaction-induced pH change is likely the hydrolysis reaction, which has a reported rate constant of ∼0.05 min−1.43 Assuming a typical diffusivity of 10−5 cm2 s−1, the corresponding reaction-diffusion length is estimated to be a* ∼ 3 mm—considerably larger than the ∼10 μm estimated for the catalase system. Additionally, the reaction-diffusion length depends on the solute diffusivity inside the drop which may be influenced by coacervate density and viscosity as well as the molecular interactions with the solute.
In designing active coacervates, it is beneficial—but not strictly necessary—that the reaction rate inside the drop be much faster that its rate outside of the drop. If the concentration of chemical fuel and destabilizing product are maintained constant outside of the droplet by an effective chemostat, the consumption of fuel outside of the drop should not affect its behavior inside the drop. In practice, however, it is desirable to limit the wasteful consumption of fuel outside of the drop as to reduce the burden on the chemostat. For transient experiments without a chemostat, pseudo-steady conditions within the drop interior can be achieved only when the reaction rate inside the drop is much faster than that outside (ESI, Section 3†). When the destabilizing product diffuses more slowly than the chemical fuel, these experiments may enable transient “sculpting” of large coacervate drops, in which locally destabilizing conditions are achieved for some time before returning to stable conditions at long time (ESI, Section 3†). Such behavior is not observed in the present system where the destabilizing product (OH−) diffuses faster that the fuel (H2O2).
Conclusions
We have shown how two-way coupling between complex coacervation and enzymatic activity can enable negative feedback control in active coacervate droplets. In this approach, an enzyme incorporated within the coacervate catalyzes the production of chemical species that destabilize the condensed phase causing the droplet to dissolve and thereby decelerating the local reaction rate. In particular, we demonstrated that catalase forms pH-responsive coacervate droplets with DEAE-dextran and that catalase activity causes pH changes that destabilize those droplets. Owing to fast enzyme kinetics within the condensed phase, we hypothesize that catalase activity leads to local pH changes in droplets larger than a critical size comparable to the reaction-diffusion length. This hypothesis is supported indirectly by reaction-diffusion models informed by experimental data on the size-dependent activity of enzymatic droplets. Importantly, such negative feedback between enzyme activity and coacervate formation could allow for self-regulation of droplet size; however, this capability has yet to be demonstrated. To realize size control in active coacervate droplets, future studies would benefit from open chemostat systems that maintain constant solution conditions and from fast enzymatic reactions that alter coacervate stability without bubble formation. In the current system, oxygen bubbles present significant challenges in quantifying droplet sizes in situ for nonequilibrium steady-states sustained by delivery of H2O2 and base. Nevertheless, the present experiments and models demonstrate that active coacervates can be rationally designed to enable negative feedback control using quantitative knowledge of their reaction kinetics and phase behavior. Looking forward, the realization of bioinspired materials with internal control mechanisms based on destabilizing activity could be useful in regulating material size, fuel consumption, and the rate of material turnover.Experimental
Materials
Materials were bought and used as received from commercial suppliers. Catalase from bovine liver and diethylaminoethyl-dextran hydrochloride (DEAE-dextran, Mw = 500 kDa) were purchased from Sigma Aldrich. Alexa Fluor™ 488 NHS Ester (succinimidyl ester) was purchased from ThermoFisher Scientific. Cytiva NAP-25 columns were purchased from Fisher Scientific.ΔpH as a function of pH and H2O2 concentration (Fig. 2)
Aqueous solutions of 100 mM H2O2 were adjusted to different pH values (pH0) by addition of concentrated solutions of HCl or NaOH (0.1–1 M). A stock solution of 1 mg mL−1 catalase was prepared by dissolving catalase in 1 mM Tris at pH 7.5 followed by filtration with a 0.2 μm surfactant-free cellulose acetate (SFCA) membrane syringe filter. A fixed volume (164 μL) of the catalase solution was added to 20 mL of the stirred H2O2 solution to achieve a final catalase concentration of 8.1 μg mL−1 for the assay. The final concentration of Tris in the 20 mL reaction solution is 8 μM due to the addition of 164 μL of catalase solution, prepared with 1 mM Tris. The solution pH was measured every 1–3 s using a pH electrode (InLab Pure Pro-ISM) connected to a pH meter (SevenCompact S210) until the pH stabilized (pH∞). Additional control experiments measured the pH change caused by the addition of a 1 mM Tris solution without the enzyme. For each initial pH, the assay and Tris control were performed in triplicate. For Fig. 2b, an aqueous solution of 200 mM H2O2 was initially prepared and adjusted to pH 9 using concentrated solutions of HCl or NaOH. H2O2 solutions at lower concentrations at a common initial pH 9 were prepared by diluting the 200 mM H2O2 solution with water adjusted to pH 9. The addition of enzyme to these H2O2 solutions and subsequent pH measurements were done in a similar fashion as described above.Turbidity analysis as a function of mixing ratio (Fig. 3a)
A 0.5 mg mL−1 catalase solution was prepared by dissolving catalase in 10 mM Tris at pH 9. After dissolution, the pH was readjusted to 9 by addition of concentrated HCl or NaOH solutions followed by filtration with a 0.2 μm SFCA syringe filter. A 0.5 mg mL−1 DEAE-dextran solution was prepared in the same way as the protein. Varying amounts of these solutions were added to 384 well glass bottom plates to a final volume of 50 μL per well. The path length in these turbidity measurements is estimated to be 0.45 cm based on the ratio between the solution volume (50 μL) and the bottom area of each well (10.9 mm2). The total macromolecule concentration was held constant at 0.5 mg mL−1 for each mixing ratio. The catalase mass fraction in the wells ranged from 0 to 1 in increments of 0.04 with each mass fraction prepared in triplicate. Mixing was done by manual pipetting. Absorbance at 600 nm (A600) was measured using a Tecan Infinite M200 Pro plate reader set to 25 °C. Turbidity was calculated using the formula: 1 − T = 1–10−A600 where T is the transmittance at 600 nm.Turbidity analysis as a function of pH (Fig. 3b)
Solutions of 1 mg mL−1 catalase and DEAE-dextran were prepared in 10 mM Tris at pH 8 as described above. The solutions were then diluted to 0.25 mg mL−1 protein or polymer using 10 mM Tris or 5 mM phosphate buffer with final pH adjustment by addition of concentrated HCl or NaOH solutions. The 0.25 mg mL−1 catalase solution at a specified pH was mixed with the 0.25 mg mL−1 DEAE-dextran solution at the same pH at a mass fraction of 0.94 (940 μL catalase solution and 60 μL DEAE-dextran solution) in a cuvette (1 cm path length). Samples at each pH were prepared in triplicate and absorbance at 600 nm was measured 15 min and 1 h after mixing. Microscopy images of the mixtures were taken 15 min after mixing by removing 3.5 μL from the cuvette into uncovered imaging chambers created using press-to-seal silicone isolators on glass slides.Fluorescent labeling of catalase (Fig. 3c)
A 1 mg mL−1 catalase solution was prepared in 50 mM phosphate buffer at pH 7.5 followed by filtration with a 0.2 μm polyethersulfone (PES) filter. Alexa Fluor 488 NHS ester (1 mg mL−1 in DMSO) was added to 40 mL of catalase solution to achieve a final dye concentration of 79 μM corresponding to a molar ratio of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dye to catalase. The pH was readjusted to 7.5 by dropwise addition of concentrated NaOH. The mixture was incubated for 4 h at 4 °C. The fluorescently labeled protein was separated from the unreacted fluorophore and buffer exchanged into 10 mM Tris at pH 9 using NAP-25 columns. The eluted fractions containing fluorescently labelled catalase were filtered again using 0.2 μm PES filters. The concentration of the enzyme was calculated using absorbance measurements at 280 nm and 495 nm using the given formula: A280(only enzyme) = A280(labeled enzyme solution) − 0.11 A495(labeled enzyme solution). This formula calculates the contribution of the unlabeled enzyme to the net absorbance of the labeled enzyme solution at 280 nm. Using the reported relationship between the extinction coefficient of the dye at 280 nm and 495 nm (ε280 nm = 0.11ε495 nm), the absorbance due to the dye at 280 nm is subtracted from the net absorbance of the labeled enzyme solution at 280 nm. The obtained absorbance at 280 nm due to only the enzyme in the labeled enzyme solution was compared to the calibration curve relating the measured absorbance of the unlabeled enzyme at 280 nm to the concentration of catalase. By assuming that all the catalase present in the eluted and purified labeled enzyme solution is associated with the dye, the above procedure was used to estimate the concentration of catalase present in the labeled enzyme solution.
1 dye to catalase. The pH was readjusted to 7.5 by dropwise addition of concentrated NaOH. The mixture was incubated for 4 h at 4 °C. The fluorescently labeled protein was separated from the unreacted fluorophore and buffer exchanged into 10 mM Tris at pH 9 using NAP-25 columns. The eluted fractions containing fluorescently labelled catalase were filtered again using 0.2 μm PES filters. The concentration of the enzyme was calculated using absorbance measurements at 280 nm and 495 nm using the given formula: A280(only enzyme) = A280(labeled enzyme solution) − 0.11 A495(labeled enzyme solution). This formula calculates the contribution of the unlabeled enzyme to the net absorbance of the labeled enzyme solution at 280 nm. Using the reported relationship between the extinction coefficient of the dye at 280 nm and 495 nm (ε280 nm = 0.11ε495 nm), the absorbance due to the dye at 280 nm is subtracted from the net absorbance of the labeled enzyme solution at 280 nm. The obtained absorbance at 280 nm due to only the enzyme in the labeled enzyme solution was compared to the calibration curve relating the measured absorbance of the unlabeled enzyme at 280 nm to the concentration of catalase. By assuming that all the catalase present in the eluted and purified labeled enzyme solution is associated with the dye, the above procedure was used to estimate the concentration of catalase present in the labeled enzyme solution.
Catalase concentration in the dilute phase (Fig. 3c)
The fluorescently labeled catalase solution described above was diluted to a final concentration of 0.5 mg mL−1 catalase using 10 mM Tris at pH 9. A 0.5 mg mL−1 solution of DEAE-dextran in 10 mM Tris at pH 9 was prepared as described above. The pH of both solutions was adjusted to 9 using concentrated solutions of HCl or NaOH. Labeled catalase and DEAE-dextran were mixed at different ratios in 1.5 mL microcentrifuge tubes up to a total volume of 400 μL. The samples were then centrifuged at 13,000 rpm for 30 min to separate the dilute phase from the dense coacervate phase. 100 μL of the supernatant was removed into 384 well glass bottom plates in triplicate, and A494 measurements were taken (Tecan M200 Pro). The concentration of the fluorophore present in the supernatant was quantified using a calibration curve for pure Alexa Fluor dye at 494 nm. This wavelength was chosen based on the reported optimum excitation wavelength of Alexa Flour 488 NHS ester. This value was divided by the total concentration of Alexa Fluor present at that mixing ratio to give the fraction of catalase present in the supernatant at that mixing ratio. The total Alexa Fluor present at a particular mixing ratio was calculated by multiplying the measured absorbance of 100 μL of labeled catalase (in the absence of additional buffer or polycation) at 494 nm with the mass fraction of catalase at that mixing ratio. As a control, this procedure was repeated with labeled catalase mixed with just buffer at mixing ratios ranging from 0.6 to 1 mass fraction of catalase.Coacervate dissolution in the presence of fuel (Fig. 4)
The pH of 2 M H2O2 solutions in water was adjusted to pH 9. The concentration of prepared H2O2 solutions was checked by measuring the A280 of the 2 M H2O2 solution diluted by a factor of 20 (extinction coefficient of H2O2 at 280 nm is 4.2 M−1 cm−1 as determined experimentally). The pH of this solution was determined by measuring the absorbance of a small amount of the solution (1 mL) at 600 nm in the presence of a known concentration (0.01 mg mL−1) of xylenol blue, a pH indicator. A 0.25 mg mL−1 catalase solution in water at pH 9 was made by diluting a stock solution of 1 mg mL−1 catalase in water at pH 9 prepared as described above. This solution was mixed with a 0.25 mg mL−1 DEAE-dextran solution in water at pH 9 (prepared in a similar manner) in a scintillation vial at a mass fraction of catalase of 0.94. The pH of the solution was measured every 1 s using an InLab Pure Pro-ISM pH electrode connected to a SevenCompact S210 pH meter with stirring at 400 rpm. H2O2 was added to this solution to a final concentration of 0.1 M H2O2. The pH was recorded until a stable reading was reached. The turbidity of this solution before the addition of H2O2 and at the end of this assay was measured by pipetting 1 mL of this solution into a cuvette and measuring the A600 (in the absence of bubbles). As a control, a similar assay was performed in 100 mM Tris pH 9 buffer.Effect of phase separation on reaction rates (Fig. 5)
A 2 M solution of H2O2 in water was prepared and the pH was adjusted to 9 using concentrated solutions of NaOH and HCl. Xylenol blue, a pH indicator, was used to assess the pH of the 2 M H2O2 solution. MilliQ water adjusted to pH 9 was used to prepare the 1 mg mL−1 catalase and 1 mg mL−1 DEAE-dextran solutions. After filtration with 0.2 μM SCFA syringe filters, the protein and polymer solutions were individually diluted to a concentration of 0.25 mg mL−1 using water at pH 9. One trial included the preparation of 5 solutions with one of the solutions being split into two parts, ultimately for a total of 6 reactions per trial. All 5 initial solutions were made by diluting the same 1 mg mL−1 catalase and 1 mg mL−1 DEAE-dextran solutions. Hence, each trial consisted of 6 assays (or 6 reactions) wherein the pH of the solution was measured over time. In each assay, 2 M H2O2 was added such that the final concentration of H2O2 at the beginning of each of the 6 assays was 0.1 M H2O2. Prior to the addition of H2O2, the pH of each solution was re-adjusted to pH 9 in case there were minor changes in the solution pH after mixing. For all of the 6 assays, an InLab Pure Pro-ISM pH electrode connected to a SevenCompact S210 pH meter was used. The pH was recorded every 1 s beginning 30 s before the addition of H2O2 fuel until the pH stabilized (4–6 min after H2O2 addition).For each of the first three out of the 5 solutions, a 20 mL mixture was made by mixing 0.25 mg mL−1 catalase and 0.25 mg mL−1 DEAE-dextran at 0.94 mass fraction of catalase. To solution 1, H2O2 was added after mixing and the pH was recorded until the pH stabilized (referred to as the coacervates in solution in Fig. 5). Solutions 2 and 3 were centrifuged at 4000 rpm for 30 min at room temperature. H2O2 was added to solution 2 directly after centrifugation (referred to as pellet + supernatant in Fig. 5). Solution 3 was separated into individual phases after centrifugation. The supernatant was separated from the dense phase by pipetting and H2O2 was added to this isolated dilute phase (referred to as the supernatant in Fig. 5). To the remaining pellet from solution 3, water at pH 9 was added to obtain a solution of volume 20 mL. H2O2 at pH 9 was added to this pellet immersed in water without further mixing (referred to as pellet in ESI Fig. S11†). Solution 4 was made by mixing 0.25 mg mL−1 catalase with water to obtain a 0.235 mg mL−1 catalase solution at pH 9 (equivalent to 0.94 mass fraction of catalase). H2O2 was added to this solution after mixing (referred to as catalase in solution in Fig. 5). The fifth solution was obtained after centrifuging a catalase solution with the same composition as solution 4. H2O2 was added to this solution 5 directly after centrifugation (referred to as centrifuged catalase in ESI Fig. S11†). The final control experiment involved the addition of 2 M H2O2 solution at pH 9 to 20 mL of water at pH 9 such that the final concentration of H2O2 in the solution was 100 mM. The pH was recorded for a period of time equivalent to the time taken by the slowest assay to confirm that the addition of H2O2 to the solution of water at an initial pH of 9 leads to a negligible pH change. Each trial consisting of the 6 assays along with the control was repeated at least three times.
Data availability
Data are available from the corresponding authors upon request.Author contributions
N. M., K. J. M. B., and A. C. O. were jointly responsible for the conception and design of the studies described here. N. M., S. C., I. N. A. A., and B. L. F. performed the experiments described herein. N. M. and K. J. M. B. created and implemented the reaction-diffusion models. N. M., K. J. M. B., and A. C. O. analyzed and presented the data and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Science Foundation under grant DMR 1938303.Notes and references
- M. Hondele, S. Heinrich, P. De Los Rios and K. Weis, Emerging Top. Life Sci., 2020, 4, 343–354 CrossRef CAS PubMed.
- A. Klosin, F. Oltsch, T. Harmon, A. Honigmann, F. Jülicher, A. A. Hyman and C. Zechner, Science, 2020, 367, 464–468 CrossRef CAS PubMed.
- E. Gomes and J. Shorter, J. Biol. Chem., 2019, 294, 7115–7127 CrossRef CAS PubMed.
- S. Alberti, A. Gladfelter and T. Mittag, Cell, 2019, 176, 419–434 CrossRef CAS PubMed.
- D. Bracha, M. T. Walls and C. P. Brangwynne, Nat. Biotechnol., 2019, 37, 1435–1445 CrossRef CAS PubMed.
- K. K. Nakashima, M. A. Vibhute and E. Spruijt, Front. Mol. Biosci., 2019, 6, 21 CrossRef CAS PubMed.
- A. S. Lyon, W. B. Peeples and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2021, 22, 215–235 CrossRef CAS PubMed.
- M. Hondele, R. Sachdev, S. Heinrich, J. Wang, P. Vallotton, B. Fontoura and K. Weis, Nature, 2019, 573, 144–148 CrossRef CAS PubMed.
- D. Tauber, G. Tauber, A. Khong, B. Van Treeck, J. Pelletier and R. Parker, Cell, 2020, 180, 411–426 CrossRef CAS PubMed.
- A. N. Milin and A. A. Deniz, Biochemistry, 2018, 57, 2470–2477 CrossRef CAS PubMed.
- M.-T. Wei, Y.-C. Chang, S. F. Shimobayashi, Y. Shin, A. R. Strom and C. P. Brangwynne, Nat. Cell Biol., 2020, 22, 1187–1196 CrossRef CAS PubMed.
- J. E. Henninger, O. Oksuz, K. Shrinivas, I. Sagi, G. LeRoy, M. M. Zheng, J. O. Andrews, A. V. Zamudio, C. Lazaris, N. M. Hannett and T. I. Lee, Cell, 2021, 184, 207–225 CrossRef CAS PubMed.
- P. A. Sharp, A. K. Chakraborty, J. E. Henninger and R. A. Young, RNA, 2022, 28, 52–57 CrossRef CAS PubMed.
- M. Palacio and D. J. Taatjes, J. Mol. Biol., 2022, 434, 167216 CrossRef CAS PubMed.
- P. R. Banerjee, A. N. Milin, M. M. Moosa, P. L. Onuchic and A. A. Deniz, Angew. Chem., 2017, 129, 11512–11517 CrossRef.
- D. Zwicker, M. Decker, S. Jaensch, A. A. Hyman and F. Jülicher, Proc. Natl. Acad. Sci., 2014, 111, E2636–E2645 CrossRef CAS PubMed.
- J. Söding, D. Zwicker, S. Sohrabi-Jahromi, M. Boehning and J. Kirschbaum, Trends Cell Biol., 2020, 30, 4–14 CrossRef PubMed.
- D. Zwicker, R. Seyboldt, C. A. Weber, A. A. Hyman and F. Jülicher, Nat. Phys., 2017, 13, 408–413 Search PubMed.
- J. T. Wang, J. Smith, B. C. Chen, H. Schmidt, D. Rasoloson, A. Paix, B. G. Lambrus, D. Calidas, E. Betzig and G. Seydoux, Elife, 2014, 3, e04591 Search PubMed.
- N. A. Yewdall, A. A. André, T. Lu and E. Spruijt, Curr. Opin. Colloid Interface Sci., 2021, 52, 101416 CrossRef CAS.
- N. N. Deng, Biomicrofluidics, 2020, 14, 051301 CrossRef CAS PubMed.
- W. Mu, Z. Ji, M. Zhou, J. Wu, Y. Lin and Y. Qiao, Sci. Adv., 2021, 7, eabf9000 CrossRef CAS PubMed.
- W. Aumiller Jr, F. Pir Cakmak, B. W. Davis and C. D. Keating, Langmuir, 2016, 32, 10042–10053 CrossRef PubMed.
- C. Love, J. Steinkühler, D. T. Gonzales, N. Yandrapalli, T. Robinson, R. Dimova and T. Y. D. Tang, Angew. Chem., 2020, 132, 6006–6013 CrossRef.
- S. Koga, D. S. Williams, A. W. Perriman and S. Mann, Nat. Chem., 2011, 3, 720–724 CrossRef CAS PubMed.
- M. G. Last, S. Deshpande and C. Dekker, ACS Nano, 2020, 14, 4487–4498 CrossRef CAS PubMed.
- W. M. Aumiller and C. D. Keating, Nat. Chem., 2016, 8, 129–137 CrossRef CAS PubMed.
- W. K. Spoelstra, E. O. Van Der Sluis, M. Dogterom and L. Reese, Langmuir, 2020, 36, 1956–1964 CrossRef CAS PubMed.
- C. Donau, F. Späth, M. Sosson, B. A. K. Kriebisch, F. Schnitter, M. Tena-Solsona, H.-S. Kang, E. Salibi, M. Sattler, H. Mutschler and J. Boekhoven, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- K. K. Nakashima, M. H. van Haren, A. A. André, I. Robu and E. Spruijt, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed.
- J. Kirschbaum and D. Zwicker, J. R. Soc., Interface, 2021, 18, 20210255 CrossRef CAS PubMed.
- H. Karoui, M. J. Seck and N. Martin, Chem. Sci., 2021, 12, 2794–2802 RSC.
- L. B. Case, J. A. Ditlev and M. K. Rosen, Annu. Rev. Biophys., 2019, 48, 465 CrossRef CAS PubMed.
- O. Alptekin, S. S. Tükel, D. Yıldırım and D. Alagöz, J. Mol. Catal. B: Enzym., 2010, 64, 177–183 CrossRef CAS.
- R. F. Beers and I. W. Sizer, J. Biol. Chem., 1952, 195, 133–140 CrossRef CAS PubMed.
- Y. Ogura, Arch. Biochem. Biophys., 1955, 57, 288–300 CrossRef CAS PubMed.
- W. C. B. McTigue and S. L. Perry, Soft Matter, 2019, 15, 3089–3103 RSC.
- A. C. Obermeyer, C. E. Mills, X. H. Dong, R. J. Flores and B. D. Olsen, Soft Matter, 2016, 12, 3570–3581 RSC.
- C. S. Cummings and A. C. Obermeyer, Biochemistry, 2018, 57, 314–323 CrossRef CAS PubMed.
- E. A. Frankel, P. C. Bevilacqua and C. D. Keating, Langmuir, 2016, 32, 2041–2049 CrossRef CAS PubMed.
- N. A. Zervoudis and A. C. Obermeyer, Soft Matter, 2021, 17, 6637–6645 RSC.
- A. Testa, M. Dindo, A. A. Rebane, B. Nasouri, R. W. Style, R. Golestanian, E. R. Dufresne and P. Laurino, Nat. Commun., 2021, 12, 1–8 CrossRef PubMed.
- Y. Pocker and E. Green, J. Am. Chem. Soc., 1973, 95, 113–119 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Model of enzymatic pH change in one and two phases as well as supporting experimental data on enzyme activity and phase behavior. See DOI: https://doi.org/10.1039/d2sc03838b |
| This journal is © The Royal Society of Chemistry 2023 |