 Open Access Article
Open Access ArticleComment on “The oxidation state in low-valent beryllium and magnesium compounds” by M. Gimferrer, S. Danés, E. Vos, C. B. Yildiz, I. Corral, A. Jana, P. Salvador and D. M. Andrada, Chem. Sci. 2022, 13, 6583
Sudip
Pan
 a and
Gernot
Frenking
a and
Gernot
Frenking
 *abc
*abc
aFachbereich Chemie, Philipps-Universität Marburg, Marburg, Germany
bDonostia International Physics Center (DIPC), 20018 San Sebastian, Spain
cInstitute of Advanced Synthesis, School of Chemistry and Molecular Engineering, Jiangsu National Synergetic Innovation Center for Advanced Materials, Nanjing Tech University, China. E-mail: frenking@chemie.uni-marburg.de
First published on 15th December 2022
Abstract
We challenge the assignment of the oxidation state +2 for beryllium and magnesium in the complexes Be(cAACDip)2 and Mg(cAACDip)2 as suggested by Gimferrer et al., Chem. Sci. 2022, 13, 6583 in a recent study. A careful review of the data in the ESI contradicts their own statement and shows that the results support the earlier suggestion that the metals are in the zero oxidation state. The authors reported wrong data for the excitation energies of Be and Mg to the 1D (np2) state. We also correct some misleading statements about the EDA method.
In a recent study by Gimferrer et al.,1 the authors report quantum chemical calculations of di-coordinated beryllium and magnesium compounds ML2 (M = Be, Mg) with various ligands L, which have been synthesized by different groups in recent years. The focus of the work lies on the assignment of the oxidation state of the metal atoms in the compounds Be(cAACDip)2 and Mg(cAACDip)2 with the ligands cAAC (cyclic Alkyl Amino Carbene) that carry bulky Dip (2,6-diisopropylphenyl) substituents. The beryllium complex Be(cAACDip)2 was isolated by Braunschweig and co-workers who also analyzed the bonding situation and suggested that it is the first example of a stable beryllium compound in the zero oxidation state Be(0).2 The magnesium homologue Mg(cAACDip)2 was postulated as an intermediate that quickly rearranges to a more stable species.3 Using a variety of methods, Gimferrer et al.1 question the assignment of the zero oxidation state and propose that Be(cAACDip)2 and Mg(cAACDip)2 are actually M(+2) (M = Be, Mg) compounds where the ligands bind as anionic diradicals with a doubly charged metal ion.
We have carefully reviewed the work, and found erroneous data and contradictions between the numerical results and the conclusions in the paper. There is also a confusing mixture of statements about the electronic structure and bonding situation in low-valent compounds and the importance of the diradicaloid character in the molecules. In addition, we encountered some misleading statements about the EDA method, which we want to clarify. Finally, we noticed that the authors did not consider the possibility that the metal atoms could be in the formal oxidation state +1. We will focus in our comment on the beryllium compound Be(cAACDip)2.
Fig. 1 shows the bonding scenarios for the compounds M(cAACDip)2 (M = Be, Mg) that were considered by Gimferrer et al.1 The authors say in the introduction that the model of dative interactions shown in Fig. 1 is unlikely, because the electronegativities of Be (1.57) and Mg (1.31) are much lower than for C (2.55). This argument does not consider the electronic state of the metal atom, which may significantly change the effective electronegativity of the atom. This was already reported a long time ago by Hinze,4 who showed that electronegativity strongly depends on the atomic orbitals. He derived electronegativity values for the atomic valence orbitals responsible for atomic electronegativities, which may differ significantly from the average value that was used by the authors. A striking example is the related boron complex (BH)(cAACDip)2, which was isolated and structurally characterized by Bertrand and co-workers in 2011.5 The bonding analysis clearly showed that it is a boron(I) complex that is best described by dative bonds (cAACDip)→(BH)←(cAACDip) where the carbon atoms of the ligands are donors and boron is an acceptor.
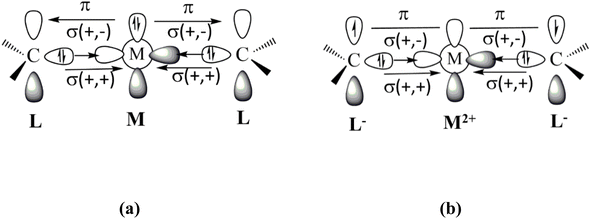 | ||
| Fig. 1 Schematic description of the metal–ligand orbital interactions in Be(cAACDip)2 and Mg(cAACDip)2 using (a) neutral fragments and (b) charged fragments. | ||
The authors then state that the model of dative bonding shown in Fig. 1a would require excitation energies of 178.3 kcal mol−1 and 399.9 kcal mol−1 for the Be and Mg atoms to acquire the atomic valence state 1D with doubly occupied (n)p2 AOs, respectively, citing a study by Moore and Russell (their ref. 24).6 The values are wrong! The cited work gives the binding energies in atomic valence orbitals of the atoms but not the double excitation energies. A value of 399.9 kcal mol−1 for the excitation energy of the magnesium atom 1S(3s2) → 1D(3p2) would be much higher than the ionization energy of Mg (176.3 kcal mol−1) which is physically unreasonable. We checked the literature and found that the experimental excitation energy to the 1D (2p2) state of Be is 162.5 kcal mol−1 (ref. 7) and that the excitation energy to the 1D (3p2) state of Mg is unknown, because it strongly interacts with the 3s and 1D series.8 Since the experimentally known promotion energies to the excited states of the third-row atom Mg are lower than for the second-row atom Be,7 it can be concluded that the excitation energy to the 1D (3p2) state of Mg is <162.5 kcal mol−1. More importantly, the alternative binding model proposed by Gimferrer et al.1 requires a dramatically higher extraction energy of 634.9 kcal mol−1 for the double ionization of Be and 523.0 kcal mol−1 for Mg,7 which is only slightly reduced by the electron affinity of the cAACDip ligands (2 × 18.4 kcal mol−1).9 The data indicate that the bonding model of dative interactions shown in Fig. 1a needs a significantly lower promotion energy than the model of diradical binding displayed in Fig. 1b.
Gimferrer et al.1 analyzed the actual interactions in Be(cAACDip)2 and Mg(cAACDip)2 with the EDA-NOCV (energy decomposition analysis with natural orbitals for chemical valence)10,11 method. Table 1 shows the numerical results, which were given in their ESI (Table S8).1 Crucial information about the most appropriate interacting fragments is provided by the orbital term, which indicates the energy change during the bond formation. Fragments which give the lowest energy change for the orbital interactions are the most suitable species to describe the bonding interaction. This has been shown to be very useful for elucidating the nature of the chemical bonds in a large variety of main-group molecules, transition metal complexes as well as lanthanide and actinide compounds.12 The authors divided the orbital term without explanations in contributions as ΔEorb and ΔEorb-HF giving a total value ΔEorb-corr, which is irrelevant for the assignment of the most suitable fragments and which are misleading nominations, because the data come from DFT calculations. The orbital interactions come from the Kohn–Sham orbitals and not from the Hartree–Fock orbitals.
| Be(cAACDip)2 | Mg(cAACDip)2 | |||
|---|---|---|---|---|
| a The lowest ΔEorb-corr value for each system is highlighted in bold. Energy values are given in kcal mol−1. b The value in parenthesis gives the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. c The values in parenthesis give the percentage contribution to the total orbital interaction ΔEorb-corr. | ||||
| E(L)2 | Be0 (1D, 2s02p2) + (cAAC)2 (CSS) | Be2+ (1S, 2s02p2) + (cAAC)22− (OSS) | Mg0 (1D, 3s03p2) + (cAAC)2 (CSS) | Mg2+ (1S, 3s03p2) + (cAAC)22− (CSS) |
| ΔEInt | −287.1 | −847.9 | −222.6 | −647.2 |
| ΔEPauli | 157.4 | 105.8 | 197.1 | 98.4 |
| ΔEdispb | −10.5 (2.4%) | −10.5 (1.1%) | −16.1 (3.8%) | −16.1 (2.1%) |
| ΔEelstatb | −202.6 (45.6%) | −449.4 (52.4%) | −210.7 (50.2%) | −466.8 (60.4%) |
| ΔEorb | −231.4 | −401.4 | −193.0 | −241.6 |
| ΔEorb-HF | 0.0 | −42.4 | −0.1 | −48.2 |
| ΔEorb-corrb | −231.4 (52.1%) | −443.8 (46.5%) | −193.1 (46.0%) | −289.8 (37.5%) |
| ΔEorb-σ(+,+)c | −18.3 (7.9%) | −45.7 (10.3%) | −13.8 (9.8%) | −41.9 (14.4%) |
| ΔEorb-σ(+,−)c | −51.9 (22.4%) | −90.3 (20.3%) | −18.6 (9.7%) | −28.4 (9.8%) |
| ΔEorb-πc | −150.7 (65.1%) | −211.6 (47.7%) | −152.0 (78.7%) | −119.5 (41.2%) |
| ΔEorb-restc | −10.4 (4.5%) | −53.9 (12.1%) | −8.6 (4.4%) | −51.8 (17.9%) |
| 〈S2〉 | 0.571 | 0.571 | 0.942 | 0.942 |
Table 1 shows that the neutral fragments M + (cAAC)2 give a significantly lower orbital interaction than the doubly charged fragments M2+ + (cAAC)22−. The smaller energy contribution of ΔEorb is the reason why Braunschweig and co-workers assigned the oxidation state zero to Be in Be(cAACDip)2.2 Gimferrer et al.1 suggested that one should use the density change rather than the energy change as a criterion for the choice of the oxidation state, saying that the electron flow to the empty pz AO of Be2+ is only 0.42e when doubly charged fragments are used, while 1.49e is transferred from the occupied pz AO of Be(0) when one uses neutral fragments. But a careful inspection of the data gives a different result. Table 1 shows that the largest orbital term for the interaction of the doubly charged fragments comes from ΔEorb-π, which amounts to −211.6 kcal mol−1 and contributes 47.7% to the total orbital interactions. Fig. 2 shows the associated deformation density, which is provided as Fig. S41 in the ESI provided by the authors. It clearly shows that the orbital interaction describes the formation of the C–Be–C π bond, which is depicted by the blue region of charge accumulation. The calculated charge migration amounts to 1.8e, which is much higher than the charge migration between the neutral fragments (1.5e). Gimferrer et al.1 mentioned the charge migration of 1.8e stating that “75% of the electron flow is associated with the internal reorganization of the fragment density, which certainly has an important energy impact, but has no influence of the oxidation state”. But the deformation density clearly reveals that the electron flow of 1.8e is associated with the charge flow from the occupied ligand orbitals to the vacant C–Be–C π orbital but not with an internal reorganization of the fragment density! The cited statement of Gimferrer et al.1 is in conflict with their own results and contradicts their suggestion to use the density change and not the energy change as a criterion for choosing the oxidation state. The deformation density in Fig. 2 clearly shows that ΔEorb-π is associated with the formation of C–Be–C π. It follows that even the size of the charge rearrangement suggests that the neutral fragments Be + (cAAC)2 are the best choice for describing the bonding in Be(cAACDip)2 and that the oxidation state of beryllium is Be(0) and not Be(+2).
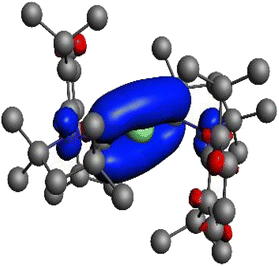 | ||
| Fig. 2 Deformation density of the orbital interaction ΔEorb-π between Be2+ and (cAACDip)22− as shown in Fig. S41 of ref. 1. The color code of the charge flow is red → blue. The value of |υαβ| = 1.8 gives the amount of the charge reorganization. | ||
The EDA-NOCV method is a very sophisticated approach for analyzing the nature of the chemical bond.13 It has been the subject of critical comments by some workers,14 which has been clarified in a recent study.15 The authors state that “EDA cannot distinguish an electron-sharing interaction from a spin-polarized one (diradicaloid)” citing a previous study by them.16 The goal of EDA is to analyze the electronic structure in the form of energy components that can be interpreted in a physically meaningful manner. This information is very useful to understand chemical bonds in terms of bonding models based on covalent (orbital) interactions, electrostatic (Coulomb) interactions and Pauli repulsion. Subtle differences, such as between electron-sharing interactions and spin-polarized interactions, fall outside the scope of EDA, and it is improper to criticize the method for not providing information about a particular property that is not the target of EDA. Clarifying notes about the EDA have recently been given in the literature.15 EDA uses the electronic structure of the respective method for an energy analysis. Information about the open-shell and closed-shell nature of the wavefunction, which may have a diradicaloid character due to a small HOMO–LUMO gap, comes from the electronic structure method which is used but not from EDA. EDA is as good as the quantum theoretical method on which it is based. But this issue is irrelevant to the assignment of the oxidation state, which is a model that is based on well-defined rules. The same holds true for EDA-NOCV. Models are not right or wrong but more or less useful. It is odd when the authors question the reliability of the KS-DFT and the energy-based EDA criterion for assigning the valence state of the metal atoms in Be(cAACDip)2 and Mg(cAACDip)2, when they are using arguments that are in conflict with their own data.
The comments by Gimferrer et al.1 could lead to the impression that the EDA-NOCV method using DFT calculations may not be used for molecules with multi-reference characters or open-shell singlet states. This is not necessarily the case. Such systems must be carefully tested for the reliability of the DFT approach, which may or may not be valid. A pertinent example is the bonding situation in the calcium complex Ca–CO2, which was recently reported.17 The complex has an open-shell singlet ground state, where the bonding interactions take place between a Ca+ (4s1) cation in the doublet ground state and a doublet ground state CO2− anion. The EDA-NOCV calculations using standard DFT calculations provided deep insights into the nature of the chemical bonds.
Since the paper by Gimferrer et al.1 focusses on the topic of oxidation state, it is useful to cite the revised definition given by the IUPAC which states “The OS of a bonded atom equals its charge after ionic approximation. In the ionic approximation, the atom that contributes more to the bonding molecular orbital (MO) becomes negative.”18 Inspection of the MOs of Be(cAACDip)2 shows that the largest coefficient of the cAACDip←Be→cAACDip π bonding MO is at beryllium (see Fig. S11, occupation 1.80, in the ESI), which suggests that Be(0) is the appropriate formal oxidation state of the metal atom. It is important to realize that the formal oxidation state of an atom is not identical to the atomic charges and the real electronic state in a molecule. This is sometimes confused. A famous example is the debate in the 90s, when Snyder questioned the assignment of the oxidation state Cu(III) in [Cu(CF3)4]−.19 A more recent example concerns the oxidation state in the coordinatively saturated metal carbonyls M(CO)8 of group 2 (M = Ca, Sr, Ba) which were recently synthesized and theoretically analyzed with the EDA-NOCV method.20a Following the Dewar–Chatt–Duncanson model of chemical bonding, all carbonyls are M(0) complexes, but the EDA-NOCV method showed that the best description for the metal–CO interactions comes from M+ + (CO)8−.20b–d
Gimferrer et al.1 report a large number of numerical results using a variety of methods which suggest that the electronic structures of some of the investigated complexes have a diradicaloid character due to a low singlet–triplet gap which are assigned as open-shell singlets. They also report a global reliability index R(%) measuring to which extent the formal OS model matches the actual electron distribution, which varies between 59 and 100% (Table 1 in their paper). But the reported bond dissociation energies (BDEs) given in Tables S5–S7 of the ESI of their work show very similar BDE values at different levels of theory, which question the value of the R(%) data. The authors also report the results of the EOS (Effective Orbital State)21 method, which is based on atomic fragments that are defined in different ways and can lead to different results. For example, the EOS analysis using the Mulliken or Löwdin approaches gives Be(0) for Be(cAACMe) whereas the NAO and QTAIM procedures suggest Be(+2).1 Another concern is the EOS result that the magnesium atom in Mg(cAACMe) is Mg(0) while in Mg(cAACDip) it is Mg(+2). A drastic alteration in the nature of the Mg-cAACR bond from Mg(0) to Mg(+2) by changing the rather remote substituent R is questionable. Another puzzling feature is the complete omission of the possibility that the metal atoms have the oxidation state +1. In the paper by Braunschweig and co-workers it was shown that the EDA-NOCV results of Be(cAACDip) using singly charged fragments give slightly higher values for the orbital term ΔEorb than using neutral fragments.2 We repeated the calculations at the same level of theory as the authors but with the inclusion of dispersion interactions, which had not been considered. We found that the ΔEorb values using singly charged and neutral fragments become nearly equal, which means that Be(cAACDip) may be described with the oxidation states Be(0) or Be(+1) but clearly not with Be(+2).
In summary, we note that the assignment of the oxidation state +2 for beryllium and magnesium in the complexes Be(cAACDip)2 and Mg(cAACDip)2 as suggested by Gimferrer et al. is not valid and that the conclusion is not supported by their own data. A critical inspection of their data corroborates the earlier assignment of the oxidation state zero. The authors reported wrong data for the excitation energies of Be and Mg to the 1D (np2) state, which are the electronic reference state of the metal atoms for the dative interactions with the cAACDip ligands.
Data availability
Full data are in this main text or in ESI of the original paper.Author contributions
GF designed the work and wrote the draft. SP carried out the calculations and checked the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
GF wants to thank Prof. Jesus Ugalde and his team at the DIPC at Donostia for their warm hospitality during his stay, during which this comment was written. The work was financially supported by the Nanjing Tech University.References
- M. Gimferrer, S. Danes, E. Vos, C. B. Yildiz, I. Corral, A. Jana, P. Salvador and D. M. Andrada, Chem. Sci., 2022, 13, 6583 RSC.
- M. Arrowsmith, H. Braunschweig, M. A. Celik, T. Dellermann, R. D. Dewhurst, W. C. Ewing, K. Hammond, T. Kramer, I. Krummenacher, J. Mies, K. Radacki and J. K. Schuster, Nat. Chem., 2016, 8, 890 CrossRef CAS PubMed.
- Z. R. Turner, Chem.–Eur. J., 2016, 22, 1164 CrossRef PubMed.
- (a) J. Hinze, Pauling's Legacy: Modem Modelling of the Chemical Bond, Theoretical and Computational Chemistry, Elsevier Science, Amsterdam, 1999, vol. 6, p. 189 Search PubMed; (b) D. Bergmann and J. Hinze, Angew. Chem., Int. Ed. Engl., 1996, 35, 150 CrossRef CAS.
- R. Kinjo, B. Donnadieu, M. A. Celik, G. Frenking and G. Bertrand, Science, 2011, 333, 610 CrossRef CAS PubMed.
- C. E. Moore and H. N. Russell, J. Res. Natl. Bur. Stand., 1952, 48, 61 CrossRef CAS.
- NIST Atomic Spectra Database Levels Form, National Institute of Standards and Technology OR National Bureau of Standards, U.S. Department of Commerce, Gaithersburg, MD, https://www.nist.gov/pml/handbook-basic-atomic-spectroscopic-data, accessed July 17, 2022.
- (a) K. Aashamar, T. M. Luke and J. D. Talman, Phys. Scr., 1986, 34, 386 CrossRef CAS; (b) P. F. O'Mahoney, Phys. Rev. A, 1985, 32, 908 CrossRef PubMed.
- M. Gernert, L. Balles-Wolf, F. Kerner, U. Müller, A. Schmiedel, M. Holzapfel, C. M. Marian, J. Pflaum, C. Lambert and A. Steffen, J. Am. Chem. Soc., 2020, 142, 8897 CrossRef CAS PubMed.
- (a) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755 CrossRef CAS; (b) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558 CrossRef CAS.
- (a) A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933 CrossRef CAS PubMed; (b) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962 CrossRef CAS PubMed.
- (a) Q. Zhang, W.-L. Li, C. Xu, M. Chen, M. Zhou, J. Li, D. M. Andrada and G. Frenking, Angew. Chem., Int. Ed., 2015, 54, 11078 CrossRef CAS PubMed; (b) D. M. Andrada and G. Frenking, Angew. Chem., Int. Ed., 2015, 54, 12319 CrossRef CAS PubMed; (c) C. Mohapatra, S. Kundu, A. N. Paesch, R. Herbst-Irmer, D. Stalke, D. M. Andrada, G. Frenking and H. W. Roesky, J. Am. Chem. Soc., 2016, 138, 10429 CrossRef CAS PubMed; (d) L. T. Scharf, M. Andrada, G. Frenking and V. H. Gessner, Chem.–Eur. J., 2017, 23, 4422 CrossRef CAS PubMed; (e) M. Hermann and G. Frenking, Chem.–Eur. J., 2017, 23, 3347 CrossRef CAS PubMed; (f) D. C. Georgiou, L. Zhao, D. J. D. Wilson, G. Frenking and J. L. Dutton, Chem.–Eur. J., 2017, 23, 2926 CrossRef CAS PubMed; (g) Z. Wu, J. Xu, L. Sokolenko, Y. L. Yagupolskii, R. Feng, Q. Liu, Y. Lu, L. Zhao, I. Fernández, G. Frenking, T. Trabelsi, J. S. Francisco and X. Zeng, Chem.–Eur. J., 2017, 23, 16566 CrossRef CAS PubMed; (h) W. Petz, D. M. Andrada, M. Hermann, G. Frenking and B. Neumüller, Z. Anorg. Allg. Chem., 2017, 643, 1096 CrossRef CAS; (i) D. M. Andrada, J. L. Casalz-Sainz, A. M. Pendas and G. Frenking, Chem.–Eur. J., 2018, 24, 9083 CrossRef CAS PubMed; (j) P. Jerabek, P. Schwerdtfeger and G. Frenking, J. Comput. Chem., 2019, 40, 247 CrossRef CAS PubMed; (k) R. Saha, S. Pan, G. Merino and P. K. Chattaraj, Angew. Chem., Int. Ed., 2019, 58, 8372 CrossRef CAS PubMed; (l) W. Fang, S. Pan, W. Su, S. Wang, L. Zhao, G. Frenking and C. Zhu, CCS Chem., 2021, 3, 2324 Search PubMed; (m) W. Su, Y. Ma, L. Xiang, J. Wang, S. Wang, L. Zhao, G. Frenking and Q. Ye, Chem.–Eur. J., 2021, 27, 10006 CrossRef CAS PubMed; (n) W. Su, S. Pan, X. Sun, S. Wang, L. Zhao, G. Frenking and C. Zhu, Nat. Commun., 2018, 9, 4997 CrossRef PubMed; (o) J. Jin, S. Pan, X. Jin, S. Lei, L. Zhao, G. Frenking and M. Zhou, Chem.–Eur. J., 2019, 25, 3229–3234 CrossRef CAS PubMed; (p) C. Chi, S. Pan, J. Jin, L. Meng, M. Luo, L. Zhao, M. Zhou and G. Frenking, Chem.–Eur. J., 2019, 25, 11772 CrossRef CAS PubMed.
- (a) L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1345 Search PubMed; (b) L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, Nat. Rev. Chem., 2019, 3, 48 CrossRef CAS; (c) L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chem. Rev., 2019, 119, 878 Search PubMed.
- (a) D. M. Andrada and C. Foroutan-Nejad, Phys. Chem. Chem. Phys., 2020, 22, 22459 RSC; (b) M. Sola, M. Duran and J. Poater, Theor. Chem. Acc., 2021, 140, 32 Search PubMed; (c) J. Poater, D. M. Andrada, M. Sola and C. Foroutan-Nejad, Phys. Chem. Chem. Phys., 2022, 24, 2344 RSC.
- F. M. Bickelhaupt, C. Fonseca Guerra, M. Mitoraj, F. Sagan, A. Michalak, S. Pan and G. Frenking, Phys. Chem. Chem. Phys., 2022, 24, 15726 RSC.
- P. Salvador, E. Vos, I. Corral and D. M. Andrada, Angew. Chem., Int. Ed., 2021, 60, 1498 CrossRef CAS PubMed.
- Y. Zhou, S. Pan, X. Dong, L. Wang, M. Zhou and G. Frenking, J. Am. Chem. Soc., 2022, 144, 8355 CrossRef CAS PubMed.
- P. Karen, P. McArdle and J. Takats, Pure Appl. Chem., 2014, 86, 1017 CAS.
- (a) J. P. Snyder, Angew. Chem., Int. Ed., 1995, 34, 986 CrossRef CAS; (b) M. Kaupp and H. G. von Schnering, Angew. Chem., Int. Ed., 1995, 34, 986 CrossRef CAS.
- (a) X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking, Science, 2018, 361, 912 CrossRef CAS PubMed; (b) C. R. Landis, R. P. Hughes and F. Weinhold, Science, 2019 DOI:10.1126/science.aay2355; (c) L. Zhao, S. Pan, M. Zhou and G. Frenking, Science, 2019 DOI:10.1126/science.aay5021; (d) G. Frenking, I. Fernández, N. Holzmann, S. Pan, I. Krossing and M. F. Zhou, JACS Au, 2021, 1, 623 CrossRef CAS PubMed.
- E. Ramos-Cordoba, V. Postils and P. Salvador, J. Chem. Theory Comput., 2015, 11, 1501 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |
