Open Access Article
Open Access ArticleBond breaking of furan–maleimide adducts via a diradical sequential mechanism under an external mechanical force†
Manuel
Cardosa-Gutierrez
a,
Guillaume
De Bo
 b,
Anne-Sophie
Duwez
b,
Anne-Sophie
Duwez
 *a and
Francoise
Remacle
*a and
Francoise
Remacle
 a
a
aUR Molecular Systems, Department of Chemistry, University of Liège, 4000 Liège, Belgium. E-mail: fremacle@uliege.be
bDepartment of Chemistry, University of Manchester, Manchester, M13 9PL, UK
First published on 4th January 2023
Abstract
Substituted furan–maleimide Diels–Alder adducts are bound by dynamic covalent bonds that make them particularly attractive mechanophores. Thermally activated [4 + 2] retro-Diels–Alder (DA) reactions predominantly proceed via a concerted mechanism in the ground electronic state. We show that an asymmetric mechanical force along the anchoring bonds in both the endo and exo isomers of proximal dimethyl furan–maleimide adducts favors a sequential pathway. The switching from a concerted to a sequential mechanism occurs at external forces of ≈1 nN. The first bond rupture occurs for a projection of the pulling force on the scissile bond at ≈4.3 nN for the exo adduct and ≈3.8 nN for the endo one. The reaction is inhibited for external forces up to ≈3.4 nN for the endo adduct and 3.6 nN for the exo one after which it is activated. In the activated region, at 4 nN, the rupture rate of the first bond for the endo adduct is computed to be ≈3 orders of magnitude larger than for the exo one in qualitative agreement with recent sonication experiments [Z. Wang and S. L. Craig, Chem. Commun., 2019, 55, 12263–12266]. In the intermediate region of the path between the rupture of the first and the second bond, the lowest singlet state exhibits a diradical character for both adducts and is close in energy to a diradical triplet state. The computed values of spin–orbit coupling along the path are too small for inducing intersystem crossings. These findings open the way for the rational design of DA mechanophores for polymer science and photochemistry.
Introduction
Dynamic covalent bonds, like the archetypal furan–maleimide Diels–Alder (DA) adduct, are vastly used in synthetic chemistry and polymer science, and are now expanding into biology.1–3 Furan–maleimide adducts are characterized by dynamic covalent bonds that are more labile and slightly longer than typical carbon–carbon covalent ones. The dynamic covalent bonds of Diels–Alder (DA) adducts make them attractive mechanophores when embedded in polymers and networks.4–11 DA reactions on these adducts proceed via a low reaction barrier that leads to reversible reactions. In solution, the adducts need to be heated at high temperatures to break open.1,12 The retro-DA reaction can also take place at room temperature when the adduct is sonicated, thus subjected to mechanical forces.5,10,11 There is however not yet a detailed understanding on the rupture mechanism of these adducts under tension, in particular on the concerted or sequential nature of the reaction path.13Beyond stabilizing intermediates and shifting chemical equilibria, due to the vector character of the force, mechanochemical reactions can follow specific pathways yielding products that may differ from those of non-directional thermal activation in solution.4,13–19 It was shown that the cis or trans anchoring of benzocyclobutene to a polymer chain controls the stereochemistry of the ring opening.20,21 Under tension, the cis attachment leads to a disrotatory ring opening in violation of the Woodward–Hoffmann rules22 and yields the same product as the trans attachment. Ab initio steered molecular dynamics simulations on cyclobutene and the determination of the minimum energy pathway provided a mechanistic interpretation on the force modified potential energy surface.14 In cis and trans gem-difluoro-cyclopropane (gDFC), it was shown that under tension, the trans gDFC undergoes a Woodward–Hoffmann thermally forbidden conrotatory ring opening, and that both cis and trans gDFC open via a diradical intermediate that is stabilized under tension.23 Upon releasing the tension, the diradical returns to the cis gDFC for which the barrier is smaller on the field free potential. The diradical character of the intermediate under tension was demonstrated by trapping it with a radical chromophore. Cyclobutane cores embedded in mechanophores were reported to open sequentially24–27 and shown to proceed via a diradical intermediate, the product stereochemistry being determined by whether or not the intermediate undergoes isomerization after the first bond rupture.28,29 Diradical intermediates were also recently reported to play a role in the mechanochemical reactivity of vinyl-addition polynorbornene that contains norbornane units30 and in the release of CO by sonication activation of the norborn 2-en-7-one scaffold.31
Various [4 + 2] mechanophores have been investigated,19 and among them furan–maleimide is a popular structural motif.5,6,9–11,32–38 Furan–maleimide adducts embedded in a polymethyl acrylate (PMA) polymer were shown to selectively break under sonication.5 Stevenson and De Bo10 pointed to the regioselectivity of the rupture of a furan–maleimide mechanophore embedded in PMA activated by sonication; the two proximal stereoisomers, where the anchoring of the polymer chain on the furan is on a carbon atom near neighbor to the furan/maleimide junction, being more labile than the distal ones where the anchoring is on the next near neighbor atom on the furan moiety. Wang et al.11 benchmarked the mechanical resistance to activation by sonication of two proximal stereoisomers with respect to the ring opening of gem-dichlorocyclopropane. They concluded that the proximal-exo adduct is mechanically less labile than the proximal-endo one. This stereoselectivity in the rupture under force follows the trend of thermal activation. It is corroborated by the differences in the computed force-free activation barriers and in the efficiency of the mechanochemical coupling to the polymer chain.
Motivated by these results,10,11 we theoretically investigated the mechanism of the [4 + 2] retro-Diels–Alder (rDA) ring opening of proximal-endo, Pendo, and proximal-exo, Pexo, dimethyl furan–maleimide adducts under tension. We report on a shift from a concerted mechanism at zero force to a sequential one at external pulling forces on the weakest scissile bond smaller than 1 nN due to the directionality of the force applied to the methyl groups used to model the tethering of the adduct into a polymer. We further show that the tension inhibits the bond rupture up to pulling forces of ≈3 nN before inducing a preferential activation of the Pendo stereoisomer in qualitative agreement with the experimental results of Wang et al.11
In the ground electronic state at room temperature, thermally activated [4 + 2] retro-Diels–Alder (rDA) reactions proceed most of the time via a concerted and stereospecific pathway involving a single concerted transition state at room temperature.39,40 Activation energies of 25–30 kcal mol−1 for the concerted rupture of the two scissile bonds at room temperature endow them with a dynamic character. Endo adducts are more reactive than exo ones because of their lower activation barriers.41–43 A sequential mechanism involving diradicals or zwitterion species is also thermally possible, depending on the substitution of DA adducts.44 Studies involving molecular dynamics showed that for some adducts at high temperature (>1000 K) and for substituted ones a small fraction of the trajectories involves two transition states (TSs) and diradical open shell singlet intermediates along the reaction path.40 The photoactivation of DA adducts with a UV pulse was shown to proceed via non-concerted pathways through successive bond cleavages, depending on the nature of the conical intersections (CoIn) leading back to the ground electronic state.45–48 Studies investigating activation by using an external static electric field also reported going through a sequential pathway involving zwitterionic intermediates.41,49
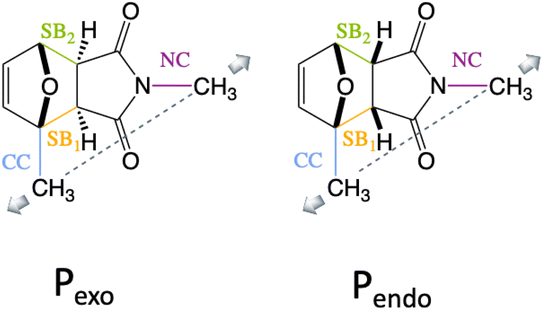
We show here that diradical intermediates can be stabilized under tension in the rDA of the substituted Pendo and Pexo furan–maleimide adducts, where the methyl groups model the anchoring on the polymer chain and control the directionality of the external force. The two adducts and the four bonds of interest, the two scissile bonds, SB1 and SB2, and the CN and the CC anchoring bonds of the methyl groups are drawn in Fig. 1. Because of the difference in the stereo-character of Pendo and Pexo, in the force free equilibrium geometry, SB1 and SB2 are essentially of equal length in Pendo (1.57 Å), while in Pexo, SB1 is longer (1.58 Å) than SB2 (1.56 Å).
Computational methods
The effect of the external force on the potential energy surface (PES) can be computed by an isometric or an isotensional approach.50 The isometric method CoGEF (constrained geometries simulate external force)51 consists in constrained geometry optimization where typically the constraint is the distance between the two atoms to which the pulling force is applied. This approach yields the most stable geometry of the system that satisfies a given value of the constraint and provides the energy and other molecular properties through electronic structure computations. In the isotensional method, the external force is explicitly added as a term in the expression of the nuclear gradient of the energy during the geometry optimization. Three approaches have been implemented, the force-modified-potential-energy surface (FMPES),14 the external force is explicit included (EFEI)15 and the enforce geometry optimization (EGO).52 The isotensional approaches can be used to determine the reactant, transition state and activation energies on the FMPES and to carry out ab initio molecular dynamics under force.14 It was shown in ref. 53 that at stationarity, the EFEI potential, VEFEI(F0), is the Legendre transform of the CoGEF potential VCoGEF(q0), so that the external force and the geometrical constraint can be considered conjugate variables: VEFEI(F0)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) VCoGEF(q0) − F0q0.
VCoGEF(q0) − F0q0.
The reaction mechanism was studied by using the CoGEF isometric protocol, for the two adducts at the UDFT level with the wB97XD54 functional and at the CAS-SCF(4,4) level with the 6-31G(d,p) basis set for the lowest singlet, S0, and triplet, T0, states. The mechanical coordinate is taken to be the distance between the two C atoms of the methyl anchoring groups (dashed line in Fig. 1). For each relaxed geometry under force, the spin–orbit coupling between S0 and T0 was computed along the CoGEF path as well as the 4 lowest singlet and three lowest triplet states at the state average (SA) complete active space55 CAS-SCF level. The CoGEF path computed at the CAS(4,4) level/6-31G(d,p) is consistent with that obtained at the UDFT level, see the ESI† for more details. The UDFT computations were carried out with the quantum chemistry software QChem56 and the CAS-SCF computation with the MOLPRO quantum chemistry package.57,58
The TSs were determined at the UDFT/wB97XD level scanning external pulling force values corresponding to the stretching coordinate.59 Consistent force modified CoGEF paths and activation barriers were obtained with the PBE0DH60 and the BH&HLYP61 functionals, Fig. S2.† These three functionals describe correctly the diradical species that appear when the pulling force induces a switch from a concerted to a sequential rupture mechanism and give results consistent with the CAS-SCF level.
The computed values of the barrier for the rupture of the weakest bond SB1 using UDFT/wB97XD/6-31G(d,p) in the gas phase at zero force are in good agreement with previously reported values in the gas phase41,42 or the M06-2X49 functional in DMSO for unsubstituted adducts. They are systematically higher by ≈5–6 kcal mol−1 than those reported values for similar furan–maleimide adducts using the B3LYP11 functional in THF. A detailed comparison with previous results at zero force and the computed values of the barriers using different functionals is provided in the ESI.†
Since the value of the stretching coordinate at equilibrium at zero force, Rpulling-0, is different in the two stereoisomers, we report below the variation of the structural and energetic observables as a function of the pulling distortion, defined as (Rpulling − Rpulling-0), where Rpulling is the stretching distortion imposed in the CoGEF protocol.
Results and discussion
Switching from a concerted to a sequential mechanism under tension
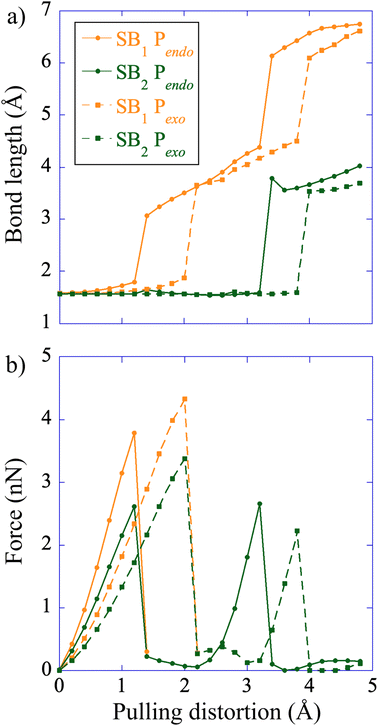
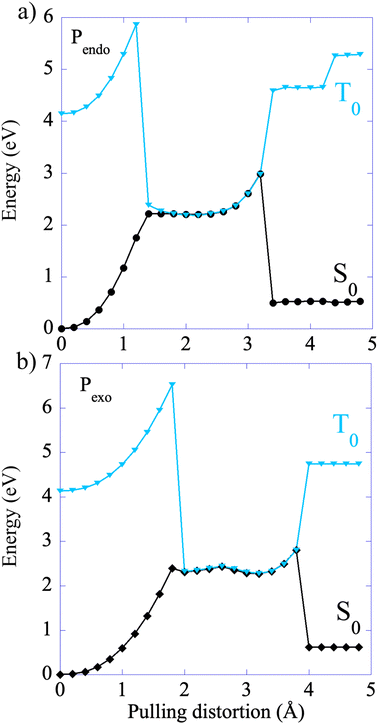
The CoGEF UDFT/wB97XD potential energy profiles are reported as a function of the pulling distortion, (Rpulling − Rpulling-0), in Fig. 2a and b for Pendo and Pexo respectively. Similar profiles are obtained at the CAS(4,4) level, see Fig. S1.† Both adducts undergo a sequential bond rupture. The energy curves exhibit two sharp rises separated by an intermediate region. The breaking of SB1 occurs at the end of the first sharp energy rise, while that of SB2 occurs at the end of the second one. This can be seen from the relaxed geometries under force reported as insets in Fig. 2a and b, and from the elongation of the bond lengths as a function of the pulling distortion plotted in Fig. 3a. During the first energy rise, SB1 is elongated while SB2 remains essentially at its equilibrium value (Fig. 3a). In this range, the projection of the pulling force on SB2 (Fig. 3b) is smaller than on SB1 and not large enough for inducing bond breaking. The SB1 bond of Pendo ruptures for a projection of the pulling force of 3.8 nN, that is slightly smaller than the breaking projection of pulling force for Pexo (4.3 nN). These values are in good agreement with those reported in ref. 10. After the SB1 breaking, the projection of the pulling force (Fig. 3b) on the two scissile bonds drops sharply to values close to zero. In the intermediate region between the two bond breakings, the energy profile of Pendo (Fig. 2a) continues to rise with a much smaller slope, starting from an anti-like unstable endo rotamer that evolves to an unstable endo gauche out one just before the breaking of SB2. On the other hand, in Pexo the anti- and gauche out rotamers correspond to minima (see Fig. 2b), separated by a small rotation barrier of 3 kcal mol−1, which is overcome by a small value of the force of 0.2 nN as can be seen from Fig. 3b. These intermediates have been reported previously for similar DA adducts for zero force reaction paths.40,44,48 Such a rotation around the unbroken bond has also been reported for the sequential ring opening of cyclobutane cores under tension.24–27,29 The breaking of SB2 occurs after a second sharp rise in the projection of the pulling force for a smaller value for Pexo (2.2 nN) than for Pendo (2.7 nN), Fig. 3b. Then the potential energy drops sharply to the dissociation asymptote.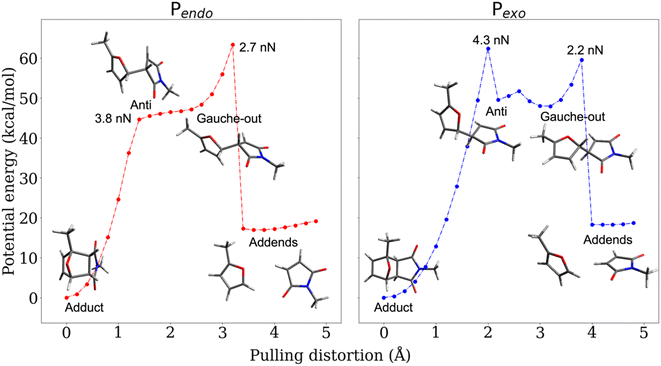 | ||
| Fig. 2 CoGEF UDFT wB97XD potential energy profiles for the Pendo (a) and Pexo (b) adducts as a function of the pulling distortion (Rpulling − Rpulling-0) as well as relaxed geometries under force for maxima and minima. The CoGEF path computed at the CAS(4,4) level is given in Fig. S1† and the one computed with the PBE0DH and BH&HLYP functionals in Fig. S2.† The relaxed geometries along the CoGEF paths computed at the DFT wB97XD and CAS(4,4) levels are given in the ESI.† | ||
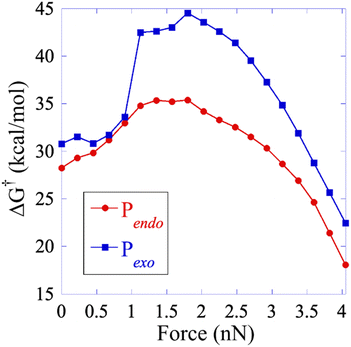
The results discussed above imply that there is a switching of the rupture mechanism from a concerted one to a sequential one at low values of the pulling force, before the rupture of the first scissile bond. In order to get further insights, we computed the transition state (TS) and the free energy of the activation barrier, 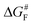 , at 298 K, using the EFEI15 isotensional protocol at the same UDFT level from zero force up to values of the pulling force on SB1 approaching that of the rupture in the UDFT CoGEF path shown in Fig. 3b. It is plotted in Fig. 4.
, at 298 K, using the EFEI15 isotensional protocol at the same UDFT level from zero force up to values of the pulling force on SB1 approaching that of the rupture in the UDFT CoGEF path shown in Fig. 3b. It is plotted in Fig. 4.
 | ||
| Fig. 4 Free energy activation barrier computed using the EFEI protocol for values of the pulling force up to the rupture of the SB1 bond. Pendo is plotted in red with full circles and Pexo in blue with diamonds. The geometries of the reactant and the transition states are given in the ESI.† | ||
At zero force, at 298 K, the free energy barrier is smaller for the Pendo adduct (28.2 kcal mol−1) than for the Pexo adduct (30.8 kcal mol−1), which leads to a computed Δ(ΔG‡) between Pexo and Pendo of 2.6 kcal mol−1. For both adducts, as the pulling force increases, the activation barrier first increases, which means that rupture is inhibited, and then goes through a plateau, before sharply decreasing up to the rupture of the SB1 bond, see Fig. 4. The maximum of the activation barrier occurs for both Pendo and Pexo at 1.8 nN. The barrier is higher for Pexo (44.5 kcal mol−1) than for Pendo (35.4 kcal mol−1). At pulling forces larger than 3.4 nN, the rupture of SB1 is activated in Pendo compared to the zero-force barrier. For Pexo, activation occurs for a pulling force larger than 3.8 nN (Fig. 4). Above 3.5 nN, the computed Δ(ΔG‡) decays sharply, but remains higher for Pexo, which makes the Pendo adduct more labile, in agreement with the experimental results of Wang et al.11 At 4 nN, just before the rupture of SB1, the computed barrier is 18 kcal mol−1 for Pendo (rate constant of 0.36 s−1 (lifetime of 2.8 s)), while it is 22.5 kcal mol−1 (rate constant of 2.1 × 10−4 s−1 (lifetime of 77 min)) for Pexo, see Fig. S3 and the ESI† for more details. The crossover from a concerted mechanism to a sequential one occurs before the first bond rupture at pulling forces ≈1 nN (1.1 nN for Pexo and 0.9 nN for Pendo). It coincides with the inflexion point of the pulling force on SB1. Above 1 nN, the sequential mechanism is favored over the concerted one and it dominates for forces above 3 nN.
Diradical species in the sequential mechanism
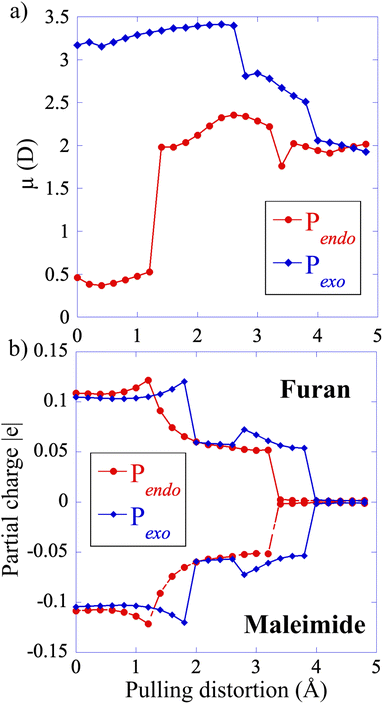
The electronic structure of S0 is very similar for both adducts along the CAS(4,4) CoGEF path. The main configurations correspond to a diradical open shell singlet in the intermediate region between the two bond ruptures, see the ESI for details and Fig. S4† that shows the coefficients of the S0 state in the electronic configurations as a function of the pulling distortion.At zero force, the value of the permanent dipole moment of Pendo is very small (0.5 D). It increases to 2.5 D in the intermediate region, after the first bond rupture, because the pulling distortion increases the extension of the Pendo adduct and makes it comparable to that of Pexo, Fig. 5. The geometry of Pexo is more extended at zero force because of its stereo-character and the dipole moment is larger, 3 D, than that of the Pendo adduct. It slightly decreases in the intermediate region to 2 D. The partial positive and negative charges on the two addends are small at zero force (furan (donor), +0.1 |e| and maleimide (acceptor), −0.1 |e|) and decrease in the intermediate region along the CoGEF path confirming the diradical character of S0 in the intermediate region.
For both adducts, the lowest triplet state, T0, becomes close in energy to S0 in the intermediate region with energy differences of the order of 0.05 eV (Fig. 6). The weight of the |2aa0> configuration in the intermediate region is 93% (Fig. S6†). In the case of Pendo, the triplet state energy becomes lower than that of S0 at the beginning of the intermediate region, for distortion in the range of 1.8 to 2.4 Å (see Fig. S7† for a plot of the S0/T0 energy difference). The spin–orbit coupling remains extremely small, of the order of 10−5 eV for both adducts throughout the intermediate region (see Table S1†), which makes intersystem crossing unlikely along the minimum energy path under force. However, the S0/T0 minimum energy crossing occurs in the vicinity of second bond rupture for both adducts, see Fig. S8.† Therefore, one could observe spin–orbit transitions using steered molecular dynamics,14,29 which will be the subject of future work. The first excited singlet state S1 which has also a diradical character in the intermediate region, is much higher in energy along the minimum path, with a S0/S1 energy difference larger than 3 eV.
 | ||
| Fig. 6 Energy profiles of the singlet S0 and the lowest triplet T0 along the CAS(4,4)-CoGEF path. The energy of the T0 state is computed in the relaxed geometry of S0. The values of the spin–orbit coupling are reported in Table S1 of the ESI.† The S0/T0 energy differences are plotted in Fig. S6† and the minimum energy intersystem crossing (MEIC) geometries in Fig. S7.† Files of geometries of the S0 state along the CoGEF path as well as at the MEIC are given in the ESI.† | ||
Conclusions
Our computations uncover a rich and complex electronic and structural reorganization of the Pendo and Pexo adducts along the stretching mechanical path. The directionality of the force as dictated by the carbon atoms of the two methyl substituents that model the anchoring into the polymer leads to an uneven activation of the two scissile bonds. This in turn induces a switch from a concerted mechanism at zero pulling force to a sequential one for force larger than 1 nN along the minimum energy path. As the external force increases, the reaction is first inhibited and then activated. Pulling forces on the most activated scissile bond larger than 3.4 nN (Pendo) and 3.6 nN (Pexo) lead to a faster rupture rate constant than at zero force. The values of the pulling force leading to the switch of the mechanism and to bond rupture for the reactant state of Pendo and Pexo are very close. However, the response Pendo occurs systematically at slightly lower forces than those computed for Pexo. The free energy activation barrier of Pendo for the first bond breaking is systematically lower by 7 to 3 kcal mol−1 as the external force increases, which explains the more labile character of Pendo under tension observed experimentally.11In the intermediate region between the two sequential bond ruptures, the singlet ground state has a diradical character and adopts an extended geometry for both adducts. In this region, the triplet state becomes very close in energy to S0 but the spin–orbit coupling remains too small to induce an intercrossing transition along the minimum energy path. However, the minimum energy crossing between T0 and S0 occurs in the vicinity of the second bond rupture along the Pexo adduct minimum energy path.
Diradical intermediates resulting from an activation by an external mechanical force have been identified experimentally in the case of ring opening of cyclopropanes23 and in the sequential opening of [2 + 2] cyclobutane mechanophores.24,25,29,62–64 Our results suggest that diradical intermediates are also formed in the mechanically activated sequential cycloreversion of [4 + 2] furan–maleimide DA adducts due to the directionality of the pulling force. The effect of the mechanical force is to modify the level structure of the various singlet and triplet states in the intermediate region, inducing several conical intersections within the singlet and triplet manifolds, as well as intersystem singlet-triplet crossings for geometries close to those of the minimum energy path. In particular, the mechanical force stabilizes the diradical intermediates in the lowest singlet and triplet states and does not induce the formation of a zwitterion, as has been reported in the case of an activation by a static electric field41,49 or for substituted addends,44 which leads to a larger charge separation. After the first bond rupture, in the case of the Pexo adduct, small forces of less than 1 nN along the minimum path induce an isomerization of the diradical intermediate from an anti- to a gauche out stereoisomer, which are separated by a small rotational barrier of 3 kcal mol−1. Such internal rotations have been reported for DA adducts undergoing a sequential cycloreversion at zero force,40,44,48 and also the opening of cyclobutane under mechanical force was observed.24,25,29,62–64
The presence of several crossings between electronic states in the vicinity of the minimum energy path as well as the fact that the rotational barriers between stereoisomers of the diradical intermediate can be overcome by small external forces could lead to different adducts upon ring closure when the force is relaxed.44 The switching to a sequential mechanism under force and the predicted production of intermediate diradicals could be potentially observed experimentally with the help of a radical trap,23 and the eventual formation of alternative adducts confirmed by spectroscopy.
Single-molecule force spectroscopy (SMFS) has contributed to further developments in mechanochemistry4,65 by enabling the mechanical activation of covalent bonds,66–68 with applications in irreversible bond scission,17,69–77 and opening of mechanophores.17,26,78–83 Our results offer new perspectives for investigating DA mechanophores by SMFS, in particular the force-clamp characterization of a reversible partial opening by breaking the weakest bond of the adduct only and the investigation of the effect of a photoexcitation of the mechanophore by UV light under force. A recent study indeed reported the involvement of fluorescent radical species in SMFS spectroscopy of a tetraaryl succinonitrile mechanophore.84 In a broader perspective, our results are also relevant for the photochemistry of DA adducts.46,47 They provide insights into the regions of the potential energy surfaces involved in a sequential bond rupture as well as on the relevant conical intersections and spin–orbit intersystem crossings between excited states along the sequential reaction path that could be probed using ultrashort few femtosecond optical pulses that became recently available.85
Data availability
Data for this paper, including optimized geometries for the COGEF path and EFEI and minimum energy intersystem crossings, are available on ZENODO at https://doi.org/10.5281/zenodo.7473211.Author contributions
M. C.-G. carried out the computations. All authors designed the research, analyzed the results and wrote the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The work of M.C.-G., A.S.D. and F.R. is supported by the action of concerted research MECHANOCHEM (ARC 19/23-20, ULiege). Computational resources have been provided by the Consortium des Equipements de Calcul Intensif (CECI), funded by the F.R.S.-FNRS under grant # 2.5020.11. G.D.B. is a Royal Society University Research Fellow.References
- S. Kotha and S. Banerjee, RSC Adv., 2013, 3, 7642–7666 RSC.
- Z. P. Zhang, M. Z. Rong and M. Q. Zhang, Prog. Polym. Sci., 2018, 80, 39–93 CrossRef CAS.
- P. Chakma and D. Konkolewicz, Angew. Chem., Int. Ed., 2019, 58, 9682–9695 CrossRef CAS PubMed.
- Polymer Mechanochemistry, ed. R. Boulatov, Springer, Cham, 2015 Search PubMed.
- H.-Y. Duan, Y.-X. Wang, L.-J. Wang, Y.-Q. Min, X.-H. Zhang and B.-Y. Du, Macromolecules, 2017, 50, 1353–1361 CrossRef CAS.
- B. Lyu, W. Cha, T. Mao, Y. Wu, H. Qian, Y. Zhou, X. Chen, S. Zhang, L. Liu, G. Yang, Z. Lu, Q. Zhu and H. Ma, ACS Appl. Mater. Interfaces, 2015, 7, 6254–6259 CrossRef CAS PubMed.
- X. Hu, M. E. McFadden, R. W. Barber and M. J. Robb, J. Am. Chem. Soc., 2018, 140, 14073–14077 CrossRef CAS PubMed.
- J. Kida, K. Imato, R. Goseki, D. Aoki, M. Morimoto and H. Otsuka, Nat. Commun., 2018, 9, 3504 CrossRef PubMed.
- Y. Min, S. Huang, Y. Wang, Z. Zhang, B. Du, X. Zhang and Z. Fan, Macromolecules, 2015, 48, 316–322 CrossRef CAS.
- R. Stevenson and G. De Bo, J. Am. Chem. Soc., 2017, 139, 16768–16771 CrossRef CAS PubMed.
- Z. Wang and S. L. Craig, Chem. Comm., 2019, 55, 12263–12266 RSC.
- A. Gandini, Prog. Polym. Sci., 2013, 38, 1–29 CrossRef CAS.
- S. Akbulatov and R. Boulatov, ChemPhysChem, 2017, 18, 1422–1450 CrossRef CAS PubMed.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, J. Am. Chem. Soc., 2009, 131, 6377–6379 CrossRef CAS PubMed.
- J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., 2009, 48, 4190–4193 CrossRef CAS PubMed.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martínez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. Niu, M. T. Ong, H. M. Klukovich, A. L. Rheingold, T. J. Martinez and S. L. Craig, Nat. Chem., 2015, 7, 323–327 CrossRef CAS PubMed.
- R. Nixon and G. De Bo, Nat. Chem., 2020, 12, 826–831 CrossRef CAS PubMed.
- E. Izak-Nau, D. Campagna, C. Baumann and R. Göstl, Polym. Chem., 2020, 11, 2274–2299 RSC.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS PubMed.
- C. L. Brown, B. H. Bowser, J. Meisner, T. B. Kouznetsova, S. Seritan, T. J. Martinez and S. L. Craig, J. Am. Chem. Soc., 2021, 143, 3846–3855 CrossRef CAS PubMed.
- R. B. Woodward and R. Hoffmann, Angew. Chem., 1969, 8, 781–853 CrossRef CAS.
- J. M. Lenhardt, M. T. Ong, R. Choe, C. R. Evenhuis, T. J. Martinez and S. L. Craig, Science, 2010, 329, 1057 CrossRef CAS PubMed.
- M. J. Kryger, M. T. Ong, S. A. Odom, N. R. Sottos, S. R. White, T. J. Martinez and J. S. Moore, J. Am. Chem. Soc., 2010, 132, 4558–4559 CrossRef CAS PubMed.
- Z. S. Kean, Z. Niu, G. B. Hewage, A. L. Rheingold and S. L. Craig, J. Am. Chem. Soc., 2013, 135, 13598–13604 CrossRef CAS PubMed.
- Z. Chen, J. A. M. Mercer, X. Zhu, J. A. H. Romaniuk, R. Pfattner, L. Cegelski, T. J. Martinez, N. Z. Burns and Y. Xia, Science, 2017, 357, 475–479 CrossRef CAS PubMed.
- M. Horst, J. Yang, J. Meisner, T. B. Kouznetsova, T. J. Martínez, S. L. Craig and Y. Xia, J. Am. Chem. Soc., 2021, 143, 12328–12334 CrossRef CAS PubMed.
- Z. Chen, X. Zhu, J. Yang, J. A. M. Mercer, N. Z. Burns, T. J. Martinez and Y. Xia, Nat. Chem., 2020, 12, 302–309 CrossRef CAS PubMed.
- Y. Liu, S. Holm, J. Meisner, Y. Jia, Q. Wu, J. Woods Toby, J. Martinez Todd and S. Moore Jeffrey, Science, 2021, 373, 208–212 CrossRef CAS PubMed.
- D. C. Lee, V. K. Kensy, C. R. Maroon, B. K. Long and A. J. Boydston, Angew. Chem., 2019, 131, 5695–5698 CrossRef.
- Y. Sun, W. J. Neary, Z. P. Burke, H. Qian, L. Zhu and J. S. Moore, J. Am. Chem. Soc., 2022, 144, 1125–1129 CrossRef CAS PubMed.
- T. Zeng, X. Hu and M. J. Robb, Chem. Commun., 2021, 57, 11173–11176 RSC.
- M. Zhang and G. De Bo, J. Am. Chem. Soc., 2020, 142, 5029–5033 CrossRef CAS PubMed.
- M. Zhang and G. De Bo, J. Am. Chem. Soc., 2018, 140, 12724–12727 CrossRef CAS PubMed.
- R. Stevenson, M. Zhang and G. De Bo, Polym. Chem., 2020, 11, 2864–2868 RSC.
- X. Hu, T. Zeng, C. C. Husic and M. J. Robb, ACS Cent. Sci., 2021, 7, 1216–1224 CrossRef CAS PubMed.
- X. Hu, T. Zeng, C. C. Husic and M. J. Robb, J. Am. Chem. Soc., 2019, 141, 15018–15023 CrossRef CAS PubMed.
- L. C. Wu and G. De Bo, Synlett, 2022, 33, st-2022-r0064-c Search PubMed.
- R. C. Cioc, M. Crockatt, J. C. van der Waal and P. C. A. Bruijnincx, Angew. Chem., 2022, 61, e202114720 CAS.
- K. Black, P. Liu, L. Xu, C. Doubleday and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12860 CrossRef CAS PubMed.
- R. Meir, H. Chen, W. Lai and S. Shaik, ChemPhysChem, 2010, 11, 301–310 CrossRef CAS PubMed.
- L. Rulíšek, P. Šebek, Z. Havlas, R. Hrabal, P. Čapek and A. Svatoš, J. Org. Chem., 2005, 70, 6295–6302 CrossRef PubMed.
- A. Ogawa and H. Fujimoto, Tetrahedron Lett., 2002, 43, 2055–2057 CrossRef CAS.
- J. Sauer and R. Sustmann, Angew. Chem., 1980, 19, 779–807 CrossRef.
- S. De Feyter, E. W. G. Diau, A. A. Scala and A. H. Zewail, Chem. Phys. Lett., 1999, 303, 249–260 CrossRef CAS.
- E. W. G. Diau, S. De Feyter and A. H. Zewail, Chem. Phys. Lett., 1999, 304, 134–144 CrossRef CAS.
- B. A. Horn, J. L. Herek and A. H. Zewail, J. Am. Chem. Soc., 1996, 118, 8755–8756 CrossRef CAS.
- S. Wilsey, K. N. Houk and A. H. Zewail, J. Am. Chem. Soc., 1999, 121, 5772–5786 CrossRef CAS.
- C. Yang, Z. Liu, Y. Li, S. Zhou, C. Lu, Y. Guo, M. Ramirez, Q. Zhang, Y. Li, Z. Liu, K. N. Houk, D. Zhang and X. Guo, Sci. Adv., 2021, 7, eabf0689 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Chem. Rev., 2016, 116, 14137–14180 CrossRef CAS PubMed.
- M. K. Beyer, J. Chem. Phys., 2000, 112, 7307–7312 CrossRef CAS.
- K. Wolinski and J. Baker, Mol. Phys., 2009, 107, 2403–2417 CrossRef CAS.
- J. Ribas-Arino, M. Shiga and D. Marx, J. Am. Chem. Soc., 2010, 132, 10609–10614 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- J. M. Seminario, Int. J. Quantum Chem., 1996, 60, 1271–1277 CrossRef.
- E. Brémond and C. Adamo, J. Chem. Phys., 2011, 135, 024106 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- M. J. Kryger, A. M. Munaretto and J. S. Moore, J. Am. Chem. Soc., 2011, 133, 18992–18998 CrossRef CAS PubMed.
- H. M. Klukovich, Z. S. Kean, S. T. Iacono and S. L. Craig, J. Am. Chem. Soc., 2011, 133, 17882–17888 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, R. Boulatov and S. L. Craig, Nat. Commun., 2016, 7, 13433 CrossRef PubMed.
- S. Garcia-Manes and A. E. M. Beedle, Nat. Chem., 2017, 1, 0083 CrossRef.
- A.-S. Duwez, S. Cuenot, C. Jérôme, S. Gabriel, R. Jérôme, S. Rapino and F. Zerbetto, Nat. Nanotechnol., 2006, 1, 122–125 CrossRef CAS PubMed.
- M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921–2948 CrossRef CAS PubMed.
- F. R. Kersey, W. C. Yount and S. L. Craig, J. Am. Chem. Soc., 2006, 128, 3886–3887 CrossRef CAS PubMed.
- A. P. Wiita, S. R. K. Ainavarapu, H. H. Huang and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7222–7227 CrossRef CAS PubMed.
- P. Zheng, G. M. Arantes, M. J. Field and H. Li, Nat. Commun., 2015, 6, 7569 CrossRef CAS PubMed.
- S. Akbulatov, Y. Tian, Z. Huang, T. J. Kucharski, Q.-Z. Yang and R. Boulatov, Science, 2017, 357, 299–303 CrossRef CAS PubMed.
- M. Grandbois, Science, 1999, 283, 1727–1730 CrossRef CAS PubMed.
- P. Zheng and H. Li, J. Am. Chem. Soc., 2011, 133, 6791–6798 CrossRef CAS PubMed.
- S. W. Schmidt, P. Filippov, A. Kersch, M. K. Beyer and H. Clausen-Schaumann, ACS Nano, 2012, 6, 1314–1321 CrossRef CAS PubMed.
- A. E. M. Beedle, A. Lezamiz, G. Stirnemann and S. Garcia-Manyes, Nat. Commun., 2015, 6, 7894 CrossRef CAS PubMed.
- M. F. Pill, A. L. L. East, D. Marx, M. K. Beyer and H. Clausen-Schaumann, Angew. Chem., 2019, 58, 9787–9790 CrossRef CAS PubMed.
- D. Schütze, K. Holz, J. Müller, M. K. Beyer, U. Lüning and B. Hartke, Angew. Chem., 2015, 54, 2556–2559 CrossRef PubMed.
- M. M. Hansmann, R. L. Melen, M. Rudolph, F. Rominger, H. Wadepohl, D. W. Stephan and A. S. K. Hashmi, J. Am. Chem. Soc., 2015, 137, 15469–15477 CrossRef CAS PubMed.
- P. A. May and J. S. Moore, Chem. Rev. Soc., 2013, 42, 7497 RSC.
- J. Li, C. Nagamani and J. S. Moore, Acc. Chem. Res., 2015, 48, 2181–2190 CrossRef CAS PubMed.
- H. M. Klukovich, Z. S. Kean, A. L. B. Ramirez, J. M. Lenhardt, J. Lin, X. Hu and S. L. Craig, J. Am. Chem. Soc., 2012, 134, 9577–9580 CrossRef CAS PubMed.
- M. F. Pill, K. Holz, N. Preußke, F. Berger, H. Clausen-Schaumann, U. Lüning and M. K. Beyer, Chem.–Eur. J., 2016, 22, 12034–12039 CrossRef CAS PubMed.
- H. Li and G. C. Walker, ACS Nano, 2017, 11, 28–30 CrossRef CAS PubMed.
- M. van Galen, J. P. Kaniraj, B. Albada and J. Sprakel, J. Phys. Chem. C, 2022, 126, 1215–1221 CrossRef CAS PubMed.
- M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martín, Chem. Rev., 2017, 117, 10760–10825 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A detailed description of computational methods and results of the thermodynamics and kinetics analysis and of the electronic structure methodology. Zip files provide the geometries of both adducts along the CoGEF path computed at the DFT and CAS(4,4) levels, the geometries of the reactant and transition states computed at the DFT level and the geometries at minimum energy intersystem crossing computed at the CAS(4,4) level. See DOI: https://doi.org/10.1039/d2sc05051j |
| This journal is © The Royal Society of Chemistry 2023 |