Open Access Article
Open Access ArticleA theoretical framework for the design of molecular crystal engines†
Cameron J.
Cook
a,
Wangxiang
Li
a,
Brandon F.
Lui
 a,
Thomas J.
Gately
a,
Thomas J.
Gately
 a,
Rabih O.
Al-Kaysi
a,
Rabih O.
Al-Kaysi
 b,
Leonard J.
Mueller
b,
Leonard J.
Mueller
 a,
Christopher J.
Bardeen
a,
Christopher J.
Bardeen
 a and
Gregory J. O.
Beran
a and
Gregory J. O.
Beran
 *a
*a
aDepartment of Chemistry, University of California Riverside, Riverside CA 92521, USA. E-mail: gregory.beran@ucr.edu
bCollege of Science and Health Professions-3124, King Saud Bin Abdulaziz University for Health Sciences, and King Abdullah International Medical Research Center, Ministry of National Guard Health Affairs, Riyadh 11426, Kingdom of Saudi Arabia
First published on 21st December 2022
Abstract
Photomechanical molecular crystals have garnered attention for their ability to transform light into mechanical work, but difficulties in characterizing the structural changes and mechanical responses experimentally have hindered the development of practical organic crystal engines. This study proposes a new computational framework for predicting the solid-state crystal-to-crystal photochemical transformations entirely from first principles, and it establishes a photomechanical engine cycle that quantifies the anisotropic mechanical performance resulting from the transformation. The approach relies on crystal structure prediction, solid-state topochemical principles, and high-quality electronic structure methods. After validating the framework on the well-studied [4 + 4] cycloadditions in 9-methyl anthracene and 9-tert-butyl anthracene ester, the experimentally-unknown solid-state transformation of 9-carboxylic acid anthracene is predicted for the first time. The results illustrate how the mechanical work is done by relaxation of the crystal lattice to accommodate the photoproduct, rather than by the photochemistry itself. The large ∼107 J m−3 work densities computed for all three systems highlight the promise of photomechanical crystal engines. This study demonstrates the importance of crystal packing in determining molecular crystal engine performance and provides tools and insights to design improved materials in silico.
1 Introduction
Organic photomechanical crystals transform light into mechanical work via the changes in solid-state structure that result from a photochemical reaction.1 These structural changes can induce elongation, bending, twisting, photosalience, and other behaviors.2–5 While numerous examples of photomechanical behaviors can be found in the literature,6–14 a predictive understanding of the relationships between molecular structure, crystal packing, photochemical transformation, and the mechanical work output remains elusive. Such understanding is vital for the rational design of photomechanical engines based on molecular crystals.15In principle, determining the work output of a light-induced crystal-to-crystal transformation should be straightforward. In practice, photomechanical crystals present specific challenges that have so far prevented the development of a comprehensive theoretical framework. First, it is often difficult to determine the structure of the product crystal after photoreaction. Performing solid-state photochemical reactions in bulk crystals often causes them to shatter, complicating diffraction experiments.6,16,17 If the photoproduct absorbs strongly at the excitation wavelength (positive photochromism), then a photostationary state is reached and complete conversion is impossible. To circumvent this problem, one might isolate the photoproduct in solution and recrystallize it. Unfortunately, the product crystal grown in this manner may have a different crystal packing from that formed by direct photoconversion in the solid-state.18 Finally, if the reaction is thermally reversible (T-type), the photoproduct may be too short-lived for practical structure determination. Progress in measuring experimental work outputs directly has been made recently,13 though such techniques are not yet widespread.
Even if the photoproduct crystal structure can be determined experimentally, this leads to a second, more fundamental challenge: how does the transformation from the reactant to the product crystal actually occur? As with gas expansion cycles in thermodynamics, this process should consist of a series of well-defined steps, each of which can be associated with an energy change. To simplify the problem, we will concentrate on complete conversion of the reactant to product that gives rise to crystal expansion and contraction. It should be noted that the most commonly reported mode of photomechanical crystal actuation involves bending due to partial conversion that yields a reactant–product bimorph structure.19–21 In principle, a bending crystal can be divided into subdomains that undergo expansion/contraction after complete conversion, so this approach should be general and adaptable to bending as well.
The significant experimental and conceptual challenges in this field motivated us to turn to computational chemistry to predict the structures, transformations, and properties of photomechanical crystals entirely from first-principles. Organic molecular crystal structure prediction has advanced considerably in recent years, thanks in large part to the development of accurate and computationally efficient electronic structure models for the solid state,22–25 which have considerably enhanced researchers' abilities to predict the thermodynamically most stable polymorphs.26–44 As a result, successful examples of crystal structure predictions in the Blind Tests,45–47 pharmaceuticals,48–52 and organic materials53–60 are accumulating rapidly.
Successful application of crystal structure prediction to photomechanical crystals would enable first-principles design and optimization of this promising class of materials. Unfortunately, this effort faces two major challenges. First, instead of generating the landscape of candidate structures for a single species, as in traditional crystal structure prediction, predicting a solid-state photomechanical response requires understanding the structures and transformations between two distinct crystal energy landscapes (reactant and product). Second, energetic stability cannot be the primary criterion for identifying the photochemical polymorph produced by the solid-state reaction. High photon energy and the steric constraints created by the solid-state reaction environment can drive the reaction toward a high-energy, thermodynamically metastable product.61 In other words, the conventional crystal structure prediction goal generating a modest number of low-energy polymorphs is replaced by the challenge of identifying the relevant structure(s) from a much larger pool of higher-energy candidate structures.
Here, we develop a new, first-principles methodology for predicting solid-state molecular crystal photomechanical transformations that overcomes these difficulties. It generates structures using crystal structure prediction, employs a crystalline topochemical hypothesis to predict the solid-state photochemical transformations, and establishes a photomechanical engine cycle that characterizes the anisotropic work produced by the structural changes. This theoretical approach is validated on two well-characterized [4 + 4] anthracene derivative photodimerization systems (9MA and 9TBAE, Fig. 1). This negative photochromic reaction permits complete conversion of the crystals to a stable photodimer form, avoiding mixtures and facilitating comparison to theory. We also use the theory to predict the photodimer crystal structure of a T-type reversible crystal (9AC) that has not yet been measured experimentally but may be more practical for actuator applications. The large ∼107 J m−3 work densities computed for all three systems demonstrate the exceptional promise of organic molecular crystal engines. Moreover, our findings demonstrate how molecular crystal packing plays a key role in determining the anisotropic work generated, emphasizing the value of theoretical tools capable of characterizing the stress and strain generated in these transformations.
2 Methods
2.1 Crystal structure prediction for 9MA
After optimizing the gas-phase monomer and photodimer structures using B3LYP/6-311+G(d)62 in Gaussian09,63 candidate crystal structures for the monomer and photodimer were generated from first-principles via a hierarchical crystal structure prediction protocol. For each species, 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystal structures from 11 common space groups were randomly generated using PyXtal,64 assuming a single molecule in the asymmetric unit (Z′ = 1). These crystal structures were relaxed using the Generalized Amber Force Field (GAFF)65 in CHARMM 45b266 and clustered to eliminate duplicates.
000 crystal structures from 11 common space groups were randomly generated using PyXtal,64 assuming a single molecule in the asymmetric unit (Z′ = 1). These crystal structures were relaxed using the Generalized Amber Force Field (GAFF)65 in CHARMM 45b266 and clustered to eliminate duplicates.
Next, all 281 monomer crystal structures lying within 10 kJ mol−1 of the lowest-energy structure, and all 255 photodimer crystal structures within 25 kJ mol−1 were further relaxed with the semi-empirical HF-3c method67 as implemented in CRYSTAL17.68 The higher energy cutoff for the photodimer landscape was chosen due to the relative sparsity of structures compared to the monomer landscape and the expectation that the SSRD could lie relatively high in energy. HF-3c refinement and another round of structure clustering reduced the landscape to 63 monomer structures within 10 kJ mol−1 and 42 photodimer structures within a 15 kJ mol−1 energy window. Final refinement of those crystal structures was performed using planewave density functional theory (DFT), using the van der Waals-corrected B86bPBE-XDM functional69–71 in QuantumEspresso.72
Energy relationships between the monomer and photodimer landscapes were computed according to,
| 2 9MA → (9MA)2 | (1) |
However, conventional density functionals used in solid-state calculations describe the anthracene photodimerization poorly.61,73–75 The issue stems from delocalization error in the approximate density functionals,76 which artificially stabilizes extended π delocalization found in the anthracene monomer by dozens of kJ mol−1 relative to the photodimer with sp3-hybridized carbon centers and more localized electron density (Fig. 1).61,74,75 Issues arising from DFT delocalization error have been identified in a number of other organic crystals as well.28,42–44,77–80
To address the delocalization error issues inherent in B86bPBE-XDM (and other density functionals) for these systems, an intramolecular correction is applied to all periodic DFT lattice energies. This single-point energy correction replaces the intramolecular energies of the monomer or photodimer with more accurate ones computed at the spin-component-scaled dispersion-corrected second-order Møller–Plesset perturbation theory (SCS-MP2D)75 level,
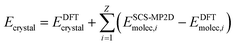 | (2) |
The molecular energies on the right-hand side are computed in the gas-phase using geometries extracted directly from the DFT-optimized crystal. The sum runs over all Z molecules in the unit cell, though space group symmetry can be exploited to compute the gas-phase molecular energies only for the molecules in the asymmetric unit. This correction has been employed successfully in several other systems.43,44,61,79 SCS-MP2D reproduces the benchmark coupled cluster single, doubles, and perturbative triples (CCSD(T)) anthracene photodimerization reaction energy to within 1.2 kJ mol−1.75 Further computational details of the crystal structure prediction can be found in ESI Section S1.†
2.2 Topochemical identification of the solid-state reacted structures
Characterizing the photomechanical transformation and the associated work performed requires identifying the solid-state reacted dimer (SSRD) crystal structure which results from the solid-state reaction. This is done topochemically, replacing the reacting monomer pairs in the monomer crystal structure with photodimers placed at the same center of mass positions and oriented to maximize overlap with the original monomer pair. Constrained DFT geometry optimization of the replaced molecules within the fixed monomer lattice parameters produces the “proto-SSRD,” while subsequent variable-cell relaxation produces the equilibrium SSRD structure. Similarly, one can construct the “proto-monomer” for the reverse dissociation reaction by substituting monomers into the photodimer unit cell. See the Results section and ESI Section S1.2† for more details.2.3 Work density calculations
The elastic work density is evaluated from the DFT-computed Cartesian stress (σ) and strain (ε) tensors for the proto-SSRD/proto-monomer relative to their fully-relaxed equilibrium structures. Tight DFT geometry-optimization criteria were employed to improve convergence of the stress and strain tensors. The orientational dependence of the work density, including both normal and shear contributions, was computed by projecting it onto different crystallographic directions defined by the unit vector![[n with combining circumflex]](https://www.rsc.org/images/entities/char_006e_0302.gif) .
.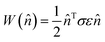 | (3) |
After scanning over all directions ![[n with combining circumflex]](https://www.rsc.org/images/entities/char_006e_0302.gif) , the absolute value of the work densities (in MJ m−3) are plotted as a heat map on the surface of a sphere. Examination of the 9MA proto-SSRD relaxation finds the stress to vary nearly linearly with strain, supporting the assumption of elastic work. See ESI Section S1.3† for further details on the work calculations.
, the absolute value of the work densities (in MJ m−3) are plotted as a heat map on the surface of a sphere. Examination of the 9MA proto-SSRD relaxation finds the stress to vary nearly linearly with strain, supporting the assumption of elastic work. See ESI Section S1.3† for further details on the work calculations.
Ref. 13 and 81 present several performance metrics that can be used to assess an actuator, including the work output (maximum force times the displacement), work capacity (Wcapacity = σmaxεmax), and the power output (work output per unit of time). The work densities computed in eqn (3) are very similar to their work capacity, though the work densities here examine the anisotropic work in various possible directions, rather than focusing on a specific actuator geometry. Consideration of process timescales and power are beyond the scope of this study.
Experimental methods are described in ESI Section S2.†
3 Results and discussion
3.1 Crystal structure prediction of key intermediates for the photomechanical cycle
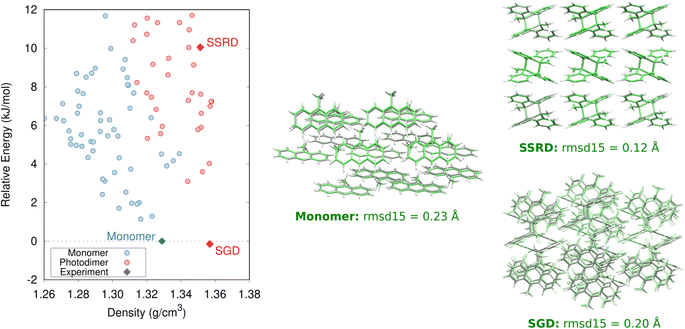
The crystal energy landscape for photomechanical materials based on the anthracene [4 + 4] photodimerization will typically contain at least three notable structures: the reactant crystal, a polymorph of the photochemical product crystallized from solution (referred to as the solution-grown dimer, or SGD), and the SSRD polymorph generated through the solid-state crystal-to-crystal photochemical reaction. The SSRD is central to the photomechanical process, and we hypothesize that the SGD and SSRD crystal structures will match only in rare cases. Our first task is to identify and characterize these structures. The monomer reactant and SGD product will frequently be the thermodynamically most stable polymorphs on their respective landscapes, while the SSRD lies quite a bit higher in energy.The predicted monomer and SGD structures match the experimentally reported crystal structures82 with excellent overlaps of 0.20–0.23 Å using the 15-molecule cluster root-mean-square deviation (rmsd15) metric (Fig. 2).83 The DFT unit cell parameters for the 9MA monomer and SGD are only 1.2% smaller than the experimental ones on average (ESI Table S3†), which is consistent with the underestimation of unit cell volumes expected for comparing 0 K DFT calculations to room-temperature experimental structures.84
While the ability to predict the thermodynamically most stable polymorphs of 9MA and its photodimer correctly is important, understanding the crystal-to-crystal transformation associated with the photomechanical response also requires identifying the SSRD polymorph on the photodimer crystal energy landscape. Energetic stability alone cannot be used as a criterion for the SSRD, since the constraints of the solid-state reaction environment can produce an SSRD that is highly metastable.61 A similar focus on high-energy structures occurs when predicting structures of porous organic materials,56,57,60 though there it stems from the models' omission of guest/solvent molecules which stabilize the pores experimentally.
A key conceptual advance in this paper lies in extending the topochemical principle to the problem of predicting the photoproduct crystal structure, rather than just the photoproduct molecule by itself. Solid-state anthracene [4 + 4] photodimerization reactions only occur when the reactive carbon atoms lie within 4.2 Å and satisfy various orientational constraints.85–87 Moreover, the steric constraints imposed by the crystalline lattice limit molecular reorganization after the photochemical transformation, thereby constraining the photoproduct crystal structure and inhibiting its relaxation to the lowest-energy SGD packing. Therefore, instead of relying on an energetic stability criterion, we identify the SSRD based on the crystal packing relationships that connect structures between the monomer and photodimer crystal energy landscapes.
Specifically, we predict the product of the crystal-to-crystal transformation with no experimental information by generating an initial topochemical SSRD crystal in which the reacting monomer pairs in the predicted monomer crystal are replaced by photodimer molecules having the same positions and orientations, as described in ESI Section S1.2.† Constrained DFT relaxation of this crystal structure with the lattice vectors held fixed at their monomer crystal values produces the proto-SSRD. Subsequent unconstrained relaxation of the proto-SSRD atoms and lattice vectors produces the final equilibrium SSRD structure. Applying this procedure to 9MA (Fig. 3a), we find that the SSRD retains the same P21/c space group as the reactant monomer crystal, and it matches the rank #27 structure on the DFT photodimer crystal structure prediction landscape (Fig. 2) with an excellent rmsd15 overlap of 0.14 Å.
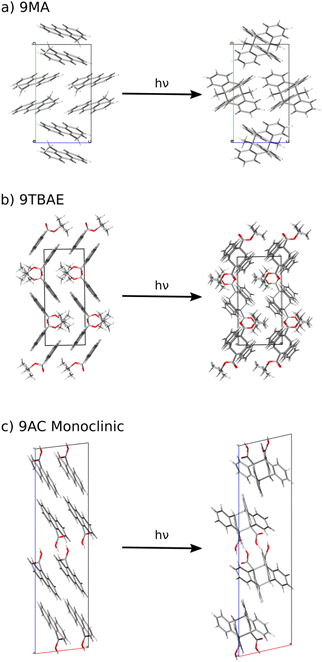 | ||
| Fig. 3 The crystalline topochemical hypothesis generates the SSRD based on the crystal packing of the monomer, as shown here for (a) 9MA, (b) 9TBAE, and (c) 9AC. | ||
Determining the 9MA SSRD crystal structure experimentally is difficult, since bulk crystals fracture after about ∼30% photodimerization under ambient conditions.88 Turowska-Tyrk and coworkers recently showed that photodimerization of single 9MA crystal can be carried to completion without fracture at elevated pressures in a diamond anvil cell.85 The SSRD structure predicted here (at 0 GPa) is an outstanding match for the experimental X-ray crystal structures reported at 0.1 and 0.4 GPa, with rmsd15 values of only 0.12 Å (Fig. 2).
Morimoto et al. observed that single microcrystal plates could expand by a factor of 1.07 along their c-axis while remaining intact.89 Presumably, these crystals also adopt the SSRD structure after conversion. To confirm this, we performed powder X-ray diffraction (PXRD) experiments on 9MA microplates after photodimerization. Fig. 4 compares the experimental PXRD pattern with a simulated one for the predicted SSRD structure. The microplates were not powdered, so their relative peak intensities are different from those in the calculated PXRD pattern. Peak positions match within 0.2°, which is consistent with the differences in volumes between the different experimental pressures and 0 K DFT calculations. Furthermore, the peak with enhanced intensity at 10.6° corresponds to the 001/100 Miller planes, which lie parallel to the bc crystal plane and thus horizontal along the substrate. The preferred orientation of the crystals should lead to enhanced intensity of this peak, as observed. Interestingly, after photoconversion the experimental SSRD pattern disappears over the course of 1 hour as the plates become almost completely amorphous (ESI Fig. S4†). Waiting for 5 days or heating the 9MA sample did not lead to recrystallization into the low energy SGD form, suggesting there is a considerable barrier to reorder the molecules into this polymorph. The rapid loss of the SSRD structure suggests that it is highly unstable. Previously, we observed that 9MA powders appeared to transform directly from monomer to the SGD photodimer structure.19 We suspect that the sample preparation process used in that work, which involved grinding the crystals after UV irradiation, facilitated the SSRD-to-SGD transition and caused us to miss the presence of the SSRD intermediate. All these observations are consistent with the SSRD being a high-energy polymorph that can be stabilized by the application of mechanical pressure.
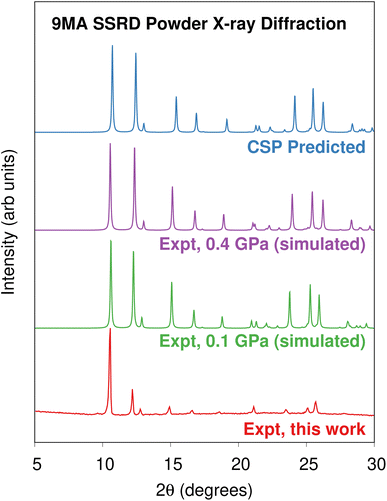 | ||
| Fig. 4 Comparison of the powder X-ray diffractograms obtained on platelets of 9MA after 40 seconds illumination against the powder diffractograms simulated using the experimentally-reported85 SSRD crystal structures obtained at 0.1 and 0.4 GPa and the SSRD structure generated via crystal structure prediction here. | ||
The 9MA monomer to SSRD structural transformation is anisotropic: the DFT-calculated cell contracts 2.6% and 3.7% along the a and b crystallographic axes, but it expands by 5.9% along c and the monoclinic angle β increases by 3.2% (Fig. 5a). The calculated expansions and contractions are slightly less than observed experimentally in the 9MA microplates,89 which may be a consequence of temperature effects since the calculations were done at 0 K. The large elongation along the c axis stems from an increase in lateral spacing between photodimers, rather than from the butterflying of the anthracene rings upon photodimerization. Energetically, the SSRD lies a rather large 10.1 kJ mol−1 above both the monomer and SGD crystal structures. Previous polymorphism surveys suggest that only ∼1–3% of polymorph pairs differ by 10 kJ mol−1 or more, and such large energy differences are even less common for rigid molecules such as 9MA and its photodimer.61,90,91
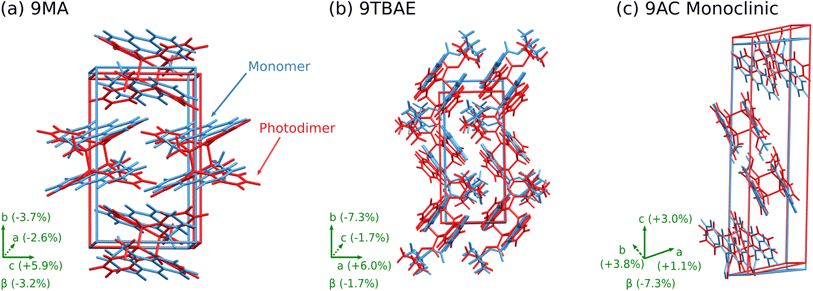 | ||
| Fig. 5 Structure overlays showing the unit cell transformation from monomer (blue) to SSRD (red) for (a) 9MA, (b) 9TBAE, and (c) monoclinic 9AC. | ||
Overall, both crystal structure prediction and the in silico topochemical SSRD formation approach independently produce the same SSRD structure. The topochemical approach identifies the SSRD based on its relationship to the monomer crystal, while full predicted crystal energy landscape of the photodimer provides confirmation of that structure and its energy relative to other observed and/or predicted photodimer polymorphs. Together with the successful prediction of the monomer and SGD crystals, these results demonstrate that the important 9MA crystal structures and the solid-state photochemical transformation can be predicted entirely from first-principles.
Previous NMR crystallography work established the structure of the 9TBAE SSRD as an ensemble of six, closely related and dynamically interconverting structures that differ only subtly in the torsional angles of the tert-butyl groups.92 Applying the topochemical approach to the 9TBAE monomer (Fig. 3b) predicts a P21/n SSRD structure that is similar to those six structures identified in the earlier study. Although the topochemical SSRD here retains the monoclinic symmetry of its parent monomer crystal, it overlaps with the six experimentally inferred orthorhombic structures with rmsd15 values around 0.4 Å. Further confirmation of the topochemically-predicted SSRD comes from the X-ray diffraction structure for a partially photodimerized 9TBAE crystal.18 Extracting photodimer components from that partially-reacted experimental structure and relaxing them with DFT produces a P21/n symmetry structure in excellent agreement with the topochemically predicted one (rmsd15 = 0.11 Å). See ESI Section S4† for additional analysis of these SSRD structures.
Structurally, solid-state photodimerization of 9TBAE induces a much larger unit cell change than 9MA (Fig. 5). The 9TBAE unit cell expands 6.0% along the a axis, largely due to the butterflying motion of the anthracene rings. Simultaneously, the monomers sliding into register as they photodimerize leads to a 7.3% contraction along the b axis. The c and β lattice parameters change only slightly, and the net volume change is small. These structural changes are consistent with the mechanism and magnitudes of nanorod elongation observed previously.6,93
The one-dimensional stacking geometry in the 9AC crystal is qualitatively different from the herringbone geometry seen in 9MA and 9TBAE. This leads to a very different morphology change. The lack of extension along a major crystal axis probably explains why it has been more difficult to detect length changes for 9AC nanorods, although bending and twisting are much more readily observed.94,96,97
3.2 Photomechanical engine cycle
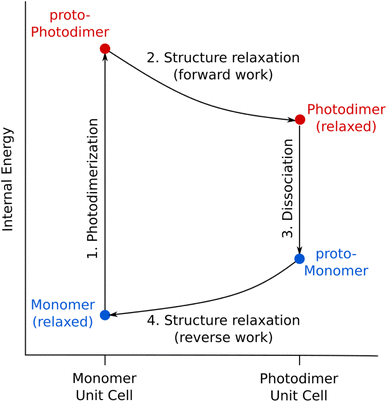
Now that the photochemical structural transformations are understood for all three systems, we need a conceptual framework to predict the work output. We establish an idealized four-step photochemical engine cycle (Fig. 6) that enables characterization of the work that could potentially be performed by a given material:1. The cycle begins with an “instantaneous” and complete solid-state photodimerization of the monomer species, converting the equilibrium monomer crystal to the proto-SSRD. The proto-SSRD retains the monomer unit cell parameters and is therefore highly strained.
2. The proto-SSRD relaxes to its equilibrium geometry. The associated stress release transforms the crystal structure anisotropically and produces “forward” mechanical work.
3. The photodimer dissociates to a strained proto-monomer—the monomer packed within the SSRD lattice parameters.
4. The proto-monomer relaxes back to the original equilibrium monomer crystal structure, producing mechanical work in the “reverse” direction.
In other words, chemical transformation creates the strained crystalline state, and relaxation of the associated stress produces work. Although the lattice parameter changes in Step 4 exactly mirror those from Step 2, the work performed in the forward and reverse directions will differ because the stress/elastic constants differ between the proto-SSRD and proto-monomer. In practice, this means that a photomechanical engine can perform net work similar to a traditional Carnot cycle based on gas expansion/compression. In the case of a photomechanical crystal, the input photon(s) act as an effective high temperature bath.
It is important to emphasize that real-world photomechanical crystals are expected to deviate from this idealized photochemical engine cycle. First, the solid-state photodimerization process does not occur instantly. Nevertheless, Raman spectroscopy experiments in certain photomechanical crystals suggest that the photochemical reaction and resulting crystal-to-crystal transformation do largely precede the relaxation of the unit cell.98,99 Solid-state photochemical reactions can also exhibit cooperative kinetics due to the changing local crystalline environment as the mixture of reacted and unreacted species evolves.100 However, such kinetic effects do not alter the final thermodynamic state achieved after complete reaction of the crystal and are therefore ignored in this idealized engine model.
Second, the solid-state photochemical reaction may not always reach 100% completion, whether due to positive photochromism or crystal packing reasons. For example, photodimerization within the one-dimensional monomer stacks in monoclinic 9AC occurs stochastically and only reaches ∼75% completion, with the remaining monomers becoming isolated and unable to react.97,101 Crystal defects, impurities, and the experimental light source can also impact the extent of reaction.
Third, many photomechanical processes are not reversible in practice. For example, the 9MA SSRD transforms to an amorphous material instead of reverting back to the monomer (ESI Fig. S3†), while the 9TBAE SSRD slowly converts to the SGD.18 On the other hand, 9AC photodimerization is thermally reversible on the timescale of minutes.97 In other photochromic and photomechanical crystals, the reverse reaction can be triggered via a different wavelength of light102,103 or external pressure.104
Despite these caveats, the idealized photomechanical engine cycle presented here provides a useful framework for quantifying the nature and magnitude of work that could hypothetically be performed by the system and for comparing the photomechanical responses of different materials.
3.3 Photomechanical performance
Having defined the photomechanical engine cycle, we analyze the photomechanical performance of 9MA, 9TBAE, and monoclinic 9AC. There are several different energies that are involved in the photomechanical cycle. We first consider the energetics of the photochemical reaction itself. The computed solid-state photodimerization reaction energies differ significantly across 9MA, 9TBAE, and 9AC. 9MA photodimerization is the least endothermic at 10.1 kJ mol−1. For 9TBAE, the photodimerization energy increases to 32.1 kJ mol−1, reflecting the steric penalty of the bulky tert-butyl ester groups. The 9TBAE SSRD is computed here to lie 12.0 kJ mol−1 above the SGD, similar to what was found previously.61 On the other hand, the 101.2 kJ mol−1 photodimerization energy for monoclinic 9AC is several-times larger than the other two systems. The constraints of maintaining the hydrogen-bonded tetramer units within the 9AC lattice make this solid-state reaction energy even larger than the already endothermic 9AC gas-phase photodimerization.95 The highly endothermic forward reaction in 9AC could imply a relatively small reverse reaction thermal barrier in accord with the Hammond postulate. This might explain why 9AC photodimerization is thermally reversible, unlike 9MA and 9TBAE. However, detailed investigation of the reaction kinetics is beyond the scope of the present study. In any case, all of these endothermic reaction energies are small relative to the 300 kJ mol−1 energy input provided by the 400 nm photons driving the dimerization.In our photomechanical engine framework, the actual mechanical work is done not by the photoreaction, but by the subsequent relaxation of the crystal lattice to accommodate the newly formed photoproduct. Fig. 7 presents the energies for each step of the cycle in each species, while Fig. 8 plots the corresponding anisotropic work densities for the forward photodimerization (Step 2) and reverse dissociation (Step 4) portions of the engine cycle.
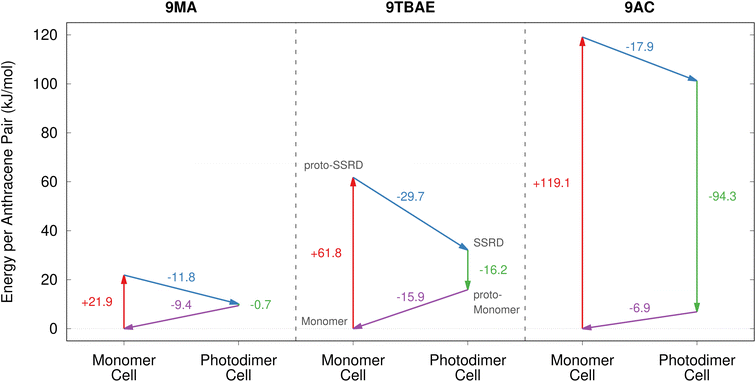 | ||
| Fig. 7 The energetics associated with the four stages of the photomechanical engine cycle differ significantly across 9MA, 9TBAE, and monoclinic 9AC. | ||
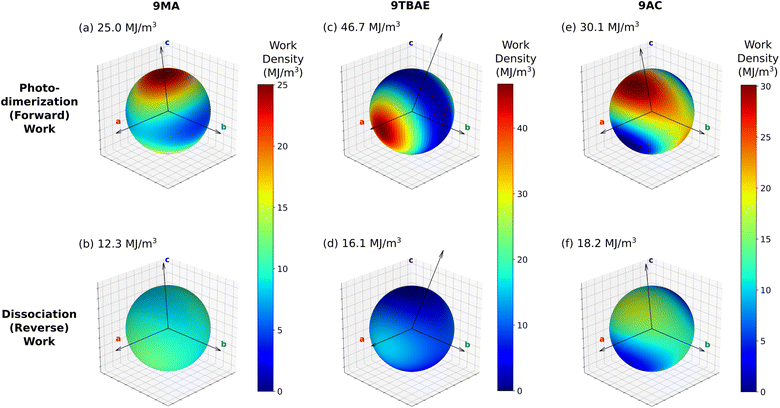
Consider first the forward photodimerization process in 9MA. The proto-SSRD lies 21.9 kJ mol−1 above the equilibrium monomer crystal. Relaxation of the proto-SSRD unit cell to its equilibrium geometry stabilizes it by 11.8 kJ mol−1 (for a net reaction energy of 10.1 kJ mol−1). Fig. 8a plots the computed elastic work produced by relaxation of the proto-SSRD. The maximal 25.0 MJ m−3 work density occurs roughly along the c axis, which is unsurprising given the large 5.4% elongation in that direction. Much less work is produced by the smaller contractions along the a and b axis.
While 9MA does not exhibit solid-state photochemical reversibility experimentally, we can examine what would happen if it completed the photomechanical engine cycle. The proto-monomer formed via dissociation within the photodimer unit cell lattice parameters is 0.7 kJ mol−1 more stable than the SSRD, and it relaxes 9.4 kJ mol−1 back to the original monomer unit cell. So while the lattice parameter changes upon dissociation mirror those from the photodimerization, the smaller stress and relaxation energy associated with photodimer dissociation translate to a maximum elastic work density of only 12.3 MJ m−3 for Step 4 of the engine cycle (Fig. 8b) that is half as large as the forward (Step 2) work.
9TBAE exhibits somewhat larger energy changes than 9MA throughout the engine cycle (Fig. 7). At the same time, the maximum forward-direction work density of 46.7 MJ m−3 for 9TBAE (Fig. 8c) is nearly double that of 9MA. Notably, the 6.0% expansion along the a axis produces far more work than the 8.5% contraction along the b. The a expansion reflects the bending out of the anthracene rings, while the b contraction stems from the energetically “softer” compression of the void space created as the monomer units slide into register to react.
As noted earlier, photodimerization of monoclinic 9AC is highly endothermic. The proto-SSRD lies 119.1 kJ mol−1 above the monomer, compared to 21.9 and 61.0 kJ mol−1 for 9MA and 9TBAE, respectively. However, the 17.9 kJ mol−1 relaxation energy of the 9AC proto-SSRD is intermediate between that of 9MA (11.8 kJ mol−1) and 9TBAE (31.5 kJ mol−1). Correspondingly, the maximal work density of 30.1 in the forward direction is closer to that of 9MA than that of 9TBAE (Fig. 8e). Whereas the maximal work density for 9MA and 9TBAE is performed along a crystallographic axis, the maximal work density in 9AC occurs in between the a and c axes—it stems largely from the 7.3% contraction of the β angle upon photodimerization. As for 9MA, the reverse work resulting from the photodimer dissociations in 9TBAE and 9AC are substantially smaller than for the forward photodimerizations (Fig. 8d and f).
Taken together, these results reveal several important features of these photomechanical crystals: first, the model predicts photomechanical crystal work densities of ∼107 J m−3, which is several orders of magnitude larger than the experimental work densities that have been reported experimentally to-date for thermosalient and photomechanical organic crystal actuators (∼10–105 J m−3)13,81,105 or photomechanical polymers (up to ∼105 J m−3).13,106 It will be important to see if future experiments can confirm these high predicted work densities. Second, the work resulting from the photodimerization is roughly double that produced by the dissociation. This reflects how the anthracene monomer crystals deform much more readily (i.e. with less stress) than the photodimer ones. Third, the anisotropic structural changes produce work that is also highly anisotropic. This highlights the importance of crystal morphology and orientation for device performance. Fourth, the amount of the work performed by a switchable photomechanical material cannot always be inferred from the crystallographic change in lattice parameters (strain) alone; the stress component of the work also depends significantly on the molecular packing. This is evident in the disparities seen for the 9TBAE work densities along the a and b axes and in the differences between the forward and reverse directions for all three systems. Fifth, the reaction energetics are somewhat decoupled from the amount of photomechanical work performed. 9AC photodimerization is much more endothermic than the other two species, but 9TBAE can perform considerably more mechanical work. This suggests that it may be possible to design materials that tune the reaction reversibility and the photomechanical work semi-independently.
Finally, we briefly consider the photon-to-work efficiencies of these photomechanical engine cycles. Based on the ∼12–30 kJ mol−1 Step 2 relaxation energies per reactive pair in the engine cycle (Fig. 7), ∼5–10% of the input 400 nm (300 kJ mol−1) photon energy is converted to forward work. Subtracting the energy change from the reverse direction (Fig. 7, Step 4), we estimate that ∼1–5% of the input photon energy is converted to net work. Of course, given the anisotropy of the structure transformation and its resulting work, not all of that relaxation energy will translate into the forward/reverse work for a given actuator mode. Nevertheless, the efficiencies will likely remain in the range of a few percent for these photomechanical engines. For comparison, experimental photon-to-work efficiencies up to 0.1% have been determined for the bending motions of azobenzenes,13 though they are frequently much lower for photomechanical actuators.13,107 At the other extreme, a simple 1-D model suggests that efficiencies of up to 55% are achievable in principle.108
3.4 Future prospects for rational design
Looking forward, the techniques described here create, for the first time, the opportunity to design new photomechanical derivatives in silico. To do so, one might perform crystal structure prediction for a series of reactant species to identify the most stable crystal structure(s), the potential for polymorphism,109 and to what extent the stable crystal packings satisfy topochemical constraints for the desired solid-state reactions.Assuming that the photochemistry is not prevented by steric or excitonic effects in the crystal, the photochemical transformation and mechanical properties can be computed inexpensively from the reactant crystal structures, as demonstrated here for 9TBAE and 9AC. Anisotropic work density calculations can provide guidance on the potential performance of a material and how one should design an actuator that maximizes the work performed for a desired task. For example, to lift an object from below using a linear actuator, one might focus on forward expansion work and let gravity facilitate the reverse contraction process. On the other hand, linear contraction work could be used to lift an object from above. From Fig. 5 and 8, we can see that the same crystal can be used for both types of work simply by changing its orientation with respect to the load. For the most promising species, one might obtain further insights into the viability, stability, and reversibility of the system by exploring the full crystal energy landscape of the photoproduct and assessing the reaction energetics and structural relationships among different photoproduct polymorphs (e.g. SSRD vs. SGD).61,95
4 Conclusions
This study demonstrates how solid-state photochemical transformations in organic crystals can be predicted entirely from first principles. It addresses several long-standing challenges surrounding the design of solid-state photoswitching and photomechanical systems, including the difficulties associated with determining the crystal structures of the photoproducts, with anticipating how changes to molecular structures will impact the crystal structures, and with understanding how crystal structure determines the mechanical response properties. The proposed photomechanical engine cycle provides a framework for characterizing the anisotropic photomechanical responses in these systems. It can be used to identify which crystal orientations or morphologies can best exploit the work produced by the photochemical transformation and to compare the potential for photomechanical work across different materials.While the present study focuses on anthracene-based crystals, these same techniques can readily be applied to other solid-state photoswitching crystals, such as azobenzenes and diarylethenes. The detailed atomistic pictures generated with these techniques could also provide the foundation for multiscale models13 that could predict photomechanical behaviors in nanoscale actuators and would facilitate the development of practical organic crystal engines.
Data availability
All relevant data is included in the ESI† materials already.Author contributions
Beran conceived the research project with Bardeen, with additional input from Mueller and Al-Kaysi. The computational studies and data analysis were carried out by Cook and Beran. The experimental studies and data analysis were performed by Li, Lui, and Gately, under Bardeen’s supervision. The manuscript was primarily written by Beran and Bardeen, with contributions from the other authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. J. O. B. acknowledges support from the National Science Foundation (CHE-1955554) and supercomputer time from XSEDE (TG-CHE110064), C. J. B. acknowledges support from the Office of Naval Research (MURI on Photomechanical Material Systems; ONR N00014-18-1-2624), and L. J. M. acknowledges support from the National Institutes of Health (R35GM145369). We thank Alex Greaney for helpful discussions.Notes and references
- P. Naumov, D. P. Karothu, E. Ahmed, L. Catalano, P. Commins, J. Mahmoud Halabi, M. B. Al-Handawi and L. Li, J. Am. Chem. Soc., 2020, 142, 13256–13272 CrossRef CAS PubMed.
- T. Kim, L. Zhu, R. O. Al-Kaysi and C. J. Bardeen, ChemPhysChem, 2014, 15, 400–414 CrossRef CAS PubMed.
- P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490 CrossRef CAS PubMed.
- Photomechanical Materials, Composites, and Systems, ed. T. J. White, Wiley, Chichester, UK, 2017 Search PubMed.
- Mechanically Responsive Materials for Soft Robotics, ed. H. Koshima, Wiley, 2020 Search PubMed.
- R. O. Al-Kaysi, A. M. Müller and C. J. Bardeen, J. Am. Chem. Soc., 2006, 128, 15938–15939 CrossRef CAS PubMed.
- S. Kobatake, S. Takami, H. Muto, T. Ishikawa and M. Irie, Nature, 2007, 446, 778–781 CrossRef CAS PubMed.
- M. Morimoto and M. Irie, J. Am. Chem. Soc., 2010, 132, 14172–14178 CrossRef CAS PubMed.
- H. Koshima, N. Ojima and H. Uchimoto, J. Am. Chem. Soc., 2009, 131, 6890–6891 CrossRef CAS PubMed.
- O. S. Bushuyev, A. Tomberg, T. Friščić and C. J. Barrett, J. Am. Chem. Soc., 2013, 135, 12556–12559 CrossRef CAS PubMed.
- H. Wang, P. Chen, Z. Wu, J. Zhao, J. Sun and R. Lu, Angew. Chem., Int. Ed., 2017, 56, 9463–9467 CrossRef CAS PubMed.
- P. Naumov, J. Kowalik, K. M. Solntsev, A. Baldridge, J.-S. Moon, C. Kranz and L. M. Tolbert, J. Am. Chem. Soc., 2010, 132, 5845–5857 CrossRef CAS PubMed.
- J. Mahmoud Halabi, E. Ahmed, S. Sofela and P. Naumov, Proc. Nat. Acad. Sci., 2021, 118, 1–7 CrossRef PubMed.
- D. Kitagawa, H. Tsujioka, F. Tong, X. Dong, C. J. Bardeen and S. Kobatake, J. Am. Chem. Soc., 2018, 140, 4208–4212 CrossRef CAS PubMed.
- A. Colin-Molina, D. P. Karothu, M. J. Jellen, R. A. Toscano, M. A. Garcia-Garibay, P. Naumov and B. Rodríguez-Molina, Matter, 2019, 1, 1033–1046 CrossRef.
- D.-K. Bučar and L. R. MacGillivray, J. Am. Chem. Soc., 2007, 129, 32–33 CrossRef PubMed.
- A. E. Keating and M. A. Garcia-Garibay, Photochemical Solid-To-Solid Reaction in Organic and Inorganic Photochemistry, eds. Ramamurthy, V. and Schanze, K., Marcel Dekker, New York, 1998, vol. 2, pp. 195–248 Search PubMed.
- L. Zhu, A. Agarwal, J. Lai, R. O. Al-Kaysi, F. S. Tham, T. Ghaddar, L. Mueller and C. J. Bardeen, J. Mater. Chem., 2011, 21, 6258–6268 RSC.
- T. Kim, L. Zhu, L. J. Mueller and C. J. Bardeen, J. Am. Chem. Soc., 2014, 136, 6617–6625 CrossRef CAS PubMed.
- D. Kitagawa and S. Kobatake, J. Phys. Chem. C, 2013, 117, 20887–20892 CrossRef CAS.
- N. K. Nath, L. Pejov, S. M. Nichols, C. Hu, N. Saleh, B. Kahr and P. Naumov, J. Am. Chem. Soc., 2014, 136, 2757–2766 CrossRef CAS PubMed.
- G. J. O. Beran, Chem. Rev., 2016, 116, 5567–5613 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- J. Hoja, A. M. Reilly and A. Tkatchenko, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1294 Search PubMed.
- J. Hermann, R. A. DiStasio and A. Tkatchenko, Chem. Rev., 2017, 117, 4714–4758 CrossRef CAS PubMed.
- A. Otero-De-La-Roza, B. H. Cao, I. K. Price, J. E. Hein and E. R. Johnson, Angew. Chem., Int. Ed., 2014, 53, 7879–7882 CrossRef CAS PubMed.
- S. R. Whittleton, A. Otero-de-la Roza and E. R. Johnson, J. Chem. Theory Comput., 2017, 13, 441–450 CrossRef CAS PubMed.
- S. R. Whittleton, A. Otero-de-la Roza and E. R. Johnson, J. Chem. Theory Comput., 2017, 13, 5332–5342 CrossRef CAS PubMed.
- D. E. Braun, J. A. McMahon, L. H. Koztecki, S. L. Price and S. M. Reutzel-Edens, Cryst. Growth Des., 2014, 14, 2056–2072 CrossRef CAS.
- D. E. Braun, S. R. Lingireddy, M. D. Beidelschies, R. Guo, P. Müller, S. L. Price and S. M. Reutzel-Edens, Cryst. Growth Des., 2017, 17, 5349–5365 CrossRef CAS PubMed.
- D. E. Braun, J. A. McMahon, R. M. Bhardwaj, J. Nyman, M. A. Neumann, J. Van De Streek and S. M. Reutzel-Edens, Cryst. Growth Des., 2019, 19, 2947–2962 CrossRef CAS.
- D. H. Case, V. K. Srirambhatla, R. Guo, R. E. Watson, L. S. Price, H. Polyzois, J. K. Cockcroft, A. J. Florence, D. A. Tocher and S. L. Price, Cryst. Growth Des., 2018, 18, 5322–5331 CrossRef CAS.
- E. Schur, J. Bernstein, L. S. Price, R. Guo, S. L. Price, S. H. Lapidus and P. W. Stephens, Cryst. Growth Des., 2019, 19, 4884–4893 CrossRef CAS.
- M.-A. Perrin, M. A. Neumann, H. Elmaleh and L. Zaske, Chem. Commun., 2009, 3181–3183 RSC.
- A. Asmadi, M. A. Neumann, J. Kendrick, P. Girard, M. A. Perrin and F. J. J. Leusen, J. Phys. Chem. B, 2009, 113, 16303–16313 CrossRef CAS PubMed.
- A. D. Bond, K. A. Solanko, J. van de Streek and M. A. Neumann, CrystEngComm, 2011, 13, 1768 RSC.
- G. R. Woollam, M. A. Neumann, T. Wagner and R. J. Davey, Faraday Discuss., 2018, 211, 209–234 RSC.
- J. Hoja and A. Tkatchenko, Faraday Discuss., 2018, 211, 253–274 RSC.
- J. Hoja, H.-Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio and A. Tkatchenko, Sci. Adv., 2019, 5, eaau3338 CrossRef PubMed.
- M. Mortazavi, J. Hoja, L. Aerts, L. Quéré, J. van de Streek, M. A. Neumann and A. Tkatchenko, Commun. Chem., 2019, 2, 70 CrossRef.
- G. Sun, X. Liu, Y. A. Abramov, S. O. Nilsson Lill, C. Chang, V. Burger and A. Broo, Cryst. Growth Des., 2021, 21, 1972–1983 CrossRef CAS.
- C. Greenwell, J. L. McKinley, P. Zhang, Q. Zeng, G. Sun, B. Li, S. Wen and G. J. O. Beran, Chem. Sci., 2020, 11, 2200–2214 RSC.
- C. Greenwell and G. J. O. Beran, Cryst. Growth Des., 2020, 20, 4875–4881 CrossRef CAS.
- G. J. O. Beran, I. J. Sugden, C. Greenwell, D. H. Bowskill, C. C. Pantelides and C. S. Adjiman, Chem. Sci., 2022, 13, 1288–1297 RSC.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Cryst. B, 2009, 65, 107–125 CrossRef CAS PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Cryst. B, 2011, 67, 535–551 CrossRef CAS PubMed.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Cryst. B, 2016, 72, 439–459 CrossRef CAS PubMed.
- M. A. Neumann, J. van de Streek, F. P. A. Fabbiani, P. Hidber and O. Grassmann, Nat. Commun., 2015, 6, 7793 CrossRef CAS PubMed.
- A. G. Shtukenberg, C. T. Hu, Q. Zhu, M. U. Schmidt, W. Xu, M. Tan and B. Kahr, Cryst. Growth Des., 2017, 17, 3562–3566 CrossRef CAS.
- A. G. Shtukenberg, M. Tan, L. Vogt-Maranto, E. J. Chan, W. Xu, J. Yang, M. E. Tuckerman, C. T. Hu and B. Kahr, Cryst. Growth Des., 2019, 19, 4070–4080 CrossRef CAS.
- E. L. Stevenson, R. W. Lancaster, A. B. M. Buanz, L. S. Price, D. A. Tocher and S. L. Price, CrystEngComm, 2019, 21, 2154–2163 RSC.
- S. Askin, J. K. Cockcroft, L. S. Price, A. D. Gonçalves, M. Zhao, D. A. Tocher, G. R. Williams, S. Gaisford and D. Q. M. Craig, Cryst. Growth Des., 2019, 19, 2751–2757 CrossRef CAS.
- A. N. Sokolov, S. Atahan-Evrenk, R. Mondal, H. B. Akkerman, R. S. Sánchez-Carrera, S. Granados-Focil, J. Schrier, S. C. Mannsfeld, A. P. Zoombelt, Z. Bao and A. Aspuru-Guzik, Nat. Commun., 2011, 2, 437 CrossRef PubMed.
- E. O. Pyzer-Knapp, H. P. G. Thompson, F. Schiffmann, K. E. Jelfs, S. Y. Chong, M. A. Little, A. I. Cooper and G. M. Day, Chem. Sci., 2014, 5, 2235–2245 RSC.
- E. H. Wolpert and K. E. Jelfs, Chem. Sci., 2022, 13, 13588–13599 RSC.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657–664 CrossRef CAS PubMed.
- P. Cui, D. P. McMahon, P. R. Spackman, B. M. Alston, M. A. Little, G. M. Day and A. I. Cooper, Chem. Sci., 2019, 10, 9988–9997 RSC.
- R. L. Greenaway, V. Santolini, A. Pulido, M. A. Little, B. M. Alston, M. E. Briggs, G. M. Day, A. I. Cooper and K. E. Jelfs, Angew. Chem., Int. Ed., 2019, 58, 16275–16281 CrossRef CAS PubMed.
- C. Y. Cheng, J. E. Campbell and G. M. Day, Chem. Sci., 2020, 11, 4922–4933 RSC.
- Q. Zhu, J. Johal, D. E. Widdowson, Z. Pang, B. Li, C. M. Kane, V. Kurlin, G. M. Day, M. A. Little and A. I. Cooper, J. Am. Chem. Soc., 2022, 144, 9893–9901 CrossRef CAS PubMed.
- G. J. O. Beran, CrystEngComm, 2019, 21, 758–764 RSC.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- S. Fredericks, K. Parrish, D. Sayre and Q. Zhu, Comput. Phys. Comm., 2021, 261, 107810 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comp. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comp. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- R. Sure and S. Grimme, J. Comp. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1986, 85, 7184–7187 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. Otero-de-la Roza and E. R. Johnson, J. Chem. Phys., 2012, 136, 174109 CrossRef CAS PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys. Condens. Mat., 2017, 29, 465901 CrossRef CAS PubMed.
- S. Grimme, C. Diedrich and M. Korth, Angew. Chem., Int. Ed., 2006, 45, 625–629 CrossRef CAS PubMed.
- J. Řezáč, C. Greenwell and G. J. O. Beran, J. Chem. Theory Comput., 2018, 14, 4711–4721 CrossRef PubMed.
- C. Greenwell, J. Řezáč and G. J. O. Beran, Phys. Chem. Chem. Phys., 2022, 24, 3695–3712 RSC.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- L. M. LeBlanc, S. G. Dale, C. R. Taylor, A. D. Becke, G. M. Day and E. R. Johnson, Angew. Chem., Int. Ed., 2018, 57, 14906–14910 CrossRef CAS PubMed.
- A. Otero-de-la Roza, L. M. LeBlanc and E. R. Johnson, J. Chem. Theory Comput., 2019, 15, 4933–4944 CrossRef CAS PubMed.
- C. Greenwell and G. J. O. Beran, J. Mater. Chem. C, 2021, 9, 2848–2857 RSC.
- G. J. O. Beran, S. E. Wright, C. Greenwell and A. J. Cruz-Cabeza, J. Chem. Phys., 2022, 156, 104112 CrossRef CAS PubMed.
- D. P. Karothu, J. Mahmoud Halabi, L. Li, A. Colin-Molina, B. Rodríguez-Molina and P. Naumov, Adv. Mater., 2020, 32, 1906216 CrossRef CAS.
- A. F. Mabied, M. Müller, R. E. Dinnebier, S. Nozawa, M. Hoshino, A. Tomita, T. Sato and S. I. Adachi, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 424–430 CrossRef CAS PubMed.
- J. A. Chisholm and W. D. S. Motherwell, J. Appl. Crystallogr., 2005, 38, 228–231 CrossRef.
- J. L. McKinley and G. J. O. Beran, J. Chem. Theory Comput., 2019, 15, 5259–5274 CrossRef CAS PubMed.
- J. Bakowicz and I. Turowska-Tyrk, Acta Cryst. B, 2022, 78, 223–230 CrossRef CAS PubMed.
- H. Ihmels, D. Leusser, M. Pfeiffer and D. Stalke, Tetrahedron, 2000, 56, 6867–6875 CrossRef CAS.
- W. N. Wang and W. Jones, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1994, 242, 227–240 CrossRef.
- I. Turowska-Tyrk and E. Trzop, Acta Cryst. B, 2003, 59, 779–786 CrossRef PubMed.
- K. Morimoto, D. Kitagawa, F. Tong, K. Chalek, L. J. Mueller, C. J. Bardeen and S. Kobatake, Angew. Chem., Int. Ed., 2022, 61, e202114089 CAS.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635 RSC.
- C. Yang, L. Zhu, R. A. Kudla, J. D. Hartman, R. O. Al-Kaysi, S. Monaco, B. Schatschneider, A. Magalhaes, G. J. O. Beran, C. J. Bardeen and L. J. Mueller, CrystEngComm, 2016, 18, 7319–7329 RSC.
- K. R. Chalek, X. Dong, F. Tong, R. A. Kudla, L. Zhu, A. D. Gill, W. Xu, C. Yan, J. D. Hartman, A. Magalhaes, R. O. Al-Kaysi, R. C. Hayward, R. J. Hooley, G. J. O. Beran, C. J. Bardeen and L. J. Mueller, Chem. Sci., 2021, 12, 453–463 RSC.
- L. Zhu, F. Tong, C. Salinas, M. K. Al-Muhanna, F. S. Tham, D. Kisailus, R. O. Al-Kaysi and C. J. Bardeen, Chem. Mater., 2014, 26, 6007–6015 CrossRef CAS.
- T. J. Gately, W. Sontising, C. J. Easley, I. Islam, R. O. Al-Kaysi, G. J. O. Beran and C. J. Bardeen, CrystEngComm, 2021, 23, 5931–5943 RSC.
- R. O. Al-Kaysi and C. J. Bardeen, Adv. Mater., 2007, 19, 1276–1280 CrossRef CAS.
- L. Zhu, R. O. Al-Kaysi and C. J. Bardeen, J. Am. Chem. Soc., 2011, 133, 12569–12575 CrossRef CAS PubMed.
- T. Salzillo and A. Brillante, CrystEngComm, 2019, 21, 3127–3136 RSC.
- T. Salzillo, I. Bilotti, R. G. Della Valle, E. Venuti and A. Brillante, J. Am. Chem. Soc., 2012, 134, 17671–17679 CrossRef CAS PubMed.
- K. Morimoto, D. Kitagawa, C. J. Bardeen and S. Kobatake, Chem. Eur. J., 2022 DOI:10.1002/chem.202203291.
- R. Moré, G. Busse, J. Hallmann, C. Paulmann, M. Scholz and S. Techert, J. Phys. Chem. C, 2010, 114, 4142–4148 CrossRef.
- M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174–12277 CrossRef CAS PubMed.
- O. Sato, Nat. Chem., 2016, 8, 644–656 CrossRef CAS PubMed.
- S. R. Jezowski, L. Zhu, Y. Wang, A. P. Rice, G. W. Scott, C. J. Bardeen and E. L. Chronister, J. Am. Chem. Soc., 2012, 134, 7459–7466 CrossRef CAS PubMed.
- D. P. Karothu, R. Ferreira, G. Dushaq, E. Ahmed, L. Catalano, J. M. Halabi, Z. Alhaddad, I. Tahir, L. Li, S. Mohamed, M. Rasras and P. Naumov, Nat. Commun., 2022, 13, 2823 CrossRef CAS PubMed.
- T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia and T. J. White, Science, 2015, 347, 982–984 CrossRef CAS PubMed.
- X. Dong, F. Tong, K. M. Hanson, R. O. Al-Kaysi, D. Kitagawa, S. Kobatake and C. J. Bardeen, Chem. Mater., 2019, 31, 1016–1022 CrossRef CAS.
- A. J. Berges and C. J. Bardeen, Photochem. Photobiol. Sci., 2022, 21, 1845–1852 CrossRef CAS PubMed.
- S. L. Price, D. E. Braun and S. M. Reutzel-Edens, Chem. Commun., 2016, 52, 7065–7077 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational details, experimental methods and data, crystal structure prediction results, comparisons of predicted and experimental crystal structures, and tabulation of the unit transformations and maximum computed work densities. See DOI: https://doi.org/10.1039/d2sc05549j |
| This journal is © The Royal Society of Chemistry 2023 |