Open Access Article
Open Access ArticleThermal site energy fluctuations in photosystem I: new insights from MD/QM/MM calculations†
Sebastian
Reiter
 a,
Ferdinand L.
Kiss
a,
Ferdinand L.
Kiss
 a,
Jürgen
Hauer
a,
Jürgen
Hauer
 b and
Regina
de Vivie-Riedle
b and
Regina
de Vivie-Riedle
 *a
*a
aDepartment of Chemistry, Ludwig-Maximilians-Universität München, Butenandtstr. 11, 81377 Munich, Germany. E-mail: regina.de_vivie@cup.uni-muenchen.de
bDepartment of Chemistry, Technical University of Munich, Lichtenbergstr. 4, Garching, 85747, Germany
First published on 6th February 2023
Abstract
Cyanobacterial photosystem I (PSI) is one of the most efficient photosynthetic machineries found in nature. Due to the large scale and complexity of the system, the energy transfer mechanism from the antenna complex to the reaction center is still not fully understood. A central element is the accurate evaluation of the individual chlorophyll excitation energies (site energies). Such an evaluation must include a detailed treatment of site specific environmental influences on structural and electrostatic properties, but also their evolution in the temporal domain, because of the dynamic nature of the energy transfer process. In this work, we calculate the site energies of all 96 chlorophylls in a membrane-embedded model of PSI. The employed hybrid QM/MM approach using the multireference DFT/MRCI method in the QM region allows to obtain accurate site energies under explicit consideration of the natural environment. We identify energy traps and barriers in the antenna complex and discuss their implications for energy transfer to the reaction center. Going beyond previous studies, our model also accounts for the molecular dynamics of the full trimeric PSI complex. Via statistical analysis we show that the thermal fluctuations of single chlorophylls prevent the formation of a single prominent energy funnel within the antenna complex. These findings are also supported by a dipole exciton model. We conclude that energy transfer pathways may form only transiently at physiological temperatures, as thermal fluctuations overcome energy barriers. The set of site energies provided in this work sets the stage for theoretical and experimental studies on the highly efficient energy transfer mechanisms in PSI.
1 Introduction
In oxygenic photosynthesis, photoautotrophic organisms harvest solar energy to drive a light-induced cascade of electron and proton transfers.1 Photosystem I (PSI) plays a crucial role in this process as it catalyzes the oxidation of plastocyanines to subsequently reduce ferredoxins. This energy conversion step occurs with a near-unity efficiency. An in-depth understanding of this remarkably high efficiency may guide future designs of artificial light harvesting (LH) systems.2–4The cyanobacterial (T. elongatus) PSI is a trimeric trans-membrane protein supercomplex.5–7 Each monomer comprises twelve protein subunits, 96 chlorophylls, 22 carotenoids, four lipids, three iron–sulfur clusters and two phylloquinones.6,7 The chlorophyll a molecules are organized in an antenna complex of 90 pigments and a reaction center (RC) of six chlorophylls arranged in two pseudo-symmetrical branches, denoted A and B.6,7 After the initial excitation of the PSI antenna complex, the generated Frenkel-exciton has an estimated lifetime of around 35 ps, followed by charge separation inside the RC.8–12 At the very center of the RC lies the special pair P700, ultimately acting as the electron donor.13–15
There are still many open questions regarding the funneling of energy from the antenna complex to the RC and the onset of charge separation therein.16 The large amount of pigments and their strongly overlapping absorption bands obscure clear experimental access to the excited state processes inside PSI.8,17–21 Here, theoretical insights can complement experiments in disentangling and explaining the measured optical responses to deduce mechanisms for the energy and charge transfer.18,19,22–27
The popular funnel theory expects downhill energy transport from the antenna complex towards the RC.8,28,29 However, experiments demonstrated reliable performance of PSI, even when excited in the red edge of the spectrum, which implicates an uphill energy transfer.8,23,30 Concerning charge-separation, several theories agree on the special pair as the primary electron donor in multiple LH complexes.8,19,31 However, time-resolved experiments on PSI14,17 as well as theoretical results for PSII32 suggest the origin of the free charges in adjacent chlorophylls in one of the two branches, preferentially the A branch. The lack of agreement between theories, experiments and computational studies emphasizes the need for an accurate model of energy and charge transfer processes.
PSI also presents significant challenges to computational methods, especially regarding the chlorophylls governing the energy and charge transfer.4,18,33 The protein environment in pigment–protein complexes such as PSI is specific for each chlorophyll, which leads to individual absorption spectra or site energies for each chromophore.32,34 In accordance with the Gouterman-model,35 these site energies correspond to the Qy state as the lowest excited state of chlorophyll. The unordered nature of the PSI antenna complex compared to e.g. LH2 in purple bacteria,36 creates additional challenges regarding the determination of the finely tuned site energies.
Given that theoretical models such as resonance energy transfers (RET) heavily depend on accurate excitation energies, the site energies lie at the core of every model for energy transfer.37–39 With previously accessible methods for the much smaller Fenna–Matthews–Olson (FMO) complex, an unambiguous assignment needs yet to be reached after more than three decades of computational and experimental studies.31,40 Similarly, there have been many attempts to obtain a set of conclusive site energies for PSI. Fitting procedures have resulted in accurate reproductions of optical spectra but did not reach a conclusive picture of energy transfer dynamics.41–43 Quantum-chemically derived site energies for static structures obtained from crystallographic data44 or an optimization by density functional theory (DFT) methods22,45 achieved predictions of the overall spectrum and an assignment of site energies. However, no study was able to prove or disprove the energy funnel theory. Subsequent works adding excitonic couplings to the site energy determination continued to refine some fundamentals of energy transfer, specifically the importance of long range electrostatics, the asymmetry in the charge transport and a lack of a continuous site energy gradient towards the RC.23,31 With increasing computational resources, site energies in other LH systems were determined computationally from samples of molecular dynamics simulations (MD).32,46–49 Such an approach requires many single-point calculations for each chlorophyll, which often leads to compromises in the electronic structure theory to retain computational feasibility. Insights into the dynamic evolution of optical properties are therefore inherently limited by the typically employed lower-level quantum mechanical (QM) methods.32 Despite their importance in RET models as diagonal elements of the excitonic Hamiltonian, an accurate determination of the absolute site energies including their energy fluctuation dynamics remains elusive. Here, we aim to close this gap by presenting a new set of chlorophyll site energies in PSI, including (i) the molecular dynamics of the trimeric and membrane-embedded supercomplex, (ii) the electrostatic influence of the natural environment in a QM/MM approach and (iii) the multireference character inherent to chlorophyll excitations via the high-level DFT/MRCI method.
This work is structured as follows: first, we introduce the relevant computational protocols and justify our choice of method by comparison to other quantum chemical approaches and to experimental steady-state spectra. Next, we discuss the obtained site energies and exciton dipole couplings in the context of temporal averages with a focus on locating low-energy chlorophylls. While the functional role of these “red chlorophylls” remains to be elucidated in detail, they may act as kinetic traps for an exciton and impede the excitation energy transfer to the reaction center,10,21,50 especially when adjacent to higher energy chlorophylls. Our findings are complemented by a dynamical perspective on site energy and exciton fluctuations, as well as electrostatic and structural influences, providing new insights on the energy funnel theory.
2 Methods
2.1 Absorption of isolated chlorophyll
To assess the performance of different quantum chemical methods, we compared calculated absorption spectra to an experimental spectrum in diethyl ether.51,52 For this purpose, the geometry of chlorophyll a, axially coordinated by two ether molecules was optimized at the r2SCAN-3c53 level of theory with Orca 5.0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 and verified as a minimum by the absence of imaginary vibrational frequencies. The r2SCAN-3c53 composite method builds on the r2SCAN meta-GGA density functional and contains three empirical corrections, namely a custom triple-ζ basis set denoted def2-mTZVPP,53 a refitted D4 dispersion correction55 and a geometric counter-poise correction56 to account for London dispersion forces and the basis set superposition error. The method has proven to yield superior ground state geometries and energies for a large variety of organic molecules, on par with or even surpassing more expensive hybrid DFT approaches.53 Further solvation effects were accounted for by the conductor-like polarizable continuum model (C-PCM),57 using a relative permittivity of εr = 4.27
54 and verified as a minimum by the absence of imaginary vibrational frequencies. The r2SCAN-3c53 composite method builds on the r2SCAN meta-GGA density functional and contains three empirical corrections, namely a custom triple-ζ basis set denoted def2-mTZVPP,53 a refitted D4 dispersion correction55 and a geometric counter-poise correction56 to account for London dispersion forces and the basis set superposition error. The method has proven to yield superior ground state geometries and energies for a large variety of organic molecules, on par with or even surpassing more expensive hybrid DFT approaches.53 Further solvation effects were accounted for by the conductor-like polarizable continuum model (C-PCM),57 using a relative permittivity of εr = 4.27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 and a refractive index of nD = 1.3526
58 and a refractive index of nD = 1.3526![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 for diethyl ether. Vertical excitation energies were calculated with the density functionals BHLYP,59,60 M06-2X,61 B3LYP,59,60,62 CAM-B3LYP,63 ωB97X-D4
58 for diethyl ether. Vertical excitation energies were calculated with the density functionals BHLYP,59,60 M06-2X,61 B3LYP,59,60,62 CAM-B3LYP,63 ωB97X-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 and SCS-ωPBEPP86
64 and SCS-ωPBEPP86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 using the Tamm–Dancoff approximation66 (TDA) and the def2-TZVP67 basis set. The RIJCOSX approximation68,69 was employed with the def2/J70 and def2-TZVP/C71 auxiliary basis sets to speed up the calculations. At the lower level of theory, we also tested the Zerner's Intermediate Neglect of Differential Overlap with parameters for Spectroscopic properties (ZINDO/S) method,72 which has been used frequently in previous studies73–77 on chlorophyll excitations. Here, the C-PCM was switched off, as the implementation of ZINDO/S we used is not parametrized for use with implicit solvation models. With each method, 20 roots were included in the calculation.
65 using the Tamm–Dancoff approximation66 (TDA) and the def2-TZVP67 basis set. The RIJCOSX approximation68,69 was employed with the def2/J70 and def2-TZVP/C71 auxiliary basis sets to speed up the calculations. At the lower level of theory, we also tested the Zerner's Intermediate Neglect of Differential Overlap with parameters for Spectroscopic properties (ZINDO/S) method,72 which has been used frequently in previous studies73–77 on chlorophyll excitations. Here, the C-PCM was switched off, as the implementation of ZINDO/S we used is not parametrized for use with implicit solvation models. With each method, 20 roots were included in the calculation.
Additionally, we tested the DFT/MRCI method78,79 in its parallel implementation.80 The DFT reference was evaluated with the BHLYP59,60 functional implemented in Orca 4.2.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81–83 and the def2-SVP67 basis set. To speed up the evaluation of Coulomb and exchange integrals, we employed the resolution of the identity (RI-JK) approximation84 with the def2-SVP/C71 and def2/JK85 auxiliary basis sets. SCF convergence was set to 10−7Eh (Orca keyword SCFCONV7) and a tighter-than-default integration grid was used (Orca keyword GRID4). The MRCI reference space was iteratively optimized, starting from a CISD expansion of four electrons in the four frontier orbitals, until it contained all leading configurations of the 10 roots included in the calculations. This starting guess corresponds to the most important transitions in the Gouterman picture.35 The R2018 Hamiltonian86 was employed with a selection threshold of 0.8 Eh and the tight parameter set to damp off-diagonal elements of the CI matrix, avoiding double counting of dynamical correlation.
81–83 and the def2-SVP67 basis set. To speed up the evaluation of Coulomb and exchange integrals, we employed the resolution of the identity (RI-JK) approximation84 with the def2-SVP/C71 and def2/JK85 auxiliary basis sets. SCF convergence was set to 10−7Eh (Orca keyword SCFCONV7) and a tighter-than-default integration grid was used (Orca keyword GRID4). The MRCI reference space was iteratively optimized, starting from a CISD expansion of four electrons in the four frontier orbitals, until it contained all leading configurations of the 10 roots included in the calculations. This starting guess corresponds to the most important transitions in the Gouterman picture.35 The R2018 Hamiltonian86 was employed with a selection threshold of 0.8 Eh and the tight parameter set to damp off-diagonal elements of the CI matrix, avoiding double counting of dynamical correlation.
2.2 Structural model of PSI
As a starting point for our investigations of PSI, we used the asymmetric unit from the 2.5 Å crystal structure of cyanobacterial PSI7 in T. elongatus (PDB: 1JB0), consisting of one monomer of the trimeric protein supercomplex. Missing amino acids were added with the Modeller interface87 to UCSF Chimera88 (cf. ESI Table S1†). Missing heavy atoms were added manually to the chlorophyll residues CLA A1402 and J1303, to β-carotene BCR A4009, and to the lipids LHG A5003 and B5004. Of the 96 Chla molecules in the asymmetric unit, 49 contain only partially resolved phytyl chains. As the phytyl chain's contributions to the absorption spectrum are negligible,89,90 we kept the intact chains but replaced all damaged phytyl residues with methyl groups (cf. ESI Fig. S1†). While there are studies that point to the role of the phytyl chain in coordinating91 or preventing coordination92 to the central Mg2+ ion, we argue that these structural effects are contained in the MD simulations. All crystal water was retained and hydrogens were added with pdb2gmx included in Gromacs 2020.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 93 or, for newly parametrized molecules, with reduce,94 distributed with AmberTools 20.
93 or, for newly parametrized molecules, with reduce,94 distributed with AmberTools 20.
To mitigate steric clashes introduced by the addition of atoms, the total energy of the asymmetric unit was minimized with the steepest descent algorithm implemented in Gromacs 2020.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 93 until the residual force was smaller than 1000 kJ mol−1 nm−1. For this, the prepared structure was placed in a cubic box with 17.664 nm edge length, solvated with TIP3P water molecules and charge neutralized by adding 15 Na+ ions. The energy-minimized asymmetric unit was subsequently replicated three times to assemble the trimeric PSI supercomplex. In the process, crystal water L4042, located exactly on the C3 axis, was removed two out of three times.
93 until the residual force was smaller than 1000 kJ mol−1 nm−1. For this, the prepared structure was placed in a cubic box with 17.664 nm edge length, solvated with TIP3P water molecules and charge neutralized by adding 15 Na+ ions. The energy-minimized asymmetric unit was subsequently replicated three times to assemble the trimeric PSI supercomplex. In the process, crystal water L4042, located exactly on the C3 axis, was removed two out of three times.
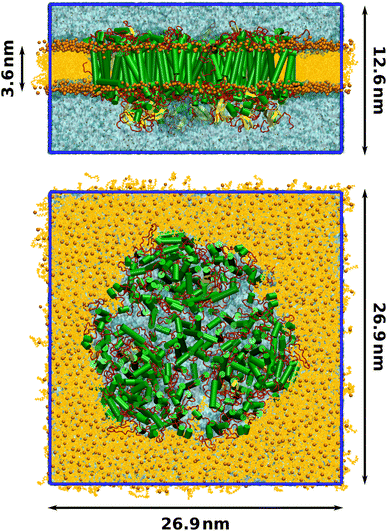
Finally, a lipid bilayer consisting of 674 lumenal and 683 stromal molecules of 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) was packed around the photosystem with packmol-memgen,95 from AmberTools 20. The membrane-embedded protein was solvated with TIP3P water and the charge was neutralized, maintaining a physiological salt concentration of 0.15 mol L−1 NaCl. The final structure contained 935![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 atoms and is illustrated in Fig. 1.
722 atoms and is illustrated in Fig. 1.
2.3 Force field parameters
To ensure that the parameters for the protein and all cofactors were compatible to each other, we employed only parameters that were derived for use with the Amber family of force fields. The protein was described with the Amber14sb96,97 force field. Parameters for the cofactors chlorophyll a and β-carotene were taken from related studies on PSII,98 which are in turn based on parameters by Ceccarelli et al.99 Iron–sulfur clusters and the coordinating CYS residues were described with parameters for oxidized, proximal Fe/S clusters derived by Smith et al.100 The available CYS residue type in Amber14sb does not describe coordination to metal clusters. We therefore introduced a new residue type CYF for the iron-coordinating CYS residues by removing the S-bound hydrogen from the CYS entry in Amber14sb, substituting the Cβ charge with the published one100 (−0.01172) and patching the Cα charge such that the overall charge of the [FeS]4/CYF4 cluster was −2. The coordination bond between the sulfur and iron atoms was described by the published100 bonded interaction parameters. The rest of the interactions between CYF and Fe4S4 were purely non-bonded and the standard parameters for CYS as defined in Amber14sb were used for this purpose. The lipids 2,3 dipalmitoyl-D-glycero-1-phosphatidylglycerol (LHG) and 1,2-distearoyl-monogalactosyl-diglyceride (LMG) were described with the LIPID17 force field.101–103 As the head group for LMG was not contained in LIPID17, parameters were generated with antechamber104 using the general Amber force field (GAFF).105 RESP charges were derived from HF/6-31G* calculations according to the Amber protocol for lipids,101 such that the total charge of the head group was zero. Parameters for phylloquinone were generated analogously.2.4 Molecular dynamics
Molecular dynamics (MD) simulations were performed with a single-precision version of Gromacs 2020.1.93 The trimeric PSI complex was placed in a tetragonal simulation box with dimensions 26.0 nm × 26.0 nm × 14.5 nm. To minimize steric clashes introduced in the membrane packing process, the total energy was minimized with the steepest descent algorithm until the maximum force was below 1000 kJ mol−1 nm−1. In all following steps, the leap-frog integrator was employed with a time step of 2 fs and bonds to hydrogens were constrained using the LINCS algorithm.106 Short-range electrostatics were calculated using Verlet lists with a cutoff distance of 1.2 nm. Particle-mesh Ewald summation107 was conducted for the long-range electrostatics using cubic interpolation and a Fourier grid spacing of 0.16 nm.Equilibration was conducted in three phases. First, the system was heated from 10 K to 100 K over 50 ps in an NVT ensemble, controlled by the V-rescale thermostat108 with a time constant of 0.1 ps. The positions of the protein and all cofactors were restrained with a force of 1000 kJ mol−1 nm−1. Two temperature coupling groups were employed, one for the membrane-embedded protein and one for water and ions. The system was propagated for another 50 ps at a constant temperature of 100 K to further minimize clashes in the membrane and solvent. In the second equilibration step, the temperature was raised from 100 K to the production temperature of 300 K over 100 ps in the NPT ensemble, keeping the position restraints. The pressure was controlled by the Berendsen barostat with a semiisotropic reference pressure of 1 bar, a coupling constant of 5 ps and using an isothermal compressibility of 4.5 × 10−5 bar−1. After annealing, the system was propagated for 900 ps at the target temperature in the NPT ensemble. In the third step, the position restraints were lifted and the system was propagated for 15 ns in an NPT ensemble, controlled by the Nosé–Hoover thermostat109,110 and the Parrinello–Rahman barostat111,112 with time constants of 0.5 ps and 5.0 ps, respectively. Proper equilibration was confirmed by the average temperature, pressure and density converging to their target values, as well as the total energy and box vectors remaining stable. The final box dimensions were 26.9 nm × 26.9 nm × 12.6 nm (Fig. 1). From the last nanosecond of this converged NPT ensemble, five production simulations over 15 ns were started. Snapshots were extracted only from the last 10 ns of each production run. During the production trajectories, the RMSDs of the protein backbone as well as that of the cofactors chlorophyll, β-carotene and phylloquinone remained stable and between 1 Å to 2 Å, further indicating that the system was equilibrated. Similarly, the area-per-lipid of the membrane had converged at 0.64 nm2, in good agreement with literature values.113–115
2.5 QM/MM protocol
Chlorophyll site energies were computed in a QM/MM scheme, where the two subsystems were coupled electrostatically.116,117 Here, the environment of each chlorophyll is expressed as a distribution of classical point charges. By including the entire model of the photosystem in the point charge distribution, all short- and long-range electrostatic interactions between a chlorophyll and the rest of the photosystem are contained in the calculations. The vertical excitation energy E is given by| E = (EQMES + EcoupES) − (EQMGS + EcoupGS), | (1) |
Unless otherwise stated, the QM region contained the respective chlorophyll molecule without the phytyl chain, which was always capped at the first carbon by a hydrogen link atom.118–120 Omitting the phytyl chain from the QM region is commonplace in the literature, as its electronic contributions to the absorption are negligible.49,89,90,121–123 We have tested this truncation also for our particular QM/MM multireference workflow and found that it performs well (ESI Table S4†). The MM region consisted of the full MD simulation box, i.e. the trimeric PSI supercomplex embedded in the solvated lipid membrane. Overpolarization at the QM/MM boundary was avoided by shifting point charges away from the link atom and introducing artificial charges to preserve the dipole moment of the former bond.120 Point charges were taken unmodified from the Amber-based classical force field (see above), where all charges were derived consistently via the established RESP protocol.124 The QM subsystem was centered in the simulation box to account for periodic boundary conditions.
2.6 Calculation of site energies
Site energies for each of the 96 chlorophylls in one asymmetric unit were calculated with the DFT/MRCI method as described above, with five singlet roots included in the MRCI part. 20 evenly spaced snapshots were extracted from the last 10 ns of two production MD simulations, resulting in 40 samples with a temporal spacing of 0.5 ns. To separate structural from electrostatic effects, these calculations were performed with and without classical point charges, resulting in 7860 individual calculations. Additional sampling was performed for the RC chlorophylls due to their special significance. Here, a total of 200 snapshots were extracted from the last 10 ns of all five production MD simulations with a temporal spacing of 0.25 ns.2.7 Excitonic coupling
To get a first estimate of excitonic effects on the energy transfer, the coupling elements Vij between pairs of chlorophylls i and j were evaluated in the point dipole approximation: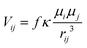 | (2) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i and
i and ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) j of the chlorophylls and the unit vector
j of the chlorophylls and the unit vector ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ij connecting their centers of mass:
ij connecting their centers of mass:κ = (![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i· i·![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) j) − 3[( j) − 3[(![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i· i·![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ij)( ij)(![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) j· j·![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ij)]. ij)]. | (3) |
To account for electrostatic screening effects by the environment, a screening factor f is introduced in eqn (2). Its value was fixed to 0.72 in this work, based on the findings by Renger et al.23
Using the site energies εi and couplings Vij, an excitonic Hamiltonian H was constructed:
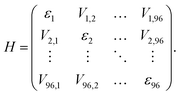 | (4) |
Diagonalization of H yields the excitonic energies as diagonal elements and the contribution coefficients ci of each chlorophyll to a respective exciton as eigenvectors. The square of ci gives the weight wi of chlorophyll i in the exciton with 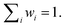 This analysis was conducted for each MD snapshot as well as for the temporal mean of site energies and couplings.
This analysis was conducted for each MD snapshot as well as for the temporal mean of site energies and couplings.
3 Results and discussion
In the following, we will refer to the chlorophylls in PSI using the nomenclature introduced by Jordan et al., where the pigments are numbered consecutively according to their associated protein subunit.7 The chlorophylls in the electron transfer chain are additionally prefixed by ‘eC’. For a translation between the naming schemes used in the crystal structure PDB, our MD simulations and the conventional nomenclature,7 please refer to ESI Table S5.†3.1 Choice of method
When discussing the energy transfer in light-harvesting processes, the site energies vary in a small window of ±100 meV.23,41–45 If the error of the quantum chemical method is much larger than this in the first place, it is hard to obtain a quantitative picture of the small energy fluctuations that govern the light-harvesting processes. The disagreement between existing sets of site energies in PSI (cf. ESI Fig. S11†) emphasizes the need for a method that can accurately reproduce not just energy differences but also the excitation energies themselves. At the same time, computational cost is a decisive factor in a problem of this scale.To find a method that satisfies both criteria, we calculated the excitation energies of the first five roots for an optimized structure of chlorophyll a at different levels of theory, ranging from the semiempirical ZINDO/S method over TDA-DFT to multireference calculations with the DFT/MRCI method. For each method we evaluated how well the overall absorption spectrum of chlorophyll a is reproduced (Fig. 2 and ESI Fig. S7†)and especially how close the calculated energy of the Qy state is to the experimentally51,52 observed one (Table 1).
 | ||
| Fig. 2 Calculated absorption spectra for an optimized (r2SCAN-3c) structure of chlorophyll a, axially coordinated by two diethyl ether molecules, compared to an experimental spectrum in diethyl ether.51,52 Stick spectra were convoluted by Gaussians (σ = 0.05 eV). Excited states with an oscillator strength <0.1 are indicated by dotted lines. A comparison with all tested density functionals is available in Fig. S7 in the ESI.† | ||
| Method | E [eV] | f |
|---|---|---|
| ZINDO/S | 1.622 | 0.3325 |
| TDA-BHLYP | 2.202 | 0.4953 |
| TDA-B3LYP | 2.148 | 0.4311 |
| TDA-M062X | 2.197 | 0.4388 |
| TDA-CAM-B3LYP | 2.158 | 0.4313 |
| TDA-ωB97X-D4 | 2.140 | 0.3896 |
| TDA-SCS-ωPBEPP86 | 1.811 | 0.3812 |
| DFT/MRCI (0.8 Eh) | 1.939 | 0.3473 |
| DFT/MRCI (1.0 Eh) | 1.903 | 0.3449 |
| Exp. (diethyl ether) | 1.876 | — |
As a semiempirical method designed for biomolecules including porphyrin-based pigments, ZINDO/S is most affordable in terms of computational effort. However, any deviations from the fitting range of ZINDO/S reveal its shortcomings. The excitation energy of the Qy band is underestimated by 0.25 eV, owing to the axial coordination with diethyl ether. Furthermore, the Qx band, which in reality is closely mixed with the vibronic progression of Qy,123,130 appears at an unreasonably high energy of 2.2 eV, separated by 0.6 eV from Qy (Fig. 2). In ensemble simulations, ZINDO/S has been shown to overestimate the red tail of the spectrum, because of its parametrization only for equilibrium structures.46,131 The hybrid density functionals vary strongly in their performance for different properties. While the Qx − Qy gap is best reproduced by CAM-B3LYP and M06-2X (ESI Fig. S7†), the error of the Qy band energy is smallest with ωB97X-D4 at the expense of a severely overestimated Qx − Qy gap. All of the tested hybrid density functionals blue-shift the entire absorption spectrum by ∼0.3 eV. The blue shift is stronger for the B bands than for the Q bands, which can be explained by non-negligible contributions of doubly excited configurations to the higher excited states.122,132 These are partially accounted for by the perturbative doubles correction included in the recently introduced65 range-separated double-hybrid functional SCS-ωPBEPP86, which is however much more expensive. At comparable cost, the DFT/MRCI method matches the experimental absorption spectrum almost exactly, in good accordance with another recent study on the spectral properties of photosynthetic pigments.133 We only observe a minor systematic blue-shift of the entire spectrum by ∼0.06 eV. Notably, we also do not observe a spurious doubly excited state between the Q- and B-bands, as predicted by earlier DFT/MRCI calculations,132 which may be rooted in the use of the completely refitted R2018 Hamiltonian.86 These results indicate that the fundamental physics of chlorophyll excitations are correctly reproduced with the new DFT/MRCI Hamiltonian. In our tests, the calculation of 10 roots required only 21 h of wall time, running on 8 CPUs. We therefore regard the DFT/MRCI method, especially with the tight parameter set, as ideally suited to compute the spectroscopic properties of chlorophylls.
Although DFT/MRCI provides highly accurate energies for individual chlorophylls at an affordable cost, it would be too expensive for pairs of pigments. However, the antenna complex of PSI features many closely packed chlorophyll aggregates,7,41 where excited state localization on one of the individual chromophores cannot be trivially assumed. We therefore tested our QM/MM partitioning scheme by computing the excitation energies for the five lowest roots of selected chlorophyll pairs from different spatial regions of PSI at the TD-ωB97X-D4/def2-TZVP level of theory. For each pair, the QM region contained both chlorophyll molecules. The natural transition orbitals of the dimer excited states (ESI Fig. S13†) confirm that the excitation is in most cases localized on one of the two pigments, supporting our QM/MM partitioning scheme and by extension affording us the high-level DFT/MRCI method.
3.2 Chlorophyll absorption in PSI
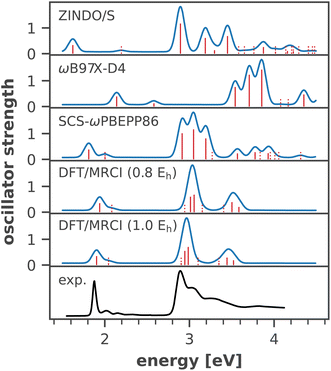
An important issue when analyzing dynamical site energy fluctuations by means of MD sampling is achieving convergence of the average energies. Fig. 3 illustrates the convergence of the arithmetic mean of the site energy for four representative chlorophyll residues with the number of considered snapshots. All other residues follow the same trend, with the average energies converged after ∼20 snapshots (ESI Fig. S10†). Thus, our sample size of 40 conformational snapshots per chlorophyll is clearly enough to obtain meaningful temporal averages. Given the importance of the six RC chlorophylls, we calculated their site energies in an additional 160 snapshots, thus increasing the data set to 200 samples. A one-way ANOVA analysis followed by Tukey's honest significant differencing (HSD) test (for details cf. ESI Section 5†) confirmed the statistical significance of the site energy differences discussed in this work.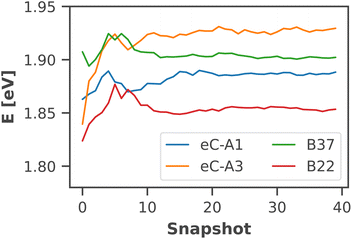 | ||
| Fig. 3 Convergence of the average site energy for four representative chlorophyll residues with the number of snapshots. 40 snapshots from two trajectories cover a time scale of 20 ns. | ||
The calculated absorption spectrum of all 96 chlorophylls in the PSI monomer (Fig. 4) is in excellent agreement with the experimental spectrum, measured previously by Di Donato et al.17 The energy gap between the Q and B bands is reproduced correctly and only a minor red-shift of 0.07 eV needs to be applied to match the experimental Qy band. This again corroborates the need for high-level quantum-chemical methods, ideally including multireference character, to model the chlorophyll absorption spectrum, as other methods exhibit much larger errors. The shoulder at 500 nm in the experimental absorption spectrum corresponds to the β-carotenes in PSI, which are not the subject of this study.
 | ||
| Fig. 4 Calculated absorption spectrum of all Chla in PSI (solid green line) compared to an experimental absorption spectrum of trimeric PSI (dashed blue line) at 293 K.17 The stick spectra signify the absorption lines of the four lowest excited states of each individual chlorophyll, colored by the energetic order of the excited state (S1: red, S2: yellow, S3: turquoise, S4: dark green). Each stick spectrum was convoluted with a Gaussian (σ = 0.025 eV) and summed up to yield the broadened absorption. The intensity was scaled to match the experimental absorption of the Qy state. A constant red-shift of 0.07 eV was applied to all calculated spectra. | ||
3.3 Site energies and couplings
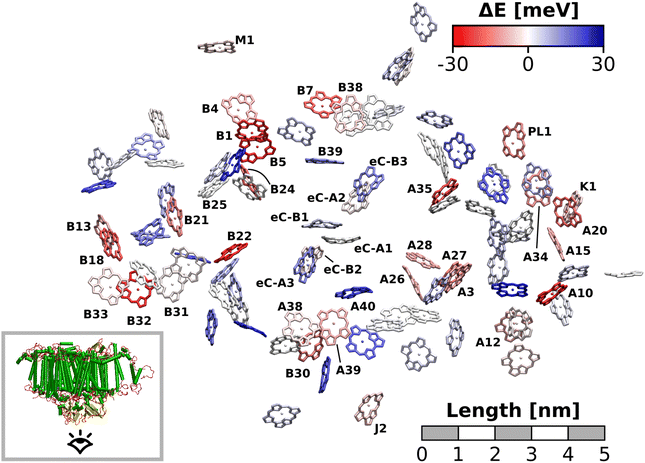
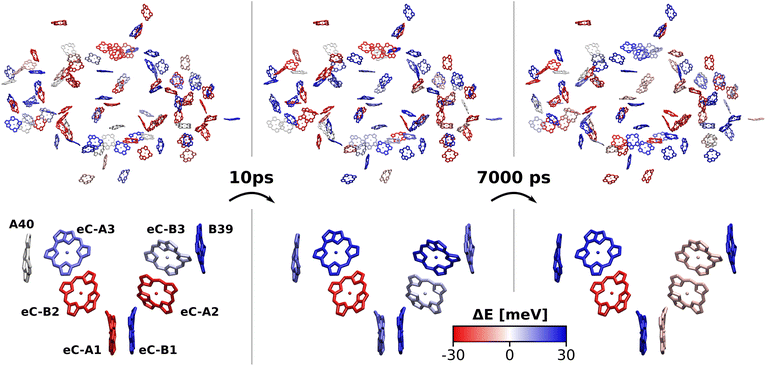
The excitation energy of each chlorophyll is tuned by the environment. These site energy shifts supposedly steer the energy transfer within the photosystem, culminating either in a redox event in the RC or in the trapping of excitation energy at low-energy sites. The average site energy shift of each chlorophyll against the total mean is illustrated in Fig. 5. Including the coupling between the chlorophylls, the lowest energy excitons are visualized in Fig. 6. In general, the mean site energies range between 1.85 eV and 1.93 eV, while the 100 largest mean couplings range between 4 meV and 43 meV. The strongest coupling is observed in P700.Many red chlorophylls, such as A10, A15, A20, A34, K1, B18 and PL1 appear in the peripheral regions of the antenna complex, far away from the RC. An often disputed red site in the periphery is the triad B31/B32/B33.20,134,135 These three chlorophylls are special because their porphyrin planes are almost parallel and their Qy transition dipole moments remain aligned with each other during the dynamics. Structural arguments7,41 and fits of optical spectra42,43 favor this triad as a red site. However, semiempirical methods,44 early DFT calculations45 and a study using the charge density coupling technique23 yield contradictory site energies. We find that only the site energy of B32 (1.86 eV) is considerably red-shifted. However, this triad of chlorophylls is subject to strong excitonic coupling,41,45 which causes an additional red-shift of the collective absorption band. The coupling matrix elements are 38 meV (B31/B32) and 33 meV (B32/B33) and thus the second largest in the entire PSI behind P700. Indeed, the time-averaged excitonic Hamiltonian yields the triad B31/B32/B33 as the lowest energy exciton domain with an excitation energy of 1.83 eV (Fig. 6). TD-DFT calculations of the entire triad, that also take short range exchange effects into account, confirm the red-shift (ESI Fig. S14†)). Considering these findings, our high-level computational results now corroborate the assignment of B31/B32/B33 as an energy sink. These results are also supported by fluorescence measurements.20,136 While this correspondence is encouraging, we note that our results refer to the initial absorption process and do not include any excited state relaxation as needed to fully capture fluorescence experiments.
Another set of low energy chlorophylls where the middle pigment B5 exhibits the strongest red-shift, B4/B5/B24, stands out in Fig. 5. In the excitonic picture (Fig. 6), B25 is also coupled to this cluster of chlorophylls. Together, the four pigments give rise to two low-energy excitons, B4/B5 (1.86 eV) and B24/B25 (1.87 eV). The red-shifted pigment B1 is located in the same region but in the stromal layer of the antenna complex, while the dimers B4/B5 and B24/B25 are located in the lumenal layer.41 While B24/B25 has been disputed before,44,45 B4/B5 has not been identified as an energy sink in preceding studies, to our knowledge.23,41–45
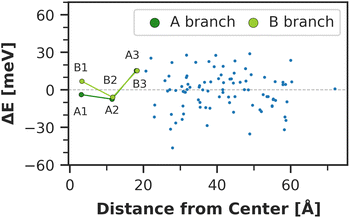
The chlorophyll with the lowest average site energy (1.85 eV) is B22, in a distance of 1.9 nm from the RC chlorophyll eC-A3, which in turn exhibits one of the highest mean energies (1.92 eV) in the entire complex. Other notable red chlorophylls, both in the site energy and in the exciton picture, include the dimers A38/A39 and B7/A32. Both dimers are subject to excitonic coupling on the order of 17 meV (A38/A39) and 29 meV (B7/A32) and are situated in close vicinity to the end points eC-A3 and eC-B3 of the two electron transfer branches in the RC. The two branches themselves are similar in that the second chlorophylls, eC-B2 in branch A and eC-A2 in branch B, exhibit almost no red- or blue-shift, while the third chlorophylls eC-A3 and eC-B3 are shifted towards higher energies. This renders the asymmetry within P700 all the more interesting. Here, the mean site energy of eC-A1 in 200 snapshots is red-shifted against eC-B1 by about 10 meV, meaning that energy will preferentially gather on the A branch once it reaches the RC. Including the coupling between the chlorophylls, the pair eC-A1 and eC-B1 contributes to two excitons with energies 1.85 eV and 1.95 eV. Again, the contributions of the two branches are asymmetric in the sense that eC-A1 contributes 49% to the lower energy exciton, while eC-B1 contributes only 37% (ESI Table S7†). The asymmetry is even more apparent when the average energy shift of each chlorophyll against the mean energy of all chlorophylls is plotted as a function of distance from P700 (Fig. 7). While there is a statistically significant downhill pathway from eC-A3 to eC-B2 and eC-A1, the energy sink in branch B is the second chlorophyll eC-A2, rather than eC-B1. The probability to transfer energy into one of the branches increases the possible number of charge transfer events therein. Therefore, assuming that charge separation indeed starts not in the special pair but in one of the two branches,14,17,32 our results correspond well with reports of branch A as slightly more active.14,137 Nevertheless, both branches in PSI are known to participate in charge transport, though there is no final consensus on the branching ratio.13,14,138
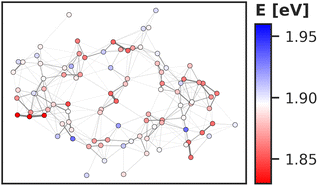
Regarding the energy transfer to the RC, we observe that P700 is neither the only nor the lowest energy sink in PSI, nor is there a distinct energy transfer pathway from the antenna complex to the RC readily apparent from Fig. 5 and 7. Instead, the terminal chlorophylls eC-A3 and eC-B3 as well as the linkers A40 and B39 to the antenna complex constitute energy barriers to P700 in the temporal average. This leaves us with two possibilities for energy transfer between the antenna complex and P700. One pathway may lead via the RC, where excitonic coupling to P700 is strongest because of the spatial proximity (cf.Fig. 6). However, uphill energy transfer is required to reach the chlorophylls A40/eC-A3 and B39/eC-B3, connecting the RC (green lines) with the antenna complex (blue dots). Another possibility is direct energy transfer from the antenna complex to P700, bypassing these high-energy chlorophylls, albeit at lower efficiency because of the smaller excitonic coupling. An argument in favor of multiple energy transfer pathways is that P700 is excitonically coupled to the entire antenna complex, rather than just to the linker chlorophylls A40 and B39, as evident from the network of coupling matrix elements in Fig. 6. Indeed, early semiempirical rate-constant calculations139 suggest that the linker chlorophylls accelerate the energy transfer time to the RC but are not critical for the process. We will show in the next section how thermal fluctuations can open new pathways towards both branches of the RC, which would seem unfavorable in the temporal average.
3.4 Thermal fluctuations
So far we have discussed the site energies and couplings in the context of temporal averages. However, when discussing energy transfer in biological systems as large and complicated as PSI, it is neither sufficient to study an average, nor a single structure, be it a crystal structure7,23,41–44 or an optimized geometry.22,45 Instead, the dynamics of the system are crucial to understand the impact of the site energy shifts in the light-harvesting process. Looking at the site and exciton energies in individual MD snapshots, we observe that chlorophylls can easily switch between higher and lower energies via thermal fluctuations. In Fig. 8, this is for example apparent for the P700 pigments, or for the chlorophyll clusters B7/A32 and B4/B5/B24/B25. In contrast, the exciton couplings are less sensitive to fluctuations, as the chlorophyll positions and orientations remain rather stable over time. The maximum standard deviation in the couplings occurs in P700 and is 5 meV. Any excitonic fluctuations are therefore mainly governed by the variance in the site energies, which will consequently be the focus of the following discussion.The complete energy distribution for each chlorophyll at 300 K is shown in Fig. 9a, where the chlorophylls are sorted in ascending order by their mean energy (blue triangles). While higher- and lower-energy pigments can be clearly distinguished in the temporal averages, the energy distributions of all chlorophylls overlap strongly (green boxes). This allows some conclusions about the energy funnel mechanism in PSI. In equilibrium, the red chlorophylls may act as energy traps and thus compete with the RC. However, at physiological temperatures this effect is mostly compensated by thermal disorder such that energy transfer pathways can open and close dynamically. This suggests that there is not one fixed pathway from the antenna complex to the reaction core but rather that energy barriers which are initially present upon excitation can be overcome via thermal motion. This type of thermally mediated energy transfer has benefits for the light-harvesting process, as the entire antenna complex with its fluctuating red sites may serve as an energy reservoir, storing excess energy until it is needed in the RC.
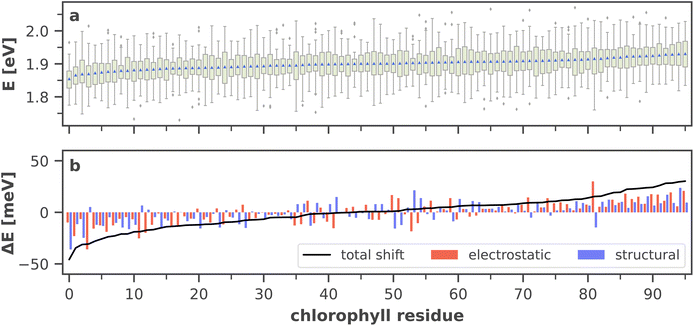 | ||
| Fig. 9 (a) Site energy distribution for each chlorophyll residue, ordered by ascending arithmetic mean (blue triangles). Green boxes extend from the beginning of the second quartile to the end of the third quartile. Whiskers extend to the minimum and maximum values of the data or to 1.5 times the interquartile range in the case of outliers (gray diamonds). A more detailed graphic including all raw data points is provided in ESI Fig. S8.† (b) Electrostatic and structural components (cf. eqn (6) and (7) to the total site energy shift from the absorption maximum, i.e. from the arithmetic mean of all site energies. The total shift (black line) is the sum of both components. A list of the chlorophyll residue IDs with the standard naming convention7,41 is available in ESI Table S5.† | ||
Moreover, the average asymmetry between the P700 chlorophylls is 10 meV and thus well within the range of the thermal fluctuations on the order of ±100 meV. This means that thermal fluctuations can open energy transfer pathways to the otherwise slightly unfavorable B-branch of the RC and thus explain the reported bidirectionality of charge transport.13,138
To further specify the time scale on which these changes happen, we computed the site energies of all chlorophylls in two consecutive MD snapshots, 10 ps apart (Fig. 8). Significant site energy fluctuations can occur on this time scale, which is well below the exciton lifetime of 35 ps between the initial excitation and a redox event in the RC.8,9 We even observe that the energy barrier on eC-A3 is removed from one snapshot to the next. This again corroborates the idea of the energy funnel as a dynamic process rather than a static pathway.
3.5 Electrostatics vs. conformation
The red- or blue-shift of the site energy Eenv from the absorption maximum 〈Eenv〉 can be separated in two components ΔEstruct and ΔEelec:| Eenv = 〈Eenv〉 + ΔEstruct + ΔEelec. | (5) |
The structural component ΔEstruct (eqn (6)) contains most of the thermal disorder and accounts for steric restrictions imposed on the pigments by the environment. The electrostatic shift ΔEelec (eqn (7)) in turn contains only the electrostatic influence of the environment on the site energies. As the environment shifts the entire site energy distribution to the red by 〈Eenv〉 − 〈Evac〉 = 17 meV, the respective absorption maxima in environment and in vacuo also enter in eqn (7).
| ΔEstruct = Evac − 〈Evac〉 | (6) |
| ΔEelec = (Eenv − 〈Eenv〉) − (Evac − 〈Evac〉) | (7) |
Fig. 9b illustrates the average magnitude of both components for each chlorophyll. The red-, blue- and unshifted site energies, almost equally distributed in thirds, are the result of almost any combination of electrostatic and structural components. A red-shift is observed from either strongly dominating electrostatic, dominating structural or collaborative/same-signed contributions. The blue-shift is achieved mostly by collaborative effects or a dominating electrostatic shift. Neutral or unshifted site energies originate either from cancelation of the respective strong contributions or from small, negligible contributions. The strongest structural shift, complemented by a weak electrostatic shift is experienced by B22 (no. 0 in Fig. 9b), which is also the overall most red-shifted chlorophyll. The also strongly red-shifted chlorophyll B5 (no. 3 in Fig. 9b) shows the opposite trend. Here, the electrostatic influence of the environment dominates the total site energy shift and is counteracted by a weak structural shift. It is also apparent that the total shift (black line) is slightly asymmetric, favoring the low-energy components. This asymmetry in the red- and blue-shifts may become more relevant at low temperatures, where a distinct red absorption side band has been observed experimentally.8,41 Again, it is informative to look at the statistics of the samples, to assess the significance of both shift contributions.
Fig. 10 visualizes the distribution of both shifts for five exemplary chlorophylls, which cover the full range of calculated site energies. In all cases, the structural shift exhibits a much broader distribution than the electrostatic shift and the shifts of all chlorophylls overlap strongly. Tukey's HSD test (cf. ESI Section 5†) reveals only 29 out of 4560 pairs of chlorophylls with statistically significant differences in the structural shift. This leads us to conclude that steric hindrance by the environment, which could in principle favor certain high- or low-energy chlorophyll conformations, does not have a significant influence on the site energies. In contrast, the electrostatic impact of the protein environment is mostly responsible for the average site energy shifts discussed above, as its distribution is much narrower. Here, Tukey's HSD test reveals 1479 pairs of chlorophylls with statistically significant differences in ΔEelec.
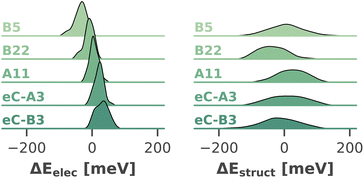 | ||
| Fig. 10 Distribution (kernel density estimate) of electrostatic and structural shifts in 40 sampled snapshots for selected chlorophylls. | ||
Explaining the electrostatic shifts by changes in the environmental charge distribution is not a trivial undertaking. Previous studies have mapped the electrostatic potential (ESP) of the environment onto the porphyrin scaffold and discussed its impact on the difference ESP between ground and excited state.23,32 While such an approach can be successful for individual pigments, a direct correlation between environmental electrostatics and site energy shifts for the entire antenna complex has yet to be discovered.
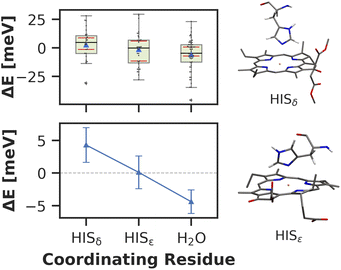
Here, we approach this challenge by investigating the axial coordination of the chlorophylls, which can reportedly tune the site energies,91,140,141 in a temporal picture. In our model, 28 chlorophylls are coordinated axially by HISδ residues which are protonated on the δ position, 14 by HISε residues protonated on the ε position and 39 by crystal water. The rest of the chlorophylls are coordinated by various different amino acids, where the sample size is not large enough to draw meaningful conclusions. Here, we define the coordinating residue as any residue within a distance of 4 Å of the central Mg2+ ion. Comparing the three classes of chlorophylls (Fig. 11), we find that HISε coordinated chlorophylls exhibit on average 5 meV lower excitation energies than HISδ coordinated chlorophylls and 5 meV higher site energies than H2O coordinated pigments. Note that this effect is not large and the energy distributions are again overlapping. Our findings are in good accordance with previous systematic studies of non-standard protonation patterns23 and illustrate that seemingly minor changes in the local environment can already induce energy shifts. While axial ligation is often discussed as an important factor on chlorophyll absorption energies,142–145 there are certainly many more effects at play in PSI than just the coordination of the central ion. This is reflected in the example of chlorophyll PL1 (cf.Fig. 5, upper right part). Its Mg2+ ion is coordinated by the anionic phosphodiester group of one of the phospholipids and therefore experiences a particularly strong negative electric potential in the axial position. Nevertheless, its average site energy (1.88 eV) is only slightly red-shifted. Its surprisingly small electrostatic shift (ΔEelec = −12 meV) indicates that collective electrostatic effects can compensate each other.
4 Conclusions
Although a long-standing subject of theoretical and experimental studies, the high efficiency of light-harvesting and charge separation in PSI is still not fully understood. In this study, we have presented a new set of quantum chemically derived chlorophyll site energies, under fully atomistic consideration of environmental effects and for the first time including molecular dynamics of the complete membrane-embedded and solvated system. Including the entire apparatus, containing the trimeric protein complex and the lipid membrane, in the simulations allows us to describe all chlorophylls in their particular natural environment. In a biological assembly, many of the antenna chlorophylls lie at protein–protein interfaces or at the outer perimeter, interacting with solvent molecules or the thylakoid membrane.146 We therefore simulate all chlorophylls in physiological conditions without artifical restraints or the need for implicitly approximated environments.The combination of the high-level DFT/MRCI method with a QM/MM approach allows an accurate reproduction of the chlorophyll absorption spectrum in PSI – a task where many other quantum chemical methods fail. Our results corroborate previously proposed red sites in the PSI antenna complex, and identify new sites of putative energy traps, which are promising targets for future experiments.21,50,147,148 Moreover, we observe a fundamental asymmetry in the two branches of the RC. Whereas the first chlorophyll eC-A1 acts as the energy sink in branch A, this role is taken by the second chlorophyll eC-A2 in branch B. These findings can be relevant for locating the initial charge transfer event and thus identifying the primary electron donor in PSI as either P700 or an adjacent chlorophyll pair in the RC.14,17,32
The origin of the site energy shifts can be distinguished in a structural and an electrostatic component. The distribution of the structural component is broad, spanning ∼100 meV and strongly overlapping in all chlorophylls. This indicates that the steric hindrance by the environment plays only a subordinate role in the observed site energy shifts. In contrast, the electrostatics clearly induce shifts of ±50 meV in the individual site energies, though clear correlations between environmental charge distributions and site energies remain to be found. In this context, we expect breakthroughs by the application of machine learning techniques.
The set of site energies and exciton couplings derived here allows us to draw conclusions about the light-harvesting process in PSI. In particular, we find that the RC is on average separated from the antenna complex by an energy barrier in the linker chlorophylls eC-A3 and eC-B3. Such a barrier may be beneficial to prevent wasting of energy when the RC is in its oxidized state. The dynamical perspective in this work reveals strong fluctuations in the site energies which in turn govern the fluctuations in the excitonic energies. Thus, excitation energy transfer within PSI should be thought of as a highly flexible process where new pathways open and close transiently on a sub-10 ps time scale via thermal thermal fluctuations in the range of kBT.
This means that even low-energy excitations can eventually culminate in a redox event,19 due to the efficient use of ambient heat,8,30 possibly even by recycling of heat dissipated by other chromophores.149 Combining these results, we propose that the antenna complex in PSI not only acts as an energy-transport system but can also store excess energy temporarily until it is needed in the RC, thereby increasing its overall efficiency.
PSI has the potential to become an integral component in artificial light-harvesting devices, providing a sustainable alternative to inorganic components.150–152 A detailed mechanistic understanding of governing energy transfer and conversion processes is crucial to harness its potential. We hope that the present work will contribute to this goal and guide future studies on the road to using PSI for green energy conversion.
Data availability
Mean site energies and shifts are provided in the ESI.† Newly derived or modified force field parameters, an optimized structure of chlorophyll a in xyz format, an equilibrated structure of the full PSI in pdb format, raw data of spectra, site energies and exciton couplings as well as statistical analyses as csv tables are openly available at Zenodo (DOI: https://doi.org/10.5281/zenodo.6576313).Author contributions
Sebastian Reiter: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review & editing; Ferdinand L. Kiss: conceptualization, validation, writing – original draft, writing – review & editing; Jürgen Hauer: conceptualization, funding acquisition, supervision, writing – review & editing; Regina de Vivie-Riedle: conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Viviana Piccinni for support in the protein crystal structure refinement. Funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the cluster of excellence e-conversion under Germany's Excellence Strategy – EXC 2089/1 – 390776260 is gratefully acknowledged. We are thankful for the computational and data resources provided by the Leibniz Supercomputing Centre (https://www.lrz.de). SR gratefully acknowledges support from the International Max Planck Research School of Advanced Photon Science (IMPRS-APS).Notes and references
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley, 3rd edn, 2021 Search PubMed.
- J. Kargul, J. D. Janna Olmos and T. Krupnik, J. Plant Physiol., 2012, 169, 1639–1653 CrossRef CAS PubMed.
- D. Ciornii, M. Riedel, K. R. Stieger, S. C. Feifel, M. Hejazi, H. Lokstein, A. Zouni and F. Lisdat, J. Am. Chem. Soc., 2017, 139, 16478–16481 CrossRef CAS PubMed.
- S. Osella, Nanomaterials, 2021, 11, 299 CrossRef CAS PubMed.
- N. Krauß, W.-D. Schubert, O. Klukas, P. Fromme, H. T. Witt and W. Saenger, Nat. Struct. Mol. Biol., 1996, 3, 965–973 CrossRef PubMed.
- P. Fromme, P. Jordan and N. Krauß, Biochim. Biophys. Acta, Bioenerg., 2001, 1507, 5–31 CrossRef CAS PubMed.
- P. Jordan, P. Fromme, H. T. Witt, O. Klukas, W. Saenger and N. Krauß, Nature, 2001, 411, 909–917 CrossRef CAS PubMed.
- L.-O. Pålsson, C. Flemming, B. Gobets, R. van Grondelle, J. P. Dekker and E. Schlodder, Biophys. J., 1998, 74, 2611–2622 CrossRef PubMed.
- A. R. Holzwarth, G. Schatz, H. Brock and E. Bittersmann, Biophys. J., 1993, 64, 1813–1826 CrossRef CAS PubMed.
- B. Gobets and R. van Grondelle, Biochim. Biophys. Acta, Bioenerg., 2001, 1507, 80–99 CrossRef CAS PubMed.
- B. Gobets, I. H. M. van Stokkum, F. van Mourik, J. P. Dekker and R. van Grondelle, Biophys. J., 2003, 85, 3883–3898 CrossRef CAS PubMed.
- D. A. Cherepanov, N. G. Brady, I. V. Shelaev, J. Nguyen, F. E. Gostev, M. D. Mamedov, V. A. Nadtochenko and B. D. Bruce, Biophys. J., 2020, 118, 337–351 CrossRef CAS PubMed.
- S. Santabarbara, L. Galuppini and A. P. Casazza, J. Integr. Plant Biol., 2010, 52, 735–749 CrossRef CAS PubMed.
- M. G. Müller, C. Slavov, R. Luthra, K. E. Redding and A. R. Holzwarth, Proc. Natl. Acad. Sci., 2010, 107, 4123–4128 CrossRef PubMed.
- H. Lokstein, G. Renger and J. P. Götze, Molecules, 2021, 26, 3378 CrossRef CAS PubMed.
- K. Brettel and W. Leibl, Biochim. Biophys. Acta, Bioenerg., 2001, 1507, 100–114 CrossRef CAS PubMed.
- M. Di Donato, A. D. Stahl, I. H. M. van Stokkum, R. van Grondelle and M.-L. Groot, Biochemistry, 2011, 50, 480–490 CrossRef CAS PubMed.
- J. R. Reimers, M. Biczysko, D. Bruce, D. F. Coker, T. J. Frankcombe, H. Hashimoto, J. Hauer, R. Jankowiak, T. Kramer, J. Linnanto, F. Mamedov, F. Müh, M. Rätsep, T. Renger, S. Styring, J. Wan, Z. Wang, Z.-Y. Wang-Otomo, Y.-X. Weng, C. Yang, J.-P. Zhang, A. Freiberg and E. Krausz, Biochim. Biophys. Acta, Bioenerg., 2016, 1857, 1627–1640 CrossRef CAS PubMed.
- D. A. Cherepanov, I. V. Shelaev, F. E. Gostev, M. D. Mamedov, A. A. Petrova, A. V. Aybush, V. A. Shuvalov, A. Y. Semenov and V. A. Nadtochenko, Biochim. Biophys. Acta, Bioenerg., 2017, 1858, 895–905 CrossRef CAS PubMed.
- S. Hatazaki, D. K. Sharma, S. Hirata, K. Nose, T. Iyoda, A. Kölsch, H. Lokstein and M. Vacha, J. Phys. Chem. Lett., 2018, 9, 6669–6675 CrossRef CAS PubMed.
- M. Russo, A. P. Casazza, G. Cerullo, S. Santabarbara and M. Maiuri, J. Chem. Phys., 2022, 156, 164202 CrossRef CAS PubMed.
- P. Canfield, M. G. Dahlbom, N. S. Hush and J. R. Reimers, J. Chem. Phys., 2006, 124, 024301 CrossRef PubMed.
- J. Adolphs, F. Müh, M. E.-A. Madjet, M. S. am Busch and T. Renger, J. Am. Chem. Soc., 2010, 132, 3331–3343 CrossRef CAS PubMed.
- G. E. Milanovsky, V. V. Ptushenko, J. H. Golbeck, A. Y. Semenov and D. A. Cherepanov, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1472–1483 CrossRef CAS PubMed.
- C. Kreisbeck and A. Aspuru-Guzik, Chem. Sci., 2016, 7, 4174–4183 RSC.
- F. Häse, C. Kreisbeck and A. Aspuru-Guzik, Chem. Sci., 2017, 8, 8419–8426 RSC.
- F. C. Ramos, M. Nottoli, L. Cupellini and B. Mennucci, Chem. Sci., 2019, 10, 9650–9662 RSC.
- Y. Shibata, S. Nishi, K. Kawakami, J.-R. Shen and T. Renger, J. Am. Chem. Soc., 2013, 135, 6903–6914 CrossRef CAS PubMed.
- S. Baghbanzadeh and I. Kassal, Phys. Chem. Chem. Phys., 2016, 18, 7459–7467 RSC.
- W. Giera, S. Szewczyk, M. D. McConnell, K. E. Redding, R. van Grondelle and K. Gibasiewicz, Photosynth. Res., 2018, 137, 321–335 CrossRef CAS PubMed.
- J. Adolphs, F. Müh, M. E.-A. Madjet and T. Renger, Photosynth. Res., 2007, 95, 197 CrossRef PubMed.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2021, 17, 1858–1873 CrossRef CAS PubMed.
- E. Cignoni, V. Slama, L. Cupellini and B. Mennucci, J. Chem. Phys., 2022, 156, 120901 CrossRef CAS PubMed.
- T. Renger, V. May and O. Kühn, Phys. Rep., 2001, 343, 137–254 CrossRef CAS.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138–163 CrossRef CAS.
- R. J. Cogdell, N. W. Isaacs, A. A. Freer, T. D. Howard, A. T. Gardiner, S. M. Prince and M. Z. Papiz, FEBS Lett., 2003, 555, 35–39 CrossRef CAS PubMed.
- S. Vassiliev and D. Bruce, Photosynth. Res., 2008, 97, 75–89 CrossRef CAS PubMed.
- M. Şener, J. Strümpfer, J. Hsin, D. Chandler, S. Scheuring, C. N. Hunter and K. Schulten, ChemPhysChem, 2011, 12, 518–531 CrossRef PubMed.
- S. Vassiliev, A. Mahboob and D. Bruce, Photosynth. Res., 2011, 110, 25 CrossRef CAS PubMed.
- T. Reinot, A. Khmelnitskiy, A. Kell, M. Jassas and R. Jankowiak, ACS Omega, 2021, 6, 5990–6008 CrossRef CAS PubMed.
- M. Byrdin, P. Jordan, N. Krauss, P. Fromme, D. Stehlik and E. Schlodder, Biophys. J., 2002, 83, 433–457 CrossRef CAS PubMed.
- B. Brüggemann, K. Sznee, V. Novoderezhkin, R. van Grondelle and V. May, J. Phys. Chem. B, 2004, 108, 13536–13546 CrossRef.
- S. Vaitekonis, G. Trinkunas and L. Valkunas, Photosynth. Res., 2005, 86, 185–201 CrossRef CAS PubMed.
- A. Damjanović, H. M. Vaswani, P. Fromme and G. R. Fleming, J. Phys. Chem. B, 2002, 106, 10251–10262 CrossRef.
- S. Yin, M. G. Dahlbom, P. J. Canfield, N. S. Hush, R. Kobayashi and J. R. Reimers, J. Phys. Chem. B, 2007, 111, 9923–9930 CrossRef CAS PubMed.
- S. Maity, B. M. Bold, J. D. Prajapati, M. Sokolov, T. Kubař, M. Elstner and U. Kleinekathöfer, J. Phys. Chem. Lett., 2020, 11, 8660–8667 CrossRef CAS PubMed.
- S. Maity, V. Daskalakis, M. Elstner and U. Kleinekathöfer, Phys. Chem. Chem. Phys., 2021, 23, 7407–7417 RSC.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2020, 142, 18174–18190 CrossRef CAS PubMed.
- A. Sirohiwal, F. Neese and D. A. Pantazis, Chem. Sci., 2021, 12, 4463–4476 RSC.
- M. Russo, A. P. Casazza, G. Cerullo, S. Santabarbara and M. Maiuri, J. Phys. Chem. B, 2021, 125, 3566–3573 CrossRef CAS PubMed.
- H. Du, R.-C. A. Fuh, J. Li, L. A. Corkan and J. S. Lindsey, Photochem. Photobiol., 1998, 68, 141–142 CAS.
- M. Taniguchi and J. S. Lindsey, Photochem. Photobiol., 2021, 97, 136–165 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1606 Search PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101 CrossRef PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, 95th edn, 2014 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. Najibi and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572 CrossRef CAS PubMed.
- M. Casanova-Páez and L. Goerigk, J. Chem. Theory Comput., 2021, 17, 5165–5186 CrossRef PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- J. Ridley and M. Zerner, Theor. Chim. Acta, 1973, 32, 111–134 CrossRef CAS.
- C. Olbrich and U. Kleinekathöfer, J. Phys. Chem. B, 2010, 114, 12427–12437 CrossRef CAS PubMed.
- C. Olbrich, J. Strümpfer, K. Schulten and U. Kleinekathöfer, J. Phys. Chem. Lett., 2011, 2, 1771–1776 CrossRef CAS PubMed.
- C. Olbrich, T. L. C. Jansen, J. Liebers, M. Aghtar, J. Strümpfer, K. Schulten, J. Knoester and U. Kleinekathöfer, J. Phys. Chem. B, 2011, 115, 8609–8621 CrossRef CAS PubMed.
- J. Gao, W.-J. Shi, J. Ye, X. Wang, H. Hirao and Y. Zhao, J. Phys. Chem. B, 2013, 117, 3488–3495 CrossRef CAS PubMed.
- L. Zhang, D.-A. Silva, H. Zhang, A. Yue, Y. Yan and X. Huang, Nat. Commun., 2014, 5, 4170 CrossRef CAS PubMed.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- C. M. Marian, A. Heil and M. Kleinschmidt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 9, e1394 Search PubMed.
- M. Kleinschmidt, C. M. Marian, M. Waletzke and S. Grimme, J. Chem. Phys., 2009, 130, 044708 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- S. Kossmann and F. Neese, Chem. Phys. Lett., 2009, 481, 240–243 CrossRef CAS.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed.
- A. Heil, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2018, 149, 164106 CrossRef PubMed.
- A. Sali and T. L. Blundell, J. Mol. Biol., 1993, 234, 779–815 CrossRef CAS PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- D. Sundholm, Chem. Phys. Lett., 1999, 302, 480–484 CrossRef CAS.
- D. Sundholm, Chem. Phys. Lett., 2000, 317, 545–552 CrossRef CAS.
- G. Mondragón-Solórzano and J. Barroso-Flores, Int. J. Quantum Chem., 2018, 118, e25663 CrossRef.
- A. Agostini, D. M. Palm, F.-J. Schmitt, M. Albertini, M. D. Valentin, H. Paulsen and D. Carbonera, Sci. Rep., 2017, 7, 7504 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- J. M. Word, S. C. Lovell, J. S. Richardson and D. C. Richardson, J. Mol. Biol., 1999, 285, 1735–1747 CrossRef CAS PubMed.
- S. Schott-Verdugo and H. Gohlke, J. Chem. Inf. Model., 2019, 59, 2522–2528 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- L. Zhang, D.-A. Silva, Y. Yan and X. Huang, J. Comput. Chem., 2012, 33, 1969–1980 CrossRef CAS PubMed.
- M. Ceccarelli, P. Procacci and M. Marchi, J. Comput. Chem., 2003, 24, 129–142 CrossRef CAS PubMed.
- D. M. A. Smith, Y. Xiong, T. P. Straatsma, K. M. Rosso and T. C. Squier, J. Chem. Theory Comput., 2012, 8, 2103–2114 CrossRef CAS PubMed.
- A. g. A. Skjevik, B. D. Madej, R. C. Walker and K. Teigen, J. Phys. Chem. B, 2012, 116, 11124–11136 CrossRef CAS PubMed.
- C. J. Dickson, B. D. Madej, A. g. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879 CrossRef CAS PubMed.
- Z. Wu, Gromacs Port of the Amber LIPID17 Force Field, Version 0.21, Zenodo, 2019, DOI:10.5281/ZENODO.3560998.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nosé and M. L. Klein, Mol. Phys., 1983, 50, 1055–1076 CrossRef.
- A. Leftin, T. R. Molugu, C. Job, K. Beyer and M. F. Brown, Biophys. J., 2014, 107, 2274–2286 CrossRef CAS PubMed.
- A. g. A. Skjevik, B. D. Madej, C. J. Dickson, K. Teigen, R. C. Walker and I. R. Gould, Chem. Commun., 2015, 51, 4402–4405 RSC.
- G. Shahane, W. Ding, M. Palaiokostas and M. Orsi, J. Mol. Model., 2019, 25, 76 CrossRef PubMed.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- D. Bakowies and W. Thiel, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1986, 7, 718–730 CrossRef CAS.
- U. Eichler, C. M. Kölmel and J. Sauer, J. Comput. Chem., 1997, 18, 463–477 CrossRef CAS.
- P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjø voll, A. Fahmi, A. Schäfer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28 CrossRef CAS.
- A. Anda, T. Hansen and L. De Vico, J. Chem. Theory Comput., 2016, 12, 1305–1313 CrossRef CAS PubMed.
- A. Anda, T. Hansen and L. De Vico, J. Phys. Chem. A, 2019, 123, 5283–5292 CrossRef CAS PubMed.
- S. Reiter, L. Bäuml, J. Hauer and R. de Vivie-Riedle, Phys. Chem. Chem. Phys., 2022, 24, 27212–27223 RSC.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- B. P. Fingerhut and S. Mukamel, J. Phys. Chem. Lett., 2012, 3, 1798–1805 CrossRef CAS PubMed.
- P. López-Tarifa, N. Liguori, N. van den Heuvel, R. Croce and L. Visscher, Phys. Chem. Chem. Phys., 2017, 19, 18311–18320 RSC.
- A. Kimura and S. Itoh, J. Phys. Chem. B, 2018, 122, 11852–11859 CrossRef CAS PubMed.
- A. Kimura, H. Kitoh-Nishioka, T. Aota, T. Hamaguchi, K. Yonekura, K. Kawakami, K. Shinzawa-Itoh, N. Inoue-Kashino, K. Ifuku, E. Yamashita, Y. Kashino and S. Itoh, J. Phys. Chem. B, 2022, 126, 4009–4021 CrossRef CAS PubMed.
- R. S. Knox and B. Q. Spring, Photochem. Photobiol., 2003, 77, 497–501 CrossRef CAS PubMed.
- J. R. Reimers, Z.-L. Cai, R. Kobayashi, M. Rätsep, A. Freiberg and E. Krausz, Sci. Rep., 2013, 3, 1–8 Search PubMed.
- N. H. List, C. Curutchet, S. Knecht, B. Mennucci and J. Kongsted, J. Chem. Theory Comput., 2013, 9, 4928–4938 CrossRef CAS PubMed.
- A. B. J. Parusel and S. Grimme, J. Phys. Chem. B, 2000, 104, 5395–5398 CrossRef CAS.
- J. P. Götze, F. Anders, S. Petry, J. F. Witte and H. Lokstein, Chem. Phys., 2022, 559, 111517 CrossRef.
- K. J. Riley, T. o. Reinot, R. Jankowiak, P. Fromme and V. Zazubovich, J. Phys. Chem. B, 2007, 111, 286–292 CrossRef CAS PubMed.
- A. Khmelnitskiy, H. Toporik, Y. Mazor and R. Jankowiak, J. Phys. Chem. B, 2020, 124, 8504–8515 CrossRef CAS PubMed.
- H. Toporik, A. Khmelnitskiy, Z. Dobson, R. Riddle, D. Williams, S. Lin, R. Jankowiak and Y. Mazor, Nat. Commun., 2020, 11, 5279 CrossRef CAS PubMed.
- N. Dashdorj, W. Xu, R. O. Cohen, J. H. Golbeck and S. Savikhin, Biophys. J., 2005, 88, 1238–1249 CrossRef CAS PubMed.
- S. Santabarbara, P. Heathcote and M. C. W. Evans, Biochim. Biophys. Acta, Bioenerg., 2005, 1708, 283–310 CrossRef CAS PubMed.
- M. Yang, A. Damjanović, H. M. Vaswani and G. R. Fleming, Biophys. J., 2003, 85, 140–158 CrossRef CAS PubMed.
- J. Heimdal, K. P. Jensen, A. Devarajan and U. Ryde, J. Biol. Inorg Chem., 2007, 12, 49–61 CrossRef CAS PubMed.
- D. Rutkowska-Zbik and T. Korona, J. Chem. Theory Comput., 2012, 8, 2972–2982 CrossRef CAS PubMed.
- T. S. Balaban, P. Fromme, A. R. Holzwarth, N. Krauß and V. I. Prokhorenko, Biochim. Biophys. Acta, Bioenerg., 2002, 1556, 197–207 CrossRef CAS PubMed.
- T. S. Balaban, P. Braun, C. Hättig, A. Hellweg, J. Kern, W. Saenger and A. Zouni, Biochim. Biophys. Acta, Bioenerg., 2009, 1787, 1254–1265 CrossRef CAS PubMed.
- B. F. Milne, Y. Toker, A. Rubio and S. B. n. Nielsen, Angew. Chem., 2015, 127, 2198–2201 CrossRef.
- M. Fortino, E. Collini, J. Bloino and A. Pedone, J. Chem. Phys., 2021, 154, 094110 CrossRef CAS PubMed.
- F. J. Van Eerden, M. N. Melo, P. W. J. M. Frederix and S. J. Marrink, Biophys. J., 2017, 113, 2669–2681 CrossRef CAS PubMed.
- A. Kell, X. Feng, C. Lin, Y. Yang, J. Li, M. Reus, A. R. Holzwarth and R. Jankowiak, J. Phys. Chem. B, 2014, 118, 6086–6091 CrossRef CAS PubMed.
- Y. Lee, M. Gorka, J. H. Golbeck and J. M. Anna, J. Am. Chem. Soc., 2018, 140, 11631–11638 CrossRef CAS PubMed.
- M. Zubik, R. Luchowski, D. Kluczyk, W. Grudzinski, M. Maksim, A. Nosalewicz and W. I. Gruszecki, J. Phys. Chem. Lett., 2020, 3242–3248 CrossRef CAS PubMed.
- K. R. Stieger, S. C. Feifel, H. Lokstein and F. Lisdat, Phys. Chem. Chem. Phys., 2014, 16, 15667–15674 RSC.
- S. C. Feifel, H. Lokstein, M. Hejazi, A. Zouni and F. Lisdat, Langmuir, 2015, 31, 10590–10598 CrossRef CAS PubMed.
- S. C. Feifel, K. R. Stieger, H. Lokstein, H. Lux and F. Lisdat, J. Mater. Chem. A, 2015, 3, 12188–12196 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details on structure modelling; further details on the MD protocol and validation; chlorophyll absorption spectra with various QM methods; mean site energies and energy shifts of each chlorophyll, sorted according to Fig. 9; convergence of site energies with the number of snapshots; comparison of the present data set with literature data; excited states of selected chlorophyll dimers and the trimer B31–B32–B33; exciton energies. See DOI: https://doi.org/10.1039/d2sc06160k |
| This journal is © The Royal Society of Chemistry 2023 |