Open Access Article
Open Access ArticleMultiscale quantum algorithms for quantum chemistry
Huan
Ma
 a,
Jie
Liu
a,
Jie
Liu
 *a,
Honghui
Shang
*c,
Yi
Fan
b,
Zhenyu
Li
*a,
Honghui
Shang
*c,
Yi
Fan
b,
Zhenyu
Li
 ab and
Jinlong
Yang
ab and
Jinlong
Yang
 *ab
*ab
aHefei National Laboratory, University of Science and Technology of China, Hefei 230088, China. E-mail: liujie86@ustc.edu.cn; jlyang@ustc.edu.cn
bHefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei 230026, China
cState Key Laboratory of Computer Architecture, Institute of Computing Technology, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: shanghonghui@ict.ac.cn
First published on 16th February 2023
Abstract
Exploring the potential applications of quantum computers in material design and drug discovery is attracting more and more attention after quantum advantage has been demonstrated using Gaussian boson sampling. However, quantum resource requirements in material and (bio)molecular simulations are far beyond the capacity of near-term quantum devices. In this work, multiscale quantum computing is proposed for quantum simulations of complex systems by integrating multiple computational methods at different scales of resolution. In this framework, most computational methods can be implemented in an efficient way on classical computers, leaving the critical portion of the computation to quantum computers. The simulation scale of quantum computing strongly depends on available quantum resources. As a near-term scheme, we integrate adaptive variational quantum eigensolver algorithms, second-order Møller–Plesset perturbation theory and Hartree–Fock theory within the framework of the many-body expansion fragmentation approach. This new algorithm is applied to model systems consisting of hundreds of orbitals with decent accuracy on the classical simulator. This work should encourage further studies on quantum computing for solving practical material and biochemistry problems.
1 Introduction
As quantum advantage has been demonstrated on different quantum computing platforms using Gaussian boson sampling,1–3 quantum computing is moving to the next stage, namely demonstrating quantum advantage in solving practical problems. Two typical problems of this kind are computational-aided material design and drug discovery, in which quantum chemistry plays a critical role in answering questions such as ∼Which one is the best?∼. Many recent efforts have been devoted to the development of advanced quantum algorithms for solving quantum chemistry problems on noisy intermediate-scale quantum (NISQ) devices,2,4–14 while implementing these algorithms for complex problems is limited by available qubit counts, coherence time and gate fidelity. Specifically, without error correction, quantum simulations of quantum chemistry are viable only if low-depth quantum algorithms are implemented to suppress the total error rate. Recent advances in error mitigation techniques enable us to model many-electron problems with a dozen qubits and tens of circuit depths on NISQ devices,9 while such circuit sizes and depths are still a long way from practical applications.The difference between the available and actually required quantum resources in practical quantum simulations has renewed the interest in divide and conquer (DC) based methods.15–19 Realistic material and (bio)chemistry systems often involve complex environments, such as surfaces and interfaces. To model these systems, the Schrödinger equations are much too complicated to be solvable. It therefore becomes desirable that approximate practical methods of applying quantum mechanics be developed.20 One popular scheme is to divide the complex problem under consideration into as many parts as possible until these become simple enough for an adequate solution, namely the philosophy of DC.21 The DC method is particularly suitable for NISQ devices since the sub-problem for each part can in principle be solved with fewer computational resources.15–18,22–25 One successful application of DC is to estimate the ground-state potential energy surface of a ring containing 10 hydrogen atoms using the density matrix embedding theory (DMET) on a trapped-ion quantum computer, in which a 20-qubit problem is decomposed into ten 2-qubit problems.18
DC often treats all subsystems at the same computational level and estimates physical observables by summing up the corresponding quantities of subsystems, while in practical simulations of complex systems, the particle–particle interactions may exhibit completely different characteristics in and between subsystems. Long-range Coulomb interactions can be well approximated as quasiclassical electrostatic interactions since empirical methods, such as empirical force filed (EFF) approaches,26 are promising to describe these interactions. As the distance between particles decreases, the repulsive exchange interactions from electrons having the same spin become important so that quantum mean-field approaches, such as Hartree–Fock (HF), are necessary to characterize these electronic interactions. Furthermore, van der Waals interactions, such as hydrogen bond and stacked π–π bond interactions and (near-)degenerate electronic interactions should be evaluated using more accurate wave function methods.27,28 Therefore, after decomposing a complex system into many subsystems, treating interactions in and between them with different computational models according to the characteristics of these interactions is an optimal way to approximate the exact results with moderate computational cost. This strategy is often referred to as multiscale modeling that aims at solving problems at multiple scales of space and/or time.29–31
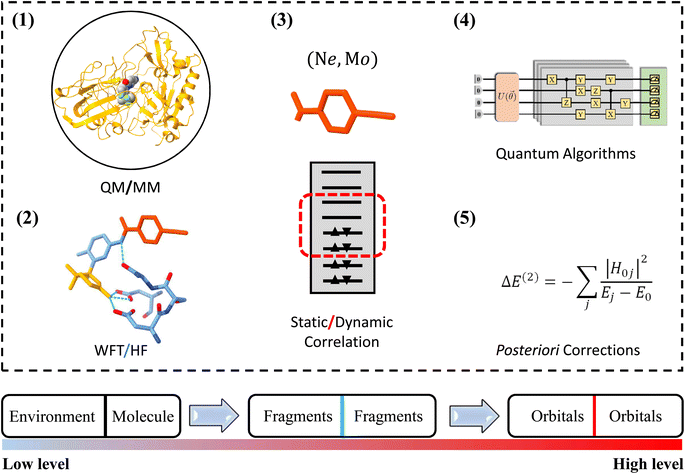
One of the most widely used multiscale models is the combination of classical and quantum mechanical (QM) principles for theoretical simulations of large biological molecules and condensed matter systems. Here, QM models are computationally demanding due to the high computational complexity of QM methods. In particular, when the QM models using the high-level wave function theory (WFT) are employed to describe the central part of a complex system, the size of the QM region to be chosen is extremely limited. Due to the potential computational power of quantum computing, QM models using quantum algorithms are a feasible way to overcome the compromise between accuracy and size. In this work, we refer to this strategy that integrates quantum computing into multiscale models as multiscale quantum computing (see a typical example in Fig. 1). Quantum algorithms are expected to provide an exact solution of the Schrödinger equation in polynomial time,10,11 which enables us to enlarge the size of the QM region without loss of efficiency.
Analogous to classical multiscale modeling, one is able to employ molecular mechanical (MM) approaches, semiempirical approaches or even quantum mean-field approaches, such as HF or density functional theory (DFT), to describe the environment and the interaction between the molecule and environment. The correlation energy should in principle be fully accounted for using quantum computing models when fault-tolerant quantum computers are available. In the NISQ era, the major challenge of multiscale quantum computing is analogous to that of classical multiscale modeling, that is, how to use limited quantum resources to approximate the exact results. In this work, we divide the QM region into fragments and build the QM model using energy-based fragmentation approaches.32 Furthermore, in each fragment, one can decompose the correlation effect into dynamic and static correlations, leaving only the latter one to the quantum computer in order to reduce quantum circuit sizes and depths. Thus, this scheme is able to extend applications of quantum simulations to complex systems.
In Section 2, we present a detailed introduction to a general framework of multiscale quantum computing for complex system simulations, including typical computational models, DC strategies and correlation energy decomposition schemes. In Section 3, we propose a practical scheme for implementing multiscale quantum computing in quantum chemistry. We focus on modeling the QM part with high accuracy on NISQ devices since its combination with low-level computational methods for modeling other surrounding parts has been extensively studied.29–31 To adapt our algorithm to contemporary quantum resources, we first employ the many-body expansion (MBE) fragmentation approach to partition the QM part of a system into small fragments. The accuracy of the MBE approach can be systematically improved toward the accurate results by including high-order many-body corrections. In each fragment, the quantum algorithm is employed to exactly solve complete active space (CAS) problems to describe the static correlation energy. The perturbation theory is applied to recover the dynamic correlation energy that is also essential in accurately characterizing energy profiles. In comparison with the DMET33 that was recently introduced in quantum computing, applying perturbation theories, such as second-order Møller–Plesset perturbation theory (MP2), in the MBE approach is straightforward. As pilot applications, our methods are used to model systems consisting of hundreds of orbitals with decent accuracy. This demonstrates that our method would be particularly applicable to near-term quantum devices.
2 Multiscale quantum computing
Applying multiscale models to complex systems has a long history in the study of biological processes and complex chemical reactions.29–31 Due to its great success, the Nobel Prize in Chemistry 2013 has been awarded to Martin Karplus, Michael Levitt and Arieh Warshel for the development of multiscale models of complex chemical systems. In multiscale modeling, one uses a variety of models at different levels of resolution and complexity to strike a balance between accuracy and efficiency.A popular multiscale scheme to deal with complex systems at the electronic scale is to combine QM models with MM models.30 The total energy of a QM/MM system can be written as
| Etotal = EQM + EMM + EQM–MM | (1) |
When commercial quantum computers become a reality, it is expected that quantum resources will be sufficient to implement the QM model straightforwardly within the framework of quantum computing. In the case of NISQ devices, it is necessary to further decompose the QM problem into sub-problems that are treated at different levels, leaving the most time-consuming sub-problem to quantum computing. Fig. 1 shows a schematic structure of multiscale quantum computing using a protein–ligand system as an example. This complex system is first divided into a molecule and a molecular environment as is commonly performed in the QM/MM scheme. The environment can be represented by a variety of low-scaling computational models, ranging from EFFs to semiempirical wave function approaches, or even to DFT. The central region should include the ligand molecule and surrounding segments of the protein, leading to a QM system containing tens or even hundreds of atoms. We further divide this QM system into many fragments, with intra-fragment interactions described by the WFT and high-order inter-fragment interactions described by the HF theory. Finally, the orbital space is divided into an active space and a frozen space. In the active space, the CAS configuration interaction (CI) problem is diagonalized on a quantum computer. After this three-step DC procedure, the CASCI problem is usually simple enough to implement on NISQ devices with low-depth quantum circuits.
2.1 Low-level computational models
A simple way to describe the environment at the all-atom level is through classical potential energy functions. For example, EFF approaches decompose the interaction energy into bond, angle, dihedral angle and van der Waals energies, which can be efficiently evaluated using analytical function forms so that large systems can be studied. Inspired by the deep insight into electron–electron interactions from quantum chemistry, QM-based potential models with no empirical parameters, e.g. effective fragment potential (EFP), have been developed for a more accurate description of the environment.35 The interaction energy of the EFP model includes electrostatics, polarization, dispersion and exchange-repulsion contributions, while, both the EFF and EFP models contribute a local embedding potential to the Hamiltonian of the QM part. In the EFF model, the coupling between the QM region and the environment is approximated with an electrostatic potential. In the EFP model, an additional polarization potential is included. The total QM Hamiltonian is expressed asĤQMtotal = ĤQM + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) es + es + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) pol pol | (2) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) es and
es and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) pol are electrostatic and polarization potentials, respectively.
pol are electrostatic and polarization potentials, respectively.
Classical potential energy function-based approaches ignore the exchange interactions. As such, they are not suitable for describing the situation where the electron density distribution changes greatly because the exchange interactions become important in this case. Alternatively, it is possible to construct a more accurate embedding potential from QM methods. Frozen-density embedding theory (FDET) constructs an exact embedding potential through a constrained optimization of the total electron density.36 Given that the FDET embedding potential has the form of a universal functional of charge densities, the formalism is in principle rigorous if the functional is exact. In practical simulations, charge densities can be determined from a non-self-consistent-field optimization or even from individual calculations of fragments to save the computational cost. The embedding potential can also be constructed from wave function-based approaches. The X-Pol method is such a theory in which the embedding potential is formulated based on the wave function of other surrounding fragments.37
2.2 High-level computational models
In order to accurately predict reaction barriers and the conformation stability, the central parts of complex systems should be described using high-level QM computational models. DFT can in principle yield the exact ground-state energy and electron density of a quantum system, as evidenced by its increasingly broad application in chemistry and materials science for predicting and interpreting complex system behaviors at an atomic scale. The accuracy of the DFT approach depends on exchange-correlation functionals while the exact form of functionals is unknown. Therefore, approximate exchange correlation functionals are adopted in practical calculations. Due to its low computational complexity, DFT has been extended to very large-scale simulations of systems containing millions of atoms.38 As a consequence, DFT is able to provide a qualitative description of most quantum chemistry problems.When accuracy in the laboratory, often referring to chemical accuracy (within 1 kcal mol−1), is required, WFT approaches are an appealing option since their accuracy can be systematically improved toward the full configuration interaction (FCI). While, due to the exponentially increasing computational cost, the largest exact diagonalization calculations were only carried out for a CAS configuration interaction (CASCI) problem with 24 electrons in 24 spatial orbitals. For nondegenerate ground-state problems, the CCSD(T) method in the complete basis set limit is considered as the gold standard for predicting relative energies of different molecular and material conformations.39,40 When systems consist of transition metal atoms, multi-reference approaches, such as CASSCF and MRCI, are necessary for describing the strong correlation effect. Both single-reference and multi-reference approaches have an unaffordable computational complexity for accurate simulations of complex systems.
Quantum algorithms are anticipated to provide an exponential speedup for exactly solving quantum chemistry problems. Quantum phase estimation (QPE) is considered a quantum algorithm that can realise quantum advantage in chemical and material simulations.41 It is worth discussing whether the QPE algorithm has real exponential acceleration when solving general quantum chemistry problems. The possibility that QPE can only achieve a polynomial acceleration still presents significant progress in quantum chemistry.42 In the current stage, the variational quantum eigensolver (VQE) is an alternative choice for exploring the potential applications of quantum computing in quantum chemistry.5
To find an exact solution to the Schrödinger equation it requires the implementation of state-of-the-art wave function ansatzes in the VQE. These ansatzes often result in deep quantum circuits that go beyond the capacity of current quantum devices even for few qubit VQE calculations due to coherence time. For example, the unitary coupled cluster (UCC) with single and double excitations (UCCSD) is one of the most widely used wave function ansatzes in the VQE. Its circuit depth scales as quartic as the system size. In addition, the UCCSD ansatz is unable to describe the strong correlation effect, such as the triple bond dissociation of molecular nitrogen.43 Many recent studies have contributed to the development of adaptive VQE algorithms to reduce circuit depth.44–48 Adaptive derivative-assembled pseudo-trotter (ADAPT) ansatz44 builds a very compact representation of electronic wave functions while maintaining high accuracy. The qubit coupled cluster (QCC) represents the electronic wave function in the qubit representation. Furthermore, in combination with the effective Hamiltonian theory, the QCC maintains a constant circuit depth for electronic structure simulations.49
2.3 Divide and conquer
In the case of quantum simulations of quantum chemistry problems involving tens or hundreds of orbitals that may find usage in practical applications, one can resort to fault-tolerant quantum computers scaling up to hundreds of logical qubits. This represents a long-term plan for quantum computing with quantum error correction. As a potential strategy tailored for NISQ devices, the DC philosophy has been recently introduced in quantum computing.15–19 With the help of the fragmentation strategy (Table 1), a complicated quantum chemistry problem can be decomposed into as many parts as possible according to available quantum circuit sizes and depths. This brings two advantages in implementing quantum algorithms:(1) The size of subsystems that determines the number of qubits used in quantum computing can adapt to available quantum resources. And then massively parallel quantum simulations of subsystems can be performed on NISQ devices. Finally, properties of subsystems are combined to obtain the corresponding quantities of the full system. This maximizes the utilization efficiency of small-scale quantum computational resources in practical applications.
(2) The circuit depth in each subsystem simulation is significantly reduced in comparison with that in the simulation of the full system. For example, the circuit depth of UCCSD scales as 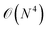 with N being the system size. If the full system is divided into Ns subsystems, the circuit depth for each subsystem is in principle reduced by Ns4. Low-depth circuits can be effectively combined with error mitigation techniques to reduce the total error rate.
with N being the system size. If the full system is divided into Ns subsystems, the circuit depth for each subsystem is in principle reduced by Ns4. Low-depth circuits can be effectively combined with error mitigation techniques to reduce the total error rate.
In the age of quantum computing without error correction, it is appealing to explore these two aspects by combining the VQE with the DC philosophy to enable large-scale simulations on NISQ devices.
Two popular DC schemes for quantum chemistry simulations are fragment-based approaches32 and quantum embedding theories.33 Fragment-based approaches usually partition a system according to chemical information, such as chemical functional groups and chemical bonds. A variety of fragment-based approaches, such as the fragment molecular-orbital method,50 the molecular fragmentation with conjugated caps method,51,52 and the (generalized) many-body expansion,53–55 have been proposed for studying complex systems. The accuracy of fragment-based approaches depends on molecular fragmentation schemes and posteriori corrections to high-order many-body interactions.32 In contrast, quantum embedding theories provide a more flexible way to partition large systems. The interaction between the subsystem and the environment is described by including bath orbitals in subsystem calculations. However, applying posteriori corrections to the DMET is not a trivial task since it involves a self-consistent iteration procedure. A pilot implementation of the DMET within the framework of the VQE has been recently realized for a ring of 10 hydrogen atoms on a trapped-ion quantum computer.18 A numerical simulation of C18 with the cc-pVDZ basis (up to 144 qubits) has been performed with the DMET-VQE method.19 Although these preliminary studies have demonstrated the advantage of the DC strategy in quantum computing, the application of the DC approaches within the VQE framework to practical quantum chemistry problems is still an open question.
2.4 Correlation energy decomposition
The Coulomb and exchange electron–electron interactions can be well described by quantum mean-field methods, such as HF, which can be efficiently implemented on classical computers. Therefore, the main task of quantum computing is to accurately recover the correlation energy, which can be further decomposed into dynamic and static correlation energies (Table 2). This decomposition is often performed according to the partition of the orbital space, including core, active and virtual spaces. The static correlation should be accounted for in the active space model. The exact solution to this problem is related to a CAS(N, M) problem, namely distributing N active electrons in the M active spin orbitals in all possible ways. Considering that the computational complexity increases exponentially as a function of N, quantum computing is anticipated to be a natural choice for solving this problem. After the static correlation is obtained, the dynamic correlation can be recovered by classical posteriori corrections.58 This procedure is often referred to as ∼static-then-dynamic∼, which has been widely used in the WFT, e.g. CASPT2 (first CASSCF and then applying second-order perturbation theory). This procedure has also been adopted in quantum computing for improving the accuracy of calculations beyond the minimal basis set. For example, posteriori corrections to the iterative qubit coupled cluster method have been proposed by Ryabinkin and co-workers, using the qubit form of the second-order Epstein–Nesbet perturbation theory equation.58Assuming that the static and dynamic correlation can be respectively treated variationally and perturbatively, an inverse scheme, namely ∼first dynamic then static∼, should also work for recovering the total correlation energy. One such framework is the effective Hamiltonian, which incorporates the dynamics correlation by a similarity transformation of the system Hamiltonian. In the context of quantum computing, this transformation often adopts a unitary form in order to construct a Hermitian form of the effective Hamiltonian. And then the diagonalization of the effective Hamiltonian is simplified to a CAS problem within a small active space. In the double UCC method, electronic excitations are decoupled into two disjoint sets so that the correlation effect for a subset of excitations can be downfolded into an effective Hamiltonian.59 In addition, the effective Hamiltonian is also able to account for the basis set convergence problem by incorporating explicit inter-electron coordinates, as is performed in the F12 methods.60,61
3 Numerical methods
We demonstrate multiscale quantum computing using practical molecular systems. The environmental effects are not taken into account since it is a trivial task to include the electrostatic potential in the Hamiltonian when the EFF is used. The reference ground-state wavefunction is computed with the HF method. The molecular systems are divided into multiple fragments. The total molecular properties are recovered using the many body expansion theory. Adaptive VQE algorithms that iteratively build a compact wave function ansatz44 are employed to find an exact solution of the ground state within the active space of fragments. For simplicity, this specific algorithm is referred to as MBE-VQE. The MP2 correction to the VQE algorithm is used to account for the dynamic correlation energy. In the following, we give a brief introduction to the theoretical methods integrated into the MBE-VQE algorithm. In Section 4, we apply MBE-VQE to study the relative energies of the hydrogen chain, the C18 ring and water hexamers. The MBE-VQE method is able to provide a reasonable description of configuration stability.Before introducing theoretical methods, we first specify the notations to be used in the following. In the MBE method, different fragments are labeled with the Greek alphabets α, β, γ…. For HF molecular orbitals (MOs) in each fragment, the occupied orbitals and the virtual orbitals are labeled with i, j, k… and a, b, c…, respectively and p, q, r, s… label general MOs. Given a set of HF orbitals ϕp, the second-quantized Hamiltonian can be written as:
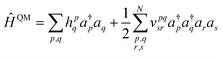 | (3) |
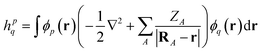 | (4) |
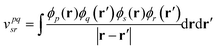 | (5) |
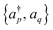 are mapped to qubit operators using the Jordan–Wigner or Bravyi–Kitaev transformation. The energy can be obtained by measuring and then summing up the expectation values of Pauli strings {
are mapped to qubit operators using the Jordan–Wigner or Bravyi–Kitaev transformation. The energy can be obtained by measuring and then summing up the expectation values of Pauli strings {![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) } ∈ {I, σx, σy, σz}⊗n as
} ∈ {I, σx, σy, σz}⊗n as | (6) |
Hereafter, we will drop the label “QM” for simplicity since the methods introduced in the following focus on QM problems.
3.1 Many body expansion theory
The MBE theory presents a simple and intuitive fragmentation scheme for large-scale simulations. Here, a large system is first partitioned into many non-overlapping fragments, often called monomers, and then the many-body effect is captured by high-order corrections from multiple fragments, namely dimers, trimers, and so forth. Without any approximation, the total energy of the whole system can be written as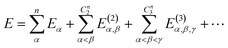 | (7) |
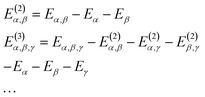 | (8) |
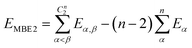 | (9) |
If one includes third-order corrections, the total energy is
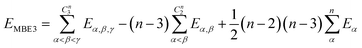 | (10) |
Note that the total energy is exact if no truncation is applied to eqn (7). When the MBE is truncated at second or third order, additional corrections to the long-range interactions are necessary to recover the exact results. The most popular scheme for MBE corrections is the electrostatic embedding approach,53 in which the energies are revised by the electrostatic interactions between the n-mer and the rest of the fragments,
En-mer = 〈Ψ|Ĥn-mer + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) es|Ψ〉 es|Ψ〉 | (11) |
To further improve the accuracy of the MBE, it is also possible to use low-scaling computational methods, such as semiempirical approaches and HF, to describe the high-order many-body interactions. A simple way to implement this strategy is the ONIOM method71 with the total energy expressed as
| Etotal = EMBEhigh + Elow − EMBElow | (12) |
One intrinsic drawback of fragment-based methods is the need to break chemical bonds resulting from molecular fragmentation. The hydrogen atom is usually chosen to saturate the severed bonds as shown in Fig. 2. It is important to guarantee that the net number of capped hydrogen atoms is zero for a valid fragmentation method. This condition is automatically satisfied in MBE methods.
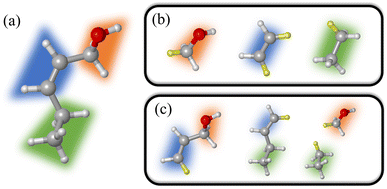 | ||
| Fig. 2 Fragmentation strategy for the MBE2 method. (a) Pentenol molecule; (b) monomers and (c) dimers. Hydrogen atoms highlighted in yellow are link atoms added to saturate the severed bonds. | ||
3.2 Adaptive VQE algorithms
The accuracy and quantum circuit depth of the VQE method depend heavily on its wave function ansatz. In contrast to the UCC ansatz, the recently proposed ADAPT ansatz72 provides an exact quantum solver for quantum chemistry problems. Meanwhile, the ADAPT ansatz bypasses the Trotterization error of the UCC ansatz by generating a pseudo-Trotter wave function with a compact sequence of unitary transformations acting on the reference state|Ψ(k)ADAPT〉 = (eθk![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) k)⋯(eθ1 k)⋯(eθ1![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) 1)|Ψ0〉 1)|Ψ0〉 | (13) |
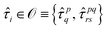 :
: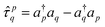 | (14) |
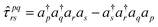 | (15) |
At the kth iteration, the energy is minimized through a conventional VQE procedure:
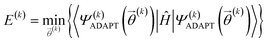 | (16) |
The residual gradient of the ith operator ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) i in
i in 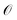 must be evaluated at each iteration to determine the sequence of the pseudo-Trotter ansatz:
must be evaluated at each iteration to determine the sequence of the pseudo-Trotter ansatz:
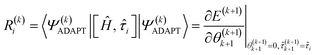 | (17) |
The operator ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) (k + 1) with the largest pre-estimated gradient R(k) is selected from
(k + 1) with the largest pre-estimated gradient R(k) is selected from 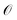 and added at the next iteration to update the wave function ansatz
and added at the next iteration to update the wave function ansatz
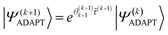 | (18) |
The convergence criteria are defined as the norm of pre-estimated gradients less than a specified threshold ε, that is,
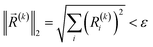 | (19) |
The fermionic creation and annihilation operators are mapped onto qubit operators {σx, σy, σz} using transformations, such as the Jordan–Wigner73,74 or Bravyi–Kitaev.75–77 The operator pool in adaptive VQE algorithms can be constructed based on a variety of operator forms. In addition to fermionic operators, another popular form is the qubit excitation operator. As introduced in the qubit-ADAPT-VQE ansatz,78 Pauli string operators with a maximal length of 4 are used to reduce the number of C-NOT gates in the quantum circuit. One scheme to construct qubit operators is to choose individual Pauli strings after the fermionic operators in the unitary coupled cluster ansatz are mapped onto qubit operators. The qubit operator generally has the form:
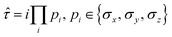 | (20) |
In contrast to the qubit-ADAPT-VQE, the qubit excitation based (QEB) VQE employs a qubit operator form that explicitly relates to creation and annihilation operators of qubits.79 In qubit-ADAPT-VQE and QEB-VQE, Pauli Z strings are discarded in order to construct shallow circuits. As a consequence, more circuit parameters may be required to restore the antisymmetry of the wave function.
3.3 MP2 corrections to the VQE algorithm
The Møller–Plesset perturbation theory is a special Rayleigh–Schrödinger perturbation theory, which uses the Fock operator![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) as the unperturbed Hamiltonian and the fluctuation potential
as the unperturbed Hamiltonian and the fluctuation potential ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) as the perturbation. The overall MP2 correlation energy is defined as:
as the perturbation. The overall MP2 correlation energy is defined as: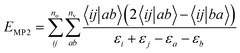 | (21) |
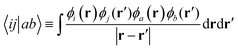 | (22) |
In the framework of a multiscale quantum algorithm, the correlation energy defined in the active space is extracted using quantum algorithms. And we use MP2 to compute the remaining part of the correlation energy as an a posteriori correction to quantum algorithms, which is defined as:
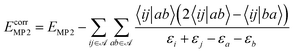 | (23) |
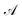 indicates the active space. If we consider
indicates the active space. If we consider 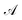 as the central part, eqn (23) can be regarded as a MP2 correction in the ONIOM form. As such, we can replace MP2 with arbitrary correlated methods, such as coupled cluster with single and double excitations (CCSD) and second-order algebraic-diagrammatic construction, to account for the dynamic correlation.
as the central part, eqn (23) can be regarded as a MP2 correction in the ONIOM form. As such, we can replace MP2 with arbitrary correlated methods, such as coupled cluster with single and double excitations (CCSD) and second-order algebraic-diagrammatic construction, to account for the dynamic correlation.
3.4 Implementation
The methods introduced above state the theoretical foundation of the MBE-VQE algorithm. The overall procedure of the MBE-VQE algorithm is shown as follows:• Dividing the full system into fragments with appropriate sizes.
• Determining the n-mers required to compute high-order many-body corrections.
• Adding link atoms at appropriate positions if necessary.
• Performing HF calculation for every n-mer structure.
• Deciding the active spaces for the VQE algorithm and performing VQE calculations.
• Adding the MP2 correction corresponding to frozen orbitals.
• Calculating the total energy following the MBE energy expression.
In this work, the C–C bonds are severed when fragments are defined for C18. A hydrogen atom is placed at a position rcap between two carbon atoms at r1 and r2. The direction of the C–H bond is the same as that of the original C–C bond, and its bond length is set to rC–H = 1.061. The coordinate of rcap is
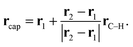 | (24) |
One of the most important merits of the MBE-VQE method is the completely independent calculations for subsystems that can be performed with massive parallelization. And this parallelization does not require extensive modification to existing VQE algorithms. Note that it is necessary to avoid severing multiple bonds in the MBE-VQE method because this will result in relatively large errors.
3.5 Dependencies
The PySCF package80 is used for restricted and unrestricted HF and CCSD calculations. The one- and two-electron integrals for constructing the second quantization Hamiltonian in VQE calculations are also extracted from PySCF. OpenFermion81 is used to carry out Jordan-Winger transformation and generate sparse matrices. An in-house VQE simulation package (Q2Chemistry)82 is used for the MBE-VQE calculations.4 Results
We apply the MBE-VQE algorithm to study the relative energies of different conformations in molecular systems. The DMET-VQE algorithm83 is also employed to study these systems for comparison. The DMET method has been well elaborated in previous studies.84 A brief introduction to implementing the DMET theory in this work is provided in the Appendix. In the following, we first demonstrate the MBE-VQE algorithm using the hydrogen chain. Here, the STO-3G basis is used. As a result, all HF orbitals are included in the active space and we don't need to add the MP2 correction to the VQE. Then, the MBE-VQE algorithm using the cc-pVDZ basis is employed to study cyclo[18]carbon. Because the HF theory makes it hard to give a reasonable description of cyclo[18]carbon when all C–C bonds tend to form double bonds, we don't employ the HF correction to the MBE method using eqn (12). Finally, we apply the MBE-VQE algorithm to study the configuration stability of eight water hexamers.4.1 Hydrogen chain
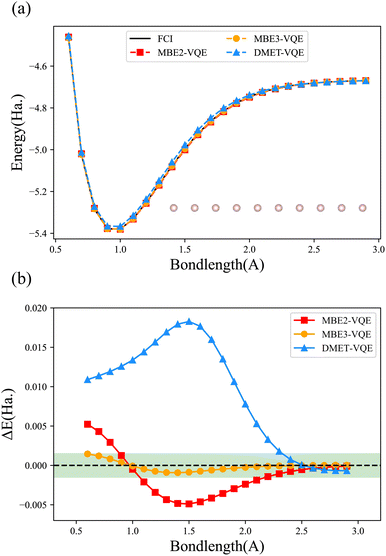
We first compute the potential energy surface (PES) of the hydrogen chain with 10 hydrogen atoms equispaced along a line using the MBE-VQE and the DMET-VQE methods. The hydrogen chain is an extremely simple model while it is essential for understanding diverse fundamental physical phenomena, such as insulator-to-metal transition and the antiferromagnetic Mott phase.85 Here, the hydrogen chain is divided into five fragments and each fragment contains 2 hydrogen atoms. Two kinds of MBE-VQE methods, including MBE2-VQE and MBE3-VQE, have been employed to describe high-order corrections. In MBE2-VQE, dimers consisting of 4 hydrogen atoms are used to obtain second-order corrections. Analogously, trimers consisting of 6 hydrogen atoms in MBE3-VQE are used to compute third-order corrections. In the DMET-VQE simulations, each fragment that contains two hydrogen atoms is considered an embedded system, and the remaining eight hydrogen atoms are considered the environment. The bath orbitals are constructed from orbitals localized at environmental hydrogen atoms. As such, two impurity orbitals and two bath orbitals are used to build the embedding Hamiltonian. All calculations are performed with the STO-3G basis. The maximal number of qubits used in MBE2-VQE, MBE3-VQE and DMET-VQE is 8, 12 and 8, respectively. The Hamiltonians in all three methods are easy to solve so all orbitals are contained in the active space.Fig. 3 shows PESs and their error curves with respect to the FCI results for H10. The errors are defined as deviations from the total energy, namely EMBE-VQE − EFCI (or EDMET-VQE − EFCI). The MBE2-VQE method and the DMET-VQE method use the same number of qubits, but the MBE2-VQE method has a lower average deviation (2.42 millihartree for MBE2-VQE and 9.00 millihartree for DMET-VQE). As shown in Fig. 3, it is clear that, as the bond length increases, the total energy deviations decrease in all three methods. This is consistent with the intuition that DC methods are more accurate when the interactions between fragments become smaller. When the hydrogen atoms are well separated, namely when the H–H bond length is larger than 2.5 Å, the errors in both MBE2-VQE and DMET-VQE are less than 1 millihartree. In comparison with MBE2-VQE, the overall errors of MBE3-VQE are much smaller. The MBE3-VQE has an average deviation of 0.45 millihartree and all MBE3-VQE results have reached chemical accuracy.
4.2 Cyclo[18]carbon
Cyclo[n]carbons have attracted much attention as a molecular carbon allotrope consisting two-coordinated carbon atoms.86–89 Recently, a cyclo[18]carbon molecule has been successfully synthesized in a solid state and its structure has been characterized by high-resolution atomic force microscopy and density functional theory.90 Here, density functional theory calculations, using the HSE hybrid functional, reveal that the cyclo[18]carbon exhibits a D9h symmetry and the short carbon–carbon (C–C) bond length is 1.195 Å and the long C–C bond length is 1.343 Å. This result is consistent with the coupled cluster calculation that estimates the bond length alternation (BLA) to be ∼0.14 Å.91 BLA is defined as the difference between the long and short C–C bond lengths.Another symmetric geometry, a doubly Hückel aromatic cumulenic D18h structure of only C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds, has also been considered.91 Therefore, cyclo[18]carbon is a good candidate to assess the MBE-VQE method. In the following calculations, we can demonstrate that the MBE-VQE method can be applied to covalent systems and gives a quite reliable description of systems that have strong intrafragment interactions but weak interfragment interactions. In addition, it is well known that the MBE method is not an appropriate method for describing delocalized correlated systems. The MBE-VQE calculations of the cyclo[18]carbon system also show the same conclusion.
C double bonds, has also been considered.91 Therefore, cyclo[18]carbon is a good candidate to assess the MBE-VQE method. In the following calculations, we can demonstrate that the MBE-VQE method can be applied to covalent systems and gives a quite reliable description of systems that have strong intrafragment interactions but weak interfragment interactions. In addition, it is well known that the MBE method is not an appropriate method for describing delocalized correlated systems. The MBE-VQE calculations of the cyclo[18]carbon system also show the same conclusion.
We apply the MBE-VQE method to study relative energies of the cyclo[18]carbon ring. A series of cyclo[18]carbon structures are generated by fixing the diameter of the ring to 7.31 Å while changing θ and BLA. Fig. 4 shows the relative energies (defined as the energy difference with the lowest point) as a function of the θ or BLA. The cc-pVDZ basis-set is utilized in all of the calculations. Considering the existence of triple bonds in cyclo[n]carbon molecules, an appropriate way to set fragments is to take two carbon atoms as one fragment. Such a fragment breaks the original single bond between fragments, so hydrogen link atoms should be added. In this situation, a monomer in the MBE calculation is an ethyne molecule, two carbon atoms and two hydrogen atoms form a total of 38 MOs. A dimer is either a butadiyne molecule or two ethyne molecules, with 66 or 76 MOs. For monomers, the five orbitals (two occupied and three virtual) closest to the Fermi level are chosen to be the active space for VQE calculation. For dimers, nine orbitals (three occupied and six virtual) form the active space. The MP2 correction to the VQE is used for describing the correlation effect resulting from orbitals not included in the active space. In the DMET-VQE simulations of cyclo[18]carbon, a single carbon atom is considered as one fragment and the other carbon atoms are considered as the environment. In each fragment, four valence orbitals (2s orbital and three 2p orbitals) are treated as impurity orbitals. The rest orbitals in that fragment are treated at the Hartree–Fock level. Four bath orbitals are constructed with orbitals from environmental carbon atoms.
 | ||
| Fig. 4 Relative energies as a function of θ and bond length alternation (BLA) computed with MBE-VQE (without HF correction, abbreviated as “-woHF”) and DMET-VQE algorithms. | ||
Fig. 4 shows that MBE-VQE agrees very well with CCSD when θ is small and BLA is large. As BLA approaches 0, the deviations resulting from MBE keep getting larger. This is because when BLA gets smaller, the bond structure exhibits a transition from an alternating single bond and triple bond to uniform double bonds. In this case, breaking the double bonds inevitably introduces large numerical errors in MBE and DMET methods. In addition, it is also improper to add a hydrogen atom as the link atom, because the bonds we serve cannot be treated as a single bond anymore. Instead of the link atom approach, ghost orbitals introduced in the FMO method92 may be a more appropriate choice to saturate the carbon atoms. However, the introduction of the FMO method cannot fix the problem of severing delocalized orbitals in the case of a small BLA. In addition, cyclo[18]carbon is a very special case in which we cannot avoid severing double bonds since it has a ring structure. In most cases, we can always choose an appropriate fragmentation scheme to avoid breaking important chemical bonds, especially when we have enough computational resources. It is also worth mentioning that CCSD may not be accurate enough to study cyclo[18]carbon when all C–C bond lengths are almost equivalent. In such a conformation, there are many degenerate orbitals so that the correlation effect becomes very strong. Table 3 shows the energy deviation of the MBE-VQE method and DMET-VQE method with respect to the CCSD method. The values of BLA at the most stable conformation are estimated to be 0.11 and 0.10 Å with the MBE-VQE and DMET-VQE methods, respectively. When the value of BLA is larger or close to that of the equilibrium geometry, the MBE-VQE method yields an excellent agreement with the CCSD method. While, as the value of BLA decreases, the MBE-VQE method deteriorates very quickly since the fragmentation method is not suitable for partitioning these strong correlation problems.
| BLA | MBE-VQE | DMET-VQE |
|---|---|---|
| 0.201 | −0.08 | 21.73 |
| 0.188 | −0.40 | 19.35 |
| 0.176 | −0.50 | 15.08 |
| 0.163 | −0.64 | 12.05 |
| 0.151 | −0.39 | 8.90 |
| 0.138 | −0.84 | 5.87 |
| 0.126 | −0.37 | 3.11 |
| 0.113 | 0.00 | 0.65 |
| 0.101 | 0.97 | −0.44 |
| 0.088 | 2.26 | −2.22 |
| 0.075 | 4.20 | −3.32 |
| 0.063 | 6.79 | −3.88 |
| 0.050 | 10.55 | −5.15 |
| 0.038 | 15.66 | −5.38 |
| BLAmin | 0.113 | 0.101 |
4.3 Water hexamers
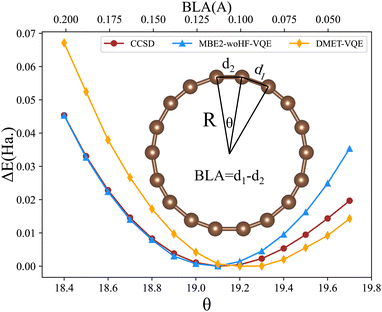
Being the most important substance for life, various properties of water have been widely studied. As the smallest piece of ice, the structure of water hexamers, namely the cluster composed of six water molecules, has attracted much attention93–96 because it helps us understand the behavior of water. It is interesting to apply multiscale quantum algorithms to study the properties of water hexamers.Fig. 5 shows eight of the most stable water hexamer structures determined in ref. 94. An annealing strategy is used to find a series of stable conformations at the MP2/6-311++g** level. The most stable structure is estimated to be the prism one. The total energies of these structures are calculated with the MBE-VQE method. The DMET-VQE method is also used as a comparison. In water hexamers, each water molecule is specified as a fragment. The cc-pVDZ basis set is employed. In the MBE-VQE method, a monomer contains one water molecule with 24 molecular orbitals and a dimer has two water molecules with 48 molecular orbitals. To achieve the best accuracy with tolerable computing resources, we choose a small active space for VQE calculations. For monomers, two occupied MOs with the lowest energy are treated as frozen orbitals, and the following four MOs are chosen as the active space to construct the effective Hamiltonian; for dimers, four MOs with the lowest energy are frozen and the following eight MOs form the active space. So in the MBE-VQE calculations, active spaces containing up to 16 qubits are used. Due to the small active space used in the VQE, the neglect of other orbitals is corrected by including a MP2 correction using eqn (23).
 | ||
| Fig. 5 A series of typical structures of water hexamers, (a) boat, (b) book, (c) cage, (d) chair, (e) cyclic (f) prism, (g) prism-book (p-b for short) and (h) twisted-boat (t-boat for short). | ||
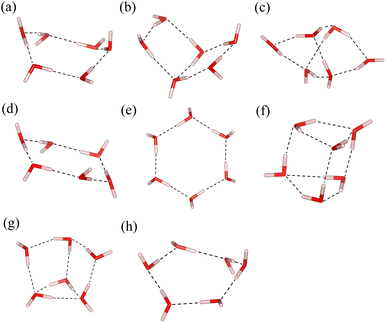
Fig. 6 shows the relative energies of eight different structures of water hexamers. Both the MBE-VQE and DMET-VQE methods give a correct prediction of the most stable water hexamer, namely the prism one. As such, relative energies are defined with respect to the energy of the prism water hexamer. For DMET-VQE, the relative energy of the cyclic structure is significantly underestimated with respect to the CCSD results, in which the energy of the cyclic structure is much higher than those of the book, cage and prism-book structures. In addition, all relative energies of other seven hexamers predicted by DMET-VQE with respect to the prism hexamer are systematically higher than the corresponding ones predicted by CCSD. As shown in Table 4, the average error of the DMET-VQE method is as large as 5.91 millihartree. As discussed in ref. 84, the accuracy of the DMET method can be improved by increasing the size of fragments, but this also results in higher computational cost. An alternative scheme to improve the DMET results is to perform posterior corrections after the DMET calculations. The DMET energy is automatically adjusted by iteratively relaxing one-particle orbitals in fragments, accompanied by a change in the global particle number and chemical potential. Therefore, formulating posterior corrections beyond the active space using the perturbation theory is very involved, requiring a comprehensive consideration of the choice of bath orbitals, the construction of one-particle orbitals and the fragment Hamiltonian. In the MBE-VQE method, we describe the correlation energy missing in the active space calculations by adding MP2 corrections. The MBE-VQE results shown in Table 4 reveal that such corrections are able to accurately restore the relative energies of eight water hexamers, with an average error of 0.58 millihartree, with respect to those from CCSD.
 | ||
| Fig. 6 Relative energies (in hartree) of different water hexamer structures computed by the MBE-VQE algorithm and DMET-VQE algorithm. The energy of the prism hexamer is used as a reference value. | ||
| Configure | DMET-VQE | MBE2-VQE |
|---|---|---|
| Boat | 8.90 | 0.76 |
| Book | 6.68 | 1.35 |
| Cage | 6.54 | 0.00 |
| Chair | 7.61 | 0.40 |
| Cyclic | 2.26 | 0.36 |
| Prism | 0.00 | 0.00 |
| Prism-book | 6.67 | 0.70 |
| Twisted-boat | 8.61 | 1.08 |
| AE | 5.91 | 0.58 |
4.4 Discussion
As one viable scheme for implementing multiscale quantum computing, the MBE-VQE algorithm combined with low-level computational methods, such as EFFs, provides an appealing tool to study complex systems on near-term quantum devices. Furthermore, we can extend the simulation scale by introducing the implicit solvation model, which accounts for the solvent or other environmental effects.97 In this work, we only apply the MBE-VQE algorithm to study the energy profiles of molecular systems containing hundreds of orbitals, while extending this algorithm to large molecular systems is straightforward, without increasing the size and depth of quantum circuits. In addition, it is easier to realize high scalability of quantum computing chips using industrial chip fabrication techniques than to improve the fidelity and coherence time of quantum gates.98 Fortunately, the MBE-VQE algorithm is inherently suitable for embarrassing parallelization since each fragment calculation is independent. And its computational complexity scales as N2 if the many-body expansion is truncated to the second order. Therefore, it is possible to realize large-scale MBE-VQE simulations of complex systems with distributed quantum devices.In energy-based fragmentation approaches, the total energy is assembled from the energies of subsystems. If the electronic structure of a subsystem is significantly different from the corresponding one in the whole system, it may result in large errors in the total energy. Therefore, we should avoid breaking bonds that leads to a remarkable change in electronic environments, such as delocalized chemical bonds and bonds involved in strongly correlated interactions, when defining fragments in the MBE-VQE algorithm. As a result, the MBE-VQE algorithm may make it difficult to describe transition metal coordination compounds or organometallic compounds because breaking metal–ligand covalent bonds makes it unlikely to maintain an accurate estimate of the energy. However, apart from this limitation, namely including these bonds in one fragment, the MBE-VQE algorithm is still expected to work for these systems. In addition, the MBE-VQE algorithm may make it difficult to describe nonlocal electronic excitations and magnetic systems, such as frustrated spin systems.
It is worth mentioning that the numerical results presented in this work are evaluated using a quantum simulator. The implementation of quantum algorithms on noisy quantum devices is quite challenging due to error accumulation. For the MBE-VQE method, the total energy is obtained by collecting many energy terms of monomers, dimers, trimers, … Therefore, in the worst case, the total error will be NtermsδE. Here, Nterms is the number of the energy terms and δE is the largest error in the energy calculations, while, in the best case, if the errors due to noise are systematically positive (or negative), a large part of the errors will cancel each other. On the other hand, when a quantum simulation of the full system is conducted on noisy quantum devices, the quantum circuit required to achieve a high accuracy will be much more complicated than those for subsystems. As the size and depth of quantum circuits increase, error accumulation due to noise will become more serious. Therefore, further studies are necessary to assess the performance of the MBE-VQE method on noisy quantum devices. In addition, in the long term, the error from the MBE-VQE method may become important if the error from noise in a small-scale quantum simulation can be remarkably suppressed.
It is well known that MBE methods suffer from the basis-set superposition error (BSSE), which originates from the fact that molecular properties calculated using the basis set of a single molecular fragment differ from those calculated using the basis set of the entire molecule. The impact of BSSE becomes more significant when diffuse basis functions are used.99,100 This is because diffuse functions centered on one fragment are more likely to have a remarkable overlap with the basis functions centered on its neighbouring fragments. Previous studies suggested several methods to avoid or minimize the BSSE effect in the MBE method.99,100 One simple strategy is to use a large basis set without diffuse functions. Another effective method is the counterpoise (CP) method,101,102 in which the energies of subsystems are calculated with the entire molecule's basis functions. In order to improve the results of the MBE-VQE calculations, it is necessary to include the BSSE effect in future studies.
5 Conclusions
In this work, we introduce a general framework for multiscale quantum computing and demonstrate its practical implementation using a MBE-VQE algorithm. The MBE-VQE algorithm can be easily implemented within the VQE framework without extensive modification to existing quantum algorithms. The MBE fragmentation approach is more suitable for describing the strongly correlated intra-fragment interactions, leaving the weak inter-fragment interactions to high-order many-body corrections. This implies that in principle multiple chemical bonds should not be severed in fragmentation. The calculations for monomers, dimers, trimers, …, in the MBE fragmentation approach are highly independent so the MBE-VQE approach is embarrassingly parallelizable if a large number of quantum processors are available. In addition, the MBE-VQE approach can be easily combined with posterior correction methods to restore the long-range interactions when the many-body expansion is truncated at a low order.The MBE-VQE algorithm has been applied to study the cyclo[18]carbon molecule and water hexamers. It gives a good description of the relative energies of these two systems with respect to the CCSD method. For the cyclo[18]carbon molecule, the equivalent bond length predicted by the MBE-VQE algorithm agrees well with the experimental results. For water hexamers, the MBE-VQE algorithm gives a good estimation of the relative stability of different configurations. The methods are expected to find promising applications in fields such as biochemistry, catalysis or other complicated chemical reactions. As discussed in Section 2, the combination of computational methods at different levels of resolution is diverse in the sense that exploring multiscale quantum computing is still an open problem in the NISQ era.
Most chemical reactions happen in complex environments, such as solution or proteins. Therefore, in order to apply quantum computers to design new catalysts or develop new drugs, we must consider the environmental effect in order to obtain reliable results. Classical multiscale simulation methods have been developed for many decades. In such a framework, the active region is often treated with quantum mechanical methods. While, limited by the computing power of classical computers, mean-field methods, such as density functional theory, or coupled cluster methods are often used to describe the electronic structure of active regions. The multiscale quantum computing framework proposed in this work can utilize quantum algorithms that can provide quantum advantage when fault-tolerant quantum computers become a reality such that it will be superior to classical multiscale simulation methods in the future. As such, the multiscale quantum computing framework provides a viable strategy for applying quantum computers to complicated material and biological molecular simulations.
6 Appendix: density matrix embedding theory
Consider that a large system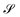 can be decomposed into two subsystems
can be decomposed into two subsystems 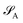 and
and 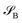 , namely
, namely 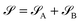 . An arbitrary quantum state |Ψ〉 of
. An arbitrary quantum state |Ψ〉 of  can be in general expressed in the Hilbert space of |ΨAI〉 ⊗ |ΨBJ〉,
can be in general expressed in the Hilbert space of |ΨAI〉 ⊗ |ΨBJ〉,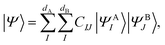 | (25) |
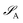
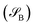 of dimension dA (dB). In quantum chemistry simulations, molecular or material systems are often composed of multiple subsystems that are small enough to enable high-level quantum mechanical calculations.
of dimension dA (dB). In quantum chemistry simulations, molecular or material systems are often composed of multiple subsystems that are small enough to enable high-level quantum mechanical calculations. 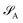 can be considered one of the local subsystems and
can be considered one of the local subsystems and 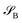 is considered the environment that is composed of the rest of the subsystems. The central idea of the DMET is to find the Schmidt decomposition of the wave function |Ψ〉. By the singular value decomposition of the coefficients C,
is considered the environment that is composed of the rest of the subsystems. The central idea of the DMET is to find the Schmidt decomposition of the wave function |Ψ〉. By the singular value decomposition of the coefficients C,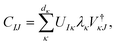 | (26) |
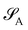 and its DMET bath,
and its DMET bath,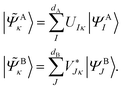 | (27) |
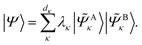 | (28) |
A simple construction of the embedding Hamiltonian in the basis of Schmidt states is
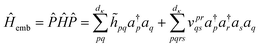 | (29) |
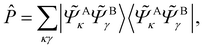 | (30) |
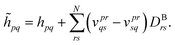 | (31) |
If the wave function of the full system is known a priori, the bath orbitals and the embedding Hamiltonian are well defined. However, due to the high computational complexity of obtaining an exact wave function of the full system, an approximate wave function from the low-level electronic structure calculation, such as HF, is used to construct the bath orbitals. These bath orbitals can be self-consistently improved by solving the embedded problems with a high-level quantum mechanical method. Given the wave function approximation introduced in the DMET, the embedding density matrix for the subsystem SA may differ from the exact one. To ensure that the total number of electrons in the subsystems adds up to NAe, a global potential μ is applied to fix the embedded Hamiltonian:
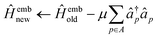 | (32) |
Furthermore a cost function is needed to evaluate the general potentials used. As was mentioned before, the mean-field ground state will cause differences in the density matrix, so the variance of the density matrix is a good cost function to use:
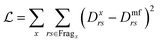 | (33) |
In ref. 84, there are some of the cost functions summarized to optimize the low-level Hamiltonian and correlation potential, including fragment plus bath fitting, fragment only fitting, and single-shot embedding. In this work, the simplest cost function
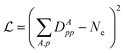 | (34) |
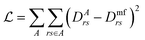 | (35) |
Data availability
The data that supports the findings of this study are available within the article and its Appendix.Author contributions
J. L. conceptualized the project. H. M., J. L. and Y. F. wrote the software. H. M. and J. L. collected data. H. M., J. L., H. H. S., Z. Y. L. and J. L. Y. analyzed data. J. L., H. M., H. H. S., Y. F., Z. Y. L. and J. L. Y. prepared the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Innovation Program for Quantum Science and Technology (2021ZD0303306), the National Natural Science Foundation of China (22073086, 21825302 and 22288201), Anhui Initiative in Quantum Information Technologies (AHY090400), and the Fundamental Research Funds for the Central Universities (WK2060000018). H. S. acknowledges support from the National Natural Science Foundation of China (T2222026 and 22003073).Notes and references
- F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin and R. Barends, et al. , Nature, 2019, 574, 505–510 CrossRef CAS PubMed.
- H.-S. Zhong, H. Wang, Y.-H. Deng, M.-C. Chen, L.-C. Peng, Y.-H. Luo, J. Qin, D. Wu, X. Ding, Y. Hu, P. Hu, X.-Y. Yang, W.-J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N.-L. Liu, C.-Y. Lu and J.-W. Pan, Science, 2020, 370, 1460–1463 CrossRef CAS PubMed.
- Y. Wu, W.-S. Bao, S. Cao, F. Chen, M.-C. Chen, X. Chen, T.-H. Chung, H. Deng, Y. Du, D. Fan, M. Gong, C. Guo, C. Guo, S. Guo, L. Han, L. Hong, H.-L. Huang, Y.-H. Huo, L. Li, N. Li, S. Li, Y. Li, F. Liang, C. Lin, J. Lin, H. Qian, D. Qiao, H. Rong, H. Su, L. Sun, L. Wang, S. Wang, D. Wu, Y. Xu, K. Yan, W. Yang, Y. Yang, Y. Ye, J. Yin, C. Ying, J. Yu, C. Zha, C. Zhang, H. Zhang, K. Zhang, Y. Zhang, H. Zhao, Y. Zhao, L. Zhou, Q. Zhu, C.-Y. Lu, C.-Z. Peng, X. Zhu and J.-W. Pan, Phys. Rev. Lett., 2021, 127, 180501 CrossRef CAS PubMed.
- J. Du, N. Xu, X. Peng, P. Wang, S. Wu and D. Lu, Phys. Rev. Lett., 2010, 104, 030502 CrossRef PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- P. J. J. O'Malley, R. Babbush, I. D. Kivlichan, J. Romero, J. R. McClean, R. Barends, J. Kelly, P. Roushan, A. Tranter, N. Ding, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, A. G. Fowler, E. Jeffrey, E. Lucero, A. Megrant, J. Y. Mutus, M. Neeley, C. Neill, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. C. White, P. V. Coveney, P. J. Love, H. Neven, A. Aspuru-Guzik and J. M. Martinis, Phys. Rev. X, 2016, 6, 031007 Search PubMed.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Nature, 2017, 549, 242 CrossRef CAS PubMed.
- C. Hempel, C. Maier, J. Romero, J. McClean, T. Monz, H. Shen, P. Jurcevic, B. P. Lanyon, P. Love, R. Babbush, A. Aspuru-Guzik, R. Blatt and C. F. Roos, Phys. Rev. X, 2018, 8, 031022 CAS.
- F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, S. Boixo, M. Broughton, B. B. Buckley, D. A. Buell, B. Burkett, N. Bushnell, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, S. Demura, A. Dunsworth, E. Farhi, A. Fowler, B. Foxen, C. Gidney, M. Giustina, R. Graff, S. Habegger, M. P. Harrigan, A. Ho, S. Hong, T. Huang, W. J. Huggins, L. Ioffe, S. V. Isakov, E. Jeffrey, Z. Jiang, C. Jones, D. Kafri, K. Kechedzhi, J. Kelly, S. Kim, P. V. Klimov, A. Korotkov, F. Kostritsa, D. Landhuis, P. Laptev, M. Lindmark, E. Lucero, O. Martin, J. M. Martinis, J. R. McClean, M. McEwen, A. Megrant, X. Mi, M. Mohseni, W. Mruczkiewicz, J. Mutus, O. Naaman, M. Neeley, C. Neill, H. Neven, M. Y. Niu, T. E. O'Brien, E. Ostby, A. Petukhov, H. Putterman, C. Quintana, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, D. Strain, K. J. Sung, M. Szalay, T. Y. Takeshita, A. Vainsencher, T. White, N. Wiebe, Z. J. Yao, P. Yeh and A. Zalcman, Science, 2020, 369, 1084–1089 CrossRef CAS PubMed.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- M. Cerezo, R. B. Andrew Arrasmith, S. C. Benjamin, S. Endo, K. Fujii, J. R. McClean, K. Mitarai, X. Yuan, L. Cincio and P. J. Coles, Nat. Rev. Phys., 2021, 3, 625–644 CrossRef.
- J. Liu, Y. Fan, Z. Li and J. Yang, Chem. Soc. Rev., 2022, 51, 3263–3279 RSC.
- H. Shang, L. Shen, Y. Fan, Z. Xu, C. Guo, J. Liu, W. Zhou, H. Ma, R. Lin, Y. Yang, F. Li, Z. Wang, Y. Zhang and Z. Li, Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, 2022 Search PubMed.
- B. Bauer, D. Wecker, A. J. Millis, M. B. Hastings and M. Troyer, Phys. Rev. X, 2016, 6, 031045 Search PubMed.
- J. M. Kreula, L. García-Álvarez, L. Lamata, S. R. Clark, E. Solano and D. Jaksch, EPJ Quantum Technology, 2016, 3, 11 CrossRef.
- T. Yamazaki, S. Matsuura, A. Narimani, A. Saidmuradov and A. Zaribafiyan, Towards the Practical Application of Near-Term Quantum Computers in Quantum Chemistry Simulations: A Problem Decomposition Approach, 2018 Search PubMed.
- Y. Kawashima, E. Lloyd, M. P. Coons, Y. Nam, S. Matsuura, A. J. Garza, S. Johri, L. Huntington, V. Senicourt, A. O. Maksymov, J. H. V. Nguyen, J. Kim, N. Alidoust, A. Zaribafiyan and T. Yamazaki, Commun. Phys., 2021, 4, 245 CrossRef.
- W. Li, Z. Huang, C. Cao, Y. Huang, Z. Shuai, X. Sun, J. Sun, X. Yuan and D. Lv, Chem. Sci., 2022, 13, 8953–8962 RSC.
- P. A. M. Dirac and R. H. Fowler, Proc. R. Soc. A, 1929, 123, 714–733 CAS.
- W. Yang, J. Mol. Struct., 1992, 255, 461–479 CrossRef.
- K. Fujii, K. Mizuta, H. Ueda, K. Mitarai, W. Mizukami and Y. O. Nakagawa, PRX Quantum, 2022, 3, 010346 CrossRef.
- T. Peng, A. W. Harrow, M. Ozols and X. Wu, Phys. Rev. Lett., 2020, 125, 150504 CrossRef CAS PubMed.
- K. Mizuta, M. Fujii, S. Fujii, K. Ichikawa, Y. Imamura, Y. Okuno and Y. O. Nakagawa, Phys. Rev. Res., 2021, 3, 043121 CrossRef CAS.
- X. Yuan, J. Sun, J. Liu, Q. Zhao and Y. Zhou, Phys. Rev. Lett., 2021, 127, 040501 CrossRef CAS PubMed.
- A. D. Mackerell Jr, J. Comput. Chem., 2004, 25, 1584–1604 CrossRef.
- P. Pulay, Int. J. Quantum Chem., 2011, 111, 3273–3279 CrossRef CAS.
- P. G. Szalay, T. Müller, G. Gidofalvi, H. Lischka and R. Shepard, Chem. Rev., 2012, 112, 108–181 CrossRef CAS PubMed.
- M. Levitt, Angew. Chem., Int. Ed., 2014, 53, 10006–10018 CrossRef CAS PubMed.
- A. Warshel, Angew. Chem., Int. Ed., 2014, 53, 10020–10031 CrossRef CAS PubMed.
- M. Karplus, Angew. Chem., Int. Ed., 2014, 53, 9992–10005 CrossRef CAS PubMed.
- A. V. Akimov and O. V. Prezhdo, Chem. Rev., 2015, 115, 5797–5890 CrossRef CAS PubMed.
- Q. Sun and G. K.-L. Chan, Acc. Chem. Res., 2016, 49, 2705–2712 CrossRef CAS PubMed.
- K. E. Ranaghan and A. J. Mulholland, Int. Rev. Phys. Chem., 2010, 29, 65–133 Search PubMed.
- M. S. Gordon, L. V. Slipchenko, H. Li and J. H. Jensen, Annu. Rep. Comput. Chem., 2007, 3, 177–193 Search PubMed.
- T. A. Wesolowski, S. Shedge and X. Zhou, Chem. Rev., 2015, 115, 5891–5928 CrossRef CAS PubMed.
- J. Gao, J. Chem. Phys., 1998, 109, 2346–2354 CrossRef CAS.
- D. R. Bowler and T. Miyazaki, J. Phys.: Condens. Matter, 2010, 22, 074207 CrossRef CAS PubMed.
- K. E. Riley, M. Pitoňák, P. Jurečka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS.
- P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2019, 15, 5275–5298 CrossRef CAS PubMed.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704 CrossRef CAS PubMed.
- S. Lee, J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z.-H. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin and G. K.-L. Chan, arXiv preprint arXiv:2208.02199, 2022.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput., 2019, 15, 311–324 CrossRef CAS PubMed.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- H. L. Tang, V. Shkolnikov, G. S. Barron, H. R. Grimsley, N. J. Mayhall, E. Barnes and S. E. Economou, PRX Quantum, 2021, 2, 020310 CrossRef.
- Y. S. Yordanov, V. Armaos, C. H. W. Barnes and D. R. M. Arvidsson-Shukur, Commun. Phys., 2021, 4, 228 CrossRef.
- J. Liu, Z. Li and J. Yang, J. Chem. Phys., 2021, 154, 244112 CrossRef CAS PubMed.
- Y. Fan, J. Liu, Z. Li and J. Yang, J. Phys. Chem. Lett., 2021, 12, 8833–8840 CrossRef CAS PubMed.
- I. G. Ryabinkin, R. A. Lang, S. N. Genin and A. F. Izmaylov, J. Chem. Theory Comput., 2020, 16, 1055–1063 CrossRef CAS PubMed.
- D. G. Fedorov, T. Nagata and K. Kitaura, Phys. Chem. Chem. Phys., 2012, 14, 7562–7577 RSC.
- D. W. Zhang and J. Z. H. Zhang, J. Chem. Phys., 2003, 119, 3599–3605 CrossRef CAS.
- X. Wang, J. Liu, J. Z. H. Zhang and X. He, J. Phys. Chem. A, 2013, 117, 7149–7161 CrossRef CAS PubMed.
- E. E. Dahlke and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 46–53 CrossRef CAS PubMed.
- R. M. Richard and J. M. Herbert, J. Chem. Phys., 2012, 137, 064113 CrossRef PubMed.
- J. Liu and J. M. Herbert, J. Chem. Theory Comput., 2016, 12, 572–584 CrossRef CAS PubMed.
- C. Vorwerk, N. Sheng, M. Govoni, B. Huang and G. Galli, Nature Computational Science, 2022, 2, 424–432 CrossRef.
- L. Song, J. Han, Y.-l. Lin, W. Xie and J. Gao, J. Phys. Chem. A, 2009, 113, 11656–11664 CrossRef CAS PubMed.
- I. G. Ryabinkin, A. F. Izmaylov and S. N. Genin, Quantum Science and Technology, 2021, 6, 024012 CrossRef.
- N. P. Bauman, E. J. Bylaska, S. Krishnamoorthy, G. H. Low, N. Wiebe, C. E. Granade, M. Roetteler, M. Troyer and K. Kowalski, J. Chem. Phys., 2019, 151, 014107 CrossRef PubMed.
- W. Kutzelnigg and W. Klopper, J. Chem. Phys., 1991, 94, 1985–2001 CrossRef CAS.
- A. Kumar, A. Asthana, C. Masteran, E. F. Valeev, Y. Zhang, L. Cincio, S. Tretiak and P. A. Dub, J. Chem. Theory Comput., 2022, 18, 5312–5324 CrossRef CAS PubMed.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Phys. Rev. X, 2020, 10, 011004 CAS.
- J. Chládek, L. Veis, J. Pittner and K. Karol, et al. , Quantum Science and Technology, 2021, 6, 034008 CrossRef.
- M. Metcalf, N. P. Bauman, K. Kowalski and W. A. De Jong, J. Chem. Theory Comput., 2020, 16, 6165–6175 CrossRef CAS PubMed.
- R. Huang, C. Li and F. A. Evangelista, arXiv preprint arXiv:2208.08591, 2022.
- S. McArdle and D. P. Tew, arXiv preprint arXiv:2006.11181, 2020.
- M. Motta, T. P. Gujarati, J. E. Rice, A. Kumar, C. Masteran, J. A. Latone, E. Lee, E. F. Valeev and T. Y. Takeshita, Phys. Chem. Chem. Phys., 2020, 22, 24270–24281 RSC.
- I. O. Sokolov, W. Dobrautz, H. Luo, A. Alavi and I. Tavernelli, arXiv preprint arXiv:2201.03049, 2022.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75–107 CrossRef CAS PubMed.
- P. Schleich, J. S. Kottmann and A. Aspuru-Guzik, Phys. Chem. Chem. Phys., 2022, 24, 13550–13564 RSC.
- S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct., 1999, 461–462, 1–21 CAS.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- P. Jordan and E. P. Wigner, Z. Phys., 1928, 47, 14–75 Search PubMed.
- J. D. Whitfield, J. Biamonte and A. Aspuru-Guzik, Mol. Phys., 2011, 109, 735–750 CrossRef CAS.
- S. Bravyi, J. M. Gambetta, A. Mezzacapo and K. Temme, arXiv preprint arXiv:1701.08213, 2017.
- A. Tranter, S. Sofia, J. Seeley, M. Kaicher, J. McClean, R. Babbush, P. V. Coveney, F. Mintert, F. Wilhelm and P. J. Love, Int. J. Quantum Chem., 2015, 115, 1431–1441 CrossRef CAS.
- J. T. Seeley, M. J. Richard and P. J. Love, J. Chem. Phys., 2012, 137, 224109 CrossRef PubMed.
- H. L. Tang, V. Shkolnikov, G. S. Barron, H. R. Grimsley, N. J. Mayhall, E. Barnes and S. E. Economou, PRX Quantum, 2021, 2, 020310 CrossRef.
- Y. S. Yordanov, V. Armaos, C. H. Barnes and D. R. Arvidsson-Shukur, Commun. Phys., 2021, 4, 1–11 CrossRef.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova and S. Sharma, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- J. R. McClean, N. C. Rubin, K. J. Sung, I. D. Kivlichan, X. Bonet-Monroig, Y. Cao, C. Dai, E. S. Fried, C. Gidney and B. Gimby, et al. , Quantum Science and Technology, 2020, 5, 034014 CrossRef.
- Y. Fan, J. Liu, X. Zeng, Z. Xu, H. Shang, Z. Li and J. Yang, arXiv preprint arXiv:2208.10978, 2022.
- W. Li, Z. Huang, C. Cao, Y. Huang, Z. Shuai, X. Sun, J. Sun, X. Yuan and D. Lv, Chem. Sci., 2022, 13, 8953–8962 RSC.
- S. Wouters, C. A. Jiménez-Hoyos, Q. Sun and G. K.-L. Chan, J. Chem. Theory Comput., 2016, 12, 2706–2719 CrossRef CAS PubMed.
- M. Motta, C. Genovese, F. Ma, Z.-H. Cui, R. Sawaya, G. K.-L. Chan, N. Chepiga, P. Helms, C. Jiménez-Hoyos, A. J. Millis, U. Ray, E. Ronca, H. Shi, S. Sorella, E. M. Stoudenmire, S. R. White and S. Zhang, Phys. Rev. X, 2020, 10, 031058 CAS.
- F. Diederich, Y. Rubin, C. B. Knobler, R. L. Whetten, K. E. Schriver, K. N. Houk and Y. Li, Science, 1989, 245, 1088–1090 CrossRef CAS PubMed.
- V. Parasuk, J. Almlof and M. W. Feyereisen, J. Am. Chem. Soc., 1991, 113, 1049–1050 CrossRef CAS.
- G. von Helden, N. Gotts and M. Bowers, Nature, 1993, 363, 60–63 CrossRef CAS.
- J. Hutter, H. P. Luethi and F. Diederich, J. Am. Chem. Soc., 1994, 116, 750–756 CrossRef CAS.
- K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299–1301 CrossRef CAS PubMed.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Chem. Commun., 2020, 56, 352–355 RSC.
- K. Kitaura, E. Ikeo, T. Asada, T. Nakano and M. Uebayasi, Chem. Phys. Lett., 1999, 313, 701–706 CrossRef CAS.
- G. Bilalbegovic, J. Phys. Chem. A, 2010, 114, 715–720 CrossRef CAS PubMed.
- G. Hincapie, N. Acelas, M. Castano, J. David and A. Restrepo, J. Phys. Chem. A, 2010, 114, 7809–7814 CrossRef CAS PubMed.
- K. Kim, K. D. Jordan and T. S. Zwier, J. Am. Chem. Soc., 1994, 116, 11568–11569 CrossRef CAS.
- K. Nauta and R. Miller, Science, 2000, 287, 293–295 CrossRef CAS PubMed.
- B. Roux and T. Simonson, Biophys. Chem., 1999, 78, 1–20 CrossRef CAS PubMed.
- A. M. J. Zwerver, T. Krähenmann, T. F. Watson, L. Lampert, H. C. George, R. Pillarisetty, S. A. Bojarski, P. Amin, S. V. Amitonov, J. M. Boter, R. Caudillo, D. Correas-Serrano, J. P. Dehollain, G. Droulers, E. M. Henry, R. Kotlyar, M. Lodari, F. Lüthi, D. J. Michalak, B. K. Mueller, S. Neyens, J. Roberts, N. Samkharadze, G. Zheng, O. K. Zietz, G. Scappucci, M. Veldhorst, L. M. K. Vandersypen and J. S. Clarke, Nat. Electron., 2022, 5, 184–190 CrossRef.
- J. F. Ouyang, M. W. Cvitkovic and R. P. Bettens, J. Chem. Theory Comput., 2014, 10, 3699–3707 CrossRef CAS PubMed.
- J. F. Ouyang and R. P. Bettens, J. Chem. Theory Comput., 2015, 11, 5132–5143 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- S. Saebo, W. Tong and P. Pulay, J. Chem. Phys., 1993, 98, 2170–2175 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |