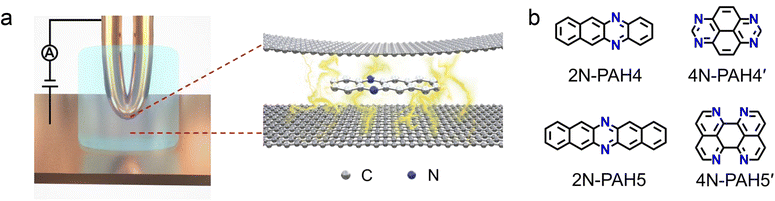
Open Access Article
Open Access ArticleAtomically well-defined nitrogen doping for cross-plane transport through graphene heterojunctions†
Hewei
Zhang‡
a,
Ping
Zhou‡
b,
Abdalghani
Daaoub‡
c,
Sara
Sangtarash
c,
Shiqiang
Zhao
a,
Zixian
Yang
a,
Yu
Zhou
a,
Yu-Ling
Zou
a,
Silvio
Decurtins
b,
Robert
Häner
b,
Yang
Yang
 *a,
Hatef
Sadeghi
*a,
Hatef
Sadeghi
 *c,
Shi-Xia
Liu
*c,
Shi-Xia
Liu
 *b and
Wenjing
Hong
*b and
Wenjing
Hong
 *a
*a
aState Key Laboratory of Physical Chemistry of Solid Surfaces, College of Chemistry and Chemical Engineering, Pen-Tung Sah Institute of Micro-Nano Science and Technology, IKKEM, Xiamen University, 361005 Xiamen, China. E-mail: yangyang@xmu.edu.cn; whong@xmu.edu.cn
bDepartment of Chemistry, Biochemistry and Pharmaceutical Sciences, University of Bern, Freiestrasse 3, 3012 Bern, Switzerland. E-mail: shi-xia.liu@unibe.ch
cDevice Modelling Group, School of Engineering, University of Warwick, Coventry CV4 7AL, UK. E-mail: Hatef.Sadeghi@warwick.ac.uk
First published on 11th May 2023
Abstract
The nitrogen doping of graphene leads to graphene heterojunctions with a tunable bandgap, suitable for electronic, electrochemical, and sensing applications. However, the microscopic nature and charge transport properties of atomic-level nitrogen-doped graphene are still unknown, mainly due to the multiple doping sites with topological diversities. In this work, we fabricated atomically well-defined N-doped graphene heterojunctions and investigated the cross-plane transport through these heterojunctions to reveal the effects of doping on their electronic properties. We found that a different doping number of nitrogen atoms leads to a conductance difference of up to ∼288%, and the conductance of graphene heterojunctions with nitrogen-doping at different positions in the conjugated framework can also lead to a conductance difference of ∼170%. Combined ultraviolet photoelectron spectroscopy measurements and theoretical calculations reveal that the insertion of nitrogen atoms into the conjugation framework significantly stabilizes the frontier molecular orbitals, leading to a change in the relative positions of the HOMO and LUMO to the Fermi level of the electrodes. Our work provides a unique insight into the role of nitrogen doping in the charge transport through graphene heterojunctions and materials at the single atomic level.
Introduction
Two-dimensional (2D) heterostructured materials not only retain the original advantages1,2 but also show unique charge transport,3–5 catalytic activity,6 mechanical strength,7 photoelectric properties,8 and magnetic properties9 beyond the classic two-dimensional materials. For instance, the doping of graphene leads to the fabrication of graphene heterojunctions with potential in electronic,10–14 sensing,15,16 photocatalytic17–19 and other applications by converting the zero bandgaps of graphene to tunable bandgaps.20 Nitrogen is widely used for doping graphene materials and devices,15,19,21,22 and there are various nitrogen-doping approaches developed, including chemical vapor deposition,23 arc discharge,24 ion irradiation25 and post-treatment.26 However, the microscopic nature and charge transport properties of atomic-level nitrogen-doped graphene remained unclear due to the complexity of the nitrogen sites and bonding topology within the carbon lattice during the doping process.20,25,27,28 Along this line, recent advances in the investigation through single-molecule junctions offer a unique insight to reveal the role of N-doping with atomically well-defined doping sites.To tackle this challenge, single-molecule junctions with gold-molecule-gold configurations offer the opportunity to investigate the role of N-doping in charge transport through molecular junctions with atomic precision. When nitrogen doping occurs in the aromatic cores of molecules, differences in the substitution positions can tune the quantum interference effects29–31 and demonstrate the different gating efficiency32 in a phenyl ring with meta connectivity. When nitrogen atoms are employed as an anchor group to form Au–N bonds,33,34 the different numbers and sites of nitrogen atoms provide different conductance pathways at molecular junctions, resulting in different conductance.35,36 However, all the above studies investigated the charge transport through the molecular skeleton using gold electrodes but not the cross-plane transport as presented in graphene heterojunctions. Recent advances in the fabrication of cross-plane heterojunctions can be considered as a microscopic model37 to investigate the role of nitrogen doping in charge transport with different numbers of nitrogen atoms at different positions of the conjugated framework in nitrogen-containing polycyclic aromatic hydrocarbons (N-PAHs).
Herein, we investigated the charge transport through nitrogen-doped graphene heterojunctions where N-PAHs are embedded between graphene electrodes by using the cross-plane break junction technique and density functional theory transport calculations. Comparing the conductance values of the corresponding polycyclic aromatic hydrocarbons (PAHs), we find that the conductance decreases with the introduction of nitrogen atoms. We further investigated the conductance of heterojunctions with nitrogen atoms at different N-PAH framework sites and observed a clear site dependence of their conductance. In conjunction with transition voltage spectroscopy (TVS), ultraviolet photoelectron spectroscopy (UPS), and theoretical calculations, it is supposed that the insertion of nitrogen atoms alters the energy level alignment between the frontier molecular orbitals and the Fermi level of graphene electrodes, thereby regulating the electrical properties.
Results and discussion
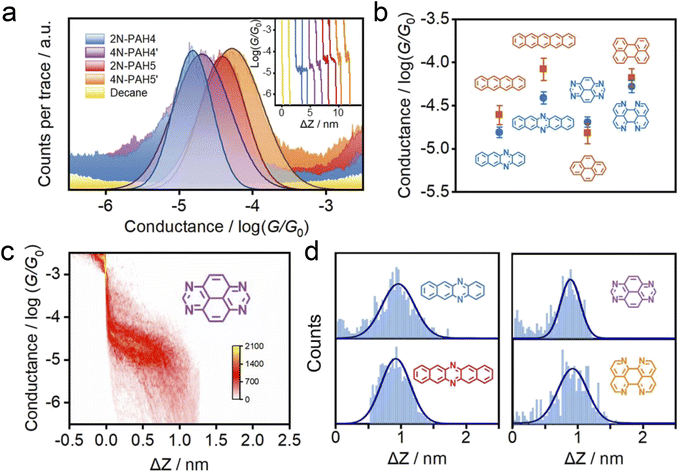
We investigate the cross-plane charge transport through the N-PAHs using a customized scanning tunneling microscopy break junction (STM-BJ) setup as shown in Fig. 1a left and Fig. S1 in the ESI.† A U-shaped Cu wire with single-layer graphene and Cu foil with single-layer graphene are chosen as substrates, and the tip is in soft contact with the substrate using the control program developed in our previous work.38–40 A push–pull process of the tip forms nanoscale gaps of varying sizes, and the molecule can be trapped in the nanogap between the graphene electrode pair and form a graphene–molecule–graphene van der Waals (vdW) heterojunction. The charge transport occurs in a cross-plane way due to the vdW interaction (Fig. 1a right). We have synthesized four N-PAH molecules as probe molecules,41–45 whose structures are shown in Fig. 1b.The conductance of the graphene-based single-molecule junctions with a bias voltage of 0.1 V ranged from 10−6.5G0 (∼24.5 pS; G0 = 2e2/h, quantum conductance) to 10−2.5G0 (∼245.4 nS) at room temperature. Direct tunneling traces were obtained in pure decane as a solvent and showed neither a discernible peak in the one-dimensional (1D) conductance histogram nor a plateau in the 2D conductance histogram. Typical individual conductance–displacement traces are shown in Fig. 2a in the inset. For all four molecules, there are distinct conductance plateaus ranging from 10−5G0 (∼775 pS) to 10−4G0 (∼7.75 nS); over 1000 individual conductance–distance traces are overlayed for statistical analysis. Distinct peaks were observed in the 1D conductance histogram (Fig. 2a), indicating that the molecular junctions of four N-PAHs were successfully constructed. The conductance of 2N-PAH4 and 4N-PAH4′ are 10−4.81G0 (∼1.20 nS) and 10−4.69G0 (∼1.58 nS) by Gaussian fitting of the peaks, respectively. Interestingly, 2N-PAH5 and 4N-PAH5′ have a conductance of 10−4.41G0 (∼3.02 nS) and 10−4.28G0 (∼4.07 nS), respectively, which are much higher than those of the former two counterparts. The relationship between the conductance and the structures of the molecules is shown in Fig. 2b, and the conductance of N-PAHs increases with the number of benzene rings, which is consistent with the conductance of PAHs.38 The cross-plane area is an essential factor affecting the conductance. The conductance of 2N-PAH5 decreases most significantly, falling to 46.8% of that of PAH5 (10−4.08G0, 6.45 nS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38), whereas the conductance of 4N-PAH4′ increases most manifestly up to 135% of that of PAH4′ (10−4.82G0, 1.17 nS
38), whereas the conductance of 4N-PAH4′ increases most manifestly up to 135% of that of PAH4′ (10−4.82G0, 1.17 nS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38), which is about ∼288% of the former decrease. Compared to their PAH counterparts,38 both 2N-PAH4 and 2N-PAH5 show a decrease in conductance by 63.1% and 46.8%, respectively, indicating that the former decrease is about ∼135% of the latter one. With the increase of the number of nitrogen atoms to four, the conductance of 4N-PAH5′ slightly decreases by 79.4%, while that of 4N-PAH4′ actually increases by 135%, which is about ∼170% of the former decrease (see Table S1 in the ESI†). Such a bipolar change can be accounted for by the fact that the insertion of nitrogen atoms stabilizes both the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), leading to a change in the relative positions of the HOMO and LUMO to the Fermi level of the electrodes. For a detailed explanation, see the section on the theoretical calculations.
38), which is about ∼288% of the former decrease. Compared to their PAH counterparts,38 both 2N-PAH4 and 2N-PAH5 show a decrease in conductance by 63.1% and 46.8%, respectively, indicating that the former decrease is about ∼135% of the latter one. With the increase of the number of nitrogen atoms to four, the conductance of 4N-PAH5′ slightly decreases by 79.4%, while that of 4N-PAH4′ actually increases by 135%, which is about ∼170% of the former decrease (see Table S1 in the ESI†). Such a bipolar change can be accounted for by the fact that the insertion of nitrogen atoms stabilizes both the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), leading to a change in the relative positions of the HOMO and LUMO to the Fermi level of the electrodes. For a detailed explanation, see the section on the theoretical calculations.
 | ||
| Fig. 2 Electrical properties with the XPBJ technique. (a) 1D conductance histograms were obtained from ∼1000 conductance–displacement traces of the pure decane solvent (yellow) and the N-PAHs using graphene electrodes. The typical individual conductance–displacement traces are shown in the inset. (b) Comparison of conductance between N-PAHs and PAHs. The data of PAH conductance come from our previous work.38 (c) 2D conductance–distance histograms of 4N-PAH4′. (d) The plateau length histograms of 2N-PAH4, 2N-PAH5, 4N-PAH4′, and 4N-PAH5′. | ||
The 2D conductance–distance histograms of N-PAHs are constructed by superimposing conductance–displacement traces to investigate the junction configurations. As shown in Fig. 2c, there are corresponding apparent intensity clouds in the range of conductance demonstrated in the 1D conductance histogram, indicating the successful construction of graphene–molecule–graphene junctions. Based on the plateau length of direct tunneling at 0.27 nm determined in pure solvent,38,39,46 the corrected plateau lengths of 2N-PAH4, 2N-PAH5, 4N-PAH4′, and 4N-PAH5′ are determined to be 0.96 nm, 0.92 nm, 0.90 nm, and 0.93 nm, respectively (Fig. 2d). They match the distance between the graphene sheet incorporated with N-PAHs, meaning that the sandwiched graphene–N-PAHs–graphene junctions are successfully fabricated. Although direct gold-aromatic ring junctions were reported,47 we tried to use gold electrodes to investigate the conductance of PAHs. Due to the absence of the anchoring group and weak van der Waals interaction at room temperature,48 PAHs which are planar molecules do not show an obvious conductance signal in the one-dimensional conductance–displacement histogram when gold electrodes are used (see Fig. S13 in the ESI†). In contrast, N-PAHs form molecular junctions through N–Au coordination bonds (see Fig. S12 in the ESI†). In remarkable contrast to graphene–molecule–graphene van der Waals heterojunctions, Au–N-PAHs–Au junctions do not seem to be able to accurately assess the influence of nitrogen atoms on charge transport through PAHs due to N–Au coordination bonds.
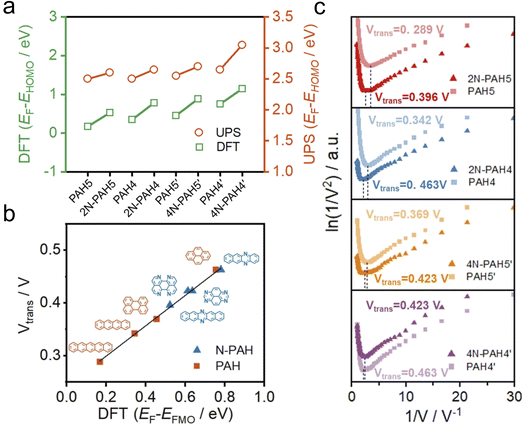
To further investigate the change of HOMO and LUMO energy levels, UPS and ultraviolet-visible (UV-Vis) spectra were used to evaluate the energy level alignment of these junctions. UPS measurements were performed using a He I light source (hν = 21.22 eV) to gauge the electronic states of monolayers on graphene.49 At an applied bias of −5 V, all the binding energy spectra are shown in Fig. S6 in the ESI.† We find that the insertion of nitrogen atoms gives rise to an increase in the energy offset between the Fermi energy EF of the electrodes and the energy of the highest occupied molecular orbital EHOMO (EF − EHOMO) as predicted by DFT calculations (Fig. 3a). The ultraviolet-visible (UV-Vis) spectra show that the HOMO–LUMO gaps of N-PAHs also decrease or remain almost unchanged compared to their PAH counterparts (see Fig. S7 in the ESI†). From the UPS and UV-Vis results, it can be deduced that the LUMO energy levels of N-PAHs decrease more rapidly than the HOMO energy levels, and notably, 4N-PAH4′ shows the most pronounced drop in the LUMO energy.
To further determine energy level alignment in the heterojunctions, we measured TVS to obtain the transition voltage (Vtrans). After the I–V measurements of all molecules, Fowler–Nordheim diagrams (describing the relationship between ln(I/V2) and 1/V) were obtained using a specific mathematical analysis method called TVS. Two trends corresponding to two different charge-transport mechanisms can be seen in the plots. The boundary between these two trends, the minimum value in the F–N plot, is defined as the transition voltage. The value of Vtrans is proportional to the energy offset between the Fermi energy EF of the electrodes and the energy of the frontier molecular orbital EFMO (EF − EFMO).50–52 The Vtrans values of N-PAHs and PAHs are linear with the absolute values of theoretical EF − EFMO (Fig. 3b). At the same time, the Vtrans values of N-PAHs and PAHs are compared (Fig. 3c). The Vtrans values of 2N-PAH5 and PAH5 are 0.396 V and 0.289 V, and the Vtrans values of 2N-PAH4 and PAH4 are 0.463 V and 0.342 V, suggesting that Vtrans increases after the insertion of nitrogen atoms. The results show that EF − EHOMO increases and EHOMO decreases due to the presence of nitrogen atoms, which is consistent with the theoretical calculations. In stark contrast, the frontier molecular orbital (the orbital which is more closed to Fermi level between the HOMO and the LUMO) shifts from the HOMO to the LUMO when the number of nitrogen atoms is increased to four. The Vtrans values of 4N-PAH5′ and PAH5′ are 0.423 V and 0.369 V, respectively. And the Vtrans value of 4N-PAH4′ (0.423 V) is slightly smaller than that of PAH4′ (0.463 V), indicative of a significantly reduced LUMO. This observation is corroborated by the UPS results mentioned earlier. It follows that 4N-PAH4′ and 4N-PAH5′ show a LUMO-dominated charge-transport mechanism that is distinct from the HOMO-dominated charge-transport through other N-PAHs and their PAH counterparts. It becomes clear that an interplay between the number of nitrogen atoms and the topology variation is applied to fine-tune the energy levels between the frontier orbitals and the Fermi level of the graphene electrodes, thereby regulating the charge-transport properties of the PAHs.
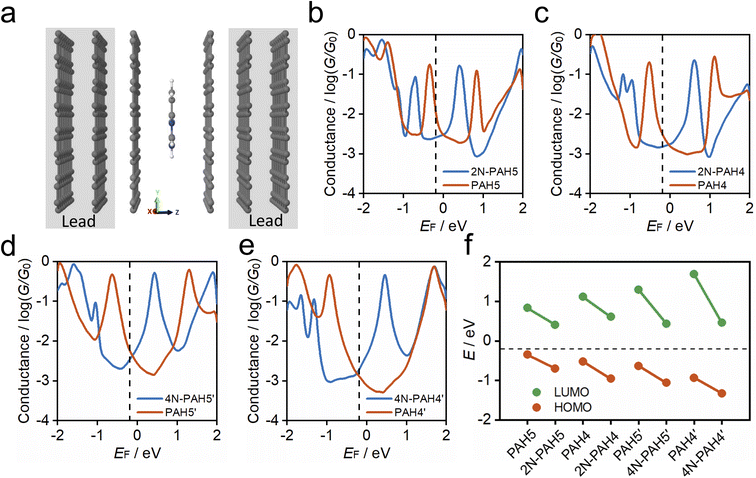
To understand the charge-transport properties of N-PAH and PAH molecules between graphene electrodes (Fig. 4a), we calculated the ground-state geometries and electronic structures of gas phase molecules using SIESTA53 implementation of density functional theory (DFT) firstly as discussed in the Computational Method section in the ESI.† We find that HOMO and LUMO energy levels for each molecule move down in energy with the insertion of nitrogen atoms (see Table S4 in the ESI†). Next, we calculated ground-state geometries and electronic structures of molecules between two graphene electrodes (see the Methods). The calculated average optimum distance between the graphene sheet and molecules is between 3.42 and 3.46 Å depending on the type of N-PAH and PAH molecule (see Table S5 in the ESI†). The smallest vdW distance (3.42 Å) is for 4N-PAH4′. The graphene electrodes are periodic in the y and x directions with multiple k-points (Fig. 4a) to resemble graphene sheets. We found that the ground state distance between graphene sheets is 3.36 Å in the transport direction (z).
To calculate cross-plane conductance through graphene-based single-molecule junctions, we obtain the mean-field Hamiltonian from density functional theory (DFT) and use the Gollum54,55 quantum transport code (see the Theoretical methods) to calculate the transmission coefficients of electrons of energy E passing from one electrode to the other. We then used the Landauer formula to calculate the electrical conductance (see the Theoretical methods). Since the molecules can interact with graphene electrodes in different stacking configurations, three different structures of AB, AA and a mixture of AA and AB stacking are considered. Fig. 4b–e show the calculated ensemble average conductance of the 3 different configurations (from AB to AA stacking) of N-PAH and PAH molecules between graphene electrodes with multiple k-points (5 × 5) perpendicular to the transport direction.
Fig. 4e shows the calculated average conductance of PAH4′ (red line) and 4N-PAH4′ (blue line) as a function of the Fermi energy EF. The HOMO resonance for 4N-PAH4′ has shifted to the left far away from the Fermi energy by ∼0.39 eV, while the LUMO resonance has shifted to the left by ∼1.23 eV and is closer to EF. This large shift of the LUMO resonance toward EF combined with its slightly smaller vdW distance increases the electrical conductance. The black dashed line at EF = −0.18 eV in Fig. 4b–e shows the Fermi energy that gives the best agreement with experiments for all molecules (see Fig. S9 in the ESI†), and several previous zero bias calculations have shown good agreement with such measurements.56–59 The LUMO resonances of 2N-PAH4 and 2N-PAH5 are also shifted downward in energy, as depicted in Fig. 4c and b, but not as much as for 4N-PAH4′. Consequently, the electrical conductance values of 2N-PAHs are lower than those of the corresponding PAHs at EF (−0.18 eV). As shown in Fig. 4d, the same holds true for 4N-PAH5′ (blue line), which has a lower conductance than PAH5′. We also performed calculations with a different graphene electrode configuration, as shown in Fig. S10 and S11 in the ESI,† and found similar results. As shown in Fig. 4f, we obtain the positions of HOMO (red circles) and LUMO (green circles) resonances relative to the Fermi energy of electrodes for each molecular junction from Fig. 4b–d. Our calculation shows that in N-PAH molecules, HOMO and LUMO energy levels move downward in energy, and the shift of the LUMO energy level is larger for molecules with a larger number of nitrogen atoms, such as 4N-PAH4′ and 4N-PAH5′. The largest shift of the LUMO energy happens to be in 4N-PAH4′. It is worth mentioning that electron transport in PAHs occurs close to the HOMO, in agreement with previous reports.38 However, electron transport in N-PAHs happens to move from the HOMO to the LUMO because the molecular orbitals move downward in energy and the FMOs change due to the larger number of nitrogen atoms. Our calculations also indicate that the conductance order between different PAHs and N-PAHs is sensitive to the choice of EF, so gating by a third electrode could lead to different orders.
Conclusions
In summary, we fabricated atomically well-defined N-doped graphene heterojunctions and investigated the cross-plane transport through these heterojunctions to reveal the effect of doping on their electronic properties. We found that the electronic cloud distribution via vdW interactions between N-PAHs and graphene electrodes plays an essential role in their conductance, and the presence of nitrogen atoms has a pronounced effect on the alignment of the energy levels of the HOMO and LUMO with respect to the Fermi level of the electrodes. Given a HOMO-dominated charge transport through PAHs and N-PAHs, the insertion of nitrogen atoms significantly stabilizes the HOMO, leading to a decrease in the conductance of N-PAH compared to that of its PAH counterpart. As the number of nitrogen atoms increases, the LUMO becomes more stabilized than the HOMO. Together with a variation in the topology and the number of phenyl rings of N-PAHs, LUMO-dominated charge transport occurs, leading to a slight decrease (4N-PAH5′) and an increase (4N-PAH4′) in the conductance of N-PAH compared with that of its PAH counterpart. Our work represented a solid step for the actual application of the graphene device via cross-plane transport and demonstrated the essential role of heteroatoms in two-dimensional heterojunctions.Methods
Materials
The Cu wires and Cu foils with single-layer graphene were purchased from 6 Carbon Technology (Shenzhen, China). 2N-PAH4,44 2N-PAH5,44 4N-PAH4′,42,45 and 4N-PAH5′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41,43 were prepared according to literature procedures.
41,43 were prepared according to literature procedures.
Single-molecule conductance measurements
We used the XPBJ technique modified from a home-built STM-BJ setup60 to perform single-molecule conductance measurements. A 0.1 V bias voltage was applied at room temperature. See more details in Section S2† and previous work.38Transition voltage spectroscopy
Conductance measurements were performed with an applied bias of 0.1 V. When a conductance plateau appeared from 10−5G0 (∼775 pS) to 10−4G0 (∼7.75 nS), the movement of the piezo was paused and the tip was stationary. The bias voltage was scanned between −1 V and 1 V and the I–V curves were recorded during the process. More than 1000 curves were collected for statistical analysis. The fitting curve was obtained from the 2D I–V histogram, and the transition voltage spectrum was plotted based on previous studies.50–52Ultraviolet photoelectron spectroscopy
UPS measurements were performed to estimate the electronic structure of N-PAHs and PAHs on graphene. The binding energy spectra were obtained using a He I light source (hν = 21.22 eV) at an applied bias of −5 V. More details are included in S25.†Theoretical calculation
The optimized geometries with ground-state Hamiltonian and overlap matrix elements for gas phase molecules and molecules between graphene electrodes were obtained using density functional theory (DFT). These results were then combined with the Green function method to calculate the phase-coherent, elastic-scattering properties of the system, consisting of two graphene electrodes and the molecule as the scattering region. From the calculated transmission functions, the electrical conductance was calculated using the Landauer formula. See the ESI† for details of computational methods.Data availability
All data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
W. H., Y. Y., H. S., and S. L. co-supervised the project. H. Z., P. Z. and A. D. prepared the manuscript with input from all authors H. Z., S. Z., Z. Y., Y. Z. and Y. Z. carried out experiments and analyzed the data. P. Z., S. D. and R. H. synthesized the molecules. A. D. and S. S. carried out the theoretical calculations. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. T2222002, 21973079, and 22032004), the Natural Science Foundation of Fujian Province (2021J06008), the National Key R&D Program of China (2017YFA0204902), the UKRI Future Leaders Fellowship (No. MR/S015329/2), the Leverhulme Trust Early Career Fellowship (No. ECF-2018-375), the Swiss NSF through the NCCR MUST “Molecular Ultrafast Science and Technology” and the Swiss NSF (200020_188468 and 200021_204053).Notes and references
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS PubMed.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. C. Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed.
- T. Taychatanapat, J. Y. Tan, Y. Yeo, K. Watanabe, T. Taniguchi and B. Özyilmaz, Nat. Commun., 2015, 6, 6093 CrossRef CAS PubMed.
- Y. Liu, C. Zeng, J. Yu, J. Zhong, B. Li, Z. Zhang, Z. Liu, Z. M. Wang, A. Pan and X. Duan, Chem. Soc. Rev., 2021, 50, 6401–6422 RSC.
- S. Wang, S. Zhao, X. Guo and G. Wang, Adv. Energy Mater., 2022, 12, 2100864 CrossRef CAS.
- D. Deng, K. S. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Nat. Nanotechnol., 2016, 11, 218–230 CrossRef CAS PubMed.
- M. El Abbassi, S. Sangtarash, X. Liu, M. L. Perrin, O. Braun, C. Lambert, H. S. J. van der Zant, S. Yitzchaik, S. Decurtins, S.-X. Liu, H. Sadeghi and M. Calame, Nat. Nanotechnol., 2019, 14, 957–961 CrossRef CAS PubMed.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- C. J. B. Ford, T. J. Thornton, R. Newbury, M. Pepper, H. Ahmed, D. C. Peacock, D. A. Ritchie, J. E. F. Frost and G. A. C. Jones, Appl. Phys. Lett., 1989, 54, 21–23 CrossRef CAS.
- J. Cai, C. A. Pignedoli, L. Talirz, P. Ruffieux, H. Söde, L. Liang, V. Meunier, R. Berger, R. Li, X. Feng, K. Müllen and R. Fasel, Nat. Nanotechnol., 2014, 9, 896–900 CrossRef CAS PubMed.
- L. Ju, J. Velasco, E. Huang, S. Kahn, C. Nosiglia, H.-Z. Tsai, W. Yang, T. Taniguchi, K. Watanabe, Y. Zhang, G. Zhang, M. Crommie, A. Zettl and F. Wang, Nat. Nanotechnol., 2014, 9, 348–352 CrossRef CAS PubMed.
- J. Han, J. Wang, M. Yang, X. Kong, X. Chen, Z. Huang, H. Guo, J. Gou, S. Tao, Z. Liu, Z. Wu, Y. Jiang and X. Wang, Adv. Mater., 2018, 30, 1804020 CrossRef PubMed.
- F. Pan, C. Sun, Y. Li, D. Tang, Y. Zou, X. Li, S. Bai, X. Wei, M. Lv, X. Chen and Y. Li, Energy Environ. Sci., 2019, 12, 3400–3411 RSC.
- A. Montenegro, C. Dutta, M. Mammetkuliev, H. Shi, B. Hou, D. Bhattacharyya, B. Zhao, S. B. Cronin and A. V. Benderskii, Nature, 2021, 594, 62–65 CrossRef CAS PubMed.
- N. R. Tanguy, M. Arjmand and N. Yan, Adv. Mater. Interfaces, 2019, 6, 1900552 CrossRef.
- T. J. Yoo, S.-Y. Kim, M. G. Kwon, C. Kim, K. E. Chang, H. J. Hwang and B. H. Lee, Laser Photonics Rev., 2021, 15, 2000557 CrossRef CAS.
- C. Li, Y. Xiao, L. Zhang, Y. Li, J.-J. Delaunay and H. Zhu, Sustainable Energy Fuels, 2018, 2, 663–672 RSC.
- Y. Yan, D. Zhai, Y. Liu, J. Gong, J. Chen, P. Zan, Z. Zeng, S. Li, W. Huang and P. Chen, ACS Nano, 2020, 14, 1185–1195 CrossRef CAS PubMed.
- Y. Li, X. Xu, X. Liu, B. Li, Y. Han, Y. Zheng, D.-f. Chen, K. W. K. Yeung, Z. Cui, Z. Li, Y. Liang, S. Zhu, X. Wang and S. Wu, Adv. Sci., 2020, 7, 2000023 CrossRef CAS PubMed.
- S. Kawai, S. Nakatsuka, T. Hatakeyama, R. Pawlak, T. Meier, J. Tracey, E. Meyer and A. S. Foster, Sci. Adv., 2018, 4, eaar7181 CrossRef PubMed.
- D. J. Rizzo, M. Wu, H.-Z. Tsai, T. Marangoni, R. A. Durr, A. A. Omrani, F. Liou, C. Bronner, T. Joshi, G. D. Nguyen, G. F. Rodgers, W.-W. Choi, J. H. Jørgensen, F. R. Fischer, S. G. Louie and M. F. Crommie, Nano Lett., 2019, 19, 3221–3228 CrossRef CAS PubMed.
- A. Taqieddin and N. R. Aluru, ACS Appl. Nano Mater., 2021, 4, 5816–5824 CrossRef CAS.
- B. Guo, Q. Liu, E. Chen, H. Zhu, L. Fang and J. R. Gong, Nano Lett., 2010, 10, 4975–4980 CrossRef CAS PubMed.
- N. Li, Z. Wang, K. Zhao, Z. Shi, Z. Gu and S. Xu, Carbon, 2010, 48, 255–259 CrossRef CAS.
- A. Sala, G. Zamborlini, T. O. Menteş and A. Locatelli, Small, 2015, 11, 5927–5931 CrossRef CAS PubMed.
- C. Zhang, L. Fu, N. Liu, M. Liu, Y. Wang and Z. Liu, Adv. Mater., 2011, 23, 1020–1024 CrossRef CAS PubMed.
- H. Wang, T. Maiyalagan and X. Wang, ACS Catal., 2012, 2, 781–794 CrossRef CAS.
- J. P. Mora-Fuentes, I. Papadopoulos, D. Thiel, R. Álvarez-Boto, D. Cortizo-Lacalle, T. Clark, M. Melle-Franco, D. M. Guldi and A. Mateo-Alonso, Angew. Chem., Int. Ed., 2020, 59, 1113–1117 CrossRef CAS PubMed.
- Y. Yang, M. Gantenbein, A. Alqorashi, J. Wei, S. Sangtarash, D. Hu, H. Sadeghi, R. Zhang, J. Pi, L. Chen, X. Huang, R. Li, J. Liu, J. Shi, W. Hong, C. J. Lambert and M. R. Bryce, J. Phys. Chem. C, 2018, 122, 14965–14970 CrossRef CAS.
- L. Wang, Z. Zhao, D. B. Shinde, Z. Lai and D. Wang, Chem. Commun., 2021, 57, 667–670 RSC.
- X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z.-Y. Xiao, W. Hong, C. J. Lambert and S.-X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176 CrossRef CAS PubMed.
- C. Tang, L. Huang, S. Sangtarash, M. Noori, H. Sadeghi, H. Xia and W. Hong, J. Am. Chem. Soc., 2021, 143, 9385–9392 CrossRef CAS PubMed.
- M. C. Walkey, C. R. Peiris, S. Ciampi, A. C. Aragonès, R. B. Domínguez-Espíndola, D. Jago, T. Pulbrook, B. W. Skelton, A. N. Sobolev, I. Díez Pérez, M. J. Piggott, G. A. Koutsantonis and N. Darwish, ACS Appl. Mater. Interfaces, 2019, 11, 36886–36894 CrossRef CAS PubMed.
- I. Diez-Perez, Z. Li, J. Hihath, J. Li, C. Zhang, X. Yang, L. Zang, Y. Dai, X. Feng, K. Muellen and N. Tao, Nat. Commun., 2010, 1, 31 CrossRef PubMed.
- L. A. Zotti, T. Kirchner, J.-C. Cuevas, F. Pauly, T. Huhn, E. Scheer and A. Erbe, Small, 2010, 6, 1529–1535 CrossRef CAS PubMed.
- D. Miguel, L. Álvarez de Cienfuegos, A. Martín-Lasanta, S. P. Morcillo, L. A. Zotti, E. Leary, M. Bürkle, Y. Asai, R. Jurado, D. J. Cárdenas, G. Rubio-Bollinger, N. Agraït, J. M. Cuerva and M. T. González, J. Am. Chem. Soc., 2015, 137, 13818–13826 CrossRef CAS PubMed.
- X.-Y. Wang, X. Yao and K. Müllen, Sci. China: Chem., 2019, 62, 1099–1144 CrossRef CAS.
- S. Zhao, Q. Wu, J. Pi, J. Liu, J. Zheng, S. Hou, J. Wei, R. Li, H. Sadeghi, Y. Yang, J. Shi, Z. Chen, Z. Xiao, C. Lambert and W. Hong, Sci. Adv., 2020, 6, eaba6714 CrossRef CAS PubMed.
- S. Zhao, Z.-Y. Deng, S. Albalawi, Q. Wu, L. Chen, H. Zhang, X.-J. Zhao, H. Hou, S. Hou, G. Dong, Y. Yang, J. Shi, C. Lambert, Y.-Z. Tan and W. Hong, Chem. Sci., 2022, 13, 5854–5859 RSC.
- Z. Tan, D. Zhang, H.-R. Tian, Q. Wu, S. Hou, J. Pi, H. Sadeghi, Z. Tang, Y. Yang, J. Liu, Y.-Z. Tan, Z.-B. Chen, J. Shi, Z. Xiao, C. Lambert, S.-Y. Xie and W. Hong, Nat. Commun., 2019, 10, 1748 CrossRef PubMed.
- T. Brietzke, W. Mickler, A. Kelling and H.-J. Holdt, Dalton Trans., 2012, 41, 2788–2797 RSC.
- S. Geib, S. C. Martens, U. Zschieschang, F. Lombeck, H. Wadepohl, H. Klauk and L. H. Gade, J. Org. Chem., 2012, 77, 6107–6116 CrossRef CAS PubMed.
- N. Kocić, P. Weiderer, S. Keller, S. Decurtins, S. X. Liu and J. Repp, Nano Lett., 2015, 15, 4406–4411 CrossRef PubMed.
- H. Kouno, Y. Kawashima, K. Tateishi, T. Uesaka, N. Kimizuka and N. Yanai, J. Phys. Chem. Lett., 2019, 10, 2208–2213 CrossRef CAS PubMed.
- P. Zhou, U. Aschauer, S. Decurtins, T. Feurer, R. Häner and S.-X. Liu, Chem. Commun., 2021, 57, 12972–12975 RSC.
- Y.-L. Zou, Q.-M. Liang, T. Lu, Y.-G. Li, S. Zhao, J. Gao, Z.-X. Yang, A. Feng, J. Shi, W. Hong, Z.-Q. Tian and Y. Yang, Sci. Adv., 2023, 9, eadf0425 CrossRef CAS PubMed.
- A. C. Aragonès, N. Darwish, S. Ciampi, L. Jiang, R. Roesch, E. Ruiz, C. A. Nijhuis and I. Díez-Pérez, J. Am. Chem. Soc., 2019, 141, 240–250 CrossRef PubMed.
- T. Yelin, R. Korytár, N. Sukenik, R. Vardimon, B. Kumar, C. Nuckolls, F. Evers and O. Tal, Nat. Mater., 2016, 15, 444–449 CrossRef CAS PubMed.
- B. Kim, J. M. Beebe, Y. Jun, X. Y. Zhu and C. D. Frisbie, J. Am. Chem. Soc., 2006, 128, 4970–4971 CrossRef CAS PubMed.
- J. M. Beebe, B. Kim, J. W. Gadzuk, C. Daniel Frisbie and J. G. Kushmerick, Phys. Rev. Lett., 2006, 97, 026801 CrossRef PubMed.
- J. M. Beebe, B. Kim, C. D. Frisbie and J. G. Kushmerick, ACS Nano, 2008, 2, 827–832 CrossRef CAS PubMed.
- Y. Yang, J. Liu, S. Feng, H. Wen, J. Tian, J. Zheng, B. Schöllhorn, C. Amatore, Z. Chen and Z. Tian, Nano Res., 2016, 9, 560–570 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 093029 CrossRef.
- H. Sadeghi, Nanotechnology, 2018, 29, 373001 CrossRef PubMed.
- N. Ferri, N. Algethami, A. Vezzoli, S. Sangtarash, M. McLaughlin, H. Sadeghi, C. J. Lambert, R. J. Nichols and S. J. Higgins, Angew. Chem., Int. Ed., 2019, 58, 16583–16589 CrossRef CAS PubMed.
- M. H. Garner, H. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. Liu, F. Ng, H. Li, S. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419 CrossRef CAS PubMed.
- L. Li, J. Z. Low, J. Wilhelm, G. Liao, S. Gunasekaran, C. R. Prindle, R. L. Starr, D. Golze, C. Nuckolls, M. L. Steigerwald, F. Evers, L. M. Campos, X. Yin and L. Venkataraman, Nat. Chem., 2022, 14, 1061–1067 CrossRef CAS PubMed.
- Y. Li, M. Buerkle, G. Li, A. Rostamian, H. Wang, Z. Wang, D. R. Bowler, T. Miyazaki, L. Xiang, Y. Asai, G. Zhou and N. Tao, Nat. Mater., 2019, 18, 357–363 CrossRef CAS PubMed.
- B.-F. Zeng, J.-Y. Wei, X.-G. Zhang, q. Liang, S. Hu, G. Wang, Z.-C. Lei, S. Zhao, H. Zhang, J. Shi, W. Hong, Z.-q. Tian and Y. Yang, Chem. Sci., 2022, 13, 7765–7772 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc00075c |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |