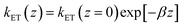Open Access Article
Open Access ArticleElectrochemical response of surface-attached redox DNA governed by low activation energy electron transfer kinetics†
Zhiyong
Zheng
 a,
Soo Hyeon
Kim
a,
Soo Hyeon
Kim
 b,
Arnaud
Chovin
a,
Nicolas
Clement
*b and
Christophe
Demaille
b,
Arnaud
Chovin
a,
Nicolas
Clement
*b and
Christophe
Demaille
 *a
*a
aUniversité Paris Cité, CNRS, Laboratoire d'Electrochimie Moléculaire, F-75013 Paris, France. E-mail: Christophe.demaille@u-paris.fr
bIIS, LIMMS/CNRS-IIS UMI2820, The Univ. of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8505, Japan. E-mail: nclement@iis.u-tokyo.ac.jp
First published on 8th March 2023
Abstract
The mechanism responsible for electron transport within layers of redox DNA anchored to electrodes has been extensively studied over the last twenty years, but remains controversial. Herein, we thoroughly study the electrochemical behavior of a series of short, model, ferrocene (Fc) end-labeled dT oligonucleotides, terminally attached to gold electrodes, using high scan rate cyclic voltammetry complemented by molecular dynamics simulations. We evidence that the electrochemical response of both single-stranded and duplexed oligonucleotides is controlled by the electron transfer kinetics at the electrode, obeying Marcus theory, but with reorganization energies considerably lowered by the attachment of the ferrocene to the electrode via the DNA chain. This so far unreported effect, that we attribute to a slower relaxation of water around Fc, uniquely shapes the electrochemical response of Fc-DNA strands and, being markedly dissimilar for single-stranded and duplexed DNA, contributes to the signaling mechanism of E-DNA sensors.
Introduction
Electrochemical conformational DNA sensors (E-DNA sensors) are sensitive, selective, and versatile modern analytical devices.1–5 They use short DNA strands (oligonucleotides) attached at one end to an electrode, and carrying a redox label at the other end as sensing elements. Molecular recognition of target molecules dispersed in solution by the anchored redox DNA modulates the electrochemical response of the sensor, which is used to report the target molecule concentration. The versatility of E-DNA sensors stems from the ability of oligonucleotides to specifically recognize many different analytes, including complementary DNA strands,1 small molecules,6 proteins,7 viruses,8 or even living cells.9,10 To optimize their sensitivity, it is of utmost importance to understand their signaling mechanism.Of particular interest here are E-DNA sensors using dilute layers of single-stranded DNA oligonucleotides as sensing elements. The oligonucleotides are end-grafted at one end and, at the other end, bear redox labels not electronically conjugated to the DNA base stack, nor able to act as intercalators. This description fits many E-DNA sensors and also excludes systems where through-DNA-chain electronic conduction was either evidenced or can be suspected.11–13 For the DNA systems considered here, a close approach of the redox label to the electrode is thus required for electron transfer events to occur. As a result, the motional dynamics of the chain and electron transfer at the electrode are the only two processes potentially kinetically controlling the electrochemical response. Which of these processes is actually rate limiting has been the subject of debate for almost 20 years.14–23
In early works from our group, fast scan rate cyclic voltammetry (CV) was used to investigate this issue.14,15,24 The response of ferrocene (Fc) labeled dT20 chains was analyzed and it was concluded that dynamic bending or rotational motion was governing the CV response of the Fc-(dT.dA)20 duplex. Subsequently, Ferapontova et al. studied the behavior of methylene blue (MB)-labeled, end-attached DNA duplexes (16–22 bases long) and also observed CV characteristics compatible with diffusional control.18,21 White et al. reported a similar diffusive-like behavior for end-grafted single-stranded MB-dT21 chains.22 Schuhmann et al. reached similar conclusions for ferrocene-labeled short DNA analogues (peptide nucleic acids, PNA, 3–16 bases long) grafted onto electrodes from high scan rate cyclic voltammetry studies.23
In a series of important contributions, Plaxco et al. reported experiments to decipher the electron transfer mechanism within redox oligonucleotide layers.17,19,20 They first used alternating current voltammetry (ACV) to study the electrochemical response of MB-labeled, end-attached single-stranded oligo-(dT) nucleotides.17 The ACV data analysis provided an apparent first-order electron transfer rate constant varying as the inverse of chain length. This was interpreted as evidence of the rate of electron transfer controlling the electrochemical signal. Later, these authors carried out the same experiments using chronoamperometry as the experimental technique.19 They then observed an inverse square dependence of the apparent electron transfer rate constant on chain length, from which they concluded that chain dynamics was actually the current limiting factor. Afterward, they applied the same technique to analyze the response of double-stranded redox DNA and reached the same conclusion.20
All of the above works report rate constants, characterizing the electrochemical response of redox-DNA systems, in the order of 1–1000 s−1 or apparent diffusion coefficients in the order of 10−10 cm2 s−1 or lower. However, it is striking that these values are orders of magnitude lower than those characterizing the dynamics of short DNA strands free in solution. For example, the translational diffusion coefficient of a single-stranded (ss) 20 bases oligonucleotide is in the order of 10−6 cm2 s−1.25 Similarly, a double-stranded (ds) DNA strand of the same length is characterized by a rotational diffusion constant in the order of μs−1.26,27
It is also intriguing that chain dynamics in the expected μs range were systematically observed in experiments where anchored oligonucleotides were end-labeled by a fluorophore and surface-induced fluorescence quenching was used to monitor the motion of the DNA chain.27,28 Fluorescence quenching and electrochemical experiments both require the end-label of the DNA chain to approach the anchoring surface within (sub)nanometer distances, albeit in fluorescence no electron transfer occurs. This suggests that the slow rate constants measured by electrochemistry reflect a kinetic control by the electron transfer step rather than by chain dynamics.
The present work aims to address this question by: (i) assembling a model end-grafted redox oligonucleotide system, (ii) characterizing its electrochemical response with fast scan rate cyclic voltammetry, and (iii) interpreting the results based on a realistic molecular dynamics model for DNA. These simulations, which were previously computationally inaccessible or not quantitative enough, have become possible with the refinement of coarse grained sequence-dependent DNA models such as oxDNA.29 For the present work, we have developed a code (Qbiol) dedicated to electrochemical application enabling the complete dynamics of the anchored DNA to be numerically reproduced and resolved in time.
We evidence that the electrochemical response of both single-stranded and duplexed redox oligonucleotides is actually kinetically controlled by the electron transfer at the electrode, complying with Marcus theory,30–32 but with a reorganization energy considerably lowered by the attachment of the redox label to the flexible DNA chain and to the electrode. This decrease in reorganization energy drastically changes the electrochemical response of redox DNA strands in a way that can be mistaken for diffusional or elastic bending control. Furthermore, the reorganization energies are markedly dissimilar for ssDNA and dsDNA, which largely contributes to making hybridization detectable electrochemically, i.e. underlies the signaling mechanism of E-DNA sensors.
Results
Design and assembly of model redox DNA layers
We studied the fast scan rate CV response of a series of short, model, poly-(dT) oligonucleotides, labeled at their 3′ extremity by a ferrocene redox tag, and 5′ end-attached to a gold electrode (Fig. 1). Oligonucleotides of sequence dTN were considered, as they have been preferably used in previous works aiming at characterizing the dynamics of surface-anchored redox-oligonucleotides.15,17,19,24 Ferrocene was chosen as a redox marker due to its fast and uncomplicated single electron transfer properties.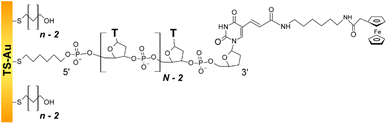 | ||
| Fig. 1 Structure of the dilute ferrocenylated DNA oligonucleotide layers. N is the number of (dT) nucleotides, n the number of CH2 units of the hydroxyl-terminated alkyl thiol surface diluent. | ||
The oligonucleotide length was systematically varied by considering N values of 10, 20, 35, and 50. The single-stranded Fc-dT chains (ssDNA) were surface thiol-attached to ultra-flat template-stripped gold surfaces, via a 6-carbon long, thiol-terminated alkyl linker. Short, hydroxyl-terminated alkyl thiol chains (HS–(CH2)n–OH) were co-adsorbed with the DNA as surface diluent. Co-adsorption was preferred over the more commonly used backfilling of already adsorbed DNA layers,33 as it produces particularly well-defined, homogeneous thiol-DNA layers, avoiding flat-lying adsorption of oligonucleotides.34,35
Alkyl chains of various lengths, featuring n = 2, 3, 4, or 6 CH2, were used. They are not longer than the C6 DNA surface linker which allows free strand motion around its 5′ end. By controlling the DNA/alkyl thiol ratio, the final Fc-DNA surface coverage could be finely tuned, and its influence on the CV response systematically studied.
We purposefully assembled diluted Fc-DNA layers with a chain surface coverage ≪10 pmol cm−2. Thorough control experiments were carried out to verify that the ssDNA chains were properly anchored via their 5′ thiol linker, and that their 3′ Fc-labeled end freely explored a small volume of solution extending from the surface and solely limited by the chain length (ESI, Section 3†).
High scan rate CV of end-attached Fc-dT35
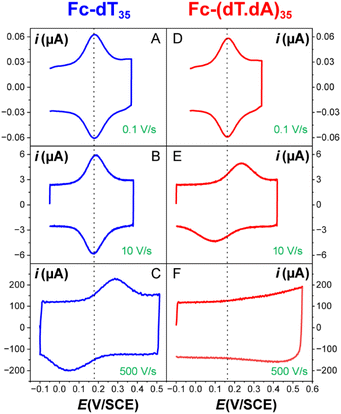
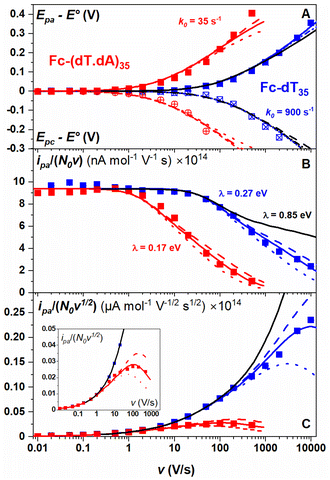
The CV responses of end-anchored DNA layers were recorded in a wide range of potential scan rate, v, from 0.01 V s−1 to 10 kV s−1, using a high-bandwidth home-designed apparatus. A 1 M ionic strength buffered NaClO4 solution was used as the electrolyte to ensure that the electrode electric field effect on DNA orientation was vanishingly small.36 We first considered Fc-(dT)35 layers, formed using mercaptohexanol (n = 6) as a surface diluent. Typical CV signals recorded at 0.1, 10, and 500 V s−1 are shown in Fig. 2A–C. At slow enough scan rates (e.g. 0.1 V s−1), the CV displayed a pair of well-defined, symmetrical peaks, located at a common peak potential value of ∼175 ± 3 mV versus SCE, corresponding to the standard potential (E°) expected for the DNA-borne Fc label.37 The intensity of the (anodic or cathodic) peak current was proportional to the scan rate and the peak full width at mid-height was ∼97 ± 3 mV. These characteristics are typical of the response of non-interacting surface-attached redox species, located outside the double layer and undergoing fast (Nernstian) electron transfer at the gold electrode. Integration of the charge under the peaks yielded the Fc-ssDNA surface coverage, 5 ± 0.5 pmol cm−2, for the CV in Fig. 2A. As the scan rate was raised, the peak separation increased and the peaks became relatively broad (Fig. 2B and C).The changes in signal characteristics with v are shown in Fig. 3. The variation of the anodic (Epa) and cathodic (Epc) peak positions and of the anodic peak intensity (ipa), normalized by v, or by 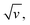 are displayed in parts a, b, and c, respectively (blue symbols). At scan rates above 10 V s−1, the anodic peak potentials shifted positively while the cathodic peak shifted negatively, so the peak separation markedly increased up to more than 0.5 V at 10 kV s−1. Such a large increase in peak separation is attributed to the electron transfer rate becoming comparable to the reciprocal of the CV characteristic “observation” time τcv = RT/Fv, with F the Faraday constant. In the same high scan rate region, the ratio ipa/v markedly decreased (Fig. 3B), while the corresponding ratio
are displayed in parts a, b, and c, respectively (blue symbols). At scan rates above 10 V s−1, the anodic peak potentials shifted positively while the cathodic peak shifted negatively, so the peak separation markedly increased up to more than 0.5 V at 10 kV s−1. Such a large increase in peak separation is attributed to the electron transfer rate becoming comparable to the reciprocal of the CV characteristic “observation” time τcv = RT/Fv, with F the Faraday constant. In the same high scan rate region, the ratio ipa/v markedly decreased (Fig. 3B), while the corresponding ratio 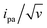 increased without reaching a plateau (Fig. 3C). Such behavior is compatible with the ssDNA chain undergoing too-fast-to-be-measured chain dynamics, the system thus behaving as a thin layer cell (TLC) where a redox species is free to “move” rapidly within a thin layer confined to the electrode surface.38,39 This is expected here since, even at the highest scan rate explored of 10 kV s−1, τcv is 2.6 μs, approaching but still larger than the expected sub-μs motional time characteristic of (dT)35.27 Such a case is also confirmed by our molecular dynamic simulations reproducing the motion of the anchored chain (vide infra).
increased without reaching a plateau (Fig. 3C). Such behavior is compatible with the ssDNA chain undergoing too-fast-to-be-measured chain dynamics, the system thus behaving as a thin layer cell (TLC) where a redox species is free to “move” rapidly within a thin layer confined to the electrode surface.38,39 This is expected here since, even at the highest scan rate explored of 10 kV s−1, τcv is 2.6 μs, approaching but still larger than the expected sub-μs motional time characteristic of (dT)35.27 Such a case is also confirmed by our molecular dynamic simulations reproducing the motion of the anchored chain (vide infra).
As discussed by Laviron39 in TLC the CV response is identical to that of a motion-less surface-attached species except that, for simple diffusion, the electron transfer rate is characterized by a standard first-order rate constant k0 = ks/L, where ks is the standard heterogeneous electron transfer rate constant of the species and L is the thin layer thickness.
In the present case, the motion of the redox label is more complex than simple diffusion, but the equivalence with a motion-less surface species still holds and one can also define a k0 value, proportional to the equilibrium probability of the presence of the redox label at the electrode and to ks (see below).
Moreover, since large overpotential values (Epa − E° and Epc − E°) were explored (Fig. 3A), the Marcus–Hush–Levich (MHL) model has to be employed to describe the electron transfer kinetics, rather than the Butler–Volmer model.30–32 The MHL model describes the electron transfer kinetics in terms of two parameters: k0 and λ, with the latter being the solvent reorganization energy, which is characteristic of the molecular structure and solvation of the redox probe.30 In CV the peak separation is only modestly dependent on the λ value,32,40,41 so that fitting of the Epa − E° and Epc − E° vs. v variations can be carried out using k0 as a single adjustable parameter (ESI, Section 4†). For Fc-dT35 this yields the best-fit value of k0 = 900 ± 100 s−1 (Fig. 3A, blue traces).
Conversely, the peak current is quite sensitive to the λ value (ESI, Section 4†).32,40,41 A typical λ value of ∼0.85 eV is reported for ferrocene species,31 both in solution and immobilized on electrodes as part of compact self-assembled thiol layers. We therefore calculated the ipa/v versus v variation with λ = 0.85 eV using the MHL/TLC model (black line in Fig. 3B). As shown, this could not account for the sharp decrease of the ipa/v ratio we experimentally observed at high scan rates. However, by using λ as an adjustable parameter (while keeping k0 = 900 s−1), the experimental ipa/v vs log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v variation could be very satisfyingly reproduced with a best-fit value of λ = 0.27 ± 0.03 eV (Fig. 3B blue solid line), and so could the
v variation could be very satisfyingly reproduced with a best-fit value of λ = 0.27 ± 0.03 eV (Fig. 3B blue solid line), and so could the 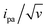 variation (Fig. 3C). Such a remarkably low λ value seemingly reflects an unexpected effect of the attachment of the ferrocene label to the surface via the flexible DNA chain.
variation (Fig. 3C). Such a remarkably low λ value seemingly reflects an unexpected effect of the attachment of the ferrocene label to the surface via the flexible DNA chain.
Hybridization of the Fc-dT35 chain: high scan rate CV of end-attached Fc-(dT.dA)35 duplex
The end-anchored, Fc-dT35 layer was exposed to fully complementary dA35 chains in solution, rinsed with the electrolyte, and thoroughly characterized again by high scan rate CV. At slow scan rates, the CV obtained was very similar to the one recorded for Fc-dT35 (Fig. 2D), even showing a similar coverage, indicating the absence of chain loss. Yet, the apparent standard potential of the ferrocene label, E°, was shifted to a more negative value of E° = 165 ± 3 mV versus SCE. At higher scan rates, the CVs differed markedly from those initially recorded for Fc-dT35: the peak separations became larger and the peak currents lower (Fig. 2E). As the scan rate was further raised, the peak current intensity relative to the capacitive background decreased, and up to the point that (from 500 V s−1), the faradaic signal was indiscernible as if “extinct” (Fig. 2F). Such changes in CV signals upon exposing the electrode to dA35 are ascribable to the full hybridization of the end-anchored Fc-dT35 chain, forming the corresponding Fc-(dT.dA)35. The reversibility and specificity of the hybridization reaction were ascertained by control experiments (ESI, Section 5†).The full CV characteristics of the Fc-(dT.dA)35 layer are presented in Fig. 3 (red symbols). Most notably, upon increasing the scan rate, the peak-to-peak separation increased while the ratio ipa/v decreased in a similar way as observed for the Fc-(dT)35 layer, but from a much lower scan rate threshold of only a few V s−1. Interestingly, the ratio 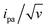 passed toward a broad peak (inset in Fig. 3C). Such a CV behavior was previously reported by us for Fc-(dT.dA)20 layers immobilized on non-MCH treated polycrystalline gold electrodes, and interpreted as a sign of diffusion or elastic rod-bending control of the CV.15,24 However, we now realize that this behavior can be quantitatively explained by the MHL/TLC model, which enables the v dependence of the CV characteristics to be perfectly reproduced (Fig. 3, red traces). This result points to fast Fc-(dT.dA)35 strand dynamics and to kinetic control of the CV by the electron transfer rate. Accordingly, our simulations predict that Fc-dsDNA strands undergo fast rotational motions around their anchored 5′ end, characterized by times in the ns range, vide infra. By contrast, even at the highest scan rate explored for Fc-(dT.dA)35 (1000 V s−1), τcv is much larger (26 μs).
passed toward a broad peak (inset in Fig. 3C). Such a CV behavior was previously reported by us for Fc-(dT.dA)20 layers immobilized on non-MCH treated polycrystalline gold electrodes, and interpreted as a sign of diffusion or elastic rod-bending control of the CV.15,24 However, we now realize that this behavior can be quantitatively explained by the MHL/TLC model, which enables the v dependence of the CV characteristics to be perfectly reproduced (Fig. 3, red traces). This result points to fast Fc-(dT.dA)35 strand dynamics and to kinetic control of the CV by the electron transfer rate. Accordingly, our simulations predict that Fc-dsDNA strands undergo fast rotational motions around their anchored 5′ end, characterized by times in the ns range, vide infra. By contrast, even at the highest scan rate explored for Fc-(dT.dA)35 (1000 V s−1), τcv is much larger (26 μs).
Fitting of the peak potentials versus log(v) yielded a best-fit k0 value of 35 ± 5 s−1 (Fig. 3A, red trace). The ipa/v variation could be nicely reproduced using the best-fit λ of 0.17 ± 0.03 eV (Fig. 3B). Notably, the peak shape of the experimental 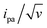 vs. v variation could nicely be reproduced by the MHL/TLC model (see inset in Fig. 3C), which predicts such shape only for low enough λ values (ESI, Section 4†).
vs. v variation could nicely be reproduced by the MHL/TLC model (see inset in Fig. 3C), which predicts such shape only for low enough λ values (ESI, Section 4†).
Effect of DNA chain length, N, on the CV of Fc-dTN and Fc-(dT.dA)N
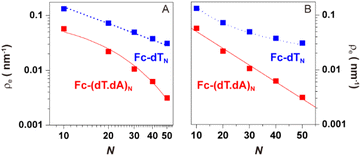
As pointed out by Plaxco et al.17,19,20 varying the DNA chain length, i.e. the number of (dT) nucleotides, N, is key to evidence whether chain motion or electron transfer kinetics controls the electrochemical response of redox-DNA. We therefore conducted high scan rate CV characterizations for Fc-dTN chains (N = 10, 20, 35, and 50), with in each case a systematic study of the effect of the chain coverage, Γ, from which sets of k0 and λ values could be derived (ESI, Section 6†). Decreasing k0vs. Γ and increasing λ vs. Γ variations were systematically observed for all chain lengths (e.g. Fig. S11–S13†). These effects translate the modulation of the electron transfer parameters due to the crowding of the surface by DNA chains.The k0 and λ values measured at the lowest coverage values explored are specifically considered below, as they are typical of isolated (non-interacting) chains, which we primarily intend to model in this work. These values are plotted as a function of N in Fig. 4.
 | ||
| Fig. 4 Variation of the kinetic parameters k0 and λ with the DNA chain length with various number of nucleotides (N). (A and B) Fc-dTN. (C and D) Fc-(dT.dA)N. Red curves in (A) and (C), and insets are fits of eqn (2) to the data, in (B) and (D) are guides to the eye. | ||
For the single-stranded chains Fc-dTN, k0 decreased rapidly with increasing chain length, N, (Fig. 4A). More precisely, k0 nicely decreased as 1/N, see log(k0) vs. log(N) plot in the inset. As shown in Fig. 4B, λ of Fc-dTN varied little with increasing N. For the Fc-(dT.dA)N duplexes, k0 also decreased rapidly with increasing chain length (Fig. 4C), while being systematically at least an order of magnitude lower than that for non-hybridized chains. Fig. 4D shows that λ increased with N, while remaining below ∼0.1 eV. Note that for N = 10, the hybridization could not be unambiguously evidenced likely due to a too-low melting point of this short duplex.
Effect of diluent length, n, on the CV of Fc-dT50 and Fc-(dT.dA)50 layers
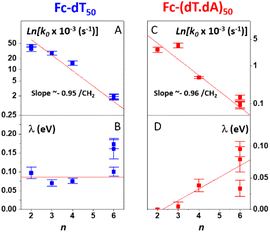
The effect of the length (i.e. number n of CH2 units) of the alkyl thiol diluent on the CV response of Fc-ssDNA and Fc-dsDNA was also studied. For this, Fc-dT50 was thiol-end adsorbed in the presence of an excess of the chosen diluent (n = 2, 3, 4, or 6). The final Fc head coverage was kept low enough (≪1 pmol cm−2) for the Fc-DNA chains to behave as isolated entities. Here again, the MHL/TLC model enabled us to fully account for the CV characteristics of the chains, both single-stranded and duplexed, for all the diluent thiols explored (Fig. S2†). The thus derived sets of k0, λ values were then plotted as a function of n, in Fig. 5.Both for Fc-(dT)50 (Fig. 5A) and Fc-(dT.dA)50 (Fig. 5C), k0 was seen to decrease exponentially with n. Such a result is strong evidence that, for our system, electron transfer to the redox Fc heads does not proceed through the DNA chain, since in this case its rate would not be affected by the length of the alkyl thiol diluent. Conversely, such dependence is expected if the electron is transferred by the Fc label to the electrode through the diluent layer. This result falls in line with the dependence of the current on the diluent thickness previously noted for some E-DNA sensors.42,43
For the dependence of λ on n, one can observe that, for Fc-(dT)50, λ remains approximately constant around a low value of 0.1 eV (Fig. 5B). For Fc-(dT.dA)50, λ values are typically even lower (Fig. 5D), going from almost zero for n = 2 and increasing to a maximum value of ∼0.1 eV for n = 6.
Molecular dynamic simulations of the behavior of end-attached Fc-DNA layers
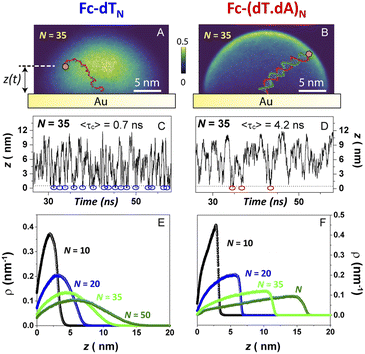
We have developed a molecular dynamics simulation code (Qbiol) based on the OxDNA package, to resolve the motional dynamics of end-anchored ss and ds Fc-DNA (ESI, Section 7†). While numerical simulations considering a molecular pendulum (rod with electrostatics) have shown to nicely reproduce the dynamics of protein-binding to double-stranded DNA and a specific antibody,44 such an approach remains too simple to capture the dynamics of protein-free DNA, and in particular for ssDNA that does not behave as a rod. In Qbiol, the 1st base (in 5′) is considered as the anchoring site attached to the surface via a strong elastic force. The position of the Fc head, assumed to correspond to the free 3′ end of the DNA, can be tracked every ∼1 ps, for periods of 10 μs, using an optimized code. This enables us to build two-dimensional heat maps, representing the distribution of the Fc head position above the electrode (more precisely above the thiol layer, ESI, Section 7†). Heat maps simulated for Fc-dT35, in its single- and double-stranded state, are shown in Fig. 6A and B, respectively.As expected, a “mushroom” – shaped distribution is found for ssDNA and a hemispherical distribution for the rigid, rod-like dsDNA. The instantaneous vertical position of Fc over the gold electrode interface, z(t), is of particular interest here and monitored throughout the simulation time. Fig. 7C and D show short samples of such time traces obtained for Fc-dT35 and Fc-(dT.dA)35, respectively. Numerous collisions of the Fc label with the electrode, defined by z < 1 Å, can be identified (blue and red circles). The average collision time 〈τc〉 is on the order of sub-ns for ssDNA and ns for dsDNA. Such very short collision times are due to the confinement of the Fc-head motion to the immediate vicinity of the electrode, within a nanometer-scale hemispherical region defined by the chain length. Similarly short collision times were obtained by White et al. from random walk simulations of the Brownian motion of a molecule confined to a hemispherical volume on an electrode.22
Most importantly, these collision times are several orders of magnitude shorter than the μs time scale one would predict from diffusion coefficients of the ss and dsDNA chains. This further supports our view on the motional dynamics of the Fc label being too fast to kinetically limit the electron transfer rate in anchored DNA layers, and validates the use of the TLC model.
Averaging the time traces enables ρ(z), the equilibrium probability of finding the Fc label at a distance z from the electrode surface, to be derived. ρ(z) vs. z profiles simulated for Fc-dTN chains of various lengths (N = 10–50) are shown in Fig. 6E and F for ss and ds DNA, respectively. The profiles obtained for ssDNA are almost ideally Gaussian-shaped, as expected for a one-dimensional elastic-diffusive motion,45 whereas they display a more complex shape for dsDNA. The probability of finding the Fc-label at the electrode surface, ρe = ρ (z = 0), is particularly relevant for interpreting CV experiments. Fig. 7 shows ρe values for different N.
For Fc-ssDNA, a clear 1/N variation of ρevs. N is seen, in agreement with the predictions of Plaxco et al. in their earlier work.19 More quantitatively, ρe is accurately given by ρe = 1/Lc, where Lc is the contour length of the ssDNA chain, counting 0.7 nm per base.46 Hence, as far as its presence probability at the electrode is concerned, the Fc head of Fc-ssDNA behaves similarly to a free species rapidly diffusing within a planar thin layer of thickness Lc. For Fc-dsDNA, a faster, approximately exponential decay of ρe with N is observed. These results illustrate that approaching the electrode is sterically “harder” for the Fc when the DNA strand is hybridized.
Discussion
Interpretation of the dependence of k0 on the DNA chain length (N), diluent length (n), and chain coverage (Γ)
In the framework of the MHL/TLC model used here, the rate of electron transfer is jointly modulated by the probability of the presence of the Fc head at the electron transfer site ρ(z), and by the rate of electron transfer between the redox probe and the electrode, kET(z). Both quantities depend on z, the distance between the Fc head and the electrode. Hence the overall electron transfer rate constant, k0, is given by integration over all transfer distances, from the distance of closest approach, set by the thickness of the alkyl thiol layer, d, to infinity: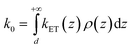 | (1) |
with a tunneling decay constant β ∼ 1 Å−1.
Eqn (1) can be a priori calculated exactly, knowing ρ(z) from the simulations. It can also be simplified by noting that ρ(z) varies much slower with z than kET(z), so that one can take ρ(z) ∼ ρ(z = 0), i.e. one can solely consider the presence probability of the Fc head at the electrode surface, noted as ρe. This yields:
| k0 = (kET(z = 0)/β)exp[−βd] × ρe = ksexp[−βd] × ρe = ksd × ρe | (2) |
Knowing ρe for any N value from our simulations, we fitted eqn (2) to the experimental k0vs. N variation for Fc-dTN, using ksd as a single adjustable parameter. The resulting best-fit curves, represented by red traces in Fig. 4A and inset, reproduce the experimental data very satisfyingly, with the best-fit value of ksd = (5.5 ± 0.5) × 10−3 cm s−1. This value is very close to the ksd value of (3 ± 0.5) × 10−3 cm s−1 we measured in solution for ferrocenedimethanol, a good model of the DNA Fc label, at an MCH-coated gold electrode (see Fig. S3†). Similarly, the experimental k0vs. N variation for Fc-(dT.dA)N duplexes could be reproduced on the basis of eqn (2), using ρe values simulated for the duplexed chains, and the best-fit value of ksd = (2.0 ± 0.5) × 10−3 cm s−1 (red trace in Fig. 4C and inset). These results are very strong evidence that the CV response of both the ss and ds Fc-DNA chains is controlled by the equilibrium presence probability of the Fc head at the surface, modulating the electron transfer rate.
Another test of the validity of the above formalism is brought by analyzing the experimental dependence of k0 on the thiol-alkyl diluent length. Fig. 5A and 6B show that, both for ss and dsDNA, k0 decayed exponentially with the diluent length (represented by n), as predicted by eqn (2). More quantitatively, linear regressions of the ln(k0) vs. n data yielded a slope of −0.95 ± 0.15 per CH2 unit, both for ss and dsDNA layers. This value is in good agreement with the decay length of ∼−1 ± 0.1 per CH2 characteristic of tunneling processes through alkyl thiols.47,48
Finally, the fact that k0 was observed to decrease as the surface coverage, Γ, was raised (Fig. S11–S13†) can simply be explained by the surface crowding lowering the presence probability of the Fc head at the electrode.
The above results evidence that the electron transfer rate through the diluent layer kinetically controls the CV response of end-anchored Fc-DNA chains.
Interpretation of the very low activation energy characterizing electron transfer of redox DNA
The unexpectedly low λ values measured here for ssDNA chains, and even more so for dsDNA chains, and their dependence on coverage, diluent, and chain length constitute an unprecedented finding for such systems. From a phenomenological point of view, such low λ values are found to be responsible for the decrease of the intensity of the CV signal of dsDNA at much lower scan rates than for ssDNA (Fig. 2), i.e. for the “extinction” phenomena we reported very early-on for the CV response of end-attached Fc-dsDNA chains.14,15Indeed, as illustrated here (ESI, Section 4†), the MHL/TLC model predicts that, only for sufficiently low values, one can obtain broad bell-shaped 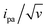 vs. v variations, within an experimentally attainable range of scan rates. Therefore, we suspect that the peak or plateau-shaped
vs. v variations, within an experimentally attainable range of scan rates. Therefore, we suspect that the peak or plateau-shaped 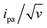 vs. v variations, or equivalently the proportionality between ipa and
vs. v variations, or equivalently the proportionality between ipa and 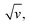 often reported in CV studies of end-attached DNA (or PNA) chains,15,18,21–24,49 actually reflect control of the electrochemical signal by the electron transfer rate associated with a low λ value, rather than by chain dynamics.
often reported in CV studies of end-attached DNA (or PNA) chains,15,18,21–24,49 actually reflect control of the electrochemical signal by the electron transfer rate associated with a low λ value, rather than by chain dynamics.
Our simulations can bring some insights into the reason why the attachment of the Fc head to a DNA chain, end-tethered to the surface, yields lower reorganization energies than typical redox species free in solution. Three hypotheses are proposed.
The first one is based on the observation that collision frequencies for Fc-DNA are much larger than what can be calculated for free Fc confined into a planar nanogap of a thickness comparable to the chain length, Lc. Indeed, in the latter case one would expect collision times in the order of 〈τc〉 ∼ Lc2/D = 100 ns, taking D = 10−5 cm2 s−1, and Lc ∼ 10 nm, i.e. a collision frequency two orders of magnitude lower than derived here for Fc-DNA.
Because of such a high collision frequency, it can be envisioned that the Fc head of DNA could, unlike free Fc, enter the Stern layer. The penetration of Fc in this electrostatic layer is to be understood in the framework of the collision theory, with Fc-DNA displacing adsorbed ions from the surface,50,51 and the displacement rate scales with the collision frequency. Within the Stern layer, the Fc head would experience a static dielectric constant, εs, lower than in the bulk and approaching the value of the optical dielectric constant, εopt = 1.78.52 The solvent reorganization energy (λ0) would consequently decrease, at the electrode, as it is given by:30
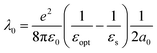 | (3) |
This effect would fall in line with the recent observation that redox molecules, immobilized on an electrode and close enough to the surface to be located within the electric double layer, display greatly decreased λ0 values.53
The total reorganization energy (λ) determined here, is the sum of the solvent (λ0) and internal (λi) reorganization energies: λ = λ0 + λi.
For ferrocene, λi was theoretically evaluated to ∼0.016 eV.54 Hence the above considerations would predict λ ∼ 0.058 + 0.016 = 0.074 eV, which is close to the minimum value we found here for Fc-ssDNA. In that framework, the increase of λ with the surface coverage (Fig. S11–S13†) could be explained by a decrease in the collision frequency due to chain crowding. The modest variation of λ with the chain length (Fig. 4B†) is also coherent with the weak dependence of the collision frequency with N as simulated (Fig. S4†). The expected independence of the collision frequency on the diluent length would also explain why λ was not found to be a function of n (Fig. 5B).
For Fc-dsDNA, the fact that we measured vanishingly small values of λ tends to show that λ0 was reduced to an even greater extent than for Fc-ssDNA, but also suggests that λi was reduced as well. This could be attributed to the rigidity of the dsDNA backbone and linker that limits the structural changes of the Fc head.55 Just like for ssDNA, the experimental increase of λ with Γ is compatible with a negative correlation of λ with the collision frequency. The increase of λ with N (Fig. 4D), and the fact that it is more pronounced than for ssDNA, parallel the simulated variation of the collision frequency with N (Fig. S4†).
The second hypothesis tentatively explaining the low λ values obtained for Fc-DNA is also based on a lower value of εs, but from a different origin, and is inspired by the studies of electrons transfer between redox centers in proteins. In these systems, low λ values have been reported and explained by the very slow relaxation of water due to the strong coupling of the redox species with slow parts of the system (here the coupling of Fc with DNA affecting water relaxation).56 Finally the Fc head may partly enter the hydrophobic layer formed by the alkyl chains of the diluent thiol, where εs is small. Future relevant work following the present study will include exploration of the temperature dependence of k0 and λ values, as well as other experiments. This will bring further insights on the microscopic mechanism of the electron transfer of Fc-DNA.
Conclusions
We have shown that the electrochemical response of short, end-attached redox DNA strands is controlled by the electron transfer rate between the redox label and the electrode. Thus, the CV behavior of Fc ss and ds DNA chains could be fully and quantitatively described by the MHL/TLC model with only two parameters: k0 and λ. Strikingly, the reorganization energy (λ) for the oxidation of the ferrocene label is markedly smaller than for the free ferrocene in solution. We developed a simulation package which reliably predicts the k0 value provided the ks value of the label is known, and can yield insights into the phenomena responsible for the lowering of the reorganization energy of the redox label.We also show that the modulation of the electrochemical response of redox DNA strands by hybridization can be fully explained by a variation of the k0 and λ parameters. Hybridization is associated with a decrease in the presence probability of the redox label in the vicinity of the electrode, lowering k0. More importantly, the formation of the DNA duplex also results in a marked decrease in the reorganization energy, which strongly alters the electrochemical response of the system. As such, this hitherto unsuspected phenomenon contributes significantly to the signaling mechanism of E-DNA sensors.
Author contributions
C. Demaille and N. Clément obtained the funding, supervised the project and designed the experiments. Z. Zheng conducted the CV characterizations and analyzed the results. A. Chovin designed the Mt/AFM-SECM setup and initial experiments, and trained Z. Zheng to conduct them. C. S. H. Kim provided scientific interactions on DNA nanoelectrochemistry and related simulations. C. Demaille, N. Clément and Z. Zheng co-wrote the paper with scientific interpretation and comments from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received financial support from the French “Agence Nationale de la Recherche” (ANR) through the “SIBI” project (ANR-19-CE42-0011-01).Notes and references
- A. A. Lubin and K. W. Plaxco, Acc. Chem. Res., 2010, 43, 496–505 CrossRef CAS.
- Y. Du and S. Dong, Anal. Chem., 2017, 89, 189–215 CrossRef CAS PubMed.
- E. E. Ferapontova, Annu. Rev. Anal. Chem., 2018, 11, 197–218 CrossRef CAS PubMed.
- S. Ranallo, A. Porchetta and F. Ricci, Anal. Chem., 2019, 91, 44–59 CrossRef CAS PubMed.
- M. A. Pellitero, A. Shaver and N. Arroyo-Currás, J. Electrochem. Soc., 2020, 167, 037529 CrossRef CAS.
- N. Arroyo-Currás, J. Somerson, P. A. Vieira, K. L. Ploense, T. E. Kippin and K. W. Plaxco, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 645–650 CrossRef PubMed.
- Y. Xiao, A. A. Lubin, A. J. Heeger and K. W. Plaxco, Angew. Chem., Int. Ed., 2005, 44, 5456–5459 CrossRef CAS PubMed.
- H. Yousefi, A. Mahmud, D. Chang, J. Das, S. Gomis, J. B. Chen, H. Wang, T. Been, L. Yip, E. Coomes, Z. Li, S. Mubareka, A. Mcgeer, N. Christie, S. Gray-Owen, A. Cochrane, J. M. Rini, E. H. Sargent and S. O. Kelley, J. Am. Chem. Soc., 2021, 143, 1722–1727 CrossRef CAS PubMed.
- J. Liu, H. Zhou, J. J. Xu and H. Y. Chen, Chem. Commun., 2011, 47, 4388–4390 RSC.
- S. Li, Y. Coffinier, C. Lagadec, F. Cleri, K. Nishiguchi, A. Fujiwara, T. Fujii, S.-H. Kim and N. Clément, Biosens. Bioelectron., 2022, 216, 114643 CrossRef CAS PubMed.
- A. A. Gorodetsky, O. Green, E. Yavin and J. K. Barton, Bioconjugate Chem., 2007, 18, 1434–1441 CrossRef CAS PubMed.
- N. K. Gupta, E. A. Wilkinson, S. K. Karuppannan, L. Bailey, A. Vilan, Z. Zhang, D. C. Qi, A. Tadich, E. M. Tuite, A. R. Pike, J. H. R. Tucker and C. A. Nijhuis, J. Am. Chem. Soc., 2021, 143, 20309–20319 CrossRef CAS PubMed.
- E. Wierzbinski, A. De Leon, X. Yin, A. Balaeff, K. L. Davis, S. Reppireddy, R. Venkatramani, S. Keinan, D. H. Ly, M. Madrid, D. N. Beratan, C. Achim and D. H. Waldeck, J. Am. Chem. Soc., 2012, 134, 9335–9342 CrossRef CAS PubMed.
- A. Anne, A. Bouchardon and J. Moiroux, J. Am. Chem. Soc., 2003, 125, 1112–1113 CrossRef CAS PubMed.
- A. Anne and C. Demaille, J. Am. Chem. Soc., 2006, 128, 542–557 CrossRef CAS PubMed.
- J. S. Swensen, Y. Xiao, B. S. Ferguson, A. A. Lubin, R. Y. Lai, A. J. Heeger, K. W. Plaxco and H. T. Soh, J. Am. Chem. Soc., 2009, 131, 4262–4266 CrossRef CAS PubMed.
- T. Uzawa, R. R. Cheng, R. J. White, D. E. Makarov and K. W. Plaxco, J. Am. Chem. Soc., 2010, 132, 16120–16126 CrossRef CAS PubMed.
- A. Abi and E. E. Ferapontova, J. Am. Chem. Soc., 2012, 134, 14499–14507 CrossRef CAS PubMed.
- P. Dauphin-Ducharme, N. Arroyo-Currás, R. Adhikari, J. Somerson, G. Ortega, D. E. Makarov and K. W. Plaxco, J. Phys. Chem. C, 2018, 122, 21441–21448 CrossRef CAS.
- P. Dauphin-Ducharme, N. Arroyo-Currás and K. W. Plaxco, J. Am. Chem. Soc., 2019, 141, 1304–1311 CrossRef CAS PubMed.
- E. Farjami, R. Campos and E. E. Ferapontova, Langmuir, 2012, 28, 16218–16226 CrossRef CAS PubMed.
- K. C. Huang and R. J. White, J. Am. Chem. Soc., 2013, 135, 12808–12817 CrossRef CAS PubMed.
- N. Hüsken, M. Gębala, F. La Mantia, W. Schuhmann and N. Metzler-Nolte, Chem.–Eur. J., 2011, 17, 9678–9690 CrossRef PubMed.
- A. Anne and C. Demaille, J. Am. Chem. Soc., 2008, 130, 9812–9823 CrossRef CAS PubMed.
- N. C. Stellwagen, S. Magnusdottir, C. Gelfi and P. G. Righetti, Biopolymers, 2001, 58, 390–397 CrossRef CAS PubMed.
- A. Ortega and J. Garcia De La Torre, J. Chem. Phys., 2003, 119, 9914–9919 CrossRef CAS.
- A. Langer, W. Kaiser, M. Svejda, P. Schwertler and U. Rant, J. Phys. Chem. B, 2014, 118, 597–607 CrossRef CAS PubMed.
- U. Rant, K. Arinaga, M. Tornow, W. K. Yong, R. R. Netz, S. Fujita, N. Yokoyama and G. Abstreiter, Biophys. J., 2006, 90, 3666–3671 CrossRef CAS PubMed.
- B. E. K. Snodin, F. Randisi, M. Mosayebi, P. Šulc, J. S. Schreck, F. Romano, T. E. Ouldridge, R. Tsukanov, E. Nir, A. A. Louis and J. P. K. Doye, J. Chem. Phys., 2015, 142, 234901 CrossRef PubMed.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- C. E. D. Chidsey, Science, 1991, 251, 919–922 CrossRef CAS PubMed.
- J.-M. Savéant, J. Phys. Chem. B, 2002, 106, 9387–9395 CrossRef.
- R. Levicky, T. M. Herne, M. J. Tarlov and S. K. Satija, J. Am. Chem. Soc., 1998, 120, 9787–9792 CrossRef CAS.
- A. Meunier, E. Triffaux, D. Bizzotto, C. Buess-Herman and T. Doneux, ChemElectroChem, 2015, 2, 434–442 CrossRef CAS.
- T. Doneux, A. De Rache, E. Triffaux, A. Meunier, M. Steichen and C. Buess-Herman, ChemElectroChem, 2014, 1, 147–157 CrossRef.
- W. Kaiser and U. Rant, J. Am. Chem. Soc., 2010, 132, 7935–7945 CrossRef CAS PubMed.
- D. Ge and R. Levicky, Chem. Commun., 2010, 46, 7190–7192 RSC.
- A. T. Hubbard and F. C. Anson, in Electroanalaytical Chemistry: A Series of Advances, 1970, pp. 129–214 Search PubMed.
- E. Laviron, J. Electroanal. Chem., 1979, 101, 19–28 CrossRef CAS.
- K. Weber and S. E. Creager, Anal. Chem., 1994, 66, 3164–3172 CrossRef CAS.
- T. M. Nahir, R. A. Clark and E. F. Bowden, Anal. Chem., 1994, 66, 2595–2598 CrossRef CAS.
- W. Yang and R. Y. Lai, Analyst, 2011, 136, 134–139 RSC.
- F. Ricci, N. Zari, F. Caprio, S. Recine, A. Amine, D. Moscone, G. Palleschi and K. W. Plaxco, Bioelectrochemistry, 2009, 76, 208–213 CrossRef CAS PubMed.
- J. Das, S. Gomis, J. B. Chen, H. Yousefi, S. Ahmed, A. Mahmud, W. Zhou, E. H. Sargent and S. O. Kelley, Nat. Chem., 2021, 13, 428–434 CrossRef CAS PubMed.
- A. Anne, C. Demaille and J. Moiroux, J. Am. Chem. Soc., 1999, 121, 10379–10388 CrossRef CAS.
- Q. Chi, G. Wang and J. Jiang, Phys. A, 2013, 392, 1072–1079 CrossRef CAS.
- H. O. Finklea and D. D. Hanshew, J. Am. Chem. Soc., 1992, 114, 3173–3181 CrossRef CAS.
- K. Slowinski, K. U. Slowinska and M. Majda, J. Phys. Chem. B, 1999, 103, 8544–8551 CrossRef CAS.
- N. Hüsken, M. Gębala, A. Battistel, F. La Mantia, W. Schuhmann and N. Metzler-Nolte, ChemPhysChem, 2012, 13, 131–139 CrossRef PubMed.
- D. Horinek and R. R. Netz, Phys. Rev. Lett., 2007, 99, 226104 CrossRef PubMed.
- R. Sivakumarasamy, R. Hartkamp, B. Siboulet, J. F. Dufrêche, K. Nishiguchi, A. Fujiwara and N. Clément, Nat. Mater., 2018, 17, 464–470 CrossRef CAS PubMed.
- D. J. Bonthuis, S. Gekle and R. R. Netz, Phys. Rev. Lett., 2011, 107, 166102 CrossRef PubMed.
- R. E. Bangle, J. Schneider, D. T. Conroy, B. M. Aramburu-Trošelj and G. J. Meyer, J. Am. Chem. Soc., 2020, 142, 14940–14946 CrossRef CAS.
- A. Paul, R. Borrelli, H. Bouyanfif, S. Gottis and F. Sauvage, ACS Omega, 2019, 4, 14780–14789 CrossRef CAS PubMed.
- H. B. Gray, B. G. Malmström and R. J. P. Williams, J. Biol. Inorg. Chem., 2000, 5, 551–559 CrossRef CAS PubMed.
- D. R. Martin and D. V. Matyushov, J. Chem. Phys., 2015, 142, 161101 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Material and methods, supporting discussions, and supporting figures. See DOI: https://doi.org/10.1039/d3sc00320e |
| This journal is © The Royal Society of Chemistry 2023 |