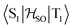Open Access Article
Open Access ArticleGold(I)-containing light-emitting molecules with an inverted singlet–triplet gap†
Daniel
Blasco
 ab,
Rinat T.
Nasibullin
c,
Rashid R.
Valiev
a and
Dage
Sundholm
ab,
Rinat T.
Nasibullin
c,
Rashid R.
Valiev
a and
Dage
Sundholm
 *a
*a
aDepartment of Chemistry, Faculty of Science, University of Helsinki, P.O. Box 55, (A.I. Virtasen Aukio 1), FIN-00014, Finland. E-mail: dage.sundholm@helsinki.fi
bDepartamento de Química, Centro de Investigación en Síntesis Química (CISQ), Universidad de La Rioja, Madre de Dios 53, 26006, Logroño, Spain
cTomsk State University, Lenin Avenue 36, 634050, Tomsk, Russian Federation
First published on 20th March 2023
Abstract
Delayed fluorescence from molecules with an inverted singlet–triplet gap (DFIST) is the consequence of the unusual reverse order of the lowest excited singlet (S1) and triplet (T1) states of thermally activated delayed fluorescence (TADF) emitters. Heptazine (1,3,4,6,7,9,9b-heptaazaphenalene) derivatives have an inverted singlet–triplet gap thanks to the combination of multiple resonance (MR) effects and a significant double excitation character. Here, we study computationally the effect of gold(I) metalation and coordination on the optical properties of heptazine (molecule 4) and the phosphine-functionalized 2,5,8-tris(dimethylphosphino)heptazine derivatives (molecules 1–3). Ab initio calculations at the approximate second-order coupled cluster (CC2) and extended multiconfigurational quasi degenerate perturbation theory at the second order (XMC-QDPT2) levels show that molecules 1–4 have an inverted singlet–triplet gap due to the alternating spatial localization of the electron and hole of the exciton in the heptazine core. A non-vanishing one-electron spin–orbit coupling operator matrix element between T1 and 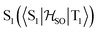 and a fast S1 ← T1 intersystem crossing rate constant (kISC) calculated at the XMC-QDPT2(12,12) level of theory for molecule 4 suggest that this new family of complexes may be the first organometallic DFIST emitters reported.
and a fast S1 ← T1 intersystem crossing rate constant (kISC) calculated at the XMC-QDPT2(12,12) level of theory for molecule 4 suggest that this new family of complexes may be the first organometallic DFIST emitters reported.
1 Introduction
In the long-standing quest for finding the most efficient photoluminescent and/or electroluminescent materials for large-scale production of organic light-emitting diodes (OLEDs), the discovery of thermally activated delayed fluorescence (TADF) emitters was a breakthrough. TADF leads to a significant increase in the spin-statistics-limited quantum yield of fluorescence without introducing practical issues associated with long-lived phosphorescing states.1–5The delayed fluorescence depends on the relative energies of the lowest excited singlet (S1) and triplet (T1) states, among other factors. Thus, the lowest singlet and triplet states must be close enough to enable singlet-exciton population from the lower triplet state by a thermally prompted reverse intersystem crossing (RISC) process. The energies of the S1 and T1 states can be almost equal when the frontier molecular orbitals (HOMO and LUMO) are spatially separated. According to the simplified two-state model of TADF, the energy gap between S1 and T1 (ΔEST) is equal to half the exchange integral between the frontier orbitals (KHL).6 However, this only holds up to a certain limit, since the oscillator strength of the vertical transition also depends on the HOMO–LUMO overlap implying that a wide spatial separation of them leads to a vanishing oscillator strength. A conceptually simple approach to design TADF emitters is to combine donor (D) and acceptor (A) fragments into a suitable scaffold, which could be an organic framework or a transition metal (TM) complex. Heavier TM complexes have advantages over pure organic molecules, since they have a more relaxed spin-selection rule thanks to the spin–orbit coupling (SOC) effect.
We are here particularly interested in gold(I)-containing TADF luminophores. Our previous experience in the field7,8 suggests that gold(I) has certain properties that justify our choice. These are: (i) its tendency towards linear dicoordination that imprints structural rigidity to the complex that minimizes non-radiative deactivation pathways, (ii) the possibility of fine-tuning the emission energy by considering subtle factors, and (iii) the chemical inertness of the complexes that makes them ideal for applications.
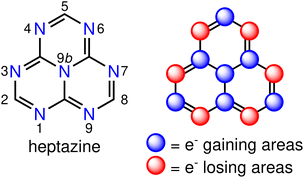
There is a growing interest in experimental and computational studies of the energy order of S1 and T1 (ΔEST < 0) in nitrogen- and/or boron-doped derivatives of the phenalenyl diradical,9–25 that violates Hund's spin-multiplicity rule.26 In such an unusual situation, reverse intersystem crossing (RISC) is a downhill process, which is expected to increase the quantum yield of fluorescence with respect to state-of-the-art TADF emitters. This phenomenon is termed as delayed fluorescence from inverted singlet–triplet gaps (DFIST)24 and the molecules displaying it are called INVEST molecules.11,12,17,25 Although the origin of the singlet–triplet inversion is still not fully understood, it is known that contributions from doubly-excited configurations increase the spatial separation of the frontier orbitals,22 which explains the stabilisation of S1 with respect to T1 and the inability of computational methods like time-dependent density functional theory (TD-DFT) or configuration interaction singles (CIS) to predict the inverted gap. The correct energy ordering of the S1 and T1 states of INVEST molecules can be obtained by using correlated wavefunction-based methods that include double excitations, such as approximate second-order coupled cluster (CC2),11,13,14,22,23 algebraic diagrammatic construction of second order (ADC(2)),11,13–15,18,22 equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) aka linear-response CCSD,11,24 state-averaged complete active space self-consistent field (SA-CASSCF),13,14,22,23 CASSCF second-order perturbation theory (CASPT2),11,22 and strongly contracted N-electron valence state second-order perturbation theory (SC-NEVPT2) methods,13,14,23 to mention the most commonly used ones. A representative example of INVEST molecules is heptazine (1,3,4,6,7,9,9b-heptaazaphenalene, Fig. 1, left), which is a member of the cyclazine (9b-azaphenalene) series composed by fusing three triazine (1,3,5-triazabenzene) rings in a D3h fashion. Optical excitation leads to a well-defined pattern of charge transfers between neighbouring atomic sites, which is called the multiple resonance (MR) effect (Fig. 1, right).5 MR-based emitters are more attractive for use in OLEDs than DA-based ones, since the former ones can be derived from highly constrained aromatic polycycles with small structural distortions of the excited states leading to narrow emission bands and small Stokes shifts.5
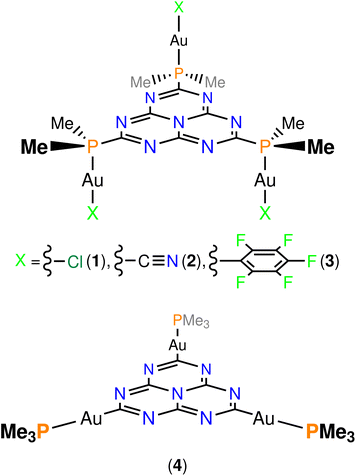
As far as we know, no-one has previously taken advantage of the MR effect in gold(I)-containing emitters for obtaining DFIST emission from gold(I) luminophores. Here, we perform the first in silico study of gold(I) complexes with an inverted singlet–triplet gap. After a careful examination of the existing bibliography on molecular heptazine chemistry and considering the pronounced tendency of gold(I) centres to coordinate to soft donor atoms (e.g. sulphur, phosphorus), we propose an analog to the previously reported 2,5,8-tris(diphenylphosphino)heptazine,27 namely, 2,5,8-tris(dimethylphosphino)heptazine for stabilizing the model compounds. The computational efforts are reduced by replacing the phenyl groups with methyl ones. The linear coordination environment of gold(I) is completed with the usual anionic ligands for preserving the electroneutrality of the final molecules. We have constructed three molecules where neutral [AuIX] (X = Cl (1), CN (2), C6F5 (3); Fig. 2, top) fragments are coordinated to the lone pair of the phosphorus atoms of the pending dimethylphosphino moieties. Also, the metalation of the corners of heptazine with cationic [AuI(PMe3)]+ fragments has been considered (molecule 4; Fig. 2, bottom). When the isolobal analogy between [AuL]+ (L = neutral, two electron donor ligand) fragments and H+ is considered,28 one obtains molecule 4, which is an isolobal analogue of heptazine with an increased SOC effect due to the presence of the heavy atoms. We have used DFT and ab initio correlated methods in calculations of the energy of the lowest excited states and in calculations of intersystem crossing (ISC) rate constants (kISC).
2 Computational details
Molecules 1–4 were built from scratch and optimized at the RI-DFT/PBE0-D3(BJ) level of theory29–37 with def2-TZVP basis sets38 on all atoms and a 60-electron effective core potential (def2-ECP)39 for gold. As the initial consideration of three-fold-axis containing point groups C3h or C3 led to saddle points on the potential energy surface, this high symmetry was broken by manually tilting the substituents in the corners of heptazine. The calculations were carried out using TURBOMOLE version 7.5.1.40,41 Further optimization at the same level of theory without symmetry constraints led to C1 (1,4) or Cs (2,3) structures that were verified as true minima by computing analytically the vibrational frequencies using the aoforce module of TURBOMOLE.42 The optimized molecular structures were used in TD-DFT/def2-TZVP38,43–47 calculations using the PBE0 (ref. 35–37) and ωB97X-D48 functionals as well as in CC2/def2-TZVP38,49–51 calculations of the first vertical singlet and triplet excitation energies of the irreducible representations a for 1,4 or a′ and a′′ for 2,3. The singlet–triplet gaps have been calculated as ΔEST = E(S1 ← S0) − E(T1 ← S0). The exciton surfaces were computed from the relaxed electron densities of the excited and ground states and calculated as Δρe = ρe(XS) − ρe(GS) (XS, excited state; GS, ground state). The optimized molecular structures, orbitals and exciton surfaces were visualized and rendered using the latest version of UCSF ChimeraX.52 The first excited singlet and triplet state structures of molecule 4 were optimized at the TD-DFT/PBE0-D3(BJ)/def2-TZVP level of theory43,53–55 and verified as true minima by computing numerically the vibrational frequencies with the NumForce module of TURBOMOLE. Since the free rotation of the Au–P bonds made it impossible to obtain a minimum (one small vibrational frequency always remained imaginary), the excited state structures were constrained to the C3 point group. All attempts to optimize the excited state structures of molecules 1–3 at the same level of theory as for molecule 4 were unsuccessful. More accurate excitation energies were obtained using the SA-CASSCF method with 12 active electrons and 12 orbitals in the active space, and a modified version of the XMC-QDPT2 method56 as implemented in the Firefly quantum chemistry package.57 The matrix element of the one-electron spin–orbit coupling operator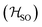 between the T1 and S1 states
between the T1 and S1 states 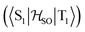 was calculated at the TD-DFT/PBE0/def2-TZVP level using MolSOC,58 at the TD-DFT/PBE0/def2-TZVP level in the zeroth-order regular approximation (ZORA)59 using ORCA,60 and at the multiconfiguration self-consistent-field (MCSCF) level using GAMESS-US.61 Since TD-DFT is not able to properly describe the singlet–triplet gap inversion, the energies of S1 and T1 were manually swapped when calculating the ISC rate constant (kISC) at the DFT level. The kISC rate constant (in s−1) for the transition S1 ← T1 was calculated using
was calculated at the TD-DFT/PBE0/def2-TZVP level using MolSOC,58 at the TD-DFT/PBE0/def2-TZVP level in the zeroth-order regular approximation (ZORA)59 using ORCA,60 and at the multiconfiguration self-consistent-field (MCSCF) level using GAMESS-US.61 Since TD-DFT is not able to properly describe the singlet–triplet gap inversion, the energies of S1 and T1 were manually swapped when calculating the ISC rate constant (kISC) at the DFT level. The kISC rate constant (in s−1) for the transition S1 ← T1 was calculated using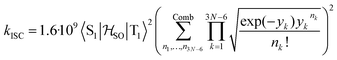 | (1) |
3 Results and discussion
3.1 Structure optimization
The minimum-energy structures of 1–3 belong to or are close to the Cs point group (see Fig. S1†). Their molecular structures resemble that of the X-ray crystal structure of 2,5,8-tris(diphenylphosphino)heptazine, where the electron lone pair of one of the three diphenylphosphino substituents points to the opposite side of the molecular plane.27 A summary of the most relevant bond distances and angles of 1–4 and a comparison with those of related structures can be found in Table S1 in the ESI.† All distances are virtually identical to those determined by others for heptazine63 and 2,4,6-tris(diphenylphosphino)heptazine,27 thus validating 1–4 as reasonable models of realistic molecules.3.2 Time-dependent density functional theory calculations
Calculations at the TD-DFT levels of theory have repeatedly failed to reproduce the correct order of the lowest-lying excited states of INVEST molecules since they do not explicitly consider double excitations.11–14 However, it is undeniable that TD-DFT provides a reasonable balance between computational cost and accuracy for applications in inorganic chemistry. Also, no previous study examining the ability of TD-DFT to predict the singlet–triplet gap inversion has dealt with heavy metal-containing molecules. Therefore, we have examined the performance of TD-DFT with two functionals, namely, PBE0 and ωB97X-D. The ωB97X-D functional introduces a long-range correction with 100% Hartree–Fock exchange (Exc[ρe]) that corrects the overestimation of the charge transfer of TD-DFT calculations, which is mandatory for addressing TADF and DFIST. Table 1 shows the lowest-energy excitation energies of the singlet and triplet manifolds of 1–4 that are obtained with the two functionals. A complete version including all irreducible representations and orbital contributions can be found in the ESI.†| Molecule | Irrepa | E(S1 ← S0) (f × 104) | E(T1 ← S0) | ΔEST |
|---|---|---|---|---|
| a Irreducible representation. | ||||
| PBE0 functional | ||||
| 1 | a′′ | 2.702 (0.200) | 2.652 | +0.050 |
| 2 | a′′ | 3.000 (3.502) | 2.760 | +0.240 |
| 3 | a | 2.281 (0.125) | 2.278 | +0.003 |
| 4 | a | 2.951 (0.005) | 2.736 | +0.215 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| ωB97X-D functional | ||||
| 1 | a′′ | 3.174 (0.509) | 2.934 | +0.240 |
| 2 | a′′ | 3.171 (0.447) | 2.928 | +0.243 |
| 3 | a | 3.187 (0.160) | 2.948 | +0.239 |
| 4 | a | 3.173 (0.002) | 2.956 | +0.217 |
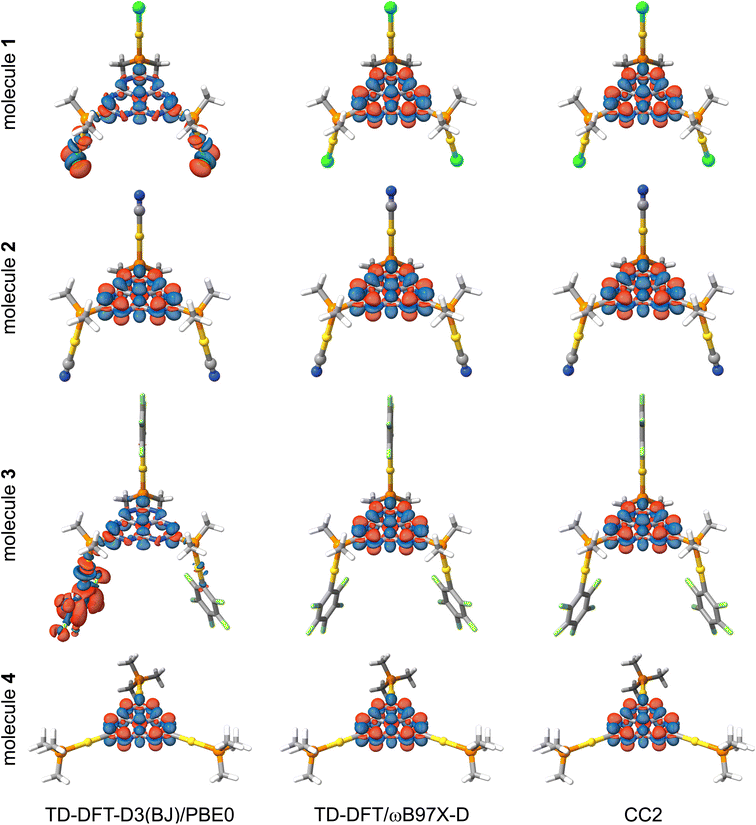
The positive ΔEST value implies that the first excited triplet state is energetically below its singlet counterpart, which is expected from previous TD-DFT calculations on INVEST molecules. The small ΔEST values can be understood from the small overlap of the frontier orbitals and the spatially localized exciton density. The ΔEST energy depends strongly on the functional for 1 (X = Cl) and 3 (X = C6F5). We only discuss the excitation character and energy levels of 1, since the same reasoning also holds for 3. Fig. 3 shows the calculated exciton densities (Δρe) of the first singlet-to-singlet excitation of 1–4. The exciton density of the first singlet-to-triplet excitation has the same shape with slightly different amplitudes. The PBE0 calculations suggest that the exciton density at the (chlorido)gold(I) fragments originates from the HOMO and HOMO-2 orbitals, whereas the LUMO contribution is fully delocalized over the heptazine core and it displays the alternating structure that has previous been obtained for heptazine. Thus, the excitation has a mixture of metal-to-ligand and ligand-to-ligand charge transfers (1MLCT + 1LLCT). However, the exciton density obtained at the ωB97X-D level is completely different and very similar to the MR excitation pattern of unsubstituted heptazine (Fig. 1, right). The exciton density calculated with ωB97X-D functional suggests that it is an intraligand charge transfer (1IL). Although the ΔEST gap calculated with the two functionals is unsatisfactory for addressing DFIST, the long-range correction to the Exc[ρe] energy obtained with the ωB97X-D functional leads to a similar exciton density as obtained at the CC2 level. The oscillator strengths (f) are small but non-vanishing thanks to the loss of the centro-symmetry of the heptazine core. Since previous studies concluded that RISC may occur when ΔEST is close to 1000 cm−1 (approx. 0.12 eV),64 the TD-DFT calculations suggest that 1–4 are likely candidates for displaying TADF.
We have also estimated ΔEST using the ΔSCF method.65–71 Previously, we showed that ΔSCF calculations at the DFT level of theory predict singlet–triplet inversion of heptazine and five other related INVEST molecules.22 However, the SCF wavefunctions of the S1 state suffer from severe spin contamination (ŝ2 > 1), and ΔEST depends heavily on the employed functional. Similar problems arose for the molecules studied here. ΔSCF calculations can be easily performed for symmetric molecules whose dominating excitation occurs between different irreducible representations, which ensures orthogonality between the ground and excited state. Therefore, we report ΔSCF energies only for molecules 1–3 belonging to the Cs point group. Molecule 3 belonging to C1 was constrained to the Cs point group for this purpose. The excitation energies and the singlet–triplet gaps are given in Table 2. The expectation values of ŝ2 are given in Table S4 of the ESI.† The ΔSCF approach predicts the correct ordering of the lowest excited singlet and triplet states and a negative ΔEST for the three molecules, regardless of the employed functional. However, the calculated ΔEST values do not agree well with those obtained at higher ab initio levels of theory (vide infra). Also, the energy gap calculated with the ωB97X-D functional is about twice the size of that obtained with the PBE0 functional. The large spin-contamination of the S1 state raises doubts about the accuracy of the ΔSCF method. It provides the correct qualitative description of the studied INVEST molecules, whereas it is not reliable enough for providing quantitative data.
3.3 Approximate second order coupled cluster calculations
Previous studies suggested that second-order coupled-cluster levels are the method of choice for describing DFIST because of their excellent trade-off between the correct energy ordering of S1 and T1 states and their cost effectiveness.11,13–15,18,22,23 We have computed the first singlet-to-singlet and singlet-to-triplet vertical excitation energies of 1–4 at the CC2/def2-TZVP level of theory. The computational requirements of CC2 calculations are still manageable even though the studied molecules contain three gold atoms. The obtained vertical excitation energies and relative contributions of doubly excited configurations are given in Table 3.In contrast to TD-DFT, CC2 calculations yield negative (meaning that S1 is lower in energy than T1) and similar ΔEST for the four molecules. The ΔEST values are −0.1 to −0.2 eV, which is in agreement with those reported in the literature for unsubstituted heptazine. Similar energies levels are obtained for the studied molecules because their exciton densities in Fig. 3 are very similar to that of unsubstituted heptazine (Fig. 1, right). The exciton density has the same pattern with local MR charge transfer from the peripheral nitrogen atoms to the carbon atoms and central nitrogen atom. The contribution from the gold(I) ligands to the excited states is negligible, precluding any possible emission tuning by simply changing the ligands attached to the metal. Extreme σ-donor or π-acceptor ligands are needed for perturbing the robust electronic structure of heptazine. However, since the introduction of such ligands is expected to shift the electron and hole of the exciton density towards them, it will be detrimental for MR-based DFIST. The contribution from double excitations to the S1 and T1 states is large (>10%). However, we recently proposed that the ca 1%-higher percentage of doubles in S1 is the reason for its energy stabilization with respect to the T1 state.22
3.4 Rate constant calculations
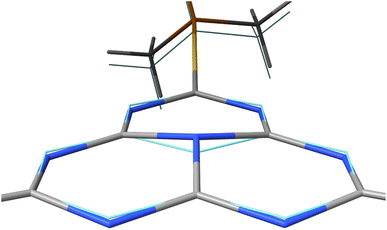
In the first excited singlet and triplet states of molecule 4, the central nitrogen atom lies above the plane and the peripheral nitrogen atoms of the heptazine core are below the plane (Fig. 4), whereas the rest of the molecule remains unperturbed by the excitation. The alternating distortion of the heptazine core may be related to the localization of the electron and hole of the exciton density. The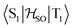 matrix element of 4 was calculated at the TD-DFT/PBE0-D3(BJ)/def2-TZVP and XMC-QDPT2(12,12)/def2-TZVP levels of theory. The scalar relativistic effects were also included by means of the zeroth-order regular approximation (ZORA) at the TD-DFT/PBE0 level. The XMC-QDPT2(12,12) perturbation theory calculations were based on the SA-CASSCF(12,12) wavefunction. The three computational levels were subsequently employed in calculations of the kISC rate constant for S1 ← T1 transition as described in the computational details section. The results are collected in Table 4. The calculated
matrix element of 4 was calculated at the TD-DFT/PBE0-D3(BJ)/def2-TZVP and XMC-QDPT2(12,12)/def2-TZVP levels of theory. The scalar relativistic effects were also included by means of the zeroth-order regular approximation (ZORA) at the TD-DFT/PBE0 level. The XMC-QDPT2(12,12) perturbation theory calculations were based on the SA-CASSCF(12,12) wavefunction. The three computational levels were subsequently employed in calculations of the kISC rate constant for S1 ← T1 transition as described in the computational details section. The results are collected in Table 4. The calculated 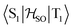 matrix element is 1.0 cm−1 and 0.8 cm−1 at the DFT and MCSCF levels, respectively, showing that the heavy-atom effect of gold(I) promotes an effective ISC enabling singlet-exciton population from the triplet state. We obtained a kISC rate constant for the S1 ← T1 transition of 4 × 108 s−1 or 7 × 107 s−1, indicating that the process is fast. At the TD-DFT/PBE0/ZORA/def2-TZVP level, the
matrix element is 1.0 cm−1 and 0.8 cm−1 at the DFT and MCSCF levels, respectively, showing that the heavy-atom effect of gold(I) promotes an effective ISC enabling singlet-exciton population from the triplet state. We obtained a kISC rate constant for the S1 ← T1 transition of 4 × 108 s−1 or 7 × 107 s−1, indicating that the process is fast. At the TD-DFT/PBE0/ZORA/def2-TZVP level, the 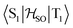 matrix element is 0.2 cm−1 leading to a kISC of 9 × 106 s−1.
matrix element is 0.2 cm−1 leading to a kISC of 9 × 106 s−1.
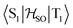 in cm−1) for molecule 4 calculated at the TD-DFT/PBE0-D3(BJ)/def2-TZVP, TD-DFT/PBE0/ZORA/def2-TZVP, and XMC-QDPT2(12,12)/def2-TZVP levels of theory
in cm−1) for molecule 4 calculated at the TD-DFT/PBE0-D3(BJ)/def2-TZVP, TD-DFT/PBE0/ZORA/def2-TZVP, and XMC-QDPT2(12,12)/def2-TZVP levels of theory
| Level of theory | E(S1 ← S0) | E(T1 ← S0) | ΔEST | k ISC | |
|---|---|---|---|---|---|
| a Since TD-DFT does not predict inversion of the singlet–triplet gap, the energies of the S1 and T1 states were manually swapped. | |||||
| TD-DFT/PBE0-D3(BJ) | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
+1215 | 4 × 108,a | 1.0 |
| TD-DFT/PBE0/ZORA | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
7860 | +1248 | 9 × 106,a | 0.2 |
| XMC-QDPT2(12,12) | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
−2300 | 7 × 107 | 0.8 |
The SOC matrix element of 0.2–1.0 cm−1 is small because the exciton is located on the heptazine moiety, whereas the gold atoms are rather far away from the exciton. The SOC matrix element also vanishes for unsubstituted heptazine for symmetry reasons, since its molecular structure belongs to the D3h point group. Even though the SOC matrix element is small, the rate for the intersystem crossing from T1 to S1 is faster than other deactivation channels of T1 leading to the desired population of the S1 state from T1.
TD-DFT calculations yield the incorrect order of the lowest excited singlet and triplet states as compared to correlated ab initio calculations. In the calculation of the kISC rate constant at the DFT level, the energies of the S1 and T1 states were swapped. Since the energy difference is slightly smaller at the TD-DFT level than at the CC2 and XMC-QDPT2(12,12) levels, the rate constant estimated at the TD-DFT level is a factor of 6 larger than the one calculated at the XMC-QDPT2(12,12) level. The excitation energy of −1573 cm−1 at the CC2 level is expected to yield a rate constant that is somewhere between the ones calculated at the TD-DFT and XMC-QDPT2(12,12) levels.
4 Conclusions
We propose substitution with gold(I)-containing moieties to 2,4,6-tris(dimethylphosphino)heptazine (1–3) and heptazine (4) as a means for obtaining bright organometallic DFIST emitters because they have non-vanishing oscillator strengths and spin–orbit coupling leading to fast intersystem crossing. The coordination or metalation with gold(I) does not significantly perturb the composition and spatial localization of the first excited states of heptazine. The inverted ΔEST values calculated at the correlated wavefunction CC2 and XMC-QDPT2 levels of theory are close to the inverted singlet–triplet gap of unsubstituted heptazine. The electron donor/acceptor nature of the gold(I) ligands is apparently irrelevant for the emission process, since the calculated excitation energies and ΔEST values are almost the same for the four studied molecules. Our computational study suggests that these complexes could be efficient DFIST emitters. Future synthetic and experimental studies on this exciting new family of gold(I)-containing complexes will be presented by us elsewhere in due time.Data availability
The cartesian coordinates of molecules 1–4 and additional data supporting this article have been uploaded as part of the ESI material.†Author contributions
DB did the calculations at the DFT, TD-DFT and CC2 levels of theory. RTN and RRV did the calculations at the SA-CASSCF and XMC-QDPT2 levels of theory. DB and DS wrote the first version of the manuscript. All authors contributed to the writing of the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research has been supported by The Academy of Finland through projects 340584 and 340583. The authors acknowledge CSC – IT Center for Science, Finland for computational resources. DB acknowledges Universidad de La Rioja for the concession of a Margarita Salas Post-Doc Scholarship financed by the Spanish Ministerio de Universidades and the European Union-NextGenerationEU program.References
- A. Endo, M. Ogasawara, A. Takahashi, D. Yokoyama, Y. Kato and C. Adachi, Adv. Mater., 2009, 21, 4802–4806 CrossRef CAS PubMed
.
- A. Endo, K. Sato, K. Yoshimura, T. Kai, A. Kawada, H. Miyazaki and C. Adachi, Appl. Phys. Lett., 2011, 98, 42 CrossRef
.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed
.
- K. Goushi, K. Yoshida, K. Sato and C. Adachi, Nat. Photonics, 2012, 6, 253–258 CrossRef CAS
.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Adv. Mater., 2016, 28, 2777–2781 CrossRef CAS PubMed
.
- P. de Silva, C. A. Kim, T. Zhu and T. Van Voorhis, Chem. Mater., 2019, 31, 6995–7006 CrossRef CAS
.
- J. M. López-de-Luzuriaga, M. Monge, M. E. Olmos, M. Rodríguez-Castillo, I. Soldevilla, D. Sundholm and R. R. Valiev, Inorg. Chem., 2020, 59, 14236–14244 CrossRef PubMed
.
- I. Soldevilla, A. García-Camacho, R. T. Nasibullin, M. E. Olmos, M. Monge, D. Sundholm, R. R. Valiev, J. M. López-de-Luzuriaga and M. Rodríguez-Castillo, J. Mater. Chem. C, 2022, 10, 4894–4904 RSC
.
- J. Li, T. Nakagawa, J. MacDonald, Q. Zhang, H. Nomura, H. Miyazaki and C. Adachi, Adv. Mater., 2013, 25, 3319–3323 CrossRef CAS PubMed
.
- J. Li, H. Nomura, H. Miyazaki and C. Adachi, Chem. Commun., 2014, 50, 6174–6176 RSC
.
- J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2019, 123, 8099–8108 CrossRef CAS PubMed
.
- P. de Silva, J. Phys. Chem. Lett., 2019, 10, 5674–5679 CrossRef CAS PubMed
.
- G. Ricci, E. San-Fabián, Y. Olivier and J. C. Sancho-García, ChemPhysChem, 2021, 22, 553–560 CrossRef CAS PubMed
.
- J. Sanz-Rodrigo, G. Ricci, Y. Olivier and J. C. Sancho-García, J. Phys. Chem. A, 2021, 125, 513–522 CrossRef CAS PubMed
.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. Lett., 2021, 12, 6852–6860 CrossRef CAS PubMed
.
- K. Bhattacharyya, Chem. Phys. Lett., 2021, 779, 138827 CrossRef CAS
.
- R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Matter, 2021, 4, 1654–1682 CrossRef CAS
.
- S. Pios, X. Huang, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2021, 23, 12968–12975 RSC
.
- F. Dinkelbach, M. Bracker, M. Kleinschmidt and C. M. Marian, J. Phys. Chem. A, 2021, 125, 10044–10051 CrossRef CAS PubMed
.
- S. Ghosh and K. Bhattacharyya, J. Phys. Chem. A, 2022, 126, 1378–1385 CrossRef CAS PubMed
.
- J. Li, Z. Li, H. Liu, H. Gong, J. Zhang, X. Li, Y. Wang and Q. Guo, Dyes Pigm., 2022, 203, 110366 CrossRef CAS
.
- L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 18713–18721 RSC
.
- G. Ricci, J.-C. Sancho-García and Y. Olivier, J. Mater. Chem. C, 2022, 10, 12680–12698 RSC
.
- N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-i. Nakayama, S. Maeda, F. Araoka and D. Miyajima, Nature, 2022, 609, 502–506 CrossRef CAS PubMed
.
- J. Li, Z. Li, H. Liu, H. Gong, J. Zhang, Y. Yao and Q. Guo, Front. Chem., 2022, 10, 999856 CrossRef CAS PubMed
.
- F. Hund, Z. Phys., 1925, 33, 345–371 CrossRef CAS
.
- C. Posern, U. Böhme and E. Kroke, Z. fur Anorg. Allg. Chem., 2018, 644, 121–126 CrossRef CAS
.
- H. G. Raubenheimer and H. Schmidbaur, Organometallics, 2012, 31, 2507–2522 CrossRef CAS
.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS
.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS
.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed
.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- J. P. Perdew and M. Ernzerhof, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- D. Andrae, U. Häussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS
.
- TURBOMOLE V7.5.1 2021, A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from https://www.turbomole.org, accessed 25.10.2022 Search PubMed.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed
.
- P. Deglmann, K. May, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2004, 384, 103–107 CrossRef CAS
.
-
F. Furche and D. Rappoport, Computational Photochemistry, Computational and Theoretical Chemistry, Elsevier, Amsterdam, 2005, ch. III, vol. 16 Search PubMed
.
- M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed
.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS
.
- R. Bauernschmitt and R. Ahlrichs, J. Chem. Phys., 1996, 104, 9047–9052 CrossRef CAS
.
- R. Bauernschmitt, M. Häser, O. Treutler and R. Ahlrichs, Chem. Phys. Lett., 1997, 264, 573–578 CrossRef CAS
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS
.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef
.
- C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951 CrossRef
.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, E. C. Meng, G. S. Couch, T. I. Croll, J. H. Morris and T. E. Ferrin, Protein Sci., 2021, 30, 70–82 CrossRef CAS PubMed
.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS
.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2004, 121, 12772–12773 CrossRef CAS
.
- D. Rappoport and F. Furche, J. Chem. Phys., 2005, 122, 064105 CrossRef PubMed
.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed
.
- A. A. Granovsky, Firefly version 8.0.0, http://classic.chem.msu.su/gran/firefly/index.html, accessed 25.10.2022 Search PubMed.
- S. G. Chiodo and M. Leopoldini, Comput. Phys. Commun., 2014, 185, 214113 CrossRef
.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed
.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS
.
- R. R. Valiev, V. N. Cherepanov, G. V. Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 6121–6133 RSC
.
- R. S. Hosmane, M. A. Rossman and N. J. Leonard, J. Am. Chem. Soc., 1982, 104, 5497–5499 CrossRef CAS
.
- T. J. Penfold, F. B. Dias and A. P. Monkman, Chem. Commun., 2018, 54, 3926–3935 RSC
.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed
.
- T. Kowalczyk, S. R. Yost and T. Van Voorhis, J. Chem. Phys., 2011, 134, 054128 CrossRef PubMed
.
- G. M. J. Barca, A. T. B. Gilbert and P. M. W. Gill, J. Chem. Phys., 2014, 141, 111104 CrossRef PubMed
.
- J. A. R. Shea and E. Neuscamman, J. Chem. Phys., 2018, 149, 081101 CrossRef PubMed
.
- G. David, T. J. P. Irons, A. E. A. Fouda, J. W. Furness and A. M. Teale, J. Chem. Theory Comput., 2021, 17, 5492–5508 CrossRef CAS PubMed
.
- R. Colle, A. Fortunelli and O. Salvetti, Theor. Chim. Acta, 1987, 71, 467–478 CrossRef CAS
.
- D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 1987, 16, 1699–1710 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Selected bond distances and angles of molecules 1–4, TD-DFT data, cartesian coordinates of molecules 1–4. See DOI: https://doi.org/10.1039/d3sc00345k |
| This journal is © The Royal Society of Chemistry 2023 |