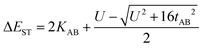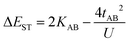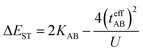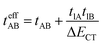Asymmetric and zwitterionic Blatter diradicals

Abstract

Asymmetric diradical molecular systems with different resonance mechanisms are largely unexplored. Herein, two conjugated asymmetric diradicals with Blatter and phenoxyl moieties (pBP and mBP) have been synthesized and studied in depth. A complete set of spectroscopic, X-ray crystallographic and magnetic techniques, together with quantum chemical calculations, have been used. The para-isomer (pBP) bears diradical and zwitterionic resonant forms, the latter by a electron delocalization mechanism, which are synergistically integrated by a sequence of nitrogen, provided by the Blatter moiety imine and amine (of different acceptor nature). In the meta-isomer (mBP), the zwitterionic form promoted in pBP by the lone-pair electron of the amine nitrogen is not available, yet it possesses a pseudo-hyperconjugation effect where the N lone pair mediates in a bonding coupling in a counter homolytic bond scission mechanism. Both electronic effects converge to promote medium diradical characters and narrow singlet–triplet gaps to the two electronic isomers. All these aspects delineate the subtle balance that shapes the electronic structure of open-shell molecules, which is even more challenging in the case of asymmetric systems, such as those described here with asymmetric phenoxyl–Blatter diradicals.

---

1 Introduction

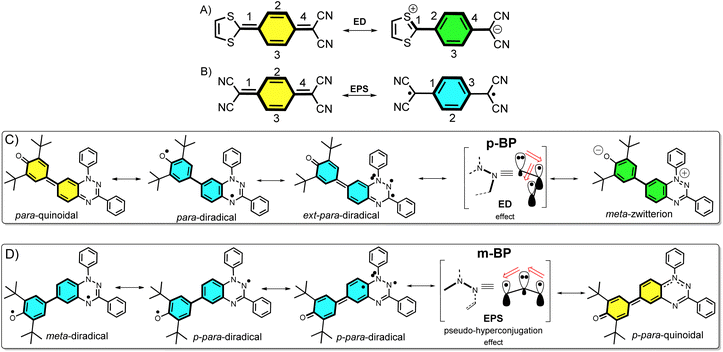
Nowadays, open-shell molecules are promising components of next-generation molecule-based magnets¹ for spintronics,² and as conductors and semiconductors in organic electronics.³ Whereas spintronics requires molecules with tunable low-to-high spin transitions, for the purpose of conducting and photoconducting materials the requirement is for materials able to stabilize charge-separated states (zwitterion-like structures). The occurrence of charge-transfer processes in the excited states is also of relevance for the application of organic chromophores in efficient organic photovoltaics (for example, singlet exciton fission³ to produce multiple triplet excitons).

Asymmetric diamagnetic π-conjugated zwitterions made by pro-aromatic spacers substituted with electron donor–acceptor groups (Scheme 1A) have been designed, historically, for electro-optical organic applications, such as in non-linear optics. The electronic property of relevance is the appearance of an electron delocalization effect (ED, Scheme 1A) by means of an intramolecular charge transfer that boosts the linear and non-linear optical responses. On the other hand, symmetric paramagnetic π-conjugated neutral diradicals based on quinonoid molecules⁴ are capable of producing neutral diradicals with low energy lying, high-spin triplet states, thanks to the gain of aromaticity in the bridge rings by means of an electron-pair splitting effect (EPS, Scheme 1B).

Scheme 1 Para-disubstituted benzoquinoid ring that transforms into a zwitterion by electron delocalization (A, ED) and into a diradical by electron-pair splitting (B, EPS). ED resonant forms have the same number of double bonds, while the diradical via EPS has one bond less, leading to the dominance of A over B if both effects act on the same π path. (C) Resonance structures of pBP (in brackets the relevant π-conjugation center is highlighted with the amine N acting as donor). (D) Resonance structures in mBP (in brackets the relevant π-conjugation center is highlighted with the amine N acting as a transmitter of the inter-radical coupling).

The majority of known π-conjugated diradicals⁵ and asymmetric zwitterions⁶ have been designed by substitution in the relative para-positions of the π-conjugated bridges (i.e., 1,4-disubstitution of the central benzene in Scheme 1A and B) with radical-bearing moieties or with donor–acceptor electroactive groups, respectively. The two concepts have thus been independently explored. It turns out, however, that the number of molecules that simultaneously execute both ED and EPS effects over the same π-core is limited, and to some extent has been disregarded. As a result, the attainment of diradicals enhanced with asymmetric zwitterionic forms is challenging, with the main difficulty being in the ability to balance both ED and EPS through bond effects (i.e., these effects are competitive in the sense that one increases to the detriment of the other). This situation is described in Scheme 1A and B, where it can be realized that, in principle, the diradical structure is disfavored with respect to the zwitterionic structure, as the former always has a smaller number of double bonds in conjugation. Hence, diradicals with charge-transfer character, or zwitterions with accessible high-spin states, are uncommon and achieving them is of interest. Some attempts along these lines have been made, such as that by Wu et al.⁷ with a series of conjugated push–pull diradicals based on quinoidal perylenes. Other cases of asymmetric donor–acceptor diradicals are those in which the radical–radical and donor–acceptor groups are connected by means of isolating non-conjugated bridges, thus neglecting the mutual benefit provided by balancing the ED and EPS effects.⁸

Structural isomerism⁹ plays an important role in diversifying the electronic and magnetic properties of molecules. For example, in disubstituted benzenes, when the isomerization pattern of the two substituting radical centers with regard to the central bridge changes from para to meta, the diradical character is increased and the ground electronic state can even vary from singlet to triplet.¹⁰

In this article, we attempt to implement the ED and EPS effects by synthesizing two asymmetric diradical isomers (pBP and mBP in Scheme 1) made by phenoxyl radical (acceptor) and Blatter radical (donor) moieties. The objective is to formulate new examples of zwitterion–diradical structures. With respect to the central benzene (Blatter benzene) of the pBP and mBP molecules, the phenoxyl oxygen and iminyl nitrogen (of the other triazine Blatter ring) are disposed in relative para-positions in pBP and in meta-positions in mBP (Scheme 1). This dual pattern of substitution gives rise to an amalgam of distinctive canonical and resonant forms in asymmetric pBP and mBP, producing in both cases charge-transfer diradicals or high-spin zwitterions, with, at the same time, some modulation from one to the other.

2 Results and discussion

2.1 Synthesis

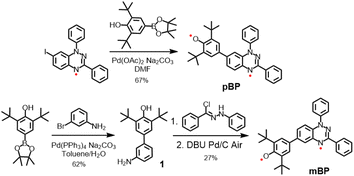
Considering the good stability and facile syntheses of Blatter radicals¹¹ and phenoxyl radicals,¹² we proposed the synthesis of asymmetric diradical isomers with these two types of scaffolds, as displayed in Scheme 2. Compound pBP was synthesized directly from 7-iodobenzotriazinyl through a modified Suzuki reaction, with an acceptable yield. pBP is very stable and can be purified by column chromatography on triethylamine treated with silica gel under ambient conditions. On the other hand, amino-substituted compound 1 was obtained from a Suzuki coupling reaction. Then, amino 1 and N-phenyl-benzenecarbohydrazonoyl chloride provided amidrazone. Subsequently, amidrazone was subjected to reductive cyclization to mBP, following an established route.¹³ The two isomers were fully characterized by electron spin resonance (ESR) spectroscopy, superconducting quantum interference device (SQUID) measurement, single-crystal X-ray diffraction (XRD), UV-visible–near-infrared (NIR), Raman and Fourier-transform infrared (FTIR) spectroscopies.

Scheme 2 Synthetic routes for pBP and mBP.

2.2 Molecular structure from X-ray diffraction

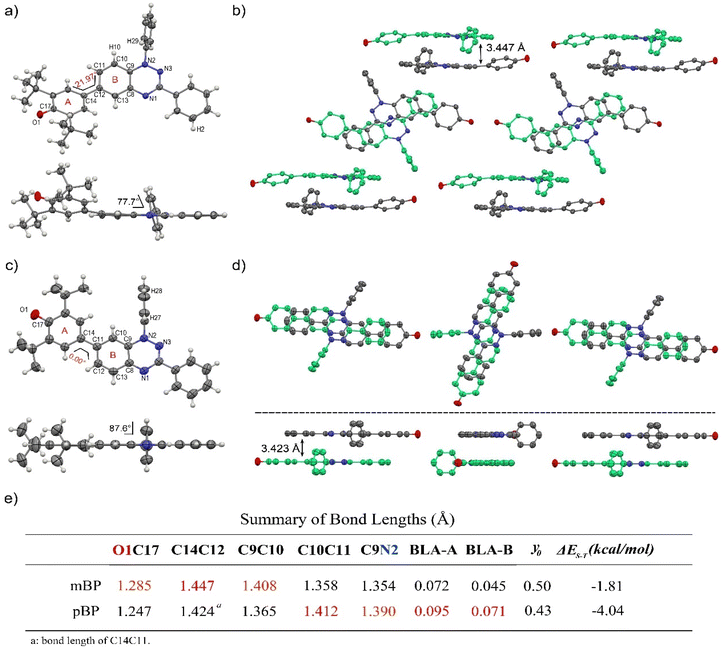
Single crystals of pBP and mBP suitable for X-ray diffraction were obtained by recrystallization from dichloromethane/hexane. As shown in Fig. 1, the phenoxyl and benzotriazinyl moieties displayed dihedral angles of 0° and 21.97° in pBP and mBP, respectively. Simultaneously, we found that: (1) the distance of the CC bond between ring A and B in Fig. 1 for pBP (1.424 Å) is shorter than that of mBP (1.447 Å), and (2) the CO bond distances are 1.247 and 1.285 Å for pBP and mBP, respectively. All these distinctive features of pBP in relation to mBP are due to the larger contribution of the quinoid closed-shell form in pBP (Scheme 1C, para-quinoidal). Despite this superior quinoidal contribution in pBP, a significant amount of diradical character persists, as deduced from the similarity of its CO bond distance with that of typical monophenoxyl radicals (1.248 Å).¹⁴ In contrast, the CN distance (C9N2 in Fig. 1) of pBP is large, 1.390 Å, revealing limited electronic interaction through this bond towards the amino nitrogen. The situation is reversed in mBP where the more distorted structure is accompanied by a CN (C9N2) bond distance that is shorter (1.354 Å) than in pBP, in agreement with the stronger electron delocalization over this bond. Using quantum chemical calculations, the bond length alternations of rings A and B of pBP and mBP were calculated (Fig. 1e) and display a larger value for pBP, in accord with the larger role of its quinoidal form.

Fig. 1 Single-crystal structures of mBP (a) pBP (c) and packing diagrams of mBP (b) and pBP (d). Thermal ellipsoids are drawn at 50% probability. Hydrogen atoms and tert-butyl groups are omitted for clarity. Dihedral angles, bond lengths (Å) and short contacts (Å) are labeled. (e) Summary of bond lengths and BLA of rings A and B.

The supramolecular structure of the mBP crystal comprises a centrosymmetric dimer linked through a pair of equivalent CH⋯N contacts (N1H29) between a triazinyl N (at position N1) and an ortho-hydrogen atom of the N-phenyl ring. The distance between dimer molecules is 3.447 Å (Fig. 1b). On the other hand, the pBP molecule has a symmetry plane and forms one-dimensional stacked columns with distances of 3.423 Å, which are also assembled through the ortho CH⋯N interactions (N1H27, Fig. 1d). Interestingly, both distances are shorter than that in the Blatter radical (3.45 Å),¹⁵ which indicates that the phenoxyl substitution could enhance the intermolecular interaction. Finally, the π-dimers are formed confronting the phenoxyl and Blatter moieties, as are typically found in donor–acceptor systems by interaction of fragments with charges of different signs.¹⁶

2.3 Magnetic properties

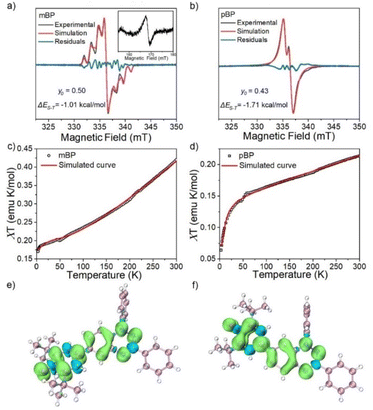
The magnetic properties of both compounds were investigated by variable-temperature ESR measurements in powder form. The intensity (I × T) of the double integral ESR intensity (I) multiplied by temperature (T in K) decreased upon cooling (Fig. S1†), suggesting depopulation of the high-spin state in favor of a low-spin ground state, or triplet to singlet transition, on cooling. From fitting of this curve with the Bleaney–Bowers equation, the energy difference between the singlet (E_S) and triplet states (E_T), ΔE_ST (2J), was estimated, and amounted to −1.01 and −1.71 kcal mol⁻¹ for mBP and pBP, respectively. Moreover, we have carried out the same variable-temperature ESR experiment in dilute solid solution (benzoquinone glassy matrices with concentration of 0.1 mM) to avoid the effect of intermolecular interactions on the magnetic properties. We found that the ΔE_ST values were similar in dilute solution and in solid powder conditions (Fig. S2†). These ΔE_ST values are well reproduced by quantum chemical calculations, at −1.81 and −4.04 kcal mol⁻¹, respectively. The quantum chemical quantity related to the diradical character,¹⁷y₀ (which is y₀ = 0 for closed-shell systems and y₀ = 1 for full open-shell diradicals), has also been estimated, giving y₀ = 0.50 for mBP and y₀ = 0.43 for pBP. In mBP the phenoxyl and iminyl radical are placed at the meta-positions of the central benzene bridge, a situation that typically produces triplet ground electronic states in benzene meta-disubstituted diradicals. However, the y₀ = 0.50 in the singlet diradical ground electronic state for mBP, compared to y₀ = 1 as would be expected for a meta-diradical triplet, indicates substantial coupling of the unpaired electrons, which takes place through the p-para-quinoidal path shown in Scheme 1D. It is noticeable that the two molecules share similar values of diradical characters in spite of their different isomeric patterns: (1) in pBP, the singlet ground electronic state is contributed by the quinoidal and zwitterionic structures, resulting in y₀ = 0.43; whereas, (2) in mBP, the y₀ = 0.50 singlet diradical character is imparted by the inter-radical bonding through the amine N along the para-conjugated path (Scheme 1D).

The small ΔE_ST values obtained for the two compounds allow facile thermal population of the lowest lying triplet excited states, which agrees with the observation of a half-field forbidden transition signal (Δm_S = ±2) for mBP. No half-field forbidden transition signal was found for pBP. Additional evidence for the presence of triplet states in the two compounds is that their ESR spectra in toluene (Fig. 2a and b) show characteristic triplet patterns at low temperature. From simulations of the ESR spectra of the triplet of mBP, the resulting ZFS parameters are D = 0.0029 cm⁻¹ and E = 0.00056 cm⁻¹, together with an average distance between the two spin centers of 9.64 Å, according to the point dipole limit. This distance is longer than that measured between the oxygen and the imine nitrogen of mBP (8.76 Å) from the single-crystal structure, in line with the role of the p-para-quinoidal form in Scheme 1D.

Fig. 2 ESR spectra of mBP (a) and pBP (b) in toluene, at 130 and 140 K, respectively. The black, red and blue lines indicate experimental, simulated and difference ESR (experimental-simulated) spectra, respectively. The inset shows the half-field ESR signal at 130 K. Magnetic susceptibilities (χT) versus T curve from the SQUID measurements on the powder of mBP (c) and pBP (d) and the fitting plot obtained with the Bleaney–Bowers equation. Calculated spin density of mBP (e) and pBP (f) based on single-crystal structure at the (u)m062x/6-311(d,p) level.

The magnetic behavior of mBP and pBP in powder forms and in dilute solid solution (benzoquinone glassy matrices with concentration of 40 mM) were studied by measuring magnetic susceptibilities (χT) using SQUID in the temperature range 2–300 K and with an applied field of 1.0 T (Fig. 2c and d). The data were corrected for both sample diamagnetism (Pascal's constants, −0.000269 emu mol⁻¹) and the diamagnetism of the sample holder (polycarbonate capsule) and benzoquinone. The measured χT–T can be fitted with the modified Bleaney–Bowers equation. The magnetic susceptibility behavior of the compounds is coherent with antiferromagnetic interactions between the unpaired electrons in the singlet diradical state, whose triplet state is populated by the thermal excitation. In addition, the majority of the calculated spin densities (α minus β spin densities) of the two isomers is spread across the phenoxyl and Blatter moieties (Fig. 2e and f).

2.4 Spectroscpic properties

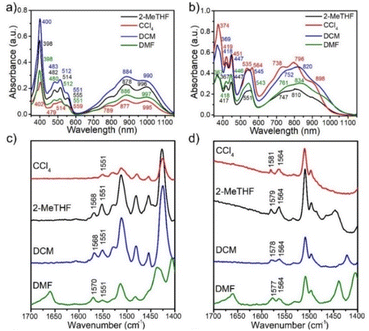
The zwitterionic character of the mBP and pBP isomers has also been investigated by electronic absorption and vibrational Raman spectroscopies. Both compounds display absorption bands in the NIR spectrum region, in line with the typical spectra of diradicaloids. Given the analyzed contributions of the zwitterionic forms, solvatochromism in solvents of different polarity has been measured, such as that displayed in Fig. 3. The wavelength of the maxima of the lowest energy absorptions of pBP displays a hypsochromic shift from dimethylformide (DMF) to tetrachloromethane (CCl₄) of 38 nm (−620 cm⁻¹), while this shift is only 8 nm (−102 cm⁻¹) in mBP, highlighting the marked negative solvatochromism¹⁸ in the two compounds. Negative solvatochromism might be ascribed to the zwitterionic contribution in the ground electronic state of pBP in Scheme 1C. On the other hand, the EPS interaction through the p-para-quinoidal path between the phenoxyl oxygen and the imine Blatter N of mBP, which causes the reduction of y₀ from 1 to 0.5, might also originate from a certain donor–acceptor polarization with subsequent modest negative solvatochromism. Overall, this reflects the more efficient establishment of a charge-separated zwitterionic state in pBP, whereas only an incipient polarized state through the p-para-quinoidal form is deduced in mBP.

Fig. 3 UV-vis–NIR electronic absorption spectra of mBP (a) and pBP (b) in solvent of different polarity (green: DMF, blue: dichloromethane (DCM), red: CCl₄, and dark: 2-methyltetrahydrofuran (2-MeTHF)). Solution-state 785 nm excitation Raman spectra of mBP (c) and pBP (d) in several solvents.

Fig. 3 displays the Raman spectra of mBP and pBP in the same solvents. In almost all cases, the 785 nm Raman spectra of mBP show a pair of bands in the 1580–1550 cm⁻¹ region due to CC stretching modes of the Blatter and of the phenoxyl moieties. pBP shows this pair of bands always at higher wavenumbers than mBP, in agreement with the contribution of a quinoidal resonant form that, as seen previously, enlarges the bond length alternation, and consequently its associated vibrational frequencies. For pBP, the 1581 cm⁻¹ band in CCl₄ moves to 1575 cm⁻¹ in DMF, while for mBP the 1570 cm⁻¹ band scarcely moves, by 2 cm⁻¹, in the studied solvents. The 1581 → 1575 cm⁻¹ shift in pBP reveals the ground electronic state contribution to the negative solvatochromic effect.

2.5 Electronic structure and operating mechanisms

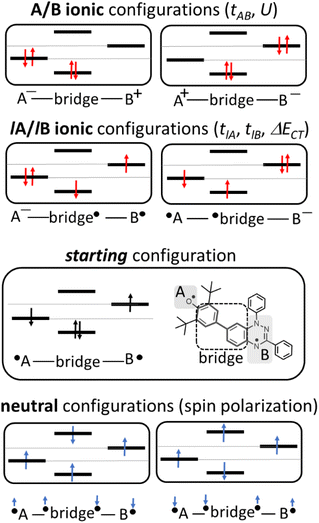
In the two-electron two-site model¹⁹ (A and B in Fig. 4) and within the second-order perturbation theory valence configuration interaction approach, the singlet–triplet gap, ΔE_ST, is obtained in terms of: (1) an exchange ferromagnetic interaction (direct exchange, K_AB, related to the direct overlap between sites A and B); (2) a transfer integral (t) between sites A and B; and (3) an energy difference between the on-site and inter-site electron repulsions (U) according to the following expression for symmetric diradicals (A and B are identical):

Fig. 4 Electronic configurations for the asymmetric diradicals studied here, where A and B are the phenoxyl oxygen and imine nitrogen in the case of pBP: ionic forms (top) and neutral tetra-radical forms (bottom).

This expression can be simplified by considering that U ≫ |t_AB|, which is reasonable in our systems given the moderate-to-large diradical character (note that U ≪ |t_AB| is the usual situation in closed-shell systems), by which the above expression for symmetric diradicals transforms to:

Which accounts for the presence of a ferromagnetic (K_AB) and an antiferromagnetic term 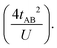The last adaptation of this formula to our case should consider the asymmetric character of the studied diradicals, which mostly affects the antiferromagnetic part by means of the transfer integrals. Hence, the above expression for asymmetric diradicals becomes:

where
where t_lA and t_lB denote the transfer integral interactions between the bridge (designated as l and located between the radical sites A and B) and sites A (t_lA) and B (t_lB). Finally, ΔE_CT provides the energy gap perturbative correction for the interaction between the bridge and the two A/B sites. Fig. 4 depicts the main electronic configurations of our asymmetric diradicals, which will serve us in dissecting two important pieces of information in this ΔE_ST description. First, the hopping integral (t) is the quantum mechanical quantity that mixes the singlet closed-shell ionic excited configurations with the diradical open-shell form (starting form in Fig. 4), which contributes to the antiferromagnetic coupling of the two radicals.²⁰ The increasing weight or mixing with the ionic configurations (i.e., larger t) makes the diradical character decrease and the ΔE_ST increase. On the other hand, the double spin-polarization effect²¹ is a through-bond bridge-mediated mechanism that tunes the ΔE_ST by stabilizing the singlet due to local reduction of the repulsion by spin polarization between the paired electrons of the bridge and of the radical centers. Double spin polarization accounts for the neutral electronic configurations of the type ˙A-˙bridge˙-B˙ in Fig. 4. Both mechanisms, ionic mixing and spin polarization, contribute to the modulation of ΔE_ST, which will be addressed below in the case of the asymmetric isomers mBP and pBP.

According to Fig. 4, for pBP, the A site is the oxygen/phenoxyl and the B site is the imine N (N1)/Blatter, which both have different electron-acceptor character. For mBP, the B site is an amine N, which is endowed with donor character, and consequently the ΔE_CT and U terms are different in mBP compared with pBP. On the other hand, for t_AB and t_lB, larger values are expected for pBP given that the sp² character of oxygen and of the N atoms, which both interact through the para-positions, would favor overlap with and through the phenyl bridge, providing significant transfer integrals that would reduce the diradical character. Conversely, the O˙ → N˙ coupling occurs through meta-positions in mBP, by which the resulting overlap with the bridge is significantly minimized. Another situation is the possibility of a zwitterionic ED from the amine N of mBP up to the phenoxyl oxygen (feasible through the para-positions), which would mediate in the transmission of the O˙ → N˙ coupling (Scheme 1D), thus increasing the t_lA and t_lB antiferromagnetic terms and concomitantly the weight of the ionic forms, thus overall decreasing the diradical character. The similarity of the y₀ and ΔE_ST values found experimentally and theoretically for the two compounds might thus be accounted for the possibility of delocalizing the spin–spin coupling between the phenoxyl oxygen and the sp² aminyl N radical through the para-position in mBP, opening up a “direct“ O˙(phenoxyl) → N˙(iminyl) interation. This electronic effect of spin–spin coupling is assisted by the lone-pair electron of the amine N, an effect that can be viewed as a result of the partial hybridization of this non-bonding orbital, which acquires bonding character in order to transmit the O˙(phenoxyl) → N˙(iminyl) coupling. This reveals a similar effect to the well-known effect of hyperconjugation,²² in the sense that conjugation acts through non-p_z carbon orbitals.²³ This pseudo-hyperconjugative effect through the lone-pair electron of mBP apparently compensates the deficient π-mesomeric effect between the O˙(phenoxyl) → N˙ through the meta-positions of the bridge.

Finally, taking into consideration the tetraradical neutral configuration, ˙A-˙bridge˙-B˙, directly connected with the double spin-polarization mechanism, we realize that in mBP, double spin polarization would be inefficient because of the disconnection through the meta-disposition of the unpaired electrons relative to the bridge. However, this would again be compensated by the feasible interaction mediated by the amine N through pseudo-hyperconjugation.

3 Conclusions

We have designed and synthesized two asymmetric isomers (mBP and pBP) made of a phenoxyl group and a Blatter radical moiety. Both molecules constitute one example of open-shell, singlet ground electronic state asymmetric diradicals with medium diradical character and rather narrow singlet–triplet gaps. The isomerisation of the O˙ → N˙ connection in pBP and mBP of direct O˙ → N˙ cascades gives rise to different resonant forms. In particular, the spin–spin coupling effect in mBP, through the lone-pair electron of its amine N, and the zwitterionic structures in pBP play distinctive roles. This is confirmed by the realization of singlet ground electronic states and the measurement of small singlet–triplet energy gaps, together with solvatochromism.

While symmetric diradicals have proliferated in the recent literature, achieving conjugated asymmetric diradicals is less common, due to the very delicate balance between the donor–acceptor character, which annihilates the diradical character in favor of closed-shell zwitterions.²⁴ This adverse situation has been saved here by incorporating an oxygen acceptor and a nitrogen donor with narrow donor–acceptor orbital energy gradient; thus, pBP is a new asymmetric diradical with a combination of zwitterion and diradical features. In the analogous isomer, mBP, the amine N lone-pair electron, instead of acting as an electronic barrier or stopper, turned out to behave as a good conjugation transmitter. This investigation delineates subtle aspects in the electronic structure of open-shell molecules and contributes to the formulation of a strategy for the design of molecules with magnetic properties in conjunction with zwitterions, which is potentially valid for the integration of molecule-based spintronics and electronics.

Data availability

NMR spectra, mass spectra, Fourier transform infrared (FT-IR) spectra, ESR spectra, SQUID spectra, low temperature absorption spectra, cyclic voltammogram, thermogravimetric analysis, electrostatic potential surface and X-ray single crystal data can be found in the ESI.†

Author contributions

Y. Z. supervised the project. F. M. carried out the synthetic work. H. C. and B. H. carried out the ESR studies. F. M., Y. J., L. C. and J. C. prepared the manuscript. S. M. Q. contributed to the Raman studies. G. X. and J. C. carried out the computational studies. All authors discussed the results and commented on the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors acknowledge financial support from the Open Research Fund of Chengdu University of Traditional Chinese Medicine State Key Laboratory Southwestern Chinese Medicine Resources (SKLTCM2022014), Guangdong Basic and Applied Basic Research Foundation (2021A1515110431) and partially funded by Grant SCITLAB (No. 20013) of Intelligent Terminal Key Laboratory of Sichuan Province. We thank MINECO/FEDER of the Spanish Government (PID2021-127127NB-I00), the Junta de Andalucía of Spain (Proyecto de Excelencia PROYEXCEL-00328) and Research Central Services (SCAI) of the University of Málaga for the access to the facilities.

Notes and references

1. (a) J. Tuček, K. Holá, A. B. Bourlinos, P. Błoński, A. Bakandritsos, J. Ugolotti, M. Dubecký, F. Karlický, V. Ranc, K. Čépe, M. Otyepka and R. Zbořil, Nat. Commun., 2017, 8, 14525; (b) E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104; (c) S. Kapuściński, J. Szczytko, D. Pociecha, M. Jasiński and P. Kaszyński, Mater. Chem. Front., 2021, 5(17), 6512–6521.
2. (a) S. Schott, U. Chopra, V. Lemaur, A. Melnyk, Y. Olivier, R. D. Pietro, I. Romanov, R. L. Carey, X. C. Jiao, C. Jellett, M. Little, A. Marks, C. R. McNeill, I. McCulloch, E. R. McNellis, D. Andrienko, D. Beljonne, J. Sinova and H. Sirringhaus, Nat. Phys., 2019, 15, 814–822; (b) S. Schott, E. McNellis, C. Nielsen, H. Y. Chen, S. Watanabe, H. Tanaka, I. McCulloch, K. Takimiya, J. Sinova and H. Sirringhaus, Nat. Commun., 2017, 8, 15200.
3. (a) M. Tsuyoshi, Y. Chiaki, F. Ko and Y. Morita, Commun. Chem., 2018, 1, 47; (b) I. Yu, Y. Jo, J. Ko, D. Y. Kim, D. Sohn and Y. Joo, Nano Lett., 2020, 20(7), 5376–5382; (c) M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936; (d) Z. Chen, W. Li, M. A. Sabuj, Y. Li, W. Zhu, M. Zeng, C. S. Sarap, M. M. Huda, X. Qiao, X. Peng, D. Ma, Y. Ma, N. Rai and F. Huang, Nat. Commun., 2021, 12, 5889.
4. (a) M. Abe, Chem. Rev., 2013, 113(9), 7011–7088; (b) X. Hu, W. Wang, D. Wang and Y. Zheng, J. Mater. Chem. C, 2018, 6(42), 11232–11242.
5. (a) R. P. Ortiz, J. Casado, V. Hernandez, J. T. L. Navarrete, P. M. Viruela, E. Orti, K. Takimiya and T. Otsubo, Angew. Chem., Int. Ed., 2007, 46(47), 9057–9061; (b) Z. Zeng, M. Ishida, J. L. Zafra, X. Zhu, Y. M. Sung, N. Bao, R. D. Webster, B. S. Lee, R.-W. Li, W. Zeng, Y. Li, C. Chi, J. T. L. Navarrete, J. Ding, J. Casado, D. Kim and J. Wu, J. Am. Chem. Soc., 2013, 135(16), 6363–6371; (c) W. Wang, L. Ge, G. Xue, F. Miao, P. Chen, H. Chen, Y. Lin, Y. Ni, J. Xiong, Y. Hu, J. Wu and Y. Zheng, Chem. Commun., 2020, 56(9), 1405–1408; (d) Y. Shen, G. Xue, Y. Dai, S. M. Quintero, H. Chen, D. Wang, F. Miao, F. Negri, Y. Zheng and J. Casado, Nat. Commun., 2021, 12, 6262.
6. (a) L. Beverina and G. A. Pagani, Acc. Chem. Res., 2014, 47(2), 319–329; (b) K. Hutchison, G. Srdanov, R. Hicks, H. Yu, F. Wudl, T. Strassner, M. Nendel and K. N. Houk, J. Am. Chem. Soc., 1998, 120(12), 2989–2990; (c) T. A. Ioannou, P. A. Koutentis, H. Krassos, G. Loizou and D. Lo Re, Org. Biomol. Chem., 2012, 10, 1339–1348; (d) C. P. Constantinides, G. A. Zissimou, A. A. Berezin, T. A. Ioannou, M. Manoli, D. Tsokkou, E. Theodorou, S. C. Hayes and P. A. Koutentis, Org. Lett., 2015, 17(16), 4026–4029; (e) G. A. Zissimou, C. P. Constantinides, M. Manoli, G. K. Pieridou, S. C. Hayes and P. A. Koutentis, Org. Lett., 2016, 18(5), 1116–1119; (f) R. Khurana, A. Bajaj and Md. E. Ali, Phys. Chem. Chem. Phys., 2022, 24, 2543–2553; (g) T. Strassner, A. Weitz, J. Rose, F. Wudl and K. N. Houk, Chem. Phys. Lett., 2000, 321(5), 459–462; (h) F. Miao, H. Chen, S. M. Quintero, G. Xue, J. Casado and Y. Zheng, Chem. Commun., 2021, 57, 8433–8436.
7. (a) Z. Zeng, S. Lee, M. Son, K. Fukuda, P. M. Burrezo, X. Zhu, Q. Qi, R.-W. Li, J. T. L. Navarrete, J. Ding, J. Casado, M. Nakano, D. Kim and J. Wu, J. Am. Chem. Soc., 2015, 137(26), 8572–8583; (b) W. Zeng and J. Wu, Mater. Chem. Front., 2019, 3(12), 2668–2672.
8. (a) B. W. Stein, C. R. Tichnell, J. Chen, D. A. Shultz and M. L. Kirk, J. Am. Chem. Soc., 2018, 140(6), 2221–2228; (b) D. A. Shultz, M. L. Kirk, J. Zhang, D. E. Stasiw, G. Wang, J. Yang, D. Habel-Rodriguez, B. W. Stein and R. D. Sommer, J. Am. Chem. Soc., 2020, 142(10), 4916–4924; (c) N. Gallagher, H. Zhang, T. Junghoefer, E. Giangrisostomi, R. Ovsyannikov, M. Pink, S. Rajca, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2019, 141(11), 4764–4774.
9. (a) J. E. Barker, J. J. Dressler, A. C. Valdivia, R. Kishi, E. T. Strand, L. N. Zakharov, S. N. MacMillan, C. J. Gómez-García, M. Nakano, J. Casado and M. M. Haley, J. Am. Chem. Soc., 2020, 142(3), 1548–1555; (b) J. J. Dressler, M. Teraoka, G. L. Espejo, R. Kishi, S. Takamuku, C. J. Gómez-García, L. N. Zakharov, M. Nakano, J. Casado and M. M. Haley, Nat. Chem., 2018, 10(11), 1134–1140; (c) G. E. Rudebusch, J. L. Zafra, K. Jorner, K. Fukuda, J. L. Marshall, I. Arrechea-Marcos, G. L. Espejo, R. P. Ortiz, C. J. Gómez-García, L. N. Zakharov, M. Nakano, H. Ottosson, J. Casado and M. M. Haley, Nat. Chem., 2016, 8(8), 753–759.
10. X. Hu, L. Zhao, H. Chen, Y. Ding, Y.-Z. Zheng, M. Miao and Y. Zheng, J. Mater. Chem. C, 2019, 7(22), 6559–6563.
11. (a) H. M. Blatter and H. Lukaszewski, Tetrahedron Lett., 1968, 9(22), 2701–2705; (b) Y. Ji, L. Long and Y. Zheng, Mater. Chem. Front., 2020, 4(12), 3433–3443; (c) A. C. Savva, S. I. Mirallai, G. A. Zissimou, A. A. Berezin, M. Demetriades, A. Kourtellaris, C. P. Constantinides, C. Nicolaides, T. Trypiniotis and P. A. Koutentis, J. Org. Chem., 2017, 82(14), 7564–7575; (d) C. P. Constantinides, E. Obijalska and P. Kaszyński, Org. Lett., 2016, 18(5), 916–919; (e) A. Berezin, G. Zissimou, C. P. Constantinides, Y. Beldjoudi, J. M. Rawson and P. A. Koutentis, J. Org. Chem., 2014, 79(1), 314–327; (f) P. A. Koutentis, H. Krassos and D. Lo Re, Org. Biomol. Chem., 2011, 9, 5228–5237; (g) C. P. Constantinides, P. A. Koutentis, H. Krassos, J. M. Rawson and A. J. Tasiopoulos, J. Org. Chem., 2011, 76(8), 2798–2806; (h) A. T. Gubaidullin, B. I. Buzykin, I. A. Litvinov and N. G. Gazetdinova, Russ. J. Gen. Chem., 2004, 74(6), 939–943; (i) F. J. M. Rogers, P. L. Norcott and M. L. Coote, Org. Biomol. Chem., 2020, 18, 8255–8277; (j) C. P. Constantinides and P. A. Koutentis, Adv. Heterocycl. Chem., 2016, 119, 173.
12. E. R. Altwicker, Chem. Rev., 1967, 67(5), 475–531.
13. P. A. Koutentis and D. L. Re, Synthesis, 2010, 12, 2075–2079.
14. V. W. Manner, T. F. Markle, J. H. Freudenthal, J. P. Roth and J. M. Mayer, Chem. Commun., 2008,(2), 256–258.
15. C. Krieger and F. A. Neugebauer, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 3124–3126.
16. H. Hu, D. A. Fishman, A. O. Gerasov, A. O. Gerasov, O. V. Przhonska, S. Webster, L. A. Padilha, D. Peceli, M. Shandura, Y. P. Kovtun, A. D. Kachkovski, I. H. Nayyar, A. E. Masunov, P. Tongwa, T. V. Timofeeva, D. J. Hagan and E. W. V. Stryland, J. Phys. Chem. Lett., 2012, 3(9), 1222–1228.
17. M. Nakano, Chem. Rec., 2017, 17(1), 27–62.
18. C. Reichardt, Chem. Rev., 1994, 94(8), 2319–2358.
19. L. Salem and C. Rowland, Angew. Chem., Int. Ed. Engl., 1972, 11(2), 92–111.
20. V. B. Koutecký, J. Koutecký and J. Michl, Angew. Chem., Int. Ed. Engl., 1987, 26(3), 170–189.
21. (a) W. T. Borden, Diradicals, Wiley, New York, 1982; (b) P. Karafiloglou, J. Chem. Educ., 1989, 66(10), 816–818.
22. A. D. McNaught and A. Wilkinson, Hyperconjugation is defined as the delocalization of the electron pair of a σ-bond over a suitable adjacent π-bond (IUPAC), Compendium of Chemical Terminology, Blackwell Scientific Publications, Oxford, 2nd edn, 1997, Online version (2019-) created by S. J. Chalk. But it is also accepted its terminology when π-delocalization/conjugation is carried out by a lone-electron pair orbital instead of a σ-bond orbital such as in our case here with the amine nitrogen.
23. A. A. Ovchinnikov, Theor. Chim. Acta, 1978, 47(4), 297–304.
24. K. Wang, Q. Zhan, B. Han, S. M. Quintero, W. Huang, Y. Ji, F. Miao, H. Chen, J. Casado and Y. Zheng, J. Mater. Chem. C, 2022, 10, 12724–12730.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic protocols, UV-vis spectra, X-ray crystallography data, theoretical computational data, and ESR and NMR spectra. CCDC 2049604 and 2049603. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc00367a

‡ These authors contributed equally to this work.

---