Metal nanoparticles supported on a nonconductive oxide undergo pH-dependent spontaneous polarization

Abstract

Electrochemical polarization, which often plays a critical role in driving chemical reactions at solid–liquid interfaces, can arise spontaneously through the exchange of ions and/or electrons across the interface. However, the extent to which such spontaneous polarization prevails at nonconductive interfaces remains unclear because such materials preclude measuring and controlling the degree of interfacial polarization via standard (i.e., wired) potentiometric methods. Herein, we circumvent the limitations of wired potentiometry by applying infrared and ambient pressure X-ray photoelectron spectroscopies (AP-XPS) to probe the electrochemical potential of nonconductive interfaces as a function of solution composition. As a model class of macroscopically nonconductive interfaces, we specifically probe the degree of spontaneous polarization of ZrO₂-supported Pt and Au nanoparticles immersed in aqueous solutions of varying pH. Shifts in the Pt-adsorbed CO vibrational band position evince electrochemical polarization of the Pt/ZrO₂–water interface with changing pH, and AP-XPS reveals quasi-Nernstian shifts of the electrochemical potential of Pt and Au with pH in the presence of H₂. These results indicate that spontaneous proton transfer via equilibrated H⁺/H₂ interconversion spontaneously polarizes metal nanoparticles even when supported on a nonconductive host. Consequently, these findings indicate that solution composition (i.e., pH) can be an effective handle for tuning interfacial electrical polarization and potential at nonconductive interfaces.

---

Introduction

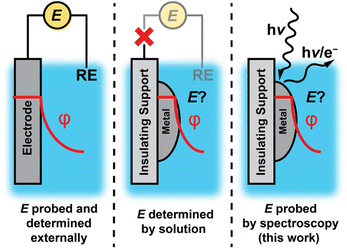
Electrochemical polarization of solid–liquid interfaces plays a critical role in energy conversion processes and chemical catalysis. Upon polarization of an interface, the electric potential gradient and corresponding electric field can drive ion/electron transfer,^1–3 organize the interfacial region of the electrolyte,^1,4–6 polarize bonds,^2,7–9 and alter the free energy and kinetics of adsorption.^1,2,10 Measuring and controlling the degree of polarization is simple for electrically conductive materials that can be readily “wired” to an external circuit (Fig. 1, left). In contrast, such potentiometric methods are inaccessible for nonconductive materials or catalyst supports, which inhibit electron flow to an external circuit (Fig. 1, middle).

Fig. 1 Different approaches for controlling and measuring solid–liquid interfacial polarization and the potential of conductive and insulating materials. Traditionally, (a) wired experiments allow for the direct measurement of interfacial potential, whereas for (b) metals supported on insulators, potentials are not as easy to determine. We report a method based on (c) a combination of X-ray photoelectron and vibrational spectroscopies to directly measure the electrochemical potential of metals supported on insulating materials.

Although electrochemical polarization is difficult to measure for nonconductive interfaces, electrochemical polarization arises at all solid–liquid interfaces as charged species (i.e., electrons and/or ions such as protons) spontaneously exchange across the interface.^1,11–23 In this scenario, the electrochemical potential of the interface would be expected to be set by the composition of the solution rather than the degree of charge flow from an external circuit. However, it remains unclear to what extent this phenomenon prevails for nonconductive materials or conductive nanomaterials on insulating supports, due to the difficulty in measuring the electrochemical potential of active sites at the surface.

Herein, we apply infrared and ambient pressure X-ray photoelectron spectroscopies (AP-XPS) to quantitatively probe the potential of oxide-supported metal nanoparticles as a model class of macroscopically nonconductive interfaces (Fig. 1, right). We employ a generalizable method based on AP-XPS that enables direct measurement of the electrochemical potential of macroscopically nonconductive materials in contact with aqueous solutions. We uncover that ZrO₂-supported Pt and Au nanoparticles immersed in aqueous solutions are likewise spontaneously polarized at ambient temperatures by spontaneous proton transfer from the bulk solution to form surface-bound hydrogen species (surface H*). Specifically, in the presence of H₂, which ensures an equilibrium coverage of surface H*, the degree of polarization scales with pH in accordance with the Nernstian expectation for quasi-equilibrated proton transfer across the interface via H⁺/H₂ interconversion. These results establish that spontaneous proton transfer reactions prevail at metal nanoparticles even when supported on nonconductive oxides while highlighting the powerful role of the solution composition in defining the degree of polarization of nonconductive solid–liquid interfaces.

Results and discussion

To investigate the degree to which varying solution composition controls the potential of nonconductive solid–liquid interfaces, we examined model systems consisting of metal nanoparticles supported on pure, undoped monoclinic ZrO₂ (M/ZrO₂, where M = Pt or Au). Such oxide-supported metal nanoparticles were chosen for this study because they are commonly used as heterogeneous catalysts and provide convenient spectroscopic markers for quantifying the degree of polarization (see below). Monoclinic ZrO₂ was specifically chosen as an insulating oxide (band gaps of 5.1–7.1 eV have been reported for monoclinic ZrO₂ (ref. 24 and 25)) with a high degree of chemical stability in aqueous solutions across a wide range of pH values.²⁶ We immersed these macroscopically nonconductive M/ZrO₂ materials in aqueous solutions of varying pH in order to alter the chemical driving force for spontaneous proton transfer from the bulk solution to form surface H* on the metal nanoparticles:

H_(aq)⁺ + e_metal⁻ + * ↔ H* ↔ ½H₂ + * (1)

It has long been appreciated that altering the chemical driving force for charge transfer across a solid–liquid interface may spontaneously electrochemically polarize that interface.^1,11–23 In the case of quasi-equilibrated proton transfer (eqn (1)), which would be described by the Nernst equation,^1,11,16,17 it has been reported for conductive Pt/C materials that the presence of H₂ establishes a quasi-equilibrated coverage of surface H*, and that the spontaneous proton transfer reaction induces pH-dependent electric fields at Pt–water interfaces.^14,23 It has not yet been demonstrated, however, that metal nanoparticles supported on an insulating support are similarly polarized by changes in pH.

To initiate our investigations, we employed attenuated total reflectance-infrared (ATR-IR) spectroscopy using adsorbed CO as an interface-specific vibrational probe of interfacial polarization. The stretching frequency of adsorbed CO, ν(CO), is sensitive to interfacial polarization.^8,27–30 These Stark shifts have been attributed to increasing negative surface charge increasing back-bonding into CO π* orbitals and shifting ν(CO) to lower wavenumbers.^8,31 As has been discussed in detail before,¹⁴ CO adsorbs strongly onto Pt surfaces across a wide pH range, permitting studies of the pH-dependence of Pt–water interfacial polarization.

We performed ATR-IR experiments with CO using two different powder samples of Pt/ZrO₂, each prepared with distinct Pt particle sizes of 1.4 nm (0.35 wt% Pt/ZrO₂) and 23 nm (7.4 wt% Pt/ZrO₂). (See ESI, Table S1 and Fig. S1† for characterization data of both Pt/ZrO₂ powder samples and calculation of Pt particle sizes from CO chemisorption data.) These measurements were performed in buffered aqueous electrolytes of varying pH saturated with 7 kPa CO, as well as 94 kPa H₂. The H₂ served to furnish a common supply of surface Pt–H to facilitate reversible proton transfer across the Pt–water interface. For the 23 nm Pt/ZrO₂ sample at pH 5.0, we observed an IR absorption peak at 2050 cm⁻¹, consistent with atop-bound CO (ν(CO_A), Fig. 2a).^{8,27,28,30,32–35} This peak redshifted to 2044 cm⁻¹ at pH 7.0 and to 2037 cm⁻¹ at pH 9.0 (Fig. 2a). For the 1.4 nm Pt/ZrO₂ sample, we likewise observed a systematic redshift in ν(CO_A) with increasing pH, going from 2043 cm⁻¹ at pH 5.0, to 2037 cm⁻¹ at pH 7.0, and 2033 cm⁻¹ at pH 9.0 (Fig. S2†). We also note the presence of a bridge-bound CO feature (Fig. S3†), consistent with prior studies,^{8,14,30,32–34} but due to its broadness and convolution from water vapor, we refrain from analysing it. The shifts in ν(CO_A) with pH are linear and comparable in magnitude for both the 1.4 nm and 23 nm Pt/ZrO₂ samples (Fig. 2b). We note that in a prior study, a distinctly nonlinear trend was observed in similar measurements with Pt/Al₂O₃ under a CO/O₂ mixture,³⁶ likely due to sluggish proton transfer equilibration under an O₂ rather than H₂ atmosphere. Indeed, the linear pH-dependent shifts in ν(CO_A) that we measured for the Pt/ZrO₂ materials under an H₂ atmosphere are similar to the shift previously reported¹⁴ for ∼5 nm Pt/C under identical conditions (data reproduced in Fig. 2b). In the case of conductive Pt/C, it was previously shown through a combination of ATR-IR and open-circuit potential (OCP) measurements that the pH-dependence of ν(CO_A) was attributable to a progressive increase in the spontaneous electrochemical polarization of the Pt–liquid interface, with increasing solution alkalinity modulating proton transfer thermodynamics across the interface.¹⁴ Similar OCP measurements are not possible for the Pt/ZrO₂ samples. While ν(COA) is known to be sensitive to the surface coverage of CO, the known strong adsorption of CO on oxide-supported Pt should lead to saturation coverage across the pH range, as observed previously for Pt/C samples.¹⁴ Thus, coverage effects are unlikely to substantially convolute the observed pH-dependent trends in ν(COA) (see ESI, Section 2.1,† for detailed discussion, as well as commentary on the role of chemical polarization from coadsorbates). Moreover, we note that atop-bound CO Stark tuning rates have been observed to be relatively invariant across carbon-supported Pt nanoparticles ranging in size from 1–30 nm when compared under similar conditions.^29,30 If it is thus assumed that the three materials in Fig. 2b (i.e., 1.4 nm and 23 nm Pt/ZrO₂ and 5 nm Pt/C) exhibit similar Stark tuning rates for atop-bound CO, then the consistency in slopes of ν(CO_A) vs. pH across all the samples provides strong indirect evidence that ZrO₂-supported Pt nanoparticles undergo spontaneous polarization with changing pH in a similar fashion to Pt nanoparticles supported on a conductive carbon support. Moreover, this phenomenon appears to prevail irrespective of Pt particle size, ranging from very small 1.4 nm Pt particles to larger 23 nm particles. While the slope in the ν(CO_A) vs. pH trends is consistent across the materials, we note that there appears to be a systematic vertical offset in the trends towards lower wavenumbers with decreasing Pt particle size. This is consistent with prior work, and has been ascribed to a combination of increased back-bonding into CO from undercoordinated Pt atoms, as well as less dipole–dipole coupling, on the smaller particles.³⁰ Taken together, these ATR-IR data strongly suggest that Pt nanoparticles are spontaneously electrochemically polarized by proton transfer even when supported on an insulating support like ZrO₂, and that the degree of polarization (i.e., the electrochemical potential) depends linearly on solution pH.

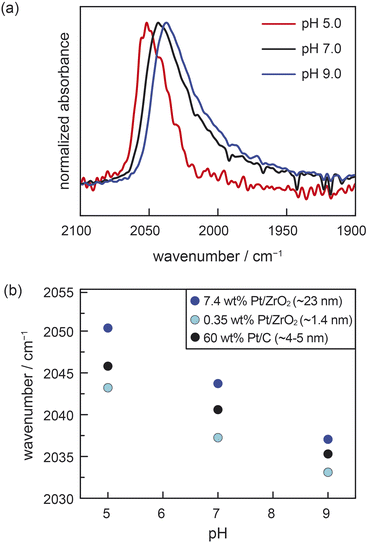Fig. 2 (a) The pH-dependence of ATR-IR spectra at saturation of atop CO adsorbed on 7.4 wt% Pt/ZrO₂ immersed in aqueous buffered electrolyte solutions. (b) pH-dependence of the peak maximum for atop-bound CO adsorbed on 7.4 wt% Pt/ZrO₂ (∼23 nm Pt nanoparticles), 0.35 wt% Pt/ZrO₂ (∼1.4 nm Pt nanoparticles), and 60 wt% Pt/C (∼5 nm Pt nanoparticles). The data for 60 wt% Pt/C are reproduced here from ref. 14. Conditions: 7 kPa CO, 94 kPa H₂, electrolyte = 0.5 M NaClO₄ in Britton–Robinson universal buffer (0.04 M acetic acid, 0.04 phosphoric acid, 0.04 M boric acid in water); pH adjusted with NaOH; experiments performed at room temperature (294 ± 1 K).

Although the foregoing ATR-IR data support that ZrO₂-supported Pt nanoparticles are spontaneously polarized by changing solution pH, these experiments rely on the assumption of a consistent Stark tuning rate and do not provide a direct, quantitative measurement of the Pt electrochemical potential. Towards this end, we examined this system using operando AP-XPS. Recent advances in AP-XPS instrumentation and methodology have enabled its use to directly quantify the electrochemical polarization and potential of conductive solid–liquid interfaces.^37–46 For a material immersed in liquid, the work required to bring an emitted photoelectron from the surface to the detector depends directly on the degree of interfacial electrochemical potential.^{38,39,42,43,47,48} Thus, by monitoring shifts in XPS peaks (corresponding to changes in electron binding energies) of components of the solid surface, we aimed to quantify changes in the magnitude of interfacial polarization as a function of solution pH.

We designed and performed operando AP-XPS experiments to quantify spontaneous polarization of the interface between ZrO₂-supported metal nanoparticles and buffered solutions of liquid water. Pt/ZrO₂ samples were prepared for these measurements by sputtering Pt onto pellets of pure monoclinic ZrO₂ (Fig. S4†) to deposit a layer of ∼8 nm Pt nanoparticles (see Fig. S5a, b and S6a†). This sample was similar to those used for ATR-IR measurements in that the Pt particles were within the size range spanned by the ATR-IR samples and supported on the same phase of ZrO₂; however, the monolithic pellet had the further benefit of facilitating the “dip-and-pull” method described below. The sample was mounted in a glass holder, which enabled dipping the sample into an aqueous electrolyte and pulling up to leave a roughly 10–20 nm liquid layer of electrolyte coating the sample.^42,49 We then probed the Pt–water interface via photoelectron spectroscopy by directing “tender” X-rays (hν = 4 keV) at the liquid-coated Pt/ZrO₂ (Fig. 3a). All AP-XPS measurements were performed in buffered aqueous electrolytes containing 0.5 M Na₂SO_4(aq). During these measurements, the atmosphere within the vacuum chamber was saturated with water vapor at ∼2.1 kPa, which corresponds to a temperature of ∼291 K assuming vapor–liquid equilibrium is established. In a fashion similar to the ATR-IR measurements, H₂ was introduced (∼0.5 kPa) in order to supply surface Pt–H and facilitate reversible proton transfer across the Pt–water interface. In this manner, we could measure Pt electron binding energies as a quantitative report of the Pt/ZrO₂ potential as a function of solution pH.

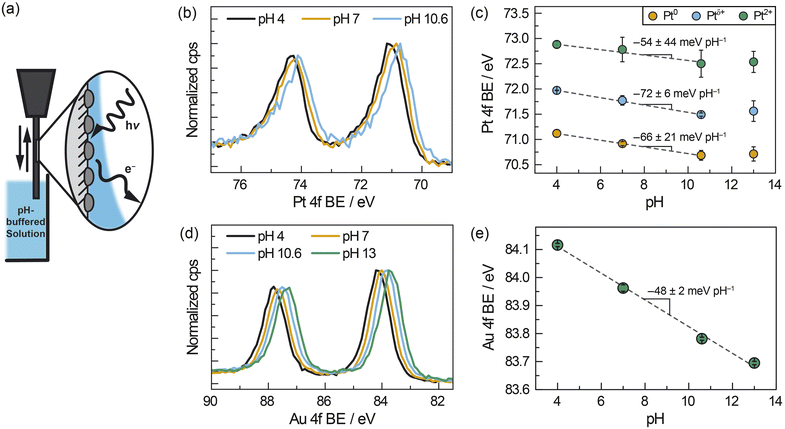Fig. 3 (a) Schematic of AP-XPS measurement for ZrO₂-supported metal nanoparticles after dip and pull in aqueous buffered electrolyte solutions of varying pH (ranging from pH 4–13) under constant H₂ pressure of ∼0.5 kPa. (b) Pt 4f spectra, corrected based on the Na 1s spectra, of ZrO₂-supported Pt nanoparticles (∼8 nm) immersed in solutions of varying pH. (c) pH-dependence of Pt 4f binding energies using a three-component fit for Pt. (d) Au 4f spectra, corrected based on the Na 1s spectra, of ZrO₂-supported Au nanoparticles (∼8 nm) immersed in solutions of varying pH. (e) pH-dependence of Au 4f binding energies using a one-component fit for Au. The fitting protocol and error analysis are described in the ESI.†

We measured the pH-dependent electrochemical potential of Pt/ZrO₂ nanoparticles by tracking shifts in the Pt 4f core level as a function of pH. We note that this quantitative analysis presupposes a pH-independent XPS reference. For this purpose, we chose the Na 1s core level as an optimal reference. First, the wetting layer of electrolytes are transparent to 4 keV X-rays, and the resultant ∼3 keV photoelectrons emitted from the Na 1s core level have a mean free path of 7 nm.⁵⁰ Thus, the Na 1s peaks we measure reflect Na_(aq)⁺ throughout the interfacial and bulk regions of the liquid layer. However, given the high ionic strength and thus low estimated Debye screening length (∼0.2 nm) relative to the liquid film thickness,⁵¹ the vast majority of Na_(aq)⁺ ions in the liquid layer are expected to be unperturbed by polarization at either the solid–liquid or liquid–vapor interfaces. Second, ²³Na NMR spectra of our buffered electrolytes indicate that Na_(aq)⁺ signals do not shift significantly or systematically with pH (Fig. S7†). This suggests that the local coordinating environment of Na_(aq)⁺ is not significantly affected by pH. Taken together, these considerations strongly suggest that the Na 1s binding energy remains invariant with pH. We further note that, although the binding energy of water and solutes have been observed to modestly depend on electrolyte concentration across a range of 0.05–8 M,⁵² in our measurements the concentration of electrolyte Na⁺ ions was constant at ∼1.1 M across the range of electrolyte pH values. Thus, we take the Na 1s binding energy to be constant at a value of 1072.1 eV (Fig. S8a†) in all measurements, thereby serving as the reference for all other XPS peaks (see ESI, Section 1.4.3,† for details of peak fitting and spectral calibration).

Relative to the Na 1s peak, the Pt 4f binding energy shifted progressively to lower values as the solution pH increased from 4 to 10.6 (Fig. 3b). Fitting the peak to three components, Pt⁰, Pt^δ+ (previously ascribed to hydrated Pt oxides),⁵³ and Pt²⁺, the Pt⁰ peak shifted from 71.1 eV at pH 4, to 70.9 eV at pH 7 and 70.7 eV at pH 10.6. We also observed binding energies of 72.0 eV (pH 4), 71.8 eV (pH 7), and 71.5 eV (pH 10.6) for Pt^δ+ and 72.9 eV (pH 4), 72.8 eV (pH 7), and 72.5 eV (pH 10.6) for Pt²⁺. These values of Pt⁰, Pt^δ+, and Pt²⁺ 4f binding energies shifted linearly with pH between pH 4–10.6, with slopes of −66 ± 21 meV pH⁻¹ for Pt⁰, −72 ± 6 meV pH⁻¹ for Pt^δ+ and −54 ± 44 meV pH⁻¹ for Pt²⁺ (Fig. 3c), respectively. This shift is largely unaffected by the number of components and type of function used in the peak fitting (see ESI, Section 2.2, and Fig. S9–S12†), with slopes varying between about −50 and −70 meV pH⁻¹. This similarity highlights the fact that the choice of fitting procedure does not have a significant impact on our quantitative analysis. We note that the Pt 4f binding energy at pH 13 (Fig. 3c) does not fall into this linear trend and this anomaly is discussed below. Notwithstanding the case of pH 13, these findings indicate that, in general, the Pt 4f binding energies are strongly dependent on the pH of the solution.

To investigate the generality of the foregoing observations on Pt/ZrO₂, we also carried out AP-XPS measurements on similarly prepared ∼8 nm Au (Fig. S5c and d†) sputtered onto the same ZrO₂ pellet but spatially separated from the Pt (Fig. S6†). Inclusion of Au and Pt on separate regions of the same ZrO₂ pellet permitted measurements of each under identical conditions. For these measurements, we monitored the Au 4f peaks referenced to the same Na 1s peak arising from Na⁺ ions in solution. Similarly to Pt, we observed that the Au 4f peak shifts to lower binding energies with increasing pH (Fig. 3d). Fitting the Au 4f peak to a single Au⁰ component (Fig. S13†), we observed that the Au 4f binding energy shifts from 84.1 eV at pH 4, to 84.0 eV, 83.8 eV, and 83.7 eV at pH 7, 10.6, and 13, respectively. This trend constitutes a linear shift with a slope of −48 ± 2 meV pH⁻¹ across a pH range of 4–13 (Fig. 3e). These findings highlight that the 4f binding energies of both Pt (between pH 4–10.6) and Au (between pH 4–13) exhibited quantitatively similar scaling relative to the Na 1s peak with changing pH. AP-XPS experiments in the gas phase suggest that the addition of 0.3 kPa H₂ to a water saturated atmosphere (∼2.1 kPa H₂O) does not change metal 4f binding energies beyond the inherent inaccuracy of shifting XPS spectra relative to the vapor phase O 1s signal (∼0.1 eV). This suggests that chemical polarization due to the dissociative adsorption of H₂ does not play a major role in the observed electrochemical polarization trends (see ESI Discussion 2.1 and Fig. S14†).

We note that the deviation at pH 13 from the linear trend in Pt 4f binding energy may be attributable to a number of factors. At pH 13 we see an additional Pt 4f XPS feature, consistent with Pt⁴⁺ (Fig. S15 and S16†). It is therefore possible, given the low H₂ partial pressure, that small quantities of highly oxidized Pt (Pt⁴⁺) and/or associated oxidation reactions at pH 13 contribute to the incomplete equilibration of the potential and deviation from Nernstian scaling (see Fig. S16† for Pt speciation across solution pHs). In separate measurements using wired electrodes, we indeed observed a substantially more sluggish change in the OCP at pH 13 than at pH 4 for both Pt and Au nanoparticles on carbon under an atmosphere of 0.7 kPa H₂ (Fig. S17†). These observations are consistent with the common understanding that hydrogen evolution/oxidation kinetics on Pt and Au are significantly slower with increasing pH.^6,54–56 Poor equilibration of the potential could also arise from a mixed potential contribution arising from oxide-based half-reactions (e.g. Pt–O + H+ + e⁻ ↔ Pt–OH), which would shift the Pt potential more positive and thus increase the Pt 4f binding energy. For Au, in contrast, we did not observe any Au oxide in the Au 4f spectrum across the full pH range, consistent with our expectation that Au oxide would not form under ambient air exposure prior to sample entry into the XPS chamber. Thus, the oxide-based mixed-potential hypothesis could explain why Pt deviates from the Nernstian expectation at pH 13, whereas the Au 4f binding energy scales linearly across the entire pH range. These pH-dependent factors may explain the poor equilibration of the Pt OCP at pH 13 with dilute H₂, a phenomenon not usually encountered under typical H₂ pressures.

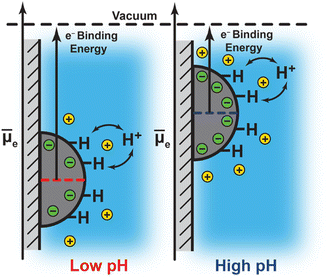
Notwithstanding the case of Pt at pH 13, the foregoing results are consistent with a picture in which the degree of interfacial polarization is controlled by quasi-equilibrated spontaneous proton transfer across the interface. In this model, increasing the solution pH (i.e., lowering H⁺ activity) drives deprotonation of surface H* (in equilibrium with H₂) to the bulk solution, leaving behind a residual electron equivalent in the metal (Fig. 4). As these electrons accumulate, the polarization of the interface inhibits subsequent deprotonation of surface H*. This process continues until proton exchange across the interface reaches equilibrium. Thus, the negative shift in Pt 4f and Au 4f binding energies with increasing pH reflect an increasing Fermi level due to a progressively more negatively polarized surface (Fig. 4). Indeed, the observed binding energy shifts of −66 ± 21 meV pH⁻¹, −72 ± 6 meV pH⁻¹, and −54 ± 44 meV pH⁻¹ for Pt 4f, and −48 ± 2 meV pH⁻¹ for Au 4f, are similar to the expected Nernstian binding energy shift of −58 meV pH⁻¹ at 291 K for proton transfer (i.e., H⁺/H₂ interconversion, Fig. 4; see ESI Section 2.3 and Scheme S1† for a derivation and detailed discussion of the Nernstian expectation). This model highlights that the proton activity in solution serves to modulate the degree of interfacial polarization of metals on nonconductive supports.

Fig. 4 pH-dependent surface charging of insulator-supported metal particles and the attendant shift in the electrochemical potential of electrons, [small mu, Greek, macron]_e, which equals the Fermi level of the metal particles.

The similarity of the scaling of Pt 4f (across pH 4–10.6) and Au 4f (pH 4–13) binding energies with pH, and their quantitative agreement with the Nernstian expectation, provide direct evidence that spontaneous proton transfer reactions play a defining and predictable role in establishing the degree of interfacial polarization for this class of macroscopically nonconductive interfaces. We also note that the consistency between Pt/ZrO₂ and Au/ZrO₂ in this regard is further remarkable in view of the dramatically different activities of Pt and Au towards H₂ activation at room temperature. These results therefore suggest that even classically more inert materials could be spontaneously polarized when immersed in liquid solutions, and that varying the solution composition (i.e., pH) provides a simple handle by which to tune the degree of interfacial polarization.

Conclusions

In conclusion, we have applied ATR-IR and AP-XPS spectroscopies to quantify spontaneous electrochemical polarization of a candidate class of macroscopically nonconductive solid–liquid interfaces, which preclude sensing with wired electrical connections. We find that ZrO₂-supported Pt and Au nanoparticles immersed in aqueous solutions are spontaneously electrochemically polarized by quasi-equilibrated proton transfer (i.e., H⁺/H₂ interconversion), resulting in pH-dependent potentials and electric fields at the Pt–water and Au–water interfaces, respectively. These experiments establish that spontaneous proton transfer reactions polarize metal nanoparticles even when supported on nonconductive oxide supports. Indeed, these findings point to the generality of spontaneous electrochemical polarization of solid–liquid interfaces, and that solution composition may serve as a predictive handle for controlling interfacial potential at nonconductive solid–liquid interfaces.

Data availability

The full experimental details, synthetic procedures, characterization data, XPS fitting procedures, IR and NMR spectra, and supplementary discussions associated with this article are provided in the ESI.†

Author contributions

T. S. W., M. J. H., K. S. W., and N. B. L. contributed equally and retain the right to list co-first authors in any order on personal documents such as curricula vitae. T. S. W. conceptualized the project. T. S. W., M. J. H., K. S. W., and N. B. L. collected and visualized the data. All authors developed methodology and analyzed the data. T. S. W. wrote the original draft of the manuscript, and all authors edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Pinar Aydogan Gokturk, Dr Rebecca Hamlyn, and Dr Terry McAfee for technical assistance during AP-XPS measurements. We also thank Dr Corey J. Kaminsky, Dr Michael L. Pegis, Dr Jaeyune Ryu, and Dr Julie E. Rorrer for helpful scientific discussions, and Dr Kaminsky, Dr Neil K. Razdan, and Dr Hai-Xu Wang for valuable feedback on our manuscript. The studies were supported by the Air Force Office of Scientific Research (AFOSR) under award number FA9550-20-1-0291 and by a Prof. Amar G. Bose Research Program Grant from MIT. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility, under contract no. DE-AC02-05CH11231. T. S. W. and K. S. W. acknowledge support from the National Science Foundation Graduate Research Fellowship under Grant No. 174530, and M. J. H. acknowledges support from Schmidt Futures for a postdoctoral fellowship. E. J. C. was partially supported by an Early Career Award in the Condensed Phase and Interfacial Molecular Science Program, in the Chemical Sciences Geosciences and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy, under Contract No. DE-AC02-05CH11231.

Notes and references

1. J. O. Bockris, A. Reddy and M. Gamboa-Aldeco, Modern Electrochemistry 2A: Fundamentals of Electrodics, Springer, Boston, MA, 2nd edn, 2000.
2. W. Schmickler and E. Santos, Interfacial Electrochemistry, Springer, Heidelberg, 2nd edn, 2010.
3. M. N. Jackson, M. L. Pegis and Y. Surendranath, ACS Cent. Sci., 2019, 5, 831–841.
4. M. F. Toney, J. N. Howard, J. Richer, G. L. Borges, J. G. Gordon, O. R. Melroy, D. G. Wiesler, D. Yee and L. B. Sorensen, Nature, 1994, 368, 444–446.
5. K. Ataka, T. Yotsuyanagi and M. Osawa, J. Phys. Chem., 1996, 100, 10664–10672.
6. I. Ledezma-Yanez, W. D. Z. Wallace, P. Sebastián-Pascual, V. Climent, J. M. Feliu and M. T. M. Koper, Nat. Energy, 2017, 2, 1–7.
7. Z.-Q. Tian, B. Ren, Y.-X. Chen, S.-Z. Zou and B.-W. Mao, J. Chem. Soc., Faraday Trans., 1996, 92, 3829–3838.
8. M. C. Figueiredo, D. Hiltrop, R. Sundararaman, K. A. Schwarz and M. T. M. Koper, Electrochim. Acta, 2018, 281, 127–132.
9. S. Sarkar, J. G. Patrow, M. J. Voegtle, A. K. Pennathur and J. M. Dawlaty, J. Phys. Chem. C, 2019, 123, 4926–4937.
10. C. G. Vayenas, S. Bebelis, C. Pliangos, S. Brosda and D. Tsiplakides, Electrochemical Activation of Catalysis: Promotion, Electrochemical Promotion, and Metal-Support Interactions, Kluwer Academic/Plenum Publishers, New York, 2001.
11. W. Nernst, Z. Phys. Chem., 1889, 4U, 129–181.
12. J. S. Adams, M. L. Kromer, J. Rodríguez-López and D. W. Flaherty, J. Am. Chem. Soc., 2021, 143, 7940–7957.
13. J. Ryu, D. T. Bregante, W. C. Howland, R. P. Bisbey, C. J. Kaminsky and Y. Surendranath, Nat. Catal., 2021, 4, 742–752.
14. T. S. Wesley, Y. Román-Leshkov and Y. Surendranath, ACS Cent. Sci., 2021, 7, 1045–1055.
15. W. C. Howland, J. B. Gerken, S. S. Stahl and Y. Surendranath, J. Am. Chem. Soc., 2022, 144, 11253–11262.
16. R. Peters, Z. Phys. Chem., 1898, 26U, 193–236.
17. V. A. Shaposhnik, J. Anal. Chem., 2008, 63, 199–201.
18. M. Spiro and A. B. Ravnö, J. Chem. Soc., 1965, 8–96.
19. M. Spiro and P. W. Griffin, J. Chem. Soc. D, 1969, 1–2.
20. M. Spiro, J. Chem. Soc., Faraday Trans. 1, 1979, 75, 1507–1512.
21. P. Bindra, D. Light and D. Rath, IBM J. Res. Dev., 1984, 28, 668–678.
22. A. Mills, Chem. Soc. Rev., 1989, 18, 285–316.
23. J. Ryu and Y. Surendranath, J. Am. Chem. Soc., 2019, 141, 15524–15531.
24. R. H. French, S. J. Glass, F. S. Ohuchi, Y. N. Xu and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5133–5142.
25. D. Ciuparu, A. Ensuque, G. Shafeev and F. Bozon-Verduraz, J. Mater. Sci. Lett., 2000, 19, 931–933.
26. W. Zouari, T. Suzuki-Muresan, T. Kobayashi, S. Utsunomiya, A. Abdelouas and B. Grambow, J. Nucl. Mater., 2021, 545, 152631.
27. B. Beden, A. Bewick and C. Lamy, J. Electroanal. Chem., 1983, 148, 147–160.
28. S.-C. Chang and M. J. Weaver, J. Chem. Phys., 1990, 92, 4582–4594.
29. C. Rice, Y. Tong, E. Oldfield, A. Wieckowski, F. Hahn, F. Gloaguen, J.-M. Léger and C. Lamy, J. Phys. Chem. B, 2000, 104, 5803–5807.
30. M. Arenz, K. J. J. Mayrhofer, V. Stamenkovic, B. B. Blizanac, T. Tomoyuki, P. N. Ross and N. M. Markovic, J. Am. Chem. Soc., 2005, 127, 6819–6829.
31. P.-A. Vuissoz, J.-P. Ansermet and A. Wieckowski, Phys. Rev. Lett., 1999, 83, 2457–2460.
32. S. D. Ebbesen, B. L. Mojet and L. Lefferts, J. Catal., 2007, 246, 66–73.
33. N. M. Marković, C. A. Lucas, A. Rodes, V. Stamenković and P. N. Ross, Surf. Sci., 2002, 499, L149–L158.
34. I. J. McPherson, P. A. Ash, R. M. J. Jacobs and K. A. Vincent, Chem. Commun., 2016, 52, 12665–12668.
35. S. D. Ebbesen, B. L. Mojet and L. Lefferts, Langmuir, 2006, 22, 1079–1085.
36. S. D. Ebbesen, B. L. Mojet and L. Lefferts, J. Catal., 2007, 246, 66–73.
37. H. S. Casalongue, S. Kaya, V. Viswanathan, D. J. Miller, D. Friebel, H. A. Hansen, J. K. Nørskov, A. Nilsson and H. Ogasawara, Nat. Commun., 2013, 4, 2817.
38. M. F. Lichterman, S. Hu, M. H. Richter, E. J. Crumlin, S. Axnanda, M. Favaro, W. Drisdell, Z. Hussain, T. Mayer, B. S. Brunschwig, N. S. Lewis, Z. Liu and H. J. Lewerenz, Energy Environ. Sci., 2015, 8, 2409–2416.
39. O. Karslioʇlu, S. Nemšák, I. Zegkinoglou, A. Shavorskiy, M. Hartl, F. Salmassi, E. M. Gullikson, M. L. Ng, C. Rameshan, B. Rude, D. Bianculli, A. A. Cordones, S. Axnanda, E. J. Crumlin, P. N. Ross, C. M. Schneider, Z. Hussain, Z. Liu, C. S. Fadley and H. Bluhm, Faraday Discuss., 2015, 180, 35–53.
40. J. J. Velasco-Velez, V. Pfeifer, M. Hävecker, R. S. Weatherup, R. Arrigo, C. H. Chuang, E. Stotz, G. Weinberg, M. Salmeron, R. Schlögl and A. Knop-Gericke, Angew. Chem., Int. Ed., 2015, 54, 14554–14558.
41. Y. T. Law, S. Zafeiratos, S. G. Neophytides, A. Orfanidi, D. Costa, T. Dintzer, R. Arrigo, A. Knop-Gericke, R. Schlögl and E. R. Savinova, Chem. Sci., 2015, 6, 5635–5642.
42. S. Axnanda, E. J. Crumlin, B. Mao, S. Rani, R. Chang, P. G. Karlsson, M. O. M. Edwards, M. Lundqvist, R. Moberg, P. Ross, Z. Hussain and Z. Liu, Sci. Rep., 2015, 5, 9788.
43. M. F. Lichterman, M. H. Richter, S. Hu, E. J. Crumlin, S. Axnanda, M. Favaro, W. Drisdell, Z. Hussain, B. S. Brunschwig, N. S. Lewis, Z. Liu and H.-J. Lewerenz, J. Electrochem. Soc., 2016, 163, H139–H146.
44. M. Favaro, B. Jeong, P. N. Ross, J. Yano, Z. Hussain, Z. Liu and E. J. Crumlin, Nat. Commun., 2016, 7, 12695.
45. M. Favaro, C. Valero-Vidal, J. Eichhorn, F. M. Toma, P. N. Ross, J. Yano, Z. Liu and E. J. Crumlin, J. Mater. Chem. A, 2017, 5, 11634–11643.
46. P. Aydogan Gokturk, R. Sujanani, J. Qian, Y. Wang, L. E. Katz, B. D. Freeman and E. J. Crumlin, Nat. Commun., 2022, 13, 5880.
47. A. T. D'Agostino and W. N. Hansen, Surf. Sci., 1986, 165, 268–276.
48. W. Zhou and D. M. Kolb, Surf. Sci., 2004, 573, 176–182.
49. M. Favaro, F. Abdi, E. Crumlin, Z. Liu, R. van de Krol and D. Starr, Surfaces, 2019, 2, 78–99.
50. A. Akkerman and E. Akkerman, J. Appl. Phys., 1999, 86, 5809–5816.
51. P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206.
52. B. Credidio, M. Pugini, S. Malerz, F. Trinter, U. Hergenhahn, I. Wilkinson, S. Thürmer and B. Winter, Phys. Chem. Chem. Phys., 2022, 24, 1310–1325.
53. R. Mom, L. Frevel, J. Velasco-Vélez, M. Plodinec, A. Knop-Gericke and R. Schlögi, J. Am. Chem. Soc., 2019, 141, 6537–6544.
54. R. Subbaraman, D. Tripkovic, D. Strmcnik, K. C. Chang, M. Uchimura, A. P. Paulikas, V. Stamenkovic and N. M. Markovic, Science, 2011, 334, 1256–1260.
55. J. Durst, A. Siebel, C. Simon, F. Hasché, J. Herranz and H. A. Gasteiger, Energy Environ. Sci., 2014, 7, 2255–2260.
56. O. Jung, M. N. Jackson, R. P. Bisbey, N. E. Kogan and Y. Surendranath, Joule, 2022, 6, 476–493.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc00884c

‡ Denotes equal contribution.

---