DOI:
10.1039/D3SC01267K
(Edge Article)
Chem. Sci., 2023,
14, 11141-11150
Dielectric response of confined water films from a classical density functional theory perspective†
Received
8th March 2023
, Accepted 21st August 2023
First published on 8th September 2023
Abstract
We re-examine the problem of the dielectric response of highly polar liquids such as water in confinement between two walls using simple two-variable density functional theory involving number and polarisation densities. In the longitudinal polarisation case where a perturbing field is applied perpendicularly to the walls, we show that the notion of the local dielectric constant, although ill-defined at a microscopic level, makes sense when coarse-graining over the typical size of a particle is introduced. The approach makes it possible to study the effective dielectric response of thin liquid films of various thicknesses in connection with the recent experiments of Fumagalli et al., [Science, 2018, 360, 1339–1342], and to discuss the notion of the interfacial dielectric constant. We argue that the observed properties as a function of slab dimensions, in particular the very low dielectric constants of the order of 2–3 measured for thin slabs of ∼1 nm thickness do not highlight any special properties of water but can be recovered for a generic polar solvent having similar particle size and the same high dielectric constant. Regarding the transverse polarisation case where the perturbing field is parallel to the walls, the associated effective dielectric constant as a function of slab dimensions reaches bulk-like values at much shorter widths than in the longitudinal case. In both cases, we find an oscillatory behaviour for slab thicknesses in the one nanometer range due to packing effects.
1 Introduction
The dielectric constant is a macroscopic concept that relates the linear response of the polarisation vector to the Maxwell electric field.1 The derivation of the dielectric constant of bulk fluids from statistical mechanics principles has a long history starting from the early studies of Debye, Onsager and Kirkwood,2–4 with major advances leading to its modern formulation in the 1970s.5–8 The extension to inhomogeneous liquids and the necessary conditions to define a local, space-dependent dielectric constant ε(r) were given by Nienhuis and Deutch5 and re-examined thirty years later by Ballenegger and Hansen.9 Such a clear definition is crucial for the implicit solvent models used, e.g., in biomolecular simulations to represent the aqueous surrounding medium or for deriving effective electrostatic interaction models based on space-dependent dielectric constants.10 That question led to a number of early studies trying to characterise ε(r) in the vicinity of biomolecules or membranes using molecular dynamics (MD) simulations.10–12 In 2005, Ballenegger and Hansen presented the first MD simulations of a model polar solvent in confinement between two repulsive walls in order to define a local ε(z) rigorously using either linear response or a small perturbing electric field.13 For a perturbation perpendicular to the walls, they were led to conclude that such ε(z) is ill-defined and “is not a useful quantity near the walls”. This pioneering work has initiated a number of subsequent MD studies of water in confinement or at interfaces using a realistic atomistic representation of both the solvent and the confining surfaces.14–19 This interest was revived recently by the experimental studies of Fumagalli et al.20 who reported local capacitance measurements for water confined between two atomically flat walls separated by various distances down to 1 nanometer. Their experiments were interpreted as revealing “the presence of an interfacial layer with vanishingly small polarisation”, that translates into an “anomalously low dielectric constant of confined water”. Historically, the question of the nature of the hydration layer close to an electrified interface goes back to the early theories of Helmholtz and Stern and has plagued the theory of electric double layers for electrolytes at charged interfaces.21 Already almost a century ago, by analysing surface capacitance data, Stern demonstrated that a thin interfacial layer exists at a solid–water interface with a dielectric constant much reduced compared to that of bulk water.22 To our knowledge, there is no clear consensus yet on the precise microscopic definition of this Stern layer and on the value of the dielectric constant that should be attributed to it. A proposed experimental reference for aqueous solutions under ambient conditions is ε ≃ 7 instead of ε ≃ 80 for the bulk,21 an already small value in the absence of extreme confinement.
The dielectric properties of interfacial and confined water have been the subject of many recent simulation studies, including, e.g., ref. 18, 19 and 23–34. However, as already stressed in the early work of ref. 13, the convergence of confined water dielectric properties by MD simulations is very difficult to achieve. Recent developments have been devoted to more efficient methods to compute the dielectric constant34 or to analytical theoretical approaches based on dielectric continuum theory (DCT)35 or a nonlocal field theoretical approach.36 Different explanations have been proposed for the observed reduction in the perpendicular dielectric constant of confined water.20 These include a dielectrically ‘dead’ interfacial water layer caused by orientational constraints imposed by the interface,20,28,29 the disruption of the water hydrogen-bond network at the interface,33 a dielectric boundary effect,35 and an excluded volume effect.19,37
Classical density functional theory (DFT) is a well-founded, efficient theoretical approach to describe atomic and molecular fluids at interfaces or in confinement; see, e.g., ref. 38–44. In this article, we re-examine the problem of the dielectric response of highly polar liquids such as water in confinement between two walls using a two-variable density functional theory, in terms of number and polarisation densities, that we have derived and used previously for either a generic dipolar fluid45,46 or for water.47,48 It is a simplified version of the full molecular density functional theory (MDFT) formalism that three of us have been developing for a number of years.49–52 This simplicity (combined with accuracy as will be seen) makes it possible first to sort out the important physical variables, secondly to derive analytical solutions and/or to provide instantaneous numerical solutions that are exempted from the statistical noise inherent to molecular simulations, for as many physical situations as desired. We note that a connected DFT approach was recently applied to the study of polarisation fluctuations in confined water; the coupling of number and polarisation densities was not considered explicitly, however, with an abrupt number density profile introduced as input.37 Our goal is three-fold: (1) to reproduce at a much simpler level and to re-examine previous MD results concerning the definition of a local (ill-defined) longitudinal dielectric constant close to a wall or in confinement and to extend this definition to that of a (well-defined) locally coarse-grained dielectric constant. (2) To contribute to the understanding of the experiments of Fumagalli et al. and of the notion of an “anomalously low dielectric constant” of water in confinement. (3) More generally to provide a theoretical foundation for describing quantitatively, at a fully molecular level, surface-induced solvent structures, as a consequence of the coupling between solvent density and solvent polarisation, in a form that can be incorporated into commonly used mean field dielectric theories.10
The outline of the paper is as follows. Section 2 introduces our two-variable, number and polarisation density free energy functional. It is applied in Section 3 to the microscopic structure and longitudinal dielectric response of a model Stockmayer fluid, having the same bulk dielectric constant as water at a similar density, in one-dimensional confinement between two graphene-like surfaces. The response is studied as a function of slab thickness from less than a nanometer to micrometers. Section 4 extends the study to a dipolar representation of SPC/E water and to the transverse response in addition to the longitudinal one. Section 5 concludes.
2 Free-energy functional for a dipolar liquid
Before discussing a more complete model of water later on, and in order to distinguish generic dielectric properties from the specific water properties emerging from its special H-bond structure, we start with an ersatz of water, namely a Stockmayer fluid composed of Lennard-Jones (LJ) particles embedding a permanent dipole μ, whose density and dielectric constant at ambient temperature are similar to those of water. We take the parameters from the early studies of Pollock and Alder:53σLJ = 3.024 Å, εLJ = 1.87 kJ mol−1, μ = 1.835 D, ρ = 0.0289 Å−3 or, in dimensionless units, 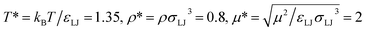 . These parameters yield a dielectric constant ε = 80. They also correspond to a state point considered by Ballenegger and Hansen when studying the dielectric properties of the closely related dipolar-soft-sphere model in confinement.13 As shown in ref. 45–48 and 54, such a dipolar liquid subjected to an external potential can be described accurately by a grand-potential functional depending on the local number density n(r) and local polarisation density P(r). This functional is determined by the chemical potential of the bulk fluid at density n0. It can be decomposed into density and polarisation terms,
. These parameters yield a dielectric constant ε = 80. They also correspond to a state point considered by Ballenegger and Hansen when studying the dielectric properties of the closely related dipolar-soft-sphere model in confinement.13 As shown in ref. 45–48 and 54, such a dipolar liquid subjected to an external potential can be described accurately by a grand-potential functional depending on the local number density n(r) and local polarisation density P(r). This functional is determined by the chemical potential of the bulk fluid at density n0. It can be decomposed into density and polarisation terms, 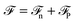 , with the density term given by
, with the density term given by| | 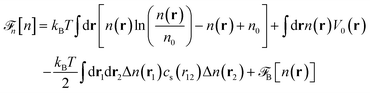 | (1) |
where Δn(r) = n(r) − n0. V0(r) represents the external LJ potential exerted at point r. 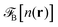 is the so called bridge functional, that we take here as a hard-sphere (HS) bridge functional based on fundamental measure theory,55–57 using the Kierlik-Rosinberg scalar version58,59 and a reference HS diameter defined conventionally as dHS = σLJ(1 + 0.298T*)/(1 + 0.3316T* + 0.001048T*2).60 The polarization part of the functional reads
is the so called bridge functional, that we take here as a hard-sphere (HS) bridge functional based on fundamental measure theory,55–57 using the Kierlik-Rosinberg scalar version58,59 and a reference HS diameter defined conventionally as dHS = σLJ(1 + 0.298T*)/(1 + 0.3316T* + 0.001048T*2).60 The polarization part of the functional reads| | 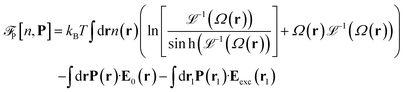 | (2) |
with Ω(r) = P(r)/μn(r) and P(r) = |P(r)|. The first term represents the ideal free energy for an ensemble of non-interacting dipoles subjected to an external electric field; there 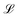 denotes the Langevin function and
denotes the Langevin function and 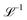 its inverse. E0(r) is the external electric field at point r. The excess electric field Eexc(r1) is defined using
its inverse. E0(r) is the external electric field at point r. The excess electric field Eexc(r1) is defined using| | 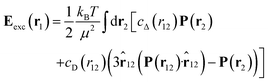 | (3) |
where ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = r12/r12. In eqn (1) and (3), cS(r), cΔ(r), and cD(r) represent the spherical and dipolar spherical-invariant projections of the angular-dependent direct correlation function of the bulk liquid at density n0. These functions are inputs in the theory and are obtained from a preliminary simulation of the bulk fluid. See ref. 45 and 48 for their behaviour in direct and Fourier space.
12 = r12/r12. In eqn (1) and (3), cS(r), cΔ(r), and cD(r) represent the spherical and dipolar spherical-invariant projections of the angular-dependent direct correlation function of the bulk liquid at density n0. These functions are inputs in the theory and are obtained from a preliminary simulation of the bulk fluid. See ref. 45 and 48 for their behaviour in direct and Fourier space.
The equilibrium number density and polarisation density are obtained by minimisation of the functional with respect to both n(r) and P(r). Minimisation of 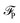 with respect to P(r) for a given n(r) gives
with respect to P(r) for a given n(r) gives
| | 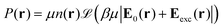 | (4) |
This accounts for dipolar saturation at high local electric fields. It does so at a fully microscopic level compared to the coarse-grained dipolar Poisson approach of Berthoumieux et al.61 For small external fields, the ideal free energy in eqn (2) can be developed at the dominant order of polarisation
| | 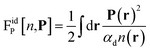 | (5) |
where
αd =
μ2/3
kBT is the orientational polarizability of a permanent dipole in a field. In that case, minimisation yields a linear relation between
P(
r) and
E0(
r), with indeed a nonlocal response function.
3 Confinement in a one-dimensional slit pore
In order to mimic the experimental setup in ref. 20, as well as to follow the simulation conditions of Ballenegger and Hansen,13 we consider a model of a one-dimensional slit pore composed of 2 graphene-like plates in the x–y-plane separated by a distance h along z. As in ref. 13, the external potential V0(z) exerted by the two walls results from the x–y integration of a 3D-Lennard-Jones potential. It is of the 9–3 type, with parameters pertinent to carbon–water interactions| | 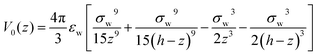 | (6) |
with σw = 3.9 Å and εw = 2.6 kJ mol−1. An external electric field E0(z) is applied along the perpendicular z-direction. For such a 1D-geometry, the polarisation field is so-called longitudinal (i.e., aligned with the electric field in q-space), and the two direct correlation functions cΔ(q), cD(q) (zeroth- and second-order Hankel transforms of cΔ(r) and cD(r), respectively) reduce in q-space to a single longitudinal function cL(q) = cΔ(q) + 2cD(q).48 The two components of the functional 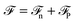 of eqn (1)–(3) can be written per surface area in the form
of eqn (1)–(3) can be written per surface area in the form| | 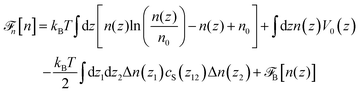 | (7) |
| | 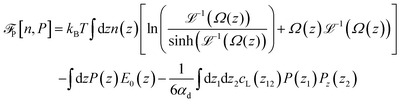 | (8) |
cS(z) and cL(z) are defined here as the inverse 1D Fourier transforms of the 3D functions cS(q) and cL(q). They are plotted in Fig. 1. It should be noted that both are of a short range and vanish beyond r ≃ 6 Å. This might be surprising for the polarisation–polarisation contribution cL(z) since dipole–dipole interactions are a priori long-range. It is a well-known fact, however, that for a longitudinal polarisation field, the long-range 1/r3 part of the dipolar tensor disappears, and the Maxwell field is rigorously defined using the local relation E(r) = E0(r) − 4πP(r). In other words the dielectric displacement is equal to the external field, D(r) = E0(r).
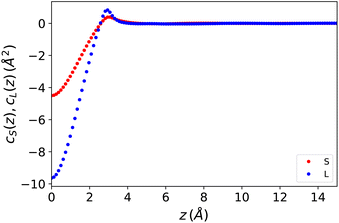 |
| | Fig. 1 One-dimensional direct correlation functions for the Stockmayer fluid model described in the text, entered in eqn (7) and (8). | |
For a small perturbing field E0(z) and when n(z) is provided independently through the minimisation of eqn (7) only (which amounts to neglecting the n–P coupling appearing in the ideal term of eqn (8)), the quadratic form of eqn (5) can be used, turning the minimisation in P(z) into a linear algebra problem that can be solved through matrix inversion. In this linear regime, the nonlocal response can be written in terms of the susceptibility χ0(z1, z2)
| | 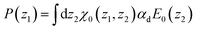 | (9) |
with
| | 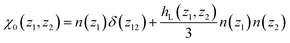 | (10) |
where the longitudinal, inhomogeneous pair distribution function
hL(
z1,
z2) relates to the bulk direct correlation function
cL(
z12) through an inhomogeneous Ornstein-Zernike (OZ) relation. See the ESI
† for details. For a constant electric field
E0(
z) ≡
E0, the integration of the second variable can be performed and a local response function can be defined as
| | 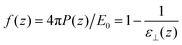 | (11) |
where
ε⊥(
z) stands for a local
longitudinal dielectric constant and formally
| | 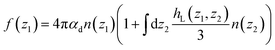 | (12) |
Variants of this formula can be readily found in the literature,9 It explains how a local dielectric constant can be defined even though the dielectric response function itself, given by χ0 or hL, is intrinsically non-local.62 It is seen that the inhomogeneous fluid density n(z) enters at two places; the first one indicates that the local response function should be zero where there is no particle, n(z1) = 0. The second one excludes the nonlocal contribution to the polarisation response coming from a region where the density is zero, n(z2) = 0. This nonlocal cut-off effect on the polarisation response near the boundaries was pointed out recently by Olivieri et al.19 Among several other worthy remarks, it is justified in the ESI† that, since hL(z1, z2) is short-ranged, the influence of the walls is expected to be short-ranged too, and the bulk values of f(z) and ε⊥(z) should be reached after only a few particle diameters from the walls.
From now on, we depart from this linear algebra formulation that implies matrix inversion. The results presented next were obtained numerically by the joint minimisation of the functional with respect to n(z) and P(z) in the presence of a small and constant external field E0 = 0.1 V nm−1. We have written a simple, dedicated Python code for that purpose. For discretisation of the fields over typically N = 1024 points, the minimisation procedure is instantaneous on a laptop (less than a second).
Following the simulations in ref. 13, we first consider a relatively wide slit of width h = 50 Å (16.5 σLJ). We plot the equilibrium density field n(z) as well as the response function f(z) in reduced units in Fig. 2. Both present strong structural oscillations up to 6 σLJ from the walls. These two curves appear very similar to the ones obtained by Ballenegger and Hansen13via MD – although their study was mainly focused on the less polar case μ* = 1.2, with the simulations for μ* = 2 proving very hard to converge. In Fig. 3-top, we plot the resulting inverse dielectric constant 1/ε⊥(z) that presents oscillations that span unphysical negative values up to ∼6σLJ from the walls. This led Ballenegger and Hansen to conclude that “ε⊥(z) is not a useful quantity near the walls”. Here we modulate this judgement by recalling that standard electrostatics is by essence a coarse grained theory, and that one should rather look at a coarse-grained ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) with a coarse-graining length of at least the size of a particle (this approach was used in ref. 13 to smooth the dipolar fluctuations). Here, this can be formalised by looking at a coarse-grained polarisation field, defined for example using
⊥(z) with a coarse-graining length of at least the size of a particle (this approach was used in ref. 13 to smooth the dipolar fluctuations). Here, this can be formalised by looking at a coarse-grained polarisation field, defined for example using
| | 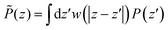 | (13) |
where the weight function
w(
z) is taken as a normalized Gaussian function with standard deviation
σP =
λσLJ,
λ of order 1. A coarse-grained dielectric constant
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥
⊥(
z) can be defined from
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif)
(
z) exactly as in
eqn (11). The inverse, coarse-grained, dielectric constant 1/
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥
⊥(
r) corresponding to
λ = 0.7 is plotted as a function of distance in
Fig. 3-top together with the bare microscopic results. This quantity now appears as a smooth curve that remains strictly positive, so that
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif)
(
r) itself is well defined and well behaved; see
Fig. 3-bottom. It presents two peaks at values higher than those in the bulk close to the walls; the main feature to be retained, however, is that the bulk value is reached after a few particle diameters, at a distance where the microscopic polarisation still presents microscopic oscillations (
z ∼ 4–5
σLJ), and there are no long-range effects induced by the walls on the local dielectric constant. We note that the coarse-graining length
σP should not be considered a fundamental quantity, but rather an observation length scale. It might also be linked to the resolution of the experiment that is realised. As soon as this observation/resolution becomes comparable to the particle size, 1/
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥
⊥(
z) and
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥
⊥(
z) appear as locally well-defined, positive quantities. As a rule of thumb, to keep a microscopic character in our analysis, we choose
σP large enough to smooth the spurious behaviour of 1/
ε(
z) (or
f(
z)), but small enough to have its overall microscopic behaviour unchanged, in particular keeping a limited penetration into the walls and an unaltered distance at which the bulk value is reached. We find both conditions typically fulfilled for 0.6 ≤
λ ≤ 1;
λ = 0.7 appears to be a good compromise. The variation of the results of
Fig. 3 with the parameter
λ is illustrated in the ESI.
† Increasing
λ from 0.7 to 1 and beyond gives a more regular behaviour for
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥
⊥(
z) but indeed a more important smoothing of the boundaries. We argue in the ESI
† that, for modelling purposes, the fundamental quantity to consider is rather the coarse-grained response
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif)
(
z) that is less sensitive to the choice of
λ and can be modelled with two inverted sigmoid-like curves, yielding smooth curves when converted to
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥
⊥(
z).
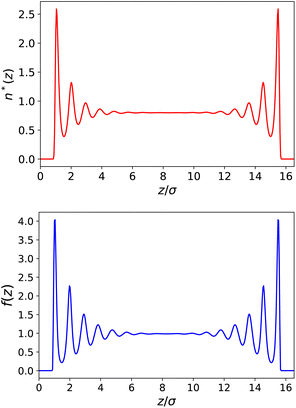 |
| | Fig. 2 Top: Reduced density n*(z) = n(z)σLJ3 for a slab of width h = 50 Å (16.5σLJ). Bottom: Local response function f(z) = 4πP(z)/E0. | |
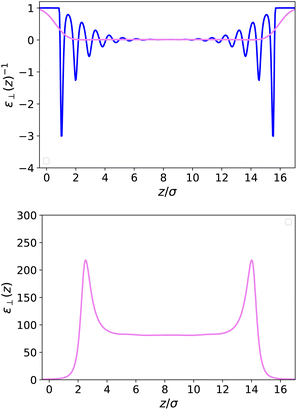 |
| | Fig. 3 Top: Local inverse dielectric constant 1/ε⊥(z) in a slab of width h = 50 Å (blue curve) and its coarse-grained version 1/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) obtained through eqn (13) with a coarse-graining length σP = 0.7σLJ (violet curve). Bottom: Coarse-grained dielectric constant ⊥(z) obtained through eqn (13) with a coarse-graining length σP = 0.7σLJ (violet curve). Bottom: Coarse-grained dielectric constant ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) whereas the corresponding microscopic ε⊥(z) is ill-defined. ⊥(z) whereas the corresponding microscopic ε⊥(z) is ill-defined. | |
In Fig. 4 and 5, we plot the results corresponding to a much narrower slab with h = 10 Å (∼3σLJ). It can be seen that only two solvent layers are allowed in-between the plates and that the density n(z) and the polarisation density P(z) remain everywhere far from their bulk values. The coarse-grained dielectric constant ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) displayed in Fig. 5 has a nice and smooth hat shape that reaches a maximum value around 10 in the middle of the slab, again far below the bulk value.
⊥(z) displayed in Fig. 5 has a nice and smooth hat shape that reaches a maximum value around 10 in the middle of the slab, again far below the bulk value.
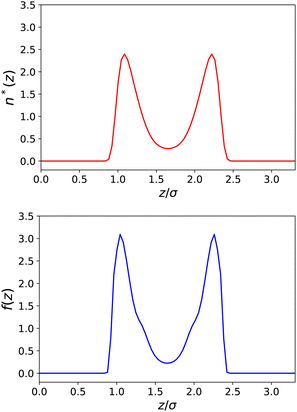 |
| | Fig. 4 Same as Fig. 2 for a slab of width h = 10 Å. | |
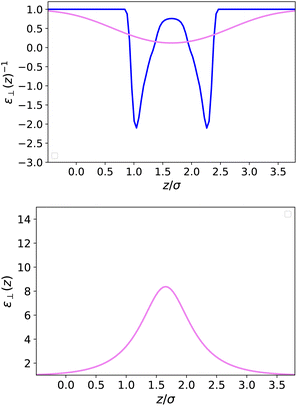 |
| | Fig. 5 Same as Fig. 3 for a slab of width h = 10 Å. | |
From the above findings, one can state that the very long range effect, up to a micrometer, observed for the measured ε⊥ as a function of slab thickness in ref. 20 cannot be attributed to any long-range effect of the walls on the local dielectric constant of the liquid. One should rather look at the effective dielectric response of the whole slab to the applied potential difference. For our slab model subjected to a constant external field (the so-called dielectric box model in ref. 18) this can be measured by relating the average polarisation in the slab to the field
| | 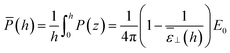 | (14) |
which yields according to
eqn (11)| | 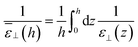 | (15) |
| | 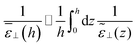 | (16) |
The second equality holds for the coarse-grained dielectric constant instead of the microscopic one if the coarse-graining length is such that ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (0) =
(0) = ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (h) ≃ 0. The microscopic expressions 14–15 remain the ones to be used in the following. Expressing the total electrostatic energy of the device, which includes the self-energy of the electric field between the plates, writing the potential difference between them as
(h) ≃ 0. The microscopic expressions 14–15 remain the ones to be used in the following. Expressing the total electrostatic energy of the device, which includes the self-energy of the electric field between the plates, writing the potential difference between them as
| | 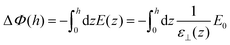 | (17) |
and equating this energy to 1/2
C(
h)Δ
ϕ(
h)
2 yields the effective capacitance
| | 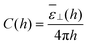 | (18) |
with
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥
⊥(
h) having the same definition as in
eqn (15). Measuring the average polarisation in the slab or the effective slab capacitance is thus equivalent. When the plate-to-plate distance
h is large enough as in
Fig. 3, one can divide the device into three regions, two interfacial regions of width
hi and an intermediate bulk region of width
h − 2
hi where
ε⊥(
z) ≃
εbulk. In that case, the choice of
hi results in the definition of an effective dielectric constant
εi for the interfacial region through
| | 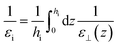 | (19) |
and the resulting dielectric constant of the whole slab can be written as
| | 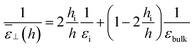 | (20) |
or alternatively as
| | 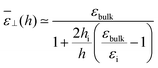 | (21) |
Visual inspection of Fig. 3 leads to the choice hi ≃ 6σLJ when looking at the bare 1/ε⊥(z) or hi ≃ 3σLJ when looking at the coarse-grained curve 1/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z). Here we can define hi unambiguously as the value at which we find that the approximation in eqn (20) departs from the exact integral in eqn (15). This criterion gives us hi ≃ 9 Å and εi ≃ 5. The approximated formulae (20) and (21) match completely the model of 3 capacitors in series that was used in ref. 20 to interpret the experimental results, except that here hi and εi are not fitting parameters but follow from a microscopic analysis. We note that the final formulae proposed in the dielectric continuum theory approach of Cox and Geissler35 or in the dividing surface model of Loche et al.27 amount in eqn (21) to reduce the interfacial width hi to the depletion length where the fluid density is zero (roughly hi = 2 Å by inspection of Fig. 3) and to fix accordingly εi = 1.
⊥(z). Here we can define hi unambiguously as the value at which we find that the approximation in eqn (20) departs from the exact integral in eqn (15). This criterion gives us hi ≃ 9 Å and εi ≃ 5. The approximated formulae (20) and (21) match completely the model of 3 capacitors in series that was used in ref. 20 to interpret the experimental results, except that here hi and εi are not fitting parameters but follow from a microscopic analysis. We note that the final formulae proposed in the dielectric continuum theory approach of Cox and Geissler35 or in the dividing surface model of Loche et al.27 amount in eqn (21) to reduce the interfacial width hi to the depletion length where the fluid density is zero (roughly hi = 2 Å by inspection of Fig. 3) and to fix accordingly εi = 1.
The three separated capacitor picture expressed using eqn (20) and (21) should not apply when h < 2hi, i.e., below ∼20 Å. In that case one has to resort merely to numerical integration in eqn (15). For the h = 10 Å case, illustrated in Fig. 4 and 5, the numerical integral yields a slab-averaged dielectric constant of ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥ = 2.3; this is a surprisingly small value compared to that of the bulk, that is in line with the experimental findings for water. In Fig. 6, we have plotted
⊥ = 2.3; this is a surprisingly small value compared to that of the bulk, that is in line with the experimental findings for water. In Fig. 6, we have plotted ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) computed over the range 0–10 nm, together with the asymptotic formula (21) starting from the same microscopic/nanoscopic distances up to the micrometer range. We use the same log–log representation as in ref. 20 for direct comparison. Although our curves correspond to a simplified water model embedded in a simplified slab (no H-bonds and no electronic polarisation), the similarities with the experimental results are striking. In particular we recover the main feature pointed out by the experimental work: the effective dielectric constant measured in slabs with a thickness in the 1 nm range is found to be around 2; this was quoted as an “anomalously low dielectric constant of confined water”. Our theoretical work makes it possible to bring some insight to the interpretation of the experimental results. Indeed the long range behaviour observed for
⊥(h) computed over the range 0–10 nm, together with the asymptotic formula (21) starting from the same microscopic/nanoscopic distances up to the micrometer range. We use the same log–log representation as in ref. 20 for direct comparison. Although our curves correspond to a simplified water model embedded in a simplified slab (no H-bonds and no electronic polarisation), the similarities with the experimental results are striking. In particular we recover the main feature pointed out by the experimental work: the effective dielectric constant measured in slabs with a thickness in the 1 nm range is found to be around 2; this was quoted as an “anomalously low dielectric constant of confined water”. Our theoretical work makes it possible to bring some insight to the interpretation of the experimental results. Indeed the long range behaviour observed for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) has no mystery since, under longitudinal conditions, the measure of the average polarisation or capacitance yields the integral of 1/ε⊥(z) which, since 1/εbulk ≪ 1, gets its main contribution from the boundaries. Very thick slabs are required for the bulk to contribute. This is clear from the slow hi/h convergence appearing in eqn (21). It should be noted that this asymptotic formula using the values hi and εi derived above works extremely well even in the h = 1 nm range, i.e., down to separation distances h < 2hi where it should not! We can only attribute this to continuity that allows the extrapolation of the curve over a limited range below its validity. Note also that since εbulk/εi ≫ 1, the results essentially depend on the ratio hi/εi so that, on an empirical ground, other choices of these parameters make it possible to reproduce the average slab dielectric constant. In particular one can take εi = 1 and hi = 9/5 = 1.8 Å, a value very close to the one suggested in the dielectric continuum theory (DCT) of Cox and Geissler;35 see Fig. 6. There is in fact much more in their analysis than considering this limit that amounts to modelling the solid–liquid interface as a step-function. Their study points out the importance, as well as the ambiguity, of locating the dielectric boundaries and of properly defining the volume of the device, which contains a molecular exclusion volume portion and one filled by the liquid. Such ambiguity is present in our definition of the device polarisation that involves its thickness h (eqn (14)). We have taken as a natural microscopic definition of h the distance between the center of the surface atoms of each plate, so that the integrated Lennard-Jones potential can be defined as in eqn (6). Other experimental choices for h are possible and the measurement of the device thickness is also subject to experimental uncertainties. The influence of this uncertainty is illustrated in the ESI.† The observed trends are in clear agreement with those in ref. 35. Although based on a simplified, step-wise, molecular representation of the solid–liquid interface, the DCT approach captures the essential balance between low and high dielectric constant volumes.
⊥(h) has no mystery since, under longitudinal conditions, the measure of the average polarisation or capacitance yields the integral of 1/ε⊥(z) which, since 1/εbulk ≪ 1, gets its main contribution from the boundaries. Very thick slabs are required for the bulk to contribute. This is clear from the slow hi/h convergence appearing in eqn (21). It should be noted that this asymptotic formula using the values hi and εi derived above works extremely well even in the h = 1 nm range, i.e., down to separation distances h < 2hi where it should not! We can only attribute this to continuity that allows the extrapolation of the curve over a limited range below its validity. Note also that since εbulk/εi ≫ 1, the results essentially depend on the ratio hi/εi so that, on an empirical ground, other choices of these parameters make it possible to reproduce the average slab dielectric constant. In particular one can take εi = 1 and hi = 9/5 = 1.8 Å, a value very close to the one suggested in the dielectric continuum theory (DCT) of Cox and Geissler;35 see Fig. 6. There is in fact much more in their analysis than considering this limit that amounts to modelling the solid–liquid interface as a step-function. Their study points out the importance, as well as the ambiguity, of locating the dielectric boundaries and of properly defining the volume of the device, which contains a molecular exclusion volume portion and one filled by the liquid. Such ambiguity is present in our definition of the device polarisation that involves its thickness h (eqn (14)). We have taken as a natural microscopic definition of h the distance between the center of the surface atoms of each plate, so that the integrated Lennard-Jones potential can be defined as in eqn (6). Other experimental choices for h are possible and the measurement of the device thickness is also subject to experimental uncertainties. The influence of this uncertainty is illustrated in the ESI.† The observed trends are in clear agreement with those in ref. 35. Although based on a simplified, step-wise, molecular representation of the solid–liquid interface, the DCT approach captures the essential balance between low and high dielectric constant volumes.
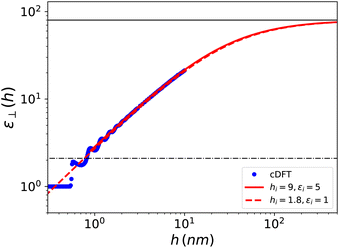 |
| | Fig. 6 Effective dielectric constant computed using cDFT for the model Stockmayer fluid embedded in a slab of width h as a function of h. The red solid curve corresponds to the asymptotic formula (21) with the parameters determined in the text; it starts at h = hi. The red dashed curve corresponds to the dielectric continuum theory of Cox and Geissler35 or dividing surface model of Loche et al.27 with εi = 1 and hi = 9/5 = 1.8 Å. These curves can be compared with the experimental results reported in ref. 20 for water in nano- to micrometric hBN slits. | |
Finally, our results show a structuration due to molecular stacking for thicknesses in the 0.6–1.2 nm range, with two clear peaks at h = 0.6 and 1 nm and damped oscillations beyond. This is in agreement with the sub-nanometer oscillatory behaviour observed by simulations by Jalali et al.30 for SPC/E water in tight confinement. The overall flattening of the curve around a value of 2 seems reminiscent, within the error bars, of the plateau detected experimentally in the 1 nm region.
4 Extension to SPC/E water
To get even closer to water, although still at a dipolar level, we extend the previous theory by introducing in the functional the parameters and the cS(z) and cL(z) direct correlation functions corresponding to SPC/E water. We take the simple weighted density approximation of ref. 52 and 63 for the bridge functional. Since the symmetry of water is beyond that of a simple dipole, at least a supplementary density-polarisation coupling has to be introduced in the functional in the form48| | 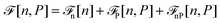 | (22) |
with| | 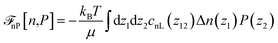 | (23) |
This introduces the fact that spontaneous polarisation exists even in a slab with a zero applied field. The corresponding polarisation profile is anti-symmetrical with respect to the two walls and the integrated polarisation of the sample is zero, as it should be. This spontaneous polarisation remains prominent when a small to moderate external field is applied. See Fig. 7 for a large slab with h = 50 Å and also ref. 51 where molecular density functional theory calculations were performed with a molecular representation of the electrodes and a constant voltage applied between the electrodes rather than an external electric field.
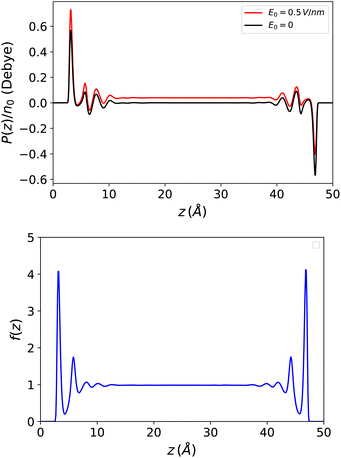 |
| | Fig. 7 Top: Polarisation in a slab of width h = 50 Å with and without an applied external electric field. Spontaneous polarisation exists due to the density/polarisation coupling of eqn (23) which remains the dominant contribution at the interfaces when a field is applied. Bottom: The resulting response function f(z) = 4π(P(z) − P0(z))/E0 which appears perfectly symmetrical. | |
On the other hand, the dielectric response f(z) = 4π(P(z) − P0(z))/E0, represented in Fig. 7, is perfectly symmetrical. It appears less oscillatory and reaches the bulk value more rapidly than in the Stockmayer case in Fig. 3; this is a sign that the damping of spatial correlations occurs more quickly in water than in a purely dipolar liquid. In Fig. 8 this response is plotted in terms of the ill-defined, local microscopic constant and of its well-defined coarse-grained version.
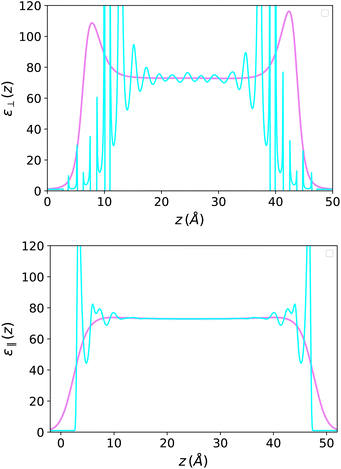 |
| | Fig. 8 Top: (III-defined) Microscopic perpendicular dielectric constant for SPC/E water in a slab of width h = 50 Å (in cyan) and its coarse-grained version with a coarse-graining length σP = 2 Å (in violet). Bottom: the same for the parallel dielectric constant when the field is applied parallel to the plates (σP = 1.5 Å). | |
We present in Fig. 9 the curve for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) which is very similar to the one obtained for the Stockmayer solvent, so that identical conclusions can be drawn. No specific properties of water emerge, beyond being a polar, molecular fluid with a high dielectric constant. This result is consistent with the observation by MD simulations28 that confined polar liquids such as methanol, acetonitrile and dichloromethane exhibit a dielectric constant reduction similar to that of water. We further note that in our results the dielectric constant reduction of confined water is reproduced by considering exclusively the number and polarisation densities, without requiring orientational constraints imposed by the interface on the water molecules. We find an interfacial width hi = 7.5 Å and an associated effective interfacial dielectric constant εi = 3.9, to be compared to hi = 7.4 and εi = 2.1 determined experimentally by Fumagalli et al.20hi appears slightly smaller for SPC/E than for the purely dipolar fluid since, as we mentioned, the spatial correlations in water have a shorter range. Concordantly, we observe oscillations of
⊥(h) which is very similar to the one obtained for the Stockmayer solvent, so that identical conclusions can be drawn. No specific properties of water emerge, beyond being a polar, molecular fluid with a high dielectric constant. This result is consistent with the observation by MD simulations28 that confined polar liquids such as methanol, acetonitrile and dichloromethane exhibit a dielectric constant reduction similar to that of water. We further note that in our results the dielectric constant reduction of confined water is reproduced by considering exclusively the number and polarisation densities, without requiring orientational constraints imposed by the interface on the water molecules. We find an interfacial width hi = 7.5 Å and an associated effective interfacial dielectric constant εi = 3.9, to be compared to hi = 7.4 and εi = 2.1 determined experimentally by Fumagalli et al.20hi appears slightly smaller for SPC/E than for the purely dipolar fluid since, as we mentioned, the spatial correlations in water have a shorter range. Concordantly, we observe oscillations of ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) around the value of 2 in the 0.6–1 nm range with a first minimum at 1.8 around h = 0.75 nm and a second higher minimum around h = 1 nm; this is in agreement with the simulation results of ref. 30. Indeed, those oscillations are dampened more quickly than in the Stockmayer case.
⊥(h) around the value of 2 in the 0.6–1 nm range with a first minimum at 1.8 around h = 0.75 nm and a second higher minimum around h = 1 nm; this is in agreement with the simulation results of ref. 30. Indeed, those oscillations are dampened more quickly than in the Stockmayer case.
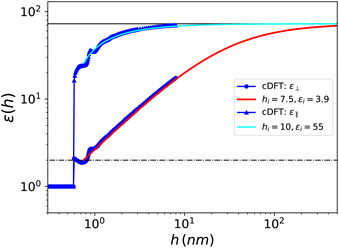 |
| | Fig. 9 Effective dielectric constant for SPC/E water embedded in a slab of width h as a function of h. The blue dots show the cDFT results for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) and the red solid curve corresponds to the asymptotic formula (21) with the parameters determined in the text and down to h = hi. The blue triangles and cyan solid curve are the same for ⊥(h) and the red solid curve corresponds to the asymptotic formula (21) with the parameters determined in the text and down to h = hi. The blue triangles and cyan solid curve are the same for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ‖(h). ‖(h). | |
Finally, although we are not aware of any experimental results to compare with, we take the opportunity here to study the transverse polarisation case, i.e., applying an external electric field in the transverse direction x parallel to the plates. All the DFT formalism developed above remains valid if the longitudinal direct correlation function cL(z) in eqn (8) is replaced by the transverse one, cT(z), defined as the inverse, 1D Fourier transform of cΔ(q) − cD(q).48 The density-polarisation coupling of eqn (23) vanishes in this case and one resorts to the joint minimisation of the equivalent of the functional in eqn (7) and (8) using cT(z). The response function to a constant field E0 is defined in this case using
| | | f(z) = 4πP(z)/E0 = ε‖(z) − 1 | (24) |
The picture is different from that in the longitudinal case since the measure now concerns ε instead of 1/ε. As seen in Fig. 8 for a 50 Å-slab, the resulting ε‖(z) presents oscillations close to the boundaries but remains everywhere positive and well-defined. This simple fact was emphasised in the early studies of Ballenegger and Hansen13 and confirmed by subsequent MD studies using molecular solvents.14,18,19,25–27 For a slab of thickness h, an effective dielectric constant can be defined as
| | 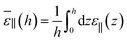 | (25) |
If the slab is thick enough to distinguish two interfacial regions from an intermediate bulk buffer, as illustrated in Fig. 8, the following simple formula pertinent to 3 capacitors in parallel can be inferred by decomposing the integral
| | 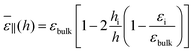 | (26) |
with
| | 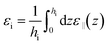 | (27) |
Again εi is fixed by the choice of a reasonable hi. Using the same unambiguous selection criterion as before (the minimal hi that fulfils the asymptotic eqn (26)), we find hi = 10 Å and εi ≃ 50, i.e., a much larger interfacial, effective value than in the perpendicular case. Besides it can be seen in Fig. 9 that the bulk value is reached for slabs of thickness h ≃ 10 nm, thus much narrower than ∼500 nm necessary for the perpendicular dielectric constant. As for the out-of-plan polarisation case, a slight oscillatory behaviour of the in-plane dielectric constant ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ‖(h) is observed for thicknesses between 0.6 and 1 nm but we do not detect the drastic drop by two orders of magnitude that Hamid et al. found in their simulations around h = 0.75 nm, that they attribute to a freezing transition occurring under that particular packing condition.31
‖(h) is observed for thicknesses between 0.6 and 1 nm but we do not detect the drastic drop by two orders of magnitude that Hamid et al. found in their simulations around h = 0.75 nm, that they attribute to a freezing transition occurring under that particular packing condition.31
Finally, let us mention that our DFT results are in overall agreement with those of previous MD simulations.14,16,18,19,25,27,28 In particular Itoh and Sakuma16 computed the perpendicular and parallel effective dielectric constants of three-dimensional graphite/SPCE-water/graphite slabs of various sizes by MD simulations. In spite of our different, simplified modelling of water and of the surface–water interactions, the DFT results in Fig. 8 are in quantitative agreement with theirs for the few slab geometries that they explored.
5 Conclusions
In this work, we presented a simple two-variable, number/polarisation density functional theory describing the microscopic structure of polar fluids at interfaces or in confinement, as well as their microscopic dielectric response to external fields. For a given system geometry the numerical solution is obtained instantaneously with a laptop and compares very well with previous MD simulations of closely related systems.9,19 It provides locally coarse-grained quantities at a modest numerical cost that can further nourish continuum Poisson-Boltzmann models. The approach made it possible to model thin water films of various thicknesses and to mimic the experimental setup in ref. 20. Our modelling is indeed incomplete and neglects physical features such as the precise chemical nature of the interface, its three-dimensional roughness, and the electronic polarisability of both the solid surfaces and the solvent. A main conclusion, however, is that finding very low effective longitudinal dielectric constants of the order of 2–3 for water in slabs of nanometer size through capacitance measurements should not be a special property of water but is true for any generic polar solvent having a high bulk dielectric constant. Fig. 6 obtained for the Stockmayer solvent or Fig. 9 for a dipolar representation of water present close similarities with the experimental curve in ref. 20. A similar conclusion is reached in ref. 35 which follows a purely macroscopic, electrostatics route. On the other hand the definition of a local, space-dependent longitudinal dielectric constant is found irrelevant at a microscopic level close to the walls but can be inferred at a molecular coarse-grained level with a smoothing length of the order of the size of a solvent particle. This local dielectric constant is shown to reach its bulk value after a short distance hi from the slab walls, typically 10 Å for water. This clearly defines a short-range interfacial solvent region with an effectively low dielectric constant εi. Since in the longitudinal polarisation case the response concerns 1/ε rather than directly ε, incorporating the intermediate bulk region with a 1/εbulk contribution turns rigorously to a three-capacitors-in-series model described by formula (20). Since the 1/εbulk is small, the low dielectric constant interfacial regions dominate and it requires large slab thicknesses for the bulk to contribute; this explains the very slow increase of ε with slab thickness. Our theoretical approach brings additional insight to this simple, phenomenological capacitor model. (1) Although it should not apply to slab width below 2hi, twice the interfacial thickness, it holds for shorter distances down to hi. We take this as a continuity effect. (2) In our microscopic analysis, the parameter hi can be defined unambiguously from the microscopic structure and it also fixes the value of the second parameter εi. Phenomenologically, since the behaviour in eqn (20) depends essentially on the ratio hi/εi, other choices of parameter couples are possible including the extreme choice εi = 1 (see Fig. 6). (3) We observe an oscillatory behaviour, leading to an effective flattening of the dielectric response around ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) = 2 for slabs below 1 nm, a saturation effect that is reminiscent of the one detected experimentally. In our case, we can relate this non-monotonic behaviour to the interplay between the polarisation response and hard-sphere packing when only one or two layers of solvent particles are allowed in the slab.
⊥(h) = 2 for slabs below 1 nm, a saturation effect that is reminiscent of the one detected experimentally. In our case, we can relate this non-monotonic behaviour to the interplay between the polarisation response and hard-sphere packing when only one or two layers of solvent particles are allowed in the slab.
We have also studied the complementary case of the transverse response when the perturbing field is applied parallel to the walls instead of perpendicular. In that case the microscopic dielectric constant ε‖(z) is well-defined although it presents some structural oscillations close to the walls; those are smoothed out by coarse-graining over particle dimensions. A three-capacitors-in-parallel model described by eqn (26) is found to apply for slabs above 1 nm and the overall slab capacitance is found to reach the bulk value for slab thickness on the order of 10 nm, i.e., much narrower than in the perpendicular case. The inferred interfacial effective dielectric constant is also much higher.
Finally, let us mention that water in confinement can be described at a much more refined molecular density functional theory level using the full MDFT formalism and its associated MDFT software that includes not only the dipolar symmetry but also all the higher multipolar symmetries and also makes it possible to represent the surface–water interaction at a fully atomistic, 3D level.51 Such calculations are underway and will be presented in a forthcoming publication.
Data availability
The data that support the findings of this study are available from the corresponding author, D. B. upon reasonable request.
Author contributions
All authors have contributed equally to this work.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Agence Nationale de la Recherche, project ANR BRIDGE AAP CE29.
References
-
W. D. Jackson, Classical Electrodynamics, Wiley, New York, 3rd edn, 1999 Search PubMed.
- L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486 CrossRef CAS.
- J. Kirkwood, J. Chem. Phys., 1939, 7, 911 CrossRef CAS.
- F. Booth, J. Chem. Phys., 1951, 19, 391–394 CrossRef CAS.
- G. Nienhuis and J. M. Deutch, J. Chem. Phys., 1971, 55, 4213–4229 CrossRef CAS.
- J. D. Ramshaw, J. Chem. Phys., 1971, 55, 1763 CrossRef CAS.
- J. D. Ramshaw, J. Chem. Phys., 1977, 66, 3134 CrossRef CAS.
-
J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids: With Applications to Soft Matter, Academic Press, Amstersdam, 4th edn, 2013 Search PubMed.
- V. Ballenegger and J. P. Hansen, Europhys. Lett., 2003, 63, 381–387 CrossRef CAS.
- B. Roux and T. Simonson, Biophys. Chem., 1999, 78, 1–20 CrossRef CAS PubMed.
- T. Simonson and D. Perahia, Proc. Natl. Acad. Sci. U.S.A., 1995, 92, 1082–1086 CrossRef CAS PubMed.
- T. Simonson and C. L. Brooks, J. Am. Chem. Soc., 1996, 118, 8452–8458 CrossRef CAS.
- V. Ballenegger and J. P. Hansen, J. Chem. Phys., 2005, 122, 114711 CrossRef CAS PubMed.
- D. J. Bonthuis, S. Gekle and R. R. Netz, Phys. Rev. Lett., 2011, 107, 1–5 CrossRef PubMed.
- A. Ghoufi, A. Szymczyk, R. Renou and M. Ding, EPL, 2012, 99, 37008 CrossRef.
- H. Itoh and H. Sakuma, J. Chem. Phys., 2015, 142, 184703 CrossRef PubMed.
- C. Schaaf and S. Gekle, Phys. Rev. E - Stat. Nonlinear Soft Matter Phys., 2015, 92, 1–9 CrossRef PubMed.
- A. Schlaich, E. W. Knapp and R. R. Netz, Phys. Rev. Lett., 2016, 117, 1–5 CrossRef PubMed.
- J. F. Olivieri, J. T. Hynes and D. Laage, J. Phys. Chem. Lett., 2021, 12, 4319–4326 CrossRef CAS PubMed.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342 CrossRef CAS PubMed.
- M. A. V. Devanathan and V. Tilak, Chem. Phys., 1965, 65, 635–684 CAS.
- O. Stern and Z. Elektrochem, Angew. Phys. Chem., 1924, 30, 508 CAS.
- C. Zhang, F. Gygi and G. Galli, J. Phys. Chem. Lett., 2013, 4, 2477–2481 CrossRef CAS.
- C. Zhang, J. Chem. Phys., 2018, 148, 156101 CrossRef PubMed.
- M. Motevaselian and N. Aluru, J. Phys. Chem. Lett., 2020, 11, 10532–10537 CrossRef CAS PubMed.
- S. Ruiz-Barragan, D. Munoz-Santiburcio, S. Korning and D. Marx, Phys. Chem. Chem. Phys., 2020, 22, 10833–10837 RSC.
- P. Loche, C. Ayaz, A. Wolde-Kidan, A. Schlaich and R. R. Netz, J. Phys. Chem. B, 2020, 124, 4365–4371 CrossRef CAS PubMed.
- M. H. Motevaselian and N. R. Aluru, ACS Nano, 2020, 14, 12761–12770 CrossRef PubMed.
- S. Mondal and B. Bagchi, Nano Lett., 2020, 20, 8959–8964 CrossRef CAS PubMed.
- H. Jalali, H. Ghorbanfekr, I. Hamid, M. Neek-Amal, R. Rashidi and F. M. Peeters, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2020, 102, 1–6 CrossRef PubMed.
- I. Hamid, H. Jalali, F. M. Peeters and M. Neek-Amal, J. Chem. Phys., 2021, 154, 114503 CrossRef CAS PubMed.
- C. Qi, Z. Zhu, C. Wang and Y. Zheng, J. Phys. Chem. Lett., 2021, 12, 931–937 CrossRef CAS PubMed.
- I. Ahmadabadi, A. Esfandiar, A. Hassanali and M. R. Ejtehadi, Phys. Rev. Mater., 2021, 5, 024008 CrossRef CAS.
- F. Deissenbeck and S. Wippermann, J. Chem. Theory Comput., 2023, 19, 1035–1043 CrossRef CAS PubMed.
- S. J. Cox and P. L. Geissler, Chem. Sci., 2022, 13, 9102–9111 RSC.
- G. Monet, H. Berthoumieux, F. Bresme and A. Kornyshev, Phys. Rev. Lett., 2021, 126, 216001 CrossRef CAS PubMed.
- J. Noji, A. Yoshimori, J. Ohnuki and M. Takano, J. Phys. Soc. Jpn., 2022, 9, 114602 CrossRef.
- S. Marčelja and N. Radić, Chem. Phys. Lett., 1976, 42, 129–130 CrossRef.
- R. Evans, Adv. Phys., 1979, 28, 143 CrossRef CAS.
-
R. Evans, Fundamentals of Inhomogeneous Fluids, Marcel Dekker, Incorporated, 1992 Search PubMed.
- P. Frodl and S. Dietrich, Phys. Rev. A, 1992, 45, 7330 CrossRef CAS PubMed.
- T. Biben, J. P. Hansen and Y. Rosenfeld, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 57, R3727–R3730 CrossRef CAS.
- A. Oleksy and J. P. Hansen, J. Chem. Phys., 2010, 132, 204702 CrossRef PubMed.
- J. Wu and Z. Li, Annu. Rev. Phys. Chem., 2007, 58, 85–112 CrossRef CAS PubMed.
- R. Ramirez, R. Gebauer, M. Mareschal and D. Borgis, Phys. Rev. E, 2002, 66, 031206 CrossRef PubMed.
- R. Ramirez and D. Borgis, J. Phys. Chem. B, 2005, 109, 6754–6763 CrossRef CAS PubMed.
- G. Jeanmairet, M. Levesque, R. Vuilleumier and D. Borgis, J. Phys. Chem. Lett., 2013, 4, 619–624 CrossRef CAS PubMed.
- G. Jeanmairet, N. Levy, M. Levesque and D. Borgis, J. Phys. Condens. Matter, 2016, 28, 244005 CrossRef PubMed.
- D. Borgis, L. Gendre and R. Ramirez, J. Phys. Chem. B, 2012, 116, 2504–2512 CrossRef CAS PubMed.
- L. Ding, M. Levesque, D. Borgis and L. Belloni, J. Chem. Phys., 2017, 147, 094107 CrossRef PubMed.
- G. Jeanmairet, B. Rotenberg, D. Borgis and M. Salanne, J. Chem. Phys., 2019, 151, 124111 CrossRef PubMed.
- D. Borgis, S. Luukkonen, L. Belloni and G. Jeanmairet, J. Chem. Phys., 2021, 155, 024117 CrossRef CAS PubMed.
- E. L. Pollock and B. J. Alder, Phys. A Stat. Mech. its Appl., 1980, 102, 1–21 CrossRef.
- M. Levesque, V. Marry, B. Rotenberg, G. Jeanmairet, R. Vuilleumier and D. Borgis, J. Chem. Phys., 2012, 137, 224107 CrossRef PubMed.
- Y. Rosenfeld, Phys. Rev. Lett., 1989, 63, 980–983 CrossRef CAS PubMed.
- R. Roth, R. Evans, A. Lang and G. Kahl, J. Phys. Condens. Matter, 2002, 14, 12063 CrossRef CAS.
- R. Roth, J. Phys.: Condens. Matter, 2010, 22, 063102 CrossRef PubMed.
- E. Kierlik and M. L. Rosinberg, Phys. Rev. A, 1990, 42, 3382–3387 CrossRef PubMed.
- M. Levesque, R. Vuilleumier and D. Borgis, J. Chem. Phys., 2012, 137, 034115 CrossRef PubMed.
- J. Fu, Y. Liu, Y. Tian and J. Wu, J. Phys. Chem. C, 2015, 119, 5374–5385 CrossRef CAS.
- H. Berthoumieux, G. Monet and R. Blossey, J. Chem. Phys., 2021, 155, 024112 CrossRef CAS PubMed.
- M. A. Vorotyntsev and A. A. Rubashkin, Chem. Phys., 2019, 521, 14–24 CrossRef CAS.
- D. Borgis, S. Luukkonen, L. Belloni and G. Jeanmairet, J. Phys. Chem. B, 2020, 124, 6885–6893 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Damien
Laage
b,
Luc
Belloni
c and
Guillaume
Jeanmairet
*ab,
Damien
Laage
b,
Luc
Belloni
c and
Guillaume
Jeanmairet
 de
de
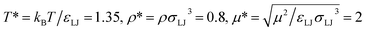 . These parameters yield a dielectric constant ε = 80. They also correspond to a state point considered by Ballenegger and Hansen when studying the dielectric properties of the closely related dipolar-soft-sphere model in confinement.13 As shown in ref. 45–48 and 54, such a dipolar liquid subjected to an external potential can be described accurately by a grand-potential functional depending on the local number density n(r) and local polarisation density P(r). This functional is determined by the chemical potential of the bulk fluid at density n0. It can be decomposed into density and polarisation terms,
. These parameters yield a dielectric constant ε = 80. They also correspond to a state point considered by Ballenegger and Hansen when studying the dielectric properties of the closely related dipolar-soft-sphere model in confinement.13 As shown in ref. 45–48 and 54, such a dipolar liquid subjected to an external potential can be described accurately by a grand-potential functional depending on the local number density n(r) and local polarisation density P(r). This functional is determined by the chemical potential of the bulk fluid at density n0. It can be decomposed into density and polarisation terms, 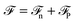 , with the density term given by
, with the density term given by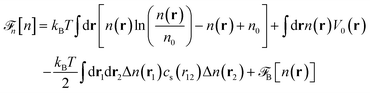
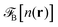 is the so called bridge functional, that we take here as a hard-sphere (HS) bridge functional based on fundamental measure theory,55–57 using the Kierlik-Rosinberg scalar version58,59 and a reference HS diameter defined conventionally as dHS = σLJ(1 + 0.298T*)/(1 + 0.3316T* + 0.001048T*2).60 The polarization part of the functional reads
is the so called bridge functional, that we take here as a hard-sphere (HS) bridge functional based on fundamental measure theory,55–57 using the Kierlik-Rosinberg scalar version58,59 and a reference HS diameter defined conventionally as dHS = σLJ(1 + 0.298T*)/(1 + 0.3316T* + 0.001048T*2).60 The polarization part of the functional reads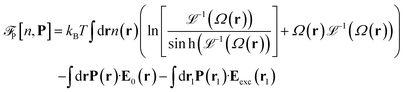
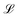 denotes the Langevin function and
denotes the Langevin function and 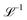 its inverse. E0(r) is the external electric field at point r. The excess electric field Eexc(r1) is defined using
its inverse. E0(r) is the external electric field at point r. The excess electric field Eexc(r1) is defined using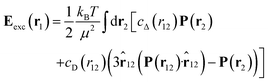
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = r12/r12. In eqn (1) and (3), cS(r), cΔ(r), and cD(r) represent the spherical and dipolar spherical-invariant projections of the angular-dependent direct correlation function of the bulk liquid at density n0. These functions are inputs in the theory and are obtained from a preliminary simulation of the bulk fluid. See ref. 45 and 48 for their behaviour in direct and Fourier space.
12 = r12/r12. In eqn (1) and (3), cS(r), cΔ(r), and cD(r) represent the spherical and dipolar spherical-invariant projections of the angular-dependent direct correlation function of the bulk liquid at density n0. These functions are inputs in the theory and are obtained from a preliminary simulation of the bulk fluid. See ref. 45 and 48 for their behaviour in direct and Fourier space.
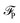 with respect to P(r) for a given n(r) gives
with respect to P(r) for a given n(r) gives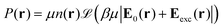
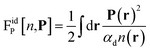
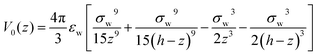
 of eqn (1)–(3) can be written per surface area in the form
of eqn (1)–(3) can be written per surface area in the form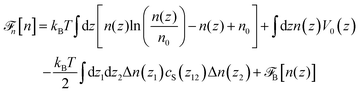
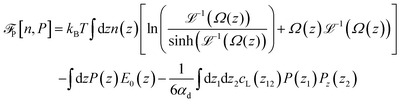

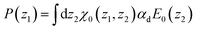
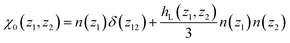
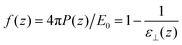
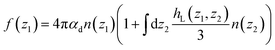
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) with a coarse-graining length of at least the size of a particle (this approach was used in ref. 13 to smooth the dipolar fluctuations). Here, this can be formalised by looking at a coarse-grained polarisation field, defined for example using
⊥(z) with a coarse-graining length of at least the size of a particle (this approach was used in ref. 13 to smooth the dipolar fluctuations). Here, this can be formalised by looking at a coarse-grained polarisation field, defined for example using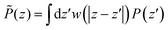
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) can be defined from
⊥(z) can be defined from ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (z) exactly as in eqn (11). The inverse, coarse-grained, dielectric constant 1/
(z) exactly as in eqn (11). The inverse, coarse-grained, dielectric constant 1/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(r) corresponding to λ = 0.7 is plotted as a function of distance in Fig. 3-top together with the bare microscopic results. This quantity now appears as a smooth curve that remains strictly positive, so that
⊥(r) corresponding to λ = 0.7 is plotted as a function of distance in Fig. 3-top together with the bare microscopic results. This quantity now appears as a smooth curve that remains strictly positive, so that ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (r) itself is well defined and well behaved; see Fig. 3-bottom. It presents two peaks at values higher than those in the bulk close to the walls; the main feature to be retained, however, is that the bulk value is reached after a few particle diameters, at a distance where the microscopic polarisation still presents microscopic oscillations (z ∼ 4–5σLJ), and there are no long-range effects induced by the walls on the local dielectric constant. We note that the coarse-graining length σP should not be considered a fundamental quantity, but rather an observation length scale. It might also be linked to the resolution of the experiment that is realised. As soon as this observation/resolution becomes comparable to the particle size, 1/
(r) itself is well defined and well behaved; see Fig. 3-bottom. It presents two peaks at values higher than those in the bulk close to the walls; the main feature to be retained, however, is that the bulk value is reached after a few particle diameters, at a distance where the microscopic polarisation still presents microscopic oscillations (z ∼ 4–5σLJ), and there are no long-range effects induced by the walls on the local dielectric constant. We note that the coarse-graining length σP should not be considered a fundamental quantity, but rather an observation length scale. It might also be linked to the resolution of the experiment that is realised. As soon as this observation/resolution becomes comparable to the particle size, 1/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) and
⊥(z) and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) appear as locally well-defined, positive quantities. As a rule of thumb, to keep a microscopic character in our analysis, we choose σP large enough to smooth the spurious behaviour of 1/ε(z) (or f(z)), but small enough to have its overall microscopic behaviour unchanged, in particular keeping a limited penetration into the walls and an unaltered distance at which the bulk value is reached. We find both conditions typically fulfilled for 0.6 ≤ λ ≤ 1; λ = 0.7 appears to be a good compromise. The variation of the results of Fig. 3 with the parameter λ is illustrated in the ESI.† Increasing λ from 0.7 to 1 and beyond gives a more regular behaviour for
⊥(z) appear as locally well-defined, positive quantities. As a rule of thumb, to keep a microscopic character in our analysis, we choose σP large enough to smooth the spurious behaviour of 1/ε(z) (or f(z)), but small enough to have its overall microscopic behaviour unchanged, in particular keeping a limited penetration into the walls and an unaltered distance at which the bulk value is reached. We find both conditions typically fulfilled for 0.6 ≤ λ ≤ 1; λ = 0.7 appears to be a good compromise. The variation of the results of Fig. 3 with the parameter λ is illustrated in the ESI.† Increasing λ from 0.7 to 1 and beyond gives a more regular behaviour for ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) but indeed a more important smoothing of the boundaries. We argue in the ESI† that, for modelling purposes, the fundamental quantity to consider is rather the coarse-grained response
⊥(z) but indeed a more important smoothing of the boundaries. We argue in the ESI† that, for modelling purposes, the fundamental quantity to consider is rather the coarse-grained response ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (z) that is less sensitive to the choice of λ and can be modelled with two inverted sigmoid-like curves, yielding smooth curves when converted to
(z) that is less sensitive to the choice of λ and can be modelled with two inverted sigmoid-like curves, yielding smooth curves when converted to ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z).
⊥(z).


![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) obtained through eqn (13) with a coarse-graining length σP = 0.7σLJ (violet curve). Bottom: Coarse-grained dielectric constant
⊥(z) obtained through eqn (13) with a coarse-graining length σP = 0.7σLJ (violet curve). Bottom: Coarse-grained dielectric constant ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) whereas the corresponding microscopic ε⊥(z) is ill-defined.
⊥(z) whereas the corresponding microscopic ε⊥(z) is ill-defined.![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z) displayed in Fig. 5 has a nice and smooth hat shape that reaches a maximum value around 10 in the middle of the slab, again far below the bulk value.
⊥(z) displayed in Fig. 5 has a nice and smooth hat shape that reaches a maximum value around 10 in the middle of the slab, again far below the bulk value.

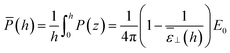
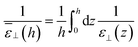
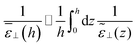
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (0) =
(0) = ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (h) ≃ 0. The microscopic expressions 14–15 remain the ones to be used in the following. Expressing the total electrostatic energy of the device, which includes the self-energy of the electric field between the plates, writing the potential difference between them as
(h) ≃ 0. The microscopic expressions 14–15 remain the ones to be used in the following. Expressing the total electrostatic energy of the device, which includes the self-energy of the electric field between the plates, writing the potential difference between them as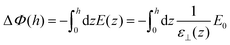
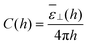
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) having the same definition as in eqn (15). Measuring the average polarisation in the slab or the effective slab capacitance is thus equivalent. When the plate-to-plate distance h is large enough as in Fig. 3, one can divide the device into three regions, two interfacial regions of width hi and an intermediate bulk region of width h − 2hi where ε⊥(z) ≃εbulk. In that case, the choice of hi results in the definition of an effective dielectric constant εi for the interfacial region through
⊥(h) having the same definition as in eqn (15). Measuring the average polarisation in the slab or the effective slab capacitance is thus equivalent. When the plate-to-plate distance h is large enough as in Fig. 3, one can divide the device into three regions, two interfacial regions of width hi and an intermediate bulk region of width h − 2hi where ε⊥(z) ≃εbulk. In that case, the choice of hi results in the definition of an effective dielectric constant εi for the interfacial region through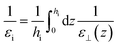
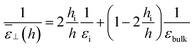
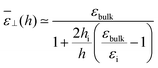
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ⊥(z). Here we can define hi unambiguously as the value at which we find that the approximation in eqn (20) departs from the exact integral in eqn (15). This criterion gives us hi ≃ 9 Å and εi ≃ 5. The approximated formulae (20) and (21) match completely the model of 3 capacitors in series that was used in ref. 20 to interpret the experimental results, except that here hi and εi are not fitting parameters but follow from a microscopic analysis. We note that the final formulae proposed in the dielectric continuum theory approach of Cox and Geissler35 or in the dividing surface model of Loche et al.27 amount in eqn (21) to reduce the interfacial width hi to the depletion length where the fluid density is zero (roughly hi = 2 Å by inspection of Fig. 3) and to fix accordingly εi = 1.
⊥(z). Here we can define hi unambiguously as the value at which we find that the approximation in eqn (20) departs from the exact integral in eqn (15). This criterion gives us hi ≃ 9 Å and εi ≃ 5. The approximated formulae (20) and (21) match completely the model of 3 capacitors in series that was used in ref. 20 to interpret the experimental results, except that here hi and εi are not fitting parameters but follow from a microscopic analysis. We note that the final formulae proposed in the dielectric continuum theory approach of Cox and Geissler35 or in the dividing surface model of Loche et al.27 amount in eqn (21) to reduce the interfacial width hi to the depletion length where the fluid density is zero (roughly hi = 2 Å by inspection of Fig. 3) and to fix accordingly εi = 1.![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥ = 2.3; this is a surprisingly small value compared to that of the bulk, that is in line with the experimental findings for water. In Fig. 6, we have plotted
⊥ = 2.3; this is a surprisingly small value compared to that of the bulk, that is in line with the experimental findings for water. In Fig. 6, we have plotted ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) computed over the range 0–10 nm, together with the asymptotic formula (21) starting from the same microscopic/nanoscopic distances up to the micrometer range. We use the same log–log representation as in ref. 20 for direct comparison. Although our curves correspond to a simplified water model embedded in a simplified slab (no H-bonds and no electronic polarisation), the similarities with the experimental results are striking. In particular we recover the main feature pointed out by the experimental work: the effective dielectric constant measured in slabs with a thickness in the 1 nm range is found to be around 2; this was quoted as an “anomalously low dielectric constant of confined water”. Our theoretical work makes it possible to bring some insight to the interpretation of the experimental results. Indeed the long range behaviour observed for
⊥(h) computed over the range 0–10 nm, together with the asymptotic formula (21) starting from the same microscopic/nanoscopic distances up to the micrometer range. We use the same log–log representation as in ref. 20 for direct comparison. Although our curves correspond to a simplified water model embedded in a simplified slab (no H-bonds and no electronic polarisation), the similarities with the experimental results are striking. In particular we recover the main feature pointed out by the experimental work: the effective dielectric constant measured in slabs with a thickness in the 1 nm range is found to be around 2; this was quoted as an “anomalously low dielectric constant of confined water”. Our theoretical work makes it possible to bring some insight to the interpretation of the experimental results. Indeed the long range behaviour observed for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) has no mystery since, under longitudinal conditions, the measure of the average polarisation or capacitance yields the integral of 1/ε⊥(z) which, since 1/εbulk ≪ 1, gets its main contribution from the boundaries. Very thick slabs are required for the bulk to contribute. This is clear from the slow hi/h convergence appearing in eqn (21). It should be noted that this asymptotic formula using the values hi and εi derived above works extremely well even in the h = 1 nm range, i.e., down to separation distances h < 2hi where it should not! We can only attribute this to continuity that allows the extrapolation of the curve over a limited range below its validity. Note also that since εbulk/εi ≫ 1, the results essentially depend on the ratio hi/εi so that, on an empirical ground, other choices of these parameters make it possible to reproduce the average slab dielectric constant. In particular one can take εi = 1 and hi = 9/5 = 1.8 Å, a value very close to the one suggested in the dielectric continuum theory (DCT) of Cox and Geissler;35 see Fig. 6. There is in fact much more in their analysis than considering this limit that amounts to modelling the solid–liquid interface as a step-function. Their study points out the importance, as well as the ambiguity, of locating the dielectric boundaries and of properly defining the volume of the device, which contains a molecular exclusion volume portion and one filled by the liquid. Such ambiguity is present in our definition of the device polarisation that involves its thickness h (eqn (14)). We have taken as a natural microscopic definition of h the distance between the center of the surface atoms of each plate, so that the integrated Lennard-Jones potential can be defined as in eqn (6). Other experimental choices for h are possible and the measurement of the device thickness is also subject to experimental uncertainties. The influence of this uncertainty is illustrated in the ESI.† The observed trends are in clear agreement with those in ref. 35. Although based on a simplified, step-wise, molecular representation of the solid–liquid interface, the DCT approach captures the essential balance between low and high dielectric constant volumes.
⊥(h) has no mystery since, under longitudinal conditions, the measure of the average polarisation or capacitance yields the integral of 1/ε⊥(z) which, since 1/εbulk ≪ 1, gets its main contribution from the boundaries. Very thick slabs are required for the bulk to contribute. This is clear from the slow hi/h convergence appearing in eqn (21). It should be noted that this asymptotic formula using the values hi and εi derived above works extremely well even in the h = 1 nm range, i.e., down to separation distances h < 2hi where it should not! We can only attribute this to continuity that allows the extrapolation of the curve over a limited range below its validity. Note also that since εbulk/εi ≫ 1, the results essentially depend on the ratio hi/εi so that, on an empirical ground, other choices of these parameters make it possible to reproduce the average slab dielectric constant. In particular one can take εi = 1 and hi = 9/5 = 1.8 Å, a value very close to the one suggested in the dielectric continuum theory (DCT) of Cox and Geissler;35 see Fig. 6. There is in fact much more in their analysis than considering this limit that amounts to modelling the solid–liquid interface as a step-function. Their study points out the importance, as well as the ambiguity, of locating the dielectric boundaries and of properly defining the volume of the device, which contains a molecular exclusion volume portion and one filled by the liquid. Such ambiguity is present in our definition of the device polarisation that involves its thickness h (eqn (14)). We have taken as a natural microscopic definition of h the distance between the center of the surface atoms of each plate, so that the integrated Lennard-Jones potential can be defined as in eqn (6). Other experimental choices for h are possible and the measurement of the device thickness is also subject to experimental uncertainties. The influence of this uncertainty is illustrated in the ESI.† The observed trends are in clear agreement with those in ref. 35. Although based on a simplified, step-wise, molecular representation of the solid–liquid interface, the DCT approach captures the essential balance between low and high dielectric constant volumes.
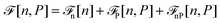
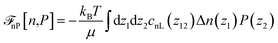

![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) which is very similar to the one obtained for the Stockmayer solvent, so that identical conclusions can be drawn. No specific properties of water emerge, beyond being a polar, molecular fluid with a high dielectric constant. This result is consistent with the observation by MD simulations28 that confined polar liquids such as methanol, acetonitrile and dichloromethane exhibit a dielectric constant reduction similar to that of water. We further note that in our results the dielectric constant reduction of confined water is reproduced by considering exclusively the number and polarisation densities, without requiring orientational constraints imposed by the interface on the water molecules. We find an interfacial width hi = 7.5 Å and an associated effective interfacial dielectric constant εi = 3.9, to be compared to hi = 7.4 and εi = 2.1 determined experimentally by Fumagalli et al.20hi appears slightly smaller for SPC/E than for the purely dipolar fluid since, as we mentioned, the spatial correlations in water have a shorter range. Concordantly, we observe oscillations of
⊥(h) which is very similar to the one obtained for the Stockmayer solvent, so that identical conclusions can be drawn. No specific properties of water emerge, beyond being a polar, molecular fluid with a high dielectric constant. This result is consistent with the observation by MD simulations28 that confined polar liquids such as methanol, acetonitrile and dichloromethane exhibit a dielectric constant reduction similar to that of water. We further note that in our results the dielectric constant reduction of confined water is reproduced by considering exclusively the number and polarisation densities, without requiring orientational constraints imposed by the interface on the water molecules. We find an interfacial width hi = 7.5 Å and an associated effective interfacial dielectric constant εi = 3.9, to be compared to hi = 7.4 and εi = 2.1 determined experimentally by Fumagalli et al.20hi appears slightly smaller for SPC/E than for the purely dipolar fluid since, as we mentioned, the spatial correlations in water have a shorter range. Concordantly, we observe oscillations of ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) around the value of 2 in the 0.6–1 nm range with a first minimum at 1.8 around h = 0.75 nm and a second higher minimum around h = 1 nm; this is in agreement with the simulation results of ref. 30. Indeed, those oscillations are dampened more quickly than in the Stockmayer case.
⊥(h) around the value of 2 in the 0.6–1 nm range with a first minimum at 1.8 around h = 0.75 nm and a second higher minimum around h = 1 nm; this is in agreement with the simulation results of ref. 30. Indeed, those oscillations are dampened more quickly than in the Stockmayer case.
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) and the red solid curve corresponds to the asymptotic formula (21) with the parameters determined in the text and down to h = hi. The blue triangles and cyan solid curve are the same for
⊥(h) and the red solid curve corresponds to the asymptotic formula (21) with the parameters determined in the text and down to h = hi. The blue triangles and cyan solid curve are the same for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ‖(h).
‖(h).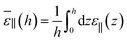
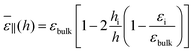
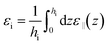
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ‖(h) is observed for thicknesses between 0.6 and 1 nm but we do not detect the drastic drop by two orders of magnitude that Hamid et al. found in their simulations around h = 0.75 nm, that they attribute to a freezing transition occurring under that particular packing condition.31
‖(h) is observed for thicknesses between 0.6 and 1 nm but we do not detect the drastic drop by two orders of magnitude that Hamid et al. found in their simulations around h = 0.75 nm, that they attribute to a freezing transition occurring under that particular packing condition.31![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ⊥(h) = 2 for slabs below 1 nm, a saturation effect that is reminiscent of the one detected experimentally. In our case, we can relate this non-monotonic behaviour to the interplay between the polarisation response and hard-sphere packing when only one or two layers of solvent particles are allowed in the slab.
⊥(h) = 2 for slabs below 1 nm, a saturation effect that is reminiscent of the one detected experimentally. In our case, we can relate this non-monotonic behaviour to the interplay between the polarisation response and hard-sphere packing when only one or two layers of solvent particles are allowed in the slab.

