Open Access Article
Open Access ArticlepH jump kinetics in colliding microdroplets: accelerated synthesis of azamonardine from dopamine and resorcinol†
Emily K.
Brown
 ab,
Grazia
Rovelli
a and
Kevin R.
Wilson
ab,
Grazia
Rovelli
a and
Kevin R.
Wilson
 *a
*a
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: krwilson@lbl.gov; Tel: +1 510-495-2474
bDepartment of Chemistry, University of California, Berkeley, CA 94720, USA
First published on 22nd May 2023
Abstract
Recent studies report the dramatic acceleration of chemical reactions in micron-sized compartments. In the majority of these studies the exact acceleration mechanism is unknown but the droplet interface is thought to play a significant role. Dopamine reacts with resorcinol to form a fluorescent product azamonardine and is used as a model system to examine how droplet interfaces accelerate reaction kinetics. The reaction is initiated by colliding two droplets levitated in a branched quadrupole trap, which allows the reaction to be observed in individual droplets where the size, concentration, and charge are carefully controlled. The collision of two droplets produces a pH jump and the reaction kinetics are quantified optically and in situ by measuring the formation of azamonardine. The reaction was observed to occur 1.5 to 7.4 times faster in 9–35 micron droplets compared to the same reaction conducted in a macroscale container. A kinetic model of the experimental results suggests that the acceleration mechanism arises from both the more rapid diffusion of oxygen into the droplet, as well as increased reagent concentrations at the air–water interface.
1. Introduction
Recent reports have provided evidence that chemical reactions occurring inside micron-sized containers (i.e., droplets) are accelerated by factors as large as 106 relative to the same reaction conducted at the macroscale.1 However, in many cases, the mechanism(s) for microdroplet accelerated chemistry remains uncertain. Electrospray ionization (ESI) mass spectrometry (MS) is a common method used to observe accelerated reactions in droplets.1–4 In these experiments variable droplet size and charge, evaporation, and gas phase reactions among other factors are difficult to control and likely contribute in some way to the acceleration mechanism.5–9 Here a branched quadrupole trap (BQT) is used to isolate the chemistry occurring in single droplets. The reaction kinetics are measured optically in individual droplets, which removes much of the mechanistic uncertainty of using ESI-MS to study reaction acceleration in microdroplets.The reaction of dopamine with resorcinol to form the fluorescent product azamonardine is selected as a model system to study reaction acceleration in micron-sized droplets. Catechols, resorcinol, and hydroquinones are common organic pollutants emitted from biomass burning and are detected in high concentrations in the atmosphere.10 Thus these molecules are frequently used as model compounds to study the oxidation of organic species in the atmosphere and the associated pathways for secondary organic aerosol (SOA) formation.11,12 The oxidation of these species in atmospheric compartments such as cloud, fog, and aerosol is still under investigation and may help answer questions about the mass of SOA in the atmosphere.13
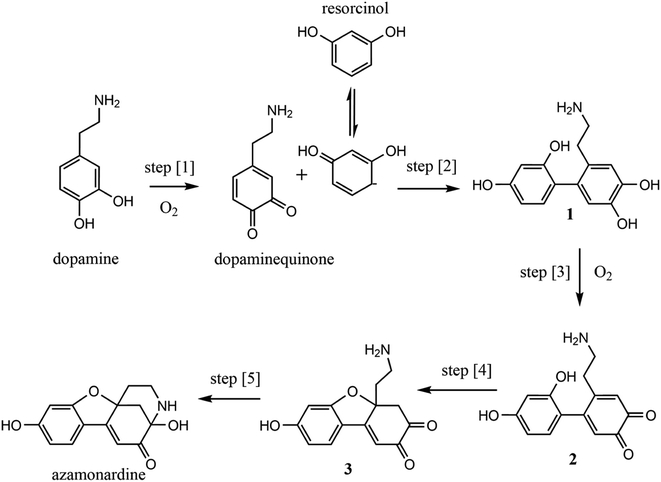
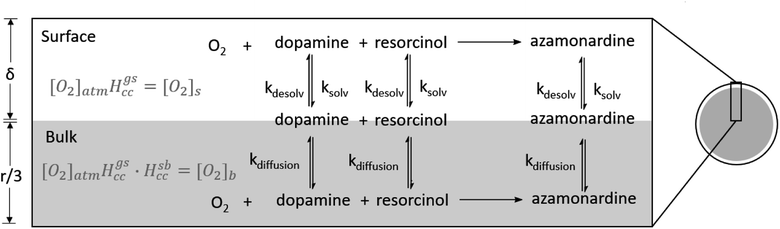
The proposed mechanism for the dopamine–resorcinol reaction is shown in Fig. 1.14,15 The reaction is pH dependent since the oxidation of dopamine (step [1], Fig. 1) to form dopaminequinone (DQ) does not proceed appreciably in acidic solution. Thus this reaction can test recent suggestions that reaction acceleration could arise from steep radial proton gradients in microdroplets.16–19 Additionally, dissolved oxygen plays an important role in the overall mechanism through the oxidation of dopamine and intermediate 1 (step [1] and step [3], Fig. 1). This O2 dependence enables us to examine more closely the role of the dissolved gas phase species in accelerating in-droplet chemistry.
As shown previously, the BQT enables the study of single droplets in an environment where droplet size, solvent evaporation, and droplet charge are finely controlled.20–22 For example, solvent evaporation, which naturally accelerates reaction kinetics by increasing reagent concentration, can be eliminated. In order to maintain a constant droplet size and eliminate evaporation these experiments are performed at high (4.6 M) sodium chloride concentrations. The strong fluorescence of azamonardine with a quantum yield of 0.47 in alkaline solution provides a non-destructive way of probing in-droplet reaction kinetics.14 This eliminates the ambiguity of monitoring kinetics using ESI-MS, which requires vaporizing the droplet and transferring its constituents to the gas phase for detection.
As will be shown below, the in-droplet synthesis of azamonardine is accelerated by 1.5–7.4 times relative to the same reaction conducted in a macroscopic container (i.e., a cuvette). The magnitude of the reaction acceleration is investigated over a range of droplet charges, sizes, and reagent concentrations. A kinetic model of the experimental results using the mechanism shown in Fig. 1 is implemented in a previously published kinetic framework,23–25 and suggests that the in-droplet accelerated synthesis of azamonardine arises from rapid oxygen diffusion and partitioning of reagents between the surface and the bulk region of the droplets.
2. Experimental
2.1 Materials
All solutions are prepared using HPLC water (Sigma-Aldrich Lot SHBM5487). For bulk and droplet experiments, dopamine hydrochloride (Sigma-Aldrich Lot BCCF4279), resorcinol (Arcos Lot A0415245), and NaCl (Sigma-Aldrich Lot SLBN3273V, 4.6 M) are combined in a volumetric flask at the desired concentrations. Solutions are confirmed to have a pH less than 5 using a pH meter (Fisher Scientific Accumet AE150). A carbonate-bicarbonate buffer is prepared from sodium carbonate (Sigma-Aldrich Lot 059K0012V) and sodium bicarbonate (Sigma-Aldrich Lot SLCG3876) with a pH of 8.9 ± 0.1.2.2 Methods
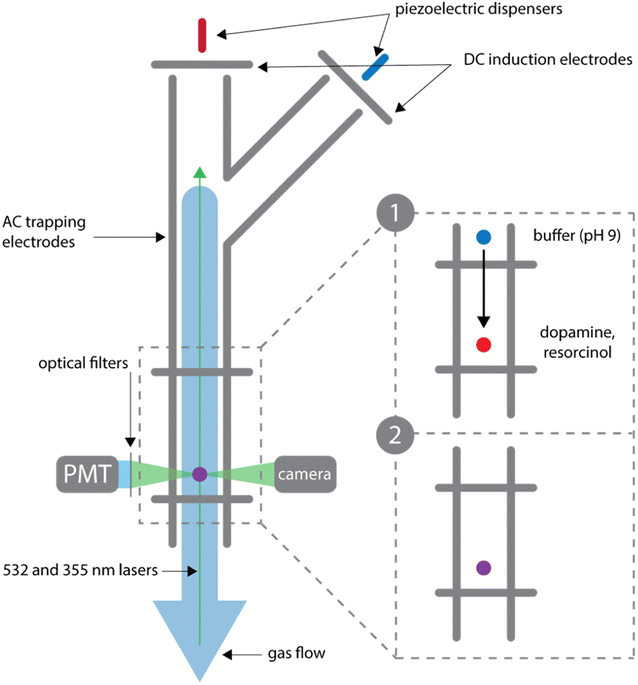
Droplet measurements are performed in a BQT as previously described and shown in Fig. 2.20,21 An acidic droplet containing dopamine and resorcinol is coalesced with a basic buffer droplet, which produces a pH jump to start the reaction. Solutions of dopamine, resorcinol, and NaCl (4.6 M) (pH <5) are prepared at the desired concentrations and dispensed into the trap through the main branch using a piezoelectric dispenser (MicroFab). NaCl is added to the droplet to control water activity and therefore droplet size during the experiment. A stable droplet size is achieved using NaCl to keep the water activity in the droplets at a constant value of 0.8; this corresponds to a NaCl concentration of 4.6 M.26,27 With this NaCl concentration, at a relative humidity of 80% (at which the BQT is maintained), the droplet will not evaporate and can be maintained at a stable size for days at a time. The charge on the droplets is controlled by the voltage applied to the induction electrode and ranges from 10−14 to 10−13 C.28 A second droplet containing the carbonate-bicarbonate buffer (0.33 M) and NaCl (2.4 M) is dispensed into the trap through the branch and suspended by the top balancing electrode. By applying a smaller and opposite polarity voltage to the induction electrode, the buffer droplets are dispensed with an opposite and smaller charge than the first droplet containing dopamine and resorcinol. Once dispensed both droplets are suspended and allowed to equilibrate to the trap environment as shown in inset 1 of Fig. 2. After equilibration the buffer droplet is released and allowed to collide with the dopamine/resorcinol droplet as illustrated in inset 2 of Fig. 2. The droplet is released by setting the balancing voltage to 0 for between 5 and 100 ms. Within ∼30 seconds of the collision the merged droplet is illuminated with a 355 nm laser (PowerChip Nanolaser, ∼20 mW) and the resulting fluorescence is recorded by a photomultiplier tube. Azamonardine has a fluorescence emission peak at 475 nm when excited at 355 nm with a maximum in fluorescence signal at pH 9 when it is in its anionic form.14,29 Filters are used to isolate the fluorescent signal between 400 and 500 nm. In Fig. S1,† we show that azamonardine is the only species contributing to the fluorescence signal. A shutter (ThorLabs KSC101) is used to turn the laser on and off over the course of the reaction in order to limit bleaching.The relative humidity (RH) in the BQT is maintained during the experiment at 80 ± 3.5% by passing air at a flow rate of 0.3 SLM through a bubbler into the BQT. In the absence of oxygen this reaction does not proceed appreciably over the course of an hour.29,30 With only nitrogen gas flowing through the BQT the reaction was not completed even after more than two days as shown in Fig. S2.†
The droplet sizes before and after collision are obtained using Mie scattering. Accurately measuring the droplet size is essential for determining reagent concentrations and for performing companion bulk measurements in a cuvette at comparable concentrations. The droplets are illuminated with a 532 nm laser (Opto Engine, 532 nm) and the Mie scattering is monitored using a line camera at 90° (ThorLabs LC100). As previously described, droplet sizes are obtained within an uncertainty of ∼0.5 μm.22 The dopamine and resorcinol concentrations in the initial droplet are known because the water content in the droplet is controlled by [NaCl] = 4.6 M and the trap RH of 80%. For example, if the dispensed solution is 1 M in dopamine and 2.3 M in sodium chloride, then after equilibration at a trap RH of 80%, the final sodium chloride concentration will be 4.6 M and the final dopamine concentration is 2 M. From the initial concentration and volume of the first droplet, it is then possible to determine the final concentration after collision using the measured final droplet size. The buffer concentration is proportional to sodium chloride concentration and its concentration in the final droplet can be similarly calculated.
For bulk measurements, dopamine, resorcinol, and NaCl (4.6 M) solutions are prepared at concentrations comparable to the droplet experiments and then pipetted into a cuvette. The carbonate-bicarbonate buffer and NaCl (4.6 M) is then rapidly mixed to initiate the reaction at the same concentration as in the droplet experiments. Fluorescence of the product azamonardine is excited using a 355 nm laser and monitored with a camera (ThorLabs DCC1645C). Air is continuously bubbled through the solution during the reaction at a flow rate of 0.3 SCCM using a mass flow controller (MKS 647C).
The reaction below pH 5 is slow and does not proceed appreciably over the time scales considered here. This is because the oxidation of dopamine to dopaminequinone (DQ), the first step of the reaction, is strongly pH dependent and does not occur at pH 5 without the presence of specific enzymes or catalysts.31,32 Thus, dopamine and resorcinol can be stored together in solution at low pH without reacting. The pH of microdroplets is a matter of some debate with some evidence that droplets may exhibit dramatic pH gradients and that the pH of microcompartments and the air water interface may be substantially different from that of similar bulk solutions.17–19,33 The fluorescence of a droplet containing dopamine and resorcinol (dispensed from a pH <5 solution) was monitored in order to determine if the reaction would proceed spontaneously in acidic droplets without the need for a pH jump to basic conditions. The fluorescence signal did not change over the course of 20 minutes (Fig. S3†) indicating that the pH of the droplet is not substantially different from the solution from which it was made. While the pH of microdroplets is still an active area of investigation, this result does agree with research that indicates microdroplet pH does not deviate from that of the corresponding bulk solution under certain conditions.34,35
3. Experimental results
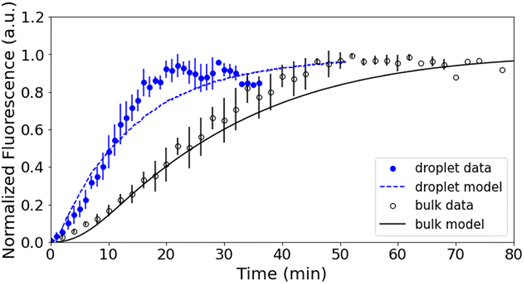
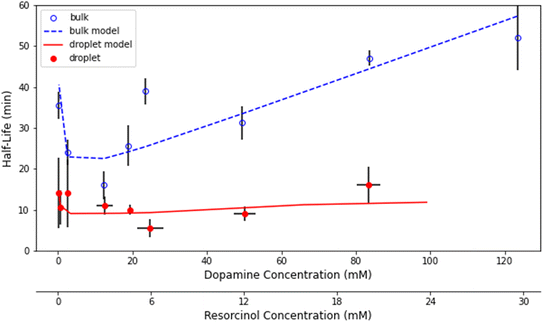
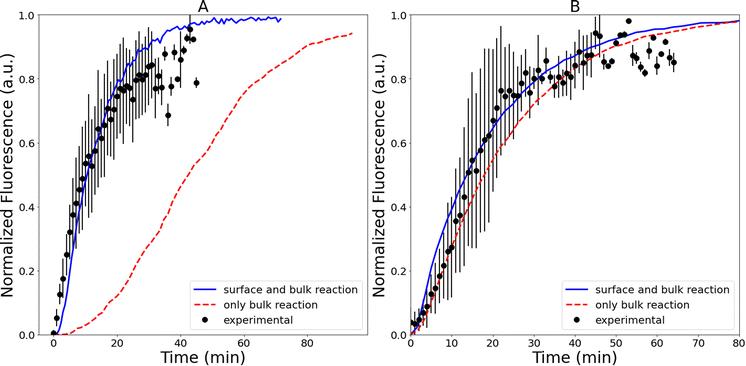
Fig. 3 shows representative kinetics for this reaction conducted in a cuvette and in a droplet. Kinetics at other reagent concentrations are shown in Fig. S4 in the ESI.† The formation of the product azamonardine vs. time, monitored by its fluorescence, shows distinctly sigmoidal kinetics as seen in Fig. 3. To compare the droplet and bulk kinetics, product half-life (τ1/2) is used, which is the amount of time required for the azamonardine fluorescence to reach half of its final value. Half-life is used in the place of a rate constant since the kinetics are non-exponential. In Fig. 3, the droplet τ1/2 = 10 ± 1.2 min compared with a bulk τ1/2 = 25 ± 4.8 min. This corresponds to an acceleration factor of 2.5, which is defined simply as the ratio bulk to droplet τ1/2.τ 1/2 was measured for a range of dopamine and resorcinol concentrations the results of which are shown in Fig. 4. The concentration ratio of dopamine to resorcinol is held constant throughout these series of measurements. Acceleration is observed for all concentrations with the droplet τ1/2 consistently smaller than the τ1/2 measured in the cuvette. As has been previously reported for this reaction, τ1/2 in the cuvette increases (i.e. reaction slows down) at higher reagent concentrations, which is attributed to the depletion of dissolved oxygen.14 In contrast, the droplet τ1/2 remains nearly invariant with increasing reagent concentration.
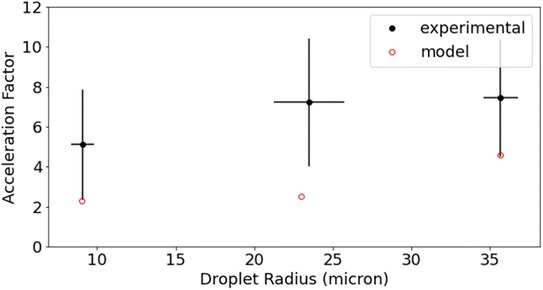
Reaction acceleration in droplets is often attributed to a variety of surface processes. These processes include partial solvation of reactants at the interface, increased concentration at the surface especially in the case of gas phase reactants, pH gradients, and charge effects.5,36 Surface effects have been shown to lead, in some cases, to an inverse dependence of the acceleration factor on droplet radius; as the surface to volume ratio increases with decreasing droplet size.25,37 The size dependence of this reaction is shown in Fig. 5 for droplet radii between 9 μm and 36 μm. While acceleration is seen for all droplet sizes, there is no statistically significant trend with droplet size. Dopamine and resorcinol concentrations are not strictly identical across all droplet sizes investigated, so the average concentrations for each droplet size investigated were used in the bulk measurements to calculate the acceleration factors in Fig. 5. The magnitude of the droplet charge is found to have no significant effect on the acceleration factor as shown in Fig. S5.†
4. Kinetic modeling
To examine the acceleration mechanism, two kinetic models are developed to explain the differences between droplet and cuvette reaction kinetics. Both models use the mechanism shown in Fig. 1.14,38 To simulate the kinetics in the cuvette a set of differential equations is solved in Mathematica (Fig. S6†).39 We assume that the solution in the cuvette is well-mixed and that the reaction occurs entirely within the bulk liquid. This is a reasonable assumption since the contribution from the air/water interface in a macroscopic container is negligible when compared to a microdroplet.25 For simplicity, we also neglect the air/water interface formed during bubbling of air through the solutions. After constraining the mechanism and rate constants used in the kinetic model to the cuvette measurements, the same reaction scheme using an identical set of rate constants is implemented in a kinetic model of a droplet, which includes contributions from the interface. Droplet kinetics are simulated in Kinetiscope,40 which uses a stochastic algorithm to propagate a chemical reaction. Kinetiscope has been used to accurately describe a wide range of chemical reactions in droplets, aerosols and emulsions with equivalent accuracy to solving systems of differential equations.25,41–44Rate constants for this reaction are constrained where possible using prior literature. Table S1† shows the rate constants for the five reaction steps in Fig. 1. The rate constant for the oxidation of dopamine (step [1], Fig. 1) is an adjustable parameter since the values reported in the literature, which range from 1.54 × 10−23 to 4.98 × 10−23 cm3 per molecule per s, are all too small to account for the experimentally observed kinetics in the cuvette.32,45 The rate constant used in the model is 1.94 × 10−20 cm3 per molecule per s. It is likely that the high ionic strength of our solutions could account for some of this deviation, as well as the presence of resorcinol, since phenols are known to increase the dopamine oxidation rate.46,47 The presence of trace amounts of iron and copper are also known to accelerate this step.45,48,49
As discussed above, dissolved O2 is critical for the reaction to proceed and thus air is continuously bubbled through the cuvette solution. To describe this in the bulk cuvette model, the rate of oxygen introduction into solution is,
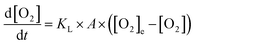 | (1) |
4.1 Bulk model results
The shape of the bulk kinetics can be satisfactorily replicated by the model as shown in Fig. 3. The simulation results are also plotted in Fig. S4† for other dopamine and resorcinol concentrations. Additionally, as shown in Fig. 4, the model can quantitatively account for the broad trends in τ1/2 as a function of reactant concentration. The model replicates the decrease in cuvette τ1/2 at low concentrations followed by the linear increase for dopamine and resorcinol concentrations above 12 mM and 4 mM, respectively. The model clearly shows that the amount of dissolved oxygen is a strong contributor to the observed kinetics. Oxygen depletion increases with increasing dopamine concentration as can be seen in Fig. S7† and is responsible for the linear increase (i.e. slowing of the reaction) in τ1/2 at high concentrations. At high dopamine and resorcinol concentrations the reaction is limited only by the rate at which oxygen enters the solution; in the absence of oxygen depletion the τ1/2 would continue to decrease monotonically. At lower dopamine (<12 mM) and resorcinol (<4 mM) concentrations dissolved oxygen is not limiting so the reaction proceeds more rapidly as dopamine/resorcinol concentrations increase.4.2 Droplet model
As discussed previously, kinetic modeling of reactions in microcompartments requires explicit consideration of the surface since at millimolar concentrations a substantial fraction of molecules within a microdroplet, relative to a macroscopic container, reside at the interface.25 The droplet is simulated in Kinetiscope using rectangular prism with two spatially distinct, well-mixed compartments.40 One compartment represents the surface, which is assumed to have a thickness (δ) of 1 nm. Below the surface compartment is a second larger volume that represents the bulk of the droplet. Following Houle et al., the height of the bulk compartment is selected to be r/3 (r is the droplet radius) to preserve the correct scaling of surface and bulk processes in a sphere.44,53 A general scheme for the model is shown in Fig. 6 and is based on work by Willis and Wilson with additional examples in Wilson et al.23,24 Molecules move between the surface and bulk compartments via Fickian diffusion, with diffusion constants constrained by the literature and shown in Table S1.† As shown in Fig. 6, species at the surface can react or solvate into the droplet bulk; species in the bulk can similarly react or desolvate back to the surface. The rate constants and mechanism constrained by the bulk cuvette model are used in the droplet model without modification in both the surface and bulk compartments.As shown in Fig. 1, oxygen plays a key role in the reaction mechanism. Thus [O2] at the surface and in the bulk of the droplet is needed. The overall dimensionless Henry's law coefficient (Hgbcc) can be expressed as the product of the gas-to-surface (Hgscc) and the surface-to-bulk (Hsbcc) Henry's law coefficients.23,24,54,55 The Henry's law coefficient for solvation of gas phase O2 at the air–water interface (Hgscc) is related to the difference in solvation free energy (ΔGgs) of a O2 molecule in the gas phase (g) and at the surface (s),
| Hgscc = e−ΔGgs/RT | (2) |
In a similar way, ΔGsb is the change in solvation free energy of moving O2 from the surface into the bulk,
| Hsbcc = e−ΔGsb/RT | (3) |
During the reaction, the oxygen concentration in the surface and bulk compartments of the droplet are not depleted relative to their Henry's law value as shown in Fig. S8.† This is because the equilibration timescales for oxygen at the surface and in the bulk of the droplet are much faster than the rate at which O2 is consumed by the reaction. For example, O2 at the surface reaches its equilibrium Henry's Law value within 100 nanoseconds, whereas the reaction occurs on timescales of minutes. The characteristic timescale for liquid phase diffusion of oxygen into the bulk droplet is 36 ms for a r = 36 μm droplet computed using the Einstein–Smoluchowski equation.24 This corresponds to a liquid phase diffusion rate constant of 28 s−1, which is ∼70 times faster than dopamine oxidation rate (i.e., 0.39 s−1 at [Dopamine] = 33 mM). Thus, in the simulation we assume that the bulk and surface oxygen concentrations remain at their Henry's Law values over the course of the reaction.
In addition to oxygen, the concentrations of the dopamine, resorcinol, intermediates 1–3 and azamonardine in the surface compartment are needed (Fig. 1). The interfacial concentrations for these species (represented generically as Y) are computed using a modified Langmuir framework as described in ref. 23–25 and shown in eqn (4),
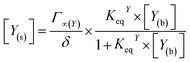 | (4) |
 | (5) |
K eq is obtained by fitting prior surface tension measurements of aqueous solutions of dopamine and resorcinol to the Szyszkowski–Langmuir equation (see ESI† for calculations).59,61,62 These fits yield Keq = 4.21 × 10−21 cm3 per molecules for dopamine and Keq = 1.89 × 10−21 cm3 per molecules for resorcinol at zero ionic strength. Unfortunately, these values fail to account for the experimentally observed droplet kinetics. This is likely due to the high ionic strength in the droplet and the well-known salting-out effects that increase an organic molecule's affinity for the air–water interface.58,63 For example, Keq for 4-hydroxyacetophenone is observed to increase ∼7 times in a 4.5 M NaCl solution (Keq = 1.389 × 10−19 cm3 per molecules) relative to pure water (Keq = 2.17 × 10−20 cm3 per molecules).58 To account for salting out, Keq for dopamine and resorcinol are both increased by approximately an order of magnitude to a final model value of 3×10−20 cm3 per molecules. Even at this increased surface activity only approximately half of the available surface sites are occupied at the highest dopamine and resorcinol concentrations. To our knowledge, Keq for the intermediates and azamonardine have not been measured and are left as adjustable parameters. We find that the model results are insensitive to the surface partitioning of all intermediates for Keq between 0 and 3 × 10−20 cm3 per molecules with the exception of intermediate 1, which can have a maximum value for Keq of ∼1 × 10−20 cm3 per molecules
4.3 Droplet model results
Fig. 4 compares the simulated droplet τ1/2 with experimental results. The droplet model captures both the magnitude of τ1/2 and its trend with reactant concentration. The droplet simulations also do a fair job of replicating the shape of the individual kinetic traces as seen in Fig. 3 and S11.† Importantly, the kinetic models, described above, quantitatively account for the observed differences in the droplet and bulk cuvette τ1/2 using the same reaction scheme (Fig. 1) and set of rate coefficients (Table S1†). This gives us some confidence that the kinetic model can yield some deeper insights into the mechanism for the in-droplet acceleration of this reaction.From the kinetic simulations, reaction acceleration can be attributed to two primary mechanisms, which in turn depend on reagent concentrations. First, as discussed above, dissolved O2 is a key reagent in this reaction and controls much of the kinetic behavior observed in the cuvette by becoming a limiting reagent at high dopamine/resorcinol concentrations. This is not the case for droplets, where because of their small size, the diffusion rate of O2 is much faster than in a macroscale system and dissolved oxygen never limits the reaction. This accounts for the nearly invariant droplet τ1/2vs. concentration observed in Fig. 4, whereas in the cuvette, τ1/2 increases linearly (reaction slows down) at high concentrations, where O2 is consumed faster than it can be resupplied by bubbling air into the cuvette (as illustrated in Fig. S7†). As will be discussed below, the faster diffusion of O2 into droplets appears to be the dominant acceleration mechanism at high concentrations (i.e., [dopamine] >∼20 mM and [resorcinol] >∼4 mM).
The second acceleration mechanism appears at lower dopamine and resorcinol concentrations. This is the concentration range ([dopamine] <10 mM and [resorcinol] <3 mM, Fig. 4) where the bulk reaction in the cuvette is not limited by dissolved O2. Thus, if O2 diffusion in droplets was the only source of reaction acceleration, one would expect that the droplet and cuvette reaction kinetics would be identical over this concentration range (i.e., both not limited by [O2]). However, as can be seen in Fig. 4 there remains a large difference between cuvette and droplet τ1/2 suggesting an additional acceleration mechanism.
Two different simulations are used to assess the importance of the interface at low (i.e., [dopamine] <10 mM, [resorcinol] <3 mM, Fig. 4), and high reagent concentrations (i.e., [dopamine] >20 mM, [resorcinol] >6 mM). Shown in Fig. 7 are droplet simulations compared with experiments at two different dopamine/resorcinol concentrations. The first simulation (solid blue line, Fig. 7) is the base model described above (Table S1†), which includes surface-bulk partitioning and reaction of all species. For comparison (red dashed line, Fig. 7) a simulation is conducted where the partitioning of reagents to the surface is turned off, effectively limiting the five reaction steps (Fig. 1) to occur only in bulk region of the droplet. At high dopamine (83 mM) and resorcinol (20 mM) concentrations, the two simulations with and without surface reactions (Fig. 7B) produce very similar results and are both within the experimental uncertainty. This suggests that surface reactions play a modest role in the observed kinetics in this concentration regime. As discussed above, at these higher dopamine/resorcinol concentrations the droplet kinetics are accelerated because dissolved O2 never becomes a limiting reagent as it does in the macroscale cuvette measurements. Characteristic times for liquid phase diffusion scale as reciprocal distance squared, so O2 is delivered into the droplet at a rate that is much faster than it can be consumed by the reaction.
However, as shown in Fig. 7A, when dopamine and resorcinol concentrations are decreased by ∼400× the difference between the two simulations becomes dramatic, clearly indicating that the interface plays a much more prominent role in the observed kinetics. The reason for this is illustrated by estimating the fraction of molecules at the droplet interface as a function of concentration,
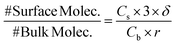 | (6) |
For example, at both low and high reactant concentration the oxidation of dopamine to DQ (Step [1], Fig. 1) occurs mainly at the interface. This can be quantified using the selection frequency of each reaction step in the simulations (see Table S4†). At high concentration (83 mM dopamine, 20 mM resorcinol, Fig. 7B) 63% of dopamine oxidation reactions occur at the interface, which increases to 86% when the concentration is lowered. This is not unexpected since [O2] at the interface is ∼300× larger than in the bulk. This enhanced concentration of O2 naturally accelerates the dopamine oxidation rate and is simply a consequence of the substantial difference between the interfacial and bulk solvation free energy of O2.
The reaction of DQ with resorcinol (Step [2], Fig. 1) occurs mainly inside the interior of the droplet at high reactant concentrations (80% are bulk reactions, Table S4†), but shifts to the interface at 0.2 mM dopamine/0.05 mM resorcinol, where 75% of the reactions that produce intermediate 1 occur at the surface. Intermediate 1 is oxidized in step [3], which occurs with equal probability in the bulk and at the surface under low dopamine/resorcinol conditions, unlike at high dopamine/resorcinol concentrations where the surface oxidation accounts for only 25% of the oxidation of intermediate 1. The simulations predict that steps [4] and [5] occur mainly in the bulk region of the droplet at all dopamine/resorcinol concentrations (Table S3†).
The lack of size dependence can be understood in light of the acceleration mechanisms discussed above. The size dependence shown in Fig. 5 is measured at high dopamine/resorcinol concentrations, where the acceleration mechanism is dominated by liquid phase O2 diffusion rates rather than by surface reactions. Therefore, the size dependence of the reaction over the droplet sizes investigated is predicted to be minimal (Fig. S11†). While the bulk model consistently underestimates the τ1/2 resulting in a higher than predicted acceleration factor for the data in Fig. 5, it nevertheless correctly predicts the linear trend in the data. The acceleration factor is expected to show a much stronger size dependence at lower dopamine and resorcinol concentrations (Fig. S10†) where the surface is expected to participate more directly in the reaction. Unfortunately, size-dependent measurements at these lower concentrations are quite challenging.
5. Conclusions
The synthesis of azamonardine from the reaction of dopamine and resorcinol is measured in a macroscopic sample and in single droplets. The reaction, which is initiated by a pH jump, is found to be accelerated in microdroplets compared to the bulk solutions for all concentrations and droplet sizes by up to ∼7.4× depending on droplet size and concentration. Using a kinetic model constrained to our experimental data, we identify two specific mechanisms to explain why azamonardine formation is accelerated in microdroplets. We would note that there are many other acceleration mechanisms reported in the literature that involve pH gradients,19 electric fields,16,19,64,65 hydroxyl radicals,66,67 H2O radical cations and anions,68,69 evaporation,5,8 and gas phase reactions.5,9 Thus, the acceleration mechanisms reported here are likely specific to our reaction and experimental conditions (e.g., ionic strength).At high dopamine and resorcinol concentrations the faster diffusion rate of oxygen into the droplet volume never limits the reaction rate, unlike the reaction in a cuvette where O2 is severely depleted. At low dopamine/resorcinol concentrations acceleration is attributed to dopamine and resorcinol partitioning to the air–water surface where the oxygen concentrations are enhanced relative to the bulk solution. The enhancement of reactant concentrations accelerates the oxidation rate at the air–water interface, which naturally leads to the observed accelerated reaction kinetics.
Although the magnitude of reaction acceleration in this system is quite modest compared to previous literature reports,1,70 we would note that a key difference in these experiments from those utilizing ESI-MS is the high ionic strength. The acceleration mechanisms identified here are suggestive of a few specific processes that might explain the differences in chemical transformations conducted in microdroplets vs. macroscale reactors. First, droplet size enhances those reactions that may be limited by diffusion, which is particularly important for those microdroplet reactions that require dissolved gases (i.e., CO2,71–74 O2 (ref. 36) or O3 (ref. 23, 75 and 76)) for example to produce key reaction intermediates. Second, as pointed out previously, reactions in micron-sized compartments provide a way to enhance the importance of surface reactions that would otherwise be obscured in macroscopic samples.25 As shown by Wilson et al., chemical reactions conducted under dilute conditions in microscale compartments naturally enhance the role that surface reactions play in the overall chemical evolution of the system (i.e., droplet or emulsion).25 This effect is clearly illustrated in Fig. 7, where surface chemistry becomes more dominant in the synthesis of azamonardine only under very dilute reaction conditions.
These results illustrate the complexity in understanding accelerated chemistry in microcompartments and the potential that multiple mechanisms may be contributing to the observed in-droplet reaction kinetics. This work also illustrates the importance of conducting well-controlled experiments where droplet size and concentration are precisely known, and where droplet kinetics are monitored in situ and are paired with companion macroscale measurements under identical reaction conditions.
Data availability
Data are available from the corresponding author upon request.Author contributions
G. R. contributed to formulation of research goals and provided mentorship. E. K. B performed the experiments and theoretical studies and analyzed the data. K. R. W provided oversight the research planning and execution. K. R. W and E. K. B wrote and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Condensed Phase and Interfacial Molecular Science (CPIMS) program, in the Chemical Sciences Geosciences and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- Z. Wei, Y. Li, R. G. Cooks and X. Yan, Accelerated Reaction Kinetics in Microdroplets: Overview and Recent Developments, Annu. Rev. Phys. Chem., 2020, 71(1), 31–51, DOI:10.1146/annurev-physchem-121319-110654.
- Y.-H. Lai, S. Sathyamoorthi, R. M. Bain and R. N. Zare, Microdroplets Accelerate Ring Opening of Epoxides, J. Am. Soc. Mass Spectrom., 2018, 29(5), 1036–1043, DOI:10.1007/s13361-018-1908-z.
- R. M. Bain, C. J. Pulliam and R. G. Cooks, Accelerated Hantzsch Electrospray Synthesis with Temporal Control of Reaction Intermediates, Chem. Sci., 2015, 6(1), 397–401, 10.1039/C4SC02436B.
- R. M. Bain, S. T. Ayrton and R. G. Cooks, Fischer Indole Synthesis in the Gas Phase, the Solution Phase, and at the Electrospray Droplet Interface, J. Am. Soc. Mass Spectrom., 2017, 28(7), 1359–1364, DOI:10.1007/s13361-017-1597-z.
- G. Rovelli, M. I. Jacobs, M. D. Willis, R. J. Rapf, A. M. Prophet and K. R. Wilson, A Critical Analysis of Electrospray Techniques for the Determination of Accelerated Rates and Mechanisms of Chemical Reactions in Droplets, Chem. Sci., 2020, 11(48), 13026–13043, 10.1039/D0SC04611F.
- A. Gallo, A. S. F. Farinha, M. Dinis, A.-H. Emwas, A. Santana, R. J. Nielsen, W. A. Goddard and H. Mishra, The Chemical Reactions in Electrosprays of Water Do Not Always Correspond to Those at the Pristine Air–Water Interface, Chem. Sci., 2019, 10(9), 2566–2577, 10.1039/C8SC05538F.
- S. Banerjee and R. N. Zare, Influence of Inlet Capillary Temperature on the Microdroplet Chemistry Studied by Mass Spectrometry, J. Phys. Chem. A, 2019, 123(36), 7704–7709, DOI:10.1021/acs.jpca.9b05703.
- C. J. Chen and E. R. Williams, The Role of Analyte Concentration in Accelerated Reaction Rates in Evaporating Droplets, Chem. Sci., 2023, 14, 4704–4713, 10.1039/D3SC00259D.
- M. I. Jacobs, R. D. Davis, R. J. Rapf and K. R. Wilson, Studying Chemistry in Micro-Compartments by Separating Droplet Generation from Ionization, J. Am. Soc. Mass Spectrom., 2019, 30(2), 339–343, DOI:10.1007/s13361-018-2091-y.
- P. Veres, J. M. Roberts, I. R. Burling, C. Warneke, J. Gouw and R. J. Yokelson, Measurements of Gas-Phase Inorganic and Organic Acids from Biomass Fires by Negative-Ion Proton-Transfer Chemical-Ionization Mass Spectrometry, J. Geophys. Res., 2010, 115, D23302, DOI:10.1029/2010JD014033.
- E. A. Pillar-Little, R. Zhou and M. I. Guzman, Heterogeneous Oxidation of Catechol, J. Phys. Chem. A, 2015, 119(41), 10349–10359, DOI:10.1021/acs.jpca.5b07914.
- Z. Finewax, J. A. de Gouw and P. J. Ziemann, Products and Secondary Organic Aerosol Yields from the OH and NO 3 Radical-Initiated Oxidation of Resorcinol, ACS Earth Space Chem., 2019, 3(7), 1248–1259, DOI:10.1021/acsearthspacechem.9b00112.
- J. D. Smith, H. Kinney and C. Anastasio, Aqueous Benzene-Diols React with an Organic Triplet Excited State and Hydroxyl Radical to Form Secondary Organic Aerosol, Phys. Chem. Chem. Phys., 2015, 17(15), 10227–10237, 10.1039/C4CP06095D.
- A. U. Acuña, M. Álvarez-Pérez, M. Liras, P. B. Coto and F. Amat-Guerri, Synthesis and Photophysics of Novel Biocompatible Fluorescent Oxocines and Azocines in Aqueous Solution, Phys. Chem. Chem. Phys., 2013, 15(39), 16704, 10.1039/c3cp52228h.
- O. Crescenzi, A. Napolitano and G. Prota, Oxidative Coupling of DOPA with Resorcinol and Phloroglucinol: Isolation of Adducts with an Unusual Tetrahydromethanobenzofuro[2,3-Dlazocine Skeleton, Tetrahedron, 1991, 47(32), 6243–6250 CrossRef CAS.
- C. Chamberlayne and R. N. Zare, Simple Model for the Electric Field and Spatial Distribution of Ions in a Microdroplet, J. Chem. Phys., 2020, 152(184702), 1–10, DOI:10.1063/5.0006550.
- H. Wei, E. P. Vejerano, W. Leng, Q. Huang, M. R. Willner, L. C. Marr and P. J. Vikesland, Aerosol Microdroplets Exhibit a Stable PH Gradient, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(28), 7272–7277, DOI:10.1073/pnas.1720488115.
- A. J. Colussi, Can the PH at the Air/Water Interface Be Different from the PH of Bulk Water?, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(34), E7887–E7887, DOI:10.1073/pnas.1811632115.
- C. F. Chamberlayne and R. N. Zare, Microdroplets Can Act as Electrochemical Cells, J. Chem. Phys., 2022, 156(5), 054705, DOI:10.1063/5.0078281.
- M. I. Jacobs, J. F. Davies, L. Lee, R. D. Davis, F. Houle and K. R. Wilson, Exploring Chemistry in Microcompartments Using Guided Droplet Collisions in a Branched Quadrupole Trap Coupled to a Single Droplet, Paper Spray Mass Spectrometer, Anal. Chem., 2017, 89(22), 12511–12519, DOI:10.1021/acs.analchem.7b03704.
- M. D. Willis, G. Rovelli and K. R. Wilson, Combining Mass Spectrometry of Picoliter Samples with a Multicompartment Electrodynamic Trap for Probing the Chemistry of Droplet Arrays, Anal. Chem., 2020, 92(17), 11943–11952, DOI:10.1021/acs.analchem.0c02343.
- J. F. Davies, Mass, Charge, and Radius of Droplets in a Linear Quadrupole Electrodynamic Balance, Aerosol Sci. Technol., 2019, 53(3), 309–320, DOI:10.1080/02786826.2018.1559921.
- M. D. Willis and K. R. Wilson, Coupled Interfacial and Bulk Kinetics Govern the Timescales of Multiphase Ozonolysis Reactions, J. Phys. Chem. A, 2022, 126(30), 4991–5010, DOI:10.1021/acs.jpca.2c03059.
- K. R. Wilson, A. M. Prophet and M. D. Willis, A Kinetic Model for Predicting Trace Gas Uptake and Reaction, J. Phys. Chem. A, 2022, 126(40), 7291–7308, DOI:10.1021/acs.jpca.2c03559.
- K. R. Wilson, A. M. Prophet, G. Rovelli, M. D. Willis, R. J. Rapf and M. I. Jacobs, A Kinetic Description of How Interfaces Accelerate Reactions in Micro-Compartments, Chem. Sci., 2020, 11(32), 8533–8545, 10.1039/D0SC03189E.
- S. L. Clegg, K. S. Pitzer and P. Brimblecombe, Thermodynamics of Multicomponent, Miscible, Ionic Solutions. Mixtures Including Unsymmetrical Electrolytes, J. Phys. Chem., 1992, 96(23), 9470–9479, DOI:10.1021/j100202a074.
- A. S. Wexler, Atmospheric Aerosol Models for Systems Including the Ions H+ , NH4+ , Na+, SO42− , NO3− , Cl− , Br− , and H2O, J. Geophys. Res., 2002, 107(D14), 4207, DOI:10.1029/2001JD000451.
- A. E. Haddrell, J. F. Davies, A. Yabushita and J. P. Reid, Accounting for Changes in Particle Charge, Dry Mass and Composition Occurring During Studies of Single Levitated Particles, J. Phys. Chem. A, 2012, 116(40), 9941–9953, DOI:10.1021/jp304920x.
- X. Zhang, Y. Zhu, X. Li, X. Guo, B. Zhang, X. Jia and B. Dai, A Simple, Fast and Low-Cost Turn-on Fluorescence Method for Dopamine Detection Using in Situ Reaction, Anal. Chim. Acta, 2016, 944, 51–56, DOI:10.1016/j.aca.2016.09.023.
- M. Iacomino, M. L. Alfieri, O. Crescenzi, M. d'Ischia and A. Napolitano, Unimolecular Variant of the Fluorescence Turn-On Oxidative Coupling of Catecholamines with Resorcinols, ACS Omega, 2019, 4(1), 1541–1548, DOI:10.1021/acsomega.8b02778.
- W. Zheng, H. Fan, L. Wang and Z. Jin, Oxidative Self-Polymerization of Dopamine in an Acidic Environment, Langmuir, 2015, 31(42), 11671–11677, DOI:10.1021/acs.langmuir.5b02757.
- E. Herlinger, R. F. Jameson and W. Linert, Spontaneous Autoxidation of Dopamine, J. Chem. Soc., Perkin Trans. 2, 1995, 2, 259, 10.1039/p29950000259.
- H. Mishra, S. Enami, R. J. Nielsen, L. A. Stewart, M. R. Hoffmann, W. A. Goddard and A. J. Colussi, Brønsted Basicity of the Air–Water Interface, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(46), 18679–18683, DOI:10.1073/pnas.1209307109.
- M. Li, Y. Kan, H. Su, U. Pöschl, S. H. Parekh, M. Bonn and Y. Cheng, Spatial Homogeneity of PH in Aerosol Microdroplets, Chem, 2023, 9(4), 1036–1046, DOI:10.1016/j.chempr.2023.02.019.
- Q. Huang, H. Wei, L. C. Marr and P. J. Vikesland, Direct Quantification of the Effect of Ammonium on Aerosol Droplet PH, Environ. Sci. Technol., 2021, 55(1), 778–787, DOI:10.1021/acs.est.0c07394.
- K. J. Angle, E. E. Neal and V. H. Grassian, Enhanced Rates of Transition-Metal-Ion-Catalyzed Oxidation of S(IV) in Aqueous Aerosols: Insights into Sulfate Aerosol Formation in the Atmosphere, Environ. Sci. Technol., 2021, 55(15), 10291–10299, DOI:10.1021/acs.est.1c01932.
- A. Fallah-Araghi, K. Meguellati, J.-C. Baret, A. E. Harrak, T. Mangeat, M. Karplus, S. Ladame, C. M. Marques and A. D. Griffiths, Enhanced Chemical Synthesis at Soft Interfaces: A Universal Reaction-Adsorption Mechanism in Microcompartments, Phys. Rev. Lett., 2014, 112(2), 028301, DOI:10.1103/PhysRevLett.112.028301.
- Y. Ogata, Y. Sawaki and M. Isono, Kinetics of the Addition of Benzenesulufinic Acid to P-Benzoquinone, Tetrahedron, 1969, 25(13), 2715–2721, DOI:10.1016/0040-4020(69)80013-X.
- Wolfram Research, Inc., Mathematica, Version 13.1, Champaign, IL, 2022 Search PubMed.
- W. Hinsberg and F. HouleKinetiscope, 2022. http://www.hinsberg.net/kinetiscope/ Search PubMed.
- M. Favaro, Stochastic Analysis of Electron Transfer and Mass Transport in Confined Solid/Liquid Interfaces, Surfaces, 2020, 3(3), 392–407, DOI:10.3390/surfaces3030029.
- M. Soniat and F. A. Houle, Swelling and Diffusion during Methanol Sorption into Hydrated Nafion, J. Phys. Chem. B, 2018, 122(34), 8255–8268, DOI:10.1021/acs.jpcb.8b03169.
- R. Alhadeff and A. Warshel, Reexamining the Origin of the Directionality of Myosin V, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(39), 10426–10431, DOI:10.1073/pnas.1711214114.
- M. J. Liu, A. A. Wiegel, K. R. Wilson and F. A. Houle, Aerosol Fragmentation Driven by Coupling of Acid–Base and Free-Radical Chemistry in the Heterogeneous Oxidation of Aqueous Citric Acid by OH Radicals, J. Phys. Chem. A, 2017, 121(31), 5856–5870, DOI:10.1021/acs.jpca.7b04892.
- Y. Sun, A. N. Pham and T. D. Waite, Elucidation of the Interplay between Fe(II), Fe(III), and Dopamine with Relevance to Iron Solubilization and Reactive Oxygen Species Generation by Catecholamines, J. Neurochem., 2016, 137(6), 955–968, DOI:10.1111/jnc.13615.
- G. E. K. Branch and M. A. Joslyn, The Kinetics of the Auto-Oxidation of Catechol in the Presence of Several Foreign Substances, J. Am. Chem. Soc., 1935, 57(12), 2388–2394, DOI:10.1021/ja01315a018.
- H. Herrmann, Kinetics of Aqueous Phase Reactions Relevant for Atmospheric Chemistry, Chem. Rev., 2003, 103(12), 4691–4716, DOI:10.1021/cr020658q.
- A. N. Pham and T. D. Waite, Cu(II)-Catalyzed Oxidation of Dopamine in Aqueous Solutions: Mechanism and Kinetics, J. Inorg. Biochem., 2014, 137, 74–84, DOI:10.1016/j.jinorgbio.2014.03.018.
- Y. Sun, A. N. Pham, D. J. Hare and T. D. Waite, Kinetic Modeling of PH-Dependent Oxidation of Dopamine by Iron and Its Relevance to Parkinson's Disease, Front. Neurosci., 2018, 12, 859, DOI:10.3389/fnins.2018.00859.
- M. Geng and Z. Duan, Prediction of Oxygen Solubility in Pure Water and Brines up to High Temperatures and Pressures, Geochim. Cosmochim. Acta, 2010, 74(19), 5631–5640, DOI:10.1016/j.gca.2010.06.034.
- M. Nishikawa, M. Nakamura, H. Yagi and K. Hashimoto, Gas Absorption in Aerated Mixing Vessels, J. Chem. Eng. Jpn., 1981, 14(3), 219–226, DOI:10.1252/jcej.14.219.
- S. A. Zieminski, R. M. Hume and R. Durham, Rates of Oxygen Transfer from Air Bubbles to Aqueous NaCl Solutions at Various Temperatures, Mar. Chem., 1976, 4(4), 333–346, DOI:10.1016/0304-4203(76)90019-0.
- A. A. Wiegel, K. R. Wilson, W. D. Hinsberg and F. A. Houle, Stochastic Methods for Aerosol Chemistry: A Compact Molecular Description of Functionalization and Fragmentation in the Heterogeneous Oxidation of Squalane Aerosol by OH Radicals, Phys. Chem. Chem. Phys., 2015, 17(6), 4398–4411, 10.1039/C4CP04927F.
- D. R. Hanson, Surface-Specific Reactions on Liquids, J. Phys. Chem. B, 1997, 101(25), 4998–5001, DOI:10.1021/jp970461f.
- R. G. Remorov and C. George, Analysis of Chemical Kinetics at the Gas-Aqueous Interface for Submicron Aerosols, Phys. Chem. Chem. Phys., 2006, 8(42), 4897, 10.1039/b606635f.
- R. Vácha, P. Slavíček, M. Mucha, B. J. Finlayson-Pitts and P. Jungwirth, Adsorption of Atmospherically Relevant Gases at the Air/Water Interface: Free Energy Profiles of Aqueous Solvation of N2 , O2 , O3 , OH, H2O, HO2 , and H2O2, J. Phys. Chem. A, 2004, 108(52), 11573–11579, DOI:10.1021/jp046268k.
- R. Sander, Henry's Law Constants, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD Search PubMed.
- K. Sahu, V. F. McNeill and K. B. Eisenthal, Effect of Salt on the Adsorption Affinity of an Aromatic Carbonyl Molecule to the Air–Aqueous Interface: Insight for Aqueous Environmental Interfaces, J. Phys. Chem. C, 2010, 114(42), 18258–18262, DOI:10.1021/jp1071742.
- B. Biswas and P. C. Singh, Protonation State of Dopamine Neurotransmitter at the Aqueous Interface: Vibrational Sum Frequency Generation Spectroscopy Study, Langmuir, 2022 DOI:10.1021/acs.langmuir.1c02505.
- G. Bleys and P. Joos, Adsorption Kinetics of Bolaform Surfactants at the Air/Water Interface, J. Phys. Chem., 1985, 89(6), 1027–1032, DOI:10.1021/j100252a028.
- M. A. Martínez-Vitela and J. Gracia-Fadrique, The Langmuir-Gibbs Surface Equation of State, Fluid Phase Equilib., 2020, 506, 112372, DOI:10.1016/j.fluid.2019.112372.
- L. E. Swearingen, Some Physical Properties of Aqueous Hydroxybenzene Solutions, J. Phys. Chem., 1928, 32(5), 785–793, DOI:10.1021/j150287a010.
- Y. Li, M. Shrestha, M. Luo, I. Sit, M. Song, V. H. Grassian and W. Xiong, Salting Up of Proteins at the Air/Water Interface, Langmuir, 2019, 35(43), 13815–13820, DOI:10.1021/acs.langmuir.9b01901.
- H. Hao, I. Leven and T. Head-Gordon, Can Electric Fields Drive Chemistry for an Aqueous Microdroplet?, Nat. Commun., 2022, 13(1), 280, DOI:10.1038/s41467-021-27941-x.
- H. Xiong, J. K. Lee, R. N. Zare and W. Min, Strong Electric Field Observed at the Interface of Aqueous Microdroplets, J. Phys. Chem. Lett., 2020, 11(17), 7423–7428, DOI:10.1021/acs.jpclett.0c02061.
- J. K. Lee, K. L. Walker, H. S. Han, J. Kang, F. B. Prinz, R. M. Waymouth, H. G. Nam and R. N. Zare, Spontaneous Generation of Hydrogen Peroxide from Aqueous Microdroplets, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(39), 19294–19298, DOI:10.1073/pnas.1911883116.
- K. Li, Y. Guo, S. A. Nizkorodov, Y. Rudich, M. Angelaki, X. Wang, T. An, S. Perrier and C. George, Spontaneous Dark Formation of OH Radicals at the Interface of Aqueous Atmospheric Droplets, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(15), e2220228120, DOI:10.1073/pnas.2220228120.
- L. Qiu and R. G. Cooks, Simultaneous and Spontaneous Oxidation and Reduction in Microdroplets by the Water Radical Cation/Anion Pair, Angew. Chem., Int. Ed., 2022, 61(41) DOI:10.1002/anie.202210765.
- L. Qiu, N. M. Morato, K.-H. Huang and R. G. Cooks, Spontaneous Water Radical Cation Oxidation at Double Bonds in Microdroplets, Front. Chem., 2022, 10, 903774, DOI:10.3389/fchem.2022.903774.
- X. Yan, R. M. Bain and R. G. Cooks, Organic Reactions in Microdroplets: Reaction Acceleration Revealed by Mass Spectrometry, Angew. Chem., Int. Ed., 2016, 55(42), 12960–12972, DOI:10.1002/anie.201602270.
- K.-H. Huang, Z. Wei and R. G. Cooks, Accelerated Reactions of Amines with Carbon Dioxide Driven by Superacid at the Microdroplet Interface, Chem. Sci., 2021, 12(6), 2242–2250, 10.1039/D0SC05625A.
- X. Song, Y. Meng and R. N. Zare, Spraying Water Microdroplets Containing 1,2,3-Triazole Converts Carbon Dioxide into Formic Acid, J. Am. Chem. Soc., 2022, 144(37), 16744–16748, DOI:10.1021/jacs.2c07779.
- H. Chen, R. Wang, J. Xu, X. Yuan, D. Zhang, Z. Zhu, M. Marshall, K. Bowen and X. Zhang, Spontaneous Reduction by One Electron on Water Microdroplets Facilitates Direct Carboxylation with CO 2, J. Am. Chem. Soc., 2023, 145(4), 2647–2652, DOI:10.1021/jacs.2c12731.
- L. Feng, X. Yin, S. Tan, C. Li, X. Gong, X. Fang and Y. Pan, Ammonium Bicarbonate Significantly Accelerates the Microdroplet Reactions of Amines with Carbon Dioxide, Anal. Chem., 2021, 93(47), 15775–15784, DOI:10.1021/acs.analchem.1c03954.
- B. J. Dennis-Smither, F. H. Marshall, R. E. H. Miles, T. C. Preston and J. P. Reid, Volatility and Oxidative Aging of Aqueous Maleic Acid Aerosol Droplets and the Dependence on Relative Humidity, J. Phys. Chem. A, 2014, 118(30), 5680–5691, DOI:10.1021/jp504823j.
- Y.-P. Chang, S.-J. Wu, M.-S. Lin, C.-Y. Chiang and G. G. Huang, Ionic-Strength and PH Dependent Reactivities of Ascorbic Acid toward Ozone in Aqueous Micro-Droplets Studied Using Aerosol Optical Tweezers, Phys. Chem. Chem. Phys., 2021, 23(16), 10108–10117, 10.1039/D0CP06493A.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc01576a |
| This journal is © The Royal Society of Chemistry 2023 |