 Open Access Article
Open Access ArticleMechanics of dynamic and deformable DNA nanostructures
Ruixin
Li
,
Anirudh S.
Madhvacharyula
,
Yancheng
Du
,
Harshith K.
Adepu
and
Jong Hyun
Choi
 *
*
School of Mechanical Engineering, Purdue University, 585 Purdue Mall, West Lafayette, Indiana 47907, USA. E-mail: jchoi@purdue.edu
First published on 6th July 2023
Abstract
In DNA nanotechnology, DNA molecules are designed, engineered, and assembled into arbitrary-shaped architectures with predesigned functions. Static DNA assemblies often have delicate designs with structural rigidity to overcome thermal fluctuations. Dynamic structures reconfigure in response to external cues, which have been explored to create functional nanodevices for environmental sensing and other applications. However, the precise control of reconfiguration dynamics has been a challenge due partly to flexible single-stranded DNA connections between moving parts. Deformable structures are special dynamic constructs with deformation on double-stranded parts and single-stranded hinges during transformation. These structures often have better control in programmed deformation. However, related deformability and mechanics including transformation mechanisms are not well understood or documented. In this review, we summarize the development of dynamic and deformable DNA nanostructures from a mechanical perspective. We present deformation mechanisms such as single-stranded DNA hinges with lock-and-release pairs, jack edges, helicity modulation, and external loading. Theoretical and computational models are discussed for understanding their associated deformations and mechanics. We elucidate the pros and cons of each model and recommend design processes based on the models. The design guidelines should be useful for those who have limited knowledge in mechanics as well as expert DNA designers.
1 Introduction
DNA usually functions under the central dogma of molecular biology.1 That is, DNA molecules are transcribed into RNA which is then translated into peptides, proteins, and enzymes. The genomic information carried by DNA can guide them to assemble into intricate structures and perform programmed functions in cells, including intracellular trafficking, apoptosis, migration, division, etc. The shapes and structures of biomolecular assemblies are critical in their functions. Thus, the understanding of the geometry and mechanics of these assemblies is the key in structural biology. In DNA nanotechnology, DNA molecules are engineered to directly assemble into complex architectures and perform similar mechanisms and functions. This is based on the Watson–Crick base-pairing principles, where A hybridizes with T and G binds with C, which may be used as a programmable bottom-up manufacturing strategy. This idea was first proposed in 1982 by Seeman who designed a four-way junction from several DNA strands.2 Since then, numerous structures and complex geometries have been explored. Initially, DNA structures were not well-defined nor rigid. A following milestone was the double-crossover motif.3–5 With the sticky-end association,6–8 1D and 2D assemblies were made possible with a reasonable stiffness. However, this type of assembly did not guarantee the structural addressability which is critical in programming functions. This method later developed into the DNA tile approach, which uses a few strands to form a unit (motif) and then associates the units via sticky ends. Recently, a similar yet distinct method called DNA bricks was introduced where a large number of unique oligonucleotides assemble into desired conformations with each behaving like a brick (analogous to Lego bricks).9 Both DNA tile and brick methods produced complex architectures with various functions and excellent addressability.A DNA origami approach pursues a different direction. This approach uses a long single-stranded DNA (ssDNA) as a scaffold in conjunction with multiple oligonucleotides (termed staples) to secure the scaffold into desired shapes. This concept was first introduced with a macromolecular octahedron made of a 1669-nucleotide (nt) long scaffold and five 40-nt staples.10 Later, Rothemund demonstrated several distinct structures in the well-recognized DNA origami work using 7249-nt M13mp18 phage DNA as a scaffold.11 With the same scaffold, various geometries can be created with different sets of staples. DNA origami has been extremely popular because arbitrary shapes can be constructed in one-step annealing and the process is reliable, robust, and fault-tolerant.12–14 The size of a single DNA origami structure is limited by the length of the scaffold. However, larger structures are possible by employing multiple orthogonal scaffold strands or by linking multiple preformed DNA origami with linkers (special staples that combines segments of different scaffolds).15–18
In addition to the development of various static constructs, dynamic and deformable structures have also been explored for resembling protein-based dynamic motors and reconfigurable assemblies. Commonly available structures with dynamics and reconfigurability are DNA walkers,19–30 molecular beacons,31–38 and switches.39–46 These dynamic DNA assemblies are typically made of one or few strands forming a motif without rigid domains and dependable connections. They are small (usually, about 10 nm or less) and rely mostly on soft ssDNA segments. Therefore, structural deformations, i.e., shape changes of rigid dsDNA parts, are missing. These all-flexible complexes are not considered in this review. Rather, this article will include another type of well-established dynamic and deformable structures which usually have two (or more) rigid parts linked with a soft connection. The reconfiguration is often realized by a ‘locking’ mechanism which forms a solid dsDNA connection between the two rigid parts. The locking mechanism may be released by strand displacement, enzymatic reactions, or molecular recognition events. Most of such structures switch between two distinct conformations, such as open and closed states. DNA boxes and DNA tweezers are good examples. In a DNA box, the lid and the box body are the two rigid parts, and the lid can open and close using a soft ssDNA connection.47 When the box is open, the lid hangs loosely around the box body. Similarly, two arms of a tweezer are rigid, and their motions are controlled by switching between dsDNA and ssDNA at the connection.48 In these cases, precise shape control may not be straightforward when the connection is soft (e.g., tweezer arm angles and the degree of box opening).
More precise progressive control may be realized by intercalators and other chemical adducts.49–55
Here, the progressive control suggests that the reconfiguration has an infinite number of states in theory. In practice, many (intermediate) conformations are possible (as opposed to two, open/closed, states) and can be prepared precisely. This method usually applies on dsDNA helices, and thus, the structures formed by closely packed dsDNA helices will be reconfigured or deformed in response to the adducts. There are also other strategies to precisely control and/or deform DNA assemblies, including optical tweezers and magnetic fields. Dynamic mechanisms and deformable structures are the major focus of this review. Recently, demand has increased for larger, more complex structures that also exhibit dynamic deformation characteristics. Given the minimum structural resolution of a single base-pair, size and complexity increase simultaneously. Dynamic motions and structural deformations also add to the complexity. Therefore, the importance of relevant mechanics has escalated. Besides, we find that although dynamic systems have been explored, those with actuation or deformation on the rigid dsDNA are neither abundant nor well-modelled. The dynamic and deformable DNA nanostructures thus call for comprehensive mechanical models for better understanding and precise predictions on the structural behaviors and an explanation for experimental observations.
We envision that the improved understanding of dynamics and deformability will benefit the designs of static structures as well. Structures often suffer from internal stresses, and thus, they may deviate from the designed conformations.16,56,57 For example, DNA tiles can be programmed to propagate indefinitely along the designed directions with sticky ends. However, they have limited sizes and often cyclize, forming unwanted aggregates.58–60 One of the important factors is the accumulation of the stresses which may become serious in large, polymerized structures. Other possible causes include entropic processes over polymerization (i.e., side reactions rather than designed tile connections). In addition, DNA assemblies are also subject to thermal fluctuations. The synthesized DNA structures may resemble the design, but their conformations may have a distribution. Sometimes the variation can be significant. Internal stresses, side reactions, and thermal fluctuations require rational designs based on the mechanics such that the structure can be compatible (i.e., the parts work together without creating unnecessary stresses at the boundaries between them) and stiff enough against small variations.
In this review, we present detailed discussion on mechanics of dynamic and deformable DNA nanostructures. Our major focus is the dynamic structures with a reasonable size and geometrical complexity, which undergo structural transformation and deformation by various methods. We first introduce the basic knowledge in mechanics relevant to DNA nanotechnology. Then we explain the mechanics of static structures so that the development of deformable DNA structures can be depicted in a conducive manner. We also discuss deformable structures by introducing different types of deformation methods based on mechanics. We provide insights on the mechanics along with models in design principles of deformable structures. Several synthesis and characterization methods are also included. Finally, we discuss representative applications of dynamic and deformable DNA structures as well as current challenges and outlook.
2 Fundamentals of structural mechanics
The excellent programmability and structural predictability make DNA ideal for creating complex structures from bottom up.61 Two complementary single strands form a double helical cylinder. There are three common forms of double-stranded (ds) DNA: A-, B-, and Z-form. They all have slightly different geometries. Among the three, B-form is the most common type with ∼2 nm in diameter and ∼3.5 nm in height in a full turn (∼10.5 base-pairs or bp per turn). The natural conditions for B-form DNA include aqueous solution with moderate ion concentrations and similar CG/AT ratios. Two double helical strands can be connected to each other by crossovers, which are the sugar-phosphate backbone. DNA strands can thus be programmed to assemble into desired geometries via arrangements of crossovers. A sound understanding of the kinematic mechanisms and theory of elastic beams will allow one to incorporate these structures with the ability to perform complex maneuvers. Previous studies demonstrated DNA as a building block to create nanoscale mechanisms.62 This section introduces the basic concepts involved in designing mechanisms and the foundations of the elasticity theory.A kinematic chain is comprised of links (or edges) and joints. A link is a rigid body that has at least two nodes, i.e., points of connection to other links. A joint is a connection between two links that allows some degree of motion.63 An essential idea in the design of mechanisms is the degrees of freedom (DOF) of a mechanism. For instance, a rigid body on a plane has three DOF, namely, x, y, and θ, as shown in Fig. 1(a). The DOF of a system are determined by the number of links and joints and the types of joints in the system. For example, a rotating pin joint and a slider joint both offer 1 DOF. In DNA nanostructures, a pin joint can be as simple as a pair of connections made of short unpaired nucleotides between two dsDNA links. If restricted to 2D, the pin joint can be further simplified into a short ssDNA strand. Examples of the rotating pin joint, slider joint, and their combined motions are shown in Fig. 1(b).64 The concept of DOF is invaluable during the design of nanostructures to decide the range of motions we want to incorporate. The DOF of the mechanisms in Fig. 1(b) are 1 DOF each. A visualization of a DNA structure as a system of links and joints is presented in Fig. 1(c)–(e).65
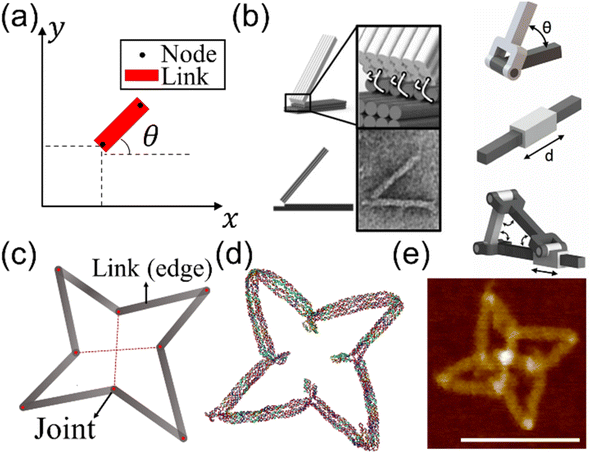 | ||
| Fig. 1 Kinematic mechanisms realized with DNA nanostructures. (a) A planar rigid body (red rectangle) with 3 degrees of freedom (DOF), i.e., the coordinates x, y, and the angle of inclination θ. The rigid body is a link. A node shown as black dots is the possible connecting point in the link to other bodies. A link must have at least two nodes. The link can be classified as a binary, ternary, and quaternary link if it has two, three, and four nodes, respectively. (b) A kinematic chain is comprised of links and joints. A joint is a connection between two links at the nodes that allows some degree of motion. An example of common kinematic chains and a nanoscale hinge realized using ssDNA connections (white lines in the inset). The transmission electron microscopy (TEM) image resembles the design. On the right side, angular (top, rotating pin joint), linear (middle, slider joint), and combined motions (bottom) are shown in schematics (Adapted from ref. 64 with permission. Copyright (2015) National Academy of Sciences). (c)–(e) Architectured auxetic metastructures from DNA (Adapted from ref. 65 with permission. Copyright (2021) Wiley-VCH GmbH). (c) Schematic of a unit cell of a rotating square design composed of links and joints. (d) Coarse-grained molecular dynamics (MD) simulation on the oxDNA platform and (e) atomic force microscopy (AFM) image of the DNA origami unit. Scale bar: 100 nm. | ||
An inherent assumption of the kinematic chain is that the links are rigid. However, the behavior of DNA assemblies which exhibit some degree of flexibility may be understood by the engineering theory of elasticity. Here, a beam is used to support and transmit forces. This theory focuses on uniform beams with high aspect ratios (length/diameter), which holds true for most DNA nanostructures. The first step in studying elasticity is the concept of stress and strain. The stress (σ) is defined as the force per unit area. An elastic beam can experience both axial and shear stress caused by longitudinal and transverse forces, respectively. The axial stress is along the axial direction, i.e., normal to the cross-sectional area of a beam, as illustrated in Fig. 2(a). In contrast, the shear stress is based on the tangential plane. A pair of distanced, equal magnitude forces acting in opposite directions generate a moment (M) or torque. Beams experience bending when moments act perpendicular to the axis (Fig. 2(b)). Torsion is caused by moments around the axis as shown in Fig. 2(c). To quantify deformation, strain (ε) is defined as the deformation of a link per unit length. Similar to stress, it can be classified into axial strain for the changes in the axial direction, and shear strain on the tangential plane.
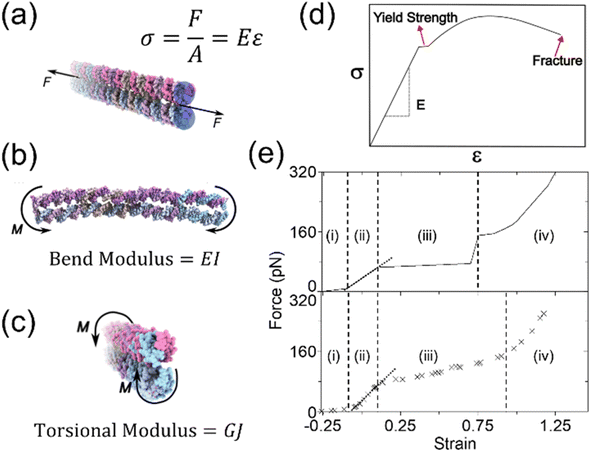 | ||
| Fig. 2 Basic mechanics and deformation behaviors. (a) A DNA beam under uniaxial loading, where σ is the stress, F represents the force, and A (blue shades) is the normal cross-sectional area. The stress σ is proportional to the strain ε (which is ΔL/L, where L is length) with the constant E, the Young's Modulus. (b) The DNA beam under bending due to moments acting perpendicular to the axis, where M is the moment, and I is the second moment of area (or area moment of inertia). (c) The beam under torsion where G is the shear modulus, and J is the second polar moment of area (or polar moment of inertia). (d) The stress–strain curve of a general material with the slope representing the Young's modulus in the linear elastic region. The turning point from the linear to non-linear regimes marks the yield strength. As the general material extends more after the yield point, fractures will happen at the end. (e) The force–strain behaviors of dsDNA component (ds-λ-DNA, top) and architectured structures (DNA crystal, bottom).67,74,155,245,246 The reference length for the strain is the length of B-form DNA. The force in the DNA crystal is the force per loaded dsDNA. There are 4 regimes upon loading: (i) un-tension, (ii) linear elasticity, (iii) dsDNA dissociation, and (iv) ssDNA stretch. Since dsDNA can dissociate into ssDNA, the force behavior is more complex than the general curve in (d). The overall magnitudes of the transition points between the regimes and stages share similarities. The deformation mechanism for each regime at similar strain corresponds to each other. However, the force-reaction of a complex DNA architecture is not a simple sum of the individual components as seen in the transition from (iii) to (iv). Both the structural complexity and the mechanics of the components must be accounted for simultaneously to fully understand the deformation behaviors (Adapted from ref. 74 with permission. Copyright (2022) Biophysical Society). | ||
Stress and strain of a body are correlated, which forms a constitutive law. A widely used constitutive law is Hooke's law which states that the resultant strain in a body is directly proportional to the stress applied. The constant of proportionality relating the two parameters is the Young's modulus (E). The Young's modulus is obtained by calculating the slope of the stress–strain curve within the linear elastic range. Analogous to the Young's modulus for axial forces, the shear modulus (G) is defined for torsion. Fig. 2(d) presents the σ–ε behavior of a general material, including both elastic and plastic ranges. While Hooke's law successfully characterizes the elastic regime, beams may also undergo irreversible deformation when subject to sufficiently high forces beyond the yield point. When a beam is unloaded after plastic loading, it will experience permanent, irreversible deformation known as residual strain.66 At significantly higher stress, the material may not sustain the load further, and fracture will take place.
Several previous studies determined the Young's modulus of DNA helices, which was found to be on the order of 100 MPa.67 The mechanical properties of DNA assemblies vary significantly depending on the surrounding environment. Thus, the medium where they are present should also be accounted for while considering their structural moduli.68–71 DNA nanostructures exhibit unique behaviors when subjected to forces.72 For example, the forces applied may lead to the dissociation between base-paired nucleotides, thus altering the properties of the structure further. Additionally, the elastic constants are affected by nicks in the DNA helices, which have been found to reduce the stiffness by more than 10 folds.73 When dsDNA bundles are under external loads, the force–strain behaviors are different from those of general materials (Fig. 2(e)).74 There are 4 distinct regimes, (i) un-tension, (ii) linear elasticity, (iii) dsDNA dissociation, and (iv) ssDNA stretch, illustrating the complex nature of DNA molecules during deformation. Notably, dsDNA strands start to dissociate before yielding. The dissociation depends on the sequence, structure, and environmental factors such as ion and temperature. The process can be somewhat reversible.75
3 Static DNA structures
Over the past four decades, DNA nanotechnology has produced complex 1D, 2D, and 3D structures with various geometries. In the early years, the assembled structures were predominantly static. These structures vary in size from small constructs (e.g., few-strand motifs) to macroscopic crystals. While DNA self-assembly may propagate indefinitely in theory, there is a size limit in practice due to the material availability, inherent curvature, and internal stresses.76 Well-defined DNA assemblies can be up to approximately 500 μm in size.77The simplest 1D structures are DNA rods which usually have a few dsDNA with double crossover connections to hold them together.78 The rods may be constructed with various cross-sections. For example, 6 dsDNA bundles may form a rod with a cross-section of 3 × 2 rectangle or a hexagonal arrangement. The respective square and honeycomb arrangements (or lattices) will have an impact on the placement of crossovers, resulting in differences in DNA helicity (vide infra).79–81 In addition, there is a correlation between the length of a rod and its cross-sectional area. That is, the thickness of the cross-section must be at least a certain percentage of the length to avoid significant structural deflection. This will be discussed in detail below in Section 5 Design requirements and guidelines. The rods (or links in the mechanics point of view) can be connected by ssDNA joints at the terminals and become wireframe structures.82–84 The wireframes may be extended into 2D or 3D structures with the joints as the corners.85–87 In such cases, there are some hollow areas in the wireframe structures. Given the same material, wireframes can be larger than the solid-piece structures without any cavities. Schmidt and coworkers constructed truss structures using DNA origami.88 Compared with regular ∼100 × 100 × 2 nm without any hollow area origami, the trusses made of the same scaffold can reach 235 × 22.5 × 22.5 nm whose volume thus increases by 6 times.
In a wireframe design, one must determine how to build the ssDNA joints. The terminals of the rods may not be on the same plane due to the nature of DNA double helix. Zhang et al. used integer numbers of full turns on dsDNA aiming for the same plane with angles controlled by the number of unhybridized nucleotides at the joints (Fig. 3(a)).83 Given the integer number, the edge length may only be certain values (e.g., approximately 3.5, 7, and 10.5 nm, etc.). This limits the possible configurations of wireframe structures. Bathe group further developed this approach towards general design principles.89 In their design, there is no need to be on the same plane. The free ssDNA segments at corners are used to form an angle and to compensate the plane disagreements. Versatile shapes are all available with some trade-off on the flatness. The structures may not stay perfectly in the same plane; however, the out-of-plane angle is ∼10°, which is not severe and generally acceptable.
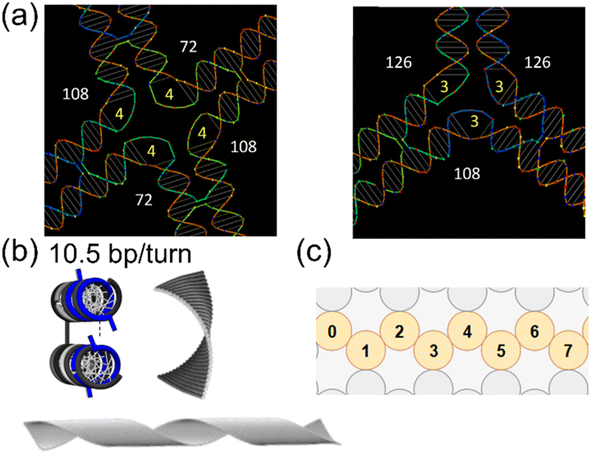 | ||
| Fig. 3 Design details for static DNA structures. (a) Schematics of possible joint designs. Left: 4-Way junction. Right: 3-Way junction. Integer full turns on dsDNA will place the joint to be on the same plane. Angles (in degree shown in white color) are then controlled by the number of un-hybridized thymine (T) nucleotides on staples (written in yellow, e.g., 4-nt and 3-nt of ploy-T) (Adapted from ref. 83 with permission. Copyright (2015) Macmillan Publishers Limited). (b) A DNA origami tile designed with a helical pitch of 10.67 bp per turn will experience strain due to the difference from the inherent 10.5 bp per turn of B-DNA. Neighboring helices will have a mismatch, which leads to a right-handed curvature as shown in the FEM computed structure on the right. This effect may be magnified if the tiles are polymerized into a long ribbon (shown in the bottom) (Adapted from ref. 16 with permission. Copyright (2016) American Chemical Society). (c) Cross-section of caDNAno design in a honeycomb lattice. In this design, a planar structure will have a wave-like corrugated arrangement of the DNA bundles. Numbers indicate the dsDNA helices. | ||
There are other 1D structures. DNA tubules or cylinders are 1D like small DNA bundles, but their diameters may be tens of nm with hollow centers and variable lengths.15,90–92 Another example is a ring-shaped DNA gear.77 It is similar to DNA tubules but has a diameter of ∼350 nm and its length ranges from ∼30 nm to microns. These constructs may also be viewed as 2D or 3D structures folded in cylindrical direction.
In 2D structures, a variety of geometries are possible by strand arrangements. If all the dsDNA bundles are closely packed, the structure will be a solid piece. Due to the close packing, slight mismatch of the length and angle in a structure can accumulate. For example, flat rectangular DNA origami is usually designed with a square lattice in caDNAno93 or similar CAD platforms. In the software, the helicity is often set as 10.67 bp per turn for simplicity of making crossovers (e.g., 32 bp for 3 turns). However, this is different from the intrinsic helicity of B-form DNA, which is ∼10.5 bp per turn.56,77 This slight difference in helicity will cause strain throughout the assembled structure, resulting in both global curvature and twist. This effect may not show up in a structure less than 100 nm, given the limited resolution in measurements (e.g., atomic force microscopy or AFM). Note there may be a flattening effect during the AFM sample preparation (see Section 4.3). Thermal fluctuation at this scale can also be comparable to the curvature and twist. The strain can accumulate and cause significant distortion in large structures. For example, polymerized DNA origami tiles show apparent structural twists (Fig. 3(b)), while individual tiles do not show significant distortion.16
Another strategy for 2D is using 10.5 bp per turn for DNA helicity in the design, which is realized in honeycomb lattices. In this lattice, a crossover is placed every 2/3 turn, which is exactly 7 bp per crossover. Therefore, there is no intrinsic mismatch and no global curvature in assembled structures.18 Due to the different crossover density, a flat plane from honeycomb lattices is thicker than one dsDNA helix. This is because the planar geometry is realized by wave-like cross-sections, as shown in Fig. 3(c). In other words, honeycomb lattices realize no curvature by sacrificing the thin flat surfaces.
3D structures are more complex to design and assemble. Due to the size limit of the scaffold in DNA origami, for example, 3D solid-piece structures are usually smaller than 50 nm. Small unit origami structures can be assembled together for larger constructs.77 This takes a significant amount of material, and the yield would suffer. As discussed above, wireframes can be larger than the solid-piece structures given same material since they are not fully filled. This causes the edges to deflect if the length is too long. The threshold is related to persistence length LP, which is the ratio between the bending modulus κ and the environmental thermal energy kBT:67,69
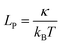 | (3.1) |
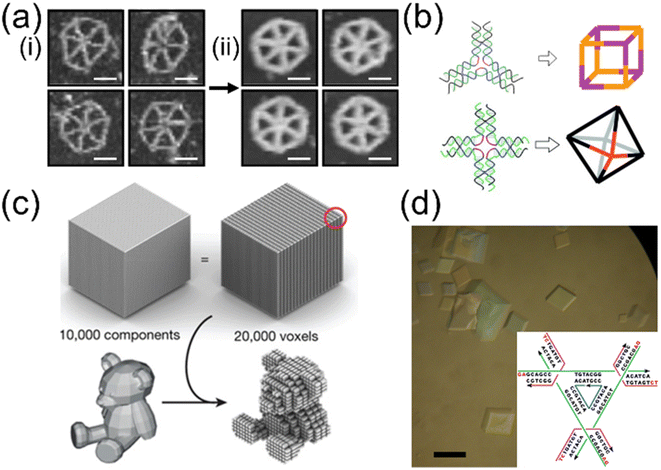 | ||
| Fig. 4 Versatility of DNA self-assembly in 2D and 3D static structures. (a) TEM images of DNA origami hexagons with the same edge length but different cross-section. The left four (i) have 2 dsDNA bundles in each edge while the right four (ii) are composed of 6 dsDNA. Therefore, the double-stranded region on the scaffold increases from ∼2.2 kbp (i) to ∼7.2 kbp (ii). Adding more dsDNA in an edge from 2 to 6 makes the edge more rigid and straight. Scale bar: 50 nm (Adapted from ref. 94 with permission. Copyright (2019)). (b) Symmetric motifs (e.g., 3- and 4-point-stars) from several oligonucleotides are assembled into cube and octahedron (Adapted from ref. 96 with permission. Copyright (2010) WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim) (Adapted from ref. 97 with permission. Copyright (2009) American Chemical Society). (c) Schematics of DNA bricks approach. Like a machining process, this method conceptually starts with a cube and removes unneeded parts in the design phase so that desired geometries such as a teddy bear will emerge from the annealing (Adapted from ref. 99 with permission. Copyright (2017) Macmillan Publishers Limited). (d) Optical image of macroscopic DNA crystals from tensegrity triangle motifs (inset). Scale bar: 200 μm (Adapted from ref. 101 with permission. Copyright (2013) American Chemical Society). | ||
The tile-based assemblies are normally not limited in size and can easily build into 2D or 3D structures similar to wireframe DNA origami.95–97 The difference is that the starting point is an n-way joint motif. The motifs can then associate with each other via sticky ends and form desired structures, such as 3D polyhedra (Fig. 4(b)). If the tile were to be completely planar and stiff, they would form a large 2D flat crystal.98 The limiting factor of the process is that the larger and more complex the final structure is, the lower the yield will be.
The DNA bricks method can generate customized 3D structures. There are two conceptual ways for the structure-building process, by either addition or subtraction. In the additive approach, the structure starts from a single strand, and neighboring strands hybridize with the first strand and propagate to occupy the space towards the target structure. In contrast, the subtractive method initiates from the entire brick with all the possible strands (which can be a cube or a rod). Like machining, strands related to the parts to be removed are taken away so that the target structure emerges from the rest of the strands. Once the structure design is set, the DNA strands will form the target structure such as a toy bear (Fig. 4(c)).99 The resolution of the assembled structures is the size of the single strands. Therefore, there exists a trade-off between resolution and yield.
There are infinite types of 2D and 3D structures. In 2D scenarios, there is a balance between flatness, curvature, stiffness, and thickness. With curvature, the assembly will either stop growing at some point or cyclize into a tube. The infinite assembly in 3D may lead to macroscopic crystals, the so-called DNA crystals. The idea was proposed by Seeman, Mao, and their coworkers.100 Most DNA assemblies are too small to be visible to naked eyes. When the tiny structures are connected, they may become large enough to observe. In their tile-based strategy, tensegrity triangle motifs were developed as an assembly unit and connected in 3 directions via sticky ends.101 3D crystals can thus be built up to hundreds of micrometers in size (Fig. 4(d)). There are other types of motifs developed by Yan and other groups with 4- to 6-arm motifs.102,103 The angle and length can be well controlled with a huge number of units coherently linking together and facing the same orientation. After the tiles are assembled, the sticky ends can be connected together by covalent bonds by ligation enzymes.104 The ligated crystals show significantly improved stability and mechanical properties. For example, they can survive in ion-free environments. They may collapse after drying out completely. However, they can restore their conformation when rehydrated. Therefore, their deformation behaviors and structural mechanics are of great interest.
4 Dynamic and deformable structures
In addition to static structures with complex geometries and structural integrity, dynamic DNA materials have been explored in pursuit of building DNA nanomachines. These nanomachines benefit from the biocompatibility and programmability of DNA-based designs. Dynamic motions and reconfigurations can originate from DNA–DNA hybridization, enzyme activities, chemical stimuli, and external loading. Here we provide a mechanical perspective on the dynamic and deformable structures along with discussions on the reconfiguration methods and tools for studying them.The simplest and most straightforward method for dynamically reconfiguring DNA structures is by reversible assembly of units. For example, DNA origami tubules may be stacked together into a long, hollow cylinder by incorporating a set of linker strands.15 By removing the linkers via toehold-mediated strand displacement, the stacked cylinder may be disassembled. It may be reassembled by reintroducing linkers. Chen et al. used this strategy for reconfigurable chirality of a long DNA origami cylinder using multiple sets of linkers and releasers.15 Here, the involvement of rigid dsDNA parts in the reconfiguration is minimal, and there are no issues or interests from the mechanics point of view. Thus, we discuss below more interesting deformation mechanics related to structural transformation.
4.1 Reconfiguration methods
To realize nanomachines, it is essential to develop mechanisms for dynamic transformation of DNA structures and understand the related mechanics. A common strategy is altering the DOF by adding or removing restrictions from DNA–DNA binding in nanostructures.48,105 This can be realized by introducing signaling strands,106 enzyme-powered reactions,107,108 photosensitive molecules,50,109 or using aptamers with target-specific affinity.110 Structural changes can also be performed by incorporating ‘jack’ strands, which alters the strain and controls the states of DNA structures. Adjusting the jack edges allows one to change the force distribution in the structures and design conformation patterns with several stages.65,111–116 Another strategy is using chemical adducts to modulate the helicity in DNA–DNA associations,49 thereby changing the force states and deforming the structures progressively. Deformation of DNA nanostructures may also be induced by external loadings. External forces are applied by multiple methods including optical tweezers,117–119 magnetic tweezers,78,120,121 electric fields,122–124 flow fields,125–127 and direct contact forces such as AFM.74,128,129 These devices can add forces or torques precisely and be used for studying deformation mechanisms as well as mechanical properties.One of the earliest demonstrations is the DNA tweezer (shown in Fig. 5(a)) designed by Yurke and coworkers.48 This nanodevice has two ssDNA arms sticking out in an open state initially. A closing strand hybridizes with the two arms upon introduction, resulting in the reduction of rotational freedom in the structure. The tweezer thus transforms into a closed state. This process can also be reversed with another strand that removes the constraints on the rotation of the arms. Since this seminal work, numerous studies have been reported using similar strategies.105,131–140 Another typical example is the DNA box shown in Fig. 5(b).47 A ‘lock-and-key’ system is designed on the lid of the box. The lid is initially held tight on the box by a pair of locks which restrict the DOF. The key strands bind to the locks via strand displacement and release the double strands into a ssDNA state. This allows the lid to recover its mobility and open up. This system is similar to DNA tubules stacking together forming a long, hollow cylinder discussed above.15 However, the difference is that the lid is connected to the box via ssDNA soft spacers, and thus, it will close the box when the lock is presented again. In contrast, the tubules were completely disconnected and finding the same neighboring tubules during reassembly would be highly unlikely.
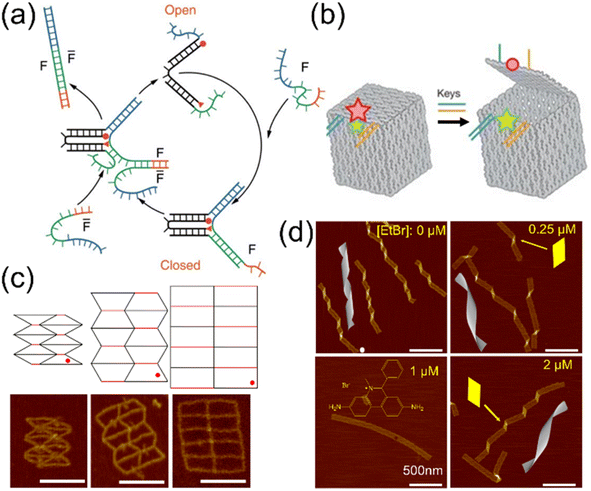 | ||
Fig. 5 Reconfigurable DNA structures using ssDNA hinges, jack edges, and helicity modulation. (a) A DNA tweezer that switches between open and closed states. The structural changes are initiated by complementary strands F and ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) that induce strand displacement (Adapted from ref. 48 with permission. Copyright (2000) Macmillan Magazines Limited). (b) A DNA box that can open and close its lid using a ssDNA hinge mechanism. The box is locked initially by DNA strands (two independent groups, marked in blue and orange) and upon addition of keys the binding is released, thus opening the lid with freedom of rotation from hinges. The Cy5 and Cy3 are depicted in red and green, respectively. Stars with different sizes represent the dye emission with different intensities. Circle indicates a loss of emission (Adapted from ref. 47 with permission. Copyright (2009) Macmillan Publishers Limited). (c) Auxetic 2D DNA origami structures (re-entrant honeycomb) with jack edges (shown in red). The jack edges can adjust its length with toehold-mediated strand displacement and addition of replacement strands. The structural deformations are performed by changing the length of jacks, demonstrating negative Poisson's ratios. The angle (noted by red dots) can vary from 30 to 60 to 90° (and vice versa). Scale bar: 100 nm (Adapted from ref. 65 with permission. Copyright (2021) Wiley-VCH GmbH). (d) Conformational control of polymerized DNA origami ribbons with chemical adducts. The increased concentration of intercalator ethidium bromide (EtBr) progressively changes the structures from right-handed to flat and then to left-handed conformations (noted by the yellow kink shape). Scale bar: 500 nm (Adapted from ref. 16 with permission. Copyright (2016) American Chemical Society). that induce strand displacement (Adapted from ref. 48 with permission. Copyright (2000) Macmillan Magazines Limited). (b) A DNA box that can open and close its lid using a ssDNA hinge mechanism. The box is locked initially by DNA strands (two independent groups, marked in blue and orange) and upon addition of keys the binding is released, thus opening the lid with freedom of rotation from hinges. The Cy5 and Cy3 are depicted in red and green, respectively. Stars with different sizes represent the dye emission with different intensities. Circle indicates a loss of emission (Adapted from ref. 47 with permission. Copyright (2009) Macmillan Publishers Limited). (c) Auxetic 2D DNA origami structures (re-entrant honeycomb) with jack edges (shown in red). The jack edges can adjust its length with toehold-mediated strand displacement and addition of replacement strands. The structural deformations are performed by changing the length of jacks, demonstrating negative Poisson's ratios. The angle (noted by red dots) can vary from 30 to 60 to 90° (and vice versa). Scale bar: 100 nm (Adapted from ref. 65 with permission. Copyright (2021) Wiley-VCH GmbH). (d) Conformational control of polymerized DNA origami ribbons with chemical adducts. The increased concentration of intercalator ethidium bromide (EtBr) progressively changes the structures from right-handed to flat and then to left-handed conformations (noted by the yellow kink shape). Scale bar: 500 nm (Adapted from ref. 16 with permission. Copyright (2016) American Chemical Society). | ||
4.1.1.1 Special cases. dsDNA may also be used as rigid joints, where elastic energy can be stored and released. Ke et al. designed a DNA origami whose corners were locked by binding strands which were compressed as a spring.108 Upon addition of a restriction enzyme, BamHI, the binding sites were cleaved and the compressed dsDNA were released, leading to an extended state of the structure. This type of dsDNA joints or spacers have some similarities with the jack edges (vide infra) but can be considered as the joints rather than edges if they are small and the elastic energy is stored within them.
The strands that bind with ssDNA spacers can be introduced by the enzymatic reactions. Schmidt and coworkers designed a wireframe DNA origami with some part of edges left unhybridized.141 As a result, the structure curves up due to soft ssDNA. They demonstrated that T4 DNA polymerase can turn the ssDNA segments into dsDNA, thus forming solid edges and gaining the rigidity in the wireframe. Accordingly, the curvature is straightened, and the wireframe origami transitions from a curved tube to a straightened tube. This method is efficient with materials since it reduces the need for chemical synthesis of DNA molecules. Once the dsDNA rods are formed, however, they cannot be removed with site-specificity (thus, no reversibility) given there is no toehold on the strands formed by the enzyme.
Similar controls on structural connections and moving space may also be realized with environmental cues.142,143 For example, guanine-rich sequences often form a unique secondary conformation called G-quadruplex where four guanine bases constitute a plane in the presence of K+ or other cations.143 The G-quadraplex may be interrupted, thus giving back freedom of movement to sequences. I-motifs are single-stranded DNA sequences which respond to pH change.144 At low pH, i-motif strands fold together and reduce the DOF. At high pH, they will unfold and can perform base-pairing. Thus, they may be used for reconfiguration mechanisms for DNA structures.145 Other environmental conditions such as UV light have also been developed. Strands with photolabile moieties or photoisomerization groups may change the base-pairing under UV irradiation, which will ultimately alter the conformation.146 It should be noted that due to the nature of the DNA binding-unbinding, a precise control of multi-states is challenging with most current designs and strategies. Though some efforts have been made (e.g., a three-state structure control by introducing more DNA strands to form intermediate steps),147 such studies are still limited and several states may coexist during the structural transitions.
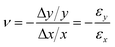 | (4.1) |
A recent study demonstrated that the helicity control may be extended with photo-modulation.50 Short- and medium-wavelength UV light, UVC and UVB, can cause photo-lesion in DNA, damage the structure, and lead to the release of internal strain. As a result, curved structures may flatten. In contrast, long-wavelength UV (UVA, 315–400 nm) does not damage the DNA strands regardless of dosage, and thus DNA assemblies are unaffected. There is a class of photo-responsive intercalators which may be utilized to control the shape of DNA constructs in conjunction with UVA, thereby regulating their intercalative binding properties.153 For example, a triarylpyridinium cation (TP1) can be biscyclized into a polycyclic form (TP2) by UVA radiation.154 TP2 is a strong intercalator with DNA, whereas TP1 is not. Under UVA radiation, it binds with DNA like EtBr, which changes the conformation of DNA assemblies.50 However, the photo-responsive molecule may not have sequence specificity. Using photoactivable intercalators with UV light may provide an alternative method to sequence-based designs and show possibilities of a progressive control of DNA structures remotely by external radiation.
4.1.4.1 Optical tweezers. Force application through optical traps is achieved by attaching DNA to micron-sized dielectric beads. The force is generated on the beads due to the change in momentum of refracted photons from a laser and the bead positions are controlled precisely. The optical method has proved useful in measuring fundamental properties of DNA such as stretch modulus155 and disassembly force.156 Pfitzner et al. used an optical tweezer to study several DNA bundles under stretch as illustrated in Fig. 6(a).117 The DNA beams were placed between a pair of beads and extended as the beads were moved apart by the optical tweezer. They first examined DNA beams in honeycomb lattices with 6, 8, 10, and 12 helices (without a hairpin) and compared the force–extension behaviors. Then, they used the 10-helix structure (with a hairpin loop in the middle) to test the hairpin with the forces to pull it open. The optical measurements provided force–extension data with exceptional precision and revealed detailed mechanical behaviors of DNA assemblies during structural transformation.
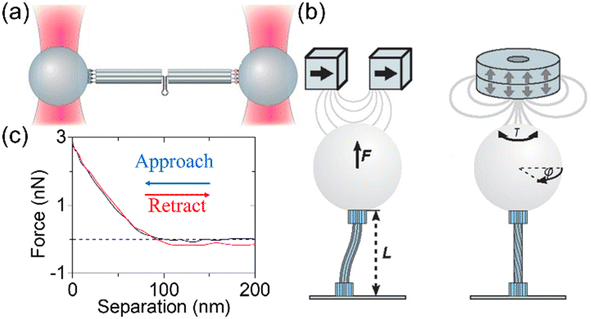 | ||
| Fig. 6 Deformation by external loading. (a) Experimental setup for optical traps. A DNA origami rod (with a length of ∼500 nm) with a hairpin in the middle is placed between two dielectric beads (with a diameter of ∼1 μm). The laser beam shown in red exerts forces on the beads, pulling them apart from each other. As a result, the DNA specimen will experience the stretch load (Adapted from ref. 117 with permission. Copyright (2013) WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim). (b) Schematics of magnetic tweezer experiments on DNA bundles with one end fixed on the surface and the other end attached to a magnetic bead. The particle moves under magnetic fields, exerting external loadings on the DNA structure (Adapted from ref. 78 with permission. Copyright (2011) American Chemical Society). (c) A pair of representative approach and retract force curves during the nanoindentation of an AFM probe tip on a single point of a macroscopic DNA crystal. The separation is the displacement from the lowest indented point. The indentation depth is approximately 100 nm (Adapted from ref. 74 with permission. Copyright (2022) Biophysical Society). | ||
4.1.4.2 Magnetic fields. In a magnetic tweezer experiment, the setting is similar to the optical trap, but the optical beads are replaced with magnetic particles. The movement of the particles is controlled by external magnetic fields. The particles can thus exert forces (e.g., bending and torsion) to the attached structures. A previous study used DNA rotors attached to magnetic particles, to impart rotational motions under magnetic fields.157 This method yielded continuous rotation with precise position control. Fig. 6(b) illustrates a study that investigated bending and torsional rigidities of DNA beams with magnetic tweezers.78 Several DNA bundles were designed with one end fixed to a coated substrate while the other end was modified with a magnetic particle. Therefore, the bending and torsional forces were exerted separately so that the respected rigidities were recovered from the force–displacement data. Magnetic fields also have been exploited to generate complex motions such as the propulsion of DNA based flagellar bundles using magnetic particles.158 This is reminiscent of bacterial flagella. Although attachment of magnetic particles to DNA devices may increase complexity, this approach offers a reliable way of controlling nanoscale devices.
4.1.4.3 Electric fields. This approach is based on the negative charge of DNA backbone. DNA assemblies will thus respond when subject to external voltage. This is different from the optical and magnetic tweezers discussed above. The electric fields subject the whole structure to forces, while the optical and magnetic fields allow application of forces on specific components of the nanostructure. Electric fields were used to estimate the mechanical properties of DNA helices.159 Rant and coworkers demonstrated the activation of a nano-lever made of DNA origami using alternating current.160 The external field enabled precise control at very high frequencies (e.g., 200 Hz). The typical response time of DNA rods to applied voltage was found to be less than 100 μs. This is extremely fast compared to the slow reaction rate of traditional methods such as strand displacement reaction which takes seconds or minutes, if not longer.27 Several recent studies have shown that electric fields can be a powerful approach to achieve precisely controlled motion in nanoscale mechanisms.161 For example, Simmel and coworkers constructed nanorobotic arms made of DNA origami and moved their rotational positions within milliseconds.123 The DNA arms were driven at angular frequencies of up to 25 Hz and positioned with precision of <2.5 nm. A follow-up work presented an elaborate rotor system from DNA controlled by alternating current (AC) fields.162 The rotor generated a maximum torque of 10 pN nm with a rotational speed up to 250 rpm. Most interestingly, the motion behaviors resembled Brownian ratchets which are common molecular machinery in nature. An analogy was drawn from biological motors such as ATP synthase, thus presenting an opportunity to further study molecular mechanisms essential in biology and create synthetic analogs.
4.1.4.4 Flow fields. External fluid flow can also exert forces on DNA assemblies. A part of a DNA structure may be fixed on a surface with another part attached to a particle. Then, this system can be subject to flow field, where the particle will be moved hydrodynamically, and the structure will experience various stretching forces depending on flow rates. Jung et al. demonstrate the feasibility of this strategy.125 They stretched 4 DNA beams with different crossover density and number of nicks using flow-induced stretching force. They found that both increasing crossovers and nicks can reduce the stretch stiffness of the beam by half. Like electric fields, this approach will introduce force actuation on the entire DNA structure.
4.1.4.5 Direct contact forces. Besides external fields, forces can be exerted on the DNA structures via direct contact. AFM is an excellent tool for this purpose, since it can apply forces on the DNA samples using its probe tip.128,129,163–167 The control of the force can be realized by adjusting the indentation depth of the tip. For example, nanoindentation was performed on self-assembled DNA crystals using AFM.74 During the indentation, the force was recorded as a function of the distance between the AFM tip and the deepest indented point of the sample (Fig. 6(c)). The mechanical deformations and elastic properties were studied. These studies provided useful tools and platforms to study deformation and mechanics of DNA structures. However, the precision, types of loadings, and the structural complexity that can be probed are still limited, and thus, more possibilities remain to be explored.
4.2 Structural reinforcement
This subsection presents methods for reinforcing DNA structures, which ultimately affect their structural properties and deformation behaviors. Suppose, for example, that a segment of a DNA structure is designed to be sturdy and withstand external forces applied by an AFM probe. This can be realized by reinforcement of the segment via physicochemical methods. The Dietz group showed that covalent bonds can be formed between proximal thymidines and become cyclobutane pyrimidine dimers within DNA origami under UV irradiation.168 This strengthened the designated part of DNA structures where pyrimidine derivatives are rich and thus improved structural stability. Their results demonstrated stable structures at temperatures up to 90 °C and in double-distilled water without salt ions, where hydrogen bond-based structures cannot remain intact. Sugiyama and coworkers demonstrated that 8-methoxypsoralen can crosslink with pyrimidine bases in DNA origami upon photo-irradiation.169 The photo-crosslinked structures showed improved resistance to high temperatures. Chemical crosslinking methods also have been developed for structural reinforcement.170,171 Anastassacos et al. used polyethylene glycol (PEG) modified oligolysines for coating DNA nanostructures. With addition of glutaraldehyde, the structures were crosslinked and showed 400-fold higher resistance to nuclease as well as improved stability in low-salt environments. The reinforced structures are also expected to have enhanced mechanical properties.4.3 Experimental characterization
Given the versatility and programmability of DNA self-assembly, one can construct complex structures, which may be static or dynamic in nature. Due to their small size on the order of nanometers, it is crucial to have a proper toolbox of measurement techniques to observe or monitor the structures after synthesis. AFM, transmission electron microscopy (TEM), and fluorescence imaging are prominent methods for visualizing nanoscale devices.172 While AFM and TEM are primarily used to measure structures in static states, several methods such as optical spectroscopy and fast-scan AFM excel in monitoring real-time dynamic changes.Apart from providing information about the topography, AFM can also be used for studying the behavior of nanostructures in response to the tip. Andersen et al. demonstrated that the tail of dolphin-shaped DNA origami was pushed to the sides by the AFM tip.182 Fundamental structural properties such as Young's modulus of DNA constructs were measured in nanoindentation experiment using AFM.74,128,167 The probe tip can also cut, fold, and stretch the surface of DNA structures.183 The versatility and multitude of options that AFM offers make it an indispensable part of any nanostructure researcher's toolbox.
Both AFM and TEM have found extensive applications in DNA nanotechnology. However, each method comes with its own share of pros and cons. While AFM is relatively fast and offers good spatial resolution, its utility is limited to 1D and 2D samples. Given the nature of the AFM probe method, precise 3D imaging is difficult. It is also hindered by the fact that the properties of the imaged structures might be different from those exhibited freely in solution. This is due to the deposition of samples on mica which leads to the flattening of the structure. This is significant with in-air imaging, likely resulting in structural deformation. Similarly, TEM sample preparation may also cause distortion. Cryo-EM can provide 3D images but requires rigorous preparation and additional postprocessing.
Given its inverse-sixth power dependence, FRET has found several applications as a molecular ruler to perform distance measurement.113 In DNA structures, FRET is introduced by strategically decorating DNA strands with fluorophore and quencher labels. An example is a DNA machine decorated with fluorophores.113 When strand displacement occurs, the reconfigurable edge shortens in length, placing the fluorophores in close proximity and leading to a change in emission signals. FRET measurements are pivotal in 2D and 3D cases involving biological entities (e.g., cells) where methods such as AFM and TEM become redundant.190 One limit is that the fluorophore-quencher pair must be within the range for FRET to occur. This can bring challenges for the placement of the pair on the structure of interest.
4.4 Theoretical and computational models
There are several models for dynamic and deformable nanostructures. This section provides an overview of available models as well as the pros and cons of each model. The models are sorted based on the lengthscale, from macroscale (continuum) to mesoscale (covering microscale to macroscale) and ultimately to microscale (interchangeable with ‘nanoscale’ in this context, that is, at atomic or molecular level). Deformable structures were originally developed from macroscopic mechanical systems. Therefore, DNA structures may use similar continuum models including elastic beam theory and finite element method (FEM) for numerical simulations. Given the dimension of DNA molecules (e.g., base stacking distance of ∼0.33 nm), mesoscale models may also be applied. An effective mesoscale model on polymers is the freely-jointed chain (FJC) model (or ideal chain model) among others. At the microscale, atomic or molecular models consider the interactions between particles (e.g., atoms), and thus, provide significantly more detailed information. Given the enormous number of particles in the calculation domain, these models are used for simulations only. One important note here is that the models discussed in this section are design driven, which means that they must benefit the design process, either by revealing the mechanical properties or ensuring the deformation schemes. Practicality (i.e., reasonable size or the number of particles to be calculated) is also important. Due to the limited computing power, it is unrealistic to simulate kDa or MDa complexes using the models developed from quantum mechanics. Therefore, full-fledged quantum mechanics models are not considered in this review.4.4.1.1 Spring network. Spring network models are the simplest form of elasticity theory. It can be rough or fine, depending on the size of the parts represented by the springs. Typically, a segment of continuous dsDNA is modeled as a spring with a given spring constant and initial length. The loading on a spring can be uniaxial, torsional, bending or their combinations. Chen et al. applied the spring system to a single-layer origami rectangle which has an original curvature.196 The cyclization process of the tile using a set of linkers was modeled as a two-step process with an intermediate state: (i) flattening the initial curvature and (ii) rolling up into a tube. The deformation was assumed to be elastic and evenly distributed on the spring system analogy. Fig. 7(a) illustrates a spring network of dsDNA bundles that experiences torsional and bending loads. The calculated energy for cyclization matched with the experiments and the simulations.197 The advantage of the model includes the simplicity and accuracy for regular deformation. For a less than 100 nm structure, the manual calculation gives a superb precision at the uncertainty level of 1%. The downsides are also obvious, nonetheless. The deformation should be small, simple, and evenly distributed without any concentrated spots. In their work, the deformation between the neighboring dsDNA helices was around 10°, which may be considered as small. Therefore, the spring constants may be assumed as constant, not varying with any parameters or under different environmental conditions. Moreover, the deformation process must be assumed in a certain way that it can be calculated. Complex deformations may not be possible in the spring model.
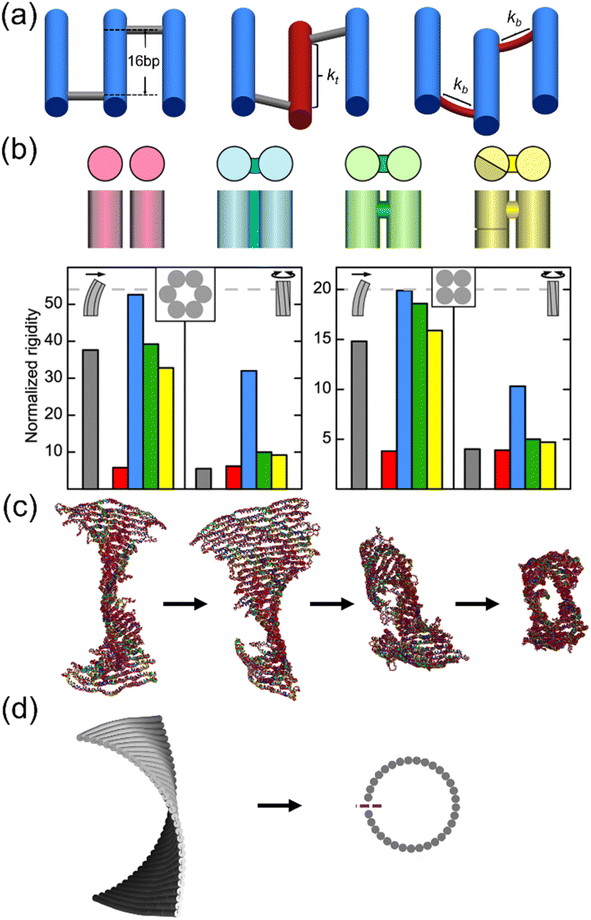 | ||
| Fig. 7 Theoretical and computational models for DNA assemblies. (a) Spring network system applied on a solid-piece origami tile, shown as a structural motif in a segment. From left to right, the schematics show the undeformed motif (with blue and gray representing dsDNA rods and ssDNA crossovers, respectively), twisting of the double helix in the middle (maroon), and bending of crossovers (maroon). The length between neighboring crossovers is 16 bp. kt is the torsional spring constant, while kb is the bending spring constant of the crossovers (Adapted from ref. 196 with permission. Copyright (2014) American Chemical Society). (b) Elastic beam theory models dsDNA bundles with different boundary conditions (red, fully disconnected; blue, fully attached; green, partially attached; and yellow, partially attached with discontinuity in the dsDNA bundles). As a comparison, FEM simulations are shown in gray (Adapted from ref. 78 with permission. Copyright (2011) American Chemical Society). (c) Coarse-grained MD simulation on cyclization of a single-layer origami tile with initial curvature. As the tile cyclizes, the initial curvature gradually disappears and the tile rolls from the boundary to the middle into a cylinder. The cylinder does not have a perfect circular cross-section (Adapted from ref. 197 with permission. Copyright (2021)). (d) Model for a spring system, where a perfect circular cross-section is assumed. (Adapted from ref. 197 with permission. Copyright (2021)). | ||
4.4.1.2 Elasticity theory. Both the spring network and the elastic beam theory are macroscale, using elastic modeling to predict structural properties and deformations. The key difference between them is that the springs in the spring model have no volume and are linked with other springs only at the terminals, whereas the beams in the elasticity theory have volume and can connect with others anywhere on the surfaces. Therefore, the beams enable more boundary conditions. For example, the elasticity theory considers how one piece of material is connected to the other. Kauert et al. modelled the DNA rods made of 4 to 6 dsDNA bundles as elastic beams, as shown in Fig. 7(b).78 They studied four different types of boundary conditions between the bundles (fully disconnected in red, fully attached in blue, and two partially attached in green and yellow). They concluded that the most reasonable conditions were the two partial attachments. A downside of the simple model is that the actual torsional rigidity may be less than predicted. There may be uncertainties in applying the elasticity theory on complex structures since it often requires additional information. For example, Li et al. applied this theory on architectured origami wireframes and found that it could roughly estimate their overall deformation behaviors.65 However, their experiment suggested that DNA nanostructures could not be predicted accurately without considering detailed mechanical properties of components (edges and joints). They concluded that the structural complexity and the mechanics of the components must be accounted for simultaneously to fully understand the structural properties and deformation behaviors.
4.4.1.3 Finite element method. FEM is a numerical method that solves a set of partial differential equations for structural analysis or other applications. The finite elements refer to smaller, simpler parts subdivided from a large system. In such a way, the equations are numerically manageable. CanDo198 is a widely used FEM platform in DNA nanotechnology. It has a single base-pair resolution, which means that the finite elements in CanDo are each base pair. The boundary conditions are set such that the neighboring bases can slide but not separate. CanDo offers reasonable initial values for DNA mechanical properties, and users can change the values for their specific conditions. All the simulations are normally performed online and finished within a few minutes. One of the challenges in CanDo is that applying forces is complex, which requires the users to install the CanDo related software locally and to adjust the structure manually. Another challenge is the representation of ssDNA in the model. No matter how long the ssDNA segment is, it is recognized as a connection without length. Thus, it cannot simulate certain structures, for example, the crank slider where many ssDNA connections are used.64 Generic FEM platforms such as COMSOL, Ansys, and ABAQUS may be good alternatives. These programs are capable of all kinds of direct mechanical loadings but may require heavy work to set the system up in the generic platforms to fully depict the base-pairs as well as unpaired nucleotides. Liedl and coworkers used the COMSOL simulations and successfully described the detailed responses to bending and twisting of DNA rods (Fig. 7(b)).78
4.4.3.1 Molecular dynamics models. MD simulations provide more detailed information with significantly better resolution. This method analyzes the physical movements of particles (e.g., atoms or molecules). The particles are subjected under interactions for a set duration, producing a view of the dynamic evolution of the whole system. The trajectories of the particles are determined by numerically solving Newton's equations of motion for the particles. MD computation often relies on coarse-grained models which use a pseudo-atom to represent a group of atoms. Thus, the resolution is pseudo-atom level. OxDNA is a commonly used coarse-grained MD platform in DNA nanotechnology.68 It uses one particle to represent one nucleotide. In a nucleotide, there are multiple sites for different association energies. For example, base-pairing is between bases, backbone connection is between backbone sites, and stacking is between base stacks. There are seven different association energies in total. The platform allows external loadings to the system. As such, this model provides significantly more details than the abovementioned methods. Li et al. performed coarse-grained MD simulations on cyclization of an origami tile (Fig. 7(c)) and compared the results with experiments, FEM results, and elasticity theory.196,197 The experiments determined the conformations before and after the cyclization, from which related energy was estimated. A simple spring network model provided results that matched with the experiments (Fig. 7(d)). However, details such as the exact deformation pathways were not revealed. The MD simulations on the oxDNA software calculated the forces needed to induce the cyclization and provided the details of structural evolution under loads.
Shi et al. performed coarse-grained MD simulations on DNA origami hinges with various lengths of ssDNA segments that led to variable configurations.202 This was realized by comparing the configuration of the ssDNA connections with applied forces. In the hinge design, there is an interplay between beam-like dsDNA edges and spring-like ssDNA joints. For example, the longer the ssDNA segment is, the more moving space there is. As a model system, they simulated the hinges with and without ssDNA joints and added hypothetical forces. The force exerted by the different length of ssDNA joints was then recovered by matching the configuration of the hinge. This work benefits the designs of intricate DNA nanostructures. Overall, coarse-grained MD models are powerful tools that can include non-specific binding of bases, the charge effect of salts, and the sequence specificity.68 Some details are not included, however; for example, the DNA form (e.g., B–Z transition), pH-dependent behaviors, and other molecular effects.203 The best way to consider such effects would be all-atom models.
4.4.3.2 All-atom models. These models include all the related atoms in the simulations for better accuracy. Thus, DNA, water molecules, free ions, and base–ion complexes will all be calculated. Therefore, direct simulations of non-Watson–Crick (or noncanonical) base pairings are possible, including i-motif, G-quadplex, and other possible bindings. Nanoscale molecular dynamics or NAMD is an all-atom software that can simulate DNA structures.204 It can also explore the DNA association with proteins, lipids, and carbohydrates. However, there are significant issues. Firstly, all-atom computations take significantly longer than coarse-grained models, because all the atoms are considered. Secondly, simulating deformations of large DNA structures may not be realistic even if it can take up to 1 billion atoms. Hübner et al. simulated the position of a fluorophore on a DNA origami using NAMD.205 The simulation suggested that the fluorophore bounced back and forth due to the thermal fluctuation. Stacking and unstacking of the bases were observed. Although all-atom models can capture details, the entire simulation domain is about 50 bp (∼17 nm) in size. It is difficult to calculate the overall deformation of large structures. Thus, the all-atom models are recommended for small segments rather than assembled structures. For example, the detailed behaviors of function groups (e.g., pH- or ion-dependent groups) may be well described.
5 Design requirements and guidelines
Given the focus of this review on dynamic and deformable structures, this section provides our recommendations for designing DNA structures with deformability during dynamic processes. Our guidelines presented below are based on three common models: elasticity theory, FEM, and coarse-grained MD models. Suppose a complex structure is being analyzed by FEM. A coarse-grained MD computation may also be performed to gain more details in exchange of design and modelling time. However, the elastic beam theory may not give sufficient information due to the complexity, and the experiment may not agree with the design. Note that other models such as FJC and WLC models as well as all-atom models are not discussed here since they may be best suited for special cases as discussed in Section 4.4. For example, FJC models are applicable for long DNA rods, while all-atom models are suitable for direct simulation of non-Watson–Crick base pairings in a small domain. In the following discussion on the general designs and models, the structures are classified into two groups: solid piece and wireframe.In solid-piece DNA nanostructures, it is generally safe to assume that dsDNA strands are rigid cylinders with deformability and ssDNA are soft spacers. Most deformations occur with ssDNA parts or thin dsDNA bundles, while thick dsDNA segments will barely deform. Conceptual designs may be verified with the elastic beam theory and examined with FEM. A rational design route may be: (1) conceptual design with assumptions on rigid dsDNA and soft ssDNA; (2) intermediate design with possible changes based on elastic beam theory; (3) final design verified by FEM simulations. Between the steps, corrections should be made on the design to reflect any parts that do not fit the design criteria (e.g., a curved edge should be reinforced to be straight). Given the simplicity of the solid-piece design, not many changes are expected.
Wireframe structures can be more complex. The complexity comes from both the dsDNA edges (links) and ssDNA joints. Depending on the expected deformation of the dynamic structures, different strategies may be used. For small deformations (<10% of relative changes), the assumptions of dsDNA as rigid cylinders and ssDNA as soft spacers still hold true. In such a case, they can be designed like static structures. Edges should be shorter than the persistence length, and ss-segments at joints should be designed accordingly for the range of adjustable angles. Yan et. al. summarized correlations between the ssDNA length at a joint and the angle between two adjacent edges.83 As depicted in Fig. 8(a), the length increases from 2 to 6 nt with the angle ranging from 180 to 0°. Each ss-segment length would be suitable within the small deformation. General FEM platforms such as COMSOL may be used for better simulations on the ss-segments.
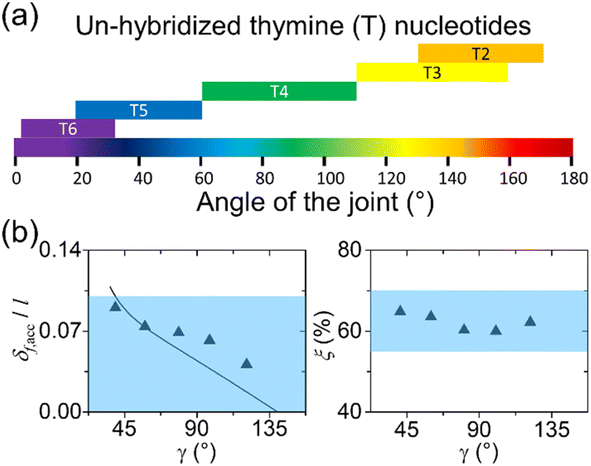 | ||
| Fig. 8 Design recommendations for deformable DNA structures. (a) Suggestions for unpaired ssDNA at the joints of a wireframe origami. Un-hybridized thymine (T) nucleotides on staples are marked as Tn (e.g., T6 means 6-nt ploy-T, or TTTTTT). The length of ploy-T increases from 2 to 6 as the angle narrows from 180 to 0° (Adapted from ref. 83 with permission. Copyright (2015) Macmillan Publishers Limited). (b) Design guidelines for wireframe DNA origami that undergoes significant structural deformation (e.g., 10–50% relative changes). Dimensionless flexure (δf,acc/l) on the left and joint stretch (ξ) on the right as a function of angle γ which defines the conformation. The line is the prediction from the elasticity theory and the filled triangles denote the deformation data from coarse-grained MD simulations. δf,acc and l are the flexure and length of an edge in a wireframe DNA origami. Joint stretch ξ is defined as the length of a ssDNA segment at a joint divided by its fully stretched length. Blue shades indicate recommended regions for edge thickness and joint stretch. If the design recommendations are met, the wireframe structures will assume straight edges and sharp angles (Adapted from ref. 65 with permission. Copyright (2021) Wiley-VCH GmbH). | ||
For a greater extent of deformation (e.g., 10–50%), the edge rigidity and joint flexibility must be considered. The Choi group developed a set of design requirements on DNA origami wireframes experiencing significant deformation (>30%).65 They explored several auxetic structures which normally have sharp angles and relatively long edges. Two key points from the work are as follows (Fig. 8(b)). Firstly, edges must have a thickness greater than 10% of their length for sufficient rigidity. Otherwise, the edges will likely have curvature. Structural deformations under external loads or thermal fluctuation are due to the limited persistence length or stiffness (see Section 2 and eqn (3.1)). At a given temperature, the persistence length is proportional to the stiffness, such as bending modulus which is the product of Young's modulus and the second moment of area of the cross-section (Fig. 2(b)). Young's modulus normally remains unchanged, and thus for a longer persistence length, a larger second moment of area is needed. Cross-sectional area is the sum of all the infinitesimal elements of area on the cross-section. Likewise, the second moment of area of the cross-section is the sum of all the infinitesimal elements of area times the square of the distance from the infinitesimal element to the bending axis. Therefore, the further the area elements are from the bending axis, the stiffer the edge is for a given cross-sectional area. The values of common cross-sections under typical bending axis can be found elsewhere.206 In summary, the edge thickness here is the thickness perpendicular to the bending axis (often, the edge axis). If the bending axis is unknown, thicknesses in all the directions must satisfy such conditions.
Secondly, joints must have a certain level of tension, quantified by a stretch level. The stretch level is defined as the length of a ssDNA segment at a joint divided by its fully stretched length and should be between 55 and 70%. For the stretch level below 55%, the joint will be loose, and as such the structural integrity will be compromised. On the other extreme, the joints with a stretch level of over 70% may experience internal stresses and likely distort (without any loading) due to the lack of sufficient deformability. If both recommendations are met, the assembled structures will have straight edges and sharp angles. Note that the joint stretch level is difficult to study with FEM simulations which also may not be able to reflect the changes of elastic properties under large deformations. Therefore, coarse-grained MD computation will be the best choice. Like any designs, corrections are needed before finalizing the design. The changes on the lengths of ssDNA segments are usually not significant, for example, from 8 to 6 nt, due to the moderate deformation.
If a structure undergoes significant deformation (>50% relative change) or is too large and complex to design, several iterations are required. A recommended design route is: (1) disassemble the structure into several components; (2) design each component based on the guidelines shown above; and (3) assemble the components and check for additional corrections on the design. Suppose a round table with four legs is the structure to be designed, and it is subjected under loads in the center of its upper surface. If the initial design is under a large force (e.g., 1 nN) that might result in a significant deflection. In this case, the table may be conceptually disassembled into five components: a round tabletop surface and four table legs. The force distributed on each leg can be estimated (e.g., 0.25 nN if the four legs are symmetric). The design of the legs may be evaluated by FEM to ensure that they remain straight under the load. The tabletop surface should be examined by coarse-grained MD simulations because of the significant deformation. Due to the possible large deformation, corrections on the thickness of the tabletop are expected. After the legs and the surface are ready for the assembly, the coarse-grained MD simulations may be performed for the assembled structure. Additional corrections on the connections between the legs and the tabletop or even the components themselves may be necessary. Eventually, the DNA table will be shaped. Castro and coworkers proposed a design flow on complex structures, which reflects the same idea of design.207
Overall, the design recommendations are closely related to possible models on dynamic and deformable structures. Simple models, such as elastic beam theory, often require additional information of the structure and components. The effectiveness of the design purely based on simple models may thus be limited. As discussed in Section 2, DNA properties can vary when subject to large deformations. Therefore, complex deformable structures would require models that can account for variation of the properties. This type of model would be able to provide more detailed information about the structure; for example, coarse-grained MD models as opposed to FEM. The time for design would then increase exponentially with respect to structural complexity.
6 Applications of dynamic and deformable structures
6.1 Dynamic nanodevices with reconfigurability and responsivity
As discussed above, ssDNA is widely used as a joint connecting rigid DNA bundles. Its flexibility and low stiffness make it an ideal joint which allows a greater degree of motion compared to dsDNA or other higher order duplexes. The combination of rigid bundles and soft hinges can thus constitute dynamic DNA nanodevices capable of programmed reconfiguration. The Castro group demonstrated the effectiveness of ssDNA hinges in the machine mechanisms constructed using DNA origami.64 They constructed the crank slider mechanism which outputs translation upon circulating the crank. DNA bundles were used as links of machine elements and ssDNA to control the motion of these links. The flexibility of ssDNA segments varied the crank angle, resulting in the translation of an outer bundle (slider) over the inner rod. Further, ssDNA was also used to change the conformations of a Bennett linkage. These basic mechanisms drive the challenge to create complex functions for nanomachines. A fully functional nanomachine may contain intricate mechanisms which contain two basic components when broken down; for example, the DNA rods are being pulled or rotated upon hinge. By standardizing the two, higher order mechanisms can be devised.Multiple groups have developed various mechanisms for controlling cargo actuation. In an attempt to using DNA as a cargo delivery vehicle, Kjems and coworkers designed a DNA origami box with internal cavity.208 The hollow volume of the DNA box may be used to carry molecular payloads and have the capability to open and close the lid with a set of locks and keys. This concept was demonstrated for drug delivery by Douglas et al. using DNA-aptamer locks which respond to an array of cues.209 The cues can be platelet-derived growth factor (PDGF) or protein tyrosine kinase 7 (PTK7).210,211 The cargo in the box can be antibodies or anti-cancer agents. Thus, delivery vehicles leveraging the programmability of DNA can be effective in finding the target cells and releasing the drug molecules.
Liposomes or lipid vesicles are often used to mimic biological cell membranes and organelles. There is a challenge on controlling the size and shape of liposomes.212 Zhang et al. created a dynamic long and thin quadrangular prism or cylindrical DNA templates for liposomes to grow on (Fig. 9(a)).130 The cylindrical template was polymerized from monomers which have two rings and four pillars each such that the distance between the rings is well defined. The liposomes formed within the rings in the presence of free ssDNA segments projected toward the center. The pillars in the monomer can be dynamically removed (changed from dsDNA to ssDNA) so that the individual liposomal spheres can merge into a single elongated liposome. This strategy is similar to DNA boxes that use ssDNA hinges to control motion. This development using DNA structures as a dynamic template can exponentially increase the functionalization of liposomes as synthetic vesicles.
 | ||
| Fig. 9 Applications of dynamic and deformable DNA. (a) A dynamic long and thin quadrangular prism or a cylindrical template polymerized from DNA monomer structures. Left: A monomer with two rings and four pillars. Middle-left: Polymerized cylindrical DNA template. Middle-right: The cylindrical DNA template with a liposome formed within each ring. Right: Liposomes merge together into a single elongated liposome by removing the pillars in the monomers (Adapted from ref. 130 with permission. Copyright (2017) Macmillan Publishers Limited). (b) 2D deployable Hoberman flight ring made of DNA origami. Left: Schematics of the reconfiguration between open (triangle overall) and closed (hexagon overall) states. The reconfiguration is driven by three jack edges (not shown). Purple arrows indicate the force exerted by one of the jacks. For simplicity, only one is depicted. The inscribed circle is marked with a dotted line. The three red triangles are on top of the blue triangles. Note that the inside vertex of each red triangle is connected to that of the blue one on the opposite layer, thus forming a trefoil knot. The jack edges are placed on these connections. Right: AFM images of open and closed states of the DNA origami. Scale bar: 100 nm (Adapted from ref. 213 with permission. Copyright (2021) Wiley-VCH GmbH). (c) Force measurement in FRET decorated DNA origami. Left: Two nucleosomes whose force interactions are to be studied by DNA origami. Middle: DNA origami force spectrometer. It has a spring-loaded hinge with generated moment or torque illustrated with a red torsional spring. Red and green dots indicate positions of the FRET pair. Right: Schematic and corresponding TEM images of the DNA origami with two nucleosomes attached at different locations. Scale bar: 50 nm (Adapted from ref. 221 with permission. Copyright (2016) American Association for the Advancement of Science). | ||
6.2 Structural deployment
Jack edges induce local strain to displace designated parts within a structure, thereby changing the conformation.65,111–116 As discussed in Section 4.1, jack edges prove to be more precise than flexible ssDNA hinges/locks. Li et al. designed jack edges as a structural transformation mechanism for a Hoberman flight ring.213 A Hoberman sphere is a 3D deployable structure developed as a kids toy and can change its finite size upon external loading (e.g., switching between compressed and extended states). Its 2D version is a Hoberman flight ring. A Hoberman flight ring was constructed with DNA origami which consisted of 6 deployable triangles in 2 layers, representing a trefoil knot. Fig. 9(b) shows that when the red triangles are located on top of blue triangles, the inscribed circle is at its largest (open state). It becomes smallest (closed state; a hexagon overall) when the red triangles slide farthest with respect to the blue ones. The structural transformation was made possible by changing the lengths of three jack edges implemented (i.e., long jacks for the hexagon; short jacks for the triangle). All joints between the triangle edges are made of unpaired ssDNA segments, with their length depending on their rotation angles. About 50% change between the two conformations marks as an excellent deployable structure. This 2D reconfiguration mechanism could be extended in 3D and the volumetric change has the potential for payload delivery.This type of deployable structure is distinct and different from regular transformable structures. Typical structures capable of reconfiguration often have the conformation changed for distinct differences. Examples includes a box that opens the lid,47 a tetrahedron which changes one of its edge lengths,113 and a set of rings that stacks and disassembles.15 After reconfiguration, the symmetry is broken and changed completely. In contrast, deployable structures preserve their global shapes during expansion and contraction.214 In the case of the flight ring, the structure is centrosymmetric in both open and closed states. To keep the structural symmetry, the open or closed parts must be either at the center (flight ring) or symmetric (with respect to the center point). The shell of cowpea chlorotic mottle virus (CCMV) is considered as deployable.215,216 Upon pH change, the shell deploys and the genetic molecules inside are released. A simplified view of the process is that the shell reconfigures from (regular or truncated) icosahedron to rhombic triacontahedron. In this process, triangle or hexagon and pentagon faces expands or merges into rhombus faces, creating channels for releasing genetic molecules from the inside cavity.217 Before and after the deployable reconfiguration, its centrosymmetric property remains the same.
6.3 Force sensing and regulation
Force sensing using DNA nanostructures offers powerful avenues to understand the mechanisms behind several essential biological processes. For example, Salaita and coworkers successfully leveraged the tunability of DNA origami to develop nanoscale tension probes capable of measuring cellular traction forces.218 The probes consist of adhesive peptides to bind to the molecule of interest and DNA hairpins as force sensors. The force was estimated by observing the unfolding of hairpins in response to applied forces using fluorescence measurements. The tunability was achieved by increasing the GC content in the hairpin to increase the unfolding force. The modular design also enabled the development of multiple sensors by controlling the number of peptides and hairpins. Additionally, the conformational transitions of DNA constructs have proven to be valuable indicators for force measurements. Nickels and coworkers showed that the two stacking conformers of a Holliday junction can indicate molecular forces.219 Previous studies by Sugiyama and coworkers also demonstrated the biosensing in optical tweezers by the unfolding of interlocks between DNA origami tiles.220 Similarly, the Dietz group measured forces using FRET decorated DNA origami, as depicted in Fig. 9(c).221 The DNA structures were analogous to a spring-loaded hinge. By measuring the angular distributions of the origami spring via FRET, the forces between the nucleosomes under different conditions were calculated.Force sensors can also probe different structural behaviors depending on how the DNA helices deform. This can be realized either through shearing or unzipping base pairs.222 For example, Darcy et al. explored force measurements using a DNA hinging mechanism.223 The hinge design is similar to the structure in Fig. 1(b) with two rigid dsDNA edges connected via ssDNA at the joint. When the two free ends are compressed, the angle between the arms indicates the forces exerted on the DNA hinge. For measuring large forces, the design can be modified with short ssDNA connections such that the hinge becomes stiffer. They showed that this hinge system can measure up to 20 pN of force. This system was used to monitor the force during unzipping of dsDNA strands with different lengths. DNA-based force sensors also have been extended to design hydrogels that exhibit different fluorescence signals depending on force inputs by embedding small DNA tension probes into the hydrogel lattice.224
Several previous reports established the utility of DNA probes in biological applications such as cell adhesion.225,226 The structural flexibility of DNA renders it useful for the mechanical regulation of biological processes. DNA springs were developed to regulate enzymatic activities by applying forces.227 This study regulated the activity of maltose binding protein (MBP) with covalently attached ssDNA.228 When bound with a complementary strand, the force exerted by the DNA made it energetically unfavorable for the protein to occupy the conformational state required for binding.
6.4 Propagation of local deformation driven by information transfer
Structural deformation mechanisms discussed thus far need local deformation on each actuation site to induce global changes in configurations. With the increase in the size of DNA assemblies and the number of reconfiguration sites it becomes a challenge to supply proportional amounts of ssDNA to act on the sites. Song et al. proposed a method that uses a single reconfiguration site to transform the entire structure.229 The nanostructure contains repeating units of four dsDNA bundles in rhombus shapes. The structure has two stable states, corresponding to the standing and falling of the dominoes. When a trigger strand is presented, the unit that recognizes the trigger changes its configuration from standing to falling, causing all other units to fall. This work proves that the information transfer of structural deformation between molecular units is possible and can be dynamically propagated with external activation. If the structure can be made larger, the sensing (of ssDNA) and actuation (reconfiguration) can be far from each other. This could be useful in building complex DNA function devices.The research on deformable DNA structures is rapidly developing yet is still in its youth. Thus, related applications have been relatively limited. Other reviews on the applications of dynamic structures can be found elsewhere.62,230–234
7 Conclusions and outlook
This article provides an overview of the development of DNA nanotechnology, the basic mechanics, and the evolution from static DNA structures to dynamic, deformable nanodevices. We have focused on mechanical perspectives on deformation mechanisms, different scales in modelling, and ultimately design recommendations. Both static and dynamic DNA nanodevices with small deformation share the same basic mechanics, and thus have similar design principles. For a greater degree of deformation (e.g., 10–50% of relative changes), the conformation changes must be considered during the design process. For significant deformation (>50%), the change of mechanical properties of DNA components needs to be accounted for as well. Design by parts and iterations on assembled structures are required for complex architectures. The mechanics and designs are also closely related to the intended applications, and thus the functionalities should be in turn reflected in the mechanics and designs. To expand our understanding of dynamic and deformable nanostructures, there are several questions that need to be answered.7.1 What we can build
The dynamic DNA nanostructures with soft ssDNA hinges have been well developed and used for various applications as discussed above. For example, DNA origami boxes have been demonstrated by multiple groups with different chemical schemes;47,208,235–237 however, the open-close mechanisms were very similar from the mechanics point of view as all used ssDNA hinges. In contrast, deformations on dsDNA parts are still underdeveloped, yet they could be developed into unique mechanisms for programming structural transformations and functions. This review summarizes the fundamentals in related mechanics and design suggestions. With a library of mechanical designs and mechanisms, one can envision a broader range of feasible structures and functionalities that may be tailored to specific applications.7.2 How we can program DNA mechanics
In any deformable structure, some parts are designed for structural integrity while the others are accounted for deformation. Under selections of materials with different stiffnesses, distributions of deformation may be arranged. For example, soft parts can deform noticeably, whereas rigid parts may have minimal deformation. The utility of DNA on this aspect is that stiffness of ssDNA is smaller than that of dsDNA by more than an order of magnitude.73 This can benefit in arranging deformations at different parts. Additional methods include cross-section designs. For example, 6 dsDNA can be arranged into a honeycomb or a 3 × 2 rectangular cross-section. Hexagonal arrangement will have almost the same bending stiffness regardless of bending directions while rectangular lattice will be stiffer if the bending is on the 3-bundle direction and softer if bent on the 2-bundle direction. Depending on the loading, cross-sections should be selected accordingly.There are several strategies for strengthening DNA, such as adding chemicals that can enhance DNA mechanics. For example, crosslinking molecules can improve the thermal stability of DNA structures,168–171 and will likely enhance the stiffness and mechanical stability. This mechanical enhancement has not been explored extensively. Given different crosslinking reactions on different bases (e.g., C and T vs. A and G),238,239 it may be possible to design sequence-based stiffness, which could open new opportunities in mechanical designs and related applications.
DNA nanostructures also offer the freedom of tailoring the mechanical properties through introducing a variety of crossovers.4,240 Crossovers between helices determine the strain experienced by the structures due to base-pair mismatch, if any, which often accumulate to introduce a global twist into the structure.16 Fine-tuning of the diameter and twist in DNA nanotubes was achieved by strategically placing the crossovers in between the helices to control the mismatch and consequently the torsion experienced by the helices.241,242 Additionally, the mechanical properties and the porosity of the nanotube structure may also be modulated by the crossover density.243 In general, the stiffness of a helical bundle is inversely proportional to the crossover spacing.
Besides, the surroundings where the DNA assemblies are present also affect the structures and related mechanics. For example, increasing Na+ from 1 mM to 1 M can reduce the DNA stiffness to ∼1/3 of the original value.244 Note that the DNA structures would be affected in this salt-based approach. If it is combined with protection methods, such as polyethylene glycol (PEG) coating on DNA, only the parts without coating would become influenced. In this scenario, DNA could possess 4 distinct rigidities (ssDNA, dsDNA, enhanced DNA, and weakened DNA). This will enable significantly more versatile structures. For example, auxetic DNA origami wireframes may benefit from different stiffness in their designs. Suppose dsDNA edges in the wireframes are replaced with enhanced DNA with higher stiffness. The edges will then likely remain straight during deformation under loading (thus maintaining structural integrity), while the deformability is preserved. Similarly, different rigidities of DNA parts can be used on a structure to enable regioselective deformations during reconfiguration to fit the design purposes.
7.3 What we can model
The designs are hinged to the available theoretical and computational models. With new types of deformable structures and distinct stiffnesses, dynamic mechanisms and deformation modes can be complex. New models or amendments on available models will be necessary to provide suitable guidance on those structures. For example, crosslinked DNA structures cannot be simulated directly by all-atom models, not to mention the three common models (elasticity theory, FEM, and coarse-grained MD models). Alternatively, the stiffness values of crosslinked double helices could be acquired from experiments, which may then be used as an input for general FEM platforms (e.g., COMSOL). Since the crosslinking typically occurs at designed sites, it will be reasonable to replace the stiffness of those sites with the experimental values in the calculation.238,239 Therefore, it may be possible for FEM to compute crosslinked structures. One downside of this approach is that FEM simulations normally do not reflect the changes of elastic properties under large deformation. If the reinforced structures experience significant deformation, the simulated results will not be accurate without additional information. One may need to measure the mechanical properties under small and significant deformations for the DNA components so that the computation can result in better accuracy. With proper modelling for newly developed structures and mechanical properties, the subfield of dynamic and deformable DNA structures will be on a fast-developing route.Author contributions
All authors contributed to the writing and editing of this review article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the US Department of Energy (award no. DE-SC0020673) and the National Science Foundation (award no. 2025187 and 2134603).References
- F. Crick, Central Dogma of Molecular Biology, Nature, 1970, 227, 561–563 CrossRef CAS PubMed.
- N. C. Seeman, Nucleic Acid Junctions and Lattices, J. Theor. Biol., 1982, 99, 237–247 CrossRef CAS PubMed.
- T. J. Fu and N. C. Seeman, DNA Double-Crossover Molecules, Biochemistry, 1993, 32, 3211–3220 CrossRef CAS PubMed.
- X. Li, X. Yang, J. Qi and N. C. Seeman, Antiparallel DNA Double Crossover Molecules As Components for Nanoconstruction, J. Am. Chem. Soc., 1996, 118, 6131–6140 CrossRef CAS.
- X. Yang, L. A. Wenzler, J. Qi, X. Li and N. C. Seeman, Ligation of DNA Triangles Containing Double Crossover Molecules, J. Am. Chem. Soc., 1998, 120, 9779–9786 CrossRef CAS.
- H. Qiu, J. C. Dewan and N. C. Seeman, A DNA Decamer with a Sticky End: The Crystal Structure of d-CGACGATCGT, J. Mol. Biol., 1997, 267, 881–898 CrossRef CAS PubMed.
- N. C. Seeman, DNA in a Material World, Nature, 2003, 421, 427–431 CrossRef PubMed.
- F. A. Aldaye, A. L. Palmer and H. F. Sleiman, Assembling Materials with DNA as the Guide, Science, 2008, 321, 1795–1799 CrossRef CAS PubMed.
- Y. Ke, L. L. Ong, W. Sun, J. Song, M. Dong, W. M. Shih and P. Yin, DNA Brick Crystals with Prescribed Depths, Nat. Chem., 2014, 6, 994–1002 CrossRef CAS PubMed.
- W. M. Shih, J. D. Quispe and G. F. Joyce, A 1.7-Kilobase Single-Stranded DNA that Folds into a Nanoscale Octahedron, Nature, 2004, 427, 618–621 CrossRef CAS PubMed.
- P. W. Rothemund, Folding DNA to Create Nanoscale Shapes and Patterns, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- S. Fan, D. Wang, A. Kenaan, J. Cheng, D. Cui and J. Song, Create Nanoscale Patterns with DNA Origami, Small, 2019, 15, 1805554 CrossRef PubMed.
- H. Bila, E. E. Kurisinkal and M. M. Bastings, Engineering a Stable Future for DNA-Origami as a Biomaterial, Biomater. Sci., 2019, 7, 532–541 RSC.
- P. D. Halley, R. A. Patton, A. Chowdhury, J. C. Byrd and C. E. Castro, Low-Cost, Simple, and Scalable Self-Assembly of DNA Origami Nanostructures, Nano Res., 2019, 12, 1207–1215 CrossRef CAS.
- H. Chen, T.-G. Cha, J. Pan and J. H. Choi, Hierarchically Assembled DNA Origami Tubules with Reconfigurable Chirality, Nanotechnology, 2013, 24, 435601 CrossRef PubMed.
- H. Chen, H. Zhang, J. Pan, T.-G. Cha, S. Li, J. Andréasson and J. H. Choi, Dynamic and Progressive Control of DNA Origami Conformation by Modulating DNA Helicity with Chemical Adducts, ACS Nano, 2016, 10, 4989–4996 CrossRef CAS PubMed.
- M. W. Grome, Z. Zhang, F. Pincet and C. Lin, Vesicle Tubulation with Self-Assembling DNA Nanosprings, Angew. Chem., Int. Ed., 2018, 57, 5330–5334 CrossRef CAS PubMed.
- Z. Li, M. Liu, L. Wang, J. Nangreave, H. Yan and Y. Liu, Molecular Behavior of DNA Origami in Higher-Order Self-Assembly, J. Am. Chem. Soc., 2010, 132, 13545–13552 CrossRef CAS PubMed.
- J. Pan, T.-G. Cha, F. Li, H. Chen, N. A. Bragg and J. H. Choi, Visible/Near-Infrared Subdiffraction Imaging Reveals the Stochastic Nature of DNA Walkers, Sci. Adv., 2017, 3, e1601600 CrossRef PubMed.
- Y. Du, J. Pan, H. Qiu, C. Mao and J. H. Choi, Mechanistic Understanding of Surface Migration Dynamics with DNA Walkers, J. Phys. Chem. B, 2021, 125, 507–517 CrossRef CAS PubMed.
- C. Jung, P. B. Allen and A. D. Ellington, A Stochastic DNA Walker that Traverses a Microparticle Surface, Nat. Nanotechnol., 2016, 11, 157–163 CrossRef CAS PubMed.
- K. Yehl, A. Mugler, S. Vivek, Y. Liu, Y. Zhang, M. Fan, E. R. Weeks and K. Salaita, High-Speed DNA-Based Rolling Motors Powered by RNase H, Nat. Nanotechnol., 2016, 11, 184–190 CrossRef CAS PubMed.
- P. Yin, H. Yan, X. G. Daniell, A. J. Turberfield and J. H. Reif, A unidirectional DNA Walker that Moves Autonomously along a Track, Angew. Chem., 2004, 116, 5014–5019 CrossRef.
- F. Zhang, J. Nangreave, Y. Liu and H. Yan, Structural DNA Nanotechnology: State of the Art and Future Perspective, J. Am. Chem. Soc., 2014, 136, 11198–11211 CrossRef CAS PubMed.
- F. Li, T. G. Cha, J. Pan, A. Ozcelikkale, B. Han and J. H. Choi, DNA Walker-Regulated Cancer Cell Growth Inhibition, ChemBioChem, 2016, 17, 1138–1141 CrossRef CAS PubMed.
- T.-G. Cha, J. Pan, H. Chen, J. Salgado, X. Li, C. Mao and J. H. Choi, A Synthetic DNA Motor that Transports Nanoparticles along Carbon Nanotubes, Nat. Nanotechnol., 2014, 9, 39–43 CrossRef CAS PubMed.
- T.-G. Cha, J. Pan, H. Chen, H. N. Robinson, X. Li, C. Mao and J. H. Choi, Design Principles of DNA Enzyme-Based Walkers: Translocation Kinetics and Photoregulation, J. Am. Chem. Soc., 2015, 137, 9429–9437 CrossRef CAS PubMed.
- J.-S. Shin and N. A. Pierce, A Synthetic DNA Walker for Molecular Transport, J. Am. Chem. Soc., 2004, 126, 10834–10835 CrossRef CAS PubMed.
- M. You, Y. Chen, X. Zhang, H. Liu, R. Wang, K. Wang, K. R. Williams and W. Tan, An Autonomous and Controllable Light-Driven DNA Walking Device, Angew. Chem., Int. Ed., 2012, 51, 2457–2460 CrossRef CAS PubMed.
- A. T. Blanchard, A. S. Bazrafshan, J. Yi, J. T. Eisman, K. M. Yehl, T. Bian, A. Mugler and K. Salaita, Highly Polyvalent DNA Motors Generate 100+ pN of Force via Autochemophoresis, Nano Lett., 2019, 19, 6977–6986 CrossRef CAS PubMed.
- W. Tan, K. Wang and T. J. Drake, Molecular Beacons, Curr. Opin. Chem. Biol., 2004, 8, 547–553 CrossRef CAS PubMed.
- T. J. Drake and W. Tan, Molecular Beacon DNA Probes and Their Bioanalytical Applications, Appl. Spectrosc., 2004, 58, 269A–280A CrossRef CAS PubMed.
- D. Selnihhin, S. M. Sparvath, S. Preus, V. Birkedal and E. S. Andersen, Multifluorophore DNA origami beacon as a biosensing platform, ACS Nano, 2018, 12, 5699–5708 CrossRef CAS PubMed.
- P. Zhang, T. Beck and W. Tan, Design of a Molecular Beacon DNA Probe with Two Fluorophores, Angew. Chem., 2001, 113, 416–419 CrossRef.
- P.-J. J. Huang and J. Liu, Molecular Beacon Lighting up on Graphene Oxide, Anal. Chem., 2012, 84, 4192–4198 CrossRef CAS PubMed.
- H. Kuhn, V. V. Demidov, J. M. Coull, M. J. Fiandaca, B. D. Gildea and M. D. Frank-Kamenetskii, Hybridization of DNA and PNA Molecular Beacons to Single-Stranded and Double-Stranded DNA Targets, J. Am. Chem. Soc., 2002, 124, 1097–1103 CrossRef CAS PubMed.
- C. H. Lu, J. Li, J. J. Liu, H. H. Yang, X. Chen and G. N. Chen, Increasing the Sensitivity and Single-Base Mismatch Selectivity of the Molecular Beacon Using Graphene Oxide as the “Nanoquencher”, Chem. – Eur. J., 2010, 16, 4889–4894 CrossRef CAS PubMed.
- K. Wang, Z. Tang, C. J. Yang, Y. Kim, X. Fang, W. Li, Y. Wu, C. D. Medley, Z. Cao and J. Li, Molecular Engineering of DNA: Molecular Beacons, Angew. Chem., Int. Ed., 2009, 48, 856–870 CrossRef CAS PubMed.
- R. P. Fahlman and D. Sen, DNA Conformational Switches as Sensitive Electronic Sensors of Analytes, J. Am. Chem. Soc., 2002, 124, 4610–4616 CrossRef CAS PubMed.
- D. Han, Y.-R. Kim, J.-W. Oh, T. H. Kim, R. K. Mahajan, J. S. Kim and H. Kim, A Regenerative Electrochemical Sensor Based on Oligonucleotide for the Selective Determination of Mercury (II), Analyst, 2009, 134, 1857–1862 RSC.
- T. Li, S. Dong and E. Wang, A Lead(II)-Driven DNA Molecular Device for Turn-On Fluorescence Detection of Lead(II) Ion with High Selectivity and Sensitivity, J. Am. Chem. Soc., 2010, 132, 13156–13157 CrossRef CAS PubMed.
- F. Wang, X. Liu and I. Willner, DNA Switches: from Principles to Applications, Angew. Chem., Int. Ed., 2015, 54, 1098–1129 CrossRef CAS PubMed.
- M. Xiao, W. Lai, F. Wang, L. Li, C. Fan and H. Pei, Programming Drug Delivery Kinetics for Active Burst Release with DNA Toehold Switches, J. Am. Chem. Soc., 2019, 141, 20354–20364 CrossRef CAS PubMed.
- Y. C. Huang and D. Sen, A Twisting Electronic Nanoswitch Made of DNA, Angew. Chem., 2014, 126, 14279–14283 CrossRef.
- J. M. Thomas, H.-Z. Yu and D. Sen, A Mechano-Electronic DNA Switch, J. Am. Chem. Soc., 2012, 134, 13738–13748 CrossRef CAS PubMed.
- Y. Yang, G. Liu, H. Liu, D. Li, C. Fan and D. Liu, An Electrochemically Actuated Reversible DNA Switch, Nano Lett., 2010, 10, 1393–1397 CrossRef CAS PubMed.
- E. S. Andersen, M. Dong, M. M. Nielsen, K. Jahn, R. Subramani, W. Mamdouh, M. M. Golas, B. Sander, H. Stark, C. L. Oliveira, J. S. Pedersen, V. Birkedal, F. Besenbacher, K. V. Gothelf and J. Kjems, Self-Assembly of a Nanoscale DNA Box with a Controllable Lid, Nature, 2009, 459, 73–76 CrossRef CAS PubMed.
- B. Yurke, A. J. Turberfield, A. P. Mills, F. C. Simmel and J. L. Neumann, A DNA-Fuelled Molecular Machine Made of DNA, Nature, 2000, 406, 605–608 CrossRef CAS PubMed.
- C. Xie, Y. Hu, Z. Chen, K. Chen and L. Pan, Tuning curved DNA origami structures through mechanical design and chemical adducts, Nanotechnology, 2022, 33, 405603 CrossRef PubMed.
- H. Chen, R. Li, S. Li, J. Andréasson and J. H. Choi, Conformational Effects of UV Light on DNA Origami, J. Am. Chem. Soc., 2017, 139, 1380–1383 CrossRef CAS PubMed.
- A. Gopinath, C. Thachuk, A. Mitskovets, H. A. Atwater, D. Kirkpatrick and P. W. Rothemund, Absolute and Arbitrary Orientation of Single-Molecule Shapes, Science, 2021, 371, eabd6179 CrossRef CAS PubMed.
- H. Ijäs, B. Shen, A. Heuer-Jungemann, A. Keller, M. A. Kostiainen, T. Liedl, J. A. Ihalainen and V. Linko, Unraveling the Interaction Between Doxorubicin and DNA Origami Nanostructures for Customizable Chemotherapeutic Drug Release, Nucleic Acids Res., 2021, 49, 3048–3062 CrossRef PubMed.
- F. Kollmann, S. Ramakrishnan, B. Shen, G. Grundmeier, M. A. Kostiainen, V. Linko and A. Keller, Superstructure-Dependent Loading of DNA Origami Nanostructures with a Groove-Binding Drug, ACS Omega, 2018, 3, 9441–9448 CrossRef CAS PubMed.
- H. L. Miller, S. Contera, A. J. Wollman, A. Hirst, K. E. Dunn, S. Schröter, D. O'Connell and M. C. Leake, Biophysical Characterisation of DNA Origami Nanostructures Reveals Inaccessibility to Intercalation Binding Sites, Nanotechnology, 2020, 31, 235605 CrossRef CAS PubMed.
- Y. Zeng, J. Liu, S. Yang, W. Liu, L. Xu and R. Wang, Time-Lapse Live Cell Imaging to Monitor Doxorubicin Release from DNA Origami Nanostructures, J. Mater. Chem. B, 2018, 6, 1605–1612 RSC.
- H. Dietz, S. M. Douglas and W. M. Shih, Folding DNA into Twisted and Curved Nanoscale Shapes, Science, 2009, 325, 725–730 CrossRef CAS PubMed.
- J. Y. Lee, J. G. Lee, G. Yun, C. Lee, Y.-J. Kim, K. S. Kim, T. H. Kim and D.-N. Kim, Rapid Computational Analysis of DNA Origami Assemblies at Near-Atomic Resolution, ACS Nano, 2021, 15, 1002–1015 CrossRef CAS PubMed.
- X. Sun, S. Hyeon Ko, C. Zhang, A. E. Ribbe and C. Mao, Surface-Mediated DNA Self-Assembly, J. Am. Chem. Soc., 2009, 131, 13248–13249 CrossRef CAS PubMed.
- P. O'Neill, P. W. Rothemund, A. Kumar and D. K. Fygenson, Sturdier DNA Nanotubes via Ligation, Nano Lett., 2006, 6, 1379–1383 CrossRef PubMed.
- K. Fujibayashi, R. Hariadi, S. H. Park, E. Winfree and S. Murata, Toward Reliable Algorithmic Self-Assembly of DNA Tiles: A Fixed-Width Cellular Automaton Pattern, Nano Lett., 2008, 8, 1791–1797 CrossRef CAS PubMed.
- J. D. Watson and F. H. Crick, Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid, Nature, 1953, 171, 737–738 CrossRef CAS PubMed.
- S. Nummelin, B. Shen, P. Piskunen, Q. Liu, M. A. Kostiainen and V. Linko, Robotic DNA Nanostructures, ACS Synth. Biol., 2020, 9, 1923–1940 CrossRef CAS PubMed.
- R. L. Norton, Design of Machinery: An Introduction to the Synthesis and Analysis of Mechanisms and Machines, McGraw-Hill/Higher Education, 2008 Search PubMed.
- A. E. Marras, L. Zhou, H.-J. Su and C. E. Castro, Programmable Motion of DNA Origami Mechanisms, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 713–718 CrossRef CAS PubMed.
- R. Li, H. Chen and J. H. Choi, Auxetic Two-Dimensional Nanostructures from DNA, Angew. Chem., Int. Ed., 2021, 60, 7165–7173 CrossRef CAS PubMed.
- S. H. Crandall, N. C. Dahl and T. Lardner, An Introduction to the Mechanics of Solids, McGraw-Hill Book Company, 3rd edn, 2012, SI Units Search PubMed.
- J. F. Marko and S. Cocco, The Micromechanics of DNA, Phys. World, 2003, 16, 37 CrossRef CAS.
- B. E. Snodin, F. Randisi, M. Mosayebi, P. Šulc, J. S. Schreck, F. Romano, T. E. Ouldridge, R. Tsukanov, E. Nir and A. A. Louis, Introducing Improved Structural Properties and Salt Dependence into a Coarse-Grained Model of DNA, J. Chem. Phys., 2015, 142, 234901 CrossRef PubMed.
- A. Aggarwal, S. Naskar, A. K. Sahoo, S. Mogurampelly, A. Garai and P. K. Maiti, What do We Know about DNA Mechanics so far?, Curr. Opin. Struct. Biol., 2020, 64, 42–50 CrossRef CAS PubMed.
- S. Naskar, M. Gosika, H. Joshi and P. K. Maiti, Tuning the Stability of DNA Nanotubes with Salt, J. Phys. Chem. C, 2019, 123, 9461–9470 CrossRef CAS.
- A. Garai, S. Saurabh, Y. Lansac and P. K. Maiti, DNA Elasticity from Short DNA to Nucleosomal DNA, J. Phys. Chem. B, 2015, 119, 11146–11156 CrossRef CAS PubMed.
- C. Bustamante, Z. Bryant and S. B. Smith, Ten Years of Tension: Single-Molecule DNA Mechanics, Nature, 2003, 421, 423–427 CrossRef PubMed.
- J. B. Hays and B. H. Zimm, Flexibility and Stiffness in Nicked DNA, J. Mol. Biol., 1970, 48, 297–317 CrossRef CAS PubMed.
- R. Li, M. Zheng, A. S. Madhavacharyula, Y. Du, C. Mao and J. H. Choi, Mechanical Deformation Behaviors and Structural Properties of Ligated DNA Crystals, Biophys. J., 2022, 121, 4078–4090 CrossRef CAS PubMed.
- M. C. Engel, D. M. Smith, M. A. Jobst, M. Sajfutdinow, T. Liedl, F. Romano, L. Rovigatti, A. A. Louis and J. P. K. Doye, Force-Induced Unravelling of DNA Origami, ACS Nano, 2018, 12, 6734–6747 CrossRef CAS PubMed.
- J. F. Berengut, C. K. Wong, J. C. Berengut, J. P. Doye, T. E. Ouldridge and L. K. Lee, Self-Limiting Polymerization of DNA Origami Subunits with Strain Accumulation, ACS Nano, 2020, 14, 17428–17441 CrossRef CAS PubMed.
- K. F. Wagenbauer, C. Sigl and H. Dietz, Gigadalton-Scale Shape-Programmable DNA Assemblies, Nature, 2017, 552, 78–83 CrossRef CAS PubMed.
- D. J. Kauert, T. Kurth, T. Liedl and R. Seidel, Direct Mechanical Measurements Reveal the Material Properties of Three-Dimensional DNA Origami, Nano Lett., 2011, 11, 5558–5563 CrossRef CAS PubMed.
- Y. Ke, S. M. Douglas, M. Liu, J. Sharma, A. Cheng, A. Leung, Y. Liu, W. M. Shih and H. Yan, Multilayer DNA Origami Packed on a Square Lattice, J. Am. Chem. Soc., 2009, 131, 15903–15908 CrossRef CAS PubMed.
- Y. Ke, N. V. Voigt, K. V. Gothelf and W. M. Shih, Multilayer DNA Origami Packed on Hexagonal and Hybrid Lattices, J. Am. Chem. Soc., 2012, 134, 1770–1774 CrossRef CAS PubMed.
- C. E. Castro, F. Kilchherr, D.-N. Kim, E. L. Shiao, T. Wauer, P. Wortmann, M. Bathe and H. Dietz, A Primer to Scaffolded DNA Origami, Nat. Methods, 2011, 8, 221–229 CrossRef CAS PubMed.
- D. Han, S. Pal, Y. Yang, S. Jiang, J. Nangreave, Y. Liu and H. Yan, DNA Gridiron Nanostructures Based on Four-Arm Junctions, Science, 2013, 339, 1412–1415 CrossRef CAS PubMed.
- F. Zhang, S. Jiang, S. Wu, Y. Li, C. Mao, Y. Liu and H. Yan, Complex Wireframe DNA Origami Nanostructures with Multi-Arm Junction Vertices, Nat. Nanotechnol., 2015, 10, 779–784 CrossRef CAS PubMed.
- S. S. Simmel, P. C. Nickels and T. Liedl, Wireframe and Tensegrity DNA Nanostructures, Acc. Chem. Res., 2014, 47, 1691–1699 CrossRef CAS PubMed.
- H. Jun, X. Wang, M. F. Parsons, W. P. Bricker, T. John, S. Li, S. Jackson, W. Chiu and M. Bathe, Rapid Prototyping of Arbitrary 2D and 3D Wireframe DNA Origami, Nucleic Acids Res., 2021, 49, 10265–10274 CrossRef CAS PubMed.
- X. Wang, H. Jun and M. Bathe, Programming 2D Supramolecular Assemblies with Wireframe DNA Origami, J. Am. Chem. Soc., 2022, 144, 4403–4409 CrossRef CAS PubMed.
- W. Wang, S. Chen, B. An, K. Huang, T. Bai, M. Xu, G. Bellot, Y. Ke, Y. Xiang and B. Wei, Complex Wireframe DNA Nanostructures from Simple Building Blocks, Nat. Commun., 2019, 10, 1067 CrossRef PubMed.
- M. Matthies, N. P. Agarwal and T. L. Schmidt, Design and Synthesis of Triangulated DNA Origami Trusses, Nano Lett., 2016, 16, 2108–2113 CrossRef CAS PubMed.
- H. Jun, F. Zhang, T. Shepherd, S. Ratanalert, X. Qi, H. Yan and M. Bathe, Autonomously Designed Free-Form 2D DNA Origami, Sci. Adv., 2019, 5, eaav0655 CrossRef PubMed.
- P. Yin, R. F. Hariadi, S. Sahu, H. M. Choi, S. H. Park, T. H. LaBean and J. H. Reif, Programming DNA Tube Circumferences, Science, 2008, 321, 824–826 CrossRef CAS PubMed.
- Y. Ke, Y. Liu, J. Zhang and H. Yan, A study of DNA Tube Formation Mechanisms Using 4-, 8-, and 12-Helix DNA Nanostructures, J. Am. Chem. Soc., 2006, 128, 4414–4421 CrossRef CAS PubMed.
- J. Choi, H. Chen, F. Li, L. Yang, S. S. Kim, R. R. Naik, P. D. Ye and J. H. Choi, Nanomanufacturing of 2D Transition Metal Dichalcogenide Materials Using Self-Assembled DNA Nanotubes, Small, 2015, 11, 5520–5527 CrossRef CAS PubMed.
- S. M. Douglas, A. H. Marblestone, S. Teerapittayanon, A. Vazquez, G. M. Church and W. M. Shih, Rapid Prototyping of 3D DNA-Origami Shapes with CaDNAno, Nucleic Acids Res., 2009, 37, 5001–5006 CrossRef CAS PubMed.
- H. Jun, X. Wang, W. P. Bricker and M. Bathe, Automated Sequence Design of 2D Wireframe DNA origami with Honeycomb Edges, Nat. Commun., 2019, 10, 5419 CrossRef PubMed.
- Y. He, T. Ye, M. Su, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, Hierarchical Self-assembly of DNA into Symmetric Supramolecular Polyhedra, Nature, 2008, 452, 198–201 CrossRef CAS PubMed.
- Y. He, M. Su, P. a. Fang, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, On the Chirality of Self-Assembled DNA Octahedra, Angew. Chem., Int. Ed., 2010, 49, 748–751 CrossRef CAS PubMed.
- C. Zhang, S. H. Ko, M. Su, Y. Leng, A. E. Ribbe, W. Jiang and C. Mao, Symmetry Controls the Face Geometry of DNA Polyhedra, J. Am. Chem. Soc., 2009, 131, 1413–1415 CrossRef CAS PubMed.
- S. H. Ko, M. Su, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, Synergistic Self-Assembly of RNA and DNA Molecules, Nat. Chem., 2010, 2, 1050–1055 CrossRef CAS PubMed.
- L. L. Ong, N. Hanikel, O. K. Yaghi, C. Grun, M. T. Strauss, P. Bron, J. Lai-Kee-Him, F. Schueder, B. Wang and P. Wang, Programmable Self-Assembly of Three-Dimensional Nanostructures from 10,000 Unique Components, Nature, 2017, 552, 72–77 CrossRef CAS PubMed.
- J. Zheng, J. J. Birktoft, Y. Chen, T. Wang, R. Sha, P. E. Constantinou, S. L. Ginell, C. Mao and N. C. Seeman, From Molecular to Macroscopic via the Rational Design of a Self-Assembled 3D DNA Crystal, Nature, 2009, 461, 74–77 CrossRef CAS PubMed.
- R. Sha, J. J. Birktoft, N. Nguyen, A. R. Chandrasekaran, J. Zheng, X. Zhao, C. Mao and N. C. Seeman, Self-Assembled DNA Crystals: The Impact on Resolution of 5′-Phosphates and the DNA Source, Nano Lett., 2013, 13, 793–797 CrossRef CAS PubMed.
- C. R. Simmons, F. Zhang, J. J. Birktoft, X. Qi, D. Han, Y. Liu, R. Sha, H. O. Abdallah, C. Hernandez, Y. P. Ohayon, N. C. Seeman and H. Yan, Construction and Structure Determination of a Three-Dimensional DNA Crystal, J. Am. Chem. Soc., 2016, 138, 10047–10054 CrossRef CAS PubMed.
- F. Zhang, C. R. Simmons, J. Gates, Y. Liu and H. Yan, Self-Assembly of a 3D DNA Crystal Structure with Rationally Designed Six-Fold Symmetry, Angew. Chem., Int. Ed., 2018, 57, 12504–12507 CrossRef CAS PubMed.
- Z. Li, L. Liu, M. Zheng, J. Zhao, N. C. Seeman and C. Mao, Making Engineered 3D DNA Crystals Robust, J. Am. Chem. Soc., 2019, 141, 15850–15855 CrossRef CAS PubMed.
- M. Liu, J. Fu, C. Hejesen, Y. Yang, N. W. Woodbury, K. Gothelf, Y. Liu and H. Yan, A DNA Tweezer-Actuated Enzyme Nanoreactor, Nat. Commun., 2013, 4, 2127 CrossRef PubMed.
- D. Wang, J. Song, P. Wang, V. Pan, Y. Zhang, D. Cui and Y. Ke, Design and Operation of Reconfigurable Two-Dimensional DNA Molecular Arrays, Nat. Protoc., 2018, 13, 2312–2329 CrossRef CAS PubMed.
- J. Deng and A. Walther, Pathway Complexity in Fuel-Driven DNA Nanostructures with Autonomous Reconfiguration of Multiple Dynamic Steady States, J. Am. Chem. Soc., 2020, 142, 685–689 CrossRef PubMed.
- Y. Ke, T. Meyer, W. M. Shih and G. Bellot, Regulation at a Distance of Biomolecular Interactions Using a DNA Origami Nanoactuator, Nat. Commun., 2016, 7, 10935 CrossRef CAS PubMed.
- D. Han, J. Huang, Z. Zhu, Q. Yuan, M. You, Y. Chen and W. Tan, Molecular Engineering of Photoresponsive Three-Dimensional DNA Nanostructures, Chem. Commun., 2011, 47, 4670–4672 RSC.
- C. Zhou, L. Xin, X. Duan, M. J. Urban and N. Liu, Dynamic Plasmonic System that Responds to Thermal and Aptamer-Target Regulations, Nano Lett., 2018, 18, 7395–7399 CrossRef CAS PubMed.
- P. Zhan, P. K. Dutta, P. Wang, G. Song, M. Dai, S.-X. Zhao, Z.-G. Wang, P. Yin, W. Zhang and B. Ding, Reconfigurable Three-Dimensional Gold Nanorod Plasmonic Nanostructures Organized on DNA Origami Tripod, ACS Nano, 2017, 11, 1172–1179 CrossRef CAS PubMed.
- D. Wang, L. Yu, C.-M. Huang, G. Arya, S. Chang and Y. Ke, Programmable Transformations of DNA Origami Made of Small Modular Dynamic Units, J. Am. Chem. Soc., 2021, 143, 2256–2263 CrossRef CAS PubMed.
- R. P. Goodman, M. Heilemann, S. Doose, C. M. Erben, A. N. Kapanidis and A. J. Turberfield, Reconfigurable, Braced, Three-Dimensional DNA Nanostructures, Nat. Nanotechnol., 2008, 3, 93–96 CrossRef CAS PubMed.
- F. A. Aldaye and H. F. Sleiman, Modular Access to Structurally Switchable 3D Discrete DNA Assemblies, J. Am. Chem. Soc., 2007, 129, 13376–13377 CrossRef CAS PubMed.
- Y. Choi, H. Choi, A. C. Lee, H. Lee and S. Kwon, A Reconfigurable DNA Accordion Rack, Angew. Chem., Int. Ed., 2018, 57, 2811–2815 CrossRef CAS PubMed.
- W. Wang, C. Chen, S. Vecchioni, T. Zhang, C. Wu, Y. P. Ohayon, R. Sha, N. C. Seeman and B. Wei, Reconfigurable Two-Dimensional DNA Lattices: Static and Dynamic Angle Control, Angew. Chem., 2021, 133, 25985–25990 CrossRef.
- E. Pfitzner, C. Wachauf, F. Kilchherr, B. Pelz, W. M. Shih, M. Rief and H. Dietz, Rigid DNA Beams for High-Resolution Single-Molecule Mechanics, Angew. Chem., Int. Ed., 2013, 52, 7766–7771 CrossRef CAS PubMed.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Stretching DNA with Optical Tweezers, Biophys. J., 1997, 72, 1335–1346 CrossRef CAS PubMed.
- U. Bockelmann, P. Thomen, B. Essevaz-Roulet, V. Viasnoff and F. Heslot, Unzipping DNA with Optical Tweezers: High Sequence Sensitivity and Force Flips, Biophys. J., 2002, 82, 1537–1553 CrossRef CAS PubMed.
- Q. Xin, P. Li, Y. He, C. Shi, Y. Qiao, X. Bian, J. Su, R. Qiao, X. Zhou and J. Zhong, Magnetic Tweezers for the Mechanical Research of DNA at the Single Molecule Level, Anal. Methods, 2017, 9, 5720–5730 RSC.
- J. Yan, D. Skoko and J. F. Marko, Near-Field-Magnetic-Tweezer Manipulation of Single DNA Molecules, Phys. Rev. E, 2004, 70, 011905 CrossRef PubMed.
- M. Gao, J. Hu, Y. Wang, M. Liu, J. Wang, Z. Song, H. Xu, C. Hu and Z. Wang, Controlled Self-Assembly of λ-DNA Networks with the Synergistic Effect of a DC Electric Field, J. Phys. Chem. B, 2019, 123, 9809–9818 CrossRef CAS PubMed.
- E. Kopperger, J. List, S. Madhira, F. Rothfischer, D. C. Lamb and F. C. Simmel, A Self-Assembled Nanoscale Robotic Arm Controlled by Electric Fields, Science, 2018, 359, 296–301 CrossRef CAS PubMed.
- L. Zheng, J. P. Brody and P. J. Burke, Electronic Manipulation of DNA, Proteins, and Nanoparticles for Potential Circuit Assembly, Biosens. Bioelectron., 2004, 20, 606–619 CrossRef CAS PubMed.
- W.-H. Jung, E. Chen, R. Veneziano, S. Gaitanaros and Y. Chen, Stretching DNA Origami: Effect of Nicks and Holliday Junctions on the Axial Stiffness, Nucleic Acids Res., 2020, 48, 12407–12414 CrossRef CAS PubMed.
- K. Hirano, T. Iwaki, T. Ishido, Y. Yoshikawa, K. Naruse and K. Yoshikawa, Stretching of Single DNA Molecules Caused by Accelerating Flow on a Microchip, J. Chem. Phys., 2018, 149, 165101 CrossRef PubMed.
- J. Wang and C. Lu, Single Molecule λ-DNA Stretching Studied by Microfluidics and Single Particle Tracking, J. Appl. Phys., 2007, 102, 074703 CrossRef.
- F. Zhou, W. Sun, C. Zhang, J. Shen, P. Yin and H. Liu, 3D Freestanding DNA Nanostructure Hybrid as a Low-Density High-Strength Material, ACS Nano, 2020, 14, 6582–6588 CrossRef CAS PubMed.
- Z. Ma, Y.-J. Kim, S. Park, Y. Hirai, T. Tsuchiya, D.-N. Kim and O. Tabata, Direct characterization of radial modulus of DNA nanotube by AFM nanoindentation, in 10th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, 2015, pp. 581–584 Search PubMed.
- Z. Zhang, Y. Yang, F. Pincet, M. C. Llaguno and C. Lin, Placing and Shaping Liposomes with Reconfigurable DNA Nanocages, Nat. Chem., 2017, 9, 653–659 CrossRef CAS PubMed.
- J. Elbaz, M. Moshe and I. Willner, Coherent Activation of DNA Tweezers: A “SET–RESET” Logic System, Angew. Chem., Int. Ed., 2009, 48, 3834–3837 CrossRef CAS PubMed.
- J. Elbaz, Z.-G. Wang, R. Orbach and I. Willner, pH-Stimulated Concurrent Mechanical Activation of Two DNA “Tweezers”. A “SET–RESET” Logic Gate System, Nano Lett., 2009, 9, 4510–4514 CrossRef CAS PubMed.
- X. Han, Z. Zhou, F. Yang and Z. Deng, Catch and Release: DNA Tweezers That Can Capture, Hold, and Release an Object Under Control, J. Am. Chem. Soc., 2008, 130, 14414–14415 CrossRef CAS PubMed.
- B. Kou, Y. Chai, Y. Yuan and R. Yuan, Dynamical Regulation of Enzyme Cascade Amplification by a Regenerated DNA Nanotweezer for Ultrasensitive Electrochemical DNA Detection, Anal. Chem., 2018, 90, 10701–10706 CrossRef CAS PubMed.
- M. Liu, S. Jiang, O. Loza, N. E. Fahmi, P. Šulc and N. Stephanopoulos, Rapid Photoactuation of a DNA Nanostructure Using an Internal Photocaged Trigger Strand, Angew. Chem., Int. Ed., 2018, 57, 9341–9345 CrossRef CAS PubMed.
- S. Liu, K. Xiang, C. Wang, Y. Zhang, G.-C. Fan, W. Wang and H. Han, DNA Nanotweezers for Biosensing Applications: Recent Advances and Future Prospects, ACS Sens., 2022, 7, 3–20 CrossRef CAS PubMed.
- B. K. Müller, A. Reuter, F. C. Simmel and D. C. Lamb, Single-Pair FRET Characterization of DNA Tweezers, Nano Lett., 2006, 6, 2814–2820 CrossRef PubMed.
- D. Saliba, T. Trinh, C. Lachance-Brais, A. L. Prinzen, F. J. Rizzuto, D. de Rochambeau and H. F. Sleiman, Asymmetric Patterning Drives the Folding of a Tripodal DNA Nanotweezer, Chem. Sci., 2022, 13, 74–80 RSC.
- L. Zhou, M. Gao, W. Fu, Y. Wang, D. Luo, K. Chang and M. Chen, Three-Dimensional DNA Tweezers Serve as Modular DNA Intelligent Machines for Detection and Regulation of Intracellular microRNA, Sci. Adv., 2020, 6, eabb0695 CrossRef CAS PubMed.
- B. Saccà, Y. Ishitsuka, R. Meyer, A. Sprengel, E. C. Schöneweiß, G. U. Nienhaus and C. M. Niemeyer, Reversible Reconfiguration of DNA Origami Nanochambers Monitored by Single-Molecule FRET, Angew. Chem., Int. Ed., 2015, 54, 3592–3597 CrossRef PubMed.
- N. P. Agarwal, M. Matthies, B. Joffroy and T. L. Schmidt, Structural Transformation of Wireframe DNA Origami via DNA Polymerase Assisted Gap-Filling, ACS Nano, 2018, 12, 2546–2553 CrossRef CAS PubMed.
- Y. Sannohe, M. Endo, Y. Katsuda, K. Hidaka and H. Sugiyama, Visualization of Dynamic Conformational Switching of the G-Quadruplex in a DNA Nanostructure, J. Am. Chem. Soc., 2010, 132, 16311–16313 CrossRef CAS PubMed.
- E. Torelli, M. Marini, S. Palmano, L. Piantanida, C. Polano, A. Scarpellini, M. Lazzarino and G. Firrao, A DNA Origami Nanorobot Controlled by Nucleic Acid Hybridization, Small, 2014, 10, 2918–2926 CrossRef CAS PubMed.
- H. Ijäs, I. Hakaste, B. Shen, M. A. Kostiainen and V. Linko, Reconfigurable DNA Origami Nanocapsule for pH-Controlled Encapsulation and Display of Cargo, ACS Nano, 2019, 13, 5959–5967 CrossRef PubMed.
- Q. Jiang, Q. Liu, Y. Shi, Z.-G. Wang, P. Zhan, J. Liu, C. Liu, H. Wang, X. Shi and L. Zhang, Stimulus-Responsive Plasmonic Chiral Signals of Gold Nanorods Organized on DNA Origami, Nano Lett., 2017, 17, 7125–7130 CrossRef CAS PubMed.
- R. E. Kohman and X. Han, Light Sensitization of DNA Nanostructures via Incorporation of Photo-Cleavable Spacers, Chem. Commun., 2015, 51, 5747–5750 RSC.
- A. Kuzuya, R. Watanabe, M. Hashizume, M. Kaino, S. Minamida, K. Kameda and Y. Ohya, Precise Structure Control of Three-State Nanomechanical DNA Origami Devices, Methods, 2014, 67, 250–255 CrossRef CAS PubMed.
- L. J. Gibson and M. F. Ashby, Cellular Solids: Structure and Properties, Cambridge University Press, 1999 Search PubMed.
- F. N. Gür, F. W. Schwarz, J. Ye, S. Diez and T. L. Schmidt, Toward Self-Assembled Plasmonic Devices: High-Yield Arrangement of Gold Nanoparticles on DNA Origami Templates, ACS Nano, 2016, 10, 5374–5382 CrossRef PubMed.
- Q. Jiang, Y. Shi, Q. Zhang, N. Li, P. Zhan, L. Song, L. Dai, J. Tian, Y. Du and Z. Cheng, A Self-Assembled DNA Origami-Gold Nanorod Complex for Cancer Theranostics, Small, 2015, 11, 5134–5141 CrossRef CAS PubMed.
- L. Song, Q. Jiang, J. Liu, N. Li, Q. Liu, L. Dai, Y. Gao, W. Liu, D. Liu and B. Ding, DNA Origami/Gold Nanorod Hybrid Nanostructures for the Circumvention of Drug Resistance, Nanoscale, 2017, 9, 7750–7754 RSC.
- M. A. Bork, C. G. Gianopoulos, H. Zhang, P. E. Fanwick, J. H. Choi and D. R. McMillin, Accessibility and External versus Intercalative Binding to DNA as Assessed by Oxygen-Induced Quenching of the Palladium (II)-Containing Cationic Porphyrins Pd (T4) and Pd (tD4), Biochemistry, 2014, 53, 714–724 CrossRef CAS PubMed.
- K. Szaciłowski, W. Macyk, A. Drzewiecka-Matuszek, M. Brindell and G. Stochel, Bioinorganic photochemistry: frontiers and mechanisms, Chem. Rev., 2005, 105, 2647–2694 CrossRef PubMed.
- M. L. Di Pietro, F. Puntoriero, F. Tuyéras, P. Ochsenbein, P. P. Lainé and S. Campagna, Photochemically Driven Intercalation of Small Molecules into DNA by In Situ Irradiation, Chem. Commun., 2010, 46, 5169–5171 RSC.
- S. B. Smith, Y. Cui and C. Bustamante, Overstretching B-DNA: The Elastic Response of Individual Double-Stranded and Single-Stranded DNA Molecules, Science, 1996, 271, 795–799 CrossRef CAS PubMed.
- P. Shrestha, T. Emura, D. Koirala, Y. Cui, K. Hidaka, W. J. Maximuck, M. Endo, H. Sugiyama and H. Mao, Mechanical Properties of DNA Origami Nanoassemblies are Determined by Holliday Junction Mechanophores, Nucleic Acids Res., 2016, 44, 6574–6582 CrossRef PubMed.
- S. Lauback, K. R. Mattioli, A. E. Marras, M. Armstrong, T. P. Rudibaugh, R. Sooryakumar and C. E. Castro, Real-time Magnetic Actuation of DNA Nanodevices via Modular Integration with Stiff Micro-Levers, Nat. Commun., 2018, 9, 1446 CrossRef PubMed.
- A. M. Maier, C. Weig, P. Oswald, E. Frey, P. Fischer and T. Liedl, Magnetic Propulsion of Microswimmers with DNA-Based Flagellar Bundles, Nano Lett., 2016, 16, 906–910 CrossRef CAS PubMed.
- J. B. Heng, A. Aksimentiev, C. Ho, P. Marks, Y. V. Grinkova, S. Sligar, K. Schulten and G. Timp, Stretching DNA Using the Electric Field in a Synthetic Nanopore, Nano Lett., 2005, 5, 1883–1888 CrossRef CAS PubMed.
- F. Kroener, A. Heerwig, W. Kaiser, M. Mertig and U. Rant, Electrical Actuation of a DNA Origami Nanolever on an Electrode, J. Am. Chem. Soc., 2017, 139, 16510–16513 CrossRef CAS PubMed.
- P. Stömmer, H. Kiefer, E. Kopperger, M. N. Honemann, M. Kube, F. C. Simmel, R. R. Netz and H. Dietz, A Synthetic Tubular Molecular Transport System, Nat. Commun., 2021, 12, 4393 CrossRef PubMed.
- A.-K. Pumm, W. Engelen, E. Kopperger, J. Isensee, M. Vogt, V. Kozina, M. Kube, M. N. Honemann, E. Bertosin, M. Langecker, R. Golestanian, F. C. Simmel and H. Dietz, A DNA Origami Rotary Ratchet Motor, Nature, 2022, 607, 492–498 CrossRef CAS PubMed.
- T.-H. Nguyen, S.-M. Lee, K. Na, S. Yang, J. Kim and E.-S. Yoon, An Improved Measurement of dsDNA Elasticity Using AFM, Nanotechnology, 2010, 21, 075101 CrossRef PubMed.
- Y. Lin, X. Shen, J. Wang, L. Bao, Z. Zhang and D. Pang, Measuring Radial Young's Modulus of DNA by Tapping Mode AFM, Chin. Sci. Bull., 2007, 52, 3189–3192 CrossRef CAS.
- L. Li, L. Liu, O. Tabata and W. J. Li, Elasticity measurement of DNA origami nanotube in liquid with tapping mode AFM, in The 9th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, 2014, pp. 684–687 Search PubMed.
- R. P. Goodman, I. A. Schaap, C. F. Tardin, C. M. Erben, R. M. Berry, C. F. Schmidt and A. J. Turberfield, Rapid Chiral Assembly of Rigid DNA Building Blocks for Molecular Nanofabrication, Science, 2005, 310, 1661–1665 CrossRef CAS PubMed.
- L. Li, P. Zhang, J. Li, Y. Wang, Y. Wei, J. Hu, X. Zhou, B. Xu and B. Li, Measurement of Nanomechanical Properties of DNA Molecules by PeakForce Atomic Force Microscopy Based on DNA Origami, Nanoscale, 2019, 11, 4707–4711 RSC.
- T. Gerling, M. Kube, B. Kick and H. Dietz, Sequence-Programmable Covalent Bonding of Designed DNA Assemblies, Sci. Adv., 2018, 4, eaau1157 CrossRef CAS PubMed.
- A. Rajendran, M. Endo, Y. Katsuda, K. Hidaka and H. Sugiyama, Photo-Cross-Linking-Assisted Thermal Stability of DNA Origami Structures and its Application for Higher-Temperature Self-Assembly, J. Am. Chem. Soc., 2011, 133, 14488–14491 CrossRef CAS PubMed.
- F. M. Anastassacos, Z. Zhao, Y. Zeng and W. M. Shih, Glutaraldehyde Cross-Linking of Oligolysines Coating DNA Origami Greatly Reduces Susceptibility to Nuclease Degradation, J. Am. Chem. Soc., 2020, 142, 3311–3315 CrossRef CAS PubMed.
- L. Sala, T. Perecko, O. Mestek, D. Pinkas, T. s. Homola and J. Kočišek, Cisplatin-Cross-Linked DNA Origami Nanostructures for Drug Delivery Applications, ACS Appl. Nano Mater., 2022, 5, 13267–13275 CrossRef CAS.
- R. Jungmann, M. Scheible and F. C. Simmel, Nanoscale Imaging in DNA Nanotechnology, WIREs: Nanomed. Nanobiotechnol., 2012, 4, 66–81 CAS.
- R. Garcia, Nanomechanical Mapping of Soft Materials with the Atomic Force Microscope: Methods, Theory and Applications, Chem. Soc. Rev., 2020, 49, 5850–5884 RSC.
- F. Li, H. Chen, J. Pan, T.-G. Cha, I. L. Medintz and J. H. Choi, A DNAzyme-Mediated Logic Gate for Programming Molecular Capture and Release on DNA Origami, Chem. Commun., 2016, 52, 8369–8372 RSC.
- F. Zhang, J. Nangreave, Y. Liu and H. Yan, Reconfigurable DNA Origami to Generate Quasifractal Patterns, Nano Lett., 2012, 12, 3290–3295 CrossRef CAS PubMed.
- H. Liu, Y. Chen, Y. He, A. E. Ribbe and C. Mao, Approaching the Limit: Can One DNA Oligonucleotide Assemble into Large Nanostructures?, Angew. Chem., Int. Ed., 2006, 45, 1942–1945 CrossRef CAS PubMed.
- C. Kielar, S. Ramakrishnan, S. Fricke, G. Grundmeier and A. Keller, Dynamics of DNA Origami Lattice Formation at Solid–Liquid Interfaces, ACS Appl. Mater. Interfaces, 2018, 10, 44844–44853 CrossRef CAS PubMed.
- M. Endo, Surface Assembly of DNA Origami on a Lipid Bilayer Observed Using High-Speed Atomic Force Microscopy, Molecules, 2022, 27, 4224 CrossRef CAS PubMed.
- Y. Yang, R. Tashiro, Y. Suzuki, T. Emura, K. Hidaka, H. Sugiyama and M. Endo, A Photoregulated DNA-Based Rotary System and Direct Observation of its Rotational Movement, Chem. – Eur. J., 2017, 23, 3979–3985 CrossRef CAS PubMed.
- D. R. Stamov, T. Neumann, A. Kraus, A. Körnig, T. Jankowski, D. Knebel, T. Jähnke, T. Henze and H. Haschke, Unraveling Molecular Dynamics with High-Speed Video-Rate Atomic Force Microscopy, Microsc. Today, 2022, 30, 10–14 CrossRef.
- M. Endo and H. Sugiyama, Single-Molecule Imaging of Dynamic Motions of Biomolecules in DNA Origami Nanostructures Using High-Speed Atomic Force Microscopy, Acc. Chem. Res., 2014, 47, 1645–1653 CrossRef CAS PubMed.
- E. S. Andersen, M. Dong, M. M. Nielsen, K. Jahn, A. Lind-Thomsen, W. Mamdouh, K. V. Gothelf, F. Besenbacher and J. Kjems, DNA Origami Design of Dolphin-Shaped Structures with Flexible Tails, ACS Nano, 2008, 2, 1213–1218 CrossRef CAS PubMed.
- S. Thamm, N. Slesiona, A. Dathe, A. Csáki and W. Fritzsche, AFM-Based Probing of the Flexibility and Surface Attachment of Immobilized DNA Origami, Langmuir, 2018, 34, 15093–15098 CrossRef CAS PubMed.
- X.-c. Bai, T. G. Martin, S. H. Scheres and H. Dietz, Cryo-EM Structure of a 3D DNA-Origami Object, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20012–20017 CrossRef CAS PubMed.
- H. Jun, T. R. Shepherd, K. Zhang, W. P. Bricker, S. Li, W. Chiu and M. Bathe, Automated Sequence Design of 3D Polyhedral Wireframe DNA Origami with Honeycomb Edges, ACS Nano, 2019, 13, 2083–2093 CAS.
- L. Zhou, A. E. Marras, H.-J. Su and C. E. Castro, DNA Origami Compliant Nanostructures with Tunable Mechanical Properties, ACS Nano, 2014, 8, 27–34 CrossRef CAS PubMed.
- W. R. Algar, N. Hildebrandt, S. S. Vogel and I. L. Medintz, FRET as a Biomolecular Research Tool — Understanding its Potential While Avoiding Pitfalls, Nat. Methods, 2019, 16, 815–829 CrossRef CAS PubMed.
- A. J. Thubagere, W. Li, R. F. Johnson, Z. Chen, S. Doroudi, Y. L. Lee, G. Izatt, S. Wittman, N. Srinivas and D. Woods, A Cargo-Sorting DNA Robot, Science, 2017, 357, eaan6558 CrossRef PubMed.
- Y. Du, J. Pan and J. H. Choi, A Review on Optical Imaging of DNA Nanostructures and Dynamic Processes, Methods Appl. Fluoresc., 2019, 7, 012002 CrossRef CAS PubMed.
- H. Qiu, F. Li, Y. Du, R. Li, J. Y. Hyun, S. Y. Lee and J. H. Choi, Programmable Aggregation of Artificial Cells with DNA Signals, ACS Synth. Biol., 2021, 10, 1268–1276 CrossRef CAS PubMed.
- J. Schnitzbauer, M. T. Strauss, T. Schlichthaerle, F. Schueder and R. Jungmann, Super-Resolution Microscopy with DNA-PAINT, Nat. Protoc., 2017, 12, 1198–1228 CrossRef CAS PubMed.
- R. Jungmann, M. S. Avendaño, J. B. Woehrstein, M. Dai, W. M. Shih and P. Yin, Multiplexed 3D Cellular Super-Resolution Imaging with DNA-PAINT and Exchange-PAINT, Nat. Methods, 2014, 11, 313–318 CrossRef CAS PubMed.
- O. K. Wade, J. B. Woehrstein, P. C. Nickels, S. Strauss, F. Stehr, J. Stein, F. Schueder, M. T. Strauss, M. Ganji and J. Schnitzbauer, 124-Color Super-Resolution Imaging by Engineering DNA-PAINT Blinking Kinetics, Nano Lett., 2019, 19, 2641–2646 CrossRef CAS PubMed.
- F. Schueder, J. Stein, F. Stehr, A. Auer, B. Sperl, M. T. Strauss, P. Schwille and R. Jungmann, An Order of Magnitude Faster DNA-PAINT Imaging by Optimized Sequence Design and Buffer Conditions, Nat. Methods, 2019, 16, 1101–1104 CrossRef CAS PubMed.
- R. Iinuma, Y. Ke, R. Jungmann, T. Schlichthaerle, J. B. Woehrstein and P. Yin, Polyhedra Self-Assembled from DNA Tripods and Characterized with 3D DNA-PAINT, Science, 2014, 344, 65–69 CrossRef CAS PubMed.
- H. Chen, T.-W. Weng, M. M. Riccitelli, Y. Cui, J. Irudayaraj and J. H. Choi, Understanding the Mechanical Properties of DNA Origami Tiles and Controlling the Kinetics of Their Folding and Unfolding Reconfiguration, J. Am. Chem. Soc., 2014, 136, 6995–7005 CrossRef CAS PubMed.
- R. Li, H. Chen, H. Lee and J. H. Choi, Elucidating the Mechanical Energy for Cyclization of a DNA Origami Tile, Appl. Sci., 2021, 11, 2357 CrossRef CAS.
- D.-N. Kim, F. Kilchherr, H. Dietz and M. Bathe, Quantitative Prediction of 3D Solution Shape and Flexibility of Nucleic Acid Nanostructures, Nucleic Acids Res., 2012, 40, 2862–2868 CrossRef CAS PubMed.
- W. Kuhn, Über die Gestalt fadenförmiger Moleküle in Lösungen, Kolloid-Z., 1934, 68, 2–15 CrossRef CAS.
- O. Kratky and G. Porod, Röntgenuntersuchung Gelöster Fadenmoleküle, Recl. Trav. Chim. Pays-Bas, 1949, 68, 1106–1122 CrossRef CAS.
- N. Balabaev and T. Khazanovich, Extension of Chains Composed of Freely Joined Elastic Segments, Russ. J. Phys. Chem. B, 2009, 3, 242–246 CrossRef.
- Z. Shi, C. E. Castro and G. Arya, Conformational Dynamics of Mechanically Compliant DNA Nanostructures from Coarse-Grained Molecular Dynamics Simulations, ACS Nano, 2017, 11, 4617–4630 CrossRef CAS PubMed.
- M. C. Engel, F. Romano, A. A. Louis and J. P. Doye, Measuring Internal Forces in Single-Stranded DNA: Application to a DNA Force Clamp, J. Chem. Theory Comput., 2020, 16, 7764–7775 CrossRef CAS PubMed.
- J. C. Phillips, D. J. Hardy, J. D. Maia, J. E. Stone, J. V. Ribeiro, R. C. Bernardi, R. Buch, G. Fiorin, J. Hénin and W. Jiang, Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD, J. Chem. Phys., 2020, 153, 044130 CrossRef CAS PubMed.
- K. Hübner, H. Joshi, A. Aksimentiev, F. D. Stefani, P. Tinnefeld and G. P. Acuna, Determining the in-Plane Orientation and Binding Mode of Single Fluorescent Dyes in DNA origami structures, ACS Nano, 2021, 15, 5109–5117 CrossRef PubMed.
- R. G. Budynas and A. M. Sadegh, Roark's Formulas for Stress and Strain, McGraw-Hill Education, 2020 Search PubMed.
- C.-M. Huang, A. Kucinic, J. A. Johnson, H.-J. Su and C. E. Castro, Integrated Computer-Aided Engineering and Design for DNA Assemblies, Nat. Mater., 2021, 20, 1264–1271 CrossRef CAS PubMed.
- R. M. Zadegan, M. D. Jepsen, K. E. Thomsen, A. H. Okholm, D. H. Schaffert, E. S. Andersen, V. Birkedal and J. Kjems, Construction of a 4 Zeptoliters Switchable 3D DNA Box Origami, ACS Nano, 2012, 6, 10050–10053 CrossRef CAS PubMed.
- S. M. Douglas, I. Bachelet and G. M. Church, A Logic-Gated Nanorobot for Targeted Transport of Molecular Payloads, Science, 2012, 335, 831–834 CrossRef CAS PubMed.
- Z. Tang, D. Shangguan, K. Wang, H. Shi, K. Sefah, P. Mallikratchy, H. W. Chen, Y. Li and W. Tan, Selection of Aptamers for Molecular Recognition and Characterization of Cancer Cells, Anal. Chem., 2007, 79, 4900–4907 CrossRef CAS PubMed.
- Y. F. Huang, D. Shangguan, H. Liu, J. A. Phillips, X. Zhang, Y. Chen and W. Tan, Molecular Assembly of an Aptamer–Drug Conjugate for Targeted Drug Delivery to Tumor Cells, ChemBioChem, 2009, 10, 862–868 CrossRef CAS PubMed.
- Y. Yang, J. Wang, H. Shigematsu, W. Xu, W. M. Shih, J. E. Rothman and C. Lin, Self-Assembly of Size-Controlled Liposomes on DNA Nanotemplates, Nat. Chem., 2016, 8, 476–483 CrossRef CAS PubMed.
- R. Li, H. Chen and J. H. Choi, Topological Assembly of a Deployable Hoberman Flight Ring from DNA, Small, 2021, 17, 2007069 CrossRef CAS PubMed.
- R. Li, Y.-A. Yao and X. Kong, A Class of Reconfigurable Deployable Platonic Mechanisms, Mech. Mach. Theory, 2016, 105, 409–427 CrossRef.
- J. A. Speir, S. Munshi, G. Wang, T. S. Baker and J. E. Johnson, Structures of the Native and Swollen Forms of Cowpea Chlorotic Mottle Virus Determined by X-Ray Crystallography and Cryo-Electron Microscopy, Structure, 1995, 3, 63–78 CrossRef CAS PubMed.
- F. Tama and C. L. Brooks III, The Mechanism and Pathway of pH Induced Swelling in Cowpea Chlorotic Mottle Virus, J. Mol. Biol., 2002, 318, 733–747 CrossRef CAS PubMed.
- J. Bancroft, G. Hills and R. Markham, A Study of the Self-Assembly Process in a Small Spherical Virus Formation of Organized Structures from Protein Subunits in Vitro, Virology, 1967, 31, 354–379 CrossRef CAS PubMed.
- P. K. Dutta, Y. Zhang, A. T. Blanchard, C. Ge, M. Rushdi, K. Weiss, C. Zhu, Y. Ke and K. Salaita, Programmable Multivalent DNA-Origami Tension Probes for Reporting Cellular Traction Forces, Nano Lett., 2018, 18, 4803–4811 CrossRef CAS PubMed.
- P. C. Nickels, B. Wünsch, P. Holzmeister, W. Bae, L. M. Kneer, D. Grohmann, P. Tinnefeld and T. Liedl, Molecular Force Spectroscopy with a DNA Origami-Based Nanoscopic Force Clamp, Science, 2016, 354, 305–307 CrossRef CAS PubMed.
- D. Koirala, P. Shrestha, T. Emura, K. Hidaka, S. Mandal, M. Endo, H. Sugiyama and H. Mao, Single-Molecule Mechanochemical Sensing Using DNA Origami Nanostructures, Angew. Chem., 2014, 126, 8275–8279 CrossRef.
- J. J. Funke, P. Ketterer, C. Lieleg, S. Schunter, P. Korber and H. Dietz, Uncovering the Forces Between Nucleosomes Using DNA Origami, Sci. Adv., 2016, 2, e1600974 CrossRef PubMed.
- C. Albrecht, K. Blank, M. Lalic-Multhaler, S. Hirler, T. Mai, I. Gilbert, S. Schiffmann, T. Bayer, H. Clausen-Schaumann and H. E. Gaub, DNA: a Programmable Force Sensor, Science, 2003, 301, 367–370 CrossRef CAS PubMed.
- M. Darcy, K. Crocker, Y. Wang, J. V. Le, G. Mohammadiroozbahani, M. A. Abdelhamid, T. D. Craggs, C. E. Castro, R. Bundschuh and M. G. Poirier, High-Force Application by a Nanoscale DNA Force Spectrometer, ACS Nano, 2022, 16, 5682–5695 CrossRef CAS PubMed.
- R. Merindol, G. Delechiave, L. Heinen, L. H. Catalani and A. Walther, Modular Design of Programmable Mechanofluorescent DNA Hydrogels, Nat. Commun., 2019, 10, 528 CrossRef CAS PubMed.
- Y. Zhang, C. Ge, C. Zhu and K. Salaita, DNA-Based Digital Tension Probes Reveal Integrin Forces During Early Cell Adhesion, Nat. Commun., 2014, 5, 5167 CrossRef CAS PubMed.
- T. Schlichthaerle, C. Lindner and R. Jungmann, Super-Resolved Visualization of Single DNA-Based Tension Sensors in Cell Adhesion, Nat. Commun., 2021, 12, 2510 CrossRef CAS PubMed.
- R. Saran, Y. Wang and I. T. Li, Mechanical Flexibility of DNA: a Quintessential Tool for DNA Nanotechnology, Sensors, 2020, 20, 7019 CrossRef CAS PubMed.
- B. Choi, G. Zocchi, S. Canale, Y. Wu, S. Chan and L. J. Perry, Artificial Allosteric Control of Maltose Binding Protein, Phys. Rev. Lett., 2005, 94, 038103 CrossRef PubMed.
- J. Song, Z. Li, P. Wang, T. Meyer, C. Mao and Y. Ke, Reconfiguration of DNA Molecular Arrays Driven by Information Relay, Science, 2017, 357, eaan3377 CrossRef PubMed.
- J. Ji, D. Karna and H. Mao, DNA Origami Nano-Mechanics, Chem. Soc. Rev., 2021, 50, 11966–11978 RSC.
- Y. Ke, C. Castro and J. H. Choi, Structural DNA Nanotechnology: Artificial Nanostructures for Biomedical Research, Annu. Rev. Biomed. Eng., 2018, 20, 375–401 CrossRef CAS PubMed.
- L. He, J. Mu, O. Gang and X. Chen, Rationally Programming Nanomaterials with DNA for Biomedical Applications, Adv. Sci., 2021, 8, 2003775 CrossRef CAS PubMed.
- A. Keller and V. Linko, Challenges and Perspectives of DNA Nanostructures in Biomedicine, Angew. Chem., Int. Ed., 2020, 59, 15818–15833 CrossRef CAS PubMed.
- H. Ramezani and H. Dietz, Building Machines with DNA Molecules, Nat. Rev. Genet., 2020, 21, 5–26 CrossRef CAS PubMed.
- J. R. Burns, B. Lamarre, A. L. Pyne, J. E. Noble and M. G. Ryadnov, DNA Origami Inside-Out Viruses, ACS Synth. Biol., 2018, 7, 767–773 CrossRef CAS PubMed.
- A. Kuzuya and M. Komiyama, Design and Construction of a Box-Shaped 3D-DNA Origami, Chem. Commun., 2009, 4182–4184 RSC.
- R. Ranjbar and M. S. Hafezi-Moghadam, Design and Construction of a DNA Origami Drug Delivery System Based on MPT64 Antibody Aptamer for Tuberculosis Treatment, Electron. Physician, 2016, 8, 1857 CrossRef PubMed.
- H.-L. Lo, S. Nakajima, L. Ma, B. Walter, A. Yasui, D. W. Ethell and L. B. Owen, Differential Biologic Effects of CPD and 6-4PP UV-Induced DNA Damage on the Induction of Apoptosis and Cell-Cycle Arrest, BMC Cancer, 2005, 5, 135 CrossRef PubMed.
- A. Scrima, R. Koníčková, B. K. Czyzewski, Y. Kawasaki, P. D. Jeffrey, R. Groisman, Y. Nakatani, S. Iwai, N. P. Pavletich and N. H. Thomä, Structural Basis of UV DNA-Damage Recognition by the DDB1–DDB2 Complex, Cell, 2008, 135, 1213–1223 CrossRef CAS PubMed.
- X. Wang, A. R. Chandrasekaran, Z. Shen, Y. P. Ohayon, T. Wang, M. E. Kizer, R. Sha, C. Mao, H. Yan and X. Zhang, Paranemic Crossover DNA: There and Back Again, Chem. Rev., 2018, 119, 6273–6289 CrossRef PubMed.
- Y.-J. Kim, C. Lee, J. G. Lee and D.-N. Kim, Configurational Design of Mechanical Perturbation for Fine Control of Twisted DNA Origami Structures, ACS Nano, 2019, 13, 6348–6355 CrossRef CAS PubMed.
- J. F. Berengut, J. C. Berengut, J. P. Doye, D. Prešern, A. Kawamoto, J. Ruan, M. J. Wainwright and L. K. Lee, Design and Synthesis of Pleated DNA Origami Nanotubes with Adjustable Diameters, Nucleic Acids Res., 2019, 47, 11963–11975 CAS.
- Z. Ma, K. Kawai, Y. Hirai, T. Tsuchiya and O. Tabata, Tuning Porosity and Radial Mechanical Properties of DNA Origami Nanotubes via Crossover Design, Jpn. J. Appl. Phys., 2017, 56, 06GJ02 CrossRef.
- P. J. Hagerman, Flexibility of DNA, Annu. Rev. Biophys. Biophys. Chem., 1988, 17, 265–286 CrossRef CAS PubMed.
- C. Bustamante, S. B. Smith, J. Liphardt and D. Smith, Single-Molecule Studies of DNA Mechanics, Curr. Opin. Struct. Biol., 2000, 10, 279–285 CrossRef CAS PubMed.
- P. Cluzel, A. Lebrun, C. Heller, R. Lavery, J.-L. Viovy, D. Chatenay and F. Caron, DNA: An Extensible Molecule, Science, 1996, 271, 792–794 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |
