DOI:
10.1039/D3SC02044D
(Edge Article)
Chem. Sci., 2023,
14, 8129-8146
A generalized protein–ligand scoring framework with balanced scoring, docking, ranking and screening powers†
Received
20th April 2023
, Accepted 3rd July 2023
First published on 4th July 2023
Abstract
Applying machine learning algorithms to protein–ligand scoring functions has aroused widespread attention in recent years due to the high predictive accuracy and affordable computational cost. Nevertheless, most machine learning-based scoring functions are only applicable to a specific task, e.g., binding affinity prediction, binding pose prediction or virtual screening, suggesting that the development of a scoring function with balanced performance in all critical tasks remains a grand challenge. To this end, we propose a novel parameterization strategy by introducing an adjustable binding affinity term that represents the correlation between the predicted outcomes and experimental data into the training of mixture density network. The resulting residue-atom distance likelihood potential not only retains the superior docking and screening power over all the other state-of-the-art approaches, but also achieves a remarkable improvement in scoring and ranking performance. We emphatically explore the impacts of several key elements on prediction accuracy as well as the task preference, and demonstrate that the performance of scoring/ranking and docking/screening tasks of a certain model could be well balanced through an appropriate manner. Overall, our study highlights the potential utility of our innovative parameterization strategy as well as the resulting scoring framework in future structure-based drug design.
Introduction
Identification of lead active compounds is one of the most vigorous and innovative stages in drug discovery. Conventionally, it relies on high-throughput screening (HTS) to screen millions of drug-like molecules against a specified target of interest, followed by multiple cycles of structural optimizations according to the expert knowledge of medicinal chemists.1,2 Owing to the rapid advancement of computational chemistry and computer technology, molecular docking, a structure-based technique that aims to predict the binding mode and binding affinity of a protein–ligand complex using a predefined scoring function (SF), has gradually become a routine tool in computer-aided drug design (CADD) in the past two decades, and has played a critical role in the discovery and design of a large number of drug candidates and approved drugs.3–6
At present, improving the reliability of SF remains to be one of the most crucial tasks in the docking field.7,8 During the last few years, the expertise accumulated on the applications of machine learning (ML) and artificial intelligence (AI) algorithms in quantitative structure–activity relationship (QSAR) models has been widely transferred to the development of SFs, thus leading to the emergence of a series of ML-based SFs (MLSFs). Unlike the additive formulated hypothesis utilized in traditional physics-based, empirical or knowledge-based SFs, most MLSFs rely on ML algorithms to learn the functional forms from the data, and has achieved remarkably improved prediction accuracy over classical approaches in numerous retrospective benchmark studies.9–15
Four main metrics are typically considered to assess the performance of a SF, i.e., the scoring power to estimate the linear correlation between the predicted and experimentally-determined binding strengths, the ranking power to assess the capability of a SF to rank the known ligands for a certain target, the docking power to evaluate the capability to discriminate near-native poses from computer-yielded decoy poses, and the screening power to evaluate the ability to identify the true binders for a certain target from a pool of decoy compounds.16,17 An ideal SF should perform well across a wide range of applications, e.g., binding affinity prediction, binding pose prediction, virtual screening (VS), etc. Classical SFs such as GlideScore18 and GOLD ChemPLP19 can obtain acceptable docking and screening powers in several retrospective assessment studies, but the scoring power is usually far from satisfaction.17,20–22 A variety of MLSFs trained on pure crystal structures as regression models always exhibit vastly superior scoring power than classical methods but are rather weak in docking and screening.10,23–25 Several data argumentation strategies have been employed to improve the situation, for example, incorporating decoy poses into the training set to construct a classification model that directly distinguishes near-native poses and those with high root-mean-square-deviations (RMSDs),26–28 or introducing plenty of decoy/inactive compounds for a specific target in the training set to train a classification model to differentiate active and inactive compounds.29–33 These task-specific MLSFs perform well in the defined task, but are inevitably lack of accuracy in other tasks, which limits their applications in a molecular docking protocol. Thus, developing a MLSF with balanced performance for multiple objectives remains a big challenge.
A few strategies have been proposed in recent years to overcome this challenge, and it is worth noting that the classical additive function form is retained in these newly-developed MLSFs.34–40 The pioneering one is the Δ-ML approach first introduced into the SF field by Zhang et al., where a correction term fitted by ML algorithms was utilized to correct the classical empirical SF score. Three MLSFs, namely ΔVinaRF20,38 ΔVinaXGB34 and ΔLin_F9XGB,39 have been successively developed and exhibit excellent performance in all four tasks in the widely-recognized Comparative Assessment of Scoring Functions (CASF) benchmarks.17 OnionNet-SFCT40 adopts an extension of the Δ-ML strategy, in which the original binding affinity regression model is replaced by a RMSD classification model to serve as the correction term. The use of the linear combination of Vina scores and predicted RMSD values achieves enhanced performance on multiple docking and screening datasets, but the scoring and ranking powers on the CASF-2016 benchmark are reduced. PIGNet proposed by Moon et al.36 can be calculated as the sum of four energy components evolved from the physics-informed parameterized equations, where neural networks are employed to fit the pairwise interactions at the atom level. The introduction of physics-informed parameterized equations and several data argumentation strategies leads to the outperforming docking and screening powers of the approach in the CASF-2016 benchmark, and their scoring and ranking powers remain competitive. Another strategy worth mentioning is the mixture density network (MDN) first employed in DeepDock,35 which inherits the function form of traditional knowledge-based SFs. The protein–ligand pairwise distance likelihood can be learned through the MDN and then aggregated into a statistical potential by summing all independent negative log-likelihood values. Inspired by this innovative idea, we recently developed an improved SF called RTMScore37 based on residue-atom distance likelihood potential with graph transformers serving as feature extractors to learn protein and ligand node representations. Our approach could achieve state-of-the-art docking and screening powers, but its scoring and ranking powers on the CASF-2016 benchmark are far below the average due to the underutilization of experimental binding data in model training.
In this study, we extend our original model to all four tasks important for a SF and propose a generalized protein–ligand scoring framework (GenScore) by introducing an adjustable binding affinity term into the training of MDN. Here we describe how the trade-off between the MDN term and the affinity term enables our approach to obtain balanced scoring, ranking, docking and screening powers. Our newly-developed framework successfully retains the excellent docking/screening power of RTMScore while exhibits significantly superior performance in binding affinity prediction/ranking task.
Materials and methods
Dataset collection
The dataset used in the training and validation of the model has been described in our previous work.37 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443 protein–ligand complexes along with their experimental binding affinity data were retrieved from the PDBbind-v2020 general set41 and preprocessed with the Protein Preparation Wizard42 module implemented in Schrödinger 2020 to add hydrogens, delete waters, and optimize hydrogen bonds. The protonation states of the co-crystallized ligands and proteins were determined with the built-in Epik43 and PropKa44 utilities, respectively with pH = 7.0. The structures were finally minimized using the OPLS3 force field45 until the RMSD of heavy atoms averaged at 0.30 Å. After eliminating the PDB entries existing in the PDBbind-v2020 core set and CASF-2016 benchmark as well as those not identified by RDKit,46 a total of 19
443 protein–ligand complexes along with their experimental binding affinity data were retrieved from the PDBbind-v2020 general set41 and preprocessed with the Protein Preparation Wizard42 module implemented in Schrödinger 2020 to add hydrogens, delete waters, and optimize hydrogen bonds. The protonation states of the co-crystallized ligands and proteins were determined with the built-in Epik43 and PropKa44 utilities, respectively with pH = 7.0. The structures were finally minimized using the OPLS3 force field45 until the RMSD of heavy atoms averaged at 0.30 Å. After eliminating the PDB entries existing in the PDBbind-v2020 core set and CASF-2016 benchmark as well as those not identified by RDKit,46 a total of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149 complexes were remained, in which 1500 were randomly selected for validation and the rest were used for training. The validation set here was employed for the judgement of early stopping in model training to avoid overfitting as well as the selection of the model that exhibited optimal performance in internal testing.
149 complexes were remained, in which 1500 were randomly selected for validation and the rest were used for training. The validation set here was employed for the judgement of early stopping in model training to avoid overfitting as well as the selection of the model that exhibited optimal performance in internal testing.
Initial graph representations
For a specific protein–ligand complex, the ligand and the protein were individually handled. Each ligand was represented as an undirected graph (Gl = (Vl, El)) with nodes and edges denoting atoms and bonds in a two-dimensional (2D) molecule. Each protein was first truncated to the binding pocket defined as the residues within a 10.0 Å radius from the reference ligand, and then represented as an undirected graph (Gp = (Vp, Ep)) at the residue level, where each node corresponded to a residue and each edge represented the interaction between any two residues with a maximum distance of 10.0 Å. The cutoff of 10.0 Å was an empirical parameter, and was determined in order to cover most important interactions with affordable cost of computing resources. The input nodes and edge features for ligands and protein pockets were the same as those employed in RTMScore,37 as summarized in Tables S1 and S2,† respectively. The former only contained some basic atom and bond features, while the latter included not only the basic amino acid types but also several three-dimensional (3D) geometric features, such as some kinds of distances and dihedral angles. The above features were primarily generated through RDKit and MDAnalysis47 toolkits, and the graphs were produced by using the Pytorch Geometric (PyG)48 package.
Model architectures
The overall model architecture (Fig. 1) was the same as that used in RTMScore, which was made up of three major components, i.e., node representation learning module, representation concatenation module and MDN.49 The 3D protein residue graphs and 2D ligand graphs yielded according to the above section were employed by the node representation learning module to learn their corresponding node representations. The learned node representations were further concatenated in a pairwise manner by the representation concatenation module, and finally the concatenated features were processed in the MDN to learn the probability density distribution of the distance between each ligand–protein pair.
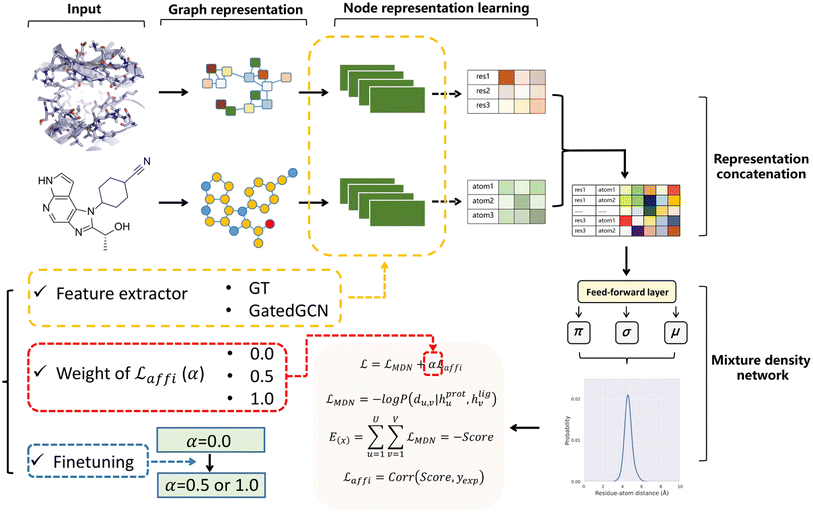 |
| | Fig. 1 Overall model architecture of GenScore. The protein and ligand graphs first go through the node representation learning module to learn their corresponding node representations, then the learned node representations are concatenated in a pairwise manner in representation concatenation module, and finally the concatenated features will be processed in a mixture density network to learn the probability density distribution of the distance between each ligand–protein pair. Three crucial settings for model performance are specially investigated, including the feature extractors employed for representation learning (GT or GatedGCN), the weight of the affinity term (α 0, 0.5 or 1.0), and whether to use finetuning technique to train the model. | |
Node representation learning module.
Two graph-based feature extractors were explored here for node representation learning, including an expanded graph transformer (GT) framework50 that was used in RTMScore, and a fork of graph convolutional neural network (GatedGCN).51,52 The protein and ligand were independently embedded with the same architecture since no remarkable improvement was observed when different architectures for the embedding of protein and ligand were used, e.g., applying protein-specific geometric vector perceptrons (GVP)53,54 to embed the protein pocket and GT or GatedGCN in ligand representation.
Specifically, for a graph G with its node features αi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dh×1 for node i and edge features βij ∈
dh×1 for node i and edge features βij ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) de×1 for the edge between node i and its neighboring node j, the initial node features αi and edge features βij were first embedded into d-dimensional hidden features h0i and e0ijvia two independent fully connected layers.
de×1 for the edge between node i and its neighboring node j, the initial node features αi and edge features βij were first embedded into d-dimensional hidden features h0i and e0ijvia two independent fully connected layers.
| | | h0i = W0ααi + b0α; e0ij = W0ββij + b0β | (1) |
where
W0α ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×dh
d×dh,
W0β ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×de
d×de and
b0α,
b0β ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d
d denote the weights and biases of linear layers. Then
h0i and
e0ij are fed into
l tandem repeated GT/GatedGCN layers to obtain the updated features
hil and
eijl. For GT, it relies on a modified multi-head self-attention (MHA) mechanism for the update of node and edge features, and the layer update equations for a layer
l are described as follows:
| |  | (2) |
| | | êijl+1 = OelDropout(Concatk∈1,…,H(ωijk,l)) | (3) |
where
| | 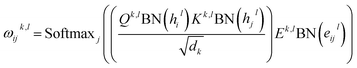 | (4) |
and
Qk,l,
Kk,l,
Vk,l,
Ek,l ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dk×d
dk×d,
Ohl,
Ohl ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d
d×d are the weight matrices for linear layers;
k ∈ 1,…,
H represents the number of attention heads;
dk denotes the dimension for each head, which can be computed as
d divided by
H;
j ∈
Ni denotes the neighboring nodes of node
i; BN, Concat, Dropout and Softmax denote batch normalization, concatenation, dropout, and softmax operations, respectively. The attention outputs
ĥil+1 and
êijl+1 are then passed to several batch normalization layers, fully connected layers and residual connections to obtain the final features of the
lth layer
hil+1 and
eijl+1 as:
| | | hil+1 = ĥil+1 + Øh2lDropout(SiLUØh1lBN(hil + ĥil+1)) | (5) |
| | | eijl+1 = êijl+1 + Øe2lDropout(SiLUØe1lBN(eijl + êijl+1)) | (6) |
where
Øh1l,
Øe1l ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2d×d
2d×d and
Øh2l,
Øe2l ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×2d
d×2d are the weight matrices for linear layers; SiLU denotes a type of nonlinear activation.
For GatedGCN, an edge gating mechanism was utilized to update the node and edge features, and for the lth layer:
| | 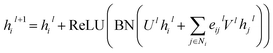 | (7) |
where
Ul,
Vl ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d
d×d, ReLU is a type of nonlinear activation, and the edge gates
eijl is defined as:
| | 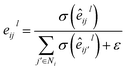 | (8) |
| | | êijl+1 = êijl + ReLU(BN(Alhil + Blhjl + Cleijl)) | (9) |
where
σ denotes sigmoid function;
ε denotes a small fixed constant for numerical stability;
Al,
Bl,
Cl ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d
d×d represent weight matrices.
Representation concatenation module and MDN.
The protein and ligand representations learned from the above module (hprotu and hligv) were pairwise-concatenated and fed into the MDN. The dm-dimensional hidden feature hu,v that represented the interactions between the uth protein node and the vth ligand node was calculated as:| | | hu,v = Dropout(ELU(BN(WcConcat([hprotu, hligv])))) | (10) |
where Wc ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2d×dm. The representation hu,v is passed into three individual fully-connected layers, and the three vectors that are necessary to parametrize a mixture density model, i.e., means (μu,v), standard deviations (σu,v), and mixing coefficients (ρu,v), are calculated as follows:
2d×dm. The representation hu,v is passed into three individual fully-connected layers, and the three vectors that are necessary to parametrize a mixture density model, i.e., means (μu,v), standard deviations (σu,v), and mixing coefficients (ρu,v), are calculated as follows:| | | μu,v = ELU(Wμhu,v) + 1 | (11) |
| | | σu,v = ELU(Wσhu,v) + 1.1 | (12) |
| | | ρu,v = Softmax(Wρhu,v) | (13) |
where Wμ, Wσ, Wρ ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dm×Ng. The mixture density model is defined as the mixture of Ng Gaussians, thus mimicking the probability density distribution of the ligand–protein distance for each ligand–protein node pair. Here, the minimum distance between a specific ligand atom and each atom is used in a specific residue as the final indicator due to its superior performance in our previous study.37 Besides, two auxiliary representations as suggested by Méndez-Lucio et al.35 are computed based on hu,v in order to learn the atom type of each ligand atom and the bond type of each bond formed between a specific atom and its neighboring atoms, thus serving as two auxiliary tasks for the memorization of molecular structures.
dm×Ng. The mixture density model is defined as the mixture of Ng Gaussians, thus mimicking the probability density distribution of the ligand–protein distance for each ligand–protein node pair. Here, the minimum distance between a specific ligand atom and each atom is used in a specific residue as the final indicator due to its superior performance in our previous study.37 Besides, two auxiliary representations as suggested by Méndez-Lucio et al.35 are computed based on hu,v in order to learn the atom type of each ligand atom and the bond type of each bond formed between a specific atom and its neighboring atoms, thus serving as two auxiliary tasks for the memorization of molecular structures.
Training procedures
We utilized the Adam optimizer with a batch size of 64, a learning rate of 10−3 and a weight decay of 10−5 for model training. The training procedure proceeded unless the validation performance would not be improved in successive 70 epochs. The detailed settings of hyperparameters were listed in Table S3.†
The loss function was defined as eqn (14), which could be described as the sum of an MDN loss 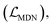 two auxiliary cross-entropy losses
two auxiliary cross-entropy losses 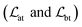 and an adjustable affinity correction term
and an adjustable affinity correction term 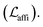 The MDN loss was computed as the negative log-likelihood of a pool of protein–ligand node distances and then summed into a potential E(x) at the protein–ligand complex level. The affinity term was defined as the correlation coefficient of the final predicted scores and experimentally-determined binding affinities. α denoted the weight of
The MDN loss was computed as the negative log-likelihood of a pool of protein–ligand node distances and then summed into a potential E(x) at the protein–ligand complex level. The affinity term was defined as the correlation coefficient of the final predicted scores and experimentally-determined binding affinities. α denoted the weight of 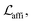 and α = 0 indicated a model without affinity term. The protein–ligand node pairs with distances less than 7.0 Å were taken into consideration when training the MDN while the cutoff was changed to 5.0 Å for model predictions, since this combination could achieve relatively better performance in our previous study.37
and α = 0 indicated a model without affinity term. The protein–ligand node pairs with distances less than 7.0 Å were taken into consideration when training the MDN while the cutoff was changed to 5.0 Å for model predictions, since this combination could achieve relatively better performance in our previous study.37
| | 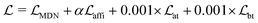 | (14) |
| | 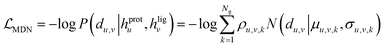 | (15) |
| | 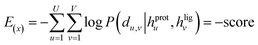 | (16) |
| | 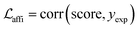 | (17) |
To explore the impact of incorporating binding affinity term on the final performance, in addition to the routine model training from scratch, we also constructed several models using transfer learning by finetuning the models without the affinity term (α = 0) to the models that incorporated the affinity term. Specifically, a model without the affinity term was pretrained as an initial, and then the parameters learned from this model was employed to initialize the models with the affinity term. For a single training-validation split, three independent models were trained and the mean performance was assessed to further demonstrate the robustness of the methodology.
Evaluation procedures
A variety of benchmark sets were included in this study to comprehensively validate our generalized protein–ligand scoring framework, including the CASF-2016 benchmark,17 three VS datasets namely the demanding evaluation kits for objective in silico screening (DEKOIS) 2.0,55 the Directory of Useful Decoys-Enhanced (DUD-E)56 and the LIT-PCBA,57 and several extra test sets, i.e., the Community Structure–Activity Resource (CSAR) NRC-HiQ benchmark,58 the Merck FEP benchmark59 and the PDBbind-CrossDocked-Core.60
CASF-2016 benchmark.
The CASF benchmark originally proposed by Cheng et al.61 in 2007 is a widely-recognized dataset for the benchmarking of classical SFs. Although a cloud of doubt has been raised for its over-estimation of MLSFs,62–64 it remains an important standard since more than 30 popular SFs have been tested on it. The most updated CASF-2016 (ref. 17) is constructed based on 285 diverse protein–ligand complexes (57 targets and 5 known ligands for each target). In this work, the performance of a SF was assessed from four different aspects, i.e., scoring, ranking, docking and screening. Scoring power was mainly evaluated by the Pearson's correlation coefficient (Rp) between the predicted and experimental binding affinities of all the 285 complexes; ranking power was primarily indicated by the average Spearman's rank correlation coefficient (Rs) across the 57 targets; docking power was measured using the success rate (SR), where a successful prediction could be marked if one of the RMSD values between the top-ranked poses and the native poses was less than 2.0 Å; screening power was divided into the forward screening power and the reverse screening power. The forward screening power calculated the SR of identifying the highest-affinity binder among the 1%, 5% or 10% top-scored ligands over all 57 targets, as well as the enrichment factor (EF) that was measured by the average percentage of the true binders observed among the top-scored candidates (1%, 5% or 10%) across all 57 targets. The reverse screening power calculated the SR of predicting the target of a ligand among the 1%, 5% or 10% top-scored candidate proteins.
DEKOIS2.0 and DUD-E.
DEKOIS2.0 and DUD-E are two crucial datasets for benchmarking VS protocols, and can be considered complementary owing to their different actives versus decoys ratios and distinct ways to generate the decoys. Some studies have doubted the applicability of these datasets for the evaluation of MLSFs due to the hidden biases.65,66 However, all the SFs in this study are trained on just crystalized ligand poses with low structural similarity to the diverse decoy compounds in the retrospective VS benchmarks, and the external testing of VS performance on the two datasets can in turn validate the generalization capability of our approach. DEKOIS2.0 consists of 81 diverse targets with 30 actives and 1200 decoys for each target. DUD-E contains a total of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886 active ligands against 102 diverse targets with 50 decoys generated for each active compound. The docking poses produced by Glide SP37 were used for model evaluation. In short, up to 10 docking poses were generated for each compound, and then rescored by each model. The VS performance was assessed according to the area under the receiver operating characteristic curve (AUROC),67 Boltzmann enhanced discrimination of receiver operating characteristic (BEDROC, α = 80.5),68 and EFs with different percentiles (0.5%, 1%, and 5%).
886 active ligands against 102 diverse targets with 50 decoys generated for each active compound. The docking poses produced by Glide SP37 were used for model evaluation. In short, up to 10 docking poses were generated for each compound, and then rescored by each model. The VS performance was assessed according to the area under the receiver operating characteristic curve (AUROC),67 Boltzmann enhanced discrimination of receiver operating characteristic (BEDROC, α = 80.5),68 and EFs with different percentiles (0.5%, 1%, and 5%).
LIT-PCBA.
LIT-PCBA is claimed as an unbiased dataset designed for benchmarking ML and VS, where the bioactivities of both the active and inactive compounds are verified by experimental results. The full set contains a total of 15 targets, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 true actives and 2
030 true actives and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798
798![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 737 true inactives. For each target, the ratio of actives to inactives is around 1
737 true inactives. For each target, the ratio of actives to inactives is around 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000, and this high imbalance could better mimic the challenging scenarios in real-word applications. The proteins and ligands were prepared as described above, and then Glide SP was employed to generate up to 10 docking poses for each compound. It should be noted that multiple PDB templates are provided for each target in the original version of the dataset. To save computational costs, we assessed the quality of each PDB entry by taking multiple factors (e.g., binding site, binding site mutations, missing residues, resolution, etc.) into account, and finally selected just one for each target for the following docking calculations. As for the molecule failing in docking, an extreme low score was exerted to it. The detailed information of the dataset employed here is summarized in Table S4.† The performance is indicated majorly according to the EF at the top 1% percentile (EF1%).
1000, and this high imbalance could better mimic the challenging scenarios in real-word applications. The proteins and ligands were prepared as described above, and then Glide SP was employed to generate up to 10 docking poses for each compound. It should be noted that multiple PDB templates are provided for each target in the original version of the dataset. To save computational costs, we assessed the quality of each PDB entry by taking multiple factors (e.g., binding site, binding site mutations, missing residues, resolution, etc.) into account, and finally selected just one for each target for the following docking calculations. As for the molecule failing in docking, an extreme low score was exerted to it. The detailed information of the dataset employed here is summarized in Table S4.† The performance is indicated majorly according to the EF at the top 1% percentile (EF1%).
CSAR NRC-HiQ benchmark.
The CSAR NRC-HiQ set updated in 2011 consists of 466 high-quality protein–ligand crystal structures with experimentally-determined binding information from the literature. A large number of the structures collected in the CSAR benchmark set are identical to those in the PDBbind-v2020 general set, and therefore, we further constructed two subsets of the CSAR NRC-HiQ set, where Setet was generated by eliminating the entries appeared in the training and validation sets and Setep was obtained by excluding all the same structures existing in PDBbind-v2020. The final numbers of structures in the subsets of Setet and Setep were 102 and 66, respectively. The complexes were then prepared using the Protein Preparation Wizard module as described above, and rescored by each model. The scoring power represented by Rp and Rs was summarized.
PDBbind-CrossDocked-Core.
The PDBbind-CrossDocked-Core set was derived from the PDBbind-v2016 core set in our previous study60 consisting of 285 diverse protein–ligand complexes. Each ligand was extracted and re-docked into the pocket of the original protein (or cross-docked into the pockets of the other four proteins belonging to the same target cluster) by using three docking programs, i.e., Surflex-Dock,69 Glide SP18 and AutoDock Vina,70 with up to 20 poses generated. The docking power was assessed by calculating the SR across the 285 complexes based on either the re-docked poses or cross-docked poses using the idea of ensemble docking. The scoring power was assessed in an end-to-end manner, i.e., using the MLSFs to select the best-scored pose of a specific ligand and to calculate the Rp and Rs that represent the capability of binding affinity prediction.
Merck FEP benchmark.
The Merck FEP benchmark set is initially developed for assessing models based on the theoretical prediction of free energy, such as Schrödinger's FEP+.71 The dataset consists of 8 pharmaceutically relevant targets and a total of 264 active ligands with their binding affinity data curated from the literature. The ligands for a specific target share a similar scaffold but include various structural transformations, thus well mimicking the real-world applications during the hit-to-lead and lead optimization stages. Given that the analogues for a specific target may exhibit similar binding poses while conventional molecular docking can hardly reproduce the binding poses of all the series, the poses provided by the authors were directly employed here for rescoring, which were predicted by using either the Flexible Ligand Alignment tool or Glide core-constrained docking based on a reference structure. The average Rs values across 8 targets was used as the major indicator of the ranking power.
Baselines
In addition to the models emphatically explored in this study, some other SFs were also included as the baselines. For the CASF benchmark, the results of several classical SFs and recently-developed MLSFs tested on the same dataset were directly retrieved for comparison. Regarding DEKOIS2.0 and DUD-E, only the docking score of Glide SP was utilized as the major baseline since it demonstrated significantly superior screening power than other tested classical SFs and a pool of generic MLSFs in our previous study.24 As for LIT-PCBA, besides the Glide SP, we also collected the results of several approaches from some relevant publications for comparison.39,72,73 When it comes to the other tests, six classical SFs, i.e., three in the latest version of AutoDock Vina74 (AD4,75 Vina70 and Vinadro76), Glide SP,18 Glide XP,77 X-Score,78 and two MLSFs of ΔLin_F9XGB39 and Pafnucy,79 were used for comparison. As for the Merck FEP benchmark, the Prime-MM/GBSA method was also performed using the prime_mmgbsa utility in Schrödinger with the residues within 5.0 Å from the ligand set as flexible.
Results and discussions
Assessment on CASF-2016 benchmark
In this study, a total of ten groups of models were constructed and the impacts of three crucial settings were emphatically investigated, including the feature extractors employed for representation learning (GT or GatedGCN), whether to use finetuning technique for model training, and the weight of the affinity term (α = 0, 0.5 or 1.0).
Our models were first tested on the routine CASF-2016 benchmark, and compared with 33 traditional SFs reported by Su et al.17 (Fig. 2) as well as several representative MLSFs (Table 1). As shown in Fig. 2, the results indicated that our methods consistently outperformed the classical SFs in terms of all four powers. Incorporation of the affinity term remarkably improved the scoring and ranking powers (Fig. 2A and B), while maintained strong docking and screening powers in most cases. Specifically, the GT model with α = 1.0 (GT_1.0) exhibited greater scoring (0.829 vs. 0.458) and ranking (0.673 vs. 0.536) powers, but decrease in the docking and screening powers could be observed. In contrast, the DT model with α = 0.5 (DT_0.5) obtained a more balanced performance compared to the DT_1.0 and DT_0.0 models. As for the finetuned models, GT_ft_0.5 and GT_ft_1.0 showed significantly improved docking and screening powers than the models trained from scratch. The average top 1 success rates of GT_ft_0.5 and GT_ft_1.0 with the crystal poses excluded from the test set were 93.6% and 94.0%, respectively, and the values increased to 97.6% and 96.6% when the crystal poses were included. In the assessment of the screening power, two finetuned models exhibited superior forward screening performance according to either the average top 1 success rate (71.4% and 71.9% vs. 64.9%) or the EF1% (28.16 and 28.12 vs. 27.54), but showed weaker reverse screening power indicated by the top 1 success rate (32.7% and 29.0% vs. 38.7%). As for the scoring and ranking power, finetuned models obtained higher ranking power (0.659 vs. 0.614; 0.684 vs. 0.673) but slightly decreased scoring power (0.773 vs. 0.787; 0.802 vs. 0.829). All the above findings demonstrated that direct use of the affinity term together with the MDN term could get higher scoring and ranking powers but lower docking and screening powers. However, the introduction of different weights to combine the two terms in a different manner or using finetuning technique to give a set of initial parameters to model training could efficiently achieve a balanced performance in terms of all four tasks. Similar results were observed when the GT feature extractor was replaced by GatedGCN. Of note, the GatedGCN models exhibited overall superior scoring and ranking powers but weaker docking and screening powers compared to GT models. For example, the scoring and ranking powers of GatedGCN_ft_0.5 (0.816 and 0.667, respectively) were higher than those of GT_ft_0.5 (0.773 and 0.659, respectively), while the docking powers (SR1 with or without native poses) and screening powers (forward SR1, EF1 and reverse SR1) of GatedGCN_ft_0.5 (93.3%, 96.4%, 67.3%, 25.43 and 29.2%, respectively) were relatively decreased compared to those of GT_ft_0.5 (93.6%, 97.6%, 71.4%, 28.16 and 32.7%, respectively). These results suggested that it would be critical to balance the scoring/ranking power and the docking/screening power in order to develop a generalized protein–ligand scoring framework.
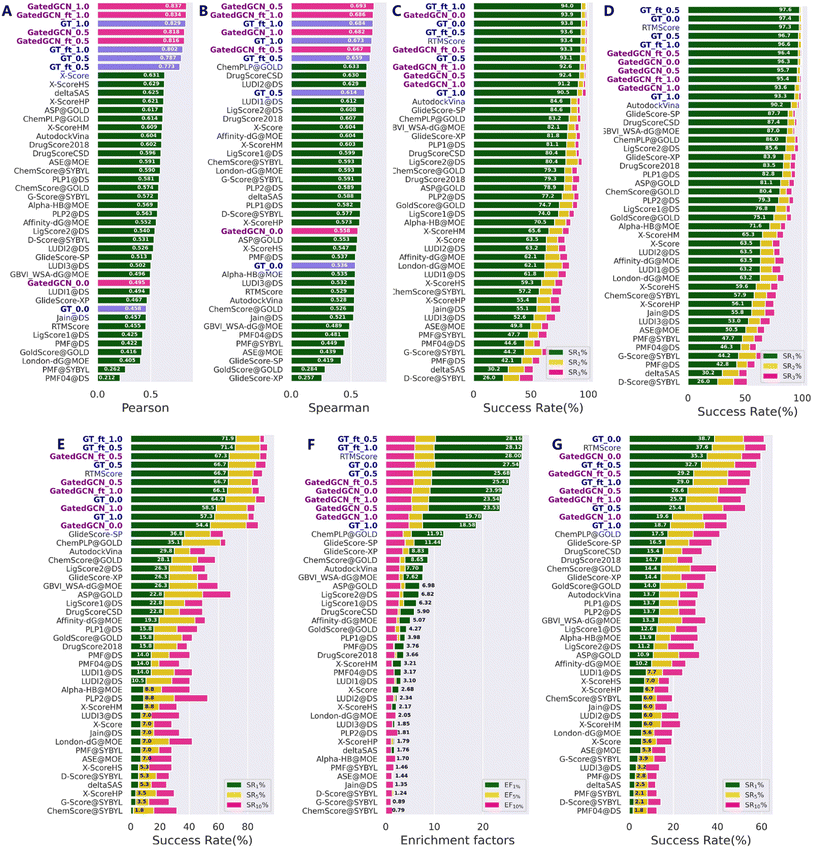 |
| | Fig. 2 Performances of scoring functions on CASF-2016 benchmark, including (A) the scoring power measured by Pearson correlation coefficient (Rp), (B) the ranking power evaluated by Spearman correlation coefficient (Rs), the docking powers indicated by success rates at the top 1%, 2% and 5% levels either (C) with or (D) without the crystalized poses in the test set, and the screening powers in terms of (E) success rates (SR1%, SR5% and SR10%) and (F) enrichment factors (EF1%, EF5% and EF10%) in forward screening and (G) success rates (SR1%, SR5% and SR10%) in reverse screening. The models constructed in this study are in bold font. The methods in each subplot are ranked in a descending order according to (A) Rp, (B) Rs, (C, D, E and G) SR1% and EF1%, respectively. | |
Table 1 Performances of several representative SFs on the CASF-2016 benchmarka
| Feature extractor |
Training mode |
α
|
Docking |
Screening |
Scoring |
Ranking |
| SR1 (native poses included) |
SR1 (native poses excluded) |
Forward SR1 |
EF1 |
Reverse SR1 |
R
p
|
R
s
|
|
The training set information of each compared approach can be found in Table S5.
|
| AutoDock Vina70 |
0.846 |
0.902 |
0.298 |
7.70 |
0.137 |
0.604 |
0.528 |
| ChemPLP@GOLD19 |
0.832 |
0.860 |
0.351 |
11.91 |
0.165 |
0.614 |
0.633 |
| GlideScore-SP18 |
0.846 |
0.877 |
0.368 |
11.44 |
0.175 |
0.513 |
0.419 |
| KORP-PL85 |
0.856 |
0.891 |
0.421 |
22.23 |
0.151 |
0.447 |
0.570 |
| KDEEP80,89 |
0.291 |
— |
— |
— |
— |
0.701 |
0.528 |
| AKScore80 |
0.360 |
— |
— |
— |
— |
0.812 |
0.670 |
| ΔVinaRF20 (ref. 38 and 39) |
0.849 |
0.891 |
0.456 |
12.36 |
— |
0.739 |
0.635 |
| ΔVinaXGB34 |
— |
0.916 |
0.368 |
13.14 |
— |
0.796 |
0.647 |
| ΔLin_F9XGB39 |
— |
0.867 |
0.404 |
12.61 |
— |
0.845 |
0.704 |
| OnionNet-SFCT + Vina40 |
— |
0.937 |
0.421 |
15.50 |
— |
0.428 |
0.393 |
| AEScore81 |
0.358 |
— |
— |
— |
— |
0.830 |
0.640 |
| Δ-AEScore81 |
0.856 |
— |
0.193 |
6.16 |
|
0.800 |
0.590 |
| PIGNet36 |
0.870 |
— |
0.554 |
19.60 |
— |
0.761 |
0.682 |
| DeepDock35 |
0.870 |
— |
0.439 |
16.41 |
0.239 |
0.460 |
0.425 |
| RTMScore37 |
0.934 ± 0.002 |
0.973 ± 0.013 |
0.667 ± 0.071 |
28.00 ± 0.94 |
0.376 ± 0.019 |
0.455 ± 0.015 |
0.529 ± 0.004 |
| GT |
— |
0 |
0.938 ± 0.011 |
0.974 ± 0.007 |
0.649 ± 0.035 |
27.54 ± 0.65 |
0.387 ± 0.011 |
0.458 ± 0.012 |
0.536 ± 0.034 |
| — |
0.5 |
0.933 ± 0.007 |
0.969 ± 0.007 |
0.667 ± 0.046 |
25.68 ± 1.60 |
0.254 ± 0.013 |
0.787 ± 0.026 |
0.614 ± 0.022 |
| — |
1.0 |
0.905 ± 0.012 |
0.933 ± 0.013 |
0.573 ± 0.041 |
18.58 ± 1.69 |
0.187 ± 0.046 |
0.829 ± 0.015 |
0.673 ± 0.009 |
| Finetune |
0.5 |
0.936 ± 0.007 |
0.976 ± 0.005 |
0.714 ± 0.053 |
28.16 ± 0.88 |
0.327 ± 0.030 |
0.773 ± 0.004 |
0.659 ± 0.016 |
| Finetune |
1.0 |
0.940 ± 0.000 |
0.966 ± 0.006 |
0.719 ± 0.035 |
28.12 ± 0.13 |
0.290 ± 0.016 |
0.802 ± 0.011 |
0.684 ± 0.024 |
| GatedGCN |
— |
0 |
0.939 ± 0.018 |
0.963 ± 0.011 |
0.544 ± 0.061 |
23.99 ± 0.54 |
0.353 ± 0.006 |
0.495 ± 0.005 |
0.558 ± 0.014 |
| — |
0.5 |
0.924 ± 0.006 |
0.957 ± 0.010 |
0.667 ± 0.031 |
23.53 ± 0.35 |
0.266 ± 0.034 |
0.818 ± 0.010 |
0.693 ± 0.029 |
| — |
1.0 |
0.912 ± 0.006 |
0.936 ± 0.005 |
0.585 ± 0.010 |
19.78 ± 0.09 |
0.196 ± 0.004 |
0.837 ± 0.011 |
0.682 ± 0.014 |
| Finetune |
0.5 |
0.933 ± 0.007 |
0.964 ± 0.005 |
0.673 ± 0.010 |
25.43 ± 0.55 |
0.292 ± 0.012 |
0.816 ± 0.001 |
0.667 ± 0.020 |
| Finetune |
1.0 |
0.926 ± 0.016 |
0.954 ± 0.004 |
0.661 ± 0.037 |
23.54 ± 1.00 |
0.259 ± 0.027 |
0.834 ± 0.014 |
0.686 ± 0.017 |
Compared with the other state-of-the-art MLSFs, our models were still competitive. Early MLSFs were always trained as non-linear regression models to directly fit the predicted scores and experimental binding data based on the pure crystal structures, thus leading to their extremely excellent scoring power with the Rp values ranging from 0.80 to 0.86.10,11 Two representative methods listed in Table 2, i.e., AKScore80 and AEScore,81 could obtain the scoring powers of 0.812 and 0.830, respectively, but their docking powers (36.0% and 35.8%) were far worse than expected. The screening powers of these two MLSFs were also quite weak, which was in accordance with our previous study that MLSFs trained in a similar way (e.g., RFscore,14,82 NNscore,15,83 OnionNet,84 and Pafnucy79) exhibited significantly worse VS performance than classical Glide SP on the DUD-E and DEKOIS2.0 datasets.24 Some SFs relying on statistical potentials such as KORP-PL85 and DeepDock35 exhibited a similar task preference as our previously-developed RTMScore, i.e., performing well in docking and screening but less accurate in scoring and ranking. Besides, in comparison to several newly-developed MLSFs, i.e., PIGNet,36 ΔVinaRF20,38 ΔVinaXGB,34 ΔLin_F9XGB39 and Δ-AEScore,81 our finetuned models consistently achieved superior docking and screening powers in all cases, and maintained leading scoring and ranking powers over most models.
Table 2 Screening powers of scoring functions on the DEKOIS2.0 dataset
| Method |
AUROC |
BEDROC (α = 80.5) |
EF0.5% |
EF1% |
EF5% |
| Mean |
Median |
Mean |
Median |
Mean |
Median |
Mean |
Median |
Mean |
Median |
| Glide SP |
0.747 |
0.754 |
0.385 |
0.314 |
14.61 |
13.30 |
12.47 |
9.61 |
6.30 |
5.97 |
| RTMScore |
0.764 ± 0.007 |
0.774 ± 0.012 |
0.550 ± 0.009 |
0.603 ± 0.003 |
20.78 ± 0.21 |
25.30 ± 0.87 |
18.39 ± 0.16 |
21.38 ± 0.33 |
8.33 ± 0.12 |
8.53 ± 0.37 |
| GT_0.0 |
0.763 ± 0.002 |
0.783 ± 0.010 |
0.539 ± 0.012 |
0.599 ± 0.022 |
20.35 ± 0.47 |
25.13 ± 1.48 |
18.13 ± 0.39 |
20.22 ± 1.30 |
8.24 ± 0.17 |
8.38 ± 0.25 |
| GT_ft_0.5 |
0.757 ± 0.002 |
0.767 ± 0.007 |
0.539 ± 0.007 |
0.588 ± 0.011 |
20.24 ± 0.52 |
24.81 ± 1.31 |
17.87 ± 0.10 |
19.82 ± 0.63 |
8.25 ± 0.11 |
8.36 ± 0.43 |
| GT_ft_1.0 |
0.761 ± 0.002 |
0.773 ± 0.004 |
0.533 ± 0.010 |
0.573 ± 0.022 |
19.79 ± 0.70 |
25.00 ± 0.42 |
17.64 ± 0.43 |
18.78 ± 1.41 |
8.28 ± 0.14 |
8.48 ± 0.25 |
| GT_0.5 |
0.762 ± 0.003 |
0.778 ± 0.008 |
0.529 ± 0.004 |
0.583 ± 0.027 |
20.12 ± 0.20 |
23.97 ± 0.71 |
17.63 ± 0.17 |
19.56 ± 1.96 |
8.13 ± 0.16 |
8.52 ± 0.61 |
| GT_1.0 |
0.757 ± 0.004 |
0.778 ± 0.003 |
0.487 ± 0.017 |
0.521 ± 0.030 |
18.76 ± 0.61 |
22.38 ± 0.61 |
16.09 ± 0.66 |
17.59 ± 1.20 |
7.78 ± 0.17 |
7.83 ± 0.45 |
| GatedGCN_0.0 |
0.758 ± 0.004 |
0.779 ± 0.002 |
0.532 ± 0.014 |
0.586 ± 0.030 |
19.64 ± 0.34 |
24.36 ± 1.18 |
17.66 ± 0.37 |
18.64 ± 0.60 |
8.21 ± 0.18 |
8.19 ± 0.40 |
| GatedGCN_ft_0.5 |
0.755 ± 0.007 |
0.767 ± 0.006 |
0.522 ± 0.009 |
0.586 ± 0.014 |
19.26 ± 0.18 |
22.95 ± 2.21 |
17.29 ± 0.35 |
18.76 ± 0.71 |
8.09 ± 0.14 |
8.25 ± 0.30 |
| GatedGCN_ft_1.0 |
0.753 ± 0.005 |
0.768 ± 0.013 |
0.503 ± 0.012 |
0.550 ± 0.028 |
18.63 ± 0.25 |
21.47 ± 1.14 |
16.98 ± 0.49 |
18.11 ± 2.54 |
7.93 ± 0.17 |
8.18 ± 0.18 |
| GatedGCN_0.5 |
0.756 ± 0.003 |
0.767 ± 0.003 |
0.507 ± 0.004 |
0.544 ± 0.014 |
18.68 ± 0.31 |
22.47 ± 2.23 |
16.93 ± 0.03 |
19.38 ± 1.00 |
7.93 ± 0.03 |
7.89 ± 0.27 |
| GatedGCN_1.0 |
0.752 ± 0.007 |
0.770 ± 0.015 |
0.468 ± 0.013 |
0.504 ± 0.027 |
17.37 ± 0.46 |
19.50 ± 1.63 |
15.38 ± 0.39 |
16.98 ± 1.61 |
7.51 ± 0.21 |
7.56 ± 0.25 |
Assessment on DEKOIS2.0, DUD-E and LIT-PCBA datasets
We further investigated the screening power of our models on two large-scale VS datasets, i.e., DEKOIS2.0 and DUD-E, which contained more diverse actives and decoys in comparison to the limited crystalized ligands in the CASF-2016 benchmark. The results on DEKOIS2.0 indicated by AUROC, BEDROC and EFs were shown in Table 2 and Fig. 3. The overall screening performance was not improved by using the affinity term in model training, which was in contrast to the results from the CASF-2016 forward screening test where the finetuned models could even outperform the models without the affinity term in regard to both the top 1 success rate and EF1%. Similar to the findings on the CASF-2016 benchmark, tuning the weight of the affinity term from 1.0 to 0.5, using GT rather than GatedGCN for representation learning, and finetuning the model from a specific set of initial parameters, benefited to improving the screening power. The optimal model GT_ft_0.5 achieved the mean BEDROC of 0.539 ± 0.007, EF0.5% of 20.24 ± 0.52, EF1% of 17.87 ± 0.10 and EF5% of 8.25 ± 0.11, which were infinitely close to the corresponding model without the affinity term (mean BEDROC = 0.539 ± 0.012, EF0.5% = 20.35 ± 0.47, EF1% = 18.13 ± 0.39 and EF5% = 8.24 ± 0.17). Notably, the worst-performed models, GatedGCN_1.0 and GT_1.0, were still better than Glide SP that was demonstrated to be one of the best-performing SFs in our previous assessment study.
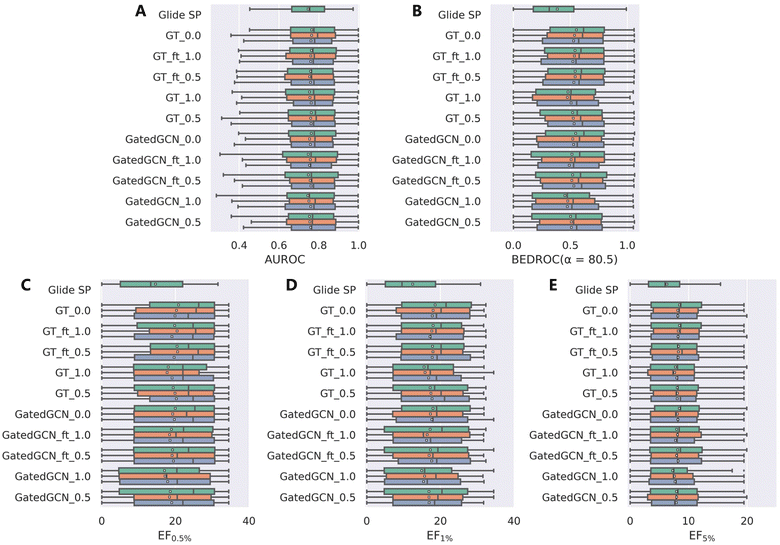 |
| | Fig. 3 Screening power of scoring functions on the DEKOIS2.0 dataset in terms of (A) AUROC, (B) BEDROC (α = 80.5), and (C–E) enrichment factors at different percentiles (0.5%, 1.0%, and 5.0%), based on the docking poses yielded by Glide SP. The color denotes the models trained with different random seeds, and the white square in the box plot denotes the mean value of each statistic. | |
The results from the DUD-E dataset (Table 3 and Fig. 4) were substantially consistent with those from the DEKOIS2.0 dataset, and were relatively more stable. GT_ft_0.5 still obtained the best enrichment performance with the mean BEDROC of 0.534 ± 0.011, EF0.5% of 41.11 ± 0.84, EF1% of 33.31 ± 0.65 and EF5% of 10.68 ± 0.15, but was less effective than GT_0.0 (mean BEDROC = 0.546 ± 0.010, EF0.5% = 44.02 ± 3.67, EF1% = 33.96 ± 0.69 and EF5% = 10.73 ± 0.20). GatedGCN_1.0 and GT_1.0 still performed the worst but superior to classical Glide SP (0.473 and 0.472 vs. 0.414; 35.54 and 35.62 vs. 29.44; 28.53 and 28.41 vs. 23.61; 9.98 and 10.02 vs. 9.24).
Table 3 Screening powers of scoring functions on the DUD-E dataset
| Method |
AUROC |
BEDROC (α = 80.5) |
EF0.5% |
EF1% |
EF5% |
| Mean |
Median |
Mean |
Median |
Mean |
Median |
Mean |
Median |
Mean |
Median |
| Glide SP |
0.820 |
0.845 |
0.414 |
0.410 |
29.44 |
33.27 |
23.61 |
23.30 |
9.24 |
9.50 |
| RTMScore |
0.829 ± 0.003 |
0.865 ± 0.004 |
0.548 ± 0.013 |
0.596 ± 0.025 |
41.73 ± 1.03 |
48.11 ± 2.37 |
34.19 ± 0.95 |
35.22 ± 1.97 |
10.81 ± 0.19 |
11.64 ± 0.19 |
| GT_0.0 |
0.828 ± 0.001 |
0.865 ± 0.003 |
0.546 ± 0.010 |
0.604 ± 0.027 |
44.02 ± 3.67 |
51.19 ± 3.07 |
33.96 ± 0.69 |
34.78 ± 0.43 |
10.73 ± 0.20 |
11.63 ± 0.27 |
| GT_ft_0.5 |
0.824 ± 0.002 |
0.862 ± 0.003 |
0.534 ± 0.011 |
0.588 ± 0.010 |
41.11 ± 0.84 |
46.44 ± 0.96 |
33.31 ± 0.65 |
34.22 ± 1.14 |
10.68 ± 0.15 |
11.67 ± 0.35 |
| GT_ft_1.0 |
0.824 ± 0.003 |
0.859 ± 0.002 |
0.532 ± 0.017 |
0.567 ± 0.024 |
40.56 ± 1.33 |
45.58 ± 1.39 |
32.65 ± 1.36 |
33.20 ± 2.19 |
10.66 ± 0.20 |
11.39 ± 0.38 |
| GT_0.5 |
0.826 ± 0.004 |
0.862 ± 0.005 |
0.535 ± 0.008 |
0.575 ± 0.010 |
41.08 ± 0.60 |
46.27 ± 2.26 |
33.00 ± 0.34 |
33.78 ± 0.17 |
10.70 ± 0.10 |
11.60 ± 0.31 |
| GT_1.0 |
0.820 ± 0.002 |
0.852 ± 0.004 |
0.472 ± 0.021 |
0.471 ± 0.031 |
35.62 ± 1.84 |
38.14 ± 1.74 |
28.41 ± 1.48 |
27.73 ± 1.90 |
10.02 ± 0.26 |
10.14 ± 0.46 |
| GatedGCN_0.0 |
0.828 ± 0.001 |
0.860 ± 0.006 |
0.537 ± 0.001 |
0.574 ± 0.014 |
40.71 ± 0.18 |
45.30 ± 0.64 |
33.28 ± 0.10 |
33.65 ± 0.81 |
10.70 ± 0.05 |
11.50 ± 0.08 |
| GatedGCN_ft_0.5 |
0.826 ± 0.003 |
0.862 ± 0.002 |
0.529 ± 0.007 |
0.556 ± 0.005 |
40.03 ± 0.42 |
44.63 ± 0.61 |
32.47 ± 0.50 |
32.32 ± 0.19 |
10.67 ± 0.17 |
11.34 ± 0.39 |
| GatedGCN_ft_1.0 |
0.824 ± 0.003 |
0.855 ± 0.010 |
0.515 ± 0.009 |
0.538 ± 0.019 |
38.91 ± 0.67 |
41.84 ± 2.19 |
31.21 ± 0.71 |
31.61 ± 1.31 |
10.56 ± 0.16 |
11.09 ± 0.22 |
| GatedGCN_0.5 |
0.822 ± 0.002 |
0.856 ± 0.002 |
0.514 ± 0.004 |
0.533 ± 0.009 |
39.14 ± 0.29 |
42.91 ± 1.82 |
31.36 ± 0.21 |
31.42 ± 1.37 |
10.48 ± 0.12 |
10.94 ± 0.01 |
| GatedGCN_1.0 |
0.816 ± 0.002 |
0.849 ± 0.003 |
0.473 ± 0.005 |
0.467 ± 0.014 |
35.54 ± 0.34 |
38.18 ± 1.11 |
28.53 ± 0.61 |
27.38 ± 1.63 |
9.98 ± 0.03 |
10.09 ± 0.45 |
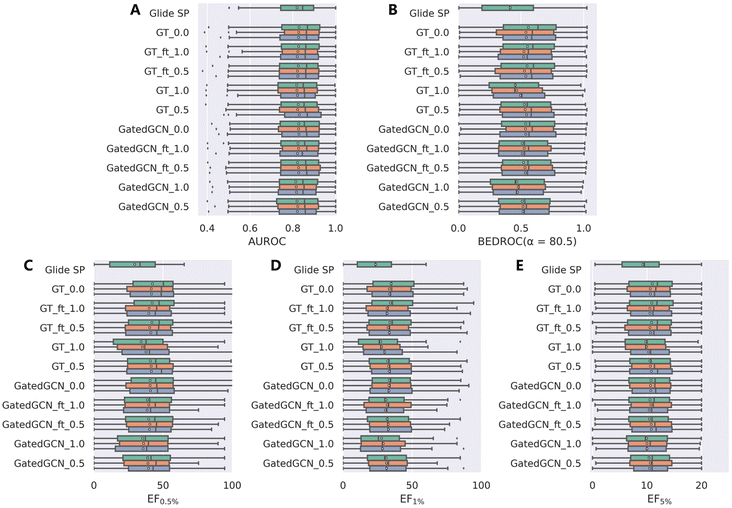 |
| | Fig. 4 Screening power of scoring functions on the DUD-E dataset in terms of (A) AUROC, (B) BEDROC (α = 80.5), and (C–E) enrichment factors at different percentiles (0.5%, 1.0%, and 5.0%), based on the docking poses yielded by Glide SP. The color denotes the models trained with different random seeds, and the white square in the box plot denotes the mean value of each statistic. | |
Despite this, it should be noticed that several MLSFs constructed based on numerous decoy compounds or trained in a target-specific way might exhibit comparable or even better results on the DUD-E or DEKOIS2.0 dataset. For example, the ROC enrichment scores at the 1.0% percentile for the models presented by Ragoza et al.,29 Torng et al.,31 and Lim et al.30 were 29.654, 29.748 and 69.037, respectively, according to the cross-validation on DUD-E, and similarly an average EF1% of 43.913 on the DUD-E could be obtained for SIEVE-Score,32 which was trained as a target-specific MLSF. RF-Score-VS86 trained in a horizontal split or per-target split way could obtain an average EF1% of 32.05–43.43 on the DUD-E dataset, but the corresponding indicators decreased to 9.52–13.5 when a vertical split was employed, and the performance further decreased in the external DEKOS 2.0 dataset (EF1% = 9.84 and 7.81 for RF-Score-VS v2 and RF-Score-VS v3, respectively). These models could not avoid the hidden biases in the training sets thus leading to their poor generalization ability in other external test sets, and it would be difficult to train and use a target-specific model without sufficient experimentally-verified compounds in real-world scenarios. The generic approach in this work was constructed based on the protein–ligand crystalized complexes that comprised a completely different composition as the DUD-E/DEKOIS dataset, and thus better avoided the potential hidden biases or the lack of training data for certain targets.
Considering the potential biases in above two datasets, we also tested our models on LIT-PCBA dataset, where both the actives and inactives had been experimentally verified and an extreme imbalance of actives and inactives was retained to mimic the challenging real screening scenarios. It should be noted that over half of the targets (8 of 15) use cell-based assays to determine the bioactivity, so whether the data is consistently reliable for benchmarking structure-based approaches remains questioned. Nevertheless, the evaluation results based on it may be still valuable to some extents. According to the average EF1% of all the 15 targets (Table 4), GatedGCN_1.0 and GT_1.0 still performed the worst among all our models (EF1% = 5.14 ± 0.62 and 5.24 ± 0.74) but slightly better than Glide SP (EF1% = 4.06). However, owing to the smaller amounts of targets in this dataset (15 vs. 102 and 81), the impacts of other settings might be a little irregular. Here the top-three performed models were GatedGCN_ft_0.5 (EF1% = 6.80 ± 0.49), GT_0.0 (EF1% = 6.51 ± 0.37) and GT_ft_1.0 (EF1% = 6.41 ± 0.71), and they could outperform Glide SP in 10, 11 and 9 of the 15 targets, respectively. Further comparison of our models with the data reported by other groups (Table 5) also demonstrated the competitiveness of our methods. Our models could just obtain lower average EF1% than IFP (EF1% = 7.46) and GRIM (EF1% = 6.87), but performed generally superior to the other approaches, e.g., Pafnucy (EF1% = 5.32), ΔVinaRF20 (EF1% = 3.18 or 5.38) and ΔLin_F9XGB (EF1% = 5.55). Of note, IFP and GRIM are not typical SFs, and they shall belong to similarity searching approaches that are highly dependent on the chosen PDB templates and target-specific, while the other approaches are all generic. Two recent studies conducted by Tran-Nguyen et al. have demonstrated the poor generalization of the simple approaches like IFP on other datasets.87,88 Additionally, just as we have mentioned above, MLSFs trained for a specific target may perform better than generic approaches on the assigned target. For example, our previous study indicates that a descriptor-based XGBoost model could achieve the average EF1% of 8.94 on seven targets of the LIT-PCBA validation set, and a 2D fingerprint-based quantitative structure–activity relationship (QSAR) model could even obtain the corresponding indicator of 14.59.33 But this type of approaches is not always available due to the insufficient data for model training. Of course, we should admit that some external factors such as docking programs to generate the binding poses and PDB entries employed for docking may exert a significant impact on the final performance, and the average indicators in our study are dominant by some extreme targets (ADRB2, ESR_ago and PPARG), so the comparison with the data reported by other groups is not absolutely convincing. Despite this, all above findings suggest that our generalized protein–ligand scoring framework could indeed retain the excellent screening power of RTMScore on large VS benchmarks.
Table 4 The screening powers of scoring functions (in terms of the EF1%) on the LIT-PCBA dataset
| Target |
Glide SP |
GT |
GatedGCN |
| 0.0 |
ft_0.5 |
ft_1.0 |
0.5 |
1.0 |
0.0 |
ft_0.5 |
ft_1.0 |
0.5 |
1.0 |
| ADRB2 |
5.88 |
17.65 ± 0.00 |
19.61 ± 3.40 |
17.65 ± 5.88 |
19.61 ± 3.40 |
15.69 ± 3.4 |
21.57 ± 3.40 |
23.53 ± 0.00 |
17.65 ± 0.00 |
17.65 ± 0.00 |
17.65 ± 5.88 |
| ALDH1 |
2.02 |
1.80 ± 0.20 |
2.11 ± 0.41 |
1.89 ± 0.21 |
1.88 ± 0.43 |
1.96 ± 0.03 |
1.81 ± 0.09 |
1.79 ± 0.23 |
1.79 ± 0.18 |
1.87 ± 0.17 |
1.98 ± 0.09 |
| ESR_ago |
7.69 |
12.81 ± 4.44 |
12.81 ± 4.44 |
15.37 ± 0.00 |
7.69 ± 0.00 |
10.25 ± 4.44 |
12.81 ± 4.44 |
12.81 ± 4.44 |
15.37 ± 0.00 |
10.25 ± 4.44 |
7.69 ± 0.00 |
| ESR_antago |
1.94 |
4.85 ± 0.00 |
2.91 ± 0.00 |
2.27 ± 0.56 |
4.21 ± 0.56 |
3.56 ± 1.12 |
3.88 ± 0.00 |
3.88 ± 1.68 |
3.24 ± 0.56 |
3.88 ± 0.97 |
2.59 ± 0.56 |
| FEN1 |
7.32 |
5.96 ± 0.98 |
5.42 ± 1.35 |
7.14 ± 0.56 |
4.88 ± 0.98 |
6.05 ± 1.84 |
5.06 ± 0.56 |
6.50 ± 0.54 |
5.87 ± 0.16 |
6.68 ± 0.78 |
6.68 ± 1.03 |
| GBA |
4.22 |
1.81 ± 1.04 |
2.41 ± 1.59 |
4.01 ± 1.84 |
2.01 ± 0.92 |
1.41 ± 1.25 |
1.20 ± 0.00 |
3.21 ± 1.39 |
7.23 ± 1.59 |
6.22 ± 3.32 |
2.81 ± 0.70 |
| IDH1 |
0.00 |
8.55 ± 1.48 |
6.84 ± 1.48 |
7.69 ± 4.44 |
5.13 ± 0.00 |
5.13 ± 2.56 |
8.55 ± 5.92 |
9.40 ± 3.92 |
6.84 ± 1.48 |
4.27 ± 1.48 |
5.13 ± 2.56 |
| KAT2A |
1.03 |
1.20 ± 0.30 |
0.86 ± 0.3 |
0.34 ± 0.30 |
1.37 ± 0.60 |
1.20 ± 0.79 |
1.20 ± 0.30 |
0.86 ± 0.30 |
1.03 ± 0.00 |
0.69 ± 0.60 |
0.86 ± 0.30 |
| MAPK1 |
3.24 |
4.54 ± 0.32 |
4.00 ± 0.75 |
4.32 ± 0.82 |
4.54 ± 0.65 |
4.87 ± 0.86 |
4.76 ± 0.68 |
4.76 ± 0.75 |
5.08 ± 0.68 |
4.76 ± 0.19 |
4.87 ± 0.65 |
| MTORC1 |
0.00 |
0.00 ± 0.00 |
0.00 ± 0.00 |
0.34 ± 0.59 |
0.34 ± 0.59 |
2.40 ± 1.19 |
0.69 ± 0.59 |
0.34 ± 0.59 |
1.37 ± 0.59 |
0.34 ± 0.59 |
0.00 ± 0.00 |
| OPRK1 |
0.00 |
4.17 ± 0.00 |
2.78 ± 2.41 |
5.55 ± 2.41 |
2.78 ± 2.41 |
2.78 ± 2.41 |
0.00 ± 0.00 |
4.17 ± 0.00 |
1.39 ± 2.41 |
2.78 ± 2.41 |
1.39 ± 2.41 |
| PKM2 |
2.75 |
3.42 ± 1.32 |
2.69 ± 0.53 |
2.38 ± 0.32 |
2.75 ± 0.18 |
1.47 ± 0.63 |
3.05 ± 0.64 |
3.05 ± 0.90 |
1.10 ± 0.32 |
1.47 ± 0.48 |
1.28 ± 0.66 |
| PPARG |
21.96 |
25.62 ± 0.00 |
25.62 ± 0.00 |
25.62 ± 3.66 |
24.4 ± 2.11 |
20.74 ± 2.11 |
24.40 ± 2.11 |
24.40 ± 2.11 |
24.4 ± 2.11 |
20.74 ± 2.11 |
21.96 ± 0.00 |
| TP53 |
2.50 |
4.17 ± 0.72 |
0.00 ± 0.00 |
0.42 ± 0.72 |
2.92 ± 0.72 |
0.00 ± 0.00 |
3.33 ± 1.91 |
2.08 ± 1.44 |
0.83 ± 0.72 |
0.42 ± 0.72 |
1.25 ± 0.00 |
| VDR |
0.34 |
1.06 ± 0.17 |
1.21 ± 0.28 |
1.13 ± 0.20 |
0.83 ± 0.17 |
1.13 ± 0.41 |
0.94 ± 0.17 |
1.17 ± 0.40 |
0.83 ± 0.13 |
0.87 ± 0.47 |
1.02 ± 0.57 |
| Average |
4.06 |
6.51 ± 0.37 |
5.95 ± 0.45 |
6.41 ± 0.71 |
5.69 ± 0.23 |
5.24 ± 0.74 |
6.22 ± 0.87 |
6.80 ± 0.49 |
6.27 ± 0.35 |
5.53 ± 0.59 |
5.14 ± 0.62 |
Table 5 Comparison of the screening powers on LIT-PCBA dataset with the data reported by other groups
| Group |
Docking programs |
Scoring function |
Average EF1% |
Number of targets (EF1% > 2) |
Number of targets (EF1% > 5) |
Number of targets (EF1% > 10) |
| Sunseri et al.73 |
Smina |
RFScore-4 |
1.28 |
4 |
1 |
0 |
| RFScore-VS |
0.73 |
5 |
2 |
0 |
| Vina |
1.1 |
6 |
1 |
0 |
| Dense (affinity) |
2.58 |
6 |
6 |
2 |
| Smina + Vinardo |
Vinardo |
0.99 |
4 |
2 |
0 |
| Yang et al.39 |
Smina + Lin_F9 |
Vina |
2.78 |
6 |
2 |
1 |
| ΔVinaRF20 |
3.18 |
6 |
3 |
2 |
| Lin_F9 |
2.21 |
8 |
1 |
0 |
| ΔLin_F9XGB |
5.55 |
13 |
8 |
2 |
| Tran-Nguyen et al.72 |
Surflex |
Surflex |
2.51 |
6 |
3 |
0 |
| Pafnucy |
5.32 |
9 |
7 |
3 |
| ΔVinaRF20 |
5.38 |
10 |
7 |
3 |
| IFP |
7.46 |
11 |
9 |
4 |
| GRIM |
6.87 |
12 |
8 |
5 |
| Ours |
Glide SP |
Glide SP |
4.06 |
9 |
4 |
1 |
| GT_0.0 |
6.51 ± 0.37 |
10.33 ± 0.58 |
5.33 ± 0.58 |
3.00 ± 1.00 |
| GT_ft_0.5 |
5.95 ± 0.45 |
9.67 ± 1.15 |
4.67 ± 0.58 |
2.67 ± 0.58 |
| GT_ft_1.0 |
6.41 ± 0.71 |
9.67 ± 0.58 |
6.00 ± 0.00 |
3.33 ± 0.58 |
| GT_0.5 |
5.69 ± 0.23 |
11.00 ± 1.00 |
5.00 ± 1.00 |
2.00 ± 0.00 |
| GT_1.0 |
5.24 ± 0.74 |
9.33 ± 0.58 |
4.67 ± 1.53 |
2.33 ± 0.58 |
| GatedGCN_0.0 |
6.22 ± 0.87 |
8.67 ± 0.58 |
5.00 ± 1.00 |
3.00 ± 1.00 |
| GatedGCN_ft_0.5 |
6.80 ± 0.49 |
10.00 ± 0.00 |
5.67 ± 0.58 |
3.33 ± 0.58 |
| GatedGCN_ft_1.0 |
6.27 ± 0.35 |
8.67 ± 1.15 |
6.33 ± 0.57 |
3.00 ± 0.00 |
| GatedGCN_0.5 |
5.53 ± 0.59 |
9.00 ± 0.00 |
5.33 ± 0.58 |
2.33 ± 0.58 |
| GatedGCN_1.0 |
5.14 ± 0.62 |
8.33 ± 0.00 |
5.00 ± 0.71 |
2.00 ± 0.00 |
Assessment on other datasets regarding binding affinity prediction/ranking
The scoring/ranking powers were further investigated on several extra datasets. We first assessed our models on the PDBbind-CrossDocked-Core set, an extension of the PDBbind-v2016 core set. Either the re-docked or cross-docked poses of the 285 protein–ligand complexes produced by Surflex-Dock, Glide SP or AutoDock Vina were rescored by each MLSF to select the top-ranked pose for a certain target, followed by the estimation of the scoring power only based on those top-ranked poses. This end-to-end procedure could well reproduce the real-world applications of MLSFs for rescoring, and both the docking and scoring powers could be evaluated within the process. The docking power in terms of top 1 success rate (SR1) and the scoring power in terms of Rp and Rs were summarized in Table 6, Fig. 5 and S1.† The integrated use of the affinity term and finetuning slightly improved docking performance in most cases, and our models could successfully identify ∼80% and ∼62% top-ranked poses as near-native (RMSD ≤ 2.0 Å) for the re-docked and cross-docked poses generated by Surflex-Dock, ∼72% and ∼56% by Glide SP, and ∼66% and ∼58% by Vina, remarkably higher than all the baselines in all the subsets of the benchmark (e.g., the corresponding SR1% of ΔLin_F9XGB were only 70.5%, 50.9%, 61.7%, 50.9%, 50.9% and 37.6%). The results of the scoring performance were consistent with the tests on the CASF-2016 benchmark, where a prominent increase could be achieved by incorporating the affinity term. Further improvements could be made by assigning a higher weight of the affinity term, training the model from scratch, or using GatedGCN for feature extraction. Our models exhibited general superiority over seven out of eight SFs except for ΔLin_F9XGB. Further analysis indicated that the scoring and docking powers of our models were highly correlated (e.g., the SR1% and Rp values for GT_ft_1.0 on the re-docked poses produced by Surflex-Dock, Glide SP and Vina are 81.5% and 0.769, 74.7% and 0.703, and 67.3% and 0.596, respectively), suggesting that the binding scores predicted by our approach were highly sensitive to the pose quality. Interestingly, ΔLin_F9XGB could still give a high Rp value of 0.747 when only 37.6% near-native ligand poses were used based on the cross-docked poses generated by Vina. What ΔLin_F9XGB actually learnt from the incorrect binding poses remained to be explored.
Table 6 Docking and scoring powers of scoring functions on the PDBbind-CrossDocked-Core set, where redocked and cross-docked poses are generated for the 285 complexes in the PDBbind-v2016 core set using Surflex-Dock, Glide SP or AutoDock Vina. The indicators on cross-docked poses are calculated with the consideration of all the poses for a certain target using the idea of ensemble docking. The standard deviations for three repetitions are omitted for the clarity of presentation
| Method |
Surflex |
Glide SP |
Vina |
| Redocked |
Cross |
Redocked |
Cross |
Redocked |
Cross |
| SR1 |
R
p
|
SR1 |
R
p
|
SR1 |
R
p
|
SR1 |
R
p
|
SR1 |
R
p
|
SR1 |
R
p
|
| AD4 |
0.702 |
−0.043 |
0.498 |
0.541 |
0.603 |
0.594 |
0.498 |
0.571 |
0.551 |
−0.166 |
0.437 |
0.531 |
| Vina |
0.691 |
0.512 |
0.505 |
0.430 |
0.606 |
0.549 |
0.505 |
0.499 |
0.540 |
0.528 |
0.380 |
0.492 |
| Vinardo |
0.677 |
0.319 |
0.477 |
0.199 |
0.628 |
0.459 |
0.477 |
0.369 |
0.558 |
0.460 |
0.391 |
0.385 |
| ΔLin_F9XGB |
0.705 |
0.783 |
0.509 |
0.776 |
0.617 |
0.814 |
0.509 |
0.787 |
0.509 |
0.726 |
0.376 |
0.747 |
| X-Score |
0.663 |
0.626 |
0.475 |
0.565 |
0.582 |
0.565 |
0.475 |
0.486 |
0.512 |
0.475 |
0.401 |
0.402 |
| Pafnucy |
0.512 |
0.597 |
0.319 |
0.558 |
0.422 |
0.562 |
0.319 |
0.519 |
0.211 |
0.441 |
0.165 |
0.442 |
| Glide SP |
0.730 |
0.475 |
0.547 |
−0.104 |
0.645 |
0.473 |
0.547 |
0.380 |
0.502 |
0.380 |
0.376 |
0.225 |
| Glide XP |
0.726 |
0.486 |
0.525 |
−0.103 |
0.610 |
0.446 |
0.525 |
0.404 |
0.470 |
0.332 |
0.366 |
0.178 |
| GT_0.0 |
0.795 |
0.469 |
0.627 |
0.372 |
0.735 |
0.408 |
0.579 |
0.296 |
0.660 |
0.370 |
0.583 |
0.255 |
| GT_ft_0.5 |
0.821 |
0.731 |
0.638 |
0.619 |
0.747 |
0.703 |
0.584 |
0.563 |
0.673 |
0.596 |
0.583 |
0.498 |
| GT_ft_1.0 |
0.815 |
0.769 |
0.636 |
0.661 |
0.743 |
0.727 |
0.585 |
0.599 |
0.660 |
0.617 |
0.590 |
0.547 |
| GT_0.5 |
0.809 |
0.764 |
0.633 |
0.684 |
0.738 |
0.734 |
0.571 |
0.624 |
0.669 |
0.603 |
0.579 |
0.561 |
| GT_1.0 |
0.787 |
0.800 |
0.603 |
0.730 |
0.712 |
0.769 |
0.539 |
0.671 |
0.658 |
0.632 |
0.551 |
0.619 |
| GatedGCN_0.0 |
0.811 |
0.504 |
0.609 |
0.415 |
0.736 |
0.448 |
0.573 |
0.344 |
0.664 |
0.394 |
0.575 |
0.304 |
| GatedGCN_ft_0.5 |
0.820 |
0.776 |
0.631 |
0.673 |
0.738 |
0.744 |
0.576 |
0.614 |
0.677 |
0.620 |
0.584 |
0.555 |
| GatedGCN_ft_1.0 |
0.822 |
0.798 |
0.627 |
0.706 |
0.719 |
0.762 |
0.575 |
0.648 |
0.674 |
0.640 |
0.581 |
0.601 |
| GatedGCN_0.5 |
0.800 |
0.783 |
0.621 |
0.694 |
0.726 |
0.748 |
0.558 |
0.642 |
0.669 |
0.624 |
0.572 |
0.589 |
| GatedGCN_1.0 |
0.805 |
0.810 |
0.600 |
0.739 |
0.716 |
0.779 |
0.545 |
0.677 |
0.664 |
0.651 |
0.542 |
0.629 |
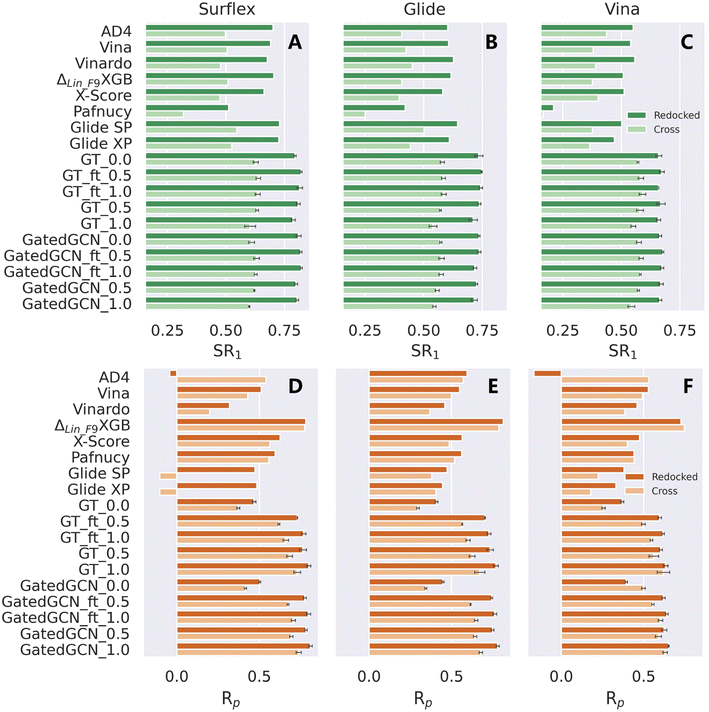 |
| | Fig. 5 Docking and scoring powers of scoring functions on PDBbind-CrossDocked-Core set indicated by (A–C) top 1 success rate (SR1) and (D–F) Pearson correlation coefficient (Rp), respectively, where the poses are generated by (A and D) Surflex-Dock, (B and E) Glide SP and (C and F) AutoDock Vina, respectively. | |
We also tested our models on the two subsets of the CSAR NRC-HiQ benchmark, as shown in Table 7 and Fig. 6. ΔLin_F9XGB was excluded from the test since both subsets were used for model training. Additionally, it should be noticed that the structures overlapped with our training set/PDBbind were all eliminated. For our models with different settings, incorporation of the affinity term could still make considerable improvements in binding affinity prediction, and the use of larger weight of the affinity term benefited to improving the scoring power. However, the impacts of finetuning and GatedGCN on model performance were not significant, partially due to the relatively small amounts of the test data. In brief, our framework remained competitive on this external benchmark for binding affinity prediction.
Table 7 Scoring powers of scoring functions on two subsets of CSAR NRC-HiQ benchmark
| Method |
Setet (102) |
Setep (66) |
|
R
p
|
R
s
|
R
p
|
R
s
|
| AD4 |
0.527 |
0.542 |
0.561 |
0.610 |
| Vina |
0.306 |
0.589 |
0.282 |
0.543 |
| Vinardo |
0.286 |
0.586 |
0.260 |
0.543 |
| X-Score |
0.617 |
0.598 |
0.528 |
0.514 |
| Pafnucy |
0.610 |
0.625 |
0.583 |
0.605 |
| Glide SP |
0.126 |
0.571 |
0.115 |
0.551 |
| Glide XP |
0.126 |
0.388 |
0.115 |
0.365 |
| GT_0.0 |
0.397 ± 0.008 |
0.409 ± 0.019 |
0.329 ± 0.012 |
0.379 ± 0.026 |
| GT_ft_0.5 |
0.624 ± 0.011 |
0.622 ± 0.024 |
0.582 ± 0.015 |
0.601 ± 0.039 |
| GT_ft_1.0 |
0.667 ± 0.014 |
0.659 ± 0.020 |
0.607 ± 0.018 |
0.622 ± 0.018 |
| GT_0.5 |
0.671 ± 0.043 |
0.668 ± 0.047 |
0.628 ± 0.039 |
0.634 ± 0.059 |
| GT_1.0 |
0.713 ± 0.036 |
0.697 ± 0.033 |
0.678 ± 0.044 |
0.674 ± 0.051 |
| GatedGCN_0.0 |
0.420 ± 0.008 |
0.431 ± 0.006 |
0.369 ± 0.013 |
0.413 ± 0.017 |
| GatedGCN_ft_0.5 |
0.676 ± 0.014 |
0.664 ± 0.010 |
0.648 ± 0.024 |
0.659 ± 0.021 |
| GatedGCN_ft_1.0 |
0.710 ± 0.027 |
0.690 ± 0.022 |
0.693 ± 0.037 |
0.684 ± 0.024 |
| GatedGCN_0.5 |
0.684 ± 0.015 |
0.681 ± 0.023 |
0.640 ± 0.026 |
0.646 ± 0.034 |
| GatedGCN_1.0 |
0.697 ± 0.007 |
0.681 ± 0.009 |
0.670 ± 0.010 |
0.651 ± 0.020 |
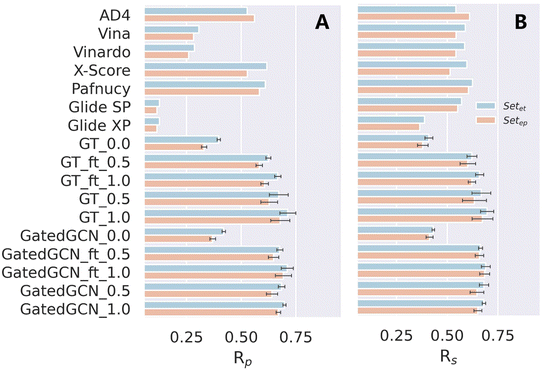 |
| | Fig. 6 Scoring power of scoring functions on two subsets of the CSAR NRC-HiQ benchmark indicated by (A) Pearson correlation coefficient (Rp) and (B) Spearman correlation coefficient (Rs). | |
Finally, we evaluated the ranking powers of these methods on the Merck FEP benchmark, a dataset initially developed for the assessment of some theory-driven free energy prediction methods. As shown in Table 8, this benchmark was challenging for all the evaluated SFs, with the average Rs values of almost all the SFs below 0.5, and the ranking power was also extremely target-specific. In terms of the average Rs across the eight targets, we could still observe an improved performance by introducing the affinity term, as well as the superiority of our approaches over the other tested methods.
Table 8 Ranking powers in terms of Spearman correlation coefficient (Rs) across eight targets on the Merck FEP benchmark. The standard deviations for three repetitions are omitted for the clarity of presentation
| Method |
hif2a (42) |
pfkfb3 (40) |
eg5 (28) |
cdk8 (33) |
shp2 (26) |
syk (44) |
cmet (24) |
tnks2 (27) |
Average (264) |
| AD4 |
0.376 |
0.530 |
−0.397 |
0.629 |
0.609 |
0.544 |
0.324 |
0.558 |
0.397 |
| Vina |
0.493 |
0.546 |
−0.520 |
0.849 |
0.569 |
0.519 |
−0.257 |
0.538 |
0.342 |
| Vinardo |
0.371 |
0.515 |
−0.475 |
0.782 |
0.490 |
0.379 |
−0.359 |
0.305 |
0.251 |
| ΔLin_F9XGB |
0.480 |
0.603 |
−0.099 |
0.826 |
0.640 |
0.103 |
0.077 |
0.458 |
0.386 |
| X-Score |
0.224 |
0.430 |
−0.316 |
0.406 |
−0.030 |
0.689 |
0.531 |
0.669 |
0.325 |
| Pafnucy |
0.224 |
0.430 |
−0.316 |
0.406 |
−0.030 |
0.689 |
0.531 |
0.669 |
0.325 |
| Glide SP |
0.445 |
0.480 |
−0.111 |
0.345 |
0.542 |
−0.006 |
0.378 |
0.316 |
0.299 |
| Glide XP |
0.410 |
0.513 |
0.017 |
0.617 |
0.490 |
0.124 |
0.165 |
0.582 |
0.365 |
| Prime-MM/GBSA_0.0 |
0.282 |
0.554 |
−0.002 |
0.649 |
0.585 |
0.108 |
0.499 |
0.158 |
0.354 |
| Prime-MM/GBSA_5.0 |
0.316 |
0.562 |
0.178 |
0.572 |
0.489 |
0.006 |
0.583 |
0.067 |
0.347 |
| GT_0.0 |
0.317 |
0.544 |
0.116 |
0.665 |
0.537 |
0.074 |
0.693 |
0.512 |
0.432 |
| GT_ft_0.5 |
0.357 |
0.450 |
0.210 |
0.671 |
0.608 |
0.230 |
0.693 |
0.540 |
0.470 |
| GT_ft_1.0 |
0.352 |
0.480 |
0.221 |
0.635 |
0.711 |
−0.006 |
0.617 |
0.555 |
0.446 |
| GT_0.5 |
0.459 |
0.590 |
0.204 |
0.682 |
0.445 |
0.099 |
0.772 |
0.580 |
0.479 |
| GT_1.0 |
0.437 |
0.571 |
0.275 |
0.675 |
0.338 |
0.144 |
0.677 |
0.578 |
0.462 |
| GatedGCN_0.0 |
0.398 |
0.533 |
0.132 |
0.685 |
0.575 |
0.106 |
0.610 |
0.464 |
0.438 |
| GatedGCN_ft_0.5 |
0.493 |
0.560 |
0.213 |
0.691 |
0.517 |
0.169 |
0.690 |
0.634 |
0.496 |
| GatedGCN_ft_1.0 |
0.519 |
0.578 |
0.206 |
0.712 |
0.609 |
0.214 |
0.727 |
0.586 |
0.519 |
| GatedGCN_0.5 |
0.395 |
0.580 |
0.221 |
0.679 |
0.490 |
0.121 |
0.746 |
0.610 |
0.480 |
| GatedGCN_1.0 |
0.455 |
0.635 |
0.293 |
0.693 |
0.489 |
−0.001 |
0.773 |
0.598 |
0.492 |
To summarize, the above results on the three independent benchmarks demonstrated that incorporation of the affinity term into the training of MDN could indeed improve the scoring and ranking powers, and the corresponding models achieved comparable or even superior performance than the other SFs, thus facilitating the development of a generalized framework with balanced scoring, docking, ranking and screening powers.
Model interpretations
Poor interpretability is one of the major limitations of deep learning models. Owing to the additive functional form inherited from the classical SFs, the predicted outcomes of our models can be easily decomposed into the contribution of each independent residue-atom pair, which can be further described as the contribution of each residue in a protein pocket or each atom in a ligand. Our previous study has demonstrated that RTMScore can provide extra information at either the atom or the residue level but is not able to reflect the relative binding affinities of a series of protein–ligand complexes due to the poor scoring/ranking power.37 Here we provide the case studies based on two targets retrieved from the CASF-2016 benchmark, i.e., Janus Kinase 1 (JAK1) and catechol-O-methyltransferase (COMT), to clarify how the atomic contributions may benefit to the real-world hit/lead optimization. The results could be found in Fig. 7, where two representative analogues were retrieved for each target and their predicted scores by GatedGCN_ft_1.0 and GatedGCN_0.0 as well as the experimentally-determined inhibitory constants (Ki) were also presented. It could be observed that GatedGCN_ft_1.0 gave a higher contribution of the acetonitrile moiety (8.08) than the carbonitrile moiety (3.36) for JAK1 and a higher contribution of the purine moiety (19.70) than the 4-(trifluoromethyl)-imidazole moiety (11.85) for COMT, while the scores of their common substructures were similar (67.67 vs. 66.52; 48.97 vs. 49.05), which was in well accordance with the change of their Ki values. The scores generated by GatedGCN_0.0 could also substantially describe the activity change for COMT (33.78 vs. 18.40; 91.47 vs. 87.63), but failed to make accurate predictions for JAK1 (8.48 vs. 3.62, 92.78 vs. 99.15). Additionally, no obvious difference was observed for the scores produced by GatedGCN_0.0 with varying Ki values, further verifying our previous finding that this score might be better to binding pose prediction/ranking rather than binding affinity prediction/ranking. In contrast, the introduction of the affinity term improved the capability of binding affinity prediction/ranking, suggesting its potential application prospect in the stage of hit/lead optimization.
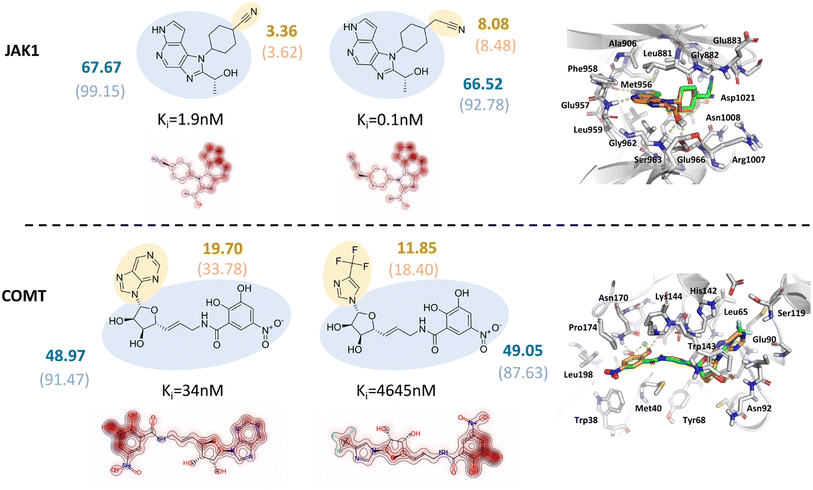 |
| | Fig. 7 Two case studies of Janus Kinase 1 (JAK1) and catechol-O-methyltransferase (COMT) for model interpretation, where two representative analogues with the atomic contributions and binding modes displayed. The blue and yellow circles indicate common and different substructures, respectively. The score of each substructure predicted by GatedGCN_ft_1.0 is shown in bold, while the corresponding score for GatedGCN_0.0 is embedded in bracket. | |
Conclusions
In this work, we propose a generalized protein–ligand scoring framework extended from our recently-developed RTMScore, where an adjustable affinity term is included into the training of MDN in order to further fit the predicted outcomes with the experimental data. The trade-off between the MDN term and the affinity term enables our models to achieve balanced scoring, docking, ranking, and screening powers on multiple benchmark datasets. Specifically, our models can well retain the outstanding docking and screening powers of RTMScore, and remarkably improve the scoring and ranking powers, which are comparable or even superior to all the tested baselines. We further emphatically explore the impacts of several important settings for model performance. The results indicate that using GT for representation learning, giving a weight of 0.5 for the affinity term, and training the models from a specific set of initial parameters can yield higher docking and screening performance, and in contrast, using GatedGCN for feature extraction, setting the weight of the affinity term to 1.0, and training the models from scratch, tend to obtain superior scoring and ranking powers. These findings suggest that it is hard to train a perfect model that preforms the best in all the tasks. Hence, we consider the model constructed here as an integrated framework for docking applications, among which GT_ft_0.5 that exhibits a relatively more balanced performance in all the four tasks may be more suitable embedded into a docking program for synthetical use. Besides, a model like GT_0.0 or the original RTMScore may serve as a rescoring tool for docking and screening, and GatedGCN_ft_1.0 and GatedGCN_1.0 could be employed for scoring or ranking. We believe our framework could serve as a reliable tool for structure-based drug design, and our innovative parameterization strategy could also provide valuable insights into the development of novel MLSFs with balanced scoring, docking, ranking and screening powers.
Data availability
The PDBbind dataset and CASF-2016 benchmark are available at https://www.pdbbind.org.cn. The docking poses for the DEKOIS2.0 and DUD-E datasets are available at https://www.zenodo.org/record/6859325, and the LIT-PCBA, the CSAR NRC-HiQ benchmark, the Merck FEP benchmark and the PDBbind-CrossDocked-Core are available at https://drugdesign.unistra.fr/LIT-PCBA/, https://www.csardock.org/, https://github.com/MCompChem/fep-benchmark, and https://www.zenodo.org/record/5525936, respectively. The codes and execution details of GenScore can be found at https://github.com/sc8668/GenScore.
Author contributions
C. Shen and X. Zhang collected the data, developed the models, analyzed the data, and wrote the manuscript; C. Hsieh, Y. Deng, D. Wang, L. Xu, J. Wu and D. Li helped interpret the results with constructive discussions; Y. Kang, T. Hou and P. Pan conceived and supervised the project, interpreted the results, and wrote the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was financially supported by National Key Research and Development Program of China (2021YFE0206400), National Natural Science Foundation of China (22220102001; 81773632; 82204279), China Postdoctoral Science Foundation (2022M722795), and the Fundamental Research Funds for the Central Universities (226-2022-00220).
References
- J. P. Hughes, S. Rees, S. B. Kalindjian and K. L. Philpott, Br. J. Pharmacol., 2011, 162, 1239–1249 CrossRef CAS PubMed.
- W. L. Jorgensen, Acc. Chem. Res., 2009, 42, 724–733 CrossRef CAS PubMed.
- T. T. Talele, S. A. Khedkar and A. C. Rigby, Curr. Top. Med. Chem., 2010, 10, 127–141 CrossRef CAS PubMed.
- V. T. Sabe, T. Ntombela, L. A. Jhamba, G. E. Maguire, T. Govender, T. Naicker and H. G. Kruger, Eur. J. Med. Chem., 2021, 224, 113705 CrossRef CAS PubMed.
- F. Ballante, A. J. Kooistra, S. Kampen, C. de Graaf and J. Carlsson, Pharmacol. Rev., 2021, 73, 527–565 CrossRef PubMed.
- Z. Wang, H. Sun, C. Shen, X. Hu, J. Gao, D. Li, D. Cao and T. Hou, Phys. Chem. Chem. Phys., 2020, 22, 3149–3159 RSC.
- D. B. Kitchen, H. Decornez, J. R. Furr and J. Bajorath, Nat. Rev. Drug Discovery, 2004, 3, 935–949 CrossRef CAS PubMed.
- I. A. Guedes, F. S. Pereira and L. E. Dardenne, Front. Pharmacol., 2018, 9, 1089 CrossRef CAS PubMed.
- Q. U. Ain, A. Aleksandrova, F. D. Roessler and P. J. Ballester, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 405–424 CAS.
- C. Shen, J. Ding, Z. Wang, D. Cao, X. Ding and T. Hou, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1429 CAS.
- H. Li, K. H. Sze, G. Lu and P. J. Ballester, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1465 CAS.
- H. Li, K. H. Sze, G. Lu and P. J. Ballester, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1478 Search PubMed.
- G. Xiong, C. Shen, Z. Yang, D. Jiang, S. Liu, A. Lu, X. Chen, T. Hou and D. Cao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1567 CAS.
- P. J. Ballester and J. B. Mitchell, Bioinformatics, 2010, 26, 1169–1175 CrossRef CAS PubMed.
- J. D. Durrant and J. A. McCammon, J. Chem. Inf. Model., 2010, 50, 1865–1871 CrossRef CAS PubMed.
- J. Liu and R. Wang, J. Chem. Inf. Model., 2015, 55, 475–482 CrossRef CAS PubMed.
- M. Su, Q. Yang, Y. Du, G. Feng, Z. Liu, Y. Li and R. Wang, J. Chem. Inf. Model., 2018, 59, 895–913 CrossRef PubMed.
- R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley and J. K. Perry, J. Med. Chem., 2004, 47, 1739–1749 CrossRef CAS PubMed.
- O. Korb, T. Stutzle and T. E. Exner, J. Chem. Inf. Model., 2009, 49, 84–96 CrossRef CAS PubMed.
- Y. Li, L. Han, Z. Liu and R. Wang, J. Chem. Inf. Model., 2014, 54, 1717–1736 CrossRef CAS PubMed.
- Z. Wang, H. Sun, X. Yao, D. Li, L. Xu, Y. Li, S. Tian and T. Hou, Phys. Chem. Chem. Phys., 2016, 18, 12964–12975 RSC.
- C. Shen, Z. Wang, X. Yao, Y. Li, T. Lei, E. Wang, L. Xu, F. Zhu, D. Li and T. Hou, Briefings Bioinf., 2020, 21, 282–297 CAS.
- J. Gabel, J. Desaphy and D. Rognan, J. Chem. Inf. Model., 2014, 54, 2807–2815 CrossRef CAS PubMed.
- C. Shen, Y. Hu, Z. Wang, X. Zhang, J. Pang, G. Wang, H. Zhong, L. Xu, D. Cao and T. Hou, Briefings Bioinf., 2021, 22, bbaa070 CrossRef PubMed.
- M. Wójcikowski, P. J. Ballester and P. Siedlecki, Sci. Rep., 2017, 7, 46710 CrossRef PubMed.
- P. G. Francoeur, T. Masuda, J. Sunseri, A. Jia, R. B. Iovanisci, I. Snyder and D. R. Koes, J. Chem. Inf. Model., 2020, 60, 4200–4215 CrossRef CAS PubMed.
- J. A. Morrone, J. K. Weber, T. Huynh, H. Luo and W. D. Cornell, J. Chem. Inf. Model., 2020, 60, 4170–4179 CrossRef CAS PubMed.
- K. A. Stafford, B. M. Anderson, J. Sorenson and H. van den Bedem, J. Chem. Inf. Model., 2022, 62, 1178–1189 CrossRef CAS PubMed.
- M. Ragoza, J. Hochuli, E. Idrobo, J. Sunseri and D. R. Koes, J. Chem. Inf. Model., 2017, 57, 942–957 CrossRef CAS PubMed.
- J. Lim, S. Ryu, K. Park, Y. J. Choe, J. Ham and W. Y. Kim, J. Chem. Inf. Model., 2019, 59, 3981–3988 CrossRef CAS PubMed.
- W. Torng and R. B. Altman, J. Chem. Inf. Model., 2019, 59, 4131–4149 CrossRef CAS PubMed.
- N. Yasuo and M. Sekijima, J. Chem. Inf. Model., 2019, 59, 1050–1061 CrossRef CAS PubMed.
- C. Shen, G. Weng, X. Zhang, E. L.-H. Leung, X. Yao, J. Pang, X. Chai, D. Li, E. Wang and D. Cao, Briefings Bioinf., 2021, 22, bbaa410 CrossRef PubMed.
- J. Lu, X. Hou, C. Wang and Y. Zhang, J. Chem. Inf. Model., 2019, 59, 4540–4549 CrossRef CAS PubMed.
- O. Méndez-Lucio, M. Ahmad, E. A. del Rio-Chanona and J. K. Wegner, Nat. Mach. Intell., 2021, 3, 1033–1039 CrossRef.
- S. Moon, W. Zhung, S. Yang, J. Lim and W. Y. Kim, Chem. Sci., 2022, 13, 3661–3673 RSC.
- C. Shen, X. Zhang, Y. Deng, J. Gao, D. Wang, L. Xu, P. Pan, T. Hou and Y. Kang, J. Med. Chem., 2022, 65, 10691–10706 CrossRef CAS PubMed.
- C. Wang and Y. Zhang, J. Comput. Chem., 2017, 38, 169–177 CrossRef PubMed.
- C. Yang and Y. Zhang, J. Chem. Inf. Model., 2022, 62, 2696–2712 CrossRef CAS PubMed.
- L. Zheng, J. Meng, K. Jiang, H. Lan, Z. Wang, M. Lin, W. Li, H. Guo, Y. Wei and Y. Mu, Briefings Bioinf., 2022, 23, bbac051 CrossRef PubMed.
- R. Wang, X. Fang, Y. Lu and S. Wang, J. Med. Chem., 2004, 47, 2977–2980 CrossRef CAS PubMed.
- G. Madhavi Sastry, M. Adzhigirey, T. Day, R. Annabhimoju and W. Sherman, J. Comput.-Aided Mol. Des., 2013, 27, 221–234 CrossRef CAS PubMed.
- J. C. Shelley, A. Cholleti, L. L. Frye, J. R. Greenwood, M. R. Timlin and M. Uchimaya, J. Comput.-Aided Mol. Des., 2007, 21, 681–691 CrossRef CAS PubMed.
- M. H. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed.
- E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren and J. L. Knight, J. Chem. Theory Comput., 2016, 12, 281–296 CrossRef CAS PubMed.
-
G. Landrum. RDKit: Open Source Cheminformatics, https://www.rdkit.org, 2019 Search PubMed.
-
R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domanski, D. L. Dotson, S. Buchoux and I. M. Kenney, MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations, Report 2575-9752, Los Alamos National Lab. (LANL), Los Alamos, NM (United States), 2019 Search PubMed.
-
M. Fey and J. E. Lenssen, arXiv, 2019, preprint, arXiv:1903.02428, DOI:10.48550/arXiv.1903.02428.
-
C. M. Bishop, Mixture density networks, 1994 Search PubMed.
-
V. P. Dwivedi and X. Bresson, arXiv, 2020, preprint, arXiv:2012.09699, DOI:10.48550/arXiv.2012.09699.
-
X. Bresson and T. Laurent, arXiv, 2017, preprint, arXiv:1711.07553, DOI:10.48550/arXiv.1711.07553.
-
V. P. Dwivedi, C. K. Joshi, T. Laurent, Y. Bengio and X. Bresson, arXiv, 2020, preprint, arXiv:2003.00982, DOI:10.48550/arXiv.2003.00982.
-
B. Jing, S. Eismann, P. Suriana, R. J. Townshend and R. Dror, arXiv, 2020, preprint, arXiv:2009.01411, DOI:10.48550/arXiv.2009.01411.
-
B. Jing, S. Eismann, P. N. Soni and R. O. Dror, arXiv, 2021, preprint, arXiv:2106.03843, DOI:10.48550/arXiv.2106.03843.
- M. R. Bauer, T. M. Ibrahim, S. M. Vogel and F. M. Boeckler, J. Chem. Inf. Model., 2013, 53, 1447–1462 CrossRef CAS PubMed.
- M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594 CrossRef CAS PubMed.
- V.-K. Tran-Nguyen, C. Jacquemard and D. Rognan, J. Chem. Inf. Model., 2020, 60, 4263–4273 CrossRef CAS PubMed.
- J. B. Dunbar Jr, R. D. Smith, C.-Y. Yang, P. M.-U. Ung, K. W. Lexa, N. A. Khazanov, J. A. Stuckey, S. Wang and H. A. Carlson, J. Chem. Inf. Model., 2011, 51, 2036–2046 CrossRef PubMed.
- C. E. Schindler, H. Baumann, A. Blum, D. Böse, H.-P. Buchstaller, L. Burgdorf, D. Cappel, E. Chekler, P. Czodrowski and D. Dorsch, J. Chem. Inf. Model., 2020, 60, 5457–5474 CrossRef CAS PubMed.
- C. Shen, X. Hu, J. Gao, X. Zhang, H. Zhong, Z. Wang, L. Xu, Y. Kang, D. Cao and T. Hou, J. Cheminf., 2021, 13, 81 Search PubMed.
- T. Cheng, X. Li, Y. Li, Z. Liu and R. Wang, J. Chem. Inf. Model., 2009, 49, 1079–1093 CrossRef CAS PubMed.
- M. Su, G. Feng, Z. Liu, Y. Li and R. Wang, J. Chem. Inf. Model., 2020, 60, 1122–1136 CrossRef CAS PubMed.
- J. Yang, C. Shen and N. Huang, Front. Pharmacol., 2020, 11, 69 CrossRef CAS PubMed.
- C. Shen, Y. Hu, Z. Wang, X. Zhang, H. Zhong, G. Wang, X. Yao, L. Xu, D. Cao and T. Hou, Briefings Bioinf., 2021, 22, 497–514 CrossRef PubMed.
- L. Chen, A. Cruz, S. Ramsey, C. J. Dickson, J. S. Duca, V. Hornak, D. R. Koes and T. Kurtzman, PLoS One, 2019, 14, e0220113 CrossRef CAS PubMed.
- J. Sieg, F. Flachsenberg and M. Rarey, J. Chem. Inf. Model., 2019, 59, 947–961 CrossRef CAS PubMed.
- N. Triballeau, F. Acher, I. Brabet, J.-P. Pin and H.-O. Bertrand, J. Med. Chem., 2005, 48, 2534–2547 CrossRef CAS PubMed.
- J.-F. Truchon and C. I. Bayly, J. Chem. Inf. Model., 2007, 47, 488–508 CrossRef CAS PubMed.
- A. N. Jain, J. Comput.-Aided Mol. Des., 2007, 21, 281–306 CrossRef CAS PubMed.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461 CAS.
- L. Wang, Y. Wu, Y. Deng, B. Kim, L. Pierce, G. Krilov, D. Lupyan, S. Robinson, M. K. Dahlgren and J. Greenwood, J. Am. Chem. Soc., 2015, 137, 2695–2703 CrossRef CAS PubMed.
- V.-K. Tran-Nguyen, G. Bret and D. Rognan, J. Chem. Inf. Model., 2021, 61, 2788–2797 CrossRef CAS PubMed.
- J. Sunseri and D. R. Koes, Molecules, 2021, 26, 7369 CrossRef CAS PubMed.
- J. Eberhardt, D. Santos-Martins, A. F. Tillack and S. Forli, J. Chem. Inf. Model., 2021, 61, 3891–3898 CrossRef CAS PubMed.
- R. Huey, G. M. Morris, A. J. Olson and D. S. Goodsell, J. Comput. Chem., 2007, 28, 1145–1152 CrossRef CAS PubMed.
- R. Quiroga and M. A. Villarreal, PLoS One, 2016, 11, e0155183 CrossRef PubMed.
- R. A. Friesner, R. B. Murphy, M. P. Repasky, L. L. Frye, J. R. Greenwood, T. A. Halgren, P. C. Sanschagrin and D. T. Mainz, J. Med. Chem., 2006, 49, 6177–6196 CrossRef CAS PubMed.
- R. Wang, L. Lai and S. Wang, J. Comput.-Aided Mol. Des., 2002, 16, 11–26 CrossRef CAS PubMed.
- M. M. Stepniewska-Dziubinska, P. Zielenkiewicz and P. Siedlecki, Bioinformatics, 2018, 34, 3666–3674 CrossRef CAS PubMed.
- Y. Kwon, W.-H. Shin, J. Ko and J. Lee, Int. J. Mol. Sci., 2020, 21, 8424 CrossRef CAS PubMed.
- R. Meli, A. Anighoro, M. J. Bodkin, G. M. Morris and P. C. Biggin, J. Cheminf., 2021, 13, 1–19 Search PubMed.
- P. J. Ballester, A. Schreyer and T. L. Blundell, J. Chem. Inf. Model., 2014, 54, 944–955 CrossRef CAS PubMed.
- J. D. Durrant and J. A. McCammon, J. Chem. Inf. Model., 2011, 51, 2897–2903 CrossRef CAS PubMed.
- L. Zheng, J. Fan and Y. Mu, ACS Omega, 2019, 4, 15956–15965 CrossRef CAS PubMed.
- M. Kadukova, K. d. S. Machado, P. Chacón and S. Grudinin, Bioinformatics, 2021, 37, 943–950 CrossRef CAS PubMed.
- M. Wójcikowski, P. J. Ballester and P. Siedlecki, Sci. Rep., 2017, 7, 1–10 CrossRef PubMed.
- V.-K. Tran-Nguyen and P. J. Ballester, J. Chem. Inf. Model., 2023, 63, 1401–1405 CrossRef CAS PubMed.
- V.-K. Tran-Nguyen, S. Simeon, M. Junaid and P. J. Ballester, Curr. Res. Struct. Biol., 2022, 4, 206–210 CrossRef CAS PubMed.
- J. Jiménez, M. Skalic, G. Martinez-Rosell and G. De Fabritiis, J. Chem. Inf. Model., 2018, 58, 287–296 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article abcd,
Xujun
Zhang
a,
Chang-Yu
Hsieh
abcd,
Xujun
Zhang
a,
Chang-Yu
Hsieh
 a,
Yafeng
Deng
d,
Dong
Wang
a,
Lei
Xu
a,
Yafeng
Deng
d,
Dong
Wang
a,
Lei
Xu
 e,
Jian
Wu
c,
Dan
Li
e,
Jian
Wu
c,
Dan
Li
 a,
Yu
Kang
a,
Yu
Kang
 *a,
Tingjun
Hou
*a,
Tingjun
Hou
 *ab and
Peichen
Pan
*ab and
Peichen
Pan
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443 protein–ligand complexes along with their experimental binding affinity data were retrieved from the PDBbind-v2020 general set41 and preprocessed with the Protein Preparation Wizard42 module implemented in Schrödinger 2020 to add hydrogens, delete waters, and optimize hydrogen bonds. The protonation states of the co-crystallized ligands and proteins were determined with the built-in Epik43 and PropKa44 utilities, respectively with pH = 7.0. The structures were finally minimized using the OPLS3 force field45 until the RMSD of heavy atoms averaged at 0.30 Å. After eliminating the PDB entries existing in the PDBbind-v2020 core set and CASF-2016 benchmark as well as those not identified by RDKit,46 a total of 19
443 protein–ligand complexes along with their experimental binding affinity data were retrieved from the PDBbind-v2020 general set41 and preprocessed with the Protein Preparation Wizard42 module implemented in Schrödinger 2020 to add hydrogens, delete waters, and optimize hydrogen bonds. The protonation states of the co-crystallized ligands and proteins were determined with the built-in Epik43 and PropKa44 utilities, respectively with pH = 7.0. The structures were finally minimized using the OPLS3 force field45 until the RMSD of heavy atoms averaged at 0.30 Å. After eliminating the PDB entries existing in the PDBbind-v2020 core set and CASF-2016 benchmark as well as those not identified by RDKit,46 a total of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149 complexes were remained, in which 1500 were randomly selected for validation and the rest were used for training. The validation set here was employed for the judgement of early stopping in model training to avoid overfitting as well as the selection of the model that exhibited optimal performance in internal testing.
149 complexes were remained, in which 1500 were randomly selected for validation and the rest were used for training. The validation set here was employed for the judgement of early stopping in model training to avoid overfitting as well as the selection of the model that exhibited optimal performance in internal testing.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dh×1 for node i and edge features βij ∈
dh×1 for node i and edge features βij ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) de×1 for the edge between node i and its neighboring node j, the initial node features αi and edge features βij were first embedded into d-dimensional hidden features h0i and e0ijvia two independent fully connected layers.
de×1 for the edge between node i and its neighboring node j, the initial node features αi and edge features βij were first embedded into d-dimensional hidden features h0i and e0ijvia two independent fully connected layers.![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×dh, W0β ∈
d×dh, W0β ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×de and b0α,b0β ∈
d×de and b0α,b0β ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d denote the weights and biases of linear layers. Then h0i and e0ij are fed into l tandem repeated GT/GatedGCN layers to obtain the updated features hil and eijl. For GT, it relies on a modified multi-head self-attention (MHA) mechanism for the update of node and edge features, and the layer update equations for a layer l are described as follows:
d denote the weights and biases of linear layers. Then h0i and e0ij are fed into l tandem repeated GT/GatedGCN layers to obtain the updated features hil and eijl. For GT, it relies on a modified multi-head self-attention (MHA) mechanism for the update of node and edge features, and the layer update equations for a layer l are described as follows:
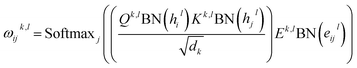
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dk×d, Ohl, Ohl ∈
dk×d, Ohl, Ohl ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d are the weight matrices for linear layers; k ∈ 1,…,H represents the number of attention heads; dk denotes the dimension for each head, which can be computed as d divided by H; j ∈ Ni denotes the neighboring nodes of node i; BN, Concat, Dropout and Softmax denote batch normalization, concatenation, dropout, and softmax operations, respectively. The attention outputs ĥil+1 and êijl+1 are then passed to several batch normalization layers, fully connected layers and residual connections to obtain the final features of the lth layer hil+1 and eijl+1 as:
d×d are the weight matrices for linear layers; k ∈ 1,…,H represents the number of attention heads; dk denotes the dimension for each head, which can be computed as d divided by H; j ∈ Ni denotes the neighboring nodes of node i; BN, Concat, Dropout and Softmax denote batch normalization, concatenation, dropout, and softmax operations, respectively. The attention outputs ĥil+1 and êijl+1 are then passed to several batch normalization layers, fully connected layers and residual connections to obtain the final features of the lth layer hil+1 and eijl+1 as:![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2d×d and Øh2l, Øe2l ∈
2d×d and Øh2l, Øe2l ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×2d are the weight matrices for linear layers; SiLU denotes a type of nonlinear activation.
d×2d are the weight matrices for linear layers; SiLU denotes a type of nonlinear activation.
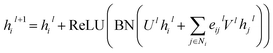
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d, ReLU is a type of nonlinear activation, and the edge gates eijl is defined as:
d×d, ReLU is a type of nonlinear activation, and the edge gates eijl is defined as: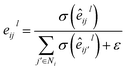
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d represent weight matrices.
d×d represent weight matrices.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2d×dm. The representation hu,v is passed into three individual fully-connected layers, and the three vectors that are necessary to parametrize a mixture density model, i.e., means (μu,v), standard deviations (σu,v), and mixing coefficients (ρu,v), are calculated as follows:
2d×dm. The representation hu,v is passed into three individual fully-connected layers, and the three vectors that are necessary to parametrize a mixture density model, i.e., means (μu,v), standard deviations (σu,v), and mixing coefficients (ρu,v), are calculated as follows:![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dm×Ng. The mixture density model is defined as the mixture of Ng Gaussians, thus mimicking the probability density distribution of the ligand–protein distance for each ligand–protein node pair. Here, the minimum distance between a specific ligand atom and each atom is used in a specific residue as the final indicator due to its superior performance in our previous study.37 Besides, two auxiliary representations as suggested by Méndez-Lucio et al.35 are computed based on hu,v in order to learn the atom type of each ligand atom and the bond type of each bond formed between a specific atom and its neighboring atoms, thus serving as two auxiliary tasks for the memorization of molecular structures.
dm×Ng. The mixture density model is defined as the mixture of Ng Gaussians, thus mimicking the probability density distribution of the ligand–protein distance for each ligand–protein node pair. Here, the minimum distance between a specific ligand atom and each atom is used in a specific residue as the final indicator due to its superior performance in our previous study.37 Besides, two auxiliary representations as suggested by Méndez-Lucio et al.35 are computed based on hu,v in order to learn the atom type of each ligand atom and the bond type of each bond formed between a specific atom and its neighboring atoms, thus serving as two auxiliary tasks for the memorization of molecular structures.
 two auxiliary cross-entropy losses
two auxiliary cross-entropy losses  and an adjustable affinity correction term
and an adjustable affinity correction term  The MDN loss was computed as the negative log-likelihood of a pool of protein–ligand node distances and then summed into a potential E(x) at the protein–ligand complex level. The affinity term was defined as the correlation coefficient of the final predicted scores and experimentally-determined binding affinities. α denoted the weight of
The MDN loss was computed as the negative log-likelihood of a pool of protein–ligand node distances and then summed into a potential E(x) at the protein–ligand complex level. The affinity term was defined as the correlation coefficient of the final predicted scores and experimentally-determined binding affinities. α denoted the weight of 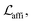 and α = 0 indicated a model without affinity term. The protein–ligand node pairs with distances less than 7.0 Å were taken into consideration when training the MDN while the cutoff was changed to 5.0 Å for model predictions, since this combination could achieve relatively better performance in our previous study.37
and α = 0 indicated a model without affinity term. The protein–ligand node pairs with distances less than 7.0 Å were taken into consideration when training the MDN while the cutoff was changed to 5.0 Å for model predictions, since this combination could achieve relatively better performance in our previous study.37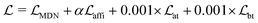
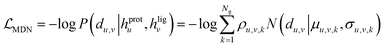
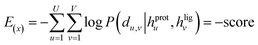
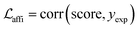
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886 active ligands against 102 diverse targets with 50 decoys generated for each active compound. The docking poses produced by Glide SP37 were used for model evaluation. In short, up to 10 docking poses were generated for each compound, and then rescored by each model. The VS performance was assessed according to the area under the receiver operating characteristic curve (AUROC),67 Boltzmann enhanced discrimination of receiver operating characteristic (BEDROC, α = 80.5),68 and EFs with different percentiles (0.5%, 1%, and 5%).
886 active ligands against 102 diverse targets with 50 decoys generated for each active compound. The docking poses produced by Glide SP37 were used for model evaluation. In short, up to 10 docking poses were generated for each compound, and then rescored by each model. The VS performance was assessed according to the area under the receiver operating characteristic curve (AUROC),67 Boltzmann enhanced discrimination of receiver operating characteristic (BEDROC, α = 80.5),68 and EFs with different percentiles (0.5%, 1%, and 5%).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 true actives and 2
030 true actives and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798
798![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 737 true inactives. For each target, the ratio of actives to inactives is around 1
737 true inactives. For each target, the ratio of actives to inactives is around 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000, and this high imbalance could better mimic the challenging scenarios in real-word applications. The proteins and ligands were prepared as described above, and then Glide SP was employed to generate up to 10 docking poses for each compound. It should be noted that multiple PDB templates are provided for each target in the original version of the dataset. To save computational costs, we assessed the quality of each PDB entry by taking multiple factors (e.g., binding site, binding site mutations, missing residues, resolution, etc.) into account, and finally selected just one for each target for the following docking calculations. As for the molecule failing in docking, an extreme low score was exerted to it. The detailed information of the dataset employed here is summarized in Table S4.† The performance is indicated majorly according to the EF at the top 1% percentile (EF1%).
1000, and this high imbalance could better mimic the challenging scenarios in real-word applications. The proteins and ligands were prepared as described above, and then Glide SP was employed to generate up to 10 docking poses for each compound. It should be noted that multiple PDB templates are provided for each target in the original version of the dataset. To save computational costs, we assessed the quality of each PDB entry by taking multiple factors (e.g., binding site, binding site mutations, missing residues, resolution, etc.) into account, and finally selected just one for each target for the following docking calculations. As for the molecule failing in docking, an extreme low score was exerted to it. The detailed information of the dataset employed here is summarized in Table S4.† The performance is indicated majorly according to the EF at the top 1% percentile (EF1%).







