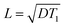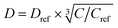Exploiting solid-state dynamic nuclear polarization NMR spectroscopy to establish the spatial distribution of polymorphic phases in a solid material

Abstract

Solid-state DNP NMR can enhance the ability to detect minor amounts of solid phases within heterogenous materials. Here we demonstrate that NMR contrast based on the transport of DNP-enhanced polarization can be exploited in the challenging case of early detection of a small amount of a minor polymorphic phase within a major polymorph, and we show that this approach can yield quantitative information on the spatial distribution of the two polymorphs. We focus on the detection of a minor amount (<4%) of polymorph III of m-aminobenzoic acid within a powder sample of polymorph I at natural isotopic abundance. Based on proposed models of the spatial distribution of the two polymorphs, simulations of ¹H spin diffusion allow NMR data to be calculated for each model as a function of particle size and the relative amounts of the polymorphs. A comparison between simulated and experimental NMR data allows the model(s) best representing the spatial distribution of the polymorphs in the system to be established.

---

Introduction

In the context of organic molecular materials, the phenomenon of polymorphism^1–5 arises when a given type of molecule can form two or more solid phases with different crystal structures, and is a critically important concept in understanding fundamental properties of solids and optimizing their applications. In the case of pharmaceutical materials, for example, physicochemical and pharmacokinetic properties such as solubility and bioavailability may differ significantly between different polymorphs of a drug molecule as a consequence of their different crystal structures. For this reason, it is essential to characterize all polymorphic forms that are accessible to the molecule of interest and to establish the relative stabilities of the polymorphs. Importantly, early detection of small amounts of a minor polymorphic phase in a mixture with a major polymorphic phase, of the type that may arise, for example, during solid-state phase transformations between polymorphs, is critical to anticipate the evolution of the molecule of interest towards a polymorph with unfavorable properties.

A wide range of diffraction, microscopy and spectroscopy techniques provide key information in polymorphism research, although the ability to detect a small amount of a minor polymorphic phase within a major polymorph remains challenging.

Solid-state NMR spectroscopy is a powerful technique for polymorph characterization as chemical shifts and relaxation times are discriminatingly sensitive to differences in the local environments that exist in different polymorphs.^6–16 Unfortunately, the intrinsically low sensitivity of NMR may limit the opportunity to detect a minor polymorphic phase in a mixture with a major polymorphic phase.^17–19

Interestingly, recent advances in dynamic nuclear polarization (DNP) NMR,^20–27 in which polarization from the electron spin of an exogenous polarizing agent^28–32 is transferred to nuclear spins through microwave irradiation, can significantly enhance the ability of NMR to detect small amounts of solid phases in heterogenous materials by enhancing the sensitivity of solid-state NMR measurements by several orders of magnitude. Furthermore, DNP NMR may also generate large polarization gradients, allowing domain sizes between ca. 200 nm and 20 µm to be probed through spin diffusion.³³ Transport of DNP-enhanced polarization from the polarizing agent by spin diffusion allows solid-state DNP NMR to be exploited to establish domain sizes in multicomponent blends, for example in biomolecules,^34,35 microcrystalline solids,³⁶ pharmaceutical formulations,³⁷ porous materials³⁸ and nanoparticles.^39,40

As polymorphs of a given molecule generally have different DNP signal enhancements,⁴¹ transport of DNP-enhanced polarization in a solid particle composed of several polymorphs may not be uniform, which represents the basis of a strategy, reported for the first time in this article, to gain detailed insights into the nature of solid materials that comprise mixtures of polymorphic phases.

More specifically, we show that NMR contrast based on distinct transport of DNP-enhanced polarization can be exploited to allow a small amount of a minor polymorphic phase to be detected within a sample of a major polymorphic phase. Furthermore, we show that these experiments can yield quantitative information on the spatial distribution and domain sizes of the two polymorphic phases within particles of the powder sample.

Results and discussion

NMR contrast based on distinct transport of DNP-enhanced polarization

To demonstrate our strategy, we focus on m-aminobenzoic acid (m-ABA; Scheme 1), a system of interest in polymorphism research.^42–46 Five polymorphs of m-ABA (denoted Forms I to V) have been reported,^42,43 which either contain the zwitterionic tautomer (Forms I, III and IV) or the non-zwitterionic tautomer (Forms II and V) of m-ABA. The crystal structures of Form II (determined⁴² by single-crystal XRD) and Forms III, IV and V (determined⁴³ from powder XRD data) are known. To date, determination of the crystal structure of Form I has proved elusive, although X-ray photoelectron spectroscopy confirms that Form I contains the zwitterionic tautomer.⁴³

Scheme 1 Molecular structure of m-ABA in the zwitterionic tautomer.

Our DNP NMR strategy is demonstrated in studies of freshly prepared samples of Form I of m-ABA at natural isotopic abundance, which show evidence (as discussed below) for the presence of a small amount of Form III. Form I is a meta-stable polymorph that is known^43,45 to transform over time to Form III, which is thermodynamically more stable. Direct evidence for the polymorphic transformation of Form I to Form III has been observed by in situ solid-state ¹³C NMR studies^45,46 of the crystallization of m-ABA from methanol.

First, we consider experiments on a freshly prepared powder sample of Form I of m-ABA impregnated with a solution (60 mM) containing the DNP polarizing agent TEKPol in 1,1,2,2-tetrachloroethane.⁴⁷ Following impregnation, the solution phase containing the polarizing agent is in contact with the surface of the solid particles in the powder sample, but the polarizing agent is not present within the particles.

To assess whether contact between the solution containing the polarizing agent and particles of Form I may induce the polymorphic transformation to Form III, powder XRD data were recorded for a sample of Form I after impregnation with the polarizing solution, both before and after quenching to liquid nitrogen temperature (see ESI; Section 1.1†). The powder XRD data do not show any detectable amount of Form III, indicating that the conditions required for the DNP experiment (i.e., impregnation with the polarizing solution and low-temperature measurements) do not induce any significant extent of formation of Form III within a freshly prepared powder sample of Form I.

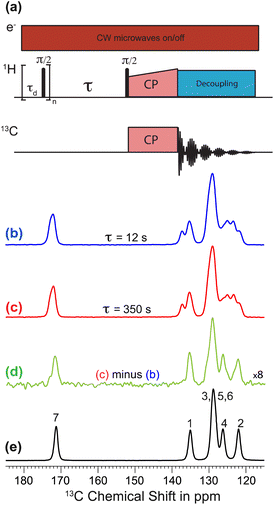
Polarization transfer from the polarizing solution to particles in the powder was monitored by ¹H–¹³C CPMAS saturation recovery measurements for different DNP polarization times τ, using the pulse sequence in Fig. 1a. ¹H–¹³C CPMAS NMR spectra recorded under microwave irradiation and using short (τ = 12 s; Fig. 1b) and long (τ = 350 s; Fig. 1c) DNP polarization times both show the spectral features characteristic of Form I.⁴⁴ However, the difference spectrum (Fig. 1d) obtained by subtracting the spectrum recorded with short polarization time from the spectrum recorded with long polarization time exhibits the spectral features characteristic of Form III (Fig. 1e). Significantly, this result indicates that the freshly prepared powder sample of Form I is actually a blend of polymorphic phases, comprising a major phase (Form I) and a minor phase (Form III). As Form I and Form III both contain the zwitterionic tautomer of m-ABA⁴³ and have similar values of isotropic ¹³C NMR chemical shifts,⁴⁴ the presence of a small amount of Form III within a sample of Form I is not readily detected by standard NMR measurements (Fig. 1b and c). We note that the behavior exhibited in Fig. 1b–d (for a sample of Form I impregnated with TEKPol/EtCl₄ solution) is also observed for a sample of Form I impregnated with AMUPol/glycerol–D₂O solution (see ESI; Section 1.2†).

Fig. 1 (a) ¹H–¹³C CPMAS saturation-recovery pulse sequence used to record solid-state ¹³C NMR spectra for different polarization times τ. (b and c) Solid-state ¹³C NMR spectra recorded at 110 K and under microwave irradiation for a powder sample of Form I of m-ABA impregnated with TEKPol/EtCl₄ solution using (b) τ = 12 s and (c) τ = 350 s. (d) Difference spectrum obtained by subtracting the spectrum in (b) from the spectrum in (c), with the intensity scale in the difference spectrum expanded by a factor of 8. (e) Solid-state ¹³C NMR spectrum recorded at 110 K with τ = 350 s for a powder sample of Form III impregnated with TEKPol/EtCl₄ solution. Peak assignments are based on the atom numbering shown in Scheme 1.

Investigation of the spatial distribution and domain sizes of the two polymorphic phases

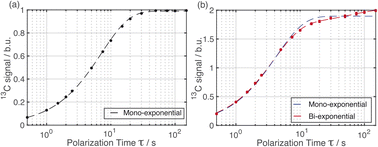
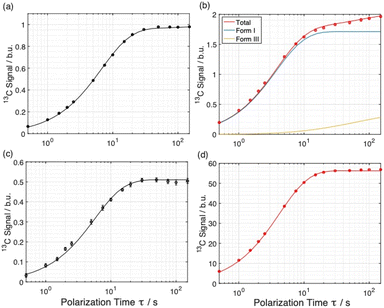
The distribution of the two polymorphs within the material was explored by examining the build-up of ¹³C resonances (Fig. 2) in spectra recorded using the ¹H–¹³C CPMAS saturation recovery pulse sequence as a function of the polarization time τ.³³ It should be noted that, although solid-state NMR has been exploited to identify the presence of structurally distinct domains within inhomogeneous materials,^48–51 it has not been used hitherto to explore the spatial distribution of polymorphic phases of a given molecule within a solid material.

Fig. 2 Experimental ¹³C NMR signal intensities for a powder sample of Form I impregnated with a solution of AMUPol in glycerol/D₂O (60/40, v/v). Data were recorded using ¹H–¹³C CPMAS saturation recovery (a) without and (b) with microwave irradiation applied. The signals are normalized to Boltzmann units (b.u.); one Boltzmann unit represents the polarization level reached without DNP or depolarization effects. Fits to the experimental data are shown by dashed lines. The experimental data in (a) are described by a mono-exponential build-up curve with build-up time T_B,_OFF = 7.2 s. The experimental data in (b) are described by a bi-exponential build-up curve with build-up times T_B,_ON(1) = 3.8 s and T_B,_ON(2) = 60 s.

For these measurements, a freshly prepared powder sample of Form I was impregnated with a solution (12 mM) containing the polarizing agent AMUPol in glycerol–D₂O (60/40, v/v). In this case, AMUPol was preferred to TEKPol as the DNP properties of AMUPol (e.g. depolarization) are understood in detail,⁵² allowing a more accurate description of the polarization source in the numerical simulations discussed below. We note that the experimental build-up curves for a powder sample of Form I impregnated with a TEKPol/EtCl₄ solution (see ESI; Section 1.3†) are essentially identical to those shown in Fig. 2.

Importantly, the build-up curves derived from solid-state DNP NMR data recorded with and without microwave irradiation are clearly different. Specifically, the build-up curve is mono-exponential with no microwave irradiation applied (Fig. 2a) and bi-exponential with microwave irradiation applied (Fig. 2b). The bi-exponential build-up curve observed with microwave irradiation confirms that the contrast between the two polymorphic phases arises from non-uniform DNP signal enhancements within the sample. We note that the build-up curves shown in Fig. 2 were obtained by monitoring all the ¹³C NMR resonances between 119 and 138 ppm as a function of the polarizing time τ. Importantly, the build-up curve for the single resonance at 137 ppm (see ESI; Fig. S7†), which is a ¹³C NMR signal for pure Form I, is mono-exponential with a build-up time of 4 s, which is comparable to the short component of the bi-exponential build-up curve shown in Fig. 2b. Significantly, the same experiments on a freshly prepared powder sample of Form I that had not been impregnated with a solution of AMUPol gave a mono-exponential build-up curve in both cases.

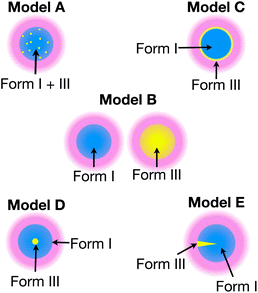
To gain more detailed structural insights from the solid-state DNP NMR data, we have carried out numerical simulations based on five models that represent different spatial distributions of the two polymorphic phases within particles in the powder sample (for more details, see ESI; Section 2†). Our models have been chosen to represent the spatial distribution of the polymorphic phases that would arise from plausible scenarios for the production of Form III by nucleation and growth within particles of Form I, while retaining a level of simplicity (based on justifiable simplifying assumptions) that is required to allow the computational analysis to remain tractable and practicable.

For each model, transport of polarization from the solution containing the polarizing agent to particles in the powder was modelled using simulations of ¹H spin diffusion³³ based on classical diffusion processes following Fick's second law. This approach allows build-up curves to be computed for the specific spatial distribution of the two polymorphs characteristic of each model, and as a function of the variables that define each model, specifically the particle size and the relative amounts of the two polymorphic phases. By comparison between experimental and simulated build-up curves, the model(s) giving best agreement with the experimental data may be deduced, thus establishing the spatial distribution of the polymorphic phases within the material.

Each model represents a different spatial distribution (shown schematically in Fig. 3) of the two polymorphic phases within particles of the powder sample, and corresponds to a plausible scenario for the production of Form III by nucleation and growth within particles of Form I (which is meta-stable with respect to transformation to Form III). For each model, it is assumed that the material comprises spherical particles of uniform size (defined by radius R) that are initially pure Form I.

Fig. 3 The distribution of the two polymorphs within particles in a powder sample of m-ABA in Models A–E. Each model assumes spherical particles of uniform size (defined by radius R), with regions containing Form I shown in blue and regions containing Form III shown in yellow. The solution (pink) containing the polarizing agent is located on the surface of the particles.

Model A (homogeneous distribution of Form III within each particle of Form I). In this model, Form III nucleates at multiple sites throughout each particle of Form I, but with no substantial growth of Form III, leading to an essentially uniform distribution of small regions of Form III within particles of Form I. In the context of probing the spatial distribution using solid-state DNP NMR, the regions of Form III in this model must be much smaller than the shortest spin-diffusion length.

Model B (distinct particles of pure Form I and pure Form III). In this model, there is a low probability of nucleation of Form III. However, after nucleation occurs, rapid growth of Form III occurs such that the whole particle becomes Form III. As a result, the powder sample comprises many particles of pure Form I and some particles of pure Form III.

Model C (core–shell particles with Form III in the shell). In this model, nucleation and growth of Form III occur at the surface of each particle of Form I, giving rise to a spherical shell of Form III and a spherical core of Form I.

Model D (core–shell particles with Form III in the core). In this model, nucleation and growth of Form III occur in the interior of each particle of Form I, represented by a spherical core of Form III at the center of the particle and a spherical shell of Form I.

Model E (Form III embedded as a region extending from the surface to the core of particles of Form I). In this case, nucleation and growth of Form III produce a region of Form III that extends from the surface to the center of each particle of Form I. The region containing Form III is represented in this model as a cone, with the apex at the center of the particle and the base at the surface of the particle. This model is indicative of a much wider range of geometric scenarios in which a region of Form III is embedded within each particle of Form I, with partial presence at the surface of the particle and extending deep within the particle.

In assessing the quality of agreement between the simulated solid-state DNP NMR data for each model and the experimental data, our numerical simulations involved variation of: (i) the radius R of the spherical particles, and (ii) the relative amounts of Form I and Form III.

Numerical simulations for Models A–E

Model A. First, we note that Model A can be ruled out as it would give mono-exponential build-up curves both with and without microwave irradiation. In fact, in this model, each particle of m-ABA in the powder sample contains distinct domains of Form I and domains of Form III, with the domains of Form III (the minor phase) distributed homogeneously within each particle of Form I (the major phase). For the model to be considered as homogeneous, the domains of both Form I and Form III must be much smaller than the shortest spin-diffusion length. The spin diffusion length is calculated as:
where D is the spin diffusion coefficient and T₁ is the longitudinal relaxation time. We choose a reference spin diffusion coefficient D_ref, using the value D_ref = 500 nm² s⁻¹ determined for polystyrene,⁵³ and the spin diffusion coefficient for the material of interest is determined as:
where C is the ¹H concentration in the material of interest and C_ref = 80 mol dm^–3 for the reference material polystyrene. For Form I and Form III of m-ABA, C = 58 mol dm^–3. For the polarizing solution containing AMUPol in glycerol–D₂O (60/40 v/v), C = 65 mol dm^–3. We note that glycerol (with natural isotopic abundances) was used within the solvent mixture in order to increase the polarizing power of the polarizing solution.^54–56

From the equations above, the spin diffusion length is determined to be L = 309 nm for Form III and L = 47 nm for Form I. In a homogeneous distribution in which the domains of Form III are smaller than 10 nm, any polarization gradient between Form I and Form III would be instantly compensated by ¹H spin-diffusion, leading to a mono-exponential build-up curve.

Model B. For Model B, comprising particles of pure Form I and particles of pure Form III, the simulated build-up curve under conditions of microwave irradiation is bi-exponential and shows good agreement with the experimental build-up curve (see ESI, Section 2.1†). The best fit between experimental and simulated data is obtained with R = 3.3 µm for each type of particle, and with 97% of particles comprising pure Form I and 3% of particles comprising pure Form III (see ESI; Section 2.1†). In this model, a significant fraction of the domain containing Form III is located far from the surface of the particle, giving rise to the long component of the bi-exponential build-up curve. We note that the presence of a larger proportion of Form III would lead to a bi-exponential build-up curve, even without microwave irradiation.

Model C. For Model C (core–shell with Form III in the shell), the calculated and experimental build-up curves are in poor agreement (see ESI; Section 2.2†). As the shell comprising Form III and the polarizing agent are in close proximity in this model, the simulated build-up curve is mono-exponential both with and without microwave irradiation, which is not consistent with the experimental results. Thus, Model C may be ruled out. This observation also suggests, independently, that impregnation of the powder sample with the solution containing the polarizing agent is not responsible for inducing the nucleation of Form III within the particles of Form I as, under these circumstances, Form III would be expected to be formed preferentially in the outer shell of the particles of Form I.

Model D. Model D (core–shell with Form III in the core) also gives a mono-exponential build-up curve. In this case, the presence of a region of Form III in the core of each particle would not be observed in the DNP experiment recorded with microwave irradiation. Indeed, the short T₁ of Form I would not permit spin diffusion to transfer the DNP polarization throughout the 7 µm from the surface to the core of the particle. For this model, the smallest deviation between the calculated and experimental build-up curves is obtained when the relative amounts of Form III and Form I are 3% and 97%, respectively, although the calculated and experimental build-up curves are in poor agreement.

Model E. For Model E, the domain containing Form III extends from the surface to the center of each particle of Form I. As the region of this domain at the surface of the particle is directly exposed to the solution containing the polarizing agent, the polarization of Form III is enhanced by spin diffusion. On the other hand, the part of the domain of Form III located far from the surface of the particle is associated with a long build-up time. As a consequence, bi-exponential behavior is expected for this model under conditions with microwave irradiation, whereas mono-exponential behavior is expected under conditions without microwave irradiation.

Simulated build-up curves for Model E are shown together with the experimental build-up curves in Fig. 4a and b, and experimental and simulated build-up curves for the polarizing solution are shown in Fig. 4c and d. Clearly, excellent agreement is observed between experimental and simulated data for all four curves. In fact, the simulations give mono-exponential behavior for the polarizing solution and for the solid phase not subjected to microwave irradiation, whereas the simulations give bi-exponential behavior under conditions of microwave irradiation. The best agreement between experimental and simulated data for Model E is obtained for particles of radius R = 4.6 µm containing 96% of Form I and 4% of Form III (see ESI; Section 2.3†).

Fig. 4 Experimental build-up curves (data points with error bars) for ¹³C resonances for: (a and b) a powder sample of Form I of m-ABA impregnated with AMUPol/glycerol–D₂O solution, and (c and d) the AMUPol/glycerol–D₂O solution. Experimental data were recorded using ¹H–¹³C CPMAS saturation recovery as a function of polarization time τ, either (b and d) with or (a and c) without microwave irradiation. Solid lines shown the best-fit simulated build-up curves for Model E obtained with R = 4.6 µm and a composition with 96% of Form I and 4% of Form III. The best-fit simulated build-up curves for the individual components of Form I (blue solid line) and Form III (yellow solid line) are also shown in (b). Signals are expressed in Boltzmann units (b.u.). Note that the error bars are larger than the data points only in (c).

In summary, only the simulated build-up curves for Model B and Model E show good agreement with the experimental build-up curves. In Model B, the two polymorphs are present in different particles, whereas in Model E, the two polymorphs are present as distinct domains within the same particle. Clearly, in order to distinguish whether Model B or Model E is a more accurate representation of the actual distribution of Form III within particles of Form I of m-ABA, information derived from complementary experimental techniques (particularly electron microscopy or Raman microspectrometry) may yield valuable insights.

Concluding remarks

Overall, our results demonstrate the ability of solid-state DNP NMR experiments to detect the presence of a minor polymorphic phase within a major polymorph in a powder sample at natural isotopic abundance, and to establish contrast between the two polymorphic phases. Furthermore, quantitative details of the spatial distribution of the two polymorphic phases within the particles can be obtained through numerical simulations of ¹H spin diffusion.

Our methodology has been illustrated in a challenging system, for which the NMR signals for the two polymorphs overlap significantly, and for which the crystal structure of the major polymorph (Form I of m-ABA) is unknown. In this regard, it is relevant to highlight the advantages of the methodology reported here compared to the use of powder XRD to characterize the mixture of polymorphic phases. Firstly, we emphasize that powder XRD could not provide insights into the spatial distribution of the different polymorphs within the mixture of polymorphic phases, in contrast to the DNP NMR approach described in this paper; in this regard, we note that Raman microspectrometry is a valuable technique for studying the spatial distributions of different phases (including polymorphic phases) in heterogenous solid materials^57–64 on length-scales comparable to the size of the polymorphic domains studied by DNP NMR in the present work. Secondly, with regard to detecting the existence of a small amount (e.g., 5%) of a minor polymorphic phase together with the major polymorphic phase, powder XRD should be able to confirm this fact qualitatively, provided the quality of the powder XRD data is sufficiently high (e.g., with better signal/noise ratio than the powder XRD data in Fig. S1†).

However, reliable quantification of the relative amount of the minor polymorphic phase by analysis of powder XRD data is not necessarily straightforward. The only rigorous way to quantify the relative amounts of the two polymorphic phases by powder XRD would be to carry out a two-phase Rietveld refinement (with the relative amounts of the two phases determined from the refined value of the relative scale factor), but a two-phase Rietveld refinement requires that the structures of both polymorphic phases are already known. In the present case, this approach would not be possible for a mixture of polymorphs involving Form I of m-ABA as the structure of this material is not known. The reason that Rietveld refinement is required in this context is that it allows the effects of “preferred orientation” in the powder sample to be taken quantitatively into account. Simpler approaches (e.g., based on assessing the relative intensities of specific peaks characteristic of the two polymorphs in the powder XRD data) do not provide a reliable or rigorous basis for quantifying the relative amounts of the two polymorphs as this type of approach does not take into account the fact that the two polymorphs in the powder sample may be affected by a different extent of preferred orientation.

Clearly, the method presented here has the potential to reveal the early onset of transformations between polymorphic forms and will thus be a highly valuable addition to existing powder XRD and electron microscopy methods for the investigation of polymorph transformation in powder samples of organic materials.

Methods

Sample preparation and characterization

Preparation of Form I of m-ABA. A sample of m-ABA with natural isotopic abundances was purchased from SIGMA ALDRICH and used as supplied. Powder samples of Form I of m-ABA were prepared by rapidly cooling a saturated solution of m-ABA in DMSO, following the procedure described by Williams et al.⁴³ For the solid-state DNP NMR experiments, a freshly prepared powder sample of Form I of m-ABA was impregnated by the incipient wetness method using a solution containing the polarizing agent (TEKPol or AMUPol).³⁶

Impregnation of the powder sample of Form I of m-ABA with TEKPol. A freshly prepared powder sample of Form I of m-ABA (30 mg) was impregnated with a solution (15 µL, 60 mM) containing TEKPol in 1,1,2,2-tetrachloroethane (EtCl₄; TCE). Within a few minutes after impregnation, the sample was loaded into a sapphire MAS NMR rotor (3.2 mm) with a Teflon insert (volume, 20 µL) for the solid-state DNP NMR experiments. The extent of dissolution of m-ABA in the TEKPol/TCE solution was assessed by comparing ¹³C CPMAS NMR spectra recorded at 100 K for a powder sample of Form I of m-ABA before (Fig. S6a†) and after (Fig. S6b†) impregnation with the TEKPol/TCE solution. The spectrum recorded after impregnation did not contain any detectable broad-line signals for m-ABA, indicating that no significant amount of m-ABA was present in the amorphous “frozen liquid” phase produced on quenching the solution to 100 K, and consistent with Form I of m-ABA having no significant solubility in the TEKPol/TCE solution (see ESI; Section 1.5†).

Impregnation of the powder sample of Form I of m-ABA with AMUPol. A freshly prepared powder sample of Form I of m-ABA (39 mg) was impregnated with a solution (20 µL, 12 mM) containing AMUPol in glycerol–D₂O (60/40 v/v). Within a few minutes after impregnation, the sample was loaded into a sapphire MAS NMR rotor (3.2 mm) with a Teflon insert (volume, 20 µL) for the solid-state DNP NMR experiments.

Solid-state DNP NMR experiments

Experimental methods. All solid-state DNP NMR experiments were carried out on a Bruker AVANCE III HD NMR spectrometer with a 9.4 T wide-bore magnet (Larmor frequencies: ¹H, 400 MHz; ¹³C, 100 MHz) using a Bruker 3.2 mm low-temperature double resonance DNP ¹H/{²⁹Si/¹³C} MAS NMR probe. The sample temperature was ca. 100 K and the MAS frequency was 10 kHz. The spectrometer was equipped with a gyrotron for microwave irradiation of the sample. The field sweep coil of the NMR magnet was set to give microwave irradiation at the maximum DNP enhancement of TOTAPOL (263.334 GHz). The estimated power of the microwave beam at the output of the probe waveguide was 4 W. A thermocouple located 8.5 mm from the sample was used to measure the temperature of the NMR experiments.

¹H NMR saturation recovery experiments were carried out to determine the different time constants of the (exponential) recovery of the polarization. A train of 90° pulses (comprising 50 pulses separated by 1 ms) was used to saturate the ¹H magnetization, with recovery of the ¹H magnetization allowed during the polarization delay τ. The magnetization was then transferred to the ¹³C spin nuclei for detection. The intensities of the ¹³C NMR signals of m-ABA were measured in the region of the spectrum between 119 and 138 ppm, which was chosen because this region contains the same number of ¹³C NMR resonances for the two polymorphic forms and the minimum amount of noise.

It is essential to clearly distinguish between the intrinsic build-up time, the effective build-up time in the presence of microwave irradiation, and the effective build-up time in the absence of microwave irradiation. In this regard, T₁ denotes the ¹H relaxation time measured from a saturation recovery experiment on a pure dry powder sample. The effective ¹H build-up time for a powder sample impregnated with the solution containing the polarizing agent is denoted T_B,ON (measured in the presence of microwave irradiation) or T_B,OFF (measured in the absence of microwave irradiation).

Theoretical build-up curves were simulated using the following parameters measured experimentally: T_1,ON(Form I) = 3 s, T_1,OFF(Form I) = 6.5 s, T_1,ON(Form III) = 214 s, T_1,OFF(Form III) = 213 s. An enhancement of 115, a depolarization factor of 0.5, T_B,ON(solution) = 4.35 s and T_B,OFF(solution) = 5.79 s were measured for the solution containing AMUPol (12 mM) dissolved in glycerol–D₂O (60/40 v/v).

The ¹³C NMR resonances in the high-resolution solid-state ¹³C NMR spectrum of Form I of m-ABA (see Fig. 1e) were assigned from a ¹³C–¹³C DQ dipolar correlation NMR spectrum recorded with a DQ excitation time of 0.4 ms.⁶⁵

Numerical simulations for Models A–E based on well-defined spatial distributions of polymorphic phases within particles in a powder sample. All numerical simulations of solid-state DNP NMR polarization build-up curves were carried out using either Matlab or COMSOL Multiphysics, according to the methodology described by Pinon et al.³³ Descriptions of Models A–E used in the numerical simulations are shown schematically in Fig. 3. For each model, it is assumed that the material comprises spherical particles of uniform size (defined by radius R), with the different models differing in the spatial distribution of Form I and Form III within the particles. Further details of the mathematical foundations for calculating the build-up curves for each model are discussed in ESI (Section 2†). In assessing the quality of agreement between the simulated NMR data for each model and the experimental NMR data, the numerical simulations involved variation of the radius R of the spherical particles, and the relative amounts of Form I and Form III.

Data availability

ESI† contains additional figures discussed in the text. The code and raw data used to carry out the numerical simulations presented in the manuscript is available at https://zenodo.org/record/8019697.

Author contributions

The specific components of the research were carried out as follows: preparation of the sample of m-ABA (C. E. H., A. C. P., S. F. C.); measurement of powder XRD data (C. E. H.); analysis of powder XRD data (C. E. H., K. D. M. H.); measurement of solid-state DNP NMR data (A. C. P., S. F. C., F. Z., S. V., G. M., P. T.); analysis of solid-state DNP NMR data (A. C. P., S. F. C., F. Z., S. V., G. M., K. D. M. H., P. T.); numerical simulations of ¹H spin diffusion (A. C. P., S. F. C.). Preparation of the manuscript was coordinated by G. M., K. D. M. H., A. C. P., P. T. with contributions from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Basile Heresanu (CINaM-CNRS/AMU laboratory) and Andrew Williams (Cardiff University) for recording the powder XRD data in Fig. S2.† This project received funding from ERC under the European Union Horizon 2020 research and innovation programme (Grant Agreement No. 758498) and from CNRS under the International Emerging Actions (Grant Agreement No. 00211). We are grateful to Cardiff University for financial support.

References

1. J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, Oxford, 2002.
2. B. Rodríguez-Spong, C. P. Price, A. Jayasankar, A. J. Matzger and N. R. Rodríguez-Hornedo, Adv. Drug Delivery Rev., 2004, 56, 241–274.
3. S. L. Price, Acc. Chem. Res., 2009, 42, 117–126.
4. A. Y. Lee, D. Erdemir and A. S. Myerson, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 259–280.
5. D.-K. Bučar, R. W. Lancaster and J. Bernstein, Angew. Chem., Int. Ed., 2015, 54, 6972–6993.
6. K. D. M. Harris and J. M. Thomas, J. Solid State Chem., 1991, 94, 197–205.
7. B. E. Padden, M. T. Zell, Z. Dong, S. A. Schroeder, D. J. W. Grant and E. J. Munson, Anal. Chem., 1999, 71, 3325–3331.
8. N. Zumbulyadis, B. Antalek, W. Windig, R. P. Scaringe, A. M. Lanzafame, T. Blanton and M. Helber, J. Am. Chem. Soc., 1999, 121, 11554–11557.
9. R. K. Harris, Analyst, 2006, 131, 351–373.
10. J. M. Griffin, D. R. Martin and S. P. Brown, Angew. Chem., Int. Ed., 2007, 46, 8036–8038.
11. R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174–S186.
12. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779.
13. D. Stueber and S. Jehle, J. Pharm. Sci., 2017, 106, 1828–1838.
14. F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Nat. Commun., 2018, 9, 4501.
15. P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53.
16. C. J. H. Smalley, H. E. Hoskyns, C. E. Hughes, D. N. Johnstone, T. Willhammar, M. T. Young, C. J. Pickard, A. J. Logsdail, P. A. Midgley and K. D. M. Harris, Chem. Sci., 2022, 13, 5277–5288.
17. K. Maruyoshi, D. Iuga, A. E. Watts, C. E. Hughes, K. D. M. Harris and S. P. Brown, J. Pharm. Sci., 2017, 106, 3372–3377.
18. Y. T. A. Wong, R. L. E. G. Aspers, M. Uusi-Penttilä and A. P. M. Kentgens, Anal. Chem., 2022, 94, 16667–16674.
19. Y. Du, P. Phyo, M. Li, B. Sorman, M. McNevin, W. Xu, Y. Liu and Y. Su, Anal. Chem., 2022, 94, 15341–15349.
20. Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941.
21. A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Acc. Chem. Res., 2013, 46, 1942–1951.
22. A. J. Rossini, J. Phys. Chem. Lett., 2018, 9, 5150–5159.
23. R. W. Hooper, B. A. Klein and V. K. Michaelis, Chem. Mater., 2020, 32, 4425–4430.
24. I. B. Moroz and M. Leskes, Annu. Rev. Mater. Res., 2022, 52, 25–55.
25. T. Biedenbänder, V. Aladin, S. Saeidpour and B. Corzilius, Chem. Rev., 2022, 122, 9738–9794.
26. W. Y. Chow, G. De Paëpe and S. Hediger, Chem. Rev., 2022, 122, 9795–9847.
27. D. Xiao, S. Xu, N. J. Brownbill, S. Paul, L.-H. Chen, S. Pawsey, F. Aussenac, B.-L. Su, X. Han, X. Bao, Z. Liu and F. Blanc, Chem. Sci., 2018, 9, 8184–8193.
28. C. Sauvée, M. Rosay, G. Casano, F. Aussenac, R. T. Weber, O. Ouari and P. Tordo, Angew. Chem., Int. Ed., 2013, 52, 10858–10861.
29. G. Mathies, M. A. Caporini, V. K. Michaelis, Y. Liu, K.-N. Hu, D. Mance, J. L. Zweier, M. Rosay, M. Baldus and R. G. Griffin, Angew. Chem., Int. Ed., 2015, 54, 11770–11774.
30. D. J. Kubicki, G. Casano, M. Schwarzwälder, S. Abel, C. Sauvée, K. Ganesan, M. Yulikov, A. J. Rossini, G. Jeschke, C. Copéret, A. Lesage, P. Tordo, O. Ouari and L. Emsley, Chem. Sci., 2016, 7, 550–558.
31. R. Yao, D. Beriashvili, W. Zhang, S. Li, A. Safeer, A. Gurinov, A. Rockenbauer, Y. Yang, Y. Song, M. Baldus and Y. Liu, Chem. Sci., 2022, 13, 14157–14164.
32. T. Halbritter, R. Harrabi, S. Paul, J. van Tol, D. Lee, S. Hediger, S. T. Sigurdsson, F. Mentink-Vigier and G. De Paëpe, Chem. Sci., 2023, 14, 3852–3864.
33. A. C. Pinon, J. Schlagnitweit, P. Berruyer, A. J. Rossini, M. Lelli, E. Socie, M. Tang, T. Pham, A. Lesage, S. Schantz and L. Emsley, J. Phys. Chem. C, 2017, 121, 15993–16005.
34. P. C. A. van der Wel, J. R. Lewandowski and R. G. Griffin, J. Am. Chem. Soc., 2007, 129, 5117–5130.
35. A. Jantschke, E. Koers, D. Mance, M. Weingarth, E. Brunner and M. Baldus, Angew. Chem., Int. Ed., 2015, 54, 15069–15073.
36. A. J. Rossini, A. Zagdoun, F. Hegner, M. Schwarzwälder, D. Gajan, C. Copéret, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2012, 134, 16899–16908.
37. A. J. Rossini, C. M. Widdifield, A. Zagdoun, M. Lelli, M. Schwarzwälder, C. Copéret, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2014, 136, 2324–2334.
38. O. Lafon, A. S. L. Thankamony, T. Kobayashi, D. Carnevale, V. Vitzthum, I. I. Slowing, K. Kandel, H. Vezin, J.-P. Amoureux, G. Bodenhausen and M. Pruski, J. Phys. Chem. C, 2013, 117, 1375–1382.
39. J. Viger-Gravel, A. Schantz, A. C. Pinon, A. J. Rossini, S. Schantz and L. Emsley, J. Phys. Chem. B, 2018, 122, 2073–2081.
40. A. C. Pinon, U. Skantze, J. Viger-Gravel, S. Schantz and L. Emsley, J. Phys. Chem. A, 2018, 122, 8802–8807.
41. A. C. Pinon, A. J. Rossini, C. M. Widdifield, D. Gajan and L. Emsley, Mol. Pharm., 2015, 12, 4146–4153.
42. A. Théorêt, Spectrochim. Acta, Part A, 1971, 27, 11–18.
43. P. A. Williams, C. E. Hughes, G. K. Lim, B. M. Kariuki and K. D. M. Harris, Cryst. Growth Des., 2012, 12, 3104–3113.
44. C. E. Hughes, P. A. Williams and K. D. M. Harris, Angew. Chem., Int. Ed., 2014, 53, 8939–8943.
45. K. D. M. Harris, C. E. Hughes and P. A. Williams, Solid State Nucl. Magn. Reson., 2015, 65, 107–113.
46. K. D. M. Harris, C. E. Hughes, P. A. Williams and G. R. Edwards-Gau, Acta Crystallogr., Sect. C: Struct. Chem., 2017, 73, 137–148.
47. A. Zagdoun, G. Casano, O. Ouari, M. Schwarzwälder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Copéret, A. Lesage, P. Tordo and L. Emsley, J. Am. Chem. Soc., 2013, 135, 12790–12797.
48. S. Schantz and N. Ljungqvist, Macromolecules, 1993, 26, 6517–6524.
49. T. N. Pham, S. A. Watson, A. J. Edwards, M. Chavda, J. S. Clawson, M. Strohmeier and F. G. Vogt, Mol. Pharm., 2010, 7, 1667–1691.
50. P. Duan, M. S. Lamm, F. Yang, W. Xu, D. Skomski, Y. Su and K. Schmidt-Rohr, Mol. Pharm., 2020, 17, 3567–3580.
51. D. Stueber and Z. E. X. Dance, Anal. Chem., 2020, 92, 11095–11102.
52. S. Hediger, D. Lee, F. Mentink-Vigier, G. De Paëpe, MAS-DNP Enhancements: Hyperpolarization, Depolarization, and Absolute Sensitivity, eMagRes, 2018, 7, 105–116.
53. T. Wenckebach, Essentials of Dynamic Nuclear Polarization, Spindrift Publications, The Netherlands, 2016.
54. P. Thureau, M. Juramy, F. Ziarelli, S. Viel and G. Mollica, Solid State Nucl. Magn. Reson., 2019, 99, 15–19.
55. K. Kundu, F. Mentink-Vigier, A. Feintuch and S. Vega, eMagRes, 2019, 8, 295–338.
56. N. A. Prisco, A. C. Pinon, L. Emsley and B. F. Chmelka, Phys. Chem. Chem. Phys., 2021, 23, 1006–1020.
57. T. Wu and L. Yu, Pharm. Res., 2006, 23, 2350–2355.
58. M. J. Henson and L. Zhang, Appl. Spectrosc., 2006, 60, 1247–1255.
59. A. Brillante, I. Bilotti, R. G. Della Valle, E. Venuti and A. Girlando, CrystEngComm, 2008, 10, 937–946.
60. K. Greco and R. Bogner, Mol. Pharm., 2010, 7, 1406–1418.
61. J. Marti-Rujas, A. Desmedt, K. D. M. Harris and F. Guillaume, J. Am. Chem. Soc., 2004, 126, 11124–11125.
62. B. A. Palmer, A. Le Comte, K. D. M. Harris and F. Guillaume, J. Am. Chem. Soc., 2013, 135, 14512–14515.
63. E. Widjaja, P. Kanaujia, G. Lau, W. K. Ng, M. Garland, C. Saal, A. Hanefeld, M. Fischbach, M. Maio and R. B. H. Tan, Eur. J. Pharm. Sci., 2011, 42, 45–54.
64. J. R. Petriglieri, E. Salvioli-Mariani, L. Mantovani, M. Tribaudino, P. P. Lottici, C. Laporte-Magoni and D. Bersani, J. Raman Spectrosc., 2015, 46, 953–958.
65. M. Dekhil, G. Mollica, T. T. Bonniot, F. Ziarelli, P. Thureau and S. Viel, Chem. Commun., 2016, 52, 8565–8568.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02063k

---