Electrically conductive [Fe₄S₄]-based organometallic polymers

Abstract

Tailoring the molecular components of hybrid organic–inorganic materials enables precise control over their electronic properties. Designing electrically conductive coordination materials, e.g. metal–organic frameworks (MOFs), has relied on single-metal nodes because the metal–oxo clusters present in the vast majority of MOFs are not suitable for electrical conduction due to their localized electron orbitals. Therefore, the development of metal-cluster nodes with delocalized bonding would greatly expand the structural and electrochemical tunability of conductive materials. Whereas the cuboidal [Fe₄S₄] cluster is a ubiquitous cofactor for electron transport in biological systems, few electrically conductive artificial materials employ the [Fe₄S₄] cluster as a building unit due to the lack of suitable bridging linkers. In this work, we bridge the [Fe₄S₄] clusters with ditopic N-heterocyclic carbene (NHC) linkers through charge-delocalized Fe–C bonds that enhance electronic communication between the clusters. [Fe₄S₄Cl₂(ditopic NHC)] exhibits a high electrical conductivity of 1 mS cm⁻¹ at 25 °C, surpassing the conductivity of related but less covalent materials. These results highlight that synthetic control over individual bonds is critical to the design of long-range behavior in semiconductors.

---

Introduction

The electronic properties of hybrid organic–inorganic materials attract widespread attention due to the vast tunability of their components and structures. In particular, electroactive coordination polymers and metal–organic frameworks (CP/MOFs)^1–3 have been extensively studied for use in diverse technologies as charge storage materials,^4,5 electrochemical catalysts,^6,7 and chemiselective sensors.⁹ Despite these intense research efforts, the structural diversities of electrically conductive CP/MOFs remain limited, with most constructed from single-metal nodes, e.g. Fe²⁺ and Ni²⁺.^10–12 On the other hand, >100 000 examples of conventional CP/MOFs have been prepared through use of multi-nuclear metal clusters, or so-called secondary building units (SBUs), largely through the rational design of the reticular chemistry.¹³ While these structures feature charge-localized metal–oxo clusters that inhibit charge mobility, redox-active, charge-delocalized SBUs suitable for electron conduction remain unexplored.¹⁴

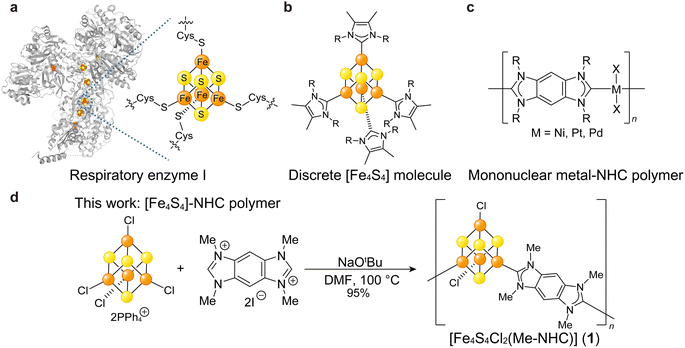
Ample studies suggest [Fe₄S₄] could serve as an electron-delocalized SBU with tunable electronic behavior. The [Fe₄S₄] cluster is a ubiquitous cofactor for electron transfer in enzymes (Fig. 1a),^15,16 and the structures and electronic properties of discrete [Fe₄S₄] clusters have been extensively studied with various capping ligands such as thiols,¹⁷ phosphines,¹⁸ halogens, and N-heterocyclic carbenes (NHCs, Fig. 1b),¹⁹ and alkyls.²⁰ Despite the broad interest in discrete [Fe₄S₄] clusters, few studies have focused on [Fe₄S₄] as a building unit of extended hybrid materials.^8,21 Recently, Anderson et al. reported (NR₄)₂[Fe₄S₄(BDT)₂] (R = Me, Bu; BDT = 1,4-benzenedithiolate) as one-dimensional chains of [Fe₄S₄] clusters bridged by Fe–S coordination bonds with electrical conductivities of 10⁻⁶ to 10⁻³ mS cm⁻¹.⁸ While indicative of semiconductor behavior, these values lie on the lower range for Fe and thiol-based CP/MOFs (10⁻³ to 10⁴ mS cm⁻¹, Table S1†). Given the delocalized bonding within [Fe₄S₄] clusters, we hypothesized that charge mobility could be improved by increasing the covalency of the cluster–linker bonds.

Fig. 1 Schematic representation of the [Fe₄S₄] and NHC molecules and materials related to this work. (a) [Fe₄S₄] clusters in the biological system. Crystal structure of respiratory enzyme I containing [Fe₄S₄]. (b) Biomimetic, discrete [Fe₄S₄] cluster with NHC capping ligands. (c) Electrically conductive mononuclear metal–NHC polymers. (d) Formation of [Fe₄S₄]–NHC polymer (1) via organometallic bond bridging.

To enhance electronic communication between [Fe₄S₄] clusters, we selected ditopic NHC compounds as linkers. Due to the strong electron-donating and π-accepting nature of NHCs and due to the similar electronegativities of transition metal ions and carbon moieties, NHCs produce strong metal–C bonds in various organometallic complexes^22,23 and give rise to single molecular wires with greater electronic conduction in comparison to analogues based on metal–S/N bonds.²⁴ Among extended network systems, polymers furnished from mono-nuclear metal ions and multi-topic NHCs exhibit high electrical conductivities exceeding 1.0 mS cm⁻¹ (Fig. 1c).²⁵ Although ditopic NHC linkers are attractive building units for electroactive CP/MOFs, limited studies have employed them.^26,27 The dearth of NHC-based materials likely stems from the synthetic difficulties in producing crystalline products given the irreversible formation of metal–C bonds. Recently, Bejger et al. reported [Co₄S₄(ⁱPr-NHC)₂] (ⁱPr-NHC = tetraisopropyl-benzobis-imidazolylidenes) showing crystallinity.²⁷ While redox the behaviour of [Co₄S₄] was explored, the electrical conductivity was not reported. Fe-based coordination materials show higher electrical conductivity than the Co-based analogues due to the high-energy valence electrons of Fe²⁺ and the Fe^3+/2+ mixed valency.^28,29 We assumed that the unique feature of Fe in enhancing electrical conductivity is applicable to the [M₄S₄] (M = Fe, Co) system as well. Here, we demonstrate the synthesis and opto-electronic behaviour of organometallic polymers with high electrical conductivities consisting of [Fe₄S₄] clusters linked by covalent Fe–C bonds bridged by ditopic NHCs (Fig. 1d).

Results and discussion

Synthesis and structural characterizations

We targeted benzobis-imidazolylidenes as NHC linkers due to the π-conjugated skeleton and modularity of the alkyl side chains.^25,30 The corresponding tetraalkyl-benzobisimidazolium salts (R–BBI–X; R = Me, Et, ⁿPr, ⁿBu; X = Br, I) were synthesized as precursors by following literature procedures (Fig. S1†).^31,32 The pre-formed [Fe₄S₄] cluster, (PPh₄)₂(Fe₄S₄Cl₄), was chosen as a precursor due to its good solubility in organic solvents and synthetic scalability, and was prepared according to literature (Fig. S2†).³³ An N,N-dimethylformamide (DMF) solution of R–BBI–X was combined with a DMF solution of NaO^tBu under N₂ to generate the NHC linker by in situ deprotonation. A DMF solution of (PPh₄)₂(Fe₄S₄Cl₄) was added to the resultant reaction mixture and heated at 100 °C for 24 h. For NHC variants with longer alkyl chains, the yields decreased such that almost no solid was obtained when using ⁿBu–BBI–Br. We ascribe the decrease in the yields for longer alkyl chain variants to the decrease in the coordination ability of the resultant NHC ligand and the increase of its solubility. The incorporation of longer alkyl chains next to the coordination site lowers the coordination ability due to the steric hindrance, thereby suppressing polymer product formation.³⁴ Additionally, products with longer alkyl chains presumably have a higher solubility due to the enhanced molecular dynamics. Both factors result in lowering the yield of the solid products with longer alkyl chains. Therefore, we focused on the product obtained from Me–BBI–I, [Fe₄S₄Cl₂(Me–NHC)] (1; Me–NHC = tetramethyl-benzobis-imidazolylidenes, 95% yield, Fig. S3†) (Fig. 1d), the composition of which was determined by acid-digested ¹H NMR and elemental analysis (Fig. S4†). The chemical composition of 1 was also confirmed from thermal gravimetric analysis (TGA). The TGA profile of 1 under N₂ displayed a weight loss of 39.4 wt% at 500 °C (Fig. S5†), which showed good agreement with the gravimetric ratio of Me–NHC for the polymeric structure of [Fe₄S₄Cl₂(Me–NHC)] (33.7 wt%) rather than the discrete structure of [Fe₄S₄Cl₂(Me–NHC)₂] (50.4 wt%).

Powder X-ray diffraction (PXRD) of 1 using a benchtop diffractometer did not produce well-defined reflections (Fig. S6†), which we ascribe to the less reversible coordination kinetics of meal–carbon bonds. The products synthesized (2-Et, 3-nPr, and 4-nBu) from Et–BBI–Br, ⁿPr–BBI–Br, and ⁿBu–BBI–Br lacked well-defined Bragg peaks as well (Fig. S6†). This result is consistent with previously reported mononuclear metal–NHC polymers consisting of metal–carbon bonds.^35,36 The insolubility of 1 in common polar solvents, e.g. dimethyl sulfoxide, acetonitrile, and methanol, also suggested the formation of polymeric structures.

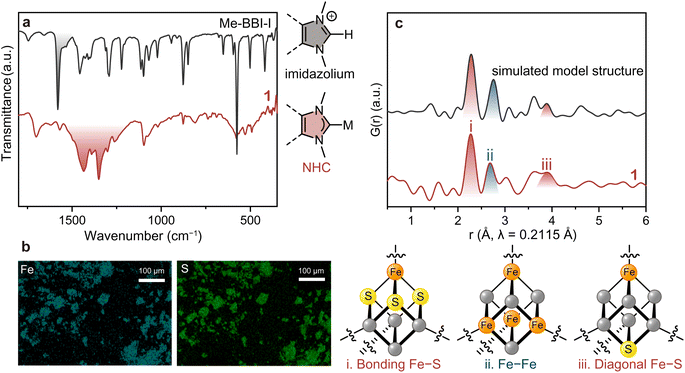
The formation of the Me–NHC carbene from the imidazolium was confirmed by Fourier-transform infrared (FT-IR) spectroscopy under N₂ (Fig. 2a). While the stretching vibration of imidazolium C=N at 1580 cm⁻¹ (highlighted in black) in Me–BBI–I disappeared in the spectrum of 1, a new set of split peaks at 1350–1500 cm⁻¹ (highlighted in red) appeared that is characteristic of the stretching vibration of C=N in NHCs bound to metal ions.^37,38 To exclude the possibility that 1 is simply alkene polymers resulting from self-reaction of NHC dimers,³¹ the control reaction without (PPh₄)₂(Fe₄S₄Cl₄) was conducted. This synthesis afforded crystalline red powder and a FT-IR spectrum that does not match with that of 1, indicating 1 does not contain the self-reacted Me–NHC dimer (Fig. S7 and S8†).

Fig. 2 Structural characterizations on 1. (a) FT-IR spectra of 1 (red) and Me–BBI–I (black) under N₂. (b) SEM-EDX mapping images of 1 for Fe (blue) and S (green). (c) PDF profiles of 1 and the simulated profile from the model structure. The intra-cluster atom–atom correlations, (i) directly bonding Fe–S, (ii) Fe–Fe, and (iii) diagonal Fe–S, are displayed, respectively.

Scanning electron microscopy with energy dispersive X-ray spectroscopy (SEM-EDX) was carried out to confirm the distribution of Fe and S (Fig. 2b). While the particle size and morphology were not uniform, as consistent with a polymeric material, the EDX mapping showed a homogeneous distribution of Fe and S in 1. This analysis produced an experimental Fe : S ratio of 1 : 0.7, in comparison to the theoretical ratio of 1 : 1. We ascribe this deviation is due to the extreme moisture sensitivity of 1. Specifically, we expect that upon air exposure to perform SEM-EDX analysis, the [Fe₄S₄] cluster partially hydrolysed to produce H₂S³⁹ and the high-vacuum conditions induced sulfur vacancy formation at the particle surfaces.

Pair distribution function (PDF) analysis was performed on 1 using synchrotron total X-ray scattering data (λ = 0.2115 Å, Fig. S9†) to identify the structural periodicity of 1. PDF analysis is a powerful tool for retrieving atom–atom correlation without being restricted to crystalline materials.⁴⁰ Interestingly, Bragg peaks were observed when using synchrotron radiation (Fig. S9†). The signal-to-noise, however, was still too low for reporting a definitive Rietveld refinement. Nevertheless, PDF analysis could be performed with these data. The cuboidal [Fe₄S₄] cluster features three intra-cluster atomic correlations: directly bound Fe–S, Fe–Fe, and diagonal Fe–S vectors (Fig. 2c). The discrete model [Fe₄S₄Cl₂(monotopic Me–NHC)₂] was employed to simulate the intra-cluster correlations in the [Fe₄S₄] (Fig. S10†). The simulated PDF profile shows directly bound Fe–S, Fe–Fe, and diagonal Fe–S at 2.28, 2.75, and 3.89 Å, respectively (Fig. 2c). The partial PDF fractions of the correlation between Fe–S, Fe–Fe, Fe–Cl, Fe–C, S–S, and C–C were also simulated (Fig. S11†). The PDF profile of 1 displayed peaks at 2.27, 2.69, and 3.91 Å, showing good agreement with the simulated model. The observed atom–atom correlations of [Fe₄S₄] also are in a reasonable range of the [Fe₄S₄] correlations reported in the Cambridge Crystallographic Data Centre (CCDC) database: (i) Fe–S: 2.270–2.335 Å, (ii) Fe–Fe: 2.673–2.766 Å, and (iii) diagonal Fe–S: 3.878–3.935 Å (Table S2†). The simulated PDF profiles of inorganic iron sulfides such as FeS, Fe₂S₃, and Fe₄S₃ do not match with that of 1, which excludes the formation of amorphous iron sulfide in 1 (Fig. S12†). The PDF results therefore confirm that 1 preserves the [Fe₄S₄] cluster.

Electronic properties

To probe the opto-electronic nature of 1, we collected its diffuse reflectance (DR) UV-vis-near infrared (NIR) spectrum under N₂ (Fig. 3a). Notably, the absorption features of 1 extend into the NIR range, which is commonly observed in highly conjugated metal–organic and organic conductive polymers.⁴¹ The solution-state UV-vis-NIR spectrum of (PPh₄)₂(Fe₄S₄Cl₄) in DMF was collected for comparison. We assign the absorption bands of (PPh₄)₂(Fe₄S₄Cl₄) according to the literature as follows: 500 nm: ligand-to-metal charge transfer (LMCT) from S to Fe and 700 nm: LMCT from Cl to Fe.⁴² The broad features of 1 at 600–640 and 808 nm are assigned as LMCT (S to Fe) and (Cl to Fe), respectively. The red-shift is ascribed to the replacement of the electron-withdrawing Cl⁻ to the strong σ donating Me–NHC. The optical band gap (E_g) of 1 was calculated as 0.5 eV by the Tauc plot of DR UV-vis-NIR spectrum (Fig. 3a).⁴³ This small E_g is comparable to those of the other highly conjugated and conductive metal–organic materials.¹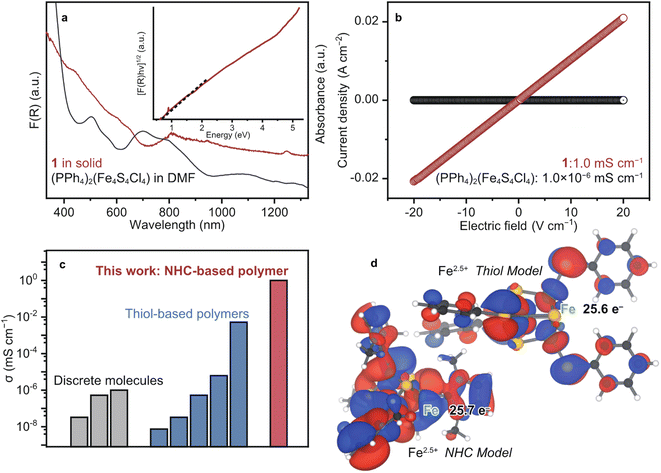

Fig. 3 Electronic properties of 1. (a) DR and solution-state UV-vis spectra of 1 (red) and (PPh₄)₂(Fe₄S₄Cl₄) in DMF (black). Inset: Tauc plot of 1. (b) LSV profiles of 1 (red) and (PPh₄)₂(Fe₄S₄Cl₄) (black) under N₂ at 25 °C. (c) Plots of the electronic conductivity for [Fe₄S₄]-based materials and molecules. The conductivity was obtained by the pressed-pellet two-probe methods at 25 °C.⁸ (d) Calculated SOMOs of the NHC (left) and thiol (right) model structures displayed at isosurface values of 0.02 and 0.05 respectively.

Solid-state cyclic voltammetry (CV) was carried out to understand the redox behavior of 1 by drop-casting a DMF suspension onto a glassy carbon electrode. An irreversible reduction peak was observed at −1.4 V vs. FeCp₂^+/0 (0.1 M [Li][PF₆], acetonitrile, Fig. S13†), which we assign to the [Fe₄S₄]^2+/+ redox couple based on similar features observed for the one-electron reduction of [Fe₄S₄]²⁺-based molecules and materials: (PPh₄)₂(Fe₄S₄Cl₄), Fe₄S₄–Sn₂S₆, and TMA₂(Fe₄S₄)(BDT)₂ display irreversible reduction waves at −1.3, −1.3, and −1.6 V vs. FeCp₂^+/0, respectively. The negative shift of 1 by −0.1 V from (PPh₄)₂(Fe₄S₄Cl₄) is reasonable as the Me–NHC possesses a greater electron-donating ability than Cl⁻.⁴⁴ We ascribe the irreversible reduction to the strong interaction between the [Fe₄S₄] cluster and incorporated Li⁺ ions or instability of 1 upon reduction.

To evaluate the electronic conductivity σ of 1, linear sweep voltammetry was carried out using a two-contact probe, pressed-pellet method at 25 °C under N₂. The current–voltage profile of 1 showed a linear behaviour in accordance with Ohm's law. Accordingly, σ of 1 was calculated to be 1.0 mS cm⁻¹ (Fig. 3b), which is higher than the σ of discrete [Fe₄S₄] complexes and [Fe₄S₄]–dithiol CP/MOFs by more than three orders of magnitude (Fig. 3c and Table S1†). The discrete [Fe₄S₄] complexes are electrically insulating due to the suppressed electron conduction between clusters by bulky counter ions (10⁻⁸ to 10⁻⁶ mS cm⁻¹, Fig. 3b and S14†), whereas the conductivity of [Fe₄S₄]–thiol CP/MOFs ranges between 10⁻⁶ and 10⁻³ mS cm⁻¹ depending on the counter cations and oxidation state of [Fe₄S₄] clusters.⁸ Therefore, we expect that the covalency of chemical bonds bridging [Fe₄S₄] clusters dictates electron conduction.

To characterize the chemical bonding of 1 and [Fe₄S₄]–thiol CP/MOFs, density functional theory (DFT) calculations were performed on model cubane clusters (Fig. 3d). Given the π-accepting nature of NHC ligands, as with CO, the frontier orbitals are expected to display Fe–C π bonding character. For the thiol-based cluster, however, we expect purely antibonding orbitals between Fe and S due to the π donating nature of thiolates as ligands. Indeed, the model cluster bearing NHC ligands has three near-degenerate frontier orbitals, which can be justified by the tetrahedral symmetry of the cluster. Examining all three of these frontier orbitals together (Fig. S15†) shows significant overlap between the cubane iron orbitals and the ligand carbon orbitals. In contrast, the model cluster with benzenethiolate ligands has a single frontier orbital with planar nodes between the cubane iron orbitals and the ligand sulfur orbitals, indicating less covalency in this cluster than in the NHC cluster. Mulliken analysis indicates a larger electron density on Fe in the case of the NHC cluster, reflecting the shorter and more electron-rich bonding. This analysis further supports the hypothesis of decreased covalency in the thiolate cluster.

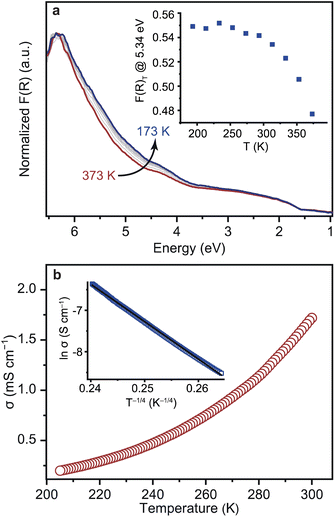
Variable-temperature (VT) DR-UV-vis spectra were collected on 1 in the temperature range of 173 to 373 K under vacuum (Fig. 4a). Carboxylate-based CP/MOFs, e.g. MUV-10, typically exhibit a large temperature dependence in their UV-vis spectra and E_g values due to dynamic metal-linker bonding.^45,46 On the other hand, the VT UV-vis spectra of 1 displayed only a slight increase in the intensities upon cooling and the change in the E_g was almost negligible. Plotting a difference curve δF(R)_T = F(R)_T − F(R)₃₇₃ indicates that the intensities between 3.5 and 6.2 eV (200–350 nm) increase at the peak maximum of 5.34 eV (232 nm, Fig. S16†) and level off at 250 K (Fig. 4a). Such absorption features typically originate from π–π* transitions of aromatic molecules. Accordingly, we assign them to the NHC linker rather than [Fe₄S₄] clusters in 1. The enhancement of the intensities likely arises from suppression of intra-molecular, local dynamics of Me–NHC, e.g. rotation and flipping, at the lower temperatures.^47,48 The structural rigidity of 1 toward temperature was also confirmed by the VT diffuse-reflectance infrared spectroscopy (DRIFTS) in the temperature range of 173 to 373 K (Fig. S17†). The shift of the peak at 1260 cm⁻¹, which corresponds to the C–N stretching mode of Me–NHC was almost negligible <1.0 × 10⁻² cm⁻¹ K⁻¹. The smaller temperature dependence of 1 reflects the rigid nature of Fe–C bonding dynamics in comparison with the typical M–O bonding in the carboxylate–CP/MOFs, and is consistent with the high stability constants measured for metal–NHC bonds.⁴⁹

Fig. 4 Temperature-dependent electronic response of 1. (a) VT DR-UV-vis of 1 under vacuum. Inset: the plot of the intensities at 232 nm as a function of temperature. (b) VT electrical conductivity of 1 by four-contact probe, pressed-pellet method. Inset: fitting of the data to the Mott 3D VRH model.

VT conductivity measurements of 1 using a four-contact probe method indicated thermally activated electronic conduction in the temperature range of 205–300 K (Fig. 4b and S18†). Charge transport in disordered conductive solids is typically characterized by a Mott viable-range hopping (VRH) model.^50,51 VRH model is expressed as follows: σ = σ₀ exp[−(T₀/T)^1/(d+1)], where T₀ is the material-specific Mott temperature and d is the dimensionality of carrier transport. The VT conductivity of 1 was satisfactorily fitted with the 3D VRH model (R² = 0.9993, Fig. 4b). The results indicate an electron transport mechanism in 1 consistent with 3D hopping. Fitting of the data to the Arrhenius equation, σ = σ₀ exp(−E_a/k_BT), where σ₀ is the pre-exponential factor, E_a is the Arrhenius activation energy, k_B is the Boltzmann constant, and T is the temperature, revealed an E_a value of 0.12 eV (Fig. S19†). The E_a value of 1 is small compared to other conductive CP/MOFs with similar conductivities of 10⁻¹ to 10 mS cm⁻¹ (0.18–0.44 eV, Table S3†). E_a represents the energy barrier that electrons overcome when they hop between sites.⁵² While grain boundaries between particles increase E_a, the small E_a of 1 indicates an especially low-energy electron transport pathway enabled by charge-delocalized Fe–C bonds.

Conclusions

We demonstrate the synthesis of a highly electronically conductive [Fe₄S₄]-based organometallic polymer, [Fe₄S₄Cl₂(Me–NHC)] (1). Bridging the [Fe₄S₄] clusters by the ditopic Me–NHC linkers with charge-delocalized Fe–C bonds leads to a high electrical conductivity of 1.0 mS cm⁻¹ at 25 °C. The variable-temperature spectroscopies and conductivity experiments reveal that rigid Fe–C bonds resulted in the small temperature response in the electronic properties, namely the band gap and electrical conductivity. The results provide synthetic guidelines for the design of electronically conductive hybrid materials based upon new classes of molecular building units.

Author contributions

K. K. performed data collection and analysis, designed experiments, and prepared the manuscript, T. C. performed VT conductivity experiments, M. D. guided analysis of VT measurements. E. G. and C. H. performed DFT calculations and assisted manuscript preparation, C. K. B. oversaw data analysis, experimental design, manuscript preparation, and initial project conception.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by the Department of Energy through the Office of Basic Energy Sciences under grant DE-SC0022147 and by the National Science Foundation through the Division of Materials Research under grant no. DMR-2114430. C. K. B. and C. H. H. acknowledges the Research Corporation for Science Advancement (Cottrell Award). K. K. acknowledges the Japan Society for the Promotion of Science (JSPS) for an Overseas Research Fellowship (application number 202160772). This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02-06CH11357. The mail-in program at beamline 11-ID-B contributed to the data. This work made use of the CAMCOR facility of the Lorry I. Lokey Laboratories at the University of Oregon.

References

1. L. S. Xie, G. Skorupskii and M. Dinca, Chem. Rev., 2020, 120, 8536–8580.
2. J. Xie, L. Wang and J. S. Anderson, Chem. Sci., 2020, 11, 8350–8372.
3. E. M. Johnson, S. Ilic and A. J. Morris, ACS Cent. Sci., 2021, 7, 445–453.
4. D. Sheberla, J. C. Bachman, J. S. Elias, C. J. Sun, Y. Shao-Horn and M. Dinca, Nat. Mater., 2017, 16, 220–224.
5. K. W. Nam, S. S. Park, R. Dos Reis, V. P. Dravid, H. Kim, C. A. Mirkin and J. F. Stoddart, Nat. Commun., 2019, 10, 4948.
6. E. M. Miner, S. Gul, N. D. Ricke, E. Pastor, J. Yano, V. K. Yachandra, T. Van Voorhis and M. Dincă, ACS Catal., 2017, 7, 7726–7731.
7. Z. Meng, J. Luo, W. Li and K. A. Mirica, J. Am. Chem. Soc., 2020, 142, 21656–21669.
8. N. E. Horwitz, J. Xie, A. S. Filatov, R. J. Papoular, W. E. Shepard, D. Z. Zee, M. P. Grahn, C. Gilder and J. S. Anderson, J. Am. Chem. Soc., 2019, 141, 3940–3951.
9. I. Stassen, J. H. Dou, C. Hendon and M. Dinca, ACS Cent. Sci., 2019, 5, 1425–1431.
10. A. J. Clough, N. M. Orchanian, J. M. Skelton, A. J. Neer, S. A. Howard, C. A. Downes, L. F. J. Piper, A. Walsh, B. C. Melot and S. C. Marinescu, J. Am. Chem. Soc., 2019, 141, 16323–16330.
11. L. E. Darago, M. L. Aubrey, C. J. Yu, M. I. Gonzalez and J. R. Long, J. Am. Chem. Soc., 2015, 137, 15703–15711.
12. T. Kambe, R. Sakamoto, T. Kusamoto, T. Pal, N. Fukui, K. Hoshiko, T. Shimojima, Z. Wang, T. Hirahara, K. Ishizaka, S. Hasegawa, F. Liu and H. Nishihara, J. Am. Chem. Soc., 2014, 136, 14357–14360.
13. M. J. Kalmutzki, N. Hanikel and O. M. Yaghi, Sci. Adv., 2018, 4, eaat9180.
14. Z. Ji, C. Trickett, X. Pei and O. M. Yaghi, J. Am. Chem. Soc., 2018, 140, 13618–13622.
15. M. M. Roessler, M. S. King, A. J. Robinson, F. A. Armstrong, J. Harmer and J. Hirst, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1930–1935.
16. P. Hinchliffe and L. A. Sazanov, Science, 2005, 309, 771–774.
17. B. V. DePamphilis, B. A. Averill, T. Herskovitz, L. Que and R. H. Holm, J. Am. Chem. Soc., 1974, 96, 4159–4167.
18. C. Goh, B. M. Segal, J. Huang, J. R. Long and R. H. Holm, J. Am. Chem. Soc., 1996, 118, 11844–11853.
19. L. Deng and R. H. Holm, J. Am. Chem. Soc., 2008, 130, 9878–9886.
20. M. Ye, N. B. Thompson, A. C. Brown and D. L. M. Suess, J. Am. Chem. Soc., 2019, 141, 13330–13335.
21. O. Salinas, J. Xie, R. J. Papoular, N. E. Horwitz, E. Elkaim, A. S. Filatov and J. S. Anderson, Dalton Trans., 2021, 50, 10798–10805.
22. C. A. Smith, M. R. Narouz, P. A. Lummis, I. Singh, A. Nazemi, C. H. Li and C. M. Crudden, Chem. Rev., 2019, 119, 4986–5056.
23. S. Ibanez, M. Poyatos and E. Peris, Acc. Chem. Res., 2020, 53, 1401–1413.
24. Y. Tanaka, Y. Kato, T. Tada, S. Fujii, M. Kiguchi and M. Akita, J. Am. Chem. Soc., 2018, 140, 10080–10084.
25. K. A. Williams, A. J. Boydston and C. W. Bielawski, J. R. Soc., Interface, 2007, 4, 359–362.
26. J. F. Longevial, M. Lo, A. Lebrun, D. Laurencin, S. Clement and S. Richeter, Dalton Trans., 2020, 49, 7005–7014.
27. J. H. Gillen, C. A. Moore, M. Vuong, J. Shajahan, M. R. Anstey, J. R. Alston and C. M. Bejger, Chem. Commun., 2022, 58, 4885–4888.
28. L. Sun, C. H. Hendon, S. S. Park, Y. Tulchinsky, R. Wan, F. Wang, A. Walsh and M. Dincă, Chem. Sci., 2017, 8, 4450–4457.
29. J. McKenzie, K. N. Le, D. J. Bardgett, K. A. Collins, T. Ericson, M. K. Wojnar, J. Chouinard, S. Golledge, A. F. Cozzolino, D. C. Johnson, C. H. Hendon and C. K. Brozek, Chem. Mater., 2022, 34, 1905–1920.
30. D. G. Gusev and E. Peris, Dalton Trans., 2013, 42, 7359–7364.
31. J. W. Kamplain and C. W. Bielawski, Chem. Commun., 2006, 1727–1729,  10.1039/b518246h.
32. Z. Guo, N. R. Song, J. H. Moon, M. Kim, E. J. Jun, J. Choi, J. Y. Lee, C. W. Bielawski, J. L. Sessler and J. Yoon, J. Am. Chem. Soc., 2012, 134, 17846–17849.
33. B. D. Yuhas, A. L. Smeigh, A. P. Samuel, Y. Shim, S. Bag, A. P. Douvalis, M. R. Wasielewski and M. G. Kanatzidis, J. Am. Chem. Soc., 2011, 133, 7252–7255.
34. J. Ha, M. Jeon, J. Park, J. Kim and H. R. Moon, Nanoscale Adv., 2023, 5, 2111–2117.
35. U. Stoeck, G. Nickerl, U. Burkhardt, I. Senkovska and S. Kaskel, J. Am. Chem. Soc., 2012, 134, 17335–17337.
36. S. Gonell, M. Poyatos and E. Peris, Chem.–Eur. J., 2014, 20, 5746–5751.
37. M. A. Iqbal, R. A. Haque, S. F. Nasri, A. M. S. A. Majid, M. B. K. Ahamed, E. Farsi and T. Fatima, Chem. Cent. J., 2013, 7, 27.
38. M. A. Iqbal, R. A. Haque, S. Budagumpi, M. B. K. Ahamed and A. M. S. A. Majid, Inorg. Chem. Commun., 2013, 28, 64–69.
39. C. T. Tran and E. Kim, Inorg. Chem., 2012, 51, 10086–10088.
40. C. Castillo-Blas, J. M. Moreno, I. Romero-Muniz and A. E. Platero-Prats, Nanoscale, 2020, 12, 15577–15587.
41. B. Dhara, S. S. Nagarkar, J. Kumar, V. Kumar, P. K. Jha, S. K. Ghosh, S. Nair and N. Ballav, J. Phys. Chem. Lett., 2016, 7, 2945–2950.
42. A. O. Schuren, V. K. Gramm, M. Durr, A. Foi, I. Ivanovic-Burmazovic, F. Doctorovich, U. Ruschewitz and A. Klein, Dalton Trans., 2016, 45, 361–375.
43. K. Fabrizio, K. N. Le, A. B. Andreeva, C. H. Hendon and C. K. Brozek, ACS Mater. Lett., 2022, 4, 457–463.
44. Y. Ohki, K. Tanifuji, N. Yamada, M. Imada, T. Tajima and K. Tatsumi, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12635–12640.
45. K. Fabrizio, K. A. Lazarou, L. I. Payne, L. P. Twight, S. Golledge, C. H. Hendon and C. K. Brozek, J. Am. Chem. Soc., 2021, 143, 12609–12621.
46. K. Fabrizio and C. K. Brozek, Nano Lett., 2023, 23, 925–930.
47. A. Pietropaolo, C. Cozza, Z. Zhang and T. Nakano, Liq. Cryst., 2018, 45, 2048–2053.
48. W. Zhang, T. Fei, T. Cheng, C. Zheng, Y. Dong, J.-Y. Yang and L. Liu, Opt. Mater. Express, 2021, 11, 895.
49. A. K. d. K. Lewis, S. Caddick, F. G. N. Cloke, N. C. Billingham, P. B. Hitchcock and J. Leonard, J. Am. Chem. Soc., 2003, 125, 10066–10073.
50. J. Xie, S. Ewing, J. N. Boyn, A. S. Filatov, B. Cheng, T. Ma, G. L. Grocke, N. Zhao, R. Itani, X. Sun, H. Cho, Z. Chen, K. W. Chapman, S. N. Patel, D. V. Talapin, J. Park, D. A. Mazziotti and J. S. Anderson, Nature, 2022, 611, 479–484.
51. Q. Yi, X. Dai, J. Zhao, Y. Sun, Y. Lou, X. Su, Q. Li, B. Sun, H. Zheng, M. Shen, Q. Wang and G. Zou, Nanoscale, 2013, 5, 6923–6927.
52. Y. Jiang, I. Oh, S. H. Joo, O. Buyukcakir, X. Chen, S. H. Lee, M. Huang, W. K. Seong, S. K. Kwak, J. W. Yoo and R. S. Ruoff, J. Am. Chem. Soc., 2019, 141, 16884–16893.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02195e

‡ Current address: Institute for Integrated Cell-Material Sciences, Institute for Advanced Study, Kyoto University, Kyoto 606-8501, Japan.

---