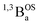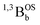Open Access Article
Open Access ArticleVariation from closed-shell to open shell electronic structures in oligothiophene bis(dioxolene) complexes†
Paul D.
Miller
a,
David A.
Shultz
 *a,
Joshua
Mengell
*a,
Joshua
Mengell
 b,
Martin L.
Kirk
b,
Martin L.
Kirk
 *bcd and
Lukasz
Wojtas
e
*bcd and
Lukasz
Wojtas
e
aDepartment of Chemistry, North Carolina State University, Raleigh, North Carolina 27695-8204, USA. E-mail: shultz@ncsu.edu
bDepartment of Chemistry and Chemical Biology, The University of New Mexico, MSC03 2060, 1 University of New Mexico, Albuquerque, NM 87131-0001, USA. E-mail: mkirk@unm.edu
cThe Center for High Technology Materials, The University of New Mexico, Albuquerque, New Mexico 87106, USA
dCenter for Quantum Information and Control (CQuIC), The University of New Mexico, Albuquerque, New Mexico 87131-0001, USA
eDepartment of Chemistry, University of South Florida, 4202 E. Fowler Avenue, CHE 205, Tampa, FL 33620-5250, USA
First published on 9th October 2023
Abstract
A series of oligothiophene bis(dioxolene) complexes, SQ–Thn–SQ (SQ = S = ½TpCum,MeZnII(3-tert-butyl-orthosemiquinonate); TpCum,Me = tris(5-cumenyl-3-methylpyrazolyl)borate anion) have been synthesized, structurally characterized, and studied as a function of the number of thiophene bridging units, n (n = 0–3) using a combination of variable–temperature (VT) electronic absorption and EPR spectroscopies, and VT magnetic susceptibility measurements. The thiophene bridge bond lengths determined by X-ray crystallography display dramatic differences across the SQ–Thn–SQ series. Bridge bond deviation values (Σ|Δi|) display a progressive change in the nature of the bridge fragment bonding as the number of thiophene groups increases, with quinoidal bridge character for n = 1 (SQ–Th–SQ) and biradical character with “aromatic” bridge bond lengths for n = 3 (SQ–Th3–SQ). Remarkably, for n = 2 (SQ–Th2–SQ) the nature of the bridge fragment is intermediate between quinoid and biradical aromatic, which we describe as having open-shell character as opposed to biradicaloid since the open-shell biradical configuration does not have the correct symmetry to mix with the quinoidal ground-state configuration. This bridge bonding character is reflected in the energies of the lowest lying open-shell states for these three molecules. The SQ–Th–SQ molecule is diamagnetic at all temperatures studied, and we provide evidence for SQ–SQ antiferromagnetic exchange coupling and population of triplet states in SQ–Th2–SQ and SQ–Th3–SQ, with JSQ–SQ(ave) = −279 cm−1 (VT EPR/electronic absorption/magnetic susceptibility) and JSQ–SQ = −117 cm−1 (VT EPR/electronic absorption/magnetic susceptibility), respectively. The results have been interpreted in the context of state configurational mixing within a simplified 4-electron, 3-orbital model that explicitly contains contributions of a bridge fragment. Variable–temperature spectroscopic- and magnetic susceptibility data are consistent with two low-lying open-shell states for SQ–Th3–SQ, but three low-lying states (one closed-shell and two open-shell) for SQ–Th2–SQ. This model provides a simple symmetry-based framework to understand the continuum of electronic and geometric structures of this class of molecules as a function of the number of thiophene units in the bridge.
Introduction
Conjugated π-systems that possess biradical character1–6 hold tremendous promise as novel architectures for molecular and molecule-based materials due to their remarkable magnetic, optical, and electronic properties. As a result, these π-conjugated biradical systems are expected to contribute to the organic semiconductor,7–9 singlet fission,1 break junction,10 spintronics,11,12 non-linear optical, and exchange-coupled electron spin qubit13–17 knowledge base and function as models for understanding the effects of dipolar coupling and molecular vibrations on spin relaxation.18 It has recently been shown that the introduction of biradicaloid character into the bridge fragment in break-junction molecular conductance studies dramatically modifies the distance dependence of the conductance,10,19,20 leading to reversed conductance decay behavior where an increase in conductance with increasing molecular wire length is observed.10,20 One-dimensional molecular wires typically display an exponential distance dependence on conductance in the coherent tunneling regime.21–24 This biradicaloid conductance study20 is important since, in the context of the Su, Schrieffer and Heeger model,25,26 biradical species have 1-D topological insulator properties. Namely, they possess occupied and unoccupied delocalized states and localized topologically protected conducting edge states in the bandgap region.Along with Chichibabin's hydrocarbon derivatives and analogs,1,27–30 phenoxy radicals are the most common organic radical employed in the construction of conjugated π-systems with biradicaloid character, and their magnetic, optical, and vibrational properties have been extensively studied (Fig. 1A).1,3,4,31–36 These compounds display small HOMO–LUMO gaps, and the large spin density on the para-carbon of 3,6-di-tert-butylphenoxy37 when bonded to thiophene bridge units results in strong through-bond coupled, closed-shell ground states that are NMR-active for bridges comprised of 0–4 thiophene units,38–40 although characteristics of open-shell configurations have been reported for Phen–Th2–Phen.32,34 In contrast to oligothiophene-bridged structures, a single para-phenyl bridge unit results in a closed-shell quinoidal electronic structure,36 but two-41,42 or more para-phenylene bridge units result in thermally-accessible open-shell character. Understanding biradical electronic structure has been complicated due to various experimental issues and the challenging nature of the open-shell computational problem. Here, we present the results of a detailed structural, magnetic, and spectroscopic study on a series of SQ–Thn–SQ (n = 0–3) molecules in order to gain greater insight into the electronic structure of these biradical systems, and discuss the results of these studies in terms of the quinoid, biradical, and biradicaloid character in the electronic ground and excited states of these molecules.
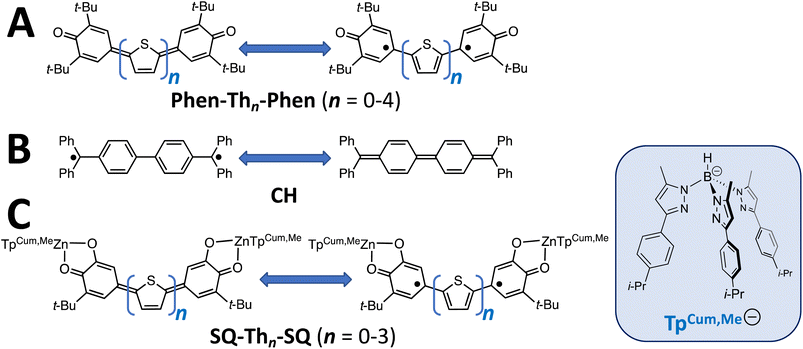 | ||
| Fig. 1 (A) Kekulé π-systems comprised of phenoxy radical-terminated oligothiophenes. (B) Chichibabin's hydrocarbon, CH. (C) Bis(semiquinone) complexes presented in this study. | ||
Biradicaloid systems have consistently been described in terms of two Lewis structures that are in resonance (Fig. 1). These resonance structures are the closed-shell quinoid form and open-shell biradical from, the latter of which derives from a HOMO → LUMO one-electron promotion. This idea leads to the possibility of a continuum of biradicaloid descriptions, with the biradical and quinoid forms at the extrema and “biradicaloid” describing a quantum mechanical admixture (i.e., resonance) of open-shell biradical and quinoid. Additional complexity exists in such systems where the open-shell biradical Lewis structure can distort (e.g., along a torsional coordinate), which leads to non-planar structures. Here, the electronic structures of the low-lying biradical and quinoid states have been described as being in thermal equilibrium with one another, although experimental evidence for this equilibrium has been limited.29
The first biradicaloid was synthesized in 1907 (Chichibabin's hydrocarbon; CH, Fig. 1B)43 and inspired decades of controversy that was described as the “Biradical Paradox”.44,45 The paradox being: solution EPR of CH indicated |J| ≪ |a| (a = isotropic proton hyperfine coupling constant), despite clear evidence that |J| was in fact much larger than |a| due to the diamagnetic character displayed by the compound. Many studies were conducted to explain this phenomenon,44–49 however it wasn't until 1987 that Montgomery, et al.50 conclusively showed through X-ray diffraction that CH contained a quinoidal bond length pattern. Upon obtaining a pure sample of CH, it was actually found to be EPR silent due to the magnitude of |J|, and paramagnetic impurities (dimers,51 or radical quenching through proton abstraction52) were responsible for the conflicting results. However, it is important to note that there are still non-covalent interactions between radicals that can complicate the analysis, and obfuscate the electronic structure description of biradicaloids.45
Metal complexes of S = ½ orthosemiquinone (SQ) are powerful alternatives to phenoxy radical-based molecules since they allow for the inclusion of both diamagnetic and paramagnetic transition metal ions into the molecular scaffold. In addition, the spin density distribution of SQ vs. phenoxy places ∼65% less spin density for SQ at the point of attachment37 to a bridging organic π-system (positions marked with “●” in Fig. 1A and C). Thus, the incorporation of SQ allows for thermal population of the triplet state at lower temperatures compared to phenoxy biradicals. Herein, we present dinuclear metal complexes comprised of two bridge terminal SQ groups, where both SQs are complexed to a diamagnetic (TpCum,MeZnII)+ complex ion (TpCum,Me = tris(5-cumenyl-3-methylpyrazolyl)borate53–55 bridged by 0–3 thiophene groups; Fig. 1C). The TpCum,Me anionic ligand was first used for steric protection of SQ groups by Pierpont,55 and subsequently by us.21,56–61 Our crystallographic results clearly show a decrease in “quinoidal” bond lengths as the number of thiophene bridge fragments increases. This observation is consistent with both variable–temperature magnetic susceptibility results as well as variable–temperature electronic absorption spectroscopic studies, which illustrate thermal population of the exchange coupled triplet state with increasing temperature. In addition, we present molecular orbital (MO) and state models that provide a fundamental symmetry-based framework to understand the continuum of electronic structures in this class of molecules as a function of the number of thiophene units in the bridge.
Results and analysis
Here, we present synthetic results, X-ray crystallographic results, and associated analyses for the SQ–SQ, SQ–Th–SQ, SQ–Th2–SQ, and SQ–Th3–SQ series of compounds. Since their ground state electronic structures span a continuum from closed-shell singlet quinoidal to open-shell singlet biradical, we will present analyses of the magnetic and spectroscopic results together for each compound at the end of this section. Detailed computations and electronic absorption band assignments for SQ–Th–SQ and SQ–Th2–SQ and SQ–Th3–SQ are beyond the scope of this manuscript and will be presented elsewhere.Synthesis and structural data
Synthetic details and structural data are presented in the ESI† and below for all complexes in this study.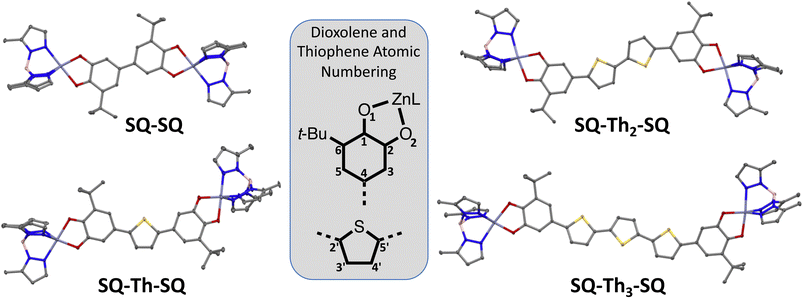 | ||
| Fig. 2 Thermal ellipsoid (50% probability) plots from 100 K crystal structures of SQ2Th, SQ2Th2, and SQ2Th3. Hydrogens and cumenyl groups are omitted for clarity. | ||
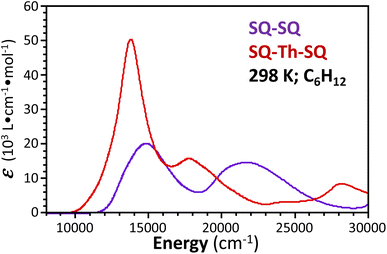
Spectroscopic and magnetic data for SQ–SQ and SQ–Th–SQ
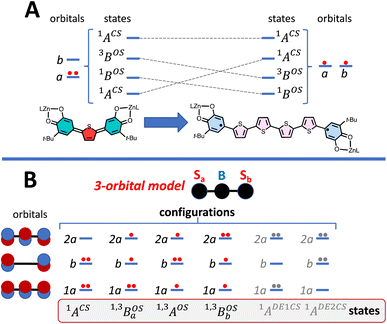
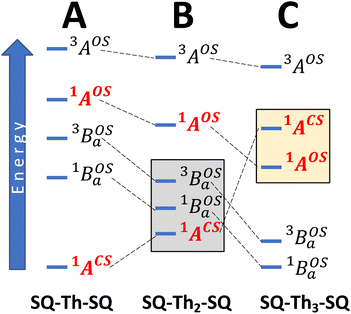
To account for any admixture of open-shell singlet character into the quinoidal 1ACS ground state the model needs to be expanded, and a minimally expanded 3-orbital, 4-electron model, with select configurations, is shown in Fig. 5B. This model includes an effective bridge orbital that provides a mechanism for excited open shell configurations to mix into the quinoidal 1ACS ground state. A partial state energy diagram is given in Fig. 6, which displays many features in common with Tanabe–Sugano diagrams71,72 used to understand the nature of ligand field excitations in transition metal complexes. As one moves from SQ–Th–SQ to SQ–Th3–SQ, the SQ–SQ interaction decreases and closed-shell configurations increase in energy, which drives the system from closed-shell quinoidal to open-shell biradical.
Crystallographically-determined bond deviation parameters and the diamagnetic nature of the complexes for SQ–SQ and SQ–Th–SQ clearly indicate that these molecules possess dominant quinoidal closed-shell S = 0 electronic ground states. As a result, the admixture of open shell configurations (e.g., the 1AOS in Fig. 5) must be quite small.
Spectroscopic and magnetic data for SQ–Th3–SQ
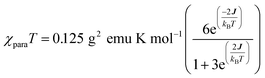 | (1) |
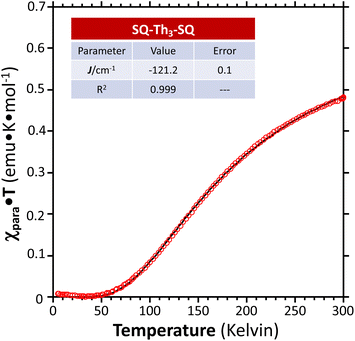
We fit eqn (1) to the data to yield J = −121 cm−1, with a corresponding singlet–triplet energy gap of 2J = ΔE(S − T) = 242 cm−1. The susceptibility data indicate an electronic structure that correlates with the state diagram shown in Fig. 6C, with a 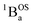 ground state and an exchange coupled
ground state and an exchange coupled 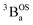 triplet state at higher energy (2J).
triplet state at higher energy (2J).
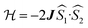 exchange Hamiltonian was used to generate eqn (2).
exchange Hamiltonian was used to generate eqn (2).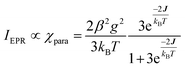 | (2) |
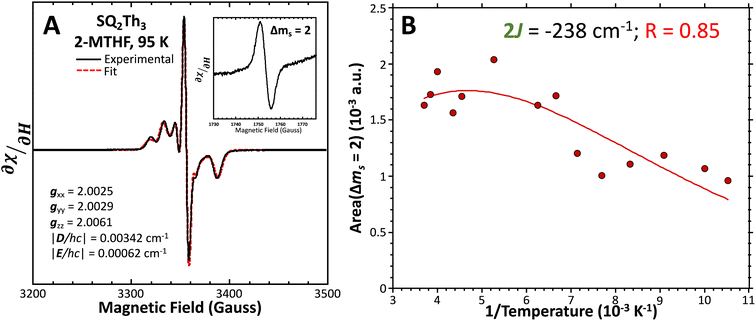 | ||
Fig. 8 (A) Powder EPR spectrum of SQ-Th3-SQ (—) and simulation parameters. (Inset) Δms = 2 transition. Fit ( ) includes 32% S = ½ impurities. For simulation details, see text and ESI.† (B) Doubly-integrated Δms = 2 EPR transition intensities ( ) includes 32% S = ½ impurities. For simulation details, see text and ESI.† (B) Doubly-integrated Δms = 2 EPR transition intensities ( ) vs. inverse temperature and fit ( ) vs. inverse temperature and fit ( ) for SQ-Th3-SQ. See text for fit details. Samples were ∼1 mM dissolved in an evaporated film of poly(vinyl chloride). ) for SQ-Th3-SQ. See text for fit details. Samples were ∼1 mM dissolved in an evaporated film of poly(vinyl chloride). | ||
We fit eqn (2) to the VT EPR data to yield J = −119 cm−1, which is in excellent agreement with the exchange parameter determined from our analysis of the VT magnetic susceptibility data (J = −121 cm−1). Thus, the VT EPR data support the solid-state magnetic susceptibility data, with both data sets being consistent with an aromatic ring-bridged biradical (i.e., open-shell singlet) ground state. This electronic structure determination is also fully consistent with the bond length patterns (Σ|Δi| values for both SQ and Th rings, vide supra) obtained from the X-ray structure of SQ–Th3–SQ.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540, 17
540, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182, and 21
182, and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 cm−1, consistent with only two species contributing to the electronic absorption spectra across the 4–196 K temperature range. Since both the variable–temperature EPR and magnetic susceptibility data indicate J ≈ −120 cm−1, this leads to an S = 0 ground state singlet and a negligible population of the exchange coupled S = 1 triplet state at 4 K (at 4 K; nS=1/nS=0 ∼ 3
150 cm−1, consistent with only two species contributing to the electronic absorption spectra across the 4–196 K temperature range. Since both the variable–temperature EPR and magnetic susceptibility data indicate J ≈ −120 cm−1, this leads to an S = 0 ground state singlet and a negligible population of the exchange coupled S = 1 triplet state at 4 K (at 4 K; nS=1/nS=0 ∼ 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−242/2.78) ∼ 0). Thus, the 4 K spectrum of SQ–Th3–SQ is that of the exchange coupled
exp(−242/2.78) ∼ 0). Thus, the 4 K spectrum of SQ–Th3–SQ is that of the exchange coupled 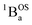 singlet ground state.
singlet ground state.
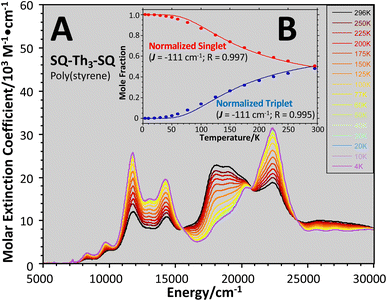
The intensities of the temperature dependent bands at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422 cm−1 and 18
422 cm−1 and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215 cm−1, which we associate with the
215 cm−1, which we associate with the 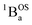 singlet ground- and
singlet ground- and 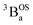 thermally-populated triplet states, respectively, are plotted as a function of temperature in Fig. 9B. A simple 2-state (singlet and triplet) Boltzmann expression was fit to these data to yield a singlet–triplet splitting of 222 cm−1 (J = −111 cm−1). This value of J determined from VT electronic absorption data is in excellent agreement with the exchange coupling parameter for SQ–Th3–SQ that was determined from both magnetic susceptibility (J = −121 cm−1) and variable–temperature EPR spectroscopy (J = −119 cm−1), vide supra. The temperature dependent
thermally-populated triplet states, respectively, are plotted as a function of temperature in Fig. 9B. A simple 2-state (singlet and triplet) Boltzmann expression was fit to these data to yield a singlet–triplet splitting of 222 cm−1 (J = −111 cm−1). This value of J determined from VT electronic absorption data is in excellent agreement with the exchange coupling parameter for SQ–Th3–SQ that was determined from both magnetic susceptibility (J = −121 cm−1) and variable–temperature EPR spectroscopy (J = −119 cm−1), vide supra. The temperature dependent 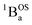 and
and  contributions to the VT electronic absorption spectra of SQ–Th3–SQ have allowed us to extract the pure individual spectra that originate from the
contributions to the VT electronic absorption spectra of SQ–Th3–SQ have allowed us to extract the pure individual spectra that originate from the  and
and  states (Fig. 10), providing additional access to the nature of the excited state manifold.
states (Fig. 10), providing additional access to the nature of the excited state manifold.
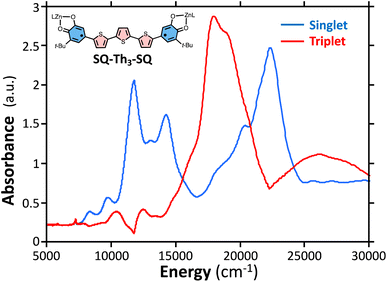 | ||
Fig. 10 Singlet spectrum of SQ–Th3–SQ ( ) collected at 4 K. Triplet spectrum of SQ–Th3–SQ ( ) collected at 4 K. Triplet spectrum of SQ–Th3–SQ ( ) derived from subtracting the weighted 4 K spectrum from the 298 K spectrum. ) derived from subtracting the weighted 4 K spectrum from the 298 K spectrum. | ||
Considering the state description in Fig. 6C, one can have spin-allowed excitations from the open shell aromatic 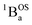 ground state to configurationally mixed excited states (e.g., configurationally mixed 1AOS and1ACS in the 3-orbital model; Fig. 5B) that possess closed-shell quinoidal character. Therefore, the electronic absorption spectrum that originates from the aromatic-bridge biradical
ground state to configurationally mixed excited states (e.g., configurationally mixed 1AOS and1ACS in the 3-orbital model; Fig. 5B) that possess closed-shell quinoidal character. Therefore, the electronic absorption spectrum that originates from the aromatic-bridge biradical 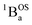 ground state contains transitions to biradicaloid/open-shell singlet excited states. In marked contrast, there are no triplet excited states that possess closed-shell quinoidal character. This is why the spectra that originate from the
ground state contains transitions to biradicaloid/open-shell singlet excited states. In marked contrast, there are no triplet excited states that possess closed-shell quinoidal character. This is why the spectra that originate from the 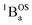 and
and 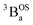 states are very different in their appearance, and strongly suggests considerable mixing between open- and closed-shell excited singlet configuration states. Strong mixing between these singlet excited states can drive one or more of these states below the lowest energy excited triplet state, and this is the likely origin for the dramatic red shift of the singlet spectrum compared to the triplet spectrum (Fig. 10).
states are very different in their appearance, and strongly suggests considerable mixing between open- and closed-shell excited singlet configuration states. Strong mixing between these singlet excited states can drive one or more of these states below the lowest energy excited triplet state, and this is the likely origin for the dramatic red shift of the singlet spectrum compared to the triplet spectrum (Fig. 10).
Spectroscopic and magnetic data for SQ–Th2–SQ
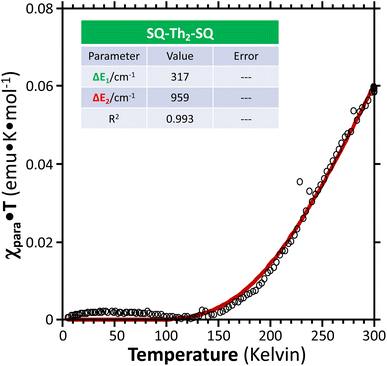 | ||
Fig. 11 Paramagnetic susceptibility-temperature product (χparaT) vs. temperature ( ) for a crystalline sample of SQ–Th2–SQ, measured by variable–temperature magnetic susceptibility experiments at a magnetic field strength of 0.1 Tesla. Data were fit ( ) for a crystalline sample of SQ–Th2–SQ, measured by variable–temperature magnetic susceptibility experiments at a magnetic field strength of 0.1 Tesla. Data were fit ( ) to the same model as the VT EPR and EAS data, see Fig. 6B and text. Regarding the magnitude of the χparaT product in this plot, note that χparaT is equal to 1.0 emu K mol−1 for a pure S = 1 triplet state. ) to the same model as the VT EPR and EAS data, see Fig. 6B and text. Regarding the magnitude of the χparaT product in this plot, note that χparaT is equal to 1.0 emu K mol−1 for a pure S = 1 triplet state. | ||
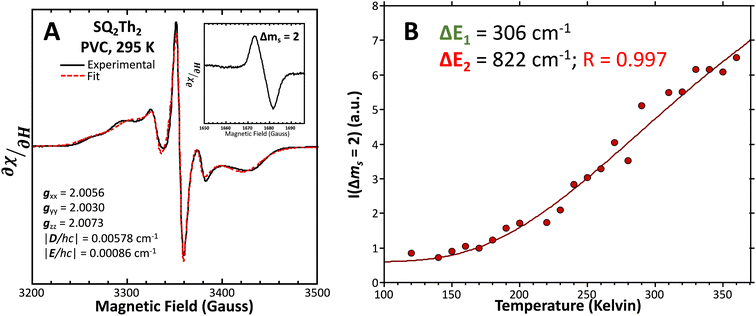 | ||
Fig. 12 (A) Powder EPR spectrum of SQ–Th2–SQ (—, left). Fit ( ) includes 34% S = ½ impurities. For simulation parameters, see text and ESI.† (B) Doubly-integrated Δms = 2 EPR transition intensities ( ) includes 34% S = ½ impurities. For simulation parameters, see text and ESI.† (B) Doubly-integrated Δms = 2 EPR transition intensities ( ) vs. inverse temperature for SQ–Th2–SQ. Samples were ∼1 mM dissolved in an evaporated film of poly(vinyl chloride). Data were fit ( ) vs. inverse temperature for SQ–Th2–SQ. Samples were ∼1 mM dissolved in an evaporated film of poly(vinyl chloride). Data were fit ( ) to a model that includes three lowest energy spin states, see text and Fig. 6B. ) to a model that includes three lowest energy spin states, see text and Fig. 6B. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 that, when compared to the VT behavior of SQ–Th3–SQ, displays a markedly weaker temperature dependence.
300 cm−1 that, when compared to the VT behavior of SQ–Th3–SQ, displays a markedly weaker temperature dependence.
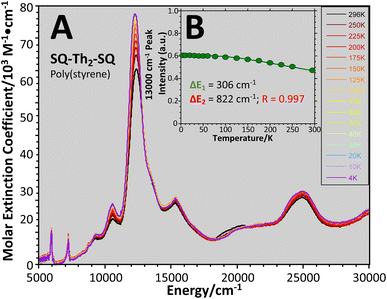 | ||
Fig. 13 (A) Variable–temperature (4–298 K) electronic absorption spectra of SQ–Th2–SQ in a poly(styrene) film. (B) Normalized transition intensity of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 band. Data fit using 3 lowest thermally-populated spin states. See Fig. 6B and text. 000 cm−1 band. Data fit using 3 lowest thermally-populated spin states. See Fig. 6B and text. | ||
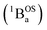 and triplet
and triplet 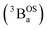 exchange-coupled states that are found at energies ΔE1 and ΔE2, respectively, above the closed-shell ground state. In this model, the energy difference ΔE1 − ΔE2 corresponds to the singlet–triplet splitting (2J) of the open shell biradical states using the exchange Hamiltonian,
exchange-coupled states that are found at energies ΔE1 and ΔE2, respectively, above the closed-shell ground state. In this model, the energy difference ΔE1 − ΔE2 corresponds to the singlet–triplet splitting (2J) of the open shell biradical states using the exchange Hamiltonian, 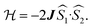 Note that these open-shell singlet
Note that these open-shell singlet 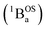 and triplet
and triplet 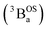 exchange-coupled states were the lowest-lying states in SQ–Th3–SQ, and the closed-shell quinoidal state for SQ–Th2–SQ represents an electronic excited state in SQ–Th3–SQ. We attribute the existence of biradicaloid and aromatic ring-bridged biradical populations to result from a temperature-dependent structural change (increased ring torsion amplitudes, Fig. 14) that leads to greater SQ–Th and Th–Th bond torsions in SQ–Th2–SQ as the temperature is increased. Thus, the potential energy surfaces for the open-shell singlet and triplet are described as being distorted along this torsional coordinate, Qtorsion, relative to the closed shell singlet ground state. Thus, eqn (3) and (4) (C = Nβ2/3kB and D represents monoradical impurity), and 5 (C is a proportionality constant) derived from the 3-state model in Fig. 6B were fit to the VT magnetic susceptibility, EPR, and electronic absorption data, respectively.
exchange-coupled states were the lowest-lying states in SQ–Th3–SQ, and the closed-shell quinoidal state for SQ–Th2–SQ represents an electronic excited state in SQ–Th3–SQ. We attribute the existence of biradicaloid and aromatic ring-bridged biradical populations to result from a temperature-dependent structural change (increased ring torsion amplitudes, Fig. 14) that leads to greater SQ–Th and Th–Th bond torsions in SQ–Th2–SQ as the temperature is increased. Thus, the potential energy surfaces for the open-shell singlet and triplet are described as being distorted along this torsional coordinate, Qtorsion, relative to the closed shell singlet ground state. Thus, eqn (3) and (4) (C = Nβ2/3kB and D represents monoradical impurity), and 5 (C is a proportionality constant) derived from the 3-state model in Fig. 6B were fit to the VT magnetic susceptibility, EPR, and electronic absorption data, respectively.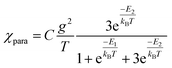 | (3) |
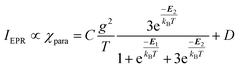 | (4) |
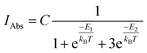 | (5) |
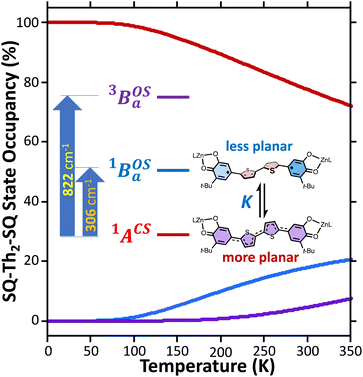
Best fits of eqn (3) to the VT magnetic susceptibility data yield ΔE1 = 317 cm−1 and ΔE2 = 959 cm−1. This results in the open-shell biradical singlet residing only 317 cm−1 above the S = 0 quinoidal ground state, with a biradical singlet–triplet splitting of ΔE1 − ΔE2 = 2J = 642 cm−1 (J = 321 cm−1). In contrast to the VT magnetic susceptibility data, the VT EPR data directly probes the thermally populated open-shell triplet state as a spectroscopic observable. The best fit of eqn (4) to the VT EPR data gives ΔE1 = 306 cm−1 and ΔE2 = 822 cm−1. The ΔE1 = 306 cm−1 quinoid – biradical singlet–singlet gap is in remarkable agreement with that determined from the VT magnetic susceptibility experiments (ΔE1 = 317 cm−1). However, the ΔE1 − ΔE2 = 2J = 516 cm−1 (J = 258 cm−1) determined for the biradical singlet–triplet gap in the solid solution (polymer) phase is reduced by ∼20% compared to that determined by magnetic susceptibility experiments on samples in the polycrystalline state.
Eqn (5) was fit to the VT electronic absorption data, which directly probes the reduction in closed-shell biradicaloid singlet state population with increasing temperature by monitoring the temperature dependence of the ∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 absorption band. The VT absorption data were collected in the solid solution (polymer matrix) phase and the temperature dependence is described with the same ΔE1 and ΔE2 parameters that were determined from the temperature dependence of the Δms = 2 EPR resonance. Thus, VT magnetic susceptibility, EPR, and electronic absorption spectroscopy all yield the same energy gap for populating the biradical singlet state (ΔE1 ave = 310 cm−1). The experimentally determined Boltzmann populations of the three thermally-accessible states for SQ–Th2–SQ are presented graphically in Fig. 14. The biradical character present in the 1ACS ground state must therefore derive from strong configurational mixing with open shell singlet biradical excited state(s), and this is described in the state energy diagram depicted in Fig. 6B (e.g., 1ACS mixing with 1AOS).
300 cm−1 absorption band. The VT absorption data were collected in the solid solution (polymer matrix) phase and the temperature dependence is described with the same ΔE1 and ΔE2 parameters that were determined from the temperature dependence of the Δms = 2 EPR resonance. Thus, VT magnetic susceptibility, EPR, and electronic absorption spectroscopy all yield the same energy gap for populating the biradical singlet state (ΔE1 ave = 310 cm−1). The experimentally determined Boltzmann populations of the three thermally-accessible states for SQ–Th2–SQ are presented graphically in Fig. 14. The biradical character present in the 1ACS ground state must therefore derive from strong configurational mixing with open shell singlet biradical excited state(s), and this is described in the state energy diagram depicted in Fig. 6B (e.g., 1ACS mixing with 1AOS).
In order to address whether the thermally-excited 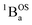 state of SQ–Th2–SQ possesses any appreciable closed-shell singlet character, or whether this state is analogous to the aromatic biradical singlet ground state of SQ–Th3–SQ, we analyzed the distance dependence of the
state of SQ–Th2–SQ possesses any appreciable closed-shell singlet character, or whether this state is analogous to the aromatic biradical singlet ground state of SQ–Th3–SQ, we analyzed the distance dependence of the 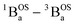 singlet–triplet splitting in SQ–Th2–SQ and SQ–Th3–SQ. We have previously determined the distance decay constant (β = 0.22) for magnetic exchange mediated by aromatic thiophene bridges.21 Since β should be a transferrable property74,75 for evaluating magnetic exchange mediated by these thiophene units, we have used this β value and the JSQ–SQ(ave) = −279 cm−1 for SQ–Th2–SQ, which was the average derived from magnetic susceptibility, VT EPR, and VT electronic absorption spectroscopy, to derive the expected J value for SQ–Th3–SQ. This analysis predicts J ≈ −119 cm−1 for SQ–Th3–SQ, which is in excellent agreement with the experimental Jave = −117 cm−1 that we determined for SQ–Th3–SQ. This analysis provides strong support for the ΔE1 − ΔE2 gap representing the JSQ-SQHeisenberg exchange interaction in both SQ–Th2–SQ and SQ–Th3–SQ, with an openshell biradical ground state configuration for SQ–Th3–SQ, and thermally accessible open-shell triplet biradical states for both SQ–Th2–SQ and SQ–Th3–SQ.
singlet–triplet splitting in SQ–Th2–SQ and SQ–Th3–SQ. We have previously determined the distance decay constant (β = 0.22) for magnetic exchange mediated by aromatic thiophene bridges.21 Since β should be a transferrable property74,75 for evaluating magnetic exchange mediated by these thiophene units, we have used this β value and the JSQ–SQ(ave) = −279 cm−1 for SQ–Th2–SQ, which was the average derived from magnetic susceptibility, VT EPR, and VT electronic absorption spectroscopy, to derive the expected J value for SQ–Th3–SQ. This analysis predicts J ≈ −119 cm−1 for SQ–Th3–SQ, which is in excellent agreement with the experimental Jave = −117 cm−1 that we determined for SQ–Th3–SQ. This analysis provides strong support for the ΔE1 − ΔE2 gap representing the JSQ-SQHeisenberg exchange interaction in both SQ–Th2–SQ and SQ–Th3–SQ, with an openshell biradical ground state configuration for SQ–Th3–SQ, and thermally accessible open-shell triplet biradical states for both SQ–Th2–SQ and SQ–Th3–SQ.
Discussion
Biradicals are distinguished by the presence of singlet and triplet configurations that derive from a HOMO → LUMO one-electron promotion relative to the closed-shell quinoidal ground state. These configurations are described by the quinoid and biradical Lewis structures presented in Fig. 1. For biradicaloids, the ground state open-shell biradical character has been described in terms of a biradical index (yi), which may be computed from natural orbital occupancies that derive from the results of spin unrestricted Hartree–Fock or DFT computations.1 Here, y0 derives from the occupancy of the lowest unoccupied natural orbital, and is often used to describe the degree of biradical character in the electronic ground state.1 Additionally, a valence configuration interaction model, effectively related to the 4-state Anderson model68 that has had a tremendous influence on our understanding of antiferromagnetic exchange in dimeric systems, has been employed to evaluate the degree of biradical character.1,69 This model derives from the asymptotic limit of the H2 molecule (very weak radical–radical coupling with no bridge orbitals) involving two effectively degenerate orbitals and the incorporation of closed-shell ionic configurations. This 2-electron, 2-orbital (4-state) model allows for configurational mixing between closed and open shell singlet configurations with ionic and covalent character. If coupling between the SQ SOMO orbitals (also a 2-electron, 2-orbital model) in actual or effective symmetry is assumed a priori, configurational mixing between closed- and open-shell singlets is symmetry forbidden. Since there are notable examples where an expanded model is required to explain the electronic structure and the nature of the radical–radical exchange interaction in biradical systems,21,57–61,76–80 we have minimally expanded the 2-electron, 2-orbital model to include a doubly-occupied bridge orbital that provides a mechanism for understanding the nature of open-shell singlet states that configurationally mix with quinoidal states.21,57–61,67,77,78With respect to the role of the thiophene bridge units in defining the ground state electronic and geometric structure of the SQ–Thn–SQ series, the explicit consideration and addition of a single bridge-orbital reveals how open-shell and low-energy closed-shell singlet configurations (e.g., 1AOS and 1ACS, respectively; Fig. 5B and 6) can mix to yield “biradicaloid” electronic structures in both ground- (Fig. 6B) and excited (Fig. 6C) states. We note that the nature of these open-shell singlet states generally need not be formal biradical states (analogous to 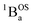 in the 3-orbital model) but could be any open-shell configuration of the proper symmetry to allow for configurational mixing with closed shell-singlet configurations (see Fig. 5 and 6 – e.g.1AOSFig. 5b). As a consequence, the cases presented here show how open-shell/closed-shell 1AOS–1ACS mixing contributes to modifying the degree of quinoidal-aromatic bond patterns in the thiophene bridge fragments. Although this configurational mixing leads to complex ground- and excited state electronic structures in these systems, a key experimental descriptor of the degree of biradical character in the electronic ground states is given by the experimentally derived bond deviation parameters Σ|Δi|,62 which can then be correlated with experimental magnetic and spectroscopic observables. This allows results of electronic structure computations to be evaluated in the context of the experimental data.
in the 3-orbital model) but could be any open-shell configuration of the proper symmetry to allow for configurational mixing with closed shell-singlet configurations (see Fig. 5 and 6 – e.g.1AOSFig. 5b). As a consequence, the cases presented here show how open-shell/closed-shell 1AOS–1ACS mixing contributes to modifying the degree of quinoidal-aromatic bond patterns in the thiophene bridge fragments. Although this configurational mixing leads to complex ground- and excited state electronic structures in these systems, a key experimental descriptor of the degree of biradical character in the electronic ground states is given by the experimentally derived bond deviation parameters Σ|Δi|,62 which can then be correlated with experimental magnetic and spectroscopic observables. This allows results of electronic structure computations to be evaluated in the context of the experimental data.
Regarding the concepts of quinoidal, biradical, and biradicaloid electronic structure descriptions, one needs to consider how these are defined. For example, the quinoidal closed-shell singlet configuration can mix with other closed- or open-shell singlet configurations of the same symmetry. One of these open-shell configurations is associated with what is described as possessing “biradical” character, where the unpaired electrons are primarily localized on the “radical” moieties of the molecule. Thus, from a Lewis structure approach, we define a true biradicaloid as representing a resonance hybrid comprised of the quinoidal and biradical Lewis structures depicted in Fig. 1. Typically, non-contributing or marginally contributing resonance structures describing the ground state (i.e., the biradical forms of SQ–SQ and SQ–Th–SQ) are thought of as representing high energy configurations. However, this is not necessarily correct. The dioxolene-bridge-dioxolene fragments of SQ–SQ and SQ–Th2–SQ possess C2h symmetry, and the closed-shell quinoid configuration and open-shell biradical configuration are forbidden to mix by symmetry even though they may be very close in energy. This is clearly highlighted for SQ–Th2–SQ, where the quinoid and biradical singlet configurations are within kBT of one another but possess different symmetries and do not mix. For these molecules, the biradicaloid character admixed into the ground-state configuration is best described as open-shell singlet character, since there is no resonance between the two Lewis structures drawn in Fig. 1. We therefore describe a ground-state electronic structure description of SQ–Th2–SQ as being quinoidal, with open-shell singlet character.
The low-energy thermally populated excited states are biradical in nature and possess SQ–SQ radical–radical Heisenberg exchange coupling interactions. The thermally accessible biradical states in SQ–Th2–SQ and SQ–Th3–SQ possess experimentally determined J values that are consistent with previously determined distance decay parameters (β values) for aromatic SQ bridge configurations.21 These low-energy open-shell states possess non-planar geometries. We suggest that this symmetry lowering derives from a two-stage pseudo Jahn–Teller effect,81 which involves vibronic coupling with specific excited states to electronically drive out-of-plane ring–ring distortions.
The SQ–Thn–SQ (n = 0–3) molecules presented in this study provide clear examples of dominantly closed-shell quinoidal (SQ–Thn–SQ; n = 0, 1) and open-shell biradical (SQ–Th3–SQ) ground states. The SQ–Th2–SQ complex is unique in this series, possessing some open-shell singlet character as evidenced by the experimentally-determined bridge bond deviation values (Σ|Δi|).62 Although the open shell biradical state of SQ–Th2–SQ is a mere 310 cm−1 above the quinoidal ground state, these states do not configurationally mix due to symmetry constraints. This thermally excited biradical state in SQ–Th2–SQ becomes the ground state in SQ–Th3–SQ (see Fig. 6). Additional evidence for admixed open- and closed-shell character in the ground state of SQ–Th2–SQ is found in the excited states of SQ–Th3–SQ, as revealed by the dramatic differences in spin-allowed 1GS → 1ES (ES = excited state configuration) and 3GS → 3ES transitions (e.g. the 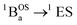 and
and  transitions in Fig. 10). This mixing of open- and closed-shell excited states naturally derives from our 3-orbital, 4-electron model that indicates the importance of bridge states in the description of closed-shell quinoidal, open-shell biradical, and admixed singlet biradical character in the ground and excited states of these molecules. Our study reveals of the power of using a combined synthetic, spectroscopic, and magnetic approach to unravel the complex nature of these and related molecules.
transitions in Fig. 10). This mixing of open- and closed-shell excited states naturally derives from our 3-orbital, 4-electron model that indicates the importance of bridge states in the description of closed-shell quinoidal, open-shell biradical, and admixed singlet biradical character in the ground and excited states of these molecules. Our study reveals of the power of using a combined synthetic, spectroscopic, and magnetic approach to unravel the complex nature of these and related molecules.
Conclusions
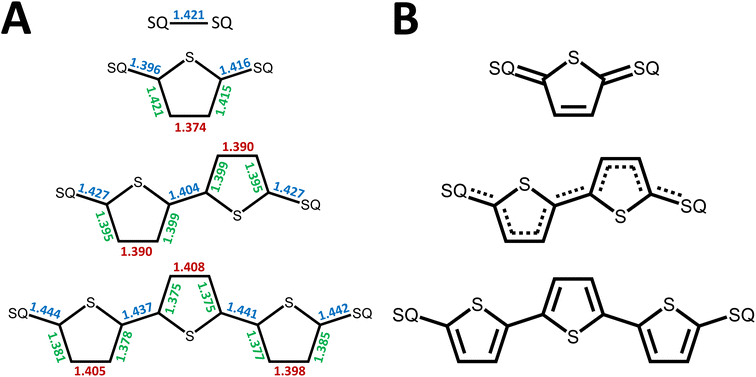
In summary, the degree of closed shell quinoidal and open-shell aromatic character in the electronic ground state and thermally accessible excited states of SQ–Th–SQ, SQ–Th2–SQ, and SQ–Th3–SQ are markedly different. The expanded 3-orbital model discussed in this work has provided insight into the nature of the closed-shell ground state singlet in SQ–Th–SQ, an open-shell singlet for SQ–Th3–SQ, and a configurationally mixed singlet ground state for SQ–Th2–SQ, which possesses some open-shell character. The pattern of bridge bond lengths shown in Fig. 3 is consistent with the predictions enabled by this model, and reveals the alternation of short- and long C–C bonds characteristic of quinoidal resonance structures being most prominent for SQ–Th–SQ and least prominent for SQ–Th3–SQ. In addition, the dioxolene bond deviation parameters62 (Σ|Δi|) clearly decrease from SQ–Th–SQ to SQ–Th3–SQ, and this indicates maximal quinoidal character for SQ–Th–SQ. The results of our structural analyses are consistent with EPR, electronic absorption spectroscopy, and magnetic susceptibility studies for all of these complexes.A primary strength of our approach to the biradicaloid problem lies in the simplicity of using symmetry/group theory to understand state mixing, and this is further exemplified by our use of a conceptually approachable, minimal basis 4-electron-, 3-orbital model that includes the bridge moiety. Thus, the degree of open-shell, closed-shell, and biradical character in the electronic ground state is determined by the molecular symmetry, and is modulated by the nature and of the bridge fragment (e.g., thiophene, phenylene, etc. and the number of bridge units). Doubly-excited states (e.g., 1ADECS; Fig. 5B) and open-shell singlet states with occupied π* and/or vacant π-bonding orbitals can attenuate the quinoidal bond length alternation pattern for closed-shell states if they have the same symmetry as the ground state. However, open-shell 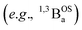 states have non-quinoidal, aromatic bridge units and do not mix with closed-shell singlet states. Importantly, the dioxolene moieties provide attenuated spin density in this series of compounds that allows for exemplars of quinoid, configurationally mixed quinoid/open-shell, and open-shell singlet biradical ground states in the complexes that we have detailed here. We are not aware of any other series of molecules that highlight the complex electronic structures associated with open-shell/closed-shell mixing as a function of the bridge repeat unit. Ongoing studies are focusing on spectral band assignments, correlating open-shell character with bond deviation parameters,62 and understanding how different bridges and metal ions can fine tune the nature of open- and closed-shell configurational mixing in analogs of the SQ–Thn–SQ series.
states have non-quinoidal, aromatic bridge units and do not mix with closed-shell singlet states. Importantly, the dioxolene moieties provide attenuated spin density in this series of compounds that allows for exemplars of quinoid, configurationally mixed quinoid/open-shell, and open-shell singlet biradical ground states in the complexes that we have detailed here. We are not aware of any other series of molecules that highlight the complex electronic structures associated with open-shell/closed-shell mixing as a function of the bridge repeat unit. Ongoing studies are focusing on spectral band assignments, correlating open-shell character with bond deviation parameters,62 and understanding how different bridges and metal ions can fine tune the nature of open- and closed-shell configurational mixing in analogs of the SQ–Thn–SQ series.
Data availability
ESI† contains synthetic- and characterization details of all new molecules and metal complexes.Author contributions
M. L. K. and D. A. S. conceptualized and supervised the project; P. D. M. synthesized and characterized all molecules and complexes; J. M. collected and analyzed variable temperature electronic absorption spectra; P. D. M., D. A. S., and M. L. K. wrote the original manuscript draft.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
D. A. Shultz thanks the National Science Foundation (CHE-1931291 and CHE-1764181) for financial support. M. L. Kirk acknowledges the National Science Foundation (NSF CHE-1900237) for financial support.References
- T. Y. Gopalakrishna, W. Zeng, X. Lu and J. Wu, Chem. Commun., 2018, 54, 2186–2199 RSC
.
- J. J. Dressler, M. Teraoka, G. L. Espejo, R. Kishi, S. Takamuku, C. J. Gomez-Garcia, L. N. Zakharov, M. Nakano, J. Casado and M. M. Haley, Nat. Chem., 2018, 10, 1134–1140 CrossRef CAS PubMed
.
- Y. Shen, G. Xue, Y. Dai, S. M. Quintero, H. Chen, D. Wang, F. Miao, F. Negri, Y. Zheng and J. Casado, Nat. Commun., 2021, 12, 6262 CrossRef CAS PubMed
.
- R. Rausch, M. I. S. Rohr, D. Schmidt, I. Krummenacher, H. Braunschweig and F. Wurthner, Chem. Sci., 2021, 12, 793–802 RSC
.
- M. Abe, Chem. Rev., 2013, 113, 7011–7088 CrossRef CAS PubMed
.
- A. Hinz, J. Bresien, F. Breher and A. Schulz, Chem. Rev., 2023, 123, 10468–10526 CrossRef CAS PubMed
.
- C. K. Frederickson, B. D. Rose and M. M. Haley, Acc. Chem. Res., 2017, 50, 977–987 CrossRef CAS PubMed
.
- F. A. Larik, M. Faisal, A. Saeed, Q. Abbas, M. A. Kazi, N. Abbas, A. A. Thebo, D. M. Khan and P. A. Channar, J. Mater. Sci.: Mater. Electron., 2018, 29, 17975–18010 CrossRef CAS
.
- Y. Dai, Z. Xie, M. Bao, C. Liu and Y. H. Su, Chem. Sci., 2023, 14, 3548–3553 RSC
.
- L. Li, J. Z. Low, J. Wilhelm, G. Liao, S. Gunasekaran, C. R. Prindle, R. h. L. Starr, D. Golze, C. Nuckolls, M. L. Steigerwald, F. Evers, L. M. Campos, X. Yin and L. Venkataraman, Nat. Chem., 2022, 14, 1061–1067 CrossRef CAS PubMed
.
- I. Bergenti, V. Dediu, M. Prezioso and A. Riminucci, Philos. Trans. R. Soc., A, 2011, 369, 3054–3068 CrossRef CAS PubMed
.
- A. Konishi, Y. Hirao, H. Kurata, T. Kubo, M. Nakano and K. Kamada, Pure Appl. Chem., 2014, 86, 497–505 CAS
.
- M. L. Kirk, D. A. Shultz, P. Hewitt and A. van der Est, J. Am. Chem. Soc., 2022, 144, 12781–12788 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, P. Hewitt and A. van der Est, J. Phys. Chem. Lett., 2022, 13, 872–878 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, P. Hewitt, D. E. Stasiw, J. Chen and A. van der Est, Chem. Sci., 2021, 12, 13704–13710 RSC
.
- M. L. Kirk, D. A. Shultz, J. Chen, P. Hewitt, D. Daley, S. Paudel and A. van Der Est, J. Am. Chem. Soc., 2021, 143, 10519–10523 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, A. R. Marri, P. Hewitt and A. van der Est, J. Am. Chem. Soc., 2022, 144, 21005–21009 CrossRef CAS PubMed
.
- H. Sato, V. Kathirvelu, G. Spagnol, S. Rajca, A. Rajca, S. S. Eaton and G. R. Eaton, J. Phys. Chem. B, 2008, 112, 2818–2828 CrossRef CAS PubMed
.
- S. Gunasekaran, D. Hernangómez-Pérez, I. Davydenko, S. Marder, F. Evers and L. Venkataraman, Nano Lett., 2018, 18, 6387–6391 CrossRef CAS PubMed
.
- L. Li, S. G. Louie, A. M. Evans, E. Meirzadeh, C. Nuckolls and L. Venkataraman, J. Am. Chem. Soc., 2023, 145, 2492–2498 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, D. E. Stasiw, G. F. Lewis, G. Wang, C. L. Brannen, R. D. Sommer and P. D. Boyle, J. Am. Chem. Soc., 2013, 135, 17144–17154 CrossRef CAS PubMed
.
- G. C. Solomon, D. Q. Andrews, T. Hansen, R. H. Goldsmith, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Chem. Phys., 2008, 129, 054701 CrossRef PubMed
.
- W. B. Davis, W. A. Svec, M. A. Ratner and M. R. Wasielewski, Nature, 1998, 396, 60–63 CrossRef CAS
.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS
.
- W. P. Su, J. R. Schrieffer and A. J. Heeger, Phys. Rev. Lett., 1979, 42, 1698–1701 CrossRef CAS
.
- A. J. Heeger, S. Kivelson, J. R. Schrieffer and W. P. Su, Rev. Mod. Phys., 1988, 60, 781–850 CrossRef CAS
.
- Z. Zeng, Y. M. Sung, N. Bao, D. Tan, R. Lee, J. L. Zafra, B. Y. Lee, M. Ishida, J. Ding, J. T. Lopez Navarrete, Y. Li, W. Zeng, D. Kim, K.-W. Huang, R. D. Webster, J. Casado and J. Wu, J. Am. Chem. Soc., 2012, 134, 14513–14525 CrossRef CAS PubMed
.
- J. Wang, X. Xu, H. Phan, T. S. Herng, T. Y. Gopalakrishna, G. Li, J. Ding and J. Wu, Angew. Chem., Int. Ed., 2017, 56, 14154–14158 CrossRef CAS PubMed
.
- P. Ravat and M. Baumgarten, PCCP Phys. Chem. Chem. Phys., 2015, 17, 983–991 RSC
.
- T. Takahashi, K. I. Matsuoka, K. Takimiya, T. Otsubo and Y. Aso, J. Am. Chem. Soc., 2005, 127, 8928–8929 CrossRef CAS PubMed
.
- D. Sakamaki, S. Yano, T. Kobashi, S. Seki, T. Kurahashi, S. Matsubara, A. Ito and K. Tanaka, Angew. Chem., Int. Ed., 2015, 54, 8267–8270 CrossRef CAS PubMed
.
- S. Di Motta, F. Negri, D. Fazzi, C. Castiglioni and E. V. Canesi, J. Phys. Chem. Lett., 2010, 1, 3334–3339 CrossRef CAS
.
- K. Takahashi, A. Gunji, K. Yanagi and M. Miki, J. Org. Chem., 1996, 61, 4784–4792 CrossRef CAS PubMed
.
- F. Tampieri, L. Colella, A. Maghsoumi, J. Martí-Rujas, E. Parisini, M. Tommasini, C. Bertarelli and A. Barbon, J. Phys. Chem. C, 2016, 120, 5732–5740 CrossRef CAS
.
- M. Lanata, C. Bertarelli, M. C. Gallazzi, A. Bianco, M. Del Zoppo and G. Zerbi, Synth. Met., 2003, 138, 357–362 CrossRef CAS
.
- R. West, J. A. Jorgenson, K. L. Stearley and J. C. Calabrese, Chem. Commun., 1991, 1234–1235, 10.1039/C39910001234
.
- J. Pannell, Chem. Ind., 1962, 1797–1800 CAS
.
- K. Takahashi, T. Suzuki, K. Akiyama, Y. Ikegami and Y. Fukazawa, J. Am. Chem. Soc., 1991, 113, 4576–4583 CrossRef CAS
.
- K. Takahashi, A. Gunji, K. Yanagi and M. Miki, J. Org. Chem., 1996, 61, 4784–4792 CrossRef CAS PubMed
.
- K. Takahashi and T. Suzuki, J. Am. Chem. Soc., 1989, 111, 5483–5485 CrossRef CAS
.
- j. Rebmann, J. Zhou, P. Schuler, H. B. Stegmann and A. Rieker, J. Chem. Res., Synop., 1996, 7, 318–319 Search PubMed
.
- A. Rebmann, J. Zhou, P. Schuler, A. Rieker and H. B. Stegmann, J. Chem. Soc., Perkin Trans. 2, 1997, 2, 1615–1618 RSC
.
- A. E. Chichibabin, Ber. Dtsch. Chem. Ges., 1907, 40, 1810–1819 CrossRef
.
- H. M. McConnell, J. Chem. Phys., 1960, 33, 1868–1869 CrossRef CAS
.
- Y. Kanzaki, D. Shiomi, K. Sato and T. Takui, J. Phys. Chem. B, 2012, 116, 1053–1059 CrossRef CAS PubMed
.
- T. Kubo, Chem. Lett., 2015, 44, 111–122 CrossRef
.
- E. Müller and I. Müller-Rodloff, Adv. Cycloaddit., 1935, 517, 134–151 Search PubMed
.
- H. S. Jarrett, G. J. Sloan and W. R. Vaughan, J. Chem. Phys., 1956, 25, 697–701 CrossRef CAS
.
- D. C. Reitz and S. I. Weissman, J. Chem. Phys., 1960, 33, 700–704 CrossRef CAS
.
- L. K. Montgomery, J. C. Huffman, E. A. Jurczak and M. P. Grendze, J. Am. Chem. Soc., 1986, 108, 6004–6011 CrossRef CAS PubMed
.
- R. K. Waring and G. J. Sloan, J. Chem. Phys., 1964, 40, 772–777 CrossRef CAS
.
- H.-D. Brauer, H. tieger, J. S. Hyde, L. D. Kispert and G. R. Luckhurst, Mol. Phys., 1969, 17, 457–471 CrossRef CAS
.
- M. Ruf, K. Weis and H. Vahrenkamp, J. Chem. Soc., Chem. Commun., 1994, 135–136 RSC
.
- M. Ruf and H. Vahrenkamp, Inorg. Chem., 1996, 35, 6571–6578 CrossRef CAS PubMed
.
- M. Ruf, B. C. Noll, M. D. Groner, G. T. Yee and C. G. Pierpont, Inorg. Chem., 1997, 36, 4860–4865 CrossRef CAS PubMed
.
- J. Chen, J. Yang, M. Yadav, D. A. Shultz and M. L. Kirk, Inorg. Chem., 2023, 62, 739–747 CrossRef CAS PubMed
.
- D. A. Shultz, M. L. Kirk, J. Zhang, D. E. Stasiw, G. Wang, J. Yang, D. Habel-Rodriguez, B. W. Stein and R. D. Sommer, J. Am. Chem. Soc., 2020, 142, 4916–4924 CrossRef CAS PubMed
.
- M. L. Kirk and D. A. Shultz, Coord. Chem. Rev., 2013, 257, 218–233 CrossRef CAS
.
- M. L. Kirk, D. A. Shultz, E. C. Depperman, D. Habel-Rodriguez and R. D. Schmidt, J. Am. Chem. Soc., 2012, 134, 7812–7819 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, D. Habel-Rodriguez, R. D. Schmidt and U. Sullivan, J. Phys. Chem. B, 2010, 114, 14712–14716 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, E. C. Depperman and C. L. Brannen, J. Am. Chem. Soc., 2007, 129, 1937–1943 CrossRef CAS PubMed
.
- S. H. Bodnar, A. Caneschi, A. Dei, D. A. Shultz and L. Sorace, Chem. Commun., 2001, 2150–2151 RSC
.
- P. Pouzet, I. Erdelmeier, D. Ginderow, P. M. Dansette, D. Mansuy and J.-P. Mornon, J. Heterocycl. Chem., 1997, 34, 1567–1574 CrossRef CAS
.
- R. Akai, K. Oka, R. Nishida and N. Tohnai, CrystEngComm, 2022, 24, 4180–4186 RSC
.
- D. D. Graf, R. G. Duan, J. P. Campbell, L. L. Miller and K. R. Mann, J. Am. Chem. Soc., 1997, 119, 5888–5899 CrossRef CAS
.
-
O. Kahn, Molecular Magnetism, VCH, New York, 1993 Search PubMed
.
- M. L. Kirk, D. A. Shultz and E. C. Depperman, Polyhedron, 2005, 24, 2880–2884 CrossRef CAS
.
- P. W. Anderson, Phys. Rev., 1959, 115, 2–13 CrossRef CAS
.
-
J. Michl and V. Bonacic-Koutecky, Electronic Aspects of Organic Photochemistry, Wiley-Interscience, New York, 1990 Search PubMed
.
- R. Nieman, N. J. Silva, A. J. A. Aquino, M. M. Haley and H. Lischka, J. Org. Chem., 2020, 85, 3664–3675 CrossRef CAS PubMed
.
- Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 753–766 CrossRef CAS
.
-
S. Sugano, Y. Tanabe and H. Kamimura, Multiplets of Transition-Metal Ions in Crystals, Academic Press, New York, 1970 Search PubMed
.
- E. Wasserman, L. C. Snyder and W. A. Yager, J. Chem. Phys., 1964, 41, 1763–1772 CrossRef CAS
.
- C. Herrmann, J. Phys. Chem. A, 2019, 123, 10205–10223 CrossRef CAS PubMed
.
- M. L. Kirk, R. Dangi, D. Habel-Rodriguez, J. Yang, D. A. Shultz and J. Zhang, Chem. Sci., 2020, 11, 11425–11434 RSC
.
- P. Hewitt, D. A. Shultz and M. L. Kirk, J. Org. Chem., 2021, 86, 15577–15587 CrossRef CAS PubMed
.
- D. E. Stasiw, J. Zhang, G. Wang, R. Dangi, B. W. Stein, D. A. Shultz, M. L. Kirk, L. Wojtas and R. D. Sommer, J. Am. Chem. Soc., 2015, 137, 9222–9225 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, D. E. Stasiw, D. Habel-Rodriguez, B. Stein and P. D. Boyle, J. Am. Chem. Soc., 2013, 135, 14713–14725 CrossRef CAS PubMed
.
- M. L. Kirk, D. A. Shultz, R. D. Schmidt, D. Habel-Rodriguez, H. Lee and J. Lee, J. Am. Chem. Soc., 2009, 131, 18304–18313 CrossRef CAS PubMed
.
- F. Miao, Y. R. Ji, B. Han, S. M. Quintero, H. Chen, G. Xue, L. Cai, J. Casado and Y. Zheng, Chem. Sci., 2023, 14, 2698–2705 RSC
.
- A. Toyota, S. Koseki and M. Shiota, J. Phys. Chem. A, 2000, 104, 5343–5350 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details. Synthetic-, X-ray crystallographic-, and magnetic susceptibility details and data. CCDC 2260981–2260983. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc02341a |
| This journal is © The Royal Society of Chemistry 2023 |