Accelerating explicit solvent models of heterogeneous catalysts with machine learning interatomic potentials

Abstract

Realistically modelling how solvents affect catalytic reactions is a longstanding challenge due to its prohibitive computational cost. Typically, an explicit atomistic treatment of the solvent molecules is needed together with molecular dynamics (MD) simulations and enhanced sampling methods. Here, we demonstrate the utility of machine learning interatomic potentials (MLIPs), coupled with active learning, to enable fast and accurate explicit solvent modelling of adsorption and reactions on heterogeneous catalysts. MLIPs trained on-the-fly were able to accelerate ab initio MD simulations by up to 4 orders of magnitude while reproducing with high fidelity the geometrical features of water in the bulk and at metal–water interfaces. Using these ML-accelerated simulations, we accurately predicted key catalytic quantities such as the adsorption energies of CO*, OH*, COH*, HCO*, and OCCHO* on Cu surfaces and the free energy barriers of C–H scission of ethylene glycol over Cu and Pd surfaces, as validated with ab initio calculations. We envision that such simulations will pave the way towards detailed and realistic studies of solvated catalysts at large time- and length-scales.

---

1. Introduction

In both homogeneous and heterogeneous catalysis, solvents play important roles by affecting chemical equilibria, rates of reaction, and product selectivities, as well as reaction yields.^1–3 Solvents exert these influences through their molecular interactions with the catalyst as well as with reactants, products, and intermediates.^3,4 To model these interactions, computationally inexpensive implicit solvation models, which treat the solvent environment as a structureless continuum,^5,6 are routinely used to model organic and organometallic catalysts,^7,8 as well as heterogeneous catalysts.^9,10

Yet, implicit solvation models have several well-known deficiencies: they fail to quantitatively account for hydrogen bonding, as well as entropic effects in free energy calculations.^11–13 Due to these deficiencies, solvation energies of the same transition state can differ by up to 5 kcal mol⁻¹ when applying different implicit solvation models.¹⁴ In addition, implicit solvation models predict overly stabilized salt bridges¹⁵ and give incorrect ion distributions in biomolecular simulations,¹⁶ which are especially pronounced in polar solvents. The failure of implicit solvation models to accurately predict solvation energetics leads to unphysical configurational sampling, further compounding the energetic errors.¹⁷

To rectify these deficiencies, an explicit atomistic description of the solvent environment is required. For example, Liu et al. demonstrated using ab initio molecular dynamics (AIMD) simulations of glycosylation reactions in explicit solvent that solute–solvent interactions and solvation-related entropic contributions were crucial for determining the correct catalytic mechanisms.¹⁸ Despite their advantages, explicit solvation is seldom used as computationally intensive MD simulations are required to adequately sample the configurational space of explicitly solvated systems. While empirical force fields (FFs) are popular in dynamical simulations of large-scale systems and are much faster than first-principles density functional theory (DFT) calculations,^19,20 their accuracy depends on how well they are parametrized. In addition, special techniques or FFs, such as the empirical valence bond (EVB)²¹ method or ReaxFF,^22,23 may be needed to model chemical reactions. However, they are challenging to parameterize and are often not generalizable. Semi-empirical methods such as density-functional tight binding (DFTB)^24,25 and GFN-xTB^26–28 have also been developed to reduce computational cost while aiming to maintain predictive accuracy. Despite these efforts, achieving ab initio accuracy at an affordable cost remains out of reach.

Recently, however, machine learning interatomic potentials (MLIPs) have demonstrated great promise, being able to reach near-DFT accuracy while maintaining near classical FF cost.^29–32 MLIPs fit the underlying potential energy surface (PES) of a training dataset of atomic configurations with associated energies and forces. This mapping is fundamentally achieved by transforming the structures into representations that are invariant or equivariant to translation, rotation, and permutation via atomic descriptors that fingerprint the local atomic environment. However, to train an MLIP with DFT-level accuracy, thousands of DFT calculations are typically required, which is a large upfront cost. It is also tricky to decide which configurations to include in the training set to produce a generalizable potential. Fortunately, both these challenges can be tackled by employing active learning techniques, which build training sets on-the-fly by judiciously selecting the next best data points to learn from.^33–36

MLIPs have been successfully applied to accelerate searches of local and global minima^37–42 and transition states,^41,43,44 and have shown good accuracy in modelling a variety of systems, including solvated metal and inorganic interfaces,^45,46 metal and metal oxide surfaces,^47–50 crystal structures of carbon and boron,⁵¹ organic molecules,^52,53 and bulk water.⁵⁴ More recently, sparse Gaussian process regression (SGPR) based ML models for training highly generalizable and transferable force fields at low computational cost have found success in a wide range of applications including macromolecules,⁵⁵ batteries,⁵⁶ solar cells,⁵⁷ and catalytic reactions.⁵⁸ Yet, there is a lack of studies and benchmarks⁵⁹ to determine if MLIPs can efficiently model solvation effects for processes in heterogeneous catalysis such as adsorption and bond breaking and formation—this is challenging as the solvent–catalyst interface comprises of two chemically very different systems. Additionally, the formation and breaking of bonds is notoriously tricky for interatomic potentials to describe as it involves changes in the local chemical environment of the involved atoms.

In this work, we therefore demonstrate the ability of MLIPs, trained on-the-fly via an active learning framework, to simulate explicitly solvated heterogeneous catalytic systems. We show that these ML-accelerated MD (MLaMD) simulations can indeed greatly accelerate the modelling of heterogeneous catalysts while maintaining near-DFT accuracy. Specifically, we will evaluate three different MLIPs to determine the most accurate MLIP for use in our MLaMD simulations. We then show that these simulations can reliably reproduce the structure of bulk water as well as water at water–metal interfaces. Finally, we validate the ability of our simulations to accurately provide catalytic properties such as adsorption energies over Cu surfaces, as well as free energy barriers over C–H bond scission over Cu(111) and Pd(111) via MLaMD-based metadynamics simulations.

2. Results

2.1 Validation and comparison of various machine learning potentials with bulk solvents

Thorough benchmarking of the accuracy of MLIPs is crucial as different MLIPs may possess strengths and weaknesses for different systems. We thus sought to determine which MLIP would be most accurate for solvated systems by probing their ability to model bulk water. We tested three MLIPs—the moment tensor potential (MTP),⁶⁰ the Accurate Neural Network Engine for Molecular Energies (ANI)⁶¹ and Schnet.⁶² Our study focused on these MLIPs as (1) they are widely used in the literature, and (2) they are based on different architectures and methods of fingerprinting local atomic environments.

We prepared a diverse training set (T1, Table S1†) consisting of 800 configurations via AIMD simulations of bulk water with 100H₂O molecules at 3 different densities, namely 0.91, 1.00, and 1.11 times the water experimental density. We additionally prepared test sets of bulk water with 60, 100, and 200H₂O molecules, each with 600–1000 configurations obtained from AIMD simulations at 300 K and 473 K (E1 and E3–E7, Table S1†), to evaluate the ability of the MLIPs to extrapolate to unseen configurations. Hyperparameters were optimized individually to achieve the best performance for each MLIP (Tables S2–S20†). Sections S1 and S2 in the ESI† contain more details of the preparation of the datasets and the screening of hyperparameters, respectively.

The results of our benchmarking are shown in Fig. 1a. MTP shows the best training and test performance across all datasets, with the smallest energy (Fig. 1a, top) and force (Fig. 1a, bottom) root mean square errors (RMSEs) of approximately 0.4 meV per atom and 0.05 eV Å⁻¹, respectively. Interestingly, these errors are almost 5 times lower than that of ANI, and 10 times lower than Schnet. The excellent performance by MTP could be due to the relatively small training set used (800 configurations); this favours potentials with less parameters, such as MTP, which is fundamentally based on simple linear combinations of polynomials, and are thus less prone to overfitting.⁶⁰

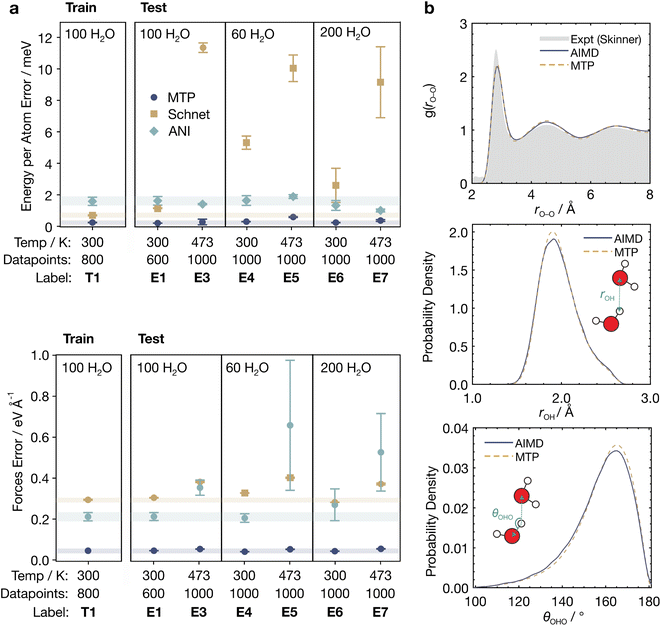Fig. 1 Energetic and geometric properties of bulk water predicted by MLIPs. (a) Root mean square errors (RMSEs) of the energy per atom (top) and force components (bottom) for MTP, Schnet, and ANI trained with the T1 dataset and evaluated on the E1, E3–E7 test datasets. Error bars represent standard errors from triplicate runs. Pale horizontal bars indicate the test set errors to aid comparison. (b) Geometric properties of bulk water from AIMD and MLaMD simulations with MTP. (Top) O–O radial distribution function, r_O–O. The experimental RDF from Skinner et al.⁶³ is provided for reference. (Middle) Hydrogen bond lengths, r_OH. (Bottom) Hydrogen bond angles, θ_OHO.

On the other hand, neural network (NN)-based MLIPs like ANI and Schnet have many more parameters and are likely overfitted with the limited training set data, as observed by their much poorer performance on the test sets as compared to on the training set (Fig. 1). Still, we did not find any significant improvement in the performance of ANI and Schnet by using a larger training set of 2400 datapoints (T2) (Fig. S2 and Section S2.5†). This could be because the configurations from T2 may be quite similar to those in T1, since T1 is a subset of T2. Training sets with more structurally diverse configurations, which are correspondingly more costly to generate, might therefore be necessary to improve the performance of ANI and Schnet. In the subsequent analyses, we therefore focus on MTP due to its excellent performance with small training sets, which are more cost-efficient for practical applications.

Besides its ability to reproduce the potential energy surface, a good MLIP should also provide realistic solvent geometries and atomic distributions (Fig. 1b). We compared the O–O radial distribution functions (RDFs) of bulk H₂O obtained via AIMD and MLaMD simulations using MTP, finding good agreement of the AIMD and MLaMD RDFs. Both the RDFs also match the experimental RDF⁶³ well (Fig. 1b, top). The MLaMD-obtained distributions of H-bond lengths and angles also match those of the AIMD simulations well (Fig. 1b, middle and bottom). These findings confirm the ability of the MLaMD simulations to faithfully reproduce the structure of bulk water, which is the first step towards accurate modelling of solvated systems.

2.2 MLIPs and active learning: MLaMD simulation framework

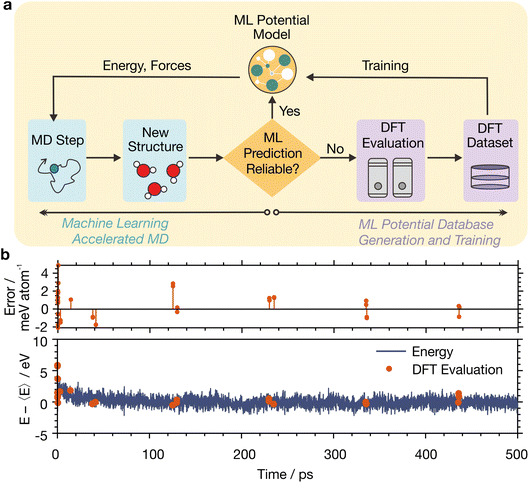
To perform MLaMD simulations, we combined the MTP with an in-house active learning scheme, which simultaneously generates training data via DFT calculations for fitting of the potential (Fig. 2a, right) whilst running MLaMD simulations (Fig. 2a, left). At its heart, the active learning algorithm decides whether more training data is required by tracking the reliability of the ML predictions as the MLaMD simulation progresses. Specifically, the Maxvol algorithm⁶⁴ in the MLIP package⁶⁵ was used to calculate an extrapolation grade, γ, for the configuration under consideration. Configurations that are interpolations of those already in the training dataset—and therefore likely well-described by ML—would have a low γ. Configurations that are extrapolations—and likely poorly described by ML—would have a high γ. When γ is above a certain threshold, the configuration is selected for DFT evaluation to augment the training dataset. Else, the potential is used as is to evaluate the configuration and continue the MD simulation. DFT calculations are also performed every 100 000 steps to periodically reaffirm the reliability of the ML predictions.

Fig. 2 Illustration of the active learning algorithm for MLaMD simulations. (a) Flow chart of the active learning algorithm. (b) Example trajectory of a 500 ps MLaMD simulation conducted at 300 K with MTP for CO* on Cu(111). The top panel shows the energetic error per atom of the ML evaluations for each DFT evaluation. No bars are present when there are no DFT evaluations. The bottom panel shows the energy of the simulation versus time. Energies are relative to the average energy of the simulation, 〈E〉.

Most implementations of active learning involve a multiple step process, such as performing several simulations to iteratively train a ML model. However, our protocol implements active learning on-the-fly during a simulation itself and does not require multiple iterations. To achieve this, we have employed an adaptive γ threshold, as explained in detail in Section S3.† In this way, our active learning procedure improves the efficiency of our simulations without compromising on accuracy.

Traditionally, comprehensive datasets have to be generated for training reliable MLIPs. However, implementing the active learning algorithm above allows us to selectively choose appropriate configurations for training, reducing the cost of generating the training database. Additionally, it increases the accuracy of the MLaMD simulations since inaccurate predictions are typically caused by extrapolated configurations: active learning can detect such configurations, evaluate them with DFT, and finally assimilate them into the training database, thereby iteratively producing better fitting PESs of the system under consideration.

An illustration of the trajectory of a MLaMD simulation is shown in Fig. 2b. At the beginning of the simulation, more DFT evaluations (Fig. 2b, red dots) are required to populate the training database whereas fewer DFT evaluations are required near the end since the MTP is already well trained.

For a typical adsorption energy calculation involving 8 MD replicas with different initial configurations (see Methods), we required ∼200 00× less DFT calls than for analogous AIMD simulations—only ∼600 DFT calculations were needed to simulate the 12 ns of total MLaMD simulation time, made up of 1 ns of equilibration and 0.5 ns of production for each MD replica (Table S24†). The high efficiency of MLaMD simulations is in large part thanks to the active learning strategy employed, which only performs DFT calculations on-the-fly during the MD simulation itself when exploring unknown configurational space. We note that the speed up of MLaMD simulations can only be computed approximately as it depends on the simulation length: the longer the simulation, the larger the speed up. This is because almost no DFT calculations will be required once the potential is well-trained.

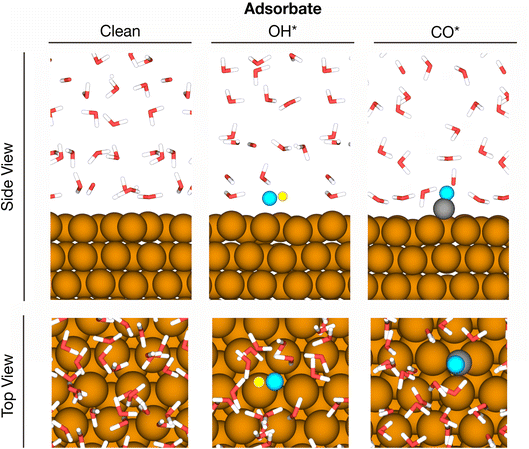
2.3 Solvation of adsorbates in water films at metal surfaces: CO* and OH* on Cu(111)

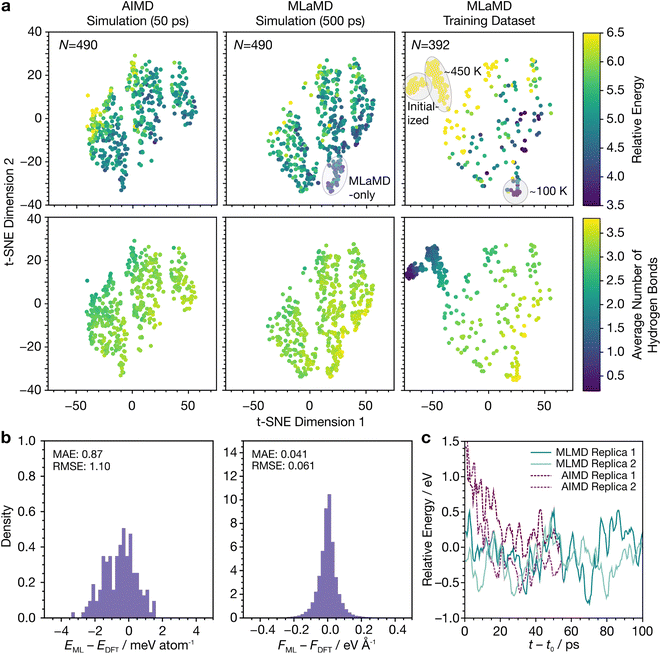
Metal–water interfaces combine two systems with very different chemistries and are therefore more complex than bulk water. We show in the following sections that MLaMD simulations can describe the solvation of adsorbates at metal–water interfaces, which model heterogeneous catalysts in an aqueous environment. Specifically, we studied in detail how water solvates a clean 3 × 3 unit cell of Cu(111), as well as two common adsorbates, CO* and OH*, adsorbed on Cu(111) (Fig. 3). These two adsorbates were chosen for in-depth study as they are representative of intermediates that are capable and incapable of hydrogen bonding, respectively. A water film of 32H₂O molecules was used to solvate all systems. More details of the system setup can be found in the Methods section.

Fig. 3 Atomic illustrations of the systems simulated—clean Cu(111), adsorbed CO*/Cu(111), and OH*/Cu(111). Side and top views are shown. Water molecules are rendered in a licorice representation, other atoms are represented as spheres. Note that for clarity, the side view does not show the entire unit cell in the z-direction. Color code: brown – Cu, red – O, white – H, grey – C, cyan – O atoms of adsorbates, yellow-H atom of OH.

2.3.1 Validation of the accuracy of MLaMD simulations. To determine how dependable MLaMD simulations are for modelling solvated interfaces, we first explored whether water structures obtained from MLaMD simulations were similar to those from AIMD simulations. We focused on the clean Cu(111) system for simplicity. The MLaMD simulations were run for 500 ps whereas the AIMD simulations were only run for 50 ps due to computational constraints; both simulations were carried out at 300 K.

To compare the water structures, we fingerprinted them with 5 commonly used structural descriptors for water, namely the (1) d₅,⁶⁶ (2) ζ,⁶⁷ (3) local structure index (LSI),⁶⁸ (4) q,⁶⁹ and (5) structural entropy (S₂)⁷⁰ descriptors. We then performed a 2-dimensional (2D) t-distributed stochastic neighbor embedding (t-SNE)⁷¹ analysis on these fingerprints. The resulting t-SNEs for structures obtained from AIMD and MLaMD are shown in Fig. 4a, where each data point represents a sampled structure. For comparison, a similar analysis was also performed on the final training set obtained from the MLaMD simulations.

Fig. 4 MLaMD simulations of solvated clean Cu(111). (a) t-SNE visualization of water configurations from AIMD and MLaMD simulations, and of the training dataset obtained from the MLaMD simulations. Data points are color coded based on their relative energy to the most stable configuration (top) and average number of hydrogen bonds between water molecules (bottom). (b) Energetic (left) and force (right) errors of 160 configurations sampled at 25 ps intervals from each of the eight production MLaMD simulation replicas. Subscripts “ML” and “DFT” represent ML- and DFT-predicted quantities, respectively. Mean absolute errors (MAEs) and root mean square error (RMSEs) are given. (c) Energies of two MLaMD and AIMD simulation replicates. Energies are zeroed to the average energy of solvated clean Cu(111) obtained from the MLaMD simulations. Times (t) are zeroed to t₀ = 10 ps, which is the initial discarded portion of the trajectory.

The configurations from the AIMD and MLaMD simulations cover similar areas of the latent space. Interestingly, the MLaMD simulations additionally cover a small space not found in the AIMD simulations (Fig. 4a, top middle panel)—these are more stable configurations with a greater degree of H-bonding (Fig. 4a, bottom middle panel). That the MLaMD simulations managed to access these configurations is likely due to their longer timescales (500 ps) compared with the AIMD simulations (50 ps): typically, longer simulation times on the order of hundreds of picoseconds to nanoseconds are necessary to obtain well-equilibrated water structures and properties.^72–74 The importance of longer simulation times to improve sampling is discussed further in the next section.

The training set structures generated from on-the-fly from the MLaMD simulation cover a larger region of the latent space as they include structures encountered in the equilibration phase conducted before production, such as the initial configurations that were randomly created and thus have high energy and little hydrogen bonding, as well as configurations encountered at high (∼450 K) and low (∼100 K) temperatures (Fig. 4a; right panels). This provides additional confidence that the configurations encountered in the MLaMD simulations are well-described by our trained models as they are interpolated from the training set.

We next analyzed the accuracy of MLaMD simulations by comparing the energies and forces of 160 configurations sampled from the MLaMD trajectories against single-point ab initio calculations. Encouragingly, the MLaMD simulations show near-DFT accuracy, with low energetic and force mean absolute errors (MAEs) of 0.87 meV per atom and 0.041 eV Å⁻¹ (Fig. 4b). Similar results were found for the Cu(111)/CO* and Cu(111)/OH* systems (Table S21 and Fig. S4, S5†). The trajectories of the AIMD and MLaMD simulations are also practically indiscernible (Fig. 4c). Overall, these results demonstrate that MLaMD simulations reproduce the ab initio potential energy surface of solvated systems with a high degree of fidelity. For the interested reader, Section S3† presents more details on how we verified the accuracy of the MLaMD simulations.

2.3.2 Energetic convergence of MLaMD simulations. Compared with AIMD simulations, a key advantage of MLaMD simulations is their ability to access extended timescales. This leads to improved configurational sampling and thus more accurately averaged quantities including binding energies. To investigate the energetic convergence of our studied systems, we tracked the evolution of three quantities as their simulations progressed (Fig. 5): (1) the total energy, (2) the autocorrelation function of the energy, which sheds light on the relaxation timescales of the system, and (3) the value of ζ, a structural descriptor of water defined as the difference between the nearest non-hydrogen-bonded neighbour distance and the farthest hydrogen-bonded neighbour distance.⁶⁷ Larger ζ values indicate a more ordered second solvation shell, increased hydrogen bonding, and a more tetrahedral structure of water.⁷⁵ Note that for clarity, we only show 4 runs out of a MLaMD bundle, however, the same trends are observed when considering all 8 runs (Fig. S9†).

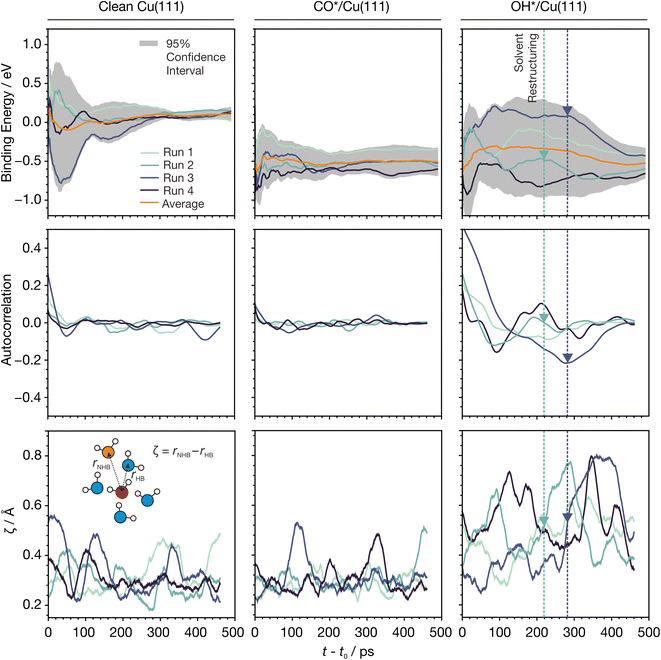Fig. 5 Evolution of MLaMD simulations versus time for Cu(111) systems. (Top) Moving average of binding energies smoothed over a window of 10 ps. Binding energies are with respect to clean Cu(111), CO(g), H₂O(g), and H₂(g), where “(g)” indicates a gas-phase species. (Middle) Moving average of the energy autocorrelation function smoothed over a window of 30 ps. (Bottom) Moving average of ζ smoothed over a window of 30 ps. Colored dashed lines and triangles highlight structural changes in water occurring in the course of the simulation. The simulation time, t, is zeroed to t₀ = 10 ps, which is the initial discarded portion of the trajectory. The inset shows the definition of ζ. Color code for atoms: white - H, red - O of water molecule under consideration, blue - O of hydrogen bonded water molecules, orange - O of non-hydrogen bonded water molecule. Only 4 out of the 8 runs of a MLaMD bundle are shown for clarity. The trajectories of all 8 runs are provided in Fig. S9.†

Interestingly, however, the energies of the OH*/Cu(111) simulations vary greatly and span a large range (∼1 eV), only beginning to converge after ∼300 ps (Fig. 5). Despite this, the average of all runs converges quickly, showing the importance of multiple replicas. Additionally, we see greater fluctuations in the energy autocorrelation function, indicating the presence of long timescale correlations in the energies. These correlations are due to restructuring of water: for example, runs 2 and 4 (Fig. 5, dark green and blue lines, respectively) show large increases in ζ from 0.4 to 0.8 at around 220 and 280 ps, respectively. This lasts for around 100 ps before ζ decreases back to ∼0.4. This indicates an increase in the ordering of water, which is also reflected in decreases in the average binding energies that occur at the same time. Such events are not observed in the simulations of clean Cu(111) or CO*/Cu(111).

The long timescales needed to observe such restructuring in the OH*/Cu(111) system is likely due to the strong hydrogen bonding of OH* to the water molecules, which reduces their mobility, as evidenced by their smaller self-diffusion coefficients.⁹ For such systems, longer timescale simulations will be beneficial for achieving more accurate energetics. For example, compared with shorter AIMD simulations,⁹ our MLaMD simulations predict OH* to bind more stably on Cu(111), as will be discussed in more detail in Section 2.3.4.

Overall, our analyses reveal that the nature of the adsorbate may influence the simulation time needed for energetic convergence. While short AIMD simulations may be sufficient for some systems, longer simulations achievable by MLaMD simulations are needed for systems with poor water mobility to ensure proper sampling of the configuration space and obtain accurate energetics.

2.3.3 Structure of water films at metal–water interfaces. We next zoomed in on how well MLaMD simulations can reproduce the properties of water near the metal–water interface, which is crucial for obtaining accurate solvation properties. To begin, we probed how the density of water—specifically, its O atoms—changes as a function of the distance, d, away from the Cu(111) surface (Fig. 6a).

Fig. 6 Properties of water at the interface of Cu(111) from MLaMD simulations. (a) Density of O and H atoms at 300 K as function of the distance from the surface, d, for clean Cu(111), CO*/Cu(111), and OH*/Cu(111). Dotted lines represent the densities of bulk water. Sample atomistic structures for each system are superimposed. Color code for atoms: brown – Cu, grey – C, red – O, white – H. (b) Surface water distribution for each of the three systems. Surface water is defined as water within d = 4.6 Å. See main text for definitions of watA and watB. Numbers may not sum up to the total due to rounding. (c) Distribution of the angle between the water bisection vector and the surface normal, θ, versus d for clean Cu(111). Brown dots represent individual data points; dark blue lines represent the mean θ ([small theta, Greek, macron]), and error bars represent standard errors of the mean.

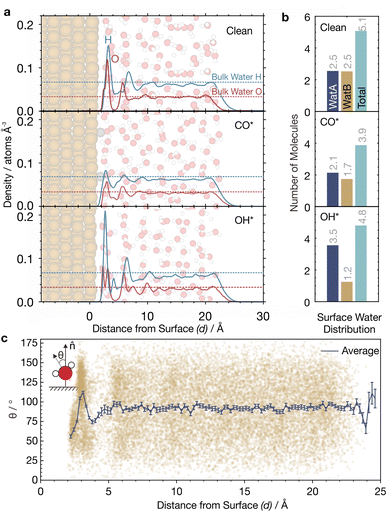
For clean Cu(111), we find a major peak and a small shoulder in the water density around d = 3 Å, which corresponds to adsorbed water. There is a smaller peak at around 6 Å, after which the density quickly levels to that of bulk water at >7 Å (black dotted lines, Fig. 6a). These findings are consistent with the literature.^45,76 The major peak and its shoulder can be deconvoluted into two components: (A) a 1st solvation layer, comprising of directly bound water molecules, also termed watA; and (B) a 2nd solvation layer, comprising of indirectly bound water molecules hydrogen-bonded to the 1st solvation layer (Fig. S11†). These molecules are also termed watB.^45,76

watA and watB molecules can be distinguished by their orientation with respect to the surface, as quantified by the angle θ between the water bisection vector and the surface normal (n̂) (Fig. 6c; inset). For most watA molecules, θ is less than 90° as they are directly bound to surface via their O atom and are in a H-up orientation. On the other hand, θ is greater than 90° for most watB molecules as they are hydrogen bonded to watA and are in a H-down orientation.^45,76

The orientations of watA and watB in their respective solvation layers were captured well by our MLaMD simulations, as observed from how the average θ, [small theta, Greek, macron], changes as a function of d (Fig. 6c). Near the surface, where d is between 0 and 3 Å, [small theta, Greek, macron] ranges between 50 and 75°, consistent with an abundance of watA in the 1st solvation layer. When d is between 3–4 Å, there is a region where [small theta, Greek, macron] increases to ∼110°, due to a larger proportion of watB in the 2nd solvation layer. At d > 4 Å, [small theta, Greek, macron] retreats back to ∼90°, corresponding to the random orientation of water found in bulk water. Consistent with our results, these variations in [small theta, Greek, macron] are also observed on Pt(111) and Au(111).⁷⁷

Quantifying the amount of watA and watB in each system can shed light onto how adsorbates alter the metal–water interface. This is, however, challenging as there is no exact definition of the distance that delineates the 1st and 2nd solvation layers. Additionally, the separation between the two solvation layers could also change with the addition of adsorbates. We therefore defined a cutoff distance, d_cut ≡ 4.6 Å, below which all water molecules belong to either the 1st or 2nd solvation layer. This cutoff was chosen as there is a minimum in the water density at this distance (Fig. 6a). Below d_cut, we classify water molecules with θ < 90° as watA, and water molecules with θ > 90° as watB.

On clean Cu(111), there are an equal number of watA and watB molecules (∼2.5), corresponding to a total (watA + watB) of 5.1 adsorbed water molecules. In the 3 × 3 unit cell, this corresponds to a coverage of 0.56 monolayers (ML), which agrees well with previous simulations.⁴⁵ Interestingly, however, adsorption of CO* and OH* alters the proportion of watA and watB molecules, as well as the total amount of water adsorbed (Fig. 6b). For the CO*/Cu(111) system, the total amount of adsorbed water decreases to 3.9. This is due to the displacement of both watA and watB from the surface upon CO adsorption. On the other hand, for the OH*/Cu(111) system, we observe a surprising increase in the amount of watA as compared with the clean surface, with a concomitant decrease in the amount of watB. This can be explained by the ability of OH* to hydrogen bond to water molecules in the 2nd solvation layer, bringing them closer to the surface.⁹

2.3.4 Adsorbate properties at metal–water interfaces. Of particular interest in heterogeneous catalysis is how solvation affects the binding geometries and energies of adsorbates as such changes can greatly impact adsorbate coverages and their reactivity. In this subsection, we will therefore look at how explicit solvation changes the properties of adsorbates compared with implicit solvation and vacuum simulations.

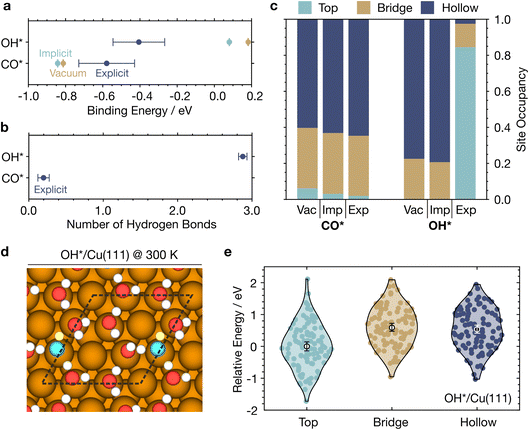
From our MLaMD simulations, we obtained binding energies of −0.62 ± 0.09 eV and −0.45 ± 0.11 eV for CO* and OH*, respectively (Fig. 7a). For comparison, the binding energies calculated by Heenan et al.⁹ with AIMD explicit solvent simulations (∼30 ps) are −0.77 ± 0.06 eV and −0.11 ± 0.05 eV. While the binding energies for CO* for the two methods agree well, discrepancies in the OH* binding energies could be due to the better sampling afforded by our longer MLaMD simulations (500 ps) which leads to more converged energetics, as also discussed in Section 2.3.2. Additional comparisons of our MLaMD simulations with AIMD simulations by Heenan et al. can be found in Section S3.3.†

Fig. 7 Energetic and geometric properties of CO* and OH* on Cu(111) from MLaMD simulations. (a) Binding energies in vacuum, implicit solvent, and explicit solvent. (b) Number of hydrogen bonds formed between the adsorbate and water. (c) Adsorbate site occupancies in vacuum (Vac), implicit (Imp), and explicit (Exp) solvent. (d) Top view of a hexagonal water structure formed by the first water layer on Cu(111) for a sample MLaMD configuration for OH*/Cu(111). Color code for atoms: brown – Cu, red – O, white – H, grey – C, cyan – O atoms of OH*, yellow – H atom of OH*. (e) Violin plot of energies for configurations with OH* binding on various sites. 100 configurations were sampled from MLaMD simulations for each site. White circles represent the mean. Error bars in all panels represent the 95% confidence intervals of the mean.

We compared these binding energies against those obtained from MLaMD simulations of the systems (1) in vacuum, and (2) in a Poisson–Boltzmann implicit solvent model as implemented in the VASPsol package⁷⁸ (Fig. 7a). The implicit solvent binding energies are similar (within 0.1 eV) to those in vacuum. Note that the MLaMD-predicted vacuum and implicit solvent binding energies are also very similar to those obtained from static DFT calculations. However, compared with explicit solvation, on average, implicit solvation overstabilizes CO* by 0.2 eV and understabilizes OH* by 0.4 eV.

These differences can be understood in terms of two main effects: (1) hydrogen bonding between the adsorbate and H₂O, and (2) displacement of H₂O molecules from the surface, also known as competitive adsorption.⁹ Our MLaMD simulations reveal that CO* forms only 0.20 hydrogen bonds with the solvent, while OH* forms 2.88 hydrogen bonds (Fig. 7b), in agreement with the trend observed in AIMD simulations, with values 0.32 and 2.39, respectively.⁹ The deficiencies of implicit solvation models in describing these stabilizing hydrogen bonding interactions are therefore especially prominent for OH*, leading to its understabilization. On the other hand, for CO* is overstabilized since implicit solvation failed to account for the endothermic displacement of adsorbed water molecules from the surface: CO* displaces ∼1.2 water molecules from the surface, whereas OH* displaces only ∼0.3 water molecules (Fig. 6b), where we define the number of displaced water molecules as the difference in the number of adsorbed water molecules on the clean surface versus that of the surface with the adsorbate. Although both adsorbates are of similar size, OH* displaces less water as it attracts water to the surface via hydrogen bonding. Besides the two main factors above, electronic effects also potentially influence the binding energies: the adsorption of water leads to significant charge buildup in the region between the water molecules and the metal surface.^77,79 This creates a significant dipole interface that changes the work function of the metal surface⁸⁰ and can interact with adsorbates.

Lastly, we studied if the binding site preferences of CO* and OH* are altered in the presence of explicit solvent as compared with implicit solvent. Interestingly, we noticed a drastic change in the preferred binding sites of OH* in explicit solvation as compared to implicit solvation or vacuum simulations (Fig. 7c). OH* occupies three-fold hollow sites (fcc and hcp) ∼80% of the time in implicit solvent and vacuum. In explicit solvent, however, OH* occupies top sites 82% of the time, bridge sites ∼17% of the time, and hollow sites less than 1% of the time. This is because H₂O tends to form hexagonal water structures on Cu(111) (Fig. S8†). When OH* binds on top sites, it can maximize its participation in these hexagonal water structures (Fig. 7d). Such configurations are ∼0.5 eV more energetically favorable than OH* binding on bridge or hollow sites with disrupted hexagonal water structures (Fig. 7e), whereas in vacuum where the top site is 0.45 eV more unstable than the hollow site (Table S25†). We note such stabilized OH* + H₂O hexagonal water structures have also been observed on Ru(0001).⁸¹

For CO*, the lack of hydrogen bonding results in very similar results for all simulations, with occupancies of ∼40% and ∼60% for the bridge and hollow sites. These results reaffirm that explicit solvation is crucial for accurate modelling of adsorbates capable of hydrogen bonding.

2.4 Activation energies via metadynamics simulations

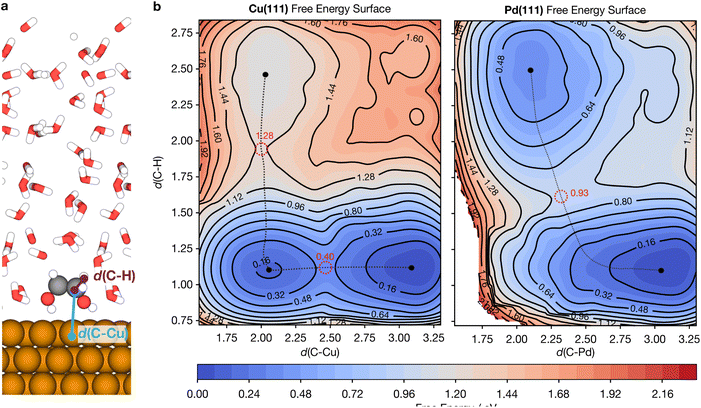
Reaction barriers are crucial for understanding the kinetics of catalytic reactions. Yet, it is highly challenging to obtain accurate barriers in explicitly solvated models particularly since static transition state calculations such as the nudged elastic band (NEB)⁸² method do not account for dynamic effects such as the formation and rearrangement of solvation shells at the transition state.⁸³ Free energy barriers in explicit solvents are therefore commonly evaluated by thermodynamic integration (TI)⁸⁴ or enhanced sampling methods such as metadynamics,⁸⁵ which can more thoroughly sample the changes in solvent configurations as reactions proceed.

Demonstrating the ability of MLaMD to model complex catalytic reactions, we performed MLaMD-based metadynamics simulations to calculate the free energy barriers for breaking of the C–H bond of ethylene glycol (EG) over Cu(111) and Pd(111). The C–H and C–Cu bond distances (Fig. 8a) were used as the collective variables (CVs) to map out the 2D free energy surfaces (FESs) for C–H bond breaking (Fig. 8b). On Cu(111), the minimum energy pathway first involves EG approaching the surface, as shown by the shorting of d(C–Cu) from 3.2 to 2.0 Å (Fig. 8b; left). This process involves a small barrier of 0.40 eV. Once close to the surface, the C–H bond of EG then breaks with d(C–H) increasing from 1.2 to 2.5 Å; the transition state occurs at a d(C–H) of 1.8 Å. This elementary step has an overall barrier of 1.28 eV with respect to the initial state. On Pd(111), however, C–H bond breaking occurs in a single step together with the approach of EG to the surface, with a barrier of 0.93 eV (Fig. 8b; right).

Fig. 8 MLaMD-based metadynamics simulations of C–H bond breaking of ethylene glycol over Cu(111) and Pd(111). (a) Atomistic illustration of the simulation setup for Cu(111); ethylene glycol and the surface are represented by spheres whereas water molecules are represented by lines. The two collective variables, d(C–H) and d(C–Cu), are marked. Color code for atoms: brown – Cu, grey – C, red – O, white – H. (b) 2D free energy surface for the C–H bond breaking of ethylene glycol over Cu(111) and Pd(111). Red dotted circles mark transition states and red text denotes their energies. Solid black circles mark minima.

The barriers from our MLaMD-based metadynamics simulations are similar to the barriers of 1.06 and 0.74 eV (ref. 86) obtained from the potential of mean force (PMF) mapped by the eSMS quantum mechanical/molecular mechanical (QM/MM) model by Heyden and coworkers.^10,87 Note that ref. 86 employed the PBE functional whereas the RPBE-D3 functional was used in this work, which may have contributed to the discrepancies observed. More importantly, however, the trends predicted by the two methods are consistent: C–H bond breaking is predicted to be more facile over Pd(111) than over Cu(111). Additionally, both methods predict a similar difference in the barriers over the two surfaces of 0.35 eV (this work) and 0.32 eV (ref. 86). These results underscore the ability of MLaMD simulations to effectively model chemically complex bond-breaking reactions.

3. Discussion

Our results demonstrate that combining active learning with MLIPs can greatly accelerate computationally costly AIMD simulations and are therefore an efficient yet accurate method for modelling the explicit solvation of heterogeneous catalytic systems. Validating our MLaMD simulations with ab initio calculations, we demonstrated low energy and force MAEs of ∼1 meV per atom and 0.06 eV per Å, respectively. To verify if our methods are applicable to a broad range of adsorbates and more complex surfaces, we performed additional simulations of 5 adsorbates—CO*, COH*, HCO*, OCCHO*, and OH*—over the Cu(211) surface, revealing similarly low errors (Section S3†).

We also find generally good agreement with the literature in terms of predicted binding energies, free energy barriers, and geometric features such as the number of hydrogen bonds formed between the adsorbate and the solvent. Yet importantly, the binding energies of certain adsorbates capable of hydrogen bonding, such as OH*/Cu(111), differed from that predicted by AIMD simulations in the literature by ∼0.3 eV. As these deviations are larger than the ab initio errors of our simulations (∼1 meV per atom, ∼0.14 eV per configuration), we suggest that these discrepancies are likely due to the shorter timescales of AIMD simulations (<100 ps) widely used. Overall, these results indicate that MLIPs can handle the complex chemical environments of solvated adsorbates on metal surfaces with high accuracy, generalizability, and transferability. Important for practical applications, they are also able to treat the breaking and formation of chemical bonds, which until now has been challenging for traditional force fields.

The low cost of MLaMD simulations enable better sampling of the configurational space via extended timescale simulations and reducing the cost of more replicas. This is especially significant given our findings that the nature of the adsorbate influences the amount of sampling needed to achieve energetic convergence. For these adsorbates, such as OH*, longer MLaMD simulations will be vital for ensuring converged energetics, as evidenced by MLaMD simulations predicting 0.34 eV more stable binding for OH*/Cu(111) than AIMD simulations.

Naturally, the choice of MLIP will play a significant role in determining the accuracy and success of MLaMD simulations. Out of the three MLIPs we tested—ANI, Schnet, and MTP—MTP performed best with energetic and force errors 4–7 times smaller than ANI and Schnet. The high accuracy of MTP is likely because of its simpler mathematical form, which prevents overfitting of the relatively small training datasets (∼500–1000 datapoints) generated during the MLaMD simulations. While having larger datasets can lead to better fitting of NN-type potentials, it also increases the time needed for retraining the model when new data arrives, which can eventually become a significant overhead. To reduce this training overhead, it will be interesting explore the use of incremental learning methods,⁸⁸ which can incorporate new data into a model without forgetting old data.

However, the main limitations of MLaMD simulations pertain to modelling systems containing charged species such as electrolytes: these limitations stem from the inability of most MLIPs to treat systems with long-range electrostatic interactions,⁸⁹ especially in solvents with low dielectric constants where there is weak charge shielding. Most current MLIPs work by fingerprinting structures using cutoff radii that are typically no larger a few coordination shells (∼5 Å).⁸⁹ They are therefore unable to capture any interactions longer than this cutoff radius. Fortunately, much research is ongoing to improve the accuracy and generalizability of MLIPs, with much effort aimed at developing MLIPs that can handle long range interactions.^90–94 For example, the equivariant NequIP⁹⁵ and MACE⁹⁶ potentials are based on message passing neural networks (MPNNs),⁹⁷ which by the nature of their architecture, could incorporate information from atoms beyond the neighbor cutoff. Long-range interactions may also be handled by explicitly including charges in the training process, as demonstrated by the 4G-HDNNPs (high-dimensional neural network potentials) developed by Behler et al.⁹⁸ In the future, it will be exciting to see how these state-of-the-art MLIPs can help further improve the speed and accuracy of MLaMD simulations and address challenging chemical problems realistically within the constraints of computational resources.

4. Conclusions

Explicit solvent models are the gold standard for modelling solvent effects in catalysis as they are able to capture key solvation phenomena such as hydrogen bonding and competitive water adsorption. Despite the wide use of solvents in catalysis and the highly influential roles that they play, our understanding of solvation phenomena remains poor, having been long stymied by the prohibitive computational cost of explicit solvent calculations. In this work, we combined MLIPs together with an active learning framework to accelerate AIMD simulations of explicitly solvated heterogeneous catalysts by more than 4 orders of magnitude and demonstrated the ability of these ML-accelerated simulations to accurately predict quantities of catalytic relevance, such as adsorption energies and reaction barriers, in these solvated environments.

By enabling explicit solvent simulations at an affordable computational cost, MLaMD simulations fill a critical gap in the realistic modelling of heterogeneous catalysts. Such simulations cannot be fully replaced by low-cost PCM-type implicit solvent models, which may predict erroneous binding energies and adsorption site preferences. This is especially true for adsorbates capable of hydrogen bonding, as we showed for the adsorption of OH* on Cu surfaces. Neither can they be replaced by AIMD simulations, as the timescales required for energetic convergence depends on the mobility of water, which may be slowed by adsorbates are capable of hydrogen bonding, such as OH*. For such systems, simulations much longer than accessible by AIMD simulations may be required.

Furthermore, compared with traditional force fields, MLaMD simulations are more generalizable and transferable: despite the vastly different chemical properties of bulk water and transition metal surfaces, we showed that MLaMD simulations were still able to reproduce the metal–water interface with high fidelity. The ability of MLaMD simulations to model the breaking and formation of bonds via metadynamics, as demonstrated by the example reaction of C–H bond scission of ethylene glycol over the (111) facets of Pd and Cu, is also a significant improvement compared with force fields, which are typically unable to handle reactions.

As MLIPs with higher accuracy and speed are continuously being developed, we expect MLaMD simulations to be able to handle increasingly more complex and larger systems. This will open avenues for probing a variety of interesting catalytic phenomena occurring at longer time and length scales, such as nanoconfined solvents. Although more work is still needed to better handle charged species due to their long ranged electrostatic interactions, we envision that MLaMD simulations can eventually become a general tool in the computational chemist's toolbox, helping to shed light onto the relatively unexplored and exciting realm of solvent effects for a wide range of different chemistries.

5. Methods

5.1 First-principles density functional theory calculations

We performed periodic, plane-wave calculations with the Vienna ab initio Simulation Package (VASP).^99,100 Valence electronic states were expanded with a plane-wave basis set with an energy cutoff of 400 eV, except for bulk water where a cutoff of 800 eV was used to minimize Pulay stresses; this is consistent with the higher energetic cutoffs used for bulk water in literature.^101,102 Core electronic states were represented with projector augmented-wave (PAW) pseudopotentials.^103,104 The Hammer et al. revision of the Perdew–Burke–Ernzerhof functional (RPBE)¹⁰⁵ was employed to account for exchange and correlation effects, together with Grimme's D3 method to account for dispersion effects.¹⁰⁶ RPBE-D3 was selected as it accurately describes both the geometrical properties of liquid water¹⁰⁷ and the chemisorption of atoms and molecules on metal surfaces.¹⁰⁵

Cu and Pd catalyst systems were modelled by five-layer (111) slabs with a 3 × 3 unit cell. The bottom two layers were fixed at their optimized bulk lattice constants of 3.57 Å for Cu and 3.91 Å for Pd (experimental:¹⁰⁸ 3.61 and 3.89 Å, respectively) and the top three layers were relaxed. The Brillouin zone was sampled by a Generalized Regular grid with 8 irreducible and 49 reducible k-points, as generated by the autoGR package.¹⁰⁹ Convergence of adsorption energies with respect to the k-points grid was confirmed. Gaussian smearing with a smearing width of 0.1 eV was applied on the Fermi surface to accelerate electronic convergence. The Fermi temperature was extrapolated to 0 K to obtain the final energies.

For explicitly solvated systems, 32H₂O molecules were added on top of the slabs, giving a ∼20 Å thick water film, which is adequate for converging the electronic and geometric properties of the solid–liquid interface.^9,45 To avoid spurious interactions between periodic images, we ensured at least 10 Å of vacuum in the z-direction, similar to the models by Groß and co-workers.^76,80 Bulk water was modelled by a cubic unit cell with 60, 100, or 200H₂O molecules.

5.2 Adsorption properties from MLaMD simulations

The binding energies of an adsorbate on Cu surfaces, E_ads, were defined with respect to the clean slab, gas-phase H₂, H₂O, and CO:

ΔE_ads = E_ads,tot − E_slab,tot − (xE_CO(g) + yE_H2(g) + zE_H2O(g)), (1)

where E_ads,tot is the total energy of the adsorbate + slab system, E_slab,tot is the total energy of the clean slab, E_CO(g), E_H2(g) and E_H2O(g) are the gas-phase total energies of CO, H₂, and H₂O, respectively, and x, y, and z are the number of CO, H₂, and H₂O molecules, respectively, that are required to form the adsorbate. All energies are time-averaged internal energies (i.e., the sum of the potential and kinetic energy). The energies of gas-phase species include a correction of since the centre of mass motion of the gas-phase molecule is not included in the MD simulations.⁹ More positive (negative) binding energies indicate weaker (stronger) binding of the adsorbate.

Time-averaged internal energies were obtained from MLaMD simulations unless otherwise stated. The NVT ensemble was sampled with a Nosé–Hoover^110,111 thermostat, as implemented in the Atomic Simulation Environment (ASE),¹¹² with timesteps of 1 fs. The hydrogen mass was adjusted to 3 amu to increase the stability of the simulation.¹¹³ To facilitate data analysis, we stored the trajectories of the simulations at every 10 timesteps.

Our workflow to obtain binding energies was conducted in two phases (Fig. S6a†). In the first phase, equilibration MLaMD simulations were performed with an initial temperature 450 K, which was ramped down to 100 K in 5 × 10⁵ steps (500 ps). This populates the database with diverse configurations, preventing overfitting of the MLIP. 8 equilibration replicas were run in parallel, each with different initial solvent configurations but sharing the same trained MLIP. All replicas contribute to the active learning of the MLIP, helping to further accelerate the simulation. We term these 8 replicas a single MLaMD bundle as the replicas are not strictly independent runs as they depend on the same potential. To further improve the diversity of the configurations in the training dataset, we ran two equilibration MLaMD bundles.

In the second phase, the two datasets generated from the equilibration MLaMD bundles were combined to populate the training database for the production MLaMD bundle. Only one production MLaMD bundle with 8 replicas was run. Initial configurations were obtained by taking the last image from the replicas of one of the equilibration bundles. The production simulations were run at 300 K for 5 × 10⁵ steps (500 ps), which was enough to ensure the convergence of the simulations (Fig. S7†). For the calculation of all properties, the first 10 ps of the production run were discarded to allow equilibration to 300 K.

The above workflow was repeated at least three times, each time with independently trained potentials and different initial solvent configurations, to obtain better statistics. Throughout the MLaMD simulations, the absolute energetic errors of the DFT calculations were consistently below 4 meV per atom (Fig. 2b and S4†).

Besides energetics, the obtained trajectories were also used to analyze how adsorbates bind to the surface via calculating how often they occupy each site on the catalyst surface. Specifically, we first enumerated all possible surface sites using the Catkit package.¹¹⁴ We then matched the position of the adsorbate at each image of the trajectory to the closest surface site. The time-averaged site occupancy across the simulation was taken.

5.3 Free energy surfaces from MLaMD-based metadynamics simulations

Well-tempered metadynamics calculations were performed with the PLUMED library^115,116 and ASE.¹¹² A hill height of 0.1 eV was chosen with a width of 0.2 Å. Hills were deposited every 100 steps, where each step was taken with a 1 fs timesteps. The workflow for calculating free energy surfaces from metadynamics simulations consists of three stages (Fig. S6b†). First, similar to the binding energy calculations, two separate equilibration bundles with 8 replicas each were created. For each replica, a normal MLaMD simulation sampling the NVT ensemble was run with an initial temperature of 450 K, which was ramped down to 100 K in 5 × 10⁵ steps (500 ps). Next, the two equilibration bundles were combined for a second equilibration run with normal MLaMD simulations at the chosen reaction temperature, 423 K, for 5 × 10⁵ steps (500 ps). Lastly, a production MLaMD-based metadynamics simulation was run at 423 K with 1 × 10⁶ steps (1000 ps) using the final configurations of the second equilibration runs as the initial state.

Data availability

Data supporting the manuscript are provided in the ESI, including the methods for generating the datasets, details of hyperparameter tuning of the machine learning interatomic potentials, evaluation of the accuracy of the trained machine learning potentials, and energetic trajectories of the simulations. Additional relevant data are available from the corresponding authors upon reasonable request.

Author contributions

B. W. J. C. obtained funding, conceptualised the project, and performed the machine learning-accelerated computational studies. X. Z. designed and performed the machine learning benchmarking studies. J. Z. provided feedback and supervised the project. All authors contributed to the analysis and the discussion of the results and co-wrote the manuscript.

Conflicts of interest

The authors declare that there are no competing interests.

Acknowledgements

This work was supported by the A*STAR Career Development Award (Grant No. 202D800017). B. W. J. C. is also grateful for support by the A*STAR SERC Central Research Fund award. The authors acknowledge high-performance computational facilities from the National Supercomputing Centre (NSCC) Singapore (https://www.nscc.sg) and A*STAR Computational Resource Centre (A*CRC).

References

1. Q. Sun, S. Wang, B. Aguila, X. Meng, S. Ma and F.-S. Xiao, Creating Solvation Environments in Heterogeneous Catalysts for Efficient Biomass Conversion, Nat. Commun., 2018, 9, 3236.
2. M. A. Mellmer, C. Sanpitakseree, B. Demir, P. Bai, K. Ma, M. Neurock and J. A. Dumesic, Solvent-Enabled Control of Reactivity for Liquid-Phase Reactions of Biomass-Derived Compounds, Nat. Catal., 2018, 1, 199–207.
3. P. J. Dyson and P. G. Jessop, Solvent Effects in Catalysis: Rational Improvements of Catalysts via Manipulation of Solvent Interactions, Catal. Sci. Technol., 2016, 6, 3302–3316.
4. N. S. Gould, S. Li, H. J. Cho, H. Landfield, S. Caratzoulas, D. Vlachos, P. Bai and B. Xu, Understanding Solvent Effects on Adsorption and Protonation in Porous Catalysts, Nat. Commun., 2020, 11, 1060.
5. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3093.
6. B. W. J. Chen, L. Xu and M. Mavrikakis, Computational Methods in Heterogeneous Catalysis, Chem. Rev., 2021, 121, 1007–1048.
7. X. Zhang and R. S. Paton, Stereoretention in Styrene Heterodimerisation Promoted by One-Electron Oxidants, Chem. Sci., 2020, 11, 9309–9324.
8. S. K. Sinha, S. Panja, J. Grover, P. S. Hazra, S. Pandit, Y. Bairagi, X. Zhang and D. Maiti, Dual Ligand Enabled Nondirected C–H Chalcogenation of Arenes and Heteroarenes, J. Am. Chem. Soc., 2022, 144, 12032–12042.
9. H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, Solvation at Metal/Water Interfaces: An Ab Initio Molecular Dynamics Benchmark of Common Computational Approaches, J. Chem. Phys., 2020, 152, 144703.
10. M. Saleheen and A. Heyden, Liquid-Phase Modeling in Heterogeneous Catalysis, ACS Catal., 2018, 8, 2188–2194.
11. A. Stirling, N. N. Nair, A. Lledós and G. Ujaque, Challenges in Modelling Homogeneous Catalysis: New Answers from Ab Initio Molecular Dynamics to the Controversy over the Wacker Process, Chem. Soc. Rev., 2014, 43, 4940–4952.
12. M. M. Heravi, M. Ghavidel and L. Mohammadkhani, Beyond a Solvent: Triple Roles of Dimethylformamide in Organic Chemistry, RSC Adv., 2018, 8, 27832–27862.
13. J. Zhang, H. Zhang, T. Wu, Q. Wang and D. Van Der Spoel, Comparison of Implicit and Explicit Solvent Models for the Calculation of Solvation Free Energy in Organic Solvents, J. Chem. Theory Comput., 2017, 13, 1034–1043.
14. R. E. Plata and D. A. Singleton, A Case Study of the Mechanism of Alcohol-Mediated Morita Baylis-Hillman Reactions. The Importance of Experimental Observations, J. Am. Chem. Soc., 2015, 137, 3811–3826.
15. R. Salari and L. T. Chong, Effects of High Temperature on Desolvation Costs of Salt Bridges across Protein Binding Interfaces: Similarities and Differences between Implicit and Explicit Solvent Models, J. Phys. Chem. B, 2012, 116, 2561–2567.
16. D. S. D. Larsson and D. Van Der Spoel, Screening for the Location of RNA Using the Chloride Ion Distribution in Simulations of Virus Capsids, J. Chem. Theory Comput., 2012, 8, 2474–2483.
17. H. Zhang, T. Tan and D. Van Der Spoel, Generalized Born and Explicit Solvent Models for Free Energy Calculations in Organic Solvents: Cyclodextrin Dimerization, J. Chem. Theory Comput., 2015, 11, 5103–5113.
18. Y. Fu, L. Bernasconi and P. Liu, Ab Initio Molecular Dynamics Simulations of the SN1/SN2 Mechanistic Continuum in Glycosylation Reactions, J. Am. Chem. Soc., 2021, 143, 1577–1589.
19. J. E. Eksterowicz and K. N. Houk, Transition-State Modeling with Empirical Force Fields, Chem. Rev., 1993, 93, 2439–2461.
20. T. Nagy and M. Meuwly, Modelling Chemical Reactions Using Empirical Force Fields, Theory Appl. Empirical Valence Bond Approach, 2017, 1–25.
21. A. Warshel and J. Florian, The Empirical Valence Bond (EVB) Method, in Encyclopedia of Computational Chemistry, John Wiley & Sons, Ltd, Chichester, UK, 2004.
22. A. C. T. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409.
23. T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik and H. M. Aktulga, et al., The ReaxFF Reactive Force-Field: Development, Applications and Future Directions, npj Comput. Mater., 2016, 2, 15011.
24. P. Koskinen and V. Mäkinen, Density-Functional Tight-Binding for Beginners, Comput. Mater. Sci., 2009, 47, 237–253.
25. G. Seifert and J.-O. Joswig, Density-Functional Tight Binding—An Approximate Density-Functional Theory Method, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 456–465.
26. S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All Spd-Block Elements (Z = 1-86), J. Chem. Theory Comput., 2017, 13, 1989–2009.
27. C. Bannwarth, S. Ehlert and S. Grimme, GFN2-XTB - An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671.
28. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended Tight-Binding Quantum Chemistry Methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493.
29. T. Zubatiuk and O. Isayev, Development of Multimodal Machine Learning Potentials: Toward a Physics-Aware Artificial Intelligence, Acc. Chem. Res., 2021, 54, 1575–1585.
30. O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K. R. Müller, Machine Learning Force Fields, Chem. Rev., 2021, 121, 10142–10186.
31. P. O. Dral, Quantum Chemistry in the Age of Machine Learning, J. Phys. Chem. Lett., 2020, 11, 2336–2347.
32. N. V. Orupattur, S. H. Mushrif and V. Prasad, Catalytic Materials and Chemistry Development Using a Synergistic Combination of Machine Learning and Ab Initio Methods, Comput. Mater. Sci., 2020, 174, 109474.
33. J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, Less Is More: Sampling Chemical Space with Active Learning, J. Chem. Phys., 2018, 148, 241733.
34. R. Jinnouchi, K. Miwa, F. Karsai, G. Kresse and R. Asahi, On-the-Fly Active Learning of Interatomic Potentials for Large-Scale Atomistic Simulations, J. Phys. Chem. Lett., 2020, 11, 6946–6955.
35. J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, On-the-Fly Active Learning of Interpretable Bayesian Force Fields for Atomistic Rare Events, npj Comput. Mater., 2020, 6, 20.
36. A. Hajibabaei, C. W. Myung and K. S. Kim, Sparse Gaussian Process Potentials: Application to Lithium Diffusivity in Superionic Conducting Solid Electrolytes, Phys. Rev. B, 2021, 103, 214102.
37. S. Jindal, S. Chiriki and S. S. Bulusu, Spherical Harmonics Based Descriptor for Neural Network Potentials: Structure and Dynamics of Au147 Nanocluster, J. Chem. Phys., 2017, 146, 204301.
38. F. Zielinski, P. I. Maxwell, T. L. Fletcher, S. J. Davie, N. Di Pasquale, S. Cardamone, M. J. L. Mills and P. L. A. Popelier, Geometry Optimization with Machine Trained Topological Atoms, Sci. Rep., 2017, 7, 1–18.
39. S. Laghuvarapu, Y. Pathak and U. D. Priyakumar, BAND NN: A Deep Learning Framework for Energy Prediction and Geometry Optimization of Organic Small Molecules, J. Comput. Chem., 2020, 41, 790–799.
40. A. Denzel and J. Kästner, Gaussian Process Regression for Geometry Optimization, J. Chem. Phys., 2018, 148, 094114.
41. S. Huang, C. Shang, P. Kang, X. Zhang and Z. Liu, LASP: Fast Global Potential Energy Surface Exploration, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415.
42. B. W. J. Chen, B. Wang, M. B. Sullivan, A. Borgna and J. Zhang, Unraveling the Synergistic Effect of Re and Cs Promoters on Ethylene Epoxidation over Silver Catalysts with Machine Learning-Accelerated First-Principles Simulations, ACS Catal., 2022, 12, 2540–2551.
43. Z. D. Pozun, K. Hansen, D. Sheppard, M. Rupp, K. R. Müller and G. Henkelman, Optimizing Transition States via Kernel-Based Machine Learning, J. Chem. Phys., 2012, 136, 174101.
44. I. Fdez. Galván, G. Raggi and R. Lindh, Restricted-Variance Constrained, Reaction Path, and Transition State Molecular Optimizations Using Gradient-Enhanced Kriging, J. Chem. Theory Comput., 2021, 17, 571–582.
45. S. K. Natarajan and J. Behler, Neural Network Molecular Dynamics Simulations of Solid-Liquid Interfaces: Water at Low-Index Copper Surfaces, Phys. Chem. Chem. Phys., 2016, 18, 28704–28725.
46. C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Machine Learning Potentials for Complex Aqueous Systems Made Simple, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 1–8.
47. P. S. Rice, Z. P. Liu and P. Hu, Hydrogen Coupling on Platinum Using Artificial Neural Network Potentials and DFT, J. Phys. Chem. Lett., 2021, 12, 10637–10645.
48. N. Artrith and J. Behler, High-Dimensional Neural Network Potentials for Metal Surfaces: A Prototype Study for Copper, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045439.
49. H. Li, Z. Zhang and Z. Liu, Application of Artificial Neural Networks for Catalysis: A Review, Catalysts, 2017, 7, 306.
50. Y. Han, J. Xu, W. Xie, Z. Wang and P. Hu, Comprehensive Study of Oxygen Vacancies on the Catalytic Performance of ZnO for CO/H₂ Activation Using Machine Learning-Accelerated First-Principles Simulations, ACS Catal., 2023, 5104–5113.
51. E. V. Podryabinkin, E. V. Tikhonov, A. V. Shapeev and A. R. Oganov, Accelerating Crystal Structure Prediction by Machine-Learning Interatomic Potentials with Active Learning, Phys. Rev. B, 2019, 99, 064114.
52. S. J. Ang, W. Wang, D. Schwalbe-Koda, S. Axelrod and R. Gómez-Bombarelli, Active Learning Accelerates Ab Initio Molecular Dynamics on Reactive Energy Surfaces, Chem, 2021, 7, 738–751.
53. S. Heinen, M. Schwilk, G. Falk, V. Rudorff, P. Van Gerwen, A. Fabrizio, M. D. Wodrich and C. Corminboeuf, Physics-Based Representations for Machine Learning Properties of Chemical Reactions, Machine Learning: Science and Technology, 2022, 3, 045005.
54. T. Young, T. Johnston-Wood, V. Deringer and F. Duarte, A Transferable Active-Learning Strategy for Reactive Molecular Force Fields, 2021.
55. A. Hajibabaei, M. Ha, S. Pourasad, J. Kim and K. S. Kim, Machine Learning of First-Principles Force-Fields for Alkane and Polyene Hydrocarbons, J. Phys. Chem. A, 2021, 125, 9414–9420.
56. M. Ha, A. Hajibabaei, D. Y. Kim, A. N. Singh, J. Yun, C. W. Myung and K. S. Kim, Al-Doping Driven Suppression of Capacity and Voltage Fadings in 4d-Element Containing Li-Ion-Battery Cathode Materials: Machine Learning and Density Functional Theory, Adv. Energy Mater., 2022, 12, 2201497.
57. C. W. Myung, A. Hajibabaei, J. H. Cha, M. Ha, J. Kim and K. S. Kim, Challenges, Opportunities, and Prospects in Metal Halide Perovskites from Theoretical and Machine Learning Perspectives, Adv. Energy Mater., 2022, 12, 2202279.
58. M. Ha, P. Thangavel, N. K. Dang, D. Y. Kim, S. Sultan, J. S. Lee and K. S. Kim, High-Performing Atomic Electrocatalyst for Chlorine Evolution Reaction, Small, 2023, 19, 2300240.
59. J. D. Morrow, J. L. A. Gardner and V. L. Deringer, How to Validate Machine-Learned Interatomic Potentials, J. Chem. Phys., 2023, 158, 121501.
60. A. V. Shapeev, Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials, Multiscale Model. Simul., 2016, 14, 1153–1173.
61. J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: An Extensible Neural Network Potential with DFT Accuracy at Force Field Computational Cost, Chem. Sci., 2017, 8, 3192–3203.
62. K. T. Schütt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Müller, SchNet - A Deep Learning Architecture for Molecules and Materials, J. Chem. Phys., 2018, 148, 241722.
63. L. B. Skinner, C. Huang, D. Schlesinger, L. G. M. Pettersson, A. Nilsson and C. J. Benmore, Benchmark Oxygen-Oxygen Pair-Distribution Function of Ambient Water from X-Ray Diffraction Measurements with a Wide Q-Range, J. Chem. Phys., 2013, 138, 074506.
64. E. V. Podryabinkin and A. V. Shapeev, Active Learning of Linearly Parametrized Interatomic Potentials, Comput. Mater. Sci., 2017, 140, 171–180.
65. I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, The MLIP Package: Moment Tensor Potentials with MPI and Active Learning, Machine Learning: Science and Technology, 2021, 2, 025002.
66. I. Saika-Voivod, F. Sciortino and P. H. Poole, Computer Simulations of Liquid Silica: Equation of State and Liquid-Liquid Phase Transition, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 1–9.
67. J. Russo and H. Tanaka, Understanding Water's Anomalies with Locally Favoured Structures, Nat. Commun., 2014, 5, 3556.
68. E. Shiratani and M. Sasai, Molecular Scale Precursor of the Liquid–Liquid Phase Transition of Water, J. Chem. Phys., 1998, 108, 3264–3276.
69. P. Chau and A. J. Hardwick, A New Order Parameter for Tetrahedral Configurations, Mol. Phys., 1998, 93, 511–518.
70. R. Sharma, S. N. Chakraborty and C. Chakravarty, Entropy, Diffusivity, and Structural Order in Liquids with Waterlike Anomalies, J. Chem. Phys., 2006, 125, 204501.
71. C. R. García-Alonso, L. M. Pérez-Naranjo and J. C. Fernández-Caballero, Multiobjective Evolutionary Algorithms to Identify Highly Autocorrelated Areas: The Case of Spatial Distribution in Financially Compromised Farms, Annals of Operations Research, 2014, 219, 187–202.
72. M. J. Gillan, D. Alfè and A. Michaelides, Perspective: How Good Is DFT for Water?, J. Chem. Phys., 2016, 144, 1–33.
73. O. Cheong, M. H. Eikerling and P. M. Kowalski, Water Structures on Pb(100) and (111) Surface Studied with the Interface Force Field, Appl. Surf. Sci., 2022, 589, 152838.
74. O. Marsalek and T. E. Markland, Quantum Dynamics and Spectroscopy of Ab Initio Liquid Water: The Interplay of Nuclear and Electronic Quantum Effects, J. Phys. Chem. Lett., 2017, 8, 1545–1551.
75. R. Shi and H. Tanaka, Microscopic Structural Descriptor of Liquid Water, J. Chem. Phys., 2018, 148, 124503.
76. S. Sakong and A. Groß, Water Structures on a Pt(111) Electrode from: Ab Initio Molecular Dynamic Simulations for a Variety of Electrochemical Conditions, Phys. Chem. Chem. Phys., 2020, 22, 10431–10437.
77. J. Le, M. Iannuzzi, A. Cuesta and J. Cheng, Determining Potentials of Zero Charge of Metal Electrodes versus the Standard Hydrogen Electrode from Density-Functional-Theory-Based Molecular Dynamics, Phys. Rev. Lett., 2017, 119, 1–6.
78. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit Self-Consistent Electrolyte Model in Plane-Wave Density-Functional Theory, J. Chem. Phys., 2019, 151, 234101.
79. P. Li, J. Huang, Y. Hu and S. Chen, Establishment of the Potential of Zero Charge of Metals in Aqueous Solutions: Different Faces of Water Revealed by Ab Initio Molecular Dynamics Simulations, J. Phys. Chem. C, 2021, 125, 3972–3979.
80. S. Sakong and A. Groß, The Electric Double Layer at Metal-Water Interfaces Revisited Based on a Charge Polarization Scheme, J. Chem. Phys., 2018, 149, 084705.
81. S. Schnur and A. Groß, Properties of Metal–Water Interfaces Studied from First Principles, New J. Phys., 2009, 11, 125003.
82. G. Henkelman, B. P. Uberuaga and H. Jonsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904.
83. V. A. Roytman and D. A. Singleton, Solvation Dynamics and the Nature of Reaction Barriers and Ion-Pair Intermediates in Carbocation Reactions, J. Am. Chem. Soc., 2020, 142, 12865–12877.
84. A. P. Bhati, S. Wan, D. W. Wright and P. V. Coveney, Rapid, Accurate, Precise, and Reliable Relative Free Energy Prediction Using Ensemble Based Thermodynamic Integration, J. Chem. Theory Comput., 2017, 13, 210–222.
85. G. Bussi and A. Laio, Using Metadynamics to Explore Complex Free-Energy Landscapes, Nat. Rev. Phys., 2020, 2, 200–212.
86. M. Zare, M. Saleheen, S. K. Kundu and A. Heyden, Dependency of Solvation Effects on Metal Identity in Surface Reactions, Commun. Chem., 2020, 3, 187.
87. M. Faheem and A. Heyden, Hybrid Quantum Mechanics/Molecular Mechanics Solvation Scheme for Computing Free Energies of Reactions at Metal-Water Interfaces, J. Chem. Theory Comput., 2014, 10, 3354–3368.
88. Z. Li and D. Hoiem, Learning without Forgetting, IEEE Trans. Pattern Anal. Mach. Intell., 2018, 40, 2935–2947.
89. V. L. Deringer, M. A. Caro and G. Csányi, Machine Learning Interatomic Potentials as Emerging Tools for Materials Science, Adv. Mater., 2019, 31, 1902765.
90. L. Zhang, H. Wang, M. C. Muniz, A. Z. Panagiotopoulos, R. Car and E. Weinan, A Deep Potential Model with Long-Range Electrostatic Interactions, J. Chem. Phys., 2022, 156, 124107.
91. D. M. Anstine and O. Isayev, Machine Learning Interatomic Potentials and Long-Range Physics, J. Phys. Chem. A, 2023, 127, 2417–2431.
92. X. Xie, K. A. Persson, D. W. Small and D. W. Small, Incorporating Electronic Information into Machine Learning Potential Energy Surfaces via Approaching the Ground-State Electronic Energy as a Function of Atom-Based Electronic Populations, J. Chem. Theory Comput., 2020, 16, 4256–4270.
93. A. Grisafi and M. Ceriotti, Incorporating Long-Range Physics in Atomic-Scale Machine Learning, J. Chem. Phys., 2019, 151, 204105.
94. J. Behler and G. Csányi, Machine Learning Potentials for Extended Systems: A Perspective, Eur. Phys. J. B, 2021, 94, 142.
95. S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials, Nat. Commun., 2022, 13, 2453.
96. I. Batatia, D. P. Kovács, G. N. C. Simm, C. Ortner and G. Csányi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, 2022.
97. T. Mueller, A. Hernandez and C. Wang, Machine Learning for Interatomic Potential Models, J. Chem. Phys., 2020, 152, 050902.
98. T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, A Fourth-Generation High-Dimensional Neural Network Potential with Accurate Electrostatics Including Non-Local Charge Transfer, Nat. Commun., 2021, 12, 398.
99. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
100. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
101. J. G. Brandenburg, T. Maas and S. Grimme, Benchmarking DFT and Semiempirical Methods on Structures and Lattice Energies for Ten Ice Polymorphs, J. Chem. Phys., 2015, 142, 124104.
102. H. Ghorbanfekr, J. Behler and F. M. Peeters, Insights into Water Permeation through HBN Nanocapillaries by Ab Initio Machine Learning Molecular Dynamics Simulations, J. Phys. Chem. Lett., 2020, 11, 7363–7370.
103. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
104. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
105. B. Hammer, L. B. Hansen and J. K. Nørskov, Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
106. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
107. K. Forster-Tonigold and A. Groß, Dispersion Corrected RPBE Studies of Liquid Water, J. Chem. Phys., 2014, 141, 064501.
108. C. Kittel, Introduction to Solid State Physics, ed. S. Johnson, John Wiley & Sons, Inc., New York, 2004, pp. 1–704.
109. W. S. Morgan, J. E. Christensen, P. K. Hamilton, J. J. Jorgensen, B. J. Campbell, G. L. W. Hart and R. W. Forcade, Generalized Regular K-Point Grid Generation on the Fly, Comput. Mater. Sci., 2020, 173, 109340.
110. W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A, 1985, 31, 1695–1697.
111. S. Nosé, A Unified Formulation of the Constant Temperature Molecular Dynamics Methods, J. Chem. Phys., 1984, 81, 511–519.
112. J. J. Blomqvist, M. Dulak, J. Friis, C. Hargus, A. Larsen, M. Jens, B. Jakob, C. Ivano, C. Rune and D. Marcin, et al., The Atomic Simulation Environment—A Python Library for Working with Atoms, J. Phys.: Condens. Matter, 2017, 29, 273002.
113. K. A. Feenstra, B. Hess and H. J. C. Berendsen, Improving Efficiency of Large Time-Scale Molecular Dynamics Simulations of Hydrogen-Rich Systems, J. Comput. Chem., 1999, 20, 786–798.
114. J. R. Boes, O. Mamun, K. Winther and T. Bligaard, Graph Theory Approach to High-Throughput Surface Adsorption Structure Generation, J. Phys. Chem. A, 2019, 123, 2281–2285.
115. The PLUMED Consortium, Promoting Transparency and Reproducibility in Enhanced Molecular Simulations, Nat. Methods, 2019, 16, 670–673.
116. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: New Feathers for an Old Bird, Comput. Phys. Commun., 2014, 185, 604–613.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02482b

---