Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Feshbach resonances in the F + CHD3 → HF + CD3 reaction†
Shu
Liu
 *ab,
Jun
Chen
*ab,
Jun
Chen
 c,
Xiaoren
Zhang
a and
Dong H.
Zhang
c,
Xiaoren
Zhang
a and
Dong H.
Zhang
 *ab
*ab
aState Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian, Liaoning 116023, China. E-mail: liushu1985@dicp.ac.cn; zhangdh@dicp.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
cState Key Laboratory of Structure Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, China
First published on 24th June 2023
Abstract
The signature of dynamics resonances was observed in the benchmark polyatomic F + CH4/CHD3 reactions more than a decade ago; however, the dynamical origin of the resonances is still not clear due to the lack of reliable quantum dynamics studies on accurate potential energy surfaces. Here, we report a six-dimensional state-to-state quantum dynamics study on the F + CHD3 → HF + CD3 reaction on a highly accurate potential energy surface. Pronounced oscillatory structures are observed in the total and product rovibrational-state-resolved reaction probabilities. Detailed analysis reveals that these oscillating features originate from the Feshbach resonance states trapped in the peculiar well on the HF(v′ = 3)–CD3 vibrationally adiabatic potential caused by HF chemical bond softening. Most of the resonance structures on the reaction probabilities are washed out in the well converged integral cross sections (ICS), leaving only one distinct peak at low collision energy. The calculated HF vibrational state-resolved ICS for CD3(v = 0) agrees quantitatively with the experimental results, especially the branching ratio, but the theoretical CD3 umbrella vibration state distribution is found to be much hotter than the experiment.
Over the past decades, a clear physical picture of the reaction resonances in the F + H2/HD/H2O/HOD/NH3 reactions has been established through close interaction between high-resolution crossed-molecular beams or transition-state spectroscopy experiments and quantum dynamics calculations on highly accurate potential energy surfaces (PESs).1–10 All these hydrogen abstraction reactions involving a F atom possess similar dynamical resonances trapped by the HF vibrational excited adiabatic potential wells in the post-barrier region.
Like the F + H2/H2O/NH3 systems, the F + CH4 → HF + CH3 reaction is another benchmark system for highly exothermic hydrogen abstraction reactions with a low and early barrier. It has a bent transition-state geometry, a shallow van der Waals (vdW) well in the entrance channel and a deeper vdW well in the exit channel, both with linear configurations. The reaction plays an important role in atmospheric chemistry and can yield a highly inverted HF(v′) vibrational distribution, which shows great potential in the production of chemical lasers.11–13 Liu and coworkers reported the first experimental signature of reactive resonances in a polyatomic reaction in the F + CH4/CHD3 reaction.14–17 In the F + CHD3(v = 0) reaction, they observed a step-like feature in the excitation function of the CD3(v = 0) + HF channel at low collision energies,15 which echoes the resonance fingerprints in the integral cross sections (ICS) of the F + HD → HF + D reaction.18,19 Furthermore, the excitation function of the CHD2(v = 0) + DF channel displays a ‘kink’ in shape at about the same energy.15 The differential cross-sections (DCS) of the two isotopic channels both show a near-threshold ridge and oscillatory forward–backward peaking, which also provide strong support for reactive resonances.16 The cross-sections of the bending-excited reaction F + CHD3(vb = 1) also show peak features for the CD3(v2 = 0,1) + HF(v′ = 3) channels.17 In addition, they observed anticorrelation in the vibrational states of the coincident product pairs of CD3(v2) and DF(v′) in the F + CD4 reaction.20–22
Theoretically, great efforts have been devoted to the construction of an accurate potential energy surface (PES) for the F + CH4 system.23–28 In 2009, Czakó et al. constructed a full-dimensional PES with permutational invariant polynomials (PIP) method called CSBB PES,29 and subsequently improved the PES by including the spin–orbit (SO) coupling term of the F atom.30 In 2014, Westermann et al.31,32 constructed the coupled diabatic WEM PESs for the entrance channel region containing vibronic as well as SO coupling effects and connected the lowest adiabatic one with the CSBB PES in the interaction region to acquire a global adiabatic PES called PWEM PES. Later, they constructed the globally defined coupled diabatic PESs33 by using the same set of diabatic electronic states in the transition state region and all four exit channels. In 2018, our group constructed a global PES for the system using a neural network (NN) fitting method based on 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 UCCSD(T)-F12a/aug-cc-pVTZ ab initio energies.34 Correction terms considering the influence of a larger basis set as well as spin–orbit couplings were further implemented with a hierarchical scheme. With a fitting error of ∼4.87 meV for energies within 2.5 eV, our NN PES is substantially more accurate than the previous ones.
000 UCCSD(T)-F12a/aug-cc-pVTZ ab initio energies.34 Correction terms considering the influence of a larger basis set as well as spin–orbit couplings were further implemented with a hierarchical scheme. With a fitting error of ∼4.87 meV for energies within 2.5 eV, our NN PES is substantially more accurate than the previous ones.
The theoretical evidence for reactive resonances in the F + CH4 reaction was first reported by Nyman et al. through the oscillations in the cumulative reaction probabilities (CRP) and the dramatic change of DCS with collision energy35 by using the time-independent three-dimensional rotating line umbrella (RLU) quantum scattering model. Wang showed the resonance features in the initial-state-selected total reaction probabilities and the ICS calculated by using the four-degree-of-freedom quantum dynamics approach on the CSBB PES.36 Westermann et al. found resonances trapped in the entrance channel vdW well of the F + CH4 system32via the transition-state spectra calculated using the full-dimensional (12D) multi-configurational time-dependent Hartree (MCTDH) approach on the WEM PESs. For the F + CHD3 reaction, von Horsten and Clary studied the reactive resonances using a two-dimensional model, which only described the bond breaking and bond forming explicitly. The final state resolved ICS for both reaction channels showed qualitative agreement with experimental results, although discrepancies remained in the branching ratios. They attributed the low energy peaks in the CRP to quasi-bound states with a quantum number v′ = 3 of the H–F stretch mode, and v′ = 4 of the D–F stretch mode in the product region.37 Qi et al. performed eight-dimensional (8D) wave packet dynamics calculations38 on the PWEM PES, and Zhao et al. performed seven-dimensional (7D) non-adiabatic wave packet dynamics calculations39 on the global vibronically and SO-coupled diabatic PESs for the F + CHD3 reaction. They both reported fast-oscillating structures on the total reaction probabilities at low collision energies, but attributed them to the resonances in the pre-reaction vdW well. Therefore, the origin of the resonances in the reaction is still not clear.
Here, we report six-dimensional (6D) state-to-state quantum dynamics studies of the F + CHD3 → HF + CD3 reaction on the NN PES. Pronounced oscillatory structures are observed in the total reaction probabilities, in particular at collision energies below 0.05 eV. Detailed analysis reveals that these oscillating features originate from the Feshbach resonance states trapped in the peculiar well on the HF(v′ = 3)–CD3 vibrational adiabatic potential (VAP) caused by HF bond softening, mainly producing HF(v′ = 2). The calculated vibrational state-specific excitation functions of HF(v′) + CD3(v = 0) are in good agreement with the experimental results. However, the theoretical CD3 umbrella vibration state distribution is found to be much hotter than the experiment.
The reduced dimensional model employed in the time-dependent wave packet (TDWP) calculations here was the free-torsion seven-dimensional (FT-7D) model we proposed for the X + YCZ3 → XY + CZ3 reaction in 2013, by assuming that the CZ3 group can rotate freely with respect to its C3v symmetry axis.40 This is an additional approximation introduced to the original eight-dimensional (8D) model of Palma and Clary with the nonreacting CZ3 group constrained in the C3v symmetry41 to reduce computational costs. With the bond length of CD fixed at its equilibrium value in the reactant (2.06 bohr) because it essentially does not change during the reaction, the number of degrees of freedom included in the calculation was reduced to six. We used the multiple-step reactant-product decoupling (MRPD) method42–44 to obtain the state-to-state information. We carried out state-to-state calculations for the total angular momentum Jtot = 0, 10, 15, 20, 25, 30, 40, 60, and 80 to converge the ICS for collision energies up to 0.3 eV. For details of the numerical parameters, please refer to the ESI.†
Fig. 1(A) shows the total reaction probabilities for the total angular momentum Jtot = 0 calculated using the 7D (with the CH bond length fixed in the original 8D model) and FT-6D models. The converged reaction probabilities rise rapidly as the collision energy increases from 0 to 0.2 eV without a reaction threshold, exhibiting many sharp and narrow oscillatory structures, especially for collision energies below 0.05 eV. Except at very low collision energies, the present reaction probabilities on the NN PES are larger than those38,39 on the PWEM and vibronically and SO-coupled diabatic PESs. It can be seen that the 6D treatment can produce similar reaction probabilities to the 7D results, except that the 6D probabilities are slightly smaller between 0.02 and 0.15 eV. We, therefore, used the 6D model to carry out state-to-state calculations to reduce computational costs.
 | ||
| Fig. 1 (A) Total and (B) product HF vibrational state-resolved Jtot = 0 reaction probabilities for the initial ground rovibrational state as a function of collision energy. | ||
Fig. 1(B) shows the 6D HF vibrational state-resolved reaction probabilities as a function of collision energy. The HF(v′ = 2) state has the largest population in the entire energy region considered here, indicating an inverted HF vibrational state distribution. With increasing collision energy, the reaction probabilities for the HF(v′ = 1) state gradually increase, and the fraction of HF(v′ = 2) decreases after 0.16 eV. The lowest vibrational state HF(v′ = 0) can only be observed at Ec > 0.1 eV as a smooth curve. The HF(v′ = 3) channel opens at a collision energy of 0.05 eV and has a probability that remains almost constant at high collision energies. The probabilities of the HF(v′ = 1, 2, 3) states all show oscillation peaks at low collision energies and become smooth in the high-energy region.
To investigate the dynamical origin of the oscillatory structures, we calculated the Jtot = 0 time-independent (TID) scattering wavefunctions at some collision energies for the reaction by performing Fourier transform of the time-dependent wavefunctions. Inspection of the two-dimensional contour of the wavefunction for the collision energy at 0.0135 eV in the product coordinates shown in Fig. 2(A) reveals that there exist three nodes along the H–F coordinate (correlating to the HF product) in the HF–CD3 complex, but only two nodes for the outgoing wavefunction with a sudden decrease in amplitude. The sudden change in the nodal structure and amplitude of the wavefunction is the characteristic feature of a Feshbach resonance, indicating that the resonance is trapped in the HF(v′ = 3) VAP well and produces mainly the HF(v′ = 2) product. Similar to the F + H2/HD/HOD(v = 1) reactions, the resonance wavefunctions of the title reaction are also narrow and located close to the barrier, and do not traverse the entire vdW well. The TID wavefunctions at the other low collision energies are found to have the same nodal structure as shown in Fig. 2(A).
To further confirm the mechanism of the resonance, we calculated the VAP for HF(v′ = 0–3) in the product region. The reaction coordinates are calculated in terms of RF–CHD3 on the reactant side and RHF–CD3 on the product side. As can be seen in Fig. 2(B), the VAP curves relevant to the vibrational states HF(v′ = 0–2) only have vdW wells. The minimum position of the vdW well moves from RHF–CD3 = 5.7 a0 for v′ = 0, to 5.6 a0 for v′ = 1, and 5.4 a0 for v′ = 2, while the well depth increases slowly with v′, from 0.082 eV for v′ = 0, to 0.103 eV for v′ = 1, and 0.137 for v′ = 2. On the other hand, the HF(v′ = 3)–CD3 VAP well is substantially deeper and is located much closer to the barrier than the HF(v′ = 0–2)–CD3 vdW wells, which is the very peculiar well caused by chemical bond softening. The HF(v′ = 3)–CD3 VAP has an asymptotic value of 0.0472 eV measured from the ground state of the reactants, and a well bottom lower than the ground state of the reactants. This means that the F + CHD3 reaction can access the Feshbach resonances supported by the HF(v′ = 3)–CD3 VAP well even with zero collision energy, which can only decay into lower HF(v′ = 0–2) vibrational states via vibrational predissociation before the HF(v′ = 3) channel opens. Therefore, the oscillating structures on the HF(v′ = 1,2) probabilities in Fig. 1(B) originate from the Feshbach resonance states trapped the peculiar HF(v′ = 3)–CD3 VAP well created by the HF bond softening. The discernible oscillating structures on the HF(v′ = 3) probabilities and HF(v′ = 2) probabilities for Ec > 0.05 eV may originate from the bending excited HF(v′ = 3)–CD3 VAP supported resonance states.
To investigate the effect of the resonance structures on the ICS, we calculated the ICS for the title reaction based on the reaction probabilities for Jtot = 0, 10, 15, 20, 25, 30, 40, 60 and 80, as shown in Fig. S1.† With increasing Jtot, the reaction probability curve shifts to higher energy, and the influence of the resonances on the reaction gradually fades. In order to take into account the change in the resonance structures with collision energy and Jtot, we estimated the reaction probabilities for partial waves J1 < J < J2 as
PJ(E) = PJ1J(E) × f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(J) + PJ2J(E) × [1 − f cos(J) + PJ2J(E) × [1 − f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(J)], cos(J)], |
P J 1 J (E) = PJ1(E − ΔE1) and PJ2J(E) = PJ2(E + ΔE2) are obtained using the J-shifting approximation with ΔE1 = [J(J + 1) − J1(J1 + 1)] × B, ΔE2 = [J2(J2 + 1) − J(J + 1)] × B. B is a varying rotational constant for different [J1, J2] intervals, which is obtained by minimizing the difference between PJ1(E − [J2(J2 + 1) − J1(J1 + 1)] × B) and PJ2(E). Fig. 3(A) shows the HF vibrational state-resolved ICS as a function of collision energy. The shapes of the excitation function are similar to the Jtot = 0 reaction probabilities in Fig. 1(B), except that the ICS of HF(v′ = 3) are higher than HF(v′ = 1) above Ec = 0.062 eV. Most resonance structures on the reaction probabilities vanish in the ICS after averaging over impact parameter Jtot, leaving only one distinct peak near Ec = 0.015 eV. In order to test the convergence of the ICS, four reaction probabilities (Jtot = 10, 15, 25, 30) were removed, and the cross-sections obtained using the 5 Jtot were in good agreement with those calculated with all 9 Jtot, even the resonance peaks, as shown in Fig. S2.† This proves that the J-shifting approximation method used here is reliable for reproducing the resonance structures on the reaction probabilities. Fig. S3† shows the normalized HF vibrational populations as a function of collision energy for the title reaction, which provide a comparison to the quasi-classical trajectories (QCT) results obtained using different methods on the CSBB PES.45 It can be seen that the GBZPVE method can reproduce the results near the threshold very well, while the GBall method is more suitable for higher energies.
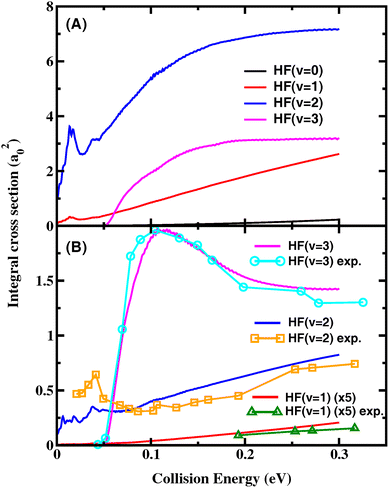 | ||
| Fig. 3 Product HF vibrational state-resolved ICS for the title reaction as a function of collision energy (A) including all the rovibrational states of CD3 and (B) for CD3(v = 0) together with the experimental excitation functions in ref. 15. | ||
Fig. 3(B) shows the HF vibrational state-resolved ICS for CD3(v = 0) as a function of collision energy, along with the experimental excitation functions in ref. 15. The experimental and theoretical vibrational branching ratios of the product HF are in quantitative agreement with each other. The HF(v′ = 2) state is the sole contributor to the ICS in the low-energy regime. After the HF(v′ = 3) channel opens at Ec = ∼0.05 eV, its ICS rises rapidly and becomes the dominant channel. After reaching its peak at 0.1 eV, the HF(v′ = 3) ICS declines with further increase in the collision energy, causing the relative branching ratio of (v′ = 3)/(v′ = 2) to decrease. Both the experimental and theoretical ICS of the HF(v′ = 1) state are very small throughout the entire energy region considered here. The experimental excitation functions of HF(v′ = 2) have a step-like feature near 0.04 eV as evidence of the resonance. Our theoretical ICS of the HF(v′ = 2) state shows a peak at about the same energy, but with a lower amplitude.
As can be seen, the theoretical ICS including all the rovibrational states of CD3 shown in Fig. 3(A) are very different from those shown in Fig. 3(B) for the vibrational ground state of CD3, indicating that the HF vibrational distributions strongly depend on the CD3 umbrella states, or there exists a strong correlation between the vibrational distributions of the two product molecules. Fig. 4 shows the correlated ICS of the HF(v′) + CD3(v2) product pair at collision energies of 0.0145 eV, 0.1 eV, 0.2 eV and 0.3 eV. The branching ratios are obtained by normalizing the CD3 umbrella vibration distribution for each HF state at a given Ec. A strong anti-correlation between the vibration excitations of the paired products is apparent. At all four collision energies, as the HF excitation increases, the umbrella mode excitations of the correlated CD3 show a noticeable decrease, and the proportion of CD3(v2 = 0) becomes increasingly larger. The CD3 umbrella state with the largest population changes from v2 = 6 for v′ = 0, to v2 = 4 for v′ = 1, to v2 = 3 for v′ = 2, and to v2 = 0 for v′ = 3. This strong anti-correlation between HF stretching and CD3 umbrella motion is in agreement with what Liu and coworkers observed in the F + CD4 reaction,20–22 but the theoretical CD3 umbrella mode excitations are much hotter than those observed in the F + CD4 experiment, which were mainly populated in v2 = 0–3. Because the umbrella angle of CD3 in the transition state and that in the product are quite different for this early barrier reaction, strong vibrational excitation for umbrella motion is expected. The QCT-correlated ICS for HF(v′) + CD3(v2) at a collision energy of 2.8 kcal mol−1 (0.121 eV) in ref. 45 showed the same anti-correlation trend, except that the present quantum mechanical (QM) CD3 excitation is slightly hotter for HF(v′ = 2) and slightly colder for HF(v′ = 3), as shown in Fig. S4.†
Fig. S5† shows the correlated ICS of the HF(v′) + CD3(v2) product pair, but the sum of the HF vibration populations for each CD3 state at a given Ec is scaled to unity. For the ground CD3 state, the HF vibration distribution is highly inverted, all peaking at v′ = 3, except that the HF(v′ = 3) channel is energetically closed at Ec = 0.0145 eV. With higher umbrella excitation of CD3, the vibration distribution of the correlated HF becomes colder, peaking at v′ = 2 for v2 = 1–6 and at v′ = 1 for v2 = 7–9 (for Ec = 0.1 eV), at v′ = 2 for v2 = 2–5 and at v′ = 1 for v2 = 6–9 (for Ec = 0.2 eV), and at v′ = 2 for v2 = 1–4 and at v′ = 1 for v2 = 5–9 (for Ec = 0.3 eV).
The anticorrelation of the HF(v′) + CD3(v2) products in terms of the energy distribution is shown in Table S1 and S2.† At a fixed Ec, the average vibration energy of CD3 (〈Ev2〉CD3) decreases with higher vibrational excitation of the correlated HF, while 〈Ev〉HF decreases when more energy is deposited into the umbrella mode of the CD3 coproduct. Because the vibrational energy levels of HF are wide enough to offset the decrease in the correlated average vibration energy of CD3, the sums of 〈Ev2〉CD3 + EHF(v′) increase with v′. On the other hand, the trend in 〈Ev〉 HF + ECD3(v2) is related to both v2 and Ec.
Therefore, our quantum dynamics study of the F + CHD3 → HF + CD3 reaction on the highly accurate NN PES revealed that there exist pronounced oscillating structures in the total reaction probabilities, in particular in the low-collision-energy region, due to dynamical resonances trapped in the peculiar HF(v′ = 3) well in the post-barrier region, similar to those in the F + H2/HD/H2O/HOD reactions. Most of the resonance structures on the reaction probabilities are washed out in the ICS, leaving only a few oscillating structures in the ICS at low collision energies, in agreement with experimental observation. The theoretical HF vibrational state-resolved excitation functions for CD3(v = 0) agree very well with the experimental results, indicating that both the NN PES and quantum-dynamics method are sufficiently accurate for this reaction. A strong anti-correlated excitation of the two product vibrators HF(v′) and CD3(v2) was found in the reaction, similar to what was observed experimentally, but the theoretical CD3 umbrella vibration state distribution is much hotter than those observed in the F + CD4 experiment.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.Author contributions
S. L. and D. H. Z. conceived the research and wrote the manuscript. S. L. performed the quantum dynamical calculation. J. C. and X. Z. developed the PES.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 22022306, 22288201), the Innovation Program for Quantum Science and Technology (Grant No. 2021ZD0303305), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB0450202), and the Dalian Innovation Support Program (Grant No. 2021RD05).References
- M. Qiu, Z. Ren, L. Che, D. Dai, S. A. Harich, X. Wang, X. Yang, C. Xu, D. Xie, M. Gustafsson, R. T. Skodje, Z. Sun and D. H. Zhang, Observation of Feshbach resonances in the F + H2 → HF + H reaction, Science, 2006, 311, 1440–1443 CrossRef CAS PubMed.
- Z. Ren, L. Che, M. Qiu, X. Wang, W. Dong, D. Dai, X. Wang, X. Yang, Z. Sun, B. Fu, S.-Y. Lee, X. Xu and D. H. Zhang, Probing the resonance potential in the F atom reaction with hydrogen deuteride with spectroscopic accuracy, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12662–12666 CrossRef CAS PubMed.
- J. B. Kim, M. L. Weichman, T. F. Sjolander, D. M. Neumark, J. Kłos, M. H. Alexander and D. E. Manolopoulos, Spectroscopic observation of resonances in the F+H2 reaction, Science, 2015, 349, 510–513 CrossRef CAS PubMed.
- T. Yang, L. Huang, C. Xiao, J. Chen, T. Wang, D. Dai, F. Lique, M. H. Alexander, Z. Sun, D. H. Zhang, X. Yang and D. M. Neumark, Enhanced reactivity of fluorine with para-hydrogen in cold interstellar clouds by resonance-induced quantum tunnelling, Nat. Chem., 2019, 11, 744–749 CrossRef CAS PubMed.
- T. Wang, J. Chen, T. Yang, C. Xiao, Z. Sun, L. Huang, D. Dai, X. Yang and D. H. Zhang, Dynamical resonances accessible only by reagent vibrational excitation in the F + HD → HF + D reaction, Science, 2013, 342, 1499–1502 CrossRef CAS PubMed.
- R. Otto, J. Ma, A. W. Ray, J. S. Daluz, J. Li, H. Guo and R. E. Continetti, Imaging dynamics on the F + H2O → HF + OH potential energy surfaces from wells to barriers, Science, 2014, 343, 396–399 CrossRef CAS PubMed.
- J. Ma and H. Guo, Reactive and nonreactive Feshbach resonances accessed by photodetachment of FH2O−, J. Phys. Chem. Lett., 2015, 6, 4822–4826 CrossRef CAS PubMed.
- X. Zhang, L. Li, J. Chen, S. Liu and D. H. Zhang, Feshbach resonances in the F + H2O → HF + OH reaction, Nat. Commun., 2020, 11, 223 CrossRef CAS PubMed.
- S. Liu, X. Zhang, J. Chen and D. H. Zhang, Feshbach resonances in the vibrationally excited F + HOD(vOH/vOD = 1) reaction due to chemical bond softening, J. Phys. Chem. Lett., 2021, 12, 6090–6094 CrossRef CAS PubMed.
- M. C. Babin, M. DeWitt, J. A. Lau, M. L. Weichman, J. B. Kim, H. Song, H. Guo and D. M. Neumark, Observation of resonances in the transition state region of the F+NH3 reaction using anion photoelectron spectroscopy, Nat. Chem., 2023, 15, 194–199 CrossRef CAS PubMed.
- N. Jonathan, C. M. Melliar-Smith and D. H. Slater, Initial vibrational energy distributions determined by infra-red chemiluminescence, Mol. Phys., 1971, 20, 93–102 CrossRef CAS.
- M. A. Nazar and J. C. Polanyi, Energy distribution among reaction products. XIV. F + CH4, F + CH3X(X = Cl, Br, I), F + CHnCl4−n(n = 1−3), Chem. Phys., 1981, 55, 299–311 CrossRef CAS.
- M. A. Wickramaaratchi, D. W. Setser, H. Hildebrandt, B. Kōrbitzer and H. Heydtmann, Evaluation of HF product distributions deduced from infrared chemiluminiscence. II. F atom reactions, Chem. Phys., 1985, 94, 109–129 CrossRef CAS.
- W. Shiu, J. J. Lin and K. Liu, Reactive resonance in a polyatomic reaction, Phys. Rev. Lett., 2004, 92, 103201 CrossRef PubMed.
- J. Zhou, J. J. Lin and K. Liu, Observation of a reactive resonance in the integral cross section of a six-atom reaction: F + CHD3, J. Chem. Phys., 2004, 121, 813–818 CrossRef CAS PubMed.
- J. Zhou, J. J. Lin and K. Liu, Deciphering the nature of the reactive resonance in F + CHD3: correlated differential cross-sections of the two isotopic channels, Mol. Phys., 2010, 108, 957–968 CrossRef CAS.
- G. Czakó, Q. Shuai, K. Liu and J. M. Bowman, Experimental and theoretical investigations of the effects of the reactant bending excitations in the F+CHD3 reaction, J. Chem. Phys., 2010, 133, 131101 CrossRef PubMed.
- R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, Observation of a transition state resonance in the integral cross section of the F+HD reaction, J. Chem. Phys., 2000, 112, 4536 CrossRef CAS.
- F. Dong, S.-H. Lee and K. Liu, Reactive excitation functions for F+p-H2/n-H2/D2 and the vibrational branching for F+HD, J. Chem. Phys., 2000, 113, 3633 CrossRef CAS.
- J. J. Lin, J. Zhou, W. Shiu and K. Liu, State-specific correlation of coincident product pairs in the F + CD4 Reaction, Science, 2003, 300, 966–969 CrossRef CAS PubMed.
- J. Zhou, J. J. Lin, W. Shiu and K. Liu, Insights into dynamics of the F+CD4 reaction via product pair correlation, J. Chem. Phys., 2003, 119, 4997 CrossRef CAS.
- J. Zhou, J. J. Lin, W. Shiu and K. Liu, State-correlation matrix of the product pair from F + CD4 → DF(v′) + CD3(0v200), Phys. Chem. Chem. Phys., 2006, 8, 3000–3006 RSC.
- J. C. Corchado and J. Espinosa-García, Theoretical study of the CH4 + F → CH3 + FH reaction. I. Ab initio reaction path, J. Chem. Phys., 1996, 105, 3152 CrossRef CAS.
- D. Troya, Ab initio and direct quasiclassical-trajectory study of the F + CH4 → HF + CH3 reaction, J. Chem. Phys., 2005, 123, 214305 CrossRef PubMed.
- C. Rángel, M. Navarrete and J. Espinosa-García, Potential energy surface for the F(2P3/2,2P1/2) + CH4 hydrogen abstraction reaction. Kinetics and dynamics study, J. Phys. Chem. A, 2005, 109, 1441–1448 CrossRef PubMed.
- J. Espinosa-García, J. L. Bravo and C. Rangel, New analytical potential energy surface for the F(2P)+CH4 hydrogen abstraction reaction: kinetics and dynamics, J. Phys. Chem. A, 2007, 111, 2761–2771 CrossRef PubMed.
- D. Troya, J. Millán and I. Baños, Ab initio potential energy surface, variational transition state theory, and quasiclassical trajectory studies of the F + CH4 → HF + CH3 reaction, J. Chem. Phys., 2004, 120, 5181 CrossRef CAS PubMed.
- J. F. Castillo, F. J. Aoiz, L. Bañares, E. Martinez-Nuñez, A. Fernández-Ramos and S. Vazquez, Quasiclassical trajectory study of the F + CH4 reaction dynamics on a Dual-level interpolated potential energy surface, J. Phys. Chem. A, 2005, 109, 8459–8470 CrossRef CAS PubMed.
- G. Czakó, B. C. Shepler, B. J. Braams and J. M. Bowman, Accurate ab initio potential energy surface, dynamics, and thermochemistry of the F + CH4 → HF + CH3 reaction, J. Chem. Phys., 2009, 130, 084301 CrossRef PubMed.
- G. Czakó and J. M. Bowman, An ab initio spin–orbit-corrected potential energy surface and dynamics for the F + CH4 and F + CHD3 reactions, Phys. Chem. Chem. Phys., 2011, 13, 8306–8312 RSC.
- T. Westermann, W. Eisfeld and U. Manthe, Coupled potential energy surface for the F(2P) + CH4 → HF + CH3 entrance channel and quantum dynamics of the CH4 · F− photodetachment, J. Chem. Phys., 2013, 139, 014309 CrossRef PubMed.
- T. Westermann, J. B. Kim, M. L. Weichman, C. Hock, T. I. Yacovitch, J. Palma, D. M. Neumark and U. Manthe, Resonances in the entrance channel of the elementary chemical reaction of fluorine and methane, Angew. Chem., Int. Ed., 2014, 53, 1122–1126 CrossRef CAS PubMed.
- T. Lenzen and U. Manthe, Vibronically and spin-orbit coupled diabatic potentials for X(P) + CH4 → HX + CH3 reactions: General theory and application for X(P) = F(2P), J. Chem. Phys., 2019, 150, 064102 CrossRef PubMed.
- J. Chen, X. Xu, S. Liu and D. H. Zhang, A neural network potential energy surface for the F+CH4 reaction including multiple channels based on coupled cluster theory, Phys. Chem. Chem. Phys., 2018, 20, 9090 RSC.
- G. Nyman and J. Espinosa-Garcia, Reduced dimensionality quantum scattering calculations on the F + CH4 → FH + CH3 reaction, J. Phys. Chem. A, 2007, 111, 11943–11947 CrossRef CAS PubMed.
- D. Wang and G. Czakó, Quantum dynamics study of the F + CH4 → HF + CH3 reaction on an ab initio potential energy surface, J. Phys. Chem. A, 2013, 117, 7124–7130 CrossRef CAS PubMed.
- H. F. von Horsten and D. C. Clary, Reactive resonances in the F+CHD3 reaction—a quantum dynamics study, Phys. Chem. Chem. Phys., 2011, 13, 4340–4356 RSC.
- J. Qi, H. Song, M. Yang, J. Palma, U. Manthe and H. Guo, Mode specific quantum dynamics of the F + CHD3 → HF + CD3 reaction, J. Chem. Phys., 2016, 144, 171101 CrossRef PubMed.
- B. Zhao and U. Manthe, Non-adiabatic transitions in the reaction of fluorine with methane, J. Chem. Phys., 2020, 152, 231102 CrossRef CAS PubMed.
- S. Liu, J. Chen, Z. Zhang and D. H. Zhang, A six-dimensional state-to-state quantum dynamics study of the H + CH4 → H2 + CH3 reaction (J = 0), J. Chem. Phys., 2013, 138, 011101 CrossRef PubMed.
- J. Palma and D. C. Clary, A quantum model Hamiltonian to treat reactions of the type X + YCZ3 → XY + CZ3: Application to O(3P) + CH4 → OH + CH3, J. Chem. Phys., 2000, 112, 1859–1867 CrossRef CAS.
- M. T. Cvitaš and S. C. Althorpe, J. Chem. Phys., 2011, 134, 024309 CrossRef PubMed.
- S. Liu, X. Xu and D. H. Zhang, Time-dependent wave packet theory for state-to-state differential cross sections of four-atom reactions in full dimensions: Application to the HD + OH → H2O + D reaction, J. Chem. Phys., 2012, 136, 144302 CrossRef PubMed.
- Z. Zhao, S. Liu and D. H. Zhang, Differential cross sections for the H + D2O → HD + OD reaction: a full dimensional state-to-state quantum dynamics study, Chin. J. Chem. Phys., 2017, 30, 16–24 CrossRef CAS.
- G. Czakó and J. M. Bowman, Quasiclassical trajectory calculations of correlated product distributions for the F + CHD3 (v1 = 0,1) reactions using an ab initio potential energy surface, J. Chem. Phys., 2009, 131, 244302 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02629a |
| This journal is © The Royal Society of Chemistry 2023 |