Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A rational design strategy of radical-type mechanophores with thermal tolerance†
Yi
Lu‡
a,
Hajime
Sugita‡
ab,
Koichiro
Mikami
 *b,
Daisuke
Aoki
*b,
Daisuke
Aoki
 a and
Hideyuki
Otsuka
a and
Hideyuki
Otsuka
 *ac
*ac
aDepartment of Chemical Science and Engineering, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8550, Japan
bSagami Chemical Research Institute, 2743-1 Hayakawa, Ayase, Kanagawa 252-1193, Japan. E-mail: r200870208tyoko@gmail.com
cLiving Systems Materialogy (LiSM) Research Group, International Research Frontiers Initiative (IRFI), Tokyo Institute of Technology, 4259 Nagatsuta-cho, Midori-ku, Yokohama 226-8501, Japan
First published on 3rd August 2023
Abstract
Radical-type mechanophores (RMs) are attractive molecules that undergo homolytic scission of their central C–C bond to afford radical species upon exposure to heat or mechanical stimuli. However, the lack of a rational design concept limits the development of RMs with pre-determined properties. Herein, we report a rational design strategy of RMs with high thermal tolerance while maintaining mechanoresponsiveness. A combined experimental and theoretical analysis revealed that the high thermal tolerance of these RMs is related to the radical-stabilization energy (RSE) as well as the Hammett and modified Swain–Lupton constants at the para-position (σp). The trend of the RSE values is in good agreement with the experimentally evaluated thermal tolerance of a series of mechanoresponsive RMs based on the bisarylcyanoacetate motif. Furthermore, the singly occupied molecular orbital (SOMO) levels clearly exhibit a negative correlation with σp within a series of RMs that are based on the same skeleton, paving the way toward the development of RMs that can be handled under ambient conditions without peroxidation.
Introduction
The development of mechanoresponsive materials (MRMs) that exhibit a variety of macroscale functionalities, including coloring, fluorescence, self-healing, and self-strengthening, upon exposure to mechanical stimuli has been a research hotspot in materials science during the past few decades.1–12 In particular, mechanophores that induce microscale chemical reactions such as scission, isomerization, and release of small molecules are essential because they enable the functionalization of polymeric materials. Radical-type mechanophores (RMs), which undergo mechanical-stimuli-induced homolytic scission of their central C–C bonds to afford radical species, have been used to study micro-to-macroscale mechanical stimuli, strengthened materials based on sacrificial bonds, or subsequent polymer propagation.13–23The nature of the central C–C bond of RMs exerts a great impact on the functionality of the resulting polymeric materials. For example, the central C–C bonds of diarylbibenzofuranone (DABBF) and tetraarylsuccinonitrile (TASN) readily dissociate even at ambient temperature, which makes it possible to endow the polymeric material with self-healing properties.18,24 In contrast, the central C–C bond of difluorenylsuccinonitrile (DFSN), which exhibits the highest thermal tolerance among hitherto reported RMs, does not dissociate up to 100 °C.22 The extraordinary thermal tolerance of DFSN inspired us to apply the radical-polymerization methodology to develop highly mechanoresponsive or shape-memory materials.15,25,26 However, despite the clear importance of decreasing the propensity of the central C–C bond to subdue to thermal scission while preserving its ability to scission upon exposure to mechanical impact, the relationship between both phenomena is still unclear, which limits the scope of RM-based materials.
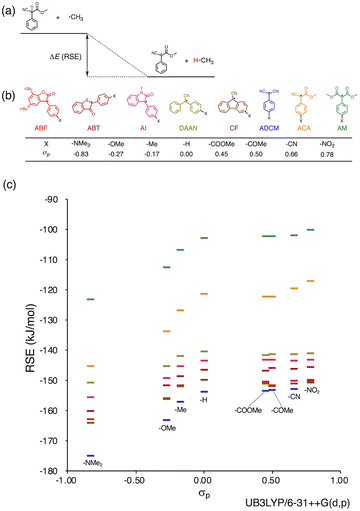
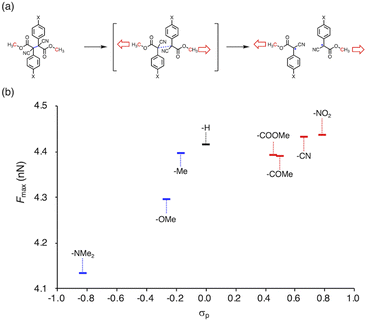
Herein, we report a rational design strategy for RMs with high thermal tolerance for the development of novel MRMs. We found that the thermal tolerance within a series of RMs that contain the same skeleton can be simply explained by the relationship between two key factors, i.e., the radical-stabilization energy (RSE) (Fig. 1a)27–31 as well as the Hammett and modified Swain–Lupton constants at the para-position (σp) (Fig. 1b).32 The RSE, which indicates the thermodynamic stability of radicals, is defined as the enthalpy change in isodesmic hydrogen-transfer reactions (Fig. 1a). We simulated the RSE values using a computational approach (Fig. 1c and S32–S34†). Meanwhile, σp is an experimental value that quantitatively represents the electron-withdrawing or electron-donating nature of substitution groups at para-position of the aromatic part (Fig. 1b).
Results and discussion
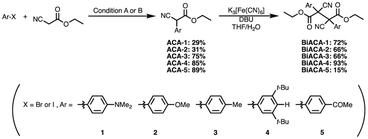
We investigated the relationship between RSE and σp in a series of representative radical molecules including derivatives of arylbenzofuranone (ABF), arylbenzothiophenone (ABT), arylindolinone (AI), diarylacetonitrile (DAAN), cyanofluorene (CF), aryldicyanomethane (ADCM), arylcyanoacetate (ACA), and arylmalonate (AM). Dimers of ABF, ABT, AI, DAAN, and CF radicals are radical-type mechanophores previously developed in our group.18,22,24,33,34 In order to elucidate the electron-donating or -withdrawing nature of these radicals, not only ADCMs, which are well-known stable radicals under ambient conditions that possess two electron-withdrawing cyano groups,35–45 but also ACAs and AMs were investigated as ADCM analogues.46,47 The relationship between RSE and σp is plotted in Fig. 1c, which shows that the change in the RSE values within the series of radical molecules that have the same skeleton depends on the σp range. The RSE value clearly increases with increasing σp value in the region of σp < 0, where the electron-donating nature of the functional groups increases with decreasing σp value. In contrast, the RSE values did not show significant changes and almost saturated in the region of σp > 0, where the electron-withdrawing nature of the functional groups increases with increasing σp value. These trends were theoretically reproduced irrespective of the computational methodology used (Fig. S32–S34†). These results thus indicate that the thermodynamic stability of these radicals can be interpreted in terms of the substituent effect within a series of radicals that share the same skeleton. Therefore, we envisioned that it should be possible to develop RMs with high thermal tolerance by designing electron-deficient radical species that bear electron-withdrawing groups.To prove this hypothesis experimentally, we synthesized ACA dimers, i.e., bisarylcyanoacetates (BiACAs), with a series of functional groups at the para-position as novel RMs (Schemes 1, S1 and S2†). In contrast to the complicated synthetic protocols for previously reported RMs such as DABBF, TASN, and DFSN,48–51 the BiACA structures provided significantly more accessible protocols to the desired electron-deficient RMs, allowing a systematic investigation of the substituent effect. All BiACAs were obtained without peroxidized products, which is indicative of low-lying singly occupied molecular orbital (SOMO) levels52–54 and slow C–C bond cleavage under ambient conditions (vide infra). We conducted variable-temperature electron paramagnetic resonance (EPR) spectroscopic measurements to determine the bond dissociation ratio (BDR) of the central C–C bond of the RMs and their dissociation constant (Kd) at 100 °C (Table S1†). In Fig. 2, the BDR values and the natural logarithms of Kd (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd) are plotted as a function of increasing RSE and σp values of the BiACAs. As expected, the BDR and ln
Kd) are plotted as a function of increasing RSE and σp values of the BiACAs. As expected, the BDR and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd values decrease with increasing RSE and σp values. Specifically, BDR and ln
Kd values decrease with increasing RSE and σp values. Specifically, BDR and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd values of 158 × 10−3% and −16.7, respectively, were obtained for BiACA-1 (RSE: −145.34 kJ mol−1, σp: −0.83), 12.1 × 10−3% and −21.6 for BiACA-2 (RSE: −133.63 kJ mol−1, σp: −0.27), 1.37 × 10−3% and −26.3 for BiACA-3 (RSE: −126.69 kJ mol−1, σp: −0.17), 0.41 × 10−3% and −27.3 for BiACA-4 (RSE: −122.17 kJ mol−1, σp: 0.00), and 0.20 × 10−3% and −28.7 for BiACA-5 (RSE: −122.17 kJ mol−1, σp: 0.50). Furthermore, BiACA-5 exhibited one of the highest levels of thermal tolerance among our previously reported RMs. These results indicate that the thermal tolerance of RMs can be correlated with the RSE values and, therefore, with the substituent effect associated with the σp value.
Kd values of 158 × 10−3% and −16.7, respectively, were obtained for BiACA-1 (RSE: −145.34 kJ mol−1, σp: −0.83), 12.1 × 10−3% and −21.6 for BiACA-2 (RSE: −133.63 kJ mol−1, σp: −0.27), 1.37 × 10−3% and −26.3 for BiACA-3 (RSE: −126.69 kJ mol−1, σp: −0.17), 0.41 × 10−3% and −27.3 for BiACA-4 (RSE: −122.17 kJ mol−1, σp: 0.00), and 0.20 × 10−3% and −28.7 for BiACA-5 (RSE: −122.17 kJ mol−1, σp: 0.50). Furthermore, BiACA-5 exhibited one of the highest levels of thermal tolerance among our previously reported RMs. These results indicate that the thermal tolerance of RMs can be correlated with the RSE values and, therefore, with the substituent effect associated with the σp value.
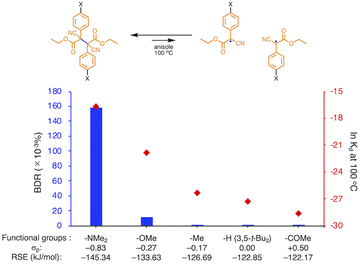 | ||
Fig. 2 Bar graph and plot of BDR and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd at 100 °C as a function of the increasing RSE and σp values for BiACA derivatives. Kd at 100 °C as a function of the increasing RSE and σp values for BiACA derivatives. | ||
The relationship between RSE/thermodynamic stability and the thermal tolerance of RMs can be explained by the Hammond–Leffler postulate (Fig. 3), which describes the transition-state (TS) geometry in an elementary step related to reactants, intermediates, and products.55,56 According to this postulate, the energy barrier between reactants, i.e., RMs, and products, i.e., radicals generated from RMs, is amenable to the thermodynamic stability of the products. Thus, RMs that bear electron-withdrawing groups, which showed shallow RSE values and, in turn, low thermodynamic stability, exhibit a higher energy barrier for thermal dissociation into the corresponding radical products, indicating higher thermal tolerance. Although DFT is a powerful tool to evaluate the dissociation of the central C–C bond and the TS in RMs, the rotation of the central C–C bond, which leads to complicated rotamers, hinders the interpretability of the results. The present approach provides a simple method for the prediction of the thermal tolerance of RMs without complicated TS searches.
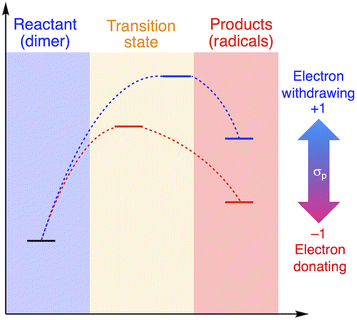 | ||
| Fig. 3 Schematic illustration of the change in the thermal tolerance according to the Hammond–Leffler postulate. | ||
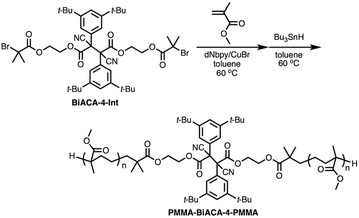
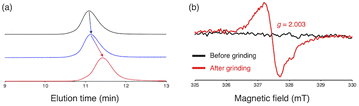
To investigate the mechanochemical reactivity of BiACAs, a poly(methyl methacrylate) (PMMA) derivative, PMMA-BiACA-4-PMMA, was synthesized via the atom transfer radical polymerization (ATRP) of methyl methacrylate using a bifunctional initiator consisting of the BiACA-4 skeleton (Scheme 2). The Br end groups were hydrogenated using tributyltin hydride to minimize possible side reactions.57 The Mn and Mw/Mn values of PMMA-BiACA-4-PMMA were determined to be 24 kDa and 1.18, respectively, by gel-permeation chromatography (GPC) (Fig. 4a, black line). To verify whether the ATRP reaction was initiated and the PMMA chains grew bidirectionally from the central BiACA-4 moiety while maintaining the dynamic covalent properties of the latter, we conducted a heating test in the absence or presence of BiACA-4-diol as a scrambling unit (Scheme S4†). A comparison of the GPC profiles before and after heating PMMA-BiACA-4-PMMA in anisole at 130 °C for 90 minutes suggested that degradation did not occur (Fig. 4a, blue line), demonstrating the high thermal tolerance of the BiACA-4 unit to radical reactions below 130 °C. To investigate the mechanochemical reactivity of the polymer, we performed a grinding test on the solid sample by ball-milling at a frequency of 30 Hz for 60 minutes. A solid-state EPR spectrum recorded after grinding showed a clear signal with a g-value of 2.003, which was attributed to carbon-centered radicals. The BDR value (0.102% ± 0.006%) is 246 times higher than that obtained at 100 °C (0.41 × 10−3%), indicating that the mechanical stimulus (grinding) greatly enhances the C–C bond dissociation. These results indicate that the thermal tolerance of an RM can be increased without significantly deactivating its mechanochemical reactivity.
To gain more insight into the relationship between the thermal- and mechanochemical scission, we performed constrained-geometries-simulate-external-force (CoGEF) calculations, which allow theoretically evaluating the mechanochemical reactivity (Fig. 5a).58–68Fig. 5b shows a plot of the maximum force (Fmax) of BiACAs vs. σp. The Fmax value increases in the region σp < 0 and was almost saturated in the region σp > 0, similar to the case of the plots of RSE vs. σp (Fig. 1c and 2). These results indicate that the nature of the thermal and mechanical bond dissociation might be the same from the viewpoint of the thermodynamic stability of the products. The CoGEF calculations showed that as the central C–C bond energy increases, not only thermal scission but also mechanochemical scission is less likely to occur. Although this may seem contradictory at first glance, it might be due to the change in the potential energy surface under mechanical force, as pointed out by Martínez et al.69 This could also explain why the bond dissociation occurs even in the case of strong C–C bonds with shallow RSE and high Fmax values. These results suggest that controlling the thermal tolerance of RMs having mechanochemical reactivity can be achieved by tuning the substituent effect, which opens new avenues for the design of RMs by controlling the dissociation bond energy of single bonds.
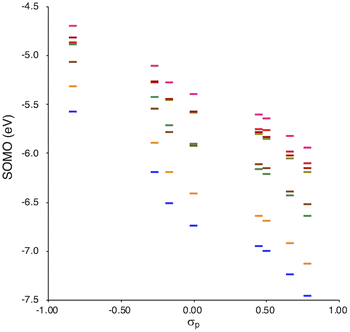
SOMO levels are often used to evaluate the reactivity of molecules; therefore, they can be considered as a good indicator for the reactivity of RMs toward oxygen molecules.54 In this study, the SOMO levels clearly show a negative correlation with the σp values within the series of radicals that share the same skeleton, reflecting the substituent effect at the para-position (Fig. 6). ADCMs, which are stable radicals under ambient conditions reported by Sakamaki and Winter,34–44 show deep SOMO levels. Interestingly, the ACAs presented here also exhibit deep SOMO levels. These results indicates that the presence of electron-withdrawing groups shallows/deepens the RSE/SOMO, provides the RMs with thermal tolerance and could enable their handling under ambient conditions without peroxidation.
Conclusions
In conclusion, we have demonstrated a rational designing strategy of RMs with high thermal tolerance. According to the relationship between the RSE and σp of the corresponding radicals, a series of thermally resistant RMs sharing similar skeletons could be simply designed. The thermal tolerance increased with increasing electron-withdrawing nature of the functional groups. The veracity of the RSE–σp relationship was experimentally validated by preparing a series of RMs that bear bisarylcyanoacetate (BiACA) skeletons with different electron density. Furthermore, not only the thermal but also the oxygen tolerance could be related to the SOMO level, and the oxygen tolerance can thus be tuned according to this parameter. Our results provide a systematic guideline for the design of RMs with various functionalities while maintaining good thermal tolerance.Data availability
The data generated in this study are available in the main text or the ESI.† Crystallographic data in the ESI† have been deposited at the joint Cambridge Crystallographic Data Centre (BiACA-4, CCDC: 2207403). The NMR and EPR spectra and the results of DFT calculation and CoGEF studies are provided in the ESI.†Author contributions
H. S., K. M. and H. O. conceptualized this work. H. S. designed the experiments and carried out DFT calculations. Y. L. performed experiments include ESR measurement. All authors wrote the manuscript. Y. L. and H. S. prepared the ESI.† All authors contributed to the editing and revision of the manuscript and ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JST CREST grant JPMJCR1991 from the Japan Science and Technology Agency (JST). We are grateful to Dr Naoki Hayakawa (Sagami Chemical Research Institute) for single-crystal X-ray diffraction measurements, and Mr Takumi Yamamoto and Mr Yuto Uchida (Tokyo Institute of Technology) for the technical support in extracting the calculation data. Computational calculations were performed at the Research Center for Computational Science, Okazaki, Japan (Project: 22-IMS-C258), and the TSUBAME3.0 supercomputer at the Tokyo Institute of Technology.References
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martínez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72 CrossRef CAS PubMed.
- J. R. Hemmer, C. Rader, B. D. Wilts, C. Weder and J. A. Berrocal, J. Am. Chem. Soc., 2021, 143, 18859–18863 CrossRef CAS PubMed.
- S. Shahi, H. Roghani-Mamaqani, R. Hoogenboom, S. Talebi and H. Mardani, Chem. Mater., 2022, 34, 468–498 CrossRef CAS.
- T. Matsuda, R. Kawakami, R. Namba, T. Nakajima and J. P. Gong, Science, 2019, 363, 504–508 CrossRef CAS PubMed.
- Y. Chen, A. J. H. Spiering, S. Karthikeyan, G. W. M. Peters, E. W. Meijer and R. P. Sijbesma, Nat. Chem., 2012, 4, 559–562 CrossRef CAS PubMed.
- Z. Wang, Z. Ma, Y. Wang, Z. Xu, Y. Luo, Y. Wei and X. Jia, Adv. Mater., 2015, 27, 6469–6474 CrossRef CAS PubMed.
- Y. Sagara, M. Karman, E. Verde-Sesto, K. Matsuo, Y. Kim, N. Tamaoki and C. Weder, J. Am. Chem. Soc., 2018, 140, 1584–1587 CrossRef CAS PubMed.
- G. A. Filonenko and J. R. Khusnutdinova, Adv. Mater., 2017, 29, 1700563–1700568 CrossRef PubMed.
- J. Fox, J. J. Wie, B. W. Greenland, S. Burattini, W. Hayes, H. M. Colquhoun, M. E. MacKay and S. J. Rowan, J. Am. Chem. Soc., 2012, 134, 5362–5368 CrossRef CAS PubMed.
- S. Coulibaly, A. Roulin, S. Balog, M. V. Biyani, E. J. Foster, S. J. Rowan, G. L. Fiore and C. Weder, Macromolecules, 2014, 47, 152–160 CrossRef CAS.
- S. L. Xiang, Q. X. Hua, P. J. Zhao, W. L. Gong, C. Li and M. Q. Zhu, Chem. Mater., 2019, 31, 5081–5088 CrossRef CAS.
- C. Nagamani, H. Liu and J. S. Moore, J. Am. Chem. Soc., 2016, 138, 2540–2543 CrossRef CAS PubMed.
- K. Imato, A. Irie, T. Kosuge, T. Ohishi, M. Nishihara, A. Takahara and H. Otsuka, Angew. Chem., Int. Ed., 2015, 54, 6168–6172 CrossRef CAS PubMed.
- H. Oka, K. Imato, T. Sato, T. Ohishi, R. Goseki and H. Otsuka, ACS Macro Lett., 2016, 5, 1124–1127 CrossRef CAS PubMed.
- T. Watabe, D. Aoki and H. Otsuka, Macromolecules, 2022, 55, 5795–5802 CrossRef CAS.
- K. Imato, T. Kanehara, S. Nojima, T. Ohishi, Y. Higaki, A. Takahara and H. Otsuka, Chem. Commun., 2016, 52, 10482–10485 RSC.
- T. Watabe, D. Aoki and H. Otsuka, Macromolecules, 2021, 54, 1725–1731 CrossRef CAS.
- T. Sumi, R. Goseki and H. Otsuka, Chem. Commun., 2017, 53, 11885–11888 RSC.
- S. Kato, K. Ishizuki, D. Aoki, R. Goseki and H. Otsuka, ACS Macro Lett., 2018, 7, 1087–1091 CrossRef CAS PubMed.
- S. Kato, D. Aoki and H. Otsuka, Polym. Chem., 2019, 10, 2636–2640 RSC.
- F. Hoshino, T. Kosuge, D. Aoki and H. Otsuka, Mater. Chem. Front., 2019, 3, 2681–2685 RSC.
- H. Sakai, T. Sumi, D. Aoki, R. Goseki and H. Otsuka, ACS Macro Lett., 2018, 7, 1359–1363 CrossRef CAS PubMed.
- K. Seshimo, H. Sakai, T. Watabe, D. Aoki, H. Sugita, K. Mikami, Y. Mao, A. Ishigami, S. Nishitsuji, T. Kurose, H. Ito and H. Otsuka, Angew. Chem., Int. Ed., 2021, 60, 8406–8409 CrossRef PubMed.
- K. Imato, M. Nishihara, T. Kanehara, Y. Amamoto, A. Takahara and H. Otsuka, Angew. Chem., Int. Ed., 2012, 51, 1138–1142 CrossRef CAS PubMed.
- Y. Mao, Y. Kubota, R. Feng, J. Gong, A. Ishigami, Y. Kobayashi, T. Watabe, D. Aoki, H. Otsuka and H. Ito, Macromolecules, 2022, 55, 3948–3957 CrossRef CAS.
- T. Watabe and H. Otsuka, Angew. Chem., Int. Ed., 2023, 62, e202216469 CrossRef CAS PubMed.
- H. Zipse, Top. Curr. Chem., 2006, 263, 163–189 CrossRef CAS.
- E. H. Krenske and M. L. Coote, J. Phys. Chem. A, 2007, 111, 8229–8240 CrossRef CAS PubMed.
- T. Kubo, Y. Katada, A. Shimizu, Y. Hirao, K. Sato, T. Takui, M. Uruichi, K. Yakushi and R. C. Haddon, J. Am. Chem. Soc., 2011, 133, 14240–14243 CrossRef CAS PubMed.
- A. S. Menon, D. J. Henry, T. Bally and L. Radom, Org. Biomol. Chem., 2011, 9, 3636–3657 RSC.
- L. M. Campos, H. Dang, D. Ng, Z. Yang, H. L. Martinez and M. A. Garcia-Garibay, J. Org. Chem., 2002, 67, 3749–3754 CrossRef CAS PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- K. Ishizuki, H. Oka, D. Aoki, R. Goseki and H. Otsuka, Chem. –Eur. J., 2018, 24, 3170–3173 CrossRef CAS PubMed.
- K. Kawasaki, D. Aoki and H. Otsuka, Macromol. Rapid Commun., 2020, 41, 1900460–1900464 CrossRef CAS PubMed.
- T. Kobashi, D. Sakamaki and S. Seki, Angew. Chem., Int. Ed., 2016, 55, 8634–8638 CrossRef CAS PubMed.
- K. Okino, S. Hira, Y. Inoue, D. Sakamaki and S. Seki, Angew. Chem., Int. Ed., 2017, 56, 16597–16601 CrossRef CAS PubMed.
- R. Zhang, A. Ellern and A. H. Winter, J. Org. Chem., 2022, 87, 1507–1511 CrossRef CAS PubMed.
- R. Zhang, J. P. Peterson, L. J. Fischer, A. Ellern and A. H. Winter, J. Am. Chem. Soc., 2018, 140, 14308–14313 CrossRef CAS PubMed.
- J. P. Peterson, R. Zhang and A. H. Winter, ACS Omega, 2019, 4, 13538–13542 CrossRef CAS PubMed.
- J. P. Peterson and A. H. Winter, J. Am. Chem. Soc., 2019, 141, 12901–12906 CrossRef CAS PubMed.
- K. Okino, D. Sakamaki and S. Seki, ACS Mater. Lett., 2019, 1, 25–29 CrossRef CAS.
- I. Badía-Domínguez, A. Pérez-Guardiola, J. C. Sancho-García, J. T. López Navarrete, V. Hernández Jolín, H. Li, D. Sakamaki, S. Seki and M. C. Ruiz Delgado, ACS Omega, 2019, 4, 4761–4769 CrossRef.
- J. P. Peterson and A. H. Winter, Org. Lett., 2020, 22, 6072–6076 CrossRef CAS PubMed.
- J. P. Peterson, A. Ellern and A. H. Winter, J. Am. Chem. Soc., 2020, 142, 5304–5313 CrossRef CAS PubMed.
- R. Zhang, A. Ellern and A. H. Winter, Angew. Chem., Int. Ed., 2021, 60, 25082–25088 CrossRef CAS PubMed.
- H. A. P. De Jongh, C. R. H. I. De Jonge and W. J. Mijs, J. Org. Chem., 1971, 36, 3160–3168 CrossRef CAS.
- H. A. P. De Jongh, C. R. H. I. De Jonge, H. J. M. Sinnige, W. J. De Klein, W. G. B. Huysmans, W. J. Mijs, W. J. Van den Hoek and J. Smidt, J. Org. Chem., 1972, 37, 1960–1966 CrossRef CAS.
- N. A. Beare and J. F. Hartwig, J. Org. Chem., 2002, 67, 541–555 CrossRef CAS PubMed.
- D. A. Culkin and J. F. Hartwig, Acc. Chem. Res., 2003, 36, 234–245 CrossRef CAS PubMed.
- Y. Jiang, N. Wu, H. Wu and M. He, Synlett, 2005, 2731–2734 CrossRef CAS.
- C. C. C. Johansson and T. J. Colacot, Angew. Chem., Int. Ed., 2010, 49, 676–707 CrossRef CAS PubMed.
- T. Nishiuchi, R. Ito, A. Takada, Y. Yasuda, T. Nagata, E. Stratmann and T. Kubo, Chem.–Asian J., 2019, 14, 1830–1836 CrossRef CAS PubMed.
- T. Kubo, Molecules, 2019, 24, 665–678 CrossRef PubMed.
- H. Sugita, Y. Lu, D. Aoki, H. Otsuka and K. Mikami, Chem. –Eur. J., 2023, 29, e202203249 CrossRef CAS PubMed.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
- F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, Part A: Structure and Mechanisms, 2007, pp. 289–293 Search PubMed.
- T. Yamamoto, D. Aoki and H. Otsuka, ACS Macro Lett., 2021, 10, 744–748 CrossRef CAS PubMed.
- M. K. Beyer, J. Chem. Phys., 2000, 112, 7307–7312 CrossRef CAS.
- M. J. Kryger, A. M. Munaretto and J. S. Moore, J. Am. Chem. Soc., 2011, 133, 18992–18998 CrossRef CAS PubMed.
- Y. Cha, T. Zhu, Y. Sha, H. Lin, J. Hwang, M. Seraydarian, S. L. Craig and C. Tang, J. Am. Chem. Soc., 2021, 143, 11871–11878 CrossRef CAS PubMed.
- H. M. Klukovich, T. B. Kouznetsova, Z. S. Kean, J. M. Lenhardt and S. L. Craig, Nat. Chem., 2013, 5, 110–114 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. S. Kean, L. Fan, B. D. Mar, T. J. Martínez and S. L. Craig, J. Am. Chem. Soc., 2014, 136, 15162–15165 CrossRef CAS PubMed.
- R. Stevenson and G. De Bo, J. Am. Chem. Soc., 2017, 139, 16768–16771 CrossRef CAS PubMed.
- M. Zhang and G. De Bo, J. Am. Chem. Soc., 2019, 141, 15879–15883 CrossRef CAS PubMed.
- I. M. Klein, C. C. Husic, D. P. Kovács, N. J. Choquette and M. J. Robb, J. Am. Chem. Soc., 2020, 142, 16364–16381 CrossRef CAS PubMed.
- Y. Sha, Z. Zhou, M. Zhu, Z. Luo, E. Xu, X. Li and H. Yan, Angew. Chem., Int. Ed., 2022, 61, e202203169 CAS.
- M. E. McFadden and M. J. Robb, J. Am. Chem. Soc., 2019, 141, 11388–11392 CrossRef CAS.
- M. E. McFadden and M. J. Robb, J. Am. Chem. Soc., 2021, 143, 7925–7929 CrossRef CAS PubMed.
- T. Kosuge, X. Zhu, V. M. Lau, D. Aoki, T. J. Martínez, J. S. Moore and H. Otsuka, J. Am. Chem. Soc., 2019, 141, 1898–1902 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all optimized structures at each calculated level (ZIP). CCDC 2207403. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc02991c |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |