Open Access Article
Open Access ArticleDynamic self-assembly of supramolecular catalysts from precision macromolecules†
Qian
Qin‡
a,
Jie
Li‡§
a,
David
Dellemme
b,
Mathieu
Fossépré
b,
Gabriella
Barozzino-Consiglio
a,
Imane
Nekkaa
a,
Adrian
Boborodea
c,
Antony E.
Fernandes
ac,
Karine
Glinel
 a,
Mathieu
Surin
a,
Mathieu
Surin
 *b and
Alain M.
Jonas
*b and
Alain M.
Jonas
 *a
*a
aInstitute of Condensed Matter and Nanosciences, Université catholique de Louvain, Croix du Sud 1 L7.04.02, Louvain-la-Neuve, Belgium. E-mail: alain.jonas@uclouvain.be
bLaboratory for Chemistry of Novel Materials, Université de Mons – UMONS, Avenue Maistriau, 17, B-7000 Mons, Belgium. E-mail: mathieu.surin@umons.ac.be
cCertech, rue Jules Bordet 45, 7180 Seneffe, Belgium
First published on 16th August 2023
Abstract
We show the emergence of strong catalytic activity at low concentrations in dynamic libraries of complementary sequence-defined oligomeric chains comprising pendant functional catalytic groups and terminal recognition units. In solution, the dynamic constitutional library created from pairs of such complementary oligomers comprises free oligomers, self-assembled di(oligomeric) macrocycles, and a virtually infinite collection of linear poly(oligomeric) chains. We demonstrate, on an exemplary catalytic system requiring the cooperation of no less than five chemical groups, that supramolecular di(oligomeric) macrocycles exhibit a catalytic turnover frequency ca. 20 times larger than the whole collection of linear poly(oligomers) and free chains. Molecular dynamics simulations and network analysis indicate that self-assembled supramolecular di(oligomeric) macrocycles are stabilized by different interactions, among which chain end pairing. We mathematically model the catalytic properties of such complex dynamic libraries with a small set of physically relevant parameters, which provides guidelines for the synthesis of oligomers capable to self-assemble into functionally-active supramolecular macrocycles over a larger range of concentrations.
Introduction
In biomolecular catalysts, the various chemical groups involved in the catalytic site self-assemble in spatially close positions, leading to optimal availability and often adaptive activity. This optimized self-assembly of active groups is intrinsically dynamic, allowing accessibility to and from the reactive site, and the realization of the reaction transition state.1,2 Reaching such an efficiency in the dynamic self-assembly of active groups and resulting catalytic activity remains challenging in synthetic molecular catalysts. Here, we show by molecular dynamics simulations and experiments that, by designing sequence-defined oligomeric chains equipped with functional catalytic groups and complementary recognition units, it is possible to induce the dynamic self-assembly of supramolecular cyclic structures displaying unusually high catalytic efficiency at low concentrations. Importantly, we also show that the catalytic properties of such oligomers can be accurately predicted by a compact mathematical model, despite the multiplicity of their possible assembly configurations.Attempts to form catalytic sites by self-assembly of synthetic macromolecules have been reported using peptides,3–7 DNA scaffolds,8–14 single-chain polymeric nanoparticles (SCNPs),15–20 peptides,21 metal organic frameworks,22,23 supramolecular polymers,24 foldamers,25 and helical (supramolecular) polymers.26–29 Additionally, supramolecular and covalent macrocycles have been synthesized to create catalytic sites involving the concerted action of different functional groups,30–34 because cyclic configurations decrease the accessible conformational space and thereby increase the probability to bring catalytically-active groups in spatially-close positions.
In our approach, we combine these ideas by designing two precision oligomers (Oa and Ob1 in Fig. 1D) that can self-assemble in a variety of configurations, including di(oligomeric) macrocycles (Fig. 1E). All these supramolecular species possess the five cooperative catalytic groups involved in the copper-catalyzed aerobic oxidation of alcohols, which are distributed between the two oligomers. We demonstrate the emergence of catalytic activity from the formed dynamic constitutional library at low concentrations, and that this activity mainly results from supramolecular di(oligomeric) macrocycles that enable the ideal positioning and connection of the cooperative catalytic residues within a confined space. Additionally, a mathematical model is developed to quantitatively predict the self-assembly of catalytic species and the catalytic properties of the constitutional library, thereby providing designing rules for self-assembled macromolecular catalytic systems.
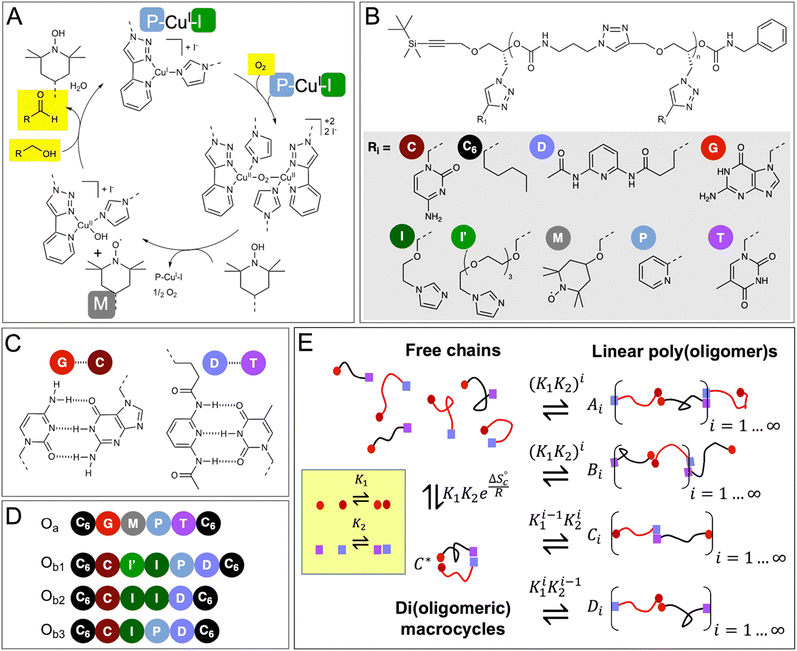 | ||
| Fig. 1 Postulated mechanism of the CuI/TEMPO-catalyzed aerobic oxidation of alcohols, and chemical structure of the oligomers and constitutional libraries. (A) Simplified catalytic cycle, adapted from reference;35 the mechanism requires the cooperative action of 2 Cu(I) atoms, 2 pyridyltriazole ligands (P), 2 imidazole co-ligands (I), and one TEMPO radical (M). (B) Chemical structure of the oligomers (n = 5 or 6). (C) Hydrogen-bond pairing of the recognition units. (D) Sequence of the oligomers synthesized in this study; two complementary chains of the Oa/Ob1 system contain all the needed catalytic groups when paired (2 × P, 2 × I, 1 × M), whereas Oa/Ob2 or Oa/Ob3 paired chains lack one functional group, i.e., 1 P or 1 I, respectively. (E) Equilibrium constitutional library of co-existing species in solutions. | ||
Results and discussion
To demonstrate the possibility to self-assemble two properly-designed precision oligomers into a catalytically-active superstructure, we selected a system developed for the sustainable aerobic oxidation of alcohols based on 2,2,6,6-tetramethylpiperidine-1-oxyl (TEMPO) and Cu(I).35–38 Although the catalytic mechanism is still discussed,39 it was proposed35,38 that the catalytic cycle requires the formation of a binuclear copper complex involving two bidentate nitrogen ligands (such as bipyridine) and two auxiliary ligands (such as N-methyl imidazole, NMI) (Fig. 1A). In support of this hypothesis, recent findings have shown the effectiveness of dinuclear copper complexes in the TEMPO-catalyzed aerobic oxidation of alcohols.40,41 As shown in ESI† (Section 12), our results also indicate that the catalytic cycle involves two Cu(I) atoms, two pyridyltriazole bidentate copper ligands (P) and two imidazole auxiliary copper ligands (I), in addition to the TEMPO radical (M).These five needed functional groups were precisely distributed between two strands Oa and Ob, each strand having intrinsically a very low catalytic activity, if any. Additionally, the two strands were equipped with complementary hydrogen-binding recognition units at their ends to favor their assembly into a variety of configurations, including supramolecular di(oligomeric) cycles, while avoiding the formation of homo-oligomeric supramolecular structures (Fig. 1B–E).
The functional groups are attached as side chains to an oligo(urethane triazole) backbone (Fig. 1B); the precise sequence of these complementary oligomers is displayed in Fig. 1D. The general synthetic procedure (Scheme 1) was demonstrated before to provide access to sequence-defined stereocontrolled oligomers.42 Here, we considerably extended the range of available side chains to include complementary nucleobase analogs (cytosine C, guanine G, thymine T and 2,6-diamidopyridine D) acting as recognition units through G⋯C and D⋯T pairing (Fig. 1C). The catalytic groups comprise two pyridyltriazole (P)–copper complexes, two imidazole co-ligands (I and I′ having different spacer lengths for optimal accessibility), and one TEMPO radical (M). Additionally, hexyl side chains (C6) were added at both ends of the chains to favor solubility in the acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dimethylsulfoxide 95
dimethylsulfoxide 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 v/v solvent system used for the experiments and possibly contribute to stabilization of the self-assembled structures. The synthetic procedures and characterization of the intermediary and final products by NMR, mass spectrometry and SEC chromatography are described in ESI† (Sections 1–5).
5 v/v solvent system used for the experiments and possibly contribute to stabilization of the self-assembled structures. The synthetic procedures and characterization of the intermediary and final products by NMR, mass spectrometry and SEC chromatography are described in ESI† (Sections 1–5).
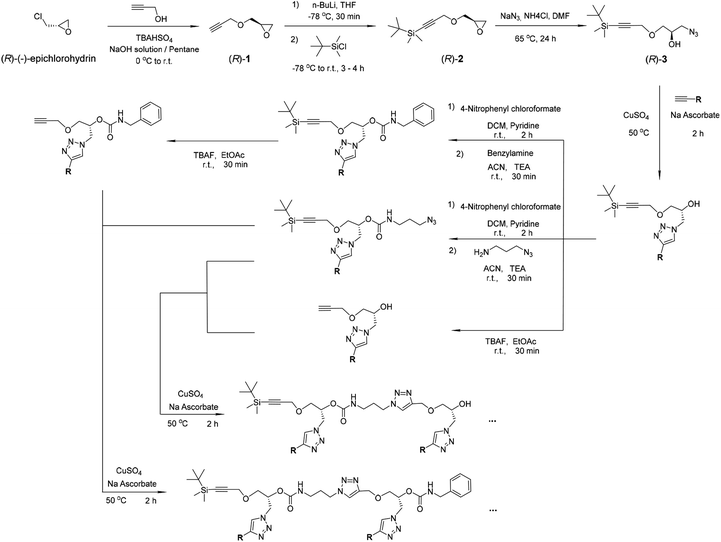 | ||
| Scheme 1 Synthesis of the oligomers. The compounds (R)-1, (R)-2 and (R)-3 were prepared according to the literature and our previous work.42–45 | ||
The first strand, Oa, consists of a 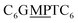 sequence (catalytic groups underlined), complementary to the second strand, Ob1, with a
sequence (catalytic groups underlined), complementary to the second strand, Ob1, with a 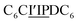 sequence (Fig. 1D). When self-assembled in a di(oligomeric) cycle in the presence of Cu(I), the two strands should provide together the five groups needed for catalysis (Fig. 1A). To demonstrate the completeness of this self-assembled active site, two other Ob strands were also synthesized, both of which can only form an incomplete catalytic site in combination with Oa: a
sequence (Fig. 1D). When self-assembled in a di(oligomeric) cycle in the presence of Cu(I), the two strands should provide together the five groups needed for catalysis (Fig. 1A). To demonstrate the completeness of this self-assembled active site, two other Ob strands were also synthesized, both of which can only form an incomplete catalytic site in combination with Oa: a 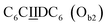 sequence that lacks a P group, and a
sequence that lacks a P group, and a 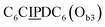 sequence that lacks a I group (Fig. 1D). Due to the removal of one unit in one strand of each of these two systems, the Ob2 and Ob3 chains are one unit shorter than the Ob1 chain of the complete system. The libraries of self-assembled configurations that form from these three systems are shown in Fig. 1E.
sequence that lacks a I group (Fig. 1D). Due to the removal of one unit in one strand of each of these two systems, the Ob2 and Ob3 chains are one unit shorter than the Ob1 chain of the complete system. The libraries of self-assembled configurations that form from these three systems are shown in Fig. 1E.
Molecular dynamics (MD) simulations of one Oa and one Ob1 chains placed in an effective solvent indicate the rapid assembly of the oligomers in a stable heteromolecular complex of ca. 1 nm radius of gyration (Fig. 2A; details in ESI Section 10†). Inside this compact globule, the two strands remain flexible and highly dynamic, allowing the different units to rearrange in space due to a vast network of interactions involving functional moieties (catalytic groups and nucleobase analogs) as well as the carbamate and triazole moieties of the backbone. Interestingly, the catalytic units are among the less buried residues and are accessible at the periphery of the globule (Fig. S164†).
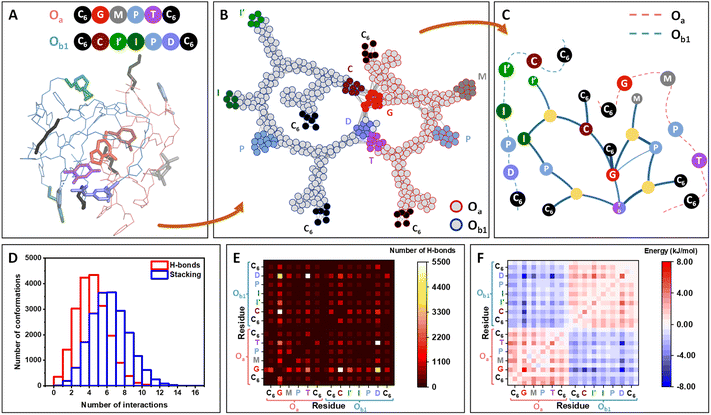 | ||
Fig. 2 Molecular simulations of the self-assembly of Oa and Ob1 oligomers. (A) Molecular dynamics snapshot of a 3D conformation of the complex, representative of the globular conformation. The two strands, Oa and Ob1, are depicted in pink and blue lines, respectively, and the functional units are depicted in sticks and coloured according to the ball representation as sketched above. (B) Network representation of the system, highlighting the persistent contacts observed during the MD simulation (see details in ESI Section 11†). Atoms (except H) constitute the nodes of the network. The nodes belonging to the strand Oa and Ob1 are circled in red and blue, respectively, with the same color code for the functional groups. (C) Modular representation of the network. The modules in yellow contain backbone or chain-ends nodes. For clarity, the primary structures of the two strands are sketched in dashed lines, showing that the sequence order is preserved in this representation, except for the complementary nucleobase analogs T and D, which are merged in the same module. (D) Distribution of the number of hydrogen-bonding and stacking interactions for the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations from MD, showing that both H-bonds and aromatic interactions strongly participate to the stabilization of the system. (E) Heatmaps showing the decomposition of the hydrogen-bonds by pair of residues (see details in ESI, Fig. S165†). Each square, localized at the crossing of a pair of residues, indicates the number of interactions detected between the two residues over the 20 000 conformations from MD, showing that both H-bonds and aromatic interactions strongly participate to the stabilization of the system. (E) Heatmaps showing the decomposition of the hydrogen-bonds by pair of residues (see details in ESI, Fig. S165†). Each square, localized at the crossing of a pair of residues, indicates the number of interactions detected between the two residues over the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations. White squares indicating the highest number of interactions are localized for the pairs G⋯C and T⋯D. Interactions are also found for the pair G⋯D. (F) Heatmaps showing the decomposition of the enthalpy of binding by pair of residues, similarly as for (E). The most stabilizing residue–residue interactions (dark blue squares) are localized for the pairs G⋯D, T⋯D and G⋯C. 000 conformations. White squares indicating the highest number of interactions are localized for the pairs G⋯C and T⋯D. Interactions are also found for the pair G⋯D. (F) Heatmaps showing the decomposition of the enthalpy of binding by pair of residues, similarly as for (E). The most stabilizing residue–residue interactions (dark blue squares) are localized for the pairs G⋯D, T⋯D and G⋯C. | ||
Network theory applied to the collection of conformations generated over a 10 μs timescale indicates that interchain connectivity arises dominantly through interactions between complementary bases, whereas intrachain connectivity replicates the primary structure of the chains (Fig. 2B). Other parameters of the network such as betweenness and average shortest path length provide further support to the formation of a globule stabilized by interactions between nucleobases (Fig. S166†). A modular representation of the network shows that the catalytic modules (M, I′, I, P in Fig. 2C) are connected via the connectivity between the bases. Analysis of MD simulations indicates that the formation of this supramolecular complex is driven both by hydrogen bonding and π-stacking interactions (Fig. 2D).
Heatmaps enumerating the frequency of hydrogen bonds (Fig. 2E) show that C⋯G and D⋯T pairings provide an important but not exclusive contribution to the persistence of the globular assembly, with D⋯G pairing providing a significant but less frequent mechanism of stabilization. Stacking interactions are far less specific, involving numerous residues including triazole groups from the backbone and aromatic catalytic units (I′, I, P) (Fig. S163†).
Heatmaps of the enthalpy of binding per residue provide a detailed view on the stabilization per residue pair, globally showing the stabilization of the supramolecular complex by interchain interactions between the different bases. This indicates that when forming the complex, intermolecular interactions outperform the intramolecular interactions of each strand when alone. The same analysis was performed on the Oa/Ob2 system and provided similar results, with the same type of interactions stabilizing the formation of a globular complex (Fig. S165†).
The catalytic systems were tested in the aerobic oxidation of benzyl alcohol (BnOH) into benzaldehyde (BzH), for different temperatures between 30 °C and 60 °C and at different molar concentrations of catalyst. Cu(I) was introduced in stoichiometric amount with respect to P groups, and catalyst concentration is expressed as the content in M units relative to the molar concentration of introduced alcohol (0.2 mol L−1). Gas chromatography was used to monitor the appearance of BzH; no other oxidation product could be found. Previous studies45 indicated that the competition of urethane and triazole motifs for Cu complexation is limited compared to P; additionally, competition of base analogs for copper binding is also limited according to NMR (ESI Section 7†). Results from a typical catalytic experiment are displayed in Fig. 3A; similar graphs for all other conditions are in ESI Fig. S158.†
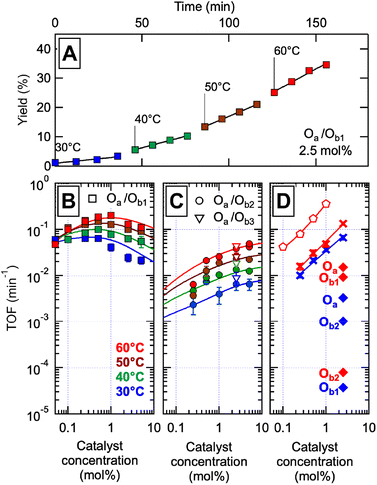 | ||
Fig. 3 Catalytic properties of the libraries of self-assembled precise oligomers. The catalyst concentration is expressed in mol% of M units relative to a reference concentration of 0.2 M benzyl alcohol (BnOH) in acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO 95 DMSO 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. (A) Typical catalytic experiment: benzaldehyde (BzH) yield versus reaction time for the conversion of BnOH (0.2 M) in the presence of oxygen, 2.5 mol% of the complete Oa/Ob1 catalytic system (with CuI), at four different temperatures. The slopes give the catalytic rates which, once divided by the concentration in catalyst, provide the turnover frequencies (TOF). (B)–(D). TOF versus catalyst concentration at four temperatures (colors as indicated), for (B) the complete Oa/Ob1 system, (C) the incomplete Oa/Ob2 (circles) and Oa/Ob3 (open triangles) systems, (D) a mixture of monomer units with the same composition as the complete oligomeric system (crosses), an equimolar mixture of MP dimers and II′P trimers lacking the hydrogen-binding groups and hydrophobic C6 units of Oa/Ob1 (pentagons), and single oligomer chains at 2.5 mol% in the presence of an equimolar amount of CuI (diamonds – blue 30 °C, red 60 °C). The continuous curves are fits of the model of Fig. 1E to the data, except in panel D where they are power law fits. 5. (A) Typical catalytic experiment: benzaldehyde (BzH) yield versus reaction time for the conversion of BnOH (0.2 M) in the presence of oxygen, 2.5 mol% of the complete Oa/Ob1 catalytic system (with CuI), at four different temperatures. The slopes give the catalytic rates which, once divided by the concentration in catalyst, provide the turnover frequencies (TOF). (B)–(D). TOF versus catalyst concentration at four temperatures (colors as indicated), for (B) the complete Oa/Ob1 system, (C) the incomplete Oa/Ob2 (circles) and Oa/Ob3 (open triangles) systems, (D) a mixture of monomer units with the same composition as the complete oligomeric system (crosses), an equimolar mixture of MP dimers and II′P trimers lacking the hydrogen-binding groups and hydrophobic C6 units of Oa/Ob1 (pentagons), and single oligomer chains at 2.5 mol% in the presence of an equimolar amount of CuI (diamonds – blue 30 °C, red 60 °C). The continuous curves are fits of the model of Fig. 1E to the data, except in panel D where they are power law fits. | ||
The turnover frequencies (TOFs) measured between 30 and 60 °C for the different oligomeric systems at different concentrations are plotted in Fig. 3B–D. The TOF is defined as the slope versus time of the BzH molar concentration at moderate conversion rates, divided by the molar concentration in catalyst; it represents the catalytic efficiency per mole of catalyst at low to moderate conversion. The catalytic activity of single oligomer chains is very low (diamonds in Fig. 3D), since they lack part of the needed catalytic groups; when combined with their complementary oligomer, they display very different catalytic activities depending on whether the two chains taken together comprise or not a complete catalytic system. Indeed, the collection of poly(oligomers) of the incomplete systems (such as in Oa/Ob2 solutions) exhibits a very low TOF despite comprising all the groups needed for catalysis (Fig. 3C); in contrast, the library of poly(oligomers) of the complete Oa/Ob1 system exhibits a much higher TOF at low concentration (Fig. 3B). Additionally, a catalytic system made of all monomer units at the same concentration as in the complete Oa/Ob1 system was measured for reference (crosses in Fig. 3D); its performance rapidly decreases upon dilution, owing to the decrease of the probability of chance encounter of the catalytic groups. This is in marked contrast with the complete Oa/Ob1 catalytic system that resists dilution and intriguingly exhibits an optimum close to 1 mol% (Fig. 3B). Likewise, the system consisting of the Oa and Ob1 oligomers devoid of H-binding G, T, D and C units and of hydrophobic C6 units (the MP dimer and the II′P trimer, pentagons in Fig. 3D), although very effective at high concentrations due to its limited steric crowding, rapidly decreases with concentration and becomes less efficient than the hydrogen-bonded system below 1 mol% of catalyst.
The complete Oa/Ob1 system is thus peculiar in its specific ability to maintain catalytic activity at low dilutions. Whereas higher catalytic activities can certainly be obtained for the other systems simply by introducing larger amounts of catalytic components (such as for the system made of separated monomer units or the MP/II′P system, Fig. 3D), the complete system is unique in its preservation of catalytic efficiency when diluted. We ascribe this resistance to dilution to the formation of self-assembled catalytic di(oligomeric) cycles.
The oligomer chains dynamically bind in a variety of configurations (Fig. 1E), resulting in the coexistence of different species including free oligomeric strands, linear poly(oligomer)s of varying length and chain ends, and di(oligomeric) cycles. In the incomplete Oa/Ob2 and Oa/Ob3 systems, self-assembly configurations comprising at least three oligomers generally contain all groups needed for catalysis, whereas di(oligomeric) configurations do not; as shown in Fig. 3C, these self-assembly configurations only provide mediocre catalytic efficiency. The fully different behavior of the complete Oa/Ob1 system thus necessarily arises from di(oligomer) assemblies, which now comprise all needed catalytic groups. Since these di(oligomeric) assemblies tend to easily form self-assembled macrocycles as shown by molecular dynamics simulations, it follows that the high catalytic efficiency at low concentrations of the Oa/Ob1 system arises from the formation of di(oligomeric) cycles.
Despite the virtually-infinite number of species in each constitutional library, their composition and catalytic activity can be modeled in a compact form by a mathematical model comprising a small set of physically-meaningful parameters, common to all libraries, temperatures and concentrations (ESI Section 9†). These parameters include two binding constants, K1 and K2 associated to chain end pairing and a standard entropy penalty 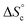 for cycle formation (Fig. 1E). The concentration in each species can be computed numerically from this model, as well as their contribution to the turnover frequencies at each temperature and concentration (ESI Section 9†). This compact mathematical model was simultaneously fitted to all experimental catalytic turnover frequencies measured at different temperatures and concentrations, for the two Oa/Ob1 and Oa/Ob2 systems taken together, leading to a quantitative reproduction of the experimental data (lines in Fig. 3B and C); parameters are reported in Table S2 (ESI Section 9†).
for cycle formation (Fig. 1E). The concentration in each species can be computed numerically from this model, as well as their contribution to the turnover frequencies at each temperature and concentration (ESI Section 9†). This compact mathematical model was simultaneously fitted to all experimental catalytic turnover frequencies measured at different temperatures and concentrations, for the two Oa/Ob1 and Oa/Ob2 systems taken together, leading to a quantitative reproduction of the experimental data (lines in Fig. 3B and C); parameters are reported in Table S2 (ESI Section 9†).
The possibility to represent at once with a compact mathematical model the catalytic properties of such complex self-assembling systems is an important outcome of this study. However, the model needs to be validated by an independent measurement of the concentration of each species in the solution (Fig. 1E), especially di(oligomeric) cycles which are of interest to us. These species are in constant dynamic equilibrium and cannot be isolated; furthermore, the oligomers they contain are involved in similar interactions in all species. Their concentrations are thus very difficult to measure by any available technique. However, each species possesses its own molecular mass and hydrodynamic volume. The diffusion coefficient of a proton attached to an oligomer included in a species of the constitutional libraries depends directly on the hydrodynamic volume of this species, which can be computed from its composition in each oligomer and from the hydrodynamic volume of the oligomers (ESI Section 9†). Additionally, the diffusion coefficient averaged over all co-existing species only depends on the hydrodynamic radii and concentrations in solution of these species. Hence, measuring the average diffusion coefficient of the protons provides an elegant way to check in situ the compositions of the constitutional libraries predicted by our model.
The diffusion coefficient of the protons of the complete Oa/Ob1 system was thus measured by DOSY NMR. A single diffusion band was seen at all concentrations by DOSY proton NMR performed in deuterated acetonitrile/DMSO 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 v/v at 300 K in the absence of copper (ESI Section 6†), indicating that fast exchange of the oligomers between the different co-existing species occurs within the NMR timeframe. In these circumstances, the average diffusion coefficient can be computed from the concentration of each co-existing species by the Stokes–Einstein equation (ESI Section 9†), with as input parameters K1, K2,
5 v/v at 300 K in the absence of copper (ESI Section 6†), indicating that fast exchange of the oligomers between the different co-existing species occurs within the NMR timeframe. In these circumstances, the average diffusion coefficient can be computed from the concentration of each co-existing species by the Stokes–Einstein equation (ESI Section 9†), with as input parameters K1, K2, 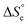 and the hydrodynamic radii of each isolated oligomer, which were measured by DOSY to be 0.50 ± 0.02 and 0.57 ± 0.02 nm for Oa and Ob1, respectively (Table S1, ESI Section 6†).
and the hydrodynamic radii of each isolated oligomer, which were measured by DOSY to be 0.50 ± 0.02 and 0.57 ± 0.02 nm for Oa and Ob1, respectively (Table S1, ESI Section 6†).
The measured and predicted diffusion coefficients of the complete Oa/Ob1 system were then compared (Fig. 4), using as parameters for the prediction the fit parameters obtained from the analysis of the catalytic data (Fig. 3). The experimental data agree very well with the predicted values assuming good solvent conditions (continuous line in Fig. 4).
 | ||
| Fig. 4 DOSY-measured average diffusion coefficient of the protons of the oligomers in the complete Oa/Ob1 system, depending on the concentration in M units (circles). The standard error is smaller than the point size. The curves are predictions based on the parameters from the fit of the catalytic activity, assuming either good (continuous curve) or Θ (dotted curve) solvent conditions (ESI Section 9†). | ||
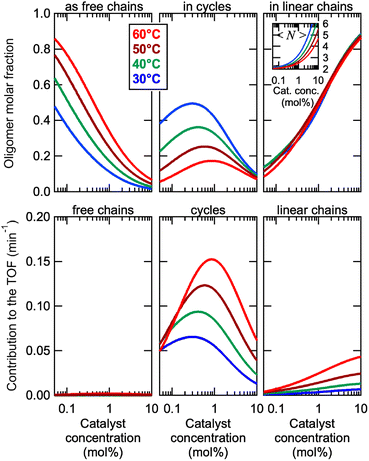
This model was thus used to compute the distribution of Oa oligomers between the different species for the Oa/Ob systems, depending on temperature and concentration (Fig. 5 top row). Oligomers are essentially free at very low concentrations, whereas they dominantly belong to linear poly(oligomeric) chains above 1 mol% of catalyst. The decrease of the binding constants K1 and K2 with temperature explains why the average degree of poly(oligomerization) of the linear chains slightly decreases with temperature (inset in top row of Fig. 5); however, the total amount of linear chains is very insensitive to temperature (Fig. 5, top right). Di(oligomeric) cycles slightly dominate the constitutional libraries at intermediate concentrations and lower temperatures, but this dominance is progressively lost as temperature increases. The decreased amount of cycles as temperature increases essentially results from the increased free energy cost associated to the entropy penalty for cycle formation 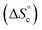 .
.
The contributions of each species to the total catalytic turnover frequency of the complete Oa/Ob1 system, which is the product between the amount of Oa in each species and the turnover frequency per Oa (ESI Section 9†), are collected in the bottom row of Fig. 5. The contribution of supramolecular di(oligomeric) cycles to the total turnover frequency is the dominant factor that explains the high catalytic activity of the complete system, even when the supramolecular cycles do not dominate the composition (e.g., at 60 °C). At this higher temperature, the relative proportion of cycles decreases but their catalytic activity increases due to thermal activation, resulting in an overall dominance of the cycles in the catalytic performance.
Cycles are thus much better than linear chains to reach a high catalytic activity, despite both configurations having all required active groups. At the concentration maximizing di(oligomeric) cycles, the ratio between the contributions to the catalytic activity of cycles versus all linear chains is ca. 30 and 10, at 30 and 60 °C, respectively. This is due to the much higher probability for the catalytic groups to be in an active site when assembled in a supramolecular cycle, compared to when in linear chains. This demonstrates that, by assembling the complementary strands in a supramolecular cycle, and thereby maximizing the probability that the five required groups meet in space, dramatic improvements of the catalytic efficiency by more than one order of magnitude can be obtained compared to linear configurations. In contrast, for the incomplete Oa/Ob2 system, supramolecular cycles cannot form complete catalytic sites and therefore do not contribute to the catalytic activity; consequently, this system only exhibits low activity associated to the low probability of formation of complete catalytic sites in linear poly(oligomeric) chains.
It is tempting to compare the efficiency of our supramolecular catalyst to other systems based on the same composition, in which the different catalytic groups are positioned differently in space.46 Depending on the sequence of units along chains45,47,48 and on their grafting configurations when heterogeneized,47,49–51 catalysts based on M, I and P units have been shown to exhibit very different catalytic efficiencies, as judged from their initial TOF. Compared to systems grafted on porous silica beads, the current supramolecular cycles are generally slightly inferior, probably because of a smaller accessibility of the substrates in the crowded globules of the cycles. In contrast, at 60 °C and below 1 mol%, the current supramolecular catalysts are better than any other homogeneous system we tested so far; this advantage is rapidly lost as concentration increases, because supramolecular cycles are disfavoured at higher concentrations while the probability of encounter is increased for other systems. However, our model can be used to predict directions for a larger range of conditions favouring the formation of the catalytically-active self-assembled di(oligomeric) cycles. For instance, increasing the chain end pairing constants by a factor of ca. 10 compared to their current geometric average value at 30 °C would result in a solution consisting almost exclusively of supramolecular cycles below 1 mol% catalyst. To favour cycles at higher concentrations, which would result in higher absolute catalytic rates, a supplementary stabilization mechanism must be given to cycles compared to linear chains. One way to achieve this is to reduce the entropy cost of cycle formation 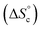 , which might be attained by increasing the rigidity of the oligomer backbones; however, this might be counter-productive with respect to the probability to have the catalytic groups meet in space. Another way would be to provide a supplementary enthalpy of stabilization specific to macrocycles, for example by using pairs of recognition units at each end of each oligomer, which would create a directionality in the pairing of ends and could thereby favour cycles over linear chains.
, which might be attained by increasing the rigidity of the oligomer backbones; however, this might be counter-productive with respect to the probability to have the catalytic groups meet in space. Another way would be to provide a supplementary enthalpy of stabilization specific to macrocycles, for example by using pairs of recognition units at each end of each oligomer, which would create a directionality in the pairing of ends and could thereby favour cycles over linear chains.
Conclusions
Our study investigated the self-assembly of complementary oligomers into a dynamic library of poly(oligomeric) species, most of which contribute little to catalytic activity. In this dynamic library, di(oligomeric) cycles were demonstrated to be highly catalytically-active, provided the two chains together comprise all the needed elements for catalysis, as in the Oa/Ob1 system. When only one element is missing as in Oa/Ob2 and Oa/Ob3, the activity drops very significantly, despite all needed elements are present in the solution. The activity can be recovered by adding the missing unit as a free component in solution (Fig. S168†). These results support the assumption35 that five functional groups, including a dinuclear copper complex, are involved in the catalytic cycle.Molecular dynamics simulations demonstrate that these self-assembled cycles form globules in which different interactions contribute to stabilization, even though the base analogs at the ends of the strands provide a continuous stabilization mechanism and connectivity between the catalytic groups, as shown by network analysis. Measurement of hydrodynamic radius also provides experimental support for the formation of di(oligomeric) cycles.
Hence, the primary structure of the oligomers is important for the emergence of catalytic activity, because the presence or absence of the needed catalytic groups on the strands directly affects the efficiency of the di(oligomeric) cycles. However, it is likely that the sequence order is not a critical factor at this stage, considering the limited length of the investigated oligomers. Nevertheless, quaternary structures are crucial for the emergence of catalytic activity, which here arises dominantly from the self-assembly of the strands in di(oligomeric) cycles. Interestingly, the self-assembly of di(oligomeric) cycles happens in a relatively dilute range of concentrations, in which cycles totally outperform simple mixtures of catalytic groups or any combination of the catalytic groups in linear chains. This demonstrates that an efficient catalytic activity can be obtained at rather high dilutions in the presence of properly self-assembled structures.
Our study also demonstrates that a small number of experimental parameters is sufficient to describe the complexity of the dynamic constitutional library of species resulting from the assembly of complementary oligomers. Indeed, the reproduction of catalytic activities and diffusion coefficients by a compact mathematical model is an important outcome of the present work, showing that the complexity of this system is still amenable to a deterministic description. Additionally, the interest of using network theory to interpret molecular dynamics simulations, and to support assumptions made in the mathematical model of the system, is another important outcome of this study.
Data availability
GC spectra and a table of values extracted therefrom (yields, turnover frequencies) are available at https://doi.org/10.14428/DVN/RYTG0V. Tables of DOSY diffusion coefficients are available at https://doi.org/10.14428/DVN/1XCNOK.Author contributions
Q. Q. and L. J. performed the synthesis and characterization of the molecules, the catalytic experiments, and the analysis of the spectroscopic results. A. E. F. contributed to define the project and provided guidance for synthesis and analysis. K. G. contributed to the definition of the project and to project guidance. I. N. contributed to the synthesis of molecules. A. B. performed the SEC analysis of the oligomers. G. B. C. performed the DOSY experiments and extracted the diffusion coefficients. M. S. led the research on the molecular dynamics simulations. D. D. and M. F. performed the molecular modeling simulations and interpretation. A. M. J. led the research and performed the modelling of the catalytic and diffusion data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Fonds de la Recherche Scientifique - FNRS and the Fonds Wetenschappelijk Onderzoek, under EOS Project No. 30650939. Computational resources are provided by the Consortium des Equipments de Calcul Intensif (CECI), funded by FNRS (Grant No. 2.5020.11) and Wallonia Region. The authors acknowledge Raoul Rozenberg for APCI-MS, Hervé Degand for ESI-MS/MS analysis, and Laurent Collard for GC analysis. K. G. is Senior Research Associate and M. S. is Research Director of the F. R. S.-FNRS.Notes and references
- A. Kohen, Role of Dynamics in Enzyme Catalysis: Substantial versus Semantic Controversies, Acc. Chem. Res., 2015, 48, 466–473 CrossRef CAS PubMed.
- P. K. Agarwal, D. N. Bernard, K. Bafna and N. Doucet, Enzyme Dynamics: Looking Beyond a Single Structure, Chemcatchem, 2020, 12, 4704–4720 CrossRef CAS PubMed.
- C. Zhang, X. Xue, Q. Luo, Y. Li, K. Yang, X. Zhuang, Y. Jiang, J. Zhang, J. Liu, G. Zou and X.-J. Liang, Self-Assembled Peptide Nanofibers Designed as Biological Enzymes for Catalyzing Ester Hydrolysis, ACS Nano, 2014, 8, 11715–11723 CrossRef CAS PubMed.
- G. Gulseren, M. A. Khalily, A. B. Tekinay and M. O. Guler, Catalytic supramolecular self-assembled peptide nanostructures for ester hydrolysis, J. Mater. Chem. B, 2016, 4, 4605–4611 RSC.
- M. Tena-Solsona, J. Nanda, S. Díaz-Oltra, A. Chotera, G. Ashkenasy and B. Escuder, Emergent Catalytic Behavior of Self-Assembled Low Molecular Weight Peptide-Based Aggregates and Hydrogels, Chem. - Eur. J., 2016, 22, 6687–6694 CrossRef CAS PubMed.
- C. Zhang, R. Shafi, A. Lampel, D. MacPherson, C. G. Pappas, V. Narang, T. Wang, C. Maldarelli and R. V. Ulijn, Switchable Hydrolase Based on Reversible Formation of Supramolecular Catalytic Site Using a Self-Assembling Peptide, Angew. Chem., Int. Ed., 2017, 56, 14511–14515 CrossRef CAS PubMed.
- M. Kurbasic, A. M. Garcia, S. Viada and S. Marchesan, Heterochiral tetrapeptide self-assembly into hydrogel biomaterials for hydrolase mimicry, J. Pept. Sci., 2022, 28, e3304 CrossRef CAS PubMed.
- E. B. Pimentel, T. M. Peters-Clarke, J. J. Coon and J. D. Martell, DNA-Scaffolded Synergistic Catalysis, J. Am. Chem. Soc., 2021, 143, 21402–21409 CrossRef CAS PubMed.
- I. Drienovská and G. Roelfes, Artificial Metalloenzymes for Asymmetric Catalysis by Creation of Novel Active Sites in Protein and DNA Scaffolds, Isr. J. Chem., 2015, 55, 21–31 CrossRef.
- M. A. A. Garcia, Y. Hu and I. Willner, Switchable supramolecular catalysis using DNA-templated scaffolds, Chem. Commun., 2015, 52, 2153–2156 RSC.
- J. J. Marek, R. P. Singh, A. Heuer and U. Hennecke, Enantioselective Catalysis by Using Short, Structurally Defined DNA Hairpins as Scaffold for Hybrid Catalysts, Chem. - Eur. J., 2017, 23, 6004–6008 CrossRef CAS PubMed.
- S. A. Green, H. R. Montgomery, T. R. Benton, N. J. Chan and H. M. Nelson, Regulating Transition-Metal Catalysis through Interference by Short RNAs, Angew. Chem., Int. Ed., 2019, 58, 16400–16404 CrossRef CAS PubMed.
- C. A. Cox, A. N. Ogorek, J. P. Habumugisha and J. D. Martell, Switchable DNA Photocatalysts for Radical Polymerization Controlled by Chemical Stimuli, J. Am. Chem. Soc., 2023, 145, 1818–1825 CrossRef CAS PubMed.
- T. Zheng, Q. Tang, L. Wan, Y. Zhao, R. Xu, X. Xu, H. Li and D. Han, Controlled Self-Assembly of the Catalytic Core of Hydrolases Using DNA Scaffolds, Nano Lett., 2023, 23, 2081–2086 CrossRef CAS PubMed.
- T. Terashima, T. Mes, T. F. A. D. Greef, M. A. J. Gillissen, P. Besenius, A. R. A. Palmans and E. W. Meijer, Single-Chain Folding of Polymers for Catalytic Systems in Water, J. Am. Chem. Soc., 2011, 133, 4742–4745 CrossRef CAS PubMed.
- J. Rubio-Cervilla, E. González and J. A. Pomposo, Advances in Single-Chain Nanoparticles for Catalysis Applications, Nanomaterials, 2017, 7, 341 CrossRef PubMed.
- H. Rothfuss, N. D. Knöfel, P. W. Roesky and C. Barner-Kowollik, Single-Chain Nanoparticles as Catalytic Nanoreactors, J. Am. Chem. Soc., 2018, 140, 5875–5881 CrossRef CAS PubMed.
- Y. Liu, S. Pujals, P. J. M. Stals, T. Paulöhrl, S. I. Presolski, E. W. Meijer, L. Albertazzi and A. R. A. Palmans, Catalytically Active Single-Chain Polymeric Nanoparticles: Exploring Their Functions in Complex Biological Media, J. Am. Chem. Soc., 2018, 140, 3423–3433 CrossRef CAS PubMed.
- T.-L. Nghiem, D. Coban, S. Tjaberings and A. H. Gröschel, Recent Advances in the Synthesis and Application of Polymer Compartments for Catalysis, Polymers, 2020, 12, 2190 CrossRef CAS PubMed.
- M. Artar, T. Terashima, M. Sawamoto, E. W. Meijer and A. R. A. Palmans, Understanding the catalytic activity of single-chain polymeric nanoparticles in water, J. Polym. Sci., Part A: Polym. Chem., 2014, 52, 12–20 CrossRef CAS.
- K. J. Prathap and G. Maayan, Metallopeptoids as efficient biomimetic catalysts, Chem. Commun., 2015, 51, 11096–11099 RSC.
- X. Zhang, C. Yang, P. An, C. Cui, Y. Ma, H. Liu, H. Wang, X. Yan, G. Li and Z. Tang, Creating enzyme-mimicking nanopockets in metal-organic frameworks for catalysis, Sci. Adv., 2022, 8, eadd5678 CrossRef CAS PubMed.
- D. Wang, H. Wu, S. Z. F. Phua, G. Yang, W. Q. Lim, L. Gu, C. Qian, H. Wang, Z. Guo, H. Chen and Y. Zhao, Self-assembled single-atom nanozyme for enhanced photodynamic therapy treatment of tumor, Nat. Commun., 2020, 11, 357 CrossRef CAS PubMed.
- M. Raynal, F. Portier, P. W. N. M. van Leeuwen and L. Bouteiller, Tunable Asymmetric Catalysis through Ligand Stacking in Chiral Rigid Rods, J. Am. Chem. Soc., 2013, 135, 17687–17690 CrossRef CAS PubMed.
- Z. C. Girvin and S. H. Gellman, Exploration of Diverse Reactive Diad Geometries for Bifunctional Catalysis via Foldamer Backbone Variation, J. Am. Chem. Soc., 2018, 140, 12476–12483 CrossRef CAS PubMed.
- T. Yamamoto, R. Murakami, S. Komatsu and M. Suginome, Chirality-Amplifying, Dynamic Induction of Single-Handed Helix by Chiral Guests to Macromolecular Chiral Catalysts Bearing Boronyl Pendants as Receptor Sites, J. Am. Chem. Soc., 2018, 140, 3867–3870 CrossRef CAS PubMed.
- Y. Nagata, R. Takeda and M. Suginome, Asymmetric Catalysis in Chiral Solvents: Chirality Transfer with Amplification of Homochirality through a Helical Macromolecular Scaffold, ACS Cent. Sci., 2019, 5, 1235–1240 CrossRef CAS PubMed.
- J. M. Zimbron, X. Caumes, Y. Li, C. M. Thomas, M. Raynal and L. Bouteiller, Real-Time Control of the Enantioselectivity of a Supramolecular Catalyst Allows Selecting the Configuration of Consecutively Formed Stereogenic Centers, Angew. Chem., Int. Ed., 2017, 56, 14016–14019 CrossRef CAS PubMed.
- Y. Li, X. Caumes, M. Raynal and L. Bouteiller, Modulation of catalyst enantioselectivity through reversible assembly of supramolecular helices, Chem. Commun., 2019, 55, 2162–2165 RSC.
- J. M. Ready and E. N. Jacobsen, Highly Active Oligomeric (salen)Co Catalysts for Asymmetric Epoxide Ring-Opening Reactions, J. Am. Chem. Soc., 2001, 123, 2687–2688 CrossRef CAS PubMed.
- N. C. Gianneschi, P. A. Bertin, S. T. Nguyen, C. A. Mirkin, L. N. Zakharov and A. L. Rheingold, A Supramolecular Approach to an Allosteric Catalyst, J. Am. Chem. Soc., 2003, 125, 10508–10509 CrossRef CAS PubMed.
- X. Zheng, C. W. Jones and M. Weck, Ring-Expanding Olefin Metathesis: A Route to Highly Active Unsymmetrical Macrocyclic Oligomeric Co-Salen Catalysts for the Hydrolytic Kinetic Resolution of Epoxides, J. Am. Chem. Soc., 2007, 129, 1105–1112 CrossRef CAS PubMed.
- Y. Liu, J. Rawlston, A. T. Swann, T. Takatani, C. D. Sherrill, P. J. Ludovice and M. Weck, The bigger, the better: Ring-size effects of macrocyclic oligomeric Co(iii)-salen catalysts, Chem. Sci., 2010, 2, 429–438 RSC.
- C. C. Bai, B. R. Tian, T. Zhao, Q. Huang and Z. Z. Wang, Cyclodextrin-Catalyzed Organic Synthesis: Reactions, Mechanisms, and Applications, Molecules, 2017, 22, 1475 CrossRef PubMed.
- J. M. Hoover, B. L. Ryland and S. S. Stahl, Mechanism of copper(I)/TEMPO-catalyzed aerobic alcohol oxidation, J. Am. Chem. Soc., 2013, 135, 2357–2367 CrossRef CAS PubMed.
- J. M. Hoover and S. S. Stahl, Highly Practical Copper(I)/TEMPO Catalyst System for Chemoselective Aerobic Oxidation of Primary Alcohols, J. Am. Chem. Soc., 2011, 133, 16901–16910 CrossRef CAS PubMed.
- J. M. Hoover, B. L. Ryland and S. S. Stahl, Copper/TEMPO-Catalyzed Aerobic Alcohol Oxidation: Mechanistic Assessment of Different Catalyst Systems, ACS Catal., 2013, 3, 2599–2605 CrossRef CAS PubMed.
- B. L. Ryland, S. D. McCann, T. C. Brunold and S. S. Stahl, Mechanism of alcohol oxidation mediated by copper(II) and nitroxyl radicals, J. Am. Chem. Soc., 2014, 136, 12166–12173 CrossRef CAS PubMed.
- J. Rabeah, U. Bentrup, R. Stößer and A. Brückner, Selective Alcohol Oxidation by a Copper TEMPO Catalyst: Mechanistic Insights by Simultaneously Coupled Operando EPR/UV-Vis/ATR-IR Spectroscopy, Angew. Chem., Int. Ed., 2015, 127, 11957–11960 CrossRef.
- K. Warm, G. Tripodi, E. Andris, S. Mebs, U. Kuhlmann, H. Dau, P. Hildebrandt, J. Roithová and K. Ray, Spectroscopic Characterization of a Reactive [Cu2(μ-OH)2]2+ Intermediate in Cu/TEMPO Catalyzed Aerobic Alcohol Oxidation Reaction, Angew. Chem., Int. Ed., 2021, 60, 23018–23024 CrossRef CAS PubMed.
- W. Zhong, J. Luo, Z. Liu, G. Zhan, L. Zhu, C. Lu, Z. Shen, X. Li and X. Liu, The mechanistic diversity of the selective aerobic oxidation of alcohols catalyzed by systems derived from CuI and a diamine ligand, Inorg. Chem. Front., 2023, 10, 3139–3150 RSC.
- J. Li, M. Leclercq, M. Fossepré, M. Surin, K. Glinel, A. M. Jonas and A. E. Fernandes, Discrete multifunctional sequence-defined oligomers with controlled chirality, Polym. Chem., 2020, 11, 4040–4046 RSC.
- J. C. Barnes, D. J. C. Ehrlich, A. X. Gao, F. A. Leibfarth, Y. Jiang, E. Zhou, T. F. Jamison and J. A. Johnson, Iterative exponential growth of stereo- and sequence-controlled polymers, Nat. Chem., 2015, 7, 810–815 CrossRef CAS PubMed.
- M. R. Golder, Y. Jiang, P. E. Teichen, H. V.-T. Nguyen, W. Wang, N. Milos, S. A. Freedman, A. P. Willard and J. A. Johnson, Stereochemical Sequence Dictates Unimolecular Diblock Copolymer Assembly, J. Am. Chem. Soc., 2018, 140, 1596–1599 CrossRef CAS PubMed.
- J. Li, Q. Qin, S. Kardas, M. Fossépré, M. Surin, A. E. Fernandes, K. Glinel and A. M. Jonas, Sequence Rules the Functional Connections and Efficiency of Catalytic Precision Oligomers, ACS Catal., 2022, 12, 2126–2131 CrossRef CAS.
- A. E. Fernandes and A. M. Jonas, Design and engineering of multifunctional silica-supported cooperative catalysts, Catal. Today, 2019, 334, 173–186 CrossRef CAS.
- P. Chandra, A. M. Jonas and A. E. Fernandes, Sequence and Surface Confinement Direct Cooperativity in Catalytic Precision Oligomers, J. Am. Chem. Soc., 2018, 140, 5179–5184 CrossRef CAS PubMed.
- S. Kardas, M. Fossépré, V. Lemaur, A. E. Fernandes, K. Glinel, A. M. Jonas and M. Surin, Revealing the Organization of Catalytic Sequence-Defined Oligomers via Combined Molecular Dynamics Simulations and Network Analysis, J. Chem. Inf. Model., 2022, 62, 2761–2770 CrossRef CAS PubMed.
- P. Chandra, A. M. Jonas and A. E. Fernandes, Spatial Coordination of Cooperativity in Silica-Supported Cu/TEMPO/Imidazole Catalytic Triad, ACS Catal., 2018, 8, 6006–6011 CrossRef CAS.
- P. Chandra, A. M. Jonas and A. E. Fernandes, Synthesis of discrete catalytic oligomers and their potential in silica-supported cooperative catalysis, RSC Adv., 2019, 9, 14194–14197 RSC.
- A. E. Fernandes, O. Riant, K. F. Jensen and A. M. Jonas, Molecular Engineering of Trifunctional Supported Catalysts for the Aerobic Oxidation of Alcohols, Angew. Chem., Int. Ed., 2016, 128, 11210–11214 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: General considerations, synthetic procedures and spectroscopic data (NMR, MS, SEC) on the oligomers and intermediate products (Sections 1–5); DOSY 2D spectra and results (Section 6); NMR study of copper pairing to base analogs (Section 7); graphs of yields versus time for the oxidation of alcohols into aldehydes (Section 8); mathematical models of the composition and properties of the constitutional libraries (Section 9); all-atom molecular dynamics simulations (Section 10); molecular network analysis (Section 11). See DOI: https://doi.org/10.1039/d3sc03133k |
| ‡ These authors contributed equally to this work. |
| § Present address: State Key Laboratory of Chemical Resource Engineering, Beijing Laboratory of Biomedical Materials, Beijing University of Chemical Technology, Beijing 100029, P. R. China. |
| This journal is © The Royal Society of Chemistry 2023 |