Open Access Article
Open Access ArticleAnti-Arrhenius behavior of electron transfer reactions in molecular dimers†
Neo
Lin
 a and
Tomoyasu
Mani
a and
Tomoyasu
Mani
 *ab
*ab
aDepartment of Chemistry, University of Connecticut, Storrs, CT 06269, USA. E-mail: tomoyasu.mani@uconn.edu; tmani@bnl.gov
bChemistry Division, Brookhaven National Laboratory, Upton, NY 11973, USA
First published on 30th October 2023
Abstract
Rates of chemical reactions typically accelerate as the temperature rises, following the Arrhenius law. However, electron transfer reactions may exhibit weak temperature dependence or counterintuitive behavior, known as anti-Arrhenius behavior, wherein reaction rates decrease as temperature increases. Solvent reorganization energy and torsion-induced changes in electronic couplings could contribute to this unusual behavior, but how each contributes to the overall temperature dependence is unclear. One can decelerate the charge recombination process in photogenerated radical pairs or charge-separated states by harnessing this often-overlooked phenomenon. This means that we could achieve long-lived radical pairs without relying on conventional cooling. Using a series of homo molecular dimers, we showed that the degree of torsional hindrance dictates temperature-dependent torsion-induced changes in electronic coupling and, therefore, charge recombination rates. The overall temperature dependence is controlled by how changes in electronic coupling and the temperature-dependent solvent reorganization energy contribute to the rates of charge recombination. Our findings pave the way for rationally designing molecules that exhibit anti-Arrhenius behavior to slow down charge recombination, opening possibilities for applications in energy-related and quantum information technologies.
1 Introduction
The Arrhenius law1 is a result of chemical kinetics, describes the temperature dependence of reaction rate constants, and is widely used as an empirical interpretation tool.2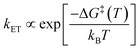 | (1) |
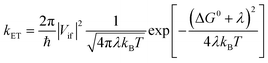 | (2a) |
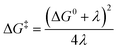 | (2b) |
Rearrangement of eqn (2a) shows that ln(kETT1/2) has a linear (negative slope) relationship with the inverse temperature 1/T.
 | (2c) |
The linearity assumes that Vif, λ, and ΔG0 are temperature independent. This linearity gives us experimental access to Vif and λ when ΔG0 can be reasonably well determined or estimated. However, some key factors governing these parameters can be temperature-dependent: solvent reorganization energy (λS), ΔG0 itself, and molecular conformations (associated Vif). Deviations from the temperature-dependent linearity of electron transfer reactions have been documented but are scarce.5 Slow solvent relaxation, most profoundly in glass-forming media,6 can generally control the reaction rates to weaken the temperature dependence.7 Electron transfer reactions in the Marcus inverted region could lead to very weak or almost no temperature dependence8 because of the contributions from the high-frequency vibrational modes in the semiclassical Marcus equation, known as the Marcus–Jortner–Levich (MJL) equation (see ESI Section 2†).9–11
The primary charge separation process in photosynthetic reaction centers exhibits an anti-Arrhenius behavior,12 where kET decreases with increasing T. Bixon and Jortner attributed this unexpected behavior to the strong coupling to the medium vibrational motion modes.13 Kim et al.14 observed a bell-shaped temperature dependence, including anti-Arrhenius behavior, in intermolecular electron transfer reactions. Conformationally rigid molecular systems could offer more detailed insights. Using donor–bridge–acceptor (D–B–A) molecules, Davis, Ratner, and Wasielewski15 later suggested that gating by torsional motion is responsible for such a counterintuitive behavior in intramolecular electron transfer reactions. Conformations of certain torsion angles can have stronger/weaker electronic couplings,16 and therefore, a larger population of such conformations at higher temperatures could lead to acceleration/deceleration of electron transfer reactions. Their study suggested that long-distance electron transfer through longer oligo-phenylenevinylenes could exhibit more pronounced dependence on torsional motions because multiple linkages imparted more complex torsional motions. While torsional gating can control the rate of electron transfer reactions,16–18 rigorous testing of its impact on temperature dependence, in particular anti-Arrhenius behavior, has been difficult because of the increasing complexity associated with D–B–A molecules such as multiple torsion angles among different units (e.g., oligo-p-phenylenevinylenes bridge) and energetic contributions. Specifically, Matyushov and co-workers have elegantly shown that the temperature-dependent solvent reorganization energy19 results in a bell-shaped dependence of kET on 1/T; charge recombination rates decelerate at high and low temperatures.20 Such temperature-dependence of solvent reorganization energy was also shown21 to contribute to the very weak or almost no temperature dependence mentioned above.8 Their results reaffirm the pronounced effects of reorganization energy in controlling electron transfer reactions while simultaneously casting the question of whether torsional motion could significantly contribute to the temperature dependence of electron transfer reactions, as suggested earlier. The effects of reorganization energies and torsion-induced changes in electronic couplings on rates of electron transfer reactions are illustrated in Fig. 1. In the Marcus inverted region, a decrease of λS and smaller V can independently lead to slower kET at elevated temperatures at comparable ΔG0.
Long-lived radical pairs (RPs) or charge-separated states are critical for efficient charge generations in photovoltaics,22 improving reactivity for photo-redox catalytic processes,23 and better spin mixing and control of spin-correlated RPs for molecular quantum sensing,24 communications, and computations.25 While cooling is often used to achieve such long-lived states, we argue that anti-Arrhenius behaviors can be exploited as an alternative way of slowing down charge recombination, reducing the reliance on low-temperature/cryogenic environments. Here, we used a set of homo molecular dimers as a model system to further understand this underexplored behavior and showed that the change in torsional flexibility of single aryl moieties could result in the different temperature dependence in the solution phase and the observation of anti-Arrhenius behavior in charge recombination.
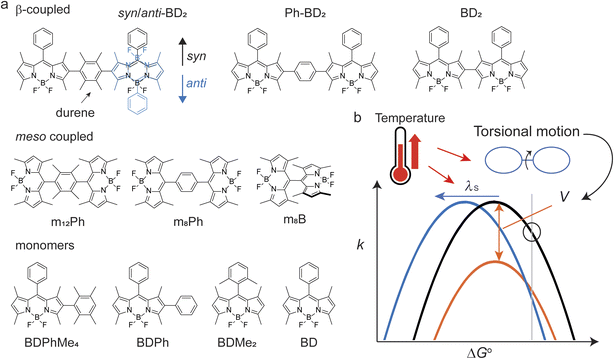
In homo molecular dimers, photoinduced electron transfer reactions are often symmetry-breaking charge separation (SBCS). SBCS has been the subject of extensive experimental and theoretical studies because of their crucial role in the light-harvesting reactions of center-specific chlorophyll molecules or “special pair”.26 Inspired by Nature's apparatus, many synthetic chromophores (dimers) and supramolecular assemblies have been designed to recreate SBCS, using polycyclic aromatic hydrocarbons and their derivatives27–29 which include boron-dipyrromethene (BODIPY) chromophores.30 BODIPY presents a unique opportunity where we can link two identical units at various locations,31–36 allowing us to investigate the effects of torsional motions. Because of reduction potentials, some BODIPY dimers can undergo SBCS. Here, we use two distinct types of homo dimers; orthogonally (or meso-) coupled and β–β (here, simply β-) coupled dimers (Fig. 1a). These two coupling sites provide different degrees of flexibility in torsion angles without changing participating donor/acceptor molecular properties. We used unsubstituted benzene and a bulky counterpart, durene (1,2,4,5-tetramethylbenzene), as a bridge to further control torsional motions between the two BODIPY units. While two torsional motions do not necessarily move in sync, they are considered identical, given structural symmetry. Because of different potential energy surfaces (PES) along their respective torsion angles, the effect of “locking” of torsional motion by a bulky bridge is different for meso- and β-coupled dimers, making them exhibit different temperature-dependent electron transfer reactions and, therefore, allowing us to help understand the controlling factors of temperature dependence. Our findings suggest the possibility of rationally designing molecular systems whose charge recombination of photogenerated radical pairs exhibits anti-Arrhenius behavior.
The paper is organized as follows. We first describe the basic photo- and electrochemical characteristics of the new β-coupled BODIPY dimers (Section 2.1–2.3). Next, we present the study of photoinduced electron transfer reactions (symmetry-breaking charge separation and recombination) in the series of meso- and β-coupled BODIPY dimers at ambient temperature (Section 2.4–2.5). We then discuss the temperature-dependent photophysical properties, including anti-Arrhenius behaviors observed in both series (Section 2.6), followed by the conclusion (Section 3).
2 Results and discussions
2.1. Synthesis and diastereomers of the β-coupled BODIPY dimers
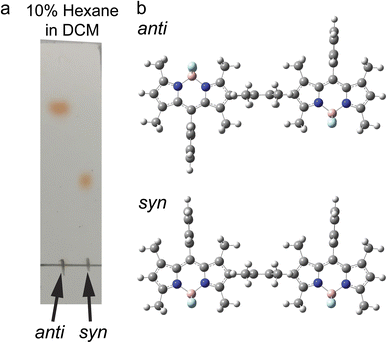
The synthetic scheme, procedures, and characterizations of the new molecules explored in this work are presented in ESI Section 1.† In addition to the dimers with benzene and tetramethylbenzene as bridges, we prepared a direct β–β coupled dimer37,38 (BD2, Fig. 1a) for comparison. We also prepared the respective monomers as controls (BD, BDPh, and BDPhMe4, Fig. 1a). The β-coupled dimer with a bulky bridge exhibits an interesting trait. Suzuki–Miyaura coupling of diiodotetramethylbenzene with mono-borylated BDs resulted in the formation of two stereoisomers of BODIPY dimers: the approximately centrosymmetric C2h conformer (syn) and the C2v non-centrosymmetric (anti) conformer. The polarities of these two conformers are significantly different from each other due to symmetry. The difference can be easily visualized by silica gel thin-layer chromatography (TLC) (Fig. 2a), making it possible to isolate them using silica column chromatography and characterize them individually. Density functional theory (DFT) calculations support this large polarity difference (Fig. 2b).As the dipole moment of BODIPY is along the short axis,39 the overall dipole moment becomes larger (μ ∼ 10 Debye in the gas phase) in syn-BD2 where the two BDs' short axis align in the same direction. On the other hand, the overall dipole moment of anti-BD2 is much smaller (μ ∼ 1 Debye), where the dipole moments of the two individual BDs align oppositely and cancel out each other. Because it is highly nonpolar, the solubility of anti-BD2 is poor in many organic solvents we tested, especially in polar solvents. While significantly different in polarity, the two stereoisomers (syn/anti diastereomers) behave almost identically within our experimental errors in the solution phase tested.
2.2. Photophysical properties of the β-coupled BODIPY dimers
We recorded absorption and emission spectra in a select number of solvents. Normalized absorption and emission spectra of the dimers and corresponding monomers in chloroform are shown in Fig. 3, and some photophysical properties are reported in Table 1. | ||
| Fig. 3 Steady-state photophysical characteristics of the β-coupled dimers and respective monomers in chloroform. (a) Normalized absorption spectra. (b) Normalized emission spectra (λex = 480 nm). | ||
| λ maxabs (nm) | λ maxem (nm) | Δνa (cm−1) | Φ em | τ (ns) | k rad (s−1) | k nr (s−1) | |
|---|---|---|---|---|---|---|---|
| a Δν = νmaxem − νmaxabs. b The values are for the emission whose peak is at 574 nm. | |||||||
| Dimers | |||||||
| syn-BD2 (C2v) | 523 | 532 | 359 | 0.83 ± 0.02 | 3.0 | 2.7 × 108 | 5.8 × 107 |
| anti-BD2 (C2h) | 523 | 532 | 323 | 0.85 ± 0.02 | 3.0 | 2.9 × 108 | 4.9 × 107 |
| Ph-BD2 | 528 | 555 | 921 | 0.74 ± 0.02 | 3.2 | 2.3 × 108 | 8.2 × 107 |
| BD2 | 534 | 523, 574 | 1305 | 0.77 ± 0.02b | 3.3b | 2.6 × 108 | 7.6 × 107 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Monomers | |||||||
| BDPhMe4 | 514 | 528 | 516 | 0.73 ± 0.02 | 4.3 | 1.7 × 108 | 6.6 × 107 |
| BDPh | 515 | 538 | 830 | 0.74 ± 0.01 | 4.6 | 1.6 × 108 | 5.6 × 107 |
| BD | 502 | 513 | 427 | 0.61 ± 0.02 | 3.7 | 1.6 × 108 | 1.1 × 108 |
The dimers' absorption and emission spectra are red-shifted compared to those of their respective monomers, and the degree of shifts varies from Ph-BD2, syn/anti-BD2, to BD2. The shift of the emission peak relative to the absorption peak (Δν = νmaxem − νmaxabs) also depends on the bridges of the dimers. These characteristics point to interesting exciton couplings. The exciton coupling is not the focus of this work, and we will present an in-depth analysis of these properties in a separate paper. The emission quantum yields of the dimers in chloroform (Φem ∼ 0.8) are slightly higher than those of the corresponding monomers (Φem ∼ 0.6–0.7). Emission lifetimes (τ = 1/kem) of the dimers are somewhat shorter than the corresponding monomers, but femtosecond transient absorption (fsTA) spectroscopy confirmed no significant additional nonradiative decay pathways (i.e., electron transfer reactions) for the dimers in chloroform (Fig. S1†). Among the dimers, Φem for syn/anti-BD2 is higher than Ph-BD2 and BD2. Nonradiative decay constants (knr), calculated by knr = (1 − Φem)kem, are smaller for syn/anti-BD2 than the corresponding monomer (BDPhMe4) and BD. This decrease in knr suggests that the improved rigidity imparted by durene, restricting rotations of both BD units, works in favor of increasing Φem.
We observed different and more complex emission properties of the dimers in a polar solvent, N,N-dimethylformamide (DMF) (Table 2); notably, we observed significantly lower Φem and shorter emission lifetimes while those of the monomers are less affected by the change in polarity. They indicate that an additional deactivation pathway exists in the dimers in a polar environment: symmetry-breaking charge separation.
| λ maxabs (nm) | λ maxem (nm) | Δνa (cm−1) | Φ em | τ (ns) | k rad (s−1) | k nr (s−1) | |
|---|---|---|---|---|---|---|---|
| a Δν = νmaxem − νmaxabs. b Φ em (fl) is the emission quantum yield of the monomer-like BODIPY fluorescence, and Φem (ex) is the quantum yield of the BODIPY dimer excitons. c The reported values are based on the global fitting of time-resolved emission decays at multiple wavelengths. These values are NOT the lifetimes of “prompt” emission. | |||||||
| Dimers | |||||||
| syn-BD2 (C2v) | 521 | 531 | 252 | 0.13 ± 0.05 | 0.76 | — | — |
| anti-BD2 (C2h) | 521 | 531 | 252 | 0.14 ± 0.05 | 0.76 | — | — |
| Ph-BD2 | 527 | 556 | 918 | 0.025 ± 0.02 (ex) | 0.16c | — | — |
| 0.005 ± 0.02 (fl)b | |||||||
| BD2 | 534 | 573 | 1205 | 0.019 ± 0.02 (ex) | 0.45 sc | — | — |
| 0.016 ± 0.02 (fl)b | |||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Monomers | |||||||
| BDPhMe4 | 512 | 526 | 861 | 0.68 ± 0.02 | 4.0 | 1.7 × 108 | 8.1 × 107 |
| BD-Ph | 514 | 540 | 406 | 0.77 ± 0.02 | 4.7 | 1.6 × 108 | 4.8 × 107 |
| BD | 501 | 512 | 349 | 0.54 ± 0.02 | 3.6 | 1.5 × 108 | 1.3 × 108 |
2.3. Electrochemical characterizations
Electrochemical data show that the charge separation processes are energetically allowed in a polar solvent. We determined the reduction potentials by cyclic voltammetry (CV) in DMF, acetonitrile (MeCN), and dichloromethane (DCM), depending on the solubility of the compounds. The voltammograms of the β-coupled dimers and monomers in DMF are shown in Fig. S2.† The reduction potentials and associated data are reported in Table 3 (DMF) and Table S1† (MeCN and DCM). Details of the analysis of electrochemical data, including comproportionation constants, are given in ESI, Section 3.†| E red 1 (●+/0, V) | E red 2 (0/●−, V) | E red 3 (●−/2−, V) | E red 4 (2−/●3−, V) | E S1 (eV) | ΔG0CSc (eV) | ΔG0CR (eV) | |
|---|---|---|---|---|---|---|---|
| a Reported vs. Fc+/0 in DMF with 0.1 TBA+PF6− unless otherwise noted. The error is generally ±0.02 V. b The peaks are irreversible, and the reported values are the peak value. c The reported values are for DMF. Determined by eqn (3). d We could not make reasonable measurements in DMF, and the values reported here are the estimations based on the data in DCM (Table S1) and scaled by the data of BDPh in DMF and DCM. e Not determined. f Reported vs. Fc+/0 in MeCN with 0.1 TBA+PF6−. | |||||||
| β-Coupled | |||||||
| syn-BD2 | 0.70 | −1.57 | −2.52 | 2.36 | −0.17 | −2.19 | |
| anti-BD2 | 0.73 | −1.56 | −2.81 | 2.36 | −0.16 | −2.20 | |
| Ph-BD2d | 0.70 | −1.49 | NDe | 2.30 | −0.19 | −2.11 | |
| BD2 | 0.76 | −1.48 | −1.66 | −2.58 | 2.24 | −0.14 | −2.10 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| meso-Coupled | |||||||
| m12Ph | 0.70 | −1.55 | −1.64 | NDe | 2.45 | −0.24 | −2.21 |
| m8Phf | 0.81 | −1.47 | −1.50 | NDe | 2.44 | −0.20 | −2.24 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Monomers | |||||||
| BDPhMe4 | 0.68 | −1.56 | −2.49 | ||||
| BDPh | 0.70 | −1.52 | −2.44 | ||||
| BDMe2 | 0.70 | −1.57 | NDe | ||||
| BD | 0.71 | −1.56 | −2.46 | ||||
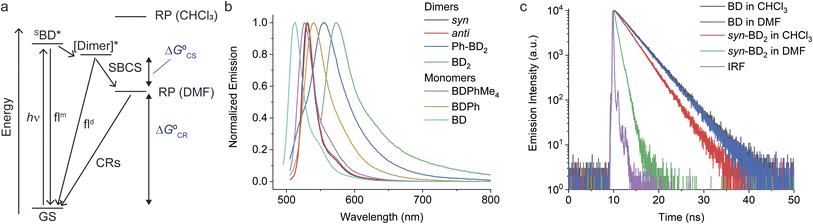
We now consider the energetics of photophysical pathways in DMF (Fig. 4a). We estimated the Gibbs energy change for charge separation by
 | (3) |
2.4. Symmetry-breaking charge separation in the β-coupled dimers
We observed SBCS for all the β-coupled dimers. The observations are similar to the meso-coupled dimers reported by Thompson, Bradforth, and co-workers (e.g., m8Ph and m8B, Fig. 1a).30 In this section and the following (Sections 2.4 and 2.5), we focus on the effect of torsional degrees of freedom on charge separation and recombination. As part of the study, we also introduced 1,2,4,5-tetramethylbenzene in the meso-coupled dimers (m12Ph, Fig. 1a, named after ref. 30) and compared the effects of a bulky bridge on these dimers.The first evidence of SBCS in the β-coupled dimers comes from emission measurements, as briefly mentioned above. Absorption and emission spectra of all the dimers in DMF are shown in Fig. S3† and 4b, respectively. The absorption spectra are similar to those in chloroform except for small blue shifts in peak wavelengths (Table 2). On the other hand, we observed some changes in emission properties. One indication of SBCS is the low quantum yield of emission. The quantum yields of the dimers in DMF are significantly smaller than those in chloroform (see Table 1 for chloroform and Table 2 for DMF). For example, Φem of syn-BD2 is 0.83 and 0.13 in chloroform and DMF, respectively. We observed only one emission peak for syn/anti-BD2, which looks more like the BD local emission. For Ph-BD2 and BD2, we observed BD local and exciton [Dimer]* emissions, and their Φem is reported separately. Emission lifetime measurements showed a monophasic decay for syn/anti-BD2 and biphasic decay for Ph-BD2 and BD2, where the faster component is dominant (∼90%). The monophasic decay for syn/anti-BD2 is faster than the corresponding monomers in both DMF and chloroform (Fig. 4c). They also correspond to the excited state/RP decays determined by fsTA spectroscopy (see below). The faster components of the biphasic decays for Ph-BD2 and BD2 agree with the rate of charge recombination determined by fsTA (see below). The slower component of the biphasic decay may be due to the monomer-like emission that might come from populations that do not undergo electron transfer reactions or slight impurities. We did not capture the “prompt” dimer exciton/local BD excited state emission decays that can reflect the rates of SBCS. Those decays in Ph-BD2 and BD2 are faster than the time-resolution of our TCSPC setup (∼20–30 ps) as shown by fsTA, and therefore we could not determine the lifetime of these emissions.
To gain further insights into time-resolved photophysical behaviors in these dimers, we performed fsTA spectroscopy. We used global fitting to analyze each fsTA data set with a sequential, irreversible, kinetic model (A → B → C →…). The spectral profiles obtained from analysis with a sequential scheme are called evolution-associated decay spectra (EADS).40 The EADS of syn-BD2 in DMF are presented in Fig. 5a, and those of Ph-BD2 and BD2 are presented in Fig. S4.†
 | ||
| Fig. 5 Photoexcitations of syn- and anti-BD2 result in the formation of RPs in DMF. (a) EADS of syn-BD2 with corresponding lifetimes upon photoexcitation at λex = 500 nm. (b) The absorption of radiolytically generated radical anions of BD˙− (ref. 41) and electrochemically generated BDPhMe4˙+. (c) Decay kinetics of syn-BD2 at 355 and 401 nm in DMF upon photoexcitation at λex = 500 nm. (d) Comparison of the decay kinetics of syn- and anti-BD2 at 401 nm in DMF upon photoexcitation at λex = 500 nm. | ||
Although we could identify a component that has the spectral signature of BD˙− (∼560 nm (ref. 41)) in the single value decomposition (SVD)'s components in all the β-coupled dimers data set in DMF, the features are not clear in the EADS likely because of the overlap with the ground state bleaching. On the other hand, we observed the absorption peak at ∼400 nm in EADS (e.g., EADS with τ = 800 ps for syn-BD2) that agrees well with the absorption band of BODIPY radical cations (BDPhMe4˙+) that we recorded spectroelectrochemically (Fig. 5b). The rise times of this peak at ∼400 nm (Fig. 5c) correspond to kSBCS obtained by global fitting: note that kSBCS ≫ kS1 in the absence of SBCS. Consistent with the emission measurements, the TA measurements showed identical (within experimental errors) photophysical pathways for syn and anti-BD2; representative kinetic traces are shown in Fig. 5d, and rate constants are reported in Table 4. Again, no electron transfer reactions were observed in less polar solvents like chloroform and toluene: fsTA data of syn-BD2 in chloroform are presented in Fig. S1.†
| Solvent | 1/kSBCS (ps) | 1/kCR (ps) | 1/(kfl + knr)b (ps) | ||
|---|---|---|---|---|---|
| fsTAa | Emissionb | ||||
| a Determined by transient absorption spectroscopy. b Determined by time-resolved emission measurements. c The decays are monophasic. d The decays are biphasic, and the short component corresponds to kCR (see Table 2). e Data were taken from ref. 30. | |||||
| β-Coupled | |||||
| syn-BD2 | DMF | 300 ± 20 | 800 ± 20 | — | 760 ± 20c |
| anti-BD2 | DMF | 300 ± 20 | 790 ± 20 | — | 760 ± 20c |
| Ph-BD2 | DMF | 17 ± 8 | 126 ± 18 | 150 ± 20d | |
| BD2 | DMF | 7 ± 1 | 340 ± 25 | 450 ± 20d | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| meso-Coupled | |||||
| m12Ph | DMF | 180 ± 10 | 1070 ± 100 | — | |
| m8Ph | DMF | 60 ± 10 | 260 ± 50 | — | |
| MeCNe | 50 ± 10 | 200 ± 80 | |||
| m8B | MeCNe | 0.8 ± 0.2 | 2000 ± 100 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Monomers | |||||
| BDPhMe4 | DMF | 4060 ± 100 | |||
| BDPh | DMF | 4790 ± 100 | |||
| BD | DMF | 3630 ± 100 | |||
Based on the TA spectra at a longer time scale, we determined that the production of triplet excited states of BDs in these dimers in DMF are negligible, meaning triplet productions by neither spin–orbit charge-transfer (SOCT-ISC)41–45 nor radical pair intersystem crossing (RP-ISC) followed by triplet charge recombination is efficient in the current systems. Therefore, we can exclude the spin effects on the charge recombination rates.
2.5. Effects of tetramethylbenzene in β- and meso-coupled dimers
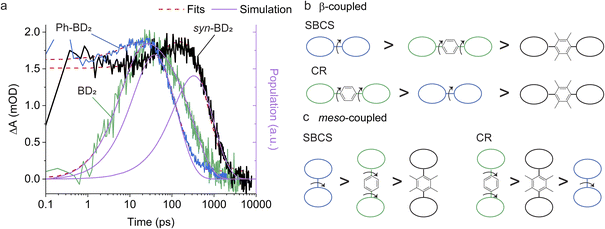
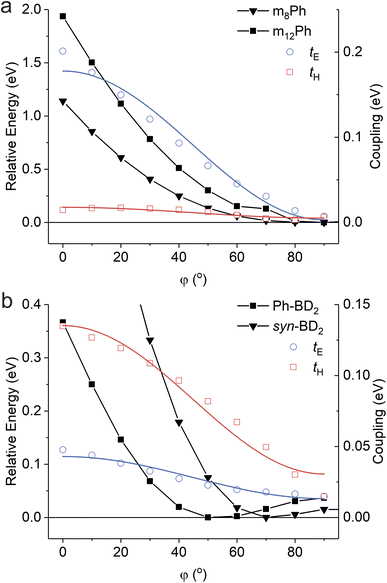
All the dimers follow the photophysical pathway depicted in Fig. 4a with varying rate constants. Charge separation (kSBCS) becomes slower, but recombination (kCR) becomes faster for Ph-BD2 than a more compact BD2. This somewhat unexpected observation of faster charge recombination at a shorter distance is similar to the meso-coupled BODIPY homo dimers previously reported (m8Ph vs. m8B where m8Ph has benzene between two BODIPYs, see Fig. 1a for the structure and rate constants for Table 4) though the effect in the β-coupled dimer case is smaller. Thompson, Bradforth, and co-workers used this observation to support the hypothesis that molecules with higher torsional rigidity exhibit longer charge-separated state lifetimes (slower kCR) because of a higher barrier to reaching resonance between the ground and CS surfaces.30 This set of our data supports this hypothesis. In contrast to Ph-BD2 and BD2, the two BODIPY planes of syn/anti-BD2 are more “locked” to a coplanar configuration because of structural hindrance by tetramethylbenzene as shown by the PES scanned along the torsion angle (φ). The comparisons of PES for BD2, BDPh, and BDPhMe4 are shown in Fig. S5.†kSBCS is about 15 and 40 times slower for syn/anti-BD2 than for the unconstrained counterpart Ph-BD2 and the more compact BD2, respectively. The effect is comparably smaller for the recombination process because kCR is only about 2 and 6 times slower for syn/anti-BD2 than for Ph-BD2 and BD2, respectively. The trends on SBCS and CR are depicted in Fig. 6a and b.To further examine the effect of the structural hindrance by tetramethylbenzene, we prepared a structurally constrained meso-coupled BODIPY dimer (m12Ph, Fig. 1a). We also prepared m8Ph for comparison. The steady-state absorption and emission spectra of m8Ph and m12Ph in DMF are reported in Fig. S6.† The synthetic scheme, characterization, and basic photophysical characterizations in chloroform and DMF are reported in ESI Experimental Section, Tables S2 and S3,† respectively. The voltammograms and electrochemical data are reported in Fig. S7† and Table 3. The Gibbs energy change of charge separation (ΔG0CS) for m12Ph and m8Ph are also reported in Table 3, using eqn (3) with rDA = 8.8 Å.29 We performed fsTA measurements in DMF, and EADS of m12Ph and m8Ph are presented in Fig. S8,† in which we could clearly identify the spectral signatures of both the BODIPY radical cation and anions. Interestingly, introducing tetramethylbenzene slowed down SBCS but did not significantly elongate the RP lifetime (Table 4). m8Ph behaves very similarly in DMF and MeCN (Table 4), and we can fairly compare the rate constants with the data set of m8B recorded in MeCN.30kCR is ∼3.5 times slower in m12Ph than m8Ph, but 2 times faster than the more compact m8B. SBCS and charge recombination are still the fastest and slowest in m8B among the three meso-coupled dimers, respectively, as illustrated in Fig. 6c, further signifying the large structural reorganization required for charge recombination in m8B.30 The differences in the effect of tetramethylbenzene on the photophysics between the β- and meso-coupled BODIPY dimers reflect the more pronounced change of conformational restrictions imposed by tetramethylbenzene in the β-coupled dimers. The PES along the phenyl ring's torsion angle (φ) in the β and meso-coupled dimers showed more flexibility at the β position. We discussed the PES data in the context of temperature dependence in Section 2.6. One interesting observation is the difference in the degree of electronic couplings, judged by the transfer integrals, for electron and hole between the β- and meso-coupled dimers: tH > tE for the β-coupled dimer and tE > tH for the meso-coupled dimer. This difference reflects how atomic orbitals contribute to the HOMO and LUMO of BODIPY. For LUMO, a significant contribution comes from the carbon at the meso position but not from the carbon at the β position. In contrast, for HOMO, more contribution comes from the carbon at the β position (Fig. S9†). These differences may indicate that the charge separation occurs through electron transfer for the meso-coupled dimers and hole transfer for the β-coupled dimers. Other details of the PES are presented in ESI Section 4.†
2.6. Temperature dependence of electron transfer reactions in the dimers
Temperature-dependent measurements show the different anti-Arrhenius behaviors for the charge recombination processes in the β- and meso-coupled dimers series. Here, we focus only on two pairs of β- and meso-coupled dimers with a bridge.First, SBCS follows the expected Arrhenius behavior for all four molecules (Fig. 7a and b). We can fit the data with eqn (2c), assuming that λ, electronic coupling between the S1 and RP states (V*), and ΔG0CS are temperature independent. In the fitting, λ and V* are variables while we keep ΔG0CS = −0.17 and −0.16 eV for syn-BD2 and Ph-BD2 and −0.24 and −0.20 eV for m12Ph and m8Ph as reported in Table 3.
 | ||
| Fig. 7 Temperature-dependent charge separation of (a) the β-coupled and (b) meso-coupled BODIPY dimers. Temperature-dependent charge recombination of (c) the β-coupled and (d) meso-coupled BODIPY dimers. The data are from fsTA measurements unless otherwise noted in the legend. The lines are fitted lines to eqn (2c). | ||
Expectedly, SBCS occurs in the Marcus normal region. Given the relatively fast rates of SBCS, the reaction is expected to occur from the excited states at the nuclear of the ground states (Franck–Condon states), and solvent reorganization energies may not change significantly over the temperature range. The obtained V* are about the same in the meso-coupled dimers, while the structurally unconstrained dimer, Ph-BD2, is about 4–5 times larger than the structurally constrained dimer syn-BD2. The fitted parameters (λ and V*) for all four dimers are reported in Table S4.† The difference in the coupling is consistent with the PES data (Fig. 8, and ESI Section 4†) that showed that the energy minima are the same for the two meso-coupled dimers (m8Ph and m12Ph) while it shifts to that of lower electronic coupling (hence slower charge separation) for a structurally constrained syn-BD2 compared to Ph-BD2.
Charge recombination processes do not follow the expected Arrhenius behavior. Temperature-dependent fsTA measurements directly monitor charge recombination and show that charge recombination rates of the unconstrained Ph-BD2 slowed dramatically at elevated temperatures. For example, 1/kCR of Ph-BD2 is 136 ± 10 ps at T = 0 °C, which slowed to 168 ± 10 ps at T = 60 °C. The charge recombination processes, determined by fsTA, are almost temperature-independent for syn/anti-BD2 (Fig. 7c). As noted above, the measured emission lifetime for the β-coupled Ph-BD2 corresponds to the charge recombination of RPs, which showed the same trend. From T = 0 °C to 60 °C, we observed an increase in exciton emission lifetime, and the nonradiative charge recombination rates slowed by ∼40% (Fig. S10†). The emission lifetime of syn-BD2 is not temperature-dependent (Fig. S11†). In clear contrast, we observed the anti-Arrhenius behavior for the constrained meso-coupled dimer m12Ph, but the charge recombination was almost temperature-independent for the unconstrained counterpart m8Ph (Fig. 7d). While the emission lifetimes do not directly reflect the charge recombination for the meso-coupled dimers, the recombination fluorescence lifetime of m12Ph increases as temperature increases while m8Ph decreases (Fig. S12†).
The fits of the CR data to eqn (2c) gave us near zero to negative activation energies (positive slopes, Fig. 7c and d). We could also not fit the data even with the MJL equation when we assumed ΔG0CR, λS, and Vif are temperature-independent (see ESI Section 2† for details). Given the structural similarity, the nature of the resulting charges within RPs is similar among the four molecules, especially among the two of the same series. Indeed, the electrochemical measurements show the almost identical ΔG0CR (Table 3). Therefore, the observed difference in the temperature dependence of the charge recombination rates must come from the structural factors associated with the bridge moieties (i.e., torsional motion).
We first look at the most structurally constrained m12Ph. The torsion angle minimum between the BD core and phenyl ring in the meso-position is φ = 90°. Please see Fig. 8a for the PES for the dimers and Fig. S13† for the control BODIPYs. The introduction of tetramethylbenzene in the meso-position does not alter the optimal φ from m8Ph to m12Ph, while it further restricts the motion with extra methyl groups locking the torsion angle more to the orthogonal configuration for m12Ph. This locking significantly raises the energy barrier to access “flatter” conformations of higher electronic couplings. We can consider m12Ph as one extreme case of “strong” torsional hindrance with a single minimum at the orthogonal configuration along 180° rotation.46 Given this steep potential barrier present in m12Ph, little structural changes occur along the torsion angle over the temperature range of our study, keeping the electronic coupling constant. This structural rigidity is corroborated by the fact that the nonradiative decay of the control BODIPY (BDMe2, Fig. 1a) is almost temperature independent, compared to the usual increase in nonradiative decay with an increase in temperature for BD (Fig. S14†). The phenyl rotation at the meso-position is responsible for the increased nonradiative decay.47,48 Their radiative decays are temperature-independent (Fig. S14†).
Therefore, we can attribute this temperature-dependent change in kCR of m12Ph to temperature-dependent solvent reorganization energies. Fitting the data to the MJL equation showed a decrease in λS as temperature increases. The fitting details are presented in ESI Section 2.† In short, we fitted the data with temperature-dependent λS and ΔG0CR while Vif was assumed to be temperature independent (see above). This decrease in λS at higher temperatures is consistent with the earlier experimental observations by Zimmt and co-workers49,50 and the models by Matyushov.19,20 The obtained electronic coupling is similar to V* obtained from the fitting of the CS data (Vif = 25 cm−1vs. V* = 30 cm−1).
As the solvent reorganization energies primarily come from the solvation surrounding the charged species, this recombination rate change with λS occurs for m8Ph as well. On top of this contribution from the temperature change in λS, we have a contribution from torsional change. Because of the shallower potential barrier, m8Ph can adopt “flatter” configurations of higher electronic couplings at higher temperatures, which are more favorable for charge recombination. This torsion-induced change in electronic couplings counteracts the change with λS, making the overall trend almost temperature-independent. Indeed, we can fit the more or less temperature-independent kCR data of m8Ph to the MJL equation by assuming a temperature-dependent Vif (ESI Section 2†). The obtained Vif for m8Ph (44 cm−1 at T = 20 °C) is higher than that for m12Ph, corroborating more flexible torsional motion and hence a higher coupling for m8Ph.
We now turn our attention to the β-coupled dimers. For the structurally unconstrained Ph-BD2, the energy minimum is at the configuration of an intermediate electronic coupling (Fig. 8b). We can classify Ph-BD2 as a “weak” torsional hindrance case.46 As the energy barrier toward the orthogonal configuration is much shallower compared to the barrier toward the “flatter” configurations, it will more likely take conformations of lower electronic couplings at higher temperatures. Coupled with the underlying change in λS, this torsion-induced change in electronic coupling slows down the charge recombination process at higher temperatures, leading to the observed anti-Arrhenius behavior. On the other hand, the tetramethylbenzene bridge fixes the phenylene ring to be more orthogonal to the BODIPY planes (φ ∼ 70° for syn-BD2vs. ∼50° for Ph-BD2) and lowers the energy barrier for the orthogonal configuration (φ ∼ 90°) significantly; ΔE = E (φ = 90°) − E (optimal φ) = 15 meV vs. 37 meV for syn-BD2 and Ph-BD2. At the same time, it raises the energy barrier for “flatter” configurations, compared to Ph-BD2. The energy minima of syn-BD2 are therefore more orthogonal, and we can also classify syn-BD2 as a “strong” torsional hindrance case.46 Yet, compared to the meso-coupled counterpart (m12Ph), the torsional motion is not as severely restricted (Fig. 8). Note that the energy scale (y-axis in Fig. 8 and S13†) is about five times larger for the meso-coupled dimers (Fig. 8a), signifying the existence of more severe torsional rigidity compared to the β-coupled dimers (Fig. 8b). Therefore, at elevated temperatures, syn-BD2 can still take conformations of higher electronic couplings and, consequently, favor charge recombination. This increase in electronic coupling counteracts the change in λS to have almost temperature-independent charge recombination for Ph-BD2 over the temperature range of our study in a similar manner to m8Ph.
3 Conclusions
While the Arrhenius law bears significant importance in chemistry, anti-Arrhenius behavior remains an underexplored phenomenon. Here, we investigated the role of torsional motion and solvent reorganization energy in the temperature dependence of the photoinduced symmetry-breaking charge separation and recombination reactions. As part of the study, we prepared a new series of β- and meso-coupled BODIPY homo dimers with 1,2,4,5-tetramethylbenzene as a bulky bridge. Because of the structural rigidity, we could identify and isolate the two stereoisomers for the β-coupled dimers (syn- and anti-BD2). The photophysical and electrochemical characterizations showed almost identical behaviors of these two stereoisomers in the solution phase we tested. Tetramethylbenzene as a bridge reduces the electronic coupling and, therefore, slows down the electron transfer processes in both β- and meso-coupled BODIPY dimers compared to the dimers with an unsubstituted phenyl bridge, but the extent of reduction differs.Temperature-dependent measurements revealed that both series of dimers exhibit anti-Arrhenius behaviors in the charge recombination process. The two series of homo dimers capture the two different cases of torsional hindrance usually observed: strong and weak. In a meso-coupled dimer, restricted torsional motion favors the conformation of the least electronic coupling (strong torsional hindrance). The severe restriction imposed by tetramethylbenzene does not allow the constrained dimer (m12Ph) to take conformations of higher electronic couplings even at elevated temperatures, effectively keeping the coupling constant fixed at the minimum over the tested temperature range. Yet, the change in solvent reorganization energy leads to anti-Arrhenius behavior in charge recombination. The unconstrained meso-coupled dimer (m8Ph) can take conformations favorable for electron transfer reactions at elevated temperatures due to a shallower energy barrier. This results in counteracting the contribution from the solvent reorganization energy and, overall, in almost temperature-independent charge recombination processes. On the other hand, because of a weaker torsional hindrance, the unconstrained β-coupled dimer (Ph-BD2) takes the conformation with intermediate electronic coupling. Temperature increase shifts it to take conformations of lower electronic coupling (φ ∼ 90°) which are unfavorable for electron transfer reactions, resulting in the anti-Arrhenius behavior. On the other hand, the constrained β-coupled dimers (syn/anti-BD2) can take the conformations of (close to) the least electronic couplings due to the structural hindrance. The elevated temperature shifts the equilibrium to conformations of higher electronic coupling and, therefore, faster electron transfer reactions. This change in couplings counteracts the solvent reorganization energy contribution to have the overall charge recombination trend temperature independent.
While the temperature dependence of solvent reorganization energy, when present, leads to anti-Arrhenius behavior of electron transfer reactions under a certain temperature range,20 we demonstrate that a simple torsional motion can significantly modify the temperature dependence. The nature of modifications depends on the strength of torsional hindrance, and we can synthetically control such a hindrance to exhibit anti-Arrhenius behavior (e.g., m12Ph in a polar solvent). The current study shows that we can rationally design the molecular systems to take advantage of this underexplored chemical phenomenon to decelerate charge recombination of SCRPs without cooling down. This strategy may be helpful in producing long-lived SCRPs for energy- and quantum information technologies.
Data availability
All relevant data are available from the corresponding author upon reasonable request.Author contributions
L. N. – investigation, writing, T. M. – conceptualization, project administration, funding acquisition, investigation, writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding by the National Science Foundation under Grant No. 2144787, an NSF CAREER Award. The computational studies were performed at the cluster located in the Chemistry Division of the Brookhaven National Laboratory through work funded by LDRD 23-030. We thank Mr Miu Tsuji and Mr Michael Vrionides for synthesizing m8Ph and BDMe2, respectively, and Dr Dariusz Niedzwiedzki for providing us with ASUfit 3.0 software.References
- S. Arrhenius, , Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren, Z. Phys. Chem., 1889, 4U, 226–248 CrossRef.
- B. Peters, Common Features of Extraordinary Rate Theories, J. Phys. Chem. B, 2015, 119, 6349–6356 CrossRef CAS PubMed.
- R. A. Marcus, On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer 1, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, Electron-Transfer Reactions in Chemistry – Theory and Experiment, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, Contemporary Issues in Electron Transfer Research, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS.
- C. A. Angell, Formation of Glasses from Liquids and Biopolymers, Science, 1995, 267, 1924–1935 CrossRef CAS PubMed.
- G. P. Wiederrecht, W. A. Svec and M. R. Wasielewski, Controlling the Adiabaticity of Electron-Transfer Reactions Using Nematic Liquid-Crystal Solvents, J. Phys. Chem. B, 1999, 103, 1386–1389 CrossRef CAS.
- N. Liang, J. R. Miller and G. L. Closs, Temperature-independent long-range electron transfer reactions in the Marcus inverted region, J. Am. Chem. Soc., 1990, 112, 5353–5354 CrossRef CAS.
- J. Ulstrup and J. Jortner, The effect of intramolecular quantum modes on free energy relationships for electron transfer reactions, J. Chem. Phys., 2008, 63, 4358–4368 CrossRef.
- M. Bixon and J. Jortner, Solvent relaxation dynamics and electron transfer, Chem. Phys., 1993, 176, 467–481 CrossRef CAS.
- M. Bixon and J. Jortner, in Advances in Chemical Physics, 1999, vol. 106, pp. 35–202 Search PubMed.
- G. R. Fleming, J. L. Martin and J. Breton, Rates of primary electron transfer in photosynthetic reaction centres and their mechanistic implications, Nature, 1988, 333, 190–192 CrossRef CAS.
- M. Bixon and J. Jortner, Activationless and pseudoactivationless primary electron transfer in photosynthetic bacterial reaction centers, Chem. Phys. Lett., 1989, 159, 17–20 CrossRef CAS.
- H. B. Kim, N. Kitamura, Y. Kawanishi and S. Tazuke, Bell-shaped temperature dependence in quenching of excited Ru(bpy)32+ by an organic acceptor, J. Am. Chem. Soc., 1987, 109, 2506–2508 CrossRef CAS.
- W. B. Davis, M. A. Ratner and M. R. Wasielewski, Conformational Gating of Long Distance Electron Transfer through Wire-like Bridges in Donor−Bridge−Acceptor Molecules, J. Am. Chem. Soc., 2001, 123, 7877–7886 CrossRef CAS PubMed.
- B. M. Hoffman and M. A. Ratner, Gated electron transfer: when are observed rates controlled by conformational interconversion?, J. Am. Chem. Soc., 1987, 109, 6237–6243 CrossRef CAS.
- H. A. Meylemans and N. H. Damrauer, Controlling Electron Transfer through the Manipulation of Structure and Ligand-Based Torsional Motions: A Computational Exploration of Ruthenium Donor−Acceptor Systems using Density Functional Theory, Inorg. Chem., 2009, 48, 11161–11175 CrossRef CAS PubMed.
- K. E. Spettel and N. H. Damrauer, Exploiting Conformational Dynamics of Structurally Tuned Aryl-Substituted Terpyridyl Ruthenium(II) Complexes to Inhibit Charge Recombination in Dye-Sensitized Solar Cells, J. Phys. Chem. C, 2016, 120, 10815–10829 CrossRef CAS.
- D. V. Matyushov, Energetics of Electron-Transfer Reactions in Soft Condensed Media, Acc. Chem. Res., 2007, 40, 294–301 CrossRef CAS PubMed.
- M. M. Waskasi, G. Kodis, A. L. Moore, T. A. Moore, D. Gust and D. V. Matyushov, Marcus Bell-Shaped Electron Transfer Kinetics Observed in an Arrhenius Plot, J. Am. Chem. Soc., 2016, 138, 9251–9257 CrossRef CAS PubMed.
- M. M. Waskasi, M. D. Newton and D. V. Matyushov, Impact of Temperature and Non-Gaussian Statistics on Electron Transfer in Donor–Bridge–Acceptor Molecules, J. Phys. Chem. B, 2017, 121, 2665–2676 CrossRef CAS PubMed.
- G. Lakhwani, A. Rao and R. H. Friend, Bimolecular Recombination in Organic Photovoltaics, Annu. Rev. Phys. Chem., 2014, 65, 557–581 CrossRef CAS PubMed.
- D. Gust, T. A. Moore and A. L. Moore, Solar Fuels via Artificial Photosynthesis, Acc. Chem. Res., 2009, 42, 1890–1898 CrossRef CAS PubMed.
- T. Mani, Molecular qubits based on photogenerated spin-correlated radical pairs for quantum sensing, Chem. Phys. Rev., 2022, 3, 021301 CrossRef CAS.
- S. M. Harvey and M. R. Wasielewski, Photogenerated Spin-Correlated Radical Pairs: From Photosynthetic Energy Transduction to Quantum Information Science, J. Am. Chem. Soc., 2021, 143, 15508–15529 CrossRef CAS PubMed.
- R. E. Blankenship, Molecular mechanisms of photosynthesis, John Wiley & Sons, Incorporated, Oxford, 2002 Search PubMed.
- E. Vauthey, Photoinduced Symmetry-Breaking Charge Separation, ChemPhysChem, 2012, 13, 2001–2011 CrossRef CAS PubMed.
- R. M. Young and M. R. Wasielewski, Mixed Electronic States in Molecular Dimers: Connecting Singlet Fission, Excimer Formation, and Symmetry-Breaking Charge Transfer, Acc. Chem. Res., 2020, 53, 1957–1968 CrossRef CAS PubMed.
- E. Sebastian and M. Hariharan, Symmetry-Breaking Charge Separation in Molecular Constructs for Efficient Light Energy Conversion, ACS Energy Lett., 2022, 7, 696–711 CrossRef CAS.
- L. Estergreen, A. R. Mencke, D. E. Cotton, N. V. Korovina, J. Michl, S. T. Roberts, M. E. Thompson and S. E. Bradforth, Controlling Symmetry Breaking Charge Transfer in BODIPY Pairs, Acc. Chem. Res., 2022, 55, 1561–1572 CrossRef CAS PubMed.
- N. Saki, T. Dinc and E. U. Akkaya, Excimer emission and energy transfer in cofacial boradiazaindacene (BODIPY) dimers built on a xanthene scaffold, Tetrahedron, 2006, 62, 2721–2725 CrossRef CAS.
- A. C. Benniston, G. Copley, A. Harriman, D. Howgego, R. W. Harrington and W. Clegg, Cofacial Boron Dipyrromethene (Bodipy) Dimers: Synthesis, Charge Delocalization, and Exciton Coupling, J. Org. Chem., 2010, 75, 2018–2027 CrossRef CAS PubMed.
- M. A. H. Alamiry, A. C. Benniston, G. Copley, A. Harriman and D. Howgego, Intramolecular Excimer Formation for Covalently Linked Boron Dipyrromethene Dyes, J. Phys. Chem. A, 2011, 115, 12111–12119 CrossRef CAS PubMed.
- J. H. Golden, L. Estergreen, T. Porter, A. C. Tadle, M. R. D. Sylvinson, J. W. Facendola, C. P. Kubiak, S. E. Bradforth and M. E. Thompson, Symmetry-Breaking Charge Transfer in Boron Dipyridylmethene (DIPYR) Dimers, ACS Appl. Energy Mater., 2018, 1, 1083–1095 CrossRef CAS.
- I. J. Arroyo-Córdoba, R. Sola-Llano, N. Epelde-Elezcano, I. L. Arbeloa, V. Martínez-Martínez and E. Peña-Cabrera, Fully Functionalizable β,β′-BODIPY Dimer: Synthesis, Structure, and Photophysical Signatures, J. Org. Chem., 2018, 83, 10186–10196 CrossRef PubMed.
- E. Sebastian and M. Hariharan, Null Exciton-Coupled Chromophoric Dimer Exhibits Symmetry-Breaking Charge Separation, J. Am. Chem. Soc., 2021, 143, 13769–13781 CrossRef CAS PubMed.
- Z. Li, Y. Liu, X. Hou, Z. Xu, C. Liu, F. Zhang and Z. Xie, The crystal structures, spectrometric, photodynamic properties and bioimaging of β-β linked Bodipy oligomers, J. Lumin., 2019, 212, 306–314 CrossRef CAS.
- X.-F. Zhang, BisBODIPY as PCT-based halogen free photosensitizers for highly efficient excited triplet state and singlet oxygen formation: Tuning the efficiency by different linking positions, Dyes Pigm., 2017, 146, 491–501 CrossRef CAS.
- F. Bergström, I. Mikhalyov, P. Hägglöf, R. Wortmann, T. Ny and L. B. Å. Johansson, Dimers of Dipyrrometheneboron Difluoride (BODIPY) with Light Spectroscopic Applications in Chemistry and Biology, J. Am. Chem. Soc., 2002, 124, 196–204 CrossRef PubMed.
- I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Global and target analysis of time-resolved spectra, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104 CrossRef CAS PubMed.
- J. T. Buck, A. M. Boudreau, A. DeCarmine, R. W. Wilson, J. Hampsey and T. Mani, Spin-Allowed Transitions Control the Formation of Triplet Excited States in Orthogonal Donor-Acceptor Dyads, Chem, 2019, 5, 138–155 CAS.
- H. vanWilligen, G. Jones and M. S. Farahat, Time-resolved EPR study of photoexcited triplet-state formation in electron-donor-substituted acridinium ions, J. Phys. Chem., 1996, 100, 3312–3316 CrossRef CAS.
- M. T. Colvin, A. B. Ricks, A. M. Scott, D. T. Co and M. R. Wasielewski, Intersystem Crossing Involving Strongly Spin Exchange-Coupled Radical Ion Pairs in Donor–bridge–Acceptor Molecules, J. Phys. Chem. A, 2012, 116, 1923–1930 CrossRef CAS PubMed.
- Z. E. X. Dance, S. M. Mickley, T. M. Wilson, A. B. Ricks, A. M. Scott, M. A. Ratner and M. R. Wasielewski, Intersystem crossing mediated by photoinduced intramolecular charge transfer: Julolidine-anthracene molecules with perpendicular pi systems, J. Phys. Chem. A, 2008, 112, 4194–4201 CrossRef CAS PubMed.
- Z. E. X. Dance, Q. X. Mi, D. W. McCamant, M. J. Ahrens, M. A. Ratner and M. R. Wasielewski, Time-resolved EPR studies of photogenerated radical ion pairs separated by p-phenylene oligomers and of triplet states resulting from charge recombination, J. Phys. Chem. B, 2006, 110, 25163–25173 CrossRef CAS PubMed.
- N. K. Lee, S. Park, M.-H. Yoon, Z. H. Kim and S. K. Kim, Effect of ring torsion on intramolecular vibrational redistribution dynamics of 1,1′-binaphthyl and 2,2′-binaphthyl, Phys. Chem. Chem. Phys., 2012, 14, 840–848 RSC.
- H. L. Kee, C. Kirmaier, L. Yu, P. Thamyongkit, W. J. Youngblood, M. E. Calder, L. Ramos, B. C. Noll, D. F. Bocian, W. R. Scheidt, R. R. Birge, J. S. Lindsey and D. Holten, Structural Control of the Photodynamics of Boron−Dipyrrin Complexes, J. Phys. Chem. B, 2005, 109, 20433–20443 CrossRef CAS PubMed.
- M. K. Kuimova, G. Yahioglu, J. A. Levitt and K. Suhling, Molecular Rotor Measures Viscosity of Live Cells via Fluorescence Lifetime Imaging, J. Am. Chem. Soc., 2008, 130, 6672–6673 CrossRef CAS PubMed.
- P. Vath and M. B. Zimmt, A Spectroscopic Study of Solvent Reorganization Energy: Dependence on Temperature, Charge Transfer Distance, and the Type of Solute−Solvent Interactions, J. Phys. Chem. A, 2000, 104, 2626–2633 CrossRef CAS.
- P. Vath, M. B. Zimmt, D. V. Matyushov and G. A. Voth, A Failure of Continuum Theory: Temperature Dependence of the Solvent Reorganization Energy of Electron Transfer in Highly Polar Solvents, J. Phys. Chem. B, 1999, 103, 9130–9140 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental methods, characterizations of new compounds, fitting details, electrochemical studies, discussions on PES, Fig. S1–S14, Tables S1–S4, additional reference, and NMR data. See DOI: https://doi.org/10.1039/d3sc03609j |
| This journal is © The Royal Society of Chemistry 2023 |