Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dimerization of confined Brønsted acids in enantioselective organocatalytic reactions†
Ingolf
Harden
 a,
Frank
Neese
a and
Giovanni
Bistoni
a,
Frank
Neese
a and
Giovanni
Bistoni
 *b
*b
aMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm Platz 1, 45470 Mülheim an der Ruhr, Germany
bDepartment of Chemistry, Biology and Biotechnology, University of Perugia, Via Elce di Sotto, 8, 06123 Perugia, Italy. E-mail: giovanni.bistoni@unipg.it
First published on 18th September 2023
Abstract
The formation of Brønsted acid aggregates in the course of asymmetric organocatalytic reactions is often overlooked in mechanistic studies, even though it might have a deep impact on the stereo-controlling factors of the transformations. In this work, we shed light on the influence of the catalyst structure and reaction conditions on the spontaneity of the aggregation process for popular chiral organocatalysts derived from phosphoric acids using high-level quantum mechanical calculations. Our study encompasses small and sterically unhindered chiral phosphoric acids as well as large and “confined” imidodiphosphates and imidodiphosphorimidates. These systems have recently proven particularly effective in promoting a large number of highly relevant asymmetric transformations. While cooperative catalytic effects of sterically less hindered chiral phosphoric acid catalysts are well appreciated in literature, it is found that the formation of catalyst dimers in solution is possible for both standard and confined catalysts. The spontaneity of the aggregation process depends on reaction conditions like solvent polarity, polarizability, temperature, the nature of the interaction with the substrate, as well as the catalyst architecture. Finally, it is shown that, at low temperatures (153 K), the aggregation process can profoundly influence the reaction kinetics and selectivity.
Introduction
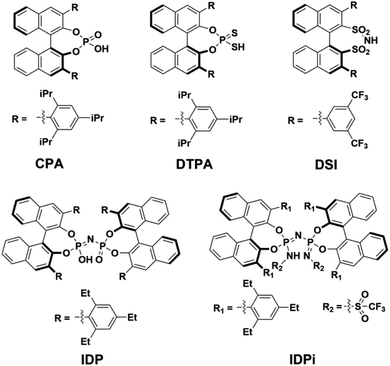
Chiral Brønsted acids derived from BINOL are commonly used as organocatalysts to promote a broad range of highly selective reactions involved in the synthesis of many valuable chemical entities, such as pharmaceuticals and agrochemicals.1They can be grouped into families with different structure and properties, such as (i) chiral phosphoric acids2–6 (CPA), (ii) dithiophosphoric acids7–9 (DTPA), (iii) disulfonimides10,11 (DSI); (iv) imidodiphosphates12–14 (IDP) and (v) imidodiphosphorimidates15,16 (IDPi). In particular, IDPi recently demonstrated remarkable activity and selectivity toward a large number of highly relevant stereoselective transformations,17–23 thanks to their confined active site, high acidity and modular architecture, which offers ample opportunities for catalyst design.
Mechanistic insights are instrumental for catalyst optimization and typically require synergistic experimental and computational efforts.23–31 Of paramount importance in this context is understanding the influence of the catalyst structure on the selectivity of the transformation and the role played by noncovalent interactions and steric effects, which might be capable of favoring/disfavoring only specific reaction pathways.32–34
Among the computational studies that addressed this problem, our group35 examined Diels–Alder reactions between cinnamate esters and cyclopentadiene and found that the stereoselectivity of the IDPi catalyst is governed by the balance of repulsive short-range steric effects and attractive long-range dispersion interactions. Wheeler and coworkers36 investigated the stereoselective synthesis of 2,3-dihydroquinazolinones catalyzed by chiral SPINOL-phosphoric acids and found that the stereoselectivity is influenced by π-stacking interactions between the substrate and the aryl ligands of the catalyst, as well as by hydrogen bonds between the substrate and the catalyst's core. The Houk group found37 stereodivergence for the CPA catalyzed allylation of aldehydes with β-akenyl allylic boronates for different substrates that was explained by noncovalent C–H–π interactions. Recently, we proposed a dispersion-driven induced fit model for the stereoselective intramolecular etherification of 4-phenylpent-4-en-1-ol, in which both catalyst distortion and the catalyst–substrate interaction are mainly governed by London dispersion.38
All previously discussed reactions assumed a monoacidic pathway, meaning that only one catalyst molecule is involved in the rate- and/or stereo-determining step. However, it is important to note that sterically unhindered phosphoric acids tend to spontaneously aggregate in solution. This aggregation can have a significant impact on the intricate network of covalent and noncovalent interactions that govern the essential properties of similar transformations. For example, Malm et al.39 demonstrated that multimers of diphenyl phosphoric acid with quinaldine (Qu) are formed in solution of aprotic solvents via NMR spectroscopy, while Detering and coworkers40 identified phosphoric acid trimers in CDF3 + CDF2Cl (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) solutions. Gschwind and coworkers presented evidence for the formation of CPA/imine aggregates in which imine molecules are nested between two CPAs.41,42
3) solutions. Gschwind and coworkers presented evidence for the formation of CPA/imine aggregates in which imine molecules are nested between two CPAs.41,42
When these aggregation processes occur, one possible consequence is a change in the electronic properties of the active site, which can have a notable impact on the catalyst's activity. For example, the groups of List and Thiel43 observed that heterodimerization of CPAs with small carboxylic acids increased the CPA acidity, resulting in increased reaction rates for epoxide ring opening reactions.
Moreover, cooperative effects between multiple catalyst molecules can also profoundly influence the selectivity of a chemical transformation. Niemeyer and coworkers44 investigated acid–acid interactions in catenated and catalytically active CPA dimers and found inversed stereoselectivities compared to the monoacidic pathway for the transfer-hydrogenation of 2-phenylquinoline. For the non-catenated CPAs,45 the monomeric and dimeric pathways compete, with the latter showing increased stereoselectivity. Toste and coworkers46 investigated the stereoselective CPA-catalyzed fluorination of allylic alcohols with Selectfluor and found reversal of stereoselectivity for catalysts with aryl substituents of increasing size. This effect was explained with dimerization processes taking place for the less sterically demanding catalysts. Recently, the groups of Yoon and Toste47 proposed a mechanism for stereoselective [2 + 2] photocycloadditions of vinylpyridines with styrene in which cooperative stereoinduction of the Ir-containing photocatalyst and the CPA catalyst determines the stereoselective outcome. Recently, Gschwind and coworkers investigated the key factors leading to the separation between the monomeric and dimeric pathways for the CPA-catalyzed transfer hydrogenation of imines. They found that high catalyst loadings, low temperatures and high absolute concentrations favor the dimeric pathway, leading to inversed stereoselectivity.48
In contrast, for “confined” catalysts like IDP or IDPi, dimerization in aprotic solvents has been largely overlooked, as well as its influence on the catalytic activity in the realm of counter-anion directed catalysis49,50 (ACDC). The aim of this work is bridging this knowledge gap by investigating the acid dimerization process in solution using state-of-the-art computational techniques for representative BINOL-derived acids (Scheme 1). In addition, the impact of a possible Brønsted acid dimerization on the activity of an asymmetric transformation is also examined in detail using the recently51 developed IDPi catalyzed stereoselective C–C coupling reaction of silyl nitronates with silyl ketene acetals as a case study.
Methodology
Unless otherwise specified, all calculations were carried out with the ORCA52,53 program package version 5.0.3.54For studying the catalyst aggregation process, an initial structural ensemble (SE) encompassing a large number of monomers and dimers for the catalysts shown in Scheme 1 was generated using the Conformer–Rotamer Ensemble Sampling Tool55–57 (CREST) at the GFN-FF58 level of theory, as implemented in the Extended Tight-Binding Program Package59 (xTB). For CPA, DTPA and DSI, all unique conformers in the SE were optimized with the Perdew–Burke–Ernzerhof60 (PBE) functional in combination with the Ahlrichs double-zeta def2-SVP61 basis set. Grimme's D3 dispersion correction62 was invoked together with Becke–Johnson damping.63 The resolution of identity64 was used in the split-RJ65 version together with the appropriate Coulomb-fitting auxiliary basis set66 to speed up the calculations. This protocol is abbreviated as PBE-D3/def2-SVP. For the larger catalytic systems (IDP and IDPi), optimization of all found dimer conformers was computationally too demanding, and hence only the lowest-in-energy conformers (in a range of 2.8 kcal mol−1) were optimized. Some of the conformers with higher energy were also included in the optimization step, i.e., those with unique and significant structural features. Importantly, for IDP and IDPi, different starting structures were used for the conformer sampling procedure to better explore the chemical space. For the most stable conformer identified, frequency calculations were carried out to compute thermal corrections. Final single point energies were obtained using the range-separated ωB97M-V67,68 functional together with the def2-TZVP basis set and the RIJCOSX69,70 approximation. Solvation corrections were computed at the B3LYP-D3/def2-TZVP60,71–73 level of theory using the SMD model (toluene).74 The final Gibbs free energy G was obtained via
| G = EωB97M-VSP + GB3LYPsolv + GPBEthermo. | (1) |
The dimerization energy of each catalyst (ΔGdim) was computed using a supramolecular approach, by subtracting from the energy of the most stable dimer the energy of the catalysts in their geometric ground state. Importantly, the key findings discussed in this work (e.g., the sign of ΔGdim indicating the spontaneity of the process under the experimental conditions) are essentially independent by the nature of the specific exchange correlation functional employed and/or by the level of theory used for incorporating solvation effects, as detailed in the ESI (see Tables S1 and S4†).
For studying the IDPi-catalyzed stereoselective C–C coupling reaction of silyl nitronates, a different protocol was used due to the increased system size. In particular, the initial GFN-FF/CREST conformational sampling on the ion pair/transition state involving two catalysts was performed by freezing the one-catalyst ion pair/transition state to its geometric ground state. Geometry optimizations of the most stable one- and two-catalyst ion pair conformers and transition states were performed at the r2SCAN-3c/GFN2-xTB level of theory using an multiscale ONIOM75 approach, as implemented in ORCA 5.0.3. As a note of caution, it is worth emphasizing here that complete exploration of the conformational space for these challenging systems with state-of-the-art computational protocols is not possible due to the challenging system size. Hence, the conformer sampling was used to identify the optimal position of a second catalyst molecule, keeping all other atoms frozen to the same position they have in the corresponding structures along the monomeric pathway. In all cases, the catalyst molecules were treated at the GFN2-xTB level of theory, while the silyl nitronate and the nucleophile were treated at the DFT level. Solvation effects were treated with the implicit ALPB solvation model.76 Numerical frequencies were obtained at the same level of theory. The reactant and product states were obtained from intrinsic reaction coordinate77 (IRC) calculations and subsequent geometry optimizations. Importantly, optimizing the entire systems at the r2SCAN-3c level does not change the associated electronic energy variations, which demonstrate that our results on the aggregation process are robust and to a large extent independent by the chosen level of electronic structure theory (see ESI, Section S10†). Final single point energies including Grimme's geometrical counterpoise correction78 (gCP) were obtained at the ωB97M-V/def2-TZVP/SMD(CH2Cl2) level of theory.
Results and discussion
Spontaneous and non-spontaneous dimerization processes in solution
The temperature dependence of the computed dimerization free energy ΔGdim in a commonly used aprotic solvent in organocatalysis (toluene in the present example) for the catalysts shown in Scheme 1 is illustrated in Fig. 1; as expected for a bimolecular process, the entropic term is largely responsible for the temperature dependence of the dimerization free energy.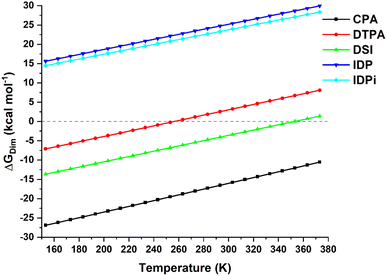 | ||
| Fig. 1 Temperature dependence of the dimerization free energy in toluene for the catalysts studied in this work. Note that the boiling point of toluene is ca. 384 K. | ||
Importantly, CPA shows negative ΔGdim at all temperatures and it is thus expected to form stable dimers in solution. In contrast, DSI and DTPA feature a much larger (less negative) ΔGdim than CPA. While DTPA and DSI are still expected to form stable dimers under mild reactions conditions, our calculations suggest that dimerization should not be favorable at higher temperatures. In particular, ΔGdim = 0 for T = 256 K for DTPA and for T = 354 K for DSI (note that a computational error of 2 kcal mol−1 in the dimerization energy estimate would lead to variations of these temperatures of about +/− 30 K). The confined catalysts IDP and IDPi show a completely different behavior, with positive free dimerization energies at all temperatures. Hence, these catalysts are not expected to dimerize under experimental conditions.
It is important to emphasize here that whether or not catalyst aggregation plays a significant role in a chemical process, e.g., by influencing its selectivity, also depends on other factors like the size of the substituents, solvent polarity, reaction kinetics and catalyst concentration, as it has been suggested in literature45 for a CPA catalyzed transformation. For example, Zhang et al.79,80 performed kinetic studies for the disulfonimide catalyzed cyanosilylation of Napthaldehyde at room temperature and with diethyl ether solvent and found an average reaction order for the catalyst of 1.23, resembling a first order influence of the catalyst on the rate constant. Moreover, Gschwind and coworkers did not find evidence supporting the formation of DSI-imine aggregates containing more than one DSI molecule in CD2Cl2 solution at 180 K, while they were able to detect the formation of CPA-imine ion pair dimers via NMR spectroscopy.81
However, aside from effects associated with specific reaction conditions, our results demonstrate that dimer stability follows the trend:
| CPA > DSI > DTPA ≫ IDP ∼ IDPi | (2) |
Effect of solute–solvent interactions on the dimerization process
The solvation contribution to ΔGdim comprises of electrostatic and non-electrostatic components, both of which were modeled using the SMD scheme.82 In the present case, both effects favor dimer dissociation, as shown in the ESI (see Tables S4 and S6†). On the one hand, electrostatic solute–solvent interactions strongly stabilize the non-interacting monomers. Thus, solvent polarity is one of the factors that can be used to experimentally control the spontaneity of the catalyst aggregation process, especially for catalysts like DTPA and DSI with relatively small dimerization free energies. On the other hand, solute–solvent dispersion interactions increase with increasing solvent accessible surface (SAS), and hence they also preferentially stabilize the monomers. Importantly, changing the shape and the polarizability of the solvent could have an impact on the strength of the solute–solvent dispersion interaction, thus affecting the energetics and hence the spontaneity of the aggregation process.82 Hence, for systems like CPA, DTPA and DSI, effects like temperature, solvent polarity and polarizability can tip the scale on whether catalyst dimers are formed in solution or not. In contrast, for the larger IDP and IDPi catalysts, the formation of supramolecular aggregates is unlikely under standard experimental conditions. As discussed in the ESI (see Section S6†), the solvation contribution to the free dimerization energy is fairly independent of the density functional. To understand the origin of these differences, a detailed analysis of the key intermolecular interactions in these dimers is carried out in the next section.Effect of intermolecular catalyst–catalyst interactions on the dimerization process
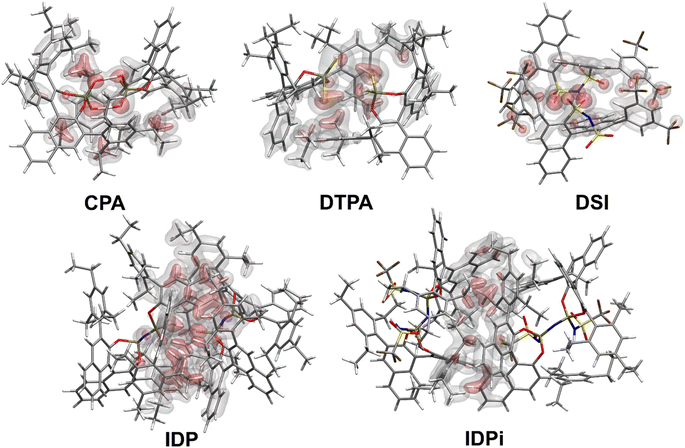
Fig. 2 shows the most stable conformers found from the sampling procedure for all the catalysts studied in this work. The corresponding dispersion interaction density (DID)83,84 plots at the HFLD/Silver level85 are also shown and provide a spatial analysis of the role played by London dispersion forces acting between the monomers.Structural analysis revealed the presence of two intermolecular hydrogen bonds in the CPA and DTPA dimers, while DSI and IDP feature only one hydrogen bond in their respective dimers. The most stable IDPi dimer does not show hydrogen bonds. While the difference between ΔGdim for CPA and DSI (Fig. 1) can be largely attributed to the relative strength of the corresponding O–H hydrogen (CPA) and S–H (DTPA) hydrogen bonds, understanding the relative stability of the other aggregates considered in this work is less straightforward and requires a deeper computational analysis.
To achieve this goal, ΔGdim at 173 K was decomposed into various terms:
| ΔGdim = ΔEgeo-prep + Edisp + ΔEnon-disp + ΔGthermo + ΔGsolv | (3) |
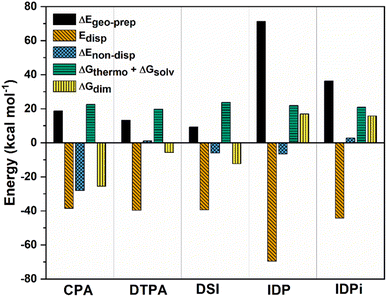 | ||
| Fig. 3 Decomposition of ΔGdim into various contributions at the ωB97M-V/def2-TZVP level of theory at 173 K for CPA, DTPA, DSI, IDP and IDPi. All energies are in kcal mol−1. | ||
ΔGthermoand ΔGsolv are roughly constant along the series and, as already discussed, favor dimer dissociation. The other repulsive contribution to the interaction is the geometric preparation associated with the catalysts' strain in the adduct, which to a large extent increases with the size of the interacting monomers. For small catalysts (CPA, DTPA, and DSI) the geometric preparation is comparable to the contribution from entropy and solvation, while its importance increases significantly for IDP and IDPi.
For CPA, the non-dispersive interaction ΔEnon-disp is large and negative. It amounts to −28.1 kcal mol−1 and can be attributed to two strong intermolecular O–H hydrogen bonds that stabilize the dimeric structure. In DTPA, on the other hand, the S–H hydrogen bonds are much weaker. Accordingly, ΔEnon-disp is slightly positive in this case due to balance of attractive (weak hydrogen bonds, electrostatic) and repulsive (charge penetration, steric repulsion) interactions. For all other dimers, ΔEnon-disp vanishes, making London dispersion Edisp the dominant energy component stabilizing the dimer.
Irrespective of the level of theory used (see Fig. S2†), CPA, DTPA, DSI and IDPi show qualitatively similar Edisp energies, even though IDPi is much larger, and hence more polarizable, than the other catalysts considered in this work. This seemingly counterintuitive effect can be understood by analyzing the DID plots shown in Fig. 2. As illustrated by the red (inner) surfaces in this figure, the strongest dispersive interactions in the dimers typically involve the catalysts' core. However, for IDPi, the catalysts' core does not contribute significantly to the interaction, probably due to steric effects originating from the substituents at the nitrogen position (R2). Such bulky groups are not present in the IDP core, and hence the corresponding dimer shows an intermolecular hydrogen bond and a very large Edisp value. However, the large value of Edisp in IDP is entirely compensated by the corresponding increase in ΔEgeo-prep, i.e., catalyst distortion increases to allow for an optimal interaction between the monomers. For these reasons, IDP and IDPi show comparable dimerization energies. It is worth mentioning here that the geometric preparation of bulky catalytic systems like IDP and IDPi is determined to a large extent by the strength of intra-catalyst dispersive interactions.38 For example, in the case of IDP, the active site is shielded by the ligands in the ground state geometric structure. Hence, significant structural rearrangement is required to allow the direct interaction between the active centers in the dimer. Similarly, for IDPi, the orientation of the 3,3′ aryl ligands is perturbed upon the formation of the dimer. Such structural rearrangements occur at the expense of intra-catalyst dispersion interactions, resulting in increased energy.
Taken together, these results suggest that the relative stability of the smaller CPA, DSI and DTPA Brønsted acid dimers is determined by the nature and number of hydrogen bonds involving the XH groups (X = S/O) in the catalysts' core. In the IDP and IDPi dimers, steric hindrance prohibits the formation of strong hydrogen bonds. In addition, intermolecular dispersion forces are fully counteracted by the repulsive catalyst strain. For these reasons, the dimers of these catalysts are unstable in solution. While different substituents might influence the magnitude of ΔGdim, we do not anticipate significant variations in these trends for the standard substituents commonly used in organocatalysis.
Dimerization processes under catalytic conditions
In the case of sterically unhindered phosphoric acids, the influence of catalyst dimerization on the mechanism and selectivity of organocatalytic transformations has already been extensively studied.45,48 In contrast, for asymmetric reactions catalyzed by bulky systems like IDPi, the role played by catalyst dimerization is not yet fully understood. To help fill this gap, we selected as a case study, the C–C bond formation of silyl nitronates with silyl ketene acetals catalyzed by IDPi.51 The proposed mechanism for the reaction is outlined in Scheme 2.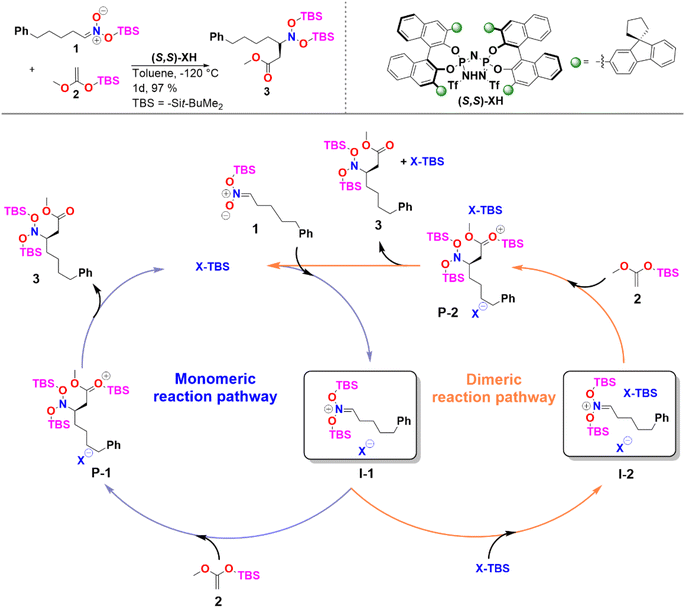 | ||
| Scheme 2 Reaction considered in this work and proposed catalytic cycle. See ref. 51 for experimental details. | ||
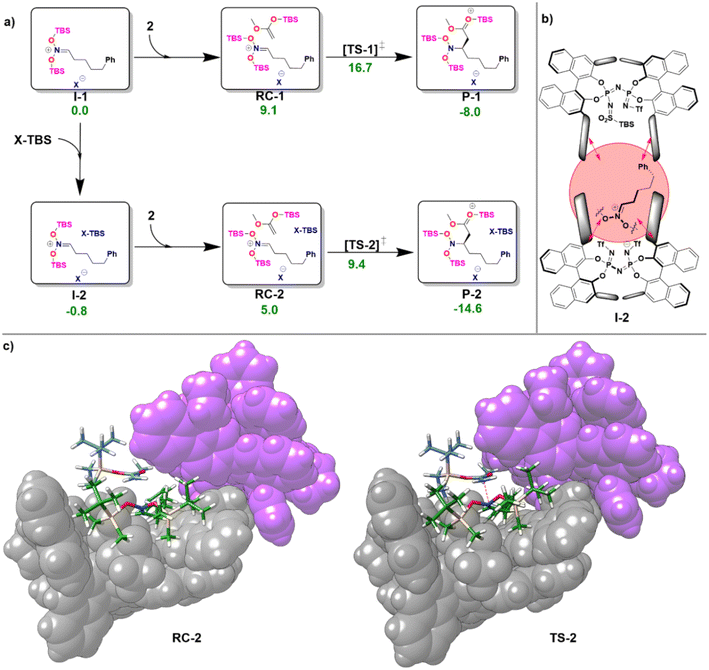
In the first step of the monomeric reaction pathway, the catalyst XH is silylated at room temperature to form X-TBS, which is the catalytically active species entering the catalytic cycle. The key step of the reaction is the formation of the chiral ion pair (I-1), which consists of the catalyst anion X− and the doubly silylated nitronate cation. I-1 is attacked by the nucleophile 2, which leads to the product P-1 in a single step. After release of X-TBS from P-1, the final product 3 is formed. In the dimeric reaction pathway, a second X-TBS molecule enters the catalytic cycle after the formation of I-1, leading to the formation of a second ion pair involving two catalyst molecules I-2. The computed monomeric and dimeric reaction profiles at 153 K, which is the experimental temperature for the C–C coupling reaction,51 are shown in Fig. 4 together with the 3D structures of the dimeric reactant and transition state.
Remarkably enough, the aggregation of I-1 with X-TBS to give I-2 features a free reaction energy (ΔGR) close to zero (−0.8 kcal mol−1). The small value of ΔGR suggests that the spontaneity of this process might change for different substituents and/or for different reaction conditions. Experimentally, the NMR characterization of the ion pair containing tert-Butyldimethylsilyl (E)-(2-phenylethylidene)azinate was carried out at 193 K and no catalyst dimerization was observed.51 Stimulated by these findings, we re-computed ΔGR at 193 K and found a positive value (1.9 kcal mol−1), which is consistent with the experimental results. These results provide further evidence for the fundamental role played by temperature in this context. In addition, it should be noted that the use of different substituents at the silyl nitronate could also influence the geometric match between the monomers, thus affecting the energy of the dimerization process.
Analysis of the noncovalent interactions between the three main fragments in I-2 (X−, bis-silyl nitronate, X-TBS) at the HFLD/Silver level revealed that electrostatic forces dominate the X−–nitronate interaction, while dispersive interactions are the dominant contribution to the interaction between the nitronate and X-TBS (see ESI, Table S8†). Importantly, the geometric preparation of the interacting fragments in I-2 (computed with respect to their geometries in I-1 or, for X-TBS, with respect to its equilibrium geometry) was found to be relatively small (−1.2 kcal mol−1 for X−, 8.8 kcal mol−1 for the nitronate, 1.2 kcal mol−1 for X-TBS at the ωB97M-V level of theory), indicating that strong interactions between the fragments can be realized without large structural changes (see Fig. 4b). This behavior is in striking contrast to our findings for the IDP and IDPi dimers (Fig. 3), which also feature strong dispersive interactions which are, however, counteracted by geometric preparation, thus making dimerization of these systems unlikely.
It can be concluded that the formation of aggregates of confined phosphoric acid derivatives (X− and X-TBS in the present example) under reaction conditions might be favored by the presence of substrates (the positively charged nitronate in this case) and/or reaction additives that sit between the two catalysts and act as a “glue” between them through electrostatic and dispersion forces.
As can be seen from Fig. 4c, for the dimeric complexes including the nucleophile (RC-2 and TS-2) the dual catalyst pocket opens up in order to facilitate interaction between the nucleophile and the nitronate. The dimeric transition state (TS-2) features a smaller relative free energy than its monomeric counterpart (TS-1). As detailed in the ESI (see Table S9†), the relative stabilization of TS-2 occurs irrespective of the specific nature of the exchange correlation functional employed. However, the complex nature of the system and of its interaction with the environment effectively limit the confidence of quantitative computational estimates of reaction barriers in this case (the difference in the activation barrier between the pathways ranges from 7.3 kcal mol−1 (ωB97M-V) to 3.1 kcal mol−1 (ωB97M-D4)). The relatively small energy difference between the two pathways suggests that experimental variables like temperature and solvent nature are likely crucial to determine the actual mechanistic details of the transformation, e.g., the reaction order with respect to the catalyst.
Conclusions
We present evidence that the formation of aggregates of chiral phosphoric acid derivatives in solution is in principle possible for both standard (e.g., CPA, DTPA and DSI) and confined (e.g., IDP, and IDPi) catalysts, but it depends heavily on the reaction conditions; this might have a profound influence on the stereo-controlling factors of potentially a large number of organocatalytic transformations.For CPA in solvents with low dielectric constants like toluene, the aggregation process is expected to be spontaneous at all temperatures (below the boiling point of the solvent). For DTPA and DSI, the aggregation process is less favorable, being spontaneous in toluene under mild reaction conditions, while higher temperatures and more polar solvents promote dissociation.
By contrast, for confined catalysts like IDPi, geometric strain makes the aggregation process much more challenging, and hence this process requires specific reaction conditions to become spontaneous. In the case study considered here, we showed that a positively charged molecule (nitronate) sitting between the phosphoric acid derivatives (the catalyst anion and the neutral silylated catalyst) drastically reduces aggregation energy and might favor the aggregation process through electrostatic and dispersion forces, while minimizing at the same time the geometrical strain. Remarkably enough, mechanistic investigations on the C–C coupling reaction with silyl ketene acetals indicate a faster reaction for the dimeric pathway at low temperatures (153 K), suggesting that cooperative catalytic effects between Brønsted acids might play an important role even for bulky and sterically demanding catalytic systems like IDPi.
Data availability
The Cartesian coordinates of all structures, the results of benchmark calculations on the influence of electronic structure method, solvation scheme, dispersive interactions and basis set size on aggregation energies and reaction barriers as well as a detailed analysis of the key noncovalent interactions are provided in the ESI.†Author contributions
I. H. performed all the calculations. G. B. conceived and directed the project. I. H. and G. B. wrote the original draft of the manuscript and prepared the figures. I. H., F. N. and G. B. contributed to the data analysis and to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Max Planck Society for financial support.References
- C. Min and D. Seidel, Asymmetric Brønsted acid catalysis with chiral carboxylic acids, Chem. Soc. Rev., 2017, 46, 5889–5902 RSC.
- M. Klussmann, L. Ratjen, S. Hoffmann, V. Wakchaure, R. Goddard and B. List, Synthesis of TRIP and Analysis of Phosphate Salt Impurities, Synlett, 2010, 2010, 2189–2192 CrossRef.
- S. Hoffmann, A. M. Seayad and B. List, A Powerful Brønsted Acid Catalyst for the Organocatalytic Asymmetric Transfer Hydrogenation of Imines, Angew. Chem., Int. Ed., 2005, 44, 7424–7427 CrossRef CAS PubMed.
- D. Uraguchi and M. Terada, Chiral Brønsted Acid-Catalyzed Direct Mannich Reactions via Electrophilic Activation, J. Am. Chem. Soc., 2004, 126, 5356–5357 CrossRef CAS PubMed.
- T. Akiyama, J. Itoh, K. Yokota and K. Fuchibe, Enantioselective Mannich-Type Reaction Catalyzed by a Chiral Brønsted Acid, Angew. Chem., Int. Ed., 2004, 43, 1566–1568 CrossRef CAS PubMed.
- M. Duan, C. D. Díaz-Oviedo, Y. Zhou, X. Chen, P. Yu, B. List, K. N. Houk and Y. Lan, Chiral Phosphoric Acid Catalyzed Conversion of Epoxides into Thiiranes: Mechanism, Stereochemical Model, and New Catalyst Design, Angew. Chem., Int. Ed., 2022, 61, e202113204 CrossRef CAS PubMed.
- Y. P. Chin and E. H. Krenske, Nazarov Cyclizations Catalyzed by BINOL Phosphoric Acid Derivatives: Quantum Chemistry Struggles To Predict the Enantioselectivity, J. Org. Chem., 2022, 87, 1710–1722 CrossRef CAS PubMed.
- G. Pousse, A. Devineau, V. Dalla, L. Humphreys, M.-C. Lasne, J. Rouden and J. Blanchet, Synthesis of BINOL derived phosphorodithioic acids as new chiral Brønsted acids and an improved synthesis of 3,3′-disubstituted H8-BINOL derivatives, Tetrahedron, 2009, 65, 10617–10622 CrossRef CAS.
- N. D. Shapiro, V. Rauniyar, G. L. Hamilton, J. Wu and F. D. Toste, Asymmetric additions to dienes catalysed by a dithiophosphoric acid, Nature, 2011, 470, 245–249 CrossRef CAS PubMed.
- P. García-García, F. Lay, P. García-García, C. Rabalakos and B. List, A Powerful Chiral Counteranion Motif for Asymmetric Catalysis, Angew. Chem., Int. Ed., 2009, 48, 4363–4366 CrossRef PubMed.
- M. Treskow, J. Neudörfl and R. Giernoth, BINBAM – A New Motif for Strong and Chiral Brønsted Acids, Eur. J. Org Chem., 2009, 2009, 3693–3697 CrossRef.
- I. Čorić and B. List, Asymmetric spiroacetalization catalysed by confined Brønsted acids, Nature, 2012, 483, 315–319 CrossRef PubMed.
- S. Das, L. Liu, Y. Zheng, M. W. Alachraf, W. Thiel, C. K. De and B. List, Nitrated Confined Imidodiphosphates Enable a Catalytic Asymmetric Oxa-Pictet–Spengler Reaction, J. Am. Chem. Soc., 2016, 138, 9429–9432 CrossRef CAS PubMed.
- J. H. Kim, I. Čorić, C. Palumbo and B. List, Resolution of Diols via Catalytic Asymmetric Acetalization, J. Am. Chem. Soc., 2015, 137, 1778–1781 CrossRef CAS PubMed.
- P. S. J. Kaib, L. Schreyer, S. Lee, R. Properzi and B. List, Extremely Active Organocatalysts Enable a Highly Enantioselective Addition of Allyltrimethylsilane to Aldehydes, Angew. Chem., Int. Ed., 2016, 55, 13200–13203 CrossRef CAS PubMed.
- L. Schreyer, R. Properzi and B. List, IDPi Catalysis, Angew. Chem., Int. Ed., 2019, 58, 12761–12777 CrossRef CAS PubMed.
- J. Ouyang, J. L. Kennemur, C. K. De, C. Farès and B. List, Strong and Confined Acids Enable a Catalytic Asymmetric Nazarov Cyclization of Simple Divinyl Ketones, J. Am. Chem. Soc., 2019, 141, 3414–3418 CrossRef CAS PubMed.
- S. Ghosh, S. Das, C. K. De, D. Yepes, F. Neese, G. Bistoni, M. Leutzsch and B. List, Strong and Confined Acids Control Five Stereogenic Centers in Catalytic Asymmetric Diels–Alder Reactions of Cyclohexadienones with Cyclopentadiene, Angew. Chem., Int. Ed., 2020, 59, 12347–12351 CrossRef CAS PubMed.
- S. Ghosh, J. E. Erchinger, R. Maji and B. List, Catalytic Asymmetric Spirocyclizing Diels–Alder Reactions of Enones: Stereoselective Total and Formal Syntheses of α-Chamigrene, β-Chamigrene, Laurencenone C, Colletoic Acid, and Omphalic Acid, J. Am. Chem. Soc., 2022, 144, 6703–6708 CrossRef CAS PubMed.
- N. Tsuji, J. L. Kennemur, T. Buyck, S. Lee, S. Prévost, P. S. J. Kaib, D. Bykov, C. Farès and B. List, Activation of olefins via asymmetric Brønsted acid catalysis, Science, 2018, 359, 1501–1505 CrossRef CAS PubMed.
- P. Zhang, N. Tsuji, J. Ouyang and B. List, Strong and Confined Acids Catalyze Asymmetric Intramolecular Hydroarylations of Unactivated Olefins with Indoles, J. Am. Chem. Soc., 2021, 143, 675–680 CrossRef CAS PubMed.
- L. Schreyer, P. S. J. Kaib, V. N. Wakchaure, C. Obradors, R. Properzi, S. Lee and B. List, Confined acids catalyze asymmetric single aldolizations of acetaldehyde enolates, Science, 2018, 362, 216–219 CrossRef CAS PubMed.
- T. Amatov, N. Tsuji, R. Maji, L. Schreyer, H. Zhou, M. Leutzsch and B. List, Confinement-Controlled, Either syn- or anti-Selective Catalytic Asymmetric Mukaiyama Aldolizations of Propionaldehyde Enolsilanes, J. Am. Chem. Soc., 2021, 143, 14475–14481 CrossRef CAS PubMed.
- J. Ouyang, R. Maji, M. Leutzsch, B. Mitschke and B. List, Design of an Organocatalytic Asymmetric (4 + 3) Cycloaddition of 2-Indolylalcohols with Dienolsilanes, J. Am. Chem. Soc., 2022, 144, 8460–8466 CrossRef CAS PubMed.
- W. M. C. Sameera, S. Maeda and K. Morokuma, Computational Catalysis Using the Artificial Force Induced Reaction Method, Acc. Chem. Res., 2016, 49, 763–773 CrossRef CAS PubMed.
- S. A. Moteki, H. Maruyama, K. Nakayama, H.-B. Li, G. Petrova, S. Maeda, K. Morokuma and K. Maruoka, Positive Effect of Water in Asymmetric Direct Aldol Reactions with Primary Amine Organocatalyst: Experimental and Computational Studies, Chem.–Asian J., 2015, 10, 2112–2116 CrossRef CAS PubMed.
- P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Quantum Mechanical Investigations of Organocatalysis: Mechanisms, Reactivities, and Selectivities, Chem. Rev., 2011, 111, 5042–5137 CrossRef CAS PubMed.
- Y.-h. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Theory and Modeling of Asymmetric Catalytic Reactions, Acc. Chem. Res., 2016, 49, 750–762 CrossRef CAS PubMed.
- Q. Peng, F. Duarte and R. S. Paton, Computing organic stereoselectivity – from concepts to quantitative calculations and predictions, Chem. Soc. Rev., 2016, 45, 6093–6107 RSC.
- A. J. Sterling, S. Zavitsanou, J. Ford and F. Duarte, Selectivity in organocatalysis—From qualitative to quantitative predictive models, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2021, 11, e1518 CrossRef CAS.
- A. C. Doney, B. J. Rooks, T. Lu and S. E. Wheeler, Design of Organocatalysts for Asymmetric Propargylations through Computational Screening, ACS Catal., 2016, 6, 7948–7955 CrossRef CAS.
- R. C. Wende, A. Seitz, D. Niedek, S. M. M. Schuler, C. Hofmann, J. Becker and P. R. Schreiner, The Enantioselective Dakin–West Reaction, Angew. Chem., Int. Ed., 2016, 55, 2719–2723 CrossRef CAS PubMed.
- Y.-h. Lam and K. N. Houk, Origins of Stereoselectivity in Intramolecular Aldol Reactions Catalyzed by Cinchona Amines, J. Am. Chem. Soc., 2015, 137, 2116–2127 CrossRef CAS PubMed.
- C. Eschmann, L. Song and P. R. Schreiner, London Dispersion Interactions Rather than Steric Hindrance Determine the Enantioselectivity of the Corey–Bakshi–Shibata Reduction, Angew. Chem., Int. Ed., 2021, 60, 4823–4832 CrossRef CAS PubMed.
- D. Yepes, F. Neese, B. List and G. Bistoni, Unveiling the Delicate Balance of Steric and Dispersion Interactions in Organocatalysis Using High-Level Computational Methods, J. Am. Chem. Soc., 2020, 142, 3613–3625 CrossRef CAS PubMed.
- C. J. Laconsay, T. J. Seguin and S. E. Wheeler, Modulating Stereoselectivity through Electrostatic Interactions in a SPINOL-Phosphoric Acid-Catalyzed Synthesis of 2,3-Dihydroquinazolinones, ACS Catal., 2020, 10, 12292–12299 CrossRef.
- S. Gao, M. Duan, L. R. Andreola, P. Yu, S. E. Wheeler, K. N. Houk and M. Chen, Unusual Enantiodivergence in Chiral Brønsted Acid-Catalyzed Asymmetric Allylation with β-Alkenyl Allylic Boronates, Angew. Chem., Int. Ed., 2022, 61, e202208908 CrossRef CAS PubMed.
- I. Harden, F. Neese and G. Bistoni, An induced-fit model for asymmetric organocatalytic reactions: a case study of the activation of olefins via chiral Brønsted acid catalysts, Chem. Sci., 2022, 13, 8848–8859 RSC.
- C. Malm, H. Kim, M. Wagner and J. Hunger, Complexity in Acid–Base Titrations: Multimer Formation Between Phosphoric Acids and Imines, Chem.–Eur. J., 2017, 23, 10853–10860 CrossRef CAS PubMed.
- C. Detering, P. M. Tolstoy, N. S. Golubev, G. S. Denisov and H. H. Limbach, Vicinal H/D Isotope Effects in NMR Spectra of Complexes with Coupled Hydrogen Bonds: Phosphoric Acids, Dokl. Phys. Chem., 2001, 379, 191–193 CrossRef.
- M. Melikian, J. Gramüller, J. Hioe, J. Greindl and R. M. Gschwind, Brønsted acid catalysis – the effect of 3,3′-substituents on the structural space and the stabilization of imine/phosphoric acid complexes, Chem. Sci., 2019, 10, 5226–5234 RSC.
- J. Gramüller, P. Dullinger, D. Horinek and R. M. Gschwind, Bidentate substrate binding in Brønsted acid catalysis: structural space, hydrogen bonding and dimerization, Chem. Sci., 2022, 13, 14366–14372 RSC.
- M. R. Monaco, D. Fazzi, N. Tsuji, M. Leutzsch, S. Liao, W. Thiel and B. List, The Activation of Carboxylic Acids via Self-Assembly Asymmetric Organocatalysis: A Combined Experimental and Computational Investigation, J. Am. Chem. Soc., 2016, 138, 14740–14749 CrossRef CAS PubMed.
- R. Mitra, H. Zhu, S. Grimme and J. Niemeyer, Functional Mechanically Interlocked Molecules: Asymmetric Organocatalysis with a Catenated Bifunctional Brønsted Acid, Angew. Chem., Int. Ed., 2017, 56, 11456–11459 CrossRef CAS PubMed.
- D. Jansen, J. Gramüller, F. Niemeyer, T. Schaller, M. C. Letzel, S. Grimme, H. Zhu, R. M. Gschwind and J. Niemeyer, What is the role of acid–acid interactions in asymmetric phosphoric acid organocatalysis? A detailed mechanistic study using interlocked and non-interlocked catalysts, Chem. Sci., 2020, 11, 4381–4390 RSC.
- A. J. Neel, A. Milo, M. S. Sigman and F. D. Toste, Enantiodivergent Fluorination of Allylic Alcohols: Data Set Design Reveals Structural Interplay between Achiral Directing Group and Chiral Anion, J. Am. Chem. Soc., 2016, 138, 3863–3875 CrossRef CAS PubMed.
- S. J. Chapman, W. B. Swords, C. M. Le, I. A. Guzei, F. D. Toste and T. P. Yoon, Cooperative Stereoinduction in Asymmetric Photocatalysis, J. Am. Chem. Soc., 2022, 144, 4206–4213 CrossRef CAS PubMed.
- M. Franta, J. Gramüller, P. Dullinger, S. Kaltenberger, D. Horinek and R. M. Gschwind, Brønsted Acid Catalysis—Controlling the Competition between Monomeric versus Dimeric Reaction Pathways Enhances Stereoselectivities, Angew. Chem., Int. Ed., 2023, 62, e202301183 CrossRef CAS PubMed.
- M. Mahlau and B. List, Asymmetric Counteranion-Directed Catalysis (ACDC): A Remarkably General Approach to Enantioselective Synthesis, Isr. J. Chem., 2012, 52, 630–638 CrossRef CAS.
- M. Mahlau and B. List, Asymmetric Counteranion-Directed Catalysis: Concept, Definition, and Applications, Angew. Chem., Int. Ed., 2013, 52, 518–533 CrossRef CAS PubMed.
- S. Das, B. Mitschke, C. K. De, I. Harden, G. Bistoni and B. List, Harnessing the ambiphilicity of silyl nitronates in a catalytic asymmetric approach to aliphatic β3-amino acids, Nat. Catal., 2021, 4, 1043–1049 CrossRef CAS.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Software update: the ORCA program system—Version 5.0, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1606 CrossRef.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- P. Pracht and S. Grimme, Calculation of absolute molecular entropies and heat capacities made simple, Chem. Sci., 2021, 12, 6551–6568 RSC.
- S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- S. Spicher and S. Grimme, Robust Atomistic Modeling of Materials, Organometallic, and Biochemical Systems, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended tight-binding quantum chemistry methods, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2021, 11, e1493 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Auxiliary basis sets to approximate Coulomb potentials, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- F. Neese, An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- N. Mardirossian and M. Head-Gordon, ωB97M-V: a combinatorially optimized, range-separated hybrid, meta-GGA density functional with VV10 nonlocal correlation, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- O. A. Vydrov and T. V. Voorhis, Nonlocal van der Waals density functional: the simpler the better, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- B. Helmich-Paris, B. D. Souza, F. Neese and R. Izsák, An improved chain of spheres for exchange algorithm, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, ONIOM: A Multilayered Integrated MO + MM Method for Geometry Optimizations and Single Point Energy Predictions. A Test for Diels–Alder Reactions and Pt(P(t-Bu)3)2 + H2 Oxidative Addition, J. Phys. Chem., 1996, 100, 19357–19363 CrossRef CAS.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, Robust and Efficient Implicit Solvation Model for Fast Semiempirical Methods, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- K. Ishida, K. Morokuma and A. Komornicki, The intrinsic reaction coordinate. An ab initio calculation for HNC → HCN and H− + CH4 → CH4 + H−, J. Chem. Phys., 1977, 66, 2153–2156 CrossRef CAS.
- H. Kruse and S. Grimme, A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree–Fock and density functional theory calculations for large systems, J. Chem. Phys., 2012, 136, 154101 CrossRef PubMed.
- Z. Zhang and B. List, Kinetics of the Chiral Disulfonimide-Catalyzed Mukaiyama Aldol Reaction, Asian J. Org. Chem., 2013, 2, 957–960 CrossRef CAS.
- Z. Zhang, M. Klussmann and B. List, Kinetic Study of Disulfonimide-Catalyzed Cyanosilylation of Aldehydes by Using a Method of Progress Rates, Synlett, 2020, 31, 1593–1597 CrossRef CAS.
- K. Rothermel, M. Žabka, J. Hioe and R. M. Gschwind, Disulfonimides versus Phosphoric Acids in Brønsted Acid Catalysis: The Effect of Weak Hydrogen Bonds and Multiple Acceptors on Complex Structures and Reactivity, J. Org. Chem., 2019, 84, 13221–13231 CrossRef CAS PubMed.
- J. M. Schümann, L. Ochmann, J. Becker, A. Altun, I. Harden, G. Bistoni and P. R. Schreiner, Exploring the Limits of Intramolecular London Dispersion Stabilization with Bulky Dispersion Energy Donors in Alkane Solution, J. Am. Chem. Soc., 2023, 145, 2093–2097 CrossRef PubMed.
- A. Wuttke and R. A. Mata, Visualizing dispersion interactions through the use of local orbital spaces, J. Comput. Chem., 2017, 38, 15–23 CrossRef CAS PubMed.
- A. Altun, F. Neese and G. Bistoni, Effect of Electron Correlation on Intermolecular Interactions: A Pair Natural Orbitals Coupled Cluster Based Local Energy Decomposition Study, J. Chem. Theory Comput., 2019, 15, 215–228 CrossRef CAS PubMed.
- A. Altun, F. Neese and G. Bistoni, Open-Shell Variant of the London Dispersion-Corrected Hartree–Fock Method (HFLD) for the Quantification and Analysis of Noncovalent Interaction Energies, J. Chem. Theory Comput., 2022, 18, 2292–2307 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc03769j |
| This journal is © The Royal Society of Chemistry 2023 |