On the σ-complex character of bis(gallyl)/digallane transition metal species

Abstract

σ-complexes of homoatomic E–E bonds are key intermediates in catalytically relevant oxidative addition reactions, but are as yet unknown for the group 13 elements. Here, stable species best described as σ-complexes of a 1,2-dichlorodigallane derivative with Ni and Pd are reported. They are readily accessed through the combination of a 1,2-dichlorodigallane derivative, which features chelating phosphine functionalities, with Ni⁰ and Pd⁰ synthons. In-depth computational analyses of these complexes importantly reveal considerable Ga–Ga bonding interactions in both Ni and Pd complexes, despite the expected elongation of the Ga–Ga bond upon complexation, suggestive of σ-complex character as opposed to more commonly described bis(gallyl) character. Finally, the well-defined disproportion of the Ni complex is described, leading to a unique Ga^I–nickel complex, with concomitant expulsion of uncomplexed Ga^III species.

---

Introduction

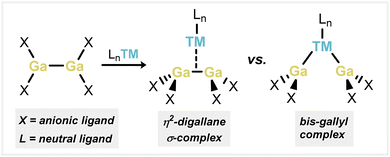
Transition metal (TM) σ-complexes have long been recognized as key intermediates on the pathway to oxidative addition and further in the σ-Complex Assisted Metathesis (σ-CAM) mechanism.^1,2 The isolation of stable σ-complexes can therefore lend key insights into their electronic nature and factors affecting the scission of E–E′ (E/E′ = C, Si, B, Al, Ga…) bonds at a TM center.³ It was only in 1984 that the landmark ‘Kubas complex’ was isolated, being the first stable example of a TM dihydrogen σ-complex.⁴ Since that time, countless examples of related H₂ complexes have been reported, and their electronic nature has been thoroughly investigated particularly in relation to the continuum of oxidation addition.⁵ Further examples of σ-complexes involving heteroatomic E–H bonds have also been discovered (E = C,⁶ Si,⁷ B,⁸ Al⁹), aligning with the importance of such E–H fragments in catalytic transformations. Accessing stable σ-complexes of homoatomic E–E bonds, beyond the H–H bond, poses a considerably greater challenge due to the lack of bond polarisation. As such, stable examples are considerably more rare. Aside from the vast number of known H₂ complexes, a number of C–C σ-complexes are known,^6b,10 whilst only two are known for disilanes.^11,12 Indeed, the first known example of the latter was initially described as a bis(silyl) species,^11a but was later found to better represent a disilane σ-complex.^11b Anionic diborane analogues (i.e., [B₂H₅]⁻) are reported to form TM complexes, due to coulombic interactions.¹³ Recently, two neutral derivatives of the [B₂H₅]⁻ unit were also found to form stable complexes with Cu at the B–B bond and are described as σ-complexes, presumably made more favorable by the electronically unsymmetrical substitution of the B–B units.¹⁴ It is interesting to note here that a degree of π-bonding in these B–B units incites a level of Dewar–Chatt–Duncanson (DCD) type bonding in their complexes.¹⁵ Nevertheless, no stable σ-complexes of group 13 R₂E-ER₂ species have yet been reported. Here, the few described examples of e.g. digallane addition to low-valent TM species have led to formal oxidative addition, typically forming trans-bis(gallyl) TM complexes (viz. Fig. 1).¹⁶ Rare examples featuring a cis-arrangement of the two Ga centers, which require a second chelating ligand at the TM center, typically bear relatively short Ga–Ga distances (i.e. <3 Å).^16c,d This may incite the presence of Ga–Ga bonding, although any degree of formal σ-complex character was not discussed in those reports. Understanding such interactions is key given the importance of group 13 E–E bonded species in catalysis, particularly true for diboranes, which are powerful reagents in borylation and diboration chemistry.¹⁷ With these points in mind, here we describe a combined experimental–computational approach in assessing the σ-complex character in [(R₄Ga₂)M] complexes (M = Ni, Pd), which feature short Ga–Ga interactions, and are stabilised through the incorporation of chelating phosphine interactions. Furthermore, the well-defined disproportionation of the described Ni species is outlined, leading to a unique Ga^I–nickel complex. These results give key insights into the electronic nature of what are best described as σ-complexes of homoatomic group 13 R₂E-ER₂ bonds.

Fig. 1 Resonance extremes in the addition of digallane species to a transition metal fragment.

Results and discussion

Synthesis and complexation of digallane

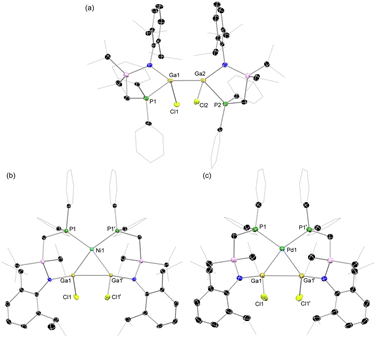
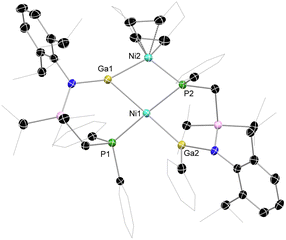
Our entry into this work first required scalable access to R₂Ga–GaR₂ species featuring our previously reported phosphine-functionalised amine pro-ligands, e.g. ^PhiPDippH (^PhiPDipp = {[Ph₂PCH₂Si(ⁱPr)₂](Dipp)N}⁻; Dipp = 2,6-ⁱPr₂C₆H₃).¹⁸ The incorporation of a phosphine brace sought to exploit the chelate effect in forming target σ-complexes, given the success of this strategy in the earlier report of a Cu-centred σ-complex.¹² Primarily, ^PhiPDippGaCl₂ (1) could be readily synthesized through addition of ^PhiPDippK to GaCl₃ in a one-pot procedure (Scheme 1). However, the reduction of this compound did not lead to the desired formation of isolable dimeric Ga^II species. We then turned our attention to the addition of two equiv. of ^PhiPDippK to the dioxane complex of Ga₂Cl₄, which did indeed lead to clean formation of the target digallane, [^PhiPDipp(Cl)Ga]₂ (2, Scheme 1 and Fig. 2(a)), which could be isolated in good crystalline yields of up to 76%.¹⁹ The asymmetric unit for 2 contains two independent molecules of this compound, with the dimeric species featuring Ga–Ga single bonds (d_Ga–Ga = 2.5283(9) and 2.5462(9) Å), and symmetrically coordinated Ga centers, each bearing one chloride ligand and one chelating ^PhiPDipp ligand, showing a singlet signal in its ³¹P{¹H} NMR spectrum (δ = −13.1 ppm). These Ga–Ga interactions are somewhat longer than reported digallanes featuring 4-coordinate Ga centers (mean of all 4-coordinate Ga–Ga distances: 2.457 Å),²⁰ and considerably longer than in the starting material, [dioxane₂·Ga₂Cl₄] (d_Ga–Ga = 2.406(1)/2.3911(17) Å),^21,22 which we attribute to the steric pressure enforced by the ^PhiPDipp ligand scaffold.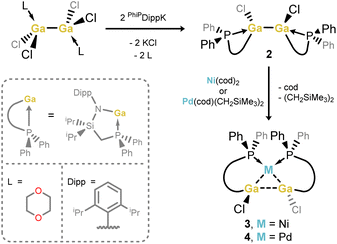

Scheme 1 Synthesis of phosphine-functionalised 1,2-bisamido-1,2-dichlorodigallane 2, and subsequent synthesis of Ni and Pd complexes 3 and 4.

Fig. 2 Molecular structures of (a) compound 2, and (b) compound 3, and (c) compound 4, with thermal ellipsoids at 30% probability, and hydrogen atoms removed for clarity. Calculated values at the BP86-(D3BJ)/def2-TZVPP level are given in brackets. Selected bond lengths (Å) and angles (°) for 2: Ga1–Ga2 2.5283(9) [2.457]; P1–Ga1 2.459(1) [2.436]; P2–Ga2 2.454(2) [2.441]; N1–Ga1 1.918(4) [1.934]; N2–Ga2 1.911(4) [1.928]; P1–Ga1–Ga2 111.12(4) [108.60]; P2–Ga2–Ga1 110.33(4) [109.38]; for 3: Ga1–Ga1′ 2.7713(7) [2.813]; Ga1–Ni1 2.3004(1) [2.331]; P1–Ni1 2.208(1) [2.190]; N1–Ga1 1.866(4) [1.887]; Ga1–Ni1-Ga1′ 74.08(1) [74.25]; P1–Ni1–P1′ 109.23(1) [108.42]; Ni1–Ga1–Ga1′ 52.96(1) [52.87]; for 4: Ga1–Ga1′ 2.8564(7) [2.924]; Ga1–Pd1 2.3862(1) [2.400]; P1–Pd1 2.3512(1) [2.326]; N1–Ga1 1.859(2) [1.887]; Ga1–Pd1–Ga1′ 73.53(1) [75.05]; P1–Pd1–P1′ 109.58(1) [106.96]; Pd1–Ga1–Ga1′ 53.24(1) [52.48].

Target TM complexes of 2 could be accessed through direct addition of this digallane to appropriate TM⁰ synthons, i.e. [Ni(cod)₂] and [Pd(cod)(CH₂SiMe₃)₂] (Scheme 1). Reactions are conducted in toluene or THF, leading to the formation of Ni (3) and Pd (4) complexes as bright orange and yellow crystalline solids, respectively, after work-up. Notably, Et₂O should be avoided in these reactions, as this leads to disproportionation processes (vide infra).²³ The ³¹P{¹H} NMR spectra for both 3 and 4 in D₈-THF indicate single species in solution, with sharp singlet signals at δ = 8.5 (3) and 4.3 (4) ppm. The ¹H NMR spectra of the same samples are extremely broadened at ambient temperature, most likely due to the chelation of the phosphine arms of the digallane at Ni and Pd, leading to hindered rotation of organic substituents. Cooling THF-d₈ samples of 3 to −55 °C leads to sharpening of signals, presumably by ‘freezing out’ ligand rotation (Fig. S24 in the ESI†). Single crystal X-ray diffraction analysis of crystals of both 3 and 4 confirmed the formation of the desired complexes, with the central [Ga₂] unit binding the Ni and Pd centres in an apparent η²-fashion (Fig. 2(b) and (c)). In both cases, an E-conformation of the 1,2-dichlorodigallane units is observed, presumably due to steric reasons, the chloride ligands being significantly less encumbering that the amide fragments. The square planar Ni centre is bound by the [Ga₂] unit and the two chelating phosphine arms. That the two Ga centres sit cis to each other is a strong indication that 3 and 4 contain formal Ga–Ga bonding interactions, given that the few known square planar bis(gallyl) TM complexes which do not feature additional chelating ligands form the trans-isomer.^16a,b The Ga–Ga distance in 3 is ≈8.6% elongated relative to that in 2 (d_Ga–Ga, 2: 2.5462(9) Å; 3: 2.7713(7) Å), as expected upon complexation. Here we note that the initial H₂ σ-complex of tungsten, reported by Kubas et al., showed ≈20% elongation of the H–H interaction.⁴ Indeed, this distance in 3 is within the known single Ga–Ga bonding interactions, and shorter than that in all so-called bis(gallyl) TM complexes (i.e. 2.910–3.039 Å).^16c,d The Ga–Ni interactions (d_Ga–Ni: 2.3004(1) Å) are within the region of known gallyl-nickel species. The acute Ga-Ni-Ga angle in 3 (∠Ga1Ni1Ga1′ = 74.08(1)°), particularly in comparison to the more open P–Ni–P angle (∠P1Ni1P1′ = 109.23(1)°), is further evidence for a Ga–Ga interaction in this complex. The Pd congener of 3, viz.4, bears a similar structural motif to 3, i.e. a square planar cis-conformation, with an elongated Ga–Ga interaction (d_Ga–Ga: 2.8564(7) Å), and Ga–Pd distances in keeping with known single bonds (d_Ga–Pd = 2.3862(1) Å). In both 3 and 4, the observed Ga–Ga distances are shorter than those in any known cis-bis(gallyl) complexes, suggesting a greater degree of Ga–Ga bonding interactions, and thus greater σ-complex character. Taken as a whole, metrical parameters in 3 and 4 give strong evidence for the presence of σ-complex character in the [Ga₂M] cores. Indeed, it is also possible that previously described bis(gallyl) complexes may in fact have a degree of ‘unassigned’ σ-complex character, as per numerous early TM-bis(hydride) complexes, which have since been reassigned as H₂ complexes following the seminal work from Kubas.

Computational evaluation of σ-complex character

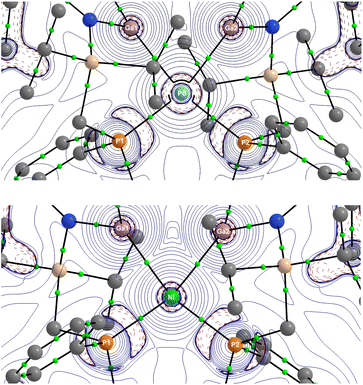
Given the historical challenges in firmly assigning σ-complexes based on structural data alone, we turned our attention to in-depth computational insights. Indeed, this has been extremely useful in uncovering the true nature of a so-called ‘Y-shaped’ bis(silyl)/disilane Pt complex, which is best described as a σ-complex due to a prominent Si–Si interaction.¹¹ We optimized the geometries of 2, 3, and 4 at the BP86-D3(BJ) level of theory using def2-SVP and larger def2-TZVPP basis sets, which gave similar results. The computed bond lengths and angles are in good agreement with the experimental data, where the differences are within the range of solid-state effects (Fig. 2). The experimental Ga–Ga distances are shorter than the calculated values, which is a well-known solid-state effect for weak interatomic interactions.²⁴ The focus of the theoretical part is on the bonding situation in 3 and 4. Table 1 shows that the atomic partial charges q of the Ga₂Cl₂ moieties are 0.95e in 3 and 0.97e in 4, with the Ga atoms carrying large positive charges and the chlorine atoms being negatively charged. The Wiberg bond orders suggest significant Ga–Ga bonding interactions with P values of 0.51 (3) and 0.46 (4), which are even larger than the Ga–N and Ga–TM values. We also analysed the electronic structure with the help of the QTAIM (Quantum Theory of Atoms in Molecules) developed by Bader.²⁵Fig. 3 shows the Laplacian distribution ∇²ρ(r) and the bond critical points (BCPs) and the associated bond paths of 3 and 4 in the Ga–Ga–TM plane. There are BCPs for the Ga–N and Ga–TM interactions but there is no Ga–Ga BCP. At first glance, this seems to contradict the calculated bond orders, which are greatest for the Ga–Ga interaction. However, it is known that the absence of BCP does not mean that there is no strong interatomic attraction: the BCP is determined by the curvature of the electron density, which often, but not always, leads to a bond path between bonded atoms. It has been pointed out that the occurrence of a bond path and a BCP must not be equated with a chemical bond.²⁶

Table 1 The calculated NBO charge (q) and Wiberg bond order (P) of 3 and 4 in the singlet state at the BP86-D3(BJ)/def2-TZVPP level

	Natural charge q			Wiberg bond order P
	3	4		3	4
Ga1	0.95	0.97	Ga1–Ga2	0.51	0.46
Ga2	0.95	0.97	Ga1–TM	0.30	0.32
TM	−0.06	−0.15	Ga2–TM	0.30	0.32
P1	0.93	0.95	TM–P1	0.28	0.28
P2	0.93	0.95	TM–P2	0.28	0.28
N1	−1.39	−1.39	Ga1–N1	0.44	0.43
N2	−1.39	−1.39	Ga2–N2	0.44	0.43
Cl1	−0.50	−0.50	Ga1–Cl1	0.70	0.70
Cl2	−0.50	−0.50	Ga2–Cl2	0.70	0.70

---

Fig. 3 Laplacian distribution at the BP86/def2-TZVPP level of 3 and 4 in the Ga1–TM–Ga2 plane. Red lines indicate the areas of charge concentration (∇²ρ(r) < 0), while blue lines show the areas of charge depletion (∇²ρ(r) > 0). The solid lines connecting the atomic nuclei are the bond paths. Green dots are bond critical points (BCPs).

A more detailed view of the bonding situation in the molecules comes from a bonding analysis using EDA (Energy Decomposition Analysis) in conjunction with NOCV (Natural Orbitals for Chemical Valence) calculations.²⁷ We carried out EDA-NOCV calculations of 3 and 4 using Ga₂Cl₂ and the remaining metal fragments [TM] in different electronic states and with different charges as interacting moieties. Previous work has shown that the best description of the chemical bonds comes from those fragments which give the smallest absolute values of the orbital interaction ΔE_orb, because they change the least during bond formation.²⁸ The smallest values for 3 and 4 were provided by neutral fragments in the electronic singlet state. The numerical results of the latter EDA-NOCV calculations are shown in Table 2. The EDA-NOCV results for all investigated combinations of the electronic state and partial charge are given in Tables S2 and S3 of the ESI.†

Table 2 EDA-NOCV results of 3 and 4 at the BP86-D3(BJ)/TZ2P + ZORA//BP86-D3(BJ)/SVP level using Ga₂Cl₂ and the remaining metal moieties [TM] in the singlet (Si) state as interacting fragments. Energy values are given in kcal mol⁻¹

Fragments	Ga2Cl2 (S) +	Ga2Cl2 (S) +
	[Ni] (S)	[Pd] (S)
a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb.
ΔEint	−231.2	−221.1
ΔEPauli	570.2	692.9
ΔEdisp^a	−50.5(6.3%)	−48.6(5.3%)
ΔEelstat^a	−369.2(46.1%)	−442.3(48.4%)
ΔEorb^a	−381.7(46.6%)	−423.1(46.3%)
ΔEorb1^b	−193.2(50.6%)	−239.0(56.5%)
ΔEorb2^b	−70.4(18.4%)	−72.4(17.1%)
ΔEorb3^b	−30.4(8.0%)	−34.9(8.2%)
ΔEorb4^b	−17.4(4.6%)	−15.2(3.6%)
ΔErest	−70.3(18.4%)	−61.6(14.6%)

---

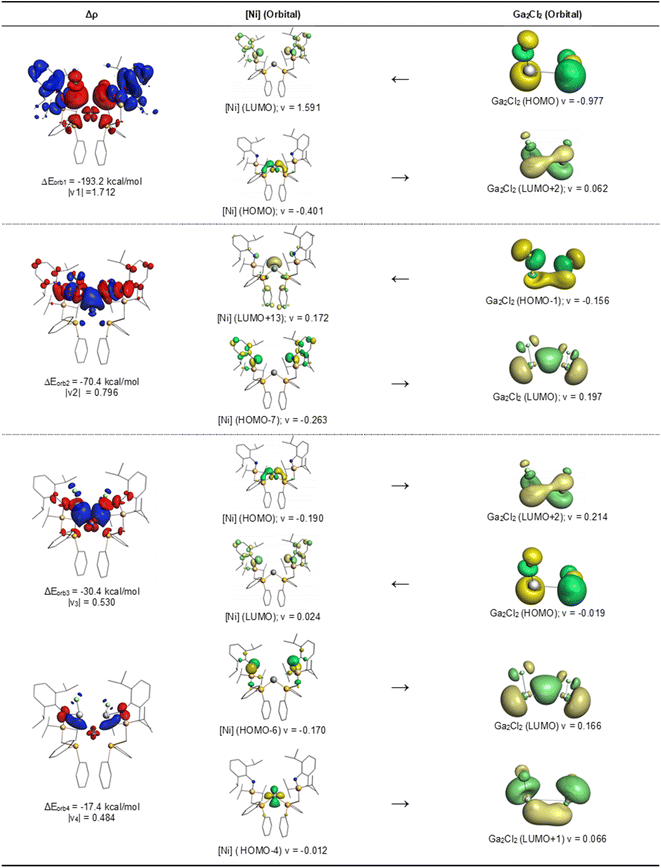
The data in Table 2 suggest that the electrostatic (Coulomb) forces ΔE_elstat and the orbital (covalent) interactions ΔE_orb have nearly the same strength and that the dispersion forces ΔE_disp are much smaller but not negligible. The biggest contribution to the intrinsic interaction energy ΔE_int comes from the Pauli repulsion, which is often neglected but crucially important for the length²⁹ and strength³⁰ of a chemical bond. The most important information for the question at hand comes from the pairwise contributions to the orbital term ΔE_orb, which accounts for about half of the total attraction. The nature of the pairwise orbital interactions, which are involved in the formation of the covalent bonds, can be identified by examination of the associated deformation densities Δρ and the fragment orbitals. The most relevant deformation densities and orbitals of 3 are shown in Fig. 4. The related drawings for 4 are shown in Fig. S55 of the ESI.†

Fig. 4 Plot of the deformation densities Δρ of the pairwise orbital interactions ΔE_orb1 − ΔE_orb4 and the shape of the most important interacting MOs of the two fragments [Ni] and Ga₂Cl₂ in the singlet states in 3. The direction of the charge flow is red → blue. The isosurface value of the plot of deformation densities is 0.001 and the isosurface value of the orbital diagram is 0.03.

There are four orbital interactions, ΔE_orb1 − ΔE_orb4, in 3 and 4, which are associated with the chemical bonds between the Ga₂Cl₂ and [TM] fragments. The orbital term ΔE_rest comes from the relaxation of the intrafragment orbitals. Each pairwise interaction ΔE_orb1 − ΔE_orb4 has two orbital components, which are associated with the formation of the Ga–N and Ga–TM bonds. Fig. 4 shows that the largest interaction ΔE_orb1 comes mainly from the donation of the HOMO of Ga₂Cl₂, which is an ClGa–GaCl antibonding orbital, into the LUMO of the metal fragment [Ni], which has the largest coefficients at the N atoms. The second component of ΔE_orb1 describes a concomitant backdonation from the HOMO of [Ni], which is a d_π AO of Ni with some bonding combination of the P atoms, into the LUMO+2 of Ga₂Cl₂. It becomes obvious that ΔE_orb1 comes from the concerted formation of the N–Ga and the Ni–Ga bonds. The same is true for ΔE_orb2, which has also two components. Fig. 4 shows that the largest charge flow arises from the donation of the HOMO-1 of Ga₂Cl₂, which is an ClGa–GaCl bonding orbital, into the LUMO+13 of [Ni], where the largest coefficient is an sd_z2 orbital at Ni. The second component of ΔE_orb2 describes the backdonation from the HOMO−7 of [Ni] into the LUMO of Ga₂Cl₂. Both orbital interactions ΔE_orb1 and ΔE_orb2 depict the simultaneous formation of the N–Ga and Ni–Ga bonds, but the two components in each term make it possible to distinguish between the two bonds. It should be noted that the notations σ and π, which are symmetry assignments, are not strictly valid, because there is no mirror plane in the fragments nor in the molecule. But the shape of the orbitals indicates that the larger component and smaller component of ΔE_orb1 and ΔE_orb2 come from interactions between in-plane and out-of-plane orbitals like in the classical donor–acceptor, in accordance with the DCD model.¹⁵Fig. 4 shows that also the two smaller orbital interactions ΔE_orb3 and ΔE_orb4 describe the simultaneous formation of the N–Ga and Ni–Ga bonds, where σ and π type orbitals are involved, which complement ΔE_orb1 and ΔE_orb2. The larger and smaller components of ΔE_orb3 are identical to the smaller and larger components of ΔE_orb1 with a reversed order of the size of charge flow. The larger component of ΔE_orb4 is identical to the smaller component of ΔE_orb2 with the smaller component of ΔE_orb4 depicting the miniscule backdonation from the HOMO-4 of [Ni] into the LUMO+1 of Ga₂Cl₂. The EDA-NOCV results clearly show that the orbital interactions between [Ni] and Ga₂Cl₂ in 3 exhibit the classical pattern of donor–acceptor interactions as described by the DCD model. The results in the ESI† reveal that the same holds true for the palladium complex 4.

Taken as a whole, these computational insights align with the classification of 3 and 4 as digallane σ-complexes, but not in the classical sense. This is due to the lack of a mirror plane in the molecule, which comprises the Ga–Ga bond. Nevertheless, the crucial orbital interaction in these species takes place in the Ga₂TM moiety, which is planar. The notation of 3 and 4 as digallane σ-complexes is also justified because the orbital interactions follow the same bonding model as in genuine σ-complexes. The key difference with classical dihydrogen σ-complexes is due the occurrence of out-of-plane π-type orbitals in 3 and 4, which are not present in complexes with H₂ ligands.

Complex disproportionation

Curious as to whether further digallane σ-complexes are accessible through simple metathesis of Ga–Cl bonds in either free digallane 2 or Ni complex 3, the reactions of these species with MeLi were carried out, with the aim of accessing the 1,2-dimethyl derivative of 3 (viz.5, Scheme 2). To our surprise, these reactions led to the formation of the isolable GaIII compound PhiPDippGaMe2,⁶ presumably through a disproportionation process, which would simultaneously form a GaI species.^31,32 No stable GaI species was observed in the disproportionation reaction of the free digallane, with only the protonated ligand observed in the ³¹P{¹H} NMR spectra of crude reaction mixtures, in addition to 6 (δ = −17.4 ppm), and an elemental gallium mirror observed within the reaction vessel. However, the reaction of σ-complex 3 with MeLi, looking to directly generate 5 (Scheme 2), gave deep red reaction mixtures featuring an additional doublet of doublets in the ³¹P{¹H} NMR spectra of reaction mixtures, at δ = 17.5 and 67.8 ppm (²J_PP = 111.3 Hz; Fig. S46 in the ESI†). Interestingly, similar spectra are observed upon the addition of 1,2-dichlorodigallane 2 to Ni(cod)₂ in Et₂O; this leads to the precipitation of (amido)(dichloro)gallane 1 and formation of one further product as ascertained by ³¹P{¹H} NMR spectroscopic analysis. This product is in keeping with that observed in the reaction of 3 with MeLi, i.e. revealing a doublet of doublets in its ³¹P{¹H} NMR spectrum. Recrystallisation of these reaction mixtures allowed for the isolation of deep red crystals of 7, a unique Ga^I nickel complex, which apparently forms through the disproportionation of 3, and subsequent ligand activation (Fig. 5). The case is likely similar when attempting to generate dimethyl complex 5 from 3, giving clear evidence for the hypothesized disproportionation reaction. More specifically, 7 most likely arises via intermediary digallene/bisgallylene complex 7′ (Scheme 2), through the activation of one Ph–P bond on a single phosphino-amide ligand, a process we have observed previously in low oxidation state iron chemistry.³³ This leads to an unsymmetrical system: one ligand remains neutral, as the κ²-[^PhiPDippGa] chelating gallylene, isoelectronic to our earlier reported cationic tetrylene ligands, [^PhiPDippE]⁺ (E = Ge, Sn).³⁴ The second ligand is dianionic, best described as a chelating (phosphide)(gallyl) ligand. In both ligand systems, the gallium centers have a formal oxidation state of +1. Given the stoichiometry of the reaction, two Ni centers are present in 7, thus having an average oxidation state of +1. Still, 7 is best described as a square-planar Ni^II complex, bearing two different Ga^I ligands, and coordinating Ni⁰ in its secondary coordination sphere, as depicted in Scheme 2. The ¹H NMR spectrum of 7 is indicative of the unsymmetrical nature of this compound, but all peaks are sharp and readily assigned, in contrast to 3 and 4. This would suggest that at ambient temperature no fluctional processes are at play in solution (e.g. Ph-migration). The ³¹P{¹H} NMR spectrum contains two clear doublet signals, in keeping with those observed in crude reaction mixtures, through coupling of the two P-centres in 7. Metrical parameters from the molecular structure of 7 are in keeping with related distances and angles in the few gallyl- and gallylene-Ni⁰/Ni^II complexes reported previously. Nevertheless, the observation of stable Ga^I ligands featuring our phosphine-functionalised amide ligands fuels our continued development of Lewis acidic donor ligands based on low oxidation state p-block species.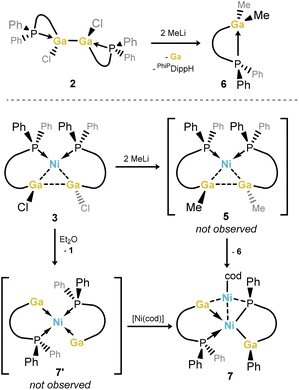

Scheme 2 The disproportionation chemistry of Ga^II species, in forming dimethyl Ga^III compound 6 and polymetallic Ga^I-Ni complex 7.

Fig. 5 Molecular structure of compound 7, with thermal ellipsoids at 30% probability, and hydrogen atoms removed for clarity. Selected bond lengths (Å) and angles (°) for 7: Ga1-Ni1 2.4149(7); Ga1–Ni2 2.2223(7); Ga2–Ni1 2.3335(7); P1–Ni1 2.158(1); P2–Ni1 2.189(1); P2–Ni2 2.1412(8); P1–Ni1–Ga1 82.79(3); P2–Ni1–Ga2 78.41(3); Ga1–Ni1–P2 99.89(3); Ga1–Ni2–P2 107.84(3).

Conclusions

The facile syntheses of Ni and Pd featuring digallane ligands are reported. In-depth computational analysis of these systems is indicative of formal σ-complex character, making them the first examples of this compound class reported to date. Computational insights suggest a bonding model akin to the Dewar–Chatt–Duncanson model, with a degree of π-symmetry in key frontier orbitals. In addition, the well-defined disproportionation of Ni-(η²-digallane) complexes is also described, leading to a unique Ga^I–nickel complex. As a whole, these key insights further deepen our understanding of σ-bond complexation and activation, which we continue to explore in our group.

Data availability

The data that support the findings of this study can be found in the article ESI,† and are additionally available from the corresponding author upon reasonable request.

Author contributions

TLK carried out all experimental work, analysis, and data collection. LQ, LZ, and GF carried out and analysed all computational work. TJH conceptualised the project and supervised experimental work. The manuscript was co-written by GF and TJH.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

TJH thanks the Fonds der Chemischen Industrie (FCI) for generous funding of this research through a Liebig Stipendium, the ERC for a Starting grant (Project 101076897 – SINGAMBI), and the Technical University Munich for the generous endowment of TUM Junior Fellow Funds. TLK thanks the FCI for the generous endowment of a Kekulé Stipendium. LZ and GF acknowledge financial support from Nanjing Tech University (Grant 39837123, 39837132, and the International Cooperation Project), National Natural Science Foundation of China (Grant 21973044), and Natural Science Foundation of the Jiangsu province (BK20211587). We also appreciate the help of the high-performance centre of Nanjing Tech University for supporting the computational resources.

Notes and references

1. R. N. Perutz, S. Sabo-Etienne and A. S. Weller, Angew. Chem., Int. Ed., 2022, 61, e202111462.
2. R. N. Perutz and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2007, 46, 2578–2592.
3. R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, John Wiley & Sons, Inc., 2014.
4. G. J. Kubas, R. R. Ryan, B. I. Swanson, P. J. Vergamini and H. J. Wasserman, J. Am. Chem. Soc., 1984, 106, 451–452.
5. (a) R. H. Crabtree, Acc. Chem. Res., 1990, 23, 95–101; (b) G. J. Kubas, Proc. Natl. Acad. Sci. U.S.A., 2007, 17, 6901–6907; (c) R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769; (d) G. J. Kubas, Metal Dihydrogen and σ-Bond Complexes, Springer, New York, NY, 2001.
6. (a) K. M. Altus and J. A. Love, Commun. Chem., 2021, 4, 174; (b) R. D. Young, Chem.–Eur. J., 2014, 20, 12704–12718; (c) M. A. Bennett, T. J. McMahon, S. Pelling, G. B. Robertson and W. A. Wickramasinghe, Organometallics, 1985, 4, 754–761; (d) H. Urtel, G. Meier, F. Eisenträger, F. Rominger, J. P. Joschek and P. Hofmann, Angew. Chem., Int. Ed., 2001, 40, 781–784; (e) R. Doyle, M. R. Galpin, S. K. Furfari, B. E. Tegner, A. J. Martínez-Martínez, A. C. Whitwood, S. A. Hicks, G. C. Lloyd-Jones, S. A. Macgregor and A. S. Weller, Organometallics, 2022, 41, 284–292.
7. (a) M. Auburn, M. Ciriano, J. A. K. Howard, M. Murray, N. J. Pugh, J. L. Spencer, F. G. A. Stone and P. Woodward, J. Chem. Soc., Dalton Trans., 1980, 659–666; (b) U. Schubert, K. Ackermann and B. Woerle, J. Am. Chem. Soc., 1982, 104, 7378–7380; (c) B. R. Jagirdar, R. Palmer, K. J. Klabunde and L. J. Radonovich, Inorg. Chem., 1995, 34, 278–283; (d) W. Chen, S. Shimada, M. Tanaka, Y. Kobayashi and K. Saigo, J. Am. Chem. Soc., 2004, 126(26), 8072–8073; (e) W. Scherer, P. Meixner, J. E. Barquera-Lozada, C. Hauf, A. Obenhuber, A. Brück, D. J. Wolstenholme, K. Ruhland, D. Leusser and D. Stalke, Angew. Chem., Int. Ed., 2013, 52, 6092–6096.
8. (a) J. F. Hartwig, C. N. Muhoro, X. He, O. Eisenstein, R. Bosque and F. Maseras, J. Am. Chem. Soc., 1996, 118, 10936–10937; (b) C. N. Muhoro and J. F. Hartwig, Angew Chem. Int. Ed. Engl., 1997, 36, 1510–1512; (c) S. Schlecht and J. F. Hartwig, J. Am. Chem. Soc., 2000, 122, 9435–9443; (d) T. J. Hebden, M. C. Denney, V. Pons, P. M. B. Piccoli, T. F. Koetzle, A. J. Schultz, W. Kaminsky, K. I. Goldberg and D. M. Heinekey, J. Am. Chem. Soc., 2008, 130, 10812–10820; (e) M. A. Esteruelas, I. Fernández, C. García-Yebra, J. Martín and E. Oñate, Organometallics, 2017, 36, 2298–2307.
9. T. Steinke, M. Cokoja, C. Gemel, A. Kempter, A. Krapp, G. Frenking, U. Zenneck and R. A. Fischer, Angew. Chem., Int. Ed., 2005, 44, 2943–2946.
10. (a) S. D. Pike, A. L. Thompson, A. G. Algarra, D. C. Apperley, S. A. Macgregor and A. S. Weller, Science, 2012, 337, 1648–1651; (b) A. S. Weller, F. M. Chadwick and A. I. McKay, Transition Metal Alkane-Sigma Complexes: Synthesis, Characterization, and Reactivity, in Advances in Organometallic Chemistry, vol. 66, Elsevier, 2016, pp. 223–276.
11. (a) G. Berthon-Gelloz, B. de Bruin, B. Tinant and I. E. Marko, Angew. Chem., Int. Ed., 2009, 48, 3161; (b) N. Takagi and S. Sakaki, J. Am. Chem. Soc., 2012, 134, 11749–11759.
12. P. Gualco, A. Amgoune, K. Miqueu, S. Ladeira and D. A. Bourissou, J. Am. Chem. Soc., 2011, 133, 4257–4259.
13. See, for example: (a) P. D. Grebenik, M. L. H. Green, M. A. Kelland, J. B. Leach, P. Mountford, G. Stringer, N. M. Walker and L.-L. Wong, J. Chem. Soc., Chem. Commun., 1988, 799–801; (b) G. Medford and S. G. Shore, J. Am. Chem. Soc., 1978, 100, 3953–3954; (c) R. S. Anju, D. K. Roy, B. Mondal, K. Yuvaraj, C. Arivazhagan, K. Saha, B. Varghese and S. Ghosh, Angew. Chem., Int. Ed., 2014, 53, 2873–2877.
14. S. R. Wang, D. Prieschl, J. D. Mattock, M. Arrowsmith, C. Pranckevicius, T. E. Stennett, R. D. Dewhurst, A. Vargas and H. Braunschweig, Angew. Chem., Int. Ed., 2018, 57, 6347–6351.
15. (a) M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C79; (b) J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939–2947; (c) G. Frenking, J. Organomet. Chem., 2001, 635, 9–23; (d) G. Frenking, Modern Coordination Chemistry: The Legacy of Joseph Chatt, ed. G. J. Leigh and N. Winterton, The Royal Society, London, 2002, p. 111.
16. (a) R. J. Baker, C. Jones and D. M. Murphy, Chem. Commun., 2005, 1339–1341; (b) S. Aldridge, R. J. Baker, N. D. Coombs, C. Jones, R. P. Rose, A. Rossin and D. J. Willock, Dalton Trans., 2006, 3313–3320; (c) C. Jones, D. P. Mills, R. P. Rose and A. Stasch, Dalton Trans., 2008, 4395–4408; (d) I. L. Fedushkin, V. G. Sokolov, V. M. Makarov, A. V. Cherkasov and G. A. Abakumova, Russ. Chem. Bull. Int. Ed., 2016, 65, 1495–1504; (e) J. K. Schuster, J. H. Muessig, R. D. Dewhurst and H. Braunschweig, Chem.–Eur. J., 2018, 24, 9692–9697.
17. (a) E. C. Neeve, S. J. Geier, I. A. I. Mkhalid, S. A. Westcott and T. B. Marder, Chem. Rev., 2016, 116, 9091–9161; (b) D. Hemming, R. Fritzemeier, S. A. Westcott, W. L. Santos and P. G. Steel, Chem. Soc. Rev., 2018, 47, 7477–7494.
18. P. M. Keil, T. Szilvási and T. J. Hadlington, Chem. Sci., 2021, 12, 5582–5590.
19. N.B. [(dioxane)₂·(Ga₂Cl₄)] was synthesized by the reaction of elemental gallium with GaCl₃ in aromatic solvents, combining two described literature procedures: (a) J. Beamish, M. Wilkinson and I. Worrall, Inorg. Chem., 1978, 17, 2026–2027; (b) J. C. Beamish, A. Boardman, R. W. Small and I. J. Worrall, Polyhedron, 1985, 4, 983–987.
20. As ascertained through a survey of the CCDC. For selected examples, see: (a) B. Quillian, P. Wei, C. S. Wannere, P. V. R. Schleyer and G. H. Robinson, J. Am. Chem. Soc., 2009, 131, 3168–3169; (b) J. Su, W. Zheng and Y. Yang, J. Organomet. Chem., 2015, 780, 1–5; (c) T. Řičica, L. Dostál, Z. Růžičková and R. Jambor, Eur. J. Inorg. Chem., 2018, 1620–1623; (d) A. Kumar, S. Banerjee, N. Sharma, M. Nazish, N. Graw, R. Herbst-Irmer, D. Stalke, U. Lourderaj and H. W. Roesky, Dalton Trans., 2022, 51, 4898–4902.
21. J. C. Beamish, R. W. H. Small and I. J. Worrall, Inorg. Chem., 1979, 18, 220–223.
22. L. Yang, J. L. Bourque, J. A. McLeod, P. Shen, K. M. Baines and L. Liu, Inorg. Chem., 2017, 56, 2985–2991.
23. Disproportionation chemistry is driven by the elimination of compound 1, which is insoluble in Et₂O.
24. V. Jonas, G. Frenking and M. T. Reetz, J. Am. Chem. Soc., 1994, 116, 8741–8753.
25. R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, Oxford, 1990.
26. (a) R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396; (b) M. Mousavi and G. Frenking, J. Organomet. Chem., 2013, 748, 2–7; (c) A. Krapp and G. Frenking, Chem.–Eur. J., 2007, 13, 8256–8270; (d) M. von Hopffgarten and G. Frenking, Chem.–Eur. J., 2008, 14, 10227–10231.
27. (a) A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939; (b) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
28. (a) L. Zhao, S. Pan, G. Wang and G. Frenking, J. Chem. Phys., 2022, 157, 034105; (b) L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, Nat. Rev. Chem., 2019, 3, 48; (c) P. Jerabek, P. Schwerdtfeger and G. Frenking, J. Comput. Chem., 2019, 40, 247–264; (d) L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chem. Rev., 2019, 119, 8781 , and further references therein..
29. A. Krapp, F. M. Bickelhaupt and G. Frenking, Chem.–Eur. J., 2006, 12, 9196–9216.
30. L. Zhao, M. Zhi and G. Frenking, Int. J. Quantum Chem., 2022, 122, e26773.
31. Dimeric aluminium(II) hydride compounds bearing chelating Nacnac or phosphino-amide ligands are known to disproportionate, and ligand-free Ga₂Cl₄ exists as the mixed-valent [Ga][GaCl₄] complex: (a) C. Chu, I. Korobkov and G. I. Nikonov, J. Am. Chem. Soc., 2014, 136, 9195–9202; (b) R. L. Falconer, G. S. Nichol, I. V. Smolyar, S. L. Cockroft and M. J. Cowley, Angew. Chem., Int. Ed., 2021, 60, 2047–2052; (c) G. Garton and H. M. Powell, J. Inorg. Nucl. Chem., 1957, 4, 84–89.
32. This compound can also be accessed through addition of two equiv. MeLi to dichlorogallane 1. See the ESI† for details.
33. P. M. Keil, A. Soyemi, K. Weisser, T. Szilvási, C. Limberg and T. J. Hadlington, Angew. Chem., Int. Ed., 2023, 62, e202218141.
34. (a) P. M. Keil and T. J. Hadlington, Angew. Chem., 2022, 134, e202114143; (b) P. M. Keil and T. J. Hadlington, Z. Anorg. Allg. Chem., 2022, 648, e202200141.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2266419–2266424. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc03772j

---