Machine learning for analysis of experimental scattering and spectroscopy data in materials chemistry

Abstract

The rapid growth of materials chemistry data, driven by advancements in large-scale radiation facilities as well as laboratory instruments, has outpaced conventional data analysis and modelling methods, which can require enormous manual effort. To address this bottleneck, we investigate the application of supervised and unsupervised machine learning (ML) techniques for scattering and spectroscopy data analysis in materials chemistry research. Our perspective focuses on ML applications in powder diffraction (PD), pair distribution function (PDF), small-angle scattering (SAS), inelastic neutron scattering (INS), and X-ray absorption spectroscopy (XAS) data, but the lessons that we learn are generally applicable across materials chemistry. We review the ability of ML to identify physical and structural models and extract information efficiently and accurately from experimental data. Furthermore, we discuss the challenges associated with supervised ML and highlight how unsupervised ML can mitigate these limitations, thus enhancing experimental materials chemistry data analysis. Our perspective emphasises the transformative potential of ML in materials chemistry characterisation and identifies promising directions for future applications. The perspective aims to guide newcomers to ML-based experimental data analysis.

---

Andy S. Anker

Andy S. Anker is postdoc at the Nanostructure group, Department of Chemistry, University of Copenhagen, where he has obtained his PhD. Andy has developed a keen interest in machine learning for analysis of experimental scattering and spectroscopy data in materials chemistry. Especially he is interested in changing the way we solve the atomic structure of inorganic nanomaterials from scattering data with the use of machine learning. As a strong advocate for open source, he shares his modelling tools on his GitHub page (http://github.com/AndySAnker) or Hugging Face page (https://huggingface.co/AndySAnker) to promote free usage, collaboration, and development within the scientific community.

Keith T. Butler

Keith Butler is associate professor for materials theory and simulation at University College London, researching the application of machine learning for materials characterization and discovery. Keith got his PhD from UCL in 2010 and has worked in the Universities of Bath and Sheffield, in the SciML Team at the Rutherford Appleton Laboratory and at Queen Mary University. Recent research has focused on several aspects of machine learning for materials science, including interpretable machine leaning, generative models, physics informed machine learning and uncertainty quantification. Keith leads/contributes to several open source packages for materials science and is an advocate of open science.

Raghavendra Selvan

Raghavendra Selvan (RS) is currently an Assistant Professor at the University of Copenhagen, with joint responsibilities at the Department of Computer Science, Neuroscience, and the Data Science Laboratory. His current research interests are broadly pertaining to Graph Neural Networks, Resource Efficient ML and Medical Image Analysis with ML. RS is keen on advancing the development and use of advanced ML methods for the sciences, with a particular focus on environmental sustainability.

Kirsten M. Ø. Jensen

Kirsten M. Ø. Jensen is an associate professor at University of Copenhagen. She obtained her PhD in 2013 from Aarhus University, and following a postdoc at Columbia University, she started the Nanostructure Group in Copenhagen in 2015. The research in her group concerns structural analysis of nanoscale materials. She focuses especially on the use of X-ray total scattering and Pair Distribution Function analysis for structure studies, and is particularly interested in applying in situ studies to uncover the chemical reactions taking place during materials synthesis. Her group has recently started using machine learning as a tool for structural analysis.

---

Introduction

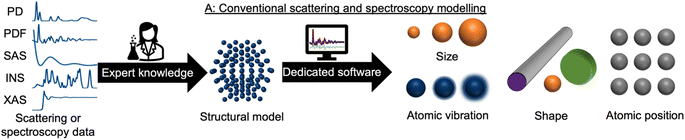
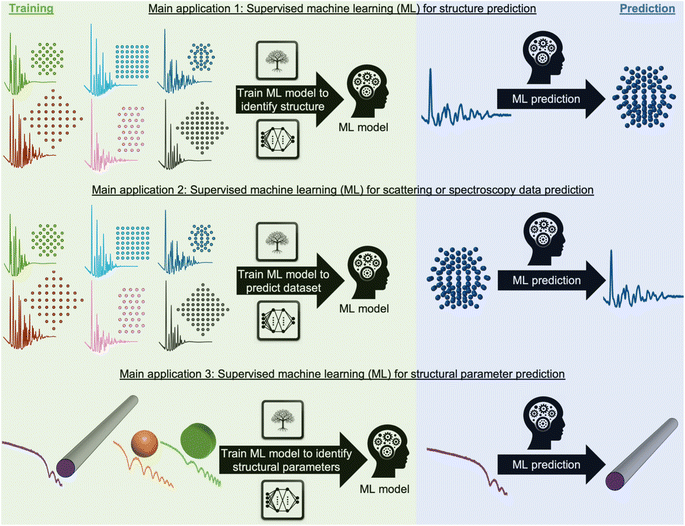
During recent decades, materials science research has been accelerated by the rapid development of large-scale radiation facilities^1,2 and the advancement of laboratory instruments.^3–5 It is now common to acquire large amounts of data from e.g. time-resolved in situ or operando experiments,^6–8 and the combination of scattering and spectroscopy with computed tomography, allowing detailed position-resolved studies^9–12 also results in large datasets. To extract information from the data, careful analysis is needed. A typical workflow for this process is sketched in Fig. 1. In conventional data modelling approaches, data are often analysed using minimisation techniques such as least-squares fitting algorithms, where the difference between experimental data and simulated data is minimised by refining parameters in a physical model, e.g., representing the atomic structure. This process is known as structure refinement. However, least-squares fitting algorithms are computationally expensive and are therefore not well suited for analysis of very large datasets. Identification of the model to use in structure refinement can furthermore be a limitation in data analysis: to identify a suitable model, extensive database and literature searches are often needed. Even then, there is a risk that an optimal structural model may not be identified, leading to the structure refinement becoming stuck in local minima. To address this automated screening of large numbers of structure models has been combined with structure refinement methods, for example for identifying a cluster¹³ or crystal structure¹⁴ from pair distribution function (PDF) data. Automated structure model identification can improve the odds of finding global minima at subsequent structure refinement. However, the high computing cost of least-squares fitting algorithms limits their use for structure model identification. Consequently, data analysis is often a major bottleneck for materials chemistry research.^15,16 With the continuing advancement of modern radiation facilities,¹⁷ the need for tools that can aid scientists in structural analysis is in increasing demand. Machine learning (ML) has recently emerged as a powerful tool for automating several aspects of scattering- and spectroscopy data analysis.^18–27 In this perspective, we describe the application of supervised and unsupervised ML to experimental scattering and spectroscopy data analysis. For a short introduction to supervised and unsupervised ML and the most popular ML algorithms, we refer to Machine Learning Algorithms – A Review, Batta Mahesh.²⁸

Fig. 1 Traditional scattering and spectroscopy modelling workflows involve an expert scientist manually creating a structural model using input data from a database or the literature. This model is refined using dedicated software to extract structural information from the dataset such as atomic positions, crystallite size, crystallite shape, and atomic vibrations. This process is repeated for each new dataset measured.

Most applications of ML in materials chemistry apply supervised ML methods. Supervised ML is broadly the task of predicting a label based on a given set of input features. As will be exemplified throughout the perspective, we observe three main applications of supervised ML for the analysis of scattering and spectroscopy data: (1) identifying a physical model from a scattering or spectroscopy dataset (main application 1, Fig. 2). Here, scattering or spectroscopy data are the input features, and the model is supervised to relate the datasets to the physical models, which are the labels. (2) Predicting scattering or spectroscopy data from a physical model. This can be achieved by using the data as labels and the physical model as input features (main application 2, Fig. 2). (3) Bypassing the model refinement step to directly obtain structural information (main application 3, Fig. 2). This is done by training the supervised ML model on data with varying structural parameters.

Fig. 2 Main application (1) use of ML for identifying a structural model. During training, a supervised ML model is trained on pairs of structural models and scattering or spectroscopy simulations, here shown for PDF data. Afterwards, the ML model can quickly and computationally inexpensively identify the structural model from (experimental) scattering or spectroscopy data. Main application (2) use of ML for predicting scattering or spectroscopy data from a structure model. During training, a supervised ML model is trained on pairs of structural models and scattering or spectroscopy simulations, here shown for PDF data. After training, the ML model quickly and computationally inexpensively predicts scattering or spectroscopy data from a structural model. Main application (3) use of ML to predict structural parameters. During training, a supervised ML model is trained on pairs of scattering or spectroscopy simulations with varying structural parameters, here shown for SAXS data. After training, the ML model quickly and computationally inexpensively identifies the structural information from the (experimental) scattering or spectroscopy data.

To train an ML model using supervised methods, one needs a dataset consisting of many pairs of labels and input features. This dataset, consisting of e.g., structure models and simulated data, is generally split into a training, validation, and test set, often in a 3 : 1 : 1 ratio. While it is critical that the data closely mirrors real-world, experimental data, labelled experimental datasets that can be used for training are not widely available. Due to this, one often resorts to simulated data that are designed to resemble experimental data. The model is trained on the training set, while being continuously evaluated on the validation set, using a user-defined objective function, called the loss function. Depending on the chosen class of models, the training will often improve on the training set until it can fit any trends in the data, including noise (overtraining). The validation set is used to ensure that the model training is stopped before it is overtrained. Once training is complete, the test set, which has not been used during training or validation, is employed to estimate the accuracy of the model on future unseen data (generalisation). It is critical that the test set closely mirrors experimental data in order to trust the reported accuracy. An intriguing possibility is to gather extensive experimental datasets from structural models, which could serve as training set for a structure-to-signal ML model (Fig. 2B) that thereby learns to include experimental effects that are otherwise challenging to simulate. The quality and size of the training set thus plays a crucial role in the model's efficiency and accuracy, with larger, higher-quality datasets typically yielding better results. A model's ability to interpolate and extrapolate, or make predictions within the range of the training data and beyond it, is generally influenced by the ML algorithm and the range and diversity of the training set. Many factors therefore need consideration when selecting and training an ML model. These include the choice of ML algorithm (tree-based methods, neural networks (NNs), genetic algorithms, etc.),^28,29 the number of parameters in the ML model, and both the quality and quantity of the training set. The model's ease of training and deployment can be influenced by the choice of ML algorithm. Interpretability of the model depends strongly on the algorithm used, for example an individual decision tree is easily interpretable, whereas a deep neural network with millions of parameters is not, and requires post hoc methods to understand its operation.³⁰ When it comes to scalability, NNs have many more trainable parameters compared to tree-based methods. This makes tree-based method efficient learners in small data regime, however, NNs often prove more effective at handling larger datasets. NNs are today commonly trained on large datasets, as used in for example, the backbone of the GPT model^31–33 and AlphaFold.³⁴ This superiority in scalability might explain why NNs have become the predominant ML algorithm for structural analysis as large databases of training data have become increasingly available.

While training an ML model can be computationally expensive, this is a one-time cost. Subsequent predictions using the ML model can be computationally inexpensive and integrated into web-based solutions, or can be done at synchrotron or neutron facilities for real-time data analysis while experiments are going on.

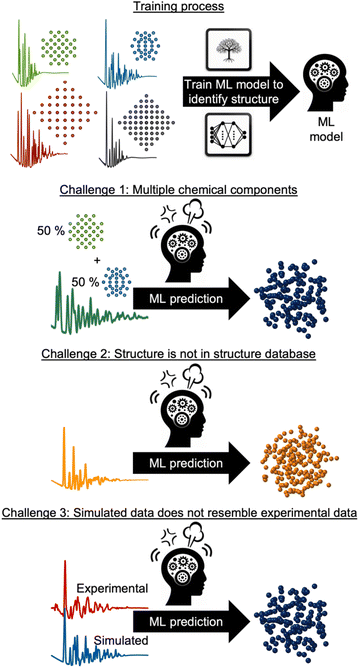
However, supervised ML is limited by its reliance on paired input data and labels for training, which can be challenging to obtain for experimental data analysis. As will be discussed and exemplified below, we observe three common challenges encountered when analysing experimental scattering and spectroscopy data with supervised ML. These are illustrated in Fig. 3: challenge (1) handling data with contributions from multiple chemical components. Challenge (2) handling data arising from structures not present in the training database and challenge (3) accounting for experimental data that contain signals not included in the simulated data. In all three scenarios, the labelled data are inadequate for solving the problem at hand, making unsupervised ML methods a more suitable alternative, or complementary tool. Unsupervised ML models work without paired labels and input features, using only input features or intermediate input-derived labels, such as in autoencoders.³⁵ Unsupervised ML is often used to present complex data in a low-dimensional space (dimensionality reduction), enabling the analysis of high-dimensional dataset similarities, clustering, and the extraction of underlying data trends that are difficult to comprehend from the input representation space.²⁸ Unsupervised methods can also be applied to ‘demix’ data, i.e., separating the signal from each component in a multi-phase scattering or spectroscopy dataset.

Fig. 3 Three common challenges when analysing experimental scattering and spectroscopy data. Supervised ML models are trained on pairs of structural models from a structural database and scattering or spectroscopy simulations. However, supervised ML methods are challenged by; challenge 1: the experimental data are obtained from a system containing multiple chemical species, which is not taken into account in the ML model. Challenge 2: the required structural model is not included in the structure database used for training the ML model. Challenge 3: the experimental data contains background noise, instrumental effects or other phenomena not encountered by the simulated data.

In the following sections, we use selected examples to provide an overview of how supervised ML has been used to identify structural models and structural information from experimental powder diffraction (PD), PDF, small-angle scattering (SAS), inelastic neutron spectroscopy (INS) and X-ray absorption spectroscopy (XAS) data or predict the dataset from a structure. We also outline and exemplify how unsupervised ML has been applied to address the three challenges presented in Fig. 3, and we discuss the potential future impact of ML in the analysis of experimental materials chemistry data.

X-ray absorption spectroscopy: large XAS databases accelerate supervised ML structure identification

XAS is a powerful experimental technique for investigating the electronic and atomic structure of materials. In XAS, a sample is exposed to a monochromatic X-ray beam, whose energy is varied in a range of ca. 10–100 eV around the K-edge or L-edge of the elements in question, i.e. the energy needed to eject electrons from the 1s or 2s orbital. This causes the sample to absorb some of the X-rays. By measuring and analysing the absorbed X-rays as a function of energy, it is possible to obtain information about the local electronic structure and chemical environment of the atoms in the sample. Information about oxidation state and coordination environment can be obtained through X-ray Absorption Near Edge Spectroscopy (XANES), while Extended X-ray Absorption Fine Structure (EXAFS) can provide knowledge of local atomic structure.

Conventional analysis of XAS data requires expertise in the complex data analysis as well as manual work. To address this, Zheng et al. created a large XANES database, XASdb, with more than 800 000 computed reference XANES entries from over 40 000 materials from the open-science Materials Project database.³⁶ Their supervised ML model, ELSIE, illustrated in Fig. 4, was used for the analysis of XANES data. Given a XANES spectrum as input, it outputs a list of the chemical compounds whose spectra are most similar to the target spectrum (main application 1, Fig. 2). From these compounds, chemical information such as oxidation state and coordination environment can be extracted. ELSIE predicts the chemical compound with 69.2% top-5 accuracy on a test set of 13 simulated XANES spectra. However, the correct oxidation state is predicted with 84.6% accuracy and the coordination environment with 76.9% accuracy. As we illustrate with challenge 3 in Fig. 3, the ML model's accuracy is lower on experimental data. On six experimental XANES spectra, ELSIE predicts oxidation state with 83.3% accuracy, coordination environment with 83.3% accuracy and the chemical compound with 33.3% top-5 accuracy.³⁷ While the predictions from ELSIE demonstrate some accuracy, they are yet to achieve the reliability of conventional methods that rely on direct comparison of measured references that are XANES spectra measured on compounds with well-known oxidation states. However, reference comparison, though grounded in empirical data, can also be inaccurate as both oxidation state and structure affect the XANES pattern, which makes it challenging to choose the chemical compounds from which the reference pattern is measured. These results highlight the impact of large databases like the open-science Materials Project³⁶ and JARVIS.³⁸ As these databases grow, they will likely catalyse supervised ML analysis of scattering and spectroscopy data in materials chemistry for example by achieving higher accuracies in the oxidation state determination from a XANES pattern. An optimal path forward might combine the ever-improving predictive capabilities of ML models like ELSIE with the established reliability of conventional reference matching.

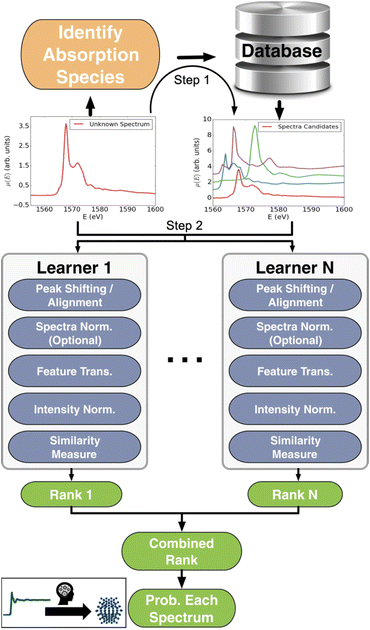Fig. 4 Workflow schema of the Ensemble-Learned Spectra IdEntification (ELSIE) algorithm. The ELSIE algorithm consists of two steps. In the first step, the absorbing species is identified and used to narrow down the candidate computed reference spectra. In the second step, the algorithm yields a rank-ordered list of computational spectra according to similarity with respect to the target spectrum. The figure is adapted from Zheng et al.³⁷ (Under Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/).

The above example shows that large XANES databases, like XASdb or the XAS data distributed via the Materials Project,³⁹ can be used to address the spectrum-to-structure problem, as illustrated with main application 1 in Fig. 2. However, it can also be used to address the inverse problem: structure-to-spectrum, as illustrated with main application 2 in Fig. 2. Calculating a XANES spectrum from a structure can be computationally demanding (CPU hours) but by using a supervised ML model to predict the spectrum, this process can be done in milliseconds to seconds.^40–42 One advantage of the spectrum calculation are that they can be performed for hypothetical structures whereas structure-to-spectrum ML models are in contrast limited by the composition of their training set.

Supervised ML can also be used to directly predict chemical information (main application 3, Fig. 2) such as average size, shape, morphology and oxidation states of first metallic nanoparticles^43,44 and metallic oxides,⁴⁵ Bader charge,⁴⁶ mean nearest neighbour distances,⁴⁶ and local chemical environment,⁴⁷ from an XANES spectrum or predict the radial distribution function from the experimental EXAFS data.^48–52

Analysing XAS data from samples containing more than one chemical species remains a challenge (challenge 1 in Fig. 3), as supervised ML models trained on data simulated from a single chemical species are constrained to be used on experimental data from individual chemical species, and attempting to account for all possible chemistries, e.g. by training on simulated data from mixed samples, leads to a combinatorial explosion. Instead, linear unsupervised ML techniques like principal component analysis (PCA) and non-negative matrix factorisation (NMF) have been used to discover trends in large XAS datasets and separate them into signals from their respective chemical components.^53–58 For example, Tanimoto et al. used NMF to identify and map spatial domains from absorption spectra in 2D-XAS images of lithium ion batteries.⁵⁶ The authors recognised that NMF can be challenged by background effects as these can be predominant in some of the NMF-extracted components. Therefore, they subtracted a reference X-ray absorption spectrum obtained on Li_0.5CoO₂, which also includes that background signal. This trick enables the NMF method to distinguish small differences in the spectra.

Small-angle scattering: supervised ML for dataset and parameter prediction

SAS is a strong technique to obtain information about the morphology, orientation and size distribution of e.g., nanoparticles in solution and solids.⁵⁹ In a SAS experiment, X-ray or neutron scattering data are measured at small scattering vectors, e.g., the Q-range from ca. 0.001 Å⁻¹ to 1 Å⁻¹. This region of the scattering signal contains structural information about the species in the sample on the nanometer to micrometer scale.

Traditional SAS data fitting is done by refining a structural model against the data as illustrated in Fig. 1. The structural model must describe the particle shape, size, and size distribution as well as possible agglomerations of e.g., nanoparticles or large molecules in the sample, and much work is often needed in deciding on a suitable structural model. This is usually done by manually comparing them, and this step can be time-consuming and prone to errors. For example, the structure refinement can become stuck in local minima.⁶⁰ Here, ML can assist by providing a more efficient approach to determine the starting model for structure refinement. The Computational Reverse-Engineering Analysis for Scattering Experiments Genetic Algorithm (CREASE-GA) tool, developed by members of Prof. A. Jayaraman's research group, can reconstruct 3D structures from SAS patterns using a genetic algorithm (main application 1, Fig. 2).^61–67 CREASE-GA compares the goodness-of-fit between the experimental SAXS pattern and simulated SAS patterns derived from a population of 3D structures. A genetic algorithm²⁹ is then used to update the 3D structure population to better describe the experimental SAS pattern. This process continues until convergence, determining the 3D structure of the sample in question. Originally, the SAS patterns from the 3D structure population were calculated using the Debye scattering equation. This posed a computational bottleneck for CREASE-GA as the computational time of the Debye scattering equation scales with the number of scatterers squared.⁶⁰ To address this, the authors have recently managed to accelerate CREASE by over 95% by employing NNs to estimate the SAS patterns (main application 2, Fig. 2).^62,65 While NNs cannot match the accuracy of the Debye scattering equation in simulating SAS patterns, they offer an additional advantage. The NN learns concurrently from the 3D structure population and their corresponding SAS patterns to predict 3D structures that align more closely with the experimental SAS pattern. Heil et al.⁶⁵ show that the accelerated CREASE method achieves similar, and sometimes superior, results when modelling particle size distribution and degree of aggregation from experimental data obtained from a one-component (melanin) nanoparticle solution and a binary (melanin and silica) nanoparticle assembly.

Supervised ML has also proved to be an efficient tool for direct parameter extraction from SAS data (main application 3, Fig. 2), which might be difficult or time-consuming for humans to detect, such as orientation,⁶⁸ shape,^69–71 or the model for SAS form factor fitting.^72–74 For example, the Scattering Ai aNalysis (SCAN) tool can predict the model for SAS form factor fitting from a SAXS pattern obtained from a nanoparticle. With the SCAN tool, the user can choose from a range of ML algorithms including tree-based algorithms and NNs. These algorithms individually achieve accuracies between 27.4% and 95.9% quantified on a test set of simulated SAXS data. However, when the ML models are combined, they achieve an accuracy of 97.3% on the same test set. We are grateful to the authors for making SCAN open source, which has made it possible to implement it as a Hugging Face app.⁷⁵ This makes it easily useable, also for users without programming experience, as illustrated in Fig. 5. Since SCAN can analyse SAXS data in seconds in an automated manner, an obvious use case would be to follow nanoparticle shape changes during an in situ SAXS experiment. This is not possible with conventional structure refinement methods which require user inputs.

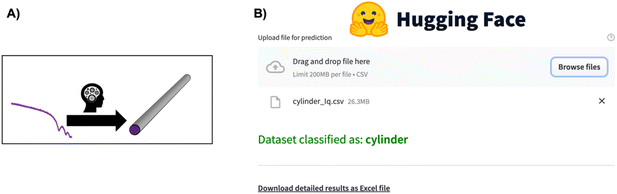Fig. 5 (A) The SCAN⁷⁴ tool directly predicts structural information such as particle shape from a SAXS pattern. (B) Overview of the SCAN⁷⁴ tool's ease of use for predicting structural information from a SAS pattern through the Hugging Face app.⁷⁵ Simply click “Browse files”, wait for the model to predict the structural information, and, if needed, download the detailed information in an Excel sheet.

Powder diffraction: structure identification

PD is a fundamental technique in materials chemistry that is used to analyse the crystal structure of a powdered sample. In PD, a powder of crystalline particles is exposed to an X-ray or neutron beam, causing Bragg diffraction due to the periodic atomic arrangement in the sample. By analysing the Bragg peak position, intensity and shape, information about the crystalline structure of the material can be obtained.

Recent advances in ML techniques offer promising new opportunities in PD data analysis. For example, it has been demonstrated that a sample's crystal system and space group can be predicted from X-ray PD or electron diffraction data using NNs^{21,26,76–78} and tree-based techniques (main application 1, Fig. 2).⁷⁹ Suzuki et al. demonstrated that an advantage of the tree-based ML approaches is that they are interpretable.⁷⁹ Interpretability enables us to understand the ML model's prediction mechanism and thus analyse when it predicts differently from a human expert. This can either indicate when the ML model is wrong and needs to be corrected or reveal when it uncovers unexpected correlations that may lead to scientific insights. In the study by Suzuki et al., it was revealed that the ML model leveraged specific parameters—namely, the number of peaks present in the PD and the Q-value of the 3^rd peak—to discern whether the data were derived from cubic or non-cubic structures. This approach mirrors the analytical strategies typically adopted by human researchers and hence builds a degree of trust in the predictions generated by the ML model.

However, the above ML models can only be used to determine the crystal system or the space group from PD data. To identify the full structural model for e.g., structure refinement, the unit cell, and unit cell content is also needed in the prediction task. Garcia-Cardona et al.⁸⁰ made progress towards this for neutron diffraction data, where the crystal system (cubic, tetragonal, trigonal, monoclinic, and triclinic) could be predicted with an accuracy of 92.65% (main application 1, Fig. 2) using convolutional NNs, which are a type of NNs that capture the relationship between neighbouring data points e.g. neighbouring intensities in the diffraction pattern. Subsequently, another supervised tree-based ML model was used to predict unit cell parameters (unit cell length and angles) from the data.⁸⁰ The authors note that the ML models possess good performance on simulated data but more sophisticated models are required before it is applicable on experimental data (challenge 3, Fig. 3). Progress is made in developing an ML model that is capable of precisely identifying a full structure model, including unit cell content, as required for e.g., Rietveld refinement of experimental PD data.^25,81–83 One such example is the probabilistic convolutional NN known as XRD-AutoAnalyzer⁸³ which achieves 93.4% accuracy on phase identification from experimental PD patterns while providing uncertainties between 0 and 100%.⁸⁴ Here, an X-ray PD pattern is measured over 10–60° (using a Cu Kα source) and fed into XRD-AutoAnalyzer, which then identifies a structure model. Should the prediction uncertainty surpass 50%, additional measurements are necessary to definitively identify the structure. In order to determine which additional measurement to perform, class activation maps, a type of interpretable ML, are used on XRD-AutoAnalyzer to highlight regions that are critical for differentiating between the most probable phase and the subsequent highest probability phase. The procedure continues repetitively with new X-ray PD measurements until the XRD-AutoAnalyzer can confirm the structure model with a confidence exceeding 50%.

If working in a more restricted chemical space with well-defined components, it is possible to use supervised ML models for direct prediction of structural parameters for the phases included in the space. Dong et al. demonstrated that it is possible to directly predict structural information such as scale factor, lattice parameter and crystallite size (main application 3, Fig. 2) from PD patterns from a system of 5 different metal oxides using a convolutional NN that they call Parameter Quantification Network (PQ-Net).² They obtained an experimental X-ray diffraction computed tomography dataset of a multi-phase Ni–Pd/CeO₂–ZrO₂/Al₂O₃ containing about 20 000 diffraction patterns with signals from multiple phases. Treating such a large quantity of data with conventional Rietveld refinements takes significant computer time. To overcome this limitation, PQ-Net was trained on simulated PD data with varying scale factors, lattice parameters and crystallite size for NiO, PdO, CeO₂, ZrO₂ and theta-Al₂O. A 2^nd degree Chebyshev polynomial background and Poisson noise were also added to the training data. After training, PQ-Net can identify the crystalline phase, scale factor, lattice parameter and crystallite size for each experimental PD pattern in the dataset, orders of magnitudes faster than done using conventional Rietveld refinement. As seen in Fig. 6, the results of using PQ-Net are comparable to those determined through Rietveld methods on experimental data. A limitation of the PQ-Net approach is that it is tied to its training set, necessitating training prior to each experiment. If unexpected phases emerge during experiments, they will result in large goodness-of-fit values. For each new experiment or when new structure types are encountered, a new training is therefore required.

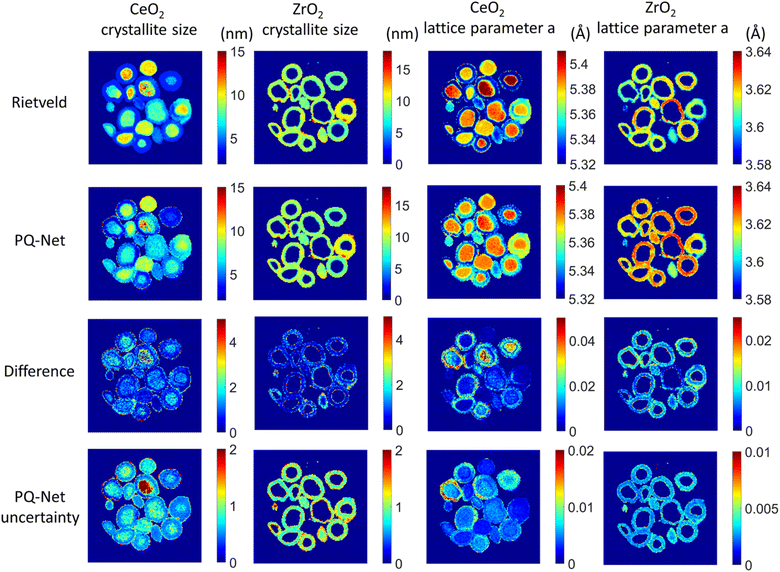Fig. 6 Crystallite size (colourbar axis corresponding to nm) and lattice parameter a (colourbar axis corresponding to Å) maps for CeO₂ and ZrO₂ obtained with the Rietveld method, results obtained with the PQ-Net, their absolute difference for the experimental multi-phase NiO–PdO–CeO₂–ZrO₂–Al₂O₃ system and the uncertainty maps of the deep ensemble PQ-Net.² (Under Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/).

Dong et al. required 100 000 datasets for training to achieve good results predicting structural information on experimental data from a chemical system with five components. For larger and complex systems with more possible components, the supervised ML model must be trained on even more data of both individual structural models and combinations of these. An example of this approach is the work by Lee et al., who used a supervised ML model for phase identification in a quaternary chemical system consisting of Sr, Al, Li, and O. This system thus spans simple to ternary oxides and multiple different polymorphs, and in total 170 inorganic compounds appear in the chemical space.⁸⁵ Here, the ML model was trained on 1 785 405 synthetic combinatorically mixed PD patterns. After training, the model was able to phase identify and give rough estimates of phase fractions of multicomponent systems from XRD data.

Instead of training the supervised ML model on large databases of combinations of phases, unsupervised ML methods, such as PCA and NMF, can demix multiphase PD patterns into individual phase patterns, as also addressed for XAS data above.^86,87 Here, a set of experimental diffraction patterns are given as input to the unsupervised ML algorithm, which decomposes it into its constituent parts. However, the PCA and NMF algorithms may encounter difficulties if the PD pattern of a chemical phase changes during the reaction, for example, through peak shifting from a unit cell change, variations in peak intensity from a change in thermal vibrations, or a change in the crystalline size, leading to different peak widths. For example, Stanev et al. encountered peak shifts induced by an alloying process in PD data.⁸⁸ To address this, they implemented a strategy that combined NMF with cross-correlation analysis of the demixed PD patterns, thus enabling the clustering of patterns that originated from the same chemical phase.

Other unsupervised ML methods can also be applied to demix signals into their constituent components (tackling challenge 2, Fig. 3). Chen et al. employed deep reasoning networks to map the crystal-structure phase diagram of Bi–Cu–V oxide using experimental PD data.⁸⁹ Based on PD data from Bi–Cu–V oxides prepared in various compositions, the ML model was trained to demix the phases in the PD patterns, and subsequently map the crystal-structure phase diagram of Bi–Cu–V oxide.⁸⁹ Once trained, the deep reasoning network can take a PD pattern from a sample in the composition space as input, and demix signals from multiple phases into their constituent components. Using a linear combination of the components, the PD pattern can be reconstructed, and the phase diagram can be constructed with phase concentrations. The authors demonstrated this process on X-ray PD patterns from a phase diagram of Bi–Cu–V containing 19 chemical phases.

Total scattering with pair distribution function: nanoparticle structure determination

Total scattering experiments are similar to PD, as the scattering of X-rays or neutrons from a sample is measured. However, for total scattering, it is not only the Bragg diffraction peaks that are analysed but also the diffuse scattering arising from local structural order. This enables structural analysis of both crystalline and non-crystalline samples. Total scattering data are often analysed in real space through PDF analysis. A PDF is generated by normalising, correcting, and Fourier-transforming the total scattering signal, and the PDF represents a histogram of interatomic distances. Like PD, PDF can be used to characterise crystalline materials, but has especially emerged as a powerful technique to characterise the atomic arrangement in non- or poorly crystalline materials such as clusters in solution and disordered, amorphous, and nanomaterials.^90,91 As for XAS, SAS and PD discussed above, ML models can help accelerate the PDF modelling process. For example, supervised ML models have been developed to predict space groups from PDF data of crystalline materials.⁹² We have furthermore shown that supervised ML can be used to identify the structure of polyoxometalate clusters.^93,94

In a slightly different application of supervised methods, we have recently demonstrated how explainable supervised ML can be used to extract information on the local atomic arrangement present in a sample.⁹⁵ The aim of PDF analysis of e.g. nanostructured materials is often to identify models for the main structural motifs in a material. Our algorithm, ML-MotEx provides this information by using SHAP (SHapley Additive exPlanation)^96,97 values to identify which atoms in a given starting model are important for the fit quality. The ML-MotEx algorithm is illustrated in Fig. 7. The starting model should be chosen to contain the main atomic arrangements expected to be found in the sample. If analysing the structure of e.g. an amorphous material, the starting model may be a related crystalline structure. However, sometimes, it can be challenging to generate a good starting model, which is a significant drawback of ML-MotEx. Based on the model, thousands of structure fragments are generated by iteratively removing atoms from the starting model (step 1), and a PDF fit is done for each of the fragments (step 2). A supervised ML model is then trained on the thousands of PDF fits (step 3), and ultimately, each atom can be assigned an atom contribution value which describes how much it contributes to the goodness-of-fit (step 4). By analysing the SHAP values, it is thus possible to identify which motifs in the starting model are important in the material to describe the data. ML-MotEx has so far been used to identify the structure of ionic clusters in solution,⁹⁵ extract structural motifs in amorphous metal oxides,⁹⁸ and identify stacking faulted domains on MnO₂ from both X-ray PD and PDF data.⁹⁹

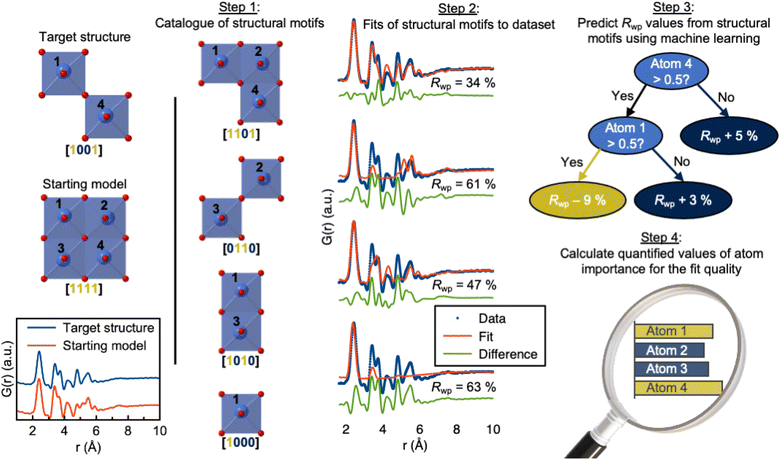Fig. 7 Use of ML-MotEx. Firstly, a starting model is provided. Using this starting model, a structure catalogue is generated, and the structures in the catalogue are fitted to the experimental data in question. An ML algorithm is then trained to predict R_wp values and finally calculating quantified values of feature importance for the fit quality. The figure is from Anker et al.⁹⁵ (Under Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/).

The supervised ML methods used for structure identification for both PD and PDF data discussed so far are limited to identifying structural models that are part of the structural database on which they have been trained. Ultimately, the aim of a PDF experiment may be to solve the structure of new nanomaterials. To explore structural models beyond any existing structural database (challenge 2 in Fig. 3), some classes of unsupervised ML could be useful. We have recently used a graph-based conditional variational autoencoder,³⁵ DeepStruc (Fig. 8A) to determine the atomic structure of metallic nanoparticles up to 200 atoms in size from PDF data.^100,101 Given a PDF, DeepStruc can output a particle structure, and we obtained mean absolute errors of 0.093 ± 0.058 Å on the atomic positions in metallic nanoparticles from simulated PDFs. Fig. 8B shows the results of applying DeepStruc to experimental PDFs obtained from three chemical systems, consisting of two magic-sized clusters (I) Au₁₄₄(p-MBA)₆₀ ¹⁰² and (II) Au₁₄₄(PET)₆₀,¹⁰² and (III) a 1.8 nm Pt nanoparticle.¹⁰³ All three structures match the structures found in the literature and provide good data fits. Although DeepStruc is supervised in the sense that it is trained on structure and PDF pairs, it also has abilities from unsupervised ML as it learns to probabilistically map cluster structures and PDFs into a two-dimensional chemically meaningful space, which we refer to as the latent space. By inspecting the latent space, it is possible to find relations between different types of cluster models. DeepStruc places decahedral (orange) structures in the latent space between face-centered cubic (fcc) (light blue) and hexagonal closed packed (hcp) (pink) structures. This spatial arrangement can be explained by considering that decahedral structures are constructed from five tetrahedrally shaped fcc crystals, separated by {111} twin boundaries.^13,104,105 The twin boundaries, resembling stacking faulted regions of fcc, justify their location in the latent space between fcc and hcp.^48,95,96 The capability of DeepStruc to interpolate between cluster structures arises from each structure in the latent space being probabilistically rather than deterministically predicted. This has been demonstrated in Anker et al.,¹⁰⁰ where we show that generative models²⁸ are necessary to go beyond the structural database used for training the ML model. Specifically, we showed that a generative model, like DeepStruc, can interpolate between structural models, as shown in Fig. 8C, while still yielding sensible results. More traditional deterministic models, which are not probabilistic, could not interpolate between structures and thereby not go beyond the structural database when predicting a structural model from a PDF.

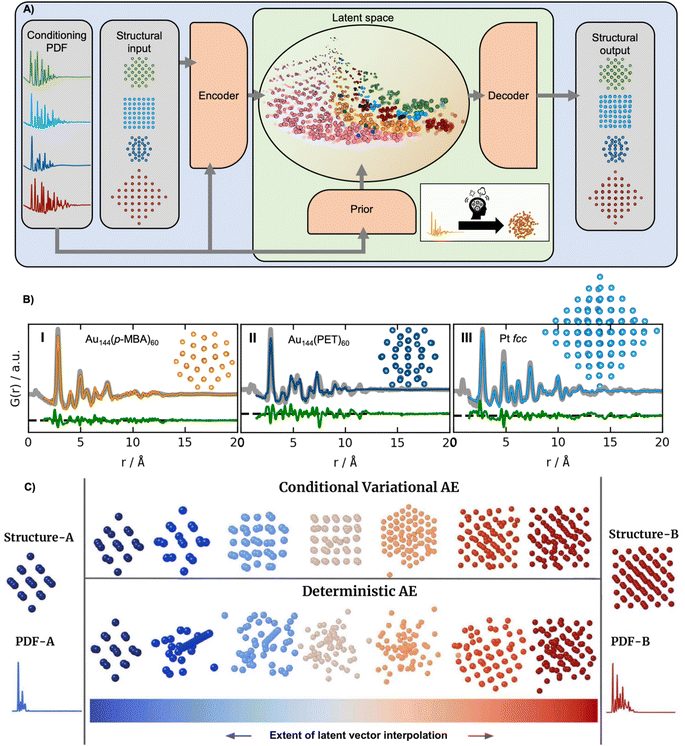Fig. 8 DeepStruc is a Conditional Variational Autoencoder that can solve the structure of a small mono-metallic nanoparticle from a PDF. (A) DeepStruc predicts the xyz-coordinates of the mono-metallic nanoparticle structure with a PDF provided as the conditional input. The encoder uses the structure and PDF as input, while the prior only takes the PDF as input. A latent space embedding is given as input to the decoder to obtain the structural output, which produces the corresponding mono-metallic nanoparticle xyz-coordinates. During the training of DeepStruc, both the blue and green regions are used, while only the green region is used for structure prediction during the inference process. (B) PDF fit of the reconstructed structure from three different nanoparticle systems: (I) Au₁₄₄(p-MBA)₆₀ PDF,¹⁰² the (II) Au₁₄₄(PET)₆₀ PDF¹⁰² using a reconstructed structure icosahedral structure and (III) a 1.8 nm Pt nanoparticle PDF from Quinson et al.¹⁰³ (A) and (B) are adapted from Kjær & Anker et al.¹⁰¹ (Under Creative Commons Attribution 3.0 Unreported License https://creativecommons.org/licenses/by/3.0/). (C) Structures generated by decoding different extents of interpolation of the latent variables obtained for PDF-A and PDF-B. The generated structures start from structure-A and progressively evolve towards structure-B. This work uses a Conditional Variational Autoencoder similar to DeepStruc and we compare it with a Deterministic Autoencoder. (C) is from Anker & Kjær et al.¹⁰⁰ (Under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License https://creativecommons.org/licenses/by-nc-nd/4.0/).

DeepStruc is integrated with the Hugging Face platform, enabling users to rapidly determine the structure of small metallic nanoparticles from PDFs using a simple two-click process.¹⁰⁶ The Hugging Face integration provides a user-friendly experience, without requiring data storage or complex software installations.

Unsupervised ML algorithms have also been employed to either uncover trends in PDFs obtained from multiple samples or to separate the signal from different phases in a PDF (challenge 2, Fig. 3).^107–109 NMF has proven to be especially useful, and has been used to analyse PDFs obtained from various materials and conditions, including battery materials, amorphous solid dispersions, or data collected under high-pressure. It has also been used to extract the interface PDF between a Fe and a Fe₃O₄ phase.^110–114 Recently, efforts have also been made to develop an efficient and accurate NMF algorithm that can be used during data measurement.^115,116 This NMF algorithm is available at PDF-in-the-cloud.^117,118

Inelastic neutron scattering: extraction of a materials Hamiltonians

INS is an inelastic experimental technique for investigating the vibrational and magnetic properties of atoms in materials. During an INS experiment, a neutron beam interacts with the atomic nuclei and the magnetic moment of the electrons in the material. By measuring the initial and final neutron energy, one can determine the energy of the interaction or excitation, which allows to study both the atomic and magnetic structure. Analysing the inelastically scattered neutrons thus provides information about the Hamiltonian, which governs atomic and magnetic interactions. However, interpreting experimental INS data or extracting the Hamiltonian can be challenging due to a large amount of measured data and the complexity of simulating accurate INS data that resembles the scattering process (challenge 3, Fig. 3).

For example, determining the appropriate spin wave model of the half-doped bilayer manganite, Pr(Ca, Sr)₂Mn₂O₇ (abbreviated as PCSMO) has been debated, with a Goodenough spin wave model (Fig. 9A),^119,120 or a Dimer spin wave model (Fig. 9A) being considered.¹²¹ Due to the subtle differences between the two models, determining which model the INS spectra correspond to has been challenging, as it requires a meticulous manual fitting process. After extensive experimentation and careful data treatment, it was ultimately determined that the Goodenough spin wave model best describes the experimental data (Fig. 9B).¹²²

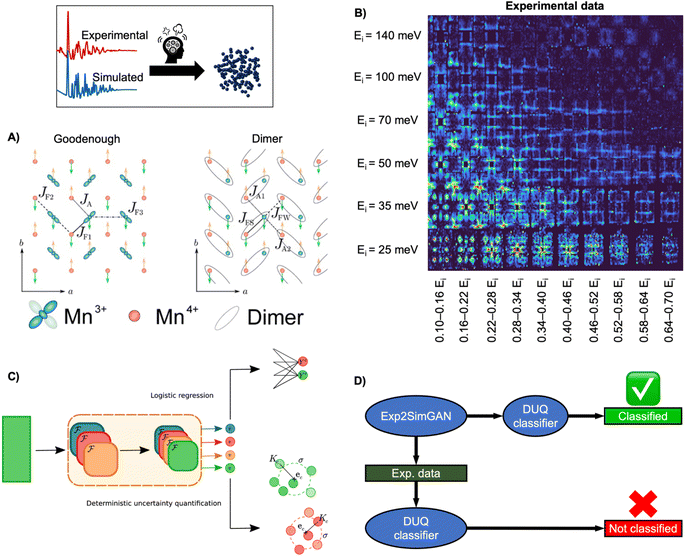Fig. 9 Determining the spin wave model from experimental INS data using ML. (A) Two magnetic exchange models in a single sheet of Mn ions in a half-doped manganite. (Left) Goodenough model (Right) Dimer model.²⁷ (B) 2D representation of experimental data of PCSMO measured at 4 K using the MAPS spectrometer.¹²² The INS spectra are arranged in terms of incident neutron energy (E_i) and bins of energy transfer ω = 0.10–0.16E_i, etc.¹²⁵ (C) Schematic representation of the DUQ method. The input initially passes through a series of convolutional NNs (orange block) to extract features. In standard logistic regression, the outputs from the convolutional NNs are classified by summing the weights connecting each filter, f_i, to the class C of interest. This is a simple binary classification. The DUQ classifier instead outputs a weight vector associated with the input that is correlated to the class predictions. If all the weights in the weight vector are close to a class (based on distances, K_c, from the weight vector to the centre, e_c, of clusters of training examples), the prediction has a large certainty, while the certainty is larger with a larger spread of weight vectors. (C) is from Butler et al.²⁷ (Under Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/). (D) The DUQ classifier cannot identify the spin wave model of an experimental dataset with high certainty. However, Exp2SimGAN matches the experimental dataset to the simulated training set of the DUQ classifier enabling the classification of the spin wave model with high certainty. A + B + D are from Anker et al.¹²⁵ (Under Creative Commons Attribution 3.0 Unreported License https://creativecommons.org/licenses/by/3.0/).

To ease this task, a supervised ML model has been developed to assist in analysing INS data. By training supervised ML models on simulated INS spectra calculated using physics-driven equations, Hamiltonians can be predicted from INS data. Specifically, Butler et al. demonstrated that NNs can predict magnetic Hamiltonians or classify the spin wave model from simulated INS data of PCSMO, saving significant time compared to manual data analysis.²⁷ They first used a logistic regression¹²³ model, illustrated in Fig. 9C, which makes a simple binary classification, either Goodenough or Dimer, but gives no indication of the reliability of the prediction. It was thereby challenging to judge when to trust the model. To resolve this problem, they used a deterministic uncertainty quantification (DUQ) classifier (Fig. 9C),^27,122 to perform uncertainty classification instead. The DUQ classifier outputs a weight vector associated with the input that is correlated to the class predictions. If all the weights in the weight vector are close to a class, the prediction has a large certainty, while the certainty is larger with a larger spread of weight vectors.

To reliably predict the spin wave model from experimental INS data (Fig. 9B), the DUQ classifier was trained on computationally expensive resolution convoluted INS spectra. Physics-driven simulations may not always capture the experimental noise, instrumental effects or other artefacts from phenomena not described by the underlying theory (challenge 3 in Fig. 3). In this example, the computationally inexpensive resolution unconvolved INS simulations did not capture any instrumental effects. To address this challenge, we introduced an unsupervised image-to-image algorithm, Exp2SimGAN, which is a generative adversarial network¹²⁴ (GAN) capable of learning the simulated and experimental data distributions and transforming between them, e.g. transforming a simulated dataset into one that resembles an experimental dataset, or vice versa.¹²⁵ By using Exp2SimGAN to convert experimental INS spectra into simulated-like data, the DUQ classifier, trained on computationally inexpensive resolution unconvolved INS spectra, can be applied to the experimental INS data (Fig. 9D).¹²⁵ This approach helps bridge the gap between simulations and experimental data, allowing for more accurate and efficient analysis (tackling challenge 3, Fig. 3).

Samarakoon et al. demonstrated an alternative approach for the analysis of INS data using autoencoders.^126–128 They showed that autoencoders can eliminate background signals and artefacts from the experimental INS spectrum by compressing them into a latent space. Once in the latent space, the magnetic behaviour can be categorised, and the autoencoder can solve the inverse problem by extracting the Hamiltonians from the experimental INS spectrum. This is achieved by decoding the INS spectrum from the latent space positions. As a result, the autoencoder works as a fast surrogate model for INS simulations accelerating the fitting procedure of the experimental INS spectrum. Later work integrates ML modelling approaches into the INS experiments enabling real-time analysis of INS data.¹²⁹

Remaining challenges and future outlook

In this perspective, we have shown how analysis of scattering and spectroscopy data is becoming increasingly feasible using supervised and unsupervised ML approaches. Especially, the progress of large open-source structural databases has catalysed the use of supervised ML. Such databases have made it possible to create datasets connecting structures with scattering and spectroscopy data for ML training.

Supervised ML is now widely used to identify structural models (main application 1, Fig. 2) from data, to predict data from structural models (main application 2, Fig. 2), or to directly provide structural information from data (main application 3, Fig. 2). However, we have highlighted three challenges that supervised ML faces in automating the analysis of scattering and spectroscopy data (Fig. 3). Challenge 1: handling datasets originating from a mix of chemical phases. Here, unsupervised ML, especially NMF, has successfully been used to demix datasets into constituent components. We anticipate the emergence of combination methods, where unsupervised ML firstly demixes complex datasets whereafter they are independently analysed using supervised ML. Challenge 2: handling data from a structural model that is not part of a database. Here, generative modelling appears promising for interpolating between structural models in a database. Challenge 3: handling experimental data. For the ML models to significantly impact the data analysis of scattering and spectroscopy data, they must perform well on experimental data and not only on simulated data. Often in materials chemistry, supervised ML models are trained on physics-driven simulations which do not include instrumental artefacts, noise or other phenomena not directly described by the underlying physics. Here, new methods are needed to make simulated data resemble experimental data. Unsupervised image-to-image algorithms could potentially address this challenge.¹²⁵

However, using ML to resolve more complicated challenges in materials chemistry is still challenged by limited sizes of datasets connecting structure and spectroscopy/scattering signal. One way to handle limited data is to constrain the ML model with chemical knowledge. Here, physics-informed NNs serve as an inspiration, as they embed partial differential equations as constraints into the NN optimisation problem, for example, when using an NN as a surrogate model for the Schrödinger equation.¹³⁰ As a result, the range of potential solutions is limited to a manageable size for ML to handle with the available information. However, not all chemistry can be expressed as differentiable equations, necessitating the development of similar approaches that can incorporate chemical knowledge into the ML architecture as ‘chemistry-driven ML’. Equivariant graph-based NNs show promise, as they leverage group representation theory to design architectures that are equivariant to specified symmetry groups, making them well-suited for analysing chemical systems with underlying symmetries.¹³¹ We expect another impact to come from interpretable and explainable ML which enables researchers to understand the underlying mechanisms behind predictions, build trust in ML model outcomes, and uncover unexpected correlations that may lead to scientific insights. For those interested, we refer to a recent review paper by Oviedo et al.³⁰ for more about interpretable and explainable ML in materials chemistry.

Currently, it is not mandatory to publish data, code, and software requirements alongside research papers, making it difficult for other researchers to apply trained ML models to their own experimental data. A paradigm shift from publishing papers with code to publishing code with papers may thus be needed. For the ML developer, we refer to N. Artrith et al.¹³² for best practices in ML for chemistry. We suggest that publishing code with papers would greatly benefit the field, allowing materials chemists to analyse data easily or automatically without domain expertise.

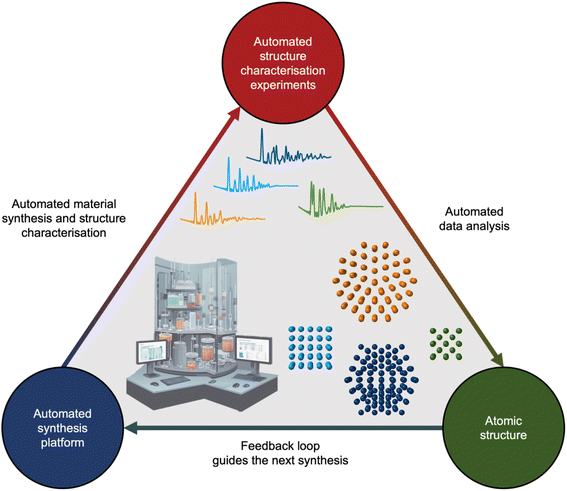
If we unceasingly share ML models, expand open-source databases, and bridge the gap between simulated and experimental data, the next decade holds promise to integrate analysis of scattering and spectroscopy data with ML into self-driving laboratories. Self-driving laboratories are currently receiving much attention for e.g. identifying new, improved photocatalysts for hydrogen production from water,¹³³ synthesising pharmaceutical compounds,¹³⁴ and optimising nanostructure synthesis based on their optical properties.^135,136 As illustrated in Fig. 10, the self-driving laboratory will synthesise a material, perform a scattering or spectroscopy experiment, and the data can be automatically analysed with ML. The findings will then be fed into an active learning framework that suggests the next experiment based on structural insight.

Fig. 10 The proposed self-driving laboratory to integrate analysis of scattering and spectroscopy data with ML into self-driving laboratories. The automated experiment platform synthesises a material and performs one or multiple structure characterisation experiments. The data from these experiments will be analysed using ML. The analysed data will be automatically fed into an active learning framework that will suggest the next experiment enabling a directed synthesis of functional materials via insight at the atomic level.

Author contributions

All authors were involved in the preparation of the manuscript and approved the final manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work is part of a project that has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (grant agreement No. 804066). Funding from the Danish Ministry of Higher Education and Science through the SMART Lighthouse is gratefully acknowledged. We acknowledge support from the Danish National Research Foundation Center for High Entropy Alloy Catalysis (DNRF 149).

References

1. C. Wang, U. Steiner and A. Sepe, Small, 2018, 14, e1802291.
2. H. Dong, K. T. Butler, D. Matras, S. W. T. Price, Y. Odarchenko, R. Khatry, A. Thompson, V. Middelkoop, S. D. M. Jacques, A. M. Beale and A. Vamvakeros, npj Comput. Mater., 2021, 7, 74.
3. M. Xia, T. Liu, N. Peng, R. Zheng, X. Cheng, H. Zhu, H. Yu, M. Shui and J. Shu, Small Methods, 2019, 3, 1900119.
4. T. Ebensperger, P. Stahlhut, F. Nachtrab, S. Zabler and R. Hanke, J. Instrum., 2012, 7, C10008.
5. B. Hornberger, J. Kasahara, M. Gifford, R. Ruth and R. Loewen, Presented in part at the SPIE Optical Engineering + Applications, 2019.
6. J. Nelson, S. Misra, Y. Yang, A. Jackson, Y. Liu, H. Wang, H. Dai, J. C. Andrews, Y. Cui and M. F. Toney, J. Am. Chem. Soc., 2012, 134, 6337–6343.
7. G. A. Elia, G. Greco, P. H. Kamm, F. García-Moreno, S. Raoux and R. Hahn, Adv. Funct. Mater., 2020, 30, 2003913.
8. E. T. S. Kjær, O. Aalling-Frederiksen, L. Yang, N. K. Thomas, M. Juelsholt, S. J. L. Billinge and K. M. Ø. Jensen, Chem. Methods, 2022, 2, e202200034.
9. H. Matsui, N. Ishiguro, T. Uruga, O. Sekizawa, K. Higashi, N. Maejima and M. Tada, Angew. Chem., Int. Ed., 2017, 56, 9371–9375.
10. A. Vamvakeros, D. Matras, T. E. Ashton, A. A. Coelho, H. Dong, D. Bauer, Y. Odarchenko, S. W. T. Price, K. T. Butler, O. Gutowski, A.-C. Dippel, M. v. Zimmerman, J. A. Darr, S. D. M. Jacques and A. M. Beale, Small Methods, 2021, 5, 2100512.
11. K. M. Ø. Jensen, X. Yang, J. V. Laveda, W. G. Zeier, K. A. See, M. D. Michiel, B. C. Melot, S. A. Corr and S. J. L. Billinge, J. Electrochem. Soc., 2015, 162, A1310–A1314.
12. J. Becher, D. F. Sanchez, D. E. Doronkin, D. Zengel, D. M. Meira, S. Pascarelli, J.-D. Grunwaldt and T. L. Sheppard, Nat. Cat., 2021, 4, 46–53.
13. S. Banerjee, C.-H. Liu, K. M. Ø. Jensen, P. Juhas, J. D. Lee, M. Tofanelli, C. J. Ackerson, C. B. Murray and S. J. L. Billinge, Acta Crystallogr., Sect. A: Found. Adv., 2020, 76, 24–31.
14. L. Yang, P. Juhás, M. W. Terban, M. G. Tucker and S. J. L. Billinge, Acta Crystallogr., Sect. A: Found. Adv., 2020, 76, 395–409.
15. A. Agrawal and A. Choudhary, APL Mater., 2016, 4, 053208.
16. K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555.
17. G. Pacchioni, Nat. Rev. Phys., 2019, 1, 100–101.
18. B. Sullivan, R. Archibald, J. Azadmanesh, V. G. Vandavasi, P. S. Langan, L. Coates, V. Lynch and P. Langan, J. Appl. Crystallogr., 2019, 52, 854–863.
19. T. W. Ke, A. S. Brewster, S. X. Yu, D. Ushizima, C. Yang and N. K. Sauter, J. Synchrotron Radiat., 2018, 25, 655–670.
20. M. Doucet, A. M. Samarakoon, C. Do, W. T. Heller, R. Archibald, D. Alan Tennant, T. Proffen and G. E. Granroth, Mach. Learn.: Sci. Technol., 2021, 2, 023001.
21. J. A. Aguiar, M. L. Gong, R. R. Unocic, T. Tasdizen and B. D. Miller, Sci. Adv., 2019, 5, eaaw1949.
22. S. Muto and M. Shiga, Microscopy, 2019, 69, 110–122.
23. H. Wang, Y. Xie, D. Li, H. Deng, Y. Zhao, M. Xin and J. Lin, J. Chem. Inf. Model., 2020, 60, 2004–2011.
24. M. Tatlier, Neural. Comput. Appl., 2011, 20, 365–371.
25. J. K. Bunn, J. Hu and J. R. Hattrick-Simpers, JOM, 2016, 68, 2116–2125.
26. F. Oviedo, Z. Ren, S. Sun, C. Settens, Z. Liu, N. T. P. Hartono, S. Ramasamy, B. L. DeCost, S. I. P. Tian, G. Romano, A. Gilad Kusne and T. Buonassisi, npj Comput. Mater., 2019, 5, 60.
27. K. T. Butler, M. D. Le, J. Thiyagalingam and T. G. Perring, J. Phys.: Condens. Matter, 2021, 33, 194006.
28. B. Mahesh, Int. J. Sci. Res., 2020, 9, 381–386.
29. S. Katoch, S. S. Chauhan and V. Kumar, Multimed. Tools Appl., 2021, 80, 8091–8126.
30. F. Oviedo, J. L. Ferres, T. Buonassisi and K. T. Butler, Acc. Mater. Res., 2022, 3, 597–607.
31. OpenAi, arXiv, 2023, preprint, arXiv:2303.08774,  DOI:10.48550/arXiv.2303.08774.
32. L. Ouyang, J. Wu, X. Jiang, D. Almeida, C. Wainwright, P. Mishkin, C. Zhang, S. Agarwal, K. Slama and A. Ray, Adv. Neural Inf. Process. Syst., 2022, 35, 27730–27744.
33. T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry and A. Askell, Adv. Neural Inf. Process. Syst., 2020, 33, 1877–1901.
34. J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek and A. Potapenko, Nature, 2021, 596, 583–589.
35. D. P. Kingma and M. Welling, arXiv, 2013, preprint, arXiv:1312.6114,  DOI:10.48550/arXiv.1312.6114.
36. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
37. C. Zheng, K. Mathew, C. Chen, Y. Chen, H. Tang, A. Dozier, J. J. Kas, F. D. Vila, J. J. Rehr, L. F. J. Piper, K. A. Persson and S. P. Ong, npj Comput. Mater., 2018, 4, 12.
38. K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, npj Comput. Mater., 2020, 6, 173.
39. K. Mathew, C. Zheng, D. Winston, C. Chen, A. Dozier, J. J. Rehr, S. P. Ong and K. A. Persson, Sci. Data, 2018, 5, 180151.
40. M. R. Carbone, M. Topsakal, D. Lu and S. Yoo, Phys. Rev. Lett., 2020, 124, 156401.
41. C. D. Rankine, M. M. M. Madkhali and T. J. Penfold, J. Phys. Chem. A, 2020, 124, 4263–4270.
42. C. Rankine and T. Penfold, J. Chem. Phys., 2022, 156, 164102.
43. J. Timoshenko, D. Lu, Y. Lin and A. I. Frenkel, J. Phys. Chem., 2017, 8, 5091–5098.
44. J. Timoshenko, S. Roese, H. Hövel and A. I. Frenkel, Radiat. Phys. Chem., 2020, 175, 108049.
45. Y. Liu, N. Marcella, J. Timoshenko, A. Halder, B. Yang, L. Kolipaka, M. J. Pellin, S. Seifert, S. Vajda and P. Liu, J. Chem. Phys., 2019, 151, 164201.
46. S. B. Torrisi, M. R. Carbone, B. A. Rohr, J. H. Montoya, Y. Ha, J. Yano, S. K. Suram and L. Hung, npj Comput. Mater., 2020, 6, 109.
47. M. R. Carbone, S. Yoo, M. Topsakal and D. Lu, Phys. Rev. Mater., 2019, 3, 033604.
48. M. Ahmadi, J. Timoshenko, F. Behafarid and B. Roldan Cuenya, J. Phys. Chem. C, 2019, 123, 10666–10676.
49. J. Timoshenko, H. S. Jeon, I. Sinev, F. T. Haase, A. Herzog and B. R. Cuenya, Chem. Sci., 2020, 11, 3727–3736.
50. J. Timoshenko, M. Ahmadi and B. Roldan Cuenya, J. Phys. Chem. C, 2019, 123, 20594–20604.
51. J. Timoshenko, A. Anspoks, A. Cintins, A. Kuzmin, J. Purans and A. I. Frenkel, Phys. Rev. Lett., 2018, 120, 225502.
52. J. Timoshenko, C. J. Wrasman, M. Luneau, T. Shirman, M. Cargnello, S. R. Bare, J. Aizenberg, C. M. Friend and A. I. Frenkel, Nano Lett., 2019, 19, 520–529.
53. A. C. Scheinost, R. Kretzschmar, S. Pfister and D. R. Roberts, Environ. Sci. Technol., 2002, 36, 5021–5028.
54. T. Ressler, J. Wong, J. Roos and I. L. Smith, Environ. Sci. Technol., 2000, 34, 950–958.
55. S. Wasserman, J. Phys. IV, 1997, 7, C2.
56. H. Tanimoto, X. Hongkun, M. Mizumaki, Y. Seno, J. Uchiwada, R. Yamagami, H. Kumazoe, K. Iwamitsu, Y. Kimura and K. Amezawa, J. Phys. Commun., 2021, 5, 115005.
57. A. A. Gambardella, M. Cotte, W. de Nolf, K. Schnetz, R. Erdmann, R. van Elsas, V. Gonzalez, A. Wallert, P. D. Iedema and M. Eveno, Sci. Adv., 2020, 6, eaay8782.
58. S. Tetef, N. Govind and G. T. Seidler, Phys. Chem. Chem. Phys., 2021, 23, 23586–23601.
59. T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016, 116, 11128–11180.
60. D. J. Beltran-Villegas, M. G. Wessels, J. Y. Lee, Y. Song, K. L. Wooley, D. J. Pochan and A. Jayaraman, J. Am. Chem. Soc., 2019, 141, 14916–14930.
61. M. G. Wessels and A. Jayaraman, Macromolecules, 2021, 54, 783–796.
62. M. G. Wessels and A. Jayaraman, ACS Polym. Au, 2021, 1, 153–164.
63. C. M. Heil and A. Jayaraman, ACS Mater. Au, 2021, 1, 140–156.
64. Z. Ye, Z. Wu and A. Jayaraman, JACS Au, 2021, 1, 1925–1936.
65. C. M. Heil, A. Patil, A. Dhinojwala and A. Jayaraman, ACS Cent. Sci., 2022, 8, 996–1007.
66. Z. Wu and A. Jayaraman, Macromolecules, 2022, 55, 11076–11091.
67. C. M. Heil, Y. Ma, B. Bharti and A. Jayaraman, JACS Au, 2023, 3, 889–904.
68. S. Liu, C. N. Melton, S. Venkatakrishnan, R. J. Pandolfi, G. Freychet, D. Kumar, H. Tang, A. Hexemer and D. M. Ushizima, MRS Commun., 2019, 9, 586–592.
69. C. Do, W.-R. Chen and S. Lee, MRS Adv., 2020, 5, 1577–1584.
70. H. Ikemoto, K. Yamamoto, H. Touyama, D. Yamashita, M. Nakamura and H. Okuda, J. Syncrotron Radiat., 2020, 27, 1069–1073.
71. G. Song, L. Porcar, M. Boehm, F. Cecillon, C. Dewhurst, Y. Le Goc, J. Locatelli, P. Mutti and T. Weber, EPJ Web Conf, 2020, 225, 01004.
72. R. K. Archibald, M. Doucet, T. Johnston, S. R. Young, E. Yang and W. T. Heller, J. Appl. Crystallogr., 2020, 53, 326–334.
73. http://www.sasview.org/) .
74. P. Tomaszewski, S. Yu, M. Borg and J. Rönnols, Swedish Workshop on Data Science (SweDS), IEEE, 2021, pp. 1–6.
75. https://huggingface.co/spaces/AndySAnker/SCattering_Ai_aNalysis .
76. A. Ziletti, D. Kumar, M. Scheffler and L. M. Ghiringhelli, Nat. Commun., 2018, 9, 2775.
77. W. B. Park, J. Chung, J. Jung, K. Sohn, S. P. Singh, M. Pyo, N. Shin and K.-S. Sohn, IUCrJ, 2017, 4, 486–494.
78. B. D. Lee, J.-W. Lee, W. B. Park, J. Park, M.-Y. Cho, S. Pal Singh, M. Pyo and K.-S. Sohn, Adv. Intell. Syst., 2022, 4, 2200042.
79. Y. Suzuki, H. Hino, T. Hawai, K. Saito, M. Kotsugi and K. Ono, Sci. Rep., 2020, 10, 21790.
80. C. Garcia-Cardona, R. Kannan, T. Johnston, T. Proffen, K. Page and S. K. Seal, IEEE International Conference on Big Data (Big Data), IEEE, 2019.
81. J. K. Bunn, S. Han, Y. Zhang, Y. Tong, J. Hu and J. R. Hattrick-Simpers, J. Mater. Res., 2015, 30, 879–889.
82. P. M. Maffettone, L. Banko, P. Cui, Y. Lysogorskiy, M. A. Little, D. Olds, A. Ludwig and A. I. Cooper, Nat. Comput. Sci., 2021, 1, 290–297.
83. N. J. Szymanski, C. J. Bartel, Y. Zeng, Q. Tu and G. Ceder, Chem. Mater., 2021, 33, 4204–4215.
84. N. J. Szymanski, C. J. Bartel, Y. Zeng, M. Diallo, H. Kim and G. Ceder, npj Comput. Mater., 2023, 9, 31.
85. J.-W. Lee, W. B. Park, J. H. Lee, S. P. Singh and K.-S. Sohn, Nat. Commun., 2020, 11, 86.
86. C. J. Long, D. Bunker, X. Li, V. L. Karen and I. Takeuchi, Rev. Sci. Instrum., 2009, 80, 103902.
87. D. Chernyshov, I. Dovgaliuk, V. Dyadkin and W. van Beek, Crystals, 2020, 10, 581.
88. V. Stanev, V. V. Vesselinov, A. G. Kusne, G. Antoszewski, I. Takeuchi and B. S. Alexandrov, npj Comput. Mater., 2018, 4, 43.
89. D. Chen, Y. Bai, S. Ament, W. Zhao, D. Guevarra, L. Zhou, B. Selman, R. B. van Dover, J. M. Gregoire and C. P. Gomes, Nat. Mach. Intell., 2021, 3, 812–822.
90. T. L. Christiansen, S. R. Cooper and K. M. Ø. Jensen, Nanoscale Adv., 2020, 2, 2234–2254.
91. S. J. L. Billinge and I. Levin, Science, 2007, 316, 561–565.
92. C.-H. Liu, Y. Tao, D. Hsu, Q. Du and S. J. L. Billinge, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 633–643.
93. https://huggingface.co/spaces/AndySAnker/POMFinder .
94. A. S. Anker, E. T. Kjær, M. Juelsholt and K. M. Ø. Jensen, 2023, preprint at https://chemrxiv.org/engage/chemrxiv/article-details/64e5fef7dd1a73847f5951b9,  DOI:10.26434/chemrxiv-2023-91xz7.
95. A. S. Anker, E. T. S. Kjær, M. Juelsholt, T. L. Christiansen, S. L. Skjærvø, M. R. V. Jørgensen, I. Kantor, D. R. Sørensen, S. J. L. Billinge, R. Selvan and K. M. Ø. Jensen, npj Comput. Mater., 2022, 8, 213.
96. S. M. Lundberg, G. Erion, H. Chen, A. DeGrave, J. M. Prutkin, B. Nair, R. Katz, J. Himmelfarb, N. Bansal and S.-I. Lee, Nat. Mach. Intell., 2020, 2, 56–67.
97. S. M. Lundberg and S.-I. Lee, Proceedings of the 31^st International Conference on Neural Information Processing Systems, 2017, pp. 4765–4774,  DOI:10.48550/arXiv.1705.07874.
98. S. L. Skjærvø, A. S. Anker, M. C. Wied, E. Kjær, M. Juelsholt, T. L. Christiansen and K. M. Ø. Jensen, Chem. Sci., 2023, 14, 4806–4816.
99. N. P. L. Magnard, A. S. Anker, O. Aalling-Frederiksen, A. Kirsch and K. M. Ø. Jensen, Dalton Trans., 2022, 51, 17150–17161.
100. A. S. Anker, E. T. S. Kjær, E. B. Dam, S. J. L. Billinge, K. M. Ø. Jensen and R. Selvan, in Proc. 16th International Workshop on Mining and Learning with Graphs (MLG), Association for Computing Machinery, New York, NY, 2020, https://www.mlgworkshop.org/2020/.
101. E. T. S. Kjær, A. S. Anker, M. N. Weng, S. J. L. Billinge, R. Selvan and K. M. Ø. Jensen, Digital Discovery, 2023, 2, 69–80.
102. K. M. Ø. Jensen, P. Juhas, M. A. Tofanelli, C. L. Heinecke, G. Vaughan, C. J. Ackerson and S. J. L. Billinge, Nat. Commun., 2016, 7, 11859.
103. J. Quinson, L. Kacenauskaite, T. L. Christiansen, T. Vosch, M. Arenz and K. M. Ø. Jensen, ACS Omega, 2018, 3, 10351–10356.
104. L. D. Marks, Philos. Mag. A, 1984, 49, 81–93.
105. S. Banerjee, C.-H. Liu, J. D. Lee, A. Kovyakh, V. Grasmik, O. Prymak, C. Koenigsmann, H. Liu, L. Wang, A. M. M. Abeykoon, S. S. Wong, M. Epple, C. B. Murray and S. J. L. Billinge, J. Phys. Chem. C, 2018, 122, 29498–29506.
106. https://huggingface.co/spaces/AndySAnker/DeepStruc .
107. S. Chen, A. Y. Sheikh and R. Ho, J. Pharm. Sci., 2014, 103, 3879–3890.
108. N. Chieng, H. Trnka, J. Boetker, M. Pikal, J. Rantanen and H. Grohganz, Int. J. Pharm., 2013, 454, 167–173.
109. K. W. Chapman, S. H. Lapidus and P. J. Chupas, J. Appl. Crystallogr., 2015, 48, 1619–1626.
110. X. Hua, A. S. Eggeman, E. Castillo-Martínez, R. Robert, H. S. Geddes, Z. Lu, C. J. Pickard, W. Meng, K. M. Wiaderek, N. Pereira, G. G. Amatucci, P. A. Midgley, K. W. Chapman, U. Steiner, A. L. Goodwin and C. P. Grey, Nat. Mater., 2021, 20, 841–850.
111. H. S. Geddes, H. D. Hutchinson, A. R. Ha, N. P. Funnell and A. L. Goodwin, Nanoscale, 2021, 13, 13220–13224.
112. X. Hua, P. K. Allan, H. S. Geddes, E. Castillo-Martínez, P. A. Chater, T. S. Dean, A. Minelli, P. G. Bruce and A. L. Goodwin, Cell Rep. Phys. Sci., 2021, 2, 100543.
113. A. Herlihy, H. S. Geddes, G. C. Sosso, C. L. Bull, C. J. Ridley, A. L. Goodwin, M. S. Senn and N. P. Funnell, J. Appl. Crystallogr., 2021, 54, 1546–1554.
114. H. S. Geddes, H. Blade, J. F. McCabe, L. P. Hughes and A. L. Goodwin, Chem. Commun., 2019, 55, 13346–13349.
115. R. Gu, S. J. Billinge and Q. Du, Acta Crystallogr., Sect. A: Found. Adv., 2023, 79.
116. C.-H. Liu, C. J. Wright, R. Gu, S. Bandi, A. Wustrow, P. K. Todd, D. O'Nolan, M. L. Beauvais, J. R. Neilson, P. J. Chupas, K. W. Chapman and S. J. L. Billinge, J. Appl. Crystallogr., 2021, 54, 768–775.
117. Z. Thatcher, C.-H. Liu, L. Yang, B. C. McBride, G. Thinh Tran, A. Wustrow, M. A. Karlsen, J. R. Neilson, D. B. Ravnsbaek and S. J. L. Billinge, Acta Crystallogr., Sect. A: Found. Adv., 2022, 78, 242–248.
118. https://PDFitc.org .
119. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
120. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
121. A. Daoud-Aladine, J. Rodríguez-Carvajal, L. Pinsard-Gaudart, M. T. Fernández-Díaz and A. Revcolevschi, Phys. Rev. Lett., 2002, 89, 097205.
122. G. E. Johnstone, T. G. Perring, O. Sikora, D. Prabhakaran and A. T. Boothroyd, Phys. Rev. Lett., 2012, 109, 237202.
123. D. W. Hosmer Jr, S. Lemeshow and R. X. Sturdivant, Applied logistic regression, John Wiley & Sons, 2013.
124. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Advances in Neural Information Processing Systems, 2014, vol. 27.
125. A. S. Anker, K. T. Butler, M. D. Le, T. G. Perring and J. Thiyagalingam, Digital Discovery, 2023, 2, 578–590.
126. A. M. Samarakoon, K. Barros, Y. W. Li, M. Eisenbach, Q. Zhang, F. Ye, V. Sharma, Z. L. Dun, H. Zhou, S. A. Grigera, C. D. Batista and D. A. Tennant, Nat. Commun., 2020, 11, 892.
127. A. M. Samarakoon, P. Laurell, C. Balz, A. Banerjee, P. Lampen-Kelley, D. Mandrus, S. E. Nagler, S. Okamoto and D. A. Tennant, Phys. Rev. Res., 2022, 4, L022061.
128. A. M. Samarakoon and D. A. Tennant, J. Phys.: Condens. Matter, 2021, 34, 044002.
129. A. Samarakoon, D. A. Tennant, F. Ye, Q. Zhang and S. A. Grigera, Commun. Mater., 2022, 3, 84.
130. M. Raissi, P. Perdikaris and G. E. Karniadakis, J. Comput. Phys., 2019, 378, 686–707.
131. S.-O. Kaba and S. Ravanbakhsh, Equivariant Networks for Crystal Structures, Advances in Neural Information Processing Systems, 2022, vol. 35,  DOI:10.48550/arXiv.2211.15420.
132. N. Artrith, K. T. Butler, F.-X. Coudert, S. Han, O. Isayev, A. Jain and A. Walsh, Nat. Chem., 2021, 13, 505–508.
133. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241.
134. S. Steiner, J. Wolf, S. Glatzel, A. Andreou, J. M. Granda, G. Keenan, T. Hinkley, G. Aragon-Camarasa, P. J. Kitson, D. Angelone and L. Cronin, Science, 2019, 363, eaav2211.
135. Y. Jiang, D. Salley, A. Sharma, G. Keenan, M. Mullin and L. Cronin, Sci. Adv., 2022, 8, eabo2626.
136. H. Tao, T. Wu, S. Kheiri, M. Aldeghi, A. Aspuru-Guzik and E. Kumacheva, Adv. Funct. Mater., 2021, 31, 2106725.

---