Micromechanical remodeling of the extracellular matrix by invading tumors: anisotropy and heterogeneity†
Austin
Naylor‡
a,
Yu
Zheng‡
b,
Yang
Jiao
 *bc and
Bo
Sun
*bc and
Bo
Sun
 *a
*a
aDepartment of Physics, Oregon State University, Corvallis, OR, USA. E-mail: sunb@oregonstate.edu
bDepartment of Physics, Arizona State University, Tempe, AZ, USA. E-mail: jiao.yang@asu.edu
cMaterials Science and Engineering, Arizona State University, Tempe, AZ, USA
First published on 21st November 2022
Abstract
Altered tissue mechanics is an important signature of invasive solid tumors. While the phenomena have been extensively studied by measuring the bulk rheology of the extracellular matrix (ECM) surrounding tumors, micromechanical remodeling at the cellular scale remains poorly understood. By combining holographic optical tweezers and confocal microscopy on in vitro tumor models, we show that the micromechanics of collagen ECM surrounding an invading tumor demonstrate directional anisotropy, spatial heterogeneity and significant variations in time as tumors invade. To test the cellular mechanisms of ECM micromechanical remodeling, we construct a simple computational model and verify its predictions with experiments. We find that collective force generation of a tumor stiffens the ECM and leads to anisotropic local mechanics such that the extension direction is more rigid than the compression direction. ECM degradation by cell-secreted matrix metalloproteinase softens the ECM, and active traction forces from individual disseminated cells re-stiffen the matrix. Together, these results identify plausible biophysical mechanisms responsible for the remodeled ECM micromechanics surrounding an invading tumor.
Introduction
During the growth and metastasis of solid tumors, reciprocal mechanical interactions between a tumor and its surrounding extracellular matrix (ECM) are of fundamental importance.1 On the one hand, cancer cells apply strong traction forces that cause nonlinear stiffening of the ECM,2,3 and build up of plastic deformations,4–6 to the point of significantly altering the microstructure of the ECM.7,8 Cancer cells and cancer associated fibroblasts also secrete matrix metalloproteinase (MMP) that degrades the ECM,9 weakens its structural integrity and even creates hollow tracks along the path of cell migration.10,11 On the other hand, the remodeled ECM mechanics provides a multitude of physical cues through cell mechanosensing, such that the growth, migration, and malignant transformation are all sensitive to the tumor's mechanical microenvironment.12–17Although the mechanics, in particular the bulk rheology of the ECM surrounding tumors, have been well documented,18–20 and are often studied for their physiological impacts,21 one may recognize the drastic discrepancies in the corresponding scales between rheology and cell-ECM interactions. Bulk rheology characterizes the elastoviscosity of the ECM at millimeter or larger scales, which is appropriate to quantify the overall property of a whole tissue or organism. In contrast, the physical interface between cells and the ECM is no more than a few micrometers in dimension. Therefore a cancer cell will directly modify and respond to the ECM micromechanics at the cellular scale,22–24 and may not have the knowledge of their physical environment at scales hundreds of times larger.25
The distinct mechanical properties of the ECM at cellular and tissue scales can be traced back to the ECM structure. Collagen ECM, for example, is a disordered assembly of fibrous scaffold with pore sizes ranging from sub-micrometer to a few micrometers.26–28 These structural features lead to anisotropic and heterogeneous mechanical moduli measured by micrometer-sized probing particles,29–31 or atomic force microscopy.32 It has been shown that local elasticity can vary by as much as 50% over a distance comparable to a single cell size.29
Mechanistic understanding of the altered cancer microenvironment requires one to fill the knowledge gap of ECM micromechanics surrounding an invading tumor. To this end, we develop an experimental system that combines confocal imaging, holographic optical tweezers,33,34 and an in vitro tumor model35 to quantify the local elastic moduli of the ECM outside of disseminating tumor diskoids. We also employ a multiscale computational model16 that explicitly accounts for the microscopic structure and physical interactions between cancer cells and 3D ECM. By integrating experiments and the model, we test putative mechanisms that contribute to the anisotropy, heterogeneity, and temporal variations of ECM micromechanics.
Results
Experimental characterization of ECM micromechanics surrounding an invading tumor
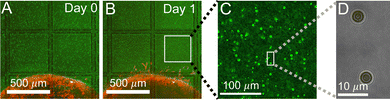
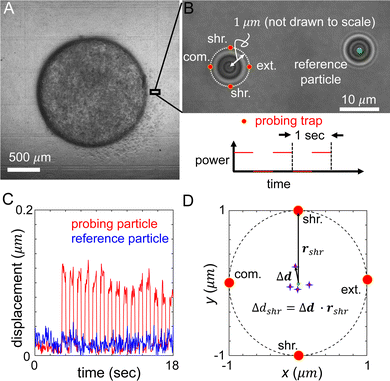
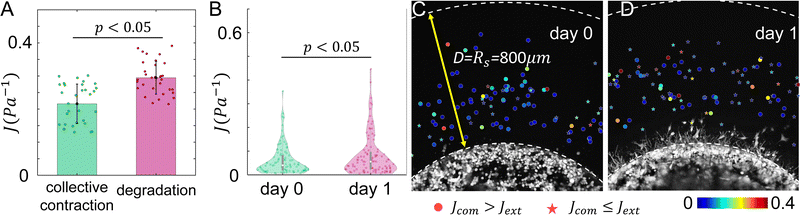
In order to measure the micromechanics of the extracellular matrix (ECM) surrounding invading solid tumors, we first create tumor diskoids using the DIGME technique we developed previously.35 This technique precisely controls the shape and size of each disk-shaped tumor model, allowing us to combine measurements of multiple tumor samples with fixed geometry. The diskoids consist of MDA-MB-231 cells, a highly invasive line of breast cancer cells that are capable of migrating in 3D ECM. The cells are confined by type-I collagen matrices at a concentration of 2 mg ml−1, which contains monodisperse polystyrene microspheres with a diameter of 3 μm as probing particles. Most microspheres are stably embedded in the ECM by attaching to multiple collagen fibers. A small fraction (∼10%) of loosely embedded polystyrene particles, likely falling in the space between ECM fibers, are excluded from further measurements. Fig. 1(A and B) show typical microscopy images of a tumor diskoid over 24 hours of invasion. We culture the diskoid in a gridded culture dish, so that microscopy images at different magnifications or at different days can be correlated. Fig. 1C shows a confocal reflection image of the collagen matrix with the bright spots indicating the location of the microspheres. The microspheres uniformly distribute in the ECM. After imaging the diskoid and its ECM on a confocal microscope (Leica SPE), we bring the sample to a home-built holographic optical tweezers (HOT) setup where a high numerical aperture objective lens (100×, NA = 1.4) is used to image and optically manipulate the microspheres as probing particles to measure the ECM micromechanics.29We choose probing particles at distances less than the radius of the diskoids (Rs ≈ 800 μm, Fig. 2A), where significant cell-induced ECM deformation is observed. The particles are illuminated by a partial coherent light source, which produces concentric diffraction patterns for high resolution particle tracking.36
In each measurement, we project optical traps to perturb the probing particle while a nearby unperturbed particle serves as a reference for drift correction (Fig. 2B). Specifically, the probing optical trap is projected at four locations each 1 μm away from the equilibrium position of the particle. The four trap locations are directed radially or tangentially from the diskoid center, which we label as extension (radially outward), compression (radially inward), and shear (tangential) directions. When switching between different microscopes (confocal and HOT), we use the grids printed at the bottom of the culture dish as alignment markers to determine the appropriate local axis with respect to the tumor diskoid.
In order to minimize the measurement error due to mechanical drift and other sources of noise, we cycle the probing trap in the four directions and repeat 15 times. Along each direction, the power of the optical traps is switched on and off for 0.5 seconds. During the whole process, positions of the reference and probing particles are tracked at a rate of 20 Hz (Fig. 2C), such that the particle displacement in response to optical forces, and the ECM micromechanics derived thereafter, are obtained by averaging reference-corrected particle positions for each probing location (Fig. 2D). The particle displacement generally has an off-axis component, and shows strong variations between different probing directions. These phenomena are related to the disordered nature of the ECM structure, and are consistent with previous reports of micromechanical measurements in cell-free matrices.29 The on-axis displacements, such as Δdshr as shown in Fig. 2D, will allow us to compute the local mechanical modulus. Note that to account for the finite particle response time to optical forces, we exclude particle trajectories at the boundaries of each power cycle (4–6 frames) when computing the average particle displacements.
ECM micromechanics is remodeled by invading tumors
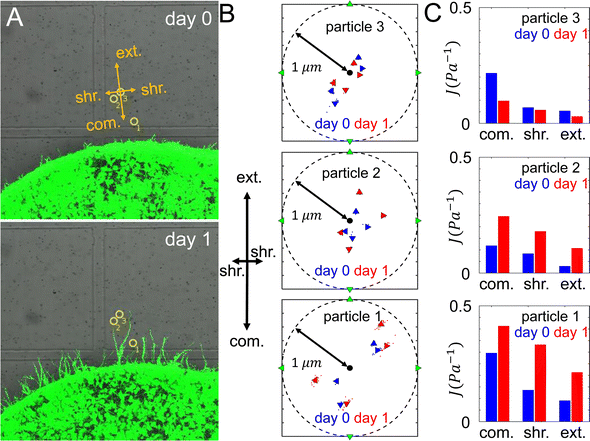
To quantify the ECM micromechanical remodeling by an invading tumor, we first focus on micromechanics measured by the same set of particles over 24 hours of invasion. Fig. 3A shows three probing particles with distances ranging between 80 μm and 180 μm to the boundary of a diskoid. For each particle, we project optical traps in the extension, compression and shear directions with respect to the diskoid, and obtain the reference-corrected displacements. Note that the off-axis displacements and anisotropy are evident for all three particles.Along each probing direction, we calculate the directional compliance:
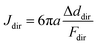 | (1) |
The directional compliance reported by the three particles are significantly different from each other. For instance particle 1 measures a local compression compliance of 0.3 Pa−1 at day 0, corresponding to a local stiffness of 3.3 Pa. This is almost three times softer than the compression modulus reported by particle 2. On the other hand, the micromechanics measured by particle 3 is stiffest in the shear direction, while particles 1 and 2 show the micromechanics are most stiff in the extension direction. The temporal evolution also differs for the three particle locations: while particles 1 and 2 show ECM softens in all directions from day 0 to day 1, particle 3 exhibit the opposite trend. In fact, the ECM at particle 2 is softened by more than doubling the compliance, while its nearby particle 3 shows modest stiffening after 24 hours of diskoid invasion. These results highlight the heterogeneity of ECM micromechanics, which would be elusive if we only had the information of bulk rheology.
Computational modeling of ECM micromechanics surrounding an invading tumor
In order to test putative physical mechanisms contributing to the ECM micromechanical remodeling, we employ a nonlinear model of the ECM network,37 in which the structure of the network is represented as a disordered 3D graph. The bonds represent fiber segments and the nodes in the graph represent cross-links. The graph was reconstructed from confocal images of 2 mg ml−1 collagen,37,38 corresponding to an average bond length of ∼1.8 μm. Upon stretching, a fiber segment (bond) first elongates elastically, which is followed by strong strain-hardening once the elongation is larger than a prescribed threshold. Upon compression, the fiber buckles and possesses a much smaller compression modulus. The elongation stiffness k of the fiber is accordingly given by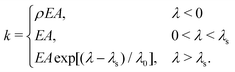 | (2) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /
/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the elongation strain, and λs = 0.02 and λ0 = 0.05 are parameters for the strain-hardening model;39ρ = 0.06 describes the effects of buckling.40 This model has been validated to realistically capture the mechanical behaviors of collagen networks in response to cellular forces.16,22,37 In its current form, we do not explicitly consider the time-dependent behaviors of the fibers, such as creep and plasticity.
is the elongation strain, and λs = 0.02 and λ0 = 0.05 are parameters for the strain-hardening model;39ρ = 0.06 describes the effects of buckling.40 This model has been validated to realistically capture the mechanical behaviors of collagen networks in response to cellular forces.16,22,37 In its current form, we do not explicitly consider the time-dependent behaviors of the fibers, such as creep and plasticity.
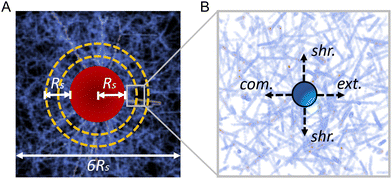
We model a diskoid embedded in the ECM as a short cylinder with radius Rs = 250 μm and height h = 80 μm and with the height along the z axis. The cylinder is placed at the center of a representative volume element (RVE) with dimensions 1500 μm × 1500 μm × 400 μm along x, y, and z direction respectively (see Fig. 4A). Although the simulation system is smaller compared to the experimental system due to computational cost, we expect the system size is sufficiently large to obtain at least qualitative insights of the physics behind the experimental observations. The contraction of the diskoid pulls the nodes residing within the diskoid region (i.e., the cylinder) towards the center along the radial direction, which is modeled by an affine transformation with a contraction ratio γ. In the subsequent simulations, we use γ = 0.93, as calibrated from experimental imaging data. After diskoid contraction, a force-based relaxation method is employed to obtain the force-equilibrium network configuration and resolve the forces on each fiber.37
The micromechanical compliance is measured following a similar but slightly different procedure used in the experiment. Specifically, spherical beads of radius a = 1.5 μm are randomly introduced in the ECM, one at a time. A bead is subsequently displaced along the extension, compression and shear directions by Δddir = 1 μm. We also investigate Δddir = 0.1 μm and 0.01 μm and verify the obtained directional compliance values are not sensitive to ddir (see the ESI†). Under this fixed displacement condition, the total response force Fdir on the bead along the corresponding direction is obtained from the force-equilibrium network configuration. The corresponding compliance Jdir is then computed following eqn (1), see (Fig. 4B).
ECM micromechanical anisotropy resulting from the collective traction force of a tumor
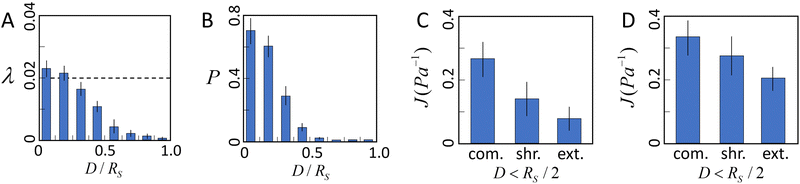
We first use the simulation to investigate the interplay of ECM nonlinear mechanics and the collective contractile force generated by a tumor. Fig. 5A shows the average elongation strain![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) of tensile fibers in the ECM as a function of D/Rs, where D is the distance to the tumor boundary, and Rs is the radius of the tumor. In the nonlinear fiber model, we consider fibers enter the strain-hardening regime once λ > λs = 0.02. It can be seen that in the vicinity of the tumor surface (e.g., D ≤ 0.2Rs),
of tensile fibers in the ECM as a function of D/Rs, where D is the distance to the tumor boundary, and Rs is the radius of the tumor. In the nonlinear fiber model, we consider fibers enter the strain-hardening regime once λ > λs = 0.02. It can be seen that in the vicinity of the tumor surface (e.g., D ≤ 0.2Rs), ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) > λs, indicating that the majority of tensile fibers in this region are in the strain-hardening regime. As D increases beyond this region,
> λs, indicating that the majority of tensile fibers in this region are in the strain-hardening regime. As D increases beyond this region, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) decreases quickly. However, as shown in Fig. 5B, there are still significant fractions of tensile fibers that are in the strain-hardening regime in the region with D < Rs/2.
decreases quickly. However, as shown in Fig. 5B, there are still significant fractions of tensile fibers that are in the strain-hardening regime in the region with D < Rs/2.
The average directional compliance obtained from simulations are shown in Fig. 5(C and D). It can be seen that in the near-tumor region (D < Rs/2), the directional compliance exhibits strong anisotropy. Specifically, the extension compliance is smaller than the shear compliance, and significantly smaller than the compression compliance. This equivalently indicates that the extension stiffness is larger than the shear stiffness, and much higher than the compression stiffness. This trend is a result of the strong strain hardening of tensile fibers in the region, which dominates the micromechanics. Specifically, when the probing bead is displaced in the tension direction, the tensile fibers already in the strain hardening regime are further pulled longer, leading to a strong and fast increasing response force, and thus, a high stiffness or low compliance. On the other hand, displacing the bead in the compression direction releases the tensile strain in the fibers, resulting in a much lower stiffness or higher compliance. Measuring the shear compliance amounts to pulling the tensile fibers sideways, with only a small component along the tensile direction, thus leading to a stiffness lower than the tension case, but higher than the compression case. A similar trend is observed in the far region (D > Rs/2), albeit the distinctions between the compliance (stiffness) are less apparent than those in the near-tumor region. This is because the strain hardening effects in the far region are significantly weaker (see Fig. 5B).
ECM degradation by cancer cells softens the ECM
Once the tumor invasion starts, cancer cells such as MDA-MB-231 cells secrete matrix metalloproteinase (MMPs) to degrade the ECM fibers and damage the structural integrity of network. This effect is likely reflected by the measured compliance for particles 1 and 2, for which the day 1 values of directional compliance Jdir are higher than the corresponding day 0 values (Fig. 3C). Here we use simulations to further verify this effect. In particular, for a given bead we first obtain Jdir as in the previous section. Subsequently, we set the fiber segments within δ = 2 μm along the line that connects the tumor center and the bead to have a much lower elongation stiffness than the original value, i.e., k = 0.01·EA, which also does not possess a strain hardening effect. This is to mimic the effects of ECM degradation by invasive cells that produce weak micro-channels in the ECM network. The values of Jdir are then computed again. We repeat the procedure for different beads in both near and far regions.Fig. 6 shows computed average Jdir along different directions in both near and far regions before (green bars) and after ECM degradation (red bars). It can clearly be seen that all Jdir increase after degradation, while the trend Jext < Jshr < Jcom is preserved. This is consistent with the experimental observations for particles 1 and 2 (see Fig. 3C).
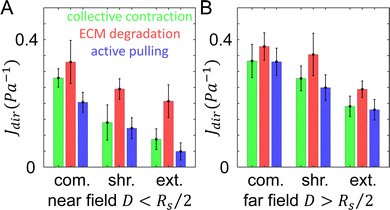 | ||
| Fig. 6 The directional compliance of the ECM from simulations. (A) Directional compliance Jdir along different directions in the near field with D < Rs/2, where D is the distance to the tumor boundary, and Rs is the radius of the tumor. (B) Directional compliance Jdir in the far field with D > Rs/2. Green: results by taking into account the collective contraction of the tumor (same as Fig. 5). Red: results when the tumor's collective contraction and ECM degradation are both considered. Blue: results when the tumor's collective contraction, ECM degradation and a nearby cell's active pulling are all considered. | ||
Active pulling by disseminated cancer cells stiffens the ECM
The directional compliance Jdir at particle 3 (Fig. 3C) exhibits very interesting behavior. Specifically, the values of Jdir on day 1 decrease compared to the corresponding values on day 0, indicating the ECM is locally stiffened. A closer examination of Fig. 3A reveals that on day 1, a branch of invading cell extends to the region near particle 3 (but not directly in front of the particle, as in the case of particle 2). As the cells at the invasion front lead the migration, they can generate contractile forces that reinforce the collective contraction of the tumor. Again we use simulations to verify this effect. For a given bead, we first obtain Jdir as in the previous section. Next, we embed a spherical cell of diameter 15 μm in a random location that is 10 μm away from the bead (as estimated from the imaging data). The cell is contracted by 15%, which pull the near-by fibers. The resulting Jdir are then computed and this procedure is repeated for all beads.Fig. 6 shows the computed mean Jdir along different directions in both near and far regions after additionally taking into account active pulling forces by nearby disseminated cancer cells (blue bars). It can be clearly seen that all Jdir decrease due to cell contraction, while the trend Jext < Jshr < Jcom is still preserved. This is consistent with the experimental observations for particles 3 (see Fig. 3C). Together, these simulation results demonstrate the effects of various mechanisms where the ECM micromechanics can be remodeled by both the whole tumor and individual disseminated cancer cells.
Further experimental verification of model predictions
Our computational model predicts several features in addition to the heterogeneity of the ECM micromechanics. To test these predictions experimentally, we leverage the precision shape control of the DIGME technique and accumulate data from multiple diskoids with the same radius. In particular, we perform micromechanical measurements on 10 diskoids at day 0 and another 10 at day 1. For each sample, we select approximately 10 probing particles with distances from the diskoid ranging from 100 to 700 μm, and close to the same focal plane as the diskoid center. We measure the local mechanics in the extension, compression and shear directions, and define the (mean) micromechanical compliance J as the average of Jdir in all four directions: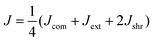 | (3) |
Our model predicts that ECM degradation by an invading tumor softens the surrounding ECM. This is the case for both directional compliance Jdir (Fig. 6) as well as the mean compliance J (Fig. 7A). Experimentally, we expect effects of ECM degradation to emerge after 24 hours of invasion. Consistent with the model prediction, the micromechanical compliance J measured at day 1 is generally softer than at day 0 (Fig. 7B). Interestingly, the measured J follow distributions exhibiting long tails, which appear to be distinct from the model calculation.
Our model also predicts that the ECM is stiffer in the extension direction than in the compression direction due to the collective contraction of the tumor, and the difference is less pronounced when ECM degradation takes place (Fig. 6). Experimentally, at day 0 we find Jcom > Jext in 75% of the instances. In contrast, only 45% measurements at day 1 show Jcom > Jext. These results again qualitatively agree with the model predictions.
Conclusion and discussions
The growth and metastasis of solid tumors involve significant mechanical remodeling of the surrounding tissue.41 Reciprocally, the altered tissue provides physical cues to the cancer cells through their mechanosensing pathways to modulate the cancer cell biology.42 Here we combine experiments and computational modeling to investigate mechanisms with which an invading tumor remodels the elastic properties of the extracellular matrix.In order to provide insights into physiologically relevant tissue mechanics at the cellular scale, we focus on the micromechanics, rather than the extensively studied bulk rheology of the ECM. To measure the ECM micromechanics, we employ holographic optical tweezers coupled with confocal microscopy (Fig. 1 and 2). We create in vitro models of solid tumors by forming breast cancer diskoids in 3D collagen ECM. The circular symmetry differentiates the tissue space outside of the tumor into compression, shear, and extension directions, along which we probe the ECM local elasticity, respectively. We find that the micromechanics of ECM surrounding an invading tumor demonstrate anisotropy in the directions probed, strong heterogeneity in space and also variations in time (Fig. 3). These results are difficult, if not impossible, to derive from bulk rheology alone. To our knowledge, detailed ECM micromechanics in proximity to a disseminating tumor has been a challenge to measure directly. We notice that the ECM micromechanical properties we have measured indicated a softer ECM compared to that suggested by a recent report of the active microrheology results.43 We suspect differences in the probing frequency and spatial statistics may contribute to the difference in the moduli measured via these two distinct techniques. This also indicates the important nonlinear dynamic-dependent micromechanics of the ECM, which should be taken into account for understanding its mechanical interaction with active cells. For future research it will be interesting to combine multiple micromechanical characterizations to better understand the physical properties of tumor associated ECM.
With a simple numerical model, we propose three independent and additive cellular mechanisms to account for the strong micromechanical heterogeneity observed in experiments. As we and other groups have reported previously, collective traction forces of the cells lead to global contraction of the ECM toward the tumor center.44 Models based on bulk rheology suggest that in regions close to the tumor ECM elastic moduli will increase due to the strain-stiffening effect.3 Our micromechanical model, on the other hand, predicts that the ECM is stiffened more in the extension direction compared to the compression direction (Fig. 5 and 6). This prediction is well supported by the experiments (Fig. 7).
Mesenchymal cancer cells, such as MDA-MB-231 cells generally execute MMP-dependent programs of 3D migration.45,46 During mesenchymal migration, cells secrete MMPs that degrade the ECM. Our model predicts and experiments confirm that ECM degradation softens the ECM micromechanics (Fig. 6 and 7). As individual cells further disseminate into the ECM, their traction force will actively pull on the nearby matrix, resulting in local stiffening. However, this latter effect depends on the location and orientation of the force-generating cell, and may further contribute to the level of heterogeneity and temporal variations in the ECM micromechanics.
While the predictions from our simplified model qualitatively agree with experiments, admittedly there are several notable discrepancies. For instance, the experimentally measured distribution of mean compliance J is approximately log-normal, which is broader compared with the distribution calculated from the model. Additionally, at day 1 of invasion only 45% of measured instances show Jcom > Jext, while the model predicts the compression compliance to be greater than extension compliance. The discrepancies could be attributed to a number of overlooked factors, such as the plasticity of the ECM at high strains,6 as well as the dynamic phases of cell migration and force generation.47 Recently, it was shown that MDA-MB-231 cells exhibit transitions between multiple migrational phenotypes.48,49 We expect the phenotypical plasticity further contributes to variations of cellular force generated and the stress state of the ECM. It is interesting for future research to include more detailed cellular dynamics and mechanosensivity in order to better model the physical interactions of invading tumors and their host tissue.50
Author contributions
Y. J. and B. S. initiated the research. A. N. conducted the experiments. Y. Z. and Y. J. constructed the computational model. All authors analyzed the data and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work is supported by the Department of Defense award W81XWH-20-1-0444 (BC190068) to A. N., the National Institute of General Medical Sciences award 1R35GM138179 to B. S. Y. Z. and Y. J. are supported by the National Science Foundation under grant no. 1916878.Notes and references
- P. Friedl and S. Alexander, Cell, 2011, 147, 992–1009 CrossRef CAS PubMed.
- H. Wang, A. S. Abhilash, C. S. Chen, R. G. Wells and V. B. Shenoy, Biophys. J., 2014, 107, 2592 CrossRef CAS PubMed.
- M. S. Hall, F. Alisafaei, E. Ban, X. Feng, C.-Y. Hui, V. B. Shenoy and M. Wu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14043–14048 CrossRef CAS PubMed.
- S. Nam, K. H. Hu, M. J. Butte and O. Chaudhuri, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5492 CrossRef CAS PubMed.
- S. Nam, J. Lee, D. G. Brownfield and O. Chaudhuri, Biophys. J., 2016, 111, 2296 CrossRef CAS PubMed.
- J. Kim, J. Feng, C. A. R. Jones, X. Mao, L. M. Sander, H. Levine and B. Sun, Nat. Commun., 2017, 8, 842 CrossRef PubMed.
- Q. Shi, R. P. Ghosh, H. Engelke, C. H. Rycroft, L. Cassereau, J. A. Sethian, V. M. Weaver and J. T. Liphardt, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 658–663 CrossRef CAS PubMed.
- W.-H. Jung, N. Yam, C.-C. Chen, K. Elawad, B. Hu and Y. Chen, Biomaterials, 2020, 234, 119756 CrossRef CAS PubMed.
- K. Wolf, Y. I. Wu, Y. Liu, J. Geiger, E. Tam, C. Overall, M. S. Stack and P. Friedl, Nat. Cell Biol., 2007, 9, 893 CrossRef CAS PubMed.
- C. Gaggioli, S. Hooper, C. Hidalgo-Carcedo, R. Grosse, J. F. Marshall, K. Harrington and E. Sahai, Nat. Cell Biol., 2007, 9, 1392–1400 CrossRef CAS PubMed.
- A. Glentis, P. Oertle, P. Mariani, A. Chikina, F. El Marjou, Y. Attieh, F. Zaccarini, M. Lae, D. Loew, F. Dingli, P. Sirven, M. Schoumacher, B. G. Gurchenkov, M. Plodinec and D. M. Vignjevic, Nat. Commun., 2017, 8, 924 CrossRef PubMed.
- D. Kim, P. P. Provenzano, C. L. Smith and A. Levchenko, J. Cell Biol., 2012, 197, 351 CrossRef CAS PubMed.
- R. Fernandez-Gonzalez, M. S. Simoes, J. C. Röper, S. Eaton and J. A. Zallen, Dev. Cell, 2009, 17, 736–743 CrossRef CAS PubMed.
- T. Lecuit, P. Lenne and E. Munro, Annu. Rev. Cell Dev. Biol., 2011, 27, 157–184 CrossRef CAS PubMed.
- H. Ahmadzadeh, M. R. Webster, R. Behera, A. M. J. Valencia, D. Wirtz, A. T. Weeraratna and V. B. Shenoy, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E1617–E1626 CrossRef CAS PubMed.
- J. Kim, Y. Zheng, A. A. Alobaidi, H. Nan, J. Tian, Y. Jiao and B. Sun, Biophysical J., 2020, 18, 1177 CrossRef PubMed.
- W. Kang, J. Ferruzzi, C.-P. Spatarelu, Y. L. Han, Y. Sharma, S. A. Koehler, J. A. Mitchel, A. Khan, J. P. Butler, D. Roblyer, M. H. Zaman, J.-A. Park, M. Guo, Z. Chen, A. F. Pegoraro and J. J. Fredberg, iScience, 2021, 24, 103252 CrossRef PubMed.
- Y. Yang, L. M. Leone and L. J. Kaufman, Biophys. J., 2009, 97, 2051–2060 CrossRef CAS PubMed.
- C. P. Broedersz and F. C. MacKintosh, Rev. Mod. Phys., 2014, 86, 995 CrossRef CAS.
- J. Feng, H. Levine, X. Mao and L. M. Sander, Soft Matter, 2016, 12, 1419–1424 RSC.
- I. Acerbi, L. Cassereau, I. Dean, Q. Shi, A. Au, C. Park, Y. Chen, J. Liphardt, E. Hwang and V. Weaver, Integr. Biol., 2015, 7, 1120 CrossRef CAS PubMed.
- Y. Zheng, H. Nan, Q. Fan, X. Wang, L. Liu, R. Liu, F. Ye, B. Sun and Y. Jiao, Phys. Rev. E, 2019, 100, 043303 CrossRef CAS PubMed.
- F. J. O'Brien, B. A. Harley, I. V. Yannas and L. J. Gibson, Biomaterials, 2005, 26, 433–441 CrossRef PubMed.
- B. M. Baker and C. S. Chen, J. Cell Sci., 2012, 125, 3015–3024 CAS.
- M. Proestaki, B. M. Burkel, E. E. Galles, S. P. Ponik and J. Notbohm, Soft Matter, 2021, 17, 10263 RSC.
- S. B. Lindström, D. A. Vader, A. Kulachenko and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051905 CrossRef PubMed.
- C. A. Jones, L. Liang, D. Lin, Y. Jiao and B. Sun, Soft Matter, 2014, 10, 8855–8863 RSC.
- B. Sun, Cell Rep. Phys. Sci., 2021, 2, 100515 CrossRef CAS PubMed.
- C. A. R. Jones, M. Cibula, J. Feng, E. A. Krnacik, D. H. McIntyre, H. Levine and B. Sun, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E5117 CrossRef CAS PubMed.
- J. Staunton, W. Vieira, K. Fung, R. Lake, A. Devine and K. Tanner, Cell. Mol. Bioeng., 2016, 9, 398 CrossRef CAS PubMed.
- Y. L. Han, P. Ronceray, G. Xu, A. Malandrino, R. D. Kamm, M. Lenz, C. P. Broedersz and M. Guo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4075–4080 CrossRef CAS PubMed.
- A. D. Doyle, N. Carvajal, A. Jin, K. Matsumoto and K. M. Yamada, Nat. Commun., 2015, 6, 8720 CrossRef CAS PubMed.
- D. G. Grier, Nature, 2003, 424, 810–816 CrossRef CAS PubMed.
- D. G. Grier and Y. Roichman, Appl. Opt., 2006, 45, 880–887 CrossRef PubMed.
- A. A. Alobaidi and B. Sun, Cancer Converge., 2017, 1, 1 CrossRef PubMed.
- R. Parthasarathy, Nat. Methods, 2012, 9, 724–726 CrossRef CAS PubMed.
- L. Liang, C. A. Jones, S. Chen, B. Sun and Y. Jiao, Phys. Biol., 2016, 13, 066001 CrossRef PubMed.
- H. Nan, L. Liang, G. Chen, L. Liu, R. Liu and Y. Jiao, Phys. Rev. E, 2018, 97, 033311 CrossRef CAS PubMed.
- J. Steinwachs, C. Metzner, K. Skodzek, N. Lang, I. Thievessen, C. Mark, S. Münster, K. E. Aifantis and B. Fabry, Nat. Methods, 2016, 13, 171–176 CrossRef CAS PubMed.
- J. Notbohm, A. Lesman, P. Rosakis, D. A. Tirrell and G. Ravichandran, J. R. Soc., Interface, 2015, 12, 20150320 CrossRef PubMed.
- M. Egeblad, M. G. Rasch and V. M. Weaver, Curr. Opin. Cell Biol., 2010, 22, 697 CrossRef CAS PubMed.
- M. Amer, L. Shi and H. Wolfenson, Cancers, 2021, 13, 4754 CrossRef CAS PubMed.
- A. Jagiełło, M. Lim and E. Botvinick, APL Bioeng., 2020, 4, 046105 CrossRef PubMed.
- A. A. Alobaidi, Y. Xu, S. Chen, Y. Jiao and B. Sun, Phys. Biol., 2017, 14, 045005 CrossRef PubMed.
- K. E. Fisher, A. Sacharidou, A. N. Stratman, A. M. Mayo, S. B. Mayo, S. B. Fisher, R. D. Mahan, M. J. Davis and G. E. Davis, J. Cell Sci., 2009, 122, 4558–4569 CrossRef CAS PubMed.
- R. J. Petrie and K. M. Yamada, J. Cell Sci., 2012, 125, 5917–5926 CrossRef CAS PubMed.
- K. Vaidžiulyte, A.-S. Macé, A. Battistella, W. Beng, K. Schauer and M. Coppey, eLife, 2022, 11, e69229 CrossRef PubMed.
- C. z Eddy, H. Raposo, A. Manchanda, R. Wong, F. Li and B. Sun, Sci. Rep., 2021, 11, 20434 CrossRef CAS PubMed.
- J. Kim, Y. Cao, C. Z. Eddy, Y. Deng, H. Levine, W.-J. Rappel and B. Sun, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024780118 CrossRef CAS PubMed.
- X. Chen, D. Chen, E. Ban, K. C. Toussaint, P. A. Janmey, R. G. Wells and V. B. Shenoy, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116718119 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01100j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |