Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Diversity of viscoelastic properties of an engineered muscle-inspired protein hydrogel†
Anders
Aufderhorst-Roberts
 ab,
Sophie
Cussons
ab,
Sophie
Cussons
 cd,
David J.
Brockwell
cd,
David J.
Brockwell
 cd and
Lorna
Dougan
cd and
Lorna
Dougan
 *bc
*bc
aDepartment of Physics, Centre for Materials Physics, University of Durham, Durham, DH1 3LE, UK
bSchool of Physics and Astronomy, University of Leeds, Leeds, LS2 9JT, UK. E-mail: l.dougan@leeds.ac.uk
cAstbury Centre for Structural Molecular Biology, University of Leeds, Leeds, UK
dSchool of Molecular and Cellular Biology, Faculty of Biological Sciences, University of Leeds, Leeds, LS2 9JT, UK
First published on 28th March 2023
Abstract
Folded protein hydrogels are prime candidates as tuneable biomaterials but it is unclear to what extent their mechanical properties have mesoscopic, as opposed to molecular origins. To address this, we probe hydrogels inspired by the muscle protein titin and engineered to the polyprotein I275, using a multimodal rheology approach. Across multiple protocols, the hydrogels consistently exhibit power-law viscoelasticity in the linear viscoelastic regime with an exponent β = 0.03, suggesting a dense fractal meso-structure, with predicted fractal dimension df = 2.48. In the nonlinear viscoelastic regime, the hydrogel undergoes stiffening and energy dissipation, indicating simultaneous alignment and unfolding of the folded proteins on the nanoscale. Remarkably, this behaviour is highly reversible, as the value of β, df and the viscoelastic moduli return to their equilibrium value, even after multiple cycles of deformation. This highlights a previously unrevealed diversity of viscoelastic properties that originate on both at the nanoscale and the mesoscopic scale, providing powerful opportunities for engineering novel biomaterials.
Introduction
Hydrogels are hydrated three-dimensional networks with significant potential in applications that involve the repair and replacement of biological tissue.1 A desired aspect of their design is that they mimic the material properties of the tissue that they are designed to replace. The ability to emulate biomechanical properties such as toughness, strain-stiffening and mechanical memory is therefore an important scientific challenge, particularly for applications involving cell growth and proliferation.2 The design challenges to recreate these properties are significant since materials must be sufficiently soft to allow cell proliferation and sufficiently stiff to protect the material from large and sudden deformations.3 In living matter, this trade-off is enabled by the unique mechanical properties of biopolymers and their ability to increase their stiffness when deformed and to accommodate large strains through force induced unfolding.4 Discovering approaches that can recreate these properties in synthetic materials remains highly challenging.An increasingly promising approach to address this challenge is to construct chemically crosslinked hydrogels from folded proteins.5–8 In nature, protein domains have precise structures which change their conformation under precise chemical and mechanical conditions. When engineered as polyproteins, their relatively small molecular size (∼10–100 kDa) distinguishes them from conventional biopolymers, however w hen crosslinked into hydrogels, polyproteins exhibit impressive mechanical properties such as high elasticity9 and resilience.6 These properties can be controlled through chemical stimuli,10,11 which suggests they may be used in applications involving shape change and shape programming.7,12,13 Their use is further advantageous since the molecular mechanics of folded protein domains have been extensively interrogated using force spectroscopy14–16 and can be correlated to bulk viscoelasticity.17,18
All hydrogels are intrinsically cross-length scale materials; however, most studies of folded protein hydrogels have focused only on the molecular scale mechanics of the protein and on the bulk properties of the resulting hydrogel. Recent findings from our group have shown that structural parameters at the meso-scale may also be of importance. These include the intermediate structural hierarchy including cross-linking,19–21 which can be used to modulate the network growth and force distribution of percolating clusters.22,23 This rich hierarchy of structural properties indicates that polyprotein hydrogels are likely to exhibit complex viscoelastic behaviours, which should manifest themselves in their mechanical response. Relating this mechanical response to the underlying structure can be achieved through shear rheology, since the time-dependent viscoelasticity of the hydrogel directly reflects the length scale of the hydrogel structure.24 However, most studies of polyprotein hydrogels have instead used dynamic mechanical analysis (DMA), which is instructive for quantifying bulk elastic properties such as toughness and failure stress but less effective in quantifying viscoelastic and structural properties. In comparison to shear rheology, DMA may also induce volumetric sample changes at high strains, which may frustrate accurate interpretation of the data.25 However, a multi-modal rheological characterisation of polyprotein hydrogels that relates time-dependent viscoelasticity to underlying structure has yet to be carried out.
In this study, we seek to bridge the gap between the molecular and bulk mechanics of folded protein hydrogels, using shear rheological tests to probe their meso-scale mechanics. We construct hydrogels using I275 polyproteins, so called because they comprise five concatenated I27 immunoglobulin domains of the muscle protein titin. Titin is an elastomeric component of the sarcomeres of striated muscle, where its I27 domains are able to unfold and refold to prevent overstretching.26 Reflecting this biological role, the I27 protein possesses mechanical stability whereas other domains in titin extend with low resistance. It also possesses a high degree of mechanical reversibility,27,28 as well as being suitable for crosslinking into a hydrogel using photochemical approaches.29 This makes it a putative robust and tough polyprotein and an excellent candidate for this study. We probe I275 hydrogels through frequency-dependent small amplitude oscillatory shear, stress relaxation and strain ramp experiments, to probe the viscoelastic properties at a range of timescales and within different regimes of deformation. By combining these different modes of rheology, we present a comprehensive rheological analysis of I275 hydrogels that infers their meso-scale structure, reveals how this structure relates to viscoelasticity and explores how this viscoelasticity determines the nonlinear and failure mechanics of the hydrogel.
Methods
Polyprotein purification
The assembly of I275 polyproteins was performed using a PCR-based Golden Gate protocol with a modified pET14b, with all original BsaI sites removed, as the destination expression vector.30 After verification of the DNA sequence, the resulting vector was transformed into BLR (DE3) pLysS E. coli cells. 2 mL LB starter culture was used to inoculate 0.5 L autoinduction medium. 10 × 0.5 L cell cultures were incubated at 28 °C, 200 rpm for 24 h, for protein expression and then harvested and lysed. The protein was loaded on to 2 × 5 mL HisTrap FF columns (Cytiva) for Ni2+ affinity chromatography. The column was then equilibrated in wash buffer (20 mM Tris, 300 mM NaCl, 10 mM imidazole, pH 8), before the protein was eluted with elution buffer (20 mM Tris, 300 mM NaCl, 500 mM imidazole, pH 8), in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to wash buffer. The protein was further purified using a 5 mL HiTrap DEAE Sepharose FF ion exchange chromatography column (Cytiva) for ion exchange purification. A gradient elution of 0–100% elution buffer (25 mM sodium phosphate pH 7.4, 0–500 mM NaCl) was performed over 300 mL. The protein was then purified by size exclusion chromatography (HiLoad 26/600 Superdex 75 pg, Cytiva) and eluted in 25 mM sodium phosphate, pH 7.4. The purified protein was dialysed into MilliQ water and freeze-dried for storage at −20 °C.
3 to wash buffer. The protein was further purified using a 5 mL HiTrap DEAE Sepharose FF ion exchange chromatography column (Cytiva) for ion exchange purification. A gradient elution of 0–100% elution buffer (25 mM sodium phosphate pH 7.4, 0–500 mM NaCl) was performed over 300 mL. The protein was then purified by size exclusion chromatography (HiLoad 26/600 Superdex 75 pg, Cytiva) and eluted in 25 mM sodium phosphate, pH 7.4. The purified protein was dialysed into MilliQ water and freeze-dried for storage at −20 °C.
Hydrogel preparation
I275 was re-suspended in 25 mM sodium phosphate, pH = 7.4 and placed on a rotary wheel for a minimum of 1 h to enable complete dissolution of protein. The suspensions were then centrifuged for 10 minutes at 5000 RCF, retaining the supernatant to ensure that any insoluble protein was removed. Protein concentration was measured by absorption at 280 nm, using an extinction coefficient of 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 M−1 cm−1. The final suspension was then diluted and mixed with an assembly buffer of tris(2,2′-bipyridyl)-dichlororuthenium(II) hexahydrate (Ru(BiPy)3) and sodium persulfate (NaPS) directly before use, with final concentrations of 0.38 mM I275, 100 μM Ru(BiPy)3 and 10 mM NaPS. Sample gelation was initiated photochemically through 60 seconds of in situ illumination with a 460 nm light emitting diode as previously described.31 The illumination intensity was calibrated to 40 mW cm−2 at 452 nm.
824 M−1 cm−1. The final suspension was then diluted and mixed with an assembly buffer of tris(2,2′-bipyridyl)-dichlororuthenium(II) hexahydrate (Ru(BiPy)3) and sodium persulfate (NaPS) directly before use, with final concentrations of 0.38 mM I275, 100 μM Ru(BiPy)3 and 10 mM NaPS. Sample gelation was initiated photochemically through 60 seconds of in situ illumination with a 460 nm light emitting diode as previously described.31 The illumination intensity was calibrated to 40 mW cm−2 at 452 nm.
Shear rheology
Rheology measurements were performed using a stress-controlled rheometer (Kinexus Malvern Pro) equipped with a 10 mm steel plate and plate geometry. The lower plate of the rheometer was replaced with a custom-built photodiode module which allowed the photochemical crosslinking to be carried out in situ. Further details of the design and calibration of this device can be found in our previous work.31 To prevent the evaporation, low viscosity (5 cSt) mineral oil was applied to the air-sample interface. All measurements were performed at 25 °C and 2 hours after crosslinking. For all measurements, rheology data was captured over at least 3 measurements on independently prepared samples.Small amplitude oscillatory measurements
All small amplitude oscillatory measurements were carried out at a strain amplitude of 1% – comfortably within the linear viscoelastic regime for all samples studied. Time dependent measurements were carried out at an angular frequency of 6.28 s−1 unless otherwise stated. All frequency sweeps were carried within a range of 0.0628–62.8 rad s−1. At high frequencies, artifacts from instrument inertia were avoided by discounting all data points for which the phase angle exceeded 150°. The duration of individual frequency sweeps was between approximately 20–35 minutes. The possible influence of sample ageing was investigated by carrying out repeated frequency sweeps in both ascending and descending frequencies, and no discernible difference was found. Power law fitting of frequency sweep data was carried out using Matlab's curve fitting toolbox.Cyclic loading measurements
Cyclic loading experiments were performed to probe the mechanical response of the polyprotein hydrogel to large deformations and to examine the effect of multiple deformations on the hydrogel mechanics. Following crosslinking, the sample was subjected to a shear strain pulse of loading rate 0.01 s−1. After each pulse, the sample was left to recover for 23 min, during which time a single oscillatory frequency sweep was carried out to assess any permanent changes to material properties. The process was then repeated with incrementally increasing strain pulse magnitudes.Stress relaxation
Stress relaxation experiments were carried out by applying a step strain to the sample for 10 min. The resulting relaxation in stress over time was fitted to a range of different constitutive models using the Rheology Open Source (RHEOS) software.32,33 A constant applied strain was typically attained within 2–3 s and any data from before this point were discarded from the analysis. For clarity, stress relaxation plots were normalised by σ0, the stress at t = 1 s, extrapolated from the fitted curves.Circular dichroism
Circular dichroism (CD) measurements were performed on an Applied Photophysics Chirascan CD spectropolarimeter using 0.01 mm path length cuvettes at a concentration of 0.5 mM. Samples were gelled inside the cuvette through photochemical crosslinking using identical buffers and the same protocol to that used in shear rheology experiments. Samples were also probed at higher dilution (5 μM), in which case the protein was probed in a phosphate buffer without crosslinking agents (25 mM sodium phosphate, pH = 7.4) in a 1 mm path length cuvette. Each measurement was averaged over 1 s and any data points for which the photomultiplier tube voltage (HV) exceeded 600 V were not included in the analysis. A minimum of 4 independently prepared samples were used for each measurement to ensure reproducibility. Standard deviations did not exceed 10% of the mean value.Results
I27 protein structure is retained following crosslinking
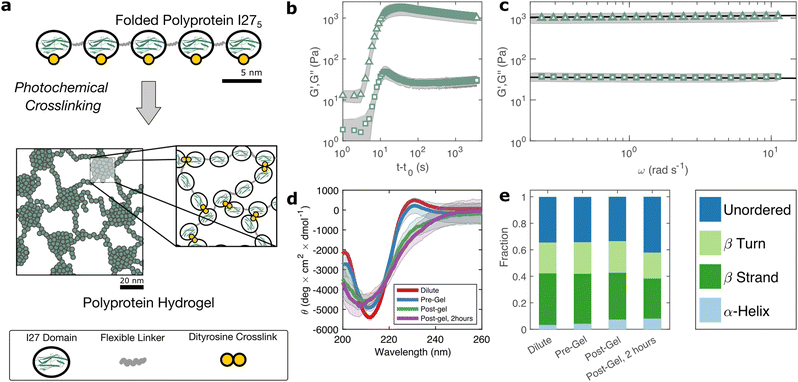
The I275 polyprotein comprises five sequential repeats of the I27 as shown in Fig. 1(a). The I27 polyproteins are assembled into hydrogels using the well-known ruthenium crosslinking strategy,34 which causes tyrosine residues on the surface of the polyproteins to radicalise and form dityrosine linkages under illumination of visible light and in the presence of sodium persulfate. Each polyprotein has five native tyrosine sites which are retained in the polyprotein design. The polyprotein also contains a hexahistidine repeat at its N-terminus and a dicysteine residue at its C-terminus, both of which are known to crosslink under the same conditions, albeit at lower efficiency.35 Therefore the polyprotein can be said to possess 7 potential crosslinking sites. The sodium persulfate that drives the crosslinking reaction is present at an approximately 4× stoichiometric excess to the potential crosslink sites to maximise the crosslinking efficiency.To probe this crosslinking process, we carry out small amplitude oscillatory shear measurements, probing the storage (G′) and loss (G′′) moduli of the sample during in situ illumination at time t = t0. As plotted in Fig. 1(b) there exists a short lag time before a sharp increase is observed in both G′ and G′′. In a recent study of BSA hydrogels we showed that this lag time31 is strongly indicative of a two-step nucleation and growth process, in which diffusion-limited pre-gel clusters mature towards eventual percolation. Although the intensity of light and the stoichiometric ratio are similar to this previous study, the observed lag time is significantly shorter (∼3 s) for I275 than for BSA (∼30 s).
The value of G′ and G′′ both increase sharply following the lag phase, reaching a peak of 1.7 ± 0.6 × 103 Pa after approximately 30 s, before undergoing a steady decrease and reaching a final G′ of 1.0 ± 0.3 × 103 Pa, after approximately 1 hour. To examine the possible molecular origins of this decrease in moduli, we carry out CD spectroscopy across each stage of the crosslinking process as shown in Fig. 1(d). Before crosslinking the mean residue ellipticity spectrum indicates an anti-parallel β-sheet structure which, in I27, is typically characterised by a negative band at 211 nm.36 A slight positive band can also be seen close to 230 nm, which reflects exciton coupling between aromatic residues.37,38 Compared with the spectra of dilute uncrosslinked I275, there is a close alignment (<10% difference in peak at 211 nm) indicating that the protein remains largely stable at the increased concentrations used for gelation, while the magnitude of the 211 nm band (5.4 ± 0.2 × 103 deg cm2 dmol−1) is comparable to previous studies of I275. Following photochemical crosslinking, the peak intensity reduces and shifts to a lower wavelength, which may indicate a decrease in the folded protein fraction. Assuming that the 211 nm peak intensity is directly proportional to the fraction of folded protein, we estimate a reduction in folded fraction of I275 of 7%. The 230 nm peak is also reduced, presumably due to the conversion of the aromatic tyrosine residues into dityrosine residues during crosslinking. Overall, this indicates a slight reduction in the folded fraction of I275. To investigate this further, we deconvoluted the CD spectra using the CONTINLL parameter set in Dichroweb,39 using protein reference set 4 (optimised for 190–240 nm). As shown in Fig. 1(e), Table 1, and Fig. S4 (ESI†) there is a slight reduction in β-sheet fraction and β-turn fraction and an increase in the proportion of the protein that is unordered. Taking this as being indicative of protein unfolding under gelation, we estimate a decrease in the fraction of folded protein of approximately 12%, which takes place in the 2 hours following gelation, the same time over which a decrease in G′ and G′′ is observed. A similar reduction in folded fraction that coincides with a decrease in G′ and G′′ has previously been observed for other folded protein hydrogels studied in our group,22,23,31 which suggests that it is a general feature of folded protein hydrogels, where it is caused by forced unfolding of weak protein domains on the molecular-scale as the hydrogel network forms.
| β-Strands | β-Turns | Unordered | |
|---|---|---|---|
| Dilute (5 μM) | 0.39 | 0.23 | 0.34 |
| Pre-crosslink | 0.38 | 0.24 | 0.34 |
| Post-crosslink | 0.35 | 0.24 | 0.34 |
| Post-gel, 2 hours | 0.30 | 0.20 | 0.42 |
Frequency sweeps are consistent with a fractal network structure
Rheological frequency sweeps (Fig. 1(c)) show that the equilibrated hydrogels are predominantly elastic in nature, with a storage modulus G′ that is over an order of magnitude higher than the loss modulus G′′ across all probed frequencies. Frequency sweeps reflect the distribution in timescales of the underlying relaxation mechanisms in the hydrogel. For our I275 hydrogels we find that the frequency dependence of G′ and G′′ are well-described by weak power law relationships (solid lines in Fig. 1(c)). Averaging over data from five independent samples of we calculate the exponent β = 0.027 ± 0.03. The estimation error of the fit can be calculated from the confidence interval of the averaged frequency sweep and is found to be ±4 × 10−4 indicating that the power law accurately describes the rheological response of the hydrogel. The high quality of the fit can be further evidenced by the observation that all fit residuals comfortably lie within one standard deviation of the data (Fig. S2, ESI†).The physical origin of power law viscoelasticity in soft and biological materials remains a matter of debate40 but it is often associated with fractal structure. The diversity of soft structured systems that display power law rheology strongly suggests that power law rheology does not only arise from fractal structure, however small angle scattering data from our group, has shown that fractal structures are a common feature of photo-chemically crosslinked folded protein hydrogels22,23 including hydrogels formed from I275.29 We have also shown that these fractal structures arise from the diffusion- and rate-limited crosslinking of constituent folded proteins31 and in situ protein unfolding.22,23
The emergence of a power law relaxation spectrum can be rationalised by considering that a fractal hydrogel network has a self-similar structure and consequentially will exhibit self-similar relaxation dynamics.41 Assuming that the excluded volume interactions are screened, this allows the fractal dimension df of the hydrogel network to be directly calculated using the following previously derived24 relation:
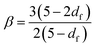 | (1) |
Hydrogel structure is responsive to deformation
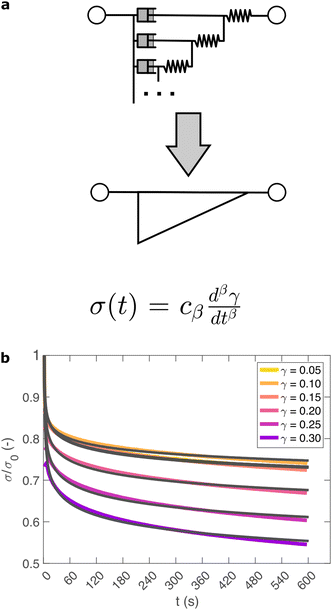
So far, we have identified that the relaxation spectrum of an I275 hydrogels can be functionally fitted to a power law model, with exponent β −0.02. This value of β is somewhat low in comparison to other soft and biological structured systems. For example cells, d have power law exponents as low as 0.2–0.3,44,45 while tissues have exponents as low as 0.1,46 and viscoelastic interfaces have exponents as low as 0.1.47 A low power law exponent indicates a very broad spectrum of relaxation times, which must be treated with caution in absence of independent verification. Such verification can best be carried out through combining different modes of rheology.40 To independently verify the validity of this exponent, we carry out a series of stress relaxation experiments, in which a step strain is applied to the sample and the sample's shear stress decays over time. This approach avoids the changes in sample strain that are inherent to creep measurements while also probing a longer range of timescales than oscillatory frequency sweeps. We probe the extent of the linear viscoelastic regime through a shear strain ramp (Fig. S5, ESI†), which confirms that the linear viscoelastic regime corresponds to γ < 0.1, with only a slightly nonlinear response at higher strains (γ < 0.3). While the exponent β is easily extracted from the frequency sweeps, extracting it from relaxation data requires a mechanical constitutive modelling approach. Here, elements of Hookean elasticity (springs) and Newtonian viscosity (dashpots) are combined in an empirical manner to approximate the viscoelastic response. In many materials, a finite number of such elements are sufficient,48 however for power law viscoelasticity the spectrum of relaxation times is broad and hence the approach requires a large number of fitting parameters making it unsuitable.49 To address this, we use a so-called fractional rheological model, which captures power law rheology using a minimal number of fitting parameters. This is achieved by reducing an arbitrary large number of springs and dashpots (Fig. 2(a)) to a single mathematical element commonly known as a springpot model50 with two fitting parameters β and cβ. The parameter cβ, is often referred to as a quasi-property49 since its SI units (Pa sβ) contain a power law exponent. From a practical perspective cβ can most simply be conceptualised as referring to the ‘firmness’ or ‘strength’ of the material.51 The springpot model describes stress relaxation σ(t) following an applied step strain γ over a measurement timescale t as: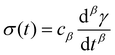 | (2) |
As shown in Fig. 2(b), eqn (2) provides an excellent fit to the stress relaxation data, both within the linear viscoelastic regime (γ < 0.1) and even for the nonlinear regime (0.1 < γ < 0.3). At low strains (γ < 0.15) the relaxation curves approximately overlay, accounting for experimental noise, which is consistent with linear viscoelasticity. For step strains that exceed 0.3 (Fig. S6, ESI†) we consistently observe an instantaneous decrease in stress during the measurement, suggesting that the sample undergoes irreversible failure. The fitted parameters β and cβ are shown in Fig. 3.
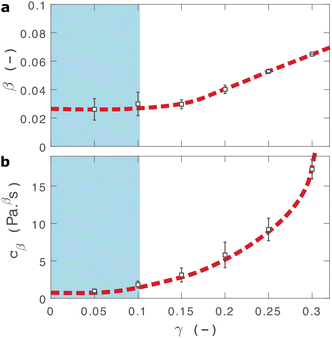 | ||
| Fig. 3 Fractional fit parameters extracted from applying eqn (2) to data in shown in Fig. 2. The shaded region indicates the linear viscoelastic regime. Dashed lines are guides for the eye. Error bars represent fits over multiple measurements. | ||
The fractional model provides an excellent fit to the relaxation data as demonstrated through plots of the fitting residuals (Fig. S7, ESI†), which show that all residuals are within one standard deviation of data, allowing for inertial errors at short timescales. We also attempted to fit several different variations of the two-component fractional model, incorporating different combinations of springs, dashpots and springpots arranged in series and in parallel in attempt to improve our model. The use of either fractional Maxwell model (two springpots in series, Fig. S8, ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57) or a modified power law model (springpot combined with a dashpot and spring, Fig. S9, ESI†
57) or a modified power law model (springpot combined with a dashpot and spring, Fig. S9, ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33) provide a poor fit to the data as both predict a plateau in σ(t) at long timescales. A fractional Kelvin Voigt model (two springpots in parallel, Fig. S10, ESI†) does provide a close fit to the data, however the additional parameters are degenerate to fitting.
33) provide a poor fit to the data as both predict a plateau in σ(t) at long timescales. A fractional Kelvin Voigt model (two springpots in parallel, Fig. S10, ESI†) does provide a close fit to the data, however the additional parameters are degenerate to fitting.
Within the linear viscoelastic regime, the value of β is independent of applied strain, as expected, and has an average measured value of 0.03 ± 0.01. This is in excellent agreement with the frequency spectra (β = 0.02), demonstrating that the power-law model accurately predicts the viscoelastic material properties of the I275 hydrogels, which are likely to originate from a cross length-scale fractal structure. Interestingly, the springpot model appears to provide an excellent fit to the relaxation data at strains that exceed the linear viscoelastic regime. The reasons for this are not immediately clear since the fractional model that we employ is only strictly valid for linear viscoelastic materials,58 although attempts have been made to extend it to nonlinear behaviour.46,59 It may be that the deviations from linear viscoelasticity for 0.1 < γ < 0.3 (Fig. S5, ESI†) are sufficiently minor so as not to invalidate the model. We find that cβ increases with strain, which suggests a strengthening of the hydrogel network. This, accompanied by an increase in β over the same range of applied strain, suggests progressive changes in network structure as the strain is increased. β reaches a maximum of approximately 0.065 for γ = 0.30, which using eqn (1), would correspond to a slight decrease in fractal dimension from df = 2.48 to df = 2.46. Assuming that our model is indeed valid at higher strains, we propose that this change may reflect the progressive unfolding of the constituent I27 domains as the applied strain is increased, leading to changes in the hydrogel network structure. At the same time, the increase in cβ would imply a strengthening or reinforcement of the network at increased strain. One explanation for this is that the polyprotein chains stiffen, by aligning with the direction of shear (leading to an increase in cβ) while simultaneously unfolding (leading to an increase in β).
Comparison can be made to a previous study by our group on crosslinked BSA hydrogels. In that study, the addition of a reducing agent resulted in breakage of covalent bonds within the BSA protein, resulting in a more force labile protein.22 Upon cross-linking, in situ protein unfolding was found to define the network architecture and mechanics, with regions of clusters of folded protein interconnected by unfolded protein. The study also noted an increase in the power law exponent when the disulphide bonds that prevent unfolding of the protein were broken through chemical reduction. Remarkably, the power law exponents before and after covalent bond breaking (0.027 ± 0.002 and 0.061 ± 0.001, respectively) are almost identical to the exponents at low and high strains measured here (0.03 ± 0.01 and 0.053 ± 0.001, respectively), providing further support for our hypothesis that the structural changes implied by our data arise from the force induced unfolding of individual protein domains.
Nonlinear mechanics indicate reversible alignment and unfolding of polyproteins
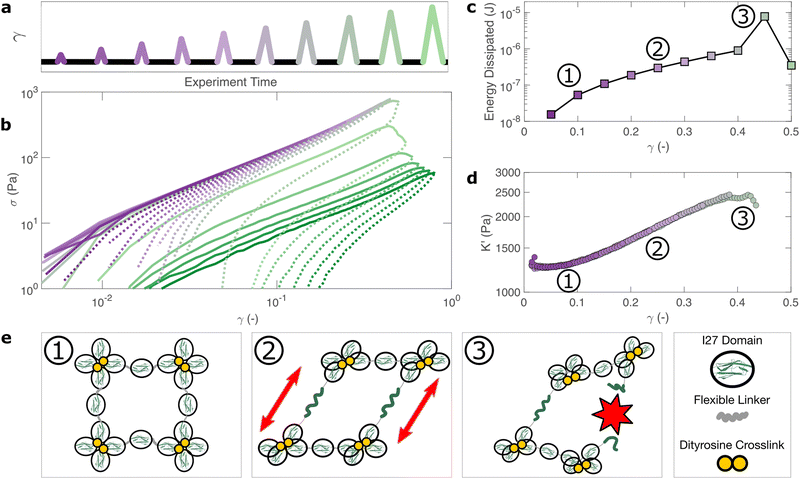
How do the structural properties of I275 hydrogels that we have encountered, change under deformation? Our relaxation data show intriguing clues that suggest network strengthening and unfolding under applied strain. To probe this independently we carry out nonlinear cyclic deformation experiments.60,61 As depicted in Fig. 4(a) and Fig. S11 (ESI†), the I275 polyprotein network is loaded and unloaded up to a threshold strain γmax through a triangular strain pulse at a constant shear rate and the magnitude of γmax is increased with each subsequent shear pulse.Within the linear viscoelastic regime, (γmax < 0.1) the loading and unloading curves (Fig. 4(a), solid and dashed lines respectively) appear to overlay closely suggesting a reversible and purely elastic response. However as γmax increases, a deviation between the loading and unloading curves begins to emerge. Calculating the energy loss in each cycle (Fig. 4(c)) from the ratio of the areas beneath the loading and unloading curves (see Methods), shows that inelastic energy dissipated during loading steadily increases with γmax. Furthermore, each subsequent loading curve appears to overlay with its predecessor, indicating that this inelastic dissipation does not bring about any permanent changes to the network stiffness. This complete reversibility of the network is unusual as most polymer networks that exhibit reversibility, such as filled rubbers62 and biological tissues also exhibit a well-defined residual cyclic softening. By contrast, we observe an almost perfect overlay between loading curves for strains up to γ = 0.4. The profile of the loading curves is also revealing of changes in hydrogel stiffness during deformation. For γ > 0.1, the stress σ required to increase the strain becomes progressively higher, indicating strain-stiffening.63 This can be most clearly seen in the evolution of the differential elastic modulus K′ with respect to strain (Fig. 4(d)), which increases approximately by a factor of 2 before the onset of rupture. As with the loading curves, the relationship between K′ and γ overlays closely across all curves, confirming that no softening takes place between loading cycles. Plotting K′ with respect to σ, reveals that the stiffening follows a power law relationship of K′ ∼ σn, where n = 0.6 is the stiffening index (Fig. S12, ESI†). Such power law stiffening is a general feature of semiflexible networks for which the distance between crosslink nodes is similar to the polymer persistence length and arises from the entropic resistance of thermal undulations against stretching.63 To assess whether our system can be considered to be semiflexible we carry out an analysis of the polyprotein dimensions (see Supplementary text, ESI†) which reveals that the distance between the crosslink sites is 5.44 nm. To calculate the persistence length of the polyproteins we draw on our previous computational calculations for a range of polyprotein dimensions.19 The most important parameter here is the ratio between the length of the linker domain and the radius of the globular domains, which for our dimensional analysis is ≈0.34. This corresponds19 to a persistence length in the range of ≈7–14 nm. Therefore, the persistence length and crosslink length are of the same order of magnitude and the polyprotein can be considered as semiflexible. For semiflexible networks it is expected that K′ ∼ σ1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 although exponents as low as 0.565 have been observed elsewhere and are thought to arise from inelastic effects such as crosslink unbinding or axial stretch.
64 although exponents as low as 0.565 have been observed elsewhere and are thought to arise from inelastic effects such as crosslink unbinding or axial stretch.
For our system, strain stiffening appears to occur concurrently with energy dissipation, which agrees with the stiffening and dissipation hypothesis that emerges from our relaxation data. From the strain ramp data, it seems likely that strain stiffening occurs due to the stretching of the constituent semiflexible polyproteins and that these polyproteins undergo force-induced unfolding concurrently (Fig. 4(e)).
Failure of polyprotein hydrogels is driven by structural adaption
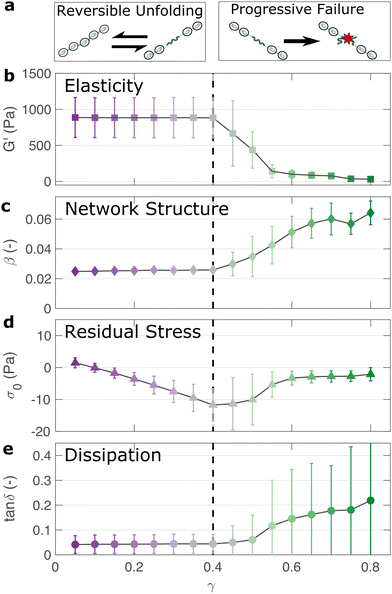
If the unfolding and refolding of I275 in the hydrogel is indeed reversible then how does the material failure, as observed from strains exceeding 0.4, take place? To investigate this further, we carry out oscillatory frequency sweep measurements after each of the triangular strain pulse measurements. Each frequency sweep therefore represents the linear viscoelastic properties of the hydrogel after each cycle of deformation. The profiles of the individual frequency sweeps of the hydrogels remain highly reproducible at pre-failure strains, (Fig. S15, ESI†) which is consistent with our previous observation that the deformations are fully reversible. At higher strains, the linear elastic modulus G′ begins to decrease (Fig. 5(a)). Over the same strain range, the power law exponent of the frequency sweeps β increases, (Fig. 5(b)) indicating permanent structural change, even after the removal of strain. At this final stage, the value β reaches 0.064 ± 0.008. Remarkably, this is identical to the maximum value of β measured through stress relaxation experiments (Fig. 3).The failure of biopolymer networks is a complex phenomenon that is challenging to model.66 In network-forming systems, the process of fracture typically occurs suddenly and is preceded by a dynamic microscopic changes.67 The eventual mechanism of fracture can originate from the dissociation of noncovalent bonds, the permanent rupture of covalent bonds, or both concurrently.68 We expect that covalent bond rupture is the most likely cause in our system since the hydrogels are covalently crosslinked. Furthermore, the high energy dissipation at γmax < 0.4 (Fig. 4) implies protein unfolding occurs pre-rupture. This observation is consistent with the unfolding forces of an I27 domain (∼0.2 nN27), which are lower than the typical rupture forces of a covalent bond (∼1–2 nN69 at a pulling speed of 10 nN s−1). One possible mechanism for failure is that as the polyprotein approaches a fully unfolded state, the tension that was previously directed to domain unfolding instead is applied to the unfolded polypeptide chain leading ultimately to irreversible peptide bond rupture. It is intuitive that such rupture would occur at the weakest bond in the chain, in this case a peptide bond in either the unfolded I27 domains or the linker region. Further evidence for the mechanism of rupture can be found by re-examining the strain pulse data in Fig. 4. Specifically, the stress required to return the hydrogel to zero strain after each pulse is denoted σ0 (shown diagrammatically in Fig. S13, ESI†). This represents the residual stress after each deformation cycle. σ0 is initially close to 0 and becomes more negative after each cycle until the onset of failure (Fig. 5(c)). Post failure, σ0 no longer becomes more negative, which may reflect the loss of tension in the network as the polyprotein chains rupture. The evolution of normal force after each loading cycle is also consistent with irreversible network remodelling (Fig. S14, ESI†). Here, the normal force decreases with increasing strain, as expected.70 However the residual normal force also increases after each cycle, indicating permanent remodelling before sharply increasing upon rupture. Finally, the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (Fig. 5(d)), which quantifies the relative viscous dissipation of the network in the form of the ratio between the elastic and viscous moduli, remains relatively low (≈0.2, at the highest values of γmax). Given that the chains are highly dissipative at high strains (Fig. 4(d)) and given the theoretical range of tan
δ (Fig. 5(d)), which quantifies the relative viscous dissipation of the network in the form of the ratio between the elastic and viscous moduli, remains relatively low (≈0.2, at the highest values of γmax). Given that the chains are highly dissipative at high strains (Fig. 4(d)) and given the theoretical range of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (0–1), a much higher dissipation would be expected if the polyprotein chains remained intact but unfolded. It is therefore likely that the network failure is determined by the reversible unfolding of the protein domains which, at significantly high tension leads to eventual bond rupture as shown diagrammatically in Fig. 5(e).
δ (0–1), a much higher dissipation would be expected if the polyprotein chains remained intact but unfolded. It is therefore likely that the network failure is determined by the reversible unfolding of the protein domains which, at significantly high tension leads to eventual bond rupture as shown diagrammatically in Fig. 5(e).
Discussion
In summary, we have applied a multi-modal rheology approach to interrogate the viscoelastic properties of folded protein hydrogels. Using these approaches, we highlight several important and previously unappreciated aspects of their material properties.Firstly, we determine that the viscoelasticity of I275 hydrogels can be accurately modelled by a simple two-parameter fractional viscoelastic constitutive model. This model manifests itself as a power law with a single exponent which is experimentally difficult to identify without validation using different approaches. Since such power laws would be challenging to computationally model due to the broad spectrum of relaxation times, we have instead compared two experimental rheological techniques and have observed the same power law behaviour in both the frequency response (Fig. 1(c) and Fig. S15, ESI†) and in the time-dependent stress relaxation response (Fig. 2). From a practical perspective, this indicates that hydrogel's stress relaxation is governed not by a single characteristic timescale but rather by a broad spectrum of timescales.
This is perhaps surprising as it suggests that the viscoelastic response of the hydrogel, at least within the linear viscoelastic regime, is not governed primarily by the narrow and well-defined unfolding timescale of the I27 protein domains when stretched axially.15 Instead the architecture of the hydrogel appears to result in a more complex spectrum of relaxation timescales, which likely arises from the orientation and arrangements of the protein domains. There are several possible mechanisms to explain this behaviour. Firstly, it could be argued that the formation of the hydrogel network causes partial unfolding, however we show a reduction of the fraction of folded protein of just 12% (Fig. 1). A more likely explanation is that the fractal structure of the hydrogel22,23,31 leads to a broad spectrum of relaxation modes, which reflects the broad spectrum of length scales within the network.71 One additional contributing factor could be the random alignment of the polyprotein chains within the hydrogel network in relation to the direction of shear deformation. In principle this could lead to changes in the relaxation timescales as the mechanical stiffness of folded proteins is known to depend on their pulling geometry.72 The broad spectrum of relaxation times we observe here appears to be common in polymeric systems,73 colloids,74 cells33,75 and tissues.76 Here, we show that this behaviour also extends to folded protein hydrogels.
Using a fractional viscoelastic model, we show that the power law exponent β is remarkably consistent between the oscillatory shear and stress relaxation experiments used in this study. Therefore, we may say that power law viscoelasticity is not an artifact of any particular technique but is instead an intrinsic property of the hydrogel and is likely to reflect the hydrogel's fractal structure. The small discrepancies we observe between model fits and experimental data are mostly accounted for by experimental noise and instrument artifacts (see Fig. S2 and S7, ESI†). Any remaining discrepancies could arise from changes in the crosslink probability over time as the hydrogel form due to the depletion of uncrosslinked protein, which would lead to variability in the power law exponent.77 Furthermore the value of the exponent β is also measured consistently after multiple cycles of deformation, indicating that this fractal structure is robust to perturbation. More surprisingly, our model also closely fits the relaxation response at larger deformations in the nonlinear viscoelastic regime (Fig. 3(a)). While our model is strictly valid only for linear viscoelasticity, we note that the fitted parameter β in this regime is close to the value of β as probed by oscillatory shear after the hydrogel failure. We speculate that this may be indicative of permanent changes to the hydrogel's structure at large deformations. Modelling this behaviour using more advanced constitutive modelling that accounts directly for nonlinear effects46,59 would an interesting topic of further study.
Within this nonlinear regime we observe that the hydrogel undergoes stiffening while subjected to shear strains, which is manifested both in relaxation data (Fig. 3(b)) and in strain ramp data (Fig. 4(d)). In line with predictions,19 this is consistent with the semiflexible nature of the polyprotein chain, a property that arises directly from the dimensions of the folded proteins. Recreating strain stiffening in synthetic hydrogels is a growing area of research78 and although the degree of stiffening is relatively low for this system (a twofold increase in modulus before failure) it is likely that a modification of the polyprotein dimensions could tune and enhance this behaviour further.
This strain-induced stiffening occurs at low strains, which corresponds to the onset of nonlinearity in stress relaxation experiments (Fig. 2) and to an observed increase in energy dissipation (Fig. 4(d)). Our relaxation data indicates an increase in the power law exponent β during deformation but notably there is no permanent changes to the hydrogel's viscoelasticity or β (Fig. 5), suggesting that the network structure is not significantly altered by repeated deformation. This stands in direct contrast to conventional rubber materials, in which the viscoelastic response from each subsequent deformation cycle is directly determined by the strain history of the sample.62 It is likely that this behaviour is a consequence of the I27 domain's propensity to re-fold upon removal of stress, since the same behaviour has been observed for hydrogels constructed from the similarly reversible GB1 domains.9 Nevertheless, our analysis of the repeated loading curves indicates that some stress accumulates in the network after each deformation cycle (Fig. 5(d)), which likely contributes to its eventual failure.
Finally, we wish to re-emphasise that the weak power-law rheology that we observe here is also commonly observed in biological tissue. Indeed, slow internal relaxation processes appear to be intrinsic to a broad range of living materials.46 The mechanical similarities between biological tissues and folded protein hydrogels are apparent and may provide further support for their potential applications in replacing and repairing living tissue.
Conclusions
We have shown that the viscoelastic response of I275 folded protein hydrogels is governed not only by the nanoscale molecular mechanics of the folded protein domains, as has commonly been assumed, but also by their meso-scale structure. Within the linear viscoelastic regime, the protein domains remain folded, and the response follows a characteristic power-law rheological behaviour. This is well described by a fractional viscoelastic model and most likely arises from the hydrogel's fractal structure. Fractal structure increasingly appears to be a general feature of folded protein hydrogels, which is evidenced by our previous findings using small angle scattering.5,22,29,31 We have recently developed a coarse-grained simulation approach to predict trends in mesostructure and porosity79 and a possible area of future research will be to directly image structural parameters such as the mesh size and porosity, for example through electron microscopy.At increased strains, nonlinear viscoelasticity is observed in the form of strain stiffening, which is accompanied by an increase in energy dissipation as the polyprotein chains align and unfold. This unfolding shows an excellent degree of reversibility, which affirms the ability of the constituent I27 domains to return to their folded confirmation upon removal of stress. Overall, we show that folded protein hydrogels exhibit a rich diversity of viscoelastic properties which reflect the hierarchy of length-scales, from their energy-dissipative properties (at the nanoscale, originating from individual proteins) to their stiffening (at the length scale of polyprotein chains) and their linear viscoelasticity and failure properties (at the mesoscopic scale, originating at the scale of the hydrogel network). We foresee that these insights will be instructive in the continuing efforts to modify and control the mechanics of folded protein hydrogels as well as for their envisaged applications as biomaterials.
Author contributions
A. A.-R., L. D. and D. J. B. conceived the experiments. A. A.-R. performed the experiments, analysed the data and wrote the manuscript with contributions from all other authors. S. C. expressed and purified proteins. L. D. is the principal investigator and corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding from the Engineering and Physcical Science Research Council in an EPSRC fellowship (EP/P02288X/1) to L. DOugan and ERC Consolidator Fellowship with UKRI guarantee (EP/X023524/1) to L. Dougan for project MESONET. The CD spectropolarimeter was funded by the Wellcome Trust with grant WT094232. The data set for the paper can be found at doi.org/10.5518/1324.Notes and references
- E. Caló and V. V. Khutoryanskiy, Eur. Polym. J., 2015, 65, 252–267 CrossRef.
- A. Vedadghavami, F. Minooei, M. H. Mohammadi, S. Khetani, A. R. Kolahchi, S. Mashayekhan and A. Sanati-Nezhad, Acta Biomater., 2017, 62, 42–63 CrossRef CAS PubMed.
- R. Langer and D. A. Tirrell, Nature, 2004, 428, 487–492 CrossRef CAS PubMed.
- F. Burla, Y. Mulla, B. E. Vos, A. Aufderhorst-Roberts and G. H. Koenderink, Nat. Rev. Phys., 2019, 1, 249–263 CrossRef.
- M. D. G. Hughes, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, ACS Nano, 2022, 16(7), 10667–10678 CrossRef CAS PubMed.
- S. Lv, Y. Cao and H. Li, Langmuir, 2012, 28, 2269–2274 CrossRef CAS PubMed.
- L. R. Khoury and I. Popa, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- J. Wu, P. Li, C. Dong, H. Jiang, B. Xue, X. Gao, M. Qin, W. Wang, B. Chen and Y. Cao, Nat. Commun., 2018, 9, 1–11 CrossRef PubMed.
- S. Lv, D. M. Dudek, Y. Cao, M. M. Balamurali, J. Gosline and H. Li, Nature, 2010, 465, 69–73 CrossRef CAS PubMed.
- N. Kong, L. Fu, Q. Peng and H. Li, ACS Biomater. Sci. Eng., 2016, 3, 742–749 CrossRef PubMed.
- L. Fu, A. Haage, N. Kong, G. Tanentzapf and H. Li, Chem. Commun., 2019, 55, 5235–5238 RSC.
- L. R. Khoury, M. Slawinski, D. R. Collison and I. Popa, Sci. Adv., 2020, 6, eaba6112 CrossRef CAS PubMed.
- Q. Bian, L. Fu and H. Li, Nat. Commun., 2022, 13, 1–8 Search PubMed.
- R. Petrosyan, A. Narayan and M. T. Woodside, J. Mol. Biol., 2021, 433, 167207 CrossRef CAS PubMed.
- M. Rief, Science, 1997, 276, 1109–1112 CrossRef CAS PubMed.
- T. Hoffmann, K. M. Tych, M. L. Hughes, D. J. Brockwell and L. Dougan, Phys. Chem. Chem. Phys., 2013, 15, 15767–15780 RSC.
- C. P. Broedersz and F. C. MacKintosh, Rev. Mod. Phys., 2014, 86, 995 CrossRef CAS.
- K. Shmilovich and I. Popa, Phys. Rev. Lett., 2018, 121, 168101 CrossRef CAS PubMed.
- B. S. Hanson, D. Head and L. Dougan, Soft Matter, 2019, 15, 8778–8789 RSC.
- B. S. Hanson and L. Dougan, Macromolecules, 2020, 53, 7335–7345 CrossRef CAS.
- B. S. Hanson and L. Dougan, Biomacromolecules, 2021, 22, 4191–4198 CrossRef CAS PubMed.
- M. D. G. Hughes, B. S. Hanson, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, ACS Nano, 2021, 15, 11296–11308 CrossRef CAS PubMed.
- M. D. G. Hughes, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, Soft Matter, 2020, 16, 6389–6399 RSC.
- M. Muthukumar, Macromolecules, 1989, 22, 4656–4658 CrossRef CAS.
- M. Gasik, A. Gantar and S. Novak, et al. , Biomed. Mater., 2017, 12, 025004 CrossRef PubMed.
- S. Improta, A. S. Politou and A. Pastore, Structure, 1996, 4, 323–337 CrossRef CAS PubMed.
- R. B. Best, S. B. Fowler, J. L. T. Herrera, A. Steward, E. Paci and J. Clarke, J. Mol. Biol., 2003, 330, 867–877 CrossRef CAS PubMed.
- H. Chen, G. Yuan, R. S. Winardhi, M. Yao, I. Popa, J. M. Fernandez and J. Yan, J. Am. Chem. Soc., 2015, 137, 3540–3546 CrossRef CAS PubMed.
- M. A. Da Silva, S. Lenton, M. Hughes, D. J. Brockwell and L. Dougan, Biomacromolecules, 2017, 18, 636–646 CrossRef CAS PubMed.
- V. Potapov, J. L. Ong, R. B. Kucera, B. W. Langhorst, K. Bilotti, J. M. Pryor, E. J. Cantor, B. Canton, T. F. Knight, T. C. Evans and G. J. S. Lohman, ACS Synth. Biol., 2018, 7, 2665–2674 CrossRef CAS PubMed.
- A. Aufderhorst-Roberts, M. D. G. Hughes, A. Hare, D. A. Head, N. Kapur, D. J. Brockwell and L. Dougan, Biomacromolecules, 2020, 21, 4253–4260 CrossRef CAS PubMed.
- J. Kaplan, A. Bonfanti and A. Kabla, J. Open Source Softw., 2019, 4, 1700 CrossRef.
- A. Bonfanti, J. L. Kaplan, G. Charras and A. Kabla, Soft Matter, 2020, 16, 6002–6020 RSC.
- D. A. Fancy and T. Kodadek, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 6020–6024 CrossRef CAS PubMed.
- D. A. Fancy, C. Denison, K. Kim, Y. Xie, T. Holdeman, F. Amini and T. Kodadek, Chem. Biol., 2000, 7, 697–708 CrossRef CAS PubMed.
- M. Wolny, M. Batchelor, P. J. Knight, E. Paci, L. Dougan and M. Peckham, J. Biol. Chem., 2014, 289, 27825–27835 CrossRef CAS PubMed.
- M. Batchelor, M. Wolny, M. Kurzawa, L. Dougan, P. J. Knight and M. Peckham, Methods in Molecular Biology, Springer, New York, 2018, pp. 185–211 Search PubMed.
- N. Sreerama, Protein Sci., 2003, 12, 384–388 CrossRef CAS PubMed.
- N. Sreerama and R. W. Woody, Anal. Biochem., 2000, 287, 252–260 CrossRef CAS PubMed.
- S. Aime, L. Cipelletti and L. Ramos, J. Rheol., 2018, 62, 1429–1441 CrossRef CAS.
- P. Patrício, C. R. Leal, J. Duarte and C. Januário, Phys. Rev. E, 2015, 92, 040702(R) CrossRef PubMed.
- F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683–697 CrossRef CAS.
- K. A. Whitaker, Z. Varga, L. C. Hsiao, M. J. Solomon, J. W. Swan and E. M. Furst, Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- J. Alcaraz, L. Buscemi, M. Grabulosa, X. Trepat, B. Fabry, R. Farré and D. Navajas, Biophys. J., 2003, 84, 2071–2079 CrossRef CAS PubMed.
- N. Desprat, A. Richert, J. Simeon and A. Asnacios, Biophys. J., 2005, 88, 2224–2233 CrossRef CAS PubMed.
- S. Nicolle, P. Vezin and J.-F. Palierne, J. Biomech., 2010, 43, 927–932 CrossRef CAS PubMed.
- A. Jaishankar and G. H. McKinley, Proc. R. Soc. A, 2013, 469, 20120284 CrossRef.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef CAS.
- G. S. Blair, B. Veinoglou and J. Caffyn, Proc. R. Soc. A, 1947, 189, 69–87 CAS.
- R. C. Koeller, J. Appl. Mech., 1984, 51, 299–307 CrossRef.
- G. W. S. Blair and F. M. V. Coppen, Am. J. Psychol., 1942, 55, 215 CrossRef.
- I. M. Sokolov, J. Klafter and A. Blumen, Phys. Today, 2002, 55, 48–54 CrossRef CAS.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- M. Muthukumar, J. Chem. Phys., 1985, 83, 3161–3168 CrossRef CAS.
- T. Faber, A. Jaishankar and G. McKinley, Food Hydrocolloids, 2017, 62, 311–324 CrossRef CAS.
- H. Schiessel, R. Metzler, A. Blumen and T. Nonnenmacher, J. Phys. A: Math. Gen., 1995, 28, 6567 CrossRef CAS.
- A. J. Holder, N. Badiei, K. Hawkins, C. Wright, P. R. Williams and D. J. Curtis, Soft Matter, 2018, 14, 574–580 RSC.
- T. Surguladze, J. Math. Sci., 2002, 112, 4517–4557 CrossRef.
- A. Jaishankar and G. H. McKinley, J. Rheol., 2014, 58, 1751–1788 CrossRef CAS.
- K. M. Schmoller, P. Fernández, R. C. Arevalo, D. L. Blair and A. R. Bausch, Nat. Commun., 2010, 1, 134 CrossRef CAS PubMed.
- N. A. Kurniawan, B. E. Vos, A. Biebricher, G. J. Wuite, E. J. Peterman and G. H. Koenderink, Biophys. J., 2016, 111, 1026–1034 CrossRef CAS PubMed.
- J. Diani, B. Fayolle and P. Gilormini, Eur. Polym. J., 2009, 45, 601–612 CrossRef CAS.
- C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nature, 2005, 435, 191–194 CrossRef CAS PubMed.
- F. C. MacKintosh, J. Käs and P. A. Janmey, Phys. Rev. Lett., 1995, 75, 4425–4428 CrossRef CAS PubMed.
- R. Tharmann, M. M. A. E. Claessens and A. R. Bausch, Phys. Rev. Lett., 2007, 99, 088102 CrossRef PubMed.
- G. Jung, Z. Qin and M. J. Buehler, Topics in Current Chemistry, Springer International Publishing, 2015, pp. 317–343 Search PubMed.
- L. Cipelletti, K. Martens and L. Ramos, Soft Matter, 2020, 16, 82–93 RSC.
- T. Ackbarow and M. J. Buehler, J. Mater. Sci., 2007, 42, 8771–8787 CrossRef CAS.
- M. Grandbois, M. Beyer, M. Rief, H. Clausen-Schaumann and H. E. Gaub, Science, 1999, 283, 1727–1730 CrossRef CAS PubMed.
- P. A. Janmey, M. E. McCormick, S. Rammensee, J. L. Leight, P. C. Georges and F. C. MacKintosh, Nat. Mater., 2007, 6, 48–51 CrossRef CAS PubMed.
- R. Metzler and J. Klafter, J. Non-Cryst. Solids, 2002, 305, 81–87 CrossRef CAS.
- H. Dietz, F. Berkemeier, M. Bertz and M. Rief, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12724–12728 CrossRef CAS PubMed.
- H. H. Winter and M. Mours, Neutron Spin Echo Spectroscopy Viscoelasticity Rheology, Springer Berlin Heidelberg, 1997, pp. 165–234 Search PubMed.
- A. Zaccone, H. Winter, M. Siebenbürger and M. Ballauff, J. Rheol., 2014, 58, 1219–1244 CrossRef CAS.
- B. Fabry, G. N. Maksym, J. P. Butler, M. Glogauer, D. Navajas and J. J. Fredberg, Phys. Rev. Lett., 2001, 87, 148102 CrossRef CAS PubMed.
- M. Kohandel, S. Sivaloganathan, G. Tenti and K. Darvish, Phys. Med. Biol., 2005, 50, 2799–2805 CrossRef CAS PubMed.
- S. B. Ross-Murphy, Polym. Bull., 2007, 58, 119–126 CrossRef CAS.
- M. Jaspers, M. Dennison, M. F. J. Mabesoone, F. C. MacKintosh, A. E. Rowan and P. H. J. Kouwer, Nat. Commun., 2014, 5, 5808 CrossRef PubMed.
- K. R. Cook, D. Head and L. Dougan, Soft Matter, 2023, 19, 2780–2791 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary text, Fig. S1–S15. See DOI: https://doi.org/10.1039/d2sm01225a |
| This journal is © The Royal Society of Chemistry 2023 |