Open Access Article
Open Access ArticleDynamics of magnetic Janus colloids studied by ultra small-angle X-ray photon correlation spectroscopy†
Thomas
Zinn
 ,
Lewis
Sharpnack
,
Lewis
Sharpnack
 and
Theyencheri
Narayanan
and
Theyencheri
Narayanan
 *
*
The European Synchrotron, 38043 Grenoble, France. E-mail: narayan@esrf.fr
First published on 16th November 2022
Abstract
The orientation behavior and the translational dynamics of spherical magnetic silica-nickel Janus colloids in an external magnetic field have been studied by small-angle X-ray scattering and X-ray photon correlation spectroscopy at ultra small-angles. For weak applied fields and at low volume fractions, the particle dynamics is dominated by Brownian motion even though the net magnetic moments of the individual particles are aligned in the direction of the field as indicated by the anisotropy in the small-angle scattering patterns. For higher fields the magnetic forces result in more complex structural changes with nickel caps of Janus particles pointing predominantly along the applied magnetic field. The alignment ultimately leads to chain-like configurations and the intensity–intensity autocorrelation functions, g2(q,t), show a second slower decay which becomes more pronounced at higher volume fractions. A direction dependent analysis of g2(q,t) revealed a faster than exponential decay perpendicular to the field which is related to the sedimentation of magnetically ordered domains. The corresponding velocity fluctuations could be decoupled from the diffusion of particles by decomposing g2(q,t) into advective and diffusive contributions. Finally, the particle dynamics becomes anisotropic at higher volume fractions and strong magnetic fields. The derived translational diffusion coefficients indicate slower particle dynamics perpendicular to the field as compared to the parallel direction.
1 Introduction
Magnetic colloids suspended in a nonmagnetic solvent show peculiar responsive dynamic behaviors when subjected to an external magnetic field.1–3 The magnetic colloids can self-assemble into various anisotropic structures including linear chains, chain-like zigzag strands or more densely packed double chains.1,4,5 The magnetic interactions can be easily manipulated by the applied field that makes such nanomaterials extremely attractive for many applications. These include for example magnetic separation methods,6 magnetically controllable colloidal crystals7,8 or biomedical applications.9,10 Many of these applications employ particles of typical sizes between 50 nm to 2 μm and recent developments in particle synthesis are not limiting the shape or magnetic structure of the particles.11,12 Hence, magnetic colloids can have either a shape or magnetic anisotropy or both. In contrast to classical isotropic magnetic particles (ferrofluids), in this study we investigate spherical composite particles with a magnetic anisotropy. The magnetic Janus particles (JPs) have recently come into focus due to their ability for magnetically guided propulsion.13,14 Nevertheless, the major challenges to be confronted with besides controlling the particle shape and magnetic properties are to predict and understand the self-assembly and their dynamics in detail. Throughout the past decades theories have been developed to comprehend the static equilibrium structure formed under the influence of an external field.3,15–18 Depending on the size of the particles these theories can be verified by optical microscopy,19 scattering methods including small angle X-ray and neutron scattering (SAXS and SANS, respectively),20–25 or by computer simulations.26–28In order to obtain the dynamic information of a magnetic responsive suspension, traditionally dynamic light scattering (DLS)29,30 is used and only in the last decades modern methods such as optical particle tracking,31 dynamic differential microscopy (DDM)32 and X-ray photon correlation spectroscopy (XPCS)33–39 became available. The high degree of coherence offered by modern synchrotron sources together with advanced photon counting pixel-array detectors (e.g. Eiger 500 K) having high spatial and temporal resolution, enable the investigation of short time scales and the direction dependent analysis of the particle dynamics.40 The ensemble averaged intensity–intensity autocorrelation functions with a high signal-to-noise ratio can be obtained even with very dilute systems, which in turn allows decoupling the diffusive and advective contributions to the particle dynamics.41–43
In this work, we study the orientation behavior and dynamics of magnetic Janus colloids at low volume fractions (ϕ) in water subjected to different applied static magnetic fields. The JP is composed of a silica sphere that bears a hemispherical nickel cap. In order to suppress magnetic dipole-dipole interactions between the particles prior to applying the magnetic field, we studied the dynamics of a dilute sample (ϕ ≈ 10−4) and a 7 times more concentrated suspension. In the dilute limit the separation distances between two particles are initially large and thermal motion can prevent the system from a rapid irreversible aggregation which would sufficiently alter the particle dynamics. This becomes immediately clear by considering the underlying magnetic interactions. For practical purposes, we reflect on identical particles with a centered magnetic dipole.3 However, theoretical simulations and experimental observations have shown that the magnetic dipole moment of JPs can be either laterally or radially off-centered.28,44 Thus, the position and direction of the magnetic moments have a significant influence on the phase diagram.45 The magnetic dipole moment, m, assuming a homogeneous spherical magnetic colloid of radius a is given by m = 4πa3B/(3μ0), where μ0 is the vacuum magnetic permeability and B is the strength of the external field. Under the influence of a magnetic field two identical magnetic moments interact via an interaction potential given by
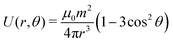 | (1) |
For a more detailed structural modeling a steric hard- or soft-sphere repulsion potential has to be added and the total magnetic field usually is a superposition of the external field and the dipole field, both factors have been omitted here for the sake of simplicity. U(r,θ) is anisotropic, and it can be easily verified that the interaction potential is attractive (U < 0) for θ < 54.7° and repulsive (U > 0) for θ > 54.7°, respectively. Its minimum and thus maximum attraction is reached for two particles in contact with their magnetic dipoles aligned in the direction of applied field (r = 2a and θ = 0°). Equally, the maximum repulsion occurs for a perpendicular configuration (r = 2a and θ = 90°). These anisotropic interactions give rise to the formation of anisotropic structures along the direction of the applied field. In addition, the self-assembly depends not exclusively on the magnetic energy but also on thermodynamic contribution. In terms of a thermodynamic equilibrium state theory,46 the balance between the entropic and magnetic energies defines the critical aggregation parameter N* and the magnetic coupling parameter Λ(m,T):
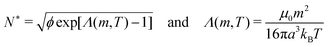 | (2) |
In order to identify the two main regimes: (i) dynamics dominated by magnetic interactions and (ii) dynamics governed by diffusive processes, only a few simple thermodynamic arguments are required. “Which of the two mechanisms dominates the particle dynamics” depends on two characteristic length scales: (i) the average particle separation without magnetic interactions and (ii) the range of the dipolar interactions. The average particle distance L in a suspension of randomly distributed particles can be analytically calculated according to L = 0.89aϕ−1/3 (the prefactor is the numerical value of gamma function at 4/3) and depends on the particle radius a and ϕ.47,48 When magnetic interactions are induced by an external field, the particle-particle interaction will be only relevant for distances where the magnetic interaction energy becomes larger than the thermal energy. This particular distance is defined by λB = 2aΛ1/3 (magnetic Bjerrum length).49 Considering the case of λB ≫ L the dynamics is deterministic, dominated by magnetic interactions and opposite for λB ≪ L the particle motion is essentially diffusive. For the latter, the particle can only feel the magnetic interaction with another particle after randomly diffusing across multiples of λB before it is magnetically captured and the dynamics becomes deterministic.
In this experimental study the static magnetic field was varied from very weak to strong fields. We will demonstrate that already at weak fields the particles feel the magnetic interactions, but with large interparticle distances, i.e. low ϕ, the particles still behave diffusive. Magnetic interactions manifest as an increase of the apparent viscosity of the suspension at stronger fields. The underlying mechanism for particle motion at higher ϕ starts to be strongly influenced due to the alignment and ultimately resulting in anisotropic dynamics.
2 Materials and methods
2.1 Materials
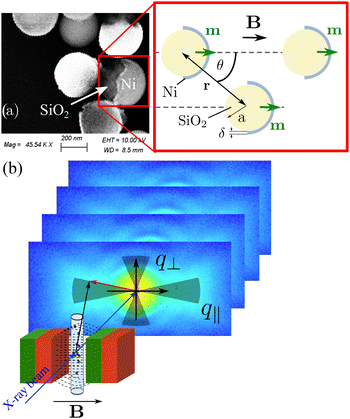
Spherical silica colloids of nominal radius (a = 220 nm) with a nickel coating (susceptibility χ ≃ 600) of thickness (δ ≃ 40 nm) on one hemisphere were synthesised according to Semeraro et al.50Fig. 1(a) shows a scanning electron microscope (SEM, ZEISS LEO 1530) image of the silica-nickel JPs in zero field. The nickel coating on the silica particles is clearly visible as a brighter region on the surface and it is likely multidomain. The asymmetric distribution of nickel on the silica particle results in a magnetic dipole shifted from its geometrical center (green arrows) which also depends on the film thickness, cf. red box in Fig. 1(a). Nickel is an isotropic magnetic material that can be magnetized in a random direction. The JPs were suspended in Milli-Q water and filled in quartz glass capillaries of 1 mm diameter.2.2 Magnetic field
A nearly homogeneous static magnetic field was generated with a set of rare earth permanent magnets in a Halbach arrangement with variable pole gap as shown in Fig. S1 in the ESI.† The sample is vertically placed on a nonmagnetic plexiglass frame at the center of the gap. By changing the directions of the magnetization, either a field perpendicular, B⊥, or parallel, B‖, to the primary beam can be applied, whose strength can be precisely tuned from 0.1 mT up to 1.0 T.2.3 X-ray scattering
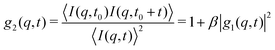 | (3) |
| g1(q,t) = exp[−Γ(q)t] | (4) |
| g1(q,t) = exp[−(t/τa)γ] | (5) |
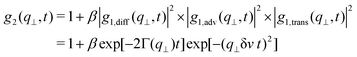 | (6) |
g1(q,t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(t/τf)γf] + (1 − A)exp[−(t/τs)γs] exp[−(t/τf)γf] + (1 − A)exp[−(t/τs)γs] | (7) |
3 Results and discussion
The structural and dynamic properties of two different concentrations of the Janus suspensions were investigated by USAXS and XPCS in the ultra small-angle range as a function of magnetic field at room temperature (295 K).3.1 Alignment behavior
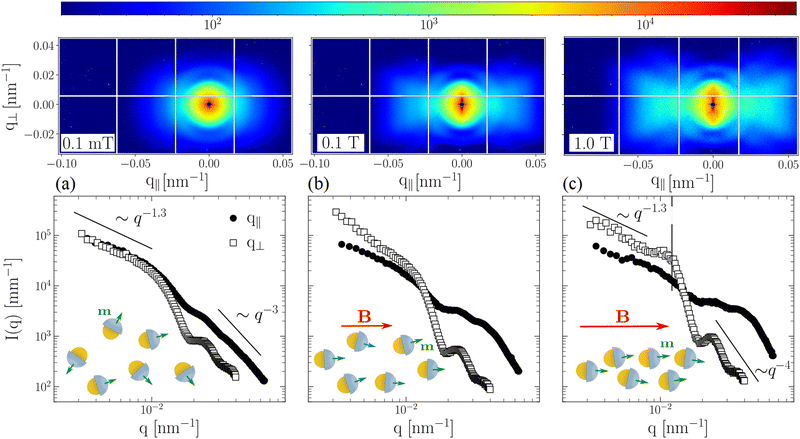
Typical USAXS patterns of the Janus suspensions (ϕ ∼ 7 × 10−4) at different applied magnetic fields (perpendicular to the X-ray beam and gravity) are shown in Fig. 2(a)–(c). More USAXS data in particular for the zero field condition and a dilute particle suspension (ϕ = 10−4) can be found in ESI,† Fig. S2 and S3, respectively. The scattering pattern for the zero-field is completely isotropic, while for the lowest applied field 0.1 mT (i.e. the magnetic setup in place), it became anisotropic in the field direction. We attribute the anisotropy even in a weak field and at low ϕ to the strong magnetic interactions. Upon the application of a magnetic field, the JPs rotate their magnetic moments in the direction of the applied field. The anisotropy became more pronounced with increasing field. On the contrary, when the magnetic field is applied parallel to the X-ray beam, the scattering pattern remained isotropic for all magnetic fields. The corresponding USAXS patterns are shown in ESI,† Fig. S4. This indicates that the JPs bear a net magnetic moment with the nickel caps pointing in the direction of the particle axis of symmetry. At low q and strong fields, we additionally observed an excess scattering intensity in the vertical direction as seen in Fig. 2(c), which is indicative of the formation of an elongated structure in the field direction.In order to better quantify the anisotropic intensity distribution, azimuthal cross-sections of the 2D images were taken parallel and perpendicular to the field. The corresponding I(q) curves are shown in Fig. 2, bottom panel. At high q we note a peculiar power-law decay I(q) ∼ q−μ with 3 ≤ μ ≤ 4, which is expected for JPs with a relatively thick and high scattering contrast cap.53 For the three different applied fields it is evident that the intensity parallel to the field, I(q‖), becomes higher with increasing field (filled symbols) as compared to the perpendicular direction I(q⊥) (open symbols) except at low q. As demonstrated for the lowest field in Fig. 2(a), the scattering tends to be isotropic for q ≤ 0.01 nm−1 and at higher q-values there is an anisotropic halo. This is qualitatively understood by the strong magnetic interactions aligning the magnetic caps in the field direction, that already happens at weak fields (U ∼ m2). In addition, I(q) ∼ q−1.3 at low q even in a weak magnetic field and this behavior is consistent with a linear organization of particles. This low q upturn becomes less pronounced at lower ϕ as depicted in ESI,† Fig. S5 and a Guinier plateau is observed in the absence of the magnetic field.
In stronger magnetic fields, the magnetic interactions overwhelm the thermal forces, and the particles start to organize preferentially in the field direction. The magnetic field-induced self-assembly is visible especially at low q perpendicular to the field direction, see Fig. 2(c). The observed excess intensity in the form of a streak is an indication of locally chain-like configuration of particles along the field direction.25 Besides, the four lobes of the pattern in the horizontal direction suggests a zigzag arrangement of particles within the chain. A closer inspection of I(q⊥) at low q reveals the signature of a structural correlation that is visible as a broad structure factor peak at q* ≈ 0.012 nm−1, see the vertical line in Fig. 2(c). This q* roughly corresponds to an interparticle separation i.e. 2π/q* ≈ 524 nm within the chains. Modeling of USAXS patterns for spherical particles with anisotropic interactions involves the coupling between the orientation-dependent form factor, and the positional and orientational correlations between the particles. As shown in the ESI,† Fig. S5, the isotropic scattering profiles can be simulated using a model presented previously50 but the agreement for a 2D anisotropic pattern was not satisfactory.
3.2 Dynamics
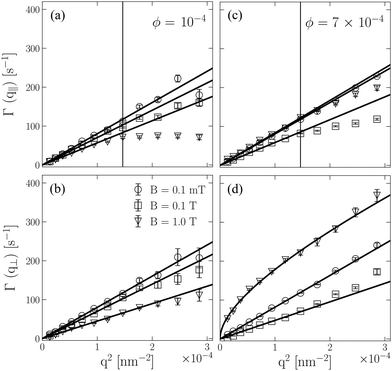
A quantitative insight into the particle organization can be obtained by XPCS. Fig. 3 shows a set of normalized correlation functions g2(q,t) measured at three different fields (a) 0.1 mT, (b) 0.1 T and (c) 1.0 T for a range of q-values within a minute after changing the field. The static intensity remained stable over this time scale. The top and bottom rows display g2(q,t) along the parallel and perpendicular field directions, respectively. Both investigated ϕ showed isotropic dynamics at 0.1 mT and the g2(q,t) could be described by a single exponential decay according to eqn (4) as indicated by the solid lines. The relaxation rates Γ(q) extracted from the autocorrelation functions yielded the typical q2-dependence as expected for free translational diffusion, see inset Fig. 3(a). The determined translational diffusion coefficient D0 = 0.81 μm2 s−1 corresponds to an apparent hydrodynamic radius RH = 281 nm, assuming η = 0.95 mPa s and a temperature of 295 K. Although RH corresponds well to the particle dimension determined by USAXS, we cannot exclude dimers or smaller aggregates due to the absence of a proper Guinier plateau at low q-values, see Fig. 2(a)–(c). By increasing the magnetic field, the g2(q,t) initially remains single exponential (0.1 T) before the magnetic field-induced self-assembly significantly changes the functional form. A comparison of the g2(q,t) at 1.0 T in Fig. 3(c) with the corresponding lower ϕ ≈ 10−4 in Fig. S6 (ESI†) reveals that the decay of g2(q,t) for the lower ϕ can still be described by a single exponential decay, whereas for the higher ϕ the relaxation changes to a bimodal decay. In addition to the fast mode, there is a clear second slower mode in g2(q,t), which is present in both parallel and perpendicular directions to the applied field. The interpretation of such a slow mode is speculative and strongly depends on the underlying structure of the system.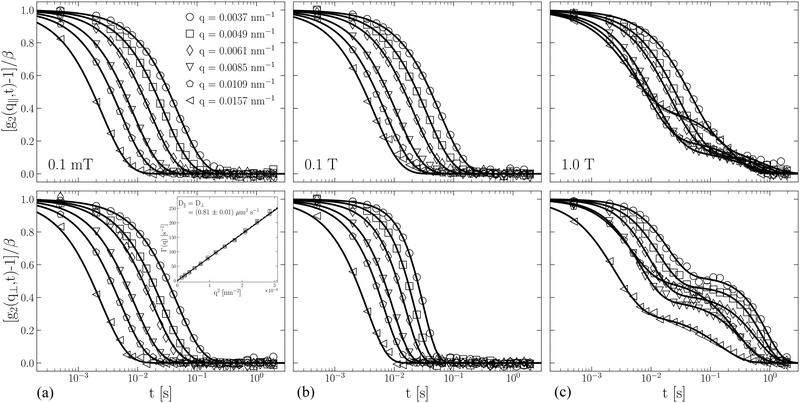 | ||
| Fig. 3 Normalized intensity–intensity autocorrelation functions, g2(q,t) for the concentrated sample (ϕ ≈ 7 × 10−4) for a range of selected q-values for magnetic fields (a) 0.1 mT, (b) 0.1 T and (c) 1.0 T. The upper and lower panels depict the behavior along horizontal and vertical directions, respectively. Solid lines are nonlinear-least-square fits according to eqn (4), (6) and (7). The inset in lower panel (a) displays Γ(q) = D0q2 behavior with D‖ = D⊥ = D0 = 0.81 μm2 s−1. | ||
In general, g2(q,t) functions are found to decay faster than that expected for freely diffusing particles in the direction perpendicular to the field. This faster relaxation can be related to the sedimentation of particle clusters. The related sedimentation velocity is likely to be not uniform and thus the mean velocity fluctuations, δv, can be described by a normal distribution, see eqn (6) with δv = 8.0 μm s−1 (ϕ ≈ 7 × 10−4 at 0.1 T). At these low ϕ, hydrodynamic interactions are not significant54 and the sedimentation velocity of a single JP is about 0.3 μm s−1. The change in the functional form of g2(q,t) appears at different values of magnetic fields, depending on ϕ. This observation reflects again the nontrivial relationship between magnetic forces caused by the external field and the entropic interactions in the suspension, as described in eqn (2)3. That is to achieve similar interactions in a dilute sample, a stronger field has to be applied in order to cause equivalent structural changes. With time the particle interactions result in larger aggregates that may further grow and thus cannot be supported by the magnetic forces and eventually sediment. The aggregation kinetics also depends on the concentration of particles. For the concentrated sample the interparticle distances become shorter and the aggregation rate is faster leading to larger particle clusters resulting in stronger velocity fluctuations.
The relaxation rates, Γ(q), parallel and perpendicular to the field determined from the direction dependent analysis are shown in a q2-representation in Fig. 4 for both ϕ. Below q* (indicated by the vertical line) most curves show a linear behavior indicative of diffusive dynamics. With increasing field the slope successively decreases i.e. the particle dynamics slows down, see Table 1. However, at the low ϕ, we observed direction independent dynamics. We may speculate two possible scenarios for the slowing down: (i) the translational motion of the particles is strongly influenced by the magnetic field or (ii) the particles form dimers or trimers that are typically found at the onset of aggregation. Most likely, we observe a combination of these two effects which cannot be easily distinguished within this study. But a qualitative understanding of the mechanism can still be reached. Firstly, at weaker fields Brownian motion of the individual particles modifies the overall structure such that a perfect alignment in the direction of the applied field is not yet achieved. But in this situation the net magnetic moment can be considered as already aligned in the direction of the field. In this state the particle can still freely rotate around its magnetic axis, which however, is not resolved by the homodyne detection scheme employed here. This reduced degree of freedom is in particular true once the particles start to organize. The magnetic domains formed can be considered as rather loose clusters, which explains the absence of a strong structure factor peak and higher structural ordering of the particles as a function of the applied magnetic field. We can account this particular behavior of the JPs suspension if we consider that the apparent viscosity of the fluid is changed under the influence of the magnetic field. This kind of dynamic behavior induces the so-called magnetic stress at higher ϕ, which has been observed in other magnetic fluids (e.g. ferrofluids).55
As ϕ is increased, the system undergoes strong structural changes and as a result the dynamic behavior becomes more complex. The underlying mechanism is consequently very different if interparticle interactions are involved. As shown by Bacri et al. the diffusion slows down perpendicular to the field and enhances along the field direction.56 The slow mode observed in Fig. 3(c) in both directions perpendicular and parallel to the field is indicative of a larger scale structural organization hindering the free diffusion of particles. This slow relaxation mode appears in both directions, is not surprising because of more complex and stronger structures are formed depending on the magnetic field and ϕ. The second slow relaxation is likely associated to the advection of these larger magnetically organized domains consisting of chain-like particle configurations. The fast mode then represents a kind of “particle rattling” inside such magnetically formed clusters. This effect becomes more pronounced at higher ϕ. The corresponding g2(q,t) at 1.0 T in Fig. 3(c) could be described by a double exponential function representing two different relaxation modes according to eqn (7). This phenomenological approach is only suited for characterizing the bimodal distribution of two well-separated dynamic processes and may not reflect the structural complexity of the system induced by the magnetic interactions. It should be stressed that the parameter A i.e. the ratio between the slow and fast mode is q-dependent, which means that the parameter A is reflecting the anisotropy in I(q) (see ESI,† Fig. S7a).
The functional form of the fast decay was modeled by a pure exponential decay parallel to the field (γ‖f = 1) and by a compressed exponential in the perpendicular direction (γ⊥f ≥ 1) (see ESI,† Fig. S7b). This deviation from the exponential behavior is likely originating from the counterflow induced by sedimentation. The slow relaxation was found to be more isotropic but showing a q-dependency, γs = γs(q). We found values tending to be larger than one, γs ≥ 1, which is due to the flow rather than a superdiffusive like motion. The corresponding values for the exponent γs are given in the ESI,† Fig. S7(c). Moreover, as explained above the faster decay along the direction of gravity is a consequence of the velocity fluctuations induced by sedimentation. Applying eqn (7) means that the advective term, exp[−(q⊥δvt)2], is not explicitly considered, and consequently Γ(q) deviates from the q2-dependency as shown in Fig. 4(d). In order to characterize the velocity fluctuations in this case Γ(q) can be expressed in terms of an effective diffusion coefficient, De, together with velocity fluctuations according to Γ(q) = Deq2 + δvq. The derived diffusion coefficients De are given in Table 1. The magnitudes of δv are found to be similar order as that obtained for the lower concentration or magnetic fields δv = 13.7 μm s−1 at 1 T. In the parallel field direction Γ(q) follows a simple q2-dependence indicating the translational diffusive dynamics. Finally, the particle dynamics became anisotropic as observed for other magnetic colloids.39,57
4 Conclusions
We have investigated the orientation and dynamic behavior of dilute suspensions of silica-nickel magnetic JPs in water by means of USAXS and XPCS. In particular, XPCS enabled probing the ensemble averaged dynamics of magnetic colloids under the influence of an external field. The quality of g2(q,t) functions allows not only a detailed direction dependent analysis, but also decomposition of the particle dynamics to advective and diffusive contributions. The magnetic interactions between the JPs quickly become dominant even at very weak fields (0.1 mT). Therefore, it is extremely important to study such systems at the emergence of the magnetic interactions at very low ϕ values. The static scattering becomes anisotropic even at low ϕ ≈ 10−4 where structural correlations are not yet present. This anisotropic scattering indicates that the particles orient their magnetic moment in the direction of the applied field, but the particles dynamics remains diffusive. Magnetic field-guided self-assembly of particles leads to more locally elongated chain-like structures in the direction of the magnetic field. The resulting shape anisotropy is responsible for the anisotropic scattering especially at low q.However, at low ϕ the particle dynamics slows down isotropically as a function of the applied field. The q2-dependence of the relaxation rates clearly indicates the translational diffusion of particles, which is influenced by the magnetic field. The isotropic nature of the particle dynamics in the very dilute regime may be considered as a change in the apparent viscosity of the medium due to magnetic forces. For higher ϕ, the interparticle distance decreases and magnetic dipole–dipole interactions quickly overwhelm entropic forces. Thus, the magnetic effects become more pronounced and chain formation results in a two-step relaxation characterized by a fast and slow modes. As a consequence the effective diffusion coefficient shows an anisotropy (D‖ > D⊥). As theoretically predicted the translational motion of the particles is slower perpendicular to the field as compared to the parallel direction. Naturally due to the complexity of the contributing interactions, there are still open questions that deserve further theoretical attention and experimental verification. Especially, for future experiments the emergence of magnetic interactions influencing the interparticle correlations and dynamics at weaker fields B ≤ 0.1 T, are of particular interest for biomedical applications. Here, we have demonstrated that XPCS in the ultra small-angle scattering geometry provides a convenient tool for the simultaneous study of the microstructure and ensemble averaged dynamics in complex systems with anisotropic interactions under the influence of an external field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y. Chushkin (ESRF) and ID02 staff are thanked for the development of the pyXPCS software package and technical support, respectively. The ESRF is acknowledged for the provision of synchrotron beamtime and funding. I. Snigireva (Microimaging laboratory, ESRF) is thanked for the SEM characterization of JPs.Notes and references
- S. A. Safran, Nat. Mater., 2003, 2, 71 CrossRef CAS PubMed.
- B. J. Lemaire, P. Davidson, J. Ferré, J.-P. Jamet, D. Petermann, P. Panine, I. Dozov, D. Stoenescu and J.-P. Jolivet, Faraday Discuss., 2005, 128, 271–283 RSC.
- J. Faraudo, J. S. Andreu, C. Calero and J. Camacho, Adv. Funct. Mater., 2016, 26, 3837 CrossRef CAS.
- M. Wang, L. He and Y. Yin, Mater. Today, 2013, 16, 110 CrossRef CAS.
- R. S. Rikken, R. J. Nolte, J. C. Maan, J. C. Van Hest, D. A. Wilson and P. C. Christianen, Soft Matter, 2014, 10, 1295 RSC.
- D. Kelland, IEEE Trans. Magn., 1998, 34, 2123 CrossRef.
- A. Pal, V. Malik, L. He, B. H. Erné, Y. Yin, W. K. Kegel and A. V. Petukhov, Angew. Chem., Int. Ed., 2015, 54, 1803 CrossRef CAS.
- Z. Li, C. Qian, W. Xu, C. Zhu and Y. Yin, Sci. Adv., 2021, 7, 1289 CrossRef.
- Q. L. Vuong, J.-F. Berret, J. Fresnais, Y. Gossuin and O. Sandre, Adv. Healthcare Mater., 2012, 1, 502–512 CrossRef CAS PubMed.
- G. N. Lucena, C. C. dos Santos, G. C. Pinto, B. E. Amantéa, R. D. Piazza, M. Jafelicci Jr and R. F. C. Marques, Drug Delivery and Magnetic Hyperthermia Based on Surface Engineering of Magnetic Nanoparticles, John Wiley and Sons, Ltd, 2021, ch. 11, p. 231 Search PubMed.
- E. Poggi and J.-F. Gohy, Colloid Polym. Sci., 2017, 295, 2083 CrossRef CAS.
- H. Su, C.-A. Hurd Price, L. Jing, Q. Tian, J. Liu and K. Qian, Mater. Today Bio, 2019, 4, 100033 CrossRef CAS.
- A. F. Demirörs, M. T. Akan, E. Poloni and A. R. Studart, Soft Matter, 2018, 14, 4741–4749 RSC.
- R. Huhnstock, M. Reginka, A. Tomita, M. Merkel, K. Dingel, D. Holzinger, B. Sick, M. Vogel and A. Ehresmann, Sci. Rep., 2021, 11, 1–11 CrossRef.
- P. De Gennes and P. Pincus, Phys. Kondens. Mater., 1970, 11, 189 CrossRef CAS.
- J. J. Cerdà, E. Elfimova, V. Ballenegger, E. Krutikova, A. Ivanov and C. Holm, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 1 CrossRef.
- J. Hernández-Rojas, D. Chakrabarti and D. J. Wales, Phys. Chem. Chem. Phys., 2016, 18, 26579 RSC.
- J. G. Ku, X. Y. Liu, H. H. Chen, R. D. Deng and Q. X. Yan, AIP Adv., 2016, 6, 025004 CrossRef.
- S. K. Smoukov, S. Gangwal, M. Marquez and O. D. Velev, Soft Matter, 2009, 5, 1285 RSC.
- F. L. D. O. Paula, Condens. Matter, 2019, 4, 55 CrossRef.
- M. A. Kamal, A. V. Petukhov and A. Pal, J. Phys. Chem. B, 2020, 124, 5754 CrossRef CAS PubMed.
- A. Wiedenmann, U. Keiderling, K. Habicht, M. Russina and R. Gähler, Phys. Rev. Lett., 2006, 97, 057202 CrossRef CAS.
- M. Barrett, A. Deschner, J. P. Embs and M. C. Rheinstädter, Soft Matter, 2011, 7, 6678 RSC.
- V. I. Petrenko, A. V. Nagornyi, I. V. Gapon, L. Vekas, V. M. Garamus, L. Almasy, A. V. Feoktystov and M. V. Avdeev, Modern Problems of Molecular Physics, 2018, p. 205 Search PubMed.
- N. Nandakumaran, L. Barnsley, A. Feoktystov, S. A. Ivanov, D. L. Huber, L. S. Fruhner, V. Leffler, S. Ehlert, E. Kentzinger, A. Qdemat, T. Bhatnagar-Schöffmann, U. Rücker, M. T. Wharmby, A. Cervellino, R. E. Dunin-Borkowski, T. Brückel and M. Feygenson, Adv. Mater., 2021, 33, 2008683 CrossRef CAS.
- S. Lago, S. López-Vidal, B. Garzón, J. A. Mejías, J. A. Anta and S. Calero, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 4 CrossRef.
- X. Peng, Y. Min, T. Ma, W. Luo and M. Yan, J. Magn. Magn. Mater., 2009, 321, 1221 CrossRef CAS.
- S. Kantorovich, R. Weeber, J. J. Cerdà and C. Holm, J. Magn. Magn. Mater., 2011, 323, 1269 CrossRef CAS.
- L. N. Donselaar and A. P. Philipse, J. Colloid Interface Sci., 1999, 212, 14 CrossRef CAS.
- F. Martínez Pedrero, M. Tirado Miranda, A. Schmitt and J. Callejas Fernández, J. Chem. Phys., 2006, 125, 084706 CrossRef PubMed.
- A. Kaiser, A. Snezhko and I. S. Aranson, Sci. Adv., 2017, 3, e1601469 CrossRef PubMed.
- A. Pal, V. A. Martinez, T. H. Ito, J. Arlt, J. J. Crassous, W. C. Poon and P. Schurtenberger, Sci. Adv., 2020, 6, eaaw9733 CrossRef CAS PubMed.
- J. Lal, D. Abernathy, L. Auvray, O. Diat and G. Grübel, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 263 CrossRef CAS.
- A. Robert, J. Wagner, T. Autenrieth, W. Härtl and G. Grübel, J. Chem. Phys., 2005, 122, 084701 CrossRef.
- J. Wagner, T. Autenrieth, A. Robert, W. Härtl and G. Grübel, J. Magn. Magn. Mater., 2005, 289, 54 CrossRef CAS.
- E. Wandersman, Y. Chushkin, E. Dubois, V. Dupuis, G. Demouchy, A. Robert and R. Perzynski, Br. J. Phys., 2009, 39, 210 CrossRef CAS.
- H. Grigoriew, L. Wiegart, A. Boczkowska and M. Mirkowska, Solid State Commun., 2010, 150, 840 CrossRef CAS.
- J. Wagner, C. Märkert, B. Fischer and L. Müller, Phys. Rev. Lett., 2013, 110, 048301 CrossRef.
- A. Pal, M. A. Kamal, T. Zinn, J. K. G. Dhont and P. Schurtenberger, Phys. Rev. Mater., 2021, 5, 035603 CrossRef CAS.
- T. Zinn, A. Homs, L. Sharpnack, G. Tinti, E. Fröjdh, P.-A. Douissard, M. Kocsis, J. Möller, Y. Chushkin and T. Narayanan, J. Synchrotron Radiat., 2018, 25, 1753 CrossRef CAS PubMed.
- R. Dattani, E. F. Semeraro and T. Narayanan, Soft Matter, 2017, 13, 2817 RSC.
- J. Möller and T. Narayanan, Phys. Rev. Lett., 2017, 118, 198001 CrossRef.
- T. Zinn, L. Sharpnack and T. Narayanan, Phys. Rev. Res., 2020, 2, 033177 CrossRef CAS.
- G. I. Vega-Bellido, R. A. DeLaCruz-Araujo, I. Kretzschmar and U. M. Córdova-Figueroa, Soft Matter, 2019, 15, 4078 RSC.
- J. A. Victoria-Camacho, R. A. DeLaCruz-Araujo, I. Kretzschmar and U. M. Córdova-Figueroa, Soft Matter, 2020, 16, 2460 RSC.
- J. Faraudo, J. S. Andreu and J. Camacho, Soft Matter, 2013, 9, 6654 RSC.
- P. Hertz, Math. Ann., 1909, 67, 387 CrossRef.
- S. Chandrasekhar, Rev. Mod. Phys., 1943, 15, 1 CrossRef.
- J. H. Promislow, A. P. Gast and M. Fermigier, J. Chem. Phys., 1995, 102, 5492 CrossRef CAS.
- E. F. Semeraro, R. Dattani and T. Narayanan, J. Chem. Phys., 2018, 148, 014904 CrossRef PubMed.
- T. Narayanan, M. Sztucki, P. Van Vaerenbergh, J. Léonardon, J. Gorini, L. Claustre, F. Sever, J. Morse and P. Boesecke, J. Appl. Crystallogr., 2018, 51, 1511 CrossRef CAS PubMed.
- B. J. Berne and R. Pecora, Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics, Dover Publications, 2000 Search PubMed.
- E. M. Anitas, Phys. Chem. Chem. Phys., 2020, 22, 536–548 RSC.
- Y. M. Wani, P. G. Kovakas, A. Nikoubashman and M. P. Howard, J. Chem. Phys., 2022, 156, 024901 CrossRef CAS PubMed.
- D. Y. Borin, A. Y. Zubarev, D. N. Chirikov and S. Odenbach, J. Phys.: Condens. Matter, 2014, 26, 406002 CrossRef PubMed.
- J.-C. Bacri, A. Cebers, A. Bourdon, G. Demouchy, B. M. Heegaard, B. Kashevsky and R. Perzynski, Eur. Phys. J. E: Soft Matter Biol. Phys., 1995, 52, 3936 CAS.
- A. Pal, T. Zinn, M. A. Kamal, T. Narayanan and P. Schurtenberger, Small, 2018, 14, 1802233 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01334g |
| This journal is © The Royal Society of Chemistry 2023 |