Open Access Article
Open Access ArticleIs there a difference between surfactant-stabilised and Pickering emulsions?
Riande I.
Dekker
*ab,
Santiago F.
Velandia
*ac,
Heleen V. M.
Kibbelaar
a,
Azeza
Morcy
a,
Véronique
Sadtler
c,
Thibault
Roques-Carmes
c,
Jan
Groenewold
b,
Willem K.
Kegel
b,
Krassimir P.
Velikov
 ad and
Daniel
Bonn
ad and
Daniel
Bonn
 a
a
avan der Waals-Zeeman Institute, Institute of Physics, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: r.i.dekker@uva.nl; s.f.velandiarodriguez@uva.nl
bVan’t Hoff Laboratory of Physical and Colloid Chemistry, Debye Institute for Nanomaterials Science, Utrecht University, Padualaan 8, 3584 CH, Utrecht, The Netherlands
cLaboratoire Réactions et Génie des Procédés, UMR 7274 CNRS, Université de Lorraine, 1 rue Grandville, 54001 Nancy, France
dUnilever Innovation Centre Wageningen, Bronland 14, 6708 WH Wageningen, The Netherlands
First published on 13th February 2023
Abstract
What measurable physical properties allow one to distinguish surfactant-stabilised from Pickering emulsions? Whereas surfactants influence oil/water interfaces by lowering the oil/water interfacial tension, particles are assumed to have little effect on the interfacial tension. Here we perform interfacial tension (IFT) measurements on three different systems: (1) soybean oil and water with ethyl cellulose nanoparticles (ECNPs), (2) silicone oil and water with the globular protein bovine serum albumin (BSA), and (3) sodium dodecyl sulfate (SDS) solutions and air. The first two systems contain particles, while the third system contains surfactant molecules. We observe a significant decrease in interfacial tension with increasing particle/molecule concentration in all three systems. We analyse the surface tension data using the Gibbs adsorption isotherm and the Langmuir equation of state for the surface, resulting in surprisingly high adsorption densities for the particle-based systems. These seem to behave very much like the surfactant system: the decrease in tension is due to the presence of many particles at the interface, each with an adsorption energy of a few kBT. Dynamic interfacial tension measurements show that the systems are in equilibrium, and that the characteristic time scale for adsorption is much longer for particle-based systems than for surfactants, in line with their size difference. In addition, the particle-based emulsion is shown to be less stable against coalescence than the surfactant-stabilised emulsion. This leaves us with the conclusion that we are not able to make a clear distinction between the surfactant-stabilised and Pickering emulsions.
Introduction
Pickering emulsions, i.e. particle-stabilised emulsions, were reported for the first time in the early 20th century by Ramsden1 and Pickering.2 However, they only gained significant interest from the beginning of the 21st century with increasing numbers of publications on Pickering emulsions.3–7 Such emulsions are believed to have strong advantages over surfactant-stabilised emulsions. They are believed to be stable over long time scales due to the particles that can completely prevent Ostwald ripening, the process where large droplets grow at the expense of small droplets.4,8,9 Furthermore, added functionality derived from the stabilising particles and their potentially much lower toxicity and environmental impact are unique properties of Pickering emulsions.10–12 However, in order to obtain stable Pickering emulsions in practice, often surfactants are added to a Pickering emulsion as co-stabiliser,13–16 albeit in lower concentrations than in conventional, surfactant-stabilised emulsions. This is major drawback in the search for surfactant-free products17,18 that are environmentally preferred. Another reason for the increased interest in Pickering emulsions, is that they are believed to be very stable against coalescence due to the high adsorption energies of the particles at the oil/water interface.19,20 The main idea is that both particles and surfactants adsorb to the oil/water interface. This results in a steric or electrostatic barrier that significantly slows down coalescence.20 Besides, surfactants are also known to reduce the oil/water interfacial tension, contributing to the emulsification and stabilisation. However, there is a large debate in literature whether particles at interfaces can also decrease the interfacial tension. Various review papers are dedicated to describing the effect of particles at interfaces and conclude that whereas many papers do report a decrease in interfacial tension caused by particle adsorption, as many papers can be found that report little or no effect of particle adsorption on the interfacial tension.21–25 Other authors considered the capillary pressure, and not the interfacial activity alone, as a reason to have emulsions highly stable against coalescence.26 Understanding what this interfacial activity means in the case of adsorbed particles could help to resolve this debate. This can be looked at from the point of view of the adsorption energy of a particle at an interface.The energy required to remove a particle with radius r from an oil/water interface with an interfacial tension of γow is given by:20,27
ΔE = πr2γow(1 ± cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 θ)2 | (1) |
To answer the question of whether there is a difference between a conventional, surfactant-stabilised emulsion and a Pickering emulsion, a good starting point would be to try and formulate a two-dimensional equation of state for the surfactants and particles at the surface. To this aim, we investigate the effect of particles to the oil/water interfacial tension in Pickering emulsions. We can relate this to the surface density and adsorption energy of the molecules and particles through the Gibbs adsorption equation and the Langmuir adsorption equation. Both are based on the assumption that there is an equilibrium between particles at the interface and particles in the continuous phase while measuring the interfacial tension. To account for more complex behavior of particles such as multilayer adsorption on heterogeneous sites or two-step adsorption theories, more detailed models can be considered.29,30 For simplicity, we limit ourselves here to the Gibbs adsorption equation and the Langmuir adsorption model as first step to address this problem. For this reason, we measure the dynamic interfacial tension over a long time and use the final, long-time constant value for the thermodynamic analysis, assuming thus that the interface is in equilibrium with the bulk.
The first Pickering system consists of ethyl cellulose nanoparticles (ENCPs). ENCPs were chosen due to their low toxicity and environmentally responsible character.11,31 We compare these results with experiments on two different emulsion stabilisers, namely the surfactant sodium dodecyl sulfate (SDS) and the globular protein bovine serum albumin (BSA). We selected this particular group of emulsifiers in part because they allow us to evaluate different Brownian particle sizes. It is important to note that Pickering emulsions can be made with a wide range of particles and particle sizes. We concentrate our study on a variety of “small” emulsifying agents because their small size allows for the production of small droplet sizes, which goes along with the various uses of Pickering emulsions. For globular proteins, an open question is whether these should be regarded as particles or as large, potentially surface-active molecules. For both the SDS and BSA, a reduction in the interfacial tension is observed. However also for the ENCPs a decrease in interfacial tension due to particle adsorption at the soybean oil/water interface is observed. This is also similar to earlier measurements on the same system of Bizmark et al.32,33
Materials and methods
Materials
Ethyl cellulose (code: 247499-100G), bovine serum albumin Fraction V, Imidazole (ReagentPlus, 99%), sodium azide (ReagentPlus, 99.5%), sodium dodecyl sulfate (ReagentPlus, 98.5%) and silicone oil (50 cSt at 25 °C) are purchased from Sigma Aldrich. Ethanol (100%, technical grade) is purchased from Interchema. Soybean oil is kindly provided by Unilever R & D. All products are used as received. All water used is purified by a Millipore apparatus (18.2 Ω cm at 25 °C).Interfacial tension of soybean oil and water with ECNPs
Aqueous dispersions of ECNPs are prepared via a modified ‘antisolvent precipitation’ technique from literature.32,34 Here, we briefly describe the method. Ethyl cellulose is dissolved in ethanol before being poured into a large volume of water under fast magnetic stirring, resulting in the spontaneous precipitation of ethyl cellulose as ECNPs due to nanoparticle nucleation. Subsequently, ethanol and some water are removed by rotary evaporation. This dispersion is then passed through a filter paper (Whatman filter paper Grade 1) to remove any large aggregates that form during the precipitation. The final concentration of the particles is determined by drying a small part of the particle dispersion. The dispersions are diluted with MilliQ water, resulting in stable aqueous dispersions of between 0.01 and 0.2 wt% of ECNPs. Note that the ENCPs preparation process does not involve the use of any surfactant.The size of the ECNPs is characterised by scanning electron microscopy (SEM, FEI XL30FEG) and dynamic light scattering (DLS, Malvern Zetasizer ZS). The SEM images are analysed in ImageJ, an average particle size is obtained from measuring at least 100 particles. The zetasizer uses dynamic light scattering to obtain a size distribution from the time-correlation function of the scattered intensity. The analysis of scattering data needed to obtain the average particle size and the size distribution is done using the CONTIN method.35 Additionally, previous measurements estimated the contact angle of the ECNPs to be 62. For details on the particle, emulsion drop size distribution and contact angle determination, see the work by Kibbelaar et al.36
Interfacial tension measurements of the interface between soybean oil and aqueous dispersions of ECNPs are performed using an OCA 20 from DataPhysics Instruments and analysed with the DataPhysics Instruments SCA 20 software module. The pendant drop measurements consist of generating a rising drop of soybean oil in a reservoir with a constant volume (5 mL) of ECNPs dispersion. The oil volume is kept constant at 20 μL for a duration of roughly 1000 s. The value for the interfacial tension is based on the shape of the oil droplet in the continuous phase and calculated by a dedicated software program.
Interfacial tension measurements of the interface between soybean oil and aqueous dispersions of ECNPs are also performed using a Krüss K100 force tensiometer with a Du Noüy ring. A waiting time of 1.5 hours is used after introducing the oil phase on top of the water phase to allow the particles to go to the oil/water interface.
Interfacial tension of silicone oil and water with BSA
MilliQ water is used to prepare an 0.5 mM imidazole buffer solution at pH = 7. Then, 1 wt% of BSA is added into 100 mL of buffer solution. The mixture is placed under agitation for 4 hours. A low-speed magnetic stirring process is used to prevent foaming in the BSA solutions. Throughout all the experiments the ionic strength remains constant at 5 mM. Subsequently, 0.02 wt% of sodium azide (antimicrobial) is added and the resulting solution is stored at 4 °C overnight before use. The maximum life time of these solutions is 5 days. The size of the BSA is characterised with dynamic light scattering (DLS) by means of an ALV LSE-5003 goniometer with a JDSU 1145P laser (wavelength 633 nm). A 8 nm hydrodynamic radius with a 0.146 polydispersity index was measured for the BSA protein.Interfacial tension measurements of the interface between silicone oil and aqueous dispersions of BSA are performed using an OCA 15EC tensiometer from DataPhysics Instruments and analysed with the DataPhysics Instruments SCA 22 software module. The pendant drop measurements consist of generating a rising drop of silicone oil in a reservoir with a constant volume (5 mL) of BSA dispersion. The BSA concentration is varied between 1 × 10−8 M and 1 × 10−3 M. The oil volume is kept constant at 20 μL for a duration of at least 1000 s. The value for the interfacial tension is calculated by the software, based on the shape of the oil droplet in the continuous phase. The Worthington number was used to determine the accuracy of interfacial tension measurements with the pendant drop method. This was defined by Berry and coworkers37 as 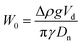 with Δρ the density difference between the pendant drop and the continuous phase, g the gravitational acceleration, Vd the drop volume, γ the interfacial tension and Dn the needle diameter. In their method the authors state that W0 ≪ 1 implies inaccurate values of interfacial tension. For both the ENCPs and BSA interfacial tension measurements we obtained W0 ≈ 0.5.
with Δρ the density difference between the pendant drop and the continuous phase, g the gravitational acceleration, Vd the drop volume, γ the interfacial tension and Dn the needle diameter. In their method the authors state that W0 ≪ 1 implies inaccurate values of interfacial tension. For both the ENCPs and BSA interfacial tension measurements we obtained W0 ≈ 0.5.
Surface tension measurements of an SDS solution
An SDS solution of 20 g L−1 is prepared by adding 20 g of SDS to 1 L of MilliQ water. The solution is stirred overnight. Surface tension measurements of the SDS solution are performed using a Krüss K100 force tensiometer with a Du Noüy ring. A microdispenser connected to the tensiometer automatically adds MilliQ water during the measurement to decrease the SDS concentration in steps to 10−6 g L−1.Microscopy study of emulsion stability
The preparation of ECNP-stabilised emulsions is described by Kibbelaar et al.36 In short, the emulsification is performed with an IKA T25 digital Ultra-Turrax homogenizer. The soybean oil is slowly added to the aqueous phase containing 2 wt% of particles, while mixing at 2k rpm. When the oil is added, the mixing speed is slowly increased. Emulsification is eventually performed at 20 k rpm for 2 min. For the stability experiments, an emulsion with ϕoil = 0.5 is used. The preparation of SDS-stabilised emulsions is described previously.38 The continuous phase is prepared by dissolving 1 wt% of SDS (Sigma-Aldrich) in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of glycerol and demineralised water. Nile red (Sigma-Aldrich) is added to the silicone oil (VWR Chemicals, viscosity 500 cSt) as a dye. The silicone oil is then slowly added to the continuous phase while stirring with a Silverson L5M-A emulsifier at 6000 rpm. This results in an emulsion with an average droplet diameter of 20 μm and ϕoil = 0.8.
50 mixture of glycerol and demineralised water. Nile red (Sigma-Aldrich) is added to the silicone oil (VWR Chemicals, viscosity 500 cSt) as a dye. The silicone oil is then slowly added to the continuous phase while stirring with a Silverson L5M-A emulsifier at 6000 rpm. This results in an emulsion with an average droplet diameter of 20 μm and ϕoil = 0.8.
A droplet of each of the emulsions is subsequently placed on a hydrophobised glass plate. The droplets are visualised with a bright field microscope. Every 10 s an image is recorded. After the first image, a hydrophobised cover slide is carefully placed on top of the droplets to induce accelerated coalescence.39 The behaviour of the droplets is recorded for two minutes.
The experiment with the ECNP-stabilised emulsion is then repeated using a Leica TCS SP8 confocal scanning microscope. Nile red is added to the oil phase, which is excited by a solid state 20 mW laser at 552 nm. This method is based on a time-pressure superposition principle that allows to consider emulsion stability through accelerated destabilization by the application of a pressure.40 It is worth clarifying that we do not assume that accelerated destabilization is equivalent to following the stability of emulsions for long periods. However, we believe that these tests can be a relative method for comparing emulsions with particles and with surfactants.
Results and discussion
Framework for analysis
The oil/water interfacial tension γ can be related to the concentration c of adsorbing species in the continuous phase via the Gibbs adsorption equation:41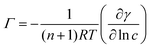 | (2) |
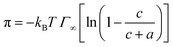 | (3) |
 | (4) |
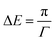 | (5) |
Interfacial tension of soybean oil and water with ECNPs
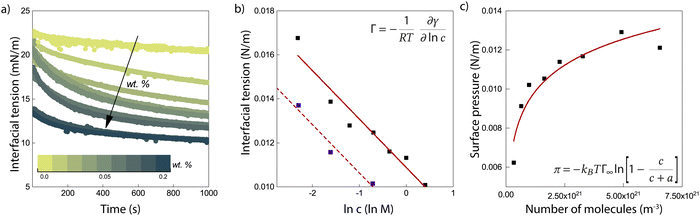
Fig. 1a shows the results of interfacial tension measurements with various nanoparticle concentrations. The results immediately show that the particles significantly decrease the interfacial tension, and an increase in particle concentration causes a faster decrease in the interfacial tension. This implies that ENCP particles are adsorbing to the water–oil interface. We do find also a very small decrease in interfacial tension over time for the oil/water system without particles. This is likely due to impurities in the soybean oil that are slightly surface active. However, the decrease in interfacial tension caused by these impurities is negligible compared to the reduction that we observe for the systems with ECNPs. A similar decrease in the interfacial tension due to ECNPs at the interface is reported for purified alkanes,33 where the same particles also cause a concentration-dependent reduction of the surface tension.44 Therefore, we believe that our data are valid and that impurities in the oil are not the explanation for this observed significant and systematic decrease in interfacial tension.We plot the interfacial tension as a function of the natural logarithm of the concentration in Fig. 1b and observe a linear decrease. From the slope of the curve, the adsorption density can be obtained via the Gibbs adsorption equation, see eqn (2). With n = 0, this results in an adsorption density of Γ = 5.3 × 1017 m−2 (Γ = 8.8 × 10−7 mol m−2) and an average area per particle 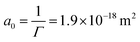 . However, we know that our particles have a diameter of 100 ± 5 nm, resulting in an area
. However, we know that our particles have a diameter of 100 ± 5 nm, resulting in an area 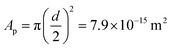 (by considering the exact contact angle and the projected radius of the particle at the interface being Rprojected = r·sin(θ), we obtain as similar value, Aprojected = 6.08 × 10−15 m2). There is thus almost a factor 1000 difference between the actual size of the particles (measured with both DLS and TEM) and the average area per particle obtained from analysing the interfacial tension results. As mentioned earlier, n will probably be somewhat different from zero, resulting in a somewhat lower adsorption density, but a factor of 1000 seems unlikely. An estimation of n can be obtained from the measured zeta potential of −30 mV, the Bjerrum length and the size of the particles. This results in a maximum n of 100. Finding the exact value for n in case of our ECNPs will be very useful for better analysis of our IFT data.
(by considering the exact contact angle and the projected radius of the particle at the interface being Rprojected = r·sin(θ), we obtain as similar value, Aprojected = 6.08 × 10−15 m2). There is thus almost a factor 1000 difference between the actual size of the particles (measured with both DLS and TEM) and the average area per particle obtained from analysing the interfacial tension results. As mentioned earlier, n will probably be somewhat different from zero, resulting in a somewhat lower adsorption density, but a factor of 1000 seems unlikely. An estimation of n can be obtained from the measured zeta potential of −30 mV, the Bjerrum length and the size of the particles. This results in a maximum n of 100. Finding the exact value for n in case of our ECNPs will be very useful for better analysis of our IFT data.
In order to check that this result is not an artifact of our measuring method, we use a second one. The blue squares in Fig. 1b shows the values for the interfacial tension as obtained with the Du Noüy ring method. These values are even a bit lower compared to the pendant drop technique, but allow for the same conclusion: a strong concentration-dependent decrease in the interfacial tension due to ECNPs at the oil/water interface. The discrepancy between the pendant drop measurements and the measurements with the Du Noüy ring arise probably from the different techniques that lay behind it, the pendant drop technique is a form of optical tensiometry, the Du Noüy ring is a form of force tensiometry.
A possible explanation for the discrepancy between the area per particle from the Gibbs equation and the actual particle size is that other, smaller, molecules contribute to the decrease in interfacial tension. A plausible hypothesis is that free ethyl cellulose molecules cause this decrease. Although ethyl cellulose is highly insoluble in water, ethyl cellulose from the nanoparticles might possibly dissolve in the oil phase during or after droplet formation. In order to verify whether free ethyl cellulose (if any) contributes to a decrease in the interfacial tension we perform interfacial tension measurements on soybean oil/water mixtures with ethyl cellulose molecules added either to the water phase or the oil phase. These measurements show that the presence of free ethyl cellulose in either the oil or water phase does not give an additional decrease in the interfacial tension compared to the oil/water system without any ethyl cellulose (nanoparticles). These results can also be found in Kibbelaar et al.36 Therefore, we can rule out the possibility that ethyl cellulose molecules go to the interface and thereby decrease the interfacial tension. We have tried to verify this further by centrifuging the particles and testing the interfacial tension between the supernatant and soybean oil. However, centrifuging these particles is a very delicate process, where not all particles sediment at too low centrifugal forces and particles are destroyed at too high centrifugal forces. We are therefore unable to draw conclusions from interfacial tension measurements with the supernatant.
Another potential explanation for the strong decrease in the interfacial tension with increasing particle concentration lies in the presence of ethanol in the particle dispersion. Ethanol is present during the antisolvent precipitation to form ethyl cellulose nanoparticles. In principle, the ethanol is removed from the particle dispersion via rotary evaporation. However, small amounts of ethanol could still be present in the dispersion. Due to the high solubility of ethanol in water, ethanol molecules are not likely to go to the interface. For example, 5 v% of ethanol is necessary to decrease the water surface tension with 25%. Therefore, we believe that any ethanol that is left after rotary evaporation will not be able to cause such a significant reduction in the interfacial tension as seen in Fig. 1a.
A fit of the data with the Langmuir model can be seen in Fig. 1c. From the fit, we obtain Γ∞ = 4.8 × 1017 m−2. This value is very similar to the value that we find by using the Gibbs adsorption equation, meaning that again we find an area per particle that is much too small for the size of the ECNPs. The adsorption energy then follows as 5–6 kBT. This is much lower than what is generally expected in literature. With r ≈ 50 nm, γow = 23 mN m−1 and θ = 62°, equation 1 gives an adsorption energy of ΔEmax = πr2γow = 1.3 × 104kBT.
Furthermore, we do a rough calculation of the percentage of particles at the oil/water interface compared to the total amount of particles in the dispersion. The lowest concentration contains 0.01 wt% of ECNPs. At a total volume of 5 mL, this gives a total of 8.4 × 1011 particles. An oil droplet of about 20 μL is formed, which has a total area of 3.6 × 10−5 m2. One particle has an area of Ap = 7.9 × 10−15 m2. Therefore, at a coverage of 100%, the total number of particles at the interface is 4.5 × 109. This is 0.5% of the total amount of particles. This calculation shows us that we have more than enough particles present to cover the oil/water interface in the way suggested by the Gibbs and Langmuir equations.
Interfacial tension of silicone oil and water with BSA
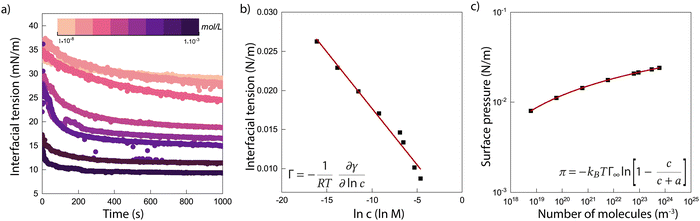
To get a better understanding of the surprising results of the interfacial tension measurements on the system with ECNPs, we perform similar experiments with the globular protein BSA at a silicone oil/water interface. Without specifying whether this protein should be considered as a particle or as a large molecule, the diameter of the protein of 10 nm makes the system interesting as its size lies in between the ECNPs and surfactants like SDS. The results are shown in Fig. 2a. We again observe a decrease in interfacial tension with increasing particle concentration. It has been reported before in literature that BSA can reduce the interfacial tension of various oil/water interfaces, as we observe here.45–47 The range of particle concentrations in our experiments is different from the ECNP system, however a very similar trend between the interfacial tension and ln c is observed (see Fig. 2b). From the Gibbs adsorption eqn (2), with n = 0, we obtain a value of Γ = 3.6 × 1017 m−2 (Γ = 5.9 × 10−7 mol m−2) and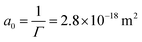 . The globular proteins are 10 nm in diameter, thus
. The globular proteins are 10 nm in diameter, thus 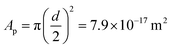 . Again we find that, according to the Gibbs adsorption equation, more proteins are at the interface than fit based on the particle size. The difference is however significantly smaller than for the ECNPs. The analysis of the interfacial tension data using the Langmuir model is shown in Fig. 2c. We obtain a good fit that gives Γ∞ = 3.4 × 1017 m−2, very close to the Gibbs adsorption isotherm. Using this analysis to obtain the energy per particle gives us ≈10 kBT. On the other hand, calculating the maximum adsorption energy using equation 1 gives ΔEmax = πr2γow = 6.5 × 102kBT (γow = 34 mN m−1).
. Again we find that, according to the Gibbs adsorption equation, more proteins are at the interface than fit based on the particle size. The difference is however significantly smaller than for the ECNPs. The analysis of the interfacial tension data using the Langmuir model is shown in Fig. 2c. We obtain a good fit that gives Γ∞ = 3.4 × 1017 m−2, very close to the Gibbs adsorption isotherm. Using this analysis to obtain the energy per particle gives us ≈10 kBT. On the other hand, calculating the maximum adsorption energy using equation 1 gives ΔEmax = πr2γow = 6.5 × 102kBT (γow = 34 mN m−1).
Surface tension measurements of an SDS solution
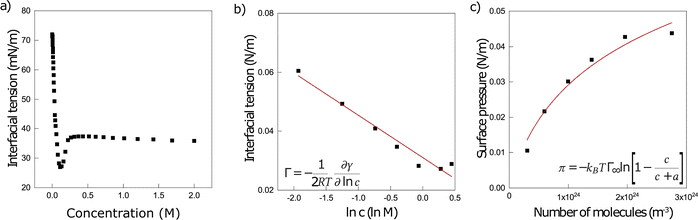
We do not understand the large decrease in interfacial tension for the ECNPs and the BSA system. The results from the Gibbs adsorption equation and the Langmuir model are not consistent with the size of the species that we obtain from characterisation with DLS. A very well studied system is sodium dodecyl sulfate (SDS), an anionic surfactant that successfully stabilises many emulsions. We perform analogous measurements on an SDS solution and analyse these data in the same way as the ECNPs and BSA interfacial tension measurements. We here use surface tension measurements that are very similar to interfacial tension measurements, but with air as one of the two phases instead of oil. These give the same information about the surface activity of the molecules. Surfactants have a relatively low energy of desorption due to the small size of the molecules.20 The size of a SDS head is approximately 40 Å2,48 and the surface tension of water is 72 mN m−1, resulting in an energy of desorption of 7.1 kBT, using equation 1. This is still rather high due to the relatively high surface tension of the water/air interface. At the soybean oil/water interface (γow = 23 mN m−1), the energy of desorption reduces to 2.3 kBT.The surface tension measurements of an SDS solution are shown in Fig. 3a. Since SDS molecules are much smaller, they adsorb at the surface much faster and the equilibrium surface tension is reached very rapidly (in a few ms). These experiments therefore only show the equilibrium surface tension over a range of concentrations. The results show three regimes. In the first regime, the surface tension decreases with increasing SDS concentration. In the second regime, we observe a small increase in surface tension with increasing SDS concentration. Then, in the third regime, the post-cmc equilibrium surface tension of 37 mN m−1 is achieved. This second regime, in which the measured surface tension is lower than the equilibrium surface tension, is a result also found by other authors and is usually related to impurities present with the SDS such as dodecyl alcohol or inorganic salts.49–51
For the Gibbs adsorption isotherm, using the first part of the measurement and using n = 1, since SDS dissociates into an SDS anion and a Na+ cation, the Gibbs adsorption isotherm gives Γ = 3.6 × 1018 m−2 (Γ = 5.9 × 10−6 mol m−2) and 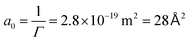 . This is in good agreement with the size of the SDS head from literature of 40 Å2.48 The Langmuir model also works very well for the surface tension of SDS, resulting in Γ∞ = 7.3 × 1018 m−2 and ΔE ≈ 2 kBT. If we calculate the energy of desorption viaeqn (1) using Γ∞, we obtain
. This is in good agreement with the size of the SDS head from literature of 40 Å2.48 The Langmuir model also works very well for the surface tension of SDS, resulting in Γ∞ = 7.3 × 1018 m−2 and ΔE ≈ 2 kBT. If we calculate the energy of desorption viaeqn (1) using Γ∞, we obtain 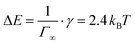 . Both methods to calculate the energy of desorption thus give the same result.
. Both methods to calculate the energy of desorption thus give the same result.
Dynamic interfacial tension
The dynamics of interfacial tension measurements allow us to say something about the rate of diffusion of the species that are going to the interface and lower the interfacial tension. Hua and Rosen52 proposed the equation: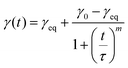 | (6) |
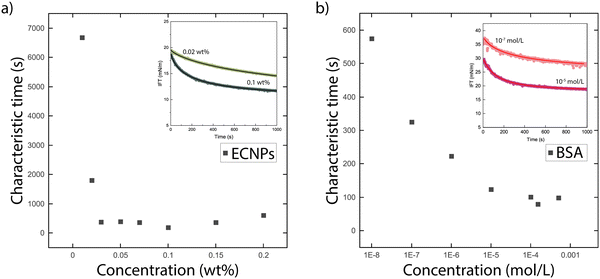 | ||
| Fig. 4 Characteristic diffusion time for particles to adsorb at the interface, obtained from a fit of the dynamic interfacial tension data with the Hua and Rosen model for (a) ECNPs and (b) BSA. The insets show fits of the IFT data with eqn (6). | ||
The second important conclusion is that the measured adsorption times are consistent with the idea that for the particle systems, it is the particles (and not for instance some impurity) that adsorb and lower the tension. This follows from both the fact that the interfacial tension consistently decrease with increasing particle concentration, and from the value of the characteristic time scale τ of the decrease. For the ECNPs system, we see that τ decreases with particle concentration, but for high enough concentrations the value becomes constant around τ ≈ 350 s (see Fig. 4a). For the BSA system, we observe similar behaviour (see Fig. 4b), with a stabilisation around τ = 100 s. For SDS, this characteristic time is much shorter, around 100 ms.53
Ward and Tordai54 developed a model that relates the characteristic time τ to the diffusion coefficient D via the surfactant concentration c in the bulk and the adsorption density Γ. Comparing the model to the data however gives unphysical results, because of the strong dependence of the time on both bulk concentration and adsorption density that is not observed in the experiments; this was already concluded previously in studies of dynamic surface tension of different surfactants.55 Nonetheless, one would expect the characteristic times to scale as the inverse of the diffusion coefficient,54 which is again inversely proportional to the size following the Stokes–Einstein equation.56 The size ratios of the ECNP, BSA and SDS is roughly 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, in rough agreement with the observed characteristic times of 350, 100 and 0.1 s. However a more detailed description of the adsorption dynamics would be needed to make this more quantitative; the large difference between BSA and SDS likely comes from the fact that the SDS is more concentrated than the BSA over the ranges probed here.
1, in rough agreement with the observed characteristic times of 350, 100 and 0.1 s. However a more detailed description of the adsorption dynamics would be needed to make this more quantitative; the large difference between BSA and SDS likely comes from the fact that the SDS is more concentrated than the BSA over the ranges probed here.
Stability of ECNP-stabilised Pickering emulsions compared to SDS-stabilised emulsions
For the stability experiments, an ECNP-stabilised emulsion with ϕoil = 0.5 is used and an SDS-stabilised emulsion with ϕoil = 0.8 is used. A small puddle of each of the emulsions is placed on a hydrophobized glass plate. The puddles are visualised with a bright field microscope. Every 10 s an image is recorded. After the first image, a hydrophobized cover slide is carefully placed on top of the pudddles. The behaviour of the puddles is recorded for two minutes. The results are shown in Fig. 5. The glass plates are hydrophobized to prevent spreading of the emulsion on a hydrophilic glass plate. For comparison, we perform the experiment comparing the ECNP-stabilised emulsion to the SDS-stabilised emulsion.The time between two images is 10 s. The left puddle is a Pickering emulsion stabilised by ECNPs, whereas the right one is the SDS-stabilised emulsion. The first image shows the situation before a cover slide is placed on top of the emulsion puddles that are a few millimeters in width. A cover slide is then carefully placed on top of the emulsions. Due to the confinement between the two plates, the diameter of both puddles increases. The hydrophobized cover slide prevents spreading of the emulsion and induces droplet coalescence by confinement.39 From the large energy necessary to remove particles, we anticipate that the Pickering emulsion puddle will take longer to present any type of phase separation under the microscope. However, in the third image something unexpected occurs. At the upper end of the Pickering emulsion puddle separation of water and oil occurs, and we see that over time this area, where separation occurs, increases. At the same time the surfactant-stabilised emulsion remains stable. This is surprising: the induced-destabilisation of the ENCP-stabilised emulsion is rapid, contrary to the usual assumption of superior stability of Pickering emulsions attributed to the high desorption energy of the relatively large particles.19,57 Such behavior might suggest that additional forces or mechanisms describe the high (or low) resistance of Pickering emulsions towards induced-destabilisation, as proposed by other authors.26,58
To get a better view of what happens to the emulsion, we investigate a droplet of Pickering emulsion with a confocal microscope. The presence of Nile red in the emulsion renders the oil phase bright. The results of the experiment are shown in Fig. 6. The left image shows the emulsion on top of a cover slide. Although the emulsion droplets are not perfectly spherical, the emulsion is stable at rest. After carefully placing a cover slide on top of the emulsion, the right image is recorded. The largest part of the image is rendered in red, due to a large area of oil. A few stable oil droplets can still be observed, but the bigger part of the emulsion is destabilised. From these observations, we can consider that the Pickering emulsions destabilise in a similar way as surfactant-stabilised emulsions since both require low energy input to induce destabilization.38,59 Intriguingly, to induce coalescence in surfactant-stabilised emulsions, the emulsion needs to be squeezed quite significantly. Our ECNP-stabilised Pickering emulsion, however, already destabilises when putting a drop on a microscope slide and simply placing a cover slide on top of it. These observations in our Pickering emulsion show that although on the shelf our emulsions are stable against coalescence for months, confinement induced-destabilisation occurs very rapidly as soon as a small amount of pressure in the form of a cover slide is applied. In the future, we foresee further research on the stability of Pickering emulsions to connect our results with bulk emulsion stability.
Conclusion
An overview of all the parameters that we have investigated based on the interfacial tension measurements on ECNPs and BSA systems and surface tension measurements on SDS solutions are listed in Table 1.| ECNPs | BSA | SDS | |
|---|---|---|---|
| d DLS (m) | 1.0 × 10−7 | 1.0 × 10−8 | 7.1 × 10−10 |
| A p (m2) | 7.9 × 10−15 | 7.9 × 10−17 | 4.0 × 10−19 |
| Γ Gibbs (m−2) | 5.3 × 1017 | 3.6 × 1017 | 3.6 × 1018 |
| a 0 (m2) | 1.9 × 10−18 | 2.8 × 10−18 | 2.8 × 10−19 |
| Γ ∞ (m−2) | 5.8 × 1017 | 3.4 × 1017 | 7.3 × 1018 |
| ΔE (kBT) | ≈5 | ≈10 | ≈2 |
| ΔEmax (kBT) | 1.3 × 104 | 6.5 × 102 | 2.4 |
| D SE (m2 s−1) | 6.6 × 10−12 | 6.6 × 10−11 | 6.0 × 10−10 |
| τ (s) | 350 | 100 | 10−2 |
| D exp (s) | 1.7 × 10−14 | 6 × 10−14 | 4.3 × 10−10 |
We have performed interfacial tension measurements on three different systems: (1) soybean oil and water with ethyl cellulose nanoparticles (ECNPs), (2) silicone oil and water with the globular protein bovine serum albumin (BSA), and (3) sodium dodecyl sulfate (SDS) solutions and air. For all three systems we observe a large and concentration-dependent decrease of the interfacial tension. There are various examples in literature that describe a similar significant reduction of the interfacial tension due to adsorption of particles at the interface.21–25 Specifically Bizmark et al.32,33 worked on ECNPs similar to ours and also observed a strong reduction. We therefore do not believe that there is some flaw in our measurement method, and have also done our very best to rule out spurious effects due to impurities.
If we accept these results, from the concentration-dependent decrease of the interfacial tension, we obtain adsorption densities from the Gibbs adsorption equation. Surprisingly, very high particle densities for the ENCPs and BSA systems are found, resulting in an average area per particle significantly smaller than the size of the particles obtained by DLS measurements. This may suggest the formation of multilayers at the interface or strong contributions from the counterions. The Langmuir isotherm gives similar adsorption densities as the Gibbs adsorption isotherm. From there we calculate an adsorption energy per particle that even for the 100 nm ECNPs is only a few kBT, in contradiction to the thousands of kBT normally reported in literature. We have to admit that these equilibrium arguments are not sufficient to explain the significant, concentration-dependent decrease of the interfacial tension for our particles.
We observe that both surfactants and particles can result in a significant decrease of the interfacial tension, making it impossible to distinguish between particles or surfactants based on the equilibrium interfacial tension. Notably, the small adsorption/desorption energy is compatible with the rapid exchange of particles between droplets observed by French et al.,60 and our observation that the ECNP-stabilised emulsions are very unstable.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank prof. Dr Bernard Binks and prof. Dr Adrian Rennie for very helpful discussions. We also would like to thank Dr Jo Janssen from Unilever R & D for helpful suggestions. We would like to thank Paul Kolpakov for his help with the surface tension measurements on SDS solutions. The work of RD is part of the research programme Controlling Multiphase Flow with project number 680-91-012, which is (partly) financed by the Dutch Research Council (NWO) and co-funded by TKI-E&I with the supplementary grant ‘TKI- Toeslag’ for Topconsortia for Knowledge and Innovation (TKI’s) of the Ministry of Economic Af- fairs and Climate Policy. This work took place within the framework of the Institute of Sustainable Process Technology. This work was partially funded by Evodos, Shell.References
- W. Ramsden, Separation of Solids in the Surface-Layers of Solutions and’Suspensions’(Observations on Surface-Membranes, Bubbles, Emulsions, and Mechanical Coagulation), Proc. R. Soc. London, 1903, 72, 156–164 CAS.
- S. Pickering, Pickering Emulsions, J. Chem. Soc., Trans., 1907, 91, 2001–2021 RSC.
- B. P. Binks and S. O. Lumsdon, Catastrophic Phase Inversion of Water-in-Oil Emulsions Stabilized by Hydrophobic Silica, Langmuir, 2000, 16, 2539–2547 CrossRef CAS.
- S. Tcholakova, N. D. Denkov and A. Lips, Comparison of solid particles, globular proteins and surfactants as emulsifiers, Phys. Chem. Chem. Phys., 2007, 9, 6313–6318 RSC.
- Y. Chevalier and M. A. Bolzinger, Emulsions stabilized with solid nanoparticles: Pickering emulsions, Colloids Surf., A, 2013, 439, 23–34 CrossRef CAS.
- Y. Yang, Z. Fang, X. Chen, W. Zhang, Y. Xie, Y. Chen, Z. Liu and W. Yuan, An overview of pickering emulsions: Solid-particle materials, classification, morphology, and applications, Front. Pharmacol., 2017, 8, 1–20 Search PubMed.
- H. Jiang, Y. Sheng and T. Ngai, Pickering emulsions: Versatility of colloidal particles and recent applications, Curr. Opin. Colloid Interface Sci., 2020, 49, 1–15 CrossRef CAS PubMed.
- Z. Du, M. P. Bilbao-Montoya, B. P. Binks, E. Dickinson, R. Ettelaie and B. S. Murray, Outstanding stability of particle-stabilized bubbles, Langmuir, 2003, 19, 3106–3108 CrossRef CAS.
- R. G. Alargova, D. S. Warhadpande, V. N. Paunov and O. D. Velev, Foam superstabilization by polymer microrods, Langmuir, 2004, 20, 10371–10374 CrossRef CAS PubMed.
- E. Dickinson, Food emulsions and foams: Stabilization by particles, Curr. Opin. Colloid Interface Sci., 2010, 15, 40–49 CrossRef CAS.
- X. Wu, L. Zhang, X. Zhang, Y. Zhu, Y. Wu, Y. Li, B. Li and S. Liu, Ethyl cellulose nanodispersions as stabilizers for oil in water Pickering emulsions, Sci. Rep., 2017, 7, 1–10 CrossRef PubMed.
- C. L. Harman, M. A. Patel, S. Guldin and G. L. Davies, Recent developments in Pickering emulsions for biomedical applications, Curr. Opin. Colloid Interface Sci., 2019, 39, 173–189 CrossRef CAS.
- C. P. Whitby, D. Fornasiero and J. Ralston, Effect of adding anionic surfactant on the stability of Pickering emulsions, J. Colloid Interface Sci., 2009, 329, 173–181 CrossRef CAS PubMed.
- J. Wang, F. Yang, J. Tan, G. Liu, J. Xu and D. Sun, Pickering emulsions stabilized by a lipophilic surfactant and hydrophilic platelike particles, Langmuir, 2010, 26, 5397–5404 CrossRef CAS PubMed.
- Z. Hu, S. Ballinger, R. Pelton and E. D. Cranston, Surfactant-enhanced cellulose nanocrystal Pickering emulsions, J. Colloid Interface Sci., 2015, 439, 139–148 CrossRef CAS PubMed.
- M. A. Khan and M. F. Haase, Stabilizing liquid drops in nonequilibrium shapes by the interfacial crosslinking of nanoparticles, Soft Matter, 2021, 17, 2034–2041 RSC.
- I. M. Banat, R. S. Makkar and S. S. Cameotra, Potential commercial applications of microbial surfactants, Appl. Microbiol. Biotechnol., 2000, 53, 495–508 CrossRef CAS PubMed.
- I. Capron and B. Cathala, Surfactant-free high internal phase emulsions stabilized by cellulose nanocrystals, Biomacromolecules, 2013, 14, 291–296 CrossRef CAS PubMed.
- R. Aveyard, B. Binks and J. Clint, Emulsions Stabilized Solely by Colloidal Particles, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
- B. P. Binks, Particles as surfactants - Similarities and differences, Curr. Opin. Colloid Interface Sci., 2002, 7, 21–41 CrossRef CAS.
- T. Okubo, Surface Tension of Structured Colloidal Suspensions of Polystyrene and Silica Spheres at the Air-Water Interface, J. Colloid Interface Sci., 1995, 171, 55–62 CrossRef CAS.
- N. Saleh, T. Sarbu, K. Sirk, G. V. Lowry, K. Matyjaszewski and R. D. Tilton, Oil-inwater emulsions stabilized by highly charged polyelectrolyte-grafted silica nanoparticles, Langmuir, 2005, 21, 9873–9878 CrossRef CAS PubMed.
- N. Glaser, D. J. Adams, A. Böker and G. Krausch, Janus Particles at Liquid-Liquid Interfaces, Langmuir, 2006, 22, 5227–5229 CrossRef CAS PubMed.
- S. Kutuzov, J. He, R. Tangirala, T. Emrick, T. P. Russell and A. Böker, On the kinetics of nanoparticle self-assembly at liquid/liquid interfaces, Phys. Chem. Chem. Phys., 2007, 9, 6351–6358 RSC.
- J. Forth, P. Y. Kim, G. Xie, X. Liu, B. A. Helms and T. P. Russell, Building Reconfigurable Devices Using Complex Liquid–Fluid Interfaces, Adv. Mater., 2019, 31, 1806370 CrossRef PubMed.
- G. Kaptay, On the Equation of the Maximum Capillary Pressure Induced by Solid Particles to Stabilize Emulsions and Foams and on the Emulsion Stability Diagrams, Colloids Surf., A, 2006, 282–283, 387–401 CrossRef.
- S. Levine, B. D. Bowen and S. J. Partridge, Stabilization of emulsions by fine particles I. Partitioning of particles between continuous phase and oil/water interface, Colloids Surf., 1989, 38, 325–343 CrossRef CAS.
- D. J. French, A. T. Brown, A. B. Schofield, J. Fowler, P. Taylor and P. S. Clegg, The secret life of Pickering emulsions: particle exchange revealed using two colours of particle, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- B.-Y. Zhu and T. Gu, Surfactant Adsorption at Solid-Liquid Interfaces, Adv. Colloid Interface Sci., 1991, 37, 1–32 CrossRef CAS.
- K. Y. Foo and B. H. Hameed, Insights into the Modeling of Adsorption Isotherm Systems, Chem. Eng. J., 2010, 156, 2–10 CrossRef CAS.
- S. Prasertmanakit, N. Praphairaksit, W. Chiangthong and N. Muangsin, Ethyl cellulose microcapsules for protecting and controlled release of folic acid, AAPS PharmSciTech, 2009, 10, 1104–1112 CrossRef CAS PubMed.
- N. Bizmark and M. A. Ioannidis, Effects of Ionic Strength on the Colloidal Stability and Interfacial Assembly of Hydrophobic Ethyl Cellulose Nanoparticles, Langmuir, 2015, 31, 9282–9289 CrossRef CAS PubMed.
- N. Bizmark and M. A. Ioannidis, Ethyl Cellulose Nanoparticles at the Alkane - WaterInterface and the Making of Pickering Emulsions, Langmuir, 2017, 33, 10568–10576 CrossRef CAS PubMed.
- D. R. Hayden, H. V. Kibbelaar, A. Imhof and K. P. Velikov, Size and Optically unable Ethyl Cellulose Nanoparticles as Carriers for Organic UV Filters, ChemNanoMat, 2018, 4, 301–308 CrossRef CAS.
- A. Scotti, W. Liu, J. S. Hyatt, E. S. Herman, H. S. Choi, J. W. Kim, L. A. Lyon, U. Gasser and A. Fernandez-Nieves, The CONTIN algorithm and its application to determine the size distribution of microgel suspensions, J. Chem. Phys., 2015, 142, 234905 CrossRef CAS PubMed.
- H. V. Kibbelaar, R. I. Dekker, A. Morcy, W. K. Kegel, K. P. Velikov and D. Bonn, Ethyl cellulose nanoparticles as stabilizers for Pickering emulsions, Colloids Surf., A, 2022, 641, 128512 CrossRef CAS.
- J. D. Berry, M. J. Neeson, R. R. Dagastine, D. Y. C. Chan and R. F. Tabor, Measurement of Surface and Interfacial Tension Using Pendant Drop Tensiometry, J. Colloid Interface Sci., 2015, 454, 226–237 CrossRef CAS PubMed.
- R. I. Dekker, A. Deblais, B. Veltkamp, P. Veenstra, W. K. Kegel and D. Bonn, Creep and drainage in the fast destabilization of emulsions, Phys. Fluids, 2021, 33, 033302 CrossRef CAS.
- A. Deblais, R. Harich, D. Bonn, A. Colin and H. Kellay, Spreading of an Oil-in-Water Emulsion on a Glass Plate: Phase Inversion and Pattern Formation, Langmuir, 2015, 31, 5971–5981 CrossRef CAS PubMed.
- T. Tsuji, K. Mochizuki, K. Okada, Y. Hayashi, Y. Obata, K. Takayama and Y. Onuki, Time–Temperature Superposition Principle for the Kinetic Analysis of Destabilization of Pharmaceutical Emulsions, Int. J. Pharm., 2019, 563, 406–412 CrossRef CAS PubMed.
- J. W. Gibbs, Scientific Papers Of J. Willard Gibbs, Dover, New York, 1961, vol. 1, p. 474 Search PubMed.
- R. P. Borwankar and D. T. Wasan, Equilibrium and dynamics of adsorption of surfactants at fluid-fluid interfaces, Chem. Eng. Sci., 1988, 43, 1323–1337 CrossRef CAS.
- P. A. Kralchevsky, K. D. Danov, G. Broze and A. Mehreteab, Thermodynamics of ionic surfactant adsorption with account for the counterion binding: Effect of salts of various valency, Langmuir, 1999, 15, 2351–2365 CrossRef CAS.
- N. Bizmark, M. A. Ioannidis and D. E. Henneke, Irreversible adsorption-driven assembly of nanoparticles at fluid interfaces revealed by a dynamic surface tension probe, Langmuir, 2014, 30, 710–717 CrossRef CAS PubMed.
- A. J. Ward and L. H. Regan, Pendant drop studies of adsorbed films of bovine serum albumin. I. Interfacial tensions at the isooctane/water interface, J. Colloid Interface Sci., 1980, 78, 389–394 CrossRef CAS.
- D. J. Burgess and N. O. Sahin, Interfacial rheological and tension properties of protein films, J. Colloid Interface Sci., 1997, 189, 74–82 CrossRef CAS.
- É. Kiss and R. Borbás, Protein adsorption at liquid/liquid interface with low interfacial tension, Colloids Surf., B, 2003, 31, 169–176 CrossRef.
- C. M. Johnson and E. Tyrode, Study of the adsorption of sodium dodecyl sulfate (SDS) at the air/water interface: Targeting the sulfate headgroup using vibrational sum frequency spectroscopy, Phys. Chem. Chem. Phys., 2005, 7, 2635–2640 RSC.
- E. A. El-Hefian and A. H. Yahaya, Investigation on some properties of SDS solutions, Aust. J. Basic Appl. Sci., 2011, 5, 1221–1227 CAS.
- L.-J. Chen, S.-Y. Lin, C.-S. Chern and S.-C. Wu, Critical Micelle Concentration of Mixed Surfactant SDS/NP(EO)40 and Its Role in Emulsion Polymerization, Colloids Surf., A, 1997, 122, 161–168 CrossRef CAS.
- L. Tofani, A. Feis, R. E. Snoke, D. Berti, P. Baglioni and G. Smulevich, Spectroscopic and Interfacial Properties of Myoglobin/Surfactant Complexes, Biophys. J., 2004, 87, 1186–1195 CrossRef CAS PubMed.
- X. Y. Hua and M. J. Rosen, Dynamic surface tension of aqueous surfactant solutions. I. Basic paremeters, J. Colloid Interface Sci., 1988, 124, 652–659 CrossRef CAS.
- M. Aytouna, Droplet Dynamics, PhD thesis, University of Amsterdam, 2012 Search PubMed.
- A. F. Ward and L. Tordai, Time-dependence of boundary tensions of solutions I. The role of diffusion in time-effects, J. Chem. Phy., 1946, 14, 453–461 CrossRef CAS.
- M. Aytouna, D. Bartolo, G. Wegdam, D. Bonn and S. Rafaï, Impact dynamics of surfactant laden drops: Dynamic surface tension effects, Exp. Fluids, 2010, 48, 49–57 CrossRef CAS.
- A. Einstein, On the movement of small particles suspended in a stationary liquid demanded by the molecular kinetic theory of heat, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- J. Bibette, D. C. Morse, T. A. Witten and D. A. Weitz, Stability Criteria for Emulsions, Phys. Rev. Lett., 1992, 69, 2439–2443 CrossRef CAS PubMed.
- N. D. Denkov, I. B. Ivanov, P. A. Kralchevsky and D. T. Wasan, A Possible Mechanism of Stabilization of Emulsions by Solid Particles, J. Colloid Interface Sci., 1992, 150, 589–593 CrossRef CAS.
- R. I. Dekker, A. Deblais, K. P. Velikov, P. Veenstra, A. Colin, H. Kellay, W. K. Kegel and D. Bonn, Emulsion Destabilization by Squeeze Flow, Langmuir, 2020, 36, 7795–7800 CrossRef CAS PubMed.
- D. J. French, P. Taylor, J. Fowler and P. S. Clegg, Making and breaking bridges in a Pickering emulsion, J. Colloid Interface Sci., 2015, 441, 30–38 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |