Magnetically induced stiffening for soft robotics†
Leah T.
Gaeta
 a,
Kevin J.
McDonald
a,
Kevin J.
McDonald
 a,
Lorenzo
Kinnicutt
a,
Megan
Le
a,
Lorenzo
Kinnicutt
a,
Megan
Le
 a,
Sidney
Wilkinson-Flicker
a,
Yixiao
Jiang
a,
Taylan
Atakuru
b,
Evren
Samur
a,
Sidney
Wilkinson-Flicker
a,
Yixiao
Jiang
a,
Taylan
Atakuru
b,
Evren
Samur
 b and
Tommaso
Ranzani
b and
Tommaso
Ranzani
 *acd
*acd
aDepartment of Mechanical Engineering, Boston University, Boston, MA 02215, USA. E-mail: tranzani@bu.edu
bDepartment of Mechanical Engineering, Boğaziçi University, Istanbul, Turkey
cDivision of Materials Science and Engineering, Boston University, Boston, MA 02215, USA
dDepartment of Biomedical Engineering, Boston University, Boston, MA 02215, USA
First published on 17th March 2023
Abstract
Soft robots are well-suited for human-centric applications, but the compliance that gives soft robots this advantage must also be paired with adequate stiffness modulation such that soft robots can achieve more rigidity when needed. For this reason, variable stiffening mechanisms are often a necessary component of soft robot design. Many techniques have been explored to introduce variable stiffness structures into soft robots, such as pneumatically-controlled jamming and thermally-controlled phase change materials. Despite fast response time, jamming methods often require a bulkier pneumatic pressure line which limits portability; and while portable via electronic control, thermally-induced methods require compatibility with high temperatures and often suffer from slow response time. In this paper, we present a magnetically-controlled stiffening approach that combines jamming-based stiffening principles with magnetorheological fluid to create a hybrid mechanical and materials approach. In doing so, we combine the advantages of fast response time from pneumatically-based jamming with the portability of thermally-induced phase change methods. We explore the influence of magnetic field strength on the stiffening of our magnetorheological jamming beam samples in two ways: by exploiting the increase in yield stress of magnetorheological fluid, and by additionally using the clamping force between permanent magnets to further stiffen the samples via a clutch effect. We introduce an analytical model to predict the stiffness of our samples as a function of the magnetic field. Finally, we demonstrate electronic control of the stiffness using electropermanent magnets. In this way, we present an important step towards a new electronically-driven stiffening mechanism for soft robots that interact safely in close contact with humans, such as in wearable devices.
1 Introduction
Soft robots are dexterous devices capable of interacting with their environment in a way rigid robots cannot.1,2 Their compliant nature allows them to conform to complex structures in a nondestructive manner.3–5 However, while the inherent compliance of soft robots affords many opportunities with regard to applications in delicate environments, the ability to adjust and reverse soft robot compliance is often required to improve force transmission,6–9 enable weight-bearing tasks,10,11 or reconfigure the robot body to adapt to different environments.12–15 Embedding variable stiffness components is often an essential feature in multiple soft robotics applications including haptics,16–19 wearables device design,11,20–24 soft surgical robots,6,8,25–27 and soft manipulation and grasping.28,29 For this reason, there has been a continuous focus on developing variable stiffness structures for soft robots and variable stiffening mechanisms are paramount to the design of soft robotic devices.14,30–33 Such structures allow a soft robot to remain flexible up to the moment when it is necessary to interact with its environment, at which point it reverts from its inherently low-stiffness state to one of more rigidity.Various techniques have been employed to implement variable stiffness structures in soft robots.30,33 Jamming remains among the most popular techniques of these as the change in stiffness occurs on the order of milliseconds.34,35 This quick stiffness change can be useful for a variety of applications, from molding objects for quick prototyping35 to safely landing an unmanned aerial vehicle.36 In jamming-based stiffening mechanisms, external stresses are applied to a compliant region of low-density packed granular, layered, or fibrous media to increase the density and solidify the structure.35 Depending on the type of jamming elements, the overall structure can have its stiffness tuned to resist deformation in different directions.35,37 The jamming transition can be induced in various ways, most commonly via the application of vacuum pressure.13,38 Recently, there have been developments in the use of positive pressure and passive activation methods.10,20,39
Jamming structures have also been used to implement clutches and brakes for soft wearable applications,40,41 such as in exoskeleton design for mobility assistance and in orthoses to control movement range of motion.42 Clutching mechanisms are particularly important in soft wearable robotics as they are used to withstand high forces from undesired human motions, and can be easily withdrawn when no longer needed.43
Variable stiffening mechanisms for soft robotics that do not rely on a pressure source have been proposed in the literature. Phase change materials in the form of low melting point metal alloys and shape memory polymers have been used to thermally adjust the stiffness of a variety of actuators, grippers, and other soft robotic structures.8,14,44–54 These systems typically contain an electrically controlled heater to induce the phase change, in turn modifying the stiffness of the soft robot itself. Though these phase change materials have the advantage of being electronically controlled and portable, locally heating these mechanisms is often slow (on the order of tens of seconds when supplied by lower power)50,55 and is not always compatible or safe in applications involving human contact. Magnetically-controlled stiffening mechanisms have also been explored. This has been primarily through the use of magnetorheological fluids and magnetorheological elastomers (MREs). MREs consist of magnetic particles suspended in an elastomeric matrix.56,57 This produces a solid structure that stiffens in the presence of a magnetic field.58 The behavior of MREs is determined by many parameters such as type of MRE, particle size and volume fraction, applied magnetic field, and polymer matrix.59–61 MREs generally require fields up to 0.8 T to provide stiffening up to 60%.62–68
Magnetorheological fluids are a class of smart fluids that solidify with a characteristic yield stress and viscosity in the presence of a magnetic field.69 Magnetorheological fluids consist of micron-scale iron particles in a carrier fluid such as water or oil along with stabilizing additives. The microscopic iron particles align themselves along magnetic field lines, leading to the macroscopic stiffening effect in the bulk fluid.70 The solidification of magnetorheological fluids occurs within a few milliseconds71–76 when a magnetic field is applied, and this solidification increases with increasing magnetic field such that the stiffness of the material can be proportionally tuned.31 This effect has historically been used in the production of active dampers77–80 and when conforming around objects for gripping.81 Magnetorheological fluid domains have been introduced into silicone structures to allow for magnetically activated variable stiffening.82,83 The modulus of these materials can increase two to thirty-fold at high magnetic fields of 1000 mT, depending on the magnetorheological fluid volume fraction in the silicone-based composite.83 Magnetically induced stiffening provides the advantage that magnetic fields can be electronically generated, thus resulting in electronically controlled stiffening. The solidification behavior of magnetorheological fluids can be electronically controlled using electromagnets84 or electropermanent magnets.85,86
Despite the development of these stiffening techniques, several issues limit their adoption. Jamming structures require an external pressure or vacuum source, limiting their portability and use in applications such as wearable devices and autonomous robots where the bulk of a pump can inhibit mobility.20,35,38,42,87 Thermally activated variable stiffening mechanisms can be slow due to their reliance on phase change materials and the heating necessary for phase transitions can limit their applicability in close contact with the body.50,55 Smart fluids by themselves provide limited stiffening in the absence of large fields that are impractical to achieve in many portable real-world systems.82,83
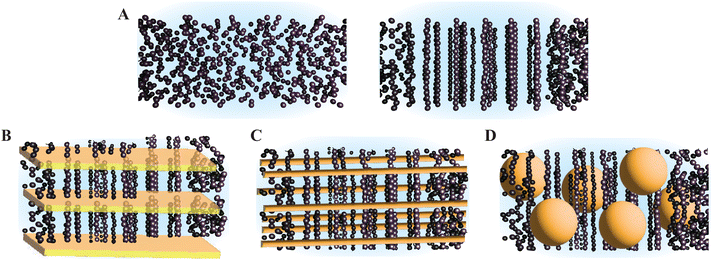
In this paper, we present a magnetically-controlled stiffening mechanism that entails scaffolding structures, typically used in jamming-based stiffening, immersed in a magnetorheological fluid, as illustrated in Fig. 1. In this way, we exploit the response to external magnetic fields of magnetorheological fluids to induce a rapid change in stiffening, while we explore how the addition of scaffolding structures can enhance and increase the achievable stiffening range. We design magnetorheological jamming beams (MRJ beams) which exploit structures such as layers, fibers, and granules as scaffolding materials suspended in magnetorheological fluid such that their stiffness can be actively tuned via an applied magnetic field (Fig. 1). While suspended in magnetorheological fluid, stacked layers are able to slide along each other in two directions, longitudinally-arranged fibers are able to redistribute themselves along one plane, and packed granules are able to rearrange themselves in all three directions. These scaffolding architectures have been shown to provide different stiffening performances in soft robotic applications.35 We characterize the effects on the stiffness of varying design parameters and magnetic field intensity as supplied by arrays of permanent magnets. We investigate how stiffening can be induced by either exploiting the increase in the yield stress of the magnetorheological fluid or by taking advantage of the pressure induced by diametrically placed permanent magnets in combination with the yield stress increase in the magnetorheological fluid. These two strategies allow us to investigate the possibility of using the proposed strategies both for tunable stiffening and as an alternative to pressure-activated clutch mechanisms for soft robotic applications. We also present an analytical beam bending model to predict stiffness as a function of the applied magnetic field. Finally, we demonstrate tunable stiffening with magnetic fields controlled electronically using electropermanent magnets (EPMs). This electronic control allows us to induce stiffness changes without producing any heat nor requiring external pressure sources.
2 Design & fabrication
When a magnetorheological fluid is exposed to a magnetic field, the particles dispersed in the fluid align to such field causing a change in its mechanical properties (Fig. 1A). In this paper, we explore how that change in the mechanical behavior can be enhanced by integrating laminar (Fig. 1B), fibrous (Fig. 1C), or granular (Fig. 1D) materials that act as a scaffolding to which the magnetorheological fluid particles can cling to. These scaffolding materials have been selected for consistency with architectures commonly used in vacuum-activated jamming structures in which fibers, granules, or sheets (layers) of materials are used to design variable stiffness architectures.13,20,35,38,87We designed and fabricated MRJ beams consisting of a flexible pouch filled with magnetorheological fluid. We then compared how the mechanical properties of these MRJ beams change when the MRJ beams contained magnetorheological fluid versus when scaffolding architectures are added into the beam interior and immersed in the magnetorheological fluid. The effectiveness of the jamming structures with scaffolding features was compared against a magnetorheological fluid-only control.
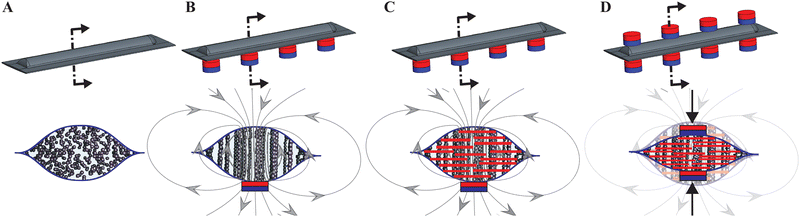
To study the effect of a magnetic field on the MRJ beam stiffness, permanent magnets were used. We studied the magnetically induced stiffening of MRJ beams using two permanent magnet architectures. First, a single row of magnets was used on the bottom of the MRJ beam such that the stiffening was due primarily to the magnetically induced change in the material properties of the fluid itself (Fig. 2B and C). This exploited the increase in magnetorheological fluid yield stress when subject to a magnetic field, which can be viewed as an increase in the friction between layers, fibers, and granules. For the remainder of this report, any results due to this particular magnet architecture will be referred to as due to the MR effect. Second, an additional row of magnets was placed on the opposite side of the MRJ beam with their polarities aligned such that MRJ beams experienced an additional clamping force, resulting in an increased stiffness due to this “clutch” effect. Clutch-inspired strategies to provide a rapid increase in resistance to motion have been proposed in soft robotics and exploit pressure-based jamming mechanisms.40,41,43 In our case, clutching is obtained by subjecting the MRJ beam sample to a magnetic field on both sides. Thus, the dual rows of magnets combine the yield stress effect from the single row magnet orientation, with the additional compression of the internal beam structure produced by magnetic attraction (Fig. 2D). Throughout this paper, any results due to this particular magnet architecture will be referred to as due to the combined MR and clutch effect.
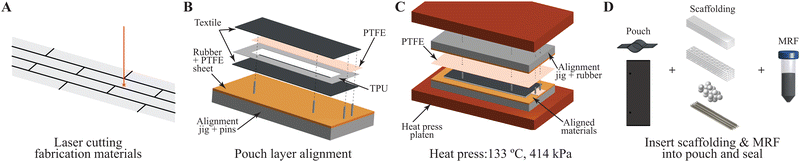
The MRJ beams consisted of a textile-based encasing manufactured using selective bonding via a heat press (Carver, Inc., 5420). The textile (FHSO-BLACK, Seattle Fabrics, Inc.) was cut to 35 mm × 100 mm pieces using a CO2 laser cutter (VersaLASER, VLS6.60), as displayed in Fig. 3A, and bonded together using 178 μm thick thermoplastic urethane (85A Shore A Polyester TPU, American Polyfilm, Inc.), see Fig. 3B. The bonding area between the textile pieces was 1 cm to ensure a large bonding area and minimize the risk of fluid leaks. Polytetrafluoroethylene, or PTFE (Teflon), was inserted between the textile pieces and over the TPU layer to act as a mask for selective bonding. This resulted in a 15 mm × 80 mm pouch for the beam to be filled with magnetorheological fluid (Fig. 3B). After aligning the materials in their respective order, the encasing was pressed at 133 °C and 414 kPa for 4 min (Fig. 3C). The PTFE was then removed, revealing a pouch opening in which scaffolding material could be inserted. Once the beams were filled with magnetorheological fluid and any scaffolding materials, the pouch openings were closed with a handheld sealer (Spot-Crimp Hand-Held Heat Sealer, McMaster-Carr) to hold the scaffolding material and magnetorheological fluid inside (Fig. 3D). The magnetorheological fluid was prepared using 80% carbonyl iron (Sigma-Aldrich) by mass, deionized water, and 0.04% xantham gum (Sigma-Aldrich) by mass. These were mixed together and allowed to sit in an enclosed container at room temperature for two hours before being measured out and inserted into the beams. All samples tested were filled with the same amount of magnetorheological fluid.
One MRJ beam was fabricated containing only magnetorheological fluid without any scaffolding. MRJ beams with three scaffolding architectures were fabricated: stacked layers, fibers, and granules. These scaffolding architectures were inserted into the previously described pouches, in which the volumes were slightly adjusted for each sample to ensure that the ratio of volume of material to volume of the pouch (i.e., packing fraction) was consistent across all samples. For the layers architecture, 78 mm × 13 mm rectangles of 51 μm thick polyester film (Duralar, McMaster-Carr) were laser cut and sanded with 220 grit sandpaper on both sides to increase friction between layers (i.e., “blank” design). Additionally, some layer architecture samples included a laser cut pattern of alternating 2 mm and 4 mm circles that was added to the polyester rectangles to promote the flow of magnetorheological fluid between layers (i.e., “dots” design). Similar to previous work in vacuum-based layer jamming, samples integrating 10 and 20 layers stacked together were tested38 to evaluate the effect of increasing the number of layers on the sample performance. For the fiber and granular materials, 7 μm-thick carbon fiber filaments (McMaster-Carr), and 2.4 mm diameter nylon ball bearings (McMaster-Carr) were used, respectively. The fiber-based MRJ beam had a packing fraction (i.e., ratio of the volume of the material to the volume of the internal pouch) of 0.91, and the granular-based MRJ beam had a packing fraction of 0.95. Across the three jamming architectures tested plus the magnetorheological fluid-only control, seven samples were manufactured (see Fig. S1 in the ESI†). Each MRJ beam contained 1 mL of magnetorheological fluid.
3 Modeling
3.1 Simulation of permanent magnet arrays
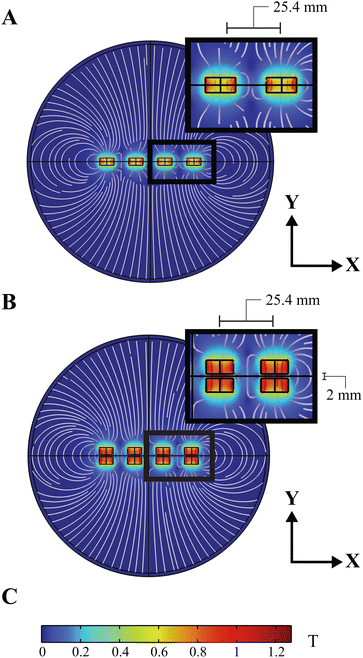
A 3D simulation was conducted in COMSOL using the AC/DC module's Magnetic Fields interface to provide an estimate of the magnetic field produced by the different permanent magnet configurations. In the case of the single row of magnets in which we test the MR effect, four magnets with a 6.35 mm thickness and 12.7 mm diameter were placed in a row with a spacing of 25.4 mm between axial center. For the double row case in which we test the MR and clutch effect, four additional magnets were added and modeled at a distance of 2 mm between the two rows. These geometries were the same used in the experimental tests (Section 4.3). In all cases, a sphere of air with a diameter of 108 mm, including a 3.2 mm infinite element boundary, surrounded the magnets. A magnetic insulation boundary condition was applied at the surface of the sphere. The Ampères law node was configured such that the magnets used the remanent flux density magnetization model as the B–H constitutive relation, with the material properties taken from the built-in BMN-52 material and the remanent flux set in the positive y direction.Fig. 4 shows an XY slice of the results of the COMSOL simulation of the single and double rows of permanent magnet arrays for the case where the row spacing was 2 mm. The color scale represents the magnetic flux density norm with the magnetic field lines shown in white. In the double row case with 2 mm spacing, the area between the magnets set by the dimensions of the MRJ beams in Section 2 experienced an average field of 344.02 mT. In the single row case, this area experienced an average field of 310.45 mT.
3.2 Bending stiffness model
We developed an analytical model to estimate the bending stiffness of the MRJ beams as a function of the applied magnetic field. The model builds upon previous modeling approaches used in pressure-based laminar jamming,35,38 in which stacked layers (similar to the scaffolding we use) are jammed together when vacuum pressure is applied. We have adapted this model to reflect that a new fluid medium, magnetorheological fluid rather than air, is being used and that the magnetic field, not the applied pressure, causes the jamming of the layers.We develop our first beam equation, taking the length of the beam, l, along the positive x-axis:
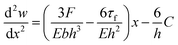 | (1) |
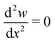 at x = 0 and x = l yields C = 0. Integrating twice and applying the three-point bending boundary conditions at each integration point yields,
at x = 0 and x = l yields C = 0. Integrating twice and applying the three-point bending boundary conditions at each integration point yields,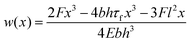 | (2) |
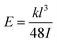 and can be substituted accordingly along with the second moment of inertia,
and can be substituted accordingly along with the second moment of inertia, 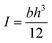 for rectangular beam bending. Taking the center of the beam, where x = l/2, we achieve a deflection equation of
for rectangular beam bending. Taking the center of the beam, where x = l/2, we achieve a deflection equation of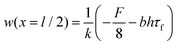 | (3) |
Since we are interested in exploring the effects of magnetically induced stiffening, we can adapt this deflection equation to incorporate this maximum frictional stress. First, F and w are taken to be the final values at the end of a three-point bend test for layer-scaffolding samples with no magnetic field applied, or 0 mT, as these are the maximum force and deflection experienced by the samples. Further substitution of b, h, and τf given the sample and the magnetic field condition yields a force over deflection, combined with an experimentally determined value, that is proportional to its stiffness, k
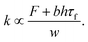 | (4) |
The maximum frictional stress, τf, is taken from the experimental characterization discussed in Section 4.2, and illustrated in Fig. 5. Additional details on the derivation of this model are reported in the ESI,† Section S2.
4 Experiments
Experiments were conducted to investigate the changes in the mechanical response of MRJ beams with varying scaffolding structures when exposed to increasing magnetic fields. We evaluated the increase in stiffness due only to the increase in the magnetorheological fluid yield stress (i.e., MR effect) and to the additional attraction of magnets on opposite sides of the sample (i.e., MR and clutch effect) exploiting the magnet arrangement described in Section 2.4.1 Magnetic field measurements
To evaluate the effect of magnetic fields of increasing strength on the stiffening of the MRJ beams, Grade N52 neodymium (Part No. 5862K118, McMaster-Carr) and alnico 8 (Part No. 57295K77, McMaster-Carr) permanent magnets of 12.7 mm diameter and 6.35 mm thickness were used.A gaussmeter (Model 425 Gaussmeter, Lake Shore Cryotronics) was used to measure the magnetic fields generated by the permanent magnets on the MRJ beams during testing. Measurements were taken with the gaussmeter probe at magnet axial center and 12.7 mm off then averaged to obtain the reported fields. With permanent magnets on one side of the sample, the neodymium and alnico magnets generated fields of 191 mT and 41 mT, respectively. When permanent magnets were held on both sides of the samples, fields of 436 mT and 69 mT were measured with the neodymium and alnico magnets, respectively.
4.2 Magnetically controlled layers cohesion testing
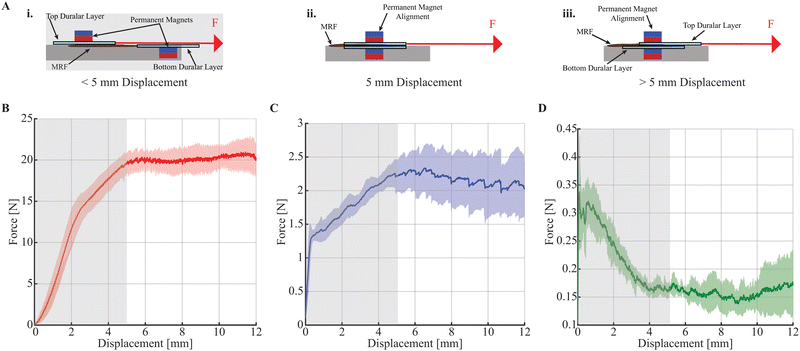
The increase in cohesion between layers of materials immersed in magnetorheological fluid as a function of the applied magnetic field was characterized by experimentally measuring the frictional stress, τf, between the layers. Testing was performed using an acrylic plate with a cavity to hold a permanent magnet. A layer of duralar was adhered to the plate and magnetorheological fluid was positioned on this duralar sheet (Fig. 5A). A second permanent magnet was positioned above another 78 mm × 13 mm duralar sheet and 5 mm away from the underlying permanent magnet, and together these were pulled at a rate of 20 mm min−1 through the magnetorheological fluid via a cable attached to a tensile testing machine (5943, Instron) configured with a 50 N load cell with 100 mN resolution (see Fig. 5A). Force data was collected for 40 s. After 5 mm of displacement, the permanent magnets were directly aligned (Fig. 5A(ii)). As such, the steady-state regimes in the non-grey regions in Fig. 5B–D indicate when the second, top permanent magnet was aligned with the underlying permanent magnet in the cavity of the acrylic plate, and the duralar sheet was dragged in between and through the strong magnetic attraction for an additional 7 mm (Fig. 5A(iii)). Tests were performed with a 436 mT field using neodymium magnets, with a 69 mT field using alnico magnets, and with no magnetic field applied using acrylic cylinders with the same geometry as the permanent magnets.4.3 Bending stiffness tests
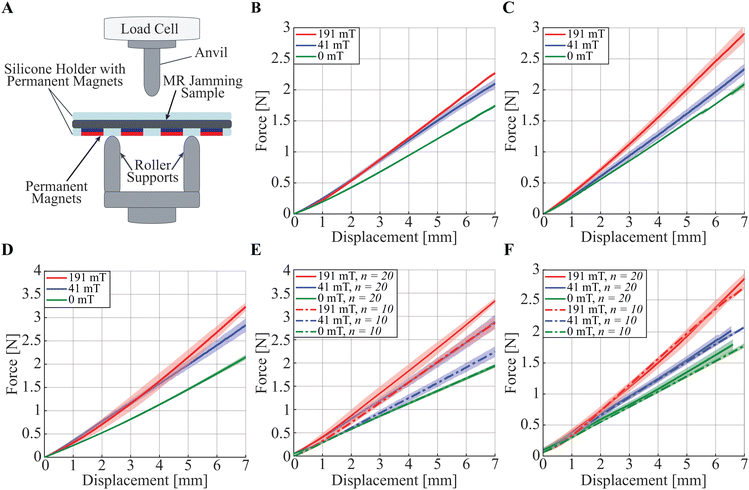
The change in mechanical properties of the MRJ beams with increasing magnetic fields was tested via a three-point bend test protocol. The materials encompassing the structures of these beams are pictured in Fig. 6. As illustrated in Fig. 7A and 8A, roller supports and an anvil required for a three-point bend test were designed and 3D-printed (Form2, FormLabs) to fit a tensile testing machine (5943, Instron) affixed with a 50 N load cell with 100 mN resolution. The roller supports and anvil each had a 5 mm radius, and the roller supports were separated by 6 cm. To hold the permanent magnets in place above and below the sample, an elastomer housing was fabricated by casting Ecoflex 00-30 (Smooth On) on 3D-printed molds (FormLabs). Ecoflex 00-3088 was selected due to its soft nature (E = 69 kPa) with respect to the samples (for instance, Duralar E = 4900 MPa).89 Each elastomer housing held four magnets at a spacing of 25.4 mm from axial centers. The overall dimensions of the elastomer were 35 mm wide, 100 mm long, and 10 mm thick, and all permanent magnets were cylinders of 6.35 mm thickness and 12.7 mm diameter. The mass of the magnets used in this study ranged between 5.6 g and 6.2 g. The spacing among the magnets allows bending of the MRJ beams in the area between the magnets. Pictures of the tests are reported in the ESI† (Fig. S2 and S3). The MRJ beams were tested by imposing a 7 mm displacement at a rate of 10 mm min−1 for all tests, and testing of these beams was performed under three conditions: (1) with no permanent magnets in the elastomer housing, (2) with permanent magnets on only one side of the sample to evaluate the stiffening due solely to the MR effect, leaving the elastomer housing above the sample empty, and (3) with permanent magnets integrated into the elastomer housing on both sides of the samples to explore the MR and clutch effect due to magnetically induced clamping.Testing of the elastomer housing with and without magnets, and with no MRJ beams in between, was conducted to ensure minimal interference on the mechanical properties of the beams due to the integration of permanent magnets. The elastomer housing stiffness without magnets was 213.82 mN mm−1, and with magnets was 227.38 mN mm−1 (6.34% maximum difference).
In addition, samples made with water as the fluid medium, rather than magnetorheological fluid, were also tested to assess the relative contribution of the MR effect with respect to the clutch effect. Layer-based scaffolding samples (both “blank” and “dots” layers) were fabricated in the same manner as the MRJ beams but the 1 mL of magnetorheological fluid was replaced with 1 mL of water. These tests were conducted using the same three-point bend test protocol previously described at no magnetic field and with permanent magnets on both sides of the samples.
4.4 Demonstration of electronically controlled stiffening
A key advantage of magnetically controlled stiffening is that magnetic fields can be generated electronically using electromagnets or electropermanent magnets (EPMs), thus paving the way toward electronically controlled stiffening. In this work, we focus on studying the dependence of the MRJ beam stiffness on the applied magnetic fields and we use permanent magnets to generate such fields for simplicity. However, we provide an example of implementing electronically controlled stiffening of MRJ beams. We used EPMs because they allow us to tune the magnetic field and require minimal energy to operate.85,90–92 Encased in a thermoplastic elastomer beam, we combine carbon fiber filaments (fiber scaffolding) with 1 mL of 80% by mass magnetorheological fluid, which surrounds four EPMs whose end caps are evenly spaced 3 mm apart with the poles aligned. The EPMs were evenly spaced 25.4 mm apart within the beam. The EPMs were manufactured by placing a 6.35 mm long, 1.6 mm diameter alnico 5 magnet (Eneflux Armtek Magnetics, Inc.) side-by-side with an equally-sized Grade N42 neodymium magnet (K&J Magnetics, Inc.). The two magnets were then placed between 3.6 × 2 × 1.6 mm A36 Low-Carbon Steel (Part No. 1388K144, McMaster-Carr) end caps. The individual components were adhered by using cyanoacrylate adhesive (RapidFuse, DAP Products Inc.), and the two magnets were wrapped with 36AWG copper wire (Part No. 7588K85, McMaster-Carr). When measuring the magnetic field directly at the end-caps using a Gaussmeter (Model 425 Gaussmeter, LakeShore Cryotronics), the EPMs exhibited a magnetic field of ∼5 mT when in the OFF state, and ∼30 mT when in the ON state. Toggling of the two bistable states was achieved using four BTS7960 Motor Drivers (Handson Technology) attached to a power supply (BK Precision) and controlled by an Arduino Mega, which supplied 500 μs pulses of current at 5 A to the coils of each EPM. This enabled electronic control of each of the individual EPMs, which require no power except when toggling between the ON and OFF states, each consuming 50 mJ.In addition, a three-point bend test using an EPM-embedded MRJ beam with fiber scaffolding was performed. In this test, an elastomer housing was not used as the magnets (EPMs) were already embedded into the MRJ beam and did not need to be held exterior to the structure. At a rate of 10 mm min−1, the anvil was lowered to impose a 5 mm displacement at the center. The embedded EPMs were evenly spaced 25.4 mm apart and bending of the EPM-embedded MRJ beam occurred directly in the center by the anvil, between the second and third EPMs.
5 Results & discussion
Seven MRJ beam samples were manufactured, six with scaffolding materials. Four layer jamming samples were made: one with 10 blank layers, one with 20 blank layers, one with 10 dotted layers, and one with 20 dotted layers. One fiber jamming sample and one granular jamming sample were made, each with jamming material packed to fill the same amount of volume of material for the MRJ beams. This resulted in packing fractions (i.e., ratio of the volume of the material to the volume of the pouch) of 0.91 and 0.95 for the fiber jamming and granular jamming cases, respectively. All MRJ beams contained the same amount of magnetorheological fluid (1 mL). An example of a fabricated MRJ beam sample with the various scaffolding materials used in this report is pictured in Fig. 6. Additional pictures of the fabricated prototypes are reported in the ESI† (Fig. S1).The maximum frictional stress τf between the layers immersed in the magnetorheological fluid was obtained from the magnetically controlled layers cohesion testing results displayed in Fig. 5. The median force was taken to be the product of the friction coefficient (μ) and the normal force (N) caused by the magnet. At 436 mT, 69 mT, and 0 mT, μN was 19.98 N, 1.83 N, and 0.15 N, respectively (see Fig. 5). τf was then obtained from dividing the median force (μ × N) by the permanent magnet area.
The results of the three-point bending tests for all MRJ beam samples are illustrated in Fig. 7 and 8. The value for the stiffness of each sample at all measured magnetic fields was derived by taking a linear fit after 1.5 mm of anvil displacement as force data collected before this point was influenced primarily by the stiffness of elastomer encasing the magnets rather than that of the samples. These stiffness values and forces required at maximum deflection are reported in Tables 1 and 2, and the stiffness values normalized with respect to their initial stiffness at 0 mT are displayed in Fig. 9.
| Scaffold type | Magnetic field (mT) | Stiffness (mN mm−1) | Stiffness % change | Force at maximum deflection (N) | Force at maximum deflection % change |
|---|---|---|---|---|---|
| No scaffold | 0 | 255.19 | — | 1.74 | — |
| 41 | 310.04 | 21.49 | 2.10 | 20.69 | |
| 191 | 337.49 | 32.25 | 2.27 | 30.46 | |
| Blank – 10 layers | 0 | 249.47 | — | 1.72 | — |
| 41 | 286.71 | 14.93 | 2.02 | 17.44 | |
| 191 | 398.15 | 59.60 | 2.66 | 54.65 | |
| Blank – 20 layers | 0 | 261.05 | — | 1.80 | — |
| 41 | 302.19 | 15.76 | 2.02 | 12.22 | |
| 191 | 399.81 | 53.15 | 2.76 | 53.33 | |
| Dots – 10 layers | 0 | 270.54 | — | 1.94 | — |
| 41 | 322.97 | 19.38 | 2.24 | 15.46 | |
| 191 | 422.05 | 56.00 | 2.86 | 47.42 | |
| Dots – 20 layers | 0 | 274.22 | — | 2.02 | — |
| 41 | 405.88 | 48.01 | 2.83 | 40.10 | |
| 191 | 478.55 | 74.51 | 3.28 | 62.38 | |
| Fibers | 0 | 332.35 | — | 2.30 | — |
| 41 | 409.14 | 23.11 | 2.84 | 23.48 | |
| 191 | 472.35 | 42.12 | 3.23 | 40.43 | |
| Granules | 0 | 301.81 | — | 2.09 | — |
| 41 | 336.47 | 11.48 | 2.33 | 11.48 | |
| 191 | 423.70 | 40.39 | 2.91 | 39.23 | |
| Scaffold type | Magnetic field (mT) | Stiffness (mN mm−1) | Stiffness % change | Force at maximum deflection (N) | Force at maximum deflection % change |
|---|---|---|---|---|---|
| No scaffold | 0 | 255.19 | — | 1.74 | — |
| 69 | 456.70 | 78.96 | 3.04 | 74.71 | |
| 436 | 462.22 | 81.13 | 3.31 | 90.23 | |
| Blank – 10 layers | 0 | 249.47 | — | 1.72 | — |
| 69 | 449.41 | 80.15 | 3.21 | 86.63 | |
| 436 | 733.28 | 193.94 | 4.84 | 181.40 | |
| Blank – 20 layers | 0 | 261.05 | — | 1.80 | — |
| 69 | 569.85 | 118.29 | 4.13 | 129.44 | |
| 436 | 1159.73 | 344.26 | 7.39 | 310.56 | |
| Dots – 10 layers | 0 | 270.54 | — | 1.94 | — |
| 69 | 485.06 | 79.29 | 3.42 | 76.29 | |
| 436 | 698.50 | 158.19 | 4.75 | 144.85 | |
| Dots – 20 layers | 0 | 274.22 | — | 2.02 | — |
| 69 | 475.67 | 73.46 | 3.57 | 76.73 | |
| 436 | 813.80 | 196.77 | 5.45 | 169.80 | |
| Fibers | 0 | 332.35 | — | 2.30 | — |
| 69 | 494.62 | 48.83 | 3.50 | 52.17 | |
| 436 | 808.03 | 143.13 | 5.14 | 123.48 | |
| Granules | 0 | 301.81 | — | 2.09 | — |
| 69 | 564.71 | 87.11 | 4.01 | 91.87 | |
| 436 | 859.41 | 184.75 | 5.70 | 172.73 | |
In the non-scaffolding sample (filled solely with magnetorheological fluid), the maximum force at full deflection reached 1.74 N at 0 mT, and the stiffness increased with the increasing magnetic field, regardless of whether the MR effect or the combined MR and clutch effect were induced. From the MR effect, the stiffness increased by 21.49% at 41 mT and by 32.25% at 191 mT, reaching maximum forces at full deflection of 2.10 N and 2.27 N, respectively. In the clutching configuration, i.e. two rows of magnets to induce the MR and clutch effect, the stiffness increased by 78.96% at 69 mT and 81.13% at 436 mT, reaching maximum forces of 3.04 N and 3.31 N, respectively. Thus, the stiffening of the non-scaffolding MRJ beam is affected by both the magnetic field, as well as the compression force on the beam caused by the attraction between the magnets. In the sample without any scaffolding, increasing the magnetic field results in only ≈10% maximum additional stiffening both in the single and double magnet row tests.
The introduction of scaffolding materials resulted overall in an amplification of the change in stiffening in all tests. All samples containing scaffolding materials demonstrated a significant increase in stiffening with increasing magnetic fields.
Results from the tests with a single row of magnets (MR effect only) are reported in Fig. 7 and in Table 1. MRJ beams with either fibers or granules show a similar increase in stiffness at 41 mT with respect to the non-scaffolding case, but then both reach more than 40% increase at 191 mT. The stiffened MRJ beam with fibers exposed to 191 mT required more than 1 N additional force for deflection in comparison to the case with no scaffolding. MRJ beams with blank layer scaffolding also show a comparable increase in stiffening compared to the case with no scaffolding when exposed to a 41 mT field. At increasing magnetic fields, however, the MRJ beams with blank layer scaffolding demonstrated a significant increase in stiffening (i.e., more than 50%). It is worth noting that increasing the number of layers from 10 to 20 did not improve the stiffening performance for the single row of magnets (MR effect only). The addition of hole patterns on the layers used in the “dots” scaffolding provided a significant improvement in the stiffening capabilities of the MRJ beams that contained them. This is likely due to the fact that the magnetorheological fluid can more easily flow across the layers and thus the layers get better entrapped by the fluid when exposed to a magnetic field. The MRJ beams that embedded 20 layers with the “dot” design achieved almost 75% stiffening at 191 mT, reaching a stiffness of 479 mN mm−1 and requiring 3.28 N for deflection, the highest increase among all samples.
Results from the tests with a double row of magnets (MR and clutch effect) are reported in Fig. 8 and in Table 2. Across all MRJ beam samples, the stiffness and force at maximum deflection increased with the increasing magnetic field when testing the MR and clutch effect. Additionally, stiffening ranges increased substantially with respect to the case of using a single row of magnets. This is because in this test we exploit the combination of the MR effect (i.e., the yield stress increases further due to the stronger magnetic fields given by the increased number of permanent magnets), and the clamping force from the diametrically placed magnets across the sample.
The MRJ beam without scaffolding reached stiffening ranges up to 81%. However, similarly to the case of the tests with a single row of magnets, increasing the magnetic field does not significantly enhance the stiffening. On the other hand, the introduction of scaffolding materials not only amplifies the achievable stiffening range but it also amplifies the difference in the amount of stiffening obtained at increasing magnetic fields.
The MRJ beams with fiber as the scaffolding material increased their stiffness by 48.83% and 143.13% at 69 mT and 436 mT, respectively. The granular MRJ beams exhibited more substantial increases in stiffness due to the MR and clutch effect, increasing by 87.11% at 69 mT and 184.75% at 436 mT. The stiffened granular MRJ beam required 2.39 N more force to deflect 7 mm at 436 mT compared to the no scaffolding MRJ beam at the same magnetic field. The layer-based scaffolding MRJ beams also exhibited significant increases in stiffness and force required for deflection. Further, increasing the number of layers, whether with “blank” or “dots” scaffolding, improved stiffening performance. This agrees with previous work in pressure-based jamming.38 The “dots” scaffolding of 10 and 20 layers produced similar increases in stiffness at 69 mT (79.29% and 73.46%, respectively) compared to the no scaffolding case at the same magnetic field (78.96%). However, as the magnetic field increased to 436 mT, the stiffness improved dramatically for the “dots” scaffolding, increasing by 158.19% to 698.50 mN mm−1 and by 196.77% to 813.80 mN mm−1 for the 10 and 20 layers, respectively, compared to only an 81.13% increase for the no scaffolding case. The 10 and 20 “blank” layers both demonstrated significant increases in stiffness with increasing magnetic field, with the 20 layer MRJ beam performing the best across all samples. At 436 mT, the 20 layer “blank” MRJ beam increased its stiffness by 344.26% to 1159.73 mN mm−1 and required over 4 N more force to deflect compared to the no scaffolding MRJ beam at the same magnetic field. Thus, the addition of hole patterns in the “dots” scaffolding did not exhibit as improved results as the “blank” layers in this case.
Further, we report the results of the samples using water rather than magnetorheological fluid as the fluid medium in the ESI,† Section S4 (see Fig. S7, S8 and Table S2, ESI†). This allowed us to isolate the component of the MR and clutch effect that is solely due to the pressure that is generated by the permanent magnets and further understand the role of magnetorheological fluid in this effect. Results show that the clutch mechanism by itself can be effective even without magnetorheological fluids and clutch mechanisms can be designed using magnetic fields instead of external pressure sources. However, the results show that using magnetorheological fluid instead of water provides consistently larger stiffening ranges across the samples at the magnetic fields tested (69 mT and 436 mT) and resulted in up to 43% increase in stiffening of the MRJ beams.
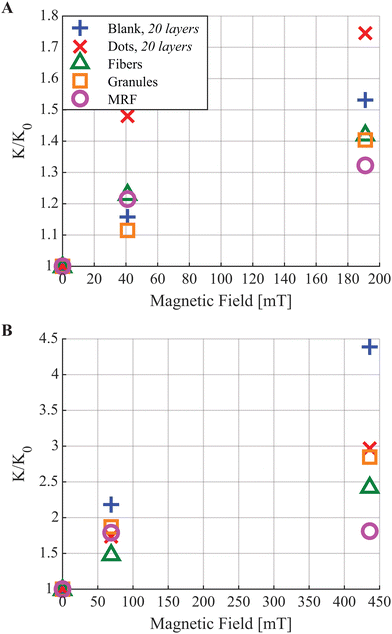
In Fig. 9 we report the stiffness of all of the MRJ beams tested normalized with respect to their initial stiffness as a function of the applied magnetic field. As displayed in Fig. 9, the stiffness of all MRJ beams increases as the applied magnetic field also increases, regardless of whether the MR effect or MR and clutch effect is being employed. Further, the differences in the mechanical response of the MRJ beams at increasing magnetic fields are amplified by the introduction of scaffolding structures. This is particularly evident in Fig. 9A at 191 mT and in Fig. 9B at 436 mT. At the smaller magnetic fields, 0–69 mT, the difference in stiffness among samples with different scaffolding designs is less evident.
Analytical model predictions based on eqn (4) are displayed in Fig. 10 in comparison with the raw data. The model applies to the MRJ beams with the “blank” layer scaffolding design with the dual rows of permanent magnets contributing stiffening due to the MR and clutch effect. The model predicts the linear regime after 1.5 mm of displacement as any data recorded before this is due more so to the nature of the elastomer housing the permanent magnets and not the layer-scaffolding MRJ beam samples. The predictions in Fig. 10 are that of the MRJ beam with 20 layers of “blank” scaffolding subject to the MR and clutch effect from two rows of magnets, which is consistent with the magnetically controlled layers cohesion testing discussed in Section 4.2 in which the frictional stress τf was obtained for the three magnetic fields (0 mT, 69 mT, and 436 mT) using two magnets. At 436 mT the analytical model predicts the stiffness to be 1283.64 mN mm−1, a 10.68% difference from the experimentally found value of 1159.73 mT. Though the prediction differs slightly from the experimental results, Fig. 10 shows the predicted slope lies close to the data after 4 mm of deflection, suggesting that other internal MRJ beam interactions could be contributing to the deviation before this point. At 69 mT and 0 mT, the analytical model predicts the MRJ beam stiffness to be 557.79 mN mm−1 and 202.16 mN mm−1, respectively. These predicted stiffness values agree with the experimental data, with differences of 2.11% at 69 mT and 22.56% at 0 mT.
 | ||
| Fig. 10 Raw data and model predictions for the MRJ beam with 20 layers of “blank” scaffolding design at 436 mT, 69 mT, and 0 mT. | ||
Finally, we demonstrate electronically controlled stiffening of an MRJ beam using fiber jamming with magnetorheological fluid, as depicted in Fig. 11. This test aims at showing a possible strategy to electronically control the magnetic field on the MRJ beams. Like in the three-point bending tests, the beam is centered as it sits upon two supports, and is provided with an initial deflection of about 5 mm. This prior deflection was initiated before demonstration as the results in Fig. 7 and 8 illustrate that stiffness increases after an initial displacement and to better hold the curvature of the mass handle (see Fig. 11). With the EPMs turned ON in Fig. 11A, the beam stiffens as it is able to hold 70 g of mass hanging from its center. When the EPMs are turned OFF, the beam resumes its initial flexible state and therefore can no longer hold the applied mass, which falls, as depicted in Fig. 11B. The demonstration can also be seen in Movie S1 from the ESI.†
A three-point bend test was also employed on an EPM-embedded MRJ beam with fibers scaffolding, using the same testing setup as for the permanent magnets. The results of this test are displayed in Section S3 in the ESI.† When the EPMs are turned to their ON state to 30 mT, there is a significant increase in MRJ beam stiffness compared to the EPM OFF state, increasing by 26%. This result is consistent with those tabulated in Table 2 using the permanent magnets, thus highlighting the fact that the stiffness of the MRJ beams increases with increasing magnetic field applied, regardless of the source.
6 Conclusions
In this paper, we investigate magnetically controlled stiffening with magnetorheological fluids and how embedding scaffolding structures immersed in the magnetorheological fluids can amplify the achievable stiffening range. This approach allows us to tune the stiffness with the applied magnetic field within a few milliseconds. We exploit the response of magnetorheological fluids to external magnetic fields supplied by either permanent magnets or EPMs to induce a rapid stiffness change while exploring how embedded scaffolding structures can enhance stiffening. We study the effect of integrating scaffolding structures typically used in pressure-based jamming in a magnetorheological fluid medium to increase the achievable stiffening range. In this way, our method combines a magnetically tunable, materials-based magnetorheological stiffening approach, with a mechanical approach borrowed from jamming.We investigated the stiffening of MRJ beams obtained due solely to the MR effect, in which the applied magnetic field increases the yield stress of the magnetorheological fluid, and due to the addition of the clutch effect in which an additional clamping force is experienced from the attraction of aligned permanent magnets (i.e., MR and clutch effect). Our results showcase that stiffening and the force needed to achieve maximum deflection increase with increasing applied magnetic field. Scaffolding design choice has a further impact on overall stiffness as well. The addition of scaffolding material increased MRJ beam stiffness compared to the beam with only magnetorheological fluid, as depicted in Tables 1 and 2. Results from the bending stiffness tests highlight how the scaffolding materials not only increase the achievable stiffening of the samples, but they enable a significant increase in stiffening with the increase in the applied magnetic field. Indeed, in the MRJ beams without scaffolding, increasing the magnetic field more than four times resulted in an increase in stiffness of only ≈10% max, while it ranged between 20% and 40% in the case of the single row of magnets tests (MR effect only) and between 100% and 200% for the double row of magnets (MR and clutch effect) depending on the type of scaffolding used. The largest observed change in stiffness came from the samples with 20 “blank” layers and 20 “dots” layers at 436 mT (in which the MR and clutch effect is induced), with individual stiffnesses increasing by 344.26% to 1159.73 mN mm−1 and by 196.77% to 813.80 mN mm−1, respectively, while the sample with no scaffolding only increased stiffness by 81.13% at this same magnetic field. These same samples also achieved large increases in maximum force at full deflection, 310.56% at 436 mT and 169.80% for the 20 “blank” and 20 “dots” layers, respectively, while the non-scaffolding only changed by 90.23%.
Therefore, the introduction of scaffolding materials also enhances the difference in the response of the MRJ beams to the applied magnetic fields. This feature can enable more granular stiffness tuning in the design of soft robotic components.
Additionally, we present an analytical model that builds upon current models used for pressure-based stiffening and we adapted that to the proposed magnetically controlled stiffening strategy. This model can provide an initial estimate of the achievable stiffening ranges.
Design and integration of variable stiffening mechanisms is often an essential component of soft robot design. The proposed stiffening strategy can provide changes in the mechanical properties without requiring external pressure sources nor causing heating. Results presented show how scaffolding allows tuning the mechanical properties of the MRJ beams as well as their stiffening ranges and capabilities. We also demonstrate how the magnetic field necessary to tune the stiffness can be generated electronically via EPMs and how the stiffening changes obtained are consistent with experiments done with permanent magnets. Demonstration of electronically controlled stiffening through the use of EPMs in a weight-bearing application is also presented in this paper. Due to the combination of magnetorheological fluid and scaffolding material, the use of EPMs allows for a change in stiffness within a few milliseconds; timing that is similar to vacuum-based jamming but without the need for a pressure source. This work can pave the way towards customizing soft robotic designs that require tunable stiffening, such as in wearable mobility-assistance applications, damping to adjust dynamic responses in robotics, and reconfigurable structures.
Author contributions
L. T. G., K. J. M., and T. R. conceptualized the topic. L. T. G., K. J. M., and T. R. designed the testing protocols, and L. T. G. carried out the data curation and analysis. L. T. G. conceived the fabrication process, and L. T. G., M. L., and S. W. F. fabricated sample materials. L. T. G. and L. K. carried out the demonstration. T. A. and E. S. contributed to the initial conceptualization of the topic and the revision of the manuscript. L. T. G., K. J. M., L. K., and T. R. contributed to the writing and revision of this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award 3R21EB028363, by the Office of Naval Research (ONR) grant number N00014-22-1-2244, and the Department of Education GAANN Award P200A210041. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the ONR. ES acknowledges the support of the Fulbright Visiting Scholar Program, and also acknowledges that the information presented here is the author's own and does not represent the Fulbright Program nor the U.S. Department of State. The authors would like to thank Jacob Rogatinsky for help capturing photos and videos for this manuscript.Notes and references
- G. M. Whitesides, Angew. Chem., Int. Ed., 2018, 57, 4258–4273 CrossRef CAS PubMed.
- B. Jumet, M. D. Bell, V. Sanchez and D. J. Preston, Adv. Intell. Syst., 2022, 4, 2100163 CrossRef.
- C. Laschi, B. Mazzolai and M. Cianchetti, Sci. Rob., 2016, 1, 1–12 Search PubMed.
- D. Rus and M. T. Tolley, Nature, 2015, 521, 467–475 CrossRef CAS PubMed.
- J. Rogatinsky, K. Gomatam, Z. H. Lim, M. Lee, L. Kinnicutt, C. Duriez, P. Thomson, K. McDonald and T. Ranzani, Adv. Intell. Syst., 2022, 2200085 CrossRef.
- T. Ranzani, G. Gerboni, M. Cianchetti and A. Menciassi, Bioinspiration Biomimetics, 2015, 10, 035008 CrossRef CAS PubMed.
- V. Wall, R. Deimel and O. Brock, Proceedings – IEEE International Conference on Robotics and Automation, 2015, pp. 252–257 Search PubMed.
- J. Lussi, M. Mattmann, S. Sevim, F. Grigis, C. De Marco, C. Chautems, S. Pané, J. Puigmartí-Luis, Q. Boehler and B. J. Nelson, Adv. Sci., 2021, 8, 2101290 CrossRef PubMed.
- J. Choi, D. Y. Lee, J. H. Eo, Y. J. Park and K. J. Cho, Soft Robot., 2021, 8, 109–118 CrossRef PubMed.
- A. Yin, H.-C. Lin, J. Thelen, B. Mahner and T. Ranzani, Adv. Intell. Syst., 2019, 1, 1900089 CrossRef.
- S. Hauser, M. Robertson, A. Ijspeert and J. Paik, IEEE Rob. Automation Lett., 2017, 2, 849–855 Search PubMed.
- B. Yang, R. Baines, D. Shah, S. Patiballa, E. Thomas, M. Venkadesan and R. Kramer-Bottiglio, Reprogrammable soft actuation and shape-shifting via tensile jamming, 2021 Search PubMed.
- D. S. Shah, E. J. Yang, M. C. Yuen, E. C. Huang and R. Kramer-Bottiglio, Adv. Funct. Mater., 2021, 31, 1–8 Search PubMed.
- D. Hwang, E. J. B. Iii, A. B. M. Tahidul Haque and M. D. Bartlett, Shape morphing mechanical metamaterials through reversible plasticity, 2022 Search PubMed.
- R. Baines, S. Freeman, F. Fish and R. Kramer-Bottiglio, Bioinspiration Biomimetics, 2020, 15, 025002 CrossRef PubMed.
- B. Aksoy and H. Shea, Adv. Funct. Mater., 2020, 30, 2001597 CrossRef CAS.
- A. A. Stanley and A. M. Okamura, IEEE Trans. Haptics, 2015, 8, 20–30 Search PubMed.
- S. Jadhav, M. R. A. Majit, B. Shih, J. P. Schulze and M. T. Tolley, Soft Robot., 2022, 9, 173–186 CrossRef PubMed.
- M. Li, T. Ranzani, S. Sareh, L. D. Seneviratne, P. Dasgupta, H. Würdemann and K. Althoefer, Smart Mater. Struct., 2014, 23, 095007 CrossRef.
- T. Liu, H. Xia, D.-Y. Lee, A. Firouzeh, Y.-L. Park and K.-J. Cho, IEEE Rob. Automation Lett., 2021, 6, 8078–8085 Search PubMed.
- A. Tonazzini, J. Shintake, C. Rognon, V. Ramachandran, S. Mintchev and D. Floreano, 2018 IEEE International Conference on Soft Robotics (RoboSoft), 2018, pp. 485–490 Search PubMed.
- A. T. Wanasinghe, W. V. Awantha, A. G. Kavindya, A. L. Kulasekera, D. S. Chathuranga and B. Senanayake, IEEE Trans. Neural Syst. Rehabil., 2021, 29, 2684–2694 CAS.
- V. Sanchez, C. J. Walsh and R. J. Wood, Adv. Funct. Mater., 2021, 31, 2008278 CrossRef CAS.
- T. P. Chenal, J. C. Case, J. Paik and R. Kramer-bottiglio, 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2014, pp. 2827–2831 Search PubMed.
- T. Ranzani, M. Cianchetti, G. Gerboni, I. D. Falco and A. Menciassi, IEEE Trans. Rob., 2016, 32, 187–200 Search PubMed.
- A. Cavallo, M. Brancadoro, S. Tognarelli and A. Menciassi, Soft Robot., 2019, 6, 161–173 CrossRef PubMed.
- Y. J. Kim, S. Cheng, S. Kim and K. D. Iagnemma, IEEE Trans. Rob., 2013, 29, 1031–1042 Search PubMed.
- Y. J. Kim, S. Cheng, S. Kim and K. D. Iagnemma, IEEE International Conference on Intelligent Robots and Systems, 2012 Search PubMed.
- E. Brown, N. Rodenberg, J. Amend, A. Mozeika, E. Steltz, M. R. Zakin, H. Lipson and H. M. Jaeger, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18809–18814 CrossRef CAS.
- M. Manti, V. Cacucciolo and M. Cianchetti, IEEE Robot. Autom. Mag., 2016, 23, 93–106 Search PubMed.
- Y. Yang, Y. Li and Y. Chen, Principles and methods for stiffness modulation in soft robot design and development, 2018 Search PubMed.
- F. Zuliani and J. K. Paik, Smart Mater. Struct., 2022, 31, 115023 CrossRef.
- L. Wang, Y. Yang, Y. Chen, C. Majidi, F. Iida, E. Askounis and Q. Pei, Mater. Today, 2018, 21, 563–576 CrossRef CAS.
- S. G. Fitzgerald, G. W. Delaney and D. Howard, Actuators, 2020, 9, 1–31 CrossRef.
- B. AktaÅŸ, Y. S. Narang, N. Vasios, K. Bertoldi and R. D. Howe, Adv. Funct. Mater., 2021, 31, 1–15 Search PubMed.
- Y. S. Narang, A. Degirmenci, J. J. Vlassak and R. D. Howe, IEEE Rob. Automation Lett., 2018, 3, 688–695 Search PubMed.
- L. Arleo, G. Bondì, S. Albini, M. Maselli and M. Cianchetti, Eng. Res. Express, 2021, 3, 1–14 Search PubMed.
- Y. S. Narang, J. J. Vlassak and R. D. Howe, Adv. Funct. Mater., 2018, 28, 1–9 CrossRef.
- Y. Li, Y. Chen, Y. Yang and Y. Wei, IEEE Trans. Rob., 2017, 33, 446–455 Search PubMed.
- A. Sadeghi, A. Mondini, M. Totaro, B. Mazzolai and L. Beccai, Adv. Eng. Mater., 2019, 21, 1–11 CrossRef.
- I. Choi, N. Corson, L. Peiros, E. W. Hawkes, S. Keller and S. Follmer, IEEE Rob. Automation Lett., 2018, 3, 450–457 Search PubMed.
- Y. S. Narang, B. Aktas, S. Ornellas, J. J. Vlassak and R. D. Howe, Soft Robot., 2020, 7, 724–735 CrossRef PubMed.
- R. J. Hinchet and H. Shea, Adv. Intell. Syst., 2022, 4, 2200174 CrossRef.
- W. Shan, T. Lu and C. Majidi, Smart Mater. Struct., 2013, 22, 1–8 CrossRef.
- Y. F. Zhang, N. Zhang, H. Hingorani, N. Ding, D. Wang, C. Yuan, B. Zhang, G. Gu and Q. Ge, Adv. Funct. Mater., 2019, 29, 1–9 Search PubMed.
- A. Firouzeh, M. Salerno and J. Paik, IEEE International Conference on Intelligent Robots and Systems, 2015, pp. 1117–1124 Search PubMed.
- R. Coulson, C. J. Stabile, K. T. Turner and C. Majidi, Soft Robot., 2022, 9, 189–200 CrossRef PubMed.
- M. C. Yuen, R. A. Bilodeau and R. K. Kramer, IEEE Rob. Automation Lett., 2016, 1, 708–715 Search PubMed.
- S. Chen, Y. Pang, Y. Cao, X. Tan and C. Cao, Adv. Mater. Technol., 2021, 6, 1–11 Search PubMed.
- A. Firouzeh, M. Salerno and J. Paik, IEEE Trans. Rob., 2017, 33, 765–777 Search PubMed.
- D. Zappetti, S. H. Jeong, J. Shintake and D. Floreano, Soft Robot., 2020, 7, 362–369 CrossRef PubMed.
- T. L. Buckner, M. C. Yuen, S. Y. Kim and R. Kramer-Bottiglio, Adv. Funct. Mater., 2019, 29, 1903368 CrossRef CAS.
- I. M. Van Meerbeek, B. C. Mac Murray, J. W. Kim, S. S. Robinson, P. X. Zou, M. N. Silberstein and R. F. Shepherd, Adv. Mater., 2016, 28, 2801–2806 CrossRef CAS PubMed.
- A. Tonazzini, S. Mintchev, B. Schubert, B. Mazzolai, J. Shintake and D. Floreano, Adv. Mater., 2016, 28, 10142–10148 CrossRef CAS PubMed.
- B. E. Schubert and D. Floreano, RSC Adv., 2013, 3, 24671–24679 RSC.
- N. Bira, P. Dhagat and J. R. Davidson, Front. Robot. AI, 2020, 7, 1–9 CrossRef PubMed.
- J. Wu, X. Gong, Y. Fan and H. Xia, Smart Mater. Struct., 2010, 19, 105007 CrossRef.
- Y. Han, W. Hong and L. E. Faidley, Int. J. Solids Struct., 2013, 50, 2281–2288 CrossRef CAS.
- W. H. Li and X. Z. Zhang, Smart Mater. Struct., 2010, 19, 035002 CrossRef.
- E. Galipeau and P. Ponte Castañeda, Int. J. Solids Struct., 2012, 49, 1–17 CrossRef.
- D. Ivaneyko, V. Toshchevikov, M. Saphiannikova and G. Heinrich, Condens. Matter Phys., 2012, 15, 33601 CrossRef.
- G. Y. Zhou, Shear properties of a magnetorheological elastomer, 2003 Search PubMed.
- Z. Varga, G. Filipcsei and M. Zrínyi, Polymer, 2006, 47, 227–233 CrossRef CAS.
- M. R. Jolly, J. David Carlson and B. C. MuñozMu, A model of the behaviour of magnetorheological materials, 1996 Search PubMed.
- L. C. Davis, J. Appl. Phys., 1999, 85, 3348–3351 CrossRef CAS.
- M. Lokander and B. Stenberg, Polym. Test., 2003, 22, 677–680 CrossRef CAS.
- M. Lokander and B. Stenberg, Polym. Test., 2003, 22, 245–251 CrossRef CAS.
- J. M. Ginder, W. F. Schlotter and M. E. Nichols, Smart Structures and Materials 2001: Damping and Isolation, 2001, pp. 103–110 Search PubMed.
- S. Genc and P. Phule, Smart Mater. Struct., 2002, 140, 140–146 CrossRef.
- A. Rendos, S. Woodman, K. McDonald, T. Ranzani and K. A. Brown, Smart Mater. Struct., 2020, 29, 1–6 CrossRef.
- M. Kubík, J. Válek, J. Žáček, F. Jeniš, D. Borin, Z. Strecker and I. Mazurek, Sci. Rep., 2022, 12, 1–10 CrossRef PubMed.
- D. S. Yoon, G. W. Kim and S. B. Choi, Mech. Syst. Signal Process, 2020, 146, 106999 CrossRef.
- M. Kubík, K. Šebesta, Z. Strecker, F. Jeniš, J. Goldasz and I. Mazurek, Smart Mater. Struct., 2021, 30, 125020 CrossRef.
- B. Horváth, P. Decsi and I. Szalai, J. Intell. Mater. Syst. Struct., 2022, 33, 918–927 CrossRef.
- T. Kikuchi, J. Noma, S. Akaiwa and Y. Ueshima, J. Intell. Mater. Syst. Struct., 2016, 27, 859–865 CrossRef CAS.
- H. M. Laun and C. Gabriel, Rheol. Acta, 2007, 46, 665–676 CrossRef CAS.
- S. J. Dyke, B. F. Spencer, M. K. Sain and J. D. Carlson, Smart Mater. Struct., 1996, 5, 565–575 CrossRef.
- G. Yang, B. F. Spencer, J. D. Carlson and M. K. Sain, Eng. Struct., 2002, 24, 309–323 CrossRef.
- R. Sukhnandan, K. Dai and V. Webster-Wood, IEEE International Conference on Robotics and Automation, 2022, pp. 11445–11451 Search PubMed.
- F. Gao, Y. N. Liu and W. H. Liao, Smart Mater. Struct., 2017, 26, 1–9 Search PubMed.
- A. Pettersson, S. Davis, J. O. Gray, T. J. Dodd and T. Ohlsson, J. Food Eng., 2010, 98, 332–338 CrossRef.
- C. Majidi and R. J. Wood, Appl. Phys. Lett., 2010, 97, 2010–2012 CrossRef.
- P. Testa, R. W. Style, J. Cui, C. Donnelly, E. Borisova, P. M. Derlet, E. R. Dufresne and L. J. Heyderman, Adv. Mater., 2019, 31, 1–6 Search PubMed.
- E. Kostamo, J. Kostamo, J. Kajaste and M. Pietola, J. Intell. Mater. Syst. Struct., 2012, 1001–1010 CrossRef.
- K. J. McDonald, L. Kinnicutt, A. M. Moran and T. Ranzani, IEEE Robot. Autom. Lett., 2022, 7, 3914–3921 Search PubMed.
- T. Leps, P. E. Glick, I. Ruffatto, A. Parness, M. T. Tolley and C. Hartzell, Smart Mater. Struct., 2020, 29, 105025 CrossRef CAS.
- M. Brancadoro, M. Manti, S. Tognarelli and M. Cianchetti, Soft Robot., 2020, 7, 663–674 CrossRef PubMed.
- Smooth-On, Ecoflex 00-30, 2022, https://www.smooth-on.com/products/ecoflex-00-30/.
- P. P. Plastics, Dura-Lar Polyester Film, 2022, https://precisionpunch.com/wp-content/pdf/polyester_film.pdf.
- A. N. Knaian, PhD thesis, Massachusetts Institute of Technology, 2010.
- A. D. Marchese, C. D. Onal and D. Rus, 2011 IEEE/RSJ international conference on intelligent robots and systems, 2011, pp. 756–761 Search PubMed.
- J. I. Padovani, S. S. Jeffrey and R. T. Howe, Technology, 2016, 4, 110–119 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01390h |
| This journal is © The Royal Society of Chemistry 2023 |