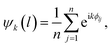Melting of a macroscale binary Coulombic crystal

Abstract

The question of melting has been addressed theoretically and experimentally for two-dimensional crystals in thermal equilibrium. However, as it pertains to out-of-equilibrium systems, the question is unresolved. Here, we present a platform to study the melting of a two-dimensional, binary Coulombic crystal composed of equal numbers of nylon and polytetrafluoroethylene (PTFE) beads that measure a couple of millimeters in diameter. The beads are tribocharged—nylon positively and PTFE negatively—and they experience long-range electrostatic interactions. They form a square crystal in which nylon and PTFE beads sit at alternating sites on a checkerboard lattice. We melt the crystal by agitating the dish in which it resides using an orbital shaker. We compare the melting behavior of the crystal without impurities to that of the crystal with impurities, where we use gold-coated nylon beads as impurities because they tribocharge negligibly. Our results reveal that impurities do not influence the melting of the crystal. Instead, the crystal undergoes shear-induced melting, beginning from its edges, due to its collisions with the dish. As a result of repetitive collisions, the beads acquire kinetic energy, undergo rearrangements, and become disordered. Unlike most examples of shear-induced melting, portions of the crystal remain locally ordered given the persistence of electrostatic interactions and the occurrence of some collisions that are favorable to ordering clusters of beads. Our work clarifies the melting behavior of sheared crystals whose constituents have persistent long-range interactions. It may prove valuable in determining the conditions under which such materials are immune to disorder.

---

1. Introduction

The melting of two-dimensional crystals in systems at thermal equilibrium has been studied theoretically.^1–3 Colloidal crystals are often used as experimental model systems to study melting.³ The crystals can melt under shear^3–5 and the presence of defects influences their melting.³ The colloidal crystals are typically composed of a single type of colloid and their melting is probed under conditions of thermal equilibrium. The melting of two-dimensional crystals in non-equilibrium systems remains poorly understood, especially when such crystals are made up of elements that interact at long-range, meaning that their screening lengths far exceed their size. For instance, the relative importance of impurities, defects, and shear is largely unknown. Melting and crystallization have been the object of study in granular systems whose entities do not interact electrostatically.^6–10 The question of non-equilibrium melting is important to address, particularly as it pertains to the fabrication of materials and the conditions under which they remain ordered.

Here, we set out to understand how a macroscale, two-dimensional binary Coulombic material melts in a non-equilibrium system. The material is composed of equal numbers of nylon and polytetrafluoroethylene (PTFE) beads, all measuring approximately 2.38 millimeters in diameter, that sit at alternating sites on a square lattice.^11–13 The beads are tribocharged¹⁴ and their electrostatic interactions are long-range. In certain cases, the material contains impurities, namely gold-coated nylon beads also measuring approximately 2.38 millimeters in diameter, that do not tribocharge appreciably.¹³ The Coulombic material, which we shall refer to as a Coulombic crystal, sits in an ungrounded, gold-coated Petri dish that is capped by an electrically grounded, optically transparent lid, as pictured in Fig. S1 (ESI†). The dish sits on the platform of an orbital shaker. To quantify the melting process, we record the positions of the beads in time with a high-speed camera. The crystal partially melts as the dish slides on the platform and the beads undergo collisions with each other and with the walls of the dish. Here, shear—of the same type and magnitude—simultaneously melts and orders the crystal. Shear melts portions of the crystal starting from its edges: some beads have enough kinetic energy to overcome attractive Coulombic interactions that would otherwise bind them to their neighbors and, as a result, rearrange. Shear simultaneously orders certain parts of the crystal through favorable collisions. The presence of impurities in the crystal, however, does not alter the mechanism of melting.

We study the melting behavior of Coulombic crystals with and without impurities. In all experiments, regardless of the presence of impurities, the nylon and PTFE beads, together, occupy about 30% of the surface area of the dish. When present in equal numbers, nylon beads tribocharge positively and PTFE beads tribocharge negatively, although the magnitude of their charge is approximately equal.¹³ In contrast, gold-coated nylon beads tribocharge positively, and the magnitude of their charge is only about 10% of that of nylon or PTFE beads.¹³ Tribocharging refers to the process by which two materials, initially uncharged, acquire charge upon contact with and separation from one another.^14,15 In the absence of impurities, we study the melting behavior at two centripetal accelerations,¹⁶ namely 21.1 m s⁻² and 26 m s⁻². We have chosen these two accelerations because they correspond to the two highest accelerations on our orbital shaker. Next, we set the centripetal acceleration to 21.1 m s⁻² and characterize the melting behavior of the Coulombic crystals when they contain one or 50 gold-coated nylon beads, which we call impurities, in addition to the 200 nylon and 200 PTFE beads. The aggregate of beads is restricted to move in two dimensions: the Petri dish is covered with a transparent lid made from acrylic to which a thin film of indium tin oxide (ITO) on polyethylene terephthalate (PET) is attached with double-sided adhesive tape. The ITO on PET film is electrically grounded; this attachment results in reduced electrostatic interactions between the beads and the lid. As the dish is agitated, it collides with the walls of a plastic enclosure that constrains its motion. In turn, the beads within the dish collide with the walls of the dish. They move as an aggregate due to both their persistent Coulombic interactions and the mechanics of their orbital agitation.¹³

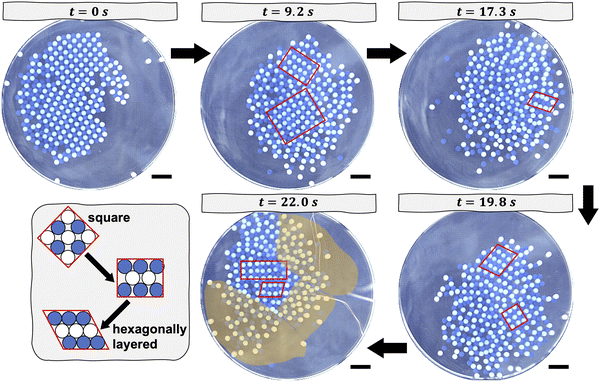
In each experiment, we begin with a square crystal at rest, as shown in Fig. 1. The crystal is formed immediately before the commencement of the melting experiment by shaking the beads, initially uncharged, at a centripetal acceleration of approximately 9.4 m s⁻². The shaker is turned off after about 10 minutes, at which point the crystal has formed. Previously, we showed that the Coulombic binding energy of a similar system, wherein the crystal had no impurities, was on the order of 10⁻³ J.¹³ The melting process commences once the orbital shaker is set to the appropriate centripetal acceleration and turned on. The aggregate of beads begins to slide across the dish and to collide with its walls. These collisions cause the beads to undergo shear transformations, which drive local regions in the crystal to transition from a square structure to a hexagonally layered structure, as captured at later snapshots in time in Fig. 1. A hexagonally layered structure refers to alternating rows of nylon beads and PTFE beads that are close-packed. As the shaking continues over the course of roughly 10 minutes, some beads have sufficient kinetic energy to overcome the local attractive Coulombic potential that holds them in place and, thus, to rearrange. These rearrangements result in disordered structures that coexist with locally ordered regions. The positions of the ordered and disordered regions are not fixed relative to the center of mass of the aggregate of beads. Depending on the orientation of the aggregate of beads relative to the direction of shear caused by a collision, a subset of beads may either adopt, for instance, a hexagonally layered structure or become disordered. Despite their collisions with the walls of the dish, the beads remain closely packed and tend to move as an aggregate. This tendency to move as an aggregate stems from the fact that the beads remain tribocharged and interact electrostatically. That said, beads—especially those located at the edge of the aggregate—may sometimes be more loosely packed than those closer to the center of mass of the aggregate, as shown in Fig. 1, because their motion is constrained by fewer neighbors. The melting behavior of crystals containing impurities is qualitatively similar to that described for crystals without impurities, as shown in Fig. S2 and S3 (ESI†). In the limit of a high impurity density of 11%, namely 50 impurities, the locally ordered regions tend to be smaller in size due to the disruptive presence of 50 impurities. We do not perform experiments with even larger densities of impurities; doing so could lead to the phase separation of the impurities from the crystal structure during the initial nucleation of the crystal¹⁷ or could alter the square symmetry of the initial crystal.

Fig. 1 Video stills captured at specific times depicting the process of melting a square crystal composed of 200 nylon beads (blue) and 200 PTFE beads (white). The crystal is mechanically agitated on an orbital shaker at a centripetal acceleration of 21.1 m s⁻². Square structures and hexagonally layered structures are outlined in red. At time t = 22 s, disordered or melted regions are highlighted in orange as a visual guide. The line in the last time panel corresponds to the reflection of the wire that connects the lid of the dish to the electrical ground. All scale bars correspond to one centimeter. The color of the images is altered for improved contrast. (inset) The shear transformation of a square lattice to a hexagonally layered structure is depicted schematically.

2. Results

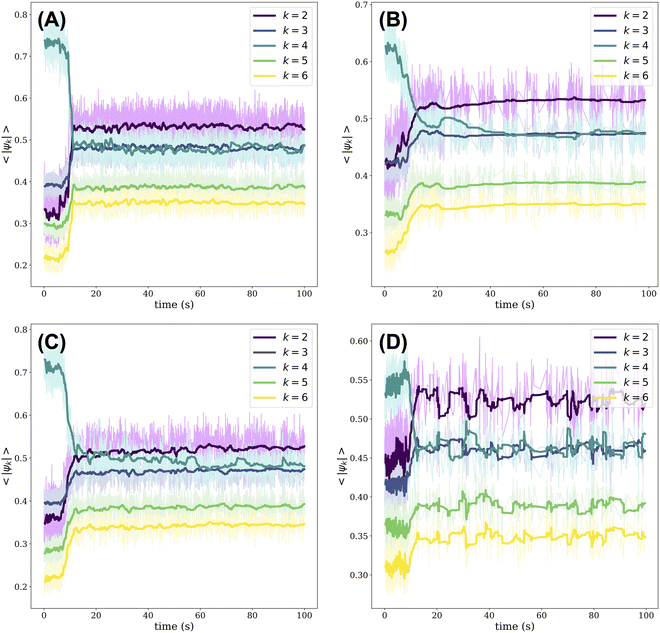
As the crystal melts, changes in the local structure can be monitored by means of the modulus of the k-atic order parameter as averaged over all beads, 〈|ψ_k|〉. The k-atic order parameter, |ψ_k|, where k = {2, 3, 4, 5, 6}, provides a measure of the orientational order of a bead relative to the beads in its local environment (see Materials and Methods for details of its calculation). The order parameter is complex and its modulus, |ψ_k|, ranges from 0 to 1; when |ψ_k| = 1, the bead has perfect k-order.¹⁸ In Fig. 2, we plot the evolution of 〈|ψ_k|〉 over time for all PTFE beads relative to their nylon neighbors. Initially, regardless of the orbital frequency of the shaker or the presence of impurities in the crystal, 〈|ψ₄|〉 is greater than the average modulus of the order parameter when k = {2, 3, 5, 6}. The dominance of 〈|ψ₄|〉 reflects the fact that the initial crystal has square symmetry. As the crystal is melted, the positions of many beads that had originally belonged to the square lattice are disturbed. These positional shifts occur as the beads collide with one another as well as with the walls of the dish. As rearrangements persist, we note a sharp decrease in 〈|ψ₄|〉 across all experiments: 〈|ψ₂|〉 overtakes 〈|ψ₄|〉 in magnitude and 〈|ψ₃|〉 becomes approximately equal to 〈|ψ₄|〉. These trends are consistent across all experiments, although we note an initial value of 〈|ψ₄|〉 ≈ 0.55 in Fig. 2(D) for the crystal with 50 impurities versus 〈|ψ₄|〉 ≈ 0.7 for the other experiments. Since the gold-coated nylon beads acquire a minor positive charge, they tend to be surrounded by PTFE beads. As such, the impurities disrupt the alternating order of nylon and PTFE beads on a square checkerboard. This disruption in ordering is reflected in the lower initial value of 〈|ψ₄|〉, since we consider the order parameter of PTFE beads relative to their nylon neighbors in generating Fig. 2.

Fig. 2 The average of the modulus of the k-atic order parameter, 〈|ψ_k|〉, where k = {2, 3, 4, 5, 6}, for all PTFE beads in each frame. The k-atic order parameter for the PTFE beads is measured relative to their nylon neighbors. Video frames are only included in the analysis if at least 80% of the nylon beads and 90% of the PTFE beads are identified. The results correspond to the melting of a square crystal composed of 200 nylon beads and 200 PTFE beads (A) without impurities when agitated orbitally at a centripetal acceleration of 26 m s⁻², (B) without impurities when agitated orbitally at a centripetal acceleration of 21.1 m s⁻², (C) with one impurity when agitated orbitally at a centripetal acceleration of 21.1 m s⁻², and (D) with 50 impurities when agitated orbitally at a centripetal acceleration of 21.1 m s⁻². Each bolded trendline corresponds to the rolling average of the raw data, which is depicted in the corresponding lightened hue.

Over time, locally ordered regions appear alongside disordered regions in the aggregate of beads. Some of these ordered regions have square symmetry, while others adopt a hexagonally layered structure. The co-existence of these ordered and disordered regions results in 〈|ψ₂|〉 overtaking 〈|ψ₄|〉. Moreover, when we consider the evolution in time of 〈|ψ_k|〉 for all PTFE beads relative to their PTFE neighbors, we note that 〈|ψ₂|〉 also overtakes 〈|ψ₄|〉 and that a local maximum in 〈|ψ₂|〉 occurs before the cross-over point, as shown in Fig. S4 (ESI†). This local maximum in 〈|ψ₂|〉 likely reflects the fact that when the crystal initially collides with the walls of the dish, all the beads belong to a well-ordered square crystal. As such, the collisions shear the crystal unidirectionally, resulting in a consistent decrease in the lattice spacing between neighboring PTFE beads and the emergence of nematic ordering.¹⁹ Ultimately, when considering the order parameter for PTFE beads relative to their PTFE neighbors or, separately, to their nylon neighbors, we find that 〈|ψ₃|〉 ≈ 〈|ψ₄|〉 after about 20 seconds of agitation, as shown in Fig. 2 and Fig. S4 (ESI†). As the melting process unfolds, the beads maintain a close-packed structure due to their binding electrostatic interactions. In examining the order parameter of PTFE beads relative to their nylon neighbors, we note that 〈|ψ₃|〉 is commensurate with 〈|ψ₄|〉 because, on average, a PTFE bead will have three nylon neighbors in a close-packed aggregate composed of equal numbers of nylon and PTFE beads. The value of 〈|ψ₂|〉 remains greater than 〈|ψ₃|〉 given the fact that disorder is patchy through the aggregate. Nearly identical trends can be drawn when considering the fraction of beads, nylon and PTFE included, whose k = {2, 3, 4, 5, 6} order parameter is the greatest in modulus as a function of time (Fig. S5, ESI†).

The extent of the orientational order in the crystal diminishes over time. In Fig. 3, we plot the 4-fold orientational correlation as a function of the radial distance, or stated equivalently the separation, between two beads. The way in which the parameter decays as a function of bead separation, namely linearly or exponentially, provides a measure of the range of orientational order in the crystal (see Materials and Methods for details of its calculation). We pay careful attention to how the parameter decays as a function of time. For crystals without impurities, the orientational order decays linearly at the early stages of melting, as shown in Fig. 3(A) and (B). Initially, when the crystal without impurities is agitated orbitally at 26 m s⁻², its 4-fold correlation does not fall off as quickly as that for the crystal without impurities agitated at 21.1 m s⁻². This discrepancy likely stems from the fact that, prior to melting, the crystal agitated at the lower acceleration contained more defects and misaligned grains (Fig. 1) as compared to that agitated at the acceleration of 26 m s⁻². The order parameter, and by extension the 4-fold orientational correlation, is sensitive to such defects in the initial crystal. In their initial, pre-melted state, the crystals with impurities show less long-range orientational order. For the case of the crystal doped with 50 impurities, before melting, its 4-fold orientational correlation decays exponentially and not linearly, as per Fig. 3(D). The impurities disturb the long-range ordering of the nylon and PTFE beads. Eventually, in all experiments, the transition from order to quasi-disorder occurs at ≈11 seconds, and it is marked by a transition from linear to exponential decay of the correlation function. The time at which this transition occurs coincides with the cross-over point of 〈|ψ₂|〉 and 〈|ψ₄|〉 in Fig. 2. Once melting has commenced, the exponential decay of the correlation function is similar for all experiments. As per Fig. 3, ordered regions in the melted crystal span about three bead diameters; this extent of order agrees with our characterization of small ordered, patches within the melted crystal shown in Fig. 1.

Fig. 3 The time-evolution of the 4-fold orientational correlation averaged over all pairs of nylon or PTFE beads that are separated by various distances. The results correspond to the melting of a square crystal composed of 200 nylon beads and 200 PTFE beads (A) without impurities when agitated orbitally at a centripetal acceleration of 26 m s⁻², (B) without impurities when agitated orbitally at a centripetal acceleration of 21.1 m s⁻², (C) with one impurity when agitated orbitally at a centripetal acceleration of 21.1 m s⁻², and (D) with 50 impurities when agitated orbitally at a centripetal acceleration of 21.1 m s⁻². In each panel, the dotted lines correspond to least squares exponential fits of the form ae^−br + c, where r is the separation between beads.

3. Discussion

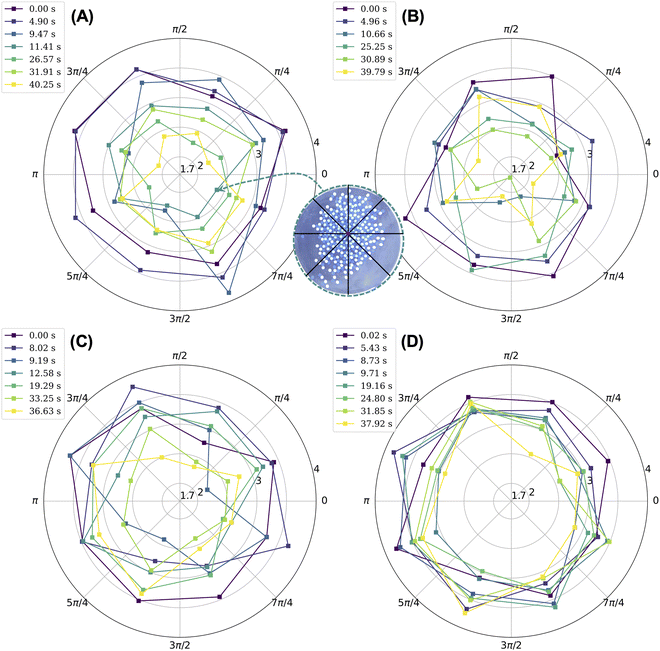
The objective of this work is to understand how crystals melt when they are not in thermal equilibrium with their environment and when their building blocks have long-range electrostatic interactions that persist in time. We use a table-top shaking experiment that allows us to visualize the melting behavior of a two-dimensional Coulombic crystal composed of tribocharged beads. We use vigorous mechanical shaking to melt the crystal. The melting of a macroscale Coulombic crystal is qualitatively unique insofar as (1) the melting does not originate from the site of impurities and (2) ordered regions appear alongside disordered, melted regions. The locations of these ordered regions relative to the center of mass of the aggregate shift in time depending on what portion of the aggregate collides with the walls of the dish. As demonstrated by the orientational correlation results in Fig. 3, the melted crystal includes ordered regions that on average span three bead diameters. The beads remain tribocharged as they are agitated. Accordingly, they continue to experience long-ranged electrostatic interactions; these interactions result in locally ordered patches under favorable shear conditions.

Unlike canonical examples of melting where melting may occur locally at the site of defects of impurities,³ our melting is shear induced, and it proceeds from the edges of the crystal into its interior despite the presence of impurities. We note that as the aggregate of melted beads collides with the walls of the dish, some beads become ordered while others become disordered. Generally, the beads that become ordered are not located at or near the point of impact of the aggregate with the wall. Moreover, these beads tend to be oriented such that the direction of the shear will induce ordering. For instance, if a subset of beads containing loosely packed rows of nylon and PTFE beads is sheared along the direction of the rows, then this shear will cause the beads to form a hexagonally layered structure. The coexistence of disordered and ordered regions within the melted crystal and their constant change in position within the aggregate can be visualized by subdividing the aggregate into sectors and considering the average coordination number of beads within each sector. We include beads at the edge of the aggregate and impurities in our calculation of the average coordination number. We define the center of the aggregate (which includes nylon, PTFE, and impurity beads) as its center of mass and consider eight sectors with equal opening angles, where the first sector starts along the positive x-axis and terminates at the angle π/4, as represented in the inset of Fig. 4. For almost all experiments, excluding that with 50 impurity beads, we note a decrease in the average coordination number by sector over time. Nevertheless, the beads in some sectors have an average coordination number of at least three, which is comparable to the average coordination number of beads at the onset of melting. In relative terms, sectors with greater coordination numbers are usually ones that include more beads that are ordered. Disordered patches tend to contain either more voids or beads that are loosely packed at the edges of the aggregate (Fig. S6, ESI†), both of which result in lower average coordination numbers. In the case of the crystal with 50 impurities, we note that the coordination number does not change as dramatically in time and that all sectors have similar coordination numbers, as shown in Fig. 4(D). Here, the impurities hold the structure together because they can retain charge capacitively.¹⁷

Fig. 4 Polar plot of the average coordination number (radial value) of the beads within each sector (angular value) at specific times. In each frame of interest, as shown in the inset, the aggregate of beads is categorized into eight sectors that are centered at the center of mass of the aggregate of beads and whose opening angle is π/4. The coordination number of a bead corresponds to the number of beads, agnostic of their kind, within 1.2 bead diameters from the bead's center. The results correspond to the melting of a square crystal composed of 200 nylon beads and 200 PTFE beads (A) without impurities when agitated orbitally at a centripetal acceleration of 26 m s⁻², (B) without impurities when agitated orbitally at a centripetal acceleration of 21.1 m s⁻², (C) with one impurity when agitated orbitally at a centripetal acceleration of 21.1 m s⁻², and (D) with 50 impurities when agitated orbitally at a centripetal acceleration of 21.1 m s⁻².

The variation of the average coordination number by sector further underscores the fact that the melting behavior of Coulombic crystals is shear induced. In some instances, some of the beads will order should the direction of shear be favorable to ordering. In other cases, the shear from repetitive collisions between the aggregate and the walls of the dish will impart enough kinetic energy to the beads for them to move about, rearrange locally, and form a disordered structure. The ability for shear to order and melt the crystal presupposes that the aggregate of beads does not occupy the entire surface area of the dish, that it can move within the dish, and that it can collide with the boundaries of the dish.

The use of shear to simultaneously order and melt portions of a crystal without changing its magnitude or frequency is a qualitatively new phenomenon. Normally, shear can either be used to crystallize or melt a crystal by altering the shear rate;⁵ however, in our system, the very same shear (in type and magnitude) can generate both order and disorder. The coexistence of ordered and disordered regions that are not pinned to specific locations in the crystal is a unique kind of shear-induced melting behavior that stems from the long-range, persistent electrostatic interactions between tribocharged beads.

4. Materials and methods

4.1. Experimental set-up

The experiments are performed at a relative humidity of ≈20% RH within a humidity-controlled glove bag (Sigma Aldrich), as shown in Fig. S1 (ESI†). Tribocharging depends on the ambient relative humidity. We and others believe that the hydroxide ions, within the thin layers of water that coat two materials in contact, redistribute themselves amongst the materials. Upon separation, one material is positively charged due to a lack of hydroxide ions and the other is negatively charged due to an excess thereof.^14,20–22 Accordingly, the humidity in the glove bag is carefully monitored using a hygrometer probe (VWR Traceable). The millimeter-sized beads, namely nylon beads (McMaster Carr 9613K12) and PTFE beads (McMaster Carr 9660K12), are placed in a gold-coated Petri dish (Corning) that is machined such that its height is approximately equal to the diameter of the beads. The beads are reported by the manufacturer to be 2.38125 ± 0.0508 millimeters in diameter. The inner diameter of the dish is reported to be about 8.63 centimeters. The nylon beads are dyed blue in batches of 100 by adding ≈20 mg of Disperse Blue 14 (Sigma Aldrich) to a vial containing the beads, 8 mL of Milli-Q water, and 2 mL of isopropyl alcohol. The mixture is heated to 60 °C overnight under constant stirring. The beads are rinsed with isopropyl alcohol or ethyl alcohol until the supernatant is clear. Undyed PTFE beads are also rinsed with isopropyl alcohol or ethyl alcohol. Both nylon and PTFE beads are dried in an oven at 40–60 °C.

The Petri dish is made from polystyrene, and it is coated with an adhesive layer of chromium, measuring approximately ≈15 nm in thickness, followed by a continuous 300-nanometer thick layer of gold. In experiments where the melting of a crystal with impurities is studied, gold-coated nylon beads are used as impurities. The nylon beads are also 2.38125 ± 0.0508 millimeters, according to manufacturing specifications, before coating. We then coat these beads with an adhesive layer of chromium followed by a layer of gold.²³ We estimate their mass to be the same as that of an uncoated nylon bead when calculating the center of mass of the aggregate. Once all the beads are inside the dish, they are neutralized in charge with a Zerostat gun (VWR). The dish is capped using an optically transparent lid, as shown in Fig. S1 (ESI†). The dish is surrounded by a custom plastic ring that has an inset lip around its circumference in which the lid fits snuggly. The lid is secured in place with some transparent adhesive tape. The lid is made from acrylic (Inventables) and a film of ITO on PET (Sigma Aldrich 639303) is attached with clear double-sided tape to the side in contact with the beads. The film is electrically grounded by means of a wire: one end is attached to electrical ground, while the other end makes conformal contact with a tab of electrically conductive tape that is attached to the ITO on PET film. The dish sits on the platform of an orbital shaker (VWR Advanced 3500 Orbital Shaker) with an orbital diameter of 19 millimeters. The platform is covered with a thin film of PTFE (McMaster Carr) to lower the coefficient of static friction between the dish and the platform. The dish is surrounded by a hard, irregularly shaped plastic enclosure.

The humidity-controlled chamber is sealed, and the humidity is adjusted to the set point of ≈20% RH by flowing wet and/or dry nitrogen into the chamber. After allowing the humidity in the glove bag to equilibrate for two hours, the beads are agitated in the dish at an orbital frequency of ≈300 rotations per minute (rpm) or, equivalently, at a centripetal acceleration of 9.4 m s⁻²: the beads form a Coulombic material. The shaker is turned off after 10 minutes. Subsequently, the orbital shaker is powered on at an orbital frequency of either 450 rpm or 500 rpm or, equivalently, at a centripetal acceleration of 21.1 m s⁻² or 26 m s⁻². The melting behavior is recorded with a fast camera (Phantom v310) for 10 minutes. The wide-angle lens (Tokina 12–24 mm f4) of the camera is sealed in the glove bag, while the body of the camera is mounted overhead to the ceiling. The dynamics are captured at a frame rate of 600 frames per second (fps) with a resolution of 640 by 480 pixels.

4.2. Data processing

After each experiment, the data are offloaded from the camera, and they are processed using a custom-built, python-based data-processing pipeline. For each frame, the same analysis is carried out. The contour of the dish is located using the Hough circle transform.²⁴ Next, the center of each bead is determined by performing Hue Saturation Value (HSV) thresholding, contour detection, watershed segmentation,²⁵ and additional filtering on candidate bead center coordinates. The identity of each bead, namely whether it is a nylon, PTFE, or gold-coated nylon bead, is recorded as the bounds for HSV thresholding depend on the color of the bead. Generally, nylon beads are not as easy to detect as impurities or PTFE beads because the ITO on PET film through which they are imaged has a very subtle blue tint, which adversely affects the contrast. The positions of the beads are determined within the frame of reference of the moving dish by subtracting the coordinates of the center of the dish from the coordinates of each bead. To characterize the melting behavior of the Coulombic material, we determine the coordination number of each bead as well as the k-atic order parameter for each bead (excluding impurities).

4.2.1. Coordination number of each bead. The coordination number of a bead corresponds to the number of neighbors, agnostic of their kind, that are within 1.2 bead diameters from the bead of interest. A bead is counted as a neighbor if its center falls within this search range.

4.2.2. k-atic order parameter for each bead. The k-atic order parameter of a bead, ψ_k, provides a measure of its local orientational order. For a bead labelled as l, the order parameter is given as:
where the summation is taken over the n = k neighbors closest to bead l and ϕ_lj is the angle that is formed between the vector connecting the bead l to its neighbor j and the positive x-axis.¹⁸ We use a python-based package²⁶ and some custom code to perform these calculations.

4.2.3. 4-fold orientational correlation. For frames where at least 80% of the nylon beads and 90% of the PTFE beads are identified by the locating algorithm, the 4-fold orientational correlation parameter is calculated in accordance with the technique reported by Cislo and coworkers.²⁷ Nylon and PTFE beads are included in the calculation, while impurity beads are excluded. For each bead, its neighbors are identified and categorized by whether they are separated from the bead by ]0,1], ]1,2], ]2,3], ]3,4], ]4,5], ]5,6], ]6,7], ]7,8], ]8,9], or ]9,10] bead diameters. Thereafter, for each pair, composed of the bead and its respective neighbor, we calculate the product of its 4-atic order parameter, ψ₄(r_i), and the complex-conjugate of its neighbor's 4-atic order parameter, ψ₄*(r_j). This exercise is repeated for all pairwise combinations of beads and the products are binned according to the spatial separation between the beads belonging to the pair. For nylon beads, we use their 4-atic order parameter as measured relative to their PTFE neighbors; conversely, for PTFE beads, we use their 4-atic order parameter as measured relative to their nylon neighbors. We note that that the sum of the products for the same pairwise combination of beads gives: ψ₄(r_i)ψ₄*(r_j) + ψ₄*(r_i)ψ₄(r_j) = 2Re[ψ₄(r_i)ψ₄*(r_j)]. Accordingly, for each spatial separation, the 4-fold orientational correlation is calculated by taking the average of all real components of the products.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Ms Grace H. Zhang, Dr Amit A. Nagarkar, Dr Farzan Vafa, Dr Suraj Shankar, Dr Mohamad Kodaimati, and Professor David R. Nelson for helpful conversations. We are grateful to the Facilities team in the Department of Chemistry and Chemical Biology at Harvard University for their assistance in building the fast-camera mount. This work was supported by the Harvard NSF MRSEC award DMR-2011754. The sputter coating of gold on select objects was performed in part at the Harvard University Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Coordinated Infrastructure Network (NNCIN), which is supported by the National Science Foundation under NSF award no. ECCS-2025158.

References

1. B. I. Halperin and D. R. Nelson, Theory of Two-Dimensional Melting, Phys. Rev. Lett., 1978, 41(2), 121–124.
2. M. J. Stevens, M. O. Robbins and J. F. Belak, Shear Melting of Colloids: A Nonequilibrium Phase Diagram, Phys. Rev. Lett., 1991, 66(23), 3004–3007.
3. F. Wang, D. Zhou and Y. Han, Melting of Colloidal Crystals, Adv. Funct. Mater., 2016, 26, 8903–8919.
4. A. Imhof, A. van Blaaderen and J. K. G. Dhont, Shear Melting of Colloidal Crystals of Charged Spheres Studied with Rheology and Polarizing Microscopy, Langmuir, 1994, 10, 3477–3484.
5. Y. L. Wu, D. Derks., A. van Blaaderen and A. Imhof, Melting and crystallization of colloid hard-sphere suspensions under shear, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(26), 10564–10569.
6. K. E. Daniels and R. P. Behringer, Hysteresis and Competition between Disorder and Crystallization in Sheared and Vibrated Granular Flow, Phys. Rev. Lett., 2005, 94, 168001.
7. P. M. Reis, R. A. Ingale and M. D. Shattuck, Crystallization of a Quasi-Two-Dimensional Granular Fluid, Phys. Rev. Lett., 2006, 96, 258001.
8. F. Pacheco-Vázquez, G. A. Caballero-Robledo and J. C. Ruiz-Suárez, Superheating in Granular Matter, Phys. Rev. Lett., 2009, 102, 170601.
9. C. May, M. Wild, I. Rehberg and K. Huang, Analog of surface melting in a macroscopic nonequilibrium system, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062201.
10. F. Rietz, C. Radin, H. L. Swinney and M. Schröter, Nucleation in Sheared Granular Matter, Phys. Rev. Lett., 2018, 120, 055701.
11. B. A. Grzybowski, A. Winkleman, J. A. Wiles, Y. Brumer and G. M. Whitesides, Electrostatic self-assembly of macroscopic crystals using contact electrification, Nat. Mater., 2003, 2, 241–245.
12. R. Cademartiri, C. A. Stan, V. M. Tran, E. Wu, L. Friar, D. Vulis, L. W. Clark, S. Tricard and G. M. Whitesides, A simple two-dimensional model system to study electrostatic-self-assembly, Soft Matter, 2012, 8, 9771–9791.
13. S. Battat, A. A. Nagarkar, F. Spaepen, D. A. Weitz and G. M. Whitesides. Kinetics of Formation of a Macroscale Binary Coulombic Material. 2023. (revision submitted).
14. L. McCarty and G. M. Whitesides, Electrostatic Charging Due to Separation of Ions at Interfaces: Contact Electrification of Ionic Electrets, Angew. Chem., Int. Ed., 2008, 47, 2188–2207.
15. W. R. Harper. Contact and Frictional Electrification. Laplacian Press. 1998.
16. J. R. Taylor, Classical Mechanics, University Science Books, 2005.
17. G. K. Kaufman, S. W. Thomas III, M. Reches, B. F. Shaw, J. Feng and G. M. Whitesides, Phase separation of 2D meso-scale Coulombic crystals from mesoscale polarizable “solvent”, Soft Matter, 2009, 5, 1188–1191.
18. D. R. Nelson, M. Rubinstein and F. Spaepen, Order in two-dimensional binary random arrays, Philos. Mag. A, 1982, 46, 105–126.
19. S. Shankar, A. Souslov, M. J. Bowick, M. C. Marchetti and V. Vitelli, Topological active matter, Nat. Rev. Phys., 2022, 4, 380–398.
20. A. Schella, S. Herminghaus and M. Schröter, Influence of humidity on tribo-electric charging and segregation in shaken granular media, Soft Matter, 2017, 13, 394–401.
21. D. J. Lacks and T. Shinbrot, Long-standing and unresolved issues in triboelectric charging, Nat. Rev. Chem., 2019, 3, 465–476.
22. I. A. Harris, M. X. Lim and H. M. Jaeger, Temperature dependence of nylon and PTFE triboelectrification, Phys. Rev. Mater., 2019, 3, 085603.
23. Our use of chromium as an adhesive layer is based on the advice of Dr Austin Akey, a specialist in metal coatings at Harvard University's Center for Nanoscale Systems.
24. H. K. Yuen, J. Princen, J. Dlingworth and J. Kittler, A Comparative Study of Hough Transform Methods for Circle Finding, in Proceedings of the Alvey Vision Conference, ed. K. D. Baker, Alvey Vision Club, 1989, pp. 169–174,  DOI:10.5244/C.3.29.
25. S. Beucher and F. Meyer, The Morphological Approach to Segmentation: The Watershed Transformation, in Mathematical Morphology in Image Processing, ed. B. J. Thomson and E. Dougherty, CRC Press, Boca Raton, 1993, pp. 433–481.
26. V. Ramasubramani, B. D. Dice, E. S. Harper, M. P. Spellings, J. A. Anderson and S. C. Glotzer, freud: A Software Suite for High Throughput Analysis of Particle Simulation Data, Comput. Phys. Commun., 2020, 254, 107275.
27. D. Cislo, H. Qin, F. Yang, M. J. Bowick and S. J. Streichan, Active cell divisions generate exotic fourfold orientationally ordered phase in living tissue, BioRxiv., 2021 DOI:10.1101/2021.07.28.453899.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01635d

---