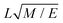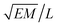Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigating anionic surfactant phase diagrams using dissipative particle dynamics: development of a transferable model†
Sarah J.
Gray
,
Martin
Walker
 ,
Rachel
Hendrikse
,
Rachel
Hendrikse
 and
Mark R.
Wilson
and
Mark R.
Wilson
 *
*
Department of Chemistry, Durham University, Lower Mountjoy, Stockton Road, Durham, DH1 3LE, UK. E-mail: mark.wilson@durham.ac.uk
First published on 11th April 2023
Abstract
Dissipative particle dynamics (DPD) provides a powerful coarse-grained simulation technique for the study of a wide range of soft matter systems. Here, we investigate the transferability of DPD models to the prediction of anionic surfactant phase diagrams, taking advantage of fast parameter sweeps to optimise the choice of DPD parameters for these systems. Parameters are developed which provide a good representation of the phase diagrams of SDS (sodium dodecyl sulfate) and three different isomeric forms of LAS (linear alkylbenzene sulfonates) across an extensive concentration range. A high degree of transferability is seen, with parameters readily transferable to other systems, such as AES (alkyl ether sulfates). Excellent agreement is obtained with experimentally measured quantities, such as the lamellar layer spacing. Isosurfaces are produced from the surfactant head group, from which the second moment M of the isosurface normal distribution is calculated for different phase structures. Lyotropic liquid crystalline phases are characterised by a combination of the eigenvalues of M, radial distribution functions, and visual inspections.
1 Introduction
Surfactants are ubiquitous in our everyday lives. However, despite their widespread use and considerable commercial value,1 accurate a priori prediction of surfactant phase diagrams remains a major challenge. This creates a barrier to the development of new surfactants and new formulations, particularly when subtle changes to molecular interactions can induce unexpected changes in phase. Consequently, industry continues to rely on empirical knowledge of previous formulations in the product development process, often resulting in huge investments to achieve the requisite properties. Therefore, it would be extremely desirable to have the ability to predict the phase behaviour of a given surfactant, or surfactant mixture, via theoretical or computational techniques.Studying the self-assembly process of surfactants using molecular dynamics (MD) simulations has traditionally been difficult, due to the long time and length scales required. As a result, MD simulations are often performed on pre-assembled surfactant systems,2–7 and studies investigating the full phase diagram are limited. These computational challenges led to the development of the mesoscopic modelling method of dissipative particle dynamics (DPD).8–10 DPD is capable of simulating very large systems while retaining chemical detail, and with its size, speed, and simplicity, DPD has seen many applications since its conception nearly twenty-five years ago, across the broad range of soft matter research.11–18
DPD has been extensively applied to surfactant systems, from simplified dumbbell models,19–21 through to more complex models fitted to reproduce the specific behaviours of individual species.22–25 Within these studies, a wide range of DPD parametrisation methods have been developed. Often these are targeted at dilute solutions where (for example) infinite dilution activity coefficients can be employed,23 or parametrisation can proceed via the surface site interaction point (SSIP) model.26,27
In common with many coarse-grained methodologies, DPD is often found to lack parameter transferability across different thermodynamic conditions, particularly with respect to large changes in concentration and/or temperature. Two-body coarse-grained models (and to a lesser extent – fully atomistic models) are not completely transferable across chemical environments, due to the limits of effective two-body potentials, which average out the effects of many-body forces in the chemical environment used for parametrisation. However, the success of theoretical approaches, such as SAFT28–31 and coarse-grained models such as MARTINI 332–34 make it clear that careful parametrisation can lead to a high degree of transferability. This is particularly true for top–down models parametrised across a range of thermodynamic conditions.35
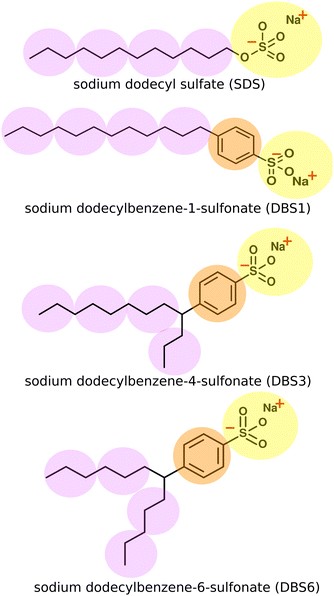
In this work, we present DPD models of two key industrial surfactants: sodium dodecylsulfate (SDS) and linear alkylbenzene sulfonate (LAS) (Fig. 1).
SDS and LAS molecules have been previously studied at a range of levels from all-atom studies of micellisation36–39 and interfacial behaviour,40,41 to coarse grain studies investigating mesophase structure, energetics, and interfacial properties.42–44 While SDS and LAS have been studied previously using DPD and other coarse-grained methods,43,45–49 only a handful of these previous studies46,47,49 have attempted to reproduce the experimental phase diagram across a range of concentrations. In this paper, we present a parametrised DPD model, which shows a high degree of transferability, not seen in previous works, which performs well across a wide concentration range and readily applies to different molecules. We make extensive use of fast parameter sweeps to optimise DPD parameters to reproduce representative phase diagrams for both SDS and three different isomeric forms of LAS using a set of transferable parameters. The results provide an excellent representation of experimental phase diagrams for SDS and for linear and two-branched forms of LAS, and provide an excellent representation of experimentally measured quantities (phase boundaries and lamellar layer spacings). Moreover, we show the same parameter set can be readily extended to other molecules, through simulations of an isomeric mixture of AES (alkyl ether sulfates).
2 Computational
2.1 Choice of DPD model and coarse-grained mapping
DPD beads can represent an enormous range of moieties: from functional groups,12,15,21 through groups of small molecules, up to much larger scales such as Kuhn length segments of a polymer chain.50,51 The coarse-grained mapping scheme used in this work is shown in Fig. 1. In each case, the sulfonate head group is represented as a single bead, a second bead type is used for the phenyl ring in LAS and the hydrocarbon chains are coarse-grained using three heavy atoms to one “tail” bead. We represented water in the system as a single bead for three water molecules. We note that both SDS and LAS are ionic surfactants but at this level of coarse-graining (for most of the phase diagram), we can successfully use a single uncharged head group bead (see below). An added advantage of this approach arises from considerable savings in computer time. The computational cost per DPD iteration, τ, changes from a linear relationship (τ ∝ N) in the absence of electrostatics, to a nonlinear relationship (τ ∝ N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) with electrostatics, therefore limiting the computational benefit of DPD calculations. We note that in dilute solutions of surfactants electrostatic interactions are known to be important in determining the critical micelle concentration and also the size of micelles,48 and ionic salts are known to perturb both of these through electrostatic shielding. However, for the current study, we are primarily interested in the liquid crystal phases formed and their position on the surfactant phase diagram. In initial tests, we found that it was possible to successfully coarse-grain both surfactants without the use of electrostatic interactions and that this was sufficient to yield good phase diagram predictions. The reason for this can be attributed to only small changes in the partial condensation of ions around aggregates as surfactant concentration changes across the majority of the phase diagram. This suggests that the bulk phase diagrams are far less sensitive to electrostatic interactions than in the low-concentration regime.
N) with electrostatics, therefore limiting the computational benefit of DPD calculations. We note that in dilute solutions of surfactants electrostatic interactions are known to be important in determining the critical micelle concentration and also the size of micelles,48 and ionic salts are known to perturb both of these through electrostatic shielding. However, for the current study, we are primarily interested in the liquid crystal phases formed and their position on the surfactant phase diagram. In initial tests, we found that it was possible to successfully coarse-grain both surfactants without the use of electrostatic interactions and that this was sufficient to yield good phase diagram predictions. The reason for this can be attributed to only small changes in the partial condensation of ions around aggregates as surfactant concentration changes across the majority of the phase diagram. This suggests that the bulk phase diagrams are far less sensitive to electrostatic interactions than in the low-concentration regime.
2.2 DPD model
The non-bonded inter-particle force is described as the sum of three pairwise forces: a conservative force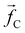 which described the chemistry of the system, a dissipative force
which described the chemistry of the system, a dissipative force 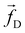 , and a random force
, and a random force 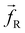 . All three of these forces apply up to a cutoff distance rC, beyond which they become zero by definition. In this work, we set the cutoff rC = 1. The conservative force takes the form
. All three of these forces apply up to a cutoff distance rC, beyond which they become zero by definition. In this work, we set the cutoff rC = 1. The conservative force takes the form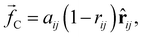 | (1) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/|rij|. The dissipative force is given by
ij = rij/|rij|. The dissipative force is given by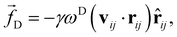 | (2) |
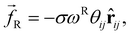 | (3) |
The random force injects small amounts of energy into the system, and the dissipative force describes the dissipation of energy due to friction – together they act as the ‘DPD thermostat’. In order to recover the Gibbs ensemble this pair of forces is coupled by a fluctuation–dissipation theorem.52 This results in the relations: σ2 = 2γkBT, and ωD = [ωR]2. The DPD thermostat parameters used in this work were γ = 5.625 and σ = 3.354 (using reduced units – see below), which are chosen in line with existing literature.10,45,53 We use the most commonly chosen function for ωR,
| ωR = (1 − rij), | (4) |
The defined cutoff of rC = 1 defines the length scale for the system. Since we chose to define the same cutoff for all bead species, our level of coarse-graining is dictated by the smallest group in our surfactants. DPD typically uses reduced units, which require scaling to map to a real system. In this work, masses are scaled such that beads have a reduced mass of m = 1 and energies E are defined by setting kBT = 1. The dimensions of various DPD parameters are provided in Table 1, where various parameters can be converted into real units using their base units.
The bead connectivity and molecular shape are maintained by a combination of two-site and three-site harmonic springs which take the form:
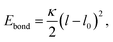 | (5) |
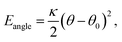 | (6) |
LAS models involve a straightforward extension of our description of SDS. We assume that the closely related sulfate and sulfonate head groups can be represented by the same bead type, with an additional bead inserted between the head and tail beads to describe the benzene ring linker group in LAS. Bonds and angles take the same form as SDS. For branched forms of LAS, two bonds are made between the chains and the benzene linker group, together with associate bond angles. We do not include an additional tail-benzene-tail angle constraint at the branch point. Bonds and angle interactions are specified in full within the ESI.†
The choice of fixing the cut-off distance for all beads rC = 1, effectively approximates the volume of all bead types to be equivalent. This approach is common in similar DPD models23,46 and is reasonable given the similarity of the volumes occupied by different beads. We expect that the approximation has little impact on transitions between liquid crystalline phases, for example between hexagonal and lamellar structures; however, we appreciate that the volume occupied by parts of the surfactant is more important in the micelle regime, for describing factors such as micellar shape, which is not considered in this work.
2.3 DPD parametrisation
To simplify the model fitting for SDS, we chose the self-interaction to be identical for all bead types (aii = 25) leaving three independent cross-interaction parameters to be chosen for head group-tail group aHT, tail-water group aTW and head-water aHW group interactions. The approach of fixing aii for all bead types is common amongst simple DPD models,57,58 where differences arising from the interaction of chemically different groups are contained entirely within the cross terms. Typically, the self-interaction is chosen to reproduce the compressibility of water, where Groot and Warren (1997)10 determine that this is achieved by setting the repulsion parameter aii = 75kBT/ρ. In this work we choose to set the bead density ρ = 3, thereby producing a self interaction value aii = 25.We primarily establish the undetermined nonbonded interaction parameters for SDS through a comprehensive sweep of parameter space. The model was then extended to other systems, as discussed in detail below. To do that we make use of Flory–Huggins parameters χ in order to demonstrate the transferability of our model. Groot and Warren10 suggest assigning aij interaction parameters by relating χ to the molecular fragments that a DPD bead represents. In the case of our fragments, χ data is not experimentally available. Instead, similarly to the method of Maiti and McGrother,59 we related the theoretical χ parameter of our fragments to their Hansen solubility data,60 taking the form
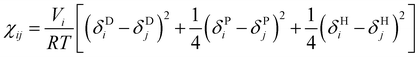 | (7) |
2.4 Simulation runs
All simulations described are performed using the DL_MESO 2.5 software package,61 applying the velocity-Verlet algorithm with a time step of δ = 0.01, for a minimum of 106 time steps. Simulations contained 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DPD beads, at a density of 3 beads per unit volume (ρrC3 = 3), and were run from an initial configuration of random molecular positional coordinates. To accommodate small concentration changes, a relatively large system is necessary given molecules can only be added/removed in integer units. The simulations are performed in cubic domains with periodic boundary conditions and edge length L = 32.2. All simulations are performed at constant volume (NVT ensemble).
000 DPD beads, at a density of 3 beads per unit volume (ρrC3 = 3), and were run from an initial configuration of random molecular positional coordinates. To accommodate small concentration changes, a relatively large system is necessary given molecules can only be added/removed in integer units. The simulations are performed in cubic domains with periodic boundary conditions and edge length L = 32.2. All simulations are performed at constant volume (NVT ensemble).
2.5 Quantifying mesophases in simulation
Isosurfaces describe a surface where the density of a predetermined molecular moiety, or bead, is approximately constant. An example of an isosurface of head groups in a micellar phase is shown in Fig. 2. These isosurfaces can be helpful in visually identifying mesophases, but they can also be used to quantify the degree to which a mesophase has a certain symmetry.We calculated our isosurfaces using the utility built into the DL_MESO software,61,62 which we will briefly summarise. The simulation box is overlaid with a regular lattice with spacing 0.25rC, on which the isosurface density will be calculated. The bead volume is smeared according to a Gaussian smearing function
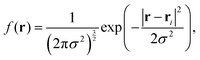 | (8) |
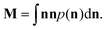 | (9) |
The three eigenvalues ε1, ε2 and ε3 of this symmetric tensor M are indicative of the mesophase present. Note that these eigenvectors are normalised such that their sum is one.
We find that the mesophases can be categorised as follows:
• if ε1 ≃ ε2 ≃ ε3 generates an isotropic phase, such as micellar or bicontinuous cubic;
• if 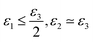 the phase has a hexagonal symmetry, i.e. hexagonal columnar (or inverse) phase;
the phase has a hexagonal symmetry, i.e. hexagonal columnar (or inverse) phase;
• if ε1 + ε2 ≤ ε3 we have a lamellar phase.
This measure, along with visual inspection, can aid the identification of the mesophases formed, which is a useful tool in iteratively improving a DPD model to reproduce experimental phase behaviour. Phase structures can additionally be characterised using pair distribution functions g(r), which describe density variation as a function of distance r, which are used in this work for calculating lamellar layer spacing. The g(r) function is computed by calculating the particle–particle distances between tail bead pairs, at every time step. For computational purposes, these distances are ‘binned’ to create a histogram of particle–particle separation distances. The g(r) function is calculated as
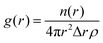 | (10) |
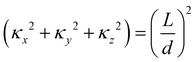 | (11) |
The layer spacing which is calculated from the distribution function g(r), can be confirmed by calculating d via another method. Suppose angle θ is the polar angle to the director of the surfactant molecules (where the director is easily calculated as the average direction vector of the molecules). Due to the periodic boundary conditions, the layers must satisfy L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = κd, where κ is the number of layers in the simulation box.49 The combination of two approaches to calculating d allows us to be confident in our calculation of the lamellar spacing.
θ = κd, where κ is the number of layers in the simulation box.49 The combination of two approaches to calculating d allows us to be confident in our calculation of the lamellar spacing.
3 Results and discussion
3.1 Initial parametrisation
The interaction parameters aij for SDS were calculated via a comprehensive sweep of the parameter space, fitting our model to the experimental phase diagram at a temperature T = 80 °C (T* = 1), where the systems of interest show multiple lyotropic phases. At lower temperatures the phase structures can be more complex, often consisting of two phase regions with hydrated crystals present (more information can be found in the ESI†). We vary aHT in the range 25 < aHT < 50 (i.e. aHT > aii = 25) in order to reproduce the hydrophobically driven head–tail separation and vary aHW in the range 12.5 < aHW < 25 for hydrophilic behaviour. aTW is varied in the range 30 < aTW < 50 to take into account enthalpic and entropic contributions to the unfavourable water-tail bead mixing free energy.Initial test simulations were performed in the high concentration regime (20% water and 80 wt% surfactant), where SDS exhibits a lamellar phase.63 In this regime, we expect better transferability of DPD parameters across the phase diagram in comparison to low concentrations. The sweep of parameter space was performed in two stages. We began by varying individual cross-interaction parameters aij, while maintaining all other cross interactions at aij = 25.
• Increasingly repulsive values of aTW were found to favour the aggregation of surfactant molecules.
• Increasingly repulsive values of aHT also favoured aggregation but to a lesser extent than aTW, noting the greater configurational freedom of water molecules in comparison to the bonded head beads.
• On its own, aHW has only a small effect on surfactant–water demixing in the higher concentration regime.
Next, we looked at the effect of varying two aij interaction parameters simultaneously to build up a picture of how synergetic effects influence aggregate formation. A sweep through aHT and aTW parameter space (Fig. 3(a)) indicated that aggregation was favoured by simultaneously high values of aHT (>35) and aTW (>40). A visual illustration of the change in aggregation behaviour is shown in Fig. 4. Here, the unusual ‘pseudo-micellar’ behaviour seen for aTW = 45 and aHT = 45 describes a fluid with a self-assembled nanostructure. This corresponds to the formation of very small aggregate nanostructures, as might be seen in a structured tertiary fluid,64 and cannot be classified as true micellar behaviour. In contrast, a sweep through parameter space for aHW and aTW (Fig. 3(b)), favour values of aHW < 20 for phase formation.
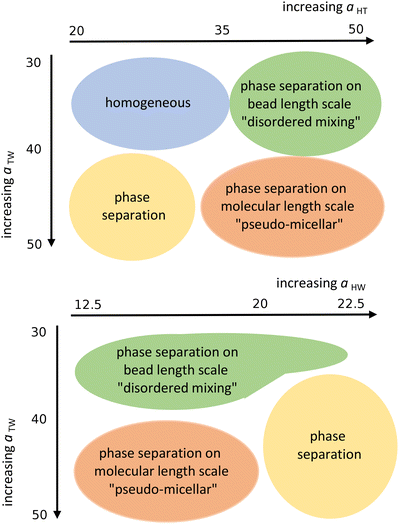 | ||
| Fig. 3 Schematic representation of the qualitative phase behaviour of our surfactant model. (Simulations conducted using 80 wt% surfactant beads and 20 wt% water). | ||
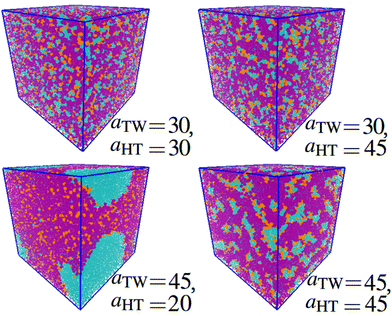 | ||
| Fig. 4 Impact of varying parameters aTW and aHT on the self-assembly behaviour. Beads are coloured according to their type: water (cyan), alkyl tail groups (purple), and head groups (orange). Cases are categorised to correspond with Fig. 3 as follows: homogeneous (aTW = 30, aHT = 30), phase separation on the bead length scale (aTW = 30, aHT = 45), phase separation (aTW = 45, aHT = 20), pseudo-micellar (aTW = 45, aHT = 45). (Simulations conducted using 80 wt% surfactant beads and 20 wt% water.) | ||
Having narrowed down the range of phase stability through Fig. 3, the final choice of parameters was made based on a successful prediction of approximate experimental phase boundaries for the hexagonal and lamellar phases. The final set of parameters chosen is shown in Table 2. The lamellar phase that results from a simulation of 80 wt% surfactant is shown in Fig. 5.
| a ij | Sulfonate (H) | Alkyl (T) | Water (W) |
|---|---|---|---|
| Sulfonate (H) | 25 | 50 | 15 |
| Alkyl (T) | — | 25 | 45 |
| Water (W) | — | — | 25 |
3.2 SDS phase diagram
At a temperature of 80 °C, SDS in water has a typical anionic surfactant experimental phase diagram, with a transition from micellar solution, L1, to a hexagonal phase, H1, at approximately 36–39 wt% surfactant, followed by a transition to the lamellar phase at roughly 60–70 wt% surfactant (with some complex, undetermined phases in between).63,65,66 The parameters presented in Table 2 are tested across a broad concentration range to investigate the phase behaviour, where we perform simulations in the range 5–95 wt% in 5 wt% intervals. The phase diagram produced for SDS is presented in Fig. 6, showing that our model gives excellent results compared to experimental data. Also shown are example eigenvalues ε1,ε2 and ε3, which are used to aid the characterisation of mesophases. Our model exhibits the L1–H1 transition at roughly 30–35 wt%, and the H1 region ends at 55–60 wt%. In the model, there is a direct transition from the H1 phase to Lα without evidence for a large two-phase region. Instead, we observe a phase region where the lamellar phase has perforations, such that the surfactant layers are not perfect (i.e. contain ‘holes’). In these cases, the water layers are able to form bridges between other periodic water layers. The structure of the micellar and hexagonal phases are shown in Fig. 7. At higher concentrations, we do not see crystalline structures. Because of the soft interaction potential (which does not readily crystallize), we expect to see liquid crystal phases forming in preference to the hydrated crystals that occur experimentally at very high-weight fractions of surfactant.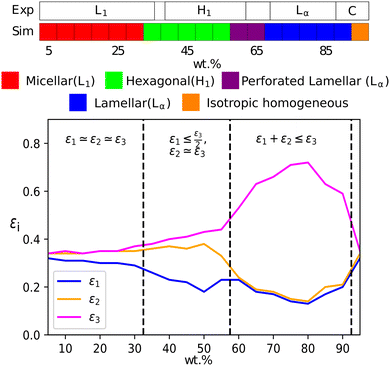 | ||
| Fig. 6 (a) A comparison of experimental phase boundaries (from Huddson et al.65 and Kékicheff et al.66) and those assigned via simulation for sodium dodecyl sulfate. Experimentally phases are identified as micellar (L1), hexagonal (H1), a region of mixed phases (62–69%), lamellar (Lα) and crystalline phases (88%+). There is also a narrow two-phase (L1 + H1) region (36–39%). (b) Also plotted is the variation of eigenvalues εi, which can be used to identify the mesophase present. | ||
The hexagonal phase is found to be more challenging to form than either the micellar or lamellar phases. This is attributed to the fact that the system needs to form large columnar aggregates, and then align these aggregates throughout the entire domain. As these columns can connect across periodic boundary conditions, most often not aligning with perfect hexagonal symmetry, large amounts of energy are required in order to break and reform the columns in the most favourable geometry. As such, a hexagonal columnar phase, that forms spontaneously, requires a larger system and longer simulation time. Therefore, in order to speed up the equilibration process, we chose to apply a gentle shear to the simulation box, which encourages hexagonal phase formation. Shear is then removed and the system is allowed to re-equilibrate in order to produce the equilibrium structure. In addition to the hexagonal phases, we occasionally require the application of shear in order to encourage the formation of lamellar bilayers. For lamellar phases which lie close to the hexagonal-lamellar phase boundary, we sometimes fail to see the formation of periodic layers under equilibrium conditions. In these cases, no clear phase structures appear, even after considerable running time. Following the application of shear, lamellar structures are able to form with layers which are parallel to the sides of the simulation box.
Fig. 8 shows typical g(r) plots for the lamellar phase of SDS, from which the layer spacing can be extracted. Layer spacings are presented in Table 3 as a function of concentration, calculated using g(r). We estimate our simulation length scale based on matching the water density simulated, to an experimentally known water density at 80 °C.48 This produces a length scale of rC ≈ 6.52 Å. This provides a mechanism for converting layer spacings in DPD units into real units. Experimentally SDS solutions at 75 wt% (T = 65 °C) have a reported layer spacing of 3.4 nm.67 This compares excellently with the value at 75 wt% calculated in this work of 3.3 nm. The lamellar phase shows a decrease in spacing as the surfactant concentration increases, which is also in agreement with experiment.67
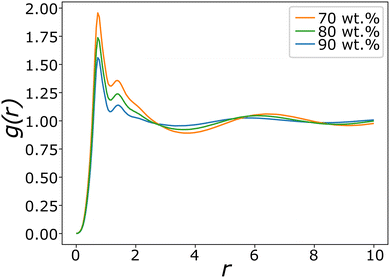 | ||
| Fig. 8 Pair distribution functions g(r) for lamellar phases of SDS with varying concentration. The difference in peak maxima measures the changing average layer separation as concentration is varied. | ||
| wt% | Layer spacing/rcut | wt% | Layer spacing/rcut |
|---|---|---|---|
| 60 | 5.37* | 80 | 5.03 |
| 65 | 5.44 | 85 | 5.03 |
| 70 | 5.29 | 90 | 4.80 |
| 75 | 5.03 |
In summary, we find that the parameters presented in Table 2 reproduce the SDS phase diagram extremely well. This result alone is not surprising, as the parameters of our model were optimised to reproduce SDS in particular. The success of this model lies in its transferability, not just across a full range of surfactant concentrations but also to different molecules.
3.3 Extension to phase diagrams of LAS
We extend our model of SDS to LAS by the introduction of an additional bead to represent the benzene ring. Bond and angle potentials take the same form as in our SDS model, with no additional angle constraints directly imposed in branched models. The nonbonded interactions between the head, tail and water beads are the same as those previously used for SDS. For interactions involving the benzene bead, interactions were selected based on the values of aij used for other beads, and their respective Hansen solubility parameters as described in Section 2.3 (i.e. no fitting was performed in extending our model to this new species).The phase behaviour of LAS is much more complex than that of SDS, as LAS refers to a whole family of molecules of different chain lengths, degrees of functionalisation, and positional isomers. In order to make a comparison to experimental data, we simulated three specific isomers of LAS, as detailed phase diagrams were unavailable for characterised isomeric mixtures. We simulated an entirely linear isomer, sodium dodecylbenzene-1-sulfonate (DBS1), and two branched isomers, sodium dodecylbenzene-4-sulfonate (DBS4) and sodium dodecylbenzene-6-sulfonate (DBS6). We chose these particular isomers as they cover the broadest range of phase behaviours exhibited by LAS.68
Flory–Huggins parameters χij for all bead pairs are calculated from Hansen solubility parameters60 using eqn (7) and are presented in Table 4. A comparison of the Flory–Huggins parameters for the existing interactions (χHW, χTW and χHT) with the Flory–Huggins for the benzene interactions (χBH, χBT, and χBW) allows us to determine the values of aij for the benzene interactions as aBH = 45, aBT = 25 and aBW = 40. Further information on how additional bead interactions are calculated can be found within the ESI,† including the Hansen solubility parameters used to obtain Table 4.
| Sulfonate (H) | Alkyl (T) | Benzene (B) | |
|---|---|---|---|
| Water (W) | 4.98 | 9.49 | 8.80 |
| Sulfonate (H) | — | 3.48 | 2.67 |
| Alkyl (T) | — | — | 0.792 |
The DPD phase diagrams of these three molecules are presented (alongside their respective experimental phase information) in Fig. 9. The linear isomer DBS1 shows a similar phase progression (micellar → hexagonal phase → lamellar phase) to that of SDS, while the branched isomers show markedly different behaviour, including the absence of a hexagonal phase. We also note here that all of our micellar solutions (for every isomer simulated) consist of elongated, worm-like micelles as opposed to spherical micelles. This is in agreement with experimental observations of LAS solutions with concentrations 5 + wt%.69
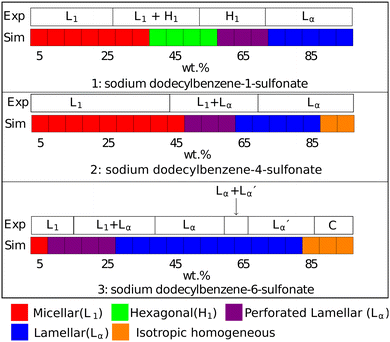 | ||
Fig. 9 Phases assigned to simulations of positional isomers of sodium para-dodecylbenzene sulfonate. Experimental phase boundaries are taken from Ma et al.68 at T = 80 °C. Note that experimental phase region denoted ‘C’ consists of a mixture of liquid crystalline phases, and that 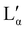 is a lamellar phase which differs from Lα. is a lamellar phase which differs from Lα. | ||
The final difference we find between model and experiment is the formation of non-crystalline structure at higher experimental concentrations (90+%). However, this behaviour only occurs in a very small region of the phase diagram at a very high concentration, which is less significant in applications of these models as these conditions are rarely encountered.
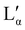 ), which are distinguished from each other by a difference in their lamellar layer spacing. We will show in the following sections that we also observe a variation in the lamellar layer spacing, for solutions at higher concentrations.
), which are distinguished from each other by a difference in their lamellar layer spacing. We will show in the following sections that we also observe a variation in the lamellar layer spacing, for solutions at higher concentrations.
At high concentrations 85 + wt%, the experimental phase diagram is complex with many phases present (including lamellar, inverse cubic and inverse hexagonal structures). Here, we do not expect an exact match between experiment and simulation. Primarily, as discussed previously, mesophase behaviour is not on the same length scale as our simulations, and our simulations would struggle to produce coexisting phase structures. Also, as previously discussed, our DPD model is not expected to target phase behaviour in the very high concentration regime.
3.4 Phase characterisation
Lamellar layer spacings are once again calculated using radial distribution function g(r), and the values found for LAS isomers are given in Table 5. It is important to note that some of the spacings (for lamellar phases which are near phase transition boundaries) are calculated from sheared simulation boxes, and the application of shear causes the lamellar phases to be orientated so that the layers are parallel to the shearing surfaces. Therefore the number of accessible spacings is reduced (when compared with those calculated from eqn (11)) and the box size L divided by the spacing must be an integer.| wt% | DBS1 | DBS4 | DBS6 |
|---|---|---|---|
| 30 | — | — | 13.1 |
| 35 | — | — | 10.7 |
| 40 | — | — | 8.93 |
| 45 | — | — | 7.03 |
| 50 | — | 6.44* | 7.80 |
| 55 | — | 6.31 | 6.31 |
| 60 | 6.44* | 5.98 | 5.69 |
| 65 | 6.31 | 5.52 | 5.37 |
| 70 | 6.31 | 5.29 | 5.09 |
| 75 | 5.98 | 5.37 | 4.85 |
| 80 | 5.88 | 5.09 | 4.75 |
| 85 | 5.69 | 4.80 | — |
| 90 | 5.61 | — | — |
| 95 | 5.37* | — | — |
We find that for the same concentration, branched molecules have a smaller layer spacing than the linear case, and the DBS6 case has a smaller spacing than DBS4. This is to be expected, given that the end-to-end distance is made smaller with the branching. For all molecules, we find that the lamellar phase exhibits a reduction in layer spacing as surfactant concentration increases. DBS6 solutions continue to form lamellar phases at relatively low concentrations and the spacing grows rapidly with decreasing concentrations. Therefore we only present lamellar spacing values at concentrations 30 + %, since at lower concentrations the spacing is so large that the layers struggle to fit inside the simulation box size. This leads to warping of the layers, which are not perfectly parallel or flat, and the spacing calculation becomes inaccurate. There are also fewer ‘available’ spacing options provided by eqn (11), as the spacing grows. For accurate spacing calculations at lower concentrations, a much larger box size would be required. A visual representation of the results in Table 5 and the available spacings can be found in the ESI.† When the concentration is higher (and the lamellar layer spacing is smaller), there are a significant number of spacings ‘available’, and therefore box size is not a significant issue for this calculation.
It is of interest that the change in lamellar layer spacing for DBS6 is discontinuous, with an anomalous increase at 50% concentration. In the experimental phase diagram, this roughly corresponds to a region in which there are two co-existing lamellar phases (Lα and 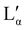 ). In our simulation, co-existing phases are unable to form (on account of the relatively small simulation length scale). However, it is possible that this is the cause of our anomalous lamellar layer spacing at this concentration. It is worth noting that this discontinuous behaviour is not a result of constraints due to the finite box size (see ESI†).
). In our simulation, co-existing phases are unable to form (on account of the relatively small simulation length scale). However, it is possible that this is the cause of our anomalous lamellar layer spacing at this concentration. It is worth noting that this discontinuous behaviour is not a result of constraints due to the finite box size (see ESI†).
Existing experimental literature values for lamellar layer spacing of LAS are from isomeric mixtures in water. At a temperature of T = 80° and concentrations 55 + wt%, the lamellar layer spacings are reported as between 3.1 and 3.6 nm.71 By comparison, our data in Table 5 measures layer spacing as between 3.1 and 4.2 nm, in reasonably good agreement with the available experimental data.
3.5 Transferability of parameters to alkyl ether sulfates (AES)
We extend our testing of the parametrisation to isomeric mixtures of alkyl ether sulfates (AES), another industrially important surfactant. AES molecules have the general chemical structure CH3 (CH2)x (OCH2CH2)nOSO3 Na, where the length of the alkyl chain typically varies between 12 and 16 carbon atoms and n varies between 0 to 6. However, shorter molecules make up the bulk of the distribution. The coarse-grained representation of the molecules is presented in Fig. 10, and the parametrisation is extended with the addition of ethylene oxide (E) beads in between the sulfate head group and the alkyl chain. Knowing polyethylene oxide displays hydrophilic behaviour, we represent ‘E’ beads as equivalent to our ‘W’ bead type, taking the same interaction aij values as water beads. In our simulations, we simplify the distribution in x and n by removing some of the longest molecules. Therefore simulations are based on an isomeric mixture, consisting of isomers with alkyl chain lengths of between 12 and 14 carbon atoms, with a degree of ethoxylation between 0 and 2. The distribution simulated is given in Table 6. | ||
| Fig. 10 Coarse-grained representation of alkyl ether sulfates (AES). The number of ethylene oxide (E) beads and alkyl beads (T) are varied in the simulation. | ||
| No. carbon atoms in alkyl tail | No. ethoxy groups | % wt |
|---|---|---|
| 12 | 0 | 29 |
| 12 | 1 | 14 |
| 12 | 2 | 7 |
| 14 | 0 | 29 |
| 14 | 1 | 14 |
| 14 | 2 | 7 |
Experimentally, AES exhibits simple phase behaviour, moving from a micellar solution at low concentrations to a hexagonal mesophase at a concentration c ≃ 25%. At higher concentrations, a transition is seen to a lamellar phase at c ≃ 60%.49 The phase progression of AES, as determined using DPD, is described in Fig. 11, and is found to be in quite good agreement with experimental data, with simulations showing the expected L1–H1–Lα phase sequence.
 | ||
| Fig. 11 Phases assigned to simulations of AES. Experimental phase boundaries are taken from Hendrikse et al.49 at 25 °C (data unavailable at higher temperatures). | ||
4 Summary and concluding thoughts
In this paper, we have detailed the phase behaviour of a DPD model parameterised to describe common sulfate- and sulfonate-based surfactants. Our results showed good agreement with experimental phase diagrams, and the model shows excellent transferability across concentrations and to different molecules. It additionally captures some rather subtle effects in phase behaviour, spontaneously forming complex architectures and being sensitive to structural changes in the molecule. Unlike DPD surfactant models elsewhere in the literature, we parametrised our initial base model to phase behaviour information, rather than more specific data such as surface tension, CMC, or partitioning behaviour. We believe this parametrisation technique is the key to our model's success, as it is transferable to different molecules and reproduces their phase behaviour, something we have not seen in many previous DPD studies.An interesting point raised in this study is that while our models were parameterised via their interaction parameters, the connectivity and shape of the molecule also influence the phase diagram. With no further parametrisation, simply describing the structural differences in two LAS isomers is sufficient for our model to reproduce two distinct sets of phase behaviour. While a simple understanding of the chemical interactions that drive surfactant mesophase formation is important, an equally important role is played by the shape of the molecule.
By simulating mesophases on these length scales, we can gain a further understanding of these complex phases that can be difficult to ascertain experimentally. For instance, the difference in stability of the hexagonal columnar phase between our SDS and our linear LAS models reflects the influence of the surface area to volume ratio in mesophase formation. One obvious limitation of this work is that we do not account for electrostatic interactions; therefore, we are unable to investigate the direct influence of salt concentration on the phase diagram by the simple addition of ions. In our model, the effects of ions are accounted for entirely via the aij parameters. The addition of salt would have an effect on water activity and thus influence the relative aij parameters between solvent and surfactants (and also to some extent the head group self-interactions). Therefore, within our model, for simulations with additional salt, the interaction parameters would need to be recalculated for a new system. Noting, for example, that a reduction in the water–water self-interaction leads to a movement of the L1 – lamellar phase boundary of LAS to lower concentrations, as seen experimentally for LAS on the addition of salt.72
For the consideration of future work, is interesting to note that it may be possible to extend the phase diagrams presented in Fig. 9 with the use of regression algorithms.73 While in this work we have performed individual simulations for each of the LAS monomers at different concentrations, one may be able to infer the phase behaviour of other LAS monomers not studied, without the need to perform additional simulations, through the use of a machine learning technique, such as the quadratic discriminant analysis algorithm (QDA).
Author contributions
SJG: data curation, formal analysis, investigation, methodology, software, visualization, writing – original draft. MW: formal analysis, methodology, software, supervision, visualization, writing – review and editing. RH: data curation, formal analysis, investigation, validation, software, visualization, writing – review and editing. MRW: conceptualization, funding acquisition, methodology, project administration, resources, software, supervision, validation, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the support of Durham University for the use of its HPC facility, Hamilton. SJG would like to thank Procter & Gamble and EPSRC for the award of a CASE studentship (grant EP/M507386/1). RH would like to acknowledge support through an EPSRC/P&G-funded Prosperity Partnership grant EP/V056891/1.Notes and references
- C. E. Fairhurst, S. Fuller, J. Gray, M. C. Holmes and G. J. T. Tiddy, Handbook of Liquid Crystals, Wiley-VCH, 1998, ch. 7, vol. 3, pp. 341–392 Search PubMed.
- B. J. Chun, J. I. Choi and S. S. Jang, Colloids Surf., A, 2015, 474, 36–43 CrossRef CAS.
- N. Yoshii and S. Okazaki, Condens. Matter Phys., 2007, 10, 573 CrossRef.
- S. Jalili and M. Akhavan, Colloids Surf., A, 2009, 352, 99–102 CrossRef CAS.
- X. Tang, P. H. Koenig and R. G. Larson, J. Phys. Chem. B, 2014, 118, 3864–3880 CrossRef CAS PubMed.
- E. Ritter, D. Yordanova, T. Gerlach, I. Smirnova and S. Jakobtorweihen, Fluid Phase Equilib., 2016, 422, 43–55 CrossRef CAS.
- F. Palazzesi, M. Calvaresi and F. Zerbetto, Soft Matter, 2011, 7, 9148–9156 RSC.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- J. M. V. A. Koelman and P. J. Hoogerbrugge, Europhys. Lett., 1993, 21, 363–368 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- R. D. Groot, T. J. Madden and D. J. Tildesley, J. Chem. Phys., 1999, 110, 9739–9749 CrossRef CAS.
- J. C. Shillcock and R. Lipowsky, J. Chem. Phys., 2002, 117, 5048–5061 CrossRef CAS.
- A. AlSunaidi, W. K. d Otter and J. H. R. Clarke, J. Chem. Phys., 2013, 138, 154904 CrossRef CAS PubMed.
- E. S. Boek, P. V. Coveney, H. N. W. Lekkerkerker and P. van der Schoot, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 3124–3133 CrossRef CAS.
- R. D. Groot and K. L. Rabone, Biophys. J., 2001, 81, 725–736 CrossRef CAS PubMed.
- M. Walker, A. J. Masters and M. R. Wilson, Phys. Chem. Chem. Phys., 2014, 16, 23074–23081 RSC.
- M. Walker and M. R. Wilson, Soft Matter, 2016, 12, 8588–8594 RSC.
- M. Walker and M. R. Wilson, Soft Matter, 2016, 12, 8876–8883 RSC.
- S. Jury, P. Bladon, M. Cates, S. Krishna, M. Hagen, N. Ruddock and P. Warren, Phys. Chem. Chem. Phys., 1999, 1, 2051–2056 RSC.
- H. Nakamura and Y. Tamura, Comput. Phys. Commun., 2005, 169, 139–143 CrossRef CAS.
- L. Rekvig, B. Hafskjold and B. Smit, J. Chem. Phys., 2004, 120, 4897–4905 CrossRef CAS PubMed.
- Z. Chen, X. Cheng, H. Cui, P. Cheng and H. Wang, Colloids Surf., A, 2007, 301, 437–443 CrossRef CAS.
- A. Vishnyakov, M.-T. Lee and A. V. Neimark, J. Phys. Chem. Lett., 2013, 4, 797–802 CrossRef CAS PubMed.
- G. Kacar, E. A. J. F. Peters and G. D. With, Europhys. Lett., 2013, 102, 40009 CrossRef.
- T. P. Liyana-Arachchi, S. N. Jamadagni, D. Eike, P. H. Koenig and J. I. Siepmann, J. Chem. Phys., 2015, 142, 044902 CrossRef PubMed.
- E. Lavagnini, J. L. Cook, P. B. Warren, M. J. Williamson and C. A. Hunter, J. Phys. Chem. B, 2020, 124, 5047–5055 CrossRef CAS PubMed.
- E. Lavagnini, J. L. Cook, P. B. Warren and C. A. Hunter, J. Phys. Chem. B, 2021, 125, 3942–3952 CrossRef CAS PubMed.
- T. Lafitte, A. Apostolakou, C. Avendaño, A. Galindo, C. S. Adjiman, E. A. Müller and G. Jackson, J. Chem. Phys., 2013, 139, 154504 CrossRef PubMed.
- C. Avendaño, T. Lafitte, C. S. Adjiman, A. Galindo, E. A. Müller and G. Jackson, J. Phys. Chem. B, 2013, 117, 2717–2733 CrossRef PubMed.
- M. Fayaz-Torshizi and E. A. Müller, Macromol. Theory Simul., 2021, 31, 2100031 CrossRef.
- J. Tasche, E. F. D. Sabattié, R. L. Thompson, M. Campana and M. R. Wilson, Macromolecules, 2020, 53, 2299–2309 CrossRef CAS PubMed.
- P. C. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. Bruininks and T. A. Wassenaar, et al. , Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed.
- T. D. Potter, M. Walker and M. R. Wilson, Soft Matter, 2020, 16, 9488–9498 RSC.
- G. Yu and M. R. Wilson, J. Mol. Liq., 2022, 345, 118210 CrossRef CAS.
- T. D. Potter, J. Tasche and M. R. Wilson, Phys. Chem. Chem. Phys., 2019, 21, 1912–1927 RSC.
- J. Shelley, K. Watanabe and M. L. Klein, Int. J. Quantum Chem., 1990, 38, 103–117 CrossRef.
- A. D. MacKerell, J. Phys. Chem., 1995, 99, 1846–1855 CrossRef CAS.
- C. D. Bruce, M. L. Berkowitz, L. Perera and M. D. E. Forbes, J. Phys. Chem. B, 2002, 106, 3788–3793 CrossRef CAS.
- M. Sammalkorpi, M. Karttunen and M. Haataja, J. Phys. Chem. B, 2007, 111, 11722–11733 CrossRef CAS PubMed.
- K. J. Schweighofer, U. Essmann and M. Berkowitz, J. Phys. Chem. B, 1997, 101, 3793–3799 CrossRef CAS.
- X. He, O. Guvench, A. D. MacKerell and M. L. Klein, J. Phys. Chem. B, 2010, 114, 9787–9794 CrossRef CAS PubMed.
- S. Jalili and M. Akhavan, Colloids Surf., A, 2009, 352, 99–102 CrossRef CAS.
- X. He, W. Shinoda, R. DeVane, K. L. Anderson and M. L. Klein, Chem. Phys. Lett., 2010, 487, 71–76 CrossRef CAS.
- W. Shinoda, R. DeVane and M. L. Klein, Mol. Simul., 2007, 33, 27–36 CrossRef CAS.
- Z. Mai, E. Couallier, M. Rakib and B. Rousseau, J. Chem. Phys., 2014, 140, 204902 CrossRef PubMed.
- M. Choudhary and S. M. Kamil, ACS Omega, 2020, 5, 22891–22900 CrossRef CAS PubMed.
- K. Y. Kim, K. Y. Kim, K.-T. Byun and H.-Y. Kwak, Korean J. Chem. Eng., 2009, 26, 1717–1722 CrossRef CAS.
- R. L. Anderson, D. J. Bray, A. Del Regno, M. A. Seaton, A. S. Ferrante and P. B. Warren, J. Chem. Theory Comput., 2018, 14, 2633–2643 CrossRef CAS PubMed.
- R. L. Hendrikse, A. E. Bayly and P. K. Jimack, J. Phys. Chem. B, 2022, 126, 8058–8071 CrossRef CAS PubMed.
- F. Lahmar, C. Tzoumanekas, D. N. Theodorou and B. Rousseau, Macromolecules, 2009, 42, 7485–7494 CrossRef CAS.
- F. Goujon, A. Ghoufi, P. Malfreyt and D. J. Tildesley, Soft Matter, 2012, 8, 4635–4644 RSC.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191 CrossRef.
- R. D. Groot and T. J. Madden, J. Chem. Phys., 1998, 108, 8713–8724 CrossRef CAS.
- L. Rekvig, M. Kranenburg, J. Vreede, B. Hafskjold and B. Smit, Langmuir, 2003, 19, 8195–8205 CrossRef CAS.
- B. Duan, X. Zhang, B. Qiao, B. Kong and X. Yang, J. Phys. Chem. B, 2009, 113, 8854–8859 CrossRef CAS PubMed.
- A. G. Goicochea, M. Romero-Bastida and R. López-Rendón, Mol. Phys., 2007, 105, 2375–2381 CrossRef CAS.
- S. Javan Nikkhah and M. Sammalkorpi, J. Colloid Interface Sci., 2023, 635, 231–241 CrossRef CAS PubMed.
- T. L. Rodgers, O. Mihailova and F. R. Siperstein, J. Phys. Chem. B, 2011, 115, 10218–10227 CrossRef CAS PubMed.
- A. Maiti and S. McGrother, J. Chem. Phys., 2004, 120, 1594–1601 CrossRef CAS PubMed.
- C. M. Hansen, Hansen solubility parameters: A user's handbook, CRC Press, 6000 Broken Sound Parkway NW, Suite 300, Boca Raton, FL, 2007, pp. 33487–2742 Search PubMed.
- M. A. Seaton, The DL_MESO Mesoscale Simulation Package, STFC Computational Science and Engineering Department, 2012, http://www.ccp5.ac.uk/DL_MESO Search PubMed.
- P. Prinsen, P. B. Warren and M. A. J. Michels, Phys. Rev. Lett., 2002, 89, 148302 CrossRef CAS PubMed.
- C. O. Rossi, M. Macchione and L. Filippelli, Mol. Cryst. Liq. Cryst., 2011, 549, 160–165 CrossRef CAS.
- T. N. Zemb, M. Klossek, T. Lopian, J. Marcus, S. Schöettl, D. Horinek, S. F. Prevost, D. Touraud, O. Diat and S. Marčelja, et al. , Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4260–4265 CrossRef CAS PubMed.
- F. Husson, H. Mustacchi and V. Luzzati, Acta Crystallogr., 1960, 13, 668–677 CrossRef CAS.
- P. Kékicheff, C. Grabielle-Madelmont and M. Ollivon, J. Colloid Interface Sci., 1989, 131, 112–132 CrossRef.
- P. Kekicheff, B. Cabane and M. Rawiso, J. Colloid Interface Sci., 1984, 102, 51–70 CrossRef CAS.
- J.-G. Ma, B. J. Boyd and C. J. Drummond, Langmuir, 2006, 22, 8646–8654 CrossRef CAS PubMed.
- A. S. Rafique, S. Khodaparast, A. S. Poulos, W. N. Sharratt, E. S. J. Robles and J. T. Cabral, Soft Matter, 2020, 16, 7835–7844 RSC.
- A. S. Poulos, M. Nania, P. Lapham, R. M. Miller, A. J. Smith, H. Tantawy, J. Caragay, J. Gummel, O. Ces, E. S. J. Robles and J. T. Cabral, Langmuir, 2016, 32, 5852–5861 CrossRef CAS PubMed.
- C. Richards, G. J. T. Tiddy and S. Casey, Langmuir, 2006, 23, 467–474 CrossRef PubMed.
- A. Sein and J. B. F. N. Engberts, Langmuir, 1995, 11, 455–465 CrossRef CAS.
- M. Panoukidou, C. R. Wand, A. Del Regno, R. L. Anderson and P. Carbone, J. Colloid Interface Sci., 2019, 557, 34–44 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01641a |
| This journal is © The Royal Society of Chemistry 2023 |