Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of prolate spheroids in the vicinity of an air–water interface†
Stefano
Villa
 *a,
Domenico
Larobina
*a,
Domenico
Larobina
 b,
Antonio
Stocco
b,
Antonio
Stocco
 c,
Christophe
Blanc
c,
Christophe
Blanc
 d,
Massimiliano M.
Villone
d,
Massimiliano M.
Villone
 e,
Gaetano
D'Avino
e,
Gaetano
D'Avino
 e and
Maurizio
Nobili
e and
Maurizio
Nobili
 *d
*d
aMax Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany. E-mail: stefano.villa@ds.mpg.de
bInstitute of Polymers, Composites, and Biomaterials, National Research Council of Italy, Naples, 80055 Portici, Italy
cInstitut Charles Sadron, CNRS UPR22, University of Strasbourg, Strasbourg, France
dLaboratoire Charles Coulomb (L2C), UMR 5221 CNRS-Université de Montpellier, Montpellier, France. E-mail: maurizio.nobili@umontpellier.fr
eDepartment of Chemical, Materials and Production Engineering, University of Naples Federico II, P.le Tecchio 80, 80125 Naples, Italy
First published on 14th March 2023
Abstract
In this article, we present the mobilities of prolate ellipsoidal micrometric particles close to an air–water interface measured by dual wave reflection interference microscopy. Particle's position and orientation with respect to the interface are simultaneously measured as a function of time. From the measured mean square displacement, five particle mobilities (3 translational and 2 rotational) and two translational–rotational cross-correlations are extracted. The fluid dynamics governing equations are solved by the finite element method to numerically evaluate the same mobilities, imposing either slip and no-slip boundary conditions to the flow at the air–water interface. The comparison between experiments and simulations reveals an agreement with no-slip boundary conditions prediction for the translation normal to the interface and the out-of-plane rotation, and with slip ones for parallel translations and in-plane rotation. We rationalize these evidences in the framework of surface incompressibility at the interface.
1 Introduction
The dynamics of spherical particles dispersed in a Newtonian fluid near an interface has been widely studied in the past both experimentally and theoretically. Although for a fluid–fluid interface the particle dynamics is expected to be governed by slip flow boundary conditions (BC),1–3 experiments often deviate from expectations. Indeed, while all experimental results relative to the movement parallel to the interface approach predictions for full-slip BC,4–6 for dynamics normal to the interface the measured mobilities range from slip to no-slip BC.6–8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ‡ Deviation from slip boundary condition has been recently rationalized considering the presence of small concentrations of interfacial active agents determining surface incompressibility.8 In brief, particle motion induces an interfacial flow perturbing the otherwise homogeneous concentration of surface active agents, which in turn builds up a Marangoni stress opposing the flow. This results in the surface incompressibility condition, i.e. zero divergence of the interfacial flow.
‡ Deviation from slip boundary condition has been recently rationalized considering the presence of small concentrations of interfacial active agents determining surface incompressibility.8 In brief, particle motion induces an interfacial flow perturbing the otherwise homogeneous concentration of surface active agents, which in turn builds up a Marangoni stress opposing the flow. This results in the surface incompressibility condition, i.e. zero divergence of the interfacial flow.
In this perspective, our group has shown that surface incompressibility at air–water interface peculiarly affects the Brownian dynamics of spherical particles, with movement normal to the interface compatible with no-slip BC predictions, while the one parallel approaching full-slip BC ones.6 This can be understood considering that the movement of a sphere normal to the interface generates a purely radial interfacial flow. As a consequence, incompressibility condition at the interface prevents interfacial flow and the particle dynamics is indistinguishable from the one normal to a solid wall8 (no-slip BC). Conversely, for a movement parallel to the interface, for which the radial component of the flow at the interface is weak, the additional condition of zero flow divergence at the interface only weakly affects the full-slip BC.9 With high-speed camera measurements we have shown that even a small concentration of surface active agents (9 × 10−4 molecules per nm2) ensures a surface incompressibility BC at the air–water interface for the typical timescales probed during a Brownian dynamics experiment. Such small concentrations are below the detection precision of available surface tension measurements and are most likely due to molecular species resulting from the chemical equilibria with the atmosphere, i.e. hydroxide or bicarbonate ions. They are therefore impossible to avoid even if all precautions are taken to keep the interface clean.8
Differently from spherical particles, the dynamics of colloids with complex morphology is still almost unexplored.10–14 Earlier studies have mostly focused on spheroidal particles close to solid boundaries,15–17 as this morphology is the simplest after the spherical one. Because of anisotropy, particle hydrodynamic interactions with the confining interface result in a complex tensorial mobility, which demands the knowledge not only of the position but also of the orientation and the aspect ratio (i.e., the ratio between the axes lengths) of the spheroid. Studies of prolate spheroids in the presence of a fluid–fluid interface concerned mainly the absorption18,19 and the 2D confined dynamics at the interface.20 Very little is known on the dynamics of an ellipsoidal particle near an air–liquid interface. This lack of knowledge contrasts with the essential role played by the mobility of micrometric non-spherical entities close to fluid interfaces. Many systems of practical interest, like the motion of bacteria in biofilm formation,21,22 the draining dynamics in flotation processes,23 and the fabrication of Pickering emulsions,24 demand indeed the knowledge of the near interface particle mobilities.
In this paper, we study the dynamic behavior of micrometric prolate ellipsoids near an air–water interface. Using Dual Wave Reflection Interference Microscopy (DW-RIM),25 we are able to measure the dynamics of five (3 translational and 2 rotational) degrees of freedom of a particle, along with its aspect ratio and its distance from the interface. In particular, we here address how the surface incompressibility affects the ellipsoid rotational degrees of freedom and the translational–rotational cross-correlations. The latter result from the presence of the interface, which breaks the homogeneity of space.26 The experimental results are compared with the outcomes of direct numerical simulations.
2 Materials and methods
2.1 Sample preparation and experimental set-up
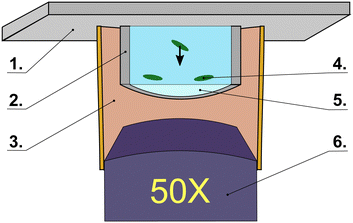
Prolate ellipsoids are produced at the desired aspect ratio A, i.e. the ratio between the major (a) and the minor (b) semi-axes, in the range 6 to 12 by stretching with a custom developed stretching device sulfate latex beads of diameter 8.7 ± 0.9 μm (MolecularProbes™) embedded in a poly(vinyl alcohol) matrix and heated at 100 °C.20 Such a large size has been chosen to reduce particles surface curvature. A low curvature for a sufficiently large surface area is indeed required to reduce the distortion of the interference fringes due to the finite numerical aperture of the microscope objective (see ESI†).Samples are prepared dispersing ellipsoids in a cell made of a hollow glass cylinder enclosed on the top by a microscope slide and exposed to air on the bottom (Fig. 1). Pinning of the three phase (air–water–glass) contact line at the lower cylinder edges prevents water falling due to gravity. This experimental geometry introduces a finite curvature of the air–water interface which nonetheless has been evaluated to negligibly affect the experimental results (see ESI†).
Because of gravity, ellipsoids sediment towards the air–water interface until they reach an equilibrium gap distance at few hundreds nanometers where gravity and DLVO interactions balance.25 If a large fluctuation normal to the interface occurs overcoming the gap distance, ellipsoids occasionally breach the interface and start the dewetting process.25,27 Due to the DLVO repulsion, however, in most cases the particle remains at the equilibrium gap distance for the entire duration of the experiment.§ In the present work we only consider the subset of ellipsoids that are not adsorbed at the interface throughout the duration of the experiment.
Ellipsoids number concentration is chosen low enough to allow neglecting inter-particles hydrodynamic couplings (mutual distance at the interface vicinity larger than 100 μm). Sample cell is located on the sample stage of the DW-RIM set-up which, in brief, consists of a custom inverted microscope working in reflection with a 50× long working distance objective.¶ The sample cell and the objectives are enclosed in a flexible chamber in order to reduce sample evaporation and to protect the air–water interface from air displacements that would introduce additional particle drifts. The set-up is designed to simultaneously illuminate with a red (wavelength λr = 625 nm) and a blue (wavelength λb = 505 nm) low coherence monochromatic light sources|| and collect the interference signal from the reflections at the particle–water and at the air–water interfaces with an RGB camera.** The choice of an RGB camera is motivated by the requirement of simultaneously recording in different channels the light incoming from the two light sources.
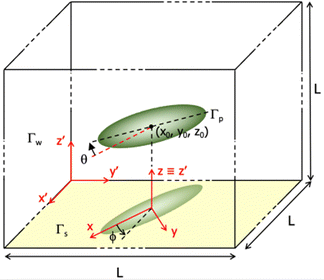
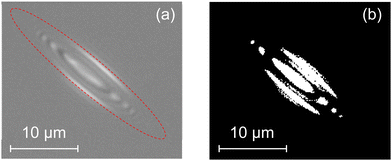
For each particle, we measure the time evolution of the particle center of mass together with the zenithal and azimuthal angles (see Fig. 2). An example of recorded interference pattern can be seen in Fig. 3a. Information on the particle movement parallel to the interface is obtained by tracking the position and the orientation on the image plane of the interference pattern, while information on the movement orthogonal to the interface is accessed from the interference pattern analysis. The superposition of the two wavelengths allows to unequivocally determine the particle-interface distance.6,25 As a matter of fact, a single channel interference pattern contains a phase ambiguity by an additive integer multiple of 2π. Consequently, from the analysis of each monochromatic interference pattern the distance z between a point of the ellipsoid surface and the air–water interface is given by the expression
zl = zl,0 + ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) lλl/(2n) lλl/(2n) | (1) |
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) l being an integer number, l = r, b for wavelengths λr and λb respectively, and zl,0 being the minimum possible value of zl obtained from the relative phase ∈ [0,2π) measured from the interference pattern. Among all possible values given by eqn (1), the real distance is found by imposing zr = zb = z. Light sources of low coherence length (in water equal to 13 μm and 5 μm for red and blue LEDs respectively) have been chosen in order to prevent residual ambiguity on the distance due to matching periodicity of zr and zb (within the experimental incertitude) for increasing values of
l being an integer number, l = r, b for wavelengths λr and λb respectively, and zl,0 being the minimum possible value of zl obtained from the relative phase ∈ [0,2π) measured from the interference pattern. Among all possible values given by eqn (1), the real distance is found by imposing zr = zb = z. Light sources of low coherence length (in water equal to 13 μm and 5 μm for red and blue LEDs respectively) have been chosen in order to prevent residual ambiguity on the distance due to matching periodicity of zr and zb (within the experimental incertitude) for increasing values of ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) r and
r and ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) b. The interference pattern for particles at distances larger than 1 μm is therefore sensibly less contrasted than the one reported in Fig. 3a, as it has been verified by following colloids from the bulk to the air–water interface during sedimentation.
b. The interference pattern for particles at distances larger than 1 μm is therefore sensibly less contrasted than the one reported in Fig. 3a, as it has been verified by following colloids from the bulk to the air–water interface during sedimentation.
Once sedimented, at equilibrium an ellipsoid lies with its major axis on average parallel to the interface, but because of thermal agitation θ fluctuates in a range of a few degrees (less than 5°) around zero. Once the fluctuating equilibrium position is reached, data are acquired for a few minutes at 30 fps in order to recover trajectories of 5000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames length.
000 frames length.
A more detailed description of the optical system and of experimental technique can be found in ref. 25.
2.2 Data analysis
Dedicated algorithms have been designed specifically for the tracking of the DW-RIM interference pattern of ellipsoidal particles. With reference to Fig. 2, we denote with (x′, y′, z′) a fixed reference frame, with x′y′ the air–water interface plane and z′ the axis normal to the interface. Hence, θ is the angle between the ellipsoid major axis and the interface plane, and ϕ is the angle formed by the projected major axis on the interface plane. The distance z′ from the interface and the zenithal angle θ are collected analyzing, for each frame, the interference pattern. A threshold is first imposed to the acquired image in order to locate the interference maxima on the binarized image (Fig. 3b). The symmetry axis of the interference pattern, corresponding to the projection of the ellipsoid major axis on the interface plane, is then identified. The movement in the plane x′y′ and the azimuthal angle ϕ are accessed by tracking the interference pattern center of mass and its orientation. A local Cartesian coordinates system xyz is also defined, where x is the direction parallel to the ellipsoids major axis projection on the interface plane, y is the orthogonal direction in the interface plane and z ≡ z′ is the direction orthogonal to the interface. From the in-plane coordinates, the displacements along the major axis projection (x) and the ones in the in-plane orthogonal direction (y) are obtained. A detailed description of the image analysis pipeline is reported in the ESI.†With this procedure the obtained resolutions are 100 nm for the ellipsoid x and y positions, a few nanometers for z and 0.3° for ϕ. Zenithal angle θ, finally, is measured with a relative error of about 10%.
The data reported in the present work refer to 18 different ellipsoids with aspect ratios in the range A ∈ [6,12] and mean distance between the air–water interface and the ellipsoid center of mass in the range z0 ∈ [2.55,3.92] μm, corresponding to a gap distance of few hundreds nanometers.
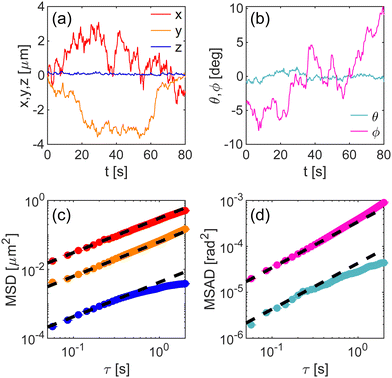
In Fig. 4, typical time evolution of the measured positions (Fig. 4a) and orientations (Fig. 4b) is shown for one representative ellipsoid.
From the tracking, the mean square displacement (MSD) (Fig. 4c) and the mean square angular displacement (MSAD) (Fig. 4d) are evaluated: MSDk(τ) = 〈[k(t + τ) − k(t)]2〉t, where k is x, y, z, θ and ϕ (for notation simplicity in equations we name MSDk both the MSD and the MSAD). From the MSD and MSAD the diffusion coefficient Dk along the freely diffusive degrees of freedom x, y and ϕ are obtained from a linear fit 2Dkτ. As expected, the in-plane translational diffusivity is larger along the major axis direction (x) than along the minor axis one (y). As it can be seen in Fig. 4a and b, the movement along z and the rotation along θ are not free but confined in the DLVO potential due to the colloid and the air–water interface interactions.25 As a consequence, MSDz and MSDθ are both characterized by sub-diffusive behavior with a plateau for large lag times. They are therefore fitted with the analytic solution of the Langevin equation assuming a harmonic potential,28,29 whose free fitting parameters are the diffusion coefficient and the potential stiffness. Translational and rotational mobilities are obtained as Dk/kBT, where kB is the Boltzmann constant and T the temperature.
The fitting procedure decouples the confinement and the viscous drag contributions present in the MSD. Consequently, inter-particle differences in the DLVO and in the gravitational potentials due to the equivalent radius†† and aspect ratio polydispersities only affect the measured mobilities by changing the particle-interface average gap distances. The mobilities measured for different ellipsoids can be therefore duly compared once they are normalized through ad hoc simulations considering same ellipsoids geometries and gap distances as the ones measured. A list of the measured geometrical parameters relative to all the considered ellipsoids together with the corresponding measured mobilities is reported in a table in the ESI.†
2.3 Simulations
Because of the lack of exact models for ellipsoids at close distance to the interface, we compare experimental results with numerical simulations. The latter are designed considering a free-buoyant rigid ellipsoid suspended in an incompressible Newtonian liquid in proximity of an interface, where both full-slip (v⊥ = 0, ∂⊥v‖ = 0) and no-slip (v⊥ = 0, v‖ = 0) BC are simulated.‡‡ Such BC have been chosen based on previous results on the Brownian diffusion of spherical particles in the same experimental conditions,6 where the surface incompressibility condition results in an effective no-slip BC for particle diffusion along the z-axis and quasi-slip BC for the parallel one. The same no-slip BC is expected to hold for an ellipsoid diffusing perpendicularly to an incompressible interface. On the ellipsoid surface, no-slip boundary conditions are imposed. The system of partial differential equations along with the BC and the numerical details are reported in the ESI.†We solve the governing equations by applying a single non-zero component of the combined force/torque vector (F,T) and compute the six components of the translational and rotational velocity vector (u,ω). By varying the imposed non-zero component of the force/torque vector, in six iterations we can compute the full mobility matrix M:30
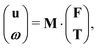 | (2) |
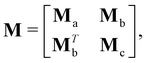 | (3) |
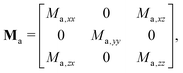 | (4) |
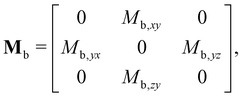 | (5) |
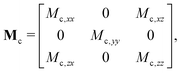 | (6) |
Due to the symmetry, for any particle-interface distance z, all the configurations obtained for different azimuthal angles ϕ (rotations around the z-axis) are equivalent. Consequently, the particle-interface hydrodynamic interactions and, in turn, the mobility matrix are functions of z and θ only, namely, M = M(z,θ). Because of the invariance for rotations around z-axis, it is sufficient to compute the mobility matrix only for configurations with the major axis of the spheroid lying in the x′z-plane; the mobility or friction matrices for orientations outside the x′z-plane are simply obtained by rotations around z-axis.
3 Results and discussions
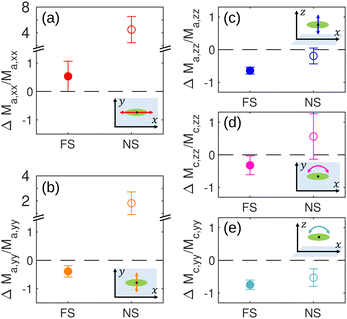
Mobilities of particles measured in our experiments depend on the particle properties (size and aspect ratio), on the average distance from the interface and on the boundary conditions at the interface. Indeed, the presence of a boundary hinders the normal dynamics and either hinders or promotes the parallel one, depending on the particular BC. Since all the relevant parameters are experimentally accessible, a benchmarking with predictions can be made at the single particle level.We therefore compare the measured mobilities 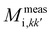 (where i = a, c and k, k′ = x, y, z according to the definitions of Section 2.3) with simulated mobilities
(where i = a, c and k, k′ = x, y, z according to the definitions of Section 2.3) with simulated mobilities 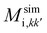 obtained using slip and no-slip BC. To this aim, for each measured ellipsoid we run a simulation having as input the measured aspect ratio and average z for the particle at hand, with θ kept fixed to zero.§§ For the five mobilities we define the mobility relative difference as:
obtained using slip and no-slip BC. To this aim, for each measured ellipsoid we run a simulation having as input the measured aspect ratio and average z for the particle at hand, with θ kept fixed to zero.§§ For the five mobilities we define the mobility relative difference as: 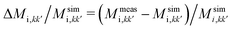 . In Fig. 5a–c, we report
. In Fig. 5a–c, we report 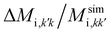 for the translational movement, in the case of slip (full circles) and no-slip (open circles) BC. The reported values with their error bars represent the averages and standard deviations on the 18 ellipsoidal particles. The experimental translational mobilities parallel to the interface (Fig. 5a and b) are close to the numerical predictions obtained with the slip BC, while the translational mobility orthogonal to the interface (Fig. 5c) approaches the result with no-slip BC.
for the translational movement, in the case of slip (full circles) and no-slip (open circles) BC. The reported values with their error bars represent the averages and standard deviations on the 18 ellipsoidal particles. The experimental translational mobilities parallel to the interface (Fig. 5a and b) are close to the numerical predictions obtained with the slip BC, while the translational mobility orthogonal to the interface (Fig. 5c) approaches the result with no-slip BC.
These results are in agreement with the findings Villa et al.6 for translational movement of spherical particles. There, the authors argue that, at low frequencies (f ≪ fc ∼ 102–103 Hz), the presence of even tiny quantity of surface active agents at the interface imposes a null divergence of the interfacial velocity field (div2D![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = 0). Such condition strongly affects the particle movement along the z-axis, that is thus equal to the one expected close to a solid wall, while the movement parallel to the interface is almost unaffected if compared to the full-slip BC case.9 As shown in ref. 6 and 8, surface incompressibility condition is the limiting case for timescales much larger than 1/fc, when a Marangoni stress induced by surface active concentration gradients hinders the interfacial radial flow. In the opposite limit, for fast dynamics at low timescales the concentration gradient at the interface has no time to build up and the interface behaves as a full-slip one. Importantly, even a tiny surface coverage of surface active species (concentration range of c0 ∼ 10−2–10−3 molecules per nm2), far below the concentrations detectable by standard surface tension instruments,31 rises the value of fc = 8c0kBT/(πηr), where r is the beads radius and η water viscosity, up to hundreds of Hz. This is a value much higher than typical acquisition frequencies of Brownian dynamics experiments. For the same experimental system, we recorded the dynamics of un-stretched 2r = 9 μm diameter sulphate latex beads using a fast camera (4000 fps). The high frame rate allowed us to measure the transition frequency from full-slip to surface incompressibility BC, resulting in fc ∼ 2000 Hz and corresponding to 9 × 10−4 molecules per nm2.6 The range of sampled Fourier components of the particle dynamics probed in the present work, determined by the acquisition frame rate of 30 fps, lies far below fc. Consequently, the Brownian dynamics can be rightfully described considering surface incompressibility at the interface. This explains the apparent discrepancy between the results retrieved for the translational mobilities. Indeed, BC are not different for dynamics normal and parallel to the interface: the unifying condition rationalizing both the directions is surface incompressibility.
= 0). Such condition strongly affects the particle movement along the z-axis, that is thus equal to the one expected close to a solid wall, while the movement parallel to the interface is almost unaffected if compared to the full-slip BC case.9 As shown in ref. 6 and 8, surface incompressibility condition is the limiting case for timescales much larger than 1/fc, when a Marangoni stress induced by surface active concentration gradients hinders the interfacial radial flow. In the opposite limit, for fast dynamics at low timescales the concentration gradient at the interface has no time to build up and the interface behaves as a full-slip one. Importantly, even a tiny surface coverage of surface active species (concentration range of c0 ∼ 10−2–10−3 molecules per nm2), far below the concentrations detectable by standard surface tension instruments,31 rises the value of fc = 8c0kBT/(πηr), where r is the beads radius and η water viscosity, up to hundreds of Hz. This is a value much higher than typical acquisition frequencies of Brownian dynamics experiments. For the same experimental system, we recorded the dynamics of un-stretched 2r = 9 μm diameter sulphate latex beads using a fast camera (4000 fps). The high frame rate allowed us to measure the transition frequency from full-slip to surface incompressibility BC, resulting in fc ∼ 2000 Hz and corresponding to 9 × 10−4 molecules per nm2.6 The range of sampled Fourier components of the particle dynamics probed in the present work, determined by the acquisition frame rate of 30 fps, lies far below fc. Consequently, the Brownian dynamics can be rightfully described considering surface incompressibility at the interface. This explains the apparent discrepancy between the results retrieved for the translational mobilities. Indeed, BC are not different for dynamics normal and parallel to the interface: the unifying condition rationalizing both the directions is surface incompressibility.
Moving from spherical particles to the ellipsoids, translation normal to the interface still induces a purely radial flow at a free interface (see ESI†). As a consequence, surface incompressibility condition for the movement normal to the interface coincides with a no-slip BC, as for the spheres.
In Fig. 5d and e, we also report the in-plane and out-of-plane rotational mobility relative difference, again for slip (full circles) and no-slip (open circles) BC. As for the translations, rotation in the plane (Fig. 5d) is closer to simulations with full-slip BC at the interface. This can also be rationalized in the framework of surface incompressibility as the rotation of a prolate ellipsoid in the plane can be regarded as the translation of its tips, with therefore a weak radial component of the flow at the interface. On the other hand, for the rotation out of the plane (Fig. 5e) the two boundary conditions give comparable results within the experimental error. For small θ, such a rotation indeed mainly consists of the vertical upward and downward movements of the two ellipsoid tips. In such an idealized picture, the interfacial velocity field would therefore have the symmetry of a dipolar field with both radial and non-radial relevant components. Please note that for both BC the significant measured deviations from the simulated values can result from the large experimental noise on θ.¶¶
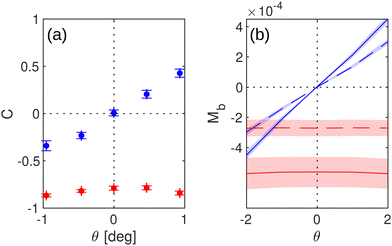
We also evaluated the cross-correlations between different degrees of freedom, comparing their trend with simulated cross-mobilities. To this aim we calculate the rotational–translational cross-correlations Cvz,ω and Cvx,ω (at time delay 0) between the angular velocity of the out-of-plane rotations ω and two components of the particle velocity, i.e. vz, along the interface normal and vx, along the ellipsoid major axis:
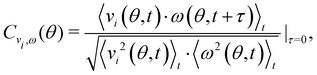 | (7) |
In the case of Cvz,ω for negative θ we observe that vz and ω are anti-correlated, while for positive θ they are correlated. To rationalize the observed cross-correlation, note that, as soon as θ deviates from zero, one tip of the ellipsoid is farther from the interface than the other. In this condition, if the particle approaches the interface (negative vz), the ellipsoid tip closer to the interface will experience a greater drag, independently from the assumed BC. Consequently the ellipsoid is subjected to a torque restoring the condition θ = 0. Therefore, if θ > 0 a vz < 0 induces an ω < 0, while vz > 0 induces an ω > 0, and thus in both cases a positive cross-correlation holds. Vice versa, if θ < 0, a vz < 0 induces an ω > 0, while a vz > 0 induces an ω < 0, and thus in both cases a negative cross-correlation. It is worth noticing that the observed cross-correlation is not a consequence of the ellipsoids-interface potential well, which also acts to restore the θ = 0 condition. Indeed, in the limit of a harmonic potential, a rotation of the ellipsoid along θ would generate only a restoring torque, with no force in the direction of the z axis.
For Cvx,ω, the negative sign observed indicates that the behaviour is anti-correlated for both θ > 0 and θ < 0, as in systems where parallel drag decreases approaching the boundary.26
In order to verify whether the cross-mobilities have the same trend as the cross-correlations, we simulated and reported in Fig. 6b the cross-mobilities Mb,zy (blue curves) and Mb,xy (red curves) versus θ, where Mb,zy corresponds to Cvz,ω, while Mb,xy corresponds to Cvx,ω. For each mobility both no-slip (dashed line) and slip (continuous line) BC are considered. The cross-mobilities are simulated for an ellipsoid of aspect ratio A = 8.6 at a particle-interface distance z0/2b = 1.167, corresponding to the average aspect ratio and distance of the experiments. Shadowed regions in Fig. 6b account for the inter-sample aspect ratio variance|||| ΔA = ±0.6. The trend of the simulated mobilities is the same of the experimental cross-correlations, for both full-slip and no-slip BC, thus implying that for the considered ellipsoids the sign of the correlation is only dictated by the presence of an interface, regardless of the specific BC applied at the interface. Since cross-mobilities are qualitatively similar for both full-slip and no-slip BC, subtle effects due to surface incompressibility condition are difficult to explore from the analysis of the cross-correlations.
This result is surprising as it is significantly different from the limit case (A = 1) of a sphere: as a consequence of a translation parallel to the interface, a bead is expected to rotate along the axis in the plane orthogonal to the translating direction with a positive correlation (Mb,xy > 0) for no-slip BC and with a negative correlation (Mb,xy < 0) for full-slip BC,26 whereas for the considered ellipsoid both mobilities are negative. This may hint at a crossover in the no-slip case from positive to negative correlation as a function of the aspect ratio which deserves further study.
4 Conclusions
In this work we first report a study on the mobilities of a micrometric ellipsoidal particle in the close vicinity of an air–water interface. Five different ellipsoidal mobilities (3 translational and 2 rotational) are measured and compared with dedicated simulations for slip and no-slip boundary conditions at the air–water interface. Moreover, the out-of-plane and the in-plane roto-translations cross-correlations are calculated and compared with simulated cross-mobilities. Analogously to the spherical particles,6 surface incompressibility rules the translational mobilities: parallel ones approach predictions for slip BC, while the orthogonal one is close to no-slip BC. The rotational degrees of freedom strengthen the importance of surface incompressibility on the mobility of the ellipsoid, as the in-plane and out-of-plane rotations relate to the corresponding translational degrees of freedom. The roto-translational cross-correlations, finally, are found in a qualitative agreement with the simulated cross-mobilities.In the current work we measured the mobilities in a limited range of particle sizes, aspect ratios and distances from the interface, but the described setup enables a wider characterization as a function of those parameters, by changing the dimensions of the produced ellipsoids and by finely tuning the particle-interface distance. Gap distance can indeed be tuned by changing the DLVO interactions with the addition of salt25 or through the use of optical tweezers.
We believe that our findings will be relevant to predict the movement of micro and nano entities close to liquid interfaces and membranes in a variety of fields ranging from biophysics to material processing. In particular, the relevance of the present results can be perceived considering the strong geometrical analogy of the investigated system with the one of a living bacteria moving close to an air water interface. Indeed, recent papers report how anomalies on the motion of Escherichia coli13 and Pseudomonas aeruginosa32 result from surface incompressibility, thus making the typical assumption of free air–water interface far from reality in such systems. By pointing out the additional effect of surface incompressibility on the rotational dynamics, we would like to take a first step towards a systematic study of surface incompressibility effects on the dynamics of micrometric organisms in water, stimulating further investigations in the field.
Author contributions
SV: data curation, formal analysis, investigation, software, visualization, writing (original draft). DL: conceptualization, visualization, writing (original draft). AS: conceptualization. CB: conceptualization, methodology. MV and GdA: data curation (simulations), writing (original draft). MN: conceptualization, funding acquisition, project administration, supervision, writing (original draft). All authors contributed to the writing (review and editing).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the French Agence Nationale de la Recherche (Contract no. ANR-14-CE07-0039-SURFANICOL), and from the LabEx NUMEV (Contract no. AAP2014-2-044). Open Access funding provided by the Max Planck Society.Notes and references
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242 CrossRef CAS.
- G. Perkins and R. Jones, Phys. A, 1991, 171, 575 CrossRef.
- A. V. Nguyen and G. M. Evans, J. Colloid Interface Sci., 2004, 273, 262–270 CrossRef CAS PubMed.
- G. M. Wang, R. Prabhakar and E. M. Sevick, Phys. Rev. Lett., 2009, 103, 248303 CrossRef CAS PubMed.
- S. Villa, G. Boniello, A. Stocco and M. Nobili, Adv. Colloid Interface Sci., 2020, 284, 102262 CrossRef CAS PubMed.
- S. Villa, C. Blanc, A. Daddi-Moussa-Ider, A. Stocco and M. Nobili, J. Colloid Interface Sci., 2023, 629, 917–927 CrossRef CAS PubMed.
- J. C. Benavides-Parra, D. Jacinto-Méndez, G. Brotons and M. D. Carbajal-Tinoco, J. Chem. Phys., 2016, 145, 114902 CrossRef.
- A. Maali, R. Boisgard, H. Chraibi, Z. Zhang, H. Kellay and A. Würger, Phys. Rev. Lett., 2017, 118, 084501 CrossRef CAS PubMed.
- J. Bławzdziewicz, M. Ekiel-Jeżewska and E. Wajnryb, J. Chem. Phys., 2010, 133, 114702 CrossRef PubMed.
- A. Chakrabarty, A. Konya, F. Wang, J. V. Selinger, K. Sun and Q.-H. Wei, Phys. Rev. Lett., 2013, 111, 160603 CrossRef PubMed.
- S. Ota, T. Li, Y. Li, Z. Ye, A. Labno, X. Yin, M.-R. Alam and X. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 053010 CrossRef PubMed.
- J. M. A. Paweł Czajka and M. Długosz, ACS Omega, 2019, 4, 17016–17030 CrossRef PubMed.
- S. Bianchi, V. C. Sosa, G. Vizsnyiczai and R. D. Leonardo, Sci. Rep., 2020, 10, 4609 CrossRef CAS PubMed.
- M. De Corato, F. Greco, G. DAvino and P. Maffettone, J. Chem. Phys., 2015, 142, 194901 CrossRef CAS PubMed.
- Y. Han, A. M. Alsayed, M. Nobili, J. Zhang, T. C. Lubensky and A. G. Yodh, Science, 2006, 314, 626–630 CrossRef CAS PubMed.
- F. Giavazzi, A. Pal and R. Cerbino, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 1–9 CrossRef PubMed.
- N. Shokeen and A. Mukhopadhyay, Colloid Polym. Sci., 2021, 229, 1595–1603 CrossRef.
- S. Coertjens, R. D. Dier, P. Moldenaers, L. Isa and J. Vermant, Langmuir, 2017, 33, 2689–2697 CrossRef CAS PubMed.
- A. Wang, W. B. Rogers and V. N. Manoharan, Phys. Rev. Lett., 2017, 119, 108004 CrossRef PubMed.
- G. Boniello, C. Blanc, D. Fedorenko, M. Medfai, N. B. Mbarek, M. In, M. Gross, A. Stocco and M. Nobili, Nat. Mater., 2015, 14, 908–911 CrossRef CAS PubMed.
- S. Bianchi, F. Saglimbeni, G. Frangipane, D. Dell'Arciprete and R. Di Leonardo, Soft Matter, 2019, 15, 3397–3406 RSC.
- D. P. Rivas, N. D. Hedgecock, K. J. Stebe and R. L. Leheny, Soft Matter, 2021, 17, 8195–8210 RSC.
- Y. Xing, X. Gui, L. Pan, B.-E. Pinchasik, Y. Cao, J. Liu, M. Kappl and H.-J. Butt, Adv. Colloid Interface Sci., 2017, 246, 105 CrossRef CAS PubMed.
- Y. Chevalier and M.-A. Bolzinger, Colloids Surf., A, 2013, 439, 23 CrossRef CAS.
- S. Villa, A. Stocco, C. Blanc and M. Nobili, Soft Matter, 2020, 16, 960–969 RSC.
- S. Lee and L. Leal, J. Fluid Mech., 1980, 98, 193–224 CrossRef.
- D. M. Kaz, R. McGorty, M. Mani, M. P. Brenner and V. N. Manoharan, Nat. Mater., 2012, 11, 138–142 CrossRef CAS PubMed.
- M. C. Wang and G. E. Uhlenbeck, Rev. Mod. Phys., 1945, 17, 323–342 CrossRef.
- S. K. T. Li, D. Medellin and M. G. Raizen, Science, 2010, 328, 1673–1675 CrossRef PubMed.
- J. Happel, Low Reynolds number hydrodynamics: with special applications to particulate media, Springer, 1983 Search PubMed.
- V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779 CrossRef CAS.
- J. Deng, M. Molaei, N. G. Chisholm and K. J. Stebe, arXiv, 2022, preprint arXiv:2204.02300.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01665f |
| ‡ In the present work we only discuss different BC at the interface, while on the particles surface we always consider no-slip BC. |
| § Since the electrostatic contribution to the DLVO potential is repulsive (both the particles and the air–water interface have a negative surface potential), the breaching probability significantly increases when the electrostatic interaction is screened. This can be done by adding salt to the solution to decrease the Debye screening length.25 In principle, salt addition can be therefore exploited for finely tuning the distance of the ellipsoids from the interface in order to characterize the space dependence of the particle dynamics. |
| ¶ Mitutoyo Apochromatic objective MY50X-805, 50×, WD 3, NA 0.55. |
| || Thorlabs collimated LEDs M625L3-C2 and M505L3-C2. |
| ** Basler dart camera daA1280-54uc. |
| †† The radius req = a1/3b2/3 of a sphere with same volume of the considered ellipsoid. |
| ‡‡ In the boundary conditions expression, ‖ and ⊥ denote respectively the direction parallel and perpendicular to the interface. The velocities are the ones of the fluid at the considered interface. |
| §§ We checked that the experimental fluctuations in z around its mean value and of θ around 0° only slightly affect the simulated mobilities. |
| ¶¶ As error on θ propagates from the error on b (see ESI†) an improved characterization of the ellipsoids semi-axes should be required for improving the measurement of θ. |
| |||| In the experimental ranges, simulations are more sensitive to the aspect ratio than to particle-interface distance. |
| This journal is © The Royal Society of Chemistry 2023 |