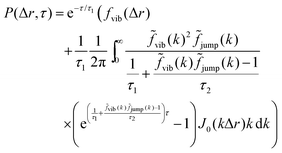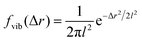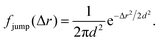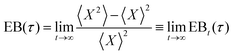Extending the analogy between intracellular motion in mammalian cells and glassy dynamics

Abstract

How molecules, organelles, and foreign objects move within living cells has been studied in organisms ranging from bacteria to human cells. In mammalian cells, in particular, cellular vesicles move across the cell using motor proteins that carry the vesicle down the cytoskeleton to their destination. We have recently noted several similarities between the motion of such vesicles and that in disordered, “glassy”, systems, but the generality of this observation remains unclear. Here we follow the motion of mitochondria, the organelles responsible for cell energy production, in mammalian cells over timescales from 50 ms to 70 s. Qualitative observations show that single mitochondria remain within a spatially limited region for extended periods of time, before moving longer distances relatively quickly. The displacement distribution is roughly Gaussian for shorter distances (≲0.05 μm) but exhibits exponentially decaying tails at longer distances (up to 0.40 μm). This behaviour is well-described by a model developed to describe the motion in glassy systems. These observations are extended to in total 3 different objects (mitochondria, lysosomes and nano-sized beads enclosed in vesicles), 3 different mammalian cell types (HEK 293, HeLa, and HT22), from 2 different organisms (human and mouse). Further evidence that supports glass-like characteristics of the motion is a difference between the time it takes to move a longer distance for the first time and subsequent times, as well as a weak ergodicity breaking of the motion. Overall, we demonstrate the ubiquity of glass-like motion in mammalian cells, providing a different perspective on intracellular motion.

---

Introduction

The living cell has a myriad of processes going on within it occurring at the same time. Some of these processes depend intimately upon transport, whether of molecules, molecular complexes, or larger lipid bilayer-decorated vesicles. While it appears that many molecular species are transported sufficiently rapid by diffusion,¹ for many vesicles (and the cargo they enclose) the cell has evolved a highly regulated transport system composed of a polymer network (the cytoskeleton) upon which the vesicles are transported, being carried by motor proteins that consume cell energy each step they take.²

We recently followed the motion of such intracellular vesicles in human (HeLa) cells using fluorescent nano-sized beads as labels.³ These beads populate vesicles^4–6 (many of them lysosomes)^4–8 that can be transported by motor proteins. We observed that the motion of the vesicles (beads) exhibited several hallmarks that are characteristic of the motion in disordered, “glassy”, systems.⁹ As opposed to diffusive motion,¹⁰ the motion in glassy systems is characterised by a highly heterogeneous dynamics where, roughly speaking, the majority of objects spend most of their time stationary and when they do move, they do so in a highly collective manner.¹¹ Glass-like motion was later reported also for chloroplasts in plant cells.¹² A similarity between the motion in glassy systems had already been noted for the motion in bacteria¹³ and other microorganisms,¹⁴ but the physical interpretation is likely quite different, since bacteria do not have motor proteins. Indeed, motor protein-driven transport is generally understood to exist to speed up transport,² so the observation that it shares characteristics with the notoriously sluggish motion in a glass may be considered somewhat surprising.

To test the generality of the observation that intracellular motion is glass-like we here followed the motion of mitochondria in three different cell types (HEK 293, HeLa, and HT22) from two different organisms (human and mouse). Mitochondria are double-membrane organelles which are essential for all eukaryotic cells. While their main function is to supply cell–energy, they are involved in multiple intracellular processes such as calcium storage, reactive oxygen species formation, and apoptosis. Mitochondrial shape, as well as the distribution of mitochondria within the cell, is highly heterogeneous due to the dynamic nature of these organelles. Most mitochondria are present as tubular elongated structures fused together to form a widespread network, which co-exists with single mitochondria detached from the network.¹⁵ The simultaneous presence of different mitochondrial configurations in the cell is due to the constant remodelling of the mitochondrial network through fission and fusion processes, mainly driven by the metabolic needs of the cell and interactions with other organelles and cytoskeleton structures.¹⁶ Crucially for our purposes here, mitochondria are transported around inside the cell along the microtubule network, being carried towards the plus ends (typically towards the cell periphery) by kinesin motor proteins, and towards the minus ends (typically towards the cell body) by dynein motor proteins.^17,18 We thus use them as another example of organelles that move by motor proteins and study their motion using live-cell fluorescence microscopy. Analysing their trajectories, we test several hallmarks characteristic of the motion in glassy systems and show that, indeed, mitochondria also move in a glass-like manner.

Experimental section

Cell culture

HEK 293 (American type culture collection, ATCC; no. CRL-1573, lot no. 63966486) cells were cultured in Dulbecco's Modified Eagle's Medium (DMEM; Gibco, Life Technologies, Eugene, OR, USA), supplemented with 10% foetal bovine serum (FBS; Gibco, Life Technologies, Eugene, OR, USA). The cells were kept in a 37 °C and 5% CO₂ incubator and were subcultured twice per week. Cells were used at passage number 6–26. HeLa cells (ATCC; no. CCL-2TM, lot no. 61647128) were cultured under the same conditions and subcultured thrice per week. Cells were used at passage number 16–30. HT22 cells were cultured in DMEM (Gibco, ThermoFisher Scientific, Landsmeer, The Netherlands) with 10% FBS (GE Healthcare Life Sciences, Eindhoven, the Netherlands), 1% sodium-pyruvate (ThermoFisher Scientific, Landsmeer, The Netherlands) and 2% penicillin–streptomycin (ThermoFisher Scientific, Landsmeer, The Netherlands), kept in a 37 °C and 5% CO₂ incubator, and subcultured twice per week. Cells were used at passage number 270. Regular mycoplasma tests were carried out and only mycoplasma negative cells were used for the experiments. For the microscopy experiments, 150 000 (HEK 293) and 50 000 (HeLa and HT22) cells were seeded onto Petri dishes with glass-bottom microwells (MatTek, Ashland, MA, USA).

Organelle staining and live cell imaging microscopy

The experiments were conducted 24 h after cell seeding. To fluorescently label the mitochondria, cells were treated with MitoTracker Deep Red (Invitrogen, Waltham, MA, USA) diluted in serum-free DMEM to a concentration of 200 nM and incubated for 25 min at 37 °C and 5% CO₂. To fluorescently label the lysosomes, cells were treated with Lysotracker Red (Invitrogen, Waltham, MA, USA) diluted in DMEM to a concentration of 0.75 μM and incubated for 1 h at 37 °C and 5% CO₂. After incubation with the relevant stain, the cells were washed three times with phosphate-buffered saline solution (Gibco, Life Technologies, Eugene, OR, USA), after which transparent live cell imaging solution (Invitrogen, Waltham, MA, USA) was added. For the experiment on fixed cells, the cells were treated with paraformaldehyde (4%) for 15 min at room temperature before microscopy. In general, microscopy was performed directly after staining. Cells were observed with a DeltaVision Elite inverted microscope (based on an Olympus IX-71 stand) using a 60× oil objective (numerical aperture 1.42), illuminating the cells with a solid-state illumination system. For MitoTracker a 621–643 nm excitation and a 662–696 nm emission filter were used, while for LysoTracker a 528–555 nm excitation and a 574–619 emission filter were used. Images were captured with a PCO-edge sCMOS camera every 50 ms for 70 s. The same settings were used for all three cell types.

Organelle tracking

Only single punctate mitochondria were considered. In each cell, all single mitochondria were tracked by selecting a region of interest to isolate one or several single mitochondria. The trajectory of each mitochondrion was then automatically determined using the TrackMate plugin (version 2.8.1), available in the Fiji distribution of ImageJ.^19–21 After the automatic tracking procedure, each trajectory was manually reviewed to ensure that no spurious “jumps” occurred to a nearby fluorescence maximum.

The same procedure was used for lysosome tracking.

Analysis

The analysis performed here follows that in our previous work.³ Briefly, the time-averaged mean square displacement for an individual trajectory was determined by calculating the square displacement (in two dimensions) between all pairs of time points along the length of the trajectory, and subsequently averaging this over all pairs with the same lag time. By subsequently averaging this quantity over all trajectories, the time- and ensemble-averaged mean square displacement was formed.

The displacement distribution was calculated starting from the radial displacement, Δr, again between all pairs of time points along the length of all trajectories. Subsequently, the histogram of all radial displacements for a given time duration was determined and finally normalised such that the integral of the distribution multiplied by 2πΔr over Δr was 1. We fitted the Chaudhuri et al. model^11,22 to the experimentally determined displacement distributions, using the two-dimensional version of the model derived in our previous work³

where J₀ is the Bessel function of order 0, tilde represents a spatial Fourier transform, and f_vib and f_jump are Gaussians representing the distribution of displacements during “rattling” and of “jumps”, respectively

This model depends on four parameters (τ₁, τ₂, l and d; see also main text for a discussion of their physical meaning) and the fit was performed on the displacement distribution for several different lag times simultaneously (a global fit). The resulting fitting parameters are shown below (Table 1 of the Result section) where the errors on the fitted parameters were estimated as the square root of the diagonal elements of the covariance matrix of the parameters. The error on the ratio τ₁/τ₂ was estimated from Gauss’ formula for error propagation.

Table 1 Parameters extracted from fits to the displacement distributions. The Chaudhuri et al. model^11,19 describing the motion in glassy systems was fitted to the experimental data (Fig. 3 and 5 bottom row). The model is formulated in terms of four different parameters: τ₁, the waiting time before the organelle makes its first jump; τ₂, the waiting time before any subsequent jump; l, the spatial extent of the organelle rattling around; and d, the size of the jump. For each system, (first column in the table) the parameters were ensured to be the same for all different lag times. The penultimate column tests the relationship between the l and d parameters that Chaudhuri et al. observed to be approximately fulfilled¹¹

System	τ 1 (s)	τ 2 (s)	l (μm)	d (μm)	2l (μm)	τ 1/τ2
HEK 293 (mitochondria)	3.77 ± 0.12	1.42 ± 0.18	0.052 ± 0.001	0.101 ± 0.003	0.104 ± 0.001	2.65 ± 0.35
HEK 293 (lysosomes)	3.01 ± 0.10	4.30 ± 1.88	0.051 ± 0.001	0.139 ± 0.005	0.101 ± 0.002	0.70 ± 0.31
HeLa (mitochondria)	7.31 ± 0.30	58.6 ± 182	0.049 ± 0.001	0.123 ± 0.003	0.098 ± 0.001	0.12 ± 0.39
HeLa (beads)	3.62 ± 0.12	1.81 ± 0.16	0.047 ± 0.001	0.082 ± 0.002	0.093 ± 0.001	2.00 ± 0.18
HT22 (mitochondria)	9.91 ± 0.57	3.60 ± 0.46	0.048 ± 0.001	0.071 ± 0.002	0.093 ± 0.001	2.75 ± 0.38

---

The time that a particle moves for the first time a certain distance and the time that it takes to move the same distance a second time were calculated as described in previous literature.^3,23 In doing so, we considered all pairs of time points, to improve statistics, and limited the calculation to the first 10 s, to reduce bias.

The degree of ergodicity breaking as a function of lag time, τ, was quantified through the ergodicity breaking parameter^24–26

where X stands for the mean square displacement of an individual trajectory at a given lag time, τ, averaged along the trajectory up to time t, and the brackets denote ensemble averaging. Since it is not possible to measure the infinite time limit experimentally, we evaluated the time-dependent parameter EB_t(τ) defined above and observed how it changed with time. Where EB_t(τ) appeared to converge with time, we took the value for 70 s to be equivalent to the infinite time-limit, EB(τ).

Results and discussion

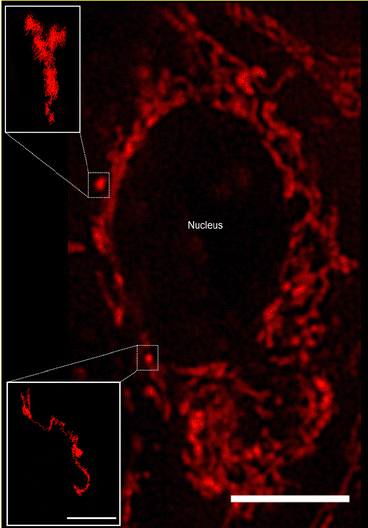
We used Human Embryonic Kidney (HEK 293) cells as our main cell model, with selected experiments repeated using HeLa (adenocarcinomic human cervical epithelial) cells and HT22 (mouse hippocampal neuronal) cells. To visualise and characterise mitochondrial motion, the mitochondria were stained with Mitotracker Deep Red and subsequently observed using live-cell fluorescence microscopy. We performed the microscopy in widefield mode, which implies a two-dimensional view of the cell. A disadvantage of this approach is that we cannot track the full three-dimensional movement of the mitochondria. On the other hand, due to the “squashed” shape of the cell, the majority of the motion is going to be in the two-dimensional plane we sample, and limiting ourselves to two dimensions implies much faster acquisition times. With a fast-acquisition camera, we were able to acquire images of cells at a size of 896 × 896 pixels (97.14 × 97.14 μm²) every 50 ms, for a total of 1400 frames (70 s).

Mitochondria are dynamic organelles present throughout the cell in different dimensions and shapes. Their diameter can vary from 0.5 to 1 μm and they can exhibit a more or less elongated tubular structure that can extend several μm in length.^27,28 The detailed mitochondrial structure is difficult to visualise through optical microscopy, due to their dimension being close to the optical resolution of typical (i.e., not super-resolution) microscopes. Nevertheless, it is possible to get a general overview of the structure and this is sufficient for our purposes here. Thus, we observe that the majority of mitochondria appear connected in a network, while some mitochondria instead appear as punctate “spots” (Fig. 1). These single (punctate) mitochondria are mostly present in the nuclear region (presumably under the cell nucleus, since mitochondria do not enter the nucleus) and closer to the outer cell membrane. In contrast, the mitochondrial network is spread out in the central part of the cell, surrounding the cell nucleus. Mitochondria are transported along the microtubule network,^17,18 whose predominant orientation is roughly radially outwards from the microtubule-organising centre close to one side of the nucleus, though more tangential orientations are also observed.²

Fig. 1 Mitochondria trajectories. Fluorescence microscopy image of a HEK 293 cell stained with MitoTracker deep red for visualising the mitochondria. The central region is occupied by the nucleus (not stained and hence only indirectly visible due to the absence of mitochondria), around which a mitochondrial network is present. Additionally, some mitochondria appear more punctate in nature and isolated from the network, as indicated by the two examples. Here we focussed on the motion of these single mitochondria. Scale bar 10 μm. (Insets) Trajectories of the two single punctate mitochondria, tracked as described in Materials and Methods. One observes phases of (nearly) unidirectional motion, interspersed by moments when the mitochondrion does not move very far. Scale bar 1 μm.

We chose to focus on the motion of the single (punctate) mitochondria as being more representative of general organelle motion than the mitochondrial network (however, see previous literature for approaches to characterise the network).^29,30 From a practical point of view, their motion is also easier to follow as we thereby avoid the densest part of the mitochondrial network. At any given time there are only a few such single mitochondria per cell, so in order to acquire sufficient amount of data we had to pool the results from several cells together (18–55 cells per condition). To characterise the motion of these single mitochondria, we determined trajectories from the microscopy images by automatic tracking using the open-source software TrackMate,¹⁹ a Fiji/ImageJ plugin,^20,21 reviewing the accuracy of each trajectory manually afterwards. Some mitochondria (e.g., Fig. 1 insets) could be followed throughout the entire duration of the “movie” (1400 frames, 70 s). However, not all of the mitochondria were easily detectable for such a long time, either because they moved to a different focal plane (not observable in two-dimensional microscopy) or because they were obscured by the widespread mitochondrial network. We thus followed the mitochondria for as long as they were visible, resulting in a distribution of trajectory lengths (Fig. S1, ESI†).

Tracked mitochondria show trajectories of sometimes several micrometres in length (Fig. 1 insets). Their motion appears highly heterogeneous, exhibiting moments in which the mitochondrion is “rattling” around in the same general area, interspersed by longer “jumps” with a considerable degree of directionality. The time spent rattling around in the same area is often longer (in both of the trajectories shown in Fig. 1 it is around 22 s) while the duration of the jumps is typically faster (around 8 s in the Fig. 1 trajectories). The unidirectionality of the jumps most likely reflects active motor protein-driven motion. Previous research has identified these active parts of the motion and analysed them separately,^31,32 but for our purposes it was not needed.³ Rather, we note that the qualitative appearance of the trajectories shows a striking similarity with the motion in a number of glassy systems, such as a colloidal glass,³³ a sheared granular material,³⁴ and a glass-forming binary Lennard-Jones mixture.¹¹ It is this similarity between intracellular motion and glassy motion³ that we want to explore further here.

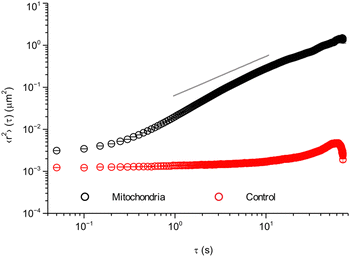
As a first characterisation of mitochondrial motion, we evaluated the mean square displacement (Fig. 2). To improve statistics, the calculations were done averaging all collected trajectories over all pairs of time points, i.e., we calculated the both time- and ensemble-averaged mean square displacement. To check the accuracy of our measurements, we started by performing the same type of experiment as in live cells, but on fixed cells (cells that are no longer alive, but with preserved intracellular structure). In these cells, the mitochondria cannot move by active processes, allowing us to assess eventual background movement due to drift of the microscope stage and thermal diffusion, as well as the finite precision with which we can localise a mitochondrion. These control experiments show (Fig. 2, red) almost no displacement, with only a small increase at longer timescales of around 20–30 s. Furthermore, the short timescale value is ∼0.0012 μm², corresponding to a distance of ∼√0.0012 μm² ≈ 0.035 μm. Whether to interpret this as localisation imprecision^35,36 or genuine short scale motion is less clear. Importantly, though, this distance is shorter than the typical length scales of interest to us here.

Fig. 2 Mean square displacement of mitochondria in HEK 293 cells. The mean square displacement was calculated from the trajectories, averaging both over (lag) time and trajectories (ensemble). Error bars represent standard error of the mean, but most are within the symbol. (Black) Mitochondrial motion in live cells (84 trajectories from 55 cells). (Red) Mitochondrial motion in fixed cells as a control (20 trajectories from 18 cells). (Grey solid line) Slope of 1, representative of Brownian motion, as a comparison. N. B. the log–log scale.

Turning to our real object of interest, the mitochondria in live cells, the mean square displacement (Fig. 2, black) shows an initial plateau at an 〈r²〉 value of ∼0.0031 μm² or a distance of ∼√0.0031 μm² ≈ 0.056 μm. The plateau is followed by a slow increase with time for short time scales (below 1 s), after which it grows roughly as a power law with an exponent higher than 1 (cf. the grey line). After ∼10 s there is possibly a decrease in the power law exponent, but it should be noted that the statistics is poorer here. The initial plateau is qualitatively consistent with the observations made above (Fig. 1 insets) and would then represent the rattling around of the mitochondrion in the same general area, with an average extent of 0.056 μm. Subsequently, at a timescale of ∼200 ms, some mitochondria start performing longer jumps and the mean square displacement starts increasing. As more and more mitochondria perform jumps and/or the mitochondria that have already jumped jump again, the mean square displacement increases further.

At the level of individual trajectories, we observe that the motion is heterogeneous (Fig. S2, ESI†). To better characterise this heterogeneity, we next calculated the displacement distribution. The displacement distribution (also referred to as the self-part of the van Hove function)^37,38 describes the probability that a particle moves a distance Δr in time τ from its starting point at time 0. We evaluated the displacement distribution in two dimensions, averaging out the angular dependence, as sampling a two-dimensional distribution requires a substantially larger amount of data. While we thereby lose information on the directionality of the motion, we can nevertheless make a number of interesting observations. We evaluated the displacement distribution for all trajectories and for all pairs of time-points (as we did for the mean square displacement), and present it for a few selected lag times, τ, between 0.5 and 3.0 s (Fig. 3; see also Fig. S3 for more times, ESI†). A first observation is that the displacement distribution is clearly not Gaussian, but rather exhibits exponentially decaying tails (Fig. 3; note the y axis log scale).^{14,23,39–48} Interestingly, the exponentially decaying tails appear to be there also for shorter timescales (Fig. S4, ESI†), though the statistics is necessarily poorer. The non-Gausssian character of the displacement distribution is most vividly demonstrated by explicitly fitting a Gaussian distribution to the data which, indeed, completely fails to describe the tails (Fig. S5, ESI†). Considering that mitochondria are transported by motor proteins along the cytoskeleton, it is perhaps not surprising that the motion is non-Gaussian. Indeed, in general multiple examples in the literature have reported a non-Gaussian behaviour of intracellular motion.^41,45,46 Still, it is telling that even at the longer timescales of a few seconds, when the mean square displacement increases close to linearly (Fig. 2), the displacement distribution remains non-Gaussian.

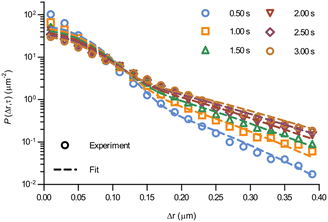Fig. 3 Displacement distribution of mitochondria in HEK 293 cells. (Data points) Displacement distributions of mitochondria observed experimentally for different lag times (84 trajectories from 55 cells). (Dotted lines) Fits of a model describing glassy motion^11,22 to the experimental data. The four fitting parameters (τ₁, τ₂, l, d) were ensured to be the same for all lag times and are reported in Table 1. For a better visualisation of the data only selected times are shown here, but more lag times were included in the fit (see Fig. S3 for a complete view, ESI†).

Even more telling is the fact that these displacement distributions (Fig. 3) are rather similar to those observed in a range of glassy systems,^{11,22,33,34,49–51} as we have previously noted for beads being moved by vesicles in HeLa cells.³ Indeed, this is consistent with the similarity between trajectories such as those shown in Fig. 1 and those reported for “real” glassy systems.^11,33,34 To evaluate if this similarity is not just qualitative but quantitative, we used the model introduced by Chaudhuri et al.^11,22 Their model describes the displacement distribution in several different experimental^22,33,34 and simulated^49–51 systems exhibiting glassy dynamics, and is based upon the following picture: particles spend some time rattling around locally, without moving larger distances. This part of the motion is described with a (time independent) Gaussian displacement distribution with characteristic distance, l. Every now and then the particle subsequently takes a longer jump, described by another Gaussian with a different characteristic distance, d. How long the particle spends rattling around before making a jump is taken from an exponentially decaying waiting time distribution with a characteristic time. To mimic “ageing”, the characteristic time before taking the first jump (the persistence time), τ₁, is allowed to be different from the characteristic time before taking a subsequent jump (the exchange time), τ₂. For the glassy systems the model was originally applied to, the reason the particle remains stalled before taking a longer jump is related to the denseness of the system (particles blocking each other from moving). We remain agnostic as to whether this is also the mechanism underlying the organelle motion and use the model only because of the similarity between organelle motion and that observed in glassy systems. It is also worth pointing out that we have not included any preferred direction of the “jumps” in the model, consistent with us determining the angular-averaged displacement distribution experimentally.

To test this model, we performed a global fit (where the parameters were ensured to be the same for the different time points analysed) to the experimentally observed displacement distributions. We observe that such a fit describes the data well (Fig. 3 dotted lines; see also Fig. S3 for more time points, ESI†) demonstrating that glassy motion is a good model to describe individual mitochondrial motion in these cells. In terms of the characteristic distances extracted from the fit (Table 1), we find that the rattling around occurs at a length scale of l = 0.05 μm, consistent with the plateau of the mean square displacement (Fig. 2 black). Similarly, we find a length scale of the jumps of d = 0.10 μm. Both lengths are much smaller than the average size of the (single, punctate) mitochondria.

In terms of the time it takes before performing a jump, we observe that the fit results in a time before taking a first jump, τ₁, that is different from the time before taking a subsequent jump, τ₂ (Table 1). Indeed, it is a typical feature of glassy systems that the distributions of these two times are different (decoupled). To provide further evidence of this observation, we proceed by evaluating the distribution of these two times directly from the experimental data (rather than indirectly from the fits). Thus, we calculated the two time distributions up to 10 s, defining the size of a “jump” as 0.10 μm, since this was the size of a jump extracted from the fit (Table 1). From this calculation it is clear (Fig. 4) that the time before making the first jump (persistence time; blue) is different from the time before making a subsequent jump (exchange time; orange). The same observation is made for other distances defining a “jump” ranging from 0.05 to 0.20 μm (Fig. S6, ESI†). For mitochondria this means that the probability to stop rattling around and perform a jump is higher after a first jump has already been performed. In a “real” glass, this is related to the probability of empty space becoming available for a particle to move into and the concept of dynamic heterogeneity. From a more theoretical point of view, it shows the ageing and non-stationary character of the motion.²⁶ Regardless, the validation of this hallmark of glassy dynamics reinforces our above finding (Fig. 3) that a model of glassy motion provides a good description of mitochondrial motion.

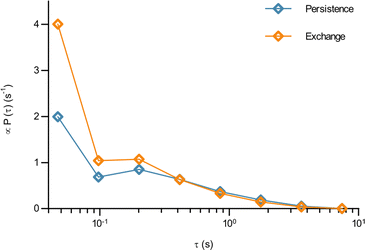Fig. 4 The waiting time before jumping the first time is different from the waiting time before jumping again for mitochondria in HEK 293 cells. How long it took a mitochondrion to move a distance of 0.1 μm for the first time, and the time it took to move the same distance a second time having already done so once, was evaluated from the experimental data as described in Methods (84 trajectories from 55 cells). The distribution of (blue) the time it takes to move the first time (persistence time) and (orange) the time it takes to move a subsequent time (exchange time). The distributions for a few other choices of the jump length are reported in Fig. S6 (ESI†). Note the log scale.

Up to this point we have demonstrated the utility of describing the motion of mitochondria in HEK 293 cells in terms of concepts borrowed from glassy dynamics. In order to expand the concept of intracellular motion being glassy to other systems, we first considered other cell lines (Fig. S7, ESI†). Thus, mitochondrial motion was assessed, following the same procedure as before, in HeLa cells and HT22 cells. HeLa cells are extensively used in cell biological research, are of epithelial nature and are, like HEK 293 cells, of human origin. HT22 cells, in contrast, are not human but of murine origin, and belong to an immortalised hippocampal neuronal cell line. In addition, we also wanted to see whether the motion of other organelles could be described in the same way, so we also tracked lysosomes in HEK 293 cells. Lysosomes are membrane-bound organelles in mammalian cells, which measure around 0.2 μm in radius⁵² and are heavily involved in metabolic processes, in particular in the degradation of cell products.⁵³ Finally, as a further comparison, we also included our previously published results³ on 40 nm (diameter) polystyrene beads being moved by vesicles, most of them lysosomes,^4–8 in HeLa cells. The motion in all of these systems is heterogeneous (Fig. S8–S10; example trajectories of our previous data are shown in the original paper, ESI†).³ As a first quantitative evaluation of the type of motion we calculated the time and ensemble-averaged mean square displacement (Fig. 5 top row), and we also fitted the Chaudhuri et al. model to the experimentally determined displacement distributions (Fig. 5 bottom row).

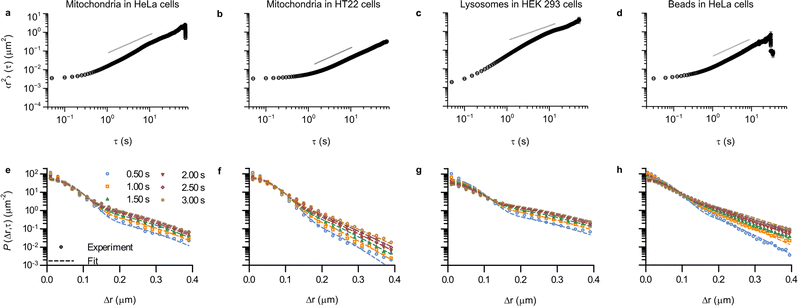Fig. 5 Ubiquity of glass-like characteristics of organelle motion in mammalian cells. (a–d) Mean square displacement as a function of lag time, τ. Error bars represent standard error of the mean, but most are within the symbol. (e–h) Displacement distribution for a few selected lag times. (Dotted lines) Fits of a model describing glassy motion^11,22 to the experimental data. The four fitting parameters (τ₁, τ₂, l, d) were ensured to be the same for all lag times and are reported in Table 1. (a and e) Mitochondria in HeLa cells (76 trajectories from 35 cells); (b and f) Mitochondria in HT22 cells (101 trajectories from 53 cells); (c and g) Lysosomes in HEK 293 cells (164 trajectories from 21 cells); and (d and h) Polystyrene beads in HeLa cells (data reproduced from literature; 157 trajectories from 17 cells).³ Note that it was possible to acquire a bit more rapidly in this case, so the mean square displacement starts already from ∼31 ms (as opposed to the 50 ms of the other systems). Trajectory length distributions are shown in Fig. S7 (ESI†).

The mean square displacements in all of the different systems exhibit a largely similar behaviour (Fig. 5 top row), with an initial plateau for short times, followed by a slow increase until ∼1 s, after which it grows more rapidly. At longer times, most of the systems have a slightly superdiffusive trend, though for mitochondria in HT22 cells the slope is actually below 1 (Fig. 5b). It is worthwhile to mention that superdiffusive behaviour is (sometimes) present also in the Chaudhuri et al. model,^11,22 and consequently there is no direct equivalence between superdiffusive behaviour and motor-protein-driven transport.

Aside from qualitative similarities, it is also interesting to note a remarkable amount of quantitative overlap. Thus the initial, 50 ms, value of the mean square displacement of the different objects in different cells is around 0.003 μm² for all tracked organelles in all cell types (Fig. 2 and 5a, b, d), though for lysosomes it is slightly lower at around 0.002 μm² (Fig. 5c). Contributing to this value is localisation imprecision, which we have already argued is not the main factor based on the value we found for mitochondria in fixed HEK 293 cells (Fig. 2, red). Different objects (mitochondria, lysosomes and beads), presumably exhibit various ease of localisation due to their different fluorescence labelling and different sizes. Furthermore, the present work (Fig. 2 and 5a–c) and our previous results reproduced here (Fig. 5d) were acquired using different microscopy set-ups, which one again would expect would give rise to a difference in localisation precision. The fact that we nevertheless find similar values under these variations thus gives further evidence that the initial plateau represents (mainly) genuine motion. In terms of quantitative agreement, it is even more encouraging to note that if we focus on HeLa cells specifically, then the mean square displacement of mitochondria and beads completely overlap for shorter times (Fig. S11, ESI†).

For the displacement distribution (Fig. 5 bottom row and Fig. 3) there is also a qualitative agreement between all the different systems. However, we also note agreement of a quantitative nature, namely that the Chaudhuri et al. model, originally developed to describe the motion in glassy systems, describes the displacement distribution in all of the different systems well. We have thereby enlarged the scope of this analogy substantially.

In terms of the parameters extracted from the fits (Table 1) the two length scales, l and d, are well-determined from the fits, as shown by the small errors. Furthermore, we observe that the range of the rattling, l ≈ 0.05 μm, is remarkably similar for all the systems. This is perhaps somewhat surprising given one might think it would be related to the size of the organelles, which are a bit different. Furthermore, the jump distance, d ≈ 0.10 μm, is also notably similar for all systems. While one should perhaps not stretch the analogy too far, we nevertheless find it interesting to note that for all the systems we investigated, one observes that the range of the jump distance, d, is roughly equal to twice the rattling, l (d ≈ 2l; compare the 5th and 6th columns of Table 1). This is the relation already noted by Chaudhuri et al.¹¹ to be approximately fulfilled for a colloidal glass,³³ a sheared granular material,³⁴ and a glass-forming binary Lennard-Jones mixture.^22,49 Whether this is a coincidence, or whether it hints at a similar mechanistic basis, we remain agnostic about.

The waiting time for the first jump, τ₁, is also well-determined from the fits (Table 1). However, the waiting-time for a successive jump, τ₂, is not well-determined for two of the systems (for lysosomes in HEK 293 cells and for mitochondria in HeLa cells). For the three systems that do give well-determined times we observe that τ₁ > τ₂, something we expect to be fulfilled on mathematical grounds.²² We also observe a variation of the two timescales between systems, with both timescales being a factor of 2 or more longer for mitochondria in HT22 cells, compared to mitochondria in HEK 293 cells and beads in HeLa cells. The larger variation of the timescales between systems is consistent with the similarity of the length scales, which implies that the observed differences between the displacement distributions (Fig. 5e–h) must mainly stem from the two timescales. Furthermore, we also estimated the ratio τ₁/τ₂ (Table 1 last column). Interestingly, for the systems where τ₂ is well-defined, we find values between 2–3, which is in the same range as a glass-forming binary Lennard-Jones mixture close to the glass transition, as well as that of a simulated silica melt.¹¹

While we have here fitted the Chaudhuri et al. model to the displacement distribution, one could also characterise it by fitting an exponential decay to the tails. For several glassy systems it has been reported that the decay length follows a power law with respect to lag time with an exponent of 1/3,^54,55 though the relevance of this result has been contested.^22,56 For the beads, we have, as a purely empirical observation, previously reported that the decay length grows as a power law with lag time with an exponent of 0.27.³ For the mitochondria and lysosomes studied here we were, however, unable to draw any definitive conclusions (Fig. S12, ESI†).

As a final characterisation of mitochondrial motion, we next tested whether it is ergodic. In this context, an ergodic behaviour would imply that averaging over a sufficient number of trajectories gives the same result as averaging over an individual trajectory during a sufficiently long time. It has been observed in several studies that intracellular and cell membrane phenomena present a nonergodic behaviour.^41,57 Moreover, like a non-linear mean square displacement and the decoupling of persistence and exchange times, ergodicity breaking is a hallmark of glassy motion, even though it is not exclusively related to this kind of motion. We quantified the degree of ergodicity breaking based on the parameter introduced by Burov, Metzler, Barkai, and co-workers.^24–26 Their parameter is a certain mathematical expression (see Methods for the explicit expression) which they then take the infinite time limit of. This poses an issue experimentally, as we clearly cannot evaluate something for an infinite length of time. We therefore evaluated the corresponding time-dependent quantity instead, and subsequently observed whether it appeared to converge within the time limit of our measurements. For several of our systems, the time-dependent ergodicity breaking parameter did not converge, so we were unable to evaluate the actual ergodicity breaking parameter (Fig. S13, ESI†). However, for mitochondria in HT22 cells, the parameter converged and we could evaluate the degree of ergodicity breaking. It should be noted that, like all our results, the ergodicity breaking parameter was evaluated by averaging over cells. However, we do not expect a major cell-to-cell variability of the motion at the subsecond timescales where we evaluated the degree of ergodicity, and, furthermore, we sampled a significant number of HT22 cells (53 cells). Nevertheless keeping this caveat in mind, the results suggest that mitochondrial motion is non-ergodic (Fig. S14, ESI†), similarly to beads enclosed in vesicles moving in HeLa cells,³ as well as lysosomes in HEK 293 cells (Fig. S15, ESI†). The lack of ergodicity naturally has consequences for interpreting time and ensemble averages,²⁶ something to keep in mind when examining observations such as mean square displacements (Fig. 2 and 5a–d).

Conclusions

Here we have followed the motion of mitochondria, the energy-supplying organelles of the cell, using live-cell fluorescence microscopy. Already qualitative observation of the trajectories suggests that their motion exhibits features that are typical of those in disordered, glassy, systems. That is, the mitochondria remain within the same region for extended periods of time, stalled, before rapidly making a longer jump. Using a model that makes this physical picture more precise, we show that it provides a good description of mitochondrial motion also from a quantitative point of view. We generalise these observations to in total three different objects (mitochondria, lysosomes, and the vesicles within which nano-sized beads reside), in three different cell lines (HEK 293, HeLa, and HT22) from two different organisms (human and mouse). While the motion is quantitatively different, strikingly, in all cases we observe that it exhibits glass-like features. From model fitting we extract the characteristic lengths of the stalled motion and the jumps, as well as the waiting time before making a jump. Interestingly, the spatial extent of the stalled motion is around 0.05 μm for all systems, despite the different sizes of the organelles and despite the different cell types, while the jump length varies a bit more between systems but nevertheless remains roughly around 0.10 μm. We also show evidence that the motion is non-ergodic.

It remains unknown what physical mechanisms are at the base of the glass-like behaviour. The cytosol of both prokaryotic and eukaryotic cells has been reported to behave like a soft glass,^13,58,59 so this could explain why the motion in bacteria and in the cytosol of eukaryotic cells exhibits glass-like features.^13,14 However, the organelles we have followed are not just freely moving in the cytosol, but rather are mostly transported by molecular motors, like dynein and kinesin, along microtubules. It is possible that a tug-of-war mechanism, that regulates the bidirectional movement of most of the cargoes along microtubules, gives rise to moments in which the organelles are pulled into different directions before one of the two takes over.^60–62 Similarly, the organelle could detach from the microtubule track, thus remaining stalled, before it attaches again to make a longer move. Alternatively, crowding within the cell, due to either other organelles and/or the cytoskeleton, could also be a reason for the stalled moments, as could a local cell energy depletion. It has also been observed that the structure of the cytoskeleton can lead to moments where the organelle remains stalled when the motor proteins meet an intersection in the mesh,⁶³ and this could also form an explanation for our observations. Insights into the physical mechanism could also come from connecting our results to the field of active matter,^64–66 in particular systems of dense active particles which often exhibits glassy features,^66–69 and sometimes similar behaviour to that shown here.^70,71 The systems studied in this field are admittedly, from a biological point of view, quite simplified. Therefore, outcomes that can be shown to be universal would be of most direct interest.

Regardless, the ubiquity of glass-like motion in mammalian cells that we have demonstrated here, suggests that it would be interesting to understand both its origins, but also its consequences.

Author contributions

C. Å. designed the research. A. M. D. contributed to the implementation of the research. B. C. performed all experiments and analysed all data, except as otherwise noted. O. H. performed the tracking of the lysosomes in HEK 293 cells. B. C. and C. Å. interpreted the data. B. C. and C. Å. wrote the manuscript. A. M. D. and O. H. reviewed the manuscript. All authors approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

B. C. was supported by a scholarship awarded under the Advanced Materials theme of the Faculty of Science and Engineering, University of Groningen. The microscopy was performed at the University Medical Center Groningen Imaging and Microscopy Center. We thank A. Salvati (University of Groningen, Groningen, The Netherlands), for providing the HEK 293 and HeLa cells. The HT22 cells were originally provided by C. Culmsee (Philipps-Universität Marburg, Marburg, Germany) for which we are grateful. We also thank Yuequ Zhang for help with culturing and seeding the HT22 cells and Steve S. Waheeb for a preliminary analysis of lysosomal motion.

Notes and references

1. R. Phillips, J. Kondev and J. Theriot, Physical biology of the cell, Garland Science, New York, 1st edn, 2008, ch. 13, pp. 481–512.
2. B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular biology of the cell, Garland Science, New York, 5th edn, 2008, ch. 16, pp. 965–1052.
3. C. Åberg and B. Poolman, Biophys. J., 2021, 120, 2355–2366.
4. A. Salvati, C. Åberg, T. dos Santos, J. Varela, P. Pinto, I. Lynch and K. A. Dawson, Nanomed. Nanotechnol. Biol. Med., 2011, 7, 818–826.
5. P. Sandin, L. W. Fitzpatrick, J. C. Simpson and K. A. Dawson, ACS Nano, 2012, 6, 1513–1521.
6. N. Vtyurina, C. Åberg and A. Salvati, Nanoscale, 2021, 13, 10436–10446.
7. C. Åberg, J. A. Varela, L. W. Fitzpatrick and K. A. Dawson, Sci. Rep., 2016, 6, 34457.
8. J. A. Varela, C. Åberg, J. C. Simpson and K. A. Dawson, Small, 2015, 11, 2026–2031.
9. K. Binder and W. Kob, Glassy materials and disordered solids: an introduction to their statistical mechanics, World Scientific, Singapore, 2005.
10. E. Frey and K. Kroy, Ann. Phys., 2005, 14, 20–50.
11. P. Chaudhuri, L. Berthier and W. Kob, Phys. Rev. Lett., 2007, 99, 060604.
12. N. Schramma, C. P. Israëls and M. Jalaal, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2216497120.
13. B. R. Parry, I. V. Surovtsev, M. T. Cabeen, C. S. O’Hern, E. R. Dufresne and C. Jacobs-Wagner, Cell, 2014, 156, 183–194.
14. M. C. Munder, D. Midtvedt, T. Franzmann, E. Nüske, O. Otto, M. Herbig, E. Ulbricht, P. Müller, A. Taubenberger, S. Maharana, L. Malinovska, D. Richter, J. Guck, V. Zaburdaev and S. Alberti, eLife, 2016, 5, e09347.
15. P. Bernardi, N. Raimundo, K. B. Busch, B. Glancy, Y. Kim, P. Katti and T. B. Willingham, Front. Physiol., 2020, 11, 1462.
16. A. S. Moore and E. L. F. Holzbaur, Curr. Opin. Physiol., 2018, 3, 94–100.
17. A. Melkov, Uri Abdu and U. Abdu, Cell. Mol. Life Sci., 2018, 75, 163–176.
18. K. Barlan and V. I. Gelfand, Cold Spring Harbor Perspect. Biol., 2017, 9, a025817.
19. J. Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90.
20. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.
21. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.
22. P. Chaudhuri, Y. Gao, L. Berthier, M. Kilfoil and W. Kob, J. Phys.: Condens. Matter, 2008, 20, 244126.
23. B. Wang, S. M. Anthony, S. Chul Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 8, 15160–15164.
24. Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101.
25. S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800–1812.
26. R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164.
27. S. Jakobs, T. Stephan, P. Ilgen and C. Brüser, Annu. Rev. Biophys., 2020, 49, 289–308.
28. B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Robert and P. Walter, Molecular biology of the cell, Garland Science, New York, 5th edn, 2008, ch. 14, pp. 813–878.
29. A. J. Valente, J. Fonseca, F. Moradi, G. Foran, A. Necakov and J. A. Stuart, Adv. Exp. Med. Biol., 2019, 1158, 183–196.
30. A. J. Valente, L. A. Maddalena, E. L. Robb, F. Moradi and J. A. Stuart, Acta Histochem., 2017, 119, 315–326.
31. D. Arcizet, B. Meier, E. Sackmann, J. O. Rädler and D. Heinrich, Phys. Rev. Lett., 2008, 101, 248103.
32. K. Chen, B. Wang, J. Guan and S. Granick, ACS Nano, 2013, 7, 8634–8644.
33. E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627–631.
34. G. Marty and O. Dauchot, Phys. Rev. Lett., 2005, 94, 015701.
35. R. E. Thompson, D. R. Larson and W. W. Webb, Biophys. J., 2002, 82, 2775–2783.
36. X. Michalet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041914.
37. K. Binder and W. Kob, Glassy materials and disordered solids: an introduction to their statistical mechanics, World Scientific, Singapore, 2005, ch. 2, pp. 35–78.
38. L. van Hove, Phys. Rev., 1954, 95, 249–262.
39. T. Toyota, D. A. Head, C. F. Schmidt and D. Mizuno, Soft Matter, 2011, 7, 3234–3239.
40. B. Stuhrmann, M. Soares, E. Silva, M. Depken, F. C. MacKintosh and G. H. Koenderink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 20901.
41. S. M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner, N. F. Scherer and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911–4916.
42. S. Stylianidou, N. J. Kuwada and P. A. Wiggins, Biophys. J., 2014, 107, 2684–2692.
43. W. He, H. Song, Y. Su, L. Geng, B. J. Ackerson, H. B. Peng and P. Tong, Nat. Commun., 2016, 7, 11801.
44. T. J. Lampo, S. Stylianidou, M. P. Backlund, P. A. Wiggins and A. J. Spakowitz, Biophys. J., 2017, 112, 532–542.
45. M. E. Grady, E. Parrish, M. A. Caporizzo, S. C. Seeger, R. J. Composto and D. M. Eckmann, Soft Matter, 2017, 13, 1873–1880.
46. P. Witzel, M. Götz, Y. Lanoiselée, T. Franosch, D. S. Grebenkov and D. Heinrich, Biophys. J., 2019, 117, 203–213.
47. A. Ravichandran, Ö. Duman, M. Hoore, G. Saggiorato, G. A. Vliegenthart, T. Auth and G. Gompper, eLife, 2019, 8, e39694.
48. E. Barkai and S. Burov, Phys. Rev. Lett., 2020, 124, 060603.
49. L. Berthier and W. Kob, J. Phys.: Condens. Matter, 2007, 19, 205130.
50. L. Berthier, G. Biroli, J. P. Bouchaud, W. Kob, K. Miyazaki and D. R. Reichman, J. Chem. Phys., 2007, 126, 184503.
51. L. Berthier, G. Biroli, J. P. Bouchaud, W. Kob, K. Miyazaki and D. R. Reichman, J. Chem. Phys., 2007, 126, 184504.
52. A. B. Novikoff, The Cell. Vol. II. Cells and Their Component Parts, Academic Press, New York, 1961, vol. II, pp. 423–488.
53. A. Ballabio and J. S. Bonifacino, Nat. Rev. Mol. Cell Biol., 2020, 21, 101–118.
54. J. M. Miotto, S. Pigolotti, A. V. Chechkin and S. Roldán-Vargas, Phys. Rev. X, 2021, 11, 031002.
55. F. Rusciano, R. Pastore and F. Greco, Phys. Rev. Lett., 2022, 128, 168001.
56. L. Berthier, E. Flenner and G. Szamel, arXiv, 2023, preprint, arxiv.2210.07119 DOI:10.48550/arxiv.2210.07119.
57. A. Weron, K. Burnecki, E. J. Akin, L. Solé, M. Balcerek, M. M. Tamkun and D. Krapf, Sci. Rep., 2017, 7, 5404.
58. M. Guo, A. J. Ehrlicher, M. H. Jensen, M. Renz, J. R. Moore, R. D. Goldman, J. Lippincott-Schwartz, F. C. Mackintosh and D. A. Weitz, Cell, 2014, 158, 822–832.
59. K. Nishizawa, K. Fujiwara, M. Ikenaga, N. Nakajo, M. Yanagisawa and D. Mizuno, Sci. Rep., 2017, 7, 15143.
60. K. Rezaul, D. Gupta, I. Semenova, K. Ikeda, P. Kraikivski, J. Yu, A. Cowan, I. Zaliapin and V. Rodionov, Traffic, 2016, 17, 475–486.
61. O. Osunbayo, J. Butterfield, J. Bergman, L. Mershon, V. Rodionov and M. Vershinin, Biophys. J., 2015, 108, 1480–1483.
62. M. J. I. Müller, S. Klumpp and R. Lipowsky, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 4609–4614.
63. M. Scholz, S. Burov, K. L. Weirich, B. J. Scholz, S. M. A. Tabei, M. L. Gardel and A. R. Dinner, Phys. Rev. X, 2016, 6, 011037.
64. S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345.
65. C. Bechinger, R. di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006.
66. L. M. C. Janssen, J. Phys.: Condens. Matter, 2019, 31, 503002.
67. L. Berthier, Phys. Rev. Lett., 2014, 112, 220602.
68. G. Szamel, E. Flenner and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062304.
69. A. Liluashvili, J. Ónody and T. Voigtmann, Phys. Rev. E, 2017, 96, 062608.
70. C. Lozano, J. R. Gomez-Solano and C. Bechinger, Nat. Mater., 2019, 18, 1118–1123.
71. J. Reichert and T. Voigtmann, Soft Matter, 2021, 17, 10492–10504.

---

Footnote

† Electronic supplementary information (ESI) available: Extended experimental results. See DOI: https://doi.org/10.1039/d2sm01672a

---