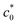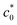Open Access Article
Open Access ArticleTransition of rupture mode of strain crystallizing elastomers in tensile edge-crack tests†
Katsuhiko
Tsunoda
*a,
Yuji
Kitamura
b and
Kenji
Urayama
 *c
*c
aSustainable and Advanced Materials Division, Bridgestone Corporation, Tokyo 187-8531, Japan. E-mail: katsuhiko.tsunoda@bridgestone.com
bSustainable and Advanced Materials Division, Bridgestone Corporation, Tokyo 187-8531, Japan
cDepartment of Material Chemistry, Graduate School of Engineering, Kyoto University, Kyoto 615-8510, Japan. E-mail: urayama.kenji.2s@kyoto-u.ac.jp
First published on 22nd February 2023
Abstract
We revisit the classical results that the fracture energy density (Wb) of strain crystallizing (SC) elastomers exhibits an abrupt change at a characteristic value (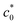 ) of initial notch length (c0) in tensile edge-crack tests. We elucidate that the abrupt change of Wb reflects the transition in rupture mode between the catastrophic crack growth without a significant SIC effect at c0 >
) of initial notch length (c0) in tensile edge-crack tests. We elucidate that the abrupt change of Wb reflects the transition in rupture mode between the catastrophic crack growth without a significant SIC effect at c0 > 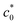 and the crack growth like that under cyclic loading (dc/dn mode) at c0 <
and the crack growth like that under cyclic loading (dc/dn mode) at c0 < 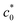 as a result of a pronounced SIC effect near the crack tip. At c0 <
as a result of a pronounced SIC effect near the crack tip. At c0 < 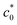 , the tearing energy (G) was considerably enhanced by hardening via SIC near the crack tip, preventing and postponing catastrophic crack growth. The fracture dominated by the dc/dn mode at c0 <
, the tearing energy (G) was considerably enhanced by hardening via SIC near the crack tip, preventing and postponing catastrophic crack growth. The fracture dominated by the dc/dn mode at c0 < 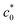 was validated by the c0-dependent G characterized by G = (c0/B)1/2/2 and the specific striations on the fracture surface. As the theory expects, coefficient B quantitatively agreed with the result of a separate cyclic loading test using the same specimen. We propose the methodology to quantify the tearing energy enhanced via SIC (GSIC) and to evaluate the dependence of GSIC on ambient temperature (T) and strain rate (
was validated by the c0-dependent G characterized by G = (c0/B)1/2/2 and the specific striations on the fracture surface. As the theory expects, coefficient B quantitatively agreed with the result of a separate cyclic loading test using the same specimen. We propose the methodology to quantify the tearing energy enhanced via SIC (GSIC) and to evaluate the dependence of GSIC on ambient temperature (T) and strain rate (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ). The disappearance of the transition feature in the Wb–c0 relationships enables us to estimate definitely the upper limits of the SIC effects for T (T*) and
). The disappearance of the transition feature in the Wb–c0 relationships enables us to estimate definitely the upper limits of the SIC effects for T (T*) and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (
(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *). Comparisons of the GSIC, T*, and
*). Comparisons of the GSIC, T*, and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * values between natural rubber (NR) and its synthetic analog reveal the superior reinforcement effect via SIC in NR.
* values between natural rubber (NR) and its synthetic analog reveal the superior reinforcement effect via SIC in NR.
Introduction
Natural rubber (NR) is one of the most widely used biomaterial polymers. NR has attracted increasing interest in environmental issues and momentum toward realizing a sustainable society.1–3 A unique feature of NR is strain-induced crystallization (SIC): NR undergoes partial crystallization when subjected to a sufficiently large strain.4,5 SIC considerably hardens rubber, resulting in a marked stress-upturn in the stress–strain relationship. SIC is a self-reinforcement function that increases the tensile strength and fracture toughness. This beneficial feature distinguishes NR from other non-crystallizing (non-SIC) rubbers.1–3 Synthetic cis-1,4-polyisoprene rubber (IR) is an NR analog. It has long been known that IR is appreciably inferior to NR in several SIC properties, such as the onset strain and the mechanical reinforcement effect.6–9 The superior SIC abilities of NR relative to IR are often attributed to the perfect stereoregularity of cis-1,4-polyisoprene and a pseudo-network via the interaction between the end-functional groups in the rubber chains and non-rubber components such as fatty acids, proteins, and lipids.10–13 Recently, it has been reported that SIC can occur even in gels with high solvent contents, significantly enhancing the mechanical toughness.14 SIC has received considerable interest as a key for toughening not only rubbers but also gels.The SIC near the crack tip subjected to large deformation contributes to enhancing the tear strength or suppressing the catastrophic crack growth.15–20 The SIC near the crack tip was revealed by investigations using the micro-beam wide-angle X-ray scattering (WAXS) technique.21,22 However, many aspects of the reinforcement effects via SIC remain to be quantified. The reinforcement effect via SIC is expected to have an upper limit for each ambient temperature (T) and imposed strain rate (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) (designated as T* and
) (designated as T* and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *, respectively), because the crystal has a melting temperature and SIC is a kinetic event. The melting temperatures (Tf) of the SIC crystals of NR and IR were investigated using WAXS experiments in the stretched state at various T.23–29 The Tf increased with imposed stretch reflecting an increase in the crystallinity index, which was thermodynamically explained by a reduction in the configurational entropy of network strands.1–3,30Tf is an equilibrium property, while the SIC kinetics is significantly affected by the ambient temperature (T). At T* the SIC kinetics becomes so slow that SIC cannot occur at
*, respectively), because the crystal has a melting temperature and SIC is a kinetic event. The melting temperatures (Tf) of the SIC crystals of NR and IR were investigated using WAXS experiments in the stretched state at various T.23–29 The Tf increased with imposed stretch reflecting an increase in the crystallinity index, which was thermodynamically explained by a reduction in the configurational entropy of network strands.1–3,30Tf is an equilibrium property, while the SIC kinetics is significantly affected by the ambient temperature (T). At T* the SIC kinetics becomes so slow that SIC cannot occur at ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) of interest.
of interest.
The effect of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) on SIC was examined by WAXS experiments using custom-made tensile instruments that could achieve high strain rates. The upper limit
on SIC was examined by WAXS experiments using custom-made tensile instruments that could achieve high strain rates. The upper limit ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) for SIC remains unclear because finite SIC was still observed at high strain rates on the order of 102 s−1.31–35 The reinforcement effect via SIC is expected to depend on T and
for SIC remains unclear because finite SIC was still observed at high strain rates on the order of 102 s−1.31–35 The reinforcement effect via SIC is expected to depend on T and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) and to disappear at sufficiently high T or
and to disappear at sufficiently high T or ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) exceeding T* and
exceeding T* and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *. However, in general, the evaluations of T* and
*. However, in general, the evaluations of T* and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * in conventional tensile tests using unnotched bulk specimens involve appreciable ambiguity, because the tensile strength (stress at break) data as a function of T or
* in conventional tensile tests using unnotched bulk specimens involve appreciable ambiguity, because the tensile strength (stress at break) data as a function of T or ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) often show scattering owing to the high susceptibility to inherent flaws.36
often show scattering owing to the high susceptibility to inherent flaws.36
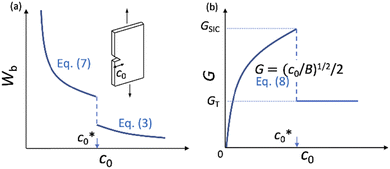
The evaluation of the tearing energy, which is the energy required for crack propagation at given T and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , in rubber-like materials has attracted considerable interest since tearing energy is a key property to characterize the fracture behavior.37–45 A classical tensile fracture test, called the “edge-crack test,” provides an important basis for characterizing the reinforcement effect via SIC.36,46–48 Thomas et al.36,46,47 and Hamed et al.48 investigated the strain energy density at break (Wb) for pre-notched NR specimens as a function of the initial notch length (c0) through tensile experiments. They found that Wb decreased with increasing c0, but with an abrupt fall at a characteristic c0 value (
, in rubber-like materials has attracted considerable interest since tearing energy is a key property to characterize the fracture behavior.37–45 A classical tensile fracture test, called the “edge-crack test,” provides an important basis for characterizing the reinforcement effect via SIC.36,46–48 Thomas et al.36,46,47 and Hamed et al.48 investigated the strain energy density at break (Wb) for pre-notched NR specimens as a function of the initial notch length (c0) through tensile experiments. They found that Wb decreased with increasing c0, but with an abrupt fall at a characteristic c0 value (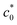 ), whereas this abrupt change was not observed for non-SIC rubber. They regarded this discontinuity as a transition between the tensile fractures with or without a significant SIC effect; at c0 <
), whereas this abrupt change was not observed for non-SIC rubber. They regarded this discontinuity as a transition between the tensile fractures with or without a significant SIC effect; at c0 < 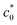 , a sufficiently wide region near the crack tip underwent SIC, resulting in an enhancement of Wb. Hamed et al. investigated the influence of cross-links and filler contents on the transition behavior of NR in edge-crack tests49,50 and discussed the synergetic effects of SIC and filler loading.
, a sufficiently wide region near the crack tip underwent SIC, resulting in an enhancement of Wb. Hamed et al. investigated the influence of cross-links and filler contents on the transition behavior of NR in edge-crack tests49,50 and discussed the synergetic effects of SIC and filler loading.
In this study, we revisit the discontinuous Wb–c0 relationships specific to the SIC rubbers and elucidate that the discontinuity results from the transition of rupture mode between the catastrophic crack growth without an appreciable SIC effect at c0 > 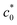 and the crack growth like that under cyclic loading (dc/dn mode) undergoing a significant SIC effect. The occurrence of the cyclic crack growth mode at c0 <
and the crack growth like that under cyclic loading (dc/dn mode) undergoing a significant SIC effect. The occurrence of the cyclic crack growth mode at c0 < 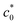 is validated by the characteristic striations on the fracture surface and the result of a separate cyclic loading test using the same specimen. We propose the methodology to quantify the tearing energy enhanced via SIC (GSIC) from the Wb–c0 data and to evaluate T* and
is validated by the characteristic striations on the fracture surface and the result of a separate cyclic loading test using the same specimen. We propose the methodology to quantify the tearing energy enhanced via SIC (GSIC) from the Wb–c0 data and to evaluate T* and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * from the disappearance of the transition feature. We demonstrate that the comparisons of the GSIC, T*, and
* from the disappearance of the transition feature. We demonstrate that the comparisons of the GSIC, T*, and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * values between NR and IR reveal the superior reinforcement effect via SIC in NR.
* values between NR and IR reveal the superior reinforcement effect via SIC in NR.
Theory for the edge-crack test of SIC rubber
Crack growth in rubber has been successfully described using fracture mechanics based on the concept of tearing energy. Tearing energy, G, which is the required energy to drive a crack with a unit area in size, is defined as follows:37,51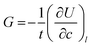 | (1) |
| G = 2kWc | (2) |
Eqn (2) was experimentally validated using the edge-crack test of non-SIC rubbers by varying the initial notch length (c0):52 the strain energy density at break (Wb) is simply proportional to c0−1, reflecting the fact that G is a material constant for non-SIC rubbers. By contrast, SIC rubbers exhibit a discontinuous transition in the Wb–c0 relationships: Wb decreases with increasing c0, and notably, Wb falls abruptly at a characteristic value of c0 (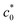 ),36,46–48 which is schematically shown in Fig. 1a. Thomas et al.36,46,47 regarded this abrupt change in Wb at
),36,46–48 which is schematically shown in Fig. 1a. Thomas et al.36,46,47 regarded this abrupt change in Wb at 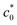 as a transition in the rupture mechanism; at c0 >
as a transition in the rupture mechanism; at c0 > 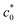 , no significant SIC occurs ahead of the advancing crack tip of the specimens, resulting in the catastrophic crack growth process observed in the non-SIC rubbers. At c0 <
, no significant SIC occurs ahead of the advancing crack tip of the specimens, resulting in the catastrophic crack growth process observed in the non-SIC rubbers. At c0 < 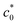 , a sufficiently large SIC region emerged near the crack tip, preventing or postponing the catastrophic crack growth process. At c0 >
, a sufficiently large SIC region emerged near the crack tip, preventing or postponing the catastrophic crack growth process. At c0 > 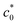 without a significant SIC effect, when the failure follows the ordinary tearing mode, the c0 dependence of Wb can be expressed by eqn (2) as follows:
without a significant SIC effect, when the failure follows the ordinary tearing mode, the c0 dependence of Wb can be expressed by eqn (2) as follows:
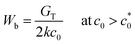 | (3) |
| G = 2kW(c0 + Δc) | (4) |
| Δc = BG2 | (5) |
| Δc = 4k2B (c0 + Δc)2W2 | (6) |
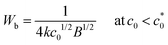 | (7) |
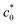 and c0 <
and c0 < 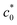 using eqn (3) and (7), respectively.
using eqn (3) and (7), respectively.
The Wb values below 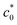 are significantly larger than those beyond
are significantly larger than those beyond 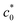 , reflecting the enhancement effect of SIC on the tearing energy. However, the corresponding effect is yet to be quantified from the Wb–c0 data. Therefore, we extend the analysis to quantify the tearing energy enhanced by the SIC effect (GSIC). Eqn (4) is expressed using eqn (7) by eliminating k as follows:
, reflecting the enhancement effect of SIC on the tearing energy. However, the corresponding effect is yet to be quantified from the Wb–c0 data. Therefore, we extend the analysis to quantify the tearing energy enhanced by the SIC effect (GSIC). Eqn (4) is expressed using eqn (7) by eliminating k as follows:
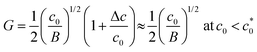 | (8) |
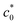 , reflecting the feature of the dc/dn mode (eqn (5); Δc = BG2). When c0 exceeds
, reflecting the feature of the dc/dn mode (eqn (5); Δc = BG2). When c0 exceeds 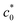 , G is expected to drop abruptly to GT in eqn (3) because the fracture occurs via catastrophic crack growth (ordinary tear manner); there is no significant SIC near the crack tip. Fig. 1b schematically illustrates the c0 dependence of G in this scenario. The maximum value of G at
, G is expected to drop abruptly to GT in eqn (3) because the fracture occurs via catastrophic crack growth (ordinary tear manner); there is no significant SIC near the crack tip. Fig. 1b schematically illustrates the c0 dependence of G in this scenario. The maximum value of G at 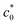 can be regarded as the characteristic tearing energy enhanced by the SIC effect (GSIC). In the case of non-SIC rubber, G in cyclic crack growth which is a subcritical process is significantly smaller than GT. In the edge-crack tensile tests of SIC rubber, G in cyclic crack growth mode can be larger than GT, because the SIC near the crack tip pronouncedly enhances G at c0 <
can be regarded as the characteristic tearing energy enhanced by the SIC effect (GSIC). In the case of non-SIC rubber, G in cyclic crack growth which is a subcritical process is significantly smaller than GT. In the edge-crack tensile tests of SIC rubber, G in cyclic crack growth mode can be larger than GT, because the SIC near the crack tip pronouncedly enhances G at c0 < 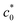 whereas it is suppressed at c0 >
whereas it is suppressed at c0 > 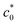 .
.
Investigations of the Wb–c0 relationships with varying ambient temperatures (T) and strain rates (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) (Fig. 1a) provide a basis for discussing the effects of T and
) (Fig. 1a) provide a basis for discussing the effects of T and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) on GSIC. In particular, the corresponding data also enable us to evaluate T* and
on GSIC. In particular, the corresponding data also enable us to evaluate T* and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * (the upper limits for the SIC effect on tearing energy) because at T > T* and
* (the upper limits for the SIC effect on tearing energy) because at T > T* and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) >
> ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *, the transition feature vanishes, and only the ordinary tearing mode (G ≈ GT; eqn (3)) appears over the entire c0 range.
*, the transition feature vanishes, and only the ordinary tearing mode (G ≈ GT; eqn (3)) appears over the entire c0 range.
Experimental section
Materials
The following compositions were employed for the preparation of the specimens designated as NR-A and IR-A: NR rubber gum (ribbed smoked sheet, RSS#3) or IR gum (IR2200, ENEOS Material Co.), stearic acid (2 phr, i.e., 2 g per 100 g of gum rubber), ZnO (5.0 phr), polymerized 2,2,4-trimethyl-1,2-dihydroquinoline (TMDQ, 0.3 phr), N-1,3-dimethylbutyl-N′-phenyl-p-phenylenediamine (6PPD, 1 phr), N-cyclohexyl-2-benzothiazole sulfenamide (CBS, 1.5 phr), and sulfur (1.5 phr).First, gum, stearic acid, ZnO, TMQD, and 6PPD were mixed, and the mixture was sheared for 2 min in a chamber at a controlled temperature of 80 °C. Next, CBS and sulfur were added for vulcanization, and the mixtures were subjected to shear for 1.5 min at 80 °C. The mixtures were further sheared using an open-roll mill for 5 min at 60 °C. Finally, specimen sheets were prepared using a hot press method at 160 °C for 8 and 13 min for NR and IR, respectively. We used the NR-A and IR-A specimens for the edge-crack tests in order to investigate the enhancement effects via SIC on tearing energy at various T and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) values.
values.
For comparing the results of the edge-crack and the cyclic loading tests, we employed the NR-B specimen which had almost the same compositions as NR-A but slightly differed in curatives: 1,3-diphenylguanidine (DPG, 0.35 phr), N-cyclohexyl-2-benzothiazole sulfenamide (CBS, 1.77 phr) and sulfur (1.4 phr). The processing procedure for the sheet specimens of NR-B was the same as that for NR-A.
NR-A and IR-A exhibited the same magnitudes of equilibrium swelling in toluene within the experimental error, indicating that they have similar cross-link densities. The average molecular weights between neighboring cross-links were estimated to be 7200 g mol−1 for NR-A and IR-A and 6400 g mol−1 for NR-B from the equilibrium swelling degrees using the Flory–Rehner equation.55
A styrene butadiene rubber (SBR) specimen was prepared as a non-SIC rubber for comparison, using SBR gum (#1500, ENEOS Material Co.). The compositions of stearic acid, ZnO, TMQD, 6PPD and sulfur were identical to those of NR-A. Diphenyl guanidine (1 phr), 2-benzothiazolyl disulfide (0.6 phr), and N-oxydiethylene-2-benzothiazole sulfenamide (0.6 phr) were used as cure accelerators. The specimen sheets were made using the same method as for NR-A at 160 °C for 6 min.
Edge-crack test
A tensile strip specimen (5 mm wide × 50 mm high × 2 mm thick) was used. An initial crack was inserted into the center of a single side of the tensile strip specimen using a specially designed cutting apparatus. The initial crack length (c0) was varied from 0.25 to 3.5 mm in an approximately 0.25 mm interval. Tensile measurements were performed using a tensile testing machine (Shimadzu AGX-Plus 1 kN and Hydroshot 1 kN) equipped with a controlled temperature chamber. To investigate the effect of T, T was varied from 25 °C to 90 °C, and the measurements were conducted at a fixed strain rate of 0.5 s−1. To examine the effect of![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ,
, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) was varied from 0.005 to 500 s−1 at 25 °C.
was varied from 0.005 to 500 s−1 at 25 °C.
The tensile force at break (fb) of a pre-notched specimen with an initial notch length (c0) was measured under the given conditions of T and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . The tearing energy (G) was calculated using eqn (2) corresponding to eqn (4) with Δc/c0 ≪ 1. The strain energy density at break (Wb) and λ in eqn (2) were obtained with the fb value using the W–σ and σ–λ relationships for the corresponding unnotched bulk specimen.
. The tearing energy (G) was calculated using eqn (2) corresponding to eqn (4) with Δc/c0 ≪ 1. The strain energy density at break (Wb) and λ in eqn (2) were obtained with the fb value using the W–σ and σ–λ relationships for the corresponding unnotched bulk specimen.
Cyclic loading test
A cyclic loading test was conducted for the pre-notched NR-B specimens (5 mm wide × 50 mm high × 2 mm thick) using a tensile tester (Shimadzu AGX-Plus 1kN). The c0 values were varied from 0.3 to 1.0 mm. The tensile specimen was cyclically loaded and unloaded between the desired extension length and zero position for 5 to 10 cycles at a crosshead speed of 200 mm min−1 and at 25 °C. The maximum stretch was varied between 3.6 and 7.0 depending on the pre-notch length of each specimen. The maximum force during each cycle was recorded, enabling the evaluation of the elastically stored energy density (Wi) and strain function (ki) for the i-th cycle, using the W–σ and σ–λ relationships for the unnotched bulk NR-B specimen. After the cyclic loading test, the initial crack length (c0) and the increment of crack length (Δci) in each cycle were precisely measured utilizing a digital video microscope as described below.Observation of the fracture surface
The fracture surface of the specimens was observed using a digital microscope (Hi-rox Co., RH-2000) equipped with a variable lighting adopter. The c0 values were measured from the fracture surface.Wide-angle X-ray scattering measurements
WAXS measurements for the unnotched bulk NR-A and IR-A specimens were performed using synchrotron radiation at beamline BL03XU of SPring-8 (JASRI). The X-ray wavelength was 0.1 nm, and the camera length was 130 mm. A CMOS camera (Hamamatsu Photonics K.K. Orca Flash-4.0) equipped with an image intensifier was used as the detector. Specially designed in-house dumbbell specimens were stretched at a strain rate of 0.1 s−1. Sequential WAXS images during the stretching process were recorded every second after the sample extension started. The X-ray scattering intensity at scattering vector q as a function of stretch (λ), Iobsx(q, λ), was obtained from the two-dimensional WAXS image by integrating β = ±10° (β: azimuth angle) after correcting for the effects of the dark noise of the detector, air scattering, and sample thickness. Because no reflection from the SIC crystals was observed at λ < 2, the corresponding scattering intensity, IOBSx (q, λ < 2), was regarded as the contribution from the amorphous phase. The scattering intensity from SIC crystals, Ix, was evaluated as follows:| Ix(q, λ) = IOBSx (q, λ) − IOBSx (q, λ < 2) | (9) |
Results and discussion
Non-SIC rubber in the edge-crack test
Fig. 2a illustrates Wb as a function of c0 for a non-SIC rubber, styrene butadiene rubber (SBR), at 25 °C and a strain rate of 0.60 s−1 obtained using the edge-crack test. Wb decreased monotonically with increasing c0. The G values calculated using the Wb data and eqn (2) are constant in the range of c0 ≤ 3.55 mm examined here (Fig. 2b). It is naturally expected because G for the non-SIC rubber can be assumed as a c0-independent critical tearing energy (GT) for the onset of catastrophic crack growth at given T and![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . Importantly, the constancy of G also validates the applicability of eqn (2) in the calculation of G for the specimens of c0 ≤ 3.55 mm in this experiment.
. Importantly, the constancy of G also validates the applicability of eqn (2) in the calculation of G for the specimens of c0 ≤ 3.55 mm in this experiment.
 | ||
| Fig. 2 (a) Strain energy density at break (Wb) as a function of the initial notch length (c0) for SBR (non-SIC rubber) at 25 °C and a strain rate of 0.60 s−1 in the edge-crack test. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). | ||
SIC rubber in the edge-crack test
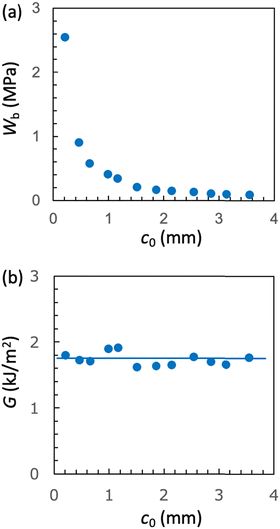
Fig. 3a shows the plots of Wbversus c0 for a SIC rubber, NR-B, at 25 °C and a strain rate of 0.11 s−1 in the edge-crack test. Wb decreased with increasing c0 but with an abrupt drop at a characteristic c0 value of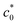 ≈ 1.8 mm, in contrast to the continuous change in a non-SIC rubber (Fig. 2a). The force–displacement data used for the evaluation of Wb at each c0 for NR-B are shown in the ESI.† The Wb–c0 relationship was qualitatively similar to the observations for NR in earlier studies36,46–48 and that shown in Fig. 1a. The c0 dependence of G, calculated from the Wb data and eqn (2), shown in Fig. 3b indicates that G increases with increasing c0 at c0 <
≈ 1.8 mm, in contrast to the continuous change in a non-SIC rubber (Fig. 2a). The force–displacement data used for the evaluation of Wb at each c0 for NR-B are shown in the ESI.† The Wb–c0 relationship was qualitatively similar to the observations for NR in earlier studies36,46–48 and that shown in Fig. 1a. The c0 dependence of G, calculated from the Wb data and eqn (2), shown in Fig. 3b indicates that G increases with increasing c0 at c0 < 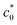 , whereas G exhibits a discontinuous change at
, whereas G exhibits a discontinuous change at 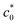 and tends to become constant at a high c0, which agrees qualitatively with Fig. 1b. Importantly, the data at c0 <
and tends to become constant at a high c0, which agrees qualitatively with Fig. 1b. Importantly, the data at c0 < 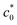 obey eqn (8), i.e., G = (c0/B)1/2/2, as indicated by the solid line in the figure which is obtained using B as an adjustable parameter (B = 3.65 × 10−13 N−2 m3). The dashed solid line depicts the result of eqn (8) using the B value (B = 4.06 × 10−13 N−2 m3) which is separately evaluated from the cyclic loading test for the same NR-B specimen at 25 °C: the B value is obtained using eqn (6) from the slope of the linear regression in the plots of Δc versus 4k2(c0 + Δc)2W2 (Fig. 3c). The B value obtained by the cyclic loading test satisfactorily agrees with the B value fitted to the G–c0 data, indicating without ambiguity that the fracture at c0 <
obey eqn (8), i.e., G = (c0/B)1/2/2, as indicated by the solid line in the figure which is obtained using B as an adjustable parameter (B = 3.65 × 10−13 N−2 m3). The dashed solid line depicts the result of eqn (8) using the B value (B = 4.06 × 10−13 N−2 m3) which is separately evaluated from the cyclic loading test for the same NR-B specimen at 25 °C: the B value is obtained using eqn (6) from the slope of the linear regression in the plots of Δc versus 4k2(c0 + Δc)2W2 (Fig. 3c). The B value obtained by the cyclic loading test satisfactorily agrees with the B value fitted to the G–c0 data, indicating without ambiguity that the fracture at c0 < 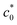 proceeds similarly to the crack growth under cyclic loading.
proceeds similarly to the crack growth under cyclic loading.
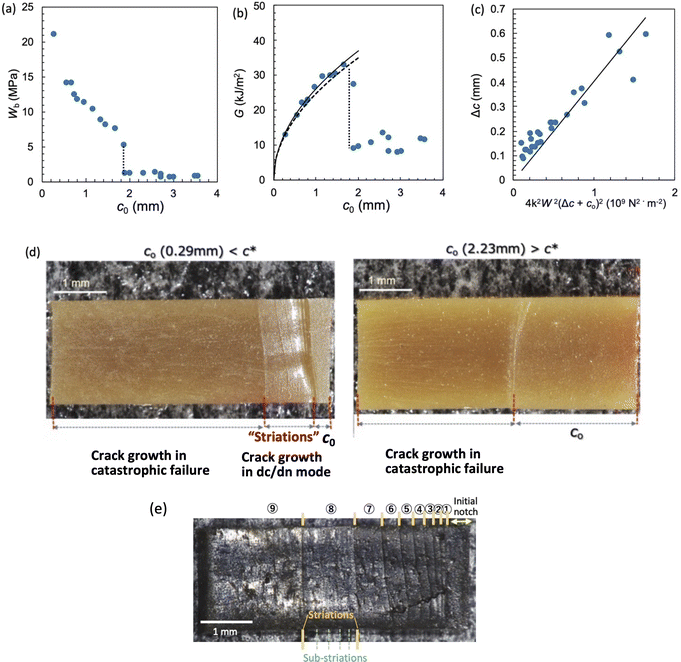 | ||
Fig. 3 (a) Strain energy density at break (Wb) as a function of the initial notch length (c0) for NR-B at 25 °C and a strain rate of 0.11 s−1 in the edge-crack test. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). The dashed line indicates the position of 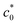 at which an abrupt change occurs. The solid line represents the fitted curve of eqn (8) to the data using B = 3.65 × 10−13 N−2 m3. The dashed solid line depicts the curve of eqn (8) with the B value (4.06 × 10−13 N−2 m3) obtained using the cyclic loading test for the same specimen. (c) Increment of crack length (Δc) as a function of 4k2B (c0 + Δc)2W2 for NR-B in the cyclic loading test. The line indicates the result of the linear regression. The slope corresponds to the B value (4.06 × 10−13 N−2 m3). (d) Fracture surfaces for NR-B of c0 = 0.29 mm (< at which an abrupt change occurs. The solid line represents the fitted curve of eqn (8) to the data using B = 3.65 × 10−13 N−2 m3. The dashed solid line depicts the curve of eqn (8) with the B value (4.06 × 10−13 N−2 m3) obtained using the cyclic loading test for the same specimen. (c) Increment of crack length (Δc) as a function of 4k2B (c0 + Δc)2W2 for NR-B in the cyclic loading test. The line indicates the result of the linear regression. The slope corresponds to the B value (4.06 × 10−13 N−2 m3). (d) Fracture surfaces for NR-B of c0 = 0.29 mm (<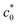 ) and c0 = 2.23 mm (> ) and c0 = 2.23 mm (>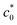 ). For c0 = 0.29 mm, the fine striation lines characteristic of the crack growth via the dc/dn mode are observed. The zone “c0” indicates the initial notch area. (e) Fracture surfaces including the striations for NR-B in the cyclic loading test. ). For c0 = 0.29 mm, the fine striation lines characteristic of the crack growth via the dc/dn mode are observed. The zone “c0” indicates the initial notch area. (e) Fracture surfaces including the striations for NR-B in the cyclic loading test. | ||
The different rupture modes at c0 > 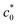 and c0 <
and c0 < 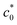 are also appreciable when comparing the fracture surfaces of the corresponding specimens, as shown in Fig. 3d. The fracture surface of the edge-crack specimen with c0 = 0.29 mm (<
are also appreciable when comparing the fracture surfaces of the corresponding specimens, as shown in Fig. 3d. The fracture surface of the edge-crack specimen with c0 = 0.29 mm (<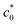 ) has characteristic marks (fine striation lines) that show the positions of the crack tip during the incremental growth of a crack. Similar striations are observed in the failure surfaces of NR in the cyclic fatigue tests,19,20 and Fig. 3e shows the striations accompanied by the sub-striations in the failure surface of NR-B in the cyclic loading tests. As the corresponding features are not observed in the non-SIC rubbers, they are attributed to SIC.19,20 The fracture surface of the edge-crack specimen of c0 = 2.23 mm (>
) has characteristic marks (fine striation lines) that show the positions of the crack tip during the incremental growth of a crack. Similar striations are observed in the failure surfaces of NR in the cyclic fatigue tests,19,20 and Fig. 3e shows the striations accompanied by the sub-striations in the failure surface of NR-B in the cyclic loading tests. As the corresponding features are not observed in the non-SIC rubbers, they are attributed to SIC.19,20 The fracture surface of the edge-crack specimen of c0 = 2.23 mm (>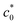 ) has no indication of striation (Fig. 3d). The fracture surface including the striations at c0 <
) has no indication of striation (Fig. 3d). The fracture surface including the striations at c0 < 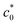 in the edge-crack tests indicates that SIC postpones the catastrophic crack growth.
in the edge-crack tests indicates that SIC postpones the catastrophic crack growth.
The successful fit of eqn (8) to the G–c0 data using the B value obtained by the cyclic loading test (Fig. 3b) and the striation characteristic of the cyclic crack growth (Fig. 3d) validate the theoretical interpretation of the data described in the previous section. The considerably different G–c0 relationships beyond and above 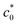 are attributed to a transition of the rupture mode. The rupture at c0 >
are attributed to a transition of the rupture mode. The rupture at c0 > 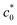 without significant SIC near the crack tip is governed by the ordinary tear mode. At c0 <
without significant SIC near the crack tip is governed by the ordinary tear mode. At c0 < 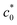 , the crack grows through a sufficiently large crystalline region, and the corresponding fracture proceeds similarly to the crack growth under cyclic loading, characterized by eqn (8). The maximum G value at
, the crack grows through a sufficiently large crystalline region, and the corresponding fracture proceeds similarly to the crack growth under cyclic loading, characterized by eqn (8). The maximum G value at 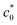 in Fig. 3b is considered a measure of the tearing energy enhanced by SIC (GSIC). The quasi-plateau G value at c0 >
in Fig. 3b is considered a measure of the tearing energy enhanced by SIC (GSIC). The quasi-plateau G value at c0 > 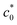 is regarded as a critical tearing energy for the onset of catastrophic crack growth without the SIC effect (GT). In Fig. 3b, the GSIC is evaluated to be 33 kJ m−2, while the GT is estimated to be 10 kJ m−2 from the average of the data at c0 >
is regarded as a critical tearing energy for the onset of catastrophic crack growth without the SIC effect (GT). In Fig. 3b, the GSIC is evaluated to be 33 kJ m−2, while the GT is estimated to be 10 kJ m−2 from the average of the data at c0 > 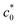 .
.
Effect of ambient temperature T
Fig. 4a and 5a show the c0 dependence of Wb at various ambient temperatures (T) for NR-A and IR-A, respectively. A discontinuous gap in Wb at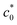 is observed at a sufficiently low T, and
is observed at a sufficiently low T, and 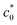 decreases with increasing T for both NR and IR. Importantly, no discontinuous change in Wb occurs when T exceeds a characteristic temperature (T*), and the T* values for NR and IR are appreciably different and are estimated to be 80 and 60 °C, the highest temperature at which the abrupt change of Wb is observed. At T > T* the SIC kinetics is so slow that SIC cannot occur sufficiently at
decreases with increasing T for both NR and IR. Importantly, no discontinuous change in Wb occurs when T exceeds a characteristic temperature (T*), and the T* values for NR and IR are appreciably different and are estimated to be 80 and 60 °C, the highest temperature at which the abrupt change of Wb is observed. At T > T* the SIC kinetics is so slow that SIC cannot occur sufficiently at ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) of interest to enhance the tearing energy.
of interest to enhance the tearing energy.
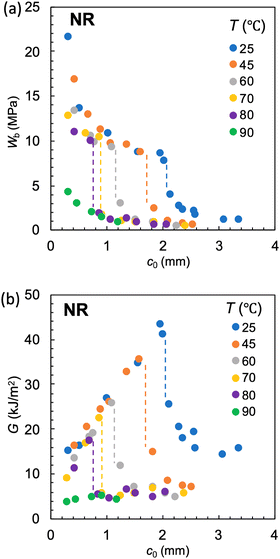 | ||
Fig. 4 (a) Strain energy density at break (Wb) as a function of the initial notch length (c0) at various ambient temperatures (T) for NR-A at a strain rate of 0.5 s−1. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). The dashed lines indicate the position of 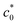 at which an abrupt change occurs for each T. No abrupt change is observed at 90 °C. at which an abrupt change occurs for each T. No abrupt change is observed at 90 °C. | ||
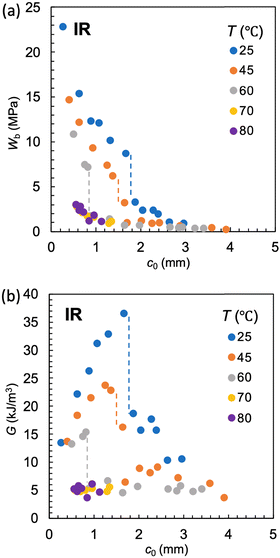 | ||
Fig. 5 (a) Strain energy density at break (Wb) as a function of the initial notch length (c0) at various ambient temperatures (T) for IR-A at a strain rate of 0.5 s−1. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). The dashed lines indicate the position of 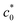 at which an abrupt change occurs for each T. No abrupt change is observed at T ≥ 70 °C. at which an abrupt change occurs for each T. No abrupt change is observed at T ≥ 70 °C. | ||
The G vs. c0 plots obtained using eqn (2) and the data in Fig. 4a and 5a are shown in Fig. 4b and 5b, respectively. At T < T*, the G values have the maximum at 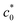 , allowing the evaluation of the GSIC at each T. GSIC tends to decrease with increasing T in both NR and IR. At T > T*, only GT is obtained, reflecting the absence of an appreciable SIC effect. In contrast to GSIC, GT is almost independent of T at T ≥ 45 °C. Thus, this method reveals the upper limit temperature (T*), beyond which the effect of SIC on tearing energy vanishes, and the T-dependence of GSIC. The G data in the vicinity of
, allowing the evaluation of the GSIC at each T. GSIC tends to decrease with increasing T in both NR and IR. At T > T*, only GT is obtained, reflecting the absence of an appreciable SIC effect. In contrast to GSIC, GT is almost independent of T at T ≥ 45 °C. Thus, this method reveals the upper limit temperature (T*), beyond which the effect of SIC on tearing energy vanishes, and the T-dependence of GSIC. The G data in the vicinity of 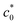 at c0 >
at c0 > 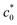 in T < T* tend to be larger than the GT value obtained at a high c0. This tendency implies that a subtle degree of the SIC effect may exist at c0 slightly beyond
in T < T* tend to be larger than the GT value obtained at a high c0. This tendency implies that a subtle degree of the SIC effect may exist at c0 slightly beyond 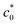 although most of the effect vanishes when c0 exceeds
although most of the effect vanishes when c0 exceeds 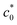 .
.
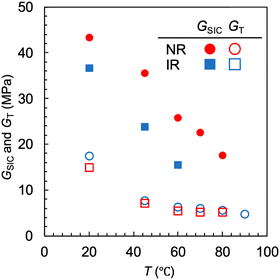
Fig. 6 shows the plots of GSIC and GT obtained in Fig. 4b and 5b against T for NR-A and IR-A. The GT values are nearly insensitive to T, except for the data at 25 °C, and there is no appreciable difference between these two rubbers. In contrast, for each rubber, the GSIC value at a given T is several times larger than GT, whereas GSIC decreases with increasing T. These results indicate that G is significantly enhanced by hardening via SIC near the crack tip, whereas this reinforcement effect decreases with a decreasing crystallinity index. Notably, these two rubbers are considerably different in T* and GSIC; T* for NR-A (80 °C) is approximately 20 °C higher than that for IR-A (60 °C), indicating that the reinforcement effect in NR emerges in a broader temperature range. Furthermore, the GSIC value for NR at each T is significantly larger than that for IR.
The effects of T on SIC are separately investigated using WAXS experiments using unnotched bulk NR-A and IR-A specimens. Fig. 7a and b show the peak area of the crystal (200) diffraction (I200) as a function of tensile strain at various T values. The evolution of I200 beyond the threshold strain reflects a continuous increase in the crystallinity index via SIC. The SIC onset strain (εSIC) was estimated from the onset of the evolution of I200. For both rubbers, as T increases, εSIC increases, and I200 decreases when compared at a given strain. At a sufficiently high T, I200 remains zero over the entire strain range, indicating no occurrence of SIC; SIC can no longer be observed even at a high strain at 110 and 80 °C for NR-A and IR-A, respectively, which explains no occurrence of significant SIC at the crack tip in the edge-crack specimens at T > T*. The upper-limit temperature for SIC (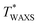 ), the highest temperature for the finite evolution of I200, is evaluated to be 90 and 70 °C for NR-A and IR-A, respectively. The
), the highest temperature for the finite evolution of I200, is evaluated to be 90 and 70 °C for NR-A and IR-A, respectively. The 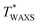 for NR-A is approximately 20 °C higher than that for IR-A, which is comparable to the difference in T* (Fig. 6). This agreement validates the evaluation of T* as the upper-limit ambient temperature in edge-crack tests. For each rubber, T* is slightly lower than
for NR-A is approximately 20 °C higher than that for IR-A, which is comparable to the difference in T* (Fig. 6). This agreement validates the evaluation of T* as the upper-limit ambient temperature in edge-crack tests. For each rubber, T* is slightly lower than 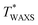 , probably because of the finite difference in the magnitudes of the effective strain and strain rate in the two measurements; the local strain and strain rate around the crack tip are higher than those in the tensile test of the unnotched bulk specimens. In addition,
, probably because of the finite difference in the magnitudes of the effective strain and strain rate in the two measurements; the local strain and strain rate around the crack tip are higher than those in the tensile test of the unnotched bulk specimens. In addition, 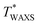 detects the threshold of SIC at the molecular level, while T* reflects the threshold of the SIC effect on macroscopic tearing energy. The emergence of the SIC effect on bulk mechanical properties requires a finite degree of crystallization. This also explains the relationship of
detects the threshold of SIC at the molecular level, while T* reflects the threshold of the SIC effect on macroscopic tearing energy. The emergence of the SIC effect on bulk mechanical properties requires a finite degree of crystallization. This also explains the relationship of 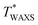 > T* for each rubber.
> T* for each rubber.
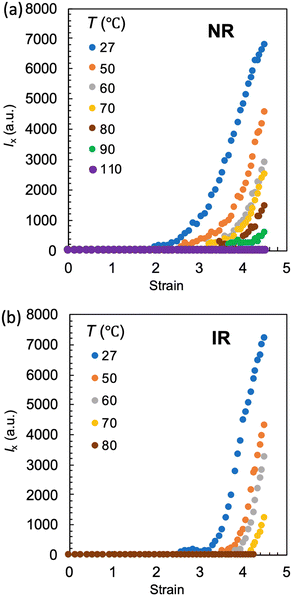 | ||
| Fig. 7 Scattering intensity of the (200) diffraction of the SIC crystal as a function of the imposed tensile strain for (a) NR-A and (b) IR-A at various ambient temperatures. | ||
In each rubber, I200 decreases with increasing T when compared at the same strain, indicating that the crystallinity index at a given strain decreases as T increases. This result explains why the GSIC decreases with increasing T for each rubber (Fig. 6).
The effects of T on the SIC for NR and IR have been studied using in-situ WAXS experiments, mainly in the sustained state with a constant strain beyond εSIC or by analyzing the stress–strain relationships.23–29 The reported values of the melting temperature of the SIC crystal (Tf) of IR range from 60 to more than 100 °C depending on the magnitude of the imposed constant strain. The 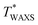 value (70 °C) for IR-A falls within the range of the reported values.
value (70 °C) for IR-A falls within the range of the reported values.
Effect of strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/h3_i_char_e0a1.gif)
Fig. 8a and 9a show the c0 dependence of Wb on NR-A and IR-A at various strain rates (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ). The ambient temperature is 25 °C. The G–c0 relationships calculated from these data are shown in Fig. 8b and 9b. For NR and IR, the effects of
). The ambient temperature is 25 °C. The G–c0 relationships calculated from these data are shown in Fig. 8b and 9b. For NR and IR, the effects of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) on the Wb–c0 and G–c0 relationships are similar to those of T (Fig. 4 and 5). A discontinuous gap in Wb and G at
on the Wb–c0 and G–c0 relationships are similar to those of T (Fig. 4 and 5). A discontinuous gap in Wb and G at 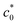 is observed at a sufficiently low
is observed at a sufficiently low ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , and the
, and the 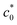 value decreases with increasing
value decreases with increasing ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . The discontinuous feature vanishes when
. The discontinuous feature vanishes when ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) exceeds the threshold value
exceeds the threshold value ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *. We regard the maximum G value at
*. We regard the maximum G value at 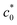 as the GSIC at each
as the GSIC at each ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , and the average of the quasi-plateau values at c0 >
, and the average of the quasi-plateau values at c0 > 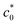 as the GT.
as the GT.
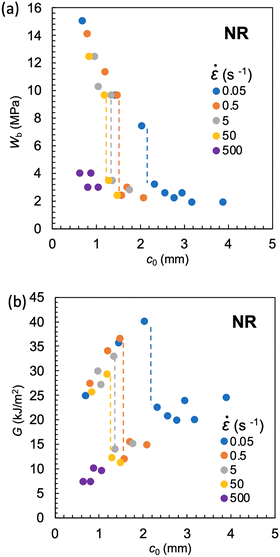 | ||
Fig. 8 (a) Strain energy density at break (Wb) as a function of the initial notch length (c0) at various strain rates (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) for NR-A at 25 °C. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). The dashed lines indicate the position of ) for NR-A at 25 °C. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). The dashed lines indicate the position of 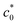 at which an abrupt change occurs for each at which an abrupt change occurs for each ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . No abrupt change is observed at 500 s−1. . No abrupt change is observed at 500 s−1. | ||
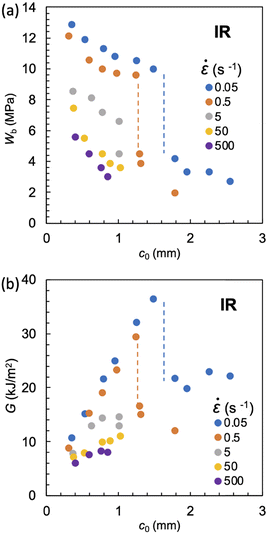 | ||
Fig. 9 (a) Strain energy density at break (Wb) as a function of the initial notch length (c0) at various strain rates (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) for IR-A at 25 °C. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). The dashed lines indicate the position of ) for IR-A at 25 °C. (b) The c0 dependence of tearing energy (G) calculated using the data in (a) with eqn (2). The dashed lines indicate the position of 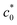 at which an abrupt change occurs for each at which an abrupt change occurs for each ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . No abrupt change is observed at . No abrupt change is observed at ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) > 5 s−1. > 5 s−1. | ||
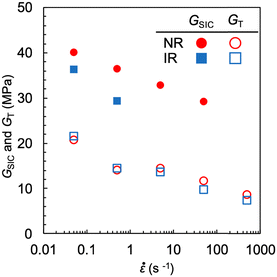
Fig. 10 shows the plots of GSIC and GT against ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) for NR-A and IR-A. An appreciable reinforcement of SIC on tearing energy (GSIC > GT) is observed at
for NR-A and IR-A. An appreciable reinforcement of SIC on tearing energy (GSIC > GT) is observed at ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) <
< ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *, while it vanishes at
*, while it vanishes at ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) >
> ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *. At
*. At ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) >
> ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *, the imposed strain rate is so high that the matrix around the crack tip cannot have enough time to undergo a sufficient degree of SIC, resulting in a catastrophic fracture governed by the GT. As this result originates from the competition between the SIC and strain rate,
*, the imposed strain rate is so high that the matrix around the crack tip cannot have enough time to undergo a sufficient degree of SIC, resulting in a catastrophic fracture governed by the GT. As this result originates from the competition between the SIC and strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *depends on T of interest. For convenience, we regard the
*depends on T of interest. For convenience, we regard the ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * from the highest
* from the highest ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) value at which finite discontinuity is observed in the G–c0 relationship because the data as a function of
value at which finite discontinuity is observed in the G–c0 relationship because the data as a function of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) are discrete. Notably, the
are discrete. Notably, the ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * value for NR-A (50 s−1) is considerably higher than that for IR-A (0.5 s−1). There exists some uncertainty in the
* value for NR-A (50 s−1) is considerably higher than that for IR-A (0.5 s−1). There exists some uncertainty in the ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * value for IR-A because of the ambiguity of the discontinuous feature in the data at 5 s−1: Finite discontinuity is appreciable in Wb (Fig. 9a) but not in G (Fig. 9b). The
* value for IR-A because of the ambiguity of the discontinuous feature in the data at 5 s−1: Finite discontinuity is appreciable in Wb (Fig. 9a) but not in G (Fig. 9b). The ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * value for IR-A may be slightly higher than 0.5 s−1. Nevertheless, we can conclude safely that
* value for IR-A may be slightly higher than 0.5 s−1. Nevertheless, we can conclude safely that ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * for NR-A is at least one order of magnitude higher than that for IR-A because of a definite difference in the discontinuity in the data at 50 s−1 between them. In addition, the GSIC for NR-A is larger than that for IR-A when compared at the same
* for NR-A is at least one order of magnitude higher than that for IR-A because of a definite difference in the discontinuity in the data at 50 s−1 between them. In addition, the GSIC for NR-A is larger than that for IR-A when compared at the same ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . As in the case of the T effect (Fig. 6), the finite superiority of NR relative to IR in reinforcing ability via SIC is appreciable in the effect of
. As in the case of the T effect (Fig. 6), the finite superiority of NR relative to IR in reinforcing ability via SIC is appreciable in the effect of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) .
.
Several researchers have studied the effect of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) on SIC for NR or IR using in situ WAXS experiments.31–35 Recently, Kitamura et al.35 showed that the times required for the occurrence of finite SIC in NR and IR were comparable and less than 0.01 s. Candau et al.34 also reported that the finite superiority of NR relative to IR in SIC ability (observed at slow strain rates) disappeared at high strain rates. According to their results, the occurrence of finite SIC and the disappearance of the difference in the reinforcement effect between NR and IR are expected at high strain rates of more than 100 s−1. However, the
on SIC for NR or IR using in situ WAXS experiments.31–35 Recently, Kitamura et al.35 showed that the times required for the occurrence of finite SIC in NR and IR were comparable and less than 0.01 s. Candau et al.34 also reported that the finite superiority of NR relative to IR in SIC ability (observed at slow strain rates) disappeared at high strain rates. According to their results, the occurrence of finite SIC and the disappearance of the difference in the reinforcement effect between NR and IR are expected at high strain rates of more than 100 s−1. However, the ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * values (50 s−1 for NR-A and 0.5 s−1 for IR-A) in the edge-crack tests are appreciably lower than this expectation, and they were considerably different between NR-A and IR-A. These discrepancies indicate that the threshold for the emergence of the SIC effect on the macroscopic mechanical strength (reflected in the edge crack tests) is different from the onset of SIC at the molecular level (detected by WAXS): the onset of the finite mechanical reinforcement effect requires a significant degree of crystallization. It should also be noted that the magnitudes of local strain and strain-rate near the crack tip are considerably larger than those in the unnotched bulk materials used in the WAXS measurements, when compared at the same degree of imposed macroscopic strain.
* values (50 s−1 for NR-A and 0.5 s−1 for IR-A) in the edge-crack tests are appreciably lower than this expectation, and they were considerably different between NR-A and IR-A. These discrepancies indicate that the threshold for the emergence of the SIC effect on the macroscopic mechanical strength (reflected in the edge crack tests) is different from the onset of SIC at the molecular level (detected by WAXS): the onset of the finite mechanical reinforcement effect requires a significant degree of crystallization. It should also be noted that the magnitudes of local strain and strain-rate near the crack tip are considerably larger than those in the unnotched bulk materials used in the WAXS measurements, when compared at the same degree of imposed macroscopic strain.
Summary
The present study demonstrates the availability of edge-crack tests to quantify the enhancement effect of SIC on tearing energy and its upper limits of T and![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) for the emergence. In the edge-crack tests using the initial notch length (c0) as a variable, the pre-notched SIC rubber specimens exhibit a discontinuous change in the strain energy density at break (Wb) at a characteristic c0 value (
for the emergence. In the edge-crack tests using the initial notch length (c0) as a variable, the pre-notched SIC rubber specimens exhibit a discontinuous change in the strain energy density at break (Wb) at a characteristic c0 value (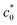 ), as a result of the transition in the rupture mechanism between the ordinary tear mode, simply governed by GT at c0 >
), as a result of the transition in the rupture mechanism between the ordinary tear mode, simply governed by GT at c0 > 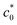 , and the cyclic growth mode via a significant degree of SIC near the crack tip at c0 <
, and the cyclic growth mode via a significant degree of SIC near the crack tip at c0 < 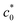 . We validated the fracture via cyclic growth mode at c0 <
. We validated the fracture via cyclic growth mode at c0 < 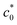 by confirming the distinctive relationship G = (c0/B)1/2/2, with the B value separately obtained using the cyclic loading test, and by observing the characteristic striations on the fracture surface.
by confirming the distinctive relationship G = (c0/B)1/2/2, with the B value separately obtained using the cyclic loading test, and by observing the characteristic striations on the fracture surface.
The maximum G value at 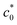 , calculated from the Wb–c0 data by extending Thomas’ theory, is regarded as a measure of the tearing energy enhanced by SIC (GSIC). The magnitude of the GSIC is several times larger than that of the GT, reflecting that the crack propagates through the matrix hardened by crystallization. The GSIC values decrease with increasing T and
, calculated from the Wb–c0 data by extending Thomas’ theory, is regarded as a measure of the tearing energy enhanced by SIC (GSIC). The magnitude of the GSIC is several times larger than that of the GT, reflecting that the crack propagates through the matrix hardened by crystallization. The GSIC values decrease with increasing T and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) due to a reduction in the crystallinity index. The upper limits of T and
due to a reduction in the crystallinity index. The upper limits of T and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) for the finite reinforcement effect via SIC (T* and
for the finite reinforcement effect via SIC (T* and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) *, respectively) are evaluated from the vanishing points of the transition feature.
*, respectively) are evaluated from the vanishing points of the transition feature.
NR exhibits a higher magnitude of GSIC at a given T or ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) than IR, whereas these rubbers show no appreciable difference in GT. NR has an approximately 20 °C higher value of T* and at least one order of magnitude larger value of
than IR, whereas these rubbers show no appreciable difference in GT. NR has an approximately 20 °C higher value of T* and at least one order of magnitude larger value of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * than IR. The WAXS measurements confirm a reduction in the crystallinity index with increasing T and an approximately 20 °C higher upper-limit temperature for the occurrence of SIC in NR. Comparisons using the GSIC, T*, and
* than IR. The WAXS measurements confirm a reduction in the crystallinity index with increasing T and an approximately 20 °C higher upper-limit temperature for the occurrence of SIC in NR. Comparisons using the GSIC, T*, and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) * values reveal that NR is obviously superior to IR in the mechanical reinforcement effect via SIC.
* values reveal that NR is obviously superior to IR in the mechanical reinforcement effect via SIC.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We appreciate Prof. James Busfield at the Queen Mary University of London for the fruitful discussion. This work was partly supported by the JST, CREST grant number JPMJCR2091, Japan. The authors thank Ayano Kozono for her assistance in making the graphs.References
-
J. E. Mark, B. Erman and C. M. Roland, The Science and Technology of Rubber, Academic Press, 2013 Search PubMed
.
-
G. R. Hamed, Engineering with Rubber, ed. A. N. Gent, Carl Hanser Verlag, Munich, 2012, p. 433 Search PubMed
.
-
S. Kohjiya and Y. Ikeda, Chemistry, Manufacture and Applications of Natural Rubber, Woodhead Publishing, 2nd edn, 2021 Search PubMed
.
- J. R. Katz, Röntgenspektrographische Untersuchungen Am Gedehnten Kautschuk Und Ihre Mögliche Bedeutung Für Das Problem Der Dehnungseigenschaften Dieser Substanz, Naturwissenschaften, 1925, 13(19), 410–416 CrossRef
.
-
K. Brüning, In-Situ Structure Characterization of Elastomers during Deformation and Fracture, Springer, Cham, 2014 Search PubMed
.
- A. N. Gent, S. Kawahara and J. Zhao, Crystallization and Strength of Natural Rubber and Synthetic Cis-1,4-Polyisoprene, Rubber Chem. Technol., 1998, 71(4), 668–678 CrossRef CAS
.
- R. Clamroth and T. Kempermann, Comparison of Methods for the Determination of Tear Strength, Polym. Test., 1986, 6(1), 3–35 CrossRef CAS
.
- M. Tosaka, S. Kohjiya, S. Murakami, S. Poompradub, Y. Ikeda, S. Toki, I. Sics and B. S. Hsiao, Effect of Network-Chain Length on Strain-Induced Crystallization of NR and IR Vulcanizates, Rubber Chem. Technol., 2004, 77(4), 711–723 CrossRef CAS
.
- S. Trabelsi, P.-A. Albouy and J. Rault, Stress-Induced Crystallization Properties of Natural and Synthetic CIS-Polyisoprene, Rubber Chem. Technol., 2004, 77(2), 303–316 CrossRef CAS
.
- Y. Tanaka, Structural Characterization of Natural Polyisoprenes: Solve the Mystery of Natural Rubber Based on Structural Study, Rubber Chem. Technol., 2001, 74(3), 355–375 CrossRef CAS
.
- J. Che, C. Burger, S. Toki, L. Rong, B. S. Hsiao, S. Amnuaypornsri and J. Sakdapipanich, Crystal and Crystallites Structure of Natural Rubber and Synthetic Cis-1,4-Polyisoprene by a New Two Dimensional Wide Angle X-Ray Diffraction Simulation Method. I. Strain-Induced Crystallization, Macromolecules, 2013, 46(11), 4520–4528 CrossRef CAS
.
- M. Oouchi, J. Ukawa, Y. Ishii and H. Maeda, Structural Analysis of the Terminal Groups in Commercial Hevea Natural Rubber by 2D-NMR with DOSY Filters and Multiple-WET Methods Using Ultrahigh-Field NMR, Biomacromolecules, 2019, 20(3), 1394–1400 CrossRef CAS
.
- M. Dixit and T. Taniguchi, Substantial Effect of Terminal Groups in Cis-Polyisoprene: A Multiscale Molecular Dynamics Simulation Study, Macromolecules, 2022, 55(21), 9650–9662 CrossRef CAS
.
- C. Liu, N. Morimoto, L. Jiang, S. Kawahara, T. Noritomi, H. Yokoyama, K. Mayumi and K. Ito, Tough Hydrogels with Rapid Self-Reinforcement, Science, 2021, 372(6546), 1078–1081 CrossRef CAS
.
- W. V. Mars and A. Fatemi, Factors That Affect the Fatigue Life of Rubber: A Literature Survey, Rubber Chem. Technol., 2004, 77(3), 391–412 CrossRef CAS
.
- N. Saintier, G. Cailletaud and R. Piques, Cyclic Loadings and Crystallization of Natural Rubber: An Explanation of Fatigue Crack Propagation Reinforcement under a Positive Loading Ratio, Mater. Sci. Eng., A, 2011, 528(3), 1078–1086 CrossRef
.
- P. Rublon, B. Huneau, E. Verron, N. Saintier, S. Beurrot, A. Leygue, C. Mocuta, D. Thiaudière and D. Berghezan, Multiaxial Deformation and Strain-Induced Crystallization around a Fatigue Crack in Natural Rubber, Eng. Fract. Mech., 2014, 123, 59–69 CrossRef
.
- F. Xiang, K. Schneider and G. Heinrich, New Observations Regarding Fatigue Crack Paths and Their Fracture Surfaces in Natural Rubber: Influences of R-Ratio and Pre-Load, Int. J. Fatigue, 2020, 135, 105508 CrossRef
.
- J.-B. Le Cam and E. Toussaint, The Mechanism of Fatigue Crack Growth in Rubbers under Severe Loading: The Effect of Stress-Induced Crystallization, Macromolecules, 2010, 43(10), 4708–4714 CrossRef CAS
.
- B. Ruellan, J.-B. Le Cam, E. Robin, I. Jeanneau, F. Canévet, G. Mauvoisin and D. Loison, Fatigue Crack Growth in Natural Rubber: The Role of SIC Investigated through Post-Mortem Analysis of Fatigue Striations, Eng. Fract. Mech., 2018, 201, 353–365 CrossRef
.
- S. Trabelsi, P.-A. Albouy and J. Rault, Stress-Induced Crystallization around a Crack Tip in Natural Rubber, Macromolecules, 2002, 35(27), 10054–10061 CrossRef CAS
.
-
Q. Demassieux, D. Berghezan and C. Creton, Microfocused Beam SAXS and WAXS Mapping at the Crack Tip and Fatigue Crack Propagation in Natural Rubber BT – Fatigue Crack Growth in Rubber Materials: Experiments and Modelling, ed. G. Heinrich, R. Kipscholl, R. Stoček, Springer International Publishing, Cham, 2021, pp. 467–491 Search PubMed
.
- J. Rault, J. Marchal, P. Judeinstein and P. A. Albouy, Stress-Induced Crystallization and Reinforcement in Filled Natural Rubbers:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H NMR Study, Macromolecules, 2006, 39(24), 8356–8368 CrossRef CAS
2H NMR Study, Macromolecules, 2006, 39(24), 8356–8368 CrossRef CAS .
- S. Toki, I. Sics, B. S. Hsiao, M. Tosaka, S. Poompradub, Y. Ikeda and S. Kohjiya, Probing the Nature of Strain-Induced Crystallization in Polyisoprene Rubber by Combined Thermomechanical and In Situ X-Ray Diffraction Techniques, Macromolecules, 2005, 38(16), 7064–7073 CrossRef CAS
.
- P.-A. Albouy, J. Marchal and J. Rault, Chain Orientation in Natural Rubber, Part I: The Inverse Yielding Effect, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 17(3), 247–259 CrossRef CAS
.
- Y. Miyamoto, H. Yamao and K. Sekimoto, Crystallization and Melting of Polyisoprene Rubber under Uniaxial Deformation, Macromolecules, 2003, 36(17), 6462–6471 CrossRef CAS
.
- N. Candau, R. Laghmach, L. Chazeau, J.-M. Chenal, C. Gauthier, T. Biben and E. Munch, Temperature Dependence of Strain-Induced Crystallization in Natural Rubber: On the Presence of Different Crystallite Populations, Polymer, 2015, 60, 115–124 CrossRef CAS
.
- P. Chen, J. Zhao, Y. Lin, J. Chang, L. Meng, D. Wang, W. Chen, L. Chen and L. Li, In Situ Characterization of Strain-Induced Crystallization of Natural Rubber by Synchrotron Radiation Wide-Angle X-Ray Diffraction: Construction of a Crystal Network at Low Temperatures, Soft Matter, 2019, 15(4), 734–743 RSC
.
- N. Candau, R. Laghmach, L. Chazeau, J.-M. Chenal, C. Gauthier, T. Biben and E. Munch, Influence of Strain Rate and Temperature on the Onset of Strain Induced Crystallization in Natural Rubber, Eur. Polym. J., 2015, 64, 244–252 CrossRef CAS
.
- P. J. Flory, Thermodynamics of Crystallization in High Polymers. I. Crystallization Induced by Stretching, J. Chem. Phys., 1947, 15(6), 397–408 CrossRef CAS
.
- K. Brüning, K. Schneider, S. V. Roth and G. Heinrich, Kinetics of Strain-Induced Crystallization in Natural Rubber Studied by WAXD: Dynamic and Impact Tensile Experiments, Macromolecules, 2012, 45(19), 7914–7919 CrossRef
.
- B. N. J. Persson, O. Albohr, G. Heinrich, H. Ueba, C.-Y. Hui, A. Jagota, S. J. Bennison and J. D. Londono, Crack Propagation in Rubber-like Materials, J. Phys.: Condens. Matter, 2005, 459(2034), 1489–1516 Search PubMed
.
- M. Tosaka, K. Senoo, K. Sato, M. Noda and N. Ohta, Detection of Fast and Slow Crystallization Processes in Instantaneously-Strained Samples of Cis-1,4-Polyisoprene, Polymer, 2012, 53(3), 864–872 CrossRef CAS
.
- N. Candau, L. Chazeau, J.-M. Chenal, C. Gauthier and E. Munch, A Comparison of the Abilities of Natural Rubber (NR) and Synthetic Polyisoprene Cis-1,4 Rubber (IR) to Crystallize under Strain at High Strain Rates, Phys. Chem. Chem. Phys., 2016, 18(5), 3472–3481 RSC
.
- Y. Kitamura, K. Okada, H. Masunaga and M. Hikosaka, Role of Strain Rate in the Strain-Induced Crystallization (SIC) of Natural and Synthetic Isoprene
Rubber, Polym. J., 2019, 51(2), 221–226 CrossRef CAS
.
- C. L. M. Bell, D. Stinson and A. G. Thomas, Measurement of Tensile Strength of Natural Rubber Vulcanizates at Elevated Temperature, Rubber Chem. Technol., 1982, 55(1), 66–75 CrossRef
.
- R. S. Rivlin and A. G. Thomas, Rupture of Rubber. I. Characteristic Energy for Tearing, J. Polym. Sci., 1953, 10(3), 291–318 CrossRef CAS
.
- H. W. Greensmith, Rupture of Rubber. IV. Tear Properties of Vulcanizates Containing Carbon Black, J. Polym. Sci., 1956, 21(98), 175–187 CrossRef
.
- G. J. Lake, C. C. Lawrence and A. G. Thomas, High-Speed Fracture of Elastomers: Part I, Rubber Chem. Technol., 2000, 73(5), 801–817 CrossRef CAS
.
- J. R. Rice, A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks, J. Appl. Mech., 1968, 35(2), 379–386 CrossRef
.
- S.-J. Chang, Path-Independent Integral for Rupture of Perfectly Elastic Materials, Z. Angew. Math. Phys., 1972, 23(1), 149–152 CrossRef
.
- Y. Qi, J. Caillard and R. Long, Fracture Toughness of Soft Materials with Rate-Independent Hysteresis, J. Mech. Phys. Solids, 2018, 118, 341–364 CrossRef
.
- R. Long, C.-Y. Hui, J. P. Gong and E. Bouchbinder, The Fracture of Highly Deformable Soft Materials: A Tale of Two Length Scales, Annu. Rev. Condens. Matter Phys., 2021, 12(1), 71–94 CrossRef
.
- E. Elmukashfi, An Experimental Method for Estimating the Tearing Energy in Rubber-like Materials Using the True Stored Energy, Sci. Rep., 2021, 11(1), 16229 CrossRef CAS
.
- C. Creton and M. Ciccotti, Fracture and Adhesion of Soft Materials: A Review, Rep. Prog. Phys., 2016, 79(4), 46601 CrossRef
.
-
A. G. Thomas, Fracture of Rubber, The Physical Basis of Yield and Fracture Conference Proceedings, Oxford, 1967, p. 134 Search PubMed
.
- A. G. Thomas and J. M. Whittle, Tensile Rupture of Rubber, Rubber Chem. Technol., 1970, 43(2), 222–228 CrossRef CAS
.
- G. Rong, G. R. Hamed and J. Jiang, Comparison of the Strength of Normal and Edge-Cut Tensile Specimens of Styrene-Butadiene Rubber and Natural Rubber with Similar Crosslink Density, Rubber Chem. Technol., 2016, 89(4), 631–639 CrossRef CAS
.
- G. R. Hamed and N. Rattanasom, Effect of Crosslink Density on Cut Growth in Black-Filled Natural Rubber Vulcanizates, Rubber Chem. Technol., 2002, 75(5), 935–942 CrossRef CAS
.
- G. R. Hamed and B. H. Park, The Mechanism of Carbon Black Reinforcement of SBR and NR Vulcanizates, Rubber Chem. Technol., 1999, 72(5), 946–959 CrossRef
.
- A. G. Thomas, Rupture of Rubber. V. Cut Growth in Natural Rubber Vulcanizates, J. Polym. Sci., 1958, 31(123), 467–480 CrossRef
.
- G. R. Hamed, Effect of Crosslink Density on the Critical Flaw Size of a Simple Elastomer, Rubber Chem. Technol., 1983, 56(1), 244–251 CrossRef CAS
.
- P. Paris and F. Erdogan, A Critical Analysis of Crack Propagation Laws, J. Basic Eng., 1963, 85(4), 528–533 CrossRef CAS
.
- A. N. Gent, P. B. Lindley and A. G. Thomas, Cut Growth and Fatigue of Rubbers. I. The Relationship between Cut Growth and Fatigue, J. Appl. Polym. Sci., 1964, 8(1), 455–466 CrossRef
.
- P. J. Flory and J. Rehner, Statistical Mechanics of Cross-Linked Polymer Networks II Swelling, J. Chem. Phys., 1943, 11(11), 521–526 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Tensile force–displacement curves for NR-B with various c0 values at 25 °C with a strain rate of 0.11 s−1 in the edge-crack test. See DOI: https://doi.org/10.1039/d3sm00060e |
| This journal is © The Royal Society of Chemistry 2023 |