Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Local structure of liquid/vapour interfaces approaching the critical point
György
Hantal
 a,
Pál
Jedlovszky
a,
Pál
Jedlovszky
 b and
Marcello
Sega
b and
Marcello
Sega
 *c
*c
aInstitute of Physics and Materials Science, University of Natural Resources and Life Sciences, Peter Jordan Strasse 82, A-1190 Vienna, Austria
bDepartment of Chemistry, Eszterhazy Karoly University, Leanyka utca 6, H-3300 Eger, Hungary
cDepartment of Chemical Engineering, University College London, London WC1E 7JE, UK. E-mail: m.sega@ucl.ac.uk
First published on 18th April 2023
Abstract
Investigating the structure of fluid interfaces at high temperatures is a particularly delicate task that requires effective ways of discriminating liquid from vapour and identifying the location of the liquid phase boundary, thereby allowing to distinguish intrinsic from capillary fluctuations. Several numerical approaches require introducing a coarse-graining length scale, often heuristically chosen to be the molecular size, to determine the location of the liquid phase boundary. Here, we propose an alternative rationale for choosing this coarse-graining length scale; we require the average position of the local liquid phase dividing surface to match its flat, macroscopic counterpart. We show that this approach provides additional insight into the structure of the liquid/vapour interface, suggesting the presence of another length scale beyond the bulk correlation one that plays an important role in determining the interface structure.
1 Introduction
A detailed understanding of liquid/vapour interfaces has proven to be an elusive objective because of the interplay between fluctuations in the bulk and surface capillary excitations. Theories dealing mainly with the effects of bulk fluctuations on the interface structure are exemplified by the approach of van der Waals,1,2 whereas the theory of Buff, Lovett, and Stillinger3 was the first to place the capillary fluctuation in focus. When approaching the critical point, fluctuations in the bulk phase are expected to become dominant, while far from it, one expects the intrinsic interface thickness to be of the order of the molecular size for simple liquids and dominated by entropic fluctuations. Several approaches tried to reconcile these two pictures. Weeks,4 for example, considered the statistical mechanics of columns of fluid separated by the bulk correlation distance ξ. In this way, all capillary fluctuations with a wavelength larger than ξ are removed from the statistical average. Further, the local equimolar Gibbs dividing surface is used to define the location of the interface. Several alternative routes have been made since then to overcome the limitations of the capillary wave theory, for example, including a wave-vector dependency into the continuous Hamiltonian that describes the coarse-grained dynamics of the interface,5–7 exploring nonlocal models8–10 or, recently, extending density functional models to asymmetric interfaces.11,12Distinguishing capillary from bulk fluctuations has been proven difficult not only in density functional treatments6 but also in computer simulations, as the abundance of different numerical approaches attests. For example, columnar averaging has been applied in simulations of polymer mixtures13–15 and water.16 Other computational strategies17–22 have taken alternative routes to the definition of the liquid/vapour interface. The computational approaches aimed at locating the local boundary between liquid and gas are characterised by the presence of an adjustable parameter (typically, a characteristic length) that influences the determination of surface atoms and, as a consequence, the distinction between capillary fluctuations and corrugations happening below that scale (intrinsic fluctuations). So, for example, the intrinsic sampling method (ISM) of Chacon and Tarazona17,18 involves a distance cutoff within which new pivot points are searched in each iteration as well as a short-wavelength cutoff for the surface modes; the ITIM and GITIM methods20,22 introduce the cutoff via the probe-sphere size; the Willard–Chandler method21 identifies the instantaneous surface with an isodensity surface determined by Gaussian kernels located at the atomic centres, and needs a choice of kernel width and isodensity threshold. These parameters are usually set initially to some physically meaningful quantity (typically, the molecular size) and refined according to some reasonable criterion, including, for example, stability of the results with respect to variation of the parameter itself.
Here, we propose a method to eliminate the ambiguity in selecting this parameter by ensuring consistency between the locally-defined and macroscopic Gibbs dividing surfaces. As it turns out, this characteristic length appears to scale with a different (smaller) exponent than that of the bulk correlation length, ξ, when approaching the critical temperature and is related to the density contrast between the liquid and the vapour phases. The appearance of another scaling might be surprising at first, but one should not forget that ξ is not the only fundamental length scale, another example being the distance between the equimolar and the zero excess energy surfaces.2 The local position of the liquid surface so defined suggests that a new length scale, smaller than the bulk correlation one, might play an important role in determining the interfacial structure of fluids.
Let us stress that according to the commonly accepted theories, only the bulk correlation length ξ, the capillary broadening Δcw, and, in case periodic boundary conditions are in place, the lateral cell size Lx enter the description of fluid interfaces close to the critical point. However, in our attempt to define a practical protocol for determining an appropriate coarse-graining length, we found, against our expectations, evidence of a different scaling from that of ξ. This empirical finding has piqued our interest, and here we present the results of our investigation.
2 Tagging liquid phase, vapour phase, and surface atoms
The first step in determining the interfacial atoms using algorithms such as GITIM or ISM is the separation between the liquid and the vapour phases. This classification is usually performed using clustering techniques (falling in the general category of unsupervised algorithms in the language of machine learning, where clustering algorithms play an important role). Far enough from the critical point, it can be safely assumed that almost all molecules are in the liquid phase and that only a few isolated molecules are found in the vapour phase. In these cases, the simplest solution is to perform a cluster analysis based on the presence of neighbours within a given cutoff radius. Molecules with no neighbours are tagged as belonging to the vapour phase, and usually, only one large cluster is found (the liquid phase). This approach can no longer distinguish between the two phases at higher temperatures because chains of molecules connecting the liquid and the vapour phase start appearing. In this case, density-based clustering approaches are more appropriate.The Density-Based Spatial Clustering of Applications with Noise23 (DBSCAN) is a popular density-based clustering algorithm. DBSCAN works by defining clusters as dense regions of data points separated by areas of lower density and requires as an input a search radius used to determine the local density and a threshold density value to distinguish points in high-density regions (called core points) from points in low-density ones. Core points and points within a cutoff radius to a core point are clustered together. In the present case, the high-density cluster represents the liquid phase.
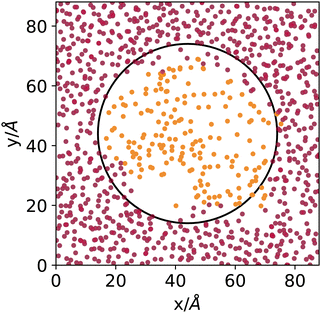
DBSCAN has been used successfully in the characterisation of fluid phases.24,25 Here, we use an automatic determination of the threshold density that assumes a bimodal local density distribution25 and a search radius of 12 Å. Fig. 1 shows the result of the DBSCAN clustering using an ad-hoc generated system, built by filling a cubic simulation box with argon atoms taken from the middle of the liquid phase of an explicit coexistence simulation (details in the Methods section) equilibrated at 153 K, in which a spherical cavity is carved and filled with a patch of atoms taken from the middle of the vapour phase of the same simulation. Fig. 1 shows a cut-out slab passing through the middle of the simulation box with the sphere's location highlighted. The points represent the centres of the argon atoms, coloured according to the way they are clustered by DBSCAN.
Even though the densities of the two phases are pretty close and the curvature radius of the carved sphere is relatively small, the algorithm does an excellent job at distinguishing molecules sampled from the original liquid or vapour phases. Notice that 153 K is, concerning argon, the highest temperature investigated in the present work, where the distinction between vapour and liquid is the most difficult due to the proximity to the critical point. The DBSCAN clustering provides, in this sense, a meaningful and reliable way to determine to which phase atoms belong, on a local basis, when interfaces are present.
Once the liquid phase is determined, one must understand which molecules have to be considered interfacial to determine the capillary fluctuations. We have chosen to use the GITIM algorithm,22 a generalisation for arbitrarily shaped interfaces of ITIM,20 as implemented in the Pytim26 package. In a nutshell, the GITIM algorithm performs the Delaunay triangulation of the atomic or molecular centres in the liquid phase. The algorithm tags as surface atoms those belonging to simplices that can host a sphere larger than a given value Rp, called the probe-sphere radius. The algorithm considers the excluded volume of the atoms. Here we use the contact distance, namely, where the pair distribution function starts differing from zero, to determine the excluded volume.
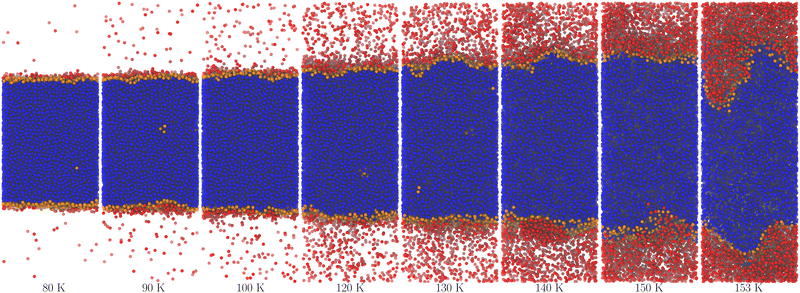
Fig. 2 and 3 show molecular dynamics simulation snapshots of the explicit coexistence simulations of argon and water at different temperatures. The simulation details are reported in the Methods section, and the snapshots were produced using the optimal coarse-graining length Rp = Rcg, as discussed later. Atoms in the liquid phase are shown in blue (the internal ones) or orange (the surface ones), whereas atoms in the vapour phase are shown in red. Hydrogen atoms are always white. The interfacial atoms appearing in the bulk liquid phase mark spontaneous cavitation effects.27 Notice also that due to the attractive potential of the liquid phase, the equilibrium vapour distribution must show an increased density close to the interface.
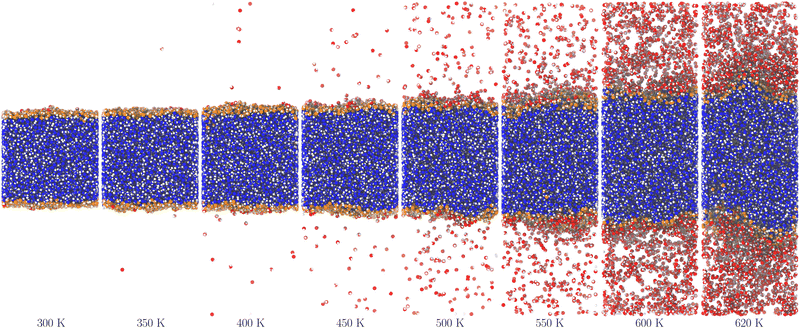 | ||
| Fig. 3 Snapshots of the water system at different temperatures. The colours are the same as in Fig. 2, except for hydrogen atoms that are always white. | ||
Even though the density-based clustering approach is quite robust, it is important to ensure that this accumulation of vapour is not an artefact of the algorithm, especially at high temperatures. We investigated this point further by building a simple model in the convolution approximation.28 In this approximation, the interface is described at the microscopic scale by the intrinsic profile and at the macroscopic scale by the capillary wave theory, neglecting the coupling between capillary fluctuations and the intrinsic structure. The apparent profile is then obtained by performing the thermal average of the intrinsic profile over the independent capillary modes, resulting in the convolution of the former with a Gaussian probability distribution with width s determined by the continuum Hamiltonian of the capillary wave theory. The effective profile ρ(z) of an interface centered at z = 0 with intrinsic profile ρI(z) is then
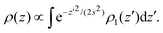 | (1) |
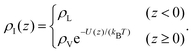 | (2) |
We have chosen the potential U(z) = Umean(z) + 3ULJ(z) as the sum of the potential obtained from integrating the contribution of a homogeneous distribution of Lennard-Jones centres in the half-space occupied by the liquid, Umean, and the contribution at close range of the three nearest neighbouring molecules, each with a Lennard-Jones potential ULJ:
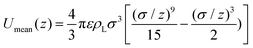 | (3) |
| ULJ(z) = 4ε[(σ/z)12 − (σ/z)6)]. | (4) |
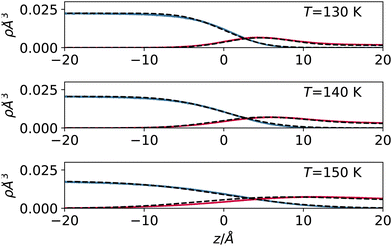
In Fig. 4, we report the result of this empirical model (with effective width s used as a fit parameter) applied to the high-temperature regime, where our approximation is applicable. The results show that despite its qualitative nature, the model can reproduce the sampled density profiles relatively well, including the vapour accumulation at the interface.
3 Local liquid phase dividing surface
The thermodynamic, macroscopic definition of the equimolar Gibbs dividing surface is the plane at which the excess surface density is identically zero. This condition is often written (liquid phase located in the region z < zeq) as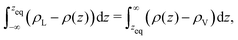 | (5) |
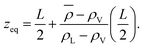 | (6) |
In an explicit coexistence simulation in the canonical ensemble, the average density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) is known precisely. In contrast, the values of the bulk liquid and vapour densities must be determined by an appropriate fit. As Stillinger noted,29 the boundary of the liquid phase (however defined) does not need to coincide with the equimolar Gibbs dividing surface. If the density profile ρ(z) is piecewise constant and equal to the two bulk densities in the respective phases, then zeq is located precisely between the two. When ρL ≫ ρV, there should be no ambiguity in this statement. If the bulk values and the distribution on the liquid side remain unchanged, but the vapour phase develops an accumulation of material at the interface, as the simple model presented before shows, then
is known precisely. In contrast, the values of the bulk liquid and vapour densities must be determined by an appropriate fit. As Stillinger noted,29 the boundary of the liquid phase (however defined) does not need to coincide with the equimolar Gibbs dividing surface. If the density profile ρ(z) is piecewise constant and equal to the two bulk densities in the respective phases, then zeq is located precisely between the two. When ρL ≫ ρV, there should be no ambiguity in this statement. If the bulk values and the distribution on the liquid side remain unchanged, but the vapour phase develops an accumulation of material at the interface, as the simple model presented before shows, then ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) must increase. Consequently, zeq will move toward the vapour phase, and it will not coincide with the location of the liquid phase surface.
must increase. Consequently, zeq will move toward the vapour phase, and it will not coincide with the location of the liquid phase surface.
We aim to start from this intuitive picture to provide a formulation for the liquid phase dividing surface along the lines of the equimolar Gibbs dividing surface, using the information about the tagged liquid phase molecules. In other words, we want to define the equimolar surface of the liquid phase, which from now on, we will call the “liquid phase dividing surface'”. To locate the liquid phase dividing surface, we start by computing the profile ρL(z) of the liquid phase (which takes the value ρL in the bulk). We define the position of the liquid phase dividing surface zL similarly to the equimolar one, eqn (5), through
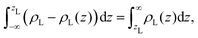 | (7) |
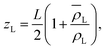 | (8) |
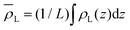 is the average density of molecules in the liquid phase over the whole box. This relation is valid only if the liquid density reaches zero far from the bulk liquid phase, which was always the case in the systems considered in this work. It is worth noticing that computing the liquid phase dividing surface zL does not require knowledge of liquid interface location, but just of the average profile ρL(z). One can think of zL as the average position of a locally corrugated dividing surface ζL(x, y) (the local liquid phase dividing surface) that contains all liquid molecules. The calculation of ζL(x, y), unlike zL, does require the knowledge of the fluid phase surface.
is the average density of molecules in the liquid phase over the whole box. This relation is valid only if the liquid density reaches zero far from the bulk liquid phase, which was always the case in the systems considered in this work. It is worth noticing that computing the liquid phase dividing surface zL does not require knowledge of liquid interface location, but just of the average profile ρL(z). One can think of zL as the average position of a locally corrugated dividing surface ζL(x, y) (the local liquid phase dividing surface) that contains all liquid molecules. The calculation of ζL(x, y), unlike zL, does require the knowledge of the fluid phase surface.
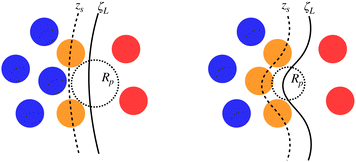
It is worth reminding the reader that our goal is to match a local definition of the surface that divides the two phases with a macroscopic one. The Gibbs equimolar dividing surface, zeq, would not be suitable because, as we discussed, it mixes liquid and vapour even in the case of a perfectly flat interface.29 This is why we are bound to choose the liquid phase dividing surface. Again, note that separating the two phases (here, using the DBSCAN algorithm) still leaves the question open of where the microscopic liquid phase surface is located. By performing the thought experiment of carving out a portion of material from a bulk liquid, it is easy to understand that, to yield the equimolar condition eqn (7), the location of ζL(x, y) must be shifted with respect to the location of the surface passing through the interfacial atomic centres (defined with some suitable interpolation scheme), zS(x, y;Rp), by the typical intermolecular distance in the liquid phase ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif)
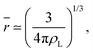 | (9) |
ζL(x, y) = zS(x, y;Rp) + ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) . . | (10) |
Fig. 5 reports a sketch to help visualise some of these quantites. As zS(x, y;Rp) depends implicitly on the probe sphere radius, we need an additional condition to find the optimal value Rp = Rcg, here named coarse-graining length, that satisfies eqn (10). A sensible condition requires that the average position along the surface normal is
| zL = 〈ζL(x, y;Rcg)〉 | (11) |
= 〈zS(x, y;Rcg)〉 + ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , , | (12) |
4 Results
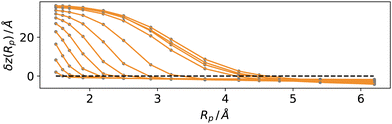
We tested these concepts on a series of molecular dynamics simulations of water and argon, performed as described in the methods section over a range of reduced temperatures 1 − T/Tc from about 0.5 to 0.03, where Tc indicates the critical temperature of the respective models. For the Lennard-Jones fluid, we have chosen30kBTc/ε = 1.3365 (the interested reader could also refer to recent reviews on simulation and equation of state results31,32). For the TIP4P-2005 water model we have used33Tc = 657.5 K.For each temperature, we computed the average position of the interfacial atoms for a set of values of the probe sphere radius Rp. We then solved eqn (12) numerically for the optimal value Rcg using a linear interpolation scheme. In Fig. 6, we report the distance δz(Rp) = zL − 〈zS(x, y;Rp)〉 − ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) between the liquid phase dividing surface zL and the mean local liquid surface position in argon, as a function of the probe-sphere radius, for different temperatures. We determined the optimal probe-sphere radius using a simple linear interpolation to find the zeroes of δz(Rp) In this way, we avoid using any assumption on the scaling of the probe-sphere radius, as the procedure relies only on the determination of the liquid phase (the DBSCAN search radius is set at 12 Å, more than twice as large as the largest Rcg). As we will show, the optimal probe-sphere radius appears to scale with an exponent smaller than that of the bulk correlation length; therefore, Rcg can not be identified with the short-wavelength cutoff that is used to define capillary waves, intended as independent surface modes driven by the restoring force provided by the (macroscopic) surface tension.
between the liquid phase dividing surface zL and the mean local liquid surface position in argon, as a function of the probe-sphere radius, for different temperatures. We determined the optimal probe-sphere radius using a simple linear interpolation to find the zeroes of δz(Rp) In this way, we avoid using any assumption on the scaling of the probe-sphere radius, as the procedure relies only on the determination of the liquid phase (the DBSCAN search radius is set at 12 Å, more than twice as large as the largest Rcg). As we will show, the optimal probe-sphere radius appears to scale with an exponent smaller than that of the bulk correlation length; therefore, Rcg can not be identified with the short-wavelength cutoff that is used to define capillary waves, intended as independent surface modes driven by the restoring force provided by the (macroscopic) surface tension.
In Fig. 7, we report the values of the coarse-graining sphere radius as a function of the reduced temperature. When approaching the critical temperature, the values of the coarse-graining radius appear to show a universal behaviour. This behaviour is apparently compatible with Rcg ∼ (1 − T/Tc)−β, where β ≃ 0.32643 is the critical exponent34 for the order parameter ρL − ρV ∼ (1 − T/Tc)β.
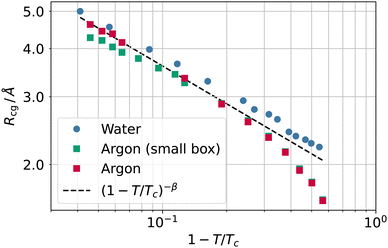 | ||
| Fig. 7 Coarse-graining length Rcg as a function of the reduced temperature 1 − T/Tc for water (circles) and argon (squares) as well as the scaling law (1 − T/Tc)−β (black dashed line). | ||
The appearance of a length scale following a scaling different from the one set by the exponent ν ≃ 0.63 of the bulk correlation length might initially seem surprising. Not all distances, however, need to scale with ν, another example of a fundamental length being the distance between two dividing surfaces (e.g., the equimolar surface and the zero excess energy surface), which scales with exponent2 2ν − 1 − β. A scaling exponent −β would imply Rcg ∼ 1/Δρ, where an inverse square length constant must appear in front of the proportionality relation.
This result underlines the dependence of the coarse-graining length on the density contrast between the two phases. This makes intuitively sense, as Rcg must be large enough to “recognise” the liquid surface, essentially by preventing the probe sphere from penetrating the liquid phase.
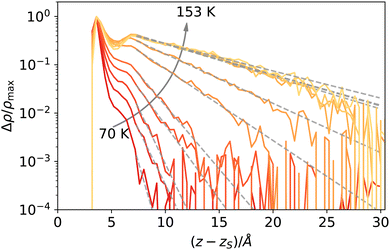
The reader might wonder if defining a length scale that is (at high enough temperatures) bound to be smaller than the bulk correlation length makes sense. Probably, the best way to convince oneself about the soundness of this approach is to look (a posteriori) at the intrinsic density profiles sampled as a function of the elevation z − zS on the liquid phase interface (here z > 0 denotes the vapour phase). As shown in Fig. 8, even at the highest temperature considered here, one can distinguish liquid from vapour as long as the first peak is considered. At low temperatures, this requires considering a neighbourhood larger than ξ, which is smaller than the molecular radius, while at high temperatures, the neighbourhood can be smaller than ξ. This can be appreciated by computing ξ directly from the decay of the intrinsic density profile in the vapour phase, reported in Fig. 9.
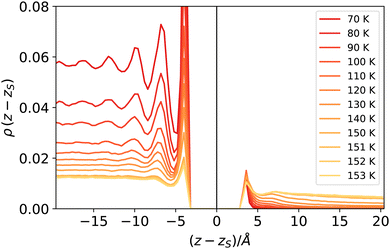 | ||
| Fig. 8 Intrinsic density profiles of argon. The vertical delta-like contribution at z = zs identifies the location of the liquid surface atoms (liquid phase corresponds to z < zs). | ||
The decay Δρ(z − zS) = ρ(z − zS) − ρbulk,vap towards the bulk vapour density ρbulk,vap can be fitted with an exponential function A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp[ − (z − z0)/ξ], with A and z0 fitting parameters, to obtain an estimate of the bulk correlation length ξ. We report ξ measured in this way in Fig. 10, showing that it follows indeed the expected scaling (1 − T/Tc)−ν. Notice that we calculated the intrinsic profiles along the macroscopic interface normal. This might become an issue at high temperatures, where the interface undulation becomes more prominent, and the direction of the local normal should be taken into account,35 but does not seem to be a problem in the present case, at least for the qualitative scaling reported in Fig. 10.
exp[ − (z − z0)/ξ], with A and z0 fitting parameters, to obtain an estimate of the bulk correlation length ξ. We report ξ measured in this way in Fig. 10, showing that it follows indeed the expected scaling (1 − T/Tc)−ν. Notice that we calculated the intrinsic profiles along the macroscopic interface normal. This might become an issue at high temperatures, where the interface undulation becomes more prominent, and the direction of the local normal should be taken into account,35 but does not seem to be a problem in the present case, at least for the qualitative scaling reported in Fig. 10.
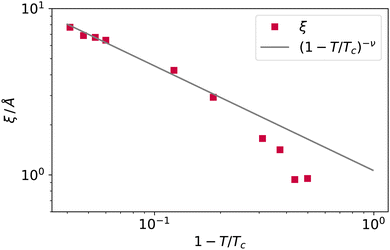 | ||
| Fig. 10 The bulk correlation length obtained from the fit of the argon intrinsic density profile decay towards the bulk vapour value, and scaling law (1 − T/Tc)−ν. | ||
At high temperatures, the bulk correlation length reaches 8 Å, but despite this, close to the interface, it is still possible to recognise in the intrinsic density profile (Fig. 8) the distinguishing features of liquid and vapour (a different local density), even below this scale. In this sense, we deem Rcg a meaningful quantity to identify the location of the liquid phase surface. Finally, let us notice that the fact that Rcg is smaller also than the cutoff radius used in DBSCAN is not a contradiction: the latter is chosen to be large enough to resolve better the local liquid and vapour distributions, but this does not influence the size that the probe sphere should have in order not to penetrate the liquid phase.
Nevertheless, the scaling of Rcg should be taken with a pinch of salt as we do not have a theory to back it, and we observed it over roughly one decade only. We underline that the highest reported temperatures, especially for the Lennard-Jones fluid, are close to the limit where the system starts fragmenting into multiple droplets (a smaller system might be more stable, but we are constrained to simulate cells larger than the bulk correlation length). In literature, explicit coexistence simulation of simple liquids usually reaches at most 1 − T/Tc ≃ 0.01; see, for example, Heyes and Woodcock.30
In addition, we checked for the influence of finite size effects by simulating a smaller box for argon (5299 atoms in a 44 × 44 × 400 Å box). The results of the smaller system are also reported in Fig. 7 and show that finite size effects provide similar results, albeit with a discrepancy from the scaling law that grows with the temperature. It is worth noticing that this finite size effect is not related to a small box size, as the side lengths are still many times larger than the bulk correlation length; rather, the number of atoms is so small that at the highest temperature, the liquid slab width starts being comparable with the bulk correlation length, and the system cannot attain a fully developed density plateau in the liquid phase. Once both the liquid and vapour phases meet the condition of being larger than the bulk correlation length at each temperature (as in the case of the larger system size), the plot of Rg falls back to the (1 − T/Tc)−β scaling.
Again, we would like to stress that the equimolar surface is not expected to coincide with the liquid phase dividing surface, even in simple model systems. As a byproduct of the coarse-graining length investigation, we can now quantify this difference. In fact, the separation between the two surfaces, zeq − zL, grows when the temperature increases, as reported in Fig. 11, for both argon and water. Although it is difficult to draw a clear picture in this case, the gap increase close to the critical point is at least not incompatible with the theoretical expectation of the separation between two dividing surfaces (like the equimolar and the surface of zero excess energy2), with exponent 2ν − 1 − β. Of course, one should also consider the possibility of this being a mere coincidence.
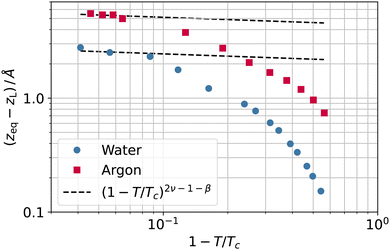 | ||
| Fig. 11 Separation between the equimolar (zeq) and liquid phase (zL) dividing surfaces as a function of the reduced temperature 1 − T/Tc for water (circles) and argon (squares). | ||
To investigate further the interfacial region, we computed the apparent interfacial widths w and wL from the profiles ρ(z) and ρL(z), respectively. We performed nonlinear least-square fits to the complementary error function, e.g., 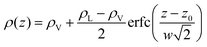 . This functional form is the prediction of the convolution approximation28 of the capillary wave theory with a step-like intrinsic profile and has also been recently proven to be the analytical solution for the three-dimensional Ising model.36 It is worth noting that there is an analytical solution for exponentially decaying intrinsic profiles,37 even though, in our case, this does not apply on the liquid side until very close to the critical temperature. In passing, we also tried to use the hyperbolic tangent solution of the Cahn–Hilliard theory,38 but it fits the profiles noticeably worse than the complementary error function. The scaling of wL and w, show in Fig. 12, is compatible with (1 − T/Tc)−ν. Here, one should not forget that the apparent interface width, even if only that of the liquid phase, emerges as the superposition of the intrinsic width, which scales indeed with the exponent −ν, and the capillary broadening Δcw in the presence of finite lateral size Lx,
. This functional form is the prediction of the convolution approximation28 of the capillary wave theory with a step-like intrinsic profile and has also been recently proven to be the analytical solution for the three-dimensional Ising model.36 It is worth noting that there is an analytical solution for exponentially decaying intrinsic profiles,37 even though, in our case, this does not apply on the liquid side until very close to the critical temperature. In passing, we also tried to use the hyperbolic tangent solution of the Cahn–Hilliard theory,38 but it fits the profiles noticeably worse than the complementary error function. The scaling of wL and w, show in Fig. 12, is compatible with (1 − T/Tc)−ν. Here, one should not forget that the apparent interface width, even if only that of the liquid phase, emerges as the superposition of the intrinsic width, which scales indeed with the exponent −ν, and the capillary broadening Δcw in the presence of finite lateral size Lx,
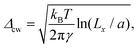 | (13) |
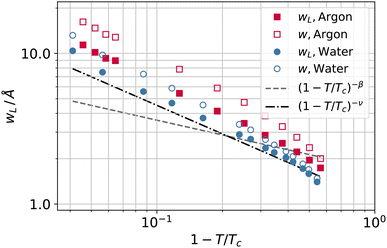 | ||
| Fig. 12 Apparent interfacial widths of the liquid phase wL and of the whole system w obtained from the profiles ρL(z) and ρ(z) for water (filled and open circles) and argon (filled and open squares). We report for comparison the scaling law of ξ from Fig. 10 (dot-dashed line) and Rcg from Fig. 7 (dashed line). | ||
In our opinion, the fact that Rcg shows the hallmark of a universal behaviour is very suggestive. The physical meaning of Rcg is that of a length scale that determines the roughness of the liquid phase surface, as a probe sphere of radius Rcg should be large enough not to penetrate the liquid phase. Since the scaling exponent of Rcg is smaller than that of the bulk correlation length ξ, this implies that sooner or later, at high temperatures, ξ must become larger than Rcg; the liquid phase surface will then be characterised, at distances larger than Rcg but smaller than ξ, by modes that are not independent. This tells us that the features of the liquid surface can be distinguished based on the local density contrast, even if their size is smaller than the bulk correlation length. Capillary waves, intended as independent modes governed by the restoring force of the surface tension, will be observed only at a larger scale. At length scales between Rcg and ξ, one can find surface modes that are not independent. Below Rcg, it is not possible anymore to distinguish any surface feature, and everything is characterised by bulk fluctuations. Notice that nonlocal effects are expected to become dominant below the scale of the bulk correlation length but can still be appreciated, for example, for argon close (T ≃ 90 K) to the triple point, at distances in the order of nanometers.9
5 Methods
We performed molecular dynamics simulations of argon with the Lennard-Jones potential and water with the TIP4P-2005 potential39 using the GROMACS package, release 2018.2.40 We integrated the equations of motion in the canonical ensemble using the Verlet algorithm with a 2 fs integration time step, a Nosé–Hoover41,42 thermostat with a time constant of 1 ps. We kept water molecules rigid using the SETTLE algorithm.43 We computed the long-range part of Coulomb and dispersion interactions using the smooth version of the particle-mesh Ewald method44 using a grid spacing of 1.2 Å, fourth order polynomial interpolation scheme, short-range cutoff of 12 Å, metallic boundary conditions and a relative interaction strength at the cutoff of 10−5 and 10−3 for the Coulomb and dispersion terms, respectively.We simulated 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133 argon atoms and 13
133 argon atoms and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 water molecules in rectangular unit cells of size 88 × 88 × 300 and 75 × 75 × 250 Å3, respectively. We started from a slab configuration with normal along the z axis and integrated the equations of motions for 10 ns, the last 5 of which we used for production. Except for the lowest temperatures, each simulation started from the last configuration of the lower-temperature run. We stored configurations to disk every ps for subsequent analysis using the MDAnalysis45 and Pytim26 analysis packages. We assigned molecules to the liquid or vapour phases according to the protocol reported first in our study on mixtures with high partial miscibility,25 which we summarise here. The protocol uses the (typically bimodal) neighbours distribution within a distance of 12 Å to determine for every frame the density threshold for the DBSCAN algorithm.23 DBSCAN was employed in the context of molecular liquids for highly miscible25 and supercritical fluids.24 In DBSCAN, points are tagged as high-density ones if either the local density (number of neighbours within a given distance rn) is higher than a threshold one (the so-called core points), or if they lie within rn from a core point (core-reachable points). If rn is large enough, the algorithm's outcome is stable and does not depend noticeably on the radius itself anymore.25 Here, we define the liquid phase as the largest cluster of high-density molecules. We consider the smaller, disconnected clusters (droplets) as part of the vapour phase to the end of the present analysis. This choice is inconsequential for determining the surface of the largest liquid cluster.
824 water molecules in rectangular unit cells of size 88 × 88 × 300 and 75 × 75 × 250 Å3, respectively. We started from a slab configuration with normal along the z axis and integrated the equations of motions for 10 ns, the last 5 of which we used for production. Except for the lowest temperatures, each simulation started from the last configuration of the lower-temperature run. We stored configurations to disk every ps for subsequent analysis using the MDAnalysis45 and Pytim26 analysis packages. We assigned molecules to the liquid or vapour phases according to the protocol reported first in our study on mixtures with high partial miscibility,25 which we summarise here. The protocol uses the (typically bimodal) neighbours distribution within a distance of 12 Å to determine for every frame the density threshold for the DBSCAN algorithm.23 DBSCAN was employed in the context of molecular liquids for highly miscible25 and supercritical fluids.24 In DBSCAN, points are tagged as high-density ones if either the local density (number of neighbours within a given distance rn) is higher than a threshold one (the so-called core points), or if they lie within rn from a core point (core-reachable points). If rn is large enough, the algorithm's outcome is stable and does not depend noticeably on the radius itself anymore.25 Here, we define the liquid phase as the largest cluster of high-density molecules. We consider the smaller, disconnected clusters (droplets) as part of the vapour phase to the end of the present analysis. This choice is inconsequential for determining the surface of the largest liquid cluster.
We identified each system's surface molecules with the GITIM algorithm in each frame using a series of different probe-sphere radii Rp. We collected the histograms of their position, ρS(z;Rp), as well as the histograms of the liquid-like and vapour-like molecules, ρL(z) and ρV(z), respectively. The function xL − zS(Rp) turned out to be always a monotonously decreasing function of Rp. Eventually, we determine the zero of the function xL − zS(Rp) by linear interpolation between the two values closest (but with opposites sign) to zero.
6 Conclusions
The equimolar Gibbs dividing surface is one of the many possible choices to separate two coexisting phases and obtain helpful thermodynamic relations between bulk values and surface-excess quantities, like the adsorption equations. However, even when defined locally, the equimolar surface does not necessarily (and in most cases, it does not) separate all molecules in the liquid phase from those in the vapour one. Here, we investigated the implications of determining the surface separating liquid from vapour using the local density as an underlying criterion. In this context, a coarse-graining length seems to emerge naturally in the definition of the surface of the liquid phase and is found to follow a universal scaling law.The procedure reported here provides solid ground for determining the otherwise free parameter (like the probe-sphere radius) in a class of algorithms for identifying interfacial molecules. While we applied this concept to the GITIM algorithm, nothing prevents following a similar procedure for different approaches, like the Willard–Chandler one, where the Gibbs condition could be used to choose the threshold density or the Gaussian kernel parameters. The coarse-graining length is set by requiring the average location of surface molecules to be compatible with the macroscopic liquid phase dividing surface. Strictly speaking, this is not a thermodynamic quantity like the Gibbs equimolar dividing surface, as the set of molecules belonging to the liquid phase cannot be determined by only thermodynamic means. However, this internal self-consistency removes the need for an assumption on how the probe-sphere radius should scale with temperature and relies only on a recipe to separate liquid-like molecules from vapour-like ones, which we implemented using a density-based clustering approach. Given that the scaling relation's prefactor is unknown, it is necessary to find the optimal probe sphere radius for at least one temperature value when simulating a new liquid.
From a more general perspective, the coarse-graining length Rcg sets the scale at which it makes sense to define the liquid surface. Below this coarse-graining length, fluctuations are not living anymore on the liquid/vapour interface but are penetrating the liquid phase. The structure of the liquid/vapour interface is only dictated by bulk fluctuations below that scale set by Rcg. On length scales between Rcg and ξ it is already possible to distinguish features of the liquid surface, even though these are composed of modes that are not independent. Eventually, at scales larger than ξ, independent capillary modes appear. In this sense, the present finding suggests the presence of another fundamental length scale, set implicitly by the order parameter Δρ, which is intermediate between strongly correlated bulk fluctuations and independent capillary waves.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
PJ acknowledges financial support from the NKFIH Foundation, Hungary (under project No. 134596). The authors acknowledge the use of the UCL Myriad High Performance Computing Facility (Myriad@UCL), and associated support services, in the completion of this work.References
- J. D. van der Waals, Verh. - K. Ned. Akad. Wet., Afd. Natuurkd., Reeks, 1893, 1, 8 Search PubMed.
- J. S. Rowlinson and B. Widom, Molecular theory of capillarity, Dover Publications, Inc., Mineola, New York, 2002 Search PubMed.
- F. P. Buff, R. A. Lovett and F. H. Stillinger Jr, Phys. Rev. Lett., 1965, 15, 621 CrossRef.
- J. D. Weeks, J. Chem. Phys., 1977, 67, 3106–3121 CrossRef CAS.
- K. R. Mecke and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 6766–6784 CrossRef CAS PubMed.
- A. O. Parry, C. Rascón, G. Willis and R. Evans, J. Phys.: Condens. Matter, 2014, 26, 355008 CrossRef CAS PubMed.
- F. Höfling and S. Dietrich, Europhys. Lett., 2015, 109, 46002 CrossRef.
- A. O. Parry, J. M. Romero-Enrique and A. Lazarides, Phys. Rev. Lett., 2004, 93, 086104 CrossRef CAS PubMed.
- E. M. Fernández, E. Chacón, P. Tarazona, A. O. Parry and C. Rascón, Phys. Rev. Lett., 2013, 111, 096104 CrossRef PubMed.
- J. Hernández-Muñoz, E. Chacón and P. Tarazona, Phys. Rev. E, 2016, 94, 062802 CrossRef PubMed.
- A. O. Parry, C. Rascón and R. Evans, J. Phys.: Condens. Matter, 2016, 28, 244013 CrossRef CAS PubMed.
- A. O. Parry and C. Rascón, Nat. Phys., 2019, 15, 287–292 Search PubMed.
- A. Werner, F. Schmid, M. Müller and K. Binder, J. Chem. Phys., 1997, 107, 8175–8188 CrossRef CAS.
- A. Werner, F. Schmid, M. Müller and K. Binder, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 728–738 CrossRef CAS.
- R. Vink, J. Horbach and K. Binder, J. Chem. Phys., 2005, 122, 134905 CrossRef CAS PubMed.
- F. Sedlmeier, D. Horinek and R. R. Netz, Phys. Rev. Lett., 2009, 103, 136102 CrossRef PubMed.
- E. Chacón and P. Tarazona, Phys. Rev. Lett., 2003, 91, 166103 CrossRef PubMed.
- P. Tarazona, E. Chacón and F. Bresme, J. Phys.: Condens. Matter, 2012, 24, 284123 CrossRef CAS PubMed.
- M. Jorge and M. N. D. Cordeiro, J. Phys. Chem. C, 2007, 111, 17612–17626 CrossRef CAS.
- L. B. Pártay, G. Hantal, P. Jedlovszky, Á. Vincze and G. Horvai, J. Comput. Chem., 2008, 29, 945–956 CrossRef PubMed.
- A. P. Willard and D. Chandler, J. Phys. Chem. B, 2010, 114, 1954–1958 CrossRef CAS PubMed.
- M. Sega, S. S. Kantorovich, P. Jedlovszky and M. Jorge, J. Chem. Phys., 2013, 138, 044110 CrossRef PubMed.
- M. Ester, H.-P. Kriegel, J. Sander and X. Xu, Proceedings of 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96), 1996, 226.
- A. Idrissi, I. Vyalov, N. Georgi and M. Kiselev, J. Phys. Chem. B, 2013, 117, 12184–12188 CrossRef CAS PubMed.
- M. Sega and G. Hantal, Phys. Chem. Chem. Phys., 2017, 19, 18968–18974 RSC.
- M. Sega, G. Hantal, B. Fábián and P. Jedlovszky, J. Comput. Chem., 2018, 39, 2118–2125 CrossRef CAS PubMed.
- D. M. Huang and D. Chandler, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 1501–1506 CrossRef CAS PubMed.
- D. Jasnow, Rep. Prog. Phys., 1984, 47, 1059 CrossRef CAS.
- F. H. Stillinger, J. Chem. Phys., 1982, 76, 1087–1091 CrossRef CAS.
- D. M. Heyes and L. V. Woodcock, Fluid Phase Equilib., 2013, 356, 301–308 CrossRef CAS.
- S. Stephan, M. Thol, J. Vrabec and H. Hasse, J. Chem. Inf. Model., 2019, 59, 4248–4265 CrossRef CAS PubMed.
- S. Stephan, J. Staubach and H. Hasse, Fluid Phase Equilib., 2020, 523, 112772 CrossRef CAS.
- M. Sega and C. Dellago, J. Phys. Chem. B, 2017, 121, 3798–3803 CrossRef CAS PubMed.
- S. El-Showk, M. F. Paulos, D. Poland, S. Rychkov, D. Simmons-Duffin and A. Vichi, J. Stat. Phys., 2014, 157, 869–914 CrossRef.
- L. G. MacDowell, Phys. Rev. E, 2017, 96, 022801 CrossRef PubMed.
- G. Delfino, W. Selke and A. Squarcini, Nucl. Phys. B, 2020, 958, 115139 CrossRef CAS.
- L. G. MacDowell, J. Benet, N. A. Katcho and J. M. Palanco, Adv. Colloid Interface Sci., 2014, 206, 150–171 CrossRef CAS PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |