Open Access Article
Open Access ArticleThe membrane regulator squalane increases membrane rigidity under high hydrostatic pressure in archaeal membrane mimics†
Josephine G.
LoRicco
 a,
Ingo
Hoffmann
a,
Ingo
Hoffmann
 b,
Antonino
Caliò
b,
Antonino
Caliò
 a and
Judith
Peters
a and
Judith
Peters
 *bcd
*bcd
aUniversité de Lyon, INSA Lyon, CNRS, MAP UMR 5240, Villeurbanne, France
bInstitut Laue-Langevin, Grenoble, France. E-mail: jpeters@ill.fr
cUniv. Grenoble Alpes, CNRS, LiPhy, Grenoble, France
dInstitut Universitaire de France, 75231 Paris, France
First published on 31st July 2023
Abstract
Apolar lipids within the membranes of archaea are thought to play a role in membrane regulation. In this work we explore the effect of the apolar lipid squalane on the dynamics of a model archaeal-like membrane, under pressure, using neutron spin echo spectroscopy. To the best of our knowledge, this is the first report on membrane dynamics at high pressure using NSE spectroscopy. Increasing pressure leads to an increase in membrane rigidity, in agreement with other techniques. The presence of squalane in the membrane results in a stiffer membrane supporting its role as a membrane regulator.
Introduction
Archaea are known to inhabit an extensive range of environments found on Earth including extremes of temperature, pH, salinity, and pressure. Marine environments, which cover over 70% of the Earth, exert around 100 bar of pressure per km of depth.1–3 At the deepest parts of the ocean, pressures can reach >1 kbar, and archaea have been found to live even under such high hydrostatic pressure (HHP) conditions.4–10 HHP is known to affect all biological molecules including nucleic acids, proteins, and lipids. Lipid membranes are particularly sensitive to pressure, and are thought to be one of the most pressure-sensitive biological structures.1,11 Membranes are known to become more tightly packed with pressure, sometimes leading to the formation of highly-ordered gel phases.11–17 Changes in packing lead to changes in membrane lipid interactions with proteins, in membrane fluidity as well as other physico-chemical properties such as permeability, which negatively impact membrane function. Hence, such properties must be tightly controlled for cells to retain membrane functionality, even under extreme conditions such as HHP. In order to conserve the functional behavior of a membrane, its lipid composition can be tuned to a particular composition, in a process known as homeoviscous adaptation, which leads cells grown at different conditions to have nearly identical membrane properties.18Mechanisms of homeoviscous adaption in bacteria/eukarya include changes in the length of the lipid chains, the degree of unsaturation, as well as the presence of membrane regulators such as sterols in eukaryotes and hopanoids in bacteria.19,20 Cholesterol, for example, has been shown to increase the rigidity of a DMPC membrane at higher molar ratios, which has been attributed to an increase in the packing of the acyl chains or an increase in leaflet coupling.21,22 Cholesterol was also seen to have a stiffening effect on unsaturated lipid membranes.23,24 In Archaea, the hydrophobic chains of lipids do not vary in size. Thus, homeoviscous adaptation is supposed to rely on the fine tuning of the number of unsaturation/cycles, the nature of polar headgroups and by the presence in the midplane of the bilayer of apolar lipids which have been proposed to play a similar regulatory role in archaea as sterols in Eukarya, and provide a mechanism of adaptation to extreme conditions.19,25–27
The membrane lipids of archaea are distinct from those found in bacteria/eukaryotes, which seems to contribute to their ability to grow under extreme conditions, such as HHP. Archaeal membranes are composed of lipids with branched isoprene-based hydrocarbon tails (phytanyl) rather than acyl chains which are linked to the glycerol backbone via ether-bonds rather than ester bonds. Unlike typical acyl-chain lipids, these phytanyl-chain lipids are found to remain in a fluid state at temperatures from −120 to 120 °C, likely due to the packing of their branched hydrocarbon tails.28 Yet, the mechanisms of adaptation in archaeal-like membranes are not as well understood as those in bacteria/eukaryotes, due to the different nature of their lipids. While most archaea produce diether lipids containing 20-carbon chains, which form bilayers, many also produce tetraether lipids with 40-carbon (biphytanyl) chains capable of forming membrane monolayers.29–31 The synthesis of monolayer-forming, tetraether lipids has been linked to high temperature and low pH adaptation32 and are thought to provide a mechanism of adaptation to extreme environments,26,33 by increasing membrane packing and impermeability to water and protons.34,35 Not all archaea, however, have been found to produce significant amounts of tetraethers,9,36–38 signifying the importance of other adaption routes, including the production of membrane regulating apolar lipids.
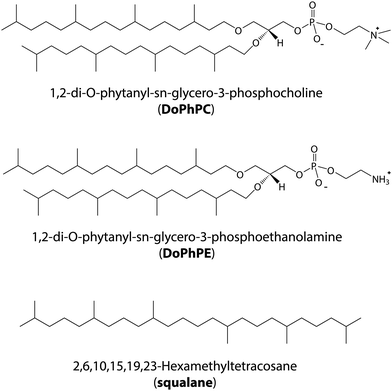
Model archaeal membranes composed of 1,2-di-O-phytanyl-sn-glycero-3-phosphocholine (DoPhPC, Fig. 1a) and 1,2-di-O-phytanyl-sn-glycero-3-phosphoethanolamine (DoPhPE, Fig. 1b) (PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE) in a 9
PE) in a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio were used in order to study the effect of HHP on the dynamics of archaeal membranes. These are synthetic lipids which resemble archaeal membrane lipids in that they have branched hydrocarbon (phytanyl) chains which are linked to the glycerol backbone via ether bonds and such choice permits to perfectly control the sample composition. To model the apolar lipids found in archaea,39 the polyisoprenoid squalane (Fig. 1c) was used. Previous studies have shown that the squalane localizes to the midplane of the bilayer and alters the physico-chemical properties of the membrane.40–44 In this work, 5 mol% squalane to PC
1 molar ratio were used in order to study the effect of HHP on the dynamics of archaeal membranes. These are synthetic lipids which resemble archaeal membrane lipids in that they have branched hydrocarbon (phytanyl) chains which are linked to the glycerol backbone via ether bonds and such choice permits to perfectly control the sample composition. To model the apolar lipids found in archaea,39 the polyisoprenoid squalane (Fig. 1c) was used. Previous studies have shown that the squalane localizes to the midplane of the bilayer and alters the physico-chemical properties of the membrane.40–44 In this work, 5 mol% squalane to PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE was chosen to model apolar membrane regulators as the maximal amount which could be accommodated within the bilayer midplane was shown to be 5–10 mol% squalane.41 Membrane dynamics of unilamellar vesicles (ULVs) were probed, in the presence or absence of squalane, using high-pressure neutron spin echo spectroscopy (HP-NSE). NSE gives access through the motions probed in the timescale up to 200 ns to information on the bending rigidity of the membranes under different conditions. Although it is possible to perform NSE experiments under high pressure, as has been done with microemulsions, to the best of our knowledge this is the first report of NSE being used to characterize biological membranes under HHP.
PE was chosen to model apolar membrane regulators as the maximal amount which could be accommodated within the bilayer midplane was shown to be 5–10 mol% squalane.41 Membrane dynamics of unilamellar vesicles (ULVs) were probed, in the presence or absence of squalane, using high-pressure neutron spin echo spectroscopy (HP-NSE). NSE gives access through the motions probed in the timescale up to 200 ns to information on the bending rigidity of the membranes under different conditions. Although it is possible to perform NSE experiments under high pressure, as has been done with microemulsions, to the best of our knowledge this is the first report of NSE being used to characterize biological membranes under HHP.
Results
To model the membranes of archaea, ULVs composed of a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of DoPhPC and DoPhPE in the absence (PC
1 molar ratio of DoPhPC and DoPhPE in the absence (PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE) and presence of 5 mol% squalane (PC
PE) and presence of 5 mol% squalane (PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq) were prepared via extrusion. Motions within vesicles can occur at many different time and length scales from whole vesicle diffusion, to bilayer undulations and thickness fluctuations, to lateral diffusion and rotational motions of individual lipids. All of these motions take place on different time and length scales that can be accessed by different techniques. A significant portion of membrane stability can be attributed to out-of-plane fluctuations called undulations, and for this reason we focused on characterizing the undulation motions of our model system. Such undulation motions can be described by the bending modulus, κ.45–47
PE + sq) were prepared via extrusion. Motions within vesicles can occur at many different time and length scales from whole vesicle diffusion, to bilayer undulations and thickness fluctuations, to lateral diffusion and rotational motions of individual lipids. All of these motions take place on different time and length scales that can be accessed by different techniques. A significant portion of membrane stability can be attributed to out-of-plane fluctuations called undulations, and for this reason we focused on characterizing the undulation motions of our model system. Such undulation motions can be described by the bending modulus, κ.45–47
In order to probe membrane dynamics in this study, neutron spin echo spectroscopy (NSE) was used.48 NSE is a quasi-elastic scattering technique which measures changes in the velocity of neutrons after interacting with the sample, using the neutron spin as a highly sensitive “clock” to access dynamic information at nanosecond time scales. NSE is able to observe motions in the 1–20 nm range, suitable for capturing membrane undulation motions.45 One of the advantages of the spin-echo technique is that it can directly access the intermediate scattering function, I(q,t), where q is the scattering vector and t is the Fourier time. The study of membrane dynamics has been an important use of the NSE technique since the development of the Zilman–Granek model.49,50 According to this model, the intermediate scattering function I(q,t) can be described by a stretched exponential function with a stretch exponent of 2/3:
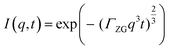 | (1) |
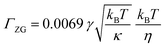 | (2) |
Membrane dynamics were measured at 25 °C and at four pressures: 50 bar, 250 bar, 500 bar and ∼1 kbar, to mimic the hydrostatic pressure faced by many archaea. At each pressure point, the intermediate scattering function was measured at six different values of q (0.043 ≥ q ≥ 0.097 Å−1) and Fourier times of up to 200 ns. Data for the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membrane and PC
PE membrane and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membrane can be found in Fig. 2. Only three q- and two pressure values are shown for clarity. The data and fits at intermediate pressures and at all q-values can be found in the ESI,† Fig. S1. The data for each sample were fit to eqn (1). Conceptually, ΓZG should not vary with q, therefore when fitting the data at each pressure point, ΓZG was used as a shared parameter. The solid lines correspond to fits of the low-pressure data, and dashed lines correspond to fits of the high-pressure data.
PE + sq membrane can be found in Fig. 2. Only three q- and two pressure values are shown for clarity. The data and fits at intermediate pressures and at all q-values can be found in the ESI,† Fig. S1. The data for each sample were fit to eqn (1). Conceptually, ΓZG should not vary with q, therefore when fitting the data at each pressure point, ΓZG was used as a shared parameter. The solid lines correspond to fits of the low-pressure data, and dashed lines correspond to fits of the high-pressure data.
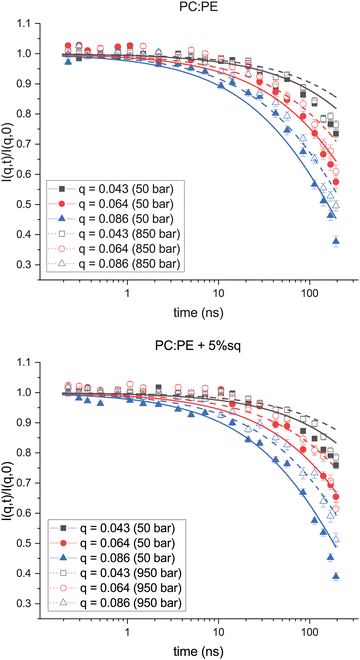 | ||
Fig. 2 Fits of I(q,t) at high and low pressure for PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE sample (Top) and PC PE sample (Top) and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq sample (Bottom). For clarity only three q-values (q = 0.043, 0.064, 0.086) are shown. Measurements made at the lowest measured pressure (50 bar) are shown in solid symbols, and measurements made at the highest pressure (≥850 bar) are shown in open symbols. Fits were made to eqn (1), and shown by solid lines for 50 bar and dashed lines for the HHP data. PE + sq sample (Bottom). For clarity only three q-values (q = 0.043, 0.064, 0.086) are shown. Measurements made at the lowest measured pressure (50 bar) are shown in solid symbols, and measurements made at the highest pressure (≥850 bar) are shown in open symbols. Fits were made to eqn (1), and shown by solid lines for 50 bar and dashed lines for the HHP data. | ||
A comparison of I(q,t) measurements taken at the lowest pressure point (solid symbols) versus the highest pressure point (open symbols) reveal a shift in the I(q,t) values at high pressure. This upward shift in the data points corresponds to a slower relaxation rate for both the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE and PC
PE and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membranes at elevated pressure. The membrane rigidities (κ) were then calculated based on the relationship between ΓZG and κ (eqn (2)). ΓZG and κ have an inverse relationship, therefore a slower relaxation rate at high pressure is indicative of a more rigid membrane.
PE + sq membranes at elevated pressure. The membrane rigidities (κ) were then calculated based on the relationship between ΓZG and κ (eqn (2)). ΓZG and κ have an inverse relationship, therefore a slower relaxation rate at high pressure is indicative of a more rigid membrane.
The rigidity of each membrane as a function of pressure is plotted in Fig. 3. From the figure it is clear that the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membrane was much more rigid than the membrane lacking squalane. The PC
PE + sq membrane was much more rigid than the membrane lacking squalane. The PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membrane had a rigidity of (20.3 ± 1.1) kBT at 50 bar which increased with pressure to a maximum of (43.7 ± 3.1) kBT at 850 bar. The PC
PE membrane had a rigidity of (20.3 ± 1.1) kBT at 50 bar which increased with pressure to a maximum of (43.7 ± 3.1) kBT at 850 bar. The PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membrane also increased with pressure from (27.0 ± 1.4) kBT at 50 bar to a maximum of (72.9 ± 6.2) kBT at 950 bar.
PE + sq membrane also increased with pressure from (27.0 ± 1.4) kBT at 50 bar to a maximum of (72.9 ± 6.2) kBT at 950 bar.
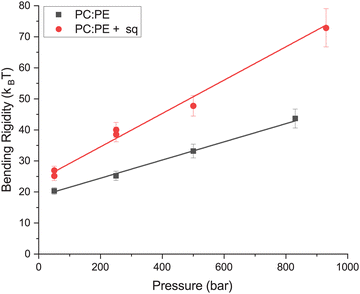 | ||
| Fig. 3 Bending rigidity as a function of pressure calculated using simple fit (eqn (1)) with shared ΓZG. Error bars are based on the goodness of the fit. Lines indicate a linear fit of the data. | ||
A linear fit to the data was used to estimate that the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membrane increased in rigidity at rate of (29.3 ± 1.4) kBT/kbar whereas the PC
PE membrane increased in rigidity at rate of (29.3 ± 1.4) kBT/kbar whereas the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membrane increased at a rate of (53.7 ± 4.6) kBT kbar−1. While both membranes increased in rigidity with pressure, the rate of the increase was larger for the PC
PE + sq membrane increased at a rate of (53.7 ± 4.6) kBT kbar−1. While both membranes increased in rigidity with pressure, the rate of the increase was larger for the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membrane, leading to a more pronounced difference in rigidity between the membranes at high pressure.
PE + sq membrane, leading to a more pronounced difference in rigidity between the membranes at high pressure.
Discussion
In order to directly compare the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE and PC
PE and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq rigidities in Fig. 3, the assumption is made that the contribution of other motions to the NSE signal, such as translational diffusion, can be ignored. While this is a fine assumption to make for vesicles of the same size, large differences in vesicle size and thus diffusion make it impossible to directly compare rigidities calculated using the present method.55 Dynamic light scattering (DLS) was performed to determine the size of the ULVs in solution. Surprisingly, it was found that the vesicles containing squalane had a significantly larger Rh (151.0 ± 3.4 nm) compared to those lacking squalane (58.4 ± 0.5 nm) at 25 °C and ambient pressure, despite being prepared by identical methodology. Squalane is known to promote more negative membrane curvature and the formation of non-lamellar membrane phases such as hexagonal and cubic phases.41,42,56 The change in preferred membrane curvature could explain the larger size of the PC
PE + sq rigidities in Fig. 3, the assumption is made that the contribution of other motions to the NSE signal, such as translational diffusion, can be ignored. While this is a fine assumption to make for vesicles of the same size, large differences in vesicle size and thus diffusion make it impossible to directly compare rigidities calculated using the present method.55 Dynamic light scattering (DLS) was performed to determine the size of the ULVs in solution. Surprisingly, it was found that the vesicles containing squalane had a significantly larger Rh (151.0 ± 3.4 nm) compared to those lacking squalane (58.4 ± 0.5 nm) at 25 °C and ambient pressure, despite being prepared by identical methodology. Squalane is known to promote more negative membrane curvature and the formation of non-lamellar membrane phases such as hexagonal and cubic phases.41,42,56 The change in preferred membrane curvature could explain the larger size of the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE vesicles containing squalane. In addition, squalane is known to promote the rigidification of the membrane. This can significantly impact the extrusion of vesicles using the extruder. Indeed, pores have a size distribution in the filter. More rigid vesicles will tend to pass through the larger pores while the more fluid ones will also pass through the smaller one. One direct consequence of this that more rigid vesicles are much harder to extrude, which we noted for the samples with 5% squalane, and that the mean vesicle size is bigger. In addition, following extrusion the behavior of rigid or fluid vesicle may also be different, since the rigid vesicles of smallest size might be unstable and burst/fuse in the solution leading to an increased mean vesicle size. Not only was the sample containing squalane more difficult to extrude, but it became progressively more difficult to extrude for each pass through the filter. This could suggest that some of the pores became obstructed, which could have promoted a rupturing of the polycarbonate filter. Indeed, a later repetition of extrusion and measurements of sample size by DLS (Fig. S3, ESI†) only showed a modest increase in vesicle size with increasing amounts of squalane.
PE vesicles containing squalane. In addition, squalane is known to promote the rigidification of the membrane. This can significantly impact the extrusion of vesicles using the extruder. Indeed, pores have a size distribution in the filter. More rigid vesicles will tend to pass through the larger pores while the more fluid ones will also pass through the smaller one. One direct consequence of this that more rigid vesicles are much harder to extrude, which we noted for the samples with 5% squalane, and that the mean vesicle size is bigger. In addition, following extrusion the behavior of rigid or fluid vesicle may also be different, since the rigid vesicles of smallest size might be unstable and burst/fuse in the solution leading to an increased mean vesicle size. Not only was the sample containing squalane more difficult to extrude, but it became progressively more difficult to extrude for each pass through the filter. This could suggest that some of the pores became obstructed, which could have promoted a rupturing of the polycarbonate filter. Indeed, a later repetition of extrusion and measurements of sample size by DLS (Fig. S3, ESI†) only showed a modest increase in vesicle size with increasing amounts of squalane.
Regardless of its origin, the difference in size, indicates the need for corrections to account for differences in diffusion between the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE and PC
PE and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq vesicles. Diffusion alone can be represented by an exponential decay function with a q2 dependence:
PE + sq vesicles. Diffusion alone can be represented by an exponential decay function with a q2 dependence:
| I(q,t) = exp(−Dq2t) | (3) |
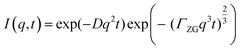 | (4) |
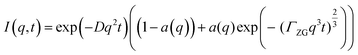 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE and PC
PE and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membranes are valid. Again, ΓZG should be q-independent, therefore we can reduce the number of free parameters by sharing ΓZG. The values of a(q) determined from fitting of the intermediate scattering function to eqn (5) for each of the samples are found in the ESI,† Fig. S2.
PE + sq membranes are valid. Again, ΓZG should be q-independent, therefore we can reduce the number of free parameters by sharing ΓZG. The values of a(q) determined from fitting of the intermediate scattering function to eqn (5) for each of the samples are found in the ESI,† Fig. S2.
The diffusion term, D, must be determined independently from the NSE data. Although IN15 is capable of performing DLS simultaneously with NSE measurements, unfortunately this was not possible with the high-pressure cell. Diffusion was determined using an independent DLS instrument at ambient pressure and the assumption was made that diffusion of the vesicles does not change appreciably within the tested pressure range. While not ideal, this may be a reasonable assumption in the pressure range used (1–1000 bar). Diffusion is correlated with viscosity and the solution viscosity (D2O) does not change significantly from 1–1000 bar58,59 and a high pressure DLS experiment performed by Kohlbrecher et al. (2007) also showed that the diffusion of lysozyme did not change in this pressure range.60
After accounting for diffusion and the limited amplitude of the undulation motion, the differences in rigidity between the samples with and without squalane became less pronounced, however the trends seen using our initial analysis still hold: (1) as the pressure was increased both samples exhibited a 2–3× increase in rigidity with pressure and (2) the sample containing squalane was generally more rigid than the membrane lacking squalane (Fig. 4). The errors in the calculated rigidities are much larger after making the diffusion and amplitude corrections due to uncertainty added by an additional parameter within the fit.
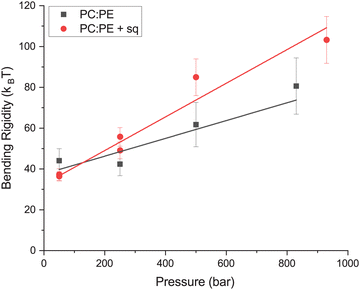 | ||
| Fig. 4 Bending rigidity as a function of pressure calculated using the diffusion and amplitude corrected equation with fixed ΓZG. Lines indicate a linear fit of the data. Error bars are based on the goodness of the fits to eqn (5). | ||
Both the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE and PC
PE and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE + sq membranes demonstrated a rigidity of ∼40 kBT at low pressure (∼50 bar) using the corrections in eqn (5) which is higher than what is typically expected for fluid membranes (10–20 kBT).47 This is likely not a reflection on the membrane system, but rather a result of the chosen prefactor in eqn (2). Many different prefactors have been used, and are often chosen to result in rigidities which agree with values determined by other methods.52 This prefactor works well for data from vesicles with a radius of ∼50 nm in analyses that do not require amplitude or diffusion corrections.
PE + sq membranes demonstrated a rigidity of ∼40 kBT at low pressure (∼50 bar) using the corrections in eqn (5) which is higher than what is typically expected for fluid membranes (10–20 kBT).47 This is likely not a reflection on the membrane system, but rather a result of the chosen prefactor in eqn (2). Many different prefactors have been used, and are often chosen to result in rigidities which agree with values determined by other methods.52 This prefactor works well for data from vesicles with a radius of ∼50 nm in analyses that do not require amplitude or diffusion corrections.
For many reasons the values calculated in Fig. 3 may not reflect the absolute rigidity values: (1) assumption that diffusion change was negligible within pressure range, (2) additional uncertainty in the fit, and (3) chosen prefactor. Despite these uncertainties, the data support the rigidification of the membranes as a function of pressure, and also a rigidifying effect of squalane on the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membrane.
PE membrane.
The increase in rigidity is consistent with previous reports of related systems under high pressure. For example, high pressure neutron spin echo (HP NSE) has been previously used to probe the rigidity of microemulsions, which have also been shown to increase in rigidity with pressure.61–63
To the best of our knowledge no lipid membrane vesicles have been measured by HP NSE so far, however the rigidity of membranes under pressure has been studied by other methods.11,14,27,64–68 For example, a DOPC membrane was shown to increase in rigidity ∼2× upon an increase in pressure to 400 bar using high pressure microscopy and the increase in rigidity was attributed to lateral compaction of the acyl-chain lipids with pressure.12–14 Increased rigidity with pressure can also be implied for systems which undergo a transition from a fluid phase to a more compact gel phase with pressure.11 While diphytanyl chain lipids are not known to undergo a fluid to gel transition,28 they nevertheless are impacted by pressure. The increase in rigidity of the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membranes suggests that archaeal lipids with diphytanyl chains, are just as susceptible to compaction and rigidification with high pressure as acyl-chain lipids. Therefore, these membranes require mechanisms to adapt to high pressure.
PE membranes suggests that archaeal lipids with diphytanyl chains, are just as susceptible to compaction and rigidification with high pressure as acyl-chain lipids. Therefore, these membranes require mechanisms to adapt to high pressure.
Apolar lipids are thought to act as membrane regulators in archaea, therefore, we might expect to see changes in membrane rigidity in the presence of squalane. Our data indicate that, indeed, the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membrane became more rigid in the presence of squalane. This is in agreement with previous findings made using the fluorescent probe laurdan, which found that 1 mol% squalane led to a slight increase in the rigidity of a PC
PE membrane became more rigid in the presence of squalane. This is in agreement with previous findings made using the fluorescent probe laurdan, which found that 1 mol% squalane led to a slight increase in the rigidity of a PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membrane64 and the finding that a related apolar lipid, squalene, facilitated tighter packing of archaeal lipids.69 This effect of squalane is reminiscent of changes in the rigidity of eukaryotic membranes in the presence of cholesterol.23,24
PE membrane64 and the finding that a related apolar lipid, squalene, facilitated tighter packing of archaeal lipids.69 This effect of squalane is reminiscent of changes in the rigidity of eukaryotic membranes in the presence of cholesterol.23,24
Experimental
Chemicals
Synthetic archaeal lipids 1,2-di-O-phytanyl-sn-glycero-3-phosphocholine (DoPhPC) and 1,2-di-O-phytanyl-sn-glycero-3-phosphoethanolamine (DoPhPE), were purchased from Avanti Polar Lipids Inc. (Alabaster, USA) as a lyophilized powder and used without further purification. 2,6,10,15,19,23-Hexamethyltetracosane (squalane) was purchased from Alfa Aesar.Sample preparation
Mixtures of DoPhPC and DoPhPE in a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio were prepared in organic solvent (2
1 molar ratio were prepared in organic solvent (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 choloroform:methanol) followed by the addition of 5 mol% squalane for one of the samples. The solvent was then evaporated under nitrogen gas to form lipid films. Residual solvent was removed by placing the lipids under vacuum overnight. Samples were hydrated with D2O to a final lipid concentration of 10 mg mL−1 (∼12 mM). Samples were allowed to sit overnight to allow for complete hydration and vortexed thoroughly to produce multilamellar vesicles (MLVs). Extrusion was then performed by passing the sample 11× though a 0.1 μm polycarbonate filter using the Avanti mini-extruder, to form unilamellar vesicles (ULVs). Extrusion was performed at 45 °C. DLS and/or NSE measurement were performed immediately following extrusion.
1 choloroform:methanol) followed by the addition of 5 mol% squalane for one of the samples. The solvent was then evaporated under nitrogen gas to form lipid films. Residual solvent was removed by placing the lipids under vacuum overnight. Samples were hydrated with D2O to a final lipid concentration of 10 mg mL−1 (∼12 mM). Samples were allowed to sit overnight to allow for complete hydration and vortexed thoroughly to produce multilamellar vesicles (MLVs). Extrusion was then performed by passing the sample 11× though a 0.1 μm polycarbonate filter using the Avanti mini-extruder, to form unilamellar vesicles (ULVs). Extrusion was performed at 45 °C. DLS and/or NSE measurement were performed immediately following extrusion.
Dynamic light scattering (DLS)
DLS was performed at the Institut Laue Langevin, (Grenoble, France) (ILL) (Partnership for Soft Condensed Matter (PSCM)) on a Malvern ZS90 zetasizer equipped with a 633 nm He–Ne laser with detection of scattering made at 90°. Measurements were performed in triplicate at 25 °C and ambient pressure.Size analysis was performed via the built-in zetasizer software. The diffusion coefficient (D) and vesicle hydrodynamic radius (Rh) are related though the Stokes–Einstein relationship:
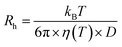 | (6) |
High pressure neutron spin echo (HP NSE)
NSE measurements were performed on the IN15 beamline70,71 at the ILL using a copper–beryllium high pressure cell equipped with sapphire windows (Liquid pressure cell 21PL30AO2) (Fig. 5). The temperature was held constant at 25 °C. Measurements were made at a wavelength of 10 Å, covering a q range of 0.043 ≥ q ≥ 0.097 Å−1. Data are identified by doi:10.5291/ILL-DATA.8-02-917.72Conclusions
We report here the bending rigidity of archaeal-like membranes determined using high pressure neutron spin echo spectroscopy, demonstrating the quality of data that can be obtained at high pressure using this technique. We were able to clearly show an increase in membrane rigidity with pressure, in agreement with data seen by other methods.The presence of squalane led to noticeable effects on the membranes. First, the size of the vesicles produced by extrusion were found to be significantly larger for the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE membranes containing squalane than those lacking squalane. Second, the membrane rigidity was higher for the membrane containing squalane, and these differences became more pronounced at high pressure. These findings are in support of the hypothesis that apolar lipids can act as membrane regulators in archaeal membranes. Whether the increase in bending rigidity occurs because of a direct stiffening of the membrane or because of an impact of the squalane molecules residing in the membrane midplane on membrane leaflet coupling could not be addressed and remains to be addressed.
PE membranes containing squalane than those lacking squalane. Second, the membrane rigidity was higher for the membrane containing squalane, and these differences became more pronounced at high pressure. These findings are in support of the hypothesis that apolar lipids can act as membrane regulators in archaeal membranes. Whether the increase in bending rigidity occurs because of a direct stiffening of the membrane or because of an impact of the squalane molecules residing in the membrane midplane on membrane leaflet coupling could not be addressed and remains to be addressed.
Author contributions
Conceptualization, J. G. L. and J. P.; investigation, J. G. L., I. H., and J. P.; formal analysis, J. G. L. and A. C.; writing – original draft preparation, J. G. L.; writing – review and editing, J. G. L., I. H., A. C., and J. P.; supervision, J. P.; funding acquisition, J. P. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Institut Laue-Langevin (ILL) for allocation of beamtime, and the ILL staff – particularly C. Payre, and J. Maurice of the high-pressure group for their technical support. The authors acknowledge the financial support of the ANR (ANR-17-CE11-0012). They would also like to thank Camille Daligault (ENS de Lyon) for her help performing experiments.Notes and references
- P. M. Oger and M. Jebbar, Res. Microbiol., 2010, 161, 799–809 CrossRef PubMed.
- F. Meersman and P. F. Mcmillan, Chem. Commun., 2014, 50, 766–775 RSC.
- R. A. Lutz and P. G. Falkowski, Science, 2012, 336, 301–302 CrossRef CAS PubMed.
- C. Dalmasso, P. Oger, G. Selva, D. Courtine, S. L’Haridon, A. Garlaschelli, E. Roussel, J. Miyazaki, J. Reveillaud, M. Jebbar, K. Takai, L. Maignien and K. Alain, Syst. Appl. Microbiol., 2016, 39, 440–444 CrossRef CAS PubMed.
- M. Jebbar, B. Franzetti, E. Girard and P. Oger, Extremophiles, 2015, 19, 721–740 CrossRef CAS PubMed.
- X. Zeng, J. L. Birrien, Y. Fouquet, G. Cherkashov, M. Jebbar, J. Querellou, P. Oger, M. A. Cambon-Bonavita, X. Xiao and D. Prieur, ISME J., 2009, 3, 873–876 CrossRef CAS PubMed.
- S. M. Kaneshiro and D. S. Clark, J. Bacteriol., 1995, 177, 3668–3672 CrossRef CAS PubMed.
- G. E. Flores, J. H. Campbell, J. D. Kirshtein, J. Meneghin, M. Podar, J. I. Steinberg, J. S. Seewald, M. K. Tivey, M. A. Voytek, Z. K. Yang and A. Reysenbach, Environ. Microbiol., 2011, 13, 2158–2171 CrossRef CAS PubMed.
- D. Hafenbradl, M. Keller and K. O. Stetter, FEMS Microbiol. Lett., 1996, 136, 199–202 CrossRef CAS.
- V. T. Marteinsson, J. L. Birrien, A. L. Reysenbach, M. Vernet, D. Marie, A. Gambacorta, P. Messner, U. B. Sleytr and D. Prieur, Int. J. Syst. Bacteriol., 1999, 49, 351–359 CrossRef PubMed.
- R. Winter and C. Jeworrek, Soft Matter, 2009, 5, 3157–3173 RSC.
- N. J. Brooks, IUCrJ, 2014, 1, 470–477 CrossRef CAS PubMed.
- N. J. Brooks, O. Ces, R. H. Templer and J. M. Seddon, Chem. Phys. Lipids, 2011, 164, 89–98 CrossRef CAS PubMed.
- S. Purushothaman, P. Cicuta, O. Ces and N. J. Brooks, J. Phys. Chem. B, 2015, 119, 9805–9810 CrossRef CAS PubMed.
- M. A. Casadei, G. Niven, E. Needs and B. M. Mackey, Appl. Environ. Microbiol., 2002, 68, 5965–5972 CrossRef CAS PubMed.
- A. Tamby, J. S. S. Damsté and L. Villanueva, Front. Mol. Biosci., 2023, 9, 1058381 CrossRef PubMed.
- M. Kato and R. Hayashi, Biosci., Biotechnol., Biochem., 1999, 63, 1321–1328 CrossRef CAS PubMed.
- M. Sinensky, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 522–525 CrossRef CAS PubMed.
- M. Salvador-Castell, M. Tourte and P. M. Oger, Int. J. Mol. Sci., 2019, 20, 4434 CrossRef CAS PubMed.
- M. F. Siliakus, J. van der Oost and S. W. M. Kengen, Extremophiles, 2017, 21, 651–670 CrossRef CAS PubMed.
- B. A. Brüning, S. Prévost, R. Stehle, R. Steitz, P. Falus, B. Farago and T. Hellweg, Biochim. Biophys. Acta - Biomembr., 2014, 1838, 2412–2419 CrossRef PubMed.
- J. Peters, J. Marion, F. J. Becher, M. Trapp, T. Gutberlet, D. J. Bicout and T. Heimburg, Sci. Rep., 2017, 7, 1–15 CrossRef PubMed.
- S. Chakraborty, M. Doktorova, T. R. Molugu, F. A. Heberle, H. L. Scott, B. Dzikovski, M. Nagao, L.-R. Stingaciu, R. F. Standaert, F. N. Barrera, J. Katsaras, G. Khelashvili, M. F. Brown and R. Ashkar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21896–21905 CrossRef CAS PubMed.
- L. R. Arriaga, I. López-Montero, F. Monroy, G. Orts-Gil, B. Farago and T. Hellweg, Biophys. J., 2009, 96, 3629–3637 CrossRef CAS PubMed.
- P. M. Oger and A. Cario, Biophys. Chem., 2013, 183, 42–56 CrossRef CAS PubMed.
- A. Cario, V. Grossi, P. Schaeffer and P. M. Oger, Front. Microbiol., 2015, 6, 1152 Search PubMed.
- L. Misuraca, B. Demé, P. Oger and J. Peters, Commun. Chem., 2021, 4, 1–8 CrossRef PubMed.
- H. Lindsey, N. O. Petersen and S. I. Chan, Biochim. Biophys. Acta, 1979, 555, 147–167 CrossRef CAS PubMed.
- M. De Rosa, A. Gambacorta and B. Nicolaus, J. Memb. Sci., 1983, 16, 287–294 CrossRef CAS.
- M. De Rosa, A. Gambacorta and A. Gliozzi, Microbiol. Rev., 1986, 50, 70–80 CrossRef CAS PubMed.
- Y. Koga and H. Morii, Biosci., Biotechnol., Biochem., 2005, 69, 2019–2034 CrossRef CAS PubMed.
- R. Huber, T. Wilharm, D. Huber, A. Trincone, S. Burggraf, H. König, R. Reinhard, I. Rockinger, H. Fricke and K. O. Stetter, Syst. Appl. Microbiol., 1992, 15, 340–351 CrossRef.
- Y. Matsuno, A. Sugai, H. Higashibata, W. Fukuda, K. Ueda, I. Uda, I. Sato, T. Itoh, T. Imanaka and S. Fujiwara, Biosci., Biotechnol., Biochem., 2009, 73, 104–108 CrossRef CAS PubMed.
- P. L. G. Chong, Chem. Phys. Lipids, 2010, 163, 253–265 CrossRef CAS PubMed.
- C. Jeworrek, F. Evers, M. Erlkamp, S. Grobelny, M. Tolan, P. Lee-Gau Chong and R. Winter, Langmuir, 2011, 27, 13113–13121 CrossRef CAS PubMed.
- G. D. Sprott, B. J. Agnew and G. B. Patel, Can. J. Microbiol., 1997, 43, 467–476 CrossRef CAS.
- H. Morii, H. Yagi, H. Akutsu, N. Nomura, Y. Sako and Y. Koga, Biochim. Biophys. Acta, 1999, 1436, 426–436 CrossRef CAS PubMed.
- N. P. Ulrih, D. Gmajner and P. Raspor, Appl. Microbiol. Biotechnol., 2009, 84, 249–260 CrossRef CAS PubMed.
- T. A. Langworthy, T. G. Tornabene and G. Holzer, Zent. Fur Bakteriol. Angew. Und Okol. Microbiol. Abt. L. Orig. C. Hyg., 1982, 3, 228–244 CAS.
- M. Salvador-Castell, B. Demé, P. Oger and J. Peters, Int. J. Mol. Sci., 2020, 21, 1816 CrossRef CAS PubMed.
- M. Salvador-Castell, B. Demé, P. Oger and J. Peters, Langmuir, 2020, 36, 7375–7382 CrossRef CAS PubMed.
- J. G. LoRicco, M. Salvador-Castell, B. Demé, J. Peters and P. M. Oger, Front. Chem., 2020, 8, 594039 CrossRef CAS PubMed.
- T. Hauß, S. Dante, T. H. Haines and N. A. Dencher, Biochim. Biophys. Acta – Bioenerg., 2005, 1710, 57–62 CrossRef PubMed.
- T. Hauß, S. Dante, N. A. Dencher and T. H. Haines, Biochim. Biophys. Acta, 2002, 1556, 149–154 CrossRef PubMed.
- I. Hoffmann, C. Hoffmann, B. Farago, S. Prévost and M. Gradzielski, J. Chem. Phys., 2018, 148, 104901 CrossRef PubMed.
- W. Helfrich, J. Phys., 1985, 46, 1263–1268 CrossRef CAS.
- S. Gupta, J. U. De Mel and G. J. Schneider, Curr. Opin. Colloid Interface Sci., 2019, 42, 121–136 CrossRef CAS.
- F. Mezei, Zeitschrift für Phys. A Hadron. Nucl., 1972, 255, 146–160 CrossRef CAS.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791 CrossRef CAS PubMed.
- A. G. Zilman and R. Granek, Chem. Phys., 2002, 284, 195–204 CrossRef CAS.
- M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler, J. Phys. Chem. Lett., 2017, 8, 4679–4684 CrossRef CAS PubMed.
- I. Hoffmann, Front. Phys., 2021, 8, 620082 CrossRef.
- U. Seifert and S. A. Langer, Europhys. Lett., 1993, 23, 71–76 CrossRef.
- M. C. Watson and F. L. H. Brown, Biophys. J., 2010, 98, L09–L11 Search PubMed.
- I. Hoffmann, R. Michel, M. Sharp, O. Holderer, M. S. Appavou, F. Polzer, B. Farago and M. Gradzielski, Nanoscale, 2014, 6, 6945–6952 RSC.
- M. Salvador-Castell, N. J. Brooks, J. Peters and P. Oger, Biochim. Biophys. Acta – Biomembr., 2020, 1862, 183130 CrossRef CAS PubMed.
- M. Mell, L. H. Moleiro, Y. Hertle, P. Fouquet, R. Schweins, I. López-Montero, T. Hellweg and F. Monroy, Eur. Phys. J. E. Soft Matter., 2013, 36, 75 CrossRef PubMed.
- K. Fukui, Y. Asakuma and K. Maeda, J. Phys.: Conf. Ser., 2010, 215, 012073 CrossRef.
- Y. Tanaka, T. Yamamoto, Y. Satomi, H. Kubota and T. Makita, Rev. Phys. Chem. Japan, 1997, 47, 12–23 Search PubMed.
- J. Kohlbrecher, A. Bollhalder, R. Vavrin and G. Meier, Rev. Sci. Instrum., 2007, 78, 125101 CrossRef CAS PubMed.
- O. Holderer, M. Klostermann, M. Monkenbusch, R. Schweins, P. Lindner, R. Strey, D. Richter and T. Sottmann, Phys. Chem. Chem. Phys., 2011, 13, 3022–3025 RSC.
- M. Klostermann, R. Strey, T. Sottmann, R. Schweins, P. Lindner, O. Holderer, M. Monkenbusch and D. Richter, Soft Matter, 2012, 8, 797–807 RSC.
- M. Nagao, H. Seto, T. Takeda and Y. Kawabata, J. Chem. Phys., 2001, 115, 10036–10044 CrossRef CAS.
- M. Salvador-Castell, M. Golub, N. Erwin, B. Demé, N. J. Brooks, R. Winter, J. Peters and P. M. Oger, Commun. Biol., 2021, 4, 653 CrossRef CAS PubMed.
- P. L.-G. Chong and A. R. Cossins, Biochimica et Biophysica Acta (BBA) - Biomembranes, 1984, 772, 197–201 CrossRef CAS PubMed.
- P. J. Quinn, F. Joo and L. Vigh, Prog. Biophys. Mol. Biol., 1989, 53, 71–103 CrossRef CAS PubMed.
- P. T. T. Wong, D. J. Siminovitch and H. H. Mantsch, Biochimica et Biophysica Acta (BBA) - Reviews on Biomembranes, 1988, 947, 139–171 CrossRef CAS PubMed.
- J. Jonas, High Pressure Chemistry, Biochemistry and Materials Science, Springer Netherlands, Dordrecht, 1993, pp. 393–441 Search PubMed.
- S. F. Gilmore, A. I. Yao, Z. Tietel, T. Kind, M. T. Facciotti and A. N. Parikh, Langmuir, 2013, 29, 7922–7930 CrossRef CAS PubMed.
- P. Schleger, B. Alefeld, J. Barthelemy, G. Ehlers, B. Farago, P. Giraud, C. Hayes, A. Kollmar, C. Lartigue, F. Mezei and D. Richter, Phys. B, 1997, 241–243, 164–165 CrossRef CAS.
- P. Schleger, G. Ehlers, A. Kollmar, B. Alefeld, J. F. Barthelemy, H. Casalta, B. Farago, P. Giraud, C. Hayes, C. Lartigue, F. Mezei and D. Richter, Phys. B, 1999, 266, 49–55 CrossRef CAS.
- P. Oger, C. Daligault, I. Hoffmann, J. G. LoRicco and J. Peters, The Effect of Bulkiness and Charges of Archaeal Lipid Polar Headgroups on Bending Rigidity of Archaeal Membranes, Institut Laue-Langevin (ILL), 2020 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The ESI contains figures with fits of the intermediate scattering functions, the amplitude a(q), the vesicle RHs and their distribution and a table with parameters obtained from DLS. See DOI: https://doi.org/10.1039/d3sm00352c |
| This journal is © The Royal Society of Chemistry 2023 |