DOI:
10.1039/D3SM00615H
(Paper)
Soft Matter, 2023,
19, 4954-4963
Size-dependent bending of a rectangular polymer film†
Received
11th May 2023
, Accepted 12th June 2023
First published on 13th June 2023
Abstract
Inhomogeneous swelling of polymer films in liquid environments may find applications in soft actuators and sensors. Among them, fluoroelastomer based films bend up spontaneously once they are placed on an acetone-soaked filter paper. The stretchability and dielectric properties of a fluoroelastomer is attractive in the fields of soft actuators and sensors, making in-depth studies on and understanding of fluoroelastomer bending behaviors important. Here, we report an abnormal size-dependent bending phenomenon of rectangular fluoroelastomer films, which transform the bending direction from the long-side bending to the short-side bending as their length or width increases or the thickness decreases. By using finite element analysis and an analytical expression obtained using a bilayer model, we reveal the key role of gravity in determining the size-dependent bending behavior. In the bilayer model, an energy quantity is obtained to characterize the role of each material and geometrical parameters in determining the size-dependent bending behavior. We further construct phase diagrams to correlate the bending modes and the film sizes based on the finite element results, which are in good agreement with experimental results. These findings can be useful for the design of future swelling-based polymer actuators and sensors.
1. Introduction
An active polymer material is responsive to external stimuli such as temperature, electric field, ion concentration, etc. Examples of such materials include, but not limited to heat-responsive liquid crystal elastomers,1,2 swellable elastomer polydimethylsiloxane (PDMS) films in an organic bath,3 voltage and cation sensitive cross-linked N,N′-dimethylyacrylamide,4 humidity responsive polyethylene oxide nanofibers,5 temperature sensitive shrinkable polymers,6 pre-stretched latex sheets,7etc. Bending in thin polymer films is a widely used deformation mode for such materials, and has been found in broad applications such as self-locomotive ratcheted actuators,5 3D self-folding devices1,8 and microgrippers.9 Similar thin active polymer structures actuated via the bending mode can also be observed in some plant tissues in nature, such as the scale of a seed-bearing pine cone10 and the keel of an ice plant seed capsule,11 which can close or open up in response to humidity change. In addition to various applications for smart actuators, the stimuli-responsive bending behavior may also be used for the design of swelling-based sensors.12,13 To understand the mechanism for the active bending phenomena and to achieve optimal design for related applications, it is of great significance to conduct theoretical studies on the bending behavior of stimuli-active polymer films.
To date, there have been multiple theoretical models focusing on understanding the relationship between the bending degree and stimuli of polymer films. One widely used model is a bilayer model where the film is simplified to be a lamella composed of a passive layer and an active layer.14 The active layer can generate active strains by expanding/shrinking its volume in response to the change of external stimuli (e.g., temperature, PH, electric field, etc.), while the passive layer does not. The mismatched strain between the two layers enables global bending of the bilayer. Early studies were focused on solving the bending curvature of two-dimensional (2D) bilayers which are assumed to deform into cylindrical shapes.15,16 Recently, some modified solutions14,17–20 were obtained in determining the bending curvature of 3D cases in comparison to Timoshenko's solution.15 In three-dimensional (3D) cases, a planar square bilayer deforms into a dome-shaped configuration with an equal curvature in different directions and bifurcates into a cylinder-like shape once the active strain exceeds a certain threshold21–23 and the bilayer can maintain in either bending direction without applying an external force.24,25 An interesting observation is that under the influence of isotropic active strains, a rectangular bilayer tends to bend along the long side rather than the short side. Such a phenomenon was observed in both numerical studies26,27 and experiments28 and has been well understood by Alben et al.,26 showing that the LS bending state has lower total strain energy than SS bending due to the edge effect. In some other situations, preferred LS bending was attributed to non-homogeneous swelling and adhesion between the polymer and substrate for a small hydrogel film.29 Athas et al.4 found that the bilayer can bend along the short side by tuning the stiffening degree at the edges of a gel bilayer with cations.
Despite significant progress, we find that the existing theories cannot explain the abnormal size-dependent bending behavior of swellable rectangular polymer films. In our experiment, we use a film made of 3 M™ Dyneon™ Fluoroelastomer FC 2230, which can swell and generate active strain by absorbing acetone, when it is placed on an acetone-soaked filter paper, the acetone diffuses into the film and has a higher concentration at its bottom side than the top side, leading to larger swelling deformation (active strain) at the bottom side than the top side (Fig. 1a). This mismatched swelling deformation across the thickness direction induces global bending of the film. We find that, depending on its size, a rectangular film can show either a short-side (SS) or a long-side (LS) bending behavior (Fig. 1b–d, Movies S1 and S2, ESI†). Here, the different bending modes are distinguished by visual observation in the initial deformation stage. We summarize some experimental observations as follows: (i) for a film with a dimension of L × W = 40 mm × 10 mm (see definition of L and W in Fig. 1a), when its thickness H decreases from 1255 μm to 174 μm, the bending direction changes from the LS to SS (Fig. 1b). (ii) If we change the length L, while keeping the aspect ratio 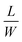 and the thickness H as constants (e.g.,
and the thickness H as constants (e.g., 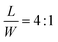 , H = 420 μm), the film tends to bend along the LS for small L and along the SS for large L (Fig. 1c). (iii) Increasing the ratio
, H = 420 μm), the film tends to bend along the LS for small L and along the SS for large L (Fig. 1c). (iii) Increasing the ratio 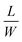 for fixed H and L leads to a shape transition from SS to LS bending (Fig. 1d, Movies S1 and S2). These observations indicate that the bending direction of the rectangular polymer film depends on all of its three geometrical parameters L, W and H.
for fixed H and L leads to a shape transition from SS to LS bending (Fig. 1d, Movies S1 and S2). These observations indicate that the bending direction of the rectangular polymer film depends on all of its three geometrical parameters L, W and H.
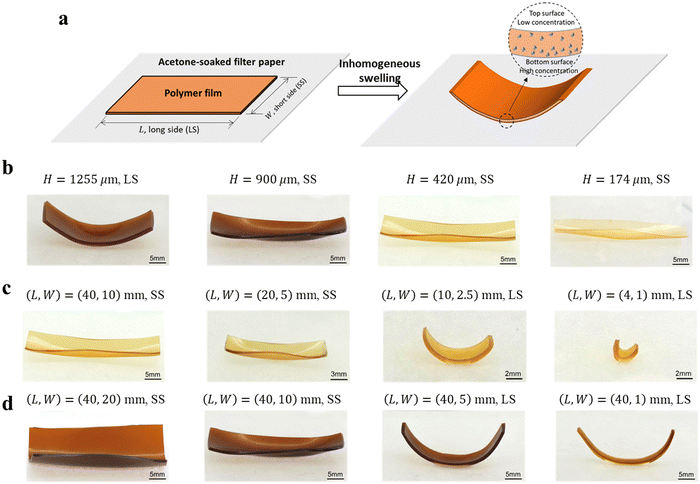 |
| | Fig. 1 (a) The initial and bending configurations of the film placed on an acetone-soaked filter paper due to inhomogeneous swelling. Bending modes of the film in which (b) H varies with L = 40 mm and W = 10 mm, (c) the overall size varies with L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W = 4 W = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and H = 420 μm, and (d) W varies with L = 40 mm and H = 900 μm. LS: long-side bending; SS: short-side bending. 1 and H = 420 μm, and (d) W varies with L = 40 mm and H = 900 μm. LS: long-side bending; SS: short-side bending. | |
The observed size-dependent bending of the rectangular film seems contradictory to the analysis reported by Alben et al.,26 where the LS bending configuration is the expected deformation mode because it corresponds to the lower energy state compared to the SS bending and no size-dependence was found. This inspires us to explore the underlying mechanism of the size-dependent bending behavior. However, we found that previous studies appear to have overlooked the impact of gravity on the bending mode, potentially due to the film's small size, yielding a negligible gravitational effect. In this study, we discover through experimental, theoretical, and finite element analysis that gravity plays a significant role in determining the transition of a film's bending direction as its size changes. It reveals that as the film bends upward, both the gravitational potential energy and bending energy increase, while the energy generated by in-plane stretching diminishes. The competition of the three kinds of energies leads to a size-dependent transition of the bending behavior along different directions. To investigate these phenomena, we first derive an analytical expression for the bending curvature of a bilayer with the gravity effect and further construct phase diagrams to identify the bending modes for given geometrical and material parameters. We then extend the model from the steady swelling of the bilayer to transient swelling of the fluoroelastomer film so that the corresponding size-dependent behavior observed in experiments can be reasonably captured. Good agreement was observed between the experimental and numerical modeling results, indicating the critical role of gravity in determining the bending behavior, particularly for large-sized films.
2. Size-dependent bending of a bilayer
As shown in Fig. 1a, the film bends due to different acetone concentrations (or swelling ratios) across the thickness direction. Due to this, the film may be simplified to the bilayer model, to a certain degree, where the bottom layer swells uniformly and the top layer does not. Such a bilayer model has also been widely used in the design of soft robotics.1,4,5,8,9 This simplification permits some useful analytical results to be obtained and thus facilitates understanding the role of each geometrical and material parameter in determining the size-dependent bending behavior.
2.1 Analytical results
2.1.1 General equations.
We use an approach of minimization of the total potential energy to solve the bending curvature of the bilayer (Fig. 2). Some assumptions are introduced to render the analysis tractable. (1) The active strain is uniformly distributed at the bottom layer and is isotropic, i.e., α(x,y) = α1, where α is the active strain. (2) The density of the bilayer, ρ, remains constant during deformation. (3) The bilayer bends into a cylindrical shape and shows a small deflection. (4) The material is linearly elastic.
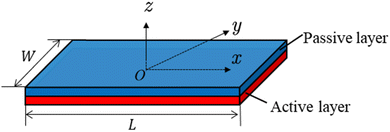 |
| | Fig. 2 Sketch of an active bilayer composed of a passive layer and an active layer. | |
The total potential energy of the bilayer comes from elastic deformation, Ue, and gravity, Ug, i.e.,
For the bilayer shown in
Fig. 2, the total elastic strain energy is given by
14| | 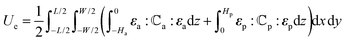 | (2) |
where the quantities with subscripts ‘a’ and ‘p’ denote those of the active layer and the passive layer, respectively,
ε is the elastic strain,
H is the thickness of each layer,
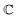
is the elastic tensor of the plate with components
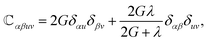 α
α,
β,
u,
v = 1, 2,
G and
λ are Lamé constants and are related to the elastic modulus
E and the Poisson's ratio
ν by
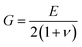
and
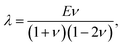 L
L and
W are the length and width of the bilayer, respectively. In the following, due to symmetry in the geometry, we consider the case for
L >
W. The origin (0,0,0) is located at the center point at the interface between the two layers (
Fig. 2).
According to differential geometry, the strains in the passive and active layers are given by
| | 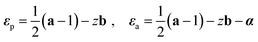 | (3) |
where
α =
α1 is the isotropic active strain,
a and
b are the first and the second fundamental forms satisfying
| |  | (4) |
the vector
R =
R(
x,
y) denotes deformed coordinates of the bilayer, and other quantities in
eqn (4) satisfy
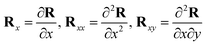
,
etc. Based on
eqn (2)–(4),
Ue can be obtained for a given
R(
x,
y).
The x–y plane of the bilayer is in the horizontal plane (perpendicular to the gravity direction), and thus the gravity potential energy is given by
| | 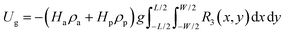 | (5) |
where
R3(
x,
y) is the third component (
z-direction) of vector
R(
x,
y),
ρ and
g are the density and acceleration due to gravity, respectively. In the following, we introduce an explicit deformed configuration
R(
x,
y) and specialize it into the case of cylindrical bending mode to obtain the solution for the bending curvature.
2.1.2 Special solutions for a cylindrical shape.
Following Liu et al.,14 the deformed shape of the bilayer is assumed to be| | 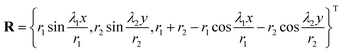 | (6) |
where λ1 and λ2 are stretches in the x and y directions, respectively, and r1 and r2 are corresponding cylindrical radii after the bending deformation. Substituting eqn (6) into eqn (4), we obtain| | 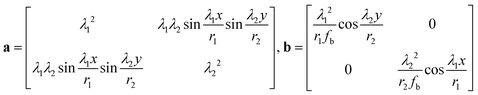 | (7) |
where 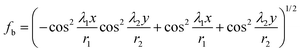 .
.
To obtain an explicit expression for Ue, we take the first order Taylor expansion of a and b at the origin (0,0), and consider the case for small deformation, i.e., λ1 ∼ 1 and λ2 ∼ 1. Then, strain tensor in eqn (3) is given by
| | 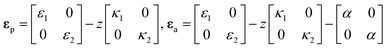 | (8) |
where the in-plane strains
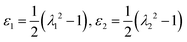
and the curvatures
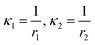
. Using
eqn (8) in
eqn (2), we can obtain the expression for the strain energy
Ue (the tedious expression is not shown here).
To obtain Ug, we compute the first-order Taylor approximation of R3(x,y) (eqn (6)) under the conditions λ1 ∼ 1 and λ2 ∼ 1, and obtain 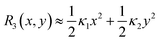 . Using this relation, the gravitational energy Ug is given by
. Using this relation, the gravitational energy Ug is given by
| | 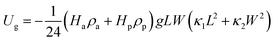 | (9) |
We can see that
Ug is proportional to the thickness
Ha and
Hp, and shows cubic dependence on
L or
W. Using the obtained
Ue and
Ug, the four unknowns can be solved by minimization of the total potential energy
U =
Ue −
Ug,
| | 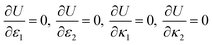 | (10) |
Considering a special case of interest that the bilayer bends into a cylindrical shape in the x direction (i.e., the long side) with vanishing curvature in the y direction (i.e., κ2 = 0), and assuming that νa = νp = ν, we obtain an analytical solution for the curvature
| | 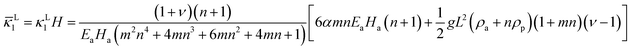 | (11) |
where
H =
Ha +
Hp is the total thickness and
m =
Ep/
Ea and
n =
Hp/
Ha. The in-plane strains are given by
| | 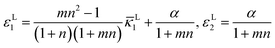 | (12) |
It can be observed that if the gravity effect is ignored, i.e., ρag = ρpg = 0, the solution reduces to the case considered in previous studies,14,18
| | 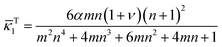 | (13) |
If the Poisson's effect is neglected (
ν = 0) or the transverse active strain is not included (
i.e.,
α = diag(1,0)),
eqn (13) reduces the classical Timoshenko's solution in 2D cases,
15i.e.,
| | 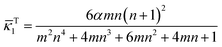 | (14) |
Due to
ν − 1 < 0, it gives that
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) T1
T1 >
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1
L1, indicating an intuitive fact that the bending degree of the bilayer is reduced by gravity.
Another possible deformation mode is that the film bends along the y direction (the short side) with κ1 = 0. Following the same procedure, we obtain the corresponding bending curvature showing a similar structure to eqn (11),
| | 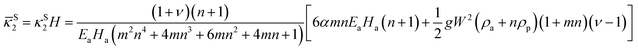 | (15) |
Comparing
eqn (11) and (15), we see that
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1
L1 <
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2
S2 due to
L >
W and
ν − 1 < 0. Considering the relation
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2
S2 <
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) T1
T1, we further obtain that
We observe that the size parameters
L and
W do not come into play in Timoshenko's solution
(14), while they have a significant effect on the curvatures
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1
L1 or
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2
S2 when the gravity effect is considered. In the following, we calculate and compare the total potential energy for LS and SS bending modes, so that we can determine the preferred bending mode which corresponds to the lower energy state among the two.
2.1.3 Energy difference between the two bending modes.
To compare the energy difference between the two bending directions, we define a quantitywhere US and UL are the total potential energy corresponding to the SS and LS bending modes, respectively. The bilayer tends to bend along the SS direction (the y-direction) if ΔU < 0 or US < UL, and vice versa. To obtain an analytical expression for ΔU, we introduce an intermediate variable ζ that controls the active strain α,| | 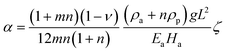 | (18) |
where ζ ≥ 1 controls the magnitude of α. From eqn (11) and (15), we see that when ζ = 1, the curvatures for the two bending modes satisfy ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2 >
S2 > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1 = 0.
L1 = 0.
To compute UL, we first use eqn (18) in κL1 (eqn (11)), and then substitute the obtained κL1, the in-plane strains εL1, εL2 (eqn (12)) and κL2 = 0 into eqn (2) and (9). The potential energy for SS bending mode, US can be obtained in a similar manner. Then, the energy difference (eqn (17)) between the two bending modes is obtained by
| | 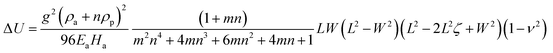 | (19) |
In
eqn (19), because
ζ ≥ 1 and
L >
W, we have
L2 − 2
L2ζ +
W2 < 0, and thus
This indicates that under the considered assumptions, the SS bending mode corresponds to the lower energy state than the LS bending one and becomes the preferred deformation mode when the influence of gravity is non-negligible. In contrast, if the gravity effect is negligible (
g = 0 in
eqn (19)), we obtain Δ
U = 0 or
US =
UL, which means that the two stable states have the same potential energy. In such a scenario, the edge effect dominates the bending behavior and the LS bending is the preferred deformation mode corresponding to a lower energy state.
17 These results indicate a trend that the bilayer tends more and more to bend along the SS as |Δ
U| increases,
i.e.,
| | | |ΔU| ↗⇒ Short-side bending; |ΔU| ↘⇒ Long-side bending | (21) |
where ‘↗’ and ‘↘’ denote the increase and decrease of |Δ
U|, respectively. In the next section, we will discuss the relationship between the bending mode and the energy difference in more detail.
2.2 Factors determining the bending behavior
In this section, we discuss the size-dependent bending in bilayer films (Fig. 2) by combining finite element results and the expression for energy difference in eqn (19). To address the effects of material and geometrical parameters explicitly, we consider a special case for ρ = ρa = ρp, and rewrite the absolute value of ΔU (eqn (19)) as| | 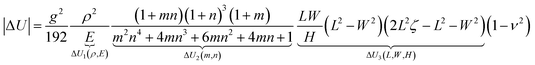 | (22) |
where E = (Ea + Ep)/2 and H = Ha + Hp, and ΔU1, ΔU2 and ΔU3 denote contributions to energy difference from the material properties, the property distinction between the two layers and the overall geometry, respectively. The finite element analysis is conducted using commercial software Abaqus and thermal strains are applied in the active layer to mimic the effect of the active isotropic expansion of the material. Once actuated by a certain value of active strain, the bilayer bends along the direction with lower total potential energy. Other numerical approaches such as the shell-based finite element method30 could also be efficient to complete the simulation. Note that the finite element model can capture both the gravity effect and the so-called edge effect addressed by Alben et al.26 The analytical expression for the curvature in eqn (19) shows good agreement with the finite element results (Fig. S5, ESI†).
The size effect is mainly determined by the term ΔU3(L,W,H) in eqn (19), i.e.,
| | 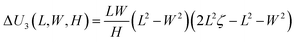 | (23) |
In the finite element calculation, we vary the size parameters
L,
W and
H and keep other parameters constant
E = 1 MPa,
ν = 0.3,
ρ = 1.8 × 10
3 kg m
−3,
α = 0.1 and
m =
n = 1. The first case is for
H = 0.2 mm for different in-plane sizes
L and
W. As shown in
Fig. 3a, the finite element simulation produces three deformation modes (denoted by triangles with different colors), including LS, SS and partial LS bending. Based on the simulation results, we identify three phase regions that distinguish the three bending modes (
Fig. 3a). Note that, in the simulation, we consider the cases for
L >
W, and the other half phase diagram for
L <
W is obtained by using symmetry of the bilayer geometry. The deformed configurations for the three bending modes are shown in
Fig. 3b at phase points
A,
B and
C. The SS bending is observed when the size of the film is small enough, while the LS bending dominates when the film size becomes large enough (points
A and
B,
Fig. 3b). For a narrow but long bilayer (large
L and small
W), partial LS bending is observed (point
C,
Fig. 3b). It is interesting to observe that even a small difference between
L and
W can lead to the size-dependent bending, as shown for the points near the symmetric axis
L =
W in
Fig. 3a. Note that if the gravity load is removed in the simulation, we observe that the film bends along the LS (see Fig. S7a, ESI
†).
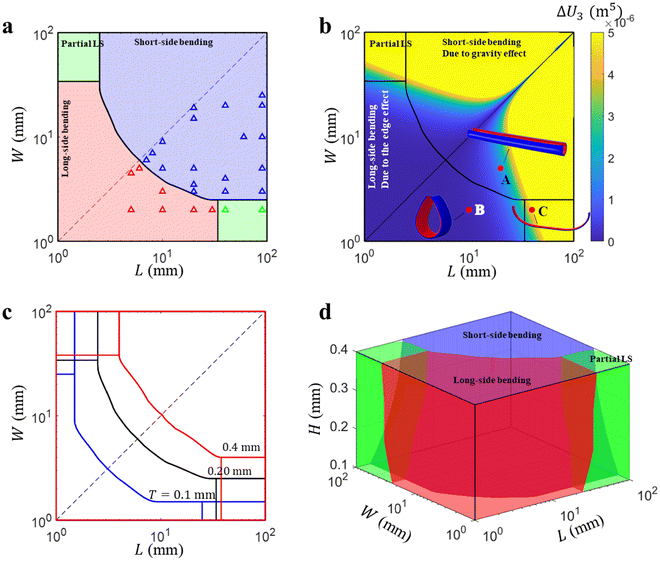 |
| | Fig. 3 (a) Phase diagram for size-dependent bending of the bilayer with the total thickness H = 0.2 mm. The finite element simulation results are marked by red (LS), blue (SS) and green (partial LS) triangles. (b) Variation of ΔU3 with respect to L and W, and three representative bending configurations at A(20, 5), B(10, 2), and C(40, 2) in three phase regions. (c) Comparison of the phase boundaries for different thicknesses H = 0.1, 0.2 and 0.4 mm. (d) The 3D phase diagram for size-dependent bending. | |
The quantity ΔU3(L,W,H) (or |ΔU|, eqn (22)) increases with either L or W (see Fig. 3b), and thus the film tends to bend along the SS as the size L or W increases (Fig. 3a and b). In the phase diagram, the area for LS bending increases with the thickness of the film, H, indicating that as the film becomes thicker, the film tends to bend along the LS, and vice versa (Fig. 3c). Eqn (23) shows that ΔU3 increases with a decrease of H and so does |ΔU|, indicating that the energy for SS bending, US, becomes increasingly smaller than that for the LS bending, UL, and thus, the bilayer tends to bend along the short side as H decreases. These results show that ΔU3 or |ΔU| well characterizes the size-dependent bending of the bilayer. For a special case L ≫ W, we observe partial LS bending (point C, Fig. 3b), which is a result of competition between the SS and LS bending modes. While eqn (20) gives a qualitative estimation of the transition of the bending mode, the phase diagram obtained by finite element simulation quantitatively distinguishes different bending modes for given geometrical parameters. Based on these data, we construct a 3D phase diagram in terms of the three size parameters L, W and T (Fig. 3d), from which the bending direction of a bilayer can be determined based on the phase region where the coordinates (L, W, H) reside.
We then discuss the mechanism of the size-dependent bending by comparing the results obtained in this study and those obtained by Alben et al.26 It can be observed that ΔU3 varies with L and W at the sixth power, which means that for a small-sized bilayer (i.e., small L and W), the gravity effect is negligible, while it becomes significant for a large-sized one. Since ΔU < 0 or US < UL (eqn (20)), the SS bending is in the lower energy state compared to the LS bending, and the energy gap between the two bending modes becomes more and more significant as L or W increases. This is the underlying mechanism for the observed SS bending for a large-sized film. During the deformation process, the energy associated with bending and stretching decreases, while that due to gravity increases because the material is lifted due to upward bending. Furthermore, from eqn (9), we find that −Ug ∼ ULg = κ1L3W for LS bending (κ2 = 0) and −Ug ∼ USg = κ2LW3 for SS bending (κ1 = 0). It is clear to see that κ1L3W > κ2LW3 for L > W, which means that the SS sided bending indeed has lower gravitational potential energy and thus becomes the preferred deformation mode. For a small-sized bilayer, the edge effect dominates, and the LS bending corresponds to lower energy than the SS bending because according to the calculation in Alben et al.,26 the length of the edge layer for LS bending with nearly zero energy is greater than that of SS bending, leading to lower total strain energy for the former than the later. Thus, we may conclude that when the gravity effect is negligible for a small-sized bilayer, it bends along the LS direction due to the edge effect; for a large-sized bilayer with a significant gravity effect, the SS bending is preferred as a result of competition between the strain energy and the gravitational energy.
The other two terms that influence |ΔU| (eqn (22)) are
| | 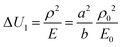 | (24) |
and
| | 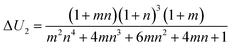 | (25) |
where
a and
b are two non-dimensional parameters satisfying
ρ =
aρ0 and
E =
bE0, respectively. The distributions of Δ
U2 and
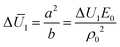
for a bilayer with
L ×
W ×
H = 20 × 5 × 0.4 mm
3 are shown in
Fig. 4a and b, respectively, in which, the bending modes at some representative points are also given. A common feature in
Fig. 4a and b is that the SS bending mode roughly appears when Δ
U2 and
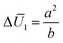
are large values (
e.g., Δ
U2 ≥ 2.5 and
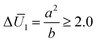
), and it transforms into the LS bending mode as Δ
U2 or
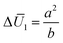
decreases. Those observations based on
Fig. 3a and b and
Fig. 4 quantitatively justify the principle for bending mode transition due to the gravity effect summarized in
eqn (21). Note that Δ
U2 in
Fig. 4a shows mirror symmetry since it can be shown that
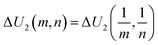
.
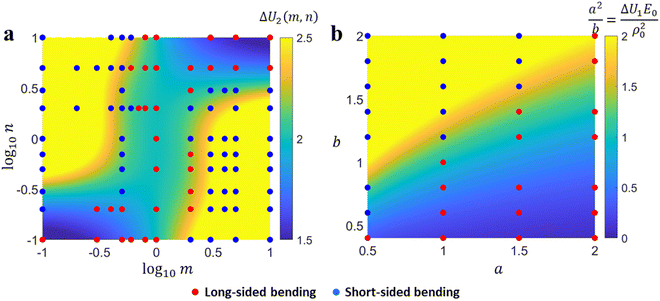 |
| | Fig. 4 Variation of (a) ΔU2 and (b) ΔŪ1 = a2/b, and some representative phase points obtained by the finite element simulation. The red circles and blue circles denote the LS and SS bending modes, respectively. Other parameters are (a) ρ = 1.8 × 103 kg m−3, E = 1 MPa and (b) m = n = 1, ρ0 = 1.8 × 103 kg m−3, and E0 = 1 MPa. The size parameters are H = 0.4 mm, L = 20 mm and W = 5 mm. | |
3. Bending of the fluoroelastomer film
In section 2, we show the profound influence of gravity on the selective bending of large-sized active rectangular bilayers. In this section, we further discuss the size-dependent bending of the fluoroelastomer film. Compared to the bilayer model, the deformation of the fluoroelastomer film placed on an acetone-soaked filter paper is involved with transient, inhomogeneous swelling and there are no clear layer-like geometric characteristics across the thickness direction. Thus, it is significant to introduce a finite element model for coupled large deformation and fluid permeation in the film and reveal the mechanism for the size-dependent bending behavior of the film.
3.1 Finite element model
As shown in Fig. 1, the deformation of the fluoroelastomer film is a process coupled with finite deformation and acetone diffusion. Thus, we may introduce the governing equations as follows| | | Balance of momentum: ∇·P + b = 0 | (26) |
and| | 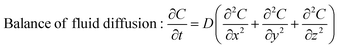 | (27) |
where P is the nominal stress, b = ρgz is the body force per unit volume with ρ the density of the material, g is the acceleration of gravity and z is the direction of gravity, C is the acetone concentration per unit volume, and D is the diffusion coefficient. Here, a Darcy-type law is used to describe the diffusion process, i.e., j = D∇C, where D is the diffusion coefficient and C is the acetone concentration per unit volume. It is noted that force b should be considered here similar to the bilayer cases to capture the size-dependent bending behavior of the rectangular films.
Though such a module for direct modeling of the coupled process is not available in Abaqus, we make an analogy between acetone diffusion and heat transfer and do the analysis using the thermo-displacement module in finite element software Abaqus. The details for the analogy are addressed in section S1 and S2 in the ESI.† The film material is described by an incompressible Mooney–Rivlin hyperelastic model and all the constitutive parameters are calibrated using experimental data (see details in the ESI†). We use fine enough mesh to perform the finite element simulation and the convergence of the results is verified. A quantitative comparison between the displacements obtained by simulation and experiment for a typical sample indicates the accuracy of the finite element model (see Fig. S6 in the ESI†).
3.2 Size-dependent bending
We conduct multiple finite element simulations for different sizes of the film (i.e., different L and W) with a fixed thickness H = 420 μm. Similar to the bilayers, the film reaches a stable bending state with lower energy, and we again identify three kinds of bending modes, including LS, SS, and partial LS bending based on multiple simulations (Fig. 5a). We divide the domain L × W into three distinct phase regions (Fig. 5a) that distinguish the different bending behavior for given values of L and W. The results show similar overall features to those of bilayers in section 2.2. For example, when the film sizes L and W are relatively small (red region in Fig. 5a), it bends along the long side, and it transits to short-side bending as the size increases (blue region). If L and W differ largely from each other (i.e., a narrow strip), the film shows partial LS bending with its middle region attached to the substrate. If the gravity effect is removed in the simulation, we observe that the film constantly bends along the LS (see e.g., Fig. S7b, ESI†).
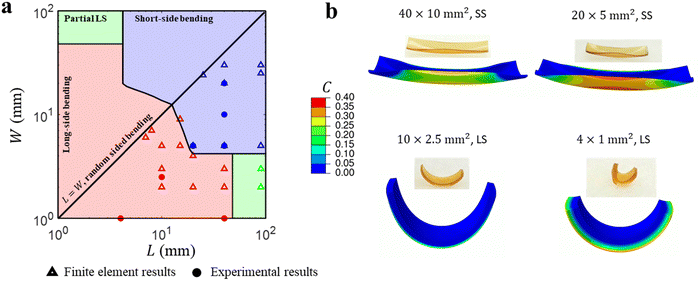 |
| | Fig. 5 (a) Phase diagram for the size-dependent bending behavior with fixed thicknesses H = 420 μm. Three bending modes can be identified, including SS, LS and partial LS. The numerical results are denoted by triangles (△) and the experimental results by solid circles (●). (b) Comparison of the bending deformation between experimental and finite element results for a fixed thickness H = 420 μm and an aspect ratio L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W = 4 W = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The contour denotes the acetone concentration or swelling strain. 1. The contour denotes the acetone concentration or swelling strain. | |
The bending modes observed in the experiments for H = 420 μm are all located in the desired phase region (Fig. 5a), indicating the accuracy of the simulation results and phase diagrams. Fig. 5b shows good agreement of the bending deformation for different overall sizes with 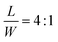 and H = 420 μm. For the case of H = 900 μm, we also observe good agreement of the deformation modes between the experiment and simulation (Fig. S8 in the ESI†). Note that, similar to the bilayers, the phase regions have a symmetric axis L = W due to the symmetry of geometry of a rectangular film and in this special case (L = W), the film can bend along either side. Even if there is a little difference between L and W, the size-dependent preferred bending is observed (see finite element results (△) near the symmetry axis L = W in Fig. 5a and Fig. S8a, ESI†).
and H = 420 μm. For the case of H = 900 μm, we also observe good agreement of the deformation modes between the experiment and simulation (Fig. S8 in the ESI†). Note that, similar to the bilayers, the phase regions have a symmetric axis L = W due to the symmetry of geometry of a rectangular film and in this special case (L = W), the film can bend along either side. Even if there is a little difference between L and W, the size-dependent preferred bending is observed (see finite element results (△) near the symmetry axis L = W in Fig. 5a and Fig. S8a, ESI†).
Compared to the applied uniform active strain in the bilayer, the fluoroelastomer film shows a larger swelling degree (denoted by the acetone concentration C, see the ESI†) in the middle bottom side than the other region (Fig. 5b) since the middle region is in continuous contact with the acetone-soaked filter paper in the bending process. This leads to a large bending curvature in the middle region (e.g., the case of 10 × 2.5 mm in Fig. 5b), while the bilayer deforms into a cylindrical shape showing a nearly uniform curvature (Fig. S7a, ESI†). In addition, due to the non-homogeneous swelling and the gravity effect, the bending shape of the fluoroelastomer film is not a perfect cylinder (Fig. 5b and Fig. S7b, ESI†), while for the bilayer model with homogeneous swelling in the active layer, the deformed shape closely resembles a cylinder (Fig. S7a, ESI†), which verifies the assumptions addressed earlier.
The phase boundaries for three thicknesses H = 0.1, 0.42 and 0.9 mm are shown in Fig. 6a. Again, similar to the results for the bilayers, as thickness H increases, the phase region for the LS bending mode increases in area, while those of the other two regions shrink within the range of interest of the film sizes (Fig. 6a). This means that for the same in-plane dimensions L and W, a thick film tends to bend along the long side while a thin one inclines to bend along the short side. Using the 2D phase diagrams for multiple  , we construct a 3D phase diagram (Fig. 6b), from which, the bending mode of a film can be identified based on the specific phase region where its size coordinate (L, W, H) resides. The 3D phase diagram provides a global map for determining the bending direction of the film based on its size.
, we construct a 3D phase diagram (Fig. 6b), from which, the bending mode of a film can be identified based on the specific phase region where its size coordinate (L, W, H) resides. The 3D phase diagram provides a global map for determining the bending direction of the film based on its size.
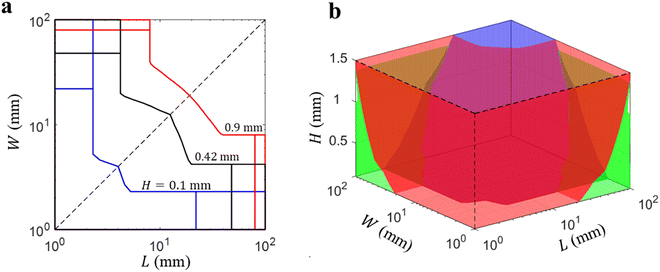 |
| | Fig. 6 (a) Phase boundaries for the size-dependent bending behavior for different thicknesses H = 0.1, 0.42 and 0.9 mm. (b) The 3D phase diagram. Red region: LS bending; blue region: SS bending; and green region: partial LS bending. | |
We then employ the expression for ΔU3(L,W,H) in eqn (23) to explain more about the experimental observations and numerical simulation in various parameter settings. We highlight again that the increase of ΔU3 means that the gravity effect becomes the dominant factor and the film shall bend along the SS; In contrast, a decrease of ΔU3 indicates the increasing importance of the edge effect which will lead to LS bending.26 For the cases discussed here, it is straightforward to see that decreasing H with fixed L and W or increasing either L or W with fixed H leads to the increase of ΔU3, and a transition from LS bending to the SS bending is expected as observed in both the experiments and simulations. In addition, we also conduct simulation and experimental study for right triangle films with a fixed edge ratio l1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l2
l2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l3 = 3
l3 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and varying overall sizes. The results show similar conclusions to those of rectangular films, that is, large-sized films tend to be affected by gravity and bend along the short side (with a long bending axis) (Fig. S9, ESI†).
5 and varying overall sizes. The results show similar conclusions to those of rectangular films, that is, large-sized films tend to be affected by gravity and bend along the short side (with a long bending axis) (Fig. S9, ESI†).
4. Conclusions
In this paper, we investigate the size-dependent bending behavior of a rectangular fluoroelastomer film placed on an acetone-soaked filter paper due to inhomogeneous swelling upon the absorption of acetone. Specifically, we observed short-side bending for large-size films while it transits to long-side bending when its size becomes smaller. We found that gravity is the factor that determines the size-dependent bending behavior. To explore the gravity effect, we first constructed a bilayer model which renders the analytical analysis tractable and results in a quantity (eqn (22)) that measures the importance of gravity in determining the bending direction. We construct finite element models for modeling the bending of bilayers and the fluoroelastomer under the influence of gravity. The simulation results agree quantitatively with the experimental results, and are consistent with the analytical results for the bilayer model. Based on the finite element results, we obtain phase diagrams for the size-dependent bending, from which the LS and SS bending modes can be determined. The analytical results and the finite element simulation indicate that gravity is the key factor that leads to the size-dependent bending phenomenon. These findings may provide broader insights into the design of swelling-based soft machines, such as soft deformable sensors and functional circuits on curved surfaces,31,32 locomotive robots5,33 and origami structures.6,9
Based on this work, we may further explore the gravity effect in other scenarios as well. For example, if the film is placed in outer space where gravity is absent, the size-dependent bending behavior cannot be observed. When the rectangular bilayer film is immersed in a solution to swell, we expect that the gravity effect is weakened by the buoyancy force4 and its bending behavior may be different from that of the one placed on a substrate (like the acetone-soaked filter paper here). As the film becomes small enough (e.g., on the scale of micro- or nanometer), the adhesive force between the film and the substrate may be another important factor determining the bending direction.29,34 It remains unknown whether gravity has an influence on the bending behavior of polygonal shaped films or not.23
The obtained results provide the opportunity to manipulate the bending direction of an active film by varying material and geometrical parameters and thus may facilitate the design of actuators capable of bending in the desired direction. In addition, when the film size is large enough (e.g., L = 100 mm, W = 90 mm and H = 0.42 mm), we observe in the experiment that the film first rolls up at the four edges, and then snaps into the SS bending mode due to dynamic instability. In such cases, the Riks path-following method35,36 can be helpful to study the shape transition between different stable states of the film under the influence of gravity.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The authors are grateful for the financial support from the National Robotics Programme, NRF, Singapore (Grant Reference No: W2025d0244).
References
- A. Agrawal, T. Yun, S. L. Pesek, W. G. Chapman and R. Verduzco, Soft Matter, 2014, 10, 1411–1415 RSC.
- J. M. Boothby and T. H. Ware, Soft Matter, 2017, 13, 4349–4356 RSC.
- A. I. Egunov, J. G. Korvink and V. A. Luchnikov, Soft Matter, 2016, 12(1), 45–52 RSC.
- J. C. Athas, C. P. Nguyen, S. Kummar and S. R. Raghavan, Soft Matter, 2018, 14, 2735–2743 RSC.
- B. Shin, J. Ha, M. Lee, K. Park, G. H. Park, T. H. Choi, K.-J. Cho and H.-Y. Kim, Sci. Robot., 2018, 3, eaar2629 CrossRef PubMed.
- J. Cui, J. G. M. Adams and Y. Zhu, Smart Mater. Struct., 2018, 27, 055009 CrossRef.
- N. A. Caruso, A. Cvetković, A. Lucantonio, G. Noselli and A. DeSimone, Int. J. Mech. Sci., 2018, 149, 481–486 CrossRef.
- G. Stoychev, S. Turcaud, J. W. C. Dunlop and L. Ionov, Adv. Funct. Mater., 2013, 23, 2295–2300 CrossRef CAS.
- P. Tyagi, N. Bassik, T. G. Leong, J.-H. Cho, B. R. Benson and D. H. Gracias, J. Microelectromech. Syst., 2009, 18, 784–791 CAS.
- C. Dawson, J. F. V. Vincent and A.-M. Rocca, Nature, 1997, 390, 668 CrossRef CAS.
- M. J. Harrington, K. Razghandi, F. Ditsch, L. Guiducci, M. Rueggeberg, J. W. C. Dunlop, P. Fratzl, C. Neinhuis and I. Burgert, Nat. Commun., 2011, 2, 337 CrossRef PubMed.
- T. Wang, A. Ramnarayanan and H. Cheng, Sensors, 2018, 18, 5 CrossRef PubMed.
- A. Jderu, D. Dorobantu, D. Ziegler and M. Enachescu, Photonic Sens., 2022, 12, 99–104 CrossRef CAS.
- Y. Liu, Y. Cao, X.-Q. Feng and C. Cao, Extreme Mech. Lett., 2019, 29, 100467 CrossRef.
- S. Timoshenko, JOSA, 1925, 11, 233–255 CrossRef CAS.
- G. G. Stoney, Proc. R. Soc. London, Ser. A, 1909, 82, 172–175 CAS.
- S. Alben, Adv. Comput. Math., 2015, 41, 1–22 CrossRef.
- C. Chen, P. Song, F. Meng, X. Li, X. Liu and J. Song, Nanotechnology, 2017, 28, 485302 CrossRef PubMed.
- J. Zang and F. Liu, Appl. Phys. Lett., 2008, 92, 021905 CrossRef.
- A. Lucantonio, P. Nardinocchi and M. Pezzulla, Proc. R. Soc. Math. Phys. Eng. Sci., 2014, 470, 20140467 CAS.
- N. J. Salamon and C. B. Masters, Int. J. Solids Struct., 1995, 32, 473–481 CrossRef.
- L. B. Freund, J. Mech. Phys. Solids, 2000, 48, 1159–1174 CrossRef CAS.
- A. M. Abdullah, P. V. Braun and K. J. Hsia, Appl. Phys. Lett., 2017, 111, 104101 CrossRef.
- M. W. Hyer, J. Compos. Mater., 1982, 16, 318–340 CrossRef.
- Z. Chen, Q. Guo, C. Majidi, W. Chen, D. J. Srolovitz and M. P. Haataja, Phys. Rev. Lett., 2012, 109(11), 114302 CrossRef PubMed.
- S. Alben, B. Balakrisnan and E. Smela, Nano Lett., 2011, 11, 2280–2285 CrossRef CAS PubMed.
- Y. Liu, H. Zhang, J. Wang and Y. Zheng, Int. J. Appl. Mech., 2016, 08, 1640003 CrossRef.
- M. Pezzulla, G. P. Smith, P. Nardinocchi and D. P. Holmes, Soft Matter, 2016, 12, 4435–4442 RSC.
- G. Stoychev, S. Zakharchenko, S. Turcaud, J. W. C. Dunlop and L. Ionov, ACS Nano, 2012, 6, 3925–3934 CrossRef CAS PubMed.
- Y. Zheng, J. Wang, H. Ye, Y. Liu and H. Zhang, Int. J. Solids Struct., 2019, 163, 87–101 CrossRef.
- W. Zhang, L. Zhang, Y. Liao and H. Cheng, Int. J. Extreme Manuf., 2021, 3, 042001 CrossRef CAS.
- N. Yi, Y. Gao, A. Lo Verso, J. Zhu, D. Erdely, C. Xue, R. Lavelle and H. Cheng, Mater. Today, 2021, 50, 24–34 CrossRef CAS PubMed.
- X. He, Y. Sun, J. Wu, Y. Wang, F. Chen, P. Fan, M. Zhong, S. Xiao, D. Zhang, J. Yang and J. Zheng, J. Mater. Chem. C, 2019, 7, 4970–4980 RSC.
- I. S. Chun, A. Challa, B. Derickson, K. J. Hsia and X. Li, Nano Lett., 2010, 10, 3927–3932 CrossRef CAS PubMed.
- Y. Liu, S. Liang, Q. Huang, H. Hu, Y. Zheng, H. Zhang and Q. Shao, Comput. Methods Appl. Mech. Eng., 2017, 323, 416–438 CrossRef.
- G. Wan, Y. Cai, Y. Liu, C. Jin, D. Wang, S. Huang, N. Hu, J. X. J. Zhang and Z. Chen, Extreme Mech. Lett., 2021, 42, 101065 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Xuemei
Fu‡
a,
Xuemei
Fu‡
 b,
Ruochen
Yang‡
b,
Ruochen
Yang‡
 b,
Jun
Liu
b,
Jun
Liu
 a,
Benjamin Chee Keong
Tee
a,
Benjamin Chee Keong
Tee
 bc and
Zhuangjian
Liu
bc and
Zhuangjian
Liu
 *a
*a
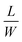 and the thickness H as constants (e.g.,
and the thickness H as constants (e.g., 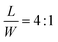 , H = 420 μm), the film tends to bend along the LS for small L and along the SS for large L (Fig. 1c). (iii) Increasing the ratio
, H = 420 μm), the film tends to bend along the LS for small L and along the SS for large L (Fig. 1c). (iii) Increasing the ratio 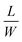 for fixed H and L leads to a shape transition from SS to LS bending (Fig. 1d, Movies S1 and S2). These observations indicate that the bending direction of the rectangular polymer film depends on all of its three geometrical parameters L, W and H.
for fixed H and L leads to a shape transition from SS to LS bending (Fig. 1d, Movies S1 and S2). These observations indicate that the bending direction of the rectangular polymer film depends on all of its three geometrical parameters L, W and H.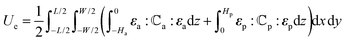
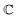 is the elastic tensor of the plate with components
is the elastic tensor of the plate with components 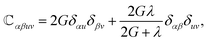 α, β, u, v = 1, 2, G and λ are Lamé constants and are related to the elastic modulus E and the Poisson's ratio ν by
α, β, u, v = 1, 2, G and λ are Lamé constants and are related to the elastic modulus E and the Poisson's ratio ν by 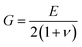 and
and 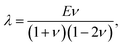 L and W are the length and width of the bilayer, respectively. In the following, due to symmetry in the geometry, we consider the case for L > W. The origin (0,0,0) is located at the center point at the interface between the two layers (Fig. 2).
L and W are the length and width of the bilayer, respectively. In the following, due to symmetry in the geometry, we consider the case for L > W. The origin (0,0,0) is located at the center point at the interface between the two layers (Fig. 2).
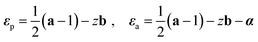

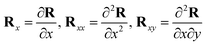 , etc. Based on eqn (2)–(4), Ue can be obtained for a given R(x,y).
, etc. Based on eqn (2)–(4), Ue can be obtained for a given R(x,y).
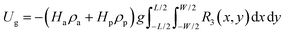
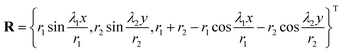
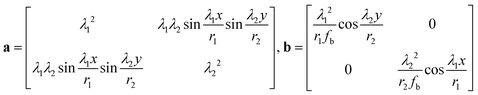
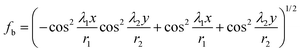 .
.
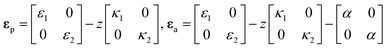
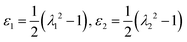 and the curvatures
and the curvatures 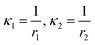 . Using eqn (8) in eqn (2), we can obtain the expression for the strain energy Ue (the tedious expression is not shown here).
. Using eqn (8) in eqn (2), we can obtain the expression for the strain energy Ue (the tedious expression is not shown here).
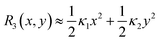 . Using this relation, the gravitational energy Ug is given by
. Using this relation, the gravitational energy Ug is given by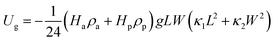
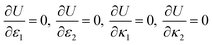
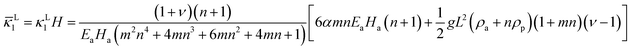
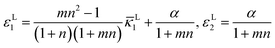
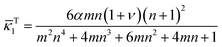
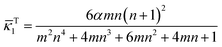
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) T1 >
T1 > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1, indicating an intuitive fact that the bending degree of the bilayer is reduced by gravity.
L1, indicating an intuitive fact that the bending degree of the bilayer is reduced by gravity.
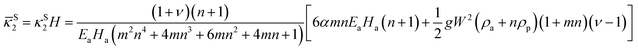
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1 <
L1 < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2 due to L > W and ν − 1 < 0. Considering the relation
S2 due to L > W and ν − 1 < 0. Considering the relation ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2 <
S2 < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) T1, we further obtain that
T1, we further obtain that![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1 <
L1 < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2 <
S2 < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) T1
T1![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1 or
L1 or ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2 when the gravity effect is considered. In the following, we calculate and compare the total potential energy for LS and SS bending modes, so that we can determine the preferred bending mode which corresponds to the lower energy state among the two.
S2 when the gravity effect is considered. In the following, we calculate and compare the total potential energy for LS and SS bending modes, so that we can determine the preferred bending mode which corresponds to the lower energy state among the two.
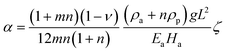
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) S2 >
S2 > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) L1 = 0.
L1 = 0.
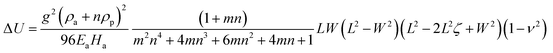
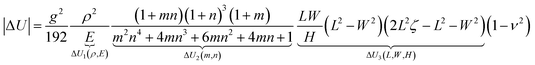
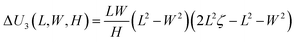
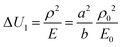
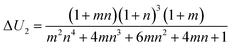
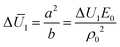 for a bilayer with L × W × H = 20 × 5 × 0.4 mm3 are shown in Fig. 4a and b, respectively, in which, the bending modes at some representative points are also given. A common feature in Fig. 4a and b is that the SS bending mode roughly appears when ΔU2 and
for a bilayer with L × W × H = 20 × 5 × 0.4 mm3 are shown in Fig. 4a and b, respectively, in which, the bending modes at some representative points are also given. A common feature in Fig. 4a and b is that the SS bending mode roughly appears when ΔU2 and 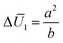 are large values (e.g., ΔU2 ≥ 2.5 and
are large values (e.g., ΔU2 ≥ 2.5 and 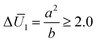 ), and it transforms into the LS bending mode as ΔU2 or
), and it transforms into the LS bending mode as ΔU2 or 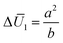 decreases. Those observations based on Fig. 3a and b and Fig. 4 quantitatively justify the principle for bending mode transition due to the gravity effect summarized in eqn (21). Note that ΔU2 in Fig. 4a shows mirror symmetry since it can be shown that
decreases. Those observations based on Fig. 3a and b and Fig. 4 quantitatively justify the principle for bending mode transition due to the gravity effect summarized in eqn (21). Note that ΔU2 in Fig. 4a shows mirror symmetry since it can be shown that 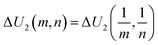 .
.
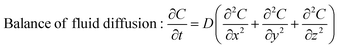
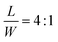 and H = 420 μm. For the case of H = 900 μm, we also observe good agreement of the deformation modes between the experiment and simulation (Fig. S8 in the ESI†). Note that, similar to the bilayers, the phase regions have a symmetric axis L = W due to the symmetry of geometry of a rectangular film and in this special case (L = W), the film can bend along either side. Even if there is a little difference between L and W, the size-dependent preferred bending is observed (see finite element results (△) near the symmetry axis L = W in Fig. 5a and Fig. S8a, ESI†).
and H = 420 μm. For the case of H = 900 μm, we also observe good agreement of the deformation modes between the experiment and simulation (Fig. S8 in the ESI†). Note that, similar to the bilayers, the phase regions have a symmetric axis L = W due to the symmetry of geometry of a rectangular film and in this special case (L = W), the film can bend along either side. Even if there is a little difference between L and W, the size-dependent preferred bending is observed (see finite element results (△) near the symmetry axis L = W in Fig. 5a and Fig. S8a, ESI†). , we construct a 3D phase diagram (Fig. 6b), from which, the bending mode of a film can be identified based on the specific phase region where its size coordinate (L, W, H) resides. The 3D phase diagram provides a global map for determining the bending direction of the film based on its size.
, we construct a 3D phase diagram (Fig. 6b), from which, the bending mode of a film can be identified based on the specific phase region where its size coordinate (L, W, H) resides. The 3D phase diagram provides a global map for determining the bending direction of the film based on its size.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l2
l2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l3 = 3
l3 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and varying overall sizes. The results show similar conclusions to those of rectangular films, that is, large-sized films tend to be affected by gravity and bend along the short side (with a long bending axis) (Fig. S9, ESI†).
5 and varying overall sizes. The results show similar conclusions to those of rectangular films, that is, large-sized films tend to be affected by gravity and bend along the short side (with a long bending axis) (Fig. S9, ESI†).





