Open Access Article
Open Access ArticleSwelling kinetics of constrained hydrogel spheres
Théotime
Cano†
ab,
Hyeonuk
Na†
 c,
Jeong-Yun
Sun
c,
Jeong-Yun
Sun
 *ce and
Ho-Young
Kim
*ce and
Ho-Young
Kim
 *ad
*ad
aDepartment of Mechanical Engineering, Seoul National University, Seoul 08826, South Korea. E-mail: hyk@snu.ac.kr
bÉcole des Mines de Saint-Étienne, Saint-Étienne 42100, France
cDepartment of Materials Science and Engineering, Seoul National University, Seoul 08826, South Korea. E-mail: jysun@snu.ac.kr
dInstitute of Advanced Machines and Design, Seoul National University, Seoul 08826, South Korea
eResearch Institute of Advanced Materials (RIAM), Seoul National University, Seoul 08826, South Korea
First published on 10th November 2023
Abstract
A cross-linked polymer network immersed in a solvent will absorb molecules from its surroundings, leading to transient swelling. Under the constraint of a semi-permeable membrane, the system will swell less and generate a larger internal pressure in return, a system rarely analyzed to date. We use a nonlinear poroelastic theory to model the kinetics of swelling under mechanical constraint. We find the simulation results agree well with our experimental data using hydrogel beads made of a mixture of 3-sulfopropyl acrylate potassium salt and acrylamide, bathed in water. Understanding and predicting the response speed and the actuation stress developed during the swelling of constrained hydrogels can guide the design of polymer-based soft actuators with unusually high strength.
1. Introduction
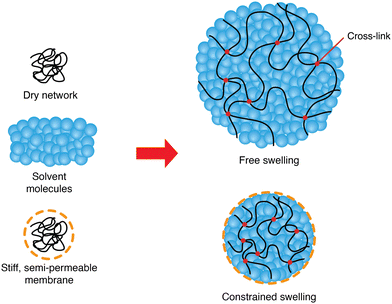
A three-dimensional polymer network can be created by cross-linking long polymers. Immersed in a solvent, this network may absorb molecules from its surroundings, thus creating a mixture called a polymer gel. If the solvent is water, it is referred to as a hydrogel. Bathed in a solvent and under no external constraint, the gel will swell by absorbing new solvent molecules until it reaches equilibrium.Gels are widely used in micromechanical systems as autonomous flow controllers,1 pH sensors2 or actuators;3 in biology for injury repair4 or as carriers for drug delivery5 and in soft robotics as stimuli-responsive muscle-like systems.6 They are biocompatible, similar to living tissues and adjustable in shapes and chemical properties.7 A major flaw exists, however, namely their slow response speed which was shown to be enhanced using electro-osmosis.3
In the field of hydrogel-based soft robotics, there is a growing need for actuators that can generate substantial forces while maintaining precise control, similar to what is achievable with rigid robots. In our prior study,3 we introduced a method to harness large swelling forces using a constrained system consisting of a hydrogel wrapped with a stiff semi-permeable membrane. However, we still lack mathematical understanding of how stress and strain develop in these constrained hydrogels.
The intrinsic swelling properties of gels have been extensively studied. Historically, one of the first attempts was conducted by Tanaka et al.,8,9 where they considered only the polymer network which swells under the effect of its own osmotic pressure. The effect of the fluid is modeled through the addition of a friction factor in the mechanical balance. Another approach based on Biot's work on soil consolidation,10 and further developed by Scherer,11 treats the gel as a continuum with the pore pressure as a state variable. Biot also later treated the same problem with a mixture theory approach and showed that these approaches are equivalent.12 Hui and Muralidharan13 showed that extending Tanaka's formalism using a momentum balance equation for the fluid leads to Biot's mixture theory. Nonetheless, all these theories are built within the restrictive framework of linear elasticity, whose assumption of small deformations hardly holds for a swelling ratio of several tens or even hundreds reached by some hydrogels including polyacrylamide-based ones.14,15
From a thermodynamic point of view, two processes are dominant in the energetic balance of the swelling. The absorption of water molecules makes the hydrogel swell and the polymer network is stretched in return. When an energetic equilibrium is reached between the energetically favourable absorption and the energetically unfavourable stretching, the swelling stops. An important aspect of hydrogels is that, as they swell, their pores expand. Hence, as the size of the pores is used to characterise the permeability, it should increase throughout the process, drastically affecting the dynamics of the swelling. Hong et al.16 built a theory for large deformations using a thermodynamic approach, based on the works of Flory17 for the mixing part, Huggins18 for the stretching part, and Grattoni19 for the deformation-dependent permeability, among others.
This study aims at analyzing the kinetics of the constrained swelling of a hydrogel coated with a stiff semi-permeable membrane (Fig. 1). In our system, swelling is solely driven by osmosis without external stimuli. When the polymer network absorbs new water molecules through the membrane, the resulting swelling stress of the inner hydrogel is applied on the membrane, which in turn acts as a constraining stress on the gel. Therefore, the constrained hydrogel will only swell slightly, and an important internal pressure will develop. This idea can be used to build hydrogel-based soft actuators, taking advantage of the aforementioned benefits of hydrogels and combining them with unusually high actuating strengths.3 Understanding its physics can allow manufacturers to tailor the strength of their actuators based on their needs and predict its response time, and designers to increase even more their strength or enhance their swelling speed.
First, we will tackle the problem of the kinetics of free swelling, namely the swelling of the hydrogel without the membrane. Then, we will consider the same question with a constrained hydrogel, referring to the swelling sphere composed of an inner core of bare hydrogel and a thin outer layer of stiff semi-permeable membrane (Fig. 1). The addition of a membrane restricts the swelling of the hydrogel, leading to smaller pore sizes within the hydrogel, which results in a reduced final swelling ratio and a slower swelling rate. On the other hand, an important internal pressure driven by the osmotic mixing potential of the polymer can grow dramatically, which can be of interest in many applications of soft actuators.
In the following, we begin with the theoretical analysis. Then, further insights into the internal behaviour during the swelling process are presented through simulations. The swelling tests were conducted on both free and constrained cases (Fig. 2) and the simulated results will be compared with experimental data. Then, the experimentally validated model will be used to perform simulations with other values for the different parameters to understand in more depth their importance. Finally, a comparison with the linear theory of Tanaka et al. is provided,8,9 assuming a linear relationship between stress and strain, will be discussed in view of small deformations in the constrained case.
2. Theoretical analysis
This section presents a combination of the theoretical frameworks proposed by Engelsberg et al.14 and Bertrand et al.,15 which are to be applied to our experimental systems of hydrogel sphere swelling. We note that the models themselves are based on the fundamental work of Hong et al.162.1 Geometry and microscopic incompressibility
We consider the problem of the swelling of a hydrogel sphere, first freely swelling in water and then constrained by a membrane. Let's consider a spherical sphere of initial radius a, the dry state being our reference state. In this study, we ignore the effects of surface instabilities that may arise during the swelling20 and assume a spherical symmetry during the whole swelling process.If ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) r is the unit vector in the radial direction,
r is the unit vector in the radial direction, ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) = R
= R![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) r is the position vector in the reference state and
r is the position vector in the reference state and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (
(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) , t) = r(R, t)
, t) = r(R, t)![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) r is the position vector in the current state at time t. We define F = ∂
r is the position vector in the current state at time t. We define F = ∂![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) /∂
/∂![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) as the gradient deformation tensor, thus assumed diagonal with the following eigenvalues, which are the stretches in the three principal directions,
as the gradient deformation tensor, thus assumed diagonal with the following eigenvalues, which are the stretches in the three principal directions,
| λr = ∂r/∂R, λθ = λϕ = r/R, | (1) |
| J = λrλθλϕ = λrλθ2. | (2) |
We state that the increase in volume of the system (polymer and fluid) can only be due to the addition of water molecules from outside the system. This microscopic incompressibility condition leads to
| 1 + ΩC = det(F) = J = 1/φ, | (3) |
2.2 Free energy density
The fundamental principle behind the swelling of a gel in water is based on two mechanisms. The first one is the spontaneous absorption of water molecules from the solvent to the gel driven by an entropic and/or enthalpic affinity between the polymer and water molecules, a process referred to as the mixing. Due to the additional water molecules, the gel will build an increasing pore pressure which will tend to stretch the cross-linked polymer network and raise the free energy of the system, a process referred to as the stretching. An equilibrium state will be reached when the energetically favourable mixing is exactly compensated by the energetically unfavourable stretching.The basic assumption of the ideal elastomeric gel theory16,21 is that the mixing and the stretching part can be totally separated in the computation of the free energy density W. The stretching part will only depend on the three eigenvalues of the deformation tensor F, and the mixing part will only depend on the amount of additional water molecules C:
| W(F, C) = Wstretch(F) + Wmix(C). | (4) |
W stretch(F) models the elastic contribution to the free energy of an arbitrarily deformed network of cross-linked polymers, ignoring the influence of the fluid on the network. The term is usually derived using a Gaussian-chain elastic model,18 which yields
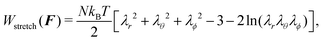 | (5) |
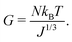 | (6) |
W mix(C) models the contribution to the free energy of the mixing of polymers and water molecules, ignoring the elastic response of the polymer network. The term is usually derived from the Flory–Huggins lattice theory,17 which yields
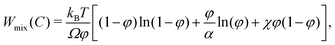 | (7) |
| χ = χ0 + χ1φ(1 − φ), | (8) |
2.3 Stress tensor and chemical potential
The condition of microscopic incompressibility leads us to introduce a Lagrange multiplier p in the expression of the free energy density| W(F, C) = Wstretch(F) + Wmix(C) + p[1 + ΩC − det(F)]. | (9) |
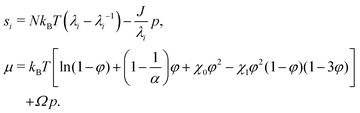 | (10) |
The elastic contribution to the true stress, 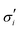 , and the Lagrange multiplier, p, thus relate to the total stress following the usual form of Biot's theory of poroelasticity:
, and the Lagrange multiplier, p, thus relate to the total stress following the usual form of Biot's theory of poroelasticity: 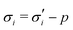 . Therefore, we interpret p as the pore pressure, i.e. the pressure of the liquid inside of the pores of the polymer network. Similarly, the chemical potential is interpreted as the sum of the osmotic pressure, Π, being the mixing contribution, and the pore pressure, p, being the mechanical contribution: μ/Ω = Π + p. This yields
. Therefore, we interpret p as the pore pressure, i.e. the pressure of the liquid inside of the pores of the polymer network. Similarly, the chemical potential is interpreted as the sum of the osmotic pressure, Π, being the mixing contribution, and the pore pressure, p, being the mechanical contribution: μ/Ω = Π + p. This yields
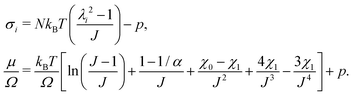 | (11) |
2.4 Kinetic law
We consider a model where the kinetic behaviour of water molecules in the gel is driven by the gradient of chemical potential. Indeed, we study a process driven by a combination of a chemical part (diffusion, represented by the osmotic pressure and following Fick's law) and a mechanical part (flow through porous media, represented by the pore pressure and following Darcy's law) combined in a single term: the chemical potential. Those two laws lead to an equivalent description of the water molecules' displacement in the gel.29 The flux of water molecules thus assumes the form of Darcy's law with a deformation-dependent permeability which accounts for the fact that the mean cross section of the pores of the polymer network increases with the swelling.The conservation of water molecules yields
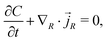 | (12) |
![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) R the nominal flux of water molecules and the divergence being taken with respect to the coordinate in the reference state.16 The true deformation-dependent Darcy's law (with
R the nominal flux of water molecules and the divergence being taken with respect to the coordinate in the reference state.16 The true deformation-dependent Darcy's law (with ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) r the true flux of solvent) is
r the true flux of solvent) is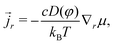 | (13) |
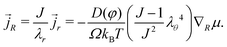 | (14) |
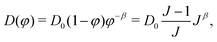 | (15) |
Inputting eqn (3), (14) and (15) into eqn (12) and taking only the radial component, we obtain the time evolution equation for J:
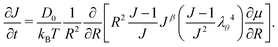 | (16) |
2.5 Mechanical equilibrium
We consider a situation with no external volumetric forces. Thus, the mechanical equilibrium requires that ∇r·σ = 0 inside the gel. Switching to the reference state and using eqn (11), we obtain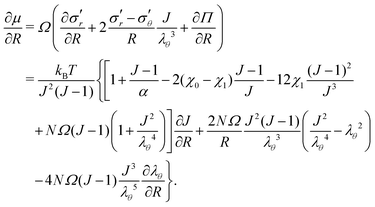 | (17) |
2.6 Governing equation
Inputting eqn (17) into eqn (16), we then proceed to non-dimensionalize the governing equation, introducing the non-dimensionalized variables ρ = R/a and τ = Dt/a2. Note that the value of the effective permeability D(J) will be different for the two cases: D should be smaller in the constrained case than in the free case. That being said, the spatio-temporal evolution of the swelling ratio is ruled by the following equation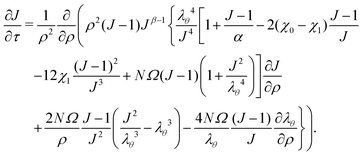 | (18) |
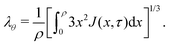 | (19) |
2.7 Boundary conditions
As will be explained in Section 4.2, the membrane of a constrained gel will be manufactured as a strengthened hydrogel. But theoretically speaking, we only consider its induced stress onto the surface of the core hydrogel as a boundary condition, i.e. we do not aim at solving for the swelling of the membrane and we consider only the mechanical aspect of the swollen membrane. Thus, for both cases we want the boundary of the gel to be in equilibrium with the surrounding fluid, namely water, so that the chemical potential on the boundary μb is expressed as μb(ρ = 1, τ) = 0.• In the case of free swelling, where the gel sphere is free to swell in water, we impose that the radial component of the true stress, σr, is equal to 0. This leads, using eqn (11) and only on the boundary, to
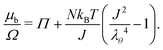 | (20) |
• In the case of constrained swelling, where the gel is coated by a semi-permeable membrane and immersed in water, we compute the radial stress–radial stretch relationship for the case of an incompressible Neo–Hookean thin shell,30 deriving the stress–stretch relationship from the incompressible simplification of eqn (5). This leads, using eqn (11) and only on the boundary, to:
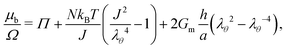 | (21) |
2.8 Numerical scheme
To integrate the governing equation, we use the Crank–Nicolson discretization method for the temporal derivative with a first-order finite difference discretization scheme for the spatial derivative. This method being semi-implicit and the governing equation being non-linear, we solve the problem by, at each time step, computing the values of J and λθ at every spatial step at once, using the Newton–Raphson method to find the root of the residue function. This method is not subject to any stability condition, so we choose the number of time steps and space steps as respectively Nτ = 1000 and Nρ = 500, which were found to yield sufficient accuracy in a reasonable computing time. For numerical reasons, the hydrogel is considered as not perfectly dried at t = 0, namely λ = 1.007 and J = 1.02. Furthermore, to let the swelling start, eqn (15) is replaced by D(φ) = D0(J − 0.9)Jβ−1, which is of negligible importance as J starts increasing.3. Simulation
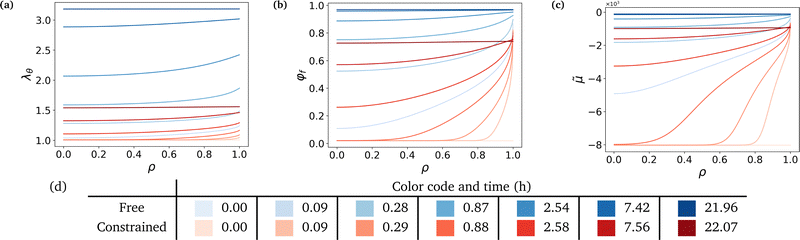
The governing equation is integrated to understand in more depth the swelling process in both cases. We proceed to plot several variables against the non-dimensional radius ρ (ρ = 0 refers to the center of the sphere and ρ = 1 to its boundary, at all time). We plot them for both the free and the most constrained case of our experiments (Gm = 2.24 MPa), at different time steps, logarithmically spaced between t = 0 and t ⋍ 20 h. Parameters used in this simulation are either fixed, computed from experiments or fitted to experimental data, as will be explained in Section 6.Fig. 3 shows that the hydrogel swells from its boundary to its center, solvent diffusion being driven by the chemical potential gradient. The gel's radius increases by a factor 3.18 in the free case and by a factor 1.56 in the constrained case (Fig. 3a). The final state in the free case is almost fully swollen with a final value of the fluid volume fraction φf ⋍ 0.97 while φf ⋍ 0.74 in the constrained case, showing the non-negligible presence of polymers in the final mixture (Fig. 3b). The chemical potential rises until it reaches a value of equilibrium almost equal to that of the solvent in the case of high swelling ratio, and lower than the said value in the constrained case to account for the non-negligible polymer presence in the mixture (Fig. 3c). Hence, there is a jump in chemical potential across the boundary of the gel. It rises rapidly near the boundary, reaching almost immediately its final value, and more slowly inside due to the slow diffusion-like process.
Fig. 4 underlines the mechanical properties of the hydrogel and especially the balance between elastic stresses and the pore pressure. The elastic stresses are always and everywhere tensile, because the polymer network has to be stretched in all directions throughout the whole swelling process to leave space for the solvent molecule to flow in the mixture (Fig. 4a and b). Solvent permeating through the boundary of the gel either stays near the boundary to inflate this region or diffuses toward the center. In the free swelling case, the fluid volume fraction increases sharply near the boundary leading to the fast growth of the outer pores and to the comparatively slow diffusion of the solvent to the inner regions. This is because pore sizes which directly affect the flux of the solvent vary across different regions (eqn (14)). The rapid increase in fluid volume fraction in the outer region indicates that the solvent tends to fill the larger pores near the boundary before gradually flowing inward. In the constrained case, the same phenomenon is witnessed, with values of the elastic radial and azimuthal stresses slightly higher but of the same order, but the final state is reached at a lower fluid volume fraction, i.e. at a lower swelling ratio due to the presence of the membrane. As the outer part of the gel rapidly reaches its final state in the constrained case, water molecules have time to flow inward and the process is closer to a uniform volumetric expansion.
 | ||
Fig. 4 Evolution of true stresses and chemical potential components against radius at logarithmically-spaced time steps. (a) Elastic radial stress 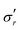 , (b) elastic azimuthal stress , (b) elastic azimuthal stress 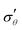 , (c) pore pressure p and (d) normalized osmotic pressure , (c) pore pressure p and (d) normalized osmotic pressure ![[capital Pi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12e.gif) = Π/(NkBT). Legends for the line colors follow those of Fig. 3. = Π/(NkBT). Legends for the line colors follow those of Fig. 3. | ||
Mechanical balance is ensured by the pore pressure, which grows largely in the constrained case and remains negligible in the free case where the polymer network can be largely stretched and its pores expanded, making room for the newly absorbed solvent. Hence, as the volume of the pores increases, their pressure decreases leading to a comparatively low pore pressure. Whereas in the constrained case, the stiffness of the membrane forces the gel to swell less (the osmotic pressure thus remains non-negligible) and the pores to remain small (the pore pressure thus becomes large), as expected3 (Fig. 4c). The pore pressure drives the transport of solvent molecules from the boundary toward the center of the gel. So does the osmotic pressure, starting at a large negative value in the dry state for both cases because polymer and solvent molecules are strictly separated in space, i.e. are not mixed at all. Then mixing spontaneously occurs, lowering (in absolute values) the value of the osmotic pressure. In the free case, the final state is almost perfectly mixed and the osmotic pressure becomes very small. In the constrained case, a larger value of the osmotic pressure remains even in the final state because of the membrane preventing the gel from swelling completely (Fig. 4d). A qualitative comparison between the chemical potential in Fig. 3c and the osmotic pressure in Fig. 4d hints towards the osmotic pressure being the driving phenomenon of the swelling process (compared to the pore pressure).
Fig. 5 puts emphasis on the mechanical aspect of the actuation, studying the developed true stresses. The combination of the two contributions in Biot's expression of the total stresses in eqn (11) shows that the total radial and total azimuthal stresses get highly compressive in the constrained case due to the large pore pressure (Fig. 5a and b). Fig. 5c shows that on the boundary, the total stress remains equal to 0 in the free swelling case as expected, with the pore pressure compensating the elastic radial stress. The pore pressure decreases in the free case, as the swelling of the pores occurs. Whereas, the total stresses of the constrained hydrogel remain substantially higher due to the presence of the stiff membrane, and consequently the pore pressure in the constrained hydrogel becomes high (∼−1.25 MPa) compared to the negligible elastic stress of the polymer network (Fig. 5a and b). This high compressive pore pressure is the primary contributor to the total stress in the constrained hydrogel. In our previous work,3 the blocking stresses of bare and constrained hydrogel were experimentally measured to be respectively 27 kPa and 1.44 MPa (at a swelling ratio of 1.53 that is similar to our experimental condition 1.56). These experimental results match well with our simulation results. Both cases show a sharp increase of the elastic radial stress at the beginning of the swelling, when the outer layer is swelling while being stuck to the inner core not yet impregnated, followed by a slow decrease as the inner part becomes swollen. In both cases, the gel absorbs solvent molecules due to chemical affinity. Indeed, the study of the decomposition of the chemical potential in terms of osmotic pressure and pore pressure in eqn (11) shows that the driving phenomenon in both cases, even though the increase of the pore pressure in the constrained case helps the diffusion process by adding a mechanical forcing, is the entropic mixing part, i.e. the osmotic pressure (Fig. 5d).
4. Materials and methods
4.1 Materials
3-Sulfopropyl acrylate potassium salt (SPA; Sigma-Aldrich 251631) and acrylamide (AAm; Sigma-Aldrich A8887) were used as monomers for the core copolymer hydrogel network. N,N′-Methylenebisacrylamide (MBAAm; Sigma-Aldrich M7279) and 1-hydroxy-cyclohexyl-phenyl-ketone (Irgacure 184; Sigma-Aldrich 405612) were respectively used as a cross-linking agent and a photoinitiator. Poly(vinyl alcohol) (PVA, Mw 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–186
000–186![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 99+% hydrolyzed; Sigma-Aldrich 363065) and Alginic acid (Alg, medium viscosity; Sigma-Aldrich A2033) were used as monomers for the shell hydrogel that is coated onto the core hydrogels. Calcium chloride (CaCl2; Sigma-Aldrich C4901) and copper(II) chloride (CuCl2; Sigma-Aldrich 222011) were used to physically crosslink the Alg chain. Ecoflex (00-10; Smooth-On Inc.) was used as a mold for the core hydrogel. Deionized water filtered with a Direct-Q®3 machine (Merck Millipore) was used to make the electrolyte solution. All chemical reagents were used without further purification.
000, 99+% hydrolyzed; Sigma-Aldrich 363065) and Alginic acid (Alg, medium viscosity; Sigma-Aldrich A2033) were used as monomers for the shell hydrogel that is coated onto the core hydrogels. Calcium chloride (CaCl2; Sigma-Aldrich C4901) and copper(II) chloride (CuCl2; Sigma-Aldrich 222011) were used to physically crosslink the Alg chain. Ecoflex (00-10; Smooth-On Inc.) was used as a mold for the core hydrogel. Deionized water filtered with a Direct-Q®3 machine (Merck Millipore) was used to make the electrolyte solution. All chemical reagents were used without further purification.
4.2 Fabrication of hydrogels
Unless otherwise specified, the precursor solution of the core hydrogel P(AAm-co-SPA) was prepared with a molar ratio of 272![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2727
2727![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 = SPA
1 = SPA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AAm
AAm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MBAAm
MBAAm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Irgacure 184, where the molar concentration of AAm and SPA monomer were respectively 0.272 M and 2.727 M. The copolymer was used to obtain appropriate swelling stress without rupturing the surrounding membrane, and therefore reliable swelling data. To create spherical hydrogel beads, the mold made of elastomer, Ecoflex™ (SMOOTH-ON 00-10), was used due to its softness and ease of use. The process began by mixing and degassing the A/B components of Ecoflex in a 1
Irgacure 184, where the molar concentration of AAm and SPA monomer were respectively 0.272 M and 2.727 M. The copolymer was used to obtain appropriate swelling stress without rupturing the surrounding membrane, and therefore reliable swelling data. To create spherical hydrogel beads, the mold made of elastomer, Ecoflex™ (SMOOTH-ON 00-10), was used due to its softness and ease of use. The process began by mixing and degassing the A/B components of Ecoflex in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio using a centrifugal mixer (THINKY, ARE-310). Subsequently, the spherical metal beads with a diameter of 4 cm were carefully embedded into the mixed solution, which was then cured into the oven at 100 °C for 1 h. After curing, the metal beads were carefully removed from the elastomer. To produce spherical hydrogels, the precursor solution was injected into the molds using a syringe and cured by exposing them to 365 nm UV irradiation for 10 min. The diameter of the core hydrogel sphere was fixed at 4 mm. To fabricate the core–shell hydrogel, first, the coating solution was prepared by dissolving Alg and PVA with a weight ratio of 2 and 3 wt% respectively in deionized water under stirring and heating (90 °C). After degassing by sonication for 1 h, a clear solution was obtained. The core hydrogel that contains multivalent ions can physically crosslink the Alg chain. To compare the effect of the modulus of the shell (Gm), two different cations were used to coat the core hydrogel. The core hydrogel was briefly immersed in 3.0 M CaCl2 or 2.0 M CuCl2 solution for 1 min and any excess solution on the surface was completely dried using an air blower. Subsequently, the spherical hydrogel was immersed into the coating solution (PVA/Alg) allowing the pre-gel to grow from the surface of the core hydrogel within a corresponding coating time. After 10 min of coating, the pre-coated hydrogel was thoroughly cleaned with deionized water to remove any excess of uncrosslinked polymers. To strengthen the shell, the pre-coated hydrogel was annealed in a 120 °C oven for 2 h. The densification of the polymer chain facilitates the additional hydrogen bonding, thereby enhancing the mechanical properties of the shell and preventing swelling in water. For further enhancement via salting-out, the annealed core–shell hydrogel was immersed into 2.0 M ZnSO4 for 15 min, followed by thorough cleaning with deionized water.
1 ratio using a centrifugal mixer (THINKY, ARE-310). Subsequently, the spherical metal beads with a diameter of 4 cm were carefully embedded into the mixed solution, which was then cured into the oven at 100 °C for 1 h. After curing, the metal beads were carefully removed from the elastomer. To produce spherical hydrogels, the precursor solution was injected into the molds using a syringe and cured by exposing them to 365 nm UV irradiation for 10 min. The diameter of the core hydrogel sphere was fixed at 4 mm. To fabricate the core–shell hydrogel, first, the coating solution was prepared by dissolving Alg and PVA with a weight ratio of 2 and 3 wt% respectively in deionized water under stirring and heating (90 °C). After degassing by sonication for 1 h, a clear solution was obtained. The core hydrogel that contains multivalent ions can physically crosslink the Alg chain. To compare the effect of the modulus of the shell (Gm), two different cations were used to coat the core hydrogel. The core hydrogel was briefly immersed in 3.0 M CaCl2 or 2.0 M CuCl2 solution for 1 min and any excess solution on the surface was completely dried using an air blower. Subsequently, the spherical hydrogel was immersed into the coating solution (PVA/Alg) allowing the pre-gel to grow from the surface of the core hydrogel within a corresponding coating time. After 10 min of coating, the pre-coated hydrogel was thoroughly cleaned with deionized water to remove any excess of uncrosslinked polymers. To strengthen the shell, the pre-coated hydrogel was annealed in a 120 °C oven for 2 h. The densification of the polymer chain facilitates the additional hydrogen bonding, thereby enhancing the mechanical properties of the shell and preventing swelling in water. For further enhancement via salting-out, the annealed core–shell hydrogel was immersed into 2.0 M ZnSO4 for 15 min, followed by thorough cleaning with deionized water.
4.3 Tensile tests
The square-shaped membranes were prepared following the above procedure. These membranes were grown on the hydrogels containing multivalent ions. Subsequently, the sheets were cut into dog-bone-shaped specimens with a gauge width of 2 mm. The thickness of each individual specimen was measured using a Vernier caliper. To gather force-displacement data, a universal testing machine (Instron 3343) with 1 kN load cell was employed, maintained at a constant strain rate of 10 mm min−1. Stress–strain curves were generated by dividing the measured force by the initial gauge cross-sectional area and the measured displacement by the initial clamp distance.4.4 Compressive tests
The disk-shaped core hydrogels were prepared by using an acrylic mold with a diameter of 10 mm and a thickness of 2 mm, followed by UV irradiation for 10 min. The swelling ratios of the specimens were controlled by making the gel swell in a specific volume of deionized water. The specimens were then kept inside a humid chamber for 24 h to reach the equilibrium state without evaporation. To determine the densities of the hydrogels, the weight of each measured sample was divided by the volume calculated from the diameter and thickness of the samples. Compressive force–displacement data were collected using a universal testing machine (Instron 3343) equipped with a 1 kN load cell. The tests were conducted at a constant strain rate of 1 mm min−1. During the tests, the specimens were positioned between the stage and load cell, with mineral oil to fill the gap between them. This setup helped to prevent evaporation and minimize the friction between the specimens and the load cell. The shear modulus was calculated from the true stress–strain curve, where the measured force was divided by the instantaneous cross-sectional area, and the measured displacement was divided by the initial thickness.4.5 Swelling rate measurement
Before measuring the swelling rate of the spherical core–shell hydrogels, all samples were completely dried at room temperature for a duration of 1 day to ensure consistent starting conditions. The swelling ratio-time curves were then generated by tracking changes in the diameters of the core–shell hydrogels over time. These measurements were facilitated by using a handheld digital microscope (Dinolite AM4815ZT) to capture the time-lapse images while the hydrogels swelled in a bath containing a substantial quantity of deionized water. The swelling ratio was determined by dividing the measured diameter at that specific swelling time by the initial diameter of the core–shell hydrogel.5. Experimental results and validation
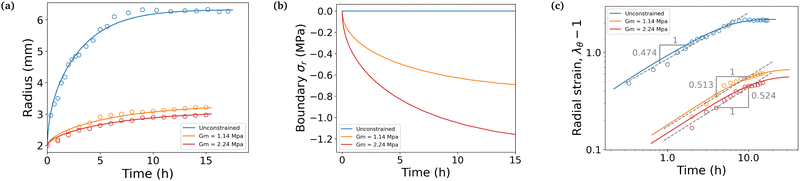
We conducted swelling tests on both unconstrained and constrained hydrogel spheres with an initial radius of a = 2 mm (Fig. 2). The results clearly demonstrate that constrained swelling leads to a slower swelling rate and a smaller final swelling ratio. In the free swelling case, the bare hydrogel reaches its equilibrium state in approximately 5 h, whereas in the constrained case, it continues to swell until approximately 15 h. Furthermore, the final radius of the bare hydrogel is approximately twice as large as that of the constrained hydrogel when measured at identical time intervals.We first aim at fitting the final swelling ratio for the free swelling case. From our experimental measurements of shear modulus and using eqn (6) at T = 298 K and J = 32, the number of chains per unit volume of dry polymer is fixed at N = 1.849 × 1025 m−3 for a shear modulus of G = 23.89 kPa. The value of G is in agreement with usual values from the literature.14 That of N is roughly one order of magnitude larger than usual values.14–16 Indeed, the goal of the present study was not to reach a very high swelling ratio and we needed the membrane to withstand the stress induced by the swelling, thus leading to the choice of a denser hydrogel. Hence, the final swelling ratio for the free swelling case now only depends on χ0 and χ1, which are fitted to match the experimental results. It gives χ0 = 0.49 and χ1 = 0.04. We note that the coordination number z ⋍ 6 is reasonable with respect to that of a simple 3D square lattice. We also underline the fact that, even though the expression of the mixing parameter in this study is different with respect to the constant approximation classically used, the value of χ still lies within the generally accepted range 0.49–0.51 for polyacrylamide hydrogels, with the value of χ being generally higher in the more constrained case, as recommended.24
We next consider the final swelling ratio for the constrained swelling case, with membranes of measured initial thickness h = 250 μm. From tensile tests performed on the membranes, we fitted the true stress–stretch curves to the theoretical expression σr(λθ) = Gm(λθ2 − λθ−4). That way, we computed their shear moduli Gm, which are of the order of the MPa, depending on the membrane.
Lastly the permeability parameter D0 is fitted to match the time scales of the experiments, which leads to D0 = 5.76 × 10−11 m2 s−1. The non-dimensionalization step done to obtain eqn (18) is conducted using the value of the effective permeability D = 1.02 × 10−8 m2 s−1 for the free case, which is of the same order of magnitude of values from other studies,14,15 and D = 4.53 × 10−10 m2 s−1 or D = 3.19 × 10−10 m2 s−1 for the two constrained cases. These values correspond to their respective final values computed from eqn (15), when the mixture has reached its equilibrium state. We note that the value of D increases throughout the swelling process by roughly two orders of magnitude in the free case and only one in the constrained cases.
The simulation is then compared with the experimental data, as shown in Fig. 6a. We obtain a satisfying fit in terms of prediction of both the final swelling ratio and the kinetics of the two processes. The theoretical model then allows us to compute the actuating pressure inside of the gel (Fig. 6b). As expected, the more constrained the gel is, the larger internal pressure it builds. The negative values of σr indicate that the stress is compressive. In all cases, at early times the power law behaviour for the radius (λθ − 1) against time resembles that of a diffusive process with an exponent close to 0.5 (Fig. 6c). The seemingly increasing exponent (with respect to the constraint) may be purely artificial, as the fitting to a power law seems to get less and less relevant as the gel gets more constrained.
6. Parametric analysis
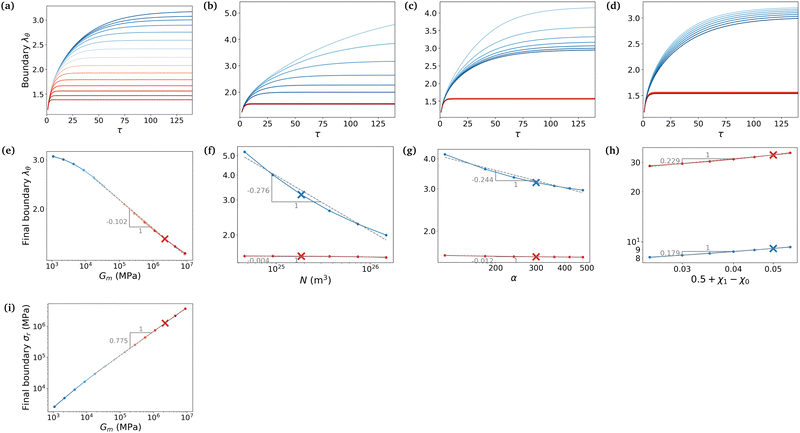
We now want to use our experimentally verified theoretical model to extend our understanding of gels with different parameters through simulations. We will investigate the importance of the shear modulus of the membrane Gm, the density of crosslinks N (which characterises the stiffness of the gel hence its ability to deform) and finally the length of polymers α and the mixing parameter χ0 (which are related to the chemical affinity between the gel and the solvent). The permeability parameter β (which rules the effect of the swelling of the pores on the gels permeability) does not affect the final swelling ratio. From eqn (11), N characterises the elastic stress and the couple (α, χ0) the osmotic pressure (at least at the two leading orders when J ≫ 1). We neglect here the effect of χ1, which is of importance in thermo-sensitive problems21 for example, but not in our problem, as will be discussed in Section 7.1.To evaluate the importance of each parameter, we plot the final azimuthal strain, which characterises the final radius, against the values of the parameters (Fig. 7a–d). As expected, the stiffer the membrane, the lower the final radius (Fig. 7a). N and α play important roles in the free case where the swelling depends on the parameters of the gel alone, but almost none in the constrained case where the membrane prevails (Fig. 7b and c). Finally the value of χ0 seems to be non-negligible in the two cases, but less relevant than the two previous parameters in the free case (Fig. 7d). We then want to relate the slopes of the log–log curves to power laws derived from the constitutive equations (eqn (20) and (21)). At equilibrium, λr = λθ = λϕ = λ = J1/3. Fig. 7e shows that for high values of Gm, λ ∼ Gm−0.102. Inputting it in σr ∼ Gm(λ2 − λ−4) and neglecting the second term, we obtain a dependence, σr ∼ Gm0.796, close to Fig. 7i. It shows that if the membrane gets stiffer, the final radius will decrease slightly but the stress produced will be much larger. Fig. 7f and g show that N and α play almost no role in the constrained case.
Now we evaluate which terms are dominant in eqn (21). Indeed the final stretch can be computed by equating the value of the chemical potential on the boundary to that of the solvent and solving for λ, namely: 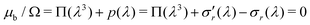 . Using J ≫ 1, we further develop in power series the expression of the first term of the osmotic pressure, ln((J −1)/J) = ln(1 − 1/J) ⋍ − 1/J − 0.5/J2 − 0.33/J3 + …, leading to (with Gm = 0 for the free case):
. Using J ≫ 1, we further develop in power series the expression of the first term of the osmotic pressure, ln((J −1)/J) = ln(1 − 1/J) ⋍ − 1/J − 0.5/J2 − 0.33/J3 + …, leading to (with Gm = 0 for the free case):
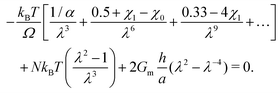 | (22) |
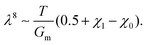 | (23) |
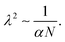 | (24) |
7. Mixing parameter and linear theory
In this last section, we briefly discuss the importance of the deformation dependence of the mixing parameter and the possibility to make the model simpler without losing most of the simulation's accuracy.7.1 Flory's constant approximation
Even though Orofino and Flory proposed a virial expansion23 of Flory's mixing parameter to better fit their experimental results, Flory's first order approximation is still widely used. Fig. 8 shows the results obtained with constant χ. Some parameter values have been changed in this simulation to match the data, namely χ1 = 0 and α = 220. χ0 = χ has been kept to its previous value to remain in the 0.49–0.51 range. We note that it closely resembles our previous simulation, and thus conclude that, for the purpose of this study, a constant mixing parameter in the hyperlinear model is sufficient to simulate the process.7.2 Tanaka and Fillmore formalism
Because in our study the hydrogels reach rather small values of swelling ratio, we conduct a comparison with the linear theory of Tanaka and Fillmore,9 referred to in the next lines as TF's model, using the same notations. This theory assumes a linear relationship between stress and strain. We solve the following problem with a simple first order explicit finite difference scheme: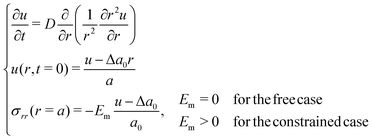 | (25) |
Some critical aspects of this model must be emphasized. First, the theoretical foundations of the model have been pointed out as somewhat artificial.31 Second, our experiments largely break the small deformation assumption of linear elasticity. Third, TF's model is not predictive: it uses the initial and final values of the radius to compute mechano-chemical properties of the gel such as its osmotic pressure. With that in mind, we allow ourselves to use TF's model in an exclusively practical way, with the only purpose of simulating the kinetics of the swelling, knowing the final state of our experiments and ignoring all physical considerations. This leads to dashed lines in Fig. 8, where again the final radius in the three cases are known and all other parameters have been fitted to match the experimental data. The simulations match strikingly well the experimental data. Also, the governing equation is much simpler, even allowing for an analytical solution for the free swelling case.9 This match to TF's model is only possible because the stretches involved in our experiments are small compared to the usual values for softer hydrogels and because the mechano-chemical aspects can be decently modelled with simple expressions. Larger swelling and finer aspects of hydrogels such as thermo-responsive behaviours or pH-driven phase transitions are absolutely impossible to model with TF's theory: one needs the hyperlinear framework.
8. Conclusion
We built a model to study the kinetics of swelling of constrained hydrogel spheres using a thermodynamic approach based on the theory of Hong et al.16 We added a constraint to the system to model the membrane around the gel, switching the key aspect of our study from swelling to actuation. That way, we managed to generate a radial stress of the order of the megapascal. Then, we used that model to simulate the process to obtain insights into finer aspects of the system's behaviour. We performed experiments to validate the model, and found that the simulation matched the experimental results satisfactorily well. We also complexified the expression of the mixing parameter χ and it turned out to be of small significance. Due to rather small deformations and simple behaviours, we finally conducted a simulation based on Tanaka et al.'s linear theory which, despite its lack of physical sense and its many fitting parameters, can predict reasonably well the process. The constrained gel, capable of generating unusually high actutation force and supporting large external load, could be employed in various fields, encompassing soft robotics, structural components, impact absorption systems, and implantable structures. Offering a predictive mechanical model for constrained hydrogels could provide guidance for the design of novel soft actuators in those application areas.Author contributions
H.-Y. K. and J.-Y. S. conceived and supervised the research. All authors contributed to preparing the manuscripts. T. C. built the theoretical model, and performed the simulation and data analysis. H. N. designed the materials, conducted the experiments and collected data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (grant no. 2018052541 and 2021017476) via SNU SOFT Foundry. Administrative support from SNU Institute of Engineering Research is acknowledged.Notes and references
- D. J. Beebe, J. S. Moore, J. M. Bauer, Q. Yu, R. H. Liu, C. Devadoss and B.-H. Jo, Nature, 2000, 404, 588–590 CrossRef CAS PubMed.
- R. Bashir, J. Z. Hilt, O. Elibol, A. Gupta and N. A. Peppas, Appl. Phys. Lett., 2002, 81, 3091–3093 CrossRef CAS.
- H. Na, Y.-W. Kang, C. S. Park, S. Jung, H.-Y. Kim and J.-Y. Sun, Science, 2022, 376, 301–307 CrossRef CAS PubMed.
- A. Jain, Y.-T. Kim, R. J. McKeon and R. V. Bellamkonda, Biomaterials, 2006, 27, 497–504 CrossRef CAS PubMed.
- Y. Xiao, W. Xu, Q. Zhu, B. Yan, D. Yang, J. Yang, X. He, S. Liang and X. Hu, Carbohydr. Polym., 2009, 77, 612–620 CrossRef CAS.
- M. Bassil, J. Davenas and M. E. L. Tahchi, Sens. Actuators, B, 2008, 134, 496–501 CrossRef CAS.
- K. Deligkaris, T. S. Tadele, W. Olthuis and A. van den Berg, Sens. Actuators, B, 2010, 147, 765–774 CrossRef CAS.
- T. Tanaka, L. O. Hocker and G. B. Benedek, J. Chem. Phys., 1973, 59, 5151–5159 CrossRef CAS.
- T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218 CrossRef CAS.
- M. A. Biot, J. Appl. Phys., 1941, 12, 155–164 CrossRef.
- G. W. Scherer, J. Non-Cryst., 1989, 113, 107–118 CrossRef CAS.
- M. A. Biot, J. Appl. Phys., 1955, 26, 182–185 CrossRef CAS.
- C.-Y. Hui and V. Muralidharan, J. Chem. Phys., 2005, 123, 154905 CrossRef PubMed.
- M. Engelsberg and W. Barros, Phys. Rev. E, 2013, 88, 062602 CrossRef CAS PubMed.
- T. Bertrand, J. Peixinho, S. Mukhopadhyay and C. W. MacMinn, Phys. Rev. Appl., 2016, 6, 064010 CrossRef.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56, 1779–1793 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- M. L. Huggins, J. Chem. Phys., 1941, 9, 440 CrossRef CAS.
- C. A. Grattoni, H. H. Al-Sharji, C. Yang, A. H. Muggeridge and R. W. Zimmerman, J. Colloid Interface Sci., 2001, 240, 601–607 CrossRef CAS PubMed.
- J. Dervaux, Y. Couder, M.-A. Guedeau-Boudeville and M. Ben Amar, Phys. Rev. Lett., 2011, 107, 018103 CrossRef PubMed.
- M. Quesada-Pérez, J. A. Maroto-Centeno, J. Forcada and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 10536–10547 RSC.
- B. Qiao and D. Zhao, J. Chem. Phys., 2004, 121, 4968–4973 CrossRef CAS PubMed.
- T. A. Orofino and P. J. Flory, J. Chem. Phys., 1957, 26, 1067–1076 CrossRef.
- J. Li, Y. Hu, J. J. Vlassak and Z. Suo, Soft Matter, 2012, 8, 8121–8128 RSC.
- R. Koningsveld and L. A. Kleintjens, Macromolecules, 1971, 4, 637–641 CrossRef CAS.
- P. L. Taylor, Y. Yu and X. Y. Wang, J. Chem. Phys., 1996, 105, 1237–1241 CrossRef CAS.
- M. G. Bawendi and K. F. Freed, J. Chem. Phys., 1988, 88, 2741–2756 CrossRef CAS.
- M. G. Bawendi, K. F. Freed and U. Mohanty, J. Chem. Phys., 1987, 87, 5534–5540 CrossRef CAS.
- S. S. L. Peppin, J. A. W. Elliott and M. G. Worster, Phys. Fluids, 2005, 17, 053301 CrossRef.
- J. Kiendl, M.-C. Hsu, M. C. Wu and A. Reali, Comput. Methods Appl. Mech. Eng., 2015, 291, 280–303 CrossRef.
- T. Komori and R. Sakamoto, Colloid Polym. Sci., 1989, 267, 179–183 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |


![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif)