Open Access Article
Open Access ArticleCombinatorial impedance spectroscopy with Bayesian analysis for triple ionic-electronic conducting perovskites†
Meagan C.
Papac
 ab,
Jake
Huang
ab,
Jake
Huang
 ba,
Andriy
Zakutayev
ba,
Andriy
Zakutayev
 *ab and
Ryan
O'Hayre
*ab and
Ryan
O'Hayre
 *b
*b
aMaterials Science Center, National Renewable Energy Laboratory, Golden, CO, USA. E-mail: andriy.zakutayev@nrel.gov
bMetallurgical and Materials Engineering Department, Colorado School of Mines, Golden, CO, USA. E-mail: rohayre@mines.edu
First published on 3rd February 2023
Abstract
Triple ionic-electronic conducting oxides (TIECs) show great promise in high-temperature electrochemical applications, including ceramic fuel cells and electrolyzers. The transport properties and electrochemical activity of TIECs strongly depend on chemical composition and environmental conditions, such as operating temperature and gas environment. Here, this dependency is investigated in a large family of TIEC oxide perovskite materials via combinatorial experimental methods and multidimensional Bayesian analysis. In total, more than 2500 impedance spectra are collected at three temperatures under dry air and humid N2 atmospheres from 432 distinct Ba(Co,Fe,Zr,Y)O3−δ (BCFZY) compositions that were synthesized by pulsed laser deposition. This study provides insight on the trends governing electrochemical performance. Combinatorial experiments demonstrate that Co-rich compositions achieve the lowest overall polarization resistance under both dry air and humid N2, while Fe substitution may increase polarization resistance. Hierarchical Bayesian analysis indicates that the performance-limiting process depends on the chemical composition, measurement temperature, and atmospheric humidity. This work provides a map of electronic properties of materials in the BCFZY perovskite family under conditions that are relevant to their application as air electrodes for protonic ceramic fuel cells and electrolyzers, and demonstrates a unique approach to studying TIECs that combines combinatorial experiments and Bayesian analysis.
Introduction
Triple ionic-electronic conducting oxides (TIECs) have recently generated interest because of their unique ability to simultaneously transport electronic charge carriers and two ionic species. Within this class of materials, Ba(Co0.4Fe0.4Zr0.1Y0.1)O3−δ (BCFZY4411) stands out for demonstrating high catalytic activity for the oxygen reduction reaction (ORR), for achieving high performance when employed as a cathode in protonic ceramic fuel cells (PCFCs),1 and for its ability to perform as an anode when a PCFC is operated in reverse as an electrolysis cell.2 While BCFZY4411 has been studied by several research groups,3–7 to our knowledge there has been no comprehensive study investigating the manipulation of cation composition to tune or optimize the transport properties of this material.Prior studies on mixed ionic-electronic conductors (MIECs), which transport two types of charge carriers, provide a baseline understanding of conduction mechanisms in these triple-conducting materials.8 In materials that contain substantial concentrations of multi-valent transition metals (TMs), electronic conduction is achieved through a small-polaron hopping mechanism and charge is transferred through the TM–O–TM bond network. Protons are transferred among oxygen sites by a Grotthuss-type mechanism,9 while oxygen ions are transported by a vacancy-diffusion mechanism. These mechanisms can be enhanced or inhibited by changes in cation concentrations.
Most known MIECs have perovskite (ABO3) or perovskite-like structures that readily accommodate A- and/or B-site substitution. However, substituting a cation to enhance transport of one carrier may inhibit transport of another carrier. Due to these various and often conflicting effects of each element on transport, a comprehensive study with high resolution in chemical composition is required to better understand how changes in cation concentrations affect transport properties in the Ba(Co,Fe,Zr,Y)O3−δ (BCFZY) materials system.
In similar materials, Zr provides stability and a large unit cell volume, which promotes oxygen ion mobility.1 Yttrium provides proton conduction and increases oxygen vacancy formation, but limits oxygen mobility.2,3 Here, the Y concentration is limited to 20% of the B-site (B) because higher concentrations may form secondary phases.4,5 The multi-valent transition metals, Co and Fe, provide electronic conduction via small polaron hopping.2,6 Iron may also improve structural stability, while the low B–O–B bond energy of Co can increase proton and oxygen ion transport and the surface oxygen exchange reaction.2,6,7
Conducting a comprehensive study of this materials family via serial experimental methods would be prohibitively time consuming. Additionally, variation in microstructure among samples from different studies or different synthesis batches can affect materials properties and convolute results. Also, manual analysis of large amounts of impedance spectroscopy data as a function of temperature and atmospheric measurement conditions is nearly intractable.
Here, we apply combinatorial experimental methods to systematically screen this composition space, and use hierarchical Bayesian models to analyse the impedance spectroscopy measurement results. We synthesize BCFZY thin films across a wide range in chemical composition by pulsed laser deposition to achieve nominally uniform microstructures, and report their electronic properties as a function of B-site cation concentrations. We demonstrate that B-site substitution with Co enhances the necessary reactions and transport, while substantial substitution with Fe may be detrimental to performance of these materials for application as fuel cell cathodes at low to intermediate temperatures. Cobalt reduces polarization resistance by enabling electronic charge transfer in both atmospheres, and by promoting oxygen vacancy formation under humid conditions. These results provide a composition-dependent property map of the BCFZY perovskite family of TIEC materials, which will enable engineering of air electrodes with improved performance for protonic ceramic fuel cell and electrolysis applications.
Combinatorial experimental methods
For this study, we employ combinatorial experimental methods to examine BCFZY thin films. First, we establish parameters for synthesizing BCFZY thin films across the required range. Second, we explore the impedance of the BCFZY materials system to uncover composition-property relationships under dry oxidizing and humid reducing gas environments.Thin film synthesis
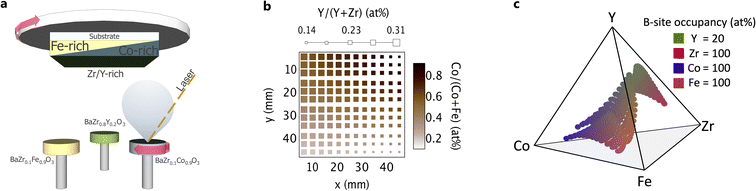
We synthesized electrolyte and electrode thin film layers in a combinatorial pulsed laser deposition (combi-PLD) chamber. Substrates were pre-heated in the vacuum chamber for 30 minutes by a radiative heater. The combi-PLD system has a rotatable carousel on which as many as six targets can be loaded simultaneously. The targets are sequentially brought into the path of a 248 nm KrF excimer laser (Fig. 1a) and are ablated 7.5 cm from the substrate. The system is equipped with a rotatable substrate holder that centres different locations on the substrate over different targets during ablation and achieves compositional gradients that span a range of 6% to 60% B-site occupation for any single element across a 2′′ × 2′′ substrate. These compositionally graded samples are called libraries. Information regarding PLD target synthesis and characterization can be found in Section S1†.Pulsed laser deposition gives access to a wide range in synthesis parameters, including substrate heater setpoint, gas partial pressures, laser energy, and laser pulse frequency. Each of these parameters was explored to establish a combination of parameters that most consistently produced crystalline films across a broad range in chemical composition. To determine the effects of substrate temperature, we loaded the substrate onto a purpose-built substrate holder that applied a temperature gradient across the substrate during deposition. We investigated pressure effects by depositing films at 1, 5, 10, 50, and 100 mT. We tested laser pulse frequencies between 5 and 40 Hz and laser energies of 200 and 300 mJ. We discuss the results of these experiments in a later section.
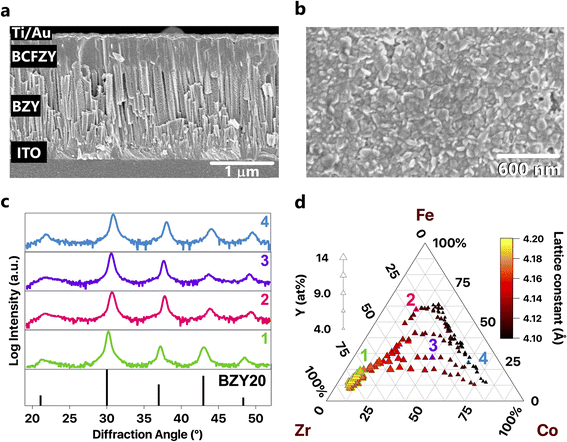
We deposited compositionally graded BCFZY thin films with thicknesses ranging between 450 and 600 nm as part of two distinct film stacks (Table 1), each for a different characterization method. Stack 1 comprised continuous film libraries deposited directly on bare, fused silica substrates (SiO2, GM Quartz, USA). These libraries served as reference samples for structure and chemical composition measurements and avoided the elemental and diffraction peak overlap that arises with additional layers. Stack 2 comprised two PLD-deposited layers on an ITO-coated glass substrate (ITO, Delta Technologies, USA) to form a library of electrochemical half cells. A compositionally uniform, continuous BaZr0.8Y0.2O3−δ (BZY20) layer, with a thickness of ∼1500 nm, served as the electrolyte. We deposited a compositionally graded BCFZY film through a shadow mask to produce a 12 × 12 point array of spatially separated and compositionally unique 1.75 mm diameter microelectrodes for characterization by electrochemical impedance spectroscopy. To improve electrical contact between the sample and probe during electrical measurements, we deposited 1 mm diameter circular contacts onto the BCFZY microelectrodes by electron beam evaporation (FC-2000, Temescal, USA). The metal contacts comprised a 50 nm layer of Ti for adhesion and 100 nm of Au. The metal contact must be larger than the probe tip for electrical measurements, while the TIEC microelectrode diameter must be small enough that the chemical composition does not substantially vary across its width.
| Stack | 1 | 2 |
|---|---|---|
| Layers | SiO2/BCFZY | Glass/ITO/BZY/BCFZY/Ti/Au |
| Substrate | Fused silica | ITO-coated glass |
| Electrolyte | None | BZY |
| Electrode | BCFZY | BCFZY |
| Electrical contacts | None | 50 nm Ti + 100 nm Au |
| Characterization method/s | XRD, XRF | Impedance spectroscopy |
Thin-film characterization
We analysed thin film structure and composition on a 4 × 11 point grid via X-ray diffraction (XRD) and X-ray fluorescence (XRF), respectively. We collected X-ray diffraction patterns by a 2D detector in a Bragg–Brentano configuration in a Bruker D8 Discover diffractometer with Cu-Kα radiation. The diffraction angle ranged from 19° to 52° with a step size of 0.05°. We indexed the peaks according to cubic barium zirconate and calculated the cubic lattice constants from the position of the most intense diffraction peak, the {110} peak. We measured energy dispersive X-ray fluorescence by a Fischerscope® X-Ray XDV®-SDD to determine film thickness and composition. A spectrum from a blank SiO2 substrate provided a base spectrum for this analysis. We processed the data from XRD, XRF, and other characterization methods with custom routines within the COMBIgor software package.10 We interpolated XRF data between measured points to obtain cation concentrations for each spatial location at which we measured impedance.Prior to electrical characterization, we annealed the as-deposited films in laboratory ambient air in a box furnace (Thermo Scientific™) for 4 hours at 500 °C, equally exposing all films to an equivalent oxygen environment at a temperature above the measurement surface temperature. We measured electrochemical impedance on the half-cell samples (Stack 2) by an Interface 1000 potentiostat (Gamry, USA) in potentiostatic mode with a 30 mV perturbation voltage. We collected spectra across a frequency range from 0.1 Hz to 1 × 106 Hz at elevated temperatures by a lab-built instrument that is described in detail elsewhere.11 Automated data collection routines measured the libraries in a through-film configuration at elevated temperature on a hot stage. After each temperature ramp, a 4 minutes dwell equilibrated the surface temperature.
A custom-built probe directed flowing gas toward each microelectrode during measurement. After the probe moved to each microelectrode, an additional 20 second dwell equilibrated the sample to the dry air flow (pH2O ≅ 7.4 × 10−5 atm). We collected impedance spectra at hot-stage setpoints of 400 °C, 450 °C and 500 °C, which correspond to film surface temperatures of 238 °C, 272 °C, and 303 °C. The surface temperature was determined from separate measurements of a blank substrate by a K-type thermocouple that was attached to the surface of the substrate by silver paste. After the entire library was mapped under dry air, the same procedure was repeated under humidified N2 (pH2O ≅ 0.028 atm) except that the probe dwelled at each electrode for 100 seconds before collecting each spectrum.
Results of combinatorial synthesis
Optimized PLD parameters synthesize crystalline films
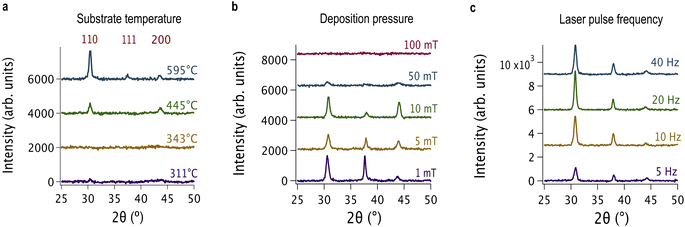
We evaluated the deposition parameters by the crystallinity of the resulting films—as determined by the FWHM of the most intense diffraction peak (the {110} peak)—and by required deposition time to achieve the desired thickness. Films deposited along a thermal gradient at a heater setpoint of 700 °C showed that crystallinity decreased with decreasing substrate temperature (Fig. 2a). Therefore, we chose 700 °C for depositing the BCFZY films. Of the pressures studied, 1 mT produced the most crystalline films (Fig. 2b). XRD analysis of single-target, end-member films confirmed that a 1 mT deposition pressure produced crystalline films across the entire composition space of interest. Both 10 Hz and 20 Hz produced more crystalline films than either 5 or 40 Hz (Fig. 2c). Both 200 mJ and 300 mJ laser energies produced films with diffraction patterns whose peaks had similar FWHM values. Thus, we chose the laser energy of 300 mJ and pulse frequency of 20 Hz to produce crystalline films at higher deposition rates. Although high deposition rates may result in rough film surfaces and low-quality interfaces, we did not observe these effects in SEM micrographs (Fig. 3a). In a similar process, we established ideal parameters for the uniform BZY layer, and found that BZY, which contains no smaller, lighter transition metals, was optimized at a heater setpoint of 800 °C with a total pressure of 50 mT and the same laser parameters that we chose for the BCFZY layer.Materials demonstrate cubic perovskite structure across chemical composition range
Crystalline films formed across the entire composition range under study (Fig. S2†). Each film displayed a cubic perovskite structure; no secondary phases were detected in as-deposited films within the resolution of the laboratory-scale diffractometer. The position of the XRD peaks moved to higher diffraction angles with decreasing B-site cation radius (Fig. 3b). This trend indicates that substitution of smaller cations (Fe and Co) for larger cations (Zr and Y) on the B-site has a measurable effect on the lattice parameter (Fig. 3c). Combined with the single-phase XRD patterns, the synchronous change of the lattice constant with the average B-site cation radius indicates that the cations form a solid solution. Chemical composition across each library varied as expected based on the deposited PLD target compositions.SEM images show a consistent, columnar microstructure in the BZY electrolyte layer (Fig. 3a). These images show neither obvious variation in surface roughness nor delamination after electrical measurements under both gas atmospheres. The BCFZY films exhibit either columnar grains or grains that are elongated parallel to the growth direction.
Multidimensional, Hierarchical Bayesian model for impedance data analysis
Electrochemical impedance spectroscopy (EIS) spectra collected from the combinatorial thin films vary both qualitatively and quantitatively: the apparent size, location, and number of impedance arcs in the complex plane varies across each library, and total polarization resistances span multiple orders of magnitude. Since there is not a well-established model for the impedance of TIEC thin films, we employed the distribution of relaxation times (DRT) for initial investigation of the EIS data. Although the DRT does not require an a priori model, the DRT must be tuned by the selection of one or more control parameters, which is typically an imprecise process.12–16 In this work, we instead obtained estimates of the DRT via the calibrated hierarchical Bayesian DRT,15 which employs hierarchical Bayesian priors and error structure estimation to systematically tune the DRT. To enable separation and quantification of discrete relaxations, we used the DRT results to construct and inform an equivalent circuit model (ECM) capable of describing all measured spectra. We determined the ECM parameters by a multidimensional, hierarchical Bayesian model, which overcomes the strong peak overlap that frequently arises for certain conditions and compositions. We describe these EIS analysis methods in more detail below.Establishing the equivalent circuit model
First, we fitted all spectra with the calibrated hierarchical Bayesian DRT, which yields a continuous distribution representing a series of resistive-capacitive relaxations with varying characteristic time constants. Peaks in the DRT are analogous to common equivalent circuit elements such as ideal RC elements, dispersed ZARC elements, and asymmetric Gerischer elements.15,17–19 Thus, analysis of peaks in the DRT provides a means for empirical construction of an ECM. However, care must be taken in the identification of peaks, as pseudo-peaks may arise due to noise in the data, while peak overlap may obscure the presence of multiple peaks. In addition, an appropriate peak shape must be selected for meaningful peak deconvolution.To robustly identify peaks in the obtained DRTs, we chose the Havriliak–Negami (HN) element as a versatile basis function for peak fitting. The HN element is an empirical equivalent circuit element that can describe behaviour ranging from ideal, symmetric relaxations (RC element) to dispersed and/or asymmetric relaxations (ZARC and Gerischer elements). The impedance of an HN element at excitation frequency ω is given by
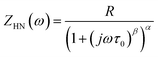 | (1) |
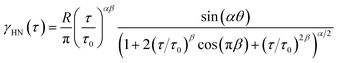 | (2) |
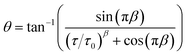 | (3) |
The DRT peak fits reveal that four peaks are present for all compositions and conditions and indicate that an ECM comprising four HN elements in series is appropriate to describe all spectra. A series resistor and inductor are included in the ECM to capture the ohmic resistance and cable inductance. However, peak positions (time constants) and magnitudes vary significantly with composition and conditions. Importantly, this often results in very strong peak overlap in individual spectra. Fig. 4 shows the distribution of DRT peak locations as a function of temperature for the spectra measured under dry air. At the lowest measurement temperature, four distinct peak positions are visible, but as the temperature increases, the distributions of the two intermediate peaks merge and become difficult to distinguish. This highlights a critical challenge in the analysis of the EIS data: it is often very difficult, if not impossible, to separate overlapping peaks in a single spectrum.
 | ||
| Fig. 4 Distribution of HN peak time constants identified in the DRTS for the dry air atmosphere as a function of measurement temperature. Darker colours indicate greater density of identified peaks. | ||
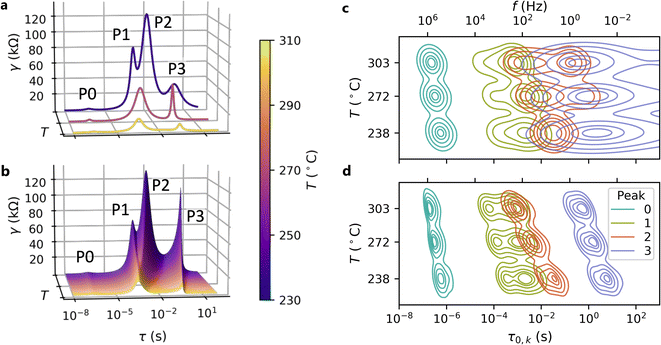 | ||
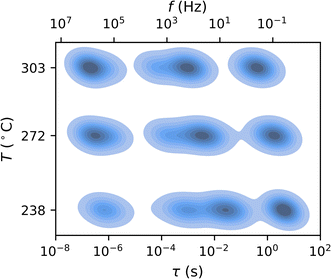
| Fig. 5 Comparison of the multidimensional model to a conventional ECM. (a and b) Equivalent DRTS of the (a) conventional ECM fit and (b) the multidimensional model fit of spectra measured at three different temperatures for a single contact. While four peaks are present at all temperatures, the conventional ECM treats each temperature independently and fails to resolve the two intermediate peaks (P1 and P2) at all but the lowest temperature, where peak separation is the greatest. Meanwhile, the multidimensional model extends each peak across all temperatures and is thus able to distinguish the two intermediate peaks even when they overlap. (c and d) The distributions of peak locations for the dry air condition identified by (c) the conventional ECM and (d) the multidimensional model as functions of measurement temperature. For each peak, the five contour lines (from outer to inner) indicate the regions outside of which 10%, 25%, 50%, 75%, and 90% of the probability mass lie. The conventional ECM shows an extremely high degree of uncertainty in the locations of Peaks 2 and 3, whereas the multidimensional model identifies much tighter peak location distributions that are consistent with the DRT results shown in Fig. 4. | ||
The multidimensional model uses the ECM derived from the DRT analysis, comprising four HN elements in series with an inductance and an ohmic resistance, as the core impedance model for a single temperature, and extends the model to multiple temperatures by incorporating activated behaviour for each HN element. Consider a single contact for which we collected impedance spectra at P distinct temperatures. The impedance is defined as a function of frequency and temperature. We select one of the measurement temperatures as the base temperature, Tbase. We may then describe the impedance by a combination of activation energies and the ECM parameters at the base temperature. The impedance of the kth HN element at any temperature T is thus given by
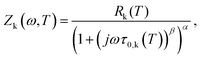 | (4) |
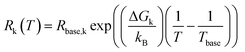 | (5) |
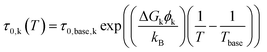 | (6) |
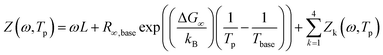 | (7) |
Because the film surface temperature may vary slightly with position and was not directly measured at the electrical probe location, we assume that temperature errors are the primary source of deviation from the Arrhenius relationship. Thus, the model allows a small temperature offset from the surface temperature at heater setpoint p:
| Tp = Tp,cal + ΔTp | (8) |
Due to the time constraints of the high-throughput measurement, it was not feasible to fully equilibrate each sample to the humid N2 atmosphere, which requires a substantially longer equilibration time than the dry air atmosphere. Thus, the humid N2 spectra represent a partially equilibrated sample state and are not compliant with Kramers–Kronig relations at low frequencies. To address this issue, we included an empirical equilibration impedance contribution in the model for the humid N2 atmosphere. The equilibration contribution cannot be assigned to a particular element of the model; it simply accounts for a contribution to the impedance that is not Kramers–Kronig compliant so that the standard ECM elements can address the Kramers–Kronig-compliant portion of the spectrum without perturbation. The effect of partial equilibration on the model parameters is further reduced by the multidimensional nature of the model because the model parameters must be in concordance across all temperatures. Still, the effect of the equilibration process on the impedance measurement cannot be ignored; the humid N2 data does not represent the equilibrium sample state, and should instead be interpreted as a qualitative indicator of how the sample state changes when exposed to lower pO2 and higher pH2O. The full definition of the equilibration contribution is given in Section S5†.
Impedance model regression
The parameters of the impedance model defined above can be regressed to the data by inputting the spectra for all P temperatures simultaneously. However, the parameter space is high-dimensional and requires careful initialization and control for meaningful results. For each contact, we used the DRT fit of the base temperature spectrum to initialize the inductance, ohmic resistance, and parameters of the HN elements. We obtained a rough initial estimate of the activation energy for each peak from manual fits of several spectra with clearly resolved peaks. Meanwhile, we used a hierarchical Bayesian prior structure to tune the parameter values determined by the model. Each prior defines a distribution of expected values for a parameter; this distribution influences the result of the optimization via a statistically derived addition to the objective function. The strength of each prior can be adjusted via the width of the distribution (broad prior distributions tend to be weaker and tight prior distributions tend to be stronger). We placed weak priors on the parameters Rk, ϕk, L, and R∞,base to prevent extreme values, and a stronger prior on ΔTp to minimize deviation from the calibrated temperatures. In addition, we applied the error model used in ref. 15 to estimate the error structure of the impedance spectra such that concordance of parameter values and priors is balanced with fit quality. The full prior structure is defined in Section S5.† For more background on the use of hierarchical Bayesian priors in analysis of EIS data, we refer the reader to ref. 15, 18, and 19. We constructed and optimized the Bayesian model using Stan, a software package for statistical modeling.20 Although it is possible to use Monte Carlo sampling to obtain credible intervals for model parameters, the computational cost is very high for a dataset of this size. Instead, the parameters are optimized via the L-BFGS-B algorithm.Analysis of impedance model results
Multidimensional model validation
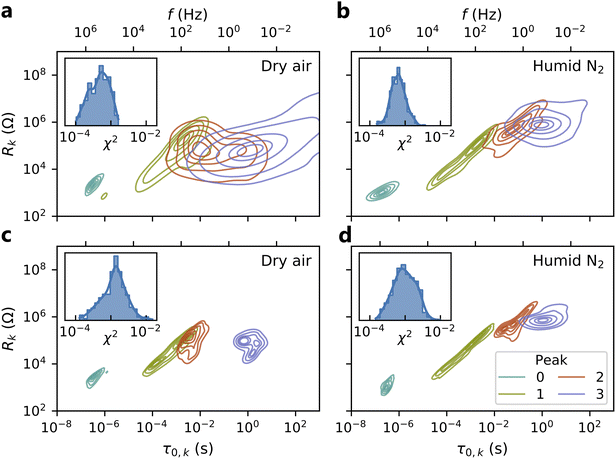
In Fig. 6, we validate the multidimensional model results by summarizing the goodness-of-fit values (χ2) and peak parameters (Rk, τ0,k) from this model compared to those obtained from conventional ECM fits. In the dry air atmosphere, the multidimensional model identifies a small peak at high frequency (Peak 0), two overlapping peaks at intermediate frequencies (Peaks 1 and 2), and a peak at low frequency (Peak 3). The conventional ECM shows similar distributions for Peaks 0 and 1, but much wider distributions of the time constants and resistances for Peaks 2 and 3. This reflects the much higher uncertainty associated with the conventional ECM due to peak overlap: a single HN element may adequately fit the impedance arising from two overlapping peaks, allowing the remaining element to be placed arbitrarily to fit noise in the data. In contrast, the elements of the multidimensional model are constrained by the Arrhenius relationship and informed by data from all temperatures, and thus cannot be placed arbitrarily. This constraint prevents overfitting of the data and results in slightly larger goodness-of-fit (χ2) values from the multidimensional model than from the conventional ECM, even though the conventional ECM has higher uncertainty.The humid N2 results (Fig. 6b and d) show similar trends: the multidimensional model identifies tighter distributions for all peaks with slightly larger χ2 values. However, Peaks 1–3 exhibit greater separation in the humid N2 atmosphere than in the dry air atmosphere, and thus the conventional ECM more consistently identifies their locations and magnitudes in the humid N2 data. In both dry air and humid N2, there is a noticeable correlation between Rk and τ0,k. This may be attributed to the direct relationship between the time constant and the product of resistance and capacitance (τ0 = RC). Since χ2 alone is not a robust indicator of fit suitability, Fig. S5† includes representative multidimensional fits corresponding to the 1st, 50th, and 99th percentile of χ2 for each atmosphere as a point of further validation. These results demonstrate that the multidimensional model dramatically reduces uncertainty in the ECM parameters while obtaining appropriate fit quality.
Trends in impedance peaks
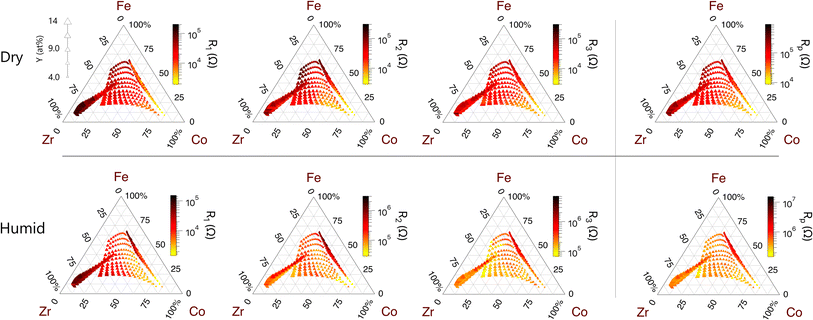
Films synthesized by PLD have inherent thickness variation and may exhibit spatially varying oxygen concentration due to plume dynamics during deposition. Although we minimized each of these variables, by centring the plume off the edge of the substrate and by annealing the films in air prior to measurement, they should not be ignored. To separate the influence of film composition from the influence of composition-independent variables, we first performed a multivariate elastic net analysis of the resistances of the individual DRT peaks. This analysis revealed that Peaks 1 and 2 are slightly correlated to film thickness, while all peaks exhibit a correlation with radial distance from the centre of the library. These non-compositional effects are largely responsible for the apparent discontinuities in peak resistance trends at the boundaries between sample libraries, but are small enough in magnitude that the compositional effects dominate when considering the results for the full composition space. Next, we examined trends in the resistances (Ri) and capacitances (Ci) of individual DRT peaks with changes in chemical composition, temperature, and gas atmosphere, to determine which peaks limit performance and to identify optimal compositions.Peak 0 is a small, high-frequency peak that is observed in all spectra. The resistance of this peak (R0) is insensitive to BCFZY composition across the sample libraries (Fig. S4†). The magnitude of R0 is consistent with the estimated conductivity and thickness of the PLD-deposited BZY thin film under the conditions of measurement; the activation energy of the R0 process (∼0.4 eV) is consistent with proton transport; and R0 decreases in humid N2 relative to dry air, a behaviour that is consistent with proton conduction. Thus, we attribute this resistance to the proton-conducting BZY thin-film electrolyte layer and not to the cathode.21,22
The ITO/BZY interface is also expected to contribute to the impedance. Like the BZY impedance, the ITO/BZY interfacial impedance should be insensitive to BCFZY chemical composition and nominally consistent across all samples. We do not observe an additional, composition-independent impedance arc. Therefore, we conclude that the impedance of this interface is obscured within one of the other impedance arcs and is small enough that it does not dominate the impedance at any given frequency.
Fig. 7 shows the resistances of the cathode-related peaks (Peaks 1–3) across all compositions under each gas condition. The corresponding capacitances of these peaks are available in Fig. S7.† Under each condition, all three of the cathode-related resistances (R1, R2, and R3) have low values when the Co concentration is high. Consequently, Co-rich compositions have the lowest total polarization resistances. The resistance (R1) and capacitance (C1) of the medium-frequency peak show only slight changes under humid N2 compared to dry air. In contrast, the medium-low-frequency peak (Peak 2) shows a much stronger response to the gas environment with a characteristic frequency that varies by up to two orders of magnitude between the two gas conditions for a single contact. Both the resistance (R2) and the capacitance (C2) corresponding to this peak increase under humid N2 compared to dry air. Finally, the resistance (R3) of the low frequency peak (Peak 3) increases significantly in humid N2 compared to dry air while the capacitance of this peak (C3) decreases significantly in humid N2 compared to dry air. Furthermore, the capacitance (C3) of the low-frequency peak is the highest among all peaks and its value is consistent with a chemical capacitance.23 The characteristics and trends of each cathode-related peak are summarized in Table 2.
| Interquartile range | ||||
|---|---|---|---|---|
| Peak 1 | Peak 2 | Peak 3 | ||
| Dry | Log10 frequency (Hz) | 2.32 to 3.28 | 2.01 to 2.38 | −0.66 to −0.21 |
| Log10 capacitance (F) | −7.92 to −7.67 | −7.71 to −7.25 | −5.02 to −4.35 | |
| Log10 resistance (Ohms) | 3.78 to 4.66 | 4.14 to 4.73 | 4.17 to 4.53 | |
| Activation energy (eV) | 0.52 to 0.69 | 1.04 to 1.19 | 0.98 to 1.11 | |
| Humid | Log10 frequency (Hz) | 2.45 to 3.29 | 0.67 to 1.28 | −0.67 to −0.21 |
| Log10 capacitance (F) | −7.92 to −7.80 | −7.02 to −6.78 | −5.86 to −5.61 | |
| Log10 resistance (Ohms) | 3.81 to 4.57 | 4.92 to 5.36 | 5.22 to 5.48 | |
| Activation energy (eV) | 0.51 to 1.06 | 0.92 to 1.18 | 0.93 to 1.15 | |
| Trend with composition | Both R1 and C1 decrease with increasing Co | R 2 decreases with Co and increases with Fe | C 3 increases and R3 decreases with increasing Co concentration | |
| Trend with change from dry air to humid N2 | R 1 slightly decreases, C1 slightly increases | R 2 and C2 increase | R 3 substantially increases, C3 substantially decreases | |
Impedance peaks represent electrochemical processes
The peaks in the DRT represent different electrochemical processes. Without a full mechanistic study, the DRT peaks cannot be definitively assigned to particular processes. However, based on the trends mentioned above and previous studies on similar materials, we propose tentative assignments for each of these peaks.We attribute Peak 1 to charge transfer at the electrode/electrolyte interface.22–25 This attribution is supported by the fact that the capacitance values are consistent with a double-layer capacitance.21,22 The trends in this peak may be moderated by the interplay between proton and electron–hole concentrations as they change with chemical composition and atmospheric conditions, specifically at the interface. In BZY, a space charge region in the grain boundaries blocks proton transport.26,27 The barrier height is reduced by hydration26 and the space charge region width is reduced by increased concentrations of Y and of mobile charge carriers.28 A similar effect at the electrode/electrolyte interface may explain the observed changes in R1. However, because our counter electrode is a buried electron-conducting layer of ITO, it is unclear whether there is a mechanism for proton exchange in the absence of a gas phase at the BZY/ITO interface. A proton-exchange process at this interface would explain why the impedance spectra approach the real axis at low frequencies, rather than exhibiting the capacitor-like shape that is expected when one electrode blocks ionic carriers. Alternatively, electronic short-circuiting through the BZY electrolyte (which is known to have some p-type electronic conductivity at high pO2) would cause the impedance spectrum to meet the real axis at the DC limit. However, the strong dependence of the impedance on the presence and composition of the BCFZY layer indicates that electronic conduction is not the primary factor that explains this phenomenon.
We attribute Peak 2 to a surface reaction process due to a drastic change in its characteristic time constant with the change in atmosphere, which may be explained by different surface reactions filling oxygen vacancies under different conditions. Under dry air, the surface reaction may comprise incorporation of adsorbed oxygen into the lattice,29 while in humid N2, the surface reaction may comprise the dissolution/formation of water.30
We attribute Peak 3 to oxygen dissociation/adsorption at the surface of the BCFZY electrode due to its exceptionally high capacitance.31 Additionally, the resistance of this peak increases substantially in humid N2 compared to dry air, which may result from water blocking the reaction sites for oxygen dissociation/adsorption.
These assignments are consistent with the observed trends and with previous literature on similar compositions. Still, a detailed, mechanistic study is urgently required to verify these claims and to conclusively define correlations between impedance peaks and electrochemical processes.
Limiting processes and optimal composition
Performance-limiting processes
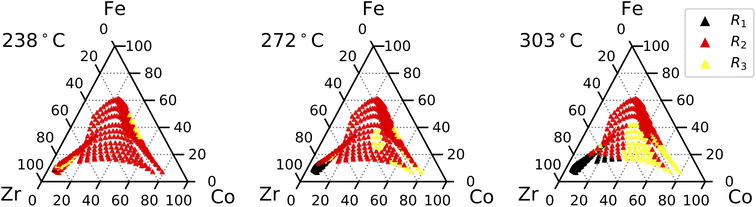
By determining which resistance is the highest for a given composition, we can identify which resistance most strongly limits performance across the composition space for the different gas conditions. However, these results are also affected by temperature, as confirmed in the literature.32Fig. 8 shows the dominant resistance at each setpoint under dry air. At 238 °C, Rp is dominated by R2 across most of the composition space. As the measurement temperature increases, R3 begins to dominate at increasingly lower Co concentrations. This indicates that R3 has a lower activation energy (lower temperature dependence) compared to R2 and overtakes it at higher temperatures. Compositions with high concentrations of Zr and Y are dominated by R2 at lower temperatures, but R1 begins to dominate as temperature increases. At 303 °C, R1 dominates for materials rich in Zr and Y, while Co-rich compositions are dominated by R3, and the overall polarization resistances of the remaining compositions are dominated by R2. Under humid N2, R3 dominates across all compositions at 303 °C, although R2 dominates in some Fe-rich and Zr-rich compositions at lower temperatures.
Optimal composition depends on temperature
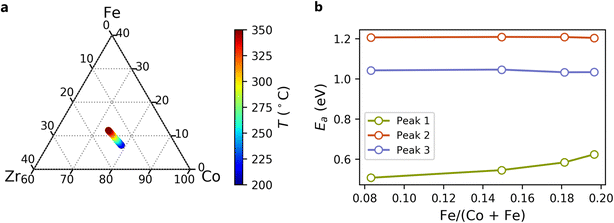
We identified the optimal BCFZY composition under a given set of conditions as the composition with the lowest total polarization resistance, which provides an overall performance metric of a given material applied as a cathode in a half fuel cell. To represent broad trends in the data rather than peculiarities of individual contacts, we determined optimal compositions through local compositionally weighted averages of resistances and activation energies. We found the optimal composition across a range in temperature by combining these activation energies and resistance values to interpolate between measured temperatures and extrapolate beyond measured temperatures.Fig. 9a illustrates the variation in optimal composition with temperature between 200 °C and 350 °C in dry air. At all temperatures, high transition metal content is favoured (Co + Fe > 80% of the B-site), reflecting the beneficial effect of Co and Fe on charge transfer and surface activity. Optimal concentrations of Zr and Y are nearly constant. At lower temperatures, Co is distinctly favoured over Fe. However, Fe becomes increasingly favourable with increasing temperature. We attribute this to the influence of Fe on the activation energy of Peak 1 (Ea,1) as shown in Fig. 9b. While the activation energies of Peak 2 and Peak 3 are nearly independent of the Fe/(Co + Fe) ratio, Ea,1 increases with increasing Fe/(Co + Fe) ratio. Consequently, as Fe concentration increases, R1 decreases more rapidly with increasing temperature, although the optimal Fe/(Co + Fe) ratio remains well below 1.
The activation energies calculated from our experimental results allow us to investigate predicted optimal compositions at higher temperatures. The results of this analysis indicate that BaCo0.4Fe0.4Zr0.1Y0.1O3−δ, which has been broadly studied for protonic ceramic electrochemical cells, may be nearly optimized for operating temperatures well above 500 °C, but that electrodes for lower-temperature applications may benefit from a substantially lower Fe/(Co + Fe) ratio.
The lowest area-specific resistance (ASR) achieved from the samples measured at 303 °C under dry air was 162.7 Ω × cm2 for the electrode composition BaCo0.77Fe0.07Zr0.14Y0.02O3−δ. However, this value is difficult to compare to literature values, given the low operating temperature. By the activation energies of Peaks 1, 2, and 3, our model predicts that at an operating temperature of 500 °C, we could achieve an ASR of 9.4 Ω × cm2 with a cathode composition of BaCo0.64Fe0.20Zr0.14Y0.02O3−δ. This is comparable to literature values, especially when we consider the reduced surface area of these dense films compared to porous, bulk electrodes.8,9
Summary and conclusions
Here, we presented a systematic study of the BCFZY family of TIEC materials by combinatorial experimental methods. We synthesized thin-film microelectrodes across a wide range of B-site cation ratios and established appropriate pulsed laser deposition parameters to achieve crystalline films across the entire range. By using the same deposition parameters for all compositions, we ensured that the microstructure varied minimally among compositions, as evidenced by cross-sectional SEM images. We showed that the lattice constant changes predictably with the cation composition, suggesting formation of a solid solution.We measured the impedance of the films under humidified N2 and dry air at 238 °C, 272 °C, and 303 °C and observed the condition-dependent changes in the impedance spectra and in the corresponding DRT. We employed a calibrated hierarchical Bayesian DRT method to identify consistent impedance features and constructed an equivalent circuit model to describe all spectra. The ECM parameters were robustly determined using a multidimensional Bayesian model that assimilates data from multiple temperatures to resolve ambiguity in individual spectra. The ECM results provide resistances, capacitances, time constants, and activation energies of discrete impedance features.
These results identify a set of optimal BCFZY cathode compositions for PCFCs that can be selected according to desired operating temperature. The investigative methods described here can be extended to other electrolyte chemistries or other cathode materials families to provide similar insight for materials discovery in additional chemical spaces.
Author contributions
MP performed the experimental investigation and initial data analysis. JH developed the methodology for impedance spectral analysis. MP and JH curated data, interpreted results, and wrote the original draft. RO and AZ were responsible for funding acquisition, review, and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work at CSM was supported by the Army Research Office under grant number W911NF-17-1-0051, with additional support provided by the Advanced Research Projects Agency-Energy (ARPA-E) through the REFUEL (award DE-AR0000808) and REBELS programs (award DEAR0000493). Work at NREL was supported by the U.S. Department of Energy, under Contract No. DEAC36-08GO28308 with the Alliance for Sustainable Energy LLC, the manager and operator of the National Renewable Energy Laboratory (NREL). Funding for the research facilities at NREL was provided by the Office of Energy Efficiency and Renewable Energy (EERE), under the Hydrogen and Fuel Cell Technologies Office (HFCO), as part of the HydroGEN Energy Materials Network (EMN) consortium (combinatorial pulsed laser deposition facilities); and Laboratory Directed Research and Development (LDRD) program (spatially resolved EIS measurement instrument). The views expressed in the article do not necessarily represent the views of the DOE or the U.S.References
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326 CrossRef CAS PubMed.
- C. Duan, R. Kee, H. Zhu, N. Sullivan, L. Zhu, L. Bian, D. Jennings and R. O'Hayre, Nat. Energy, 2019, 4, 230–240 CrossRef CAS.
- F. S. Baumann, J. Maier and J. Fleig, Solid State Ionics, 2008, 179, 1198–1204 CrossRef CAS.
- C. Duan, D. Hook, Y. Chen, J. Tong and R. O'Hayre, Energy Environ. Sci., 2017, 176, 176–182 RSC.
- S. Ryu, S. Lee, W. Jeong, A. Pandiyan, S. B. Krishna Moorthy, I. Chang, T. Park and S. W. Cha, Surf. Coat. Technol., 2019, 369, 265–268 CrossRef CAS.
- Y. Chen, T. Hong, P. Wang, K. Brinkman, J. Tong and J. Cheng, J. Power Sources, 2019, 440, 227122 CrossRef CAS.
- X. Kuai, G. Yang, Y. Chen, H. Sun, J. Dai, Y. Song, R. Ran, W. Wang, W. Zhou and Z. Shao, Adv. Energy Mater., 2019, 9, 1902384 CrossRef CAS.
- M. Papac, V. Stevanović, A. Zakutayev and R. O'Hayre, Nat. Mater., 2021, 20, 301–313 CrossRef CAS PubMed.
- K. D. Kreuer, Solid State Ionics, 1999, 125, 285–302 CrossRef CAS.
- K. R. Talley, S. R. Bauers, C. L. Melamed, M. C. Papac, K. N. Heinselman, I. Khan, D. M. Roberts, V. Jacobson, A. Mis, G. L. Brennecka, J. D. Perkins and A. Zakutayev, ACS Comb. Sci., 2019, 21, 537–547 CrossRef CAS PubMed.
- M. C. Papac, K. R. Talley, R. O'Hayre and A. Zakutayev, Rev. Sci. Instrum., 2021, 92, 065105 CrossRef CAS PubMed.
- S. Effendy, J. Song and M. Z. Bazant, J. Electrochem. Soc., 2020, 167, 106508 CrossRef CAS.
- B. A. Boukamp, J. Phys.: Energy, 2020, 2, 042001 CAS.
- M. Hahn, S. Schindler, L. C. Triebs and M. A. Danzer, Batteries, 2019, 5, 43 CrossRef CAS.
- J. Huang, M. Papac and R. O'Hayre, Electrochim. Acta, 2021, 367, 137493 CrossRef CAS.
- N. Schlüter, S. Ernst and U. Schröder, ChemElectroChem, 2020, 7, 3445–3458 CrossRef.
- B. A. Boukamp and A. Rolle, Solid State Ionics, 2017, 302, 12–18 CrossRef CAS.
- M. B. Effat and F. Ciucci, Electrochim. Acta, 2017, 247, 1117–1129 CrossRef CAS.
- F. Ciucci and C. Chen, Electrochim. Acta, 2015, 167, 439–454 CrossRef CAS.
- B. Carpenter, A. Gelman, M. D. Hoffman, D. Lee, B. Goodrich, M. Betancourt, M. A. Brubaker, J. Guo, P. Li and A. Riddell, J. Stat. Softw., 2017, 76, 1–32 Search PubMed.
- F. Mauvy, C. Lalanne, J.-M. Bassat, J.-C. Grenier, H. Zhao, L. Huo and P. Stevens, J. Electrochem. Soc., 2006, 153, A1547 CrossRef CAS.
- A. Grimaud, F. Mauvy, J. M. Bassat, S. Fourcade, L. Rocheron, M. Marrony and J. C. Grenier, J. Electrochem. Soc., 2012, 159, B683–B694 CrossRef CAS.
- F. S. Baumann, J. Fleig, G. Cristiani, B. Stuhlhofer, H.-U. Habermeier and J. Maier, J. Electrochem. Soc., 2007, 154, B931–B941 CrossRef CAS.
- H. Sumi, H. Shimada, Y. Yamaguchi, Y. Mizutani, Y. Okuyama and K. Amezawa, Sci. Rep., 2021, 11, 10622 CrossRef CAS PubMed.
- J. Dailly, F. Mauvy, M. Marrony, M. Pouchard and J.-C. Grenier, J. Solid State Electrochem., 2011, 15, 245–251 CrossRef CAS.
- C. Kjølseth, H. Fjeld, Ø. Prytz, P. I. Dahl, C. Estournès, R. Haugsrud and T. Norby, Solid State Ionics, 2010, 181, 268–275 CrossRef.
- S. Ricote, N. Bonanos, H. J. Wang and B. A. Boukamp, Solid State Ionics, 2012, 213, 36–41 CrossRef CAS.
- G. Gregori, R. Merkle and J. Maier, Prog. Mater. Sci., 2017, 89, 252–305 CrossRef CAS.
- A. Grimaud, F. Mauvy, J. M. Bassat, F. Sebastien, M. Marrony and J. C. Grenier, J. Mater. Chem., 2012, 22, 16017–16025 RSC.
- D. Poetzsch, R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2014, 16, 16446–16453 RSC.
- F. S. Baumann, J. Fleig, H.-U. Habermeier and J. Maier, Solid State Ionics, 2006, 177, 1071–1081 CrossRef CAS.
- H. Zhao, F. Mauvy, C. Lalanne, J. M. Bassat, S. Fourcade and J. C. Grenier, Solid State Ionics, 2008, 179, 2000–2005 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta01736a |
| This journal is © The Royal Society of Chemistry 2023 |