Large second harmonic generation in a penta-CdO2 sheet exfoliated from its bulk phase†
Changsheng
Hou
a,
Yiheng
Shen
a,
Qian
Wang
 *a,
Y.
Kawazoe
bcd and
P.
Jena
*a,
Y.
Kawazoe
bcd and
P.
Jena
 e
e
aCAPT, School of Materials Science and Engineering, BKL-MEMD, Peking University, Beijing, 100871, China. E-mail: qianwang2@pku.edu.cn
bNew Industry Creation Hatchery Center, Tohoku University, Sendai, 980-8577, Japan
cDepartment of Physics, Suranaree University of Technology, Nakhon Ratchasima, 30000, Thailand
dDepartment of Physics and Nanotechnology, SRM Institute of Science and Technology, Kattankulathur, Tamil Nadu 603203, India
eDepartment of Physics, Virginia Commonwealth University, Richmond, VA 23284, USA
First published on 25th November 2022
Abstract
Two-dimensional (2D) materials composed solely of pentagonal motifs are of particular interest due to their unique geometries and novel properties. Especially, the broken centrosymmetry and in-plane mirror symmetry in penta-graphene-like materials result in both in-plane and out-of-plane second harmonic generation (SHG). Transition metal cations with a filled d10 shell (d10-TM) can significantly enhance the SHG response as found in many previously studied bulk materials. Here, based on first-principles calculations combined with independent particle approximation, we show that large SHG can also exist in some 2D d10-TM oxides, such as penta-CdO2, which can be chemically exfoliated from its bulk phase with its dynamical, thermal, and mechanical stability intact. We further find that penta-CdO2 possesses extraordinary in-plane and out-of-plane SHG responses with large static SHG susceptibilities of χsheet14(0) = χsheet25(0) = χsheet36(0) = 8.86 pm2 V−1 due to the phase-matching between fundamental and second-harmonic light. In addition, the low thermal expansion and a large optical band gap of 3.24 eV endow the penta-CdO2 sheet with a high laser-induced damage threshold. Discussions are also made on the penta-ZnO2 sheet. This study expands the family of 2D materials with outstanding SHG performance.
1. Introduction
Nonlinear optics has attracted significant interest due to its important role in photonic applications including ultrafast lasers,1 frequency conversion,2 photodetectors,3 and optical modulator/switches/memories.4 As one of the leading nonlinear optical responses, second harmonic generation (SHG) is one of the hotly pursued topics because it is more easily observed in experiments as compared to other higher-order nonlinear optical effects. In general, SHG materials are non-centrosymmetric and non-metallic. Therefore, even order terms can exist in their electric polarization expansion (P = ε0χ(2)E2 + ε0χ(4)E4 + … + ε0χ(2n)E2n). Since the few-atom thickness of the 2D materials is far below the coherence length of photons, the phase-matching condition is usually satisfied, making the SHG response strong enough for observation and utilization.5 Thus, many non-centrosymmetric 2D materials with large SHG responses have been theoretically predicted and experimentally observed in recent years, including 2H-MoS2,6 h-BN,7 2D CrI3,8 2D GaSe,9 2D SnSe,10 2D perovskite,11 α-Sb and α-Bi.12 In addition, the inversion symmetry of some centrosymmetric bulk materials is broken when thinned down to 2D materials, providing more opportunities to generate SHG responses.13 However, the mirror symmetry in the out-of-plane direction hinders the out-of-plane components of the SHG matrix. For instance, odd-layer MoS2 sheets with D3h symmetry possess only one inequivalent in-plane SHG coefficient.6 If the out-of-plane mirror symmetry could be broken, the SHG performance would be enhanced. Currently, one of the successful approaches to break the out-of-plane mirror symmetry for a remarkable out-of-plane SHG signal is to construct Janus structures, as in the case with α-In2Se3,14 where the out-of-plane SHG susceptibility spectra enable ultrafast, simple, and noninvasive characterization of the vertical polarization, lattice symmetry, number of layers, and stacking sequence.Comparied with most 2D non-centrosymmetric materials constructed from highly symmetric hexagonal motifs, penta-graphene-like materials exhibit both in-plane and out-of-plane SHG responses, as found in penta-ZnS2.15 Since the theoretical prediction of penta-graphene,16 over one hundred new pentagonal 2D materials have been theoretically proposed and some, experimentally synthesized.17,18 It is interesting to note that the top-down approach has been successfully used for the synthesis of pentagonal 2D materials. For example, penta-PdSe2 was prepared by exfoliating bulk PdSe2 in the marcasite phase,19 and penta-FeS2 was synthesized by chemically cleaving bulk iron pyrite via liquid-phase exfoliation.20 Thus, it is important to find new stable pentagonal sheets with extraordinary SHG performance that could potentially be synthesized from marcasite and pyrite materials. Techniques such as chemical vapor deposition21 and molecular beam epitaxy22 have also been used in the past to synthesize 2D pentagonal sheets. These include penta-PdSe2, penta-silicene nanoribbon synthesized via physical vapor deposition,23 penta-PdS2 fabricated by sulfurization of a Pd film,24 and penta-NiN2 synthesized using a high-pressure approach.25
For the application in an optical device, high-quality SHG materials should satisfy several requirements including high SHG efficiency (a large static SHG susceptibility), moderate birefringence (0.06 ≤ Δn ≤ 0.1) to achieve phase-matching, and a high laser-induced damage threshold (LIDT) value in addition to high chemical and physical stabilities and easy-to-synthesize single crystals.26 Since metal oxides have a strong absorption edge, and usually exhibit wide optical band gaps and high LIDT, they have received extensive attention in the design of high-performance SHG materials.27 Since d10-transition metal (d10-TM) cations (e.g. Zn2+, Cd2+, Hg2+, etc.) are electron rich, have flexible bonding, and possess polar displacement features, they can be expected to induce much larger polarizability and deformability, stimulating great interest in the design of bulk SHG materials containing d10-TM.28–32 Thus, it is possible that 2D d10-TM oxides, entirely composed of pentagon motifs, would exhibit large SHG susceptibility, moderate birefringence to achieve phase-matching, and high LIDT. This expectation motivated us to carry out this study.
2. Computational methods
First-principles calculations are performed within the framework of density functional theory (DFT) implemented in the Vienna Ab initio Simulation Package (VASP).33 The projected augmented wave (PAW)34 method is used to treat interactions between ion cores and valence electrons. The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA)35 is used to describe the electronic exchange–correlation interaction. The hybrid Heyd–Scuseria–Ernzerhof (HSE06)36 functional is further applied to obtain accurate band structures. The energy cutoff, the convergence thresholds of total energy and inter-atomic force are set to 600 eV, 10−8 eV, and 10−6 eV Å−1, respectively. The first Brillouin zone is represented by a 11 × 11 × 1 k-point grid using the Monkhorst–Pack scheme.37 The vacuum space is set to 18.28 Å in the nonperiodic direction to avoid interaction between two adjacent layers. The phonon spectra are calculated using the finite displacement method implemented in the Phonopy code38 and a 5 × 5 × 1 supercell. The temperature in ab initio molecular dynamics (AIMD) simulations is controlled by using the Nosé–Hoover thermostat.39 The elastic constants are calculated using the finite difference methods.40The SHG susceptibility is described by using a third-rank tensor χabc(2)(−2ω, ω, ω), defined as Pa(2ω) = χabc(2)(−2ω, ω, ω)Eb(ω)Ec(ω), where P(2ω) is the second-order term of electric polarization, E(ω) is the fundamental light induced electric field, and a, b, c ∈ {x, y, z}. The χabc(ω) is calculated within the independent particle approximation41 by using the package developed by Zhang's group,42 where the SHG tensor can be expressed by the sum of contributions from the pure inter-band process χabc,e(ω) and the mixed inter-band and intra-band process χabc,i(ω), both of which can be deduced from the electronic structure. The tensor component χbulkabc(ω) of a bulk material is calculated by using
| χbulkabc(ω) = χbulkabc,e(ω) + χbulkabc,i(ω). | (1) |
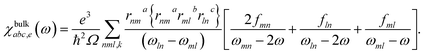 | (2) |
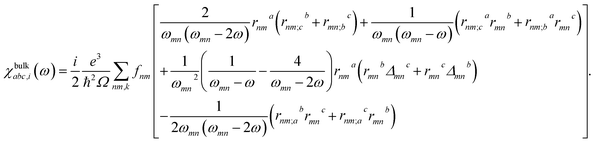 | (3) |
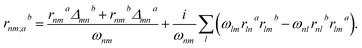 | (4) |
The static SHG susceptibility can be obtained by using the Kramers–Kronig transformation,43
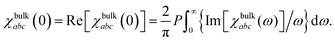 | (5) |
To obtain a converged SHG susceptibility tensor, the electronic structures are calculated at the PBE level with a very dense k-point sampling of 99 × 99 × 1. Since the PBE/GGA underestimates the band gap in the calculation of optical properties, the scissor approximation is applied where the difference between the band gaps is obtained at the PBE and HSE06 levels in SHG calculations.44 For 2D materials, it is necessary to replace the volume Ω in eqn (2) and (3) with the area of the 2D plane of the unit cell, as the volume depends on the thickness of the vacuum space in the normal direction of 2D materials.10 Thus, the unit of the sheet SHG susceptibility χsheetabc is pm2 V−1.
The linear optical properties of bulk materials are obtained from the complex frequency-dependent dielectric function εbulkij(ω). The imaginary part Im[εbulkij(ω)] is calculated by using the following equation:45
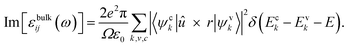 | (6) |
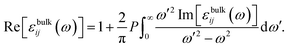 | (7) |
The real and imaginary dielectric functions of 2D materials also need to be renormalized due to the thickness-dependent volume Ω in eqn (6). Therefore, we use the following formulae47 to calculate the dielectric functions of the penta-CdO2 sheet εsheetij(ω):
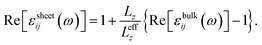 | (8) |
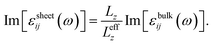 | (9) |
3. Results and discussion
3.1 Structure and stability
The 2D frameworks featuring the Cairo pentagonal tessellation exist in the marcasite and pyrite materials with Pnnm symmetry (space group no. 58), and Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry (space group no. 206), respectively.48 Hence, it is possible to obtain the corresponding pentagon-based sheets by using physical or chemical exfoliation techniques. We rationally search for pentagonal d10-TM oxide sheets from their bulk counterparts containing internal pentagonal layers. The searching starts from an initial set of crystals extracted from the Materials Project (MP) database,49 retrieving entries with one d10-TM element and oxygen, where we only consider the compounds matching the experimentally determined materials in the Inorganic Crystal Structure Database (ICSD).50 Under these conditions, the initial dataset provides 45 bulk structures for further analysis, as summarized in Table S1 in the ESI.† Then, according to the features of the marcasite and pyrite unit cells, we use the space group symmetry (Pnnm, Pbca or Pa
symmetry (space group no. 206), respectively.48 Hence, it is possible to obtain the corresponding pentagon-based sheets by using physical or chemical exfoliation techniques. We rationally search for pentagonal d10-TM oxide sheets from their bulk counterparts containing internal pentagonal layers. The searching starts from an initial set of crystals extracted from the Materials Project (MP) database,49 retrieving entries with one d10-TM element and oxygen, where we only consider the compounds matching the experimentally determined materials in the Inorganic Crystal Structure Database (ICSD).50 Under these conditions, the initial dataset provides 45 bulk structures for further analysis, as summarized in Table S1 in the ESI.† Then, according to the features of the marcasite and pyrite unit cells, we use the space group symmetry (Pnnm, Pbca or Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ), the stoichiometry (1
), the stoichiometry (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 or 2
2 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), and 12 atoms per unit cell as descriptors to identify bulk materials with a pentagonal configuration. These combined criteria reduce the original set of the 45 bulk structures to 3 structures (ZnO2, CdO2, and HgO2). We then directly extract pentagonal sheets from the bulk materials. The fully optimized geometries of the pentagonal sheets extracted from bulk ZnO2 and CdO2 exhibit a penta-graphene-like configuration with P
1), and 12 atoms per unit cell as descriptors to identify bulk materials with a pentagonal configuration. These combined criteria reduce the original set of the 45 bulk structures to 3 structures (ZnO2, CdO2, and HgO2). We then directly extract pentagonal sheets from the bulk materials. The fully optimized geometries of the pentagonal sheets extracted from bulk ZnO2 and CdO2 exhibit a penta-graphene-like configuration with P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m symmetry (space group no. 113), which are termed as penta-ZnO2 and penta-CdO2, respectively. The fully optimized pentagonal sheet extracted from bulk HgO2 possesses a penta-PdSe2-like19 configuration with P21/c symmetry (space group no. 14), which is named penta-HgO2. In the next step, we obtain their phonon spectra to check their dynamic stabilities. The results plotted in Fig. S2† show that penta-ZnO2, penta-CdO2 and penta-HgO2 are all dynamically stable as no any imaginary modes are found in the first Brillouin zones of their phonon spectra. Only the penta-graphene-like configuration of pentagon-based sheets can exhibit both in-plane and out-of-plane SHG responses.15 The other two typical types including penta-PdSe2-like and penta-NiN2-like25 configurations are centrosymmetric, which do not meet the basic requirements to exhibit SHG, thus reducing the original set of the three structures to two stable structures, namely, penta-ZnO2 and penta-CdO2. Since the difference in electronegativity of Cd and O atoms (1.75) is smaller than that of Zn and O atoms (1.79), the Cd–O bond is more covalent than the Zn–O bond, and the electrons in the Cd–O bond are expected to exhibit a stronger response under an electric field than that in the Zn–O bond, implying a stronger SHG response in penta-CdO2. Hence, we choose the penta-CdO2 sheet for further investigation. More details on penta-ZnO2 can be found in the ESI.†
21m symmetry (space group no. 113), which are termed as penta-ZnO2 and penta-CdO2, respectively. The fully optimized pentagonal sheet extracted from bulk HgO2 possesses a penta-PdSe2-like19 configuration with P21/c symmetry (space group no. 14), which is named penta-HgO2. In the next step, we obtain their phonon spectra to check their dynamic stabilities. The results plotted in Fig. S2† show that penta-ZnO2, penta-CdO2 and penta-HgO2 are all dynamically stable as no any imaginary modes are found in the first Brillouin zones of their phonon spectra. Only the penta-graphene-like configuration of pentagon-based sheets can exhibit both in-plane and out-of-plane SHG responses.15 The other two typical types including penta-PdSe2-like and penta-NiN2-like25 configurations are centrosymmetric, which do not meet the basic requirements to exhibit SHG, thus reducing the original set of the three structures to two stable structures, namely, penta-ZnO2 and penta-CdO2. Since the difference in electronegativity of Cd and O atoms (1.75) is smaller than that of Zn and O atoms (1.79), the Cd–O bond is more covalent than the Zn–O bond, and the electrons in the Cd–O bond are expected to exhibit a stronger response under an electric field than that in the Zn–O bond, implying a stronger SHG response in penta-CdO2. Hence, we choose the penta-CdO2 sheet for further investigation. More details on penta-ZnO2 can be found in the ESI.†
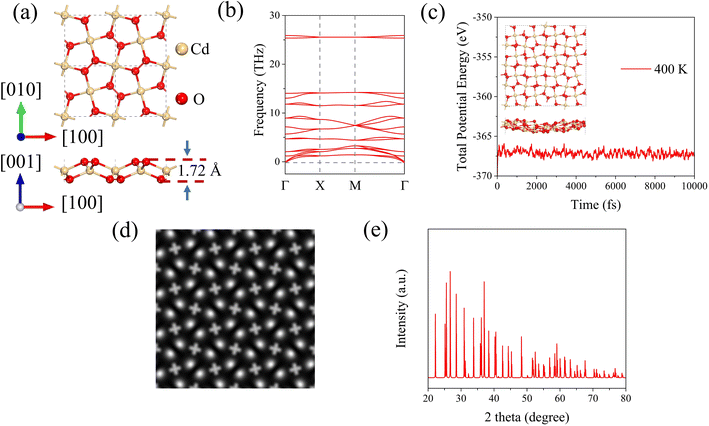
The optimized geometry and phonon spectrum of the penta-CdO2 sheet are presented in Fig. 1(a and b). The unit cell contains two Cd and four O atoms, which occupy two nonequivalent Wyckoff positions, namely, 2b (0.500, 0.500, and 0.500) and 4e (0.605, 0.105, and 0.543), respectively. Its lattice parameters are a = b = 5.00 Å. The Cd–O, and O–O bond lengths are 2.22 Å and 1.49 Å, respectively. The buckling height of the penta-CdO2 sheet is 1.72 Å. To explore the feasibility of its experimental synthesis, we calculate the exfoliation energies of the monolayer and bilayer penta-CdO2, which are defined as
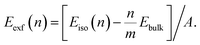 | (10) |
The thermal stability of penta-CdO2 is examined by performing AIMD simulations at 400 K. The duration of the simulation is 10 ps with a time step of 1 fs. To ensure that the observed stability is not caused by the constraints of periodic boundary conditions, a 4 × 4 × 1 supercell is used in the simulations. As shown in Fig. 1(c), the total potential energy fluctuates slightly around a constant value during the simulation and the geometry does not suffer significant distortion at the end of the simulation, which indicates that the penta-CdO2 sheet is thermally stable at 400 K.
The simulated scanning tunneling microscopy (STM) image is graphically plotted as shown in Fig. 1(d). One can see that some O–O dimers are brighter than the others, reflecting the buckled feature of this sheet. The simulated X-ray diffraction (XRD) of penta-CdO2 is also carried out, which is presented in Fig. 1(e). Finally, we examine the mechanical stability of penta-CdO2. The calculated linear elastic constants are C11 = 28.67 N m−1, C12 = −0.86 N m−1, and C66 = 13.72 N m−1. These values satisfy the requirements of Born–Huang criteria,53 namely, C11 > 0, C11 > C12 and C66 > 0 for 2D materials, confirming that penta-CdO2 is mechanically stable.
3.2 Mechanical properties
Having confirmed the stability of penta-CdO2, we study the mechanical properties of penta-CdO2 based on its linear elastic constants. The in-plane Young's modulus (E) and Poisson's ratio (ν) along an arbitrary direction (θ) are deduced from the following formulae:54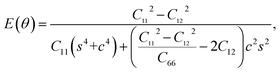 | (11) |
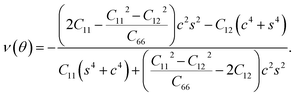 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, c = cos
θ, c = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, and θ represents the in-plane angle with respect to the [100] direction. As shown in Fig. 2(a), the Young's modulus E shows weak anisotropy, and its maximum value is 28.64 N m−1 along the [100] direction, which is only about 8% that of graphene (345 N m−1).55 The Poisson ratio ν of penta-CdO2 is highly anisotropic, exhibiting butterfly-like characteristics. Interestingly, we note that C12 is negative for penta-CdO2, leading to a negative Poisson's ratio (NPR) along most directions. The largest value of a positive Poisson's ratio is 0.01 along the [110] and its equivalent directions, while the largest absolute value of a negative Poisson's ratio is −0.03 along the [100] and its equivalent directions. Therefore, penta-CdO2 with NPR may have applications in nanomechanical devices as a nano-auxetic material.
θ, and θ represents the in-plane angle with respect to the [100] direction. As shown in Fig. 2(a), the Young's modulus E shows weak anisotropy, and its maximum value is 28.64 N m−1 along the [100] direction, which is only about 8% that of graphene (345 N m−1).55 The Poisson ratio ν of penta-CdO2 is highly anisotropic, exhibiting butterfly-like characteristics. Interestingly, we note that C12 is negative for penta-CdO2, leading to a negative Poisson's ratio (NPR) along most directions. The largest value of a positive Poisson's ratio is 0.01 along the [110] and its equivalent directions, while the largest absolute value of a negative Poisson's ratio is −0.03 along the [100] and its equivalent directions. Therefore, penta-CdO2 with NPR may have applications in nanomechanical devices as a nano-auxetic material.
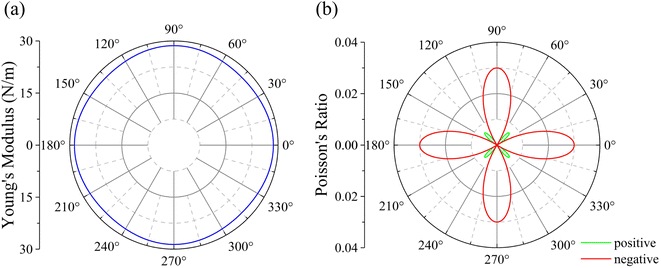 | ||
| Fig. 2 Variation of (a) the in-plane Young's modulus, and (b) Poisson's ratio with the direction in penta-CdO2. | ||
3.3 Electronic properties
The electronic properties of penta-CdO2 are studied by calculating its band structure and corresponding total and partial density of states (DOS) at the HSE06 level, and the results are plotted and shown in Fig. 3(a). The band structure calculated at the PBE level is also given for comparison. One can see that penta-CdO2 is semiconducting with an indirect bandgap of 1.54 eV at the PBE level, as the valence band maximum (VBM) and conduction band minimum (CBM) are located at different points along the M–Γ path in the first Brillouin zone. The electronic band structure at the HSE06 level has a similar dispersion but with a larger band gap of 3.28 eV due to the well-known fact that the PBE functional underestimates the band gaps. The partial DOS (PDOS) shows that the VBM is mainly contributed by the O atoms, while the CBM comes from both the Cd and O atoms.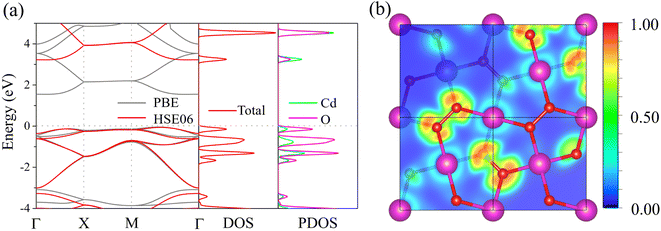 | ||
| Fig. 3 (a) Electronic band structure, and total and partial DOS of penta-CdO2. (b) ELF distribution on the plane formed by the ∠O–O–Cd in penta-CdO2. | ||
Next, we calculate the electron localization function (ELF)56 for this sheet. The ELF is a dimensionless parameter normalized in the range [0.0, 1.0], where 0.0 corresponds to a low electron density, 1.0 corresponds to fully localized electrons and 0.5 corresponds to completely delocalized electrons, as shown in Fig. 3(b). One can see that the ELF values in the vicinity of the O–O dimers (yellow and orange clouds) are in between 0.5 and 1.0, indicating that these electrons exhibit a covalent nature. The free electrons (green cloud) surrounding the O–O dimers being separated by the blue regions with low charge density further confirm the semiconducting feature of the penta-CdO2 sheet. Using the Bader charge analysis,57,58 we find that each Cd atom transfers 1.21 electrons to each of the O–O dimers, which is larger than that in the penta-ZnS2 sheet15 (0.88 electrons). Hence, the electrons of O–O dimers in penta-CdO2 are more delocalized than those of S–S dimers in penta-ZnS2, indicating that the electrons of O–O dimers can exhibit a more obvious response under an electric field, leading to a strong SHG response in penta-CdO2.
3.4 SHG susceptibility
We then evaluate the SHG properties of penta-CdO2. Because the penta-CdO2 sheet belongs to P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m symmetry (space group no. 113), only two independent nonzero components χsheetxyz(ω) = χsheetyxz(ω) and χsheetzxy(ω) are allowed by the symmetry constraints, which are further reduced to χsheet14(ω) = χsheet25(ω) and χsheet36(ω) under the Voigt notation.59 These tensor components show a crossover between the direction of the SHG response and the incident electric field, where the out-of-plane electric field contributes to the in-plane polarization via χsheet14(ω) and χsheet25(ω), and the in-plane electric field is also necessary for the out-of-plane polarization via χsheet36(ω). Hence, penta-CdO2 can exhibit both in-plane and out-of-plane SHG susceptibilities. To compensate for the underestimated band gap at the PBE level, we use the scissor correction of the band gap difference Δ = 1.74 eV in the calculations of SHG for higher accuracy.44 Besides, we find that the SHG properties converge at a k-point mesh of 99 × 99 × 1, which is illustrated in Fig. S3.†
21m symmetry (space group no. 113), only two independent nonzero components χsheetxyz(ω) = χsheetyxz(ω) and χsheetzxy(ω) are allowed by the symmetry constraints, which are further reduced to χsheet14(ω) = χsheet25(ω) and χsheet36(ω) under the Voigt notation.59 These tensor components show a crossover between the direction of the SHG response and the incident electric field, where the out-of-plane electric field contributes to the in-plane polarization via χsheet14(ω) and χsheet25(ω), and the in-plane electric field is also necessary for the out-of-plane polarization via χsheet36(ω). Hence, penta-CdO2 can exhibit both in-plane and out-of-plane SHG susceptibilities. To compensate for the underestimated band gap at the PBE level, we use the scissor correction of the band gap difference Δ = 1.74 eV in the calculations of SHG for higher accuracy.44 Besides, we find that the SHG properties converge at a k-point mesh of 99 × 99 × 1, which is illustrated in Fig. S3.†
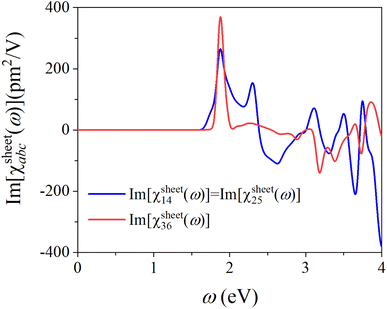
Next, we calculate the static SHG susceptibilities of penta-CdO2, which are the zero-frequency limit of the SHG susceptibilities. The static SHG susceptibilities satisfy Kleinman's symmetry, where only one independent value χsheet14(0) = χsheet25(0) = χsheet36(0) = 8.86 pm2 V−1 exists in penta-CdO2, which is much larger than that of penta-ZnS2 [χsheet14(0) = χsheet36(0) = −1.22 pm2 V−1, χsheet31(0) = χsheet15(0) = 0.69 pm2 V−1].15 In addition, to compare with the results of the SHG of bulk materials, the sheet SHG susceptibility χsheetabc(ω) of 2D materials can be converted to the corresponding bulk SHG susceptibility χbulkabc(ω) via the equation χsheetabc(ω) = χbulkabc(ω) × Leffz, where Leffz is the effective length used for the correction of the dielectric function. The converted static bulk SHG susceptibility χ14bulk(0) = χ25bulk(0) = χ36bulk(0) of penta-CdO2 is 1.04 pm V−1, which is about twice that of the well-known KBBF [experimental value of 0.47 pm V−1 at a low photon energy of ω = 1.17 eV,60 while our calculated value is 0.45 pm V−1, as presented in Fig. S4 in the ESI†]. Such large static SHG susceptibility indicates a strong frequency-doubling effect in penta-CdO2, which is promising for optical device applications.
To study the thickness dependence of the SHG of penta-CdO2, we carry out calculations for the bilayer and trilayer penta-CdO2 sheets using the Grimme's semiempirical van der Waals correction (DFT-D3).61 The AA-stacking configuration is found to be the most stable for the bilayer penta-CdO2 sheet (see Fig. S5†). On the other hand, the optimized trilayer penta-CdO2 (see Fig. S6†) undergoes a phase transition toward its bulk pyrite phase without an SHG response due to the Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) centro-symmetry with the space group of no. 206. Thus, we only focus on the bilayer configuration. The static SHG susceptibility of bilayer penta-CdO2 is calculated to be χsheet14(0) = χsheet25(0) = χsheet36(0) = 13.17 pm2 V−1, which is larger than the value of the penta-CdO2 sheet [χsheet14(0) = χsheet25(0) = χsheet36(0) = 8.86 pm2 V−1]. The calculated results for the SHG susceptibility of the bilayer penta-CdO2 sheet are plotted and shown in Fig. S7 in the ESI.†
centro-symmetry with the space group of no. 206. Thus, we only focus on the bilayer configuration. The static SHG susceptibility of bilayer penta-CdO2 is calculated to be χsheet14(0) = χsheet25(0) = χsheet36(0) = 13.17 pm2 V−1, which is larger than the value of the penta-CdO2 sheet [χsheet14(0) = χsheet25(0) = χsheet36(0) = 8.86 pm2 V−1]. The calculated results for the SHG susceptibility of the bilayer penta-CdO2 sheet are plotted and shown in Fig. S7 in the ESI.†
Next, we calculate the frequency-dependent SHG susceptibility of penta-CdO2, especially considering its imaginary part (Im[χsheetabc(ω)]). The imaginary parts of different nonzero independent SHG tensor components are plotted and shown in Fig. 4, while the real parts and modulus are plotted in Fig. S8.† Unlike previously reported 2D materials with a major in-plane SHG response,10 the penta-CdO2 sheet has both strong in-plane and out-of-plane SHG responses. One can see that Im[χsheet14(ω)] and Im[χsheet36(ω)] have the most significant peak value of 264.12 pm2 V−1 and 368.92 pm2 V−1 at 1.88 eV, respectively. From eqn (5), it can be inferred that the low-energy region of Im[χsheetabc(ω)] primarily determines the value of χsheetabc(0) due to the existence of denominator ω in the integrand. Hence, the first several peaks in Im[χsheetabc(ω)] make dominant contributions to χsheetabc(0). For reference, the most significant peak Im[χsheet36(ω)] value in penta-ZnS2 is −13.76 pm2 V−1 at 3.19 eV, which is pushed away from the low energy range due to its larger band gap of 3.34 eV. Thus, the larger value of the most significant peak in penta-CdO2 and its larger contribution lead to a larger χsheetabc(0) value as compared to that in penta-ZnS2. In addition, all of the major peaks in Im[χsheetabc(ω)] of penta-CdO2 are located within the photon energy range of 1.63–3.10 eV (400–760 nm), showing good visible nonlinear optical properties.
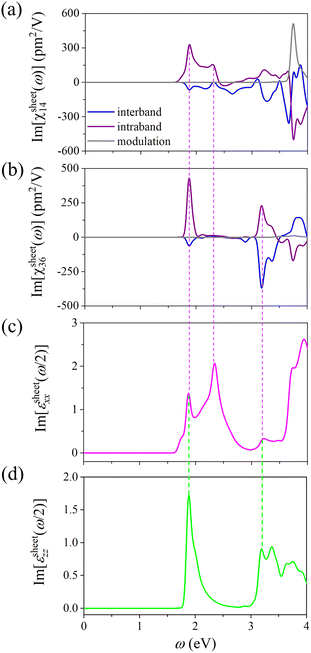
For the SHG response in a semiconductor, the light-induced electric polarization (P = ∑p + ∫tjdt) includes two main physical contributions, which are the inter-band contribution (a dipole moment p created by a pure inter-band transition) and intra-band contribution (a polarization current j generated by electrons moving within their original bands driven by the E-field). We calculate the contribution from different mechanisms to the Im[χsheetabc(ω)] of penta-CdO2. As shown in Fig. 5(a and b), we plot the different contributions to the imaginary part of SHG in penta-CdO2. We see that the inter-band and intra-band contributions to each SHG susceptibility tend to oppose each other, and the major peaks are mostly contributed by the intra-band term. Hence, the intra-band contribution to each SHG susceptibility is larger in magnitude compared to that from the inter-band contribution.
We then calculate the imaginary part of the dielectric function Im[εsheetxx(ω/2)] and Im[εsheetzz(ω/2)] at the PBE level using an identical k-point mesh in the SHG calculations. The calculated results are plotted and shown in Fig. 5(c and d). To explore the connection between the SHG properties and the linear optical properties of penta-CdO2, the mutual extrema in Im[χsheetabc(ω)] and Im[εsheetij(ω/2)] are marked in Fig. 5 by the dashed lines. One can see that the major peak of Im[χsheet14(ω)] and Im[χsheet36(ω)] at 1.88 eV is related to both Im[εsheetxx(ω/2)] and Im[εsheetzz(ω/2)]. On the other hand, the minor peak of Im[χsheet14(ω)] at 2.35 eV is related to Im[εsheetxx(ω/2)]. Because SHG is a two-photon process, the incident light with frequencies of both 2ω and ω can induce resonance for a band energy difference of 2ℏω. For penta-CdO2, the spectra of Im[εsheetij(ω/2)] exhibit significant absorption peaks at ω = 3.76, 4.70, and 6.40 eV, respectively. Hence, the peaks in Im[χsheetabc(ω)] at ω = 1.88, 2.35, and 3.20 eV are induced by two-photon resonance, indicating a strong SHG response. Meanwhile, the k-point-dependent distributions of dielectric functions are used to analyze the connection between the SHG properties and the band structure, which are illustrated in Fig. S9.† Here, we focus on the peaks of Im[εsheetxx(ω/2)] and Im[εsheetzz(ω/2)] at ω/2 = 1.88 eV, which are both relevant to that of Im[χsheet14(ω)] and Im[χsheet36(ω)]. One can see that the main contributions to Im[εsheetxx(ω/2)] and Im[εsheetzz(ω/2)] are from the transitions at the high symmetry point M and the M–Γ path. We further decompose the summed-up contribution from all band-to-band transitions at each k-point to particular band-to-band transitions. The major contribution to the peak value of Im[εsheetxx(ω/2)] is from the degenerate VBM-2-CBM and VBM-3-CBM+1 transitions at the high symmetry point M, and that of Im[εsheetzz(ω/2)] is mainly from the VBM-2-CBM transition along the M–Γ path. These are marked by pink and green arrows in Fig. S9(c).† It is also worth mentioning that the excited electron tends to transfer from the negatively charged O atoms to the positively charged Cd atoms, as shown in the band decomposed charge density in Fig. S10,† implying that the electronic states of the Cd–O bonds are the origin of the strong SHG susceptibility of penta-CdO2.
3.5 Phase-matching
In addition to the SHG susceptibility, phase-matching is another crucial factor for high-quality SHG materials. This is closely related to the incident laser wavelength.62 To show the phase-matching behavior of penta-CdO2, we calculate the refractive index n and birefringence Δn by using the previously calculated dielectric function εxx and εzz. The refractive index n is obtained according to the formula:63 | (13) |
| (αhν)n = K(hν − Eg). | (14) |
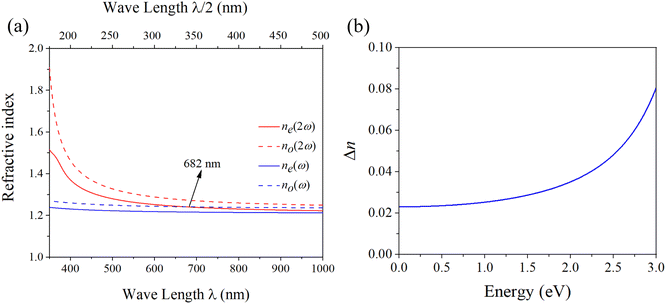 | ||
| Fig. 6 (a) Wavelength-dependent refractive indices and (b) energy-dependent birefringence of penta-CdO2. | ||
In this equation, α is the absorption coefficient, hν is the incident photon energy, K is an energy independent constant, and Eg is the optical band gap. Besides, for a direct band gap material n = 2, while for an indirect material n = 1/2. The calculated optical band gap of penta-CdO2 is 3.24 eV, indicating high LIDT for penta-CdO2. Note that only the SHG signal below the minimal band pair energy of 3.24 eV is considered in the above analysis, because of the dominant linear optical absorption beyond this limit. We also calculate the thermal expansion from 0 K to 400 K of penta-CdO2 by using the quasi harmonic approximation method66 as implemented in the Phonopy code.38 The results are plotted and shown in Fig. S11(b).† The low thermal expansion also favors its high LIDT.
4. Conclusions
In summary, the SHG performance of 2D d10-TM oxides, the penta-CdO2 sheet, is studied for the first time using first-principles calculations combined with independent particle approximation. We show that the penta-CdO2 sheet can be chemically exfoliated from its bulk phase with a low exfoliation energy of 0.85 J m−2, and is dynamically, thermally and mechanically stable. Penta-CdO2 is semiconducting with an indirect band gap of 3.28 eV at the HSE06 level, and possesses a negative Poisson's ratio of ν12 = ν21 = C12/C11 = −0.03. More interestingly, it exhibits both in-plane and out-of-plane static SHG susceptibilities with a value of χsheet14(0) = χsheet25(0) = χsheet36(0) = 8.86 pm2 V−1, which is larger than that of penta-ZnS2 [χsheet14(0) = χsheet36(0) = −1.22 pm2 V−1, χsheet31(0) = χsheet15(0) = 0.69 pm2 V−1]. The Im[χsheet14(ω)] and Im[χsheet36(ω)] have the most significant peak values of 264.12 pm2 V−1 and 368.92 pm2 V−1 at 1.88 eV, respectively, showing good visible nonlinear optical properties. The low thermal expansion together with a large optical band gap of 3.24 eV makes penta-CdO2 promising for a high laser-induced damage threshold. In addition, we extend this study to the penta-ZnO2 sheet, another 2D d10-TM oxide, which also exhibits a large SHG response: χsheet14(0) = χsheet25(0) = χsheet36(0) = −5.60 pm2 V−1. We hope that these intriguing features will stimulate experimental efforts in the synthesis of such 2D pentagonal materials for the applications in nano-SHG devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by grants from the National Natural Science Foundation of China (Grant No. NSFC-11974028) and NSFC-12274007, and the Ministry of Science and Technology of China (Grant No. 2021YFB4000601), and was also supported by the High-Performance Computing Platform of Peking University, China. P. J. acknowledges partial support by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under award DE-FG02-96ER45579. Y. K. acknowledges partial support by Suranaree University of Technology (SUT), Thailand Science Research and Innovation (TSRI), and National Science Research and Innovation Fund (NSRF) (NRIIS Project Number 90465). The authors thank the crew of the Center for Computational Materials Science, the Institute for Materials Research, Tohoku University (Japan) for their continuous support of the MASAMUNE-IMR supercomputing facility.References
- U. Keller, Recent developments in compact ultrafast lasers, Nature, 2003, 424, 831–838 CrossRef CAS PubMed.
- D. Cyranoski, Materials science: China's crystal cache, Nature, 2009, 457, 953–955 CrossRef CAS PubMed.
- F. Zhou, I. Abdelwahab, K. Leng, K. P. Loh and W. Ji, 2D Perovskites with giant excitonic optical nonlinearities for high-performance sub-bandgap photodetection, Adv. Mater., 2019, 31, 1904155 CrossRef CAS PubMed.
- Z. Sun, A. Martinez and F. Wang, Optical modulators with 2D layered materials, Nat. Photonics, 2016, 10, 227–238 CrossRef CAS.
- M. Zhao, Z. Ye, R. Suzuki, Y. Ye, H. Zhu, J. Xiao, Y. Wang, Y. Iwasa and X. Zhang, Atomically phase-matched second-harmonic generation in a 2D crystal, Light: Sci. Appl., 2016, 5, e16131 CrossRef CAS PubMed.
- Y. Li, Y. Rao, K. F. Mak, Y. You, S. Wang, C. R. Dean and T. F. Heinz, Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation, Nano Lett., 2013, 13, 3329–3333 CrossRef CAS PubMed.
- C. J. Kim, L. Brown, M. W. Graham, R. Hovden, R. W. Havener, P. L. McEuen, D. A. Muller and J. Park, Stacking order dependent second harmonic generation and topological defects in h-BN bilayers, Nano Lett., 2013, 13, 5660–5665 CrossRef CAS PubMed.
- Z. Sun, Y. Yi, T. Song, G. Clark, B. Huang, Y. Shan, S. Wu, D. Huang, C. Gao, Z. Chen, M. McGuire, T. Cao, D. Xiao, W. T. Liu, W. Yao, X. Xu and S. Wu, Giant nonreciprocal second-harmonic generation from antiferromagnetic bilayer CrI3, Nature, 2019, 572, 497–501 CrossRef CAS PubMed.
- X. Zhou, J. Cheng, Y. Zhou, T. Cao, H. Hong, Z. Liao, S. Wu, H. Peng, K. Liu and D. Yu, Strong second-harmonic generation in atomic layered GaSe, J. Am. Chem. Soc., 2015, 137, 7994–7997 CrossRef CAS PubMed.
- H. Wang and X. Qian, Giant optical second harmonic generation in two-dimensional multiferroics, Nano Lett., 2017, 17, 5027–5034 CrossRef CAS PubMed.
- W. J. Wei, X. X. Jiang, L. Y. Dong, W. W. Liu, X. B. Han, Y. Qin, K. Li, W. Li, Z. S. Lin, X. H. Bu and P. X. Lu, Regulating second-harmonic generation by van der waals interactions in two-dimensional lead halide perovskite nanosheets, J. Am. Chem. Soc., 2019, 141, 9134–9139 CrossRef PubMed.
- Y. Guo, H. Zhu and Q. Wang, Large second harmonic heneration in elemental α-Sb and α-Bi monolayers, J. Phys. Chem. C, 2020, 124, 5506–5513 CrossRef CAS.
- F. Liu, W. Wu, Y. Bai, S. H. Chae, Q. Li, J. Wang, J. Hone and X. Y. Zhu, Disassembling 2D van der waals crystals into macroscopic monolayers and reassembling into artificial lattices, Science, 2020, 367, 903–906 CrossRef CAS PubMed.
- L. Hu and X. Huang, Peculiar electronic, strong in-plane and out-of-plane second harmonic generation and piezoelectric properties of atom-thick α-M2X3 (M = Ga, In; X = S, Se): role of spontaneous electric dipole orientations, RSC Adv., 2017, 7, 55034–55043 RSC.
- Y. Shen, Y. Guo and Q. Wang, Large out-of-plane second harmonic generation susceptibility in penta-ZnS2 sheet, Adv. Theory Simul., 2020, 3, 2000027 CrossRef CAS.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Penta-graphene: a new carbon allotrope, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377 CrossRef CAS PubMed.
- M. A. Nazir, A. Hassan, Y. Shen and Q. Wang, Research progress on penta-graphene and its related materials: Properties and applications, Nano Today, 2022, 44, 101501 CrossRef CAS.
- Y. Shen and Q. Wang, Pentagon-based 2D materials: Classification, properties and applications, Phys. Rep., 2022, 964, 1–42 CrossRef CAS.
- A. D. Oyedele, S. Yang, L. Liang, A. A. Puretzky, K. Wang, J. Zhang, P. Yu, P. R. Pudasaini, A. W. Ghosh, Z. Liu, C. M. Rouleau, B. G. Sumpter, M. F. Chisholm, W. Zhou, P. D. Rack, D. B. Geohegan and K. Xiao, PdSe2: Pentagonal two-dimensional layers with high air stability for electronics, J. Am. Chem. Soc., 2017, 139, 14090–14097 CrossRef CAS PubMed.
- A. B. Puthirath, A. P. Balan, E. F. Oliveira, V. Sreepal, F. C. R. Hernandez, G. Gao, N. Chakingal, L. M. Sassi, P. Thibeorchews, G. Costin, R. Vajtai, D. S. Galvao, R. R. Nair and P. M. Ajayan, Apparent ferromagnetism in exfoliated ultrathin pyrite sheets, J. Phys. Chem. C, 2021, 125, 18927–18935 CrossRef CAS.
- Y. Gu, H. Cai, J. Dong, Y. Yu, A. N. Hoffman, C. Liu, A. D. Oyedele, Y. C. Lin, Z. Ge, A. A. Puretzky, G. Duscher, M. F. Chisholm, P. D. Rack, C. M. Rouleau, Z. Gai, X. Meng, F. Ding, D. B. Geohegan and K. Xiao, Two-dimensional palladium diselenide with strong in-plane optical anisotropy and high mobility grown by chemical vapor deposition, Adv. Mater., 2020, 32, 1906238 CrossRef CAS PubMed.
- E. Li, D. Wang, P. Fan, R. Zhang, Y. Y. Zhang, G. Li, J. Mao, Y. Wang, X. Lin, S. Du and H. J. Gao, Construction of bilayer PdSe2 on epitaxial graphene, Nano Res., 2018, 11, 5858–5865 CrossRef CAS.
- J. I. Cerdá, J. Sławińska, G. L. Lay, A. C. Marele, J. M. G. Rodríguez and M. E. Dávila, Unveiling the pentagonal nature of perfectly aligned single and double strand Si nano-ribbons on Ag(110), Nat. Commun., 2016, 7, 13076 CrossRef PubMed.
- X. Zhang, G. Su, J. Lu, W. Yang, W. Zhuang, K. Han, X. Wang, Y. Wan, X. Yu and P. Yang, Centimeter scale few-layer PdS2: Fabrication and physical properties, ACS Appl. Mater. Interfaces, 2021, 13, 43063–43074 CrossRef CAS PubMed.
- M. Bykov, E. Bykova, A. V. Ponomareva, F. Tasnádi, S. Chariton, V. B. Prakapenka, K. Glazyrin, J. S. Smith, M. F. Mahmood, I. A. Abrikosov and A. F. Goncharov, Realization of an ideal Cairo tessellation in nickel diazenide NiN2: High-pressure route to pentagonal 2D materials, ACS Nano, 2021, 15, 13539–13546 CrossRef CAS PubMed.
- K. M. Ok, E. O. Chi and P. S. Halasyamani, Bulk characterization methods for non-centrosymmetric materials: Second-harmonic generation, piezoelectricity, pyroelectricity, and ferroelectricity, Chem. Soc. Rev., 2006, 35, 710–717 RSC.
- C. Wu, X. Jiang, L. Lin, Y. Hu, T. Wu, Z. Lin, Z. Huang, M. G. Humphrey and C. Zhang, A congruent-melting mid-infrared nonlinear optical vanadate exhibiting strong second-harmonic generation, Angew. Chem., Int. Ed., 2021, 60, 22447–22453 CrossRef CAS PubMed.
- H. Yu, H. Wu, S. Pan, Z. Yang, X. Hou, X. Su, Q. Jing, K. R. Poeppelmeier and J. M. Rondinelli, Cs3Zn6B9O21: A chemically benign member of the KBBF family exhibiting the largest second harmonic generation response, J. Am. Chem. Soc., 2014, 136, 1264–1267 CrossRef CAS PubMed.
- C. Hu, B. Zhang, B. H. Lei, S. Pan and Z. Yang, Advantageous units in antimony sulfides: Exploration and design of infrared nonlinear optical materials, ACS Appl. Mater. Interfaces, 2018, 10, 26413–26421 CrossRef CAS PubMed.
- Z. Xie, M. Mutailipu, G. He, G. Han, Y. Wang, Z. Yang, M. Zhang and S. Pan, A series of rare-earth borates K7MRE2B15O30 (M = Zn, Cd, Pb; RE = Sc, Y, Gd, Lu) with Large Second Harmonic Generation Responses, Chem. Mater., 2018, 30, 2414–2423 CrossRef CAS.
- J. A. Brant, D. J. Clark, Y. S. Kim, J. I. Jang, J. H. Zhang and J. A. Aitken, Li2CdGeS4, A diamond-like semiconductor with strong second-order optical nonlinearity in the infrared and exceptional laser damage threshold, Chem. Mater., 2014, 26, 3045–3048 CrossRef CAS.
- X. Dong, L. Huang, H. Zeng, Z. Lin, K. M. Ok and G. Zou, High-performance sulfate optical materials exhibiting giant second harmonic generation and large birefringence, Angew. Chem., Int. Ed., 2022, 134, e202116790 Search PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- C. Braga and K. P. Travis, A configurational temperature Nosé-Hoover thermostat, J. Chem. Phys., 2005, 123, 134101 CrossRef PubMed.
- X. Wu, D. Vanderbilt and D. R. Hamann, Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035105 CrossRef.
- J. E. Sipe and E. Ghahramani, Nonlinear optical response of semiconductors in the independent-particle approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11705–11722 CrossRef CAS PubMed.
- Z. Fang, J. Lin, R. Liu, P. Liu, Y. Li, X. Huang, K. Ding, L. Ning and Y. Zhang, Computational design of inorganic nonlinear optical crystals based on a genetic algorithm, CrystEngComm, 2014, 16, 10569–10580 RSC.
- S. N. Rashkeev and W. R. L. Lambrecht, Second-harmonic generation of I-III-VI2 halcopyrite semiconductors: Effects of chemical substitutions, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 165212 CrossRef.
- Z. H. Levine and D. C. Allan, Calculation of the nonlinear susceptibility for optical second-harmonic generation in III-V semiconductors, Phys. Rev. Lett., 1991, 66, 41–44 CrossRef CAS PubMed.
- Q. J. Liu, Z. T. Liu, L. P. Feng and H. Tian, First-principles study of structural, elastic, electronic and optical properties of rutile GeO2 and and α-quartz GeO2, Solid State Sci., 2010, 12, 1748–1755 CrossRef CAS.
- G. W. Milton, D. J. Eyre and J. V. Mantese, Finite frequency range Kramers–Kronig relations: bounds on the dispersion, Phys. Rev. Lett., 1997, 79, 3062–3065 CrossRef CAS.
- G. Yang and S. P. Gao, A method to restore the intrinsic dielectric functions of 2D materials in periodic calculations, Nanoscale, 2021, 13, 17057–17067 RSC.
- Y. Guo, J. Zhou, H. Xie, Y. Chen and Q. Wang, Screening transition metal-based polar pentagonal monolayers with large piezoelectricity and shift current, npj Comput. Mater., 2022, 8, 1–9 CrossRef.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, The Perdew–Burke–Ernzerhof exchange-correlation functional applied to the G2-1 test set using a plane-wave basis set, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed.
- M. Hellenbrandt, The inorganic crystal structure database (ICSD) — Present and future, Crystallogr. Rev., 2014, 10, 17–22 CrossRef.
- R. Zacharia, H. Ulbricht and T. Hertel, Interlayer cohesive energy of graphite from thermal desorption of polyaromatic hydrocarbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406 CrossRef.
- J. H. Jung, C. H. Park and J. Ihm, A rigorous method of calculating exfoliation energies from first principles, Nano Lett., 2018, 18, 2759–2765 CrossRef CAS PubMed.
- J. Li, X. Fan, Y. Wei and G. Chen, Penta-BxNy sheet: A density functional theory study of two-dimensional material, Sci. Rep., 2016, 6, 31840 CrossRef CAS PubMed.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Elastic properties of hydrogenated graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- Y. L Page and P. Saxe, Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef.
- C. T. Chen, G. L. Wang, X. Y. Wang and Z. Y. Xu, Deep-UV nonlinear optical crystal KBe2BO3F2—discovery, growth, optical properties and applications, Appl. Phys. B, 2009, 97, 9–25 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- L. Q. Yang, X. M. Jiang and G. C. Guo, LiGa0.54In0.46S2: A new infrared nonlinear optical material with large laser damage threshold designed by gallium substitution in LiInS2, Inorg. Chem. Commun., 2020, 115, 107852 CrossRef CAS.
- T. V. Vu, A. A. Lavrentyev, B. V. Gabrelian, D. D. Vo, K. D. Pham, N. M. Denysyuk, L. I. Isaenko, A. Y. Tarasova and O. Y. Khyzhun, DFT study and XPS measurements elucidating the electronic and optical properties of KPb2Cl5, Opt. Mater., 2020, 102, 109793 CrossRef CAS.
- H. Lin, L. Chen, J. S. Yu, H. Chen and L. M. Wu, Infrared SHG materials CsM3Se6 (M = Ga/Sn, In/Sn): Phase match ability controlled by dipole moment of the asymmetric building unit, Chem. Mater., 2017, 29, 499–503 CrossRef CAS.
- P. Makuła, M. Pacia and W. Macyk, How to correctly determine the band gap energy of modified semiconductor photocatalysts based on UV–Vis spectra, J. Phys. Chem. Lett., 2018, 9, 6814–6817 CrossRef PubMed.
- N. S. Abraham and M. R. Shirts, Thermal gradient approach for the quasi-harmonic approximation and its application to improved treatment of anisotropic expansion, J. Chem. Theory Comput., 2018, 14, 5904–5919 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting information on the forty-five d10-TM oxides from the Materials Project (MP) database, phonon spectra, SHG susceptibility, band-decomposed charge density distribution, optical band gap, optimized geometry, and electronic band structure. See DOI: https://doi.org/10.1039/d2ta07589j |
| This journal is © The Royal Society of Chemistry 2023 |