Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accelerating anhydrous proton conduction via anion rotation and hydrogen bond recombination: a machine-learning molecular dynamics†
Saori
Minami
 * and
Ryosuke
Jinnouchi
* and
Ryosuke
Jinnouchi

Toyota Central R&D Labs., Inc., 41-1 Yokomichi, Nagakute, Aichi 480-1192, Japan. E-mail: e1778@mosk.tytlabs.co.jp
First published on 12th July 2023
Abstract
Phosphonic-acid-based electrolytes are key materials for anhydrous proton transport in fuel cells that are operatable at medium temperatures. However, these materials suffer from a severe tradeoff between proton conductivity and stability. Immobilizing phosphonic anion groups prevents anion leaching while suppressing proton transport. To reveal the origin of this relationship, we performed nanosecond-scale molecular dynamics simulations of phosphoric and phosphonic acids with different alkyl chains using machine-learned force fields. Simulations indicate that proton diffusivity is strongly correlated to the reorientation speed of anions. Thus, as the alkyl chain length increases, both the proton diffusivity and reorientation frequency decrease. Detailed analyses show that in all the materials, protons are shuttled between a pair of anions with a high frequency of approximately 10 ps−1. However, only 0.1% of the shuttling protons are transported to the adjacent anion because of three orders of magnitude slower reorientation of anions that require recombination of H-bond network. Retaining the rotational freedom of anions is essential for enhancing anhydrous proton conductivity.
Introduction
Proton exchange membrane fuel cells (PEMFCs) show great potential as power sources for light- and heavy-duty vehicles.1,2 PEMFCs employ perfluorinated ionomers as proton exchange membranes. These membranes absorb water and form heterogeneous nanosized cluster domains comprising ions and water molecules.3–6 Under sufficiently humidified conditions, the cluster domains connect with each other and provide proton transport pathways. Owing to their high proton conductivity and chemical and mechanical stability, these membranes stably realize low ohmic resistance below the boiling temperature of water, enabling the quick starts and stops of fuel cells required for automobile applications.6,7 However, at higher temperatures, the membranes dry up, and the proton conductivity significantly decreases. Therefore, the operational temperature and humidity are limited, and humidified inlet streams and large radiators are required to dissipate the waste heat. In addition, low-temperature operation requires purified hydrogen gas without contaminant species, such as CO, which poison the electrocatalysts. For simpler and more compact systems, advanced electrolyte materials that can extend the upper temperature limit, such as to 120 or 150 °C, are desired.8–11Amphoteric molecules, such as phosphoric acid (PA) and imidazole, which act as both proton doners and accepters, are attracting attention as electrolytes that can exhibit anhydrous proton conduction at high temperatures.12–16 PA is known to be a highly anhydrous proton-conductive electrolyte in the temperature range of 60–200 °C15–17 and is used as an electrolyte of PA fuel cells (PAFCs). However, PAFCs have severe durability problems because PA leaches out during operation. In addition, the energy conversion efficiency of PAFCs is reduced by the low oxygen permeability and catalyst poisoning by PA anions. To improve the durability, mechanical strength, and conductivity of PAFCs, intensive studies have been conducted on the hybridization of PA with polymers, ionic liquids, and inorganic compounds.18–26 PA-doped poly-benzimidazole (PA-PBI) exhibits a high proton conductivity in the temperature range of 100–200 °C and has been widely investigated.14,18,23,27–29 However, this acid-doped polymer suffers from PA loss because PA does not have strong attractive interactions with polymers.27 To enhance these interactions, Lee et al.19 suggested that PA be hybridized with a relatively strong base, such as quaternary ammonium-biphosphate ion-pair-coordinated polyphenylene, which improved the PA retention from 67% in PBI to 77% after 50 h of operation at 200 °C and a relative humidity of 0%. However, higher retention is desired for practical applications. It should also be noted that PA poisoning of the catalysts is inevitable in this advanced hybrid material. To further improve the stability and performance, polymers that fix anion groups via covalent bonds have been proposed.9,15,30,31 Their introduction improves the durability compared to liquid PA. However, the proton conductivity is significantly decreased in these materials. Notably, the proton conductivity rapidly decreased from 350 to 43 mS cm−1 by connecting only one methyl group to the anion (CH3PO3H2).15,32 In addition, proton transport is severely hindered by the immobilization of anions. To overcome the tradeoff between proton conductivity and anion retention, the proton transport mechanism needs to be clarified.
Generally, proton transfer occurs via vehicle and Grotthuss mechanisms. In the vehicle mechanism, protons are transported by mobile ionic molecules. In contrast, proton transport occurs via sequential hopping between anions in the Grotthuss mechanism.17,33 Ideally, the latter mechanism could significantly contribute to high proton conduction because sequential proton hopping via extended Grotthuss chains enables long-range proton transport without significant anion diffusion. The significant contribution of the Grotthuss mechanism to liquid PA is supported by the diffusion coefficients measured by Aihara et al.,16 who showed that the diffusion coefficient of hydrogen atoms is 4.5 times larger than that of phosphorus atoms. However, in reality, sequential proton hopping requires the rearrangement of molecular anions, and thus, proton hopping and the molecular rearrangement complex interplay in proton conduction.
First principles molecular dynamics (FPMD) simulations have provided valuable insights into microscopic transport mechanisms.34–37 An FPMD simulation by Vilčiauskas et al.35 showed that long Grotthuss chains developed in neat liquid PA enables fast proton conduction. Another FPMD simulation of a mixed PA and imidazole system performed by the same group38 showed that the Grotthuss chains were significantly shortened in the mixed system. However, applications of FPMD simulations remain scarce and have never been performed on phosphonic acid groups with alkyl chains because of their high computational cost. Accurate predictions of diffusion coefficients require sufficient statistics over hundreds pico second trajectories started from statistically uncorrelated multiple initial configurations.39 Performing the calculations in a brute force manner is simply out of question, since the simulations on several materials require several years. Although classical MD simulations employing empirical force fields are several orders of magnitude faster than FPMD simulations, they do not accurately represent the Grotthuss mechanism, which involves bond breaking and formation in complex molecular systems. Machine-learned force fields (MLFFs)40–48 are ideal for addressing this problem. Their flexible functional forms enable accurate reproductions of the complex FP energy landscape of the bond breaking and formation without solving the wave equation. In particular, emerging active-learning schemes coupled with reduced descriptor space39,49 enable the efficient training of MLFFs for complex multi-elemental amorphous materials with minimum human intervention. Overall, the state-of-the-art MLFF algorithm realizes three orders of magnitude faster computations of proton transfers.
In this study, we employed the MLFF scheme to reveal the relationship between proton and anion mobilities in liquid PA (H3PO4) and phosphonic acids with linear alkyl chains [(CnH2n+1PO3H2, n = 1, 4, and 7)]. Systematic comparisons of the four systems demonstrated that proton mobility decreases with increasing alkyl chain length, as in previously reported experiments,15,32 and revealed a significant contribution of anion reorientation to proton transport.
Methods
Models and simulations
Liquid PA and phosphonic acids with different alkyl chain lengths were modeled using unit cells with three-dimensional periodic boundary conditions. The numbers of molecules in the unit cell are listed in Table S1,† and the models are shown in Fig. 1. In this study, we denote PA as nC = 0 and CnH2n+1PO3H2 as nC = 1, 4, and 7, where nC denotes the number of carbon atoms in the alkyl chains.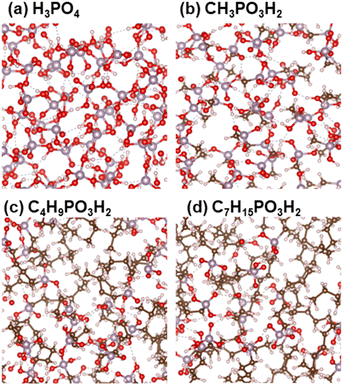 | ||
| Fig. 1 Models of (a) H3PO4, (b) CH3PO3H2, (c) C4H9PO3H2, and (d) C7H15PO3H2. White, red, brown, and purple spheres indicate H, O, C, and P atoms, respectively. | ||
All MD simulations for production runs were performed using the MLFF method implemented in the Vienna Ab initio Simulation Package (VASP).45,50,51 MLFFs were generated using the method described later in the text. The equilibrium lattice structures of each system were determined by 100 ps-NpzT-ensemble MD simulations at 393, 423, and 463 K and 0.1 MPa, where the symbol NpzT refers to the cell length only along the z-direction is allowed to relax. The cell lengths in the x–y direction were fixed to prevent significant distortions in the liquid systems. The temperature and pressure were controlled by Langevin thermostat52 and Parrinello–Rahman method,53 respectively. For efficient equilibration, the hydrogen mass and time step (Δt) were set to 4 a.u. and 2 fs, respectively. The lattice parameters were determined as the averages over the NpzT-ensemble MD simulations. After equilibration, 200 ps-NVT-ensemble MD simulations were conducted at 393, 423, and 463 K to examine static and dynamic properties. During the production runs, the hydrogen mass and Δt were set to 1 a.u. and 0.5 fs, respectively.
Initial structures for the equilibrations by using MLFFs were prepared by 1 ns-NpT-ensemble classical MD simulations at 500 K and 0.1 MPa with the COMPASS54 empirical force field and FORCITE MD package implemented in Materials Studio 2020.55 Initial configurations for these MD simulations were prepared by the amorphous cell generator in Material Studio 2020.
Analysis of dynamical properties
The diffusion coefficients (D) of the hydrogen and phosphorus atoms were calculated from their mean square displacements (MSDs) as follows: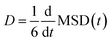 | (1) |
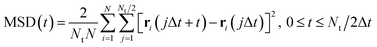 | (2) |
A previous FPMD study showed that the high proton conductivity of liquid PA owes to Grotthuss mechanism.35 In this simulation, frequent proton hopping via extended Grotthuss chains was reported. The same result was also reported by a previous MD simulation using an MLFF.49 Following the previous studies, we examined the effects of the alkyl chain length on the proton hopping frequency. The proton hopping frequency was determined as the lifetime of the electrically neutral state (H3PO4 for liquid PA and CnH2n+1PO3H2 for liquid phosphonic acids), which appeared and disappeared because of proton hopping between adjacent anions. The lifetime was evaluated using a method proposed in previous studies.36,49 In this method, the number of H–O bonds per phosphorus atom at each time step is listed. From this list, a histogram N(lΔt), which is defined as the number of neutral species that break after precisely l time steps, can be constructed. The fraction of neutral species that remains unbroken after time step m (m = 1, …, Nt) is obtained as follows:
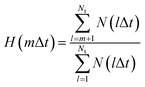 | (3) |
The fraction of neutral species that change from a neutral state to charged ions during time steps m and m + 1 is H(mΔt) − H((m + 1)Δt). Lifetimes were calculated as [m + (m + 1)]Δt/2. Therefore, the average lifetime (τL) of molecules in the electrically neutral state can be calculated as
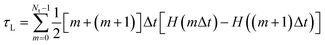 | (4) |
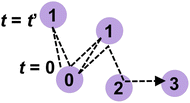
The lifetime provides a timescale for proton hopping. However, as shown later, most protons shuttle only along a single H-bond between a local pair of anions within hundreds of femtoseconds and are irrelevant to progressive proton transport. A limited number of protons were progressively transferred from one anion to another and contributed to proton conduction. To reveal the timescale of these progressive proton transfers, the dynamic transitions of phosphorus atoms holding a specific proton were tracked. For this purpose, we assigned numbers to phosphorus atoms in the system and introduced a function Pi(t) that records the number of phosphorus atoms in an anion holding a covalent bond with the ith proton at time t. Because the proton transfers from one anion to another via the Grotthuss mechanism, the number changes with time. Hence, Pi(t) varies with time t. This number was defined as shown in Fig. 2. First, we assigned the number 0 to the phosphorus atom that holds the ith proton at t = 0. Therefore, Pi(0) was equal to 0. At t = t′, the proton was transferred to an adjacent anion via an H-bond. We define the number of phosphorus atom in this proton acceptor as one. Hence, Pi(t′) was set to 1. At t = t′′, the proton was transferred from the anion to an adjacent anion. If this acceptor anion contained a phosphorus atom numbered 0, then Pi(t′′) was set to 0. Otherwise, the phosphorus atom in the acceptor anion was assigned a value of 2, and Pi(t′′) was set to 2. In this manner, the phosphorus atoms were numbered, and the dynamic transition of the phosphorus atom holding the ith proton was recorded as Pi(t). The average of Pi(t) over i, which was defined as P(t), was used to indicate the averaged number of anions a proton passed through within time range t, excluding the effects of local shuttles as well as vehicle diffusion. In other words, the time that satisfies P(t) = 1 indicated the average time required for a proton to move from one anion to another.
In addition to the proton hopping frequencies, we investigated the time required for reorientations of anions because the reorientation time is strongly correlated to the diffusion coefficient of the hydrogen atoms in liquid PA, a solid acid, and the coordination polymer in the previous MLFF study.49 The reorientation time was determined from the autocorrelation function (〈rrot(t)〉) defined as:37,49
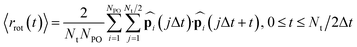 | (5) |
| 〈rrot(t)〉 ≅ c0e−t/τ0 + (1 − c0)e−t/τrot | (6) |
To examine the microscopic dynamical relations between reorientations and proton hopping, we further compared the function Pi(t) by recording the transient of the phosphorus atom holding the ith proton, with the individual autocorrelation function defined as
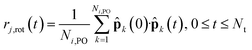 | (7) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) k is the P–O unit vector and Nj,PO is the number of P–O bonds in the jth anion.
k is the P–O unit vector and Nj,PO is the number of P–O bonds in the jth anion.
All analyses were performed using trajectories obtained by 200 ps MD simulations. We confirmed that D and τrot calculated from 200 ps trajectories are in good agreement with those calculated from 1 ns trajectories as shown in Fig. S1.†
Machine-learned force field
An active-learning MLFF scheme implemented in VASP45,50,51 was used to generate the MLFFs. In this method, the potential energy of a system is written as the sum of atomic energies, similar to the Gaussian approximation potential (GAP):41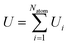 | (8) |
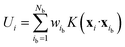 | (9) |
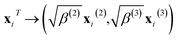 | (10) |
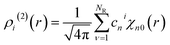 | (11) |
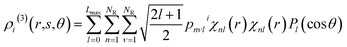 | (12) |
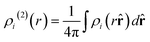 | (13) |
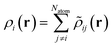 | (14) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ij(r) = fcut(rij)g(r − rij) ij(r) = fcut(rij)g(r − rij) | (15) |
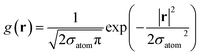 | (16) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) denotes the unit vector of r and r = |r|. The three-body distribution function ρi(3) is defined as follows:
denotes the unit vector of r and r = |r|. The three-body distribution function ρi(3) is defined as follows: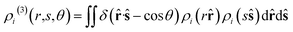 | (17) |
The kernel function K evaluates the structural similarity between the surrounding atom i and reference atom ib. The kernel function is written as a polynomial function of the inner product and is referred to as the smooth overlap of atomic positions (SOAP) which was defined by Bartók et al.57 as
K(xi,xib) = (![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) i, i,![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ib)ζ ib)ζ | (18) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) i is a unit vector of xi. The normalization of xi and exponentiation by ζ in eqn (18) introduces the higher-order atomic interaction terms from the two- and three-body components of xi.56
i is a unit vector of xi. The normalization of xi and exponentiation by ζ in eqn (18) introduces the higher-order atomic interaction terms from the two- and three-body components of xi.56
The accuracy and transferability of the MLFF are influenced by three factors: the number of structures Nst, number of kernels Nb, and descriptors xi for the structures, where Nst provides (3Natom + 7) × Nst training data, including energy, force, and stress tensor components. For the descriptor xi, we employ a set of parameters that enable compact representations of the local chemical environments of complex multi-elemental amorphous structures, as discussed in our previous study.39 The parameter set is provided in Table S2.†
MLFFs are generated on the fly during MD simulations using an active-learning algorithm, which was recently improved to efficiently learn multi-elemental amorphous materials.45 The uncertainty of the atomic energy and force for atom i predicted by the MLFF is evaluated by a spilling factor45,58 defined as
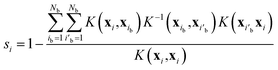 | (19) |
If either atom has an si value larger than 0.02, the FP calculation is conducted. The training data and reference atoms were selected using a CUR sparcification algorithm,59 and the MLFF was updated. If all si values are smaller than 0.02, the atomic positions are updated by solving the equation of motion using the energy, force, and stress tensor components predicted by the MLFF. In this manner, most FP calculations are bypassed and the training data and reference atoms are efficiently selected from a wide phase space that cannot be explored using the FP method.
Unit cells smaller than those used in the production runs were used for the training runs. The numbers of molecules in the unit cell are listed in Table S3.† For all materials, isobaric MD simulations at 500 and 600 K were performed. For each temperature, a 100 ps-MD simulation was executed. The pressure was set at 0.1 MPa.
In the FP calculations for the training runs, the revised Perdew–Burke–Ernzerhof (RPBE) functional60 with Grimme's D3 dispersion correction61 was used to describe the exchange–correlation interactions between electrons. The Γ point was employed for the Brillouin zone integration. Plane-wave basis sets with a cutoff energy of 520 eV were used to describe the one-electron wave functions, and the projector-augmented wave (PAW) method62,63 was used to describe the interactions between valence electrons and effective cores composed of nuclei and core electrons. The PAW atomic configurations are 1s1 for H, 2s22p2 for C, 2s2p4 for O, and 3s23p3 for P.
To validate the accuracy of the MLFF produced by the parameter set in this study, preliminary 10 ps-NpT-ensemble MD simulations for the PA were performed with MLFF and FPMD. As shown in Fig. S2,† the MLFF accurately reproduced the radial distribution functions (RDFs) calculated using the FP method. The energies, forces, and stress tensor components predicted by the MLFF were also similar to those calculated using the FP method, as shown in Fig. S3.† The root mean square errors of the energy, force and stress tensor components were 2.5 meV per atom, 0.15 eV Å−1, and 0.83 kbar, respectively, which were comparable to those of the conventional MLFFs.40,41,47,48 As shown in Table S4,† the generated MLFFs realized 3000 times faster MD simulations than the FPMD method. The balanced accuracy and high efficiency allowed us to systematically compare dynamical properties relevant to the proton transfers in four materials.
Results and discussion
The proton conductivities of liquid PA and liquid phosphonic acids decreased significantly with the introduction of the alkyl chain. A previous experimental study reported that the proton conductivity decreased from 350 mS cm−1 for PA to 43 mS cm−1 by introducing only one methyl group.15,17,32 The Nernst–Einstein equation64,65 and proton concentrations predicted by our MD simulations (Table 1) indicate that 46% decrease (from 350 to 189 mS cm−1) is attributed to the dilution of charge carriers by the introduction of methyl groups. The remaining 42% decrease to 43 mS cm−1 was likely attributed to the decreased diffusivity of the protons. This experimental observation was reproduced using diffusion coefficients simulated using the MLFF method. Fig. 3 shows the diffusion coefficients of hydrogen atoms (DH) and phosphorus atoms (DP) obtained from eqn (1) as a function of the alkyl chain length nC. The MSDs of the hydrogen and phosphorus atoms are shown in Fig. S4.† The DH values for nC = 0 at 400 K and nC = 7 at 427 K were in good agreement with the experimental values measured by pulse-gradient spin-echo (PGSE) NMR.15,32 The diffusion coefficients of the protons (Dσ) estimated from the experimental proton conductivity at 400 K15,32 using the Nernst–Einstein equation are also shown in Fig. 3a. The estimated Dσ is reproduced by the DH values obtained by the MD simulations. The DH values decreases by 60% upon introducing a methyl group to the molecule, whereas the DP values are nearly constant independent of nC. For all nC values at all temperatures, the DH values were larger than the DP values (Fig. 3c). The DH/DP ratio decreased with increasing nC values. The DH/DP ratio did not depend strongly on the temperature, although both the DH and DP values increased with increasing temperatures. DH is larger than DP because hydrogen diffusion involves both the Grotthuss and vehicle mechanisms,16,35 whereas phosphorus atoms diffuse only via the vehicle mechanism. The decrease in DH/DP with increasing nC indicated that the Grotthuss mechanism was suppressed by the alkyl chains. The small dependence of DH/DP on the temperature indicates that the suppression of the Grotthuss mechanism by the alkyl chains occurs at all temperature ranges.| Number of carbon atoms (nC) | T (K) | Density (g cm−3) | Proton concentration (mmol cm−3) |
|---|---|---|---|
| 0 | 393 | 1.74 | 53.3 |
| 423 | 1.73 | 53.1 | |
| 463 | 1.71 | 52.5 | |
| 1 | 393 | 1.38 | 28.7 |
| 423 | 1.38 | 28.7 | |
| 463 | 1.36 | 28.3 | |
| 4 | 393 | 1.09 | 15.8 |
| 423 | 1.11 | 16.1 | |
| 463 | 1.10 | 16.0 | |
| 7 | 393 | 0.892 | 11.3 |
| 423 | 0.906 | 11.3 | |
| 463 | 0.900 | 10.8 |
 | ||
| Fig. 3 (a) Diffusion coefficients hydrogen atoms and protons (DH and Dσ, respectively), (b) the diffusion coefficient of phosphorus atoms (DP), and (c) their ratio (DH/DP) as functions of the alkyl chain length (nC). Experimental values of DH for nC = 0 at 400 K and nC = 7 at 427 K are taken from ref. 15 and 32, respectively. The experimental proton conductivity used to estimate the values of Dσvia the Nernst–Einstein equation are taken from ref. 15 and 32. | ||
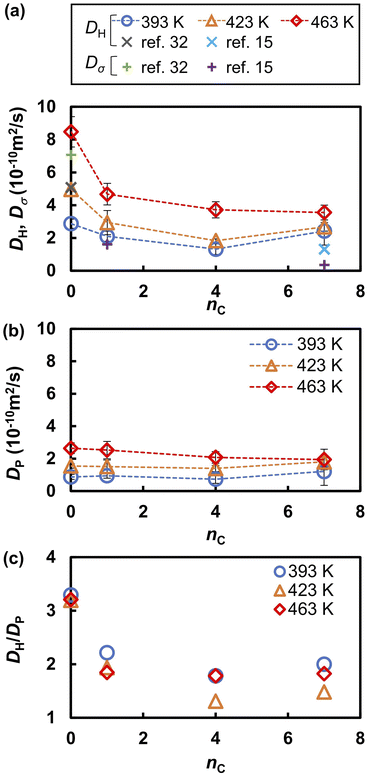
Fig. 4 compares the RDFs and running integration numbers (RINs) for P–P and O–H pairs. The first peak of the RDF of the P–P pairs (gPP) indicates that the average nearest neighbor distance of the anions is 4.7 Å. The height of the first peak increased and the RIN at the first peak decreased as nC increased. This trend indicates that the anions are diluted and localized with increasing nC. The first peak of gOH at 1.1 Å is attributed to the intramolecular covalent O–H bonds, and the second peak at 1.5 Å is attributed to intermolecular hydrogen bonds (O⋯H–O). As observed in previous FPMD and MLFF studies36,49 of liquid PA, these peaks overlapped regardless of the alkyl chain length, indicating that protons were frequently transferred between adjacent anions. The intensity of the hydrogen bonds peak decreases with increasing nC values, and the RINs of hydrogen bonds between phosphonic acid anions, which is evaluated from the nOH at 2.2 Å, decreases from 1.9 at nC = 0 to 1.3 at nC = 7.
 | ||
| Fig. 4 Radial distribution functions (solid lines) and running integration numbers (dashed lines) of (a) P–P and (b) O–H for various nC values at 463 K. | ||
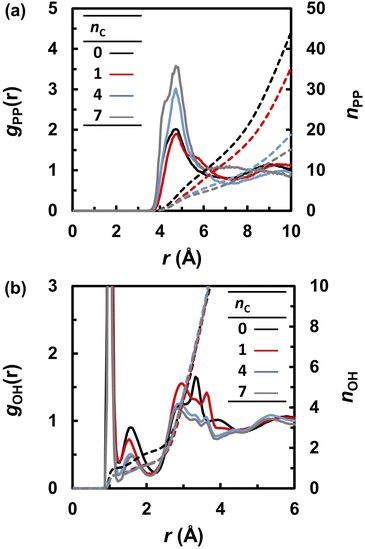
The frequent proton transfer between adjacent anions is supported by the lifetime τL of the neutral species (H3PO4 and CnH2n+1PO3H2), which were calculated using eqn (4). The lifetime τL at 463 K is shown as a function of the alkyl chain length nC in Fig. 5a. The lifetime τL increased from 100 to 300 fs with an increase in nC. These results indicate that the proton hopping frequency decreases with increasing nC values. This trend also appeared in the probability of finding a neutral state in the MD trajectories. As shown in Fig. 5b, the probability gradually increased with increasing nC values. Hence, it was concluded that alkyl chains hinder proton hopping. However, the proton hopping frequency was high and did not correlate with the DH values. For example, DH significantly decreased from nC = 0 to 1, whereas τL did not change significantly. This indicates that proton hopping does not dominate proton transport.
 | ||
| Fig. 5 (a) The lifetime (τL) of electrically neutral species (H3PO4 and CnH2n+1PO3H2) at 463 K and (b) probability of finding neutral species during the molecular dynamics simulations. | ||
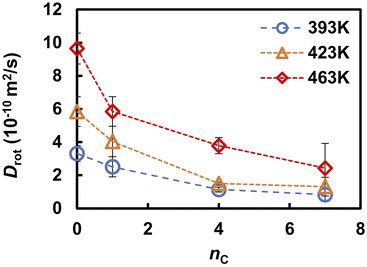
Previous FPMD and MLFF studies indicated that the molecular reorientation involved in proton transport strongly influences the proton diffusivity in liquid PA, solid acids, and coordination polymers containing PA anions.37,49 A similar trend, but a clearer correlation, was observed in the liquid PA and phosphonic acid electrolytes examined in this study. Table 2 summarizes the reorientation times τrot of the anions, as determined from the autocorrelation function in eqn (6). Under all conditions, the reorientation time τrot was three orders of magnitude longer than that of proton hopping, as shown in Fig. 5. The value of τrot computed for liquid PA is close to the reorientation correlation time of the 10 ps timescale for 1H–1H dipolar interactions in liquid PA measured by PGSE NMR.16 At 463 K, the reorientation time increased from 26 to 130 ps as the alkyl chain length increased from 0 to 7. The same trend was observed at 393 and 423 K. It should also be noted that the frequency of reorientation, defined as the inverse of τrot, is strongly correlated with DH, as shown in Fig. 6. This indicates that anion reorientation limits proton transport. The reorientation was decelerated by increasing the alkyl chain length, which likely led to slower hydrogen diffusion.
| Number of carbons(nC) | Temperature (K) | τ rot (ps) |
|---|---|---|
| 0 | 393 | 78.0 |
| 423 | 44.1 | |
| 463 | 26.5 | |
| 1 | 393 | 104 |
| 423 | 64.8 | |
| 463 | 44.1 | |
| 4 | 393 | 226 |
| 423 | 170 | |
| 463 | 67.9 | |
| 7 | 393 | 342 |
| 423 | 214 | |
| 463 | 131 |
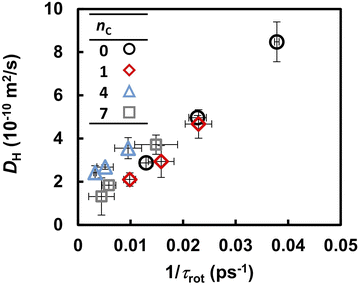 | ||
| Fig. 6 Correlation between the anion reorientation frequency (1/τrot) and diffusion coefficient of hydrogen atoms (DH). | ||
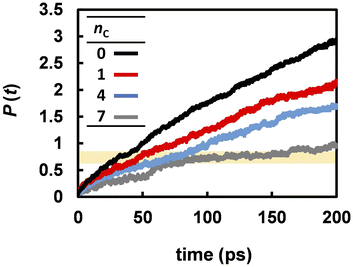
Fig. 3 suggests that the Grotthuss mechanism is suppressed by the alkyl chains. However, the proton hopping frequency shown in Fig. 5 was high and could not be strongly correlated with the DH. In contrast, the reorientation frequency exhibited a strong correlation with DH although its timescale was three times longer than that of proton hopping. To reveal the mechanism by which anion reorientation participates in proton transport, we examined the number of phosphorus atoms P(t) that a proton crossed up to time t. The computed P(t) values at 463 K are shown in Fig. 7. The value of P(t) decreased with increasing nC values. Notably, in all the electrolytes, P(t) reaches 0.7 ± 0.1 at t = τrot, as indicated by the yellow band in Fig. 7. This result means that roughly 70% of protons transported from one anion to the other every anion rotation by 90°.
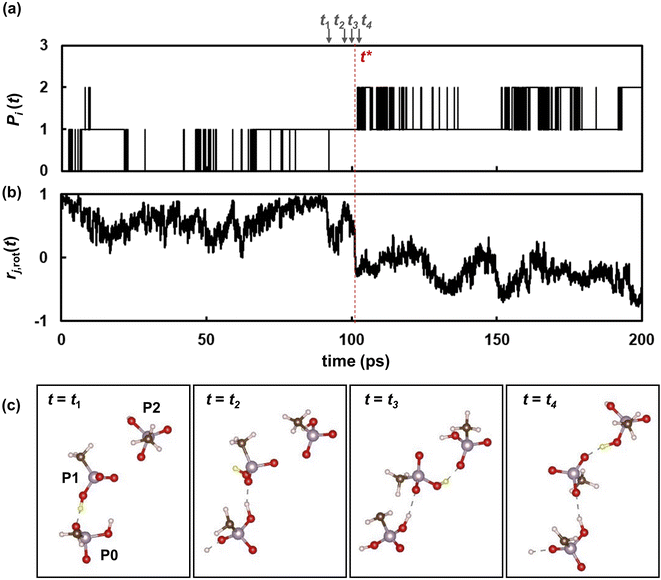
To further reveal the microscopic dynamic mechanisms, we compared the number Pi(t) of the ith proton with the autocorrelation rj,rot(t) of a phosphonic anion that passes the ith proton from one adjacent anion to the other as shown in Fig. 8. Four snapshots of the proton transfer at t = t1, t2, t3, and t4 are shown in the same figure. In these snapshots, the ith proton is indicated by a yellow sphere. As shown in Fig. 8a, Pi(t) initially oscillates between 0 and 1, indicating that the proton shuttles between the phosphonic anions P0 and P1 in Fig. 8c. At t = t2, the pair of anions formed an H-bond via another proton, as shown in the second snapshot in Fig. 8c. This induces a remarkably fast rotation of anion P1 at t = t3, which leads to a significant decrease in the autocorrelation functions rj,rot(t) of anion P1, as shown in Fig. 8b. This rotation allows anion P1 to form a H-bond with another anion, P2, via the ith proton. At t = 101 ps (denoted as t*), slightly after t = t3, the ith proton is transferred from P1 to another anion (P2). Therefore, Pi(t) increases from 1 to 2. Atomic-scale dynamics clearly indicate that progressive proton transfer occurs when the anions rotate. Thus, anion rotation limits proton transport. However, it should be noted that rotations are strongly correlated with the recombination dynamics of H-bonds because additional H-bond formation at t = t2 promotes anion rotation. Hence, concerted anion rotation and H-bond recombination enabled high proton conductivity. Based on this mechanism, we estimated the proton diffusion coefficients. As shown in Fig. 7, 70% of protons are transferred to adjacent anions every anion rotation. This means that 70% of protons move by the nearest neighbor P–P distance ΔrPP of 4.7 Å per reorientation time τrot on average. This mechanism leads to the diffusion coefficient of Drot = 0.70 × 〈ΔrPP2〉/6τrot. As shown in Fig. 9 and 3a, Drot agrees reasonably well with the DH calculated using the MSDs.
Conclusions
The origin of the decrease in proton diffusivity with an increasing number of alkyl chains to phosphonic acid groups was investigated by MD simulations employing MLFFs. Our systematic MD simulations of liquid PA and phosphonic acids indicated that in all materials, the protons were shuttle between a pair of anions with a high frequency of approximately 10 ps−1. However, only 0.1% of the shuttling protons were successfully transported to adjacent anions. This was due to the speed of the anion reorientation, which is three orders of magnitude slower than that of the proton hopping. Detailed atomic-scale dynamic analyses revealed that an anion could only pass a proton from one adjacent anion to another when rotating. This rotation was promoted by the recombination of H-bonds. Hence, concerted rotation and H-bond recombination are indispensable for proton conduction. When phosphonic acid anions are bonded to alkyl chains, increasing the alkyl chain length caused a significant deceleration of the anion rotation, which led to the suppression of fast Grotthuss proton transfer. Accordingly, retaining the rotational freedom of anions as well as H-bond recombination is the key to balancing the proton conductivity and stability of anhydrous proton-conductive electrolytes based on phosphoric and phosphonic acid anions. Based on the present results and past studies, we can consider several approaches, such as acid/base ion pairs,19 solid acids,49 and their hybridizations, which retain high rotational motions of anions and prevent reaching out of anions. As demonstrated by Lee and co-workers,19 acid/base ion pairs achieved high anion retention in durability tests while retained the high proton conductivity due to the attractive interaction between the ions. Although further high durability is required for practical applications, we expect that proper designs of acid and base molecules can realize balanced conductivity and durability. Solid acids in the high-temperature phase achieved the high proton conductivity owing to high anion rotations in their cation frame as shown in our previous MLFF study.49 Although their poor water resistances are the problem, we expect that a variety of frame architectures, such as metal- and covalent-organic frameworks,66,67 will provide flexible designing of proton conducting mediums. We believe that high anion rotation is a key to designing proton conductive materials, and the MLFF will provide a useful platform to explore the new materials in silico.Conflicts of interest
The authors declare that they have no competing financial interests or personal relationships that may have influenced the research reported in this study.Acknowledgements
This study was partially supported by NEDO (New Energy and Industrial Technology Development Organization) financially. The authors wish to acknowledge Professor Osamu Yamamuro for fruitful discussion.Notes and references
- D. A. Cullen, K. Neyerlin, R. K. Ahluwalia, R. Mukundan, K. L. More, R. L. Borup, A. Z. Weber, D. J. Myers and A. Kusoglu, New roads and challenges for fuel cells in heavy-duty transportation, Nat. Energy, 2021, 6(5), 462–474 CrossRef CAS.
- T. Yoshida and K. Kojima, Toyota MIRAI fuel cell vehicle and progress toward a future hydrogen society, Electrochem. Soc. Interface, 2015, 24(2), 45–49 CrossRef CAS.
- M. Falk, An infrared study of water in perfluorosulfonate (Nafion) membranes, Can. J. Chem., 1980, 58(14), 1495–1501 CrossRef CAS.
- T. D. Gierke, G. Munn and F. Wilson, The morphology in nafion perfluorinated membrane products, as determined by wide-and small-angle x-ray studies, J. Polym. Sci., Polym. Phys. Ed., 1981, 19(11), 1687–1704 CrossRef CAS.
- J.-C. Perrin, S. Lyonnard and F. Volino, Quasielastic neutron scattering study of water dynamics in hydrated nafion membranes, J. Phys. Chem. C, 2007, 111(8), 3393–3404 CrossRef CAS.
- A. Kusoglu and A. Z. Weber, New insights into perfluorinated sulfonic-acid ionomers, Chem. Rev., 2017, 117(3), 987–1104 CrossRef CAS.
- S. Samms, S. Wasmus and R. Savinell, Thermal stability of Nafion® in simulated fuel cell environments, J. Electrochem. Soc., 1996, 143(5), 1498–1504 CrossRef CAS.
- E. Qu, X. Hao, M. Xiao, D. Han, S. Huang, Z. Huang, S. Wang and Y. Meng, Proton exchange membranes for high temperature proton exchange membrane fuel cells: challenges and perspectives, J. Power Sources, 2022, 533, 231386 CrossRef CAS.
- K. H. Lim, A. S. Lee, V. Atanasov, J. Kerres, E. J. Park, S. Adhikari, S. Maurya, L. D. Manriquez, J. Jung and C. Fujimoto, Protonated phosphonic acid electrodes for high power heavy-duty vehicle fuel cells, Nat. Energy, 2022, 7(3), 248–259 CrossRef CAS.
- New Energy and Industrial Technology Development Organization (NEDO), Fuel Cell Development Progress 2022 Report. https://www.nedo.go.jp/content/100944011.pdf Search PubMed.
- R. Haider, Y. Wen, Z.-F. Ma, D. P. Wilkinson, L. Zhang, X. Yuan, S. Song and J. Zhang, Proton exchange membranes for high temperature proton exchange membrane fuel cells: challenges and perspectives, Chem. Soc. Rev., 2021, 50(2), 1138–1187 RSC.
- A. S. Lee, Y.-K. Choe, I. Matanovic and Y. S. Kim, The energetics of phosphoric acid interactions reveals a new acid loss mechanism, J. Mater. Chem. A, 2019, 7(16), 9867–9876 RSC.
- E. Quartarone, S. Angioni and P. Mustarelli, Polymer and Composite Membranes for Proton-Conducting, High-Temperature Fuel Cells: A Critical Review, Materials, 2017, 10(7), 687 CrossRef.
- A. Schechter and R. F. Savinell, Imidazole and 1-methyl imidazole in phosphoric acid doped polybenzimidazole, electrolyte for fuel cells, Solid State Ionics, 2002, 147(1–2), 181–187 CrossRef CAS.
- H. Steininger, M. Schuster, K. Kreuer, A. Kaltbeitzel, B. Bingöl, W. H. Meyer, S. Schauff, G. Brunklaus, J. Maier and H. W. Spiess, Intermediate temperature proton conductors for PEM fuel cells based on phosphonic acid as protogenic group: a progress report, Phys. Chem. Chem. Phys., 2007, 9(15), 1764–1773 RSC.
- Y. Aihara, A. Sonai, M. Hattori and K. Hayamizu, Ion conduction mechanisms and thermal properties of hydrated and anhydrous phosphoric acids studied with 1H, 2H, and 31P NMR, J. Phys. Chem. B, 2006, 110(49), 24999–25006 CrossRef CAS PubMed.
- T. Norby, Solid-state protonic conductors: principles, properties, progress and prospects, Solid State Ionics, 1999, 125(1–4), 1–11 CrossRef CAS.
- J. Wainright, J. T. Wang, D. Weng, R. Savinell and M. Litt, Acid-doped polybenzimidazoles: a new polymer electrolyte, J. Electrochem. Soc., 1995, 142(7), L121–L123 CrossRef CAS.
- K.-S. Lee, J. S. Spendelow, Y.-K. Choe, C. Fujimoto and Y. S. Kim, An operationally flexible fuel cell based on quaternary ammonium-biphosphate ion pairs, Nat. Energy, 2016, 1(9), 1–7 Search PubMed.
- S. M. Haile, D. A. Boysen, C. R. Chisholm and R. B. Merle, Solid acids as fuel cell electrolytes, Nature, 2001, 410(6831), 910–913 CrossRef CAS.
- S. M. Haile, C. R. Chisholm, K. Sasaki, D. A. Boysen and T. Uda, Solid acid proton conductors: from laboratory curiosities to fuel cell electrolytes, Faraday Discuss., 2007, 134, 17–39 RSC.
- D. A. Boysen, T. Uda, C. R. Chisholm and S. M. Haile, High-performance solid acid fuel cells through humidity stabilization, Science, 2004, 303(5654), 68–70 CrossRef CAS PubMed.
- O. Kongstein, T. Berning, B. Børresen, F. Seland and R. Tunold, Polymer electrolyte fuel cells based on phosphoric acid doped polybenzimidazole (PBI) membranes, Energy, 2007, 32(4), 418–422 CrossRef CAS.
- S. Horike, D. Umeyama, M. Inukai, T. Itakura and S. Kitagawa, Coordination-network-based ionic plastic crystal for anhydrous proton conductivity, J. Am. Chem. Soc., 2012, 134(18), 7612–7615 CrossRef CAS.
- D. Umeyama, S. Horike, M. Inukai, T. Itakura and S. Kitagawa, Inherent proton conduction in a 2D coordination framework, J. Am. Chem. Soc., 2012, 134(30), 12780–12785 CrossRef CAS PubMed.
- V. Atanasov, A. S. Lee, E. J. Park, S. Maurya, E. D. Baca, C. Fujimoto, M. Hibbs, I. Matanovic, J. Kerres and Y. S. Kim, Synergistically integrated phosphonated poly (pentafluorostyrene) for fuel cells, Nat. Mater., 2021, 20(3), 370–377 CrossRef CAS PubMed.
- J. Chen, L. Wang and L. Wang, Highly conductive polybenzimidazole membranes at low phosphoric acid uptake with excellent fuel cell performances by constructing long-range continuous proton transport channels using a metal–organic framework (UIO-66), ACS Appl. Mater. Interfaces, 2020, 12(37), 41350–41358 CrossRef CAS.
- S. Zhu, L. Yan, D. Zhang and Q. Feng, Molecular dynamics simulation of microscopic structure and hydrogen bond network of the pristine and phosphoric acid doped polybenzimidazole, Polymer, 2011, 52(3), 881–892 CrossRef CAS.
- S. Pahari, C. K. Choudhury, P. R. Pandey, M. More, A. Venkatnathan and S. Roy, Molecular dynamics simulation of phosphoric acid doped monomer of polybenzimidazole: a potential component polymer electrolyte membrane of fuel cell, J. Phys. Chem. B, 2012, 116(24), 7357–7366 CrossRef CAS PubMed.
- T. Rager, M. Schuster, H. Steininger and K. D. Kreuer, Poly (1, 3-phenylene-5-phosphonic Acid), a Fully Aromatic Polyelectrolyte with High Ion Exchange Capacity, Adv. Mater., 2007, 19(20), 3317–3321 CrossRef CAS.
- M. Tanaka, Y. Takeda, T. Wakiya, Y. Wakamoto, K. Harigaya, T. Ito, T. Tarao and H. Kawakami, Acid-doped polymer nanofiber framework: three-dimensional proton conductive network for high-performance fuel cells, J. Power Sources, 2017, 342, 125–134 CrossRef CAS.
- J.-P. Melchior, K.-D. Kreuer and J. Maier, Proton conduction mechanisms in the phosphoric acid–water system (H4P2O7–H3PO4·2H2O): a 1H, 31P and 17O PFG-NMR and conductivity study, Phys. Chem. Chem. Phys., 2017, 19(1), 587–600 RSC.
- K.-D. Kreuer, Proton conductivity: materials and applications, Chem. Mater., 1996, 8(3), 610–641 CrossRef CAS.
- Y.-K. Choe, E. Tsuchida, T. Ikeshoji, S. Yamakawa and S.-a. Hyodo, Nature of proton dynamics in a polymer electrolyte membrane, nafion: a first-principles molecular dynamics study, Phys. Chem. Chem. Phys., 2009, 11(20), 3892–3899 RSC.
- L. Vilčiauskas, M. E. Tuckerman, G. Bester, S. J. Paddison and K.-D. Kreuer, The mechanism of proton conduction in phosphoric acid, Nat. Chem., 2012, 4(6), 461–466 CrossRef PubMed.
- E. Tsuchida, Ab initio molecular-dynamics simulation of concentrated phosphoric acid, J. Phys. Soc. Jpn., 2006, 75(5), 054801 CrossRef.
- C. Dreßler and D. Sebastiani, Effect of anion reorientation on proton mobility in the solid acids family CsHyXO4 (X = S, P, Se, y = 1, 2) from ab initio molecular dynamics simulations, Phys. Chem. Chem. Phys., 2020, 22(19), 10738–10752 RSC.
- L. Vilčiauskas, M. E. Tuckerman, J. P. Melchior, G. Bester and K.-D. Kreuer, First principles molecular dynamics study of proton dynamics and transport in phosphoric acid/imidazole (2: 1) system, Solid State Ionics, 2013, 252, 34–39 CrossRef.
- R. Jinnouchi, S. Minami, F. Karsai, C. Verdi and G. Kresse, Proton Transport in Perfluorinated Ionomer Simulated by Machine-Learned Interatomic Potential, J. Phys. Chem. Lett., 2023, 14(14), 3581–3588 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98(14), 146401 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104(13), 136403 CrossRef PubMed.
- A. V. Shapeev, Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials, Multiscale Model. Simul., 2016, 14(3), 1153–1173 CrossRef.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics, Phys. Rev. Lett., 2018, 120(14), 143001 CrossRef CAS PubMed.
- K. T. Schutt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Muller, SchNet - a deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148(24), 241722 CrossRef CAS.
- R. Jinnouchi, F. Karsai and G. Kresse, On-the-fly machine learning force field generation: application to melting points, Phys. Rev. B, 2019, 100(1), 014105 CrossRef CAS.
- R. Drautz, Atomic cluster expansion for accurate and transferable interatomic potentials, Phys. Rev. B, 2019, 99(1), 014104 CrossRef CAS.
- A. E. Allen, G. Dusson, C. Ortner and G. Csányi, Atomic permutationally invariant polynomials for fitting molecular force fields, Mach. Learn.:Sci. Technol., 2021, 2(2), 025017 Search PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E (3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13(1), 1–11 Search PubMed.
- R. Jinnouchi, Molecular dynamics simulations of proton conducting media containing phosphoric acid, Phys. Chem. Chem. Phys., 2022, 24(25), 15522–15531 RSC.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017 Search PubMed.
- M. Parrinello and A. Rahman, Crystal structure and pair potentials: a molecular-dynamics study, Phys. Rev. Lett., 1980, 45(14), 1196–1199 CrossRef CAS.
- H. Sun, COMPASS: an ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds, J. Phys. Chem. B, 1998, 102(38), 7338–7364 CrossRef CAS.
- BIOVIA Materials Studio, Dassault, San Diego, 2020 Search PubMed.
- R. Jinnouchi, F. Karsai, C. Verdi, R. Asahi and G. Kresse, Descriptors representing two-and three-body atomic distributions and their effects on the accuracy of machine-learned inter-atomic potentials, J. Chem. Phys., 2020, 152(23), 234102 CrossRef CAS PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B, 2013, 87(18), 184115 CrossRef.
- K. Miwa and H. Ohno, Interatomic potential construction with self-learning and adaptive database, Phys. Rev. Mater., 2017, 1(5), 053801 CrossRef.
- M. W. Mahoney and P. Drineas, CUR matrix decompositions for improved data analysis, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(3), 697–702 CrossRef CAS PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(11), 7413–7421 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS.
- T. A. Zawodzinski Jr, M. Neeman, L. O. Sillerud and S. Gottesfeld, Determination of water diffusion coefficients in perfluorosulfonate ionomeric membranes, J. Phys. Chem., 1991, 95(15), 6040–6044 CrossRef.
- S. Ochi, O. Kamishima, J. Mizusaki and J. Kawamura, Investigation of proton diffusion in Nafion® 117 membrane by electrical conductivity and NMR, Solid State Ionics, 2009, 180(6–8), 580–584 CrossRef CAS.
- N. Ma and S. Horike, Metal-Organic Network-Forming Glasses, Chem. Rev., 2022, 122(3), 4163–4203 CrossRef CAS PubMed.
- H. Xu, S. Tao and D. Jiang, Proton conduction in crystalline and porous covalent organic frameworks, Nat. Mater., 2016, 15(7), 722–726 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta03164k |
| This journal is © The Royal Society of Chemistry 2023 |