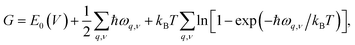Accelerating materials discovery using integrated deep machine learning approaches

Abstract

We present an integrated deep machine learning (ML) approach that combines crystal graph convolutional neural networks (CGCNN) for predicting formation energies and artificial neural networks (ANN) for constructing interatomic potentials. Using the La–Si–P ternary system as a proof-of-concept, we achieve a remarkable speed-up of at least 100 times compared to high-throughput first-principles calculations. The ML approach successfully identifies known compounds and uncovers 16 new P-rich compounds with formation energies within 100 meV per atom above the convex hull, including a stable La₂SiP₃ phase. We also employ the developed ML interatomic potential in a genetic algorithm for efficient structure search, leading to the discovery of more metastable compounds. Moreover, substitution of La atoms with Ba reveals a new stable quaternary compound, BaLaSiP₃. Our generic and robust approach holds great promise for accelerating materials discovery in various compounds, enabling more efficient exploration of complex chemical spaces and enhancing the prediction of material properties.

---

Introduction

Knowledge of plausible energetically favorable crystal structures in a given phase space and their relative thermodynamic stabilities is essential for rational materials design, discovery, and optimization. However, it is quite challenging to map out such a comprehensive structure–energy landscape for compounds containing three or more chemical elements. The number of possible combinations obtained by varying chemical composition and potential crystal structure is enormous. It is impossible to search for low-energy structures for all these combinations by experiment or computational algorithms, although several advanced computational crystal structure prediction methods based on genetic algorithm (GA), particle swarm optimization (PSO), or other algorithms are available.^1–8 Straightforward high-throughput first-principles calculations by chemical substitution of known crystal structures from experimental databases are also not efficient due to the heavy computational cost.^9–14

Rapid advances in AI/ML algorithms, information infrastructures and data science, as well as computer hardware/software, offer great opportunities to develop new transformative strategies for materials design and discovery.^15–22 Recently, machine learning (ML) techniques have been employed to assist in rapidly screening vast composition-structure spaces to select promising candidates for first-principles calculations. Successful application of such ML-guided approaches in accelerating materials discovery has been demonstrated.^23–27 However, the efficiency of these ML-guided approaches relies heavily on the accuracy of the ML model predictions. ML models with poor accuracy can either substantially overestimate the number of candidate structures, thus putting an unnecessary burden on subsequent first-principles calculations, or badly miss promising target structures. Thus, it is highly desirable to have a robust approach to provide accurate ML screening, selecting only a minimal number of promising candidate structures for first-principles calculations, and the success rate of the ML-guided predictions is boosted to dramatically accelerate the pace of materials discovery.

In this paper, we show that a crystal graph convolutional neural network (CGCNN) ML model, trained by first-principles calculation data specifically focus on the material system of interest, gives much more accurate prediction of ternary compound formation energies to efficiently select a small fraction of candidate structures (<1.5%) from a large hypothetical structure pool. Subsequent structure relaxation for the structures selected by CGCNN using interatomic potentials trained by an artificial neural network ML (ANN-ML) method, further reduces the candidate structures to a very small number for final refinement by fist-principles calculations, thus substantially boosting the efficiency of the ML-guided approach. Moreover, the developed ANN-ML interatomic potentials can be used to perform efficient and reliable structure searches based on GA. Such an integrated ML-guided approach is illustrated in Fig. 1.

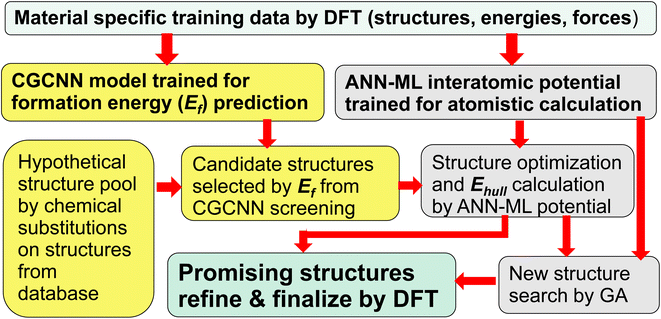Fig. 1 Flowchart of the proposed integrated ML-guided approach for accelerating materials discovery.

Results and discussion

ML accelerated discovery of La–Si–P ternary compounds

We use La–Si–P ternary system to demonstrate the accuracy and efficiency of the proposed integrated ML approach for the discovery of novel ternary compounds. Due to the complexity of the interatomic interactions in La–Si–P ternary system, it is very challenging for computational approaches to correctly and efficiently predict the low-energy stable and metastable ternary compounds. This system therefore can serve as a good test bed for our new approach. Another motivation in choosing La–Si–P system is to search for new non-centrosymmetric (NCS) ternary compounds. There have been reported that silicon phosphides of transition and/or rare-earth metals can crystallize in non-centrosymmetric (NCS) crystal structures. NCS ternary compounds are interesting because absence of inversion symmetry and significant hybridization of d-, f-, and p-orbitals promotes a plethora of emergent properties such as unconventional superconductivity, topologically non-trivial quantum properties over large energy windows, and quasiparticle behavior as have been discussed in the literature.^28–31

We use La–Si–P ternary system as a test bed to demonstrate the accuracy and efficiency of the proposed integrated ML approach for the discovery of novel ternary compounds. Many reported silicon phosphides of transition and/or rare-earth metals crystallize in noncentrosymmetric (NCS) crystal structures. The absence of inversion symmetry and significant hybridization of d-, f-, and p-orbitals promotes a plethora of emergent properties such as unconventional superconductivity, topologically non-trivial quantum properties over large energy windows, and quasiparticle behavior.^28–31

Two experimentally-observed ternary compounds (La(SiP₃)₂ and LaSiP₃) have been reported,^32,33 and another compound (La₂SiP₄) has also been recently synthesized by experiment³⁴ along with a high-temperature disordered polymorph of LaSiP₃. The discovery of new ternary phases in this system is both intriguing and challenging due to the complex interatomic interactions involved. Our proposed integrated ML approach not only correctly captures the three known ternary phases, but also efficiently predicts a novel energetically stable La₂SiP₃ phase and 15 other low-energy metastable P-rich ternary phases (P composition ≥ 50%) with formation energies within 0.1 eV per atom above the ternary convex hull. Among the 15 low-energy metastable P-rich ternary phases (P composition ≥ 50%), 5 of them are NCS crystals.

In CGCNN, a crystal structure is represented by a crystal graph that encodes both atomic information and bonding interactions between atoms. A convolutional neural network is added on top of the crystal graph to construct the proper descriptors, which are optimized for predicting target properties.²³ In this way, composition–structure–property relationships can be efficiently learned and predicted by CGCNN. The training data in CGCNN are primarily generated by first-principles calculations, which enables a sufficient volume of data for the supervision training. 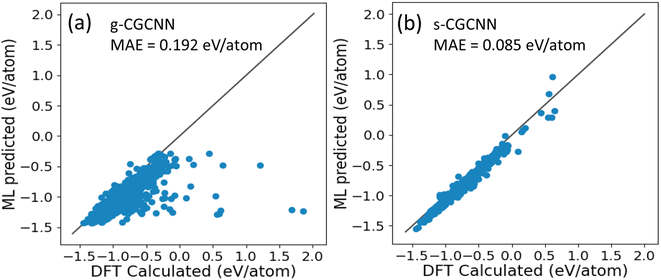The first CGCNN motel for formation energy predictions of compounds was proposed and trained by Xie and Grossman²³ using the structures and formation energies of 28 046 structures from first-principles calculations from the Materials Project (MP) database.³⁵ The training structures in this model cover a wide range of chemical elements and composition ratios, and we refer to this model as a general CGCNN (g-CGCNN) model. While the g-CGCNN model has been shown to be very useful for accelerating the discovery of novel complex ternary compounds,^25–27 the accuracy and efficiency of the CGCNN model can be significantly improved further if the model is retrained using the data specifically targeting the materials being studied.^25,36 For La–Si–P ternary system, we retrained the CGCNN using 228 284 structures and formation energies from the dataset that was prepared to train an ANN-ML interatomic potential for the La–Si–P system (see below and ESI†). We refer to this later CGCNN model as a specific CGCMM (s-CGCNN) model. In the training of both g-CGCNN and s-CGCNN, we use the exact same descriptors, size of neural network, and all other hyperparameters. The only difference is the training data. While the training data for g-CGCNN cover many chemical elements in the periodic table, the training data for the s-CGCNN model focuses on the structures containing only the three relevant elements La, Si, and P. To compare the prediction accuracy of these two CGCNN models for La–Si–P ternary compounds, we applied the models to a set of 806 La–Si–P ternary compounds studied in ref. 27. The first-principles calculation results for formation energies of these ternary compounds were studied in ref. 27, but the first-principles results were not included in the training dataset for either CGCNN model. The comparison of the formation energy from the CGCNN models and first-principles calculation results are shown in Fig. 2, in which mean absolute error (MAE) are provided. We can see that the g-CGCNN model substantially underestimates the formation energies of these compounds (Fig. 2a), while the agreement with the first-principles results is much better by the s-CGCNN predictions (Fig. 2b).

Fig. 2 (a) The g-CGCNN model predicted formation energy (E_f) compared to the calculated DFT-PBE results (b) the s-CGCNN model predicted formation energy (E_f) compared to the calculated DFT-PBE results.

We then applied the two CGCNN models to perform a fast screening of the formation energies of ternary La–Si–P compounds in a hypothetical structure pool, which was generated based on known ternary structure lattices. We collected 28 472 known ternary structures from the MP database and replaced the three elements with La, Si, and P. For each ternary structure from the MP database, five hypothetical lattices were generated by uniformly scaling the bond lengths of the structure such that the volume of the unit cell varied from the original by a factor of 0.96 to 1.04 in increments of 0.02. The use of the scaling factor for the crystal unit cell volume helps the CGCNN model differentiate the energetic stability of the same structure with different bond lengths. There are also six ways to shuffle the three elements in a given template ternary structure. Therefore, by multiplying reported ternary structures by 6 compositional combinations and 5 volume steps, 854 070 hypothetical ternary La–Si–P structures were generated.

The distributions of the formation energies (E_f) from the g-CGCNN and s-CGCNN predictions for this set of structures are shown in Fig. 3, where E_f is defined with respect to the elemental ground-state bulk phases of the constituent elements La, Si, and P, i.e., 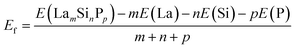, with E(La_mSi_nP_p) as the total energy of the La_mSi_nP_p compound, E(La), E(Si) and E(P) as the per-atom energy of the ground state of La, Si and P crystals, respectively. Negative formation energies indicates that the formation of the ternary compounds is energetically favorable with respect to the three elemental phases.

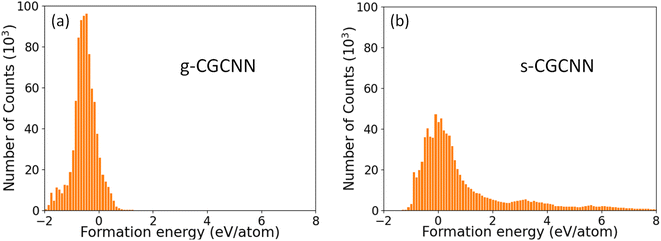Fig. 3 The formation energies (E_f) of 854 070 hypothetical ternary La–Si–P compounds as predicted by (a) the g-CGCNN model and (b) the s-CGCNN model.

From Fig. 3a, we can see that more than 80% of the ternary La–Si–P structures from the hypothetical structure pool are predicted to have negative formation energies by the g-CGCNN model. In particular, the three known ternary compounds lie in the 42nd percentile low-energy region, meaning that about the 42% of the structures from the hypothetical structures must be selected as candidate structures in order to capture these known phases. Thus the g-CGCNN model is not efficient in accelerating materials discovery for this system. In comparison, the prediction from the s-CGCNN model, as shown in Fig. 3b, shows dramatic improvement in the efficiency of candidate structure selection. The fraction of the structures that have negative formation energy is much less (33%), and the three known ternary phases lie in the 5.6th percentile low-energy region, meaning that only 5.6% of the structures must be selected as candidates to capture the three experimentally-observed phases.

After removing very similar structures, our s-CGCNN screening revealed 12 383 La–Si–P structures with negative formation energies that could be selected for further evaluations. While using first-principles calculation to optimize the unit cell shape and the atomic positions of the 12 383 structures is manageable, we found that using an interatomic potential trained by an artificial neural network ML (ANN-ML) method can further boost the efficiency of the ML-guided approach. More details of the ANN-ML interatomic potential for the La–Si–P system are given in the ESI.† Structural optimization with the ANN-ML potential using the LAMMPs code is 10⁵–10⁶ times faster than that using regular DFT potentials,³⁷ and enables the optimization of the 12 383 structures to be done much quickly. The accuracy and efficiency of the ANN-ML interatomic potentials also enable efficient exploration of the temperature effects on the thermodynamic stability and the phase formation kinetics of the predicted phases, as will be discussed below.

The artificial neural network (ANN) machine learning (ML) interatomic potential for La–Si–P system is developed by the deep learning software package DeePMD-kit.⁴⁴ The training data including the energies and forces are generated by ab initio MD (AIMD) simulations and ab initio calculations using the VASP package^39,40 with the projector-augmented-wave (PAW) method.⁴¹ The exchange and correlation energy functional with non-spin-polarized generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) form⁴¹ is used. The energy cutoff for the plane wave basis set is 270 eV. The time step is 3 fs and NVT ensemble with Nose–Hoover thermostat^45,46 are employed in AIMD simulations. The Brillouin zone is sampled by the gamma point. The training data set consists of 228 284 structures and their formation energies, including liquid snapshot structures of La₂₀Si₂₀P₆₀, La₁₀Si₁₀P₈₀, La₁₀Si₄₅P₄₅, La₁₀Si₈₀P₁₀, La₅Si₉₀P₅, La₅Si₅P₉₀, La, Si, P, and the distorted crystalline structures of LaSi, LaP, SiP, LaSiP₃, etc. from Materials Project database.³⁵ The local structure configuration information within a cutoff radial of 7.0 Å is sampled to train the ANN-ML model with four hidden layers and 120 nodes per layer. The tanh function is used as activation function in neural network model.

The binding energies of 12 383 structures and the known ternary and binary compounds obtained from the ANN-ML potential optimization enabled us to calculate the formation energy above convex hull (denoted as E_hull) for these structures, which gives a better quantitative description of the thermodynamic stability in comparison with using E_f. E_hull of any given phase on the ternary convex hull can be calculated by comparing the phase's formation energy with respect to three nearby known phases on the convex hull. These three known phases can be ternaries, binaries, or elemental crystalline phases, and the chemical compositions of these three phases correspond to the vertexes of a triangle (called a Gibbs triangle) that encloses the composition of the phase of interest for which E_hull is calculated. Therefore, E_hull determines the thermodynamic stability of the given phase against decomposition into the nearby three known phases.

The distribution of formation energies above convex hull (E_hull) of the 12 383 structures predicted by the ANN-ML potentials is shown in Fig. 4. We can see that only a very small fraction of structures has E_hull below or close to the convex hull from the ANN-ML potential prediction. The known LaSiP₃, La(SiP₃)₂, and La₂SiP₄ phases are predicted to have E_hull values of −0.036 eV per atom, 0.007 eV per atom, and 0.041 eV per atom respectively – all very close to the convex hull. Applying an E_hull cutoff value of 0.05 eV per atom to select candidate structures with composition ratio P ≥ 50%, we obtain 29 candidates including the three known ternary phases. These results indicate the ANN-ML potentials has sufficient accuracy to efficiently select promising candidate structures for the discovery of low-energy ternary compounds. To search for more low-energy metastable structures and to take into the consideration that the ANN-ML would have some errors in the E_hull predictions, we selected structures with E_hull ≤ 0.3 eV per atom and composition ratio P ≥ 50% predicted by the ANN-ML potential for further evaluation by first-principles calculations. These were 353 structures to be studied by first-principles calculations which could easily be performed within a few days using commonly available cluster computers, since most of the structures after the ANN-ML potential relaxation are already very close to the final first-principles calculation results. Therefore, using ANN-ML potentials to relax the structure can substantially reduce the number of candidate structures for first-principles calculations and provides another significant speed up to materials discovery on the top of s-CGCNN screening.

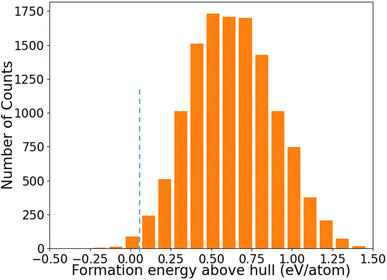Fig. 4 The distribution of formation energies above convex hull (E_hull) of the 12 383 structures predicted by the ANN-ML potential.

The first-principles calculations were performed using the projector augmented wave (PAW) method³⁸ within DFT as implemented in VASP code.^39,40 The exchange and correlation energy is treated by the generalized gradient approximation (GGA) and parameterized by the Perdew–Burke–Ernzerhof formula (PBE).⁴¹ A plane-wave basis set with a kinetic energy cutoff of 520 eV was used to expand the electronic wave functions, ensuring high accuracy in our DFT calculations for the candidate structures identified by the ML process. The convergence criterion for the total energy was set to 10⁻⁵ eV. Monkhorst–Pack's sampling scheme⁴² was adopted for the Brillouin zone sampling with a k-point grid of 2π × 0.033 Å⁻¹, and the unit cell lattice vectors (both the unit cell shape and size) were fully relaxed together with the atomic coordinates until the forces on each atom was less than 0.01 eV Å⁻¹.

Stability of La₂SiP₃

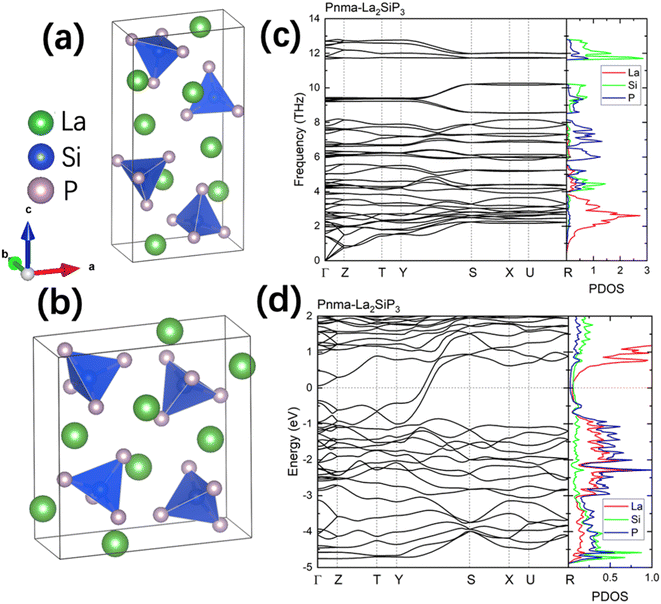
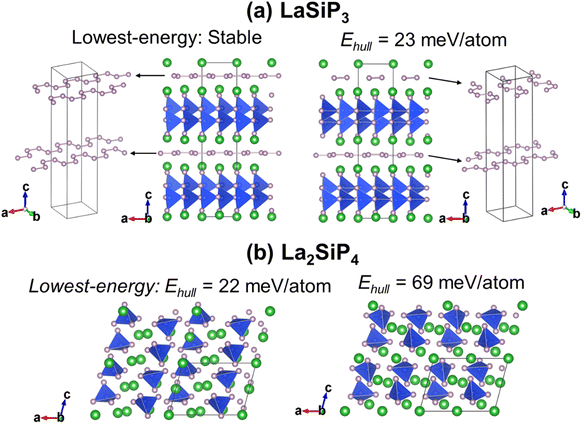
The first-principles calculations on these 353 structures correctly captured the three known ternary phases: the Pna2₁-LaSiP₃ with an E_hull value of −0.017 eV per atom, the Cmc2₁-La(SiP3)₂ with an E_hull value of −0.017 eV per atom and the P2₁/c-La₂SiP₄ with an E_hull value of 0.022 eV per atom. The calculations also revealed 16 metastable structures with E_hull < 0.1 eV per atom. More details about these 16 structures are given in the ESI (Table S1).† Among the discovered 16 metastable structures, we found one new La₂SiP₃ structure with E_hull = 0.001 eV per atom, essentially located the convex hull. Another metastable La₂SiP₃ structure also has a small E_hull of 0.033 eV per atom. These two La₂SiP₃ structures are shown in Fig. 5a and b. Both La₂SiP₃ phases are centrosymmetric orthorhombic structures with Pnma symmetry, whose conventional cells contain four formula units (Z = 4). They share one important structural feature, that is they both contain Si-centered tetrahedron with P atoms on the vertices. The orientation and arrangement of these (SiP₄) tetrahedra are different. In addition, in the higher energy phase (E_hull = 33 meV per atom), the La and P atoms form octahedra. Although these two phases have the same composition with the same number of atoms, their lattice vectors are different. The lower energy phase (E_hull = 1 meV per atom) has a unit cell of a = 8.14 Å, b = 4.19 Å, and c = 16.12 Å (volume = 549.88 ų). While the high energy phase has a unit cell of a = 4.14 Å, b = 11.32 Å, and c = 11.73 Å (volume = 549.51 ų). The average bond lengths of La–P and Si–P interactions in the two compounds are 3.04 Å and 2.31 Å, respectively.

Fig. 5 (a and b) The structures of the predicted two La₂SiP₃ phases. The formation energies above the convex hull are 1 meV per atom and 33 meV per atom, respectively. (c and d) The phonon dispersion and density of states of the two predicted La₂SiP₃ phases.

We also performed phonon calculations to investigate the dynamic stabilities of the two predicted La₂SiP₃ phases. The Phonopy package was used with the finite displacement method. A supercell of 2 × 2 × 2 is created, and the forces were calculated with the supercell with displacement along different directions. These DFT calculations adopted the same parameters used previously in the structural optimization as well as the formation energy calculations. Force constants were then calculated from the set of forces. Dynamic matrices were built from the force constants and thus phonon frequencies and eigenvectors were obtained with the specified q points. The phonon dispersion along with the phonon density of states are shown in Fig. 5c and d. No imaginary vibrational frequencies were found, indicating that these two phases are both dynamically stable. La atoms dominate the contribution of low frequency vibrational modes up to 4 THz in both structures. Both Si and P atoms contribute mostly to high frequency modes from 4 to 13 THz. The calculated band structures at the DFT-PBE level for these two structures are shown in Fig. S5a and b respectively in the ESI.† They both show metallic character but with small density of states around Fermi level. The bands across the Fermi level indicate a layered-like character formed. By investigating the density of states around the Fermi level, we found that the contribution mostly comes from La atoms, which is consistent with the arrangement of La atoms as layers in the two structures.

To investigate the effect of temperature on thermodynamics stability of the two newly discovered La₂SiP₃ compounds with respect to the three reported ternary compounds, we evaluated the Gibbs free energy as a function of temperature for the two La₂SiP₃ phases, the ordered LaSiP₃ polymorph, LaSi₂P₆, and La₂SiP₄. Without pressure and at a given temperature T and volume V, the Gibbs free energy G of a crystalline compound is given by:

where E₀(V) is the energy at T = 0 K, k_B and ℏ are the Boltzmann constant and the reduced Planck constant, respectively, and ω_q,ν is the phonon frequency at q and ν, where q and ν are the wave vector and band index, respectively.⁴³

The results of the Gibbs free energy as the function of temperature for the five ternary La–Si–P phases from our calculations are shown in Fig. S6 in the ESI.† To characterize the thermodynamic stability of these ternary structures with different compositions, we calculated the formation Gibbs energies G_hull of each ternary phase with respect to the nearby competing binary and ternary phases in the ternary convex hull at each temperature. To this end, we have also calculated the temperature-dependent Gibbs free energies of relevant binary (LaP, LaP₂, LaSi, LaSi₂, SiP, SiP₂) as shown in Fig. S6 in the ESI.† As long as the Gibbs free energies of the relevant phases at each temperature are obtained, G_hull of each ternary phase with respect to the ternary convex hull at each temperature can be calculated in the same way as E_hull calculation, by simply replacing the total energies of the competing phases with the corresponding Gibbs free energies G of the phases.

The calculated G_hull as the function of temperature for the five La–Si–P ternary phases are plotted in Fig. 6. We can see that two of the known phases, LaSiP₃ and LaSi₂P₆ are the most stable ones at low temperature below 1100 K. However, La₂SiP₃ becomes more stable than the LaSi₂P₆ above 1200 K, and same for La₂SiP₄ above 1800 K. Since the La₂SiP₄ has been recently successfully synthesized,³⁴ we expect that the newly discovered La₂SiP₃ phases, which is more thermodynamically favorable than La₂SiP₄ phase at all temperatures below 2000 K, can be synthesized as well. The results from this Gibbs energy analysis are important for understanding the thermodynamic stability of the compounds to guide experimental synthesis.

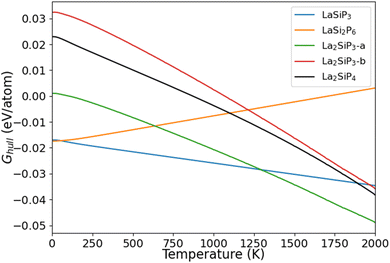Fig. 6 Calculated G_hull as a function of temperature for the four competitive La–Si–P ternary phases.

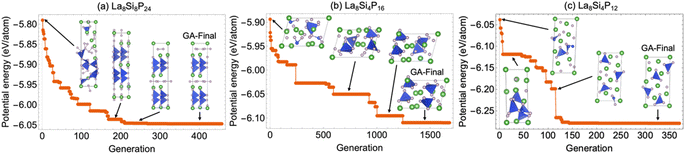
Genetic algorithm search

Since the La–Si–P ternary structures are very complex, involving mixed metallic and covalent bonding, it has been a great challenge for stable structure searching with the currently available methods.^1–8 The developed ANN-ML interatomic potential enabled us to efficiently and accurately search for the low-energy structures of the La–Si–P ternary compounds by genetic algorithm (GA) based on the promising compositions suggested by the CGCNN-ML. As shown in Fig. 7, the GA search with the developed ANN-ML potential can quickly capture the correct structures of the low-energy ternary LaSiP₃, La₂SiP₄, and La₂SiP₃ phases. As far as we know, no other available search methods in the literature can efficiently and accurately capture the correct structures of such complex ternary phases.

Fig. 7 The potential energy and crystal structure evolutions in the process of A GA search using the ANN-ML interatomic potential. (a) The LaSiP₃ phase (with 8 formula units (f.u.)), (b) the La₂SiP₄ phase (with 4 f.u.), and (c) the La₂SiP₃ phase (with 4 f.u.). The green and the smaller grey atoms indicate the La and P atoms respectively. The Si atoms are located in the center of the tetrahedra colored with blue. The structures labeled as “GA-Final” are the final structures from the GA search which correctly captured the lowest-energy structures of the corresponding compositions and corroborate well with the experimentally determined structures.

Moreover, GA searches using the developed ANN-ML interatomic potential also reveal additional new metastable La–Si–P phases as compared to the results from the CGCNN-ML. In the right panel of Fig. 8a and b, we show new metastable structures of the LaSiP₃ and La₂SiP₄ phases, respectively, obtained from our GA search. In comparison with the lowest-energy structures of the two phases (which were also captured by our GA search) in the left panels of the figure, the new metastable structures have formation energies very close to those of lowest-energy structures (within 50 meV per atom). These new metastable structures could be accessible in experiment at higher temperatures. It is interesting to note that the metastable LaSiP₃ structure is very similar to the lowest-energy one with the same noncentrosymmetric Pna2₁ space group, except the subtle difference in the orientation of the 1D P cis–trans chains. In the lowest-energy structure, all P-chains run parallel to the axis a direction, while in the metastable structure, the P-chains run along the a and b directions alternatively. In the La₂SiP₄ structures, the difference between the lowest energy and metastable structures is the relative orientation of the SiP₄ tetrahedra (shown in blue in the figure).

Fig. 8 Comparison of the structures and energies of the lowest-energy compounds (left panels) and new metastable compounds (right panels) of (a) LaSiP₃ and (b) La₂SiP₄ phases obtained from the GA search using the ANN-ML interatomic potential.

Quaternary BaLaSiP₃

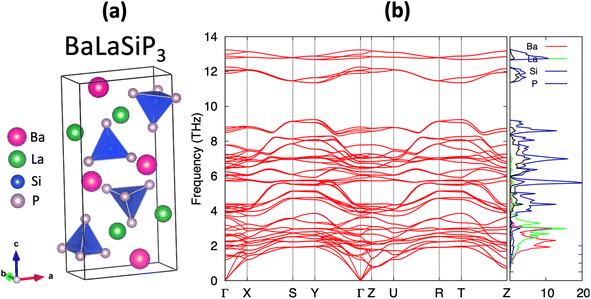
The efficient discovery of stable ternary compounds opens a useful avenue for exploring new stable quaternary compounds by chemical substitution. Applying simple electron-counting rules, we predict La₂SiP₃ to exhibit metallic behavior since it is not electron-balanced. From the covalent approach, which assumes Si–P bonding, we find (La³⁺)₂Si₀(P²⁻)₂(P¹⁻) gives a net non-zero charge while the ionic approach yields (La³⁺)₂Si⁴⁺(P³⁻)₃ which is also non-zero. This metallic behavior is corroborated by our band structure calculations. To compensate for the extra charge in the chemical composition, we considered substituting 1 La atoms in the predicted structure of La₂SiP₃ with divalent Ba, i.e., BaLaSiP₃. After the structure relaxation and total energy calculations by DFT, the quaternary BaLaSiP₃ phase (with 4 f.u. per cell) as shown in Fig. 9a was found to be energetically stable with a formation energy of 23 meV per atom below the currently known Ba–La–Si–P quaternary convex hull. This formation energy is determined by considering the possible decomposition of the BaLaSiP₃ phase into 4 known phases – Ba₃P₂, LaP, LaSiP₃, Ba₃(Si₂P₃)₂ – at the four vertexes of a tetrahedron which encloses the composition of the BaLaSiP₃ phase. Phonon calculations by DFT also showed that the BaLaSiP₃ phase is dynamically stable without any imaginal vibrational modes, as one can see from Fig. 9b. The electronic structure of this quaternary compound is given in Fig. S7 in the ESI.†

Fig. 9 (a) The crystal structure of the proposed BaLaSiP₃ quaternary compound obtained by substituting half of the La atoms by Ba atoms in the newly predicted La₂SiP₃ structure. (b) The phonon dispersion curve and density-of-states of the BaLaSiP₃ compound obtained by DFT calculations.

Similarly, we calculated the Gibbs free energies as the function of temperature for the BaLaSiP₃ quaternary phase, as well as the relevant binary and ternary phases (LaP, LaSiP₃, Ba₃P₂, Ba₃(Si₂P₃)₂). The results are shown in Fig. S6 and S8 respectively in the ESI.† Using these free energy data, we calculated Ghull as the function of temperature for the BaLaSiP₃ quaternary phase and plotted it in Fig. S9.† We can see that BaLaSiP₃ phase stays below the convex hull at all temperatures below 2000 K, which we expect it can be synthesized as well.

Conclusion

One significant advance of the integrated deep machine learning approach presented in this paper over that used in ref. 25 and 36 is that interatomic potential trained by artificial neural network (ANN) has been incorporated into our ML framework. The accuracy of the ANN-ML interatomic potentials for complex materials was also demonstrated. The speed of the structural relaxations using the developed NN-ML is 5–6 orders in magnitude faster than the first-principles calculations. Moreover, the training dataset developed for the ANN-ML potential training can simultaneously be used for training much more accurate CGCNN models for the system of interest. As such, more accurate and efficient CGCNN screenings of compositions/structures to identify better candidates for further relaxation by ANN-ML interatomic potentials can be achieved. Because of the incorporation of the ANN-ML interatomic potential, only a few tens or a few hundred structures (instead of several thousand structures with the approach in ref. 25 and 36) need to be final checked by first-principles calculations. Thus, the pace of the novel compound discovery can be sped up 100–1000 times without losing the accuracy of first-principles predictions. The developed ANN-ML interatomic potentials can also be used to efficiently and reliably explore new unknown structures by GA searches.

Using the La–Si–P ternary system as a proof-of-concept, we show that, needing only 29 structures to be checked by first-principles calculations, the integrated ML approach correctly captures the three known ternary phases (La(SiP₃)₂, and ordered LaSiP₃, La₂SiP₄) and predicted a novel stable La₂SiP₃ phase in the P-rich (P ≥ 50%) regime. The GA search using the developed ANN-ML interatomic potential quickly captured the three stable La–Si–P ternary phases and reveal several new low-energy metastable phases. The described approach is generic and robust which can be readily applied to any compounds of interest. Finally, combining these algorithms with chemical intuition, we expanded this work to explore quaternary Ba–La–Si–P phases by substituting half of the La atoms in the newly predicted La₂SiP₃ phase to yield an electron-balanced phase, BaLaSiP₃, and probe its stability.

Our band structure calculations as shown in Fig. S5 and S7† indicate these two compounds are metallic but with only small number of bands across the Fermi level. Especially, the bands across the Fermi level in the La₂SiP₃ compound exhibit linear-like dispersion, suggesting that electrons in this compound would have high mobility. In order to propose potential applications of the newly discovered compounds (La₂SiP₃, BaLaSiP₃ and other metastable phases shown in the ESI†), more evaluation and understanding on the properties of these compounds will be needed. This will be an interesting topic of future investigations.

For ordered crystalline compounds, it has been widely shown that vibrational entropy plays an important role in determining the relative thermodynamical stability and phase transition between different competing phases as the temperature varies.^47–49 Our calculation results on the temperature effects as shown in Fig. 6 also support this point of view. For most materials, including the La–Si–P ternary compounds studied in this paper, the vibrational entropy can be accurately calculated by first-principles DFT calculations. Therefore, the method for calculating temperature-dependent G_hull to determine the temperature effects on the relative stability of the competing compounds described in this paper can also be applied to other compounds.

Author contributions

W. X., L. T, H. S. and C. Z. performed machine learning analysis and first-principles calculations. W. X. and L. T. performed the genetic algorithm structure search and construction of interatomic potentials. G. V., K. K. K.-M. H. and C.-Z. W. conceptualized and planned the research. C.-Z. W. coordinates the research. All authors contributed to the discussions, analyses of the data, and writing of the paper.

Conflicts of interest

The authors declare that they have no competing interests. All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.†

Acknowledgements

Work at Ames Laboratory was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division including a grant of computer time at the National Energy Research Supercomputing Center (NERSC) in Berkeley. Ames Laboratory is operated for the U.S. DOE by Iowa State University under contract # DE-AC02-07CH11358.

References

1. S. Wu, M. Ji, C. Wang, M. Nguyen, X. Zhao, K. Umemoto, R. Wentzcovitch and K. M. Ho, Adaptive genetic algorithm method for crystal structure prediction, J. Phys.: Condens.Matter, 2014, 26, 035402.
2. X. Zhao, M. C. Nguyen, W. Y. Zhang, C. Z. Wang, M. J. Kramer, D. J. Sellmyer, X. Z. Li, F. Zhang, L. Q. Ke, V. P. Antropov and K. M. Ho, Exploring the structural complexity of intermetallic compounds by an adaptive genetic algorithm, Phys. Rev. Lett., 2014, 112, 045502.
3. X. Zhao, Q. Shu, M. C. Nguyen, Y. Wang, M. Ji, H. Xiang, K. M. Ho, X. Gong and C. Z. Wang, Interface structure prediction from first-principles, J. Phys. Chem. C, 2014, 118, 9524.
4. A. R. Oganov and C. W. Glass, Evolutionary crystal structure prediction as a tool in materials design, J. Phys.: Condens.Matter, 2008, 20, 064210.
5. A. O. Lyakhov, A. R. Oganov, H. Stokes and Q. Zhu, New developments in evolutionary structure prediction algorithm USPEX, Comput. Phys. Commun., 2013, 184, 1172.
6. Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A method for crystal structure prediction, Comput. Phys. Commun., 2012, 83, 2063.
7. C. J. Pickard and R. J. Needs, Ab initio random structure searching, J. Phys.: Condens.Matter, 2011, 23, 053201.
8. M. Amsler and S. Goedecker, Crystal structure prediction using minima hopping method, J. Chem. Phys., 2010, 133, 224104.
9. S. Arapan, P. Nieves and S. Cuesta-López, A high-throughput exploration of magnetic materials by using structure predicting methods, J. Appl. Phys., 2018, 123, 083904.
10. G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: Recent approaches to materials science-a review, J. Phys. Mater., 2019, 2, 032001.
11. W. Chen, High-throughput computing for accelerated materials discovery, in Computational Materials System Design, ed. D. Shin and J. Saal, Springer International Publishing, 2018, p. 169.
12. L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Data-driven materials science: status, challenges, and perspectives, Adv. Sci., 2019, 6, 1900808.
13. H. Zhang, High-throughput design of magnetic materials, Electron. Struct., 2021, 3, 033001.
14. D. Torelli, H. Moustafa, K. W. Jacobsen and T. Olsen, High-throughput computational screening for two-dimensional magnetic materials based on experimental databases of three dimensional compounds, npj Comput. Mater., 2020, 6, 158.
15. J. E. Gubernatis and T. Lookman, Machine learning in materials design and discovery: examples from the present and suggestions for the future, Phys. Rev. Mater., 2021, 129, 070401.
16. R. Vasudevan, G. Pilania and P. V. Balachandran, Machine learning for materials design and discovery, J. Appl. Phys., 2021, 129, 070401.
17. A. G. Kusne, T. Gao, A. Mehta, L. Q. Ke, M. C. Nguyen, K. M. Ho, V. Antropov, C. Z. Wang, M. J. Kramer, C. Long and I. Takeuchi, On-the-fly machine-learning for high-throughput experiments: search for rare-earth-free permanent magnets, Sci. Rep., 2014, 4, 6367.
18. A. Kabiraj, M. Kumar and S. Mahapatra, High-throughput discovery of high curie point two-dimensional ferromagnetic materials, npj Comput. Mater., 2020, 6, 35.
19. J. Cai, X. Chu, K. Xu, H. Li and J. Wei, Machine learning-driven new material discovery, Nanoscale Advances, 2020, 2, 3115.
20. G. Katsikas, S. Charalampos and K. Joseph, Machine learning in magnetic materials, Phys. Status Solidi (B), 2021, 258, 2000600.
21. T. D. Rhone, W. Chen, S. Desai, S. B. Torrisi, D. T. Larson, A. Yacoby and E. Kaxiras, Data-driven studies of magnetic two-dimensional materials, Sci. Rep., 2020, 10, 15795.
22. G. A. Landrum and H. Genin, Application of machine-learning methods to solid-state chemistry: Ferromagnetism in transition metal alloys, J. Solid State Chem., 2003, 176, 587.
23. T. Xie and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120, 145301.
24. C. W. Park and C. Wolverton, Developing an improved crystal graph convolutional neural network framework for accelerated materials discovery, Phys. Rev. Mater., 2020, 4, 063801.
25. W. Xia, M. Sakurai, B. Balasubramanian, T. Liao, R. Wang, C. Zhang, H. Sun, K. M. Ho, J. R. Chelikowsky, D. J. Sellmyer and C. Z. Wang, Accelerating novel magnetic materials discovery using a machine learning guided adaptive feedback, Proc. Natl. Acad. Sci. U.S.A., 2022, 119, e2204485119.
26. R. H. Wang, W. Y. Xia, T. J. Slade, X. Y. Fan, H. F. Dong, K. M. Ho, P. C. Canfield and C. Z. Wang, ML-guided discovery of ternary compounds involving La and immiscible Co and Pb elements, npj Comput. Mater., 2022, 8, 258.
27. H. J. Sun, C. Zhang, W. Y. Xia, L. Tang, G. Akopov, R. H. Wang, K. M. Ho, K. Kovnir and C. Z. Wang, Machine learning guided discovery of ternary compounds containing La, P and group IV elements, Inorg. Chem., 2022, 61, 16699.
28. E. Bauer and M. Sigrist, Non-Centrosymmetric Superconductors: Introduction and Overview, Heidelberg, Ger, Springer, 2012.
29. E. M. Carnicom, W. Xie, T. Klimczuk, J. Lin, K. Górnicka, Z. Sobczak, N. P. Ong and R. J. Cava, TaRh2B2 and NbRh2B2: Superconductors with a chiral noncentrosymmetric crystal structure, Sci. Adv., 2018, 4, eaar7969.
30. M. Smidman, M. B. Salamon, H. Q. Yuan and D. F. Agterberg, Superconductivity and spin–orbit coupling in non-centrosymmetric materials: a review, Rep. Prog. Phys., 2017, 80, 036501.
31. F. Kneidinger, E. Bauer, L. Zeiringer, P. Rogl, C. Blaas-Schenner, D. Reith and R. Podloucky, Superconductivity in non-centrosymmetric materials, Phys. C, 2015, 514, 388–398.
32. P. Kaiser and W. Jeitschko, The Rare Earth Silicon Phosphides LnSi₂P₆(Ln= La, Ce, Pr, and Nd), J. Solid State Chem., 1996, 124, 346–352.
33. G. Akopov, J. Mark, G. Viswanathan, S. J. Lee, B. C. McBride, J. Won, F. A. Perras, A. L. Paterson, B. Yuan, S. Sen, A. N. Adeyemi, F. Zhang, C. Z. Wang, K. M. Ho, G. J. Miller and K. Kovnir, Third time's the charm: intricate non-centrosymmetric polymorphism in LnSiP₃ (Ln = La and Ce) induced by distortions of phosphorus square layers, Dalton Trans., 2021, 50(19), 6463–6476.
34. G. Akopov, G. Viswanathan and K. Kovnir, Synthesis, Crystal and Electronic Structure of La₂SiP₄, Z. Anorg. Allg. Chem., 2021, 647, 91.
35. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002.
36. T. Liao, W. Xia, M. Sakurai, R. Wang, C. Zhang, H. Sun, K. M. Ho, C. Z. Wang and J. R. Chelikowsky, Magnetic iron cobalt silicides discovered using machine learning, Phys. Rev. Mater., 2023, 7, 034410.
37. C. Zhang, L. Tang, Y. Sun, K. M. Ho, R. M. Wentzcovitch and C. Z. Wang, Deep machine learning potential for atomistic simulation of Fe-Si-O systems under Earth's outer core conditions, Phys. Rev. Mater., 2022, 6, 063802.
38. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994, 50, 17953–17979.
39. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
40. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169–11186.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13, 5188.
43. A. Togo and I. Tanaka, First Principles Phonon Calculations in Materials Science, Scr. Mater., 2015, 108, 1–5.
44. H. Wang, L. Zhang, J. Han and W. E, DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics, Comput. Phys. Commun., 2018, 228, 178–184.
45. S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519.
46. W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695–1697.
47. N. O. Yamamuro, T. Matsuo and H. Suga, Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II), J. Phys. Chem. Solids, 1990, 51, 1383–1395.
48. A. Planes and L. Mañosa, Vibrational properties of shape-memory alloys, Solid State Phys., 2001, 55, 159–267.
49. S. Vela, F. Mota, M. Deumal, R. Suizu, Y. Shuku, A. Mizuno, K. Awaga, M. Shiga, J. Novoa and J. R. Arino, The key role of vibrational entropy in the phase transitions of dithiazolyl-based bistable magnetic materials, Nat. Commun., 2014, 5, 4411.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta03771a

---