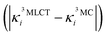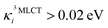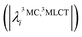Ultrafast ³MLCT quenching and vibrational coherence: excited-state dynamics of the first-discovered Fe(II)–carbene sensitiser resolved

Abstract

The application of N-heterocyclic carbene (NHC) ligands represents a groundbreaking advance towards environment-friendly light-harvesting complexes, yet, even the excited-state dynamics of the first-discovered Fe–NHC photosensitiser [Fe(bmip)₂]²⁺ (bmip = 2,6-bis(3-methyl-imidazole-1-ylidine)-pyridine) remain controversial. Using full-dimensional trajectory surface hopping (TSH) spin-vibronic dynamics simulations, we fully resolve and clarify the deactivation mechanism of [Fe(bmip)₂]²⁺. In agreement with the most recent fs-resolved X-ray experiments, we find that the excited-state population branches into triplet metal-to-ligand charge transfer (³MLCT) and metal-centered states (³MC) on early sub-ps timescales (∼200 fs). The ultrafast ³MLCT quenching by ³MC is driven by multidimensional excited-state ligand motion; it is this deactivation process that ultimately weakens the photosensitising efficiency of [Fe(bmip)₂]²⁺. Crucially, the preservation of vibrational coherence along the covalent Fe–C bonds (∼300 fs vibrational period) and the appearance of resulting coherent oscillations in various time-resolved experimental data unambiguously evidence the presence of the early sub-ps ³MC component.

---

1 Introduction

Transition metal complexes have received throughout the past decades grand attention due to their fascinating functionalities. Among the variety of functional transition-metal containing molecules, the class of light-harvesting complexes is especially intriguing, being a key component of technologies based on clean and green energy, such as solar energy conversion and photocatalysis.^1,2 In both transition-metal based solar cells and photocatalytic assemblies, the process is initiated by a light-induced electron transfer from the metal to the ligand in a photosensitiser, leading to a metal-to-ligand charge transfer (MLCT) excited state.

Extensive research efforts have continuously been devoted to developing efficient sensitisers absorbing in the visible range, with the most important aspects being the price and/or toxicity of the metal and the lifetime of the relevant MLCT states.³ An immense achievement was made a decade ago towards replacing photosensitisers based on precious metals, such as Ru and Ir, with Earth-abundant Fe complexes. This breakthrough was obtained owing to the utilisation of strongly σ-donating N-heterocyclic carbene (NHC) ligands,^4–6 which destabilise metal-centered (MC) excited states⁷ that otherwise rapidly, in ca. 100 fs, quench the MLCTs in common Fe complexes such as Fe(II) polypyridines.^8–12 Across the years, numerous Fe–NHC complexes have been synthesised and characterised with MLCT lifetimes ranging from 9 ps for the first-discovered Fe(II) sensitiser¹³ up to 528 ps;¹⁴ even higher excited-state lifetimes have been achieved for Fe(II) complexes containing amide donor atoms (2.0–2.7 ns)¹⁵ and for ligand-to-metal charge transfer (LMCT) states in an Fe(III)–carbene complex (2 ns).¹⁶

Despite the remarkable progress made in the coordination chemistry and photophysics of Fe–carbene complexes, consistent mechanistic understanding of the undergoing excited-state dynamics is often still lacking; this profound knowledge could in fact also be the key for real-life applications for solar cells and photocatalysts. Inconsistencies may typically be rooted in discrepancies in interpretations, stemming from the complexity of data acquired by time-resolved (pump–probe) experiments and/or approximations made in theoretical models for excited-state simulations. For Fe–NHCs, the scenario is best illustrated by the case of the very first discovered Fe–NHC photosensitiser, [Fe(bmip)₂]²⁺ (bmip = 2,6-bis(3-methyl-imidazole-1-ylidine)-pyridine), shown in Fig. 1, right. Utilising transient optical absorption spectroscopy (TOAS) with 485 nm pump excitation, Liu et al.¹³ identified two timescales, <100 fs and 9 ps, which they attributed to ¹MLCT → ³MLCT intersystem crossing (ISC) and ³MLCT → ³MC decay, respectively, see Fig. 1a. Our spin-vibronic¹⁷ quantum wavepacket dynamics simulations in highly-reduced nuclear configurational space (4D¹⁸ and 5D¹⁹) supported this assignment, identifying an ∼100 fs ¹MLCT → ³MLCT ISC process, and the ³MLCT → ³MC transition occurring on ps timescales (with time constants of ∼1 ps and ∼4 ps). More recently, utilising fs-resolved X-ray emission spectroscopy (XES) Kunnus et al.²⁰ identified that upon 400 nm excitation, the ³MLCT decay exhibits branching with an ∼110 fs ³MLCT → ³MC component (40%) and an ∼9 ps one (60%), the latter being identical to the ³MLCT lifetime determined by TOAS; we note that a similar branching was observed for a COOH-derivative of [Fe(bmip)₂]²⁺ by vibrational coherence spectroscopy.²¹ Furthermore, coherent oscillations with a 278 fs period were identified in the time-resolved XES and X-ray solution scattering (XSS) signals, assigned to breathing wavepacket motion in the ³MC state; such oscillations are also apparent in the TOAS data but were not analysed and in no other cases were observed by XES. Clearly, there is a significant difference in these experimental assignments, i.e., TOAS (485 nm excitation) vs. XES (400 nm excitation), as well as the XES data vs. theory in the appearance of the ∼100 fs ³MC component. This ultrafast ³MLCT quenching channel could in fact have a vital role as it challenges the general picture of Fe–carbenes possessing long-lived MLCT states and potentially weakens the complex's photosensitising ability. Crucially, using full-dimensional hybrid quantum-classical excited-state simulations, we herein clarify and explain all important aspects and ambiguities of [Fe(bmip)₂]²⁺, fully resolving its excited-state dynamics.

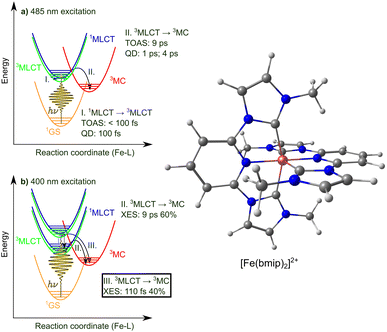Fig. 1 Left: Schematic illustration of the photophysics of [Fe(bmip)₂]²⁺ photoexcited at (a) 485 nm and (b) 400 nm, as concluded from the analysis of time-resolved experiments (TOAS¹³ and XES²⁰) and QD simulations.¹⁸ The focus of this work is (III), i.e., the sub-ps ³MLCT → ³MC process, which is highlighted in panel (b). Right: Molecular structure of the [Fe(bmip)₂]²⁺ complex.

2 Results and discussion

2.1 Theory overview

In the following, we address the ultrafast (sub-ps) quenching of ³MLCT states by ³MC, observed by fs-resolved XES. In fact, this is a remarkable result in light of the known photophysical behaviour of [Fe(bmip)₂]²⁺. This pathway was not considered in the TOAS assignment of Liu et al.¹³ in their original work reporting [Fe(bmip)₂]²⁺, and also challenges theoretical studies. For the theoretical modelling of this complex, first Fredin et al.⁷ calculated its potential energy surfaces (PESs) using density functional theory (DFT) and time-dependent DFT (TD-DFT). Subsequently, as mentioned in the Introduction, we performed quantum dynamics²² (QD) simulations^18,19 using TD-DFT PESs along 4 and 5 chosen normal modes, which were all identified to possess a dominant Fe–N/Fe–C stretching character. We stress that this means a necessary drastic reduction in nuclear degrees of freedom, albeit the modes were carefully chosen based on calculated ab initio data and symmetry considerations.²² All these results supported the existence of a long-lived ³MLCT state, without any sub-ps ³MC component. Herein, we employ an alternative approach based on trajectory surface hopping (TSH). Importantly, in contrast to QD, which delivers a solution to the time-dependent Schrödinger equation, TSH is not restricted by the number of nuclear degrees of freedom (DoF), as nuclear motion is described classically with electronic transitions approximated by stochastic hops. The dynamics thus occur on the full-dimensional PES and properties are calculated by averaging over numerous trajectories.

The electronic structure description of the PES has a decisive impact on the simulated dynamics. For transition metal complexes, in particular in the case of excited states, quantum chemistry faces immense challenges such as the description of electronic degeneracies, high density of states, and charge transfer excited states. Ideally, a balanced multiconfigurational treatment such as multiconfigurational second-order perturbation theory (CASPT2) would be the method of choice, however, computational feasibility issues as well as variance of the utilised active space for the nuclear configurational space explored by the dynamics severely limit its applicability. Herein, we use our efficient DFT/TD-DFT framework based on the B3LYP* exchange-correlation functional,²³ which we benchmarked extensively against experimental^24,25 and CASPT2 data.^12,26 We carry out TSH dynamics simulations both on DFT/TD-DFT PESs, according to a linear vibronic coupling (LVC) harmonic model²⁷ (which allows simulations up to several ps), and full on-the-fly ab initio PESs (in order to assess the validity of the LVC model for short sub-ps timescales). Details of the utilised methodology are described in the Methods section and the ESI.†

2.2 Ultrafast ³MLCT quenching: excited-state population dynamics

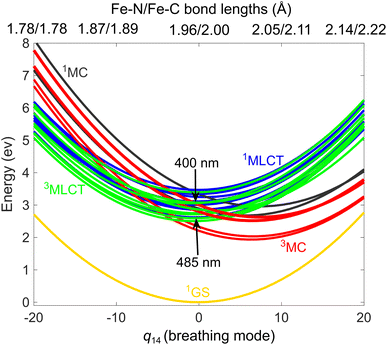
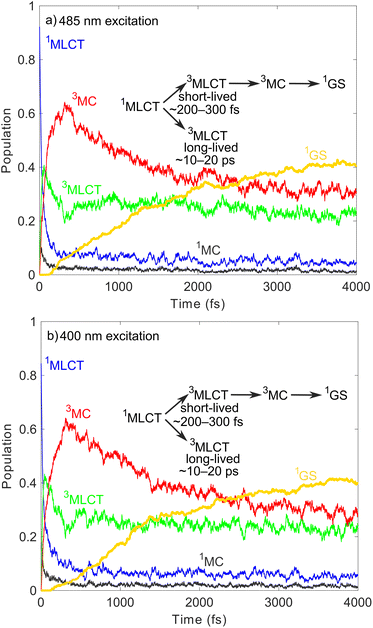
According to the two sets of experiments, i.e., TOAS¹³/XES,²⁰ we simulate the photoexcitation of [Fe(bmip)₂]²⁺ at 485/400 nm; this is illustrated in Fig. 2, in which we display the ground and excited-state diabatic PESs along the breathing mode ν₁₄,²⁸ known to be the dominant mode for dynamics involving MC states.^12,29,30 Our excited-state model includes 11 ¹MLCT, 3 ¹MC, 12 ³MLCT, and 6 ³MC states (we here note that the PESs and electronic couplings can vary for different components of a given manifold such as ¹MLCT, etc.) The excitation process is simulated by projection of the ground-state nuclear (Wigner) distribution to the excited-state PES using a 0.1 eV energy window centered at the 2.55/3.10 eV (485/400 nm) excitation energies (see ESI, Section S1,† for further details). As seen in Fig. 2, the two excitation schemes lead to different initial ¹MLCT states, with the lower one matching the initial ¹MLCT state of our previous QD simulations.^18,19

Fig. 2 Diabatic LVC-DFT/TD-DFT ground and excited-state potentials of [Fe(bmip)₂]²⁺ along the breathing normal mode ν₁₄, expressed in the dimensionless mass-frequency scaled normal mode coordinate q₁₄; the corresponding Fe–N/Fe–C bond lengths are also shown (top axis).

Fig. 3 shows the simulated electronic population dynamics for the lower-energy 485 nm (Fig. 3a) and higher-energy 400 nm (Fig. 3b) excitation. We note that we base all further analysis on the diabatic electronic representation, as it is suited for discussion of MLCT–MC dynamics, i.e., it maintains the electronic character at any nuclear geometry. It is clear from Fig. 3 that the pump energy does not have any considerable effect on the simulated dynamics. In both cases, i.e., 485/400 nm, the initial excited state has a dominant ¹MLCT character, which is in line with the matching excitation energies and considerable oscillator strengths calculated at the Franck–Condon (FC) equilibrium geometry (see ESI, Table S1†); excitation into ¹MC states only appears as a minor component. The ¹MLCT population almost promptly, in ∼50 fs, decays to ³MLCT via singlet-triplet ISC. We find that the ³MLCT population consists of two branches: a component converted into ³MC in ∼200–300 fs, which then decays on a ps timescale (in qualitative agreement with the 1.5 ps time constant determined by XES²⁰), repopulating the ground state (¹GS), and a second one with a ³MLCT population stable up to well beyond 4 ps. We recall that in our previous QD simulations,^18,19 we did observe the latter long-lived (∼few ps) ³MLCT component, but not the former sub-ps ³MLCT → ³MC pathway. Note that in principle, the ³MC states could also be populated directly from the ¹MLCTs,²¹ however, we find that this direct channel is negligible (due to its very low occurrence), as revealed by the inspection of individual trajectories (see ESI, Section S3†); this analysis also confirms that the ground state is dominantly repopulated from the ³MC states (90%) with a minor ³MLCT → ¹GS component (10%).

Fig. 3 Simulated diabatic TSH population dynamics of [Fe(bmip)₂]²⁺ excited at (a) 485 nm and (b) 400 nm obtained by averaging over 267 and 279 trajectories for (a) and (b), respectively. Also shown is a schematic of the excited-state mechanism and the approximate ³MLCT lifetimes, as obtained from the simulations.

Importantly, our simulated ³MLCT–³MC population dynamics are in excellent agreement with the XES experiment of Kunnus et al.²⁰ with the only discrepancy being in the branching ratio, as we identify the ³MC component as the one with larger weight, whereas in the XES experiment it is ³MLCT. However, the observed early sub-ps ³MC component is missing in the assignment of the TOAS experiment of Liu et al.,¹³ as well as in our previous QD studies.^18,19

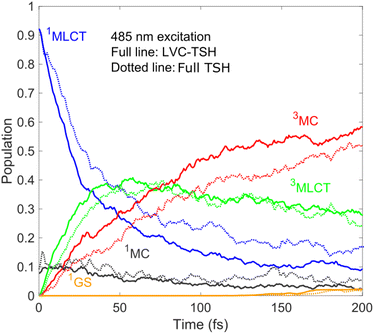
Based on the above, we thus identify a branching electronic relaxation mechanism with two components: (i) ¹MLCT → ³MLCT → ³MC → ¹GS with a short-lived ³MLCT component (∼200–300 fs), and (ii) ¹MLCT → ³MLCT with a long-lived ³MLCT intermediate (∼10 ps or longer lived). The population dynamics up to 200 fs and thus the early appearance of ³MC are supported by our simulation utilising the full (unconstrained) PESs and SOCs calculated on the fly, see Fig. 4; as is clear, the simulated LVC and full dynamics for 485 nm excitation show rather good agreement.

Fig. 4 Diabatic population dynamics of [Fe(bmip)₂]²⁺ excited at 485 nm simulated by LVC-TSH (full lines, 269 trajectories) and on-the-fly full TSH based on full unconstrained PESs (dotted lines, 100 trajectories).

In the following, we analyse the key ultrafast early ³MLCT → ³MC deactivation pathway focusing on nuclear motion and vibrational coherence.

2.3 Ultrafast ³MLCT quenching: nuclear motion

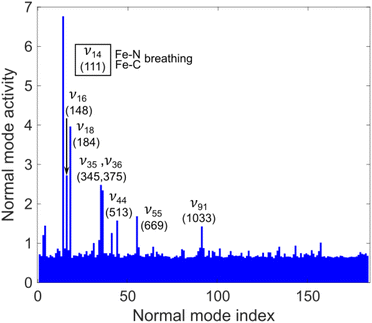
A key aspect of our simulated dynamics is that it unfold in full dimension, thus allowing us to analyse nuclear motion along all 183 modes of [Fe(bmip)₂]²⁺. Fig. 5 shows the mode activity of nuclear motion for the case of 400 nm excitation, calculated as a standard deviation of nuclear displacements projected onto dimensionless mass-frequency weighted normal mode coordinates, see ESI, Section S1.† As is clear from Fig. 5, nuclear motion during the excited-state dynamics of [Fe(bmip)₂]²⁺ is dominated by 5 modes: ν₁₄ (as anticipated, the most dominant one, i.e., we chose this breathing mode to visualize the PESs in Fig. 2), ν₁₆, ν₁₈, ν₃₅, and ν₃₆, which are all identified to possess Fe–N/Fe–C stretching characters; we note that this result is very similar for the case of 485 nm excitation, see ESI, Fig. S1.† Among these 5 modes, 4 are identical to those used in our previous QD simulations (instead of the fifth mode ν₃₅, we used mode ν₃₄, which appears here with smaller mode activity), supporting that we indeed chose the most dominant modes. However, the population dynamics obtained with QD based on these modes are very different from our present full-D TSH results, in particular regarding the appearance of the ∼200–300 fs ³MC component. Our interpretation for this discrepancy is as follows: all identified dominant Fe–N/Fe–C stretching modes are activated and operative in the ³MC states, due to occupation of an antibonding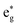 orbital, but for the ³MLCT → ³MC transition, nuclear motion in the ³MLCT states is in fact decisive. However, the MLCT potentials are typically thought to be parallel with respect to the one of the ground state, see Fig. 2; this was indeed the case in our QD simulations utilising Fe–N/Fe–C stretching modes only, with negligible nuclear motion in the MLCT states. This is the reason why the ³MC states were only found to be populated on longer (∼ps) timescales, as the ³MLCT–³MC energy gap near the ground state equilibrium geometry is significantly larger (∼hundreds of meV) than the coupling between the states.

Fig. 5 Normal mode activity of the [Fe(bmip)₂]²⁺ complex excited at 400 nm; in parentheses, the frequency of dominant modes is given (in cm⁻¹). All dominant modes possess a major Fe–N or Fe–C stretching character; ν₅₅ and ν₉₁ are deformation modes of the middle pyridine ring.

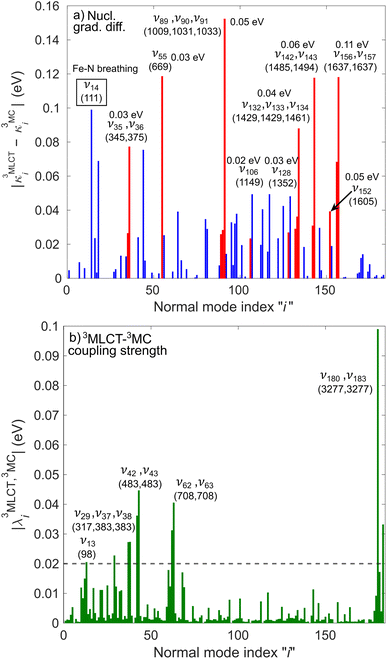
In the following, we show that nuclear motion in the lowest ³MLCT states is non negligible and is in fact the key to the ultrafast ³MLCT quenching mechanism by ³MC states. Nuclear motion and thus excited-state dynamics are dictated by the nuclear gradient of the potential energy for the excited states. The ³MLCT → ³MC dynamics are governed by the difference of ³MLCT–³MC nuclear gradients that mediates the ³MLCT–³MC energy gap. For simplicity, we here analyse the lowest out of the numerous triplet states: Fig. 6 shows the largest differences in nuclear gradients at the FC geometry between the lowest four ³MLCT and three ³MC states; we note that a similar approach to analyse vibronic effects was reported in ref. 22. We here focus on nuclear motion in the ³MLCT states and its effect on the ³MLCT–³MC dynamics, and therefore, in Fig. 6a, we highlight in red the most significant absolute gradient differences (above 0.02 eV; note that all nuclear gradients are given for unit nuclear displacement expressed in dimensionless normal mode coordinates) for which the ³MLCT gradient is also significant (at least 0.02 eV). As seen in Fig. 6a (red bars), excited-state ³MLCT nuclear motion will occur along several modes. Importantly, all these modes, with the exception of ν₃₅ and ν₃₆, will reduce the ³MLCT–³MC energy gap (∼0.16–0.39 eV for the analysed 4 ³MLCT and 3 ³MC states, see ESI, Table S1†), as movement from the FC region towards the ³MLCT minimum for these modes raises the ³MC energy (for ν₃₅ and ν₃₆, the opposite effect is observed, i.e., the ³MLCT–³MC gap slightly increases upon ³MLCT geometry relaxation). All 13 identified modes possess dominant ligand ring deformation and/or internal ligand bending character, in accordance with nuclear motion triggered by MLCT excitation (for animation of the modes, see the ESI†). Furthermore, we identified 10 additional modes which are the most important to couple the ³MLCT–³MC states (with the absolute value of the off-diagonal coupling constant being larger than 0.02 eV, see Fig. 6b); 8 of these, ν₁₃, ν₂₉, ν₄₂, ν₄₃, ν₆₂, ν₆₃, ν₁₈₀, and ν₁₈₃ have a dominant ligand character (out-of-plane twisting, out-of-plane deformation of the middle pyridine ring, C–H stretching), and the remaining two, ν₃₇ and ν₃₈ are characterised by off-center movement of the central Fe atom and bending modes of the ligand rings.

Fig. 6 Analysis of vibronic effects for the lowest four ³MLCT and three ³MC states of [Fe(bmip)₂]²⁺ at the FC geometry. (a) Largest absolute difference of nuclear gradients for all normal modes. For each mode, the ³MLCT–³MC component leading to the largest absolute difference is selected. Absolute differences above 0.02 eV originating from a significant value are highlighted in red. The numbers in eV next to mode labels are the absolute values of the largest ³MLCT gradient components. (b) ³MLCT–³MC coupling strengths for all normal modes. For each mode, the ³MLCT–³MC component leading to the largest coupling strength is selected. In parentheses, the frequency of the most important modes is given (in cm⁻¹, for both panels).

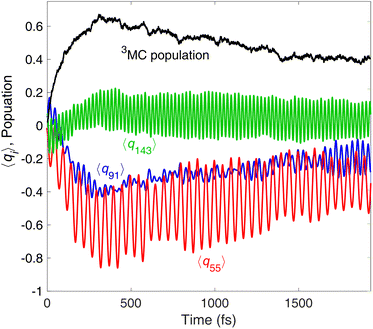
The above analysis clearly demonstrates that in contrast to the general discussion scheme of excited-state transition metal complexes, the ³MLCT PESs of [Fe(bmip)₂]²⁺ are displaced from the ground-state potential along several modes (i.e., the 13 modes identified above by the magnitude of ³MLCT nuclear gradient, see Fig. 6a). All of these modes possess a dominant ligand character, which will be activated by electronic MLCT excitation. As seen above, several of these activated modes should be capable of facilitating the ³MLCT → ³MC conversion either by reducing the ³MLCT–³MC energy gap or by accounting for the ³MLCT–³MC coupling. Equipped with these insights, we now explicitly analyse the interplay of nuclear and ³MLCT–³MC electronic population dynamics. Fig. 7 shows the average trajectory along three out of the above identified ligand modes, as well as the ³MC population, for the simulation with 400 nm excitation. The three modes, selected by the ³MLCT and ³MC nuclear gradients (see Fig. 6a), are ν₅₅ and ν₉₁, which are deformation modes of the middle pyridine rings with symmetric stretching/compression of the Fe–N bonds, and ν₁₄₃, a more complex mode involving deformation of all ligand rings as well as C–H wagging motion of the methyl groups. As seen in Fig. 7, significant vibrational dynamics occur along all three modes during the initial 0–300 fs period, with the mean displacement along the selected modes continuously shifting towards a structure distorted from the initial equilibrium geometry 〈q_i〉 = 0. Crucially, these structural dynamics correlate excellently with the initial ³MC population increase (Fig. 7, black curve), signalling the role of excited-state ligand motion in the sub-ps ³MLCT → ³MC deactivation. We here recall that nuclear motion and electronic coupling can vary for different components of the ³MLCT and ³MC manifolds. Therefore, for certain components and initial conditions, no early ³MLCT → ³MC transition occurs (because, e.g., the ³MLCT ligand motion is not strong enough to significantly decrease the ³MLCT–³MC energy gap), which is the reason for the branching observed in Fig. 3 (i.e., sub-ps ³MLCT → ³MC transition vs. long-lived ³MLCT).

Fig. 7 Average trajectories 〈q₅₅〉 (red, pyridine ring deformation), 〈q₉₁〉 (blue, pyridine ring deformation), and 〈q₁₄₃〉 (green, internal ligand bending/wagging) of [Fe(bmip)₂]²⁺ corresponding to three selected ligand modes, as obtained from the simulation with 400 nm excitation. Also shown are the population dynamics of the ³MC state (black).

2.4 Vibrational coherence

Importantly, our results are consistent with the time-resolved XES experiment of Kunnus et al.,²⁰ in particular supporting the branching of the excited-state population into ³MLCT and ³MC on early sub-ps timescales. As TOAS, in contrast to XES, is not directly sensitive to the electronic state, it is reasonable to expect that the <100 fs features of the TOAS data should in fact also contain a ³MLCT → ³MC component (although was assigned previously¹³ solely to ¹MLCT → ³MLCT). By analysis of coherent oscillations in the Fe–N/Fe–C bond lengths, we below show that this interpretation should indeed be correct, evidencing that the branching does occur.

Both the XES and XSS data for [Fe(bmip)₂]²⁺ photoexcited at 400 nm (ref. 20) show oscillations with the same period of 278 fs and an exponential damping time constant of 500 fs. The XSS oscillations clearly identify coherent vibrational motion along the Fe–N/Fe–C stretching nuclear coordinate. Interestingly, the breathing vibration is also reflected in the oscillatory XES signal;³¹ based on the XES data, the coherent vibrations were assigned to the ³MC states. Fig. 8 displays the nuclear dynamics averaged over all trajectories (400 nm excitation case) along the Fe–N and Fe–C bonds, as well as projected onto the breathing normal mode ν₁₄. In agreement with the XES/XSS experiments and their assignments, in our simulations, we observe coherent oscillations along the breathing mode with a period of ∼300 fs, which is clear in the Fe–C, but less in the Fe–N bond lengths (in the latter, the oscillations are dominated by faster components). Metal–ligand bonding and covalency has recently been proposed to be a key factor in rationalising the remarkable sensitivity of core-to-core XES to structural changes.^20,32 Namely, the Fe–ligand interaction modulates the screening of the relevant core holes (e.g., 1s and 2p, for Kα); as this modulation varies with the Fe–ligand distance, the structural dynamics will be reflected in the time-dependent XES signal. Our results also indicate the importance of covalency, as we clearly observe the coherent oscillations with a period reasonably matching the experimental one for the Fe–C bonds, which are significantly more covalent than the Fe–N. We note that (i) the coherent oscillations are very similar for the case of 485 nm excitation (see ESI, Fig. S6†), and (ii) damping (decoherence) of our oscillations is slower than the experimental one; we attribute this discrepancy to the underestimation of intermode interactions and the absence of solvent in our model. It is important to stress, however, that the appearance of vibrational coherence and the period of oscillations are in good agreement with the XES/XSS experiments, and decoherence does occur, even if it is slower than observed experimentally.

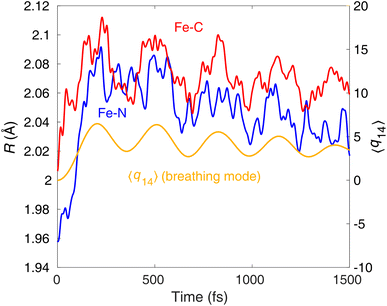Fig. 8 Average trajectories of [Fe(bmip)₂]²⁺ along the Fe–N and Fe–C bond, as well as the breathing normal mode ν₁₄, as obtained from the simulation with 400 nm excitation.

Finally, we analyse the origin of the observed vibrational coherence and the case of the TOAS experiment with 485 nm excitation. The vibrational dynamics along the Fe–N/Fe–C bonds are triggered by electronic structure changes in the ³MC states, dominated by the population of an antibonding 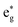orbital (d_x²–y² or d_z² combined with the corresponding ligand orbitals). Any considerable contribution of MLCT states to such dynamics along the breathing mode (see Fig. 8) is ruled out, since an MLCT excitation does not lead to significant changes in the Fe–N/Fe–C bond lengths (i.e., the case of the nested ground-state and ³MLCT oscillators,²¹ see also Fig. 2). As seen in Fig. 3, the ³MC population rises fast, within an oscillation period of the breathing mode (∼300 fs), and hence vibrational coherence is preserved, as evidenced by the observation of coherent oscillations (Fig. 8). Therefore, the appearance of coherent oscillations, with a period matching the vibrational period of the breathing mode, can be used as a fingerprint for any significant ³MC component. Importantly, the TOAS data also contain oscillations with a rather similar period to those obtained by XES and XSS (see ref. 13, ESI, Fig. S12†), appearing already at ∼300 fs. Given the connection between the ³MC population rise and the coherent oscillations, this clearly means that the ³MC states have to be populated already at early times (∼100–300 fs), otherwise the coherent oscillations could not have been observed. All this agrees excellently with our simulated dynamics, unambiguously evidencing the existence of the observed early sub-ps ³MC component and thus the branching mechanism of the excited-state population into ³MLCT and ³MC.

3 Conclusions

In this work, we resolved the excited-state dynamics of the first-discovered photosensitiser, [Fe(bmip)₂]²⁺, using full-dimensional TSH dynamics simulations. In agreement with the recent XES experiment of Kunnus et al.,²⁰ we observe branching of the excited-state population into ³MLCT and ³MC, on early sub-ps timescales. According to the branching, we identify two main relaxation pathways: (i) ¹MLCT → ³MLCT → ³MC → ¹GS with a short-lived ³MLCT component (∼200–300 fs), and (ii) ¹MLCT → ³MLCT with a long-lived ³MLCT intermediate (∼10 ps or longer lived). Similarly to our recent work¹² on the singlet-triplet-quintet dynamics of the [Fe(terpy)₂]² complex (terpy = 2,2′:6′,2′′-terpyridine), we obtain convincing agreement with experimentally resolved dynamics, which justifies the accuracy of the utilised B3LYP* DFT/TD-DFT framework for MLCT–MC energetics and dynamics. Moreover, the consistency achieved for the initial dynamics using LVC and unconstrained full ab initio PESs further validates our results.

Based on the analysis of vibronic interactions and nuclear dynamics, we found that the early transition into ³MC states is driven by ligand motion triggered by the MLCT electronic excitation; this challenges the common photophysical 1D picture with the MLCT surfaces parallel to the one of the ground state. We explicitly showed that the early ³MC population increase occurs concurrently with nuclear dynamics along ligand modes, such as deformation of the middle pyridine ring and internal ligand bending/wagging, which reduce the ³MLCT–³MC energy gap and thus facilitate the electronic transition. We explained that this mechanism does not occur for all trajectories, depending on different states of the ³MLCT/³MC manifolds and initial conditions, giving rise to the component of the branching with a long-lived ³MLCT state. As the early sub-ps ³MLCT quenching by ³MC is a highly multidimensional process, it is not likely that this channel can be suppressed by blocking the relevant modes, as there are too many of them; a more efficient strategy would be to further increase the ligand field strength to even more destabilise the ³MC states. We note that in line with this interpretation, in the absence of ligand motion such as the case of the previous QD simulations,^18,19 the early ³MC is completely missing.

Finally, we analysed coherent oscillations along the Fe–N/Fe–C bonds in the ³MC states. We emphasise that these oscillations can only be observed, i.e., vibrational coherence is preserved, if the ³MC population rises fast enough with respect to the period of the oscillations (∼300 fs). As both the more recent XES/XSS data by Kunnus et al.²⁰ and the TOAS data from the original work on [Fe(bmip)₂]²⁺ by Liu et al.¹³ contain the same oscillatory component, appearing already at early times, this means that the ³MC states had to be populated already at early sub-ps timescales; this thus clarifies the branching mechanism. We attribute the lack of the early ³MC component in the TOAS assignment to the lower sensitivity of TOAS to the electronic character. Our simulated coherent oscillations are in good agreement with those extracted from the time-resolved experiments, even if the damping (decoherence) is underestimated. We showed that the coherent oscillations with a period of ∼300 fs stem mostly from nuclear dynamics of the Fe–C bonds, which underlines the effect of covalency that has been identified as a key factor in the sensitivity of core-to-core XES to structural dynamics.^20,32

4 Methods

The dynamics were simulated by full-dimensional trajectory surface hopping (TSH) based on Tully's fewest switches³³ a three-step propagator technique,³⁴ and local diabatisation,^35,36 as implemented in the SHARC2.1 software.^37,38 Our model includes the lowest 15 singlet and 18 triplet electronic states of [Fe(bmip)₂]²⁺. The B3LYP*/TZVP DFT/TD-DFT calculations for the LVC and full (on-the-fly) PESs were carried out using the ORCA5.0 quantum chemistry program package.^39,40 Further details of the utilised methodology are given in the ESI.†

Data availability

Numerical LVC parameters are provided in the ESI† files. Further data are available from the corresponding author upon reasonable request.

Author contributions

Mátyás Pápai: conceptualisation, methodology, validation, formal analysis, investigation, data curation, writing – original draft, visualisation, project administration, funding acquisition. Tamás Rozgonyi: writing – review & editing. György Vankó: conceptualisation, writing – review & editing, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research leading to the presented results has received funding from the Hungarian National Research, Development and Innovation Fund under grant numbers NKFIH PD 134976 and TKP2021-NVA-04. MP acknowledges support from the János Bolyai Scholarship of the Hungarian Academy of Sciences. Guest access to the central HPC cluster of the Technical University of Denmark is acknowledged.⁴¹

Notes and references

1. H. B. Gray and A. W. Maverick, Science, 1981, 214, 1201–1205.
2. X. Zhang, Y. Hou, X. Xiao, X. Chen, M. Hu, X. Geng, Z. Wang and J. Zhao, Coord. Chem. Rev., 2020, 417, 213371.
3. N. Sinha and O. S. Wenger, J. Am. Chem. Soc., 2023, 145, 4903–4920.
4. Y. Liu, P. Persson, V. Sundström and K. Wärnmark, Acc. Chem. Res., 2016, 49, 1477–1485.
5. L. Lindh, P. Chábera, N. W. Rosemann, J. Uhlig, K. Wärnmark, A. Yartsev, V. Sundström and P. Persson, Catalysts, 2020, 10, 315.
6. P. Dierks, Y. Vukadinovica and M. Bauer, Inorg. Chem. Front., 2022, 9, 206–220.
7. L. A. Fredin, M. Pápai, E. Rozsályi, G. Vankó, K. Wärnmark, V. Sundström and P. Persson, J. Phys. Chem. Lett., 2014, 5, 2066–2071.
8. C. Brady, J. J. McGarvey, J. K. McCusker, H. Toftlund and D. N. Hendrickson, in Time-Resolved Relaxation Studies of Spin Crossover Systems in Solution, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 1–22.
9. W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. Hadt, R. Hartsock, T. Kroll, K. Kjær, K. Kubiček, H. Lemke, H. Liang, D. Meyer, M. Nielsen, C. Purser, J. Robinson, E. Solomon, Z. Sun, D. Sokaras, T. Van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. Gaffney, Nature, 2014, 509, 345–348.
10. G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633.
11. K. S. Kjær, T. B. Van Driel, T. C. B. Harlang, K. Kunnus, E. Biasin, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, A. O. Dohn, M. I. Pápai, K. B. Møller, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, M. Jarenmark, J. Uhlig, V. Sundström, K. Wärnmark, P. Persson, Z. Németh, D. S. Szemes, É. Bajnóczi, G. Vankó, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, S. E. Canton, H. T. Lemke and K. J. Gaffney, Chem. Sci., 2019, 10, 5749–5760.
12. T. Rozgonyi, G. Vankó and M. Pápai, Commun. Chem., 2023, 6, 7.
13. Y. Liu, T. Harlang, S. E. Canton, P. Chábera, K. Suárez-Alcántara, A. Fleckhaus, D. A. Vithanage, E. Göransson, A. Corani, R. Lomoth, V. Sundström and K. Wärnmark, Chem. Commun., 2013, 49, 6412–6414.
14. P. Chábera, K. S. Kjær, O. Prakash, A. Honarfar, Y. Liu, L. A. Fredin, T. C. B. Harlang, S. Lidin, J. Uhlig, V. Sundström, R. Lomoth, P. Persson and K. Wärnmark, J. Phys. Chem. Lett., 2018, 9, 459–463.
15. J. D. Braun, I. B. Lozada, C. Kolodziej, C. Burda, K. M. E. Newman, J. van Lierop, R. L. Davis and D. E. Herbert, Nat. Chem., 2019, 11, 1144–1150.
16. K. S. Kjær, N. Kaul, O. Prakash, P. Chábera, N. W. Rosemann, A. Honarfar, O. Gordivska, L. A. Fredin, K.-E. Bergquist, L. Häggström, T. Ericsson, L. Lindh, A. Yartsev, S. Styring, P. Huang, J. Uhlig, J. Bendix, D. Strand, V. Sundström, P. Persson, R. Lomoth and K. Wärnmark, Science, 2019, 363, 249–253.
17. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025.
18. M. Pápai, G. Vankó, T. Rozgonyi and T. J. Penfold, J. Phys. Chem. Lett., 2016, 7, 2009–2014.
19. M. Pápai, T. Rozgonyi, T. J. Penfold, M. M. Nielsen and K. B. Møller, J. Chem. Phys., 2019, 151, 104307.
20. K. Kunnus, M. Vacher, T. C. B. Harlang, K. S. Kjær, K. Haldrup, E. Biasin, T. B. van Driel, M. Pápai, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, E. Källman, M. Delcey, R. W. Hartsock, M. E. Reinhard, S. Koroidov, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, L. Sandberg, Z. Németh, D. S. Szemes, É. Bajnóczi, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, H. T. Lemke, S. E. Canton, K. B. Møller, M. M. Nielsen, G. Vankó, K. Wärnmark, V. Sundström, P. Persson, M. Lundberg, J. Uhlig and K. J. Gaffney, Nat. Commun., 2020, 11, 634.
21. F. Hainer, N. Alagna, A. Reddy Marri, T. J. Penfold, P. C. Gros, S. Haacke and T. Buckup, J. Phys. Chem. Lett., 2021, 12, 8560–8565.
22. C. Daniel, Phys. Chem. Chem. Phys., 2021, 23, 43–58.
23. M. Reiher, O. Salomon and B. Artur Hess, Theor. Chem. Acc., 2001, 107, 48–55.
24. D. Sárosiné Szemes, T. Keszthelyi, M. Papp, L. Varga and G. Vankó, Chem. Commun., 2020, 56, 11831–11834.
25. M. Papp, T. Keszthelyi, A. Vancza, É. G. BajnÓczi, É. Kováts, Z. Németh, C. Bogdán, G. Bazsó, T. Rozgonyi and G. Vankó, Inorg. Chem., 2023, 62, 6397–6410.
26. M. Pápai, G. Vankó, C. de Graaf and T. Rozgonyi, J. Chem. Theory Comput., 2013, 9, 509–519.
27. H. Köppel, W. Domcke and L. S. Cederbaum, in Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation, John Wiley & Sons, Ltd, 1984, pp. 59–246.
28. Note that in our previous QD studies,^18,19 this mode was denoted as ν₆.
29. A. Hauser, C. Enachescu, M. L. Daku, A. Vargas and N. Amstutz, Coord. Chem. Rev., 2006, 250, 1642–1652.
30. C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Chem.–Eur. J., 2013, 19, 17541–17551.
31. Note that core-to-core XES for transition metal complexes is primarily sensitive to the spin of the transition metal atom. So far, the case of [Fe(bmip)₂]²⁺ is the only one for which the structural dynamics are reflected in the core-to-core XES signal.²⁰.
32. M. Vacher, K. Kunnus, M. G. Delcey, K. J. Gaffney and M. Lundberg, Struct. Dyn., 2020, 7, 044102.
33. J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071.
34. S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231.
35. G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615.
36. F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico and H. Lischka, J. Chem. Phys., 2012, 137, 22A514.
37. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
38. S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
39. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
40. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
41. DTU Computing Center, DTU Computing Center Resources, 2022,  DOI:10.48714/DTU.HPC.0001.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the utilised methodology, linear vibronic coupling (LVC) parameters, supplementary results for population dynamics and Fe–N/Fe–C bond oscillations, animation of key normal modes. See DOI: https://doi.org/10.1039/d3ta05985e

---