A new avenue to relaxor-like ferroelectric behaviour found by probing the structure and dynamics of [NH₃NH₂]Mg(HCO₂)₃

Abstract

The field of relaxor ferroelectrics has long been dominated by ceramic oxide materials exhibiting large polarisations with temperature and frequency dependence. Intriguingly, the dense metal–organic framework (MOF) [NH₃NH₂]Mg(HCO₂)₃ was reported as one of the first coordination frameworks to exhibit relaxor-like properties. This work clarifies the origin of these relaxor-like properties through re-examining its unusual phase transition using neutron single crystal diffraction, along with solid-state NMR, quasielastic neutron scattering and dielectric spectroscopy studies. This reveals that the phase transition is caused by the partial reorientation of NH₃NH₂ within the pores of the framework, from lying in the planes of the channel at lower temperatures to along the channel direction above the transition temperature. The transition occurs via a dynamic process such that the NH₃NH₂ cations can slowly interconvert between parallel and perpendicular orientations, with an estimated activation energy of 50 kJ mol⁻¹. Furthermore these studies are consistent with proton hopping between the hydrazinium cations oriented along the channel direction via a proton site intermediate. This study suggests the ferroelectric properties of [NH₃NH₂]Mg(HCO₂)₃ are likely driven by a hydrogen bonding mechanism. The relaxor behaviour is proposed to be the result of polar regions, which likely fluctuate due to increased cation dynamics at high temperature. The combination of cation reorientation and proton hopping fully describes this material's relaxor-like behaviour, suggesting a route to the future design of non-oxide-based relaxor ferroelectrics.

---

Introduction

Ferroelectric materials exhibit a spontaneous polarisation that can be reversed by an applied electrical field and have wide-reaching applications in the energy sector as capacitors and data storage.^1,2 These materials can also be used as piezoelectrics, in which polarisation is achieved through the application of mechanical force, or vice versa, allowing for use in energy harvesting or as sensors and actuators for high-precision motors and sonar or ultrasound sensing.^3–7 These systems crystallise in non-centrosymmetric structures and must belong to polar point groups to have the switchable polarisation characteristic of ferroelectric materials.^8,9 One of the earliest discovered and most widely utilised classes of ferroelectrics are perovskites, such as BaTiO₃,¹⁰ whose properties stem from the B site titanium cation, which has a degree of mobility within the BaO₃ cage.¹¹ Rochelle's salt was one of the first reported ferroelectric materials, but it was not until decades later, following a neutron diffraction study, that the origin of the ferroelectricity was recognised as being hydrogen bond driven;^12,13 such ferroelectricity derives from the displacement of the hydrogen atom within the intermolecular bond, highlighting that ferroelectric properties are not restricted to inorganic perovskites.^14–16

Relaxor ferroelectrics are a subclass of ferroelectric materials used in capacitors for energy storage and piezoelectric sensing, particularly where high polarisation over a broader range of temperatures is needed. Relaxors have broad and typically large maxima in the temperature-dependent dielectric permittivity, and both the maximum permittivity and the temperature at which it occurs are frequency-dependent.¹⁷ In such materials, conventionally, no symmetry breaking on a macroscopic scale is observed. The origins of these unusual behaviours are not entirely understood, although these are typically explained by the random field model, which links relaxor properties to the existence of polar nanoregions, which are commonly thought to be nano-scale polar domains within a non-polar average structure.^18–20 The vast majority of relaxor ferroelectrics are perovskite oxides and, in these materials relaxor behaviour arises from doping leading to static disorder of their A and/or B site cations; this introduces chemical inhomogeneity into the materials enabling the emergence of polar nanoregions.^18–20 Relaxor perovskites usually contain Pb, but there has been a recent resurgence of interest in relaxors due to the discovery of lead-free systems, such as (Bi_1/2Na_1/2)TiO₃, although these typically remain reliant on using heavy elements.^20,21

Recently there have been reports of inorganic–organic hybrid perovskites and closely related phases with dielectric properties similar to relaxor ferroelectrics.^22–29 Hybrid perovskites have attracted attention for their photovoltaic, ferroelectric, barocaloric and magnetic properties.^30–35 Such materials have the typical formula of ABX₃ of purely inorganic perovskites, but have organic molecular A-site cations or X-site anions; this enables great diversity in chemical composition because of the variety of molecular building blocks that can be incorporated. This leads to perovskite-related structures and non-perovskite chiral cubic and hexagonal structures, many of which have dielectric anomalies caused by hydrogen bond driven ordering of their A-site cations.^36–39

The chiral dense MOF [NH₃NH₂]Mg(HCO₂)₃ was reported to have relaxor-like dielectric properties in 2014 by Chen et al.²⁴ This material has a chiral hexagonal structure with the six co-ordinated magnesium octahedra linked by bidentate formate bridges in the anti–anti bridging mode, resulting in a honeycomb-like arrangement of hexagonal channels in which the A-site NH₃NH₂⁺ cations reside. The relaxor behaviour was attributed to an order–disorder transition at 348 K driven by the displacement of NH₃NH₂⁺ cations, with the maxima occurring near this temperature. Unusually the framework adopts an anti-ferroelectric orthorhombic P2₁2₁2₁ at lower temperatures and a polar P6₃ hexagonal structure at higher temperatures. [NH₃NH₂]Mg(HCO₂)₃ is also unusual compared to the vast majority of relaxor ferroelectrics since it lacks any doping-induced disorder, although there are a small number of organic relaxors where this originates from intrinsic defects or molecular reorientation.^17,40–42

This work aims to establish the origin of relaxor-like properties in [NH₃NH₂]Mg(HCO₂)₃. To do so, we have reanalysed its phase transition through a neutron single crystal diffraction study of the structure, alongside solid-state NMR and quasielastic neutron scattering (QENS) studies of the dynamics and local environments. In doing so, we observe the reorientation of NH₃NH₂⁺ cations during a complex phase transition (PT), leading to a high temperature phase with populations of NH₃NH₂⁺ cations that adopt two different orientations rather than a simple order–disorder phase transition as previously proposed.²⁴ There are also indications of proton migration between cations aligned parallel to the channels that could be polarised by an electric field, and that the two orientations slowly interconvert in the high temperature phase. This leads to the interpretation of the relaxor-like properties of (NH₃NH₂)Mg(HCO₂)₃ emerging from these two populations of polar and non-polar arrangements of molecular cations. A reexamination of the dielectric properties of [NH₃NH₂]Mg(HCO₂)₃ reveals three distinct dielectric relaxations at temperatures that are consistent with the diffraction and spectroscopic studies.

Results and discussion

Crystallography

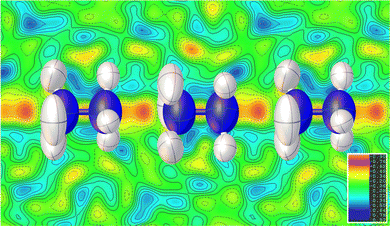
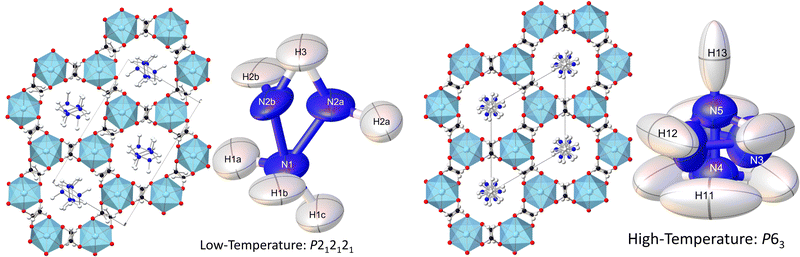
Consistent with the previous work of Chen et al.,²⁴ our initial X-ray study modelled the low-temperature phase of the framework in the orthorhombic P2₁2₁2₁ space group, which is a Sohncke-type group that allows chirality in the Mg(HCO₂)₃ anionic framework. The cations occupy the pores perpendicularly and are stacked antiparallel along the channel direction. Shown in Fig. 1, this overall arrangement is confirmed by single crystal neutron diffraction (SCND) models of the low temperature phase, but additional disorder is revealed by these experiments (see Table S1, ESI† for crystallographic details). This involves the NH₂ group, with the nitrogen atom and one of the hydrogen atoms split across two positions with a single wholly occupied hydrogen atom common between the two; nitrogen atom fractional occupancies were constrained throughout to retain nominal stoichiometry, with hydrogen atom occupancies fixed to that of their associated nitrogen atoms. Refined occupancies of the nitrogen atoms are given in Table S2 (ESI†). The shift in the atomic positions of the NH₃ end is subtle and so modelled as part of the atomic displacement parameters (ADPs). As the temperature increases within the low temperature phase, the N2a and N2b disordered site occupancies tend to a 2 : 1 ratio within experimental uncertainty (see Table S2, ESI†). The cations form strong hydrogen bonds with the formates of the framework, and there is also hydrogen bonding between the NH₃ group and adjacent NH₂ group, these interactions are shown in Fig. S1 (ESI†) and summarised by fingerprint plots⁴³ in Fig. S2 (ESI†). The most significant distances of these interactions are H2b⋯O6 as 2.2(2) Å and H2a⋯O5 as 2.52(6) Å at 250 K, showing that the cation tends to one side of the pore. There also appears to be a bifurcated hydrogen bond with the H3⋯O1/O4 distances being 2.22(6) Å and 2.15(5) Å, respectively. The hydrogen bonding between the cations is between H1b⋯N2a with a distance of 2.08(6) Å; further details can be found in Table S4 (ESI†). The three crystallographically distinct formate ions of the low temperature phase also appear disordered, with hydrogen atoms modelled as being split across two positions, each with a site occupancy fixed at 0.5.

Fig. 1 The crystal structure of [NH₃NH₂]Mg(HCO₂)₃ modelled from the single crystal neutron diffraction in both the orthorhombic low-temperature phase at 250 K and the hexagonal high-temperature phase at 400 K, with the cation disorder shown for clarity to the right of each structure. At high temperature N3 atoms lie in a plane perpendicular to the c-axis generated by the six-fold screw axis along which N4, N5 and H13 sit. The atom labelled N3 in the figure is at the equivalent general positions (x̄ +y, x̄, z).

Our findings for the higher temperature P6₃ crystal structure using neutron diffraction deviate considerably from the previous work of Chen et al.²⁴ with respect to the position of the hydrazinium cations. Their X-ray crystal structures described a single nitrogen position, subjected to the sixfold screw axis of the P6₃ hexagonal cell, which lies along the pore direction, resulting in a disordered cation perpendicular to the pore direction. Our SCND model retains a similar nitrogen position (N3) to that found by Chen et al.²⁴ Additionally, however, the model contains two further distinct nitrogen positions (N4 and N5) centred along the sixfold screw axis (see Fig. 1). These additional positions indicate that a population of cations have re-orientated along the pore direction in the high-temperature phase. The disordered nitrogen position associated with NH₃NH₂⁺ cations lying in the plane perpendicular to the channel direction persists up to 400 K, the maximum temperature explored in our study due to the decomposition of this material above 420 K.²⁴ The refined occupancies of the three nitrogen atom positions suggest there is no significant increase in the fraction of NH₃NH₂⁺ cations aligned along the pores with increasing temperature along the phase transition, settling at a 2 : 1 ratio of cations oriented perpendicular and parallel to the channel direction, respectively.

The substantial disorder of the NH₃NH₂⁺ cations in the high temperature phase prevents full modelling of all hydrogen atoms, see Fig. 1, particularly concerning those in the cations lying perpendicular to the plane that are 3-fold disordered cations. In total, three hydrogen sites were located via their expected strong negative scattering, which had their site occupancies constrained to maintain the overall stoichiometry of the compound, reported in Table S3 (ESI†). The ADPs of these sites also accommodate any weak negative scattering from the disordered components. The first two of these sites can be associated with the NH₃NH₂⁺ cations oriented parallel to the channel direction, which due to the threefold disorder, both resemble partially occupied NH₃ groups. These hydrogen atoms are, however, also in chemically feasible positions to be bonded to the hydrazinium cations lying in the ab plane perpendicular to the channel direction. The third observable site is associated with a more diffuse negative scattering in the Fourier difference map between the cations, (see Fig. 2). This scattering was accommodated by adding a hydrogen site centred equidistant from the nitrogen atoms of neighbouring cations. The existence of the intermediate proton site between the NH₃NH₂⁺ parallel to the channel pores suggests there may be proton exchange between cations. This is consistent with the displacement parameter being elongated along the c-axis suggesting this proton is not well localised to a discrete site.

Fig. 2 Fourier difference map showing the experimentally observed nodes of negative scattering (red) between the modelled NH₂NH₃⁺ cation chains. The proton site between cations is omitted to display the residual negative scattering. The rest of the difference map shows the experimental background that exhibits a combination of low-intensity residual positive (blue-green) and negative (orange-yellow) scattering.

Although there is only one crystallographically distinct formate cation in the high temperature phase, similar hydrogen disorder is present with the hydrogen split across two positions of occupancy 0.5. The NMR below, shows this formate disorder to be dynamic in the high temperature phase in contrast to the static disorder of the low temperature phase. The cations retain short hydrogen bond distances with the oxygen atoms of the formate framework H11⋯O1 and H12⋯O2 at 1.89(8) Å and 2.26(10) Å, respectively; further details can be found in Table S5 (ESI†).⁴⁴ The fingerprint plots, Fig. S2 (ESI†), show that the hydrogen bonding in the high temperature phase is weaker than in the low temperature phase, but is more abundant.

The gradual convergence of occupancies in the low temperature phase with increasing temperature indicates the presence of an intermediate regime, during which the A-site cations are becoming progressively disordered before a portion rapidly re-orientates from perpendicular to parallel to the pore direction at the phase transition. To complement our understanding of the structure of these phases by understanding their dynamics, given the limited insights possible into the latter using diffraction methods, we explored this material with solid-state NMR and QENS.

Solid-state NMR

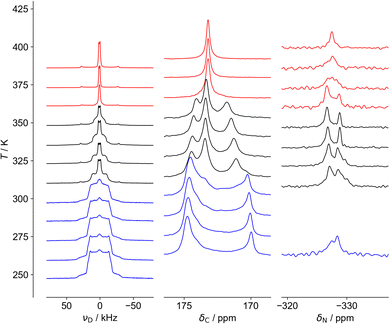
As shown in Fig. 3 and 4, three distinct regions are seen clearly in the ²H and ¹³C spectra and, to a lesser extent, the ¹⁵N spectra. These regions, also observed in ¹H linewidth data (cf.Fig. 5 below), correspond well to the behaviour observed in DSC,²⁴ in which weaker features are detected over an ∼40 K range before the stronger feature associated with the crystallographic phase transition. NMR suggests the symmetry change at 348 K is preceded by changes to the local cation environments, to which it is more sensitive than crystallography, revealing a more complex transition than is evident in average structure.

Fig. 3 NMR spectra as a function of temperature (baseline of each spectrum indicates sample temperature). Left: ²H spectra of [ND₃ND₂]Mg(HCO₂)₃. Centre: ¹³C spectra of [ND₃ND₂]Mg(HCO₂)₃. Right: ¹⁵N spectra of [NH₃NH₂]Mg(HCO₂)₃. The three distinct temperature regimes observed are highlighted using colour: (red) high temperature phase, (blue) low temperature phase, (black) intermediate regime.

Fig. 4 Fitting of representative ²H NMR spectra of [ND₃ND₂]Mg(HCO₂)₃ from low, intermediate and high temperature regions. (Left) experimental spectra (black) and overall fittings (red). (Right) Individual fitting components: (blue) high C_Q, (green) low C_Q. Additional components were required in some fittings: (purple) intermediate C_Q and (grey) small zero-frequency artefact.

Fig. 5 Static ¹H NMR linewidth of [NH₃NH₂]Mg(HCO₂)₃ as a function of temperature.

The ²H spectra are particularly sensitive to the dynamics of the cation, while the ¹³C spectra show significant changes to the host framework, as observed via the formate ion. As most clearly seen in the ¹³C spectra, the intermediate region contains features of the low and high temperature regions, consistent with a first-order transition, but there is a clear evolution of the low temperature structure towards the high temperature limit, i.e. the intermediate region is not a simple first-order transition involving separate domains of two materials. Another important feature of the ¹³C NMR results is that the low temperature spectra can only be explained in terms of significant static disorder; rather than consisting of a limited number of resonances corresponding to crystallographically distinct carbon sites, there is a continuous distribution of chemical shifts between 170 and 175 ppm, implying a distribution of local environments. This is consistent with the disorder of H positions of the formate ligand observed in the diffraction experiments being static, which creates a continuous distribution of local formate environments. In contrast, the ¹³C spectrum of the high temperature phase contains a single sharp resonance, corresponding to a highly homogeneous environment, and implying the disorder of the hydrogen atom of the formate ligand is extensively dynamically disordered.

The ¹⁵N spectra are more difficult to interpret due to the intrinsically poor NMR receptivity of ¹⁵N and the limited chemical shift range. There is no clear resolution of the –NH₃vs. –NH₂ moieties of hydrazinium in the low temperature phase. This strongly suggests that the developing peak at −327 ppm in the intermediate region is associated with a distinctly different cation population, presumably the more dynamic component observed in the ²H NMR. The most interesting feature is the distinctive “coalescence” of the two signals at ∼350 K, which would correspond to an exchange process interchanging the sites with a rate of about 200 Hz. This suggests that “perpendicular” and “parallel” orientations can slowly interconvert. This rate of exchange is slow; the frequency difference of the peaks is only about 150 Hz (∼3 ppm at 50.6 MHz) and so the exchange rates can only be on the kHz frequency scale at the highest temperatures measured. This is consistent with the ¹³C NMR spectra which cover a similarly narrow frequency range; although the disorder is “extensive”, rendering all C and N sites equivalent, some components are slow.

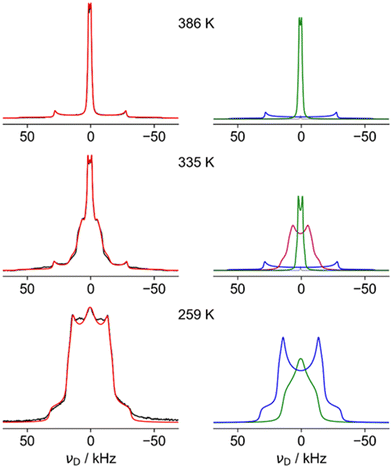
Fig. 4 shows fits of representative ²H NMR spectra from the three regions, with the fitting parameters summarised in Table S6 of the ESI.† The 259 K spectrum can be confidently fitted to a site with a quadrupole coupling, C_Q, of 43 kHz and a low asymmetry parameter, η (blue), but a second component with smaller C_Q and large η (green) is required to fit the overall shape. The higher C_Q value corresponds to deuterium sites in which the N–D vectors are undergoing symmetrical rotational diffusion about the N–N axis; the unaveraged quadrupole coupling is averaged by P₂(cos 70.5°) = −0.33. For an isolated N–D bond, this would lead to values of the order of 200 kHz × 0.33 ≈ 70 kHz. The significantly smaller measured value of 43 kHz is consistent with strongly hydrogen-bonded sites (see ref. 45 and references contained). The “green” spectrum can only be explained if the N–D is jumping between sites with different occupancies; as shown in Fig. S5 (ESI†), only a small imbalance in populations between the occupancy of the three possible positions of the ND₂ is required to generate an average ²H NMR spectrum with a high η value.

The 386 K spectrum of Fig. 4 also contains two distinct components, which can both be fitted to a single set of parameters (C_Q and η) describing a motionally averaged quadrupolar coupling tensor. These fitted parameters effectively probe the symmetry of the averaged tensor describing the electric field gradient (EFG) at the ²H nucleus. The higher C_Q component (blue) corresponds to an average tensor with a well-defined axial symmetry, e.g. resulting from rotational diffusion about a C_n axis with n > 2. This is consistent with N–D bonds undergoing C₃ rotation along the N–N, as previously observed in the LT phase, but the larger C_Q (77 kHz vs. 43 kHz) implies there is much weaker hydrogen bonding. This is in excellent agreement with the model of cations parallel to the c axis from the neutron study. The second component of the 386 K spectrum has a very small C_Q (3 kHz, green). This implies that the N–D bonds (which determine the principal axis of the EFG tensor) are undergoing quasi-isotropic reorientation. Specifically, the averaged tensors must have close to cubic local symmetry (i.e. x, y, z spanned by a T-type irreducible representation). The NMR thus clearly shows that a significant fraction of the hydrazinium cations are highly dynamic, and, as such, are unlikely to be modelled in the diffraction study. The apparent intensity ratio between the small and large C_Q components of 2 : 1 should be interpreted cautiously since there may be differential signal losses during the echo period for sites with very different dynamics. This suggests the protons of the cations perpendicular to the channels are undergoing quasi-isotropic motion. The distinct “intermediate” H site observed in diffraction is not observed in the ²H NMR. The most plausible rationalisation is that the H sites of the “parallel” cations are indeed disordered over seven sites as in the model used to fit the QENS data (see below). This model has the axial symmetry required by the NMR data.

The spectrum in the intermediate region (335 K) is also consistent with a highly dynamic phase (no strong hydrogen bonding), but the “intermediate C_Q” spectrum (purple) is clearly connected with the low temperature phase. Although fitted to a simple average C_Q spectrum of 21 kHz, the lineshape is likely to result from a site-exchange process; this would be a natural evolution of the “softening” of the ²H spectra observed in the low temperature region below the transition to the intermediate regime. The non-trivial nature of the limiting phases, however, means that detailed interpretation of the intermediate regime is necessarily speculative. The fact that a distinct intermediate region is clearly observed in all NMR spectra and DSC, but not in diffraction experiments, can be rationalised if the high temperature phase is appearing in the form of localised fluctuations; the diffraction experiments see an overall low temperature phase, but the high temperature form fluctuations lack the time and length-scales needed for measurable Bragg diffraction. At a local level, however, individual sites can exist in both low temperature and high temperature arrangements, resulting in spectra corresponding to a mix of forms. A similar rationalisation has been used in the context of an order–disorder phase transition in ZrW₂O₈.⁴⁶

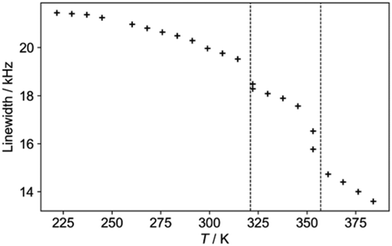
The ¹H NMR linewidths shown in Fig. 5 provide complementary qualitative insight into the dynamics. In contrast to the ²H NMR, there will be some contribution from the formate H, although this will be largely a constant “background” since the formate disorder (which will be dynamic in the high temperature phase) has very limited amplitude (see Fig. S1, ESI†). On the other hand, the ¹H linewidth will be sensitive to any motion that moves one H relative to another; the ²H NMR is only sensitive to re-orientational motions of the quadrupolar coupling tensor. The ²H NMR demonstrates that the ND_n dynamics is fast over the temperature range studied, and so the changes observed must correspond to other processes. The gradual decrease in linewidth in the low temperature regime suggests the slow onset of additional motions of the cations in an otherwise frozen glassy state, consistent with the “softening” of the ²H spectrum. The slight drop at around 320 K is suggestive of a glass transition in polymeric materials, i.e. the onset of a more dynamic “rubbery” regime. This permits additional motion until a more significant evolution at the upper transition. There is a steady drop in linewidth above 350 K, which contrasts to the ²H NMR which does not show an increase in overall dynamics in this region. The relaxation data (below) implies that there is a continued increase in cation motion, which could include processes such as switching in the direction of the “aligned” cations, proton hopping or other translational motions that the ²H NMR would not pick up.

Fig. 6 shows the evolution of the ¹H T₁ and T_1ρ relaxation time constants with temperature. These are complementary to spectra-based measurements as they specifically probe dynamics at well-defined frequencies: the ¹H NMR frequency (here 400 MHz) and the ¹H RF nutation frequency (here 50 kHz) respectively.⁴⁷ Distinctive “T₁ minima” are observed in the lower temperature regions, which allow the data to be fitted to simple dynamical models (see ESI† for full details). Different dynamical models generally give indistinguishable overall fits, and so we are fitting to simple isotropic reorientation of the internuclear vectors. Hence the fitted activation parameters (summarised in Table S7 of the ESI†) should be treated as empirical parameters that describe the relaxation behaviour rather than exact modelling of the dynamics.

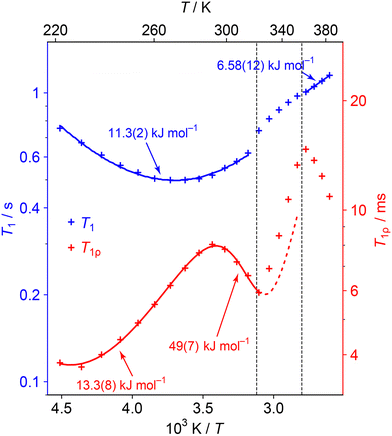Fig. 6 ¹H T₁ (blue) and T_1ρ (red) relaxation time constants as a function of temperature. Error bars are not shown as they are of a similar magnitude to the size of symbols used. Curves show fits to relaxation models (see ESI† for details of the fittings). The straight line fit in the HT phase is a guide for the eye and this E_a value should be interpreted cautiously. The data is not fitted in the transition region since the material is changing; the dashed line extrapolates the behaviour from the low temperature region fit.

The minima in the relaxation data at low temperature can be assigned to the fast ND_n motion observed in the ²H spectra. As discussed in the text associated with Table S7 in the ESI,† the fitted parameters should be interpreted cautiously since the ND₃vs. ND₂ dynamics are not distinguished. More interestingly, an additional process becomes active (moving into the 50 kHz window of the T_1ρ measurements) as the lower phase transition is approached. The parameters for this process can be fitted by including a second process with an activation energy of about 50 kJ mol⁻¹. The fitting of the higher energy process is poorly constrained since the material soon enters the intermediate phase. Indeed, the activation of this process is likely to trigger the phase evolution. This process is likely to correspond to the “softening” and coalescence of the ²H NMR spectra through the lower temperature transition, and the “glass transition” suggested by the ¹H linewidth data. Interestingly a 67 kJ mol⁻¹ (16 kcal mol⁻¹) process, ascribed to whole molecule movement of hydrazinium, has been measured in Li(N₂H₅)SO₄.⁴⁸

The ¹H T_1ρ increases rapidly and approximately linearly through the intermediate regime, which presumably reflects the evolving composition. A new minimum begins to appear at the high temperature phase. This activation of low frequency dynamics is consistent with the line narrowing observed in the ¹H lineshape data, although there is insufficient data to fit the activation parameters with any confidence. Such a slow process could correspond to inter-change of the dynamic and aligned cation populations, which is required to explain the convergence of the ¹⁵N spectrum to a single resonance. It is possible that this process also involves H⁺ hopping, although it is more consistent with the ²H NMR and QENS modelling for the latter to be a relatively fast process.

Quasielastic neutron scattering

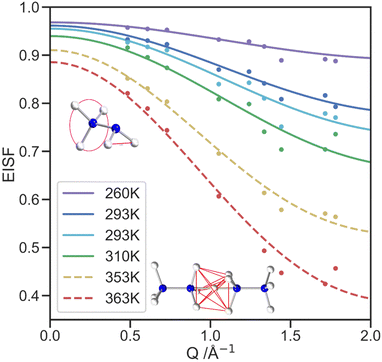
The QENS signal is specifically sensitive to ¹H dynamics, so selectively deuterated samples of [NH₃NH₂]Mg(DCO₂)₃ were produced to analyse the cation dynamics exclusively. Local cationic motion is observed as a broadening of the elastic peak and is well fitted with a single Lorentzian model, Fig. S6 (ESI†). At higher temperatures, the FWHM of the elastic peak shows little variation with the scattering vector, Q, shown in Fig. S7 (ESI†), which suggests a lack of significant long-range translational motion. Overall, the increase in FWHM with temperature above 310 K indicates the thermal motion in the IRIS energy window increases, with the mean FWHM for each temperature shown in Fig. S7 (ESI†), alongside the mean residency time, τ, calculated from the FWHM of the quasielastic lines (see Table 1). The τ values assume the motion is dominated by diffusional rotation of the NH₂ and NH₃ groups, below the transition temperature and NH₃ rotation above the transition temperature (see QENS section of ESI†).⁴⁹ These values are consistent with the NMR data in which rotation about N–N is always fast compared to the spectral lineshape (100s kHz).

Table 1 The mean FWHM of the quasielastic peak and calculated residency times for the modelled hydrogen positions using equations (10–13) in the ESI

Temperature/K	Mean FWHM/meV^a	τ/ps
a In the 260 K and 293 K data the FWHM is consistent with the 310 K data at high values of Q, but an experimental artefact results in non-meaningful values for mean FWHM at these temperatures.
310	0.052(12)	80(18)
353	0.112(18)	54(9)
363	0.147(9)	41(2)

---

The elastic incoherent structure factor (EISF) comprises contributions of the total scattering that are solely elastic and how these change as a function of Q. The EISF encodes the equilibrium geometry of the motion, and models constructed to describe the expected proton motion were developed using the atomic positions of the hydrogen atoms for the NH₃NH₂⁺ cation from the neutron crystallography. These models were fit to the EISF data collected in the PG(002) configuration Fig. 7, with contamination from Bragg peaks becoming more significant as Q increases. Because of this contamination, the PG(004) analyser configuration, which covers a wider Q range, (Fig. S9, ESI†) has insufficient resolution to fit the developed models, but the data does qualitatively show the trends expected continue to higher Q. For the low temperature phase, a model was constructed to describe the rotation of the NH₃ and NH₂ groups, consistent with both the neutron crystal structure and dynamics revealed by NMR. This model consists of a 3-site hop component and a 2-site jump model, weighted in a 3 : 2 ratio respectively, to reflect the number of hydrogen atoms in the NH₃ and NH₂ groups. The model fits the data well, especially at lower Q.⁴⁹

Fig. 7 EISF data collected in the PG(002) configuration and associated models for low temperature in solid lines and high temperature in dashed lines. Visual representations of the low temperature (magenta) and high temperature (red) site exchanges are overlayed.

The high temperature model of the EISF was constructed using the two facing NH₃ ends of neighbouring cations with the additional proton site in the centre to incorporate the hydrogen site between cations. proton site in the centre to incorporate the hydrogen site between cations. The model incorporates the fractional occupancies of the proton sites and describes the motion of a proton to jump from any of the seven sites to another through the lowest energy route. It thus allows for both three-fold rotation of the NH₃ groups and migration of protons between nitrogen atoms both within the same molecule and between molecules. The migration route between neighbouring cations is likely through the central site, allowing this to be observed by the SCND. The possibility of the NH₃NH₂⁺ cations reorienting is not included in the modelling of the EISF since the NMR suggests this process is likely occurring on a kHz timescale, which is too slow to be captured by IRIS.

The fraction of molecules contributing to the modelled motion, f, is one of the two refined parameters of the models, along with a multiple scattering correction, m, as presented in Table S10 (ESI†). With increasing temperature, f increases, as expected.⁵⁰

Dielectric behaviour

The results obtained from the diffraction and spectroscopic methods in this study led to us reexamining the dielectric properties of [NH₃NH₂]Mg(HCO₂)₃. Fig. 8 displays the temperature-dependent dielectric spectra of the [NH₃NH₂]Mg(HCO₂)₃ sample. The dielectric constant and loss tan δ exhibit pronounced frequency dispersion, and multiple dielectric anomalies are observed. Two step-like increases of the dielectric constant are unambiguously identified at T₁ ∼ 320 K and T₂ ∼ 360 K, respectively. Additionally, a strong dielectric relaxation process is observed around T₃ ∼ 400 K, as evidenced by the peak in the dielectric loss measured at the low frequency.

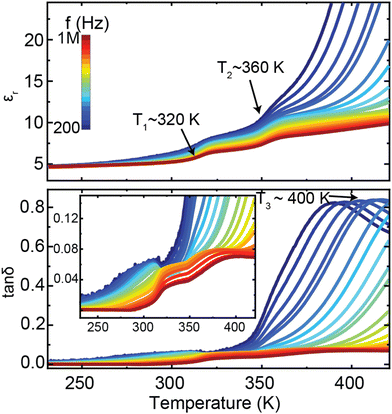Fig. 8 Temperature-dependent dielectric constant (ε_r) and losses (tan δ) of [NH₃NH₂]Mg(HCO₂)₃. The inset is the enlargement of the dielectric losses.

The measured dielectric properties are generally consistent with the previous report,²⁴ while the specific values present large differences, which may be attributed to variations in measurement methods. The observed T₁ and T₂ dielectric anomalies are consistent with the diffraction and spectroscopic studies, indicating that the dielectric properties mainly arise from the phase transition associated with the reorientation of NH₃NH₂⁺ within the pores of the framework, from lying in the planes of the channel at lower temperatures to along the channel direction above the transition temperature. The solid-state NMR studies reveal that the reorientation of NH₃NH₂⁺ initially occurs at the local scale as the sample enters the intermediate state from the low-temperature phase, corresponding to the T₁ dielectric anomaly. With further increasing temperature up to around 360 K, the sample transfers to the high-temperature disordered phase, where the cations align both parallel and perpendicular to the channel direction. It thus can be deduced that the T₁ and T₂ dielectric relaxation processes are closely linked with the thermal activation of NH₃NH₂⁺ molecular ions, which is similar to the results reported in other formate analogues.⁵¹

The anisotropic thermal expansion (ATE) of the framework, first observed by Chen et al.,²⁴ and consistently observed by our study, leads to a reduction in the a and b lattice parameters, corresponding to reduction of the pore diameters, but an increase in c corresponding to a lengthening of the pore channel. The change in the lattice parameters starts gradually at low temperatures and then increases dramatically at the transition. This could be interpreted as the cation reorientations being driven by the contraction of the pore diameter once it reaches a critical value, reorienting to align along the expanded pore length to minimise steric pressures. The reorientation of some of the cations then leads to a further contraction of the pore diameters and lengthening of the pore channel they are aligned along.

Crystallography and spectroscopy results confirm the proton hopping between the hydrazinium cations oriented along the channel direction via an intermediate proton site. This proton exchange between NH₃NH₂⁺ would allow for easy alignment to an external electric field. The change in dipole direction can occur without the whole chain of molecules reorienting, much like the hydrogen bond driven ferroelectricity in materials such as Rochelle's Salt and AH₂PO₄ phases.⁵² Furthermore, the proton diffusion will also favour the alignments of the NH₃NH₂⁺ cations along the same direction. Such local alignments could form the polar nanoregions in the sample. The proton hopping process is also reflected by the dielectric spectra. The low-frequency dielectric constant and loss present a significant increase in the temperature range over 360 K, indicating an increase in the conductivity, which possibly resulted from the long-range charge transfer induced by the proton hopping between aligned cations.

Intriguingly, the obtained high-temperature dielectric relaxation around T₃ is very similar to the properties of relaxor ferroelectrics perovskite oxide, in which oxygen vacancy motion plays a key role.⁵³ The dielectric data measured at the low frequency can be fitted by Arrhenius’ law (see equation 14 in the ESI† for details). The fitting results (Fig. S11, ESI†) estimate that E_a is around 82 kJ mol⁻¹ (0.85 eV), which is comparable to the energy for NH₃NH₂⁺ reorientation.²⁴ This is consistent with application of significant electric fields leading to cation reorientation, so more or even all cations re-orientate to the polar population. The NH₃NH₂⁺ cations lying perpendicular to the chains of the channels lack the potential for proton migration between neighbouring cations so may not contribute to net polarisation.

The somewhat higher E_a reported here, 82 kJ mol⁻¹, and also by Chen et al., ∼99 kJ mol⁻¹ (∼1.03 eV), compared to the 49(7) kJ mol⁻¹E_a calculated from the low temperature NMR data may suggest that larger scale phenomena, such as domains, play some role in the relaxor-like behaviour of this material.²⁴ As has been seen in the organic polyvinylidene-fluoride (PVDF) based polymer relaxors, this can significantly alter the E_a of relaxor properties.^40,41 However, it is likely in (NH₃NH₂)Mg(HCO₂)₃, this will have only a secondary effect. Unlike these polymers, NMR results suggest this material is homogeneous, and the highly crystalline diffraction patterns suggest it lacks the amorphous regions that play a key role in the properties the PVDF-based polymer relaxors.

The relaxor-like properties of [NH₃NH₂]Mg(HCO₂)₃ likely emerge from having NH₃NH₂⁺ cations with different orientations in neighbouring regions of the structure. This is consistent with needing neighbouring cations orientated along the channel to allow for the proposed proton migration and, also, the local distortions likely required to the anionic framework to allow for the different orientations; specifically elongated narrow channels around the NH₃NH₂⁺ lying along the channel direction while wider channels accommodate NH₃NH₂⁺ cations lying perpendicular to them. Furthermore it is consistent with previous suggestions that the related [NH₃NH₂]Mn(HCO₂)₃ phase features polar nanoregions, based on dielectric spectroscopy analysis.⁵⁴ The origins of the proposed polar nanoregions in [NH₃NH₂]Mn(HCO₂)₃ have not been investigated, and this previous study is complicated by the sample being a mixture of chiral hexagonal and perovskite polymorphs. There are also interesting connections to the relaxor ferroelectric phase of TEA(TCNQ)₂. In this material, a direct connection was established between its dielectric anomaly and the motion of the tetraethylammonium (TEA) cations observed by ¹H NMR, with the frequency-dependent dielectric response being related to the thermally activated reorientation of the TEA cations.⁴²

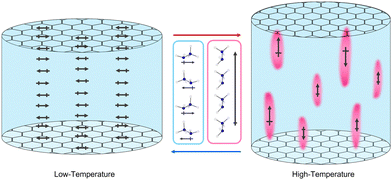
The precise arrangement of these polar and non-polar regions is not clear. The ratio of NH₃NH₂⁺ cations parallel and perpendicular to the channels does not appear to change within the high temperature phase but NMR spectroscopy suggests these are gradually interconverting. This would give rise to dynamic polar and non-polar regions fluctuating in the material, visualised in Fig. 9. X-ray diffraction studies do not reveal any obvious diffuse scattering, restricting insight into the local structure of this material, likely as a result of these dynamics. Regardless of the exact arrangement of the domains it is clear their origin is heavily reliant on the channels of the framework, which confines the thermal motion of the guest, preventing all guests from becoming dynamic before thermal degradation. Other AB(HCO₂)₃ phases and related hybrid perovskites with A-site cations that form significant hydrogen bonds exhibit dielectric anomalies similar to relaxor ferroelectrics.^{22,24,25,27–29,55} These relaxor-like properties are currently not clearly explained and it is likely that related mechanisms may apply to a significant number of them.

Fig. 9 Visualisation of left) antiparallel dipoles in the anti-ferroelectric low-temperature phase (blue). Right) the high temperature phase with dynamic polar nanoregions (pink), with dipoles aligned along the polar axis, amongst the bulk non-polar dipoles (blue). The distortion of the framework is also alluded to in the lengthening of the channel direction and contraction of the pore diameter.

Conclusions

In this study we have reanalysed the order–disorder phase transition reported by Chen et al.,²⁴ and found evidence to establish the origin of relaxor-like behaviour in [NH₃NH₂]Mg(HCO₂)₃. The nature of the transition between the non-polar and polar phases is tied to the crystallographic phase transition through a reorientation of a population of NH₃NH₂⁺ cations, determined by neutron single crystallography. These exist alongside other NH₃NH₂⁺ cations retaining their orientation perpendicular to the channel direction. The reorientation of the cations and framework dynamics were confirmed using complementary SSNMR, QENS and dielectric spectroscopy, suggesting the presence of hydrogen bond driven ferroelectricity along the cation chains permitted by proton migration between them. Reinvestigation of the dielectric properties of [NH₃NH₂]Mg(HCO₂)₃ indicates three distinct relaxations, two of which are consistent with the temperatures at which the intermediate phase observed by NMR and crystallographic phase transition occur and a third that suggests an increase in cation motion above 390 K. The relaxor-like properties of the material likely stem from fluctuating nanodomains with different orientations of NH₃NH₂⁺ cations.

Experimental

Synthesis

For the SCND samples, hydrazinium monochloride (0.9924 g, 14.50 mmol) was combined with sodium formate (3.9272 g, 57.74 mmol) in 124 mL of 7% by volume mixture of water and methanol. The solution was distributed between three crystallisation vials and layered, using a needle, with 50 mL of a magnesium chloride hexahydrate solution (2.4372 g, 11.20 mmol) in methanol (150 mL). The vials were left undisturbed for 4–5 days and then filtered. The crystals were washed with small amounts of cold ethanol.

For the selectively deuterated samples used for QENS, the framework itself only contains a single non-labile hydrogen meaning that the samples could be produced by combining hydrazinium monochloride (0.3755 g, 5.48 mmol) and sodium formate-d (1.5096 g, 21.87 mmol) in 7% by volume mixture of water and methanol. This was then layered with a solution of magnesium chloride hexahydrate (1.0158 g, 5.00 mmol) in 50 mL of methanol. While the deuterons associated with the formic acid are not generally considered labile, the samples were stored in a desiccator to reduce further the likelihood of exchange with hydrogen from moisture in the atmosphere. Four batches were produced and combined to give a sample of ∼2 g. The deuterated sample used for SSNMR was synthesised in the same manner, but deuterated methanol was used resulting in partial deuteration of the labile NH₂NH₃⁺ molecules only. Powder diffraction was collected using the Rigaku Miniflex powder diffractometer and fit using the Le Bail method using the programme GSAS II⁵⁶ to confirm phase purity (see Fig. S12 and S13, ESI†).

Single crystal neutron diffraction

Hydrogenated samples were analysed using the KOALA Laue diffractometer at the OPAL reactor,⁵⁷ which utilises white thermal neutron beams with a wavelength range of ∼0.8 Å < λ < 5.2 Å. The crystals were mounted, and diffraction patterns were collected using image plate detectors with a 1 hour exposure, with the φ-angle, perpendicular to the neutron beam, increasing from −90° to +90° in rotation steps of 20°. Data were collected at 250 K, 330 K, 350 K and 400 K, with temperature control achieved using a Cobra Cryostream. The collected data were then processed using the LaueG⁵⁸ software to reorient the frames and integrated to extract hkl intensities. The structural solution was performed using the atomic positions located by X-ray crystallography, and refinements performed in Olex2⁵⁹ with SHELXL.⁶⁰ All atoms were refined anisotropically with the occupancy of the disordered atoms of the cation refined using the SUMP SHELX command, allowing a maximum occupancy to be fixed across multiple to retain nominal stoichiometry (see Table S2, ESI† for values). Structures from this experiment are also deposited in the CSD at entries 2237784–2237788.

Solid-state NMR

Samples of [NH₃NH₂]Mg(HCO₂)₃ and [ND₃ND₂]Mg(HCO₂)₃ were packed into 4 mm zirconia rotors.

¹H NMR experiments were carried out on the [NH₃NH₂]Mg(HCO₂)₃ sample using a Bruker Avance III HD spectrometer at 400.2 MHz using a Bruker 5 mm static probe where, in the interests of sample conservation and preserving sample history, the packed rotor from magic-angle spinning (MAS) experiments was placed inside the 5 mm glass tube sample holder. ¹H spectra were acquired using a solid echo pulse sequence with an inter-pulse delay of 15 μs and full width at half maximum linewidths were determined using TopSpin 3.0.

Variable temperature ²H, ¹³C and ¹⁵N NMR experiments were carried out using a Bruker Avance III HD spectrometer at frequencies of 76.7 MHz, 125.7 MHz and 50.6 MHz respectively using a Bruker 4 mm MAS probe. Attempts to resolve distinct ²H NMR signals using MAS were unsuccessful and so all ²H spectra were taken on static samples with a 90° static echo pulse (6.4 μs) and an inter-pulse delay of 55.2 μs. ¹³C and ¹⁵N spectra were acquired using 10 kHz MAS and cross polarisation. There was no evidence of significant temperature hysteresis; the spectra shown were acquired with increasing temperature however, spectra taken with reducing temperatures were indistinguishable. ²H spectra were fitted to sums of quadrupolar lineshapes using SOLA in Topspin.

¹H T₁ relaxation measurements used a saturation recovery pulse sequence with 16 delay values for both data. Peak areas were plotted against recovery time and fitted well to single-exponential recoveries. ¹H T_1ρ values were measured using an RF nutation rate of 50 kHz. Peak area was plotted against spin-lock duration length; these fitted also well to mono-exponential decays. ²H relaxation data was also acquired. This was consistent with, but was less globally informative, than the ¹H data; see ESI† for further details. Where possible, the temperature dependence of the relaxation time constants was fitted to standard expressions to extract activation parameters for motions involved (for details see ESI†).

The temperatures for static experiments were calibrated using ethylene glycol and methanol (details in data archive), and the sample heating due to 10 kHz MAS was estimated from previous work to be 10 K. The estimated uncertainty on individual presented temperatures is ±5 K.

Quasielastic neutron scattering

High-resolution quasielastic neutron scattering was performed using IRIS, an indirect-geometry, time-of-flight spectrometer situated at the Rutherford Appleton Laboratory, UK.^61,62 The spectrometer used pyrolytic graphite (PG) single crystal analysers with neutrons detected by two 51-element ZnS scintillator detector banks and a diffraction detector bank at 2θ = 170° that contained ten ³He gas tubes, allowing for simultaneous collection of QENS and diffraction patterns. IRIS was operated in both the PG(002) and PG(004) configuration giving energy windows of −0.4 meV < ħω < 0.4 meV, and −3.5 meV < ħω < 4.0 meV, with energy resolutions of ΔE_resPG(002) of 17.5 μeV and ΔE_resPG(004) of 54.5 μeV, respectively. This gives a Q-range of 0.42 Å < Q_PG(002) < 1.85 Å for the PG(002) and a wider Q-range for the PG(004) 0.84 Å < Q_PG(004) < 3.70 Å at the cost of lower energy resolution. The timescale window of IRIS is sensitive to motions of approximately 1–100 ps.

Selectively deuterated samples [NH₃NH₂]Mg(DCO₂)₃ were loaded into a pan and shielded from the sample environment using cadmium to reduce background scattering. All measurements were collected over a temperature range of base temperature (∼13 K) to 363 K using a closed cycle refrigerator. Elastic window scans were collected at 10 K intervals from base temperature to 353 K. QENS data were collected with a ∼4 h counting time at base temperature to generate the resolution function, and at 260 K, 293 K, 310 K, 353 K and 363 K and again at 293 K on cooling for the PG(002) configuration. For the PG(004) configuration, the QENS was collected at 310 K, 353 K to 363 K with ∼4 h counting times and again on cooling at 310 K with a ∼9 h counting time.

Data reduction and integration of the elastic peaks were performed using Mantid Workbench⁶³ using the MSDFit algorithm. The experimentally measured incoherent scattering function, S(Q, ω) was fitted to the spectra using a Bayesian algorithm. A resolution function, collected at base temperature, was used to nullify the effects of any peak broadening from the instrument.

Dielectric spectroscopy

The temperature-dependent dielectric permittivity measurements were carried out on a precise LCR meter Agilent E4980A under the applied voltage of 1.0 V with a close-cycled cryo-furnace. The powder [NH₃NH₂]Mg(HCO₂)₃ sample was pressed into pellets under the pressure of ∼6 MPa. The two faces of the pellets were painted with the silver conducting paste. The measurement was undertaken in high vacuum conditions in order to avoid the influence of moisture.

Author contributions

The study was conceived by PJS in collaboration with PH and AEP, with PJS and PH responsible for funding acquisition. Sample synthesis was performed by AKS, PJS and TJH. Dielectric relaxation data acquisition was performed by TL and YL. Crystallographic experiments were performed by PJS, AKS, RP and TJH. QENS experiments were performed by FD with AEP and PJS. Formal analysis of crystallographic and QENS data was performed by TJH, supervised by PJS and AEP. SSNMR experiments were performed by HMW and GULP, along with formal analysis, supervised by PH.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

EPSRC supported PJS and AKS for this project via EP/R011524/1 and via a funded PhD studentship to TJH. PH and HMW were supported during this work through a Project Grant from the Leverhulme Trust (RPG-2018-288). The single crystal neutron diffraction measurements were performed at the Australian Centre for Neutron Scattering (proposal #8237). QENS experiments at the ISIS Pulsed Neutron and Muon Source were supported by a beamtime allocation from the Science and Technology Facilities Council.

References

1. B. L. Gersten, Cryst. Growth Technol., 2003, 299–333.
2. J. F. Scott, Science, 2007, 315, 954–959.
3. D. Damjanovic, Rep. Prog. Phys., 1998, 61, 1267–1324.
4. G. H. Haertling, J. Am. Ceram. Soc., 1999, 82, 797–818.
5. Di. Li, C. Wang, X. Cui, D. Chen, C. Fei and Y. Yang, Nano Energy, 2022, 94, 106938.
6. M. I. H. Yaacob, M. R. Arshad and A. A. Manaf, Acoust. Phys., 2011, 57, 151–158.
7. J. Wook, R. Dittmer, M. Acosta, J. Zang, C. Groh, E. Sapper, K. Wang and J. Rödel, J. Electroceramics, 2012, 29, 71–93.
8. K. M. Ok, E. O. Chi and P. S. Halasyamani, Chem. Soc. Rev., 2006, 35, 710–717.
9. P. S. Halasyamani and K. R. Poeppelmeier, Chem. Mater., 1998, 10, 2753–2769.
10. W. F. Forrester and R. M. Hinde, Nature, 1945, 156, 177.
11. A. Bussmann-Holder, J. Phys.: Condens. Matter, 2012, 24, 273202.
12. J. Valasek, Phys. Rev., 1921, 17, 475–481.
13. Y. Shiozaki, K. Shimizu, A. Oka, N. Noda and R. Nozaki, Ferroelectrics, 1999, 229, 183–188.
14. S. Horiuchi, R. Kumai and Y. Tokura, Chem. Commun., 2007, 2321–2329.
15. S. Horiuchi, R. Kumai and Y. Tokura, J. Mater. Chem., 2009, 19, 4421–4434.
16. X. J. Song, Z. X. Zhang, X. G. Chen, H. Y. Zhang, Q. Pan, J. Yao, Y. M. You and R. G. Xiong, J. Am. Chem. Soc., 2020, 142, 9000–9006.
17. B.-Y. Choi, H.-S. Han, C.-H. Hong, J.-S. Lee, C. W. Ahn, K. Wang, H.-P. Kim, W. Jo, I. W. Kim, Y. Hwang and J.-F. Li, J. Korean Phys. Soc., 2016, 68, 1481–1494.
18. R. A. Cowley, S. N. Gvasaliya, S. G. Lushnikov, B. Roessli and G. M. Rotaru, Adv. Phys., 2011, 60, 229–327.
19. G. A. Samara, J. Phys.: Condens. Matter, 2003, 15, R367.
20. V. V. Shvartsman and D. C. Lupascu, J. Am. Ceram. Soc., 2012, 95, 1–26.
21. X. X. Wang, X. G. Tang and H. L. W. Chan, Appl. Phys. Lett., 2004, 85, 91.
22. R. Shang, G. C. Xu, Z. M. Wang and S. Gao, Chem. – Eur. J., 2014, 20, 1146–1158.
23. M. A. Señarís-Rodríguez, S. Castro-García, C. Gracia-Fernández, B. Pato-Doldán, M. Sánchez-Andújar, A. A. Haghighirad, S. Yáñez-Vilar, J. López-Beceiro, L. C. Gómez-Aguirre and F. Ritter, Phys. Chem. Chem. Phys., 2012, 14, 8498.
24. S. Chen, R. Shang, K.-L. Hu, Z.-M. Wang and S. Gao, Inorg. Chem. Front., 2014, 1, 83–98.
25. J. Luo, Q. Fu, H. Wang, D. Zhao, L. Luo and W. Li, AIP Adv., 2017, 7, 105119.
26. M. Mączka, A. Pietraszko, B. Macalik and K. Hermanowicz, Inorg. Chem., 2014, 53, 787–794.
27. G. C. Xu, X. M. Ma, L. Zhang, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2010, 132, 9588–9590.
28. G. C. Xu, W. Zhang, X. M. Ma, Y. H. Chen, L. Zhang, H. L. Cai, Z. M. Wang, R. G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948–14951.
29. C. Shi, J. J. Ma, J. Y. Jiang, M. M. Hua, Q. Xu, H. Yu, Y. Zhang and H. Y. Ye, J. Am. Chem. Soc., 2020, 142, 9634–9641.
30. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
31. W. Zhang and R. G. Xiong, Chem. Rev., 2011, 112, 1163–1195.
32. J. M. Bermúdez-García, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga and M. A. Señarís-Rodríguez, Nat. Commun., 2017, 8, 1–8.
33. J. Li, M. Barrio, D. J. Dunstan, R. Dixey, X. Lou, J.-L. Tamarit, A. E. Phillips, P. Lloveras, J. Li, D. J. Dunstan, R. Dixey, A. E. Phillips, X. Lou, M. Barrio, J.-L. Tamarit and P. Lloveras, Adv. Funct. Mater., 2021, 31, 2105154.
34. P. J. Saines and N. C. Bristowe, Dalton Trans., 2018, 47, 13257–13280.
35. R. J. C. Dixey and P. J. Saines, Inorg. Chem., 2018, 57, 12543–12551.
36. W. J. Xu, S. Kopyl, A. Kholkin and J. Rocha, Coord. Chem. Rev., 2019, 387, 398–414.
37. C. Shi, X. Bin Han and W. Zhang, Coord. Chem. Rev., 2019, 378, 561–576.
38. S. M. Bovill and P. J. Saines, CrystEngComm, 2015, 17, 8319–8326.
39. H. L. B. Boström, M. S. Senn and A. L. Goodwin, Nat. Commun., 2018, 9, 1–7.
40. M. R. Gadinski, Q. Li, G. Zhang, X. Zhang and Q. Wang, Macromolecules, 2015, 48, 2731–2739.
41. A. Pramanick, N. C. Osti, N. Jalarvo, S. T. Misture, S. O. Diallo, E. Mamontov, Y. Luo, J. K. Keum and K. Littrell, AIP Adv., 2018, 8, 045204.
42. A. Berlie, I. Terry, M. Szablewski, M. Telling, D. Apperley, P. Hodgkinson and D. Zeller, Phys. Chem. Chem. Phys., 2022, 24, 7481–7492.
43. M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392.
44. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
45. R. Webber and G. H. Penner, Solid State Nucl. Magn. Reson., 2012, 47–48, 10–18.
46. M. R. Hampson, J. S. O. Evans and P. Hodgkinson, J. Am. Chem. Soc., 2005, 127, 15175–15181.
47. D. C. Apperley, R. K. Harris and P. Hodgkinson, Solid-State NMR: Basic Principles and Practice, Momentum Press, New York, 2012.
48. R. R. Knispel and H. E. Petch, Can. J. Phys., 2011, 49, 870–875.
49. M. Bée, Quasielastic neutron scattering: Principles and applications in solid state chemistry, biology and materials science, Adam Hilger, IOP Publishing, Bristol and Philadelphia, 1989.
50. M. Songvilay, Z. Wang, V. G. Sakai, T. Guidi, M. Bari, Z. G. Ye, G. Xu, K. L. Brown, P. M. Gehring and C. Stock, Phys. Rev. Mater., 2019, 3, 1–9.
51. T. Lu, D. Cortie, Z. X. Li, N. Narayanan, Z. Liu, Q. Sun, T. J. Frankcombe, G. J. McIntyre, D. Yu and Y. Liu, Chem. Mater., 2021, 33, 9666–9676.
52. S. Horiuchi, R. Kumai and Y. Tokura, Chem. Commun., 2007, 2321–2329.
53. L. Liu, Y. Huang, Y. Li, M. Wu, L. Fang, C. Hu and Y. Wang, Phys. B, 2012, 407, 136–139.
54. J. Trzmiel, A. Sieradzki, S. Pawlus and M. Mączka, Mater. Sci. Eng. B, 2018, 236–237, 24–31.
55. M. Ma̧czka, A. Ga̧gor, B. Macalik, A. Pikul, M. Ptak and J. Hanuza, Inorg. Chem., 2014, 53, 457–467.
56. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
57. A. J. Edwards, Aust. J. Chem., 2011, 64, 869–872.
58. R. O. Piltz, J. Appl. Crystallogr., 2018, 51, 635–645.
59. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
60. G. M. Sheldrick, Acta Crystallogr Sect and C. Struct, Chem, 2015, 71, 3–8.
61. C. J. Carlile and M. A. Adams, Phys. B, 1992, 182, 431–440.
62. M. T. F. Telling, S. I. Campbell, D. D. Abbley, D. A. Cragg, J. J. P. Balchin and C. J. Carlile, Appl. Phys. A Mater. Sci. Process., 2002, 74, s61–s63.
63. O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.

---

Footnote

† Electronic supplementary information (ESI) available: This includes further details of neutron crystallography, NMR, quasielastic neutron scattering and synthesis. CCDC 2237784–2237788. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3tc00480e

---