Open Access Article
Open Access ArticleCrystal structure and magnetic properties of EuZrO3 solid solutions†
Sihui
Li
 *,
Shinya
Konishi
*,
Shinya
Konishi
 ,
Takuya
Kito
,
Koji
Fujita
,
Takuya
Kito
,
Koji
Fujita
 and
Katsuhisa
Tanaka
and
Katsuhisa
Tanaka
 *
*
Department of Material Chemistry, Graduate School of Engineering, Kyoto University, Nishikyo-ku, Kyoto 615-8510, Japan. E-mail: li.sihui.26k@st.kyoto-u.ac.jp; tanaka.katsuhisa.4n@kyoto-u.ac.jp
First published on 24th May 2023
Abstract
It is theoretically proposed that perovskite-type EuZrO3 becomes a ferromagnet when the lattice volume is increased or the structure is changed from orthorhombic to cubic in contrast to the fact that the stable phase of EuZrO3, the structure of which is orthorhombic, is antiferromagnetic. To investigate the change in crystal structure and magnetic properties of EuZrO3 with the variation of lattice volume, we have synthesized polycrystals of solid solutions AxEu1−xZrO3 (A = Ba, Ca, Sr); Eu2+ is substituted by group 2 elements with different ionic radius to realize the change in lattice volume and crystal structure of EuZrO3. The stable magnetic structure of EuZrO3 solid solutions is tuned with the change of lattice volume. In particular, the ferromagnetic state is stabilized by the increase in lattice volume, which experimentally verifies the prediction by the first-principles calculations. Furthermore, this phenomenon is explainable in terms of the competition between ferromagnetic and antiferromagnetic interactions that is highly related to the volume variation and the rotation of ZrO6 octahedron. The present results indicate that the magnetic structure can be systematically tuned by controlling the chemical pressure in solid solutions.
1. Introduction
Multiferroics display two or more primary ferroic orderings, such as ferroelectricity (FE), ferro-, antiferro-, or ferri-magnetism, ferrotoroidicity, and ferroelasticity in a single-phase, and the coupling between these multiple order parameters leads to novel effects, specifically, the magnetoelectric (ME) effect.1–3 Much attention has been paid to the multiferroic properties of perovskite-type oxides the composition of which is denoted by ABO3, especially since the discovery of enhancement of polarization in constrained thin films of ferroelectromagnet BiFeO3 and manipulation of the electric polarity of TbMnO3 with a magnetic field.4,5 Currently, studies of ABO3 perovskite oxides with ME effect have focused on several compounds including divalent europium-based perovskite oxides with a general formula of EuMO3 (M: group 4 elements).6 For the multiferroic EuMO3, the correlation between magnetic and dielectric properties through the spin-lattice coupling was experimentally demonstrated for EuTiO3 (paraelectric and G-type antiferromagnetic).7–9 Specifically, the dielectric constant manifests a drastic drop at the antiferromagnetic phase transition temperature, i.e., the Néel temperature (TN), due to the hardening of soft phonon modes and subsequent saturation disruption of the dielectric constant at low temperature. The decrease of dielectric constant can be suppressed by applying a magnetic field below TN and the dielectric constant is altered by 7% at 1.5 T, corresponding to a large ME effect.9 Moreover, ferromagnetism of EuTiO3 (ETO) induced by an external electric field exhibits another aspect of ME effect.10 Such an ME effect was observed for EuZrO3 as well.11 For magnetic properties closely related to the ME effect of EuMO3, the critical balance was proposed between the antiferromagnetic (AFM) superexchange interaction via the nd orbitals of M elements and ferromagnetic (FM) indirect exchange interaction via the Eu 5d states based on the hybrid Hartree–Fock density functional calculations.12Due to the strong correlation between the degrees of freedom in crystal structure and order parameters related to the dielectric and magnetic properties, ME effects can be modified via various engineering techniques.13–22 Density functional theory (DFT) calculations and subsequent experiments have proposed that through the strain engineering, ETO thin film deposited on a substrate can be converted from a paraelectric (PE)-AFM phase to a FE-FM phase.23,24 A change in the magnetic interactions of FM ordering induced by engineering techniques in EuMO3 is anticipated to modify the ME effects. The influence of engineering techniques including strain and stress as well as lattice volume change on the magnetic structure and properties of ETO has been studied theoretically and experimentally. DFT calculations revealed that when a biaxial compressive strain is induced in the surface, both FM and FE states become stable in ETO thin films.23 This was supported by the appearance of nanometer-sized FM clusters in ETO films when an electric field is applied under a moderate compressive strain.10 The observation of FM properties has been also reported for ETO thin films with a in-plane biaxial tensile strain and a vertical strain.25–27 Furthermore, it was suggested by the hybrid Hartree–Fock density functional calculations that the lattice volume-expanded EuMO3 prefers the FM interaction through the Eu 5d states to the AFM one via the M nd states, as a consequence of the reduced hybridization of the Eu 4f and M nd orbitals.28 The volume expansions induced by the lattice mismatch between ETO thin films and different substrates can change the magnetic ground state of ETO from AFM to FM, experimentally supporting the theoretical calculations.29 Based on the critical balance between AFM superexchange interaction via the M nd orbitals and FM indirect exchange interaction via Eu 5d states, the FM state resulting from the modification of crystal structure of EuMO3 by engineering techniques was confirmed by the works mentioned above. However, those works were conducted on biaxially strained EuMO3 thin films, and the strain engineering was restricted by the substrate and could not realize three-dimensionally isotropic volume change. On the other hand, a uniform three-dimensional strain-induced negative pressure was realized by Zhao et al.30 in a composite thin film of EuTiO3 in which MgO phases of cylindrical shape were embedded. They observed the FM state in the ETO nanocomposite film and explained the magnetic state in terms of a different critical balance between the out-of-plane AFM nearest exchange interaction and the in-plane FM exchange interaction. Thus, the mechanism of the magnetic interaction in EuMO3 under three-dimensional strain or stress remains controversial.
EuZrO3, another kind of EuMO3, shows an orthorhombic crystal structure (Pbnm) and exhibits structural distortions associated with octahedral rotations, thereby having a lower symmetry than the ETO which adopts the ideal cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) perovskite structure.31–34 As for the magnetism, Eu2+ ions in EuZrO3 favor the G-type AFM structure, which has been verified by the analysis of the sign and magnitude of the magnetic exchange constants based on the Heisenberg spin Hamiltonian.6,35 This theoretical analysis along with experimental observations of the AFM transition at 4.1 K indicates that EuZrO3 is magnetically similar to ETO.11,34 Moreover, the calculations by Akamatsu et al. propose that the exchange coupling constant also can be varied by the lattice volume, showing its potential for modulating the magnetic order.28 This prediction provided an insight that not only the volume expansion of lattice but the decrease of octahedral rotation involved in the structural change from orthorhombic Pbnm to cubic Pm
m) perovskite structure.31–34 As for the magnetism, Eu2+ ions in EuZrO3 favor the G-type AFM structure, which has been verified by the analysis of the sign and magnitude of the magnetic exchange constants based on the Heisenberg spin Hamiltonian.6,35 This theoretical analysis along with experimental observations of the AFM transition at 4.1 K indicates that EuZrO3 is magnetically similar to ETO.11,34 Moreover, the calculations by Akamatsu et al. propose that the exchange coupling constant also can be varied by the lattice volume, showing its potential for modulating the magnetic order.28 This prediction provided an insight that not only the volume expansion of lattice but the decrease of octahedral rotation involved in the structural change from orthorhombic Pbnm to cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures leads to the weakening of the AFM interaction via Zr 4d orbitals and even triggering the occurrence of FM order in EuZrO3. Furthermore, the calculations extended an understanding of the competition between AFM superexchange interaction via the M nd orbitals and FM indirect exchange interaction via Eu 5d states in EuMO3.
m structures leads to the weakening of the AFM interaction via Zr 4d orbitals and even triggering the occurrence of FM order in EuZrO3. Furthermore, the calculations extended an understanding of the competition between AFM superexchange interaction via the M nd orbitals and FM indirect exchange interaction via Eu 5d states in EuMO3.
A chemical pressure, often observed in solid solutions, can induce the three-dimensional strain or stress, which is important to clarify the mechanism of magnetic interaction in EuMO3 as mentioned above, and can change the lattice volume as well as crystal structure that has influence on the magnetic interactions and structures.29,36,37 The formation of solid solutions through the A-site cation substitution has been reported to modulate the lattice volume and the accompanying structural evolution of ABO3 perovskite oxides.38–43 The alkaline earth metal zirconates AZrO3 (A = Ba, Ca and Sr) have different crystal structures and crystal lattice volumes at room temperature; the structure is cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m for A = Ba and orthorhombic Pbnm for A = Ca and Sr.44–48 Thus, the substitution of the A-site (Eu2+) by group 2 elements has the potential to induce variations in lattice volume and crystal structure and to fine-tune the magnetic properties of EuZrO3. In this study, we aimed to qualitatively verify the theoretical prediction deduced by Akamatsu et al. and reveal the underlying intrinsic mechanism of tuning the relative strengths of the competing magnetic interactions by changing the lattice volume for EuZrO3.28 The change of magnetic ordering state of EuZrO3 with a systematic variation in the lattice volume was experimentally elucidated by an A-site substitution. Through a conventional solid-state reaction method, the A-site (Eu2+) substitution was realized by group 2 elements (Ba, Ca, and Sr) with different ionic radii. The lattice volume, crystal structure, local environment, chemical state of europium ions, and magnetic properties of solid solutions AxEu1−xZrO3 (A = Ba, Ca, and Sr) were investigated using powder X-ray diffraction (XRD), high-resolution X-ray fluorescence spectrometry (HRXRF), and superconducting quantum interference device (SQUID) magnetometer. We found that the solid solutions based on EuZrO3 are AFM even when Sr2+ or Ca2+ is incorporated and an enhanced AFM behavior is observed in Ca0.3Eu0.7ZrO3 while the ferromagnetic ordering occurs in Ba0.3Eu0.7ZrO3. Overall, this study demonstrates the correlation between magnetic structure at low temperatures and the lattice volume of the EuZrO3 solid solutions. It is an important point that under the scenarios of three-dimensional chemical pressure, the present study provides direct evidence to control the competition between AFM and FM interactions among Eu2+ ions by changing the ZrO6 octahedral rotation.
m for A = Ba and orthorhombic Pbnm for A = Ca and Sr.44–48 Thus, the substitution of the A-site (Eu2+) by group 2 elements has the potential to induce variations in lattice volume and crystal structure and to fine-tune the magnetic properties of EuZrO3. In this study, we aimed to qualitatively verify the theoretical prediction deduced by Akamatsu et al. and reveal the underlying intrinsic mechanism of tuning the relative strengths of the competing magnetic interactions by changing the lattice volume for EuZrO3.28 The change of magnetic ordering state of EuZrO3 with a systematic variation in the lattice volume was experimentally elucidated by an A-site substitution. Through a conventional solid-state reaction method, the A-site (Eu2+) substitution was realized by group 2 elements (Ba, Ca, and Sr) with different ionic radii. The lattice volume, crystal structure, local environment, chemical state of europium ions, and magnetic properties of solid solutions AxEu1−xZrO3 (A = Ba, Ca, and Sr) were investigated using powder X-ray diffraction (XRD), high-resolution X-ray fluorescence spectrometry (HRXRF), and superconducting quantum interference device (SQUID) magnetometer. We found that the solid solutions based on EuZrO3 are AFM even when Sr2+ or Ca2+ is incorporated and an enhanced AFM behavior is observed in Ca0.3Eu0.7ZrO3 while the ferromagnetic ordering occurs in Ba0.3Eu0.7ZrO3. Overall, this study demonstrates the correlation between magnetic structure at low temperatures and the lattice volume of the EuZrO3 solid solutions. It is an important point that under the scenarios of three-dimensional chemical pressure, the present study provides direct evidence to control the competition between AFM and FM interactions among Eu2+ ions by changing the ZrO6 octahedral rotation.
2. Results and discussion
2.1. Structural characterization
The structural characterization was performed at room temperature in the present study. It is known that EuZrO3 takes the orthorhombic Pbnm structure with the lattice parameters at room temperature (a = 5.8192 Å, b = 8.1958 Å, and c = 5.7958 Å) and 1.4 K (a = 5.8163 Å, b = 8.1854 Å, and c = 5.7816 Å).49 For BaZrO3 with space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and SrZrO3 with space group Pbnm, the normalized molar volume approximately changes from 1.000 to 1.003 and 1.000 to 1.004, respectively, when the temperature is varied from 4.2 to 300 K.50 In addition, CaZrO3 with Pbnm structure has an average volume thermal expansion coefficient of 8.5192 × 10−6 K−1 at temperatures from approximately 0 to 350 K. Thus, the crystal structures of the AxEu1−xZrO3 series remains stable even if the temperature is varied from room temperature (300 K) to very low temperature.51
m and SrZrO3 with space group Pbnm, the normalized molar volume approximately changes from 1.000 to 1.003 and 1.000 to 1.004, respectively, when the temperature is varied from 4.2 to 300 K.50 In addition, CaZrO3 with Pbnm structure has an average volume thermal expansion coefficient of 8.5192 × 10−6 K−1 at temperatures from approximately 0 to 350 K. Thus, the crystal structures of the AxEu1−xZrO3 series remains stable even if the temperature is varied from room temperature (300 K) to very low temperature.51
The powder X-ray diffraction (XRD) patterns of the AxEu1−xZrO3 series recorded at ∼300 K are shown in Fig. 1. Each of the samples is almost entirely composed of a single phase with perovskite structure, although a trace amount of ZrO2 is detectable as an impurity phase in most of the AxEu1−xZrO3 series (Fig. S1, ESI†). Compared to pure EuZrO3, the diffraction peaks systematically shift to lower angles upon the incorporation of the larger Ba2+. This result confirms an increase in the unit lattice volume of BaxEu1−xZrO3 solid solutions, as the ionic radius of Ba2+ in coordination number (CN) 8 (1.61 Å) is larger than that of Eu2+ (1.43 Å) in CN 8.48 In contrast, oposite diffraction peak shifts are observed when the Eu2+ is substituted by Ca2+ in CN 8 (1.37 Å), indicating a smooth lattice contraction for all synthesized members of CaxEu1−xZrO3. Additionally, since the ionic radius of Sr2+ in CN 8 (1.44 Å) is almost the same as Eu2+, no apparent peak shift is observed for SrxEu1−xZrO3 as shown in Fig. 1.48 All trends in XRD patterns indicate that the replacement of Eu2+ with group 2 elements is indeed an effective strategy for compositional tuning of lattice volume by utilizing the chemical pressure.
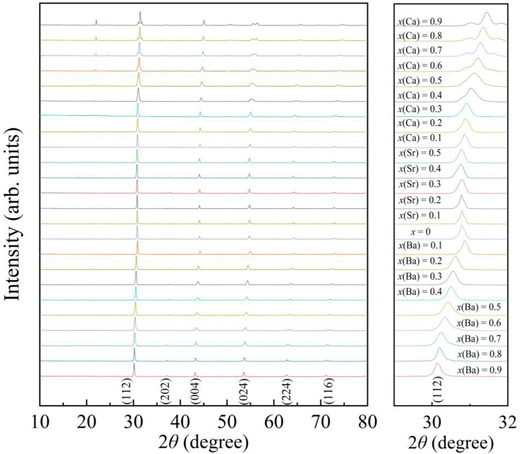 | ||
| Fig. 1 The powder X-ray diffraction (XRD) patterns of AxEu1−xZrO3 (0 ≤ x ≤ 1), where A is Ca, Sr, or Ba. The right panel shows enlarged patterns of the most intense peak for samples. | ||
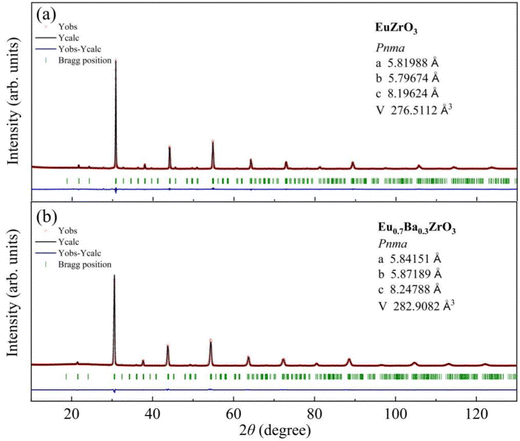
Part of the result of Rietveld analysis is illustrated in Fig. 2. All the patterns were well described by assuming that the sample was composed of a single-phase. Based on the refinement results, all the solid solutions are assigned to most probable space group. Fig. 2a confirms that EuZrO3 is identified as an orthorhombic unit cell with space group Pbnm and the lattice constants, which are in good agreement with the values reported previously.33,34 Moreover, the XRD patterns of CaxEu1−xZrO3 and SrxEu1−xZrO3 solid solutions are assigned to orthorhombic Pbnm structure, coincident with the fact that EuZrO3, CaZrO3 and SrZrO3 have the same structure.44–46 For BaxEu1−xZrO3 solid solutions, because BaZrO3 takes a cubic structure with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group at room temperature, the phase is changed from orthorhombic Pbnm to cubic Pm
m space group at room temperature, the phase is changed from orthorhombic Pbnm to cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with an increase in Ba concentration.44,47,52 The Pbnm and Pm
m with an increase in Ba concentration.44,47,52 The Pbnm and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure are represented by a−a−c+ and a0a0a0 of Glazer notation, respectively.32 The sequence of phases in the BaxEu1−xZrO3 series at room temperature and the accompanying crystal symmetry can be deduced as follows (Table 1): 0 ≤ x ≤ 0.3, orthorhombic Pbnm (a−a−c+); 0.4 ≤ x ≤ 0.6, orthorhombic Ibmm (a−a−c0); x = 0.7, tetragonal I4/mcm (a0a0c−); and 0.80 ≤ x ≤ 1, cubic Pm
m structure are represented by a−a−c+ and a0a0a0 of Glazer notation, respectively.32 The sequence of phases in the BaxEu1−xZrO3 series at room temperature and the accompanying crystal symmetry can be deduced as follows (Table 1): 0 ≤ x ≤ 0.3, orthorhombic Pbnm (a−a−c+); 0.4 ≤ x ≤ 0.6, orthorhombic Ibmm (a−a−c0); x = 0.7, tetragonal I4/mcm (a0a0c−); and 0.80 ≤ x ≤ 1, cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (a0a0a0).28 These deductions agree with the results given by Howard and Stokes for structural transition of ABO3 perovskites. All of the fitted patterns are given in Fig. S1 (ESI†).38,53
m (a0a0a0).28 These deductions agree with the results given by Howard and Stokes for structural transition of ABO3 perovskites. All of the fitted patterns are given in Fig. S1 (ESI†).38,53
| BaxEu1−xZrO3 | a (Å) | b (Å) | c (Å) | V (Å3) | Space group | R wp (%) | R B (%) | S |
|---|---|---|---|---|---|---|---|---|
| x = 0 | 5.79674(4) | 5.81988(4) | 8.19624(5) | 276.511(3) | Pbnm | 2.316 | 4.799 | 1.746 |
| x = 0.1 | 5.82575(8) | 5.81277(7) | 8.20967(9) | 278.010(5) | Pbnm | 10.29 | 6.814 | 2.208 |
| x = 0.2 | 5.83588(8) | 5.84784(8) | 8.23440(11) | 281.017(6) | Pbnm | 10.12 | 7.702 | 2.200 |
| x = 0.3 | 5.84151(11) | 5.87189(11) | 8.24788(16) | 282.908(9) | Pbnm | 10.77 | 8.171 | 2.370 |
| x = 0.4 | 5.86280(13) | 5.85745(12) | 8.27547(19) | 284.188(10) | Ibmm | 5.573 | 3.922 | 3.719 |
| x = 0.5 | 5.88447(10) | 5.87592(9) | 8.28320(14) | 286.405(8) | Ibmm | 3.681 | 4.087 | 2.466 |
| x = 0.6 | 5.90892(12) | 5.89129(12) | 8.31516(18) | 289.460(10) | Ibmm | 5.315 | 4.192 | 3.608 |
| x = 0.7 | 5.90694(10) | 5.90694(10) | 8.32721(14) | 290.552(8) | I4/mcm | 7.046 | 5.115 | 4.647 |
| x = 0.8 | 4.18186(3) | 73.1322(9) |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
6.544 | 4.316 | 3.956 | ||
| x = 0.9 | 4.18862(2) | 73.4873(7) |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
6.110 | 5.148 | 3.695 |
| CaxEu1−xZrO3 | a (Å) | b (Å) | c (Å) | V (Å3) | Space group | R wp (%) | R B (%) | S |
|---|---|---|---|---|---|---|---|---|
| x = 0.1 | 5.77804(6) | 5.81272(6) | 8.17967(9) | 274.723(5) | Pbnm | 2.529 | 4.348 | 2.154 |
| x = 0.2 | 5.75758(6) | 5.80380(6) | 8.16325(9) | 272.781(5) | Pbnm | 2.437 | 8.470 | 2.927 |
| x = 0.3 | 5.75090(5) | 5.79130(5) | 8.16550(8) | 271.953(4) | Pbnm | 2.452 | 4.521 | 2.505 |
| x = 0.4 | 5.72996(14) | 5.80064(15) | 8.15116(20) | 270.923(11) | Pbnm | 3.554 | 7.375 | 2.638 |
| x = 0.5 | 5.71224(20) | 5.79369(20) | 8.13813(28) | 269.331(16) | Pbnm | 11.84 | 8.138 | 2.638 |
| x = 0.6 | 5.69244(15) | 5.78965(16) | 8.11824(21) | 267.554(12) | Pbnm | 4.261 | 6.172 | 4.664 |
| x = 0.7 | 5.65930(7) | 5.77553(7) | 8.07929(10) | 264.075(6) | Pbnm | 3.626 | 3.741 | 3.414 |
| x = 0.8 | 5.64155(6) | 5.77700(7) | 8.07081(9) | 263.037(5) | Pbnm | 3.580 | 3.658 | 3.982 |
| x = 0.9 | 5.61377(9) | 5.75465(10) | 8.03228(13) | 259.485(7) | Pbnm | 5.085 | 2.238 | 4.467 |
| SrxEu1−xZrO3 | a (Å) | b (Å) | c (Å) | V (Å3) | Space group | R wp (%) | R B (%) | S |
|---|---|---|---|---|---|---|---|---|
| x = 0.1 | 5.79485(2) | 5.81957(2) | 8.19647(3) | 276.413(2) | Pbnm | 2.817 | 5.870 | 0.246 |
| x = 0.2 | 5.79604(2) | 5.81993(2) | 8.20028(4) | 276.616(2) | Pbnm | 2.748 | 3.294 | 0.216 |
| x = 0.3 | 5.79672(19) | 5.82203(20) | 8.19981(28) | 276.732(17) | Pbnm | 8.621 | 7.278 | 2.205 |
| x = 0.4 | 5.79668(2) | 5.82164(2) | 8.20036(4) | 276.730(2) | Pbnm | 2.131 | 3.408 | 2.252 |
| x = 0.5 | 5.79763(4) | 5.82151(4) | 8.20247(6) | 276.841(4) | Pbnm | 10.32 | 6.961 | 2.278 |
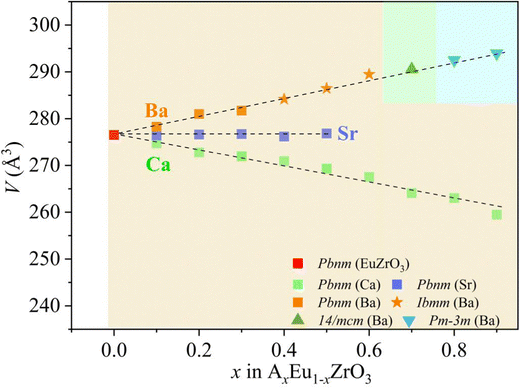
Gradual changes in the lattice constants and volume induced by A-site isovalent substitution are found from the results of refinement (Table 1), and the correlation between the composition x and the lattice volume for the AxEu1−xZrO3 series is clearly seen in Fig. 3. All the compositional dependences of lattice volume follow the Vegard's law.54,55 The lattice volume linearly increases, linearly decreases, and remains constant with Ba, Ca, and Sr concentrations, respectively, confirming the formation of all-proportional solid solutions.
2.2 Magnetic properties
The temperature dependence of magnetic susceptibility χ (T) was obtained via field-cooling (FC) process under an applied magnetic field of 100 Oe for AxEu1−xZrO3. The results are illustrated in Fig. 4. The χ(T) curve for the zero-field-cooling (ZFC) process coincides with that for the FC process within experimental errors. The magnetic phase transition temperatures (Néel temperature, TN and Curie temperature, TC) were acquired by taking the 1st derivation of χ(T) curves. The results are summarized in Table 2. Since the presence of a trace trivalent europium (6%) is confirmed by 151Eu Mössbauer spectroscopy and high-resolution X-ray fluorescence spectrometry (Fig. S2 and S3, ESI†), both Curie paramagnetism of Eu2+ and Van Vleck paramagnetism of Eu3+ are taken into consideration for analyzing the magnetic susceptibility of AxEu1−xZrO3 solid solutions in the high-temperature region. In the present case, the following equations were used:| χ = nχEu2+ + (1 − n)χEu3+ + χ0 | (1) |
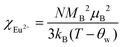 | (2) |
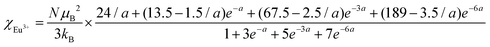 | (3) |
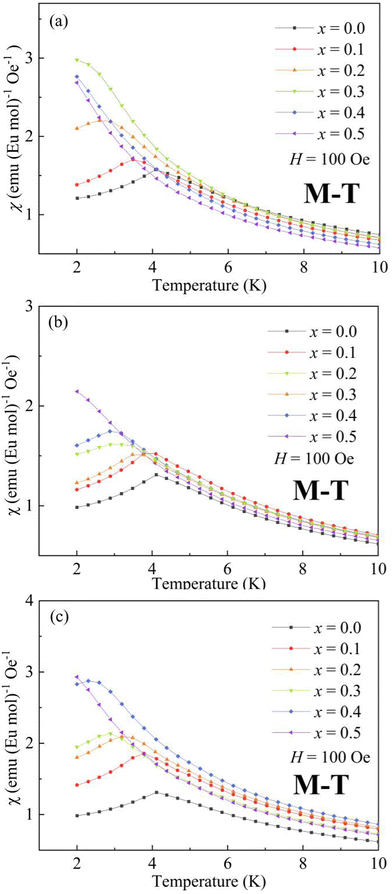 | ||
| Fig. 4 Temperature dependence of magnetic susceptibility χ (T) for (a) BaxEu1−xZrO3, (b) CaxEu1−xZrO3, and (c) SrxEu1−xZrO3 solid solutions. | ||
| BaxEu1−xZrO3 | Transition temperature (K) | θ W (K) | M S (μB) |
|---|---|---|---|
| x = 0.0 | T N = 4.1 | −0.19(2) | 7.80(1) |
| x = 0.1 | T N = 3.5 | 0.11(1) | 7.28(5) |
| x = 0.2 | 0.12 (1) | 7.45(1) | |
| x = 0.3 | T C = 3.1 | 0.67(1) | 7.19(3) |
| x = 0.4 | 0.16(1) | 7.33(3) | |
| x = 0.5 | 0.15(2) | 7.39(1) |
| CaxEu1−xZrO3 | Transition temperature (K) | θ W (K) | M S (μB) |
|---|---|---|---|
| x = 0.0 | T N = 4.1 | −0.19(2) | 7.80(1) |
| x = 0.1 | T N = 4.0 | −0.22(1) | 7.13(2) |
| x = 0.2 | T N = 3.1 | −0.45(2) | 7.07(2) |
| x = 0.3 | T N = 3.0 | −0.86(1) | 7.18(6) |
| x = 0.4 | T N = 2.9 | −0.27(1) | 7.31(4) |
| x = 0.5 | −0.09(1) | 7.58(2) |
| SrxEu1−xZrO3 | Transition temperature (K) | θ W (K) | M S (μB) |
|---|---|---|---|
| x = 0.0 | T N = 4.1 | −0.19(2) | 7.80(1) |
| x = 0.1 | T N = 3.8 | −0.12(1) | 7.31(10) |
| x = 0.2 | T N = 3.3 | −0.07(1) | 6.90(4) |
| x = 0.3 | T N = 2.8 | −0.14(3) | 6.98(1) |
| x = 0.4 | T N = 2.2 | −0.09(1) | 7.81(2) |
| x = 0.5 | −0.075(7) | 7.61(2) |
In eqn (1), n is the molar ratio of Eu2+ to the total europium ions the value of which is 0.94 (Fig. S2 and S3, ESI†), χ0 is the temperature-independent term. χEu2+ is the magnetic susceptibility of Eu2+ according to the Curie–Weiss law [eqn (2)], where N is the number of magnetic moment, kB is the Boltzmann constant, μB is the Bohr magneton, and MB is the effective number of Bohr magnetons with the theoretical value of 7.94. χEu3+ is the magnetic susceptibility of trivalent Eu ions based on the Van Vleck paramagnetism [eqn (3)], where a (a = λ/kBT) is the ratio of the multiplet width with the value of 370 cm−1 for the spin–orbit coupling constant λ.56,57 The experimental data are fitted well with the theoretical curves (Fig. S4, ESI†). The Weiss temperature (θW) obtained by the fitting was also listed in Table 2.
The present EuZrO3 sample manifests a clear AFM transition (TN = 4.1 K) in line with the previous study.11,34 The AxEu1−xZrO3 (A = Ca, Sr) solid solutions also exhibit AFM behavior for x = 0.1–0.4 while PM behavior is observed for x = 0.5 due to the dilution of magnetic moment assigned to Eu2+ ion. Besides, BaxEu1−xZrO3 solid solutions with x = 0.1 and 0.2 show AFM-like behavior. When x reaches 0.3, the compound exhibits FM behavior; the magnetization drastically increases below TC with a decrease of temperature.58 For x = 0.4 and 0.5, since significant magnetic dilution reduces the spin–spin interactions, magnetic ordering is not observed and the compounds show PM behavior.
The Weiss temperature, θW, reflects the magnitude and the sign of the magnetic interaction among Eu2+ ions. For BaxEu1−xZrO3, as the fraction of Ba is increased, θW initially increases from −0.19 (x = 0) to 0.67 (x = 0.3), and subsequently decreases to 0.15 (x = 0.5). The change of sign of θW from negative to positive when x increases from 0 to 0.3 suggests that the dominant interaction is switched from AFM to FM when the fraction of Ba is increased up to x = 0.3. The switch of magnetic interaction reflects the fact that the AFM and FM interactions compete with each other in EuZrO3. The value of θW is decreased dramatically above x = 0.4 and the compounds are PM even at low temperatures as indicated by Fig. 4(a). For SrxEu1−xZrO3, due to the weakening of AFM interaction caused by the magnetic dilution with an increase in the fraction of Sr, θW is gradually increased to approach 0 from a negative value with the increase of x. For CaxEu1−xZrO3, θW is negative independent of the composition, suggesting that the AFM interaction is dominant in all the solid solutions of this system. There seems a tendency that θW deceases, takes a minimum at x = 0.3, and then increases as the fraction of Ca is increased. Overall, the lattice expansion induced by the substitution of Ba2+ for Eu2+ inhibits the AFM interaction, leading to a situation that FM state is dominant. In contrast, enhancement of AFM interaction is realized through the lattice compression in CaxEu1−xZrO3. For SrxEu1−xZrO3, the value of θW is negative and increases to approach zero with an increase in the fraction of Sr. This phenomenon simply indicates that the magnetic structure is changed from AFM to PM by the dilution of magnetic moments belonging to Eu2+ because the lattic volume is almost independent of the composition of SrxEu1−xZrO3 due to the fact that the ionic radius of Sr2+ and Eu2+ is almost the same as each other.
The magnetic field (μ0H) dependence of magnetization (M) at 2 K for AxEu1−xZrO3 is illustrated in Fig. 5. The data at low μ0H are magnified in the insets. For SrxEu1−xZrO3 at low μ0H, the continuous increase of slope of the M–H curves indicates the gradual weakening of AFM interaction due to the dilution of Eu2+ ions. On the other hand, a decrease in the slope at low μ0H indicates an enhanced AFM interaction for Ca0.3Eu0.7ZrO3. For Ba0.3Eu0.7ZrO3, an abrupt increase in the slope at around 1000 Oe is found and the hysteresis loop is observed unlike A0.3Eu0.7ZrO3 (A = Sr and Ca) in Fig. S5 (ESI†), corresponding to the FM states of Ba0.3Eu0.7ZrO3 for Eu2+ spins. This FM state can also be confirmed by the steep increase of magnetic susceptibility with decreasing temperature below TC when a magnetic field of 100 Oe is applied. Furthermore, Fig. 5 demonstrates that the saturation magnetization (MS) for the AxEu1−xZrO3 series ranges from 7.19 μB to 7.80 μB (also summarized in Table 2). These values are almost identical to the theoretical magnetic moment of Eu2+ (7 μB), suggesting that almost all the europium ions are present as a divalent state in the AxEu1−xZrO3 solid solutions. This fact indicates that the reduction process of Eu3+ into Eu2+ by using ZrN is effective.
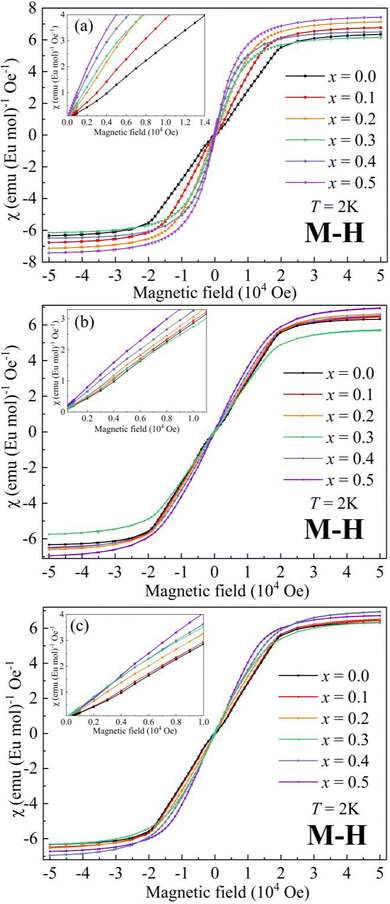 | ||
| Fig. 5 Dependence of magnetization on magnetic field at 2 K for (a) BaxEu1−xZrO3, (b) CaxEu1−xZrO3, and (c) SrxEu1−xZrO3. | ||
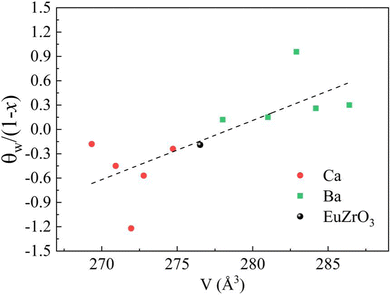
Since the linear relationship between the lattice volume and composition x is found, the compositional change can directly reflect the variation of lattice volume and accompanying crystal structural change of EuZrO3. Therefore, the compositional dependence of magnetic properties and crystal structure can lead to the relationship between the lattice volume and magnetic order. Here it should be noted that we can reasonably discuss magnetic properties at very low temperatures in terms of the crystal structure at room temperature because the crystal structure remains stable for EuZrO3, BaZrO3, SrZrO3, and CaZrO3 even when the temperature is varied from room temperature to very low temperature as described in section 2.1. According to the simple mean field theory, the Weiss temperature depends on the number of magnetic moment as well as the magnitude of magnetic interaction. Thus, it is thought that the parameter, θW/(1−x), reflects the magnitude of magnetic interaction between Eu2+ ions in the first approximation. In Fig. 6, we present the lattice volume dependence of θW/(1−x). It is found that θW/(1−x) is apt to increase with an increase in the lattice volume. It is worth noting that the tuning of magnetic interaction and the resultant magnetic transition are considered to be induced by the lattice expansion and shrinkage rather than the changes in crystal symmetry since the crystal structure retains orthorhombic Pbnm in the range of lattice volume shown in Fig. 6. The results elucidate the relationship between the lattic volume and magnetic order which has been predicted by the theoretical calculations for EuZrO3.28
2.3 Microscopic origin of magnetic behavior
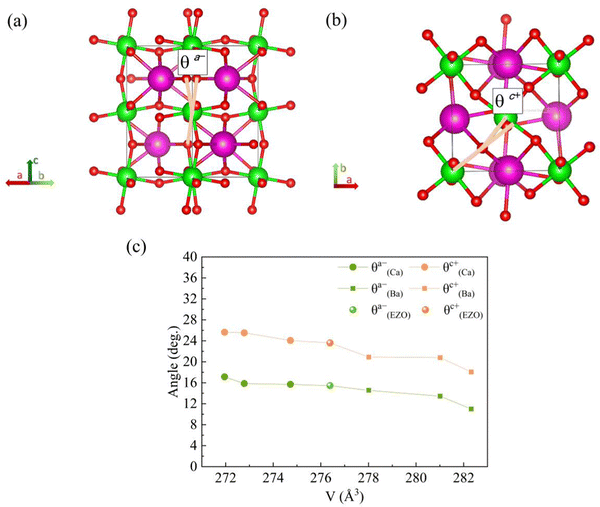
To get a better understanding of the effect of the variation of lattice volume on the magnetic behavior, the origin and magnitude of the effect are discussed from a microscopic point of view. The cooperative rotation of ZrO6 octahedra needs to be taken into account since it has been microscopically verified on the basis of first principles calculations that the octahedral rotation, related to the change of lattice volume of the orthorhombic structure, facilitates the AFM superexchange interactions between Eu2+ ions via vacant 4d state of Zr4+ in the orthorhombic EuZrO3.28 For the series of Ba-substituted solid solutions, an increase in the lattice volume is accompanied by the continuous conversion of the crystal structure from Pbnm (a−a−c+) to Ibmm (a−a−c0), I4/mcm (a0a0c−), and then Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (a0a0a0) at room temperature. For the series of Ca- and Sr-substituted solid solutions, the crystal structure retain Pbnm (a−a−c+) even when the fraction of Ca and Sr is altered. Fig. 7 illustrates the octahedral rotations with two types of angles θa− and θc+ and the relationship between these rotation angles and the lattice volume. Here the lattice volume and the corresponding θa− and θc+ were extracted from the data for EuZrO3, BaxEu1−xZrO3 and CaxEu1−xZrO3 solid solutions with the structure of Pbnm (a−a−c+). It is found that both θa− and θc+ are increased with the decrease of lattce volume. As the relationship between the magnetism and the lattice volume is verified in Fig. 6, the result shown in Fig. 7 indicates that the AFM interaction is weakened by descending the octahedral rotations, leading to the situation that the FM interaction is more dominant. Consequently, the present experimental result supports the theoretical suggestions that the octahedral rotation has great influence on the overlap between the Eu2+ 4f orbital and the Zr4+ 4d orbital and hence, changes the magnitude of AFM interaction between Eu2+ ions via 4d state of Zr4+ in EuZrO3.
m (a0a0a0) at room temperature. For the series of Ca- and Sr-substituted solid solutions, the crystal structure retain Pbnm (a−a−c+) even when the fraction of Ca and Sr is altered. Fig. 7 illustrates the octahedral rotations with two types of angles θa− and θc+ and the relationship between these rotation angles and the lattice volume. Here the lattice volume and the corresponding θa− and θc+ were extracted from the data for EuZrO3, BaxEu1−xZrO3 and CaxEu1−xZrO3 solid solutions with the structure of Pbnm (a−a−c+). It is found that both θa− and θc+ are increased with the decrease of lattce volume. As the relationship between the magnetism and the lattice volume is verified in Fig. 6, the result shown in Fig. 7 indicates that the AFM interaction is weakened by descending the octahedral rotations, leading to the situation that the FM interaction is more dominant. Consequently, the present experimental result supports the theoretical suggestions that the octahedral rotation has great influence on the overlap between the Eu2+ 4f orbital and the Zr4+ 4d orbital and hence, changes the magnitude of AFM interaction between Eu2+ ions via 4d state of Zr4+ in EuZrO3.
3. Conclusions
We experimentally provide an insight into the relative strengths of the competing magnetic interactions between Eu2+ ions in EuZrO3, which is dependent on the lattice volume and crystal structure, as suggested by the first principles calculations. The variation of lattice volume was realized by synthesizing EuZrO3-based solid solutions; Eu2+ was replaced by alkaline-earth metal ions with different radii, that is Ba, Sr, and Ca. The experimental results indicate that the magnetic ground state of EuZrO3 can be switched from AFM to FM by increasing the lattice volume. This is consistent with the first-principles calculations reported previously. Furthermore, the results also demonstrate that there is a strong coupling between the magnetic structure and the rotation of ZrO6 octahedra. Specifically, the AFM superexchange interaction between Eu2+ ions via Zr 4d state is enhanced by the rotations of the ZrO6 octahedra. The expansion of lattice volume and concomitant reduction of ZrO6 octahedral rotation lead to the situation that the FM indirect exchange interaction via Eu2+ 5d state overcomes the AFM interaction via Zr4+ 4d state.4. Experimental details
4.1. Sample preparation
Polycrystalline AxEu1−xZrO3 (A = Ba, Ca; x ≤ 0.9 and Sr; x ≤ 0.5) were synthesized by the conventional solid-state reaction method. The stoichiometric mixture of reagent-grade Eu2O3, ZrO2, ACO3, and ZrN (both 99.9% pure, sourced from Kanto Chemicals, Japan) with the molar ratio of 2–2x, 3 + x, 4x and 1−x was pressed into a pellet. The ZrN was added as a reducing agent to convert Eu3+ into Eu2+. The pellet was sintered in a carbon crucible at 1300 °C for 10 h under a reducing atmosphere of Ar (97 vol%)/H2 (3 vol%). The resultant EuZrO3 pellet was greenish-yellow, while the solid solutions of BaxEu1−xZrO3, CaxEu1−xZrO3, and SrxEu1−xZrO3 were light greenish, light yellow, and light greenish-yellow, respectively.4.2. Measurements of structural and magnetic properties
The crystal structure and purity of the sintered materials were characterized by XRD at room temperature using Cu Kα radiation (RINT2500, Rigaku). Structural parameters were determined by Rietveld refinement of the X-ray diffraction data using RIETAN-FP.59–61 In order to estimate the structural distortions related to the ZrO6 octahedral rotations, the two rotation angles θa− and θc+ shown in Fig. 7 were determined by performing VESTA based on the Rietveld refinement results.27,62 The chemical valence states of europium ions in AxEu1−xZrO3 were examined using HRXRF spectroscopy, Eu2O3 was used as a reference for trivalent Eu ions. Peak position corrections were performed using Mn Kα12 standard spectra for each sample measurement. A Savitzky-Golay smoothing method was used (smoothing points = 7) to pretreat data before analysis.63 The valence state of europium ions of EuZrO3 was evaluated using the 151Eu Mössbauer spectrum in a standard transmission geometry at room temperature, which employed γ-ray source of 151Sm2O3. The velocity calibration was done with the magnetic hyperfine spectrum of α-Fe foil using 57Co γ-ray source. In addition, the Mössbauer spectrum of EuF3 was utilized as a Doppler velocity standard.64 To understand the influence of structural change on the magnetic properties of solid-state solutions AxEu1−xZrO3, temperature and magnetic field dependence of magnetization was measured using the superconducting quantum interference device magnetometer (MPMS, Quantum Design). The temperature dependence of magnetic susceptibilities was measured in a range of 2–300 K under both ZFC and FC processes at an external magnetic field of 100 Oe. The field dependence of magnetization was recorded at 2 K under magnetic fields up to 5 T.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI, Grant-in-Aid for Challenging Research (Exploratory), Grant Number 21K19025. The authors are grateful to Michiru Yamashita and Hirokazu Izumi at Hyogo Prefectural Institute of Technology for their help with HRXRF measurement.Notes and references
- H. Schmid, Ferroelectrics, 1994, 162, 317–338 CrossRef.
- R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6, 21–29 CrossRef CAS PubMed.
- N. A. Spaldin and R. Ramesh, Nat. Mater., 2019, 18, 203–212 CrossRef CAS PubMed.
- J. Wang, J. Neaton, H. Zheng, V. Nagarajan, S. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. Schlom and U. Waghmare, Science, 2003, 299, 1719–1722 CrossRef CAS PubMed.
- T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T.-H. Arima and Y. Tokura, Nature, 2003, 426, 55–58 CrossRef CAS PubMed.
- H. Akamatsu, K. Fujita, H. Hayashi, T. Kawamoto, Y. Kumagai, Y. Zong, K. Iwata, F. Oba, I. Tanaka and K. Tanaka, Inorg. Chem., 2012, 51, 4560–4567 CrossRef CAS PubMed.
- T. Katsufuji and H. Takagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 054415 CrossRef.
- A. Bussmann-Holder, E. Liarokapis and K. Roleder, Sci. Rep., 2021, 11, 1–8 CrossRef PubMed.
- H. Wu and W. Shen, Solid State Commun., 2005, 133, 487–491 CrossRef CAS.
- P. Ryan, J. Kim, T. Birol, P. Thompson, J. Lee, X. Ke, P. Normile, E. Karapetrova, P. Schiffer and S. Brown, Nat. Commun., 2013, 4, 1–8 Search PubMed.
- T. Kolodiazhnyi, K. Fujita, L. Wang, Y. Zong, K. Tanaka, Y. Sakka and E. Takayama-Muromachi, Appl. Phys. Lett., 2010, 96, 252901 CrossRef.
- H. Akamatsu, Y. Kumagai, F. Oba, K. Fujita, H. Murakami, K. Tanaka and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 214421 CrossRef.
- M. Itoh, T. Shimura, J.-D. Yu, T. Hayashi and Y. Inaguma, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 12522 CrossRef CAS PubMed.
- T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801–3803 CrossRef CAS.
- P. Radaelli, G. Iannone, M. Marezio, H. Hwang, S. Cheong, J. Jorgensen and D. Argyriou, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8265 CrossRef CAS.
- M. Uehara, S. Mori, C. Chen and S.-W. Cheong, Nature, 1999, 399, 560–563 CrossRef CAS.
- J. Haeni, P. Irvin, W. Chang, R. Uecker, P. Reiche, Y. Li, S. Choudhury, W. Tian, M. Hawley and B. Craigo, Nature, 2004, 430, 758–761 CrossRef CAS PubMed.
- K. J. Choi, M. Biegalski, Y. Li, A. Sharan, J. Schubert, R. Uecker, P. Reiche, Y. Chen, X. Pan and V. Gopalan, Science, 2004, 306, 1005–1009 CrossRef CAS PubMed.
- M.-W. Chu, I. Szafraniak, R. Scholz, C. Harnagea, D. Hesse, M. Alexe and U. Gösele, Nat. Mater., 2004, 3, 87–90 CrossRef CAS PubMed.
- D. G. Schlom, L.-Q. Chen, C.-B. Eom, K. M. Rabe, S. K. Streiffer and J.-M. Triscone, Annu. Rev. Mater. Res., 2007, 37, 589–626 CrossRef CAS.
- D. G. Schlom, L.-Q. Chen, C. J. Fennie, V. Gopalan, D. A. Muller, X. Pan, R. Ramesh and R. Uecker, MRS Bull., 2014, 39, 118–130 CrossRef CAS.
- Y. Yokoyama, Y. Yamasaki, M. Taguchi, Y. Hirata, K. Takubo, J. Miyawaki, Y. Harada, D. Asakura, J. Fujioka and M. Nakamura, Phys. Rev. Lett., 2018, 120, 206402 CrossRef CAS PubMed.
- C. J. Fennie and K. M. Rabe, Phys. Rev. Lett., 2006, 97, 267602 CrossRef PubMed.
- J. H. Lee, L. Fang, E. Vlahos, X. Ke, Y. W. Jung, L. F. Kourkoutis, J.-W. Kim, P. J. Ryan, T. Heeg and M. Roeckerath, Nature, 2010, 466, 954–958 CrossRef CAS PubMed.
- K. Kugimiya, K. Fujita, K. Tanaka and K. Hirao, J. Magn. Magn. Mater., 2007, 310, 2268–2270 CrossRef CAS.
- K. Fujita, N. Wakasugi, S. Murai, Y. Zong and K. Tanaka, Appl. Phys. Lett., 2009, 94, 062512 CrossRef.
- Y. Lin, E.-M. Choi, P. Lu, X. Sun, R. Wu, C. Yun, B. Zhu, H. Wang, W. Li and T. Maity, ACS Appl. Mater. Interfaces, 2020, 12, 8513–8521 CrossRef CAS PubMed.
- H. Akamatsu, Y. Kumagai, F. Oba, K. Fujita, K. Tanaka and I. Tanaka, Adv. Funct. Mater., 2013, 23, 1864–1872 CrossRef CAS.
- K. Tanaka, K. Fujita, Y. Maruyama, Y. Kususe, H. Murakami, H. Akamatsu, Y. Zong and S. Murai, J. Mater. Res., 2013, 28, 1031–1041 CrossRef CAS.
- R. Zhao, C. Yang, H. Wang, K. Jiang, H. Wu, S. Shen, L. Wang, Y. Sun, K. Jin and J. Gao, Nat. Commun., 2022, 13, 2364 CrossRef CAS PubMed.
- M. Shafer, J. Appl. Phys., 1965, 36, 1145–1152 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- V. Viallet, J.-F. Marucco, J. Saint, M. Herbst-Ghysel and N. Dragoe, J. Alloys Compd., 2008, 461, 346–350 CrossRef CAS.
- Y. Zong, K. Fujita, H. Akamatsu, S. Murai and K. Tanaka, J. Solid State Chem., 2010, 183, 168–172 CrossRef CAS.
- B. Alho, E. Nóbrega, V. de Sousa, A. M. G. Carvalho, N. De Oliveira and P. Von Ranke, J. Appl. Phys., 2011, 109, 083942 CrossRef.
- J. Coey, M. Viret and S. Von Molnar, Adv. Phys., 1999, 48, 167–293 CrossRef CAS.
- G. Cuono, F. Forte, A. Romano, X. Ming, J. Luo, C. Autieri and C. Noce, Phys. Rev. Mater., 2021, 5, 064402 CrossRef CAS.
- B. Kennedy, C. Howard, G. Thorogood and J. Hester, J. Solid State Chem., 2001, 161, 106–112 CrossRef CAS.
- L. Li, B. J. Kennedy, Y. Kubota, K. Kato and R. F. Garrett, J. Mater. Chem., 2004, 14, 263–273 RSC.
- C. J. Howard, G. R. Lumpkin, R. I. Smith and Z. Zhang, J. Solid State Chem., 2004, 177, 2726–2732 CrossRef CAS.
- N. L. Henderson, X. Ke, P. Schiffer and R. E. Schaak, J. Solid State Chem., 2010, 183, 631–635 CrossRef CAS.
- Y. Ren, R. Küngas, R. J. Gorte and C. Deng, Solid State Ion., 2012, 212, 47–54 CrossRef CAS.
- M. Y. Liu, T. L. Sun, X. L. Zhu, X. Q. Liu, H. Tian and X. M. Chen, J. Am. Ceram. Soc., 2021, 104, 6393–6403 CrossRef CAS.
- H. D. Megaw, Proc. Phys. Soc., 1946, 58, 133 CrossRef CAS.
- H. Koopmans, G. Van De Velde and P. Gellings, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 1323–1325 CrossRef.
- B. J. Kennedy, C. J. Howard and B. C. Chakoumakos, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 4023 CrossRef CAS.
- A.-M. Azad, S. Subramaniam and T. W. Dung, J. Alloys Compd., 2002, 334, 118–130 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. Avdeev, B. J. Kennedy and T. Kolodiazhnyi, J. Condens. Matter Phys., 2014, 26, 095401 CrossRef CAS PubMed.
- K. Knight, J. Mater. Sci., 2020, 55, 6417–6428 CrossRef CAS.
- A. Shukla, V. Parey and N. Gaur, AIP Conf. Proc., 2016, 020011 CrossRef.
- E. Slonimskaya and A. Belyakov, Glass Ceram., 2001, 58, 54–56 CrossRef CAS.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789 CrossRef.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- A. R. Denton and N. W. Ashcroft, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 3161 CrossRef CAS PubMed.
- J. Van Vleck, The Theory of Electric and Magnetic Susceptibilities, Clarendon, Oxford, 1932 Search PubMed.
- L. Holmes, R. Sherwood, L. Van Uitert and S. Hüfner, Phys. Rev., 1969, 178, 576 CrossRef CAS.
- Y. Zong, K. Fujita, H. Akamatsu, S. Murai and K. Tanaka, Phys. Status Solidi C, 2011, 8, 3051–3054 CrossRef CAS.
- H. Rietveld, Acta Crystallogr., 1967, 22, 151–152 CrossRef CAS.
- D. L. Bish and S. Howard, J. Appl. Crystallogr., 1988, 21, 86–91 CrossRef CAS.
- F. Izumi and K. Momma, Solid State Phenom., 2007, 15–20 CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- T. Konishi, J. Kawai, M. Fujiwara, T. Kurisaki, H. Wakita and Y. Gohshi, X-Ray Spectrom., 1999, 28, 470–477 CrossRef CAS.
- G. Shenoy and B. Dunlap, Nucl. Instrum. Methods, 1969, 71, 285–291 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc00888f |
| This journal is © The Royal Society of Chemistry 2023 |